Abstract
Individualized prediction is a hallmark of clinical medicine and decision making. However, most existing prediction models rely on biomarkers and clinical outcomes available at a single time. This is in contrast to how health states progress and how physicians deliver care, which relies on progressively updating a prognosis based on available information. With the use of joint models of longitudinal and survival data, it is possible to dynamically adjust individual predictions regarding patient prognosis. This article aims to introduce the reader to the development of dynamic risk predictions and to provide the necessary resources to support their implementation and assessment, such as adaptable R code, and the theory behind the methodology. Furthermore, measures to assess the predictive performance of the derived predictions and extensions that could improve the predictions are presented. We illustrate personalized predictions using an online dataset consisting of patients with chronic liver disease (primary biliary cirrhosis).
Keywords: Joint model, longitudinal outcome, survival outcome, dynamic predictions, personalized risk predictions
Introduction
The prediction of future health outcomes supports medical decision making, health systems planning, including medical triage, and patient-informed decision making. Prediction models are widely used in medicine and generally use static inputs, such as values at the time of a clinic visit or hospital admission. Using values at a single time point does not account for changes in covariate profiles over time and how these profiles modify the risk of an event. Intuitively, physicians update their prognosis with the change in some biomarkers and clinical status of the patients. Therefore, optimal prediction should use a methodology that appropriately includes all available changes in the prediction variables.
Key Messages
Statistical innovation in joint modelling and the increasing availability of longitudinal clinical measures (e.g. electronic medical records) supports adaptive prediction for individuals but is used limitedly in clinical research.1,2 A potential criticism of these model is computational burden. Furthermore, even though a wide range of extensions have been introduced in the statistical literature, mainly the basic joint model has been used in clinical research. In this article, we seek to introduce readers to dynamic risk predictions using simplified illustrations while providing direction to additional and more advanced resources such as theory and code. We also focus on measures to assess the predictive performance and on extensions that might improve predictions.
The interest in personalized medicine continues to grow. To guide clinical decisions, physicians follow the progression of several biomarkers of each patient and, if needed, update their prognosis.
‘Joint models’ of longitudinal and survival data are a valuable tool to obtain dynamic, or evolving, risk predictions.
As publicly available software to fit joint models continues to evolve and become more computationally efficient, larger and more complex data structures can be integrated for dynamic risk predictions.
The ability to use a statistical model that incorporates all the information of a patient to inform future risk prediction should be widely applied in clinical practice. We provide accessible tutorials and selected references to promote wider use of joint models for dynamic risk prediction.
For illustration, we use an online dataset consisting of patients with chronic liver disease,3 available within R along with the package survival. The rest of the article is organized as follows. The following section describes the formulation of the standard joint model. We then describe how the dynamic risk predictions are derived, and present measures to assess the predictive performance of the model. Furthermore, we present an overview of some extensions that have been proposed to improve the predictions. We show the results for the primary biliary cirrhosis dataset and we close with a discussion. Finally, we built a webpage [https://erandrinopoulou.github.io/EducationalCorner_JMpred/] that includes the code to obtain the figures and results in R, with a detailed explanation.
We used a publicly available dataset available in the R package survival [https://stat.ethz.ch/R-manual/R-devel/library/survival/html/pbc.html].3
Joint model of longitudinal and survival data
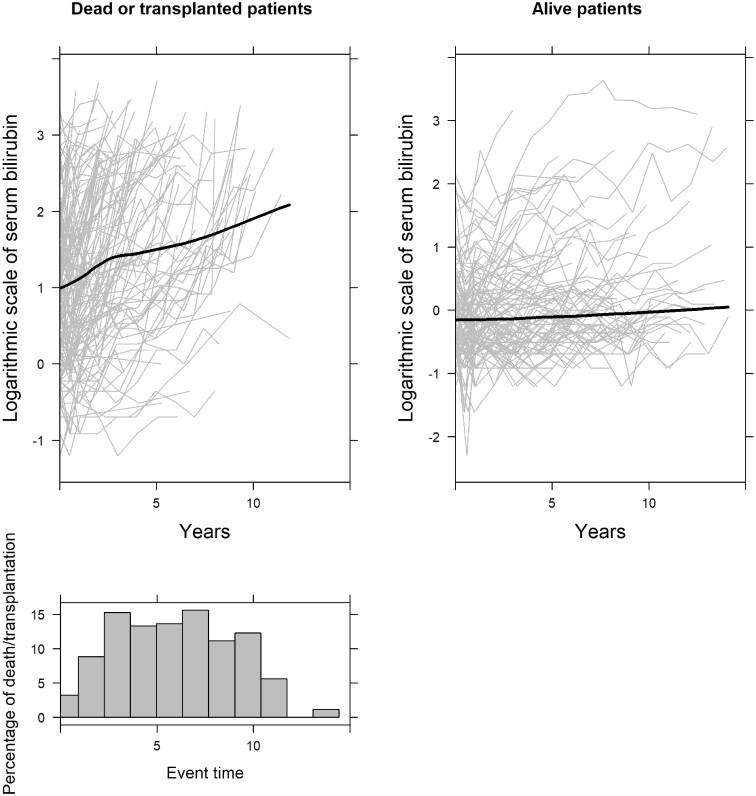
In the primary biliary cirrhosis dataset, several markers measured on the patient are available. These include serum bilirubin, serum cholesterol, serum albumin and hepatomegaly. Patients, due to their medical condition, have an increased risk of both requiring transplantation to survive or dying. The biomarkers mentioned above could provide useful information to the treating physician about the risk of each patient to require transplantation or to die. For example, it is expected that a patient with an increasing serum bilirubin evolution would have an increased risk compared with patients with a steady evolution. To illustrate these different evolutions over time, we present in Figure 1 the individualized and averaged evolutions of serum bilirubin for the different risk groups of patients. Time represents years since enrolment in the study. As can been seen, patients who did not experience transplantation or death have a low and stable serum bilirubin evolution. On the other hand, the evolution of serum bilirubin increases sharply before death/transplantation. Therefore, considering the evolution of biomarkers for predicting the risk of the event is of high relevance in clinical practice. Joint modelling is a popular statistical approach used to link longitudinal and time-to-event processes.4–6 The idea behind these models is that a mixed-effects model is fitted to describe the evolution of the longitudinal outcome, and this information is included in a time-to-event model.7–10
Figure 1.
Evolution of serum bilirubin of all patients per event group, and histogram of event times. The grey lines in the two upper plots represent the serum bilirubin measurements per patient in each event group, and the black solid lines represent the smooth evolution of all the patients in each event group. The histogram indicates the percentage of death/transplantation
Model definition
Let us assume that we are interested in the longitudinal biomarker serum bilirubin. Assuming n subjects, we let denote the follow-up measurements for the longitudinal serum bilirubin for patient i, where , at time point t. Measurements are taken at different moments and could be of different lengths for each patient. To describe the subject-specific evolution over time of serum bilirubin, we rely on a mixed-effects model. In particular we postulate:
| (1) |
where denotes the regression coefficient vector associated with the design vector for the fixed effects and, denotes the row vectors of the design matrices for the random effects . The random effects are assumed to follow a normal distribution with mean zero and covariance matrix Σ, independent of the error terms . The fixed effects part describes the average evolution in time of the longitudinal outcome of interest. The random effects (patient-specific) part of this model describes the evolution in time for each of the patients under study, and accounts for the within-person correlation over time.
For the survival submodel, let us assume that we are interested in modelling the time to death or transplantation. For simplicity, we assume the composite event of death/transplantation. However, more sophisticated survival models are possible for use by analysts (e.g. competing risks). We let Ti denote the observed failure time for patient i, taken as with indicating the true failure time in which the ith individual experiences the event and Ci the censored time. Furthermore, is the event indicator where zero indicates censoring. To model the risks of the event, we postulate the proportional hazard model:
| (2) |
where denotes row vectors of the design matrix of the covariates (or/and possibly exogenous time-varying covariates), is the corresponding transposed regression coefficients vector and α is the coefficient that links the longitudinal serum bilirubin and the time-to-event outcome survival/transplant-free probabilities. The interpretation of α is: for a one-unit increase in the underlying value of the serum bilirubin, the hazard ratio is assuming that the covariates remain the same.
Dynamic predictions
It is of high clinical interest to obtain personalized risk predictions for death and transplantation, using all the available information on the patient including the evolution of serum bilirubin. A unique feature is that each time a new measurement is available for the longitudinal outcome, the risk predictions can be updated.11–13 In particular, using the joint modelling of longitudinal and survival data, we would like to predict event-free probabilities for a new patient l who has provided us with a set of serum bilirubin measurements and some baseline characteristics. Given that no event occurred up to t, we want to obtain death or transplant-free probabilities up to a future time u > t:
| (3) |
where denotes the sample on which the joint model was fitted.
The most recent extensions and implementations in the literature of dynamic predictions using joint models have been derived under the Bayesian framework.14,15 This approach facilitates propagating the parameter uncertainty in the derived predictions and calculating credible intervals. The estimation of is based on the corresponding posterior predictive distributions, namely:
| (4) |
where is the parameter vector for both the longitudinal and survival outcomes. The second term of the integrand (4), , is the posterior distribution of the parameters given the observed data. The first term of the integrand in (4) can be written as:
| (5) |
where denotes the conditional survival function on the random effects of patient l. More details about equation (5) can be found in the Supplementary material, available as Supplementary data at IJE online. An estimate of can be obtained using the following Monte Carlo simulation scheme:
draw from the MCMC sample of the posterior ,
draw from ,
compute ,
where indicates the MCMC sample that is used each time. We then repeat the above steps several times and derive the estimates of the as,
A 95% credible interval (CI) can be obtained using the Monte Carlo sample percentiles.
Predictive performance
It is crucial for physicians to have a good prognostic tool for planning the next interventions. Therefore, assessing the predictive performance of the joint model is an important task.16,17
Overall performance measures
The distance between the predicted outcome and the actual outcome is fundamental to quantifying overall model performance. Using all available information for a particular patient l, we are interested in comparing the predicted event-free probability of this patient with the observed truth. In particular, we define the prediction error (PE) as: , where is the event status at time t. Positive and negative prediction errors could have different practical significance in some applications. In particular, in our case, a positive prediction error is when we obtain a high probability for a patient to experience the event (death/transplantation), but he/she does not experience the event. On the other hand, a negative prediction error is when we obtain a low probability of experiencing the event, but he/she does experience the event.
Discrimination
A key feature of a dynamic prediction model would be to distinguish between patients who are going to experience the event within a time frame after the last measurement, from patients that are not going to experience the event. In particular, for a future patient l with repeated measurements up to time point t, we are interested in investigating whether the patient will experience the event before a future time point u within which the physician could intervene to improve the survival outcome. The future time point u, where predictions will be obtained, should be within the range of time points available in the dataset. Predictions past the available data might not be realistic. To obtain sensitivity and specificity, we assume if subject l experiences the event and if he/she did not experience the event, for a specific . Then, we can define sensitivity and specificity as respectively. We can evaluate the discriminative capability of the model using the area under the receiver operating characteristic curve (AUC). In particular, assuming two patients (l1, l2), we have If patient l1 experiences the event before the future time point u, whereas patient l2 does not, then we would expect the model to assign higher risk probability during the predefined period for patient l1.
Further diagnostic accuracy measures include positive and negative predictive values, which are more important from the patient’s point of view. Positive predictive value is defined as the probability that subjects classified by the biomarker as having the event truly experience the event. Negative predictive value is the probability that subjects classified by the marker as not having the event truly do not experience it. Depending on the population’s prevalence, even a test with both high sensitivity and specificity can end up with a low positive predictive value.
Calibration
Calibration is how well the model predicts the observed event rates across the distribution of participant risk. A graphical way to assess the calibration of a model is to plot the predictions on the x-axis and the outcome on the y-axis. Perfect predictions should be on the 45-degree line. For binary outcomes such as in our case, smoothing techniques can be used to estimate the observed probabilities of the outcome in relation to the predicted probabilities. Using all available information up to time point t and predicting the event until a future time point u > t, the calibration accuracy CAL(t, u) can be estimated using a Cox proportional hazards model with restricted cubic splines to model the relationship between the predictions and the observed values. Based on this model, an estimated probability of the occurrence of the outcome for each predicted value can be obtained. A calibration curve using these estimated probabilities can be created.18 Further numerical metrics for calibration can be obtained, where the difference is calculated between the calibration curve and the diagonal line of best fit.18
Extensions
Several extensions of the standard joint model mentioned above have been proposed which, in some cases, might improve personalized risk predictions. Below, we provide brief introductions to selected extensions.
Multiple longitudinal outcomes
The standard joint model of longitudinal and survival data focuses on the use of a single biomarker for prediction. In the primary biliary cirrhosis dataset, multiple biomarkers are collected simultaneously, and it might be clinically relevant to model them all together instead of choosing a primary longitudinal biomarker. Furthermore, by using multiple biomarkers in the proposed model, the dynamic predictions of the survival outcome might improve.
Assuming P longitudinal outcomes that could be of different type (continuous, binary), we would focus on the risk probabilities of a new patient l at a future time point t, given that the patient did not experience the event up to time point t and has provided us with a set of longitudinal measurements . The event-free probabilities will then be More details can be found at in Rizopoulos9and Andrinopoulou et al.19
Multiple time-to-event outcomes
As in the primary biliary cirrhosis dataset, we have multiple events (death and transplantation). Therefore, the interest might lie in the risk of each event separately. Given that no event occurred up to t, we focus on the cumulative incidence probabilities at time u > t. If indicates the different time-to-event outcomes, the event probabilities will then be More details can be found inAndrinopoulou et al19 and Ferrer et al.20
Association structures
An important element of prediction that needs to be considered when building a joint model is how the longitudinal and survival outcomes are associated. There are a variety of different features of the longitudinal process that may be related to the risk of an event. For example, not only the underlying value of a marker in (1) but also the slope (how fast the marker progresses) could be associated with the time-to-event outcome. Therefore, it is important to investigate how predictions are affected by assuming different types of association structures between the longitudinal and event time processes. The event-free probabilities will be as in equation (3). More details on alternative association parameters are provided in Rizopoulos et al.21 and Papageorgiou et al.22
Time-varying association parameter
A final feature of the standard joint model is that the parameter that measures the association’s strength between the longitudinal and survival outcome is assumed to be constant in time. However, in some cases, it is more relevant to assume that the longitudinal outcome’s effect on the survival outcome is changing over time. For example, serum bilirubin’s effect on survival could be different at the beginning of the study compared with the end of the study. It has been previously shown that the dynamic risk predictions could be improved by incorporating a time-dependent association parameter.23 The event-free probabilities are defined as in equation (3).
Application
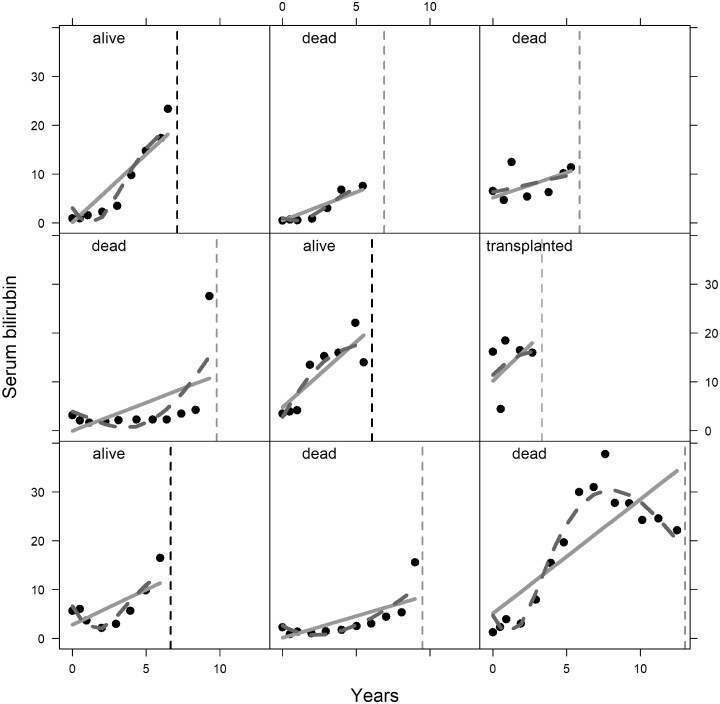
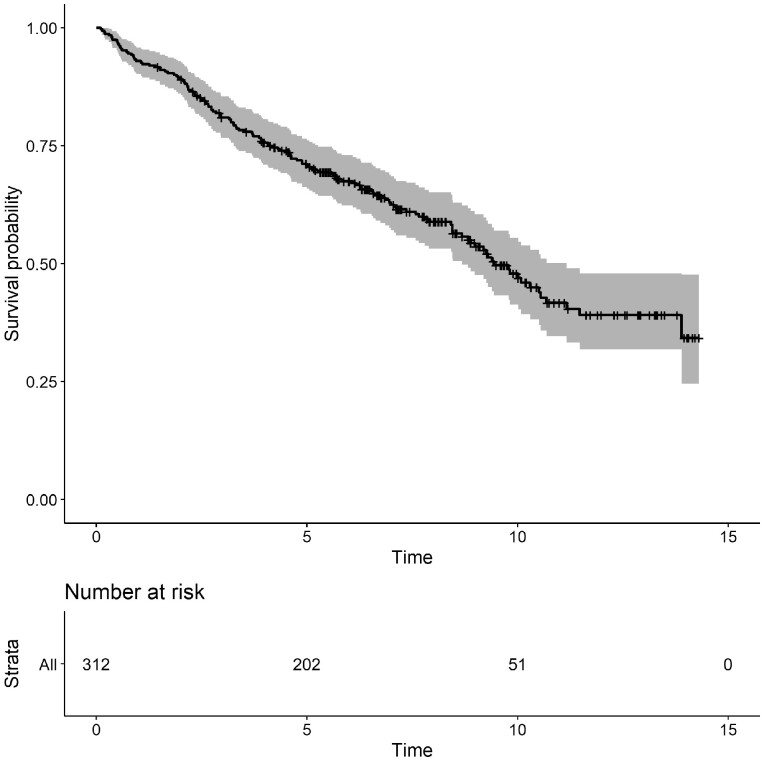
In this section, we present the analysis of the primary biliary cirrhosis dataset, which is available in the JMbayes R package.24 The survival outcomes are time to transplantation and time to death. During follow-up, several biomarkers were recorded which are known to be related to disease progression. Tests to identify the disease include measuring the levels of serum bilirubin, where high values indicate liver damage or disease. A total of 312 patients participated in this study and 50% of the patients received the drug. Most of the patients were females, 45% of the patients died and 9% were transplanted during the follow-up period. In Figure 1, we present the evolution of all patients per event group and in Figure 2, we illustrate the evolution of serum bilirubin of nine randomly selected patients. Figure 3, represents the Kaplan-Meier plot for the event-free probabilities. We assume the composite event of death/transplantation. In that case, we consider that death and transplantation indicate an equal health condition for the patient before the event occurred, which clinically might not be correct. More sophisticated survival models are possible for use by analysts (e.g. competing risks); however, these models are not always applicable using standard software. An alternative approach would be to assume death as the only event and censor the patients who experience transplantation. Only 29 out of the 312 patients were transplanted; therefore, we do not expect any essential changes in the results. The following steps illustrate the use of the joint models of longitudinal and survival outcome to obtain predictions.
Figure 2.
Evolution of serum bilirubin for nine randomly selected patients. Solid lines represent the linear evolution and the dashed lines represent the nonlinear evolution. The circles represent the observed serum bilirubin measurements. The vertical dashed lines indicate the event time.
Figure 3.
Kaplan-Meier plot for the event-free probability. Event is specified as death or transplantation
Step 1: Build and fit a joint model
Let us assume that we are interested in including the baseline covariates age, sex and drug in both the longitudinal and survival submodels. In the longitudinal submodel, it is important to investigate the evolution of our outcome over time. The decision of using a linear versus a nonlinear structure for the fixed and random effects can be based on the individual profiles and the Akaike information criterion (AIC). However, it is not always clear whether the difference in the AIC between two or more models is large and clinically important. Extra investigation can be done based on the predictive performance of the models. In Figure 2, we have illustrated that some patients have nonlinear profiles; therefore, we assumed a flexible linear mixed-effects submodel including natural cubic splines for time with two internal knots at 1 and 4 years (corresponding to 33.3% and 66.7% of the observed follow-up times; i.e. quantiles) in both the fixed-effects and random-effects parts of the models.25 We did not further investigate the models’ performance assuming different fixed- and random-effects structures in the mixed-effects model since this manuscript’s primary focus is to illustrate the dynamic predictions in the joint modelling case. Due to convergence problems, we assume a diagonal matrix for the variance-covariance of the random effects. This structure is useful when high-dimensional random-effects structures are considered. Alternatively, researchers could assume a less flexible time structure and a full variable-covariance matrix of the random effects. Then the predictive performance of the two models could be investigated. The logarithmic scale of the serum bilirubin was used because the assumption that the variance of the error terms is constant (homoscedasticity) was not satisfied in the original scale. In Figure 4, we present the results of the mixed-effects models. In complicated settings, such as models with nonlinear time structure, the coefficients do not have a straightforward interpretation. Therefore, a figure might be more informative than a table with coefficients. Here, we illustrate the average evolution of serum bilirubin’s logarithmic scale for the two treatment groups, assuming median age and female patients.
Figure 4.
Estimated average effect of treatment on log(serum bilirubin) over time for an average patient. Estimate obtained using a linear mixed-effects model
In the joint model, the baseline risk function is approximated using B-splines, assuming five knots placed on the percentiles of the observed event times (default setting in JMbayes). Note that we assumed the splines approaches previously used in the framework of joint models of longitudinal and survival models, default options in the software presented. More information on the different types of splines can be found at in Perperoglou et al.25 The association between the logarithmic scale of serum bilirubin with time to event seems to be strong. In particular, the log hazard is increased by 1.28, with 95% CI (1.1, 1.5), for each unit increase in the current value of log serum bilirubin (see Supplementary material), given that all other baseline variables remain the same. In other words, a 10% increase in serum bilirubin, holding all other variables constant, is associated with a 0.12% increase in the hazard of death/transplant.
Step 2: Obtain dynamic predictions
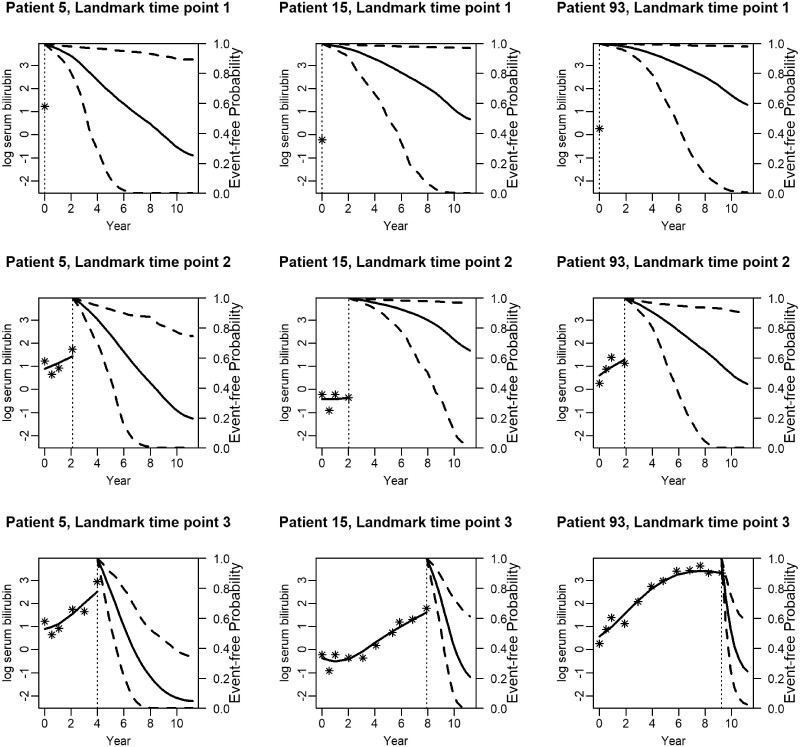
We now present predictions that are updated as more information is available for the patient. In particular, in Figure 5, we illustrate predictions from three different patients (5, 15 and 93), presented at three landmark time points. Note that the third landmark time point is different for the three patients. This is explained by the fact that these patients have measurements of different length and at different time points. Patient 5 has his/her latest measurement at 4 years, patient 15 at 10 years and patient 93 at 12 years. At landmark time point one, patients 5 and 15 seem to have event-free probabilities close to 0.3–0.4 in year 11. Patient 93 has a higher event-free probability. However, after the third visit, we obtain a lower event-free probability for patient 5 compared with patients 15 and 93. This can be explained by the fact that the longitudinal measurements of patient 5 increase rapidly over time, indicating that the patient’s condition is getting worse. On the other hand, patients 15 and 93 have a less steep evolution.
Figure 5.
Dynamic survival/transplantation-free predictions for three randomly selected patients. The x-axis represents years, and the vertical dotted line indicates the time point of the latest measurement. The y-axis of the left side represents the serum bilirubin measurements in the logarithmic scale that are available up to the latest visit. In particular, the stars represent the observed values and the solid line the fitted longitudinal trajectory. The y-axis on the right side represents the mean estimator of the predictions and the dashed lines the corresponding 95% confidence interval
Step 3: Evaluate the predictions
An essential procedure before using the dynamic predictions for future patients is to investigate their predictive performance. In the previous step, we have presented a dynamic prediction model; however, we did not investigate whether alternative models would improve those predictions. Let us assume that we want to compare the predictive performance of the following models.
A linear mixed-effects submodel with a linear time structure in both the fixed and the random effects: this model is a more simplified version of the model presented in steps 1 and 2.
A linear mixed-effects submodel with a nonlinear time structure in both the fixed and the random effects: in particular, we use natural cubic splines with three degrees of freedom. We assume a diagonal covariance-variance matrix for the random effects. This model is presented in steps 1 and 2.
A multivariate mixed-effects submodel including both serum bilirubin and spiders (which indicates whether there exist blood vessel malformations in the skin) as longitudinal outcomes: a linear time structure in both the fixed and the random effects is used. A random intercept and slope are assumed for the outcome serum bilirubin and a random intercept is assumed for the outcome spiders. The same baseline covariates are assumed as in steps 1 and 2.
A multivariate mixed-effects submodel including different features of the longitudinal outcomes: since repeated serum bilirubin and spider measurements are available for each patient, different summaries of these longitudinal outcomes might be associated with the survival outcome. We assume the underlying value and how fast the biomarker serum bilirubin is progressing (slope). Furthermore, the underlying value of spiders is assumed. A linear time structure in both the fixed and the random effects is used. A random intercept and slope are assumed for the outcome serum bilirubin and a random intercept is assumed for the outcome spiders. The same baseline covariates are assumed as in steps 1 and 2.
In order to compare the predictive performance of the models above, we will use the AUC(t, u), PE(t, u) and CAL(t, u) measures. We will assume all the repeated measurements up to the follow-up time t = 5 and the future time point u = 7. Overfitting-corrected estimates of these measures will be obtained using an internal validation procedure developed by Harrell et al.26 In particular, given that the number of patients is relatively small, the same data will be used for fitting the model and evaluating the performance of the model. Then, corrections for the optimism will be done by a bootstrap method. The steps that are followed are described below:
Fit the model on the original data and calculate the apparent predictive measures on the same data: and .
Create a bootstrap sample (assuming the same number of patients) of the data and fit the model on the bootstrap sample.
Calculate the predictive measures on the bootstrap data from the model fitted on the bootstrap sample: and .
Calculate the predictive measures on the original data from the model fitted on the bootstrap sample: and .
- Calculate the optimism in this bootstrap sample by:
Repeat steps 2-5 100 times.
- Finally, correct the apparent predictive measure with each optimism:
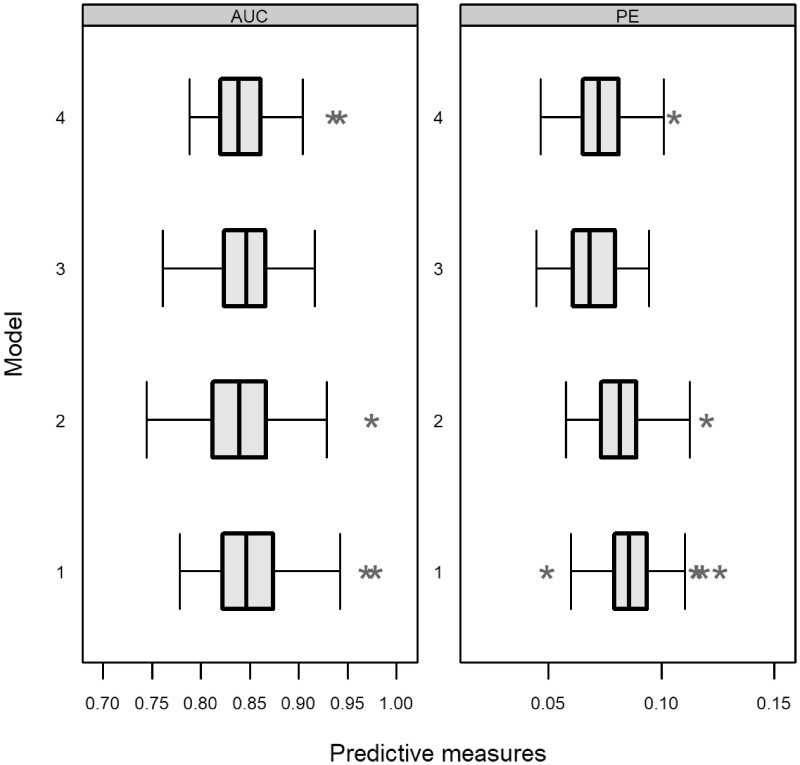
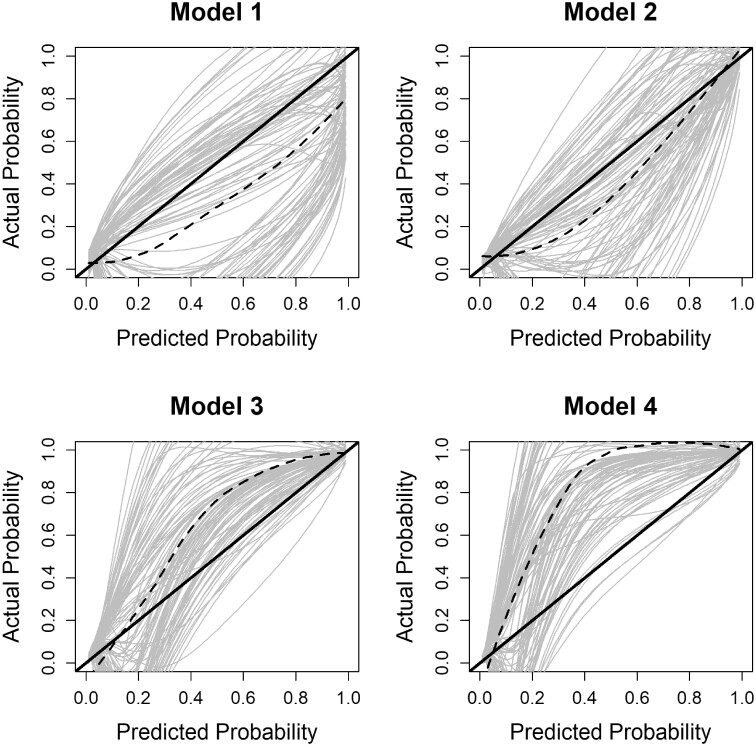
The results for each model are presented in Figures 6 and 7. In particular, we obtain small differences between the models assuming the AUC(t, u) and PE(t, u) measures. Using the PE(t, u) measure, we obtain a smaller value for models 3 and 4 compared with models 1 and 2. From the calibration plots, we observe that model 2 performs better. Even though the differences are small, these predictive performance measurements are essential in comparing the models when the focus is on predictions.
Figure 6.
AUC(t, u) and PE(t, u) corrected measures per model. In particular, each boxplot includes measures from each bootstrap iteration
Figure 7.
CAL(t, u) corrected measure per model. The solid black line represents the ideal scenario, whereas the dashed black line represents the average calibration accuracy using a Cox proportional hazards model assuming the event indicator as the outcome and the prediction probability with splines as the covariate. The grey lines represent the calibration accuracy from each bootstrap iteration
Identifying a good prediction model assuming the primary biliary cirrhosis dataset is outside the scope of this manuscript. We aim to guide researchers on the appropriate steps that they need to follow and combine with their clinical knowledge. Therefore, other joint models might exist that have a better predictive performance compared with the models presented here.
Selecting the most appropriate prediction model is a challenging task. Researchers should combine their clinical knowledge with the statistical results. A more complicated model might be slightly better according to predictive performance, but could make the interpretation more difficult, and the model less useful. In that case, researchers could decide to use a simpler model for obtaining predictions. Another reason for not selecting a complex model is that some information required by that model might be difficult to obtain. In such a scenario, the researchers might decide to use the simpler model without this type of information, even though the predictive performance is not as good as using all information.
Discussion
Herein we have provided a detailed educational tutorial on how to obtain individualized, dynamic risk predictions using the framework for joint models of longitudinal and survival data. We have used a dataset that is available online, and we have provided guidance on obtaining and interpreting dynamic predictions. Additionally, we have investigated the predictive performance assuming different models. The syntax that was used in this manuscript is available online.
There are alternative approaches for individualized risk predictions not presented in this paper. For example, the time-dependent Cox model could be used to obtain dynamic risk predictions. However, this model assumes a step function between the repeated measurements, which is not realistic for biomarkers such as serum bilirubin because such outcomes cannot be assumed to be constant between visits. One other method, that has been previously compared with the joint modelling framework, is landmarking.20,27,28 This approach uses a Cox proportional hazards model with patients still alive at a particular time point, and then predicts the survival probability for a future time point. Furthermore, latent class joint models are useful for heterogeneous populations. Using different submodel linking assumptions, each latent class is characterized by its own biomarker trajectory and class-specific event risk. Readers interested in latent class models are referred to Proust-Lima et al.29 Dynamic predictions derived from these types of models have been discussed in the literature.30,31 Additionally, other joint model extensions that are possible have not been discussed, such as how personalized dynamic predictions can be obtained for the longitudinal outcome.
The dynamic risk predictions illustrated in this research (and as shown in Figure 5) could provide the physician with a useful tool to investigate the impact of the longitudinal outcomes on patient prognosis. The calculated risk probabilities can be used as an early warning system, allowing the necessary time for the physicians to prepare and plan an intervention. Joint models are an important tool for dynamic prediction of an individual’s disease prognosis. The ability to use all of a patient’s trajectory to inform future outcome prediction should be used more widely in the clinical care. A detailed explanation on how to fit the joint models and obtain the dynamic prediction in R can be found at [https://erandrinopoulou.github.io/EducationalCorner_JMpred/].
Funding
M.O.H. is partially supported by grants R00-HL141678 and R01-DK123041 from the United States (US) National Institutes of Health (NIH). S.J.R. is partially supported by grants R01-GM104470 and R01-DK123041 from the US NIH. E.R.A. is partially supported by the NIH/National Heart, Lung, and Blood Institute (grant R01 HL141286).
Supplementary Material
Acknowledgements
The authors would like to thank the two anonymous reviewers for critically reading the manuscript and suggesting substantial improvements.
Conflict of Interest
None declared.
Contributor Information
Eleni-Rosalina Andrinopoulou, Department of Biostatistics, Erasmus MC, Rotterdam, The Netherlands.
Michael O Harhay, Department of Biostatistics, Epidemiology, and Informatics, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA; Palliative and Advanced Illness Research (PAIR) Center, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA; Pulmonary, Allergy, and Critical Care Division, Department of Medicine, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, USA.
Sarah J Ratcliffe, Division of Biostatistics, Department of Public Health Sciences, University of Virginia, Charlottesville, VA, USA.
Dimitris Rizopoulos, Department of Biostatistics, Erasmus MC, Rotterdam, The Netherlands.
References
- 1. Andrinopoulou ER, Rizopoulos D, Geleijnse ML et al. Dynamic prediction of outcome for patients with severe aortic stenosis: application of joint models for longitudinal and time-to-event data. BMC Cardiovasc Disord 2015;15:28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Al-Huniti N, Onishchenko D, Dunyak J et al. Dynamic predictions of patient survival using longitudinal tumor size in non-small cell lung cancer: Approach towards personalized medicine. J Clin Oncol 2017;35:e20606-e20606 (Suppl 15):. [Google Scholar]
- 3. Murtaugh PA, Dickson ER, Van Dam GM et al. Primary biliary cirrhosis: prediction of short-term survival based on repeated patient visits. Hepatology 1994;20:126–34. [DOI] [PubMed] [Google Scholar]
- 4. Tsiatis AA, Davidian M. Joint modeling of longitudinal and time-to-event data: an overview. Statistica Sinica 2004;14:809–34. [Google Scholar]
- 5. Asar Ö, Ritchie J, Kalra PA et al. Joint modelling of repeated measurement and time-to-event data: an introductory tutorial. Int J Epidemiol 2015;44:334–44. [DOI] [PubMed] [Google Scholar]
- 6. Papageorgiou G, Mauff K, Tomer A et al. An overview of joint modeling of time-to-event and longitudinal outcomes. Annu Rev Stat Appl 2019;6:223–40. [Google Scholar]
- 7. Wulfsohn MS, Tsiatis AA. A joint model for survival and longitudinal data measured with error. Biometrics 1997;53:330–39. [PubMed] [Google Scholar]
- 8. Henderson R, Diggle P, Dobson A. Identification and efficacy of longitudinal markers for survival. Biostatistics 2002;3:33–50. [DOI] [PubMed] [Google Scholar]
- 9. Rizopoulos D, Joint Models for Longitudinal and Time-to-event Data: With Applications in R. Boca Raton FL: Chapman and Hall/CRC Biostatistics Series, 2012. [Google Scholar]
- 10. Hickey GL, Philipson P, Jorgensen A et al. Joint modelling of time-to-event and multivariate longitudinal outcomes: recent developments and issues. BMC Med Res Methodol 2016;16:117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Taylor JM, Yu M, Sandler HM. Individualized predictions of disease progression following radiation therapy for prostate cancer. J Clin Oncol 2005;23:816–25. [DOI] [PubMed] [Google Scholar]
- 12. Yu M, Taylor JMG, Sandler HM. Individual prediction in prostate cancer studies using a joint longitudinal survival–cure model. J Am Stat Assoc 2008;103:178–87. [Google Scholar]
- 13. Rizopoulos D. Dynamic predictions and prospective accuracy in joint models for longitudinal and time-to-event data. Biometrics 2011;67:819–29. [DOI] [PubMed] [Google Scholar]
- 14. Rizopoulos D, Taylor JM, Van Rosmalen J et al. Personalized screening intervals for biomarkers using joint models for longitudinal and survival data. Biostatistics 2016;17:149–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Li K, Luo S. Dynamic predictions in Bayesian functional joint models for longitudinal and time-to-event data: An application to Alzheimer’s disease. Stat Methods Med Res 2019;28:327–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Steyerberg EW, Vickers AJ, Cook NR et al. Assessing the performance of prediction models: a framework for some traditional and novel measures. Epidemiology 2010;21:128–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Harrell FE Jr Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis. New York, NY: Springer, 2015. [Google Scholar]
- 18. Rizopoulos D, Molenberghs G, Lesaffre EM. Dynamic predictions with time-dependent covariates in survival analysis using joint modeling and landmarking. Biom J 2017;59:1261–76. [DOI] [PubMed] [Google Scholar]
- 19. Andrinopoulou ER, Rizopoulos D, Takkenberg JJ et al. Combined dynamic predictions using joint models of two longitudinal outcomes and competing risk data. Stat Methods Med Res 2017;26:1787–801. [DOI] [PubMed] [Google Scholar]
- 20. Ferrer L, Putter H, Proust-Lima C. Individual dynamic predictions using landmarking and joint modelling: validation of estimators and robustness assessment. Stat Methods Med Res 2019;28:3649–66. [DOI] [PubMed] [Google Scholar]
- 21. Rizopoulos D, Hatfield LA, Carlin BP et al. Combining dynamic predictions from joint models for longitudinal and time-to-event data using Bayesian model averaging. J Am Stat Assoc 2014;109:1385–97. [Google Scholar]
- 22. Papageorgiou G, Mokhles MM, Takkenberg JJ et al. Individualized dynamic prediction of survival with the presence of intermediate events. Stat Med 2019;38:5623–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Andrinopoulou ER, Eilers PH, Takkenberg JJ et al. Improved dynamic predictions from joint models of longitudinal and survival data with time-varying effects using p-splines. Biometrics 2018;74:685–93. [DOI] [PubMed] [Google Scholar]
- 24. Rizopoulos D. The r package jmbayes for fitting joint models for longitudinal and time-to-event data using mcmc. J Stat Softw 2016;72:1–46. [Google Scholar]
- 25. Perperoglou A, Sauerbrei W, Abrahamowicz M et al. A review of spline function procedures in r. BMC Med Res Methodol 2019;19:46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Austin PC, Harrell FE Jr, van Klaveren D. Graphical calibration curves and the integrated calibration index (ici) for survival models. Stat Med 2020;39:2714–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Harrell FE Jr, Lee KL, Mark DB. Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors. Stat Med 1996;15:361–87. [DOI] [PubMed] [Google Scholar]
- 28. Suresh K, Taylor JM, Spratt DE et al. Comparison of joint modeling and landmarking for dynamic prediction under an illness-death model. Biom J 2017;59:1277–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Proust-Lima C, Séne M, Taylor JM et al. Joint latent class models for longitudinal and time-to-event data: A review. Stat Methods Med Res 2014;23:74–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Proust-Lima C, Taylor JM. Development and validation of a dynamic prognostic tool for prostate cancer recurrence using repeated measures of posttreatment PSA: a joint modeling approach. Biostatistics 2009;10:535–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Proust-Lima C, Liquet PV. B. Estimation of extended mixed models using latent classes and latent processes: the r package lcmm. J Stat Softw 2015;78:1–56. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.