Unraveling the origin of extra strengthening in gradient nanotwinned metals

Significance

The emergence of heterogeneous nanostructured metals offers exciting opportunities for achieving extraordinary mechanical properties. Gradient nanotwinned Cu is a prominent class of heterogeneous nanostructured metals, as it exhibits a superior extra strength compared with nongradient counterparts. However, the mechanistic origin of the extra strength remains elusive. At a more fundamental level, the strengthening effects of plastically inhomogeneous deformation in heterogeneous nanostructured metals are not well understood. Here, we use a combination of controlled material processing, back-stress measurement, dislocation microstructure characterization, and strain gradient plasticity modeling to unravel the origin of the extra strength in gradient nanotwinned Cu. The combined experimental and modeling framework may be applied to accelerate the rational design of heterogeneous nanostructured metals with enhanced mechanical performance.

Abstract

Materials containing heterogeneous nanostructures hold great promise for achieving superior mechanical properties. However, the strengthening effect due to plastically inhomogeneous deformation in heterogeneous nanostructures has not been clearly understood. Here, we investigate a prototypical heterogeneous nanostructured material of gradient nanotwinned (GNT) Cu to unravel the origin of its extra strength arising from gradient nanotwin structures relative to uniform nanotwin counterparts. We measure the back and effective stresses of GNT Cu with different nanotwin thickness gradients and compare them with those of homogeneous nanotwinned Cu with different uniform nanotwin thicknesses. We find that the extra strength of GNT Cu is caused predominantly by the extra back stress resulting from nanotwin thickness gradient, while the effective stress is almost independent of the gradient structures. The combined experiment and strain gradient plasticity modeling show that an increasing structural gradient in GNT Cu produces an increasing plastic strain gradient, thereby raising the extra back stress. The plastic strain gradient is accommodated by the accumulation of geometrically necessary dislocations inside an unusual type of heterogeneous dislocation structure in the form of bundles of concentrated dislocations. Such a heterogeneous dislocation structure produces microscale internal stresses leading to the extra back stress in GNT Cu. Altogether, this work establishes a fundamental connection between the gradient structure and extra strength in GNT Cu through the mechanistic linkages of plastic strain gradient, heterogeneous dislocation structure, microscale internal stress, and extra back stress. Broadly, this work exemplifies a general approach to unraveling the strengthening mechanisms in heterogeneous nanostructured materials.

Heterogeneous nanostructured metals exhibit excellent mechanical properties such as ultrahigh strength, ductility, toughness, and their combinations (1–7). The strengthening effects arising from various types of heterogeneous nanostructures have been recently studied from different perspectives, including back and forward stresses (8–13), Bauschinger effect (14, 15), plastic strain gradient (16–19), and geometrically necessary dislocations (GNDs) (20–23), among others (5, 6, 24, 25). However, there is a critical lack of a general framework and associated exemplary studies that unify these different perspectives. Such unification is essential to vastly accelerating efforts for understanding the origin of strengthening caused by heterogeneous nanostructures and therefore enabling more advanced development of heterogeneous nanostructured metals.

Recently, gradient nanotwinned (GNT) Cu has been fabricated by stacking four homogeneous nanotwinned (HNT) components with increasing twin thickness (4, 17). Through tuning processing conditions, GNT Cu exhibits a periodic variation of nanotwin thickness through sample thickness. As a result, its overall yield strength surpasses the rule-of-mixture average of yield strengths of four HNT components, giving a substantial extra strength of GNT Cu. An increase of nanotwin thickness gradient (hereafter referred to as structural gradient) can result in a marked increase of the extra strength. Given the excellent control of structural gradient and the resultant tunability of extra strength, GNT Cu can serve as a prototypical heterogeneous nanostructured material to unravel the origin of extra strengthening in heterogeneous nanostructures.

Fig. 1 presents a general framework for understanding the mechanics of heterogeneous nanostructures with GNT Cu as an example. Here it is important to take into consideration the size of a selected representative volume element (RVE) relative to the characteristic length scales of GNT Cu, which feature the wavelength of periodically varying twin thickness (on the order of hundreds of micrometers) as well as the nanotwin thickness (on the order of tens of nanometers). As shown in the red panel of Fig. 1, when the entire sample of GNT Cu is taken as a “large” RVE, the strengthening effect of structural gradient inside the RVE can be characterized by partitioning the overall stress into its back and effective stress components based on the local plasticity theory of kinematic hardening (26–28). The back stress reflects the directional, long-range internal stresses arising from plastically inhomogeneous deformation in gradient structures, while the effective stress represents the nondirectional, short-range resistance to gliding dislocations from lattice friction and local pinning obstacles (12). Hence, quantification of the back and effective stresses can provide critical mechanistic information on the origin of strengthening in heterogeneous nanostructures. In contrast, the blue panel of Fig. 1 shows an alternative approach of choosing a “small” RVE that contains twin lamellae with a uniform thickness. Suppose a “small” RVE represents a “soft” region containing uniformly thick twin lamellae, while an adjacent “small” RVE represents a “hard” region containing uniformly thin twin lamellae. A structural gradient across the two RVEs results in a spatial gradient of plastic strains, whose strengthening effect can be characterized by the nonlocal theory of strain gradient plasticity (SGP) (17). Note that these “small” RVEs with uniform twin thickness also contain structural heterogeneity due to the presence of twin boundaries (TBs) and twin lamellae with different orientations. The strengthening effect of this type of structural heterogeneity can be characterized by the back and effective stresses that prevail locally within each “small” RVE (29). Therefore, the strengthening effects arising from the nanotwin gradients and uniform nanotwins are separated in the “small-RVE” approach, while these two strengthening effects are combined in the “large-RVE” approach.

Fig. 1.

A general framework to study the mechanics of heterogeneous nanostructures (with GNT Cu as an example) in terms of large and small RVEs at different length scales.

In this work, we first measure the back stress and effective stress for four types of freestanding HNT Cu samples with different average twin thicknesses, and each type of HNT Cu is treated as a “small” RVE. Then, we measure the sample-level back stress and effective stress for four types of GNT Cu samples with different structural gradients, and each type of GNT Cu is considered as a “large” RVE. These results enable us to establish a direct connection between the structural gradient and extra back stress. Moreover, the small-RVE approach is applied to study GNT Cu via SGP modeling, in order to quantitatively evaluate the effect of plastic strain gradients across small RVEs on the generation of extra back stress as a function of structural gradient. The combined experimental results from the two RVE approaches, in conjunction with SGP modeling, allow us to quantitatively understand the origin of extra back stress and resultant extra strength in GNT Cu, thereby enabling an in-depth mechanistic understanding of the strengthening mechanisms in heterogeneous nanostructures.

Results

Back Stress and Effective Stress of HNT Cu.

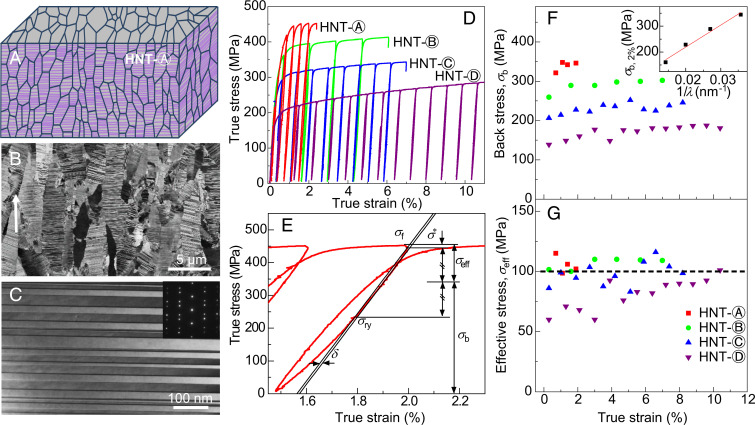
Four HNT Cu samples, referred to as HNT-Ⓐ, HNT-Ⓑ, HNT-Ⓒ, and HNT-Ⓓ, respectively, were prepared by direct-current electrodeposition (Materials and Methods). From HNT-Ⓐ to HNT-Ⓓ, the average twin thickness increases from 28, 37, and 50 to 70 nm, respectively. These HNT Cu samples consist of columnar-shaped grains along their growth direction. Inside grains, most of the nanotwins are preferentially oriented with TBs perpendicular to the growth direction, as shown by the schematic illustration, scanning electron microscope (SEM), and transmission electron microscope (TEM) images for HNT-Ⓐ as an example (Fig. 2 A–C), respectively.

Fig. 2.

Microstructure, back stress and effective stress in HNT Cu. Schematic (A), SEM image (B), and TEM image (C) of HNT-Ⓐ. The white arrow in B indicates the growth direction of HNT Cu. (D) Loading–unloading tensile true stress–strain curves of HNT-Ⓐ to -Ⓓ samples. (E) Determination of back stress σ_b and effective stress σ_eff based on Dickson’s method in a magnified unloading–reloading branch of the stress–strain curve of an HNT-Ⓐ sample. σ_f, flow stress; σ_ry, reverse yield stress; σ*, stress interval past the peak stress; δ, offset stain. (F) Back stress σ_b against tensile strain for HNT-Ⓐ to -Ⓓ. (Inset) The back stresses of HNT-Ⓐ to -Ⓓ at the applied strain of 2%, denoted as ${\sigma }_{\text{b,} \text{2\%}}$, follow a linear relationship with the reciprocal of twin thickness $\lambda$. (G) Same as F except for effective stress σ_eff.

Fig. 2D shows the tensile true stress–strain curves with multiple unloading–reloading branches for the four HNT Cu samples. The tensile stress $\sigma$ exhibits rapid increase at small strain ε and then switches to slow increase when ε exceeds about 2%. This type of two-stage hardening response is also measured for GNT Cu, as will be shown. Hence, the tensile stress $\sigma$ at ε = 2%, denoted as ${\sigma }_{2\%}$, is taken as the representative value of yield strength for both HNT and GNT Cu. From HNT-Ⓐ to HNT-Ⓓ, ${\sigma }_{2\%}$ decreases from 448, 392, and 320 to 228 MPa, showing a strong dependence on twin thickness in HNT Cu.

Fig. 2E shows a representative unloading–reloading branch of HNT-Ⓐ, where Dickson’s method (30) is applied to partition the applied tensile stress into the back stress ${\sigma }_{\text{b}}$ and effective stress ${\sigma }_{\text{eff}}$. Once unloading begins at ε = 2%, the unloading curve deviates markedly from the reference curve of linear elastic unloading. Particularly, reverse plastic yielding occurs while the applied stress is still tensile, indicative of a strong Bauschinger effect associated with a high back stress and accordingly a low effective stress.

From multiple unloading–reloading branches (Fig. 2D), ${\sigma }_{\text{b}}$ and ${\sigma }_{\text{eff}}$ were determined as a function of ε for the four types of HNT Cu. From HNT-Ⓓ to HNT-Ⓐ, ${\sigma }_{\text{b}}$ increases markedly with decreasing twin thickness $\lambda$ (Fig. 2F). For example, ${\sigma }_{\text{b}}$ at ε = 2%, denoted as ${\sigma }_{\text{b,} \text{2\%}}$, is 160 MPa in the softest HNT-Ⓓ with the largest $\lambda$ of 70 nm, as compared with 346 MPa in the strongest HNT-Ⓐ with the smallest $\lambda$ of 28 nm. Fig. 2F, Inset shows that ${\sigma }_{\text{b,} \text{2\%}}$ follows approximately a linear relationship with 1/$\lambda$. In contrast, ${\sigma }_{\text{eff}}$ exhibits a weak dependence on $\lambda$ at low ε and approaches a saturated value close to 100 MPa (Fig. 2G). There is no significant increase in ${\sigma }_{\text{eff}}$ with increasing ε, except for HNT-Ⓓ whose ${\sigma }_{\text{eff}}$ increases from ∼60 MPa at small ε to the saturated value close to 100 MPa at ε ∼8%. Altogether, the above results indicate that the back stress of HNT Cu at ε = 2% is much higher than the corresponding effective stress and accounts for about 70% of the overall tensile stress. The twin thickness dependence of the overall tensile stress is caused almost entirely by that of the back stress, while the effective stress depends weakly on twin thickness.

Back Stress and Effective Stress of GNT Cu.

Taking HNT-Ⓐ, HNT-Ⓑ, HNT-Ⓒ, and HNT-Ⓓ as building blocks, four types of GNT Cu (SI Appendix, Fig. S1 A and B) were fabricated with the stacking sequence of ⒶⒷⒸⒹ, ⒶⒷⒸⒹⒹⒸⒷⒶ, 2×ⒶⒷⒸⒹⒹⒸⒷⒶ, and 4×ⒶⒷⒸⒹⒹⒸⒷⒶ, referred to as GNT-1, GNT-2, GNT-3, and GNT-4, respectively. Taking GNT-3 as an example, we show the schematic illustration (Fig. 3A) and SEM image (Fig. 3B) of gradient nanotwin structure. A series of microhardness measurements were conducted through sample thickness (SI Appendix, Fig. S1C). The measured hardness gradient, denoted as s, increases from 1.75 to 11.6 GPa/mm for GNT-1 to GNT-4. For clarity of discussion, hereafter these hardness gradient values will be used to represent both the structural and strength gradients of GNT Cu.

Fig. 3.

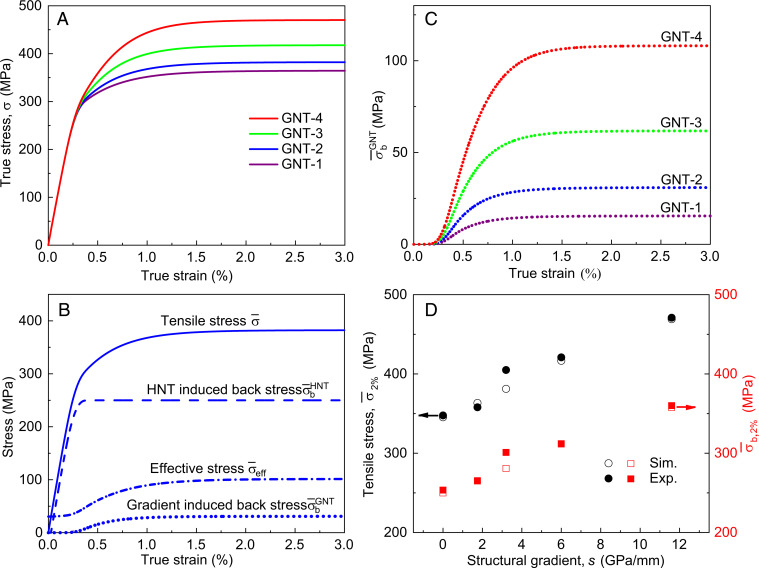
Microstructure, back stress and effective stress in GNT Cu. (A) Schematic of microstructure in GNT-3. (B) Corresponding SEM image. (C) Loading–unloading tensile true stress–strain curves of GNT-1 to -4. (D) Back stress ${\overline{\sigma }}_{\text{b}}$ against true strain of GNT-1 to -4. (E) Same as D except for effective stress ${\overline{\sigma }}_{\text{eff}}$. (F) Back stress at the applied tensile strain $\overline{\epsilon }=2\%$, denoted as ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ (y axis on the left), against structural gradient s; also shown is the corresponding back stress induced by structural gradient ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{GNT}}$ (y axis on the right). The open symbol and the horizontal dashed line represent the HNT-induced back stress ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{HNT}}$, which is estimated by the rule of mixture in terms of back stresses of HNT-Ⓐ to -Ⓓ. ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{GNT}}$ is the difference between ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ and ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{HNT}}$. The error bars are evaluated from three to five measured values around $\overline{\epsilon }=2\%$. (G) Same as F except for the effective stress at $\overline{\epsilon }=2\%$, denoted as ${\overline{\sigma }}_{\text{eff,} \text{2\%}}$.

Fig. 3C shows the tensile true stress–strain curves for the four types of GNT Cu. From GNT-1 to GNT-4, the sample-level tensile stress at the applied tensile strain $\overline{\epsilon }=2\%$, denoted as ${\overline{\sigma }}_{2\%}$, increases from 358, 406, and 420 to 460 MPa, which demonstrate a strong dependence of ${\overline{\sigma }}_{2\%}$ on structural gradient. Note that the sample-level stress and strain in GNT Cu are different from their local counterparts in the sample’s cross-section. Hence, we add an overbar to each sample-level quantity for GNT Cu. It should be noted that all four types of GNT Cu have the same volume fraction (∼25%) of four homogeneous components of HNT-Ⓐ to HNT-Ⓓ. Based on the ${\sigma }_{2\%}$ of these four HNT components, a simple rule-of-mixture estimate of the ${\overline{\sigma }}_{2\%}$ of GNT Cu gives 348 MPa. However, the measured ${\overline{\sigma }}_{2\%}$ values of all four types of GNT Cu surpass the rule-of-mixture value of 348 MPa, giving the extra strength of 10, 58, 70, and 112 MPa from GNT-1 to GNT-4, respectively. These results clearly demonstrate the extra strengthening effects of structural gradients in GNT Cu.

To assess the contributions of back and effective stresses to the extra strengths, Fig. 3D shows the back stress versus tensile strain for the four types of GNT Cu. For each type of GNT Cu, ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ is high and accounts for about 75% of ${\overline{\sigma }}_{2\%}$; ${\overline{\sigma }}_{\text{b}}$ can further increase by less than 10% with increasing tensile strain until failure. From GNT-1 to GNT-4, ${\overline{\sigma }}_{\text{b}}$ increases markedly with structural gradient. Particularly, the ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ of GNT-4 reaches 360 MPa, surpassing the ${\sigma }_{\text{b,} \text{2\%}}$ of the strongest component HNT-Ⓐ. This further demonstrates a strong extra strengthening effect associated with the back stress arising from structural gradient. In contrast, for each type of GNT Cu, ${\overline{\sigma }}_{\text{eff}}$ is much lower than ${\overline{\sigma }}_{\text{b}}$ (Fig. 3E). From GNT-1 to GNT-4, ${\overline{\sigma }}_{\text{eff}}$ exhibits a weak dependence on structural gradient and quickly reaches similar saturated values close to 100 MPa at $\overline{\epsilon }=2\%$.

To further correlate the back and effective stresses with structural gradients, Fig. 3F shows the measured ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ (see the left y axis) as a function of structural gradient s for GNT-1 to GNT-4. Based on the measured values of ${\sigma }_{\text{b,} \text{2\%}}$ from HNT-Ⓐ to HNT-Ⓓ, a rule-of-mixture estimate of ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ for GNT Cu gives 253 MPa, which corresponds to ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ in the limit of zero structural gradient (indicated by the dashed line in Fig. 3F). For each type of GNT Cu, the extra back stress at $\overline{\epsilon }=2\%$, denoted as ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{GNT}}$, was determined from the difference between the measured ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ and its rule-of-mixture estimate of 253 MPa. As shown in Fig. 3F (see the right y axis), ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{GNT}}$ increases markedly with the structural gradient s from GNT-1 to GNT-4. In contrast, Fig. 3G shows the measured effective stress at $\overline{\epsilon }=2\%$, ${\overline{\sigma }}_{\text{eff,} \text{2\%}}$, as a function of s for GNT-1 to GNT-4. Based on the measured values of ${\sigma }_{\text{eff,} \text{2\%}}$ from HNT-Ⓐ to HNT-Ⓓ, a rule-of-mixture estimate of ${\overline{\sigma }}_{\text{eff,} \text{2\%}}$ for GNT Cu gives 94 MPa, which corresponds to ${\overline{\sigma }}_{\text{eff,} \text{2\%}}$ in the limit of zero structural gradient (indicated by the dashed line in Fig. 3G). The measured ${\overline{\sigma }}_{\text{eff,} \text{2\%}}$ of GNT Cu is only slightly higher than the rule-of-mixture estimate, indicative of its weak dependence on structural gradient. Altogether, the above quantitative evaluation of back and effective stresses shows that the extra strength of GNT Cu ${\overline{\sigma }}_{\text{b,} \text{2\%}}$ is caused primarily by the extra back stress ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{\text{GNT}}$ arising from its structural gradient.

Dislocation Mechanisms in GNT Cu.

To determine the dislocation mechanism responsible for the extra back stress in GNT Cu, we conducted the SEM and TEM analysis of deformed HNT and GNT samples. An unusual type of heterogeneous dislocation structure in the form of bundles of concentrated dislocations (BCDs) was found to only develop in deformed GNT Cu, but not HNT Cu. The density of GNDs was estimated from TEM orientation mapping, showing the accumulation of GNDs in BCDs for accommodating the gradients of plastic strain. These GNDs can produce microscale internal stresses that give rise to the extra back stress and accordingly the extra strength in GNT Cu.

Fig. 4A shows the SEM image of BCDs inside columnar grains in GNT-4 deformed to $\overline{\epsilon }=1\%$. These BCDs appear as long contrast strips aligned with the direction of twin thickness gradient. The BCD width along the horizontal direction increases from component Ⓐ to Ⓓ, ranging from 0.3 to 1.5 μm. The number fraction of grains with BCDs increases from 15 to 45%, indicating the variation of BCD morphology with gradient twin structure. To estimate the GNDs associated with BCDs, Fig. 4B shows the magnified TEM image of a BCD in the component Ⓓ of GNT-4. Across this BCD, the local contrast changes along the direction parallel to TBs. The orientation mapping technique (31) in TEM was used to characterize the variation of local contrast in terms of lattice misorientation $\mathrm{\Delta }\theta$, which reaches ∼8° across the BCD. It follows that the local density of GNDs associated with this BCD ${\rho }_{\text{G}}^{\text{BCD}}$ was estimated as 3.6 × 10¹⁴ m⁻², and the corresponding average density of GNDs inside grain ${\rho }_{\text{G}}^{\text{GNT}}$ is 6.5 × 10¹¹ m⁻². The density of dislocations in BCDs is also analyzed from TEM images (SI Appendix, Discussions S1 and S2). Hence, the GNDs associated with BCDs serve to accommodate the gradients of plastic strain arising from gradient nanotwin structures. Moreover, these GNDs can generate microscale internal stresses giving rise to the sample-level extra back stress, as will be discussed next. In addition, the dislocation types inside BCDs were analyzed using a two-beam diffraction technique in TEM (32, 33) (SI Appendix, Fig. S2 and Discussion S3). As illustrated in Fig. 4C, we identified dislocation lines traversing several twin lamellae as Mode II dislocations (with slip plane inclined to TBs and Burgers vector parallel to TBs) (32–34); we also observed BCDs consisting of tangled dislocation lines that can be Mode II or Mode I (with both the slip plane and Burgers vector inclined to TBs); many dislocation segments near TBs were also observed, and they are either Mode II or Mode III (with both slip plane and Burgers vector parallel to TBs).

Fig. 4.

Deformation mechanisms in GNT Cu. (A) BCDs (indicated by the red arrows) in the SEM image of a GNT-4 sample at $\overline{\epsilon }=1\%$. (B) TEM image of a BCD in component Ⓓ of GNT-4. Squares represent points where local crystal orientation was measured to estimate the lattice misorientation and associated GND density along a twin lamella as indicated by a solid line. (C) Schematic illustration of dislocation structures in gradient nanotwins developed under applied stress σ, based on TEM results. Dislocations of Modes I, II, and III are represented by green, brown, and orange lines, respectively, and the corresponding Burgers vectors are shown on the Thompson tetrahedron. GNDs associated with HNT and GNT are denoted as GNDs_HNT and GNDs_GNT, respectively. (D) Incompatible deformation (e.g., opening and overlap) between adjacent nanotwins (indicated by pink and blue layers) without mutual constraints in an HNT structure, and (E) accumulation of GNDs_HNT due to mutual constraints between adjacent nanotwins. (F) Incompatible deformation (e.g., opening) without deformation continuity requirement, as induced by sample-level plastic strain gradient resulting from structural gradient in a GNT structure, and (G) accumulation of GNDs_GNT to satisfy the requirement of deformation continuity.

Based on the above results, we can separate the contributions to strengthening in GNT Cu from various types of dislocations indicated in Fig. 4C. First, the effective stress is likely controlled by the glide dislocations of Mode II traversing several twin lamellae. As discussed earlier, we measured the effective stresses that are almost independent of twin thickness and approach similar saturated values around 100 MPa in both HNT and GNT Cu. From Taylor’s hardening law (35, 36), the characteristic length scale associated with the effective stress of about 100 MPa can be estimated as ∼100 nm (SI Appendix, Discussion S4), which is two and five times the twin thickness of NT-Ⓓ and NT-Ⓐ, respectively. Hence, such type of Mode II dislocation should consist of connected segments that traverse several nanotwin lamellae and move concertedly as a continuous line on the corrugated {111} glide plane in those nanotwin lamellae (37, 38).

Next, we consider dislocations responsible for the back stress arising in HNT Cu that exhibits a strong dependence on twin thickness. This type of back stress can result from the microscale internal stresses caused by GNDs_HNT accumulated at TBs. During plastic deformation, glide dislocations on different slip systems in nanotwins produce deformation incompatibility at TBs (20, 21). Such incompatibility would lead to overlap or opening if adjacent nanotwin lamellae were allowed to deform independently (Fig. 4D). To accommodate the incompatibility, GNDs_HNT of Mode I can be accumulated at TBs (Fig. 4E). Their density ${\rho }_{\text{G}}^{\text{HNT}}$ should scale with $\mathrm{\Delta }{\gamma }^p/\left(\lambda b\right)$, where $\mathrm{\Delta }{\gamma }^p$ is the local incompatible strain at a TB. Hence, the back stress associated with ${\rho }_{\text{G}}^{\text{HNT}}$ in HNT Cu will increase with decreasing twin thickness. Note that the same kind of back stress can arise from the locally homogeneous nanotwin components in GNT Cu as well.

Finally, we consider dislocations dictating the extra back stress that increases with structural gradient. In GNT Cu, the BCDs represent a new type of heterogeneous dislocation structure. A typical BCD appears to consist of tangled dislocation lines of Modes I and II traversing several nanotwin lamellae (Fig. 4C). These dislocations can act as forest obstacles (39–41) to facilitate the accumulation of GNDs_GNT at this BCD, which produce an effective misorientation across the BCD, as illustrated in Fig. 4 F and G. More specifically, the yield strength gradient of a GNT sample under tension generates a gradient distribution of plastic strains. Such gradient plastic strains are similar to those developed in a bent beam where the top/bottom surface region has a larger plastic strain than the neural plane in the middle of the beam. In both cases, GNDs are needed to accommodate the lattice curvature associated with gradient plastic strains (Fig. 4F), and these GNDs should be the edge dislocations with both Burgers vector and dislocation line vector residing in the bent lattice planes (23, 42). These bent planes correspond to the {111} slip planes parallel to TBs in GNT samples. Hence, the most efficient GND configurations in GNT Cu should consist of Mode III dislocations (Fig. 4G), which could result from the reaction products of Mode I and Mode II dislocations with TBs. Based on the previous analysis of back stress for conventional dislocation cell structures (11, 43, 44), the GNDs_GNT in BCDs could play a role similar to the GNDs in dislocation cell walls and thus produce long-range, directional microscale back stresses to hinder dislocation glide in between BCDs. It follows that such microscale back stresses could collectively result in the sample-level extra back stress measured from GNT Cu (Fig. 3F). This analysis is supported by the fact that the measured effective density of GNDs associated with BCDs, denoted as ${\rho }_{\text{G}}^{\text{GNT}}$, matches the gradient of plastic strain arising from the structural gradient in GNT Cu (SI Appendix, Discussions S1 and S2).

SGP Modeling.

The above results indicate that the principal effect of gradient structure is to generate the extra strength through the formation of plastic strain gradients that produce GNDs_GNT and resultant extra back stresses. Here, we develop an SGP model to quantitatively evaluate the extra strengthening effect of plastic strain gradient by accounting for the associated GNDs_GNT and extra back stresses (SI Appendix, Discussion S5). Fig. 5A shows the SGP-simulated tensile stress–strain curves for GNT-1 to GNT-4, which agree with the experimental results in Fig. 3C. Taking GNT-2 as an example, Fig. 5B shows the SGP-simulated sample-level tensile stress $\overline{\sigma }$ along with its components of effective stress ${\overline{\sigma }}_{\text{eff}}$, back stress associated with HNT ${\overline{\sigma }}_{\text{b}}^{\text{HNT}}$, and extra back stress arising from structural gradient ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$. In this case, ${\overline{\sigma }}_{\text{b}}^{\text{HNT}}$ provides a relatively large contribution to $\overline{\sigma }$ relative to ${\overline{\sigma }}_{\text{eff}}$ and ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$. However, ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$ increases substantially with structural gradient (Fig. 5C), while ${\overline{\sigma }}_{\text{b}}^{\text{HNT}}$ and ${\overline{\sigma }}_{\text{eff}}$ do not (SI Appendix, Fig. S3), thereby underscoring the effect of increasing structural gradient on elevating ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$ and $\overline{\sigma }$. Moreover, SI Appendix, Fig. S4 shows the SGP-simulated cross-sectional distributions of tensile stress $\sigma \left(y\right)$, plastic strain ${\epsilon }_{}^{\text{p}}\left(y\right)$, back stress associated with HNT ${\sigma }_{\text{b}}^{\text{HNT}}(y)$, and extra back stress arising from structural gradient ${\sigma }_{\text{b}}^{\text{GNT}}(y)$ in GNT-2 at different $\overline{\epsilon }$. These results directly reveal the spatiotemporal evolution of gradient plastic strain and associated extra back stress during progressive yielding. Since the local yield strength decreases from component Ⓐ to Ⓓ, component Ⓓ first yields, resulting in a plastic region with nonuniform ${\epsilon }_{}^{\text{p}}\left(y\right)$ and ${\sigma }_{\text{b}}^{\text{GNT}}(y)$. The plastic region expands gradually to component Ⓐ with increasing $\overline{\epsilon }$ (SI Appendix, Fig. S4C), leading to the increasing range and magnitude of ${\sigma }_{\text{b}}^{\text{GNT}}(y)$. After progressive yielding is completed around $\overline{\epsilon }=0.3\%$, a nearly linear distribution of ${\epsilon }_{}^{\text{p}}\left(y\right)$ with a constant plastic strain gradient is maintained with increasing $\overline{\epsilon }$. Attaining a saturated gradient of plastic strain in GNT Cu can be also verified through a scaling analysis of plastic strain gradient (SI Appendix, Discussion S2).

Fig. 5.

SGP simulation results of GNT Cu, showing the evolution of back and effective stresses in GNT-1 to GNT-4. (A) Simulated sample-level stress–strain curves of GNT-1 to GNT-4. (B) Simulated sample-level tensile stress $\overline{\sigma }$ for GNT-2, along with the corresponding components of effective stress ${\overline{\sigma }}_{\text{eff}}$, back stress associated with HNT ${\overline{\sigma }}_{\text{b}}^{\text{HNT}}$, and extra back stress arising from structural gradient ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$. (C) Simulated sample-level extra back stress arising from structural gradient ${\overline{\sigma }}_{\text{b}}^{\text{GNT}}$ against tensile strain for GNT-1 to GNT-4. (D) Comparison between simulation and experimental results of the sample-level tensile stress ${\overline{\sigma }}_{\text{2\%}}$ and total back stress ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{}$ at $\overline{\epsilon }=2\%$ versus structural gradient. The effective stress in B is evaluated from the isotropic flow resistance S (SI Appendix, Discussion S5).

The saturated gradient of plastic strain should lead to the saturation of GNDs_GNT that might give the saturated extra back stress (SI Appendix, Discussion S5). However, our SGP simulations indicate that the extra strength becomes saturated until $\overline{\epsilon }\approx 1\%$, which is larger than $\overline{\epsilon }\approx 0.3\%$ when the gradient of plastic strain is saturated due to completion of progressive yielding. Specifically, SI Appendix, Fig. S4D shows that ${\sigma }_{\text{b}}^{\text{GNT}}\left(y\right)$ continues to increase after the entire cross-section becomes yielded plastically and thus achieves the saturated gradient of plastic strain. Nonetheless, the nonlinear hardening effect of plastic strain gradient can still cause a further increase of ${\sigma }_{\text{b}}^{\text{GNT}}\left(y\right)$. As a result, a uniform distribution of saturated ${\sigma }_{\text{b}}^{\text{GNT}}\left(y\right)$ is achieved until $\overline{\epsilon }\approx 1\%$, leading to the saturated extra strength at the sample level. This result demonstrates a strong nonlinear coupling between the gradient distributions of plastic strain and extra back stress in GNT Cu, which requires future in-depth study through coupled experiment and modeling. Finally, Fig. 5D shows a close agreement between the SGP-simulated and experimental results of ${\overline{\sigma }}_{\text{2\%}}$ and ${\overline{\sigma }}_{\text{b,} \text{2\%}}^{}$ as a function of structural gradient. This comparison not only validates SGP simulations but also underscores the notion that the extra strengthening of GNT Cu results predominantly from its plastic strain gradient that produces GNDs_GNT and associated extra back stress.

Conclusion

Our combined experimental and modeling results have identified the primary source of the extra strength in GNT Cu as the extra back stress arising from its nanotwin structure gradient. This type of extra back stress is induced by the GNDs associated with BCDs that only form in the gradient nanotwin structures for accommodating plastic strain gradients. An increase in nanotwin structure gradient can result in a substantial increase in plastic strain gradient, leading to rising extra strength. In contrast, the strengthening effect of HNT Cu largely comes from a different type of back stress originating from incompatible deformation between neighboring nanotwin lamellae. Such back stress is enhanced with decreasing twin thickness. On the other hand, the effective stress is much less sensitive to the thickness of nanotwins (being either uniform or nonuniform) in both GNT and HNT Cu. Altogether, these results underscore the predominant strengthening effect of the plastic strain gradient and resultant extra back stress in GNT Cu arising from its gradient structure and thus point to a “going for nano” strategy for further enhancing its strength by a simultaneous decrease of nanotwin thickness and increase of nanotwin thickness gradient. This strategy requires innovations in material processing to push the limit of attainable nanostructure geometry in the future.

Broadly, this work exemplifies a general mechanistic approach to unraveling the strengthening mechanisms in heterogeneous nanostructures. We demonstrate that in a material with hierarchical nanostructures such as GNT Cu, there generally exist multiple sources of back stresses, due to the presence of structural heterogeneities with distinct characteristic length scales. A combination of the “large-RVE” and “small-RVE” studies enables us to separate various sources of strength enhancement originating from different types of structural heterogeneities. Future mechanistic studies along this approach can provide deep insight and thus pave the way for a rational development of heterogeneous nanostructured materials with outstanding mechanical performance.

Materials and Methods

Sample Preparation.

A direct-current electrodeposition technique was used to prepare HNT and GNT Cu samples. When the electrolyte temperature was fixed at 20, 25, 30, and 35 °C and other parameters were identical, HNT Cu samples, referred to as HNT-Ⓐ, HNT-Ⓑ, HNT-Ⓒ, and HNT-Ⓓ, were fabricated, respectively. When the electrolyte temperature was increased stepwise from 20, 25, and 30 to 35 °C or decreased by an opposite sequence of temperature, GNT Cu samples were fabricated by stacking four components Ⓐ, Ⓑ, Ⓒ, and Ⓓ. As the temperature rate was adjusted to be 0.94, 1.88, 3.75, and 7.5 °C/h, the resulting four GNT Cu samples were referred to as GNT-1, GNT-2, GNT-3, and GNT-4, respectively. The total electrodeposition time of four HNT Cu samples and four GNT Cu samples was kept at ∼16 h, resulting in the same sample thickness of ∼400 μm. From GNT-1 to GNT-4, the wavelength of the triangular wave of twin thickness decreases approximately from 800 to 100 μm. More details of HNT and GNT Cu sample preparation can be found in a previous publication (4).

Loading and Unloading Tensile Tests.

Flat tensile specimens with a dog-bone shape and a gauge section of 5 mm in length and 2 mm in width were cut from as-deposited HNT and GNT Cu sheets by an electro-spark machine and then polished mechanically and electrochemically to reduce surface roughness. The tensile loading and unloading tests were performed on an Instron 5982 machine with a load cell of 5 kN at ambient temperature and a strain rate of 1 × 10⁻⁴ s⁻¹. A digital image correlation–based contactless strain gauging system (29) was used to measure the tensile strain. Before tensile tests, random spark patterns with a dot size of ∼10 μm were made by spraying diluted black ink using a medical atomizer onto the surface of tensile samples.

Measurement of Back Stress and Effective Stress.

The classical Dickson’s method (30) was used to measure the back stress and effective stress that partition the tensile stress applied to HNT Cu and GNT Cu samples. As shown by a typical unloading curve of HNT-Ⓐ in Fig. 2E, the back stress, σ_b, and effective stress, σ_eff, are respectively given by

$${\sigma }_{\text{b}}=\frac{{\sigma }_{\text{f}}+{\sigma }_{\text{ry}}}{2}-\frac{{\sigma }^{*}}{2},$$ [1]

$${\sigma }_{\text{eff}}={\sigma }_{\text{f}}-{\sigma }_{\text{b}},$$ [2]

where σ_f is the true tensile stress before unloading, σ_ry is the reverse yield stress upon unloading, and ${\sigma }^{*}$ is the stress interval past the peak stress, such that the back stress corresponds to the middle point of the elastic unloading curve. σ_ry was determined by the reference elastic unloading curve with a slope of elastic modulus (120 GPa for Cu) and an offset strain δ intercepted by the unloading curve, as schematically shown in Fig. 2E. δ was chosen as 0.01% for HNT and GNT Cu samples to capture the elastic unloading stage during which the back stress is relaxed slightly due to reverse plastic deformation, so that the constant back stress assumption in the Dickson’s method (Eq. 1) is satisfied as much as possible.

Microstructure Characterization.

An SEM (FEI Verios 460) equipped with a circular back-scattered detector was used to observe the cross-sectional microstructures of as-deposited and deformed HNT and GNT Cu samples. The SEM specimen of deformed samples was cut from the gauge section along the tensile axis. Before SEM observation, the specimen was mechanically polished and then electrochemically polished in a solution of phosphoric acid (25%), alcohol (25%), and deionized water (50%) at ambient temperature. A TEM (FEI Tecnai G2 F20) operated at 200 kV was applied to examine cross-sectional microstructures of as-deposited and as-tensioned HNT Cu and GNT Cu samples. A two-beam diffraction technique (33) in TEM was used to identify dislocations one by one under diffraction vectors of g_T = 111 and g_T = 200, respectively. The average density of each dislocation type was obtained by counting dislocations per area from at least 50 TEM images. An electron precession diffraction technique (31) with a NanoMEGAS hardware and ASTAR system was used in TEM to map the orientation of individual BCD regions, and the misorientation across a BCD was measured along twin lamellae. During this process, TBs were kept edge-on, and the nanoscale beam diffraction mode was used with a scanning step of 3.6 nm. TEM foils were also cut from the gauge section along the tensile axis of deformed samples, mechanically polished before attached into a Cu ring, and finally thinned by twin-jet electrochemical polishing in a solution of phosphoric acid (25%), alcohol (25%), and deionized water (50%) at about –10 °C.

Data Availability

All study data are included in the article and/or SI Appendix.