Microestimates of wealth for all low- and middle-income countries

Significance

Many critical policy decisions rely on data about the geographic distribution of wealth and poverty, yet only half of all countries have access to adequate data on poverty. This paper creates a complete and publicly available set of microestimates of the distribution of relative poverty and wealth across all 135 low- and middle-income countries. We provide extensive evidence of the accuracy and validity of the estimates and also provide confidence intervals for each microestimate to facilitate responsible downstream use. These methods and maps provide a set of tools to study economic development and growth, guide interventions, monitor and evaluate policies, and track the elimination of poverty worldwide.

Abstract

Many critical policy decisions, from strategic investments to the allocation of humanitarian aid, rely on data about the geographic distribution of wealth and poverty. Yet many poverty maps are out of date or exist only at very coarse levels of granularity. Here we develop microestimates of the relative wealth and poverty of the populated surface of all 135 low- and middle-income countries (LMICs) at 2.4 km resolution. The estimates are built by applying machine-learning algorithms to vast and heterogeneous data from satellites, mobile phone networks, and topographic maps, as well as aggregated and deidentified connectivity data from Facebook. We train and calibrate the estimates using nationally representative household survey data from 56 LMICs and then validate their accuracy using four independent sources of household survey data from 18 countries. We also provide confidence intervals for each microestimate to facilitate responsible downstream use. These estimates are provided free for public use in the hope that they enable targeted policy response to the COVID-19 pandemic, provide the foundation for insights into the causes and consequences of economic development and growth, and promote responsible policymaking in support of sustainable development.

Many critical decisions require accurate, quantitative data on the local distribution of wealth and poverty. Governments and nonprofit organizations rely on such data to target humanitarian aid and design social protection systems (1, 2); businesses use this information to guide marketing and investment strategies (3); these data also provide the foundation for entire fields of basic and applied social science research (4).

Yet reliable economic data are expensive to collect, and only half of all countries have access to adequate data on poverty (5). In some cases, the data that do exist are subject to political capture and censorship (6, 7) and often cannot be disaggregated below the largest administrative level (8). The scarcity of quantitative data impedes policymakers and researchers interested in addressing global poverty and inequality and hinders the broad international coalition working toward the Sustainable Development Goals, in particular toward the first goal of ending poverty in all its forms everywhere (9).

To address these data gaps, researchers have developed approaches to construct poverty maps from nontraditional data. These include methods from small area statistics that combine household sample surveys with comprehensive census data (10), as well as more recent use of satellite “nightlights” (11–13), mobile phone data (14, 15), social media (16), high-resolution satellite imagery (17–21), or a combination of these (22, 23). But to date these efforts have focused on a single continent or a select set of countries, limiting their relevance to development objectives that require a global perspective.

Results

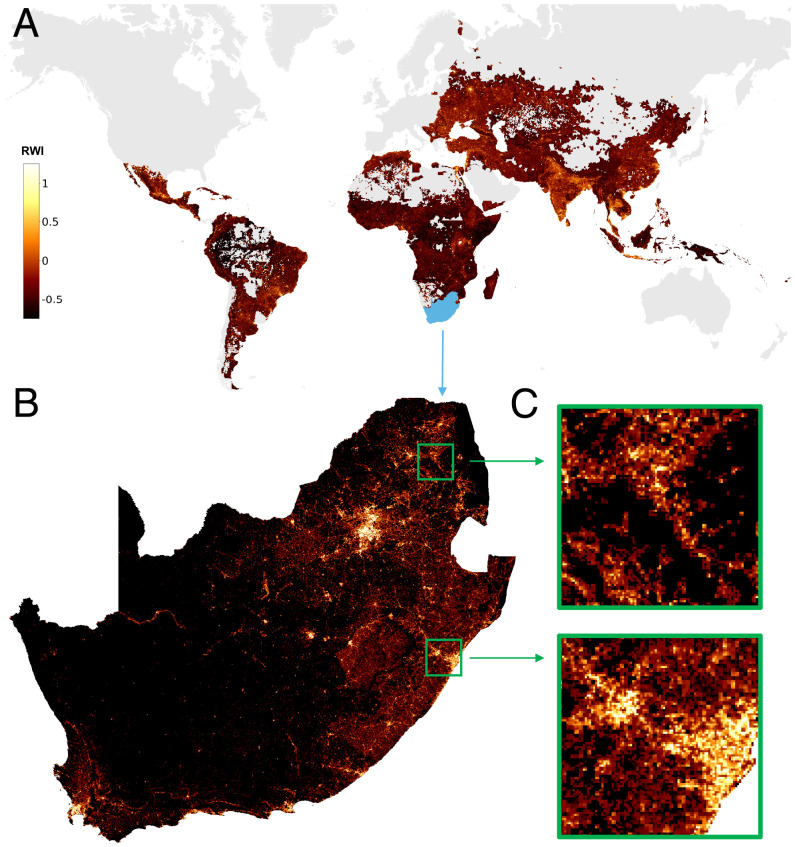
Here we develop an approach to construct microregional wealth estimates and use this method to create a complete set of microestimates of the distribution of poverty and wealth across all 135 low- and middle-income countries (LMICs) (Fig. 1A). We use this method to generate, for each of roughly 19.1 million unique 2.4-km microregions in all global LMICs, an estimate of the average absolute wealth (in dollars) and relative wealth (relative to others in the same country) of the people living in that region. These estimates, which are more granular and comprehensive than previous approaches, make it possible to see extremely local variation in wealth disparities (Fig. 1 B and C).

Fig. 1.

Microestimates of wealth for all low- and middle-income countries. (A) Estimates of the relative wealth of each populated 2.4-km gridded region of all 135 LMICs. Interactive version is available at http://www.povertymaps.net. (B and C) Enlargements show (B) the countries of South Africa and Lesotho and (C) the regions around Durban and Polokwane.

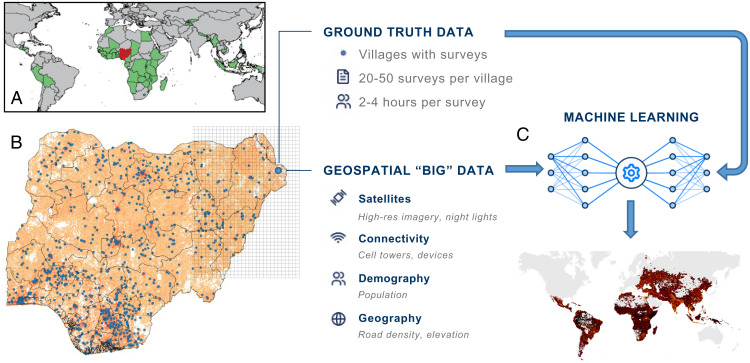
Our approach, outlined in Fig. 2, relies on “ground-truth” measurements of household wealth collected through traditional face-to-face surveys with 1,457,315 unique households living in 66,819 villages in 56 different LMICs around the world (SI Appendix, Table S1). These Demographic and Health Surveys (DHSs), which are independently funded by the US Agency for International Development, contain detailed questions about the economic circumstances of each household and make it possible to compute a standardized indicator of the average asset-based wealth of each village (Materials and Methods). We then use spatial markers in the survey data to link each village to a vast array of nontraditional digital data. This includes high-resolution satellite imagery, data from mobile phone networks, and topographic maps, as well as aggregated and deidentified connectivity data from Facebook (SI Appendix, Table S2). These data are processed using deep learning and other computational algorithms, which convert the raw data to a set of quantitative features of each village (SI Appendix, Fig. S2). We use these features to train a supervised machine-learning (ML) model that predicts the relative wealth (Fig. 1A) and absolute wealth (SI Appendix, Fig. S3A) of every populated 2.4-km grid cell in LMICs (Materials and Methods).

Fig. 2.

Overview of approach. (A) Nationally representative household survey data are obtained from 56 different countries around the world. (B) In Nigeria, for example, there are 40,680 households surveyed in 899 unique survey locations (“villages”). Geospatial “big” data from satellites and other existing sensors are also sourced from each location. (C) These data are used to train a machine-learning algorithm that predicts microregional poverty from nontraditional data, even in regions where no ground-truth data exists.

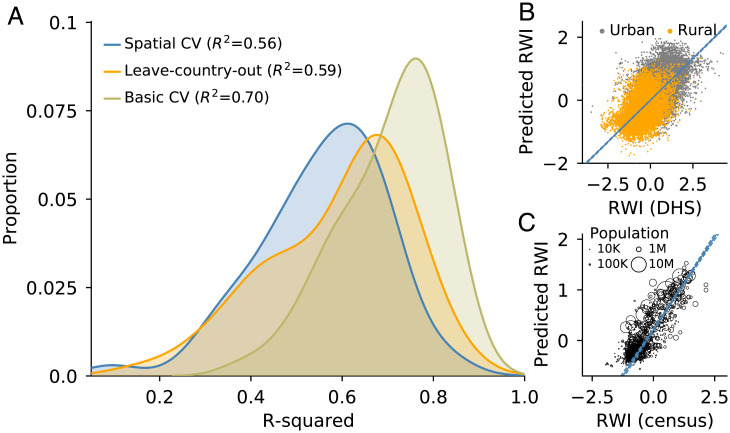
The estimates of wealth and poverty are quite accurate. Depending on the method used to evaluate performance, the model explains 56 to 70% of the actual variation in household-level wealth in LMICs (Fig. 3A). This performance compares favorably to state-of-the-art methods that focus on single countries or continents (Materials and Methods) (17, 21).

Fig. 3.

Model performance. (A) Distribution of model performance, across 56 countries with ground-truth data, using three different approaches to cross-validation. Average R² across 56 countries shown in parentheses. (B) Much of the model’s predictive power comes from being able to differentiate between rural and urban locations, but the model also detects wealth differentials within urban and rural locations. (C) The ML model explains 72% of the variation in wealth, as measured with independent census data from 15 LMICs. Population-weighted regression lines are in blue; 95% confidence intervals are shown with dashes.

To validate the accuracy of these estimates, and to eliminate the possibility that the ML model is “overfit” on the DHS surveys, we compare the model’s estimates to four independent sources of ground-truth data. The first test uses data from 15 LMICs that have collected and published census data since 2001 (SI Appendix, Table S3). These data contain census survey responses from 27 million unique individuals, including questions about the economic circumstances of each household. Importantly, the census data are independently collected and are never used to train the ML model. In each country, we aggregate the census data at the smallest administrative unit possible and calculate a “census wealth index” as the average wealth of households in that census unit. We separately aggregate the 2.4-km wealth estimates from the ML model to the same administrative unit. The ML model explains 72% of the variation in household wealth across the 979 census units formed by pooling data from the 15 censuses (Fig. 3C) and, on average, 86% of the variation in household wealth within each of the 15 countries (SI Appendix, Fig. S4).

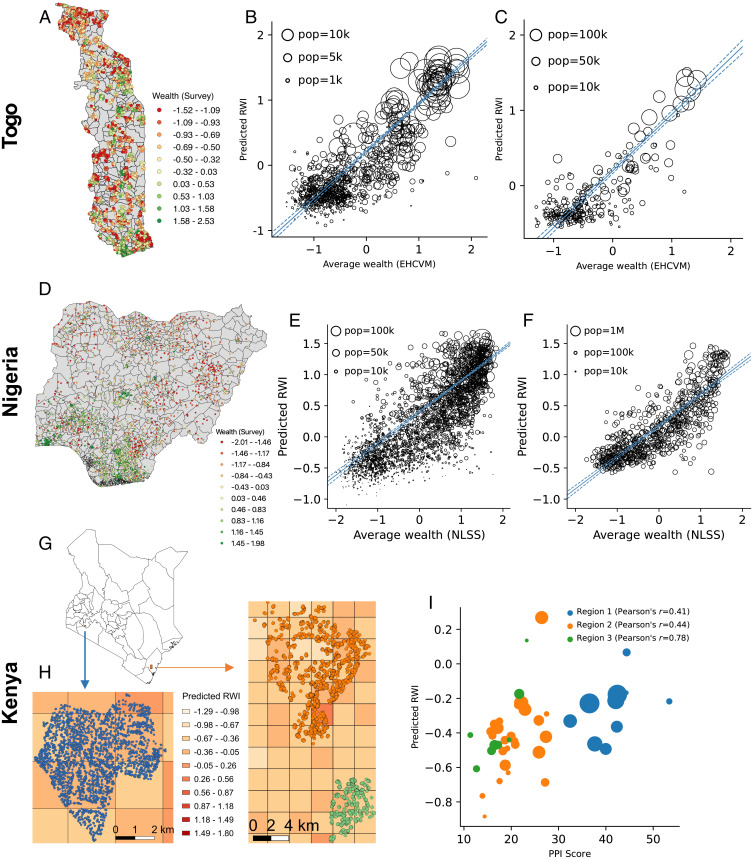
To test the accuracy of the model at the most granular level possible, we obtain three additional sources of survey data that link household wealth information to the exact geocoordinates of each surveyed household. The first dataset, collected by the government of the Togolese Republic (Togo) from 2018 to 2019, contains a nationally representative sample of 6,172 households located in 922 unique 2.4-km grid cells (Fig. 4A). We find that the ML model’s predictions explain 76% of the variation in wealth of these grid cells (Fig. 4B) and 84% of the variation in wealth of cantons, Togo’s smallest administrative unit (Fig. 4C). The second dataset, similar to the first one but independently collected by the government of Nigeria in 2019, contains a nationally representative sample of 22,104 households in 2,446 grid cells (Fig. 4D). We find that the ML estimates explain 50% of the variation in grid cell wealth (Fig. 4E) and 71% of the variation in wealth of local government areas (Fig. 4F).

Fig. 4.

Validation with independently collected microdata in Togo, Nigeria, and Kenya. (A) Map of Togo showing locations of surveyed households (jitter added to map to preserve household privacy). (B) Scatterplot of the predicted RWI of each grid cell against the average wealth of the grid cell, as reported in a nationally representative government survey. Points are sized by population. Population-weighted regression lines are in blue; 95% confidence intervals are shown with dashes. (C) Scatterplot of predicted RWI against average wealth of each canton, the smallest administrative unit in Togo. (D) Map of surveyed households in Nigeria (jitter added). (E) Scatterplot of predicted RWI against average wealth of each grid cell. (F) Scatterplot of predicted RWI against average wealth of each local government area (LGA). (G) Map of Kenya showing the regions surveyed by GiveDirectly. (H) Enlargement of the three survey regions, showing the location of each of 5,703 surveyed households. Colors of background grid cells indicate RWI predicted from the ML model. In both enlargements, the width of the grid cell is 2.4 km. (I) Scatterplot of the predicted RWI of each grid cell (y axis) against the average PPI of all surveyed households in the grid cell (x axis). Points are sized by the number of households in the grid cell and colored by region.

We further validate the grid-level predictions using a dataset collected by GiveDirectly, a nonprofit organization that provides humanitarian aid to poor households. In 2018, GiveDirectly surveyed 5,703 households in two counties in Kenya (Fig. 4G), recording a poverty probability index as well as the exact geocoordinates of each household (Fig. 4H). Using these data, we show that even within small rural villages, the ML model’s predictions correlate with GiveDirectly’s estimates of poverty and wealth (Fig. 4I; Pearson’s ρ between 0.41 and 0.78).

In addition to providing point estimates of the average wealth of the households in each grid cell, we calculate estimates of the expected error of each grid cell (SI Appendix, Fig. S3B). These are obtained by using a linear regression to predict the absolute value of the residuals (i.e., the model error) from the wealth prediction model, as a function of observable characteristics of each location (see Materials and Methods for details of this procedure and additional analysis of model error). While this linear regression has limited explanatory power (average $R^2=0.09$ using spatially stratified cross-validation; SI Appendix, Fig. S16A), it is evident that prediction errors are larger in regions that are far from areas covered by the DHS data (SI Appendix, Table S4). While measures of uncertainty are not common in prior work on subregional wealth estimation, we believe this is an important step to help promote the responsible use of such estimates in research and policy settings (24).

While our primary focus is on constructing, validating, and disseminating this resource, the process of building this dataset produces several insights relevant to the construction of high-resolution poverty maps. For instance, we find that different sources of input data complement each other in improving predictive performance (22, 23). While prior work has focused heavily on satellite imagery, we find that models trained only on satellite data do not perform as well as models that include other input data (SI Appendix, Fig. S7A). In particular, information on mobile connectivity is highly predictive of subregional wealth, with 5 of the 10 most important features in the model related to connectivity (SI Appendix, Fig. S2).

The global scale of our analysis also reveals intuitive patterns in the geographic generalizability of machine-learning models (17, 25, 26). We find that models trained using data in one country are most accurate when applied to neighboring countries (SI Appendix, Fig. S6). Models also perform better in countries when trained on countries with similar observable characteristics (SI Appendix, Fig. S14). And while much of the model’s performance derives from being able to differentiate between urban and rural areas, the model can differentiate variation in wealth within these regions as well (Fig. 3B).

We are making these microregional estimates of wealth and poverty, along with the associated confidence intervals, freely available for public use and analysis (27). These estimates are provided through an open and interactive data interface that allows scientists and policymakers to explore and download the data (SI Appendix, Fig. S1; available online at http://www.povertymaps.net).

Discussion

How might these estimates be used to guide real-world policy-making decisions? One key application is in the targeting of social assistance and humanitarian aid. In the months following the onset of the COVID-19 pandemic, hundreds of new social protection programs were launched in LMICs, and in each case, program administrators faced difficult decisions about whom to prioritize for assistance (28). This is because in many LMICs, planners do not have comprehensive data on the income or consumption of individual households (29). Our microestimates provide one potential solution.

In simulations, we find that geographic targeting using our microestimates allocates a higher share of benefits to the poor (and a lower share of benefits to the nonpoor) than geographic targeting approaches based on recent nationally representative household survey data (see Table 1 and Materials and Methods for targeting simulations). This is because the microestimates make it possible to target smaller geographic regions than would be possible with traditional survey data—a finding that is consistent with prior work that suggests that more granular targeting can produce large gains in welfare (2, 30, 31). For instance, the most recent DHS in Nigeria surveyed households in only 13.8% of all Nigerian wards (the smallest administrative unit in the country); by contrast, the microestimates cover 100% of wards. In Togo, existing government surveys provide poverty estimates that are only representative at the regional level (of which there are only five); we provide estimates for 9,770 distinct tiles.

Table 1.

Targeting simulations in Togo and Nigeria

	1)	2)	3)	4)	5)
	No. of spatial units	No. of units with estimates	$R^2$	Targeting accuracy, poorest 25%	Targeting accuracy poorest 50%
Togo
A) High-resolution estimates
Tile targeting	10,187	10,187	0.60	0.73	0.79
Canton targeting	387	387	0.56	0.73	0.77
B) Imputation based on DHS data
Prefecture targeting	40	40	0.49	0.70	0.70
Canton targeting	387	185	0.52	0.76	0.80
Nigeria
C) High-resolution estimates
Tile targeting	159,147	159,147	0.53	0.79	0.79
Ward targeting	8,808	8,808	0.51	0.78	0.78
D) Imputation based on DHS data
State targeting	37	37	0.37	0.75	0.74
LGA targeting	774	631	0.47	0.78	0.76
Ward targeting	8,808	1,218	0.54	0.83	0.79

A and C simulate the performance of antipoverty programs that geographically target households using the ML estimates of tile wealth, under scenarios where the program is implemented at the tile level (first row) or smallest administrative unit in the country (second row). B and D simulate geographic targeting based on the most recent DHS survey, using administrative units of different sizes. For B and D, when an admin-unit has no surveyed households, the wealth of the unit is imputed based on the wealth of the geographic unit closest to the household. Column 1 indicates the number of units in the country; column 2 indicates the number of units where data exist—see also SI Appendix, Fig. S19 for maps highlighting the regions in Togo and Nigeria that were surveyed in the most recent DHS. Column 3 indicates the R² from a weighted least-squares regression, at the household level, of the ground-truth wealth of each household (from the EHCVM or NLSS) and the estimate of the wealth of the spatial unit in which that household is located, weighted using the EHCVM or NLSS household weight. Columns 4 and 5 assume that the government has a fixed budget, sufficient to cover 25% (column 4) or 50% (column 5) of the population, and provides benefits to all households in the poorest administrative units; we then report the accuracy at targeting the 25% or 50% of the poorest households (in the EHCVM or NLSS).

Based on the strength of these results, the Government of Nigeria is using these estimates as the basis for social protection programs that are providing benefits to millions of poor families (32). Likewise, the Government of Togo is using these estimates to target mobile money transfers to hundreds of thousands of the country’s poorest mobile subscribers (33). These examples highlight how the ML estimates can improve targeting performance even in countries with robust national statistical offices, like Nigeria and Togo. In the large number of LMICs that have not conducted a recent nationally representative household survey, these microestimates create an option for geographic targeting that would otherwise not exist.

The standardized procedure through which these estimates are produced may also be attractive in contexts where political economy considerations might lead to systematic misreporting of data (7) or influence whether new data are collected at all (6). However, this does not imply the ML estimates are apolitical, as maps have a historical tendency to perpetuate existing relations of power (34). One particular concern is that the technology used to construct these estimates may not be transparent to the average user; if not produced or validated by independent bodies, such opacity might create alternative mechanisms for manipulation and misreporting.

Our hope is that these methods and maps can provide an additional set of tools to study economic development and growth, guide interventions, monitor and evaluate policies, and track the elimination of poverty worldwide.

Materials and Methods

Ground-Truth Wealth Measurements.

The ground-truth wealth data used to train the predictive models are derived from household surveys conducted by the Demographic and Health Survey (DHS) Program. The DHS collects “nationally representative household surveys that provide data for a wide range of monitoring and impact evaluation indicators in the areas of population, health, and nutrition” (35). We elected to train our model exclusively on DHS data because it is the most comprehensive single source of publicly available, internationally standardized wealth data that provides household-level wealth estimates with subregional geomarkers.

We use the DHS “relative wealth index” as our ground-truth measure of wealth and poverty. This means that our machine-learning algorithms are being trained to reconstruct a specific, asset-based relative wealth index—albeit at a much finer spatial resolution and in areas where DHSs did not occur. This is because we believe the DHS version of a relative wealth index is the best publicly available instrument for consistently measuring wealth across a large number of LMICs. However, it posits a specific, asset-based definition of wealth that does not necessarily capture a broader notion of human development. More broadly, a rich social science literature debates the appropriateness of different measures of human welfare and wellbeing (4, 36). Our decision to focus on estimating asset-based wealth, rather than a different measure of socioeconomic status, was motivated by several considerations. First, in developing economies, where large portions of the population do not earn formal wages, measures of income are notoriously unreliable. Instead, researchers and policymakers rely on asset-based wealth indexes or measures of consumption expenditures. Between these two, wealth is much less time consuming to record in a survey; as a result, wealth data are more commonly collected in a standardized format for a large number of countries (37).

We obtain the most recent publicly available DHS survey data from 56 countries (SI Appendix, Table S1). The criteria for inclusion are that the data are available for download through the DHS website (as of March 2020), the data contain asset/wealth information and subregional geomarkers, and the most recent survey was conducted since 2000. The combined dataset contains the survey responses from 1,457,315 household surveys taken across Africa, Asia, Europe, and Latin America. Each individual household survey lasts several hours and contains several questions related to the socioeconomic status of the household. We focus on a standardized set of questions about assets and housing characteristics (electricity in household, telephone, automobile, motorcycle, refrigerator, TV, radio, water supply, cooking fuel, trash disposal, toilet, floor material, wall material, roof material, and rooms in house). From the responses to these questions, and following standard practice (8, 38), the DHS calculates a single continuous measure of relative household wealth, the relative wealth index (RWI), by taking the first principal component of these 15 questions. It is this DHS-computed RWI that we rely upon as a ground-truth measure of wealth.

As noted in the DHS documentation, the DHS relative wealth index “is constructed as a relative index within each country at the time of the survey. Each wealth index has a mean value of zero and a standard deviation of one. Thus, specific scores cannot be directly compared across countries or over time” (39). In our analysis, we similarly standardize the satellite imagery and other input data within each country, to have a mean value of zero and a SD of one. Thus, our supervised-learning models recover how relative values of input data (relative to other locations in that country) correlate with relative values of wealth (also relative to other locations in that country).

In addition to providing measures of wealth for each household, the DHS indicates the cluster in which each household is located. The 1.5 million households are associated with 66,819 unique clusters, where a cluster is roughly equivalent to a village in rural areas and a neighborhood in urban areas. We calculate the average wealth of each “village” cluster by taking the mean RWI of all surveyed households in that cluster.* This village-level average RWI is the target variable for the machine-learning model.

Input Data.

The prediction algorithms rely on data from several different sources (SI Appendix, Table S2). To facilitate downstream analysis, all data are converted into features that are aggregated at the level of a 2.4-km grid cell. We use 2.4-km cells because that is the highest resolution at which many of our input data are available, and it is best suited to the spatial merge with the survey data (see Supervised Machine Learning below). We were also concerned that providing estimates of wealth at even smaller grid cells might compromise the privacy of individual households. Thus, if the native resolution of a data source is higher than 2.4 km, we aggregate the smaller cells to the 2.4-km level by taking the average of the smaller cells.

The features input into the model indicate, for each cell, properties such as the average road density, the average elevation, and the average annual precipitation. Several features related to telecommunications connectivity are obtained from Facebook, which uses proprietary methods to estimate the availability and use of telecommunications infrastructure from deidentified Facebook usage data.^† All estimates are regionally aggregated at the 2.4-km level to preserve individual privacy. We use estimates of the number of mobile cellular towers in each grid cell, as well as the number of WiFi access points and the number of mobile devices of different types. These measures are based on the infrastructure used by Facebook users, so may not be representative of the full population. To the extent that these features are predictive of regional wealth (which they are), no deeper inference or causal interpretation should be drawn from the empirical association. Rather, these patterns simply indicate that the regional distribution of wealth is correlated with these nonrepresentative measures of telecommunications use.

Since the raw satellite imagery is extremely high dimensional, we use unsupervised-learning algorithms to compress the raw data into a set of 100 features. Specifically, following Jean et al. (17), we use a pretrained, 50-layer convolutional neural network (CNN) to convert each 256 × 256-pixel image into 2,048 features and then extract the first 100 principal components of these 2,048-dimensional vectors.^‡ These 100 components explain 97% of the variance of the 2,048 features (SI Appendix, Fig. S9).

All input features are normalized by subtracting the country-specific mean and dividing by the country-specific SD.

Spatial Join.

We match the ground-truth wealth data to the input data using spatial information present in both datasets. The 2.4-km grid cells are defined by absolute latitude and longitude coordinates specified by the Bing tile system.^§ The DHS data include approximate information about the global positioning system (GPS) coordinate of the centroid of each of the 66,819 villages. However, the exact geocoordinates are masked by the DHS program with up to 2 km of jitter in urban areas and up to 5 km of jitter in rural areas.

To ensure that the input data associated with each village cover the village’s true location, we include a 2 × 2 grid of 2.4-km cells around the centroid in urban areas and a 4 × 4 grid in rural areas. For each village, we then take the population-weighted average of the 112-dimensional feature vectors across a 2 × 2 or a 4 × 4 set of cells, using existing estimates of the population of 2.4-km grid cells (42). This leaves us with a training set of 66,819 villages with wealth labels (calculated from the ground-truth data) and 112-dimensional feature vectors (computed from the input data).

Supervised Machine Learning.

We use machine-learning algorithms to predict the average RWI of each village from the 112 features associated with that village. We do not perform ex ante feature selection prior to fitting the model. We use a gradient-boosted regression tree, a popular and flexible supervised-learning algorithm, to map the inputs to the response variable. To tune the hyperparameters of the gradient-boosted tree, we use three different approaches to cross-validation:^¶

• •K-fold cross-validation (labeled “basic CV” in Fig. 3A). For each country, the labeled data are pooled and then randomly partitioned into k = 5 equal subsets. A model is trained on all but one subset and tested on the held-out subset. The process is repeated k times and we report average held-out performance for that country. This approach to cross-validation is used most frequently in prior work, but can substantially overestimate performance (43). This bias arises because both the input (e.g., satellite) and response (RWI) data are spatially autocorrelated, leaving the training and test data not independent and identically distributed (44).^#
• •Leave-one-country-out cross-validation (“leave-country-out”). For each country, a model is trained using the pooled data from all other 55 countries; the test performance is evaluated on the held-out country (21).
• •Spatially stratified cross-validation (“spatial CV”). This method ensures that training and test data are sampled from geographically distinct regions (43, 44). In each country, we select a random cell as the training centroid and then define the training dataset as the nearest $(k-1)/k$ percent of cells to that centroid. The remaining $1/k$ cells from that country form the test dataset. This procedure is repeated k = 10 times in each country.

Fig. 3A compares the performance of these three methods, by showing the distribution of R² values for each approach to cross-validation (the distribution is formed from 56 countries, where a separate model is trained and cross-validated in each country). The difference in R² resulting from different approaches to cross-validation highlights the potential upward bias in performance that results from spatial autocorrelation in training and test data. By comparison, recent work on wealth prediction in Africa found that a mixture of remote sensing and nightlight imagery explains on average 67% of the variation in wealth (21). That benchmark was based on an approach similar to the “leave-country-out” method shown in Fig. 3A, evaluated on a more homogenous set of 23 African nations. When we restrict our analysis to the same 23 countries evaluated by ref. 21, our model explains 71% of the variation in ground-truth wealth, using leave-country-out cross-validation (SI Appendix, Fig. S8).

Unless noted otherwise, all analysis in this paper uses models based on spatially stratified cross-validation. While this has the effect of lowering the R² values that we report, we believe it is the most conservative and appropriate method for training machine-learning models on geographic data with spatial autocorrelation.

Feature Importance.

To explore which input data are driving the model’s predictions, SI Appendix, Fig. S2 provides two different indicators of feature importance. SI Appendix, Fig. S2 A, Left indicates the unconditional correlation between the true wealth label and each individual feature, calculated as the R² from a univariate regression of the wealth label on each single feature (each row is a separate regression; with 56 countries, there are 56 R² values that form the distribution of each boxplot). SI Appendix, Fig. S2 B, Right indicates the model gain, which provides an indication of the relative contribution of each feature to the final model (specifically, it is the average gain across all splits in the random forest that use that feature) (45). In general, we find that data related to connectivity, such as the number of cell towers and mobile devices in a region, are the most predictive features; nightlight radiance and population density are also predictive. While no single feature derived from satellite imagery is especially predictive in isolation, the large number of satellite features collectively contributes to model accuracy—this can be seen most directly in SI Appendix, Fig. S7A, which compares the predictive performance of models with and without satellite imagery.

Out-of-Sample Estimates.

To produce the final maps and microestimates, as well as the public dataset, we pool data from all 56 countries and train a single model using spatially stratified cross-validation to tune the model parameters.^ǁ This model maps 112-dimensional feature vectors to wealth estimates. We then pass the 112-dimensional feature vector for each 2.4-km grid cell located in a LMIC through this trained model to produce an estimate of the relative wealth (RWI) of each grid cell (Fig. 1). We use the World Bank’s List of Country and Lending Groups to define the set of 135 low- and middle-income countries.** Since we do not normalize these predictions at the country level after they have been generated, we do not expect that each country will have the same within-country RWI distribution.

The 2.4-km grid cell estimates are more granular than the data that were used to train and cross-validate the model, which used 2 × 2 or 4 × 4 grids of 2.4-km cells to account for the jitter in the DHS data. It is possible to generate these 2.4-km estimates because that is the native resolution of much of the input data, so it is possible to construct input vectors for each 2.4-km grid cell. However, it is possible that performance at this finer resolution would be different from the performance that is cross-validated at coarser resolution. We cannot test this possibility with the DHS data; however, subsequent validation of the 2.4-km estimates using microdata with actual GPS coordinates suggests that, at least in the three countries we can check, the accuracy of the 2.4-km estimates is similar to that of the 2 × 2 and 4 × 4 grids tested through cross-validation.

To help preserve the privacy of individuals and households, we do not display wealth estimates for 2.4-km regions where existing population layers indicate the presence of 10 or fewer individuals in the region (42). Instead, we aggregate neighboring 2.4-km tiles (by taking the population-weighted average RWI) until the total estimated population of the larger area is at least 10. The “neighbors” of a tile are those tiles that fall within the larger tile, using the tile boundaries defined by the Bing tile system (the 2.4-km estimates correspond to Bing tile level 14; the next largest tile, Bing tile level 13, defines 4.8-km grid cells, and so forth). All of the neighboring 2.4-km cells in the larger tile are then assigned the same estimate of RWI (i.e., the population-weighted average).

Cross-Sectional Estimation.

Our main objective is to produce accurate estimates of the current, cross-sectional distribution of wealth and poverty within LMICs. In training the machine-learning model described above, we thus use the most recently available version of each data source. The ground-truth wealth measurements cover a wide range of years (SI Appendix, Table S1); the input data are primarily generated in 2018 (SI Appendix, Table S2). This often creates a mismatch between the dates of the input variables and the survey labels for a given region. In practice, this means that our estimates are best at capturing within-country variation in wealth that does not change over a relatively short time horizon (i.e., between the prior survey date and 2018). Analysis of DHS data from LMICs with multiple surveys suggests a high degree of persistence in the within-country variation in wealth (SI Appendix, Fig. S12). For instance, across the 33 countries with two or more DHS surveys conducted since 2000, the median R² between regional Administrative Level 2 (admin-2) wealth estimates from the most recent DHS survey and the preceding DHS survey is 0.81. Still, this approximation likely introduces error into our model and suggests that these estimates are better suited toward applications that require a measure of permanent income than to applications that require an understanding of poverty dynamics. More broadly, we see this model’s performance as a benchmark that can be improved upon as more input and survey data become available.

Ideally, we would obtain historical input data from the same years in which each survey was conducted. Unfortunately, historical versions of most of the input data in SI Appendix, Table S2 do not exist. Alternatively, we could restrict our analysis to input data that do exist in a historical panel. However, as shown in SI Appendix, Fig. S7A, excluding key predictors substantially limits the model’s predictive accuracy. Another option would be to train the model using only more recent surveys. In SI Appendix, Fig. S10A, we observe that the accuracy of a model trained on the subset of 24 countries that conducted DHS surveys since 2015 is similar to the performance of a model trained on all 56 countries with DHS data since 2000. Related, when we validate the model’s performance using independently collected census data (Independent Validation with Census Data), we find no evidence to suggest that a shorter gap between the date of the DHS training data and the date of the census increases the predictive accuracy of the model (SI Appendix, Fig. S11).

Independent Validation with Census Data.

We validate the accuracy of the ML estimates using census data that are collected independently from the DHS data used to train the models. Specifically, we obtain census data from all countries with public IPUMS-I data, where the census occurred since 2000 and where asset data are complete (46). In total, these data cover 15 countries on three continents and capture the survey responses of 27 million individuals (SI Appendix, Table S3). We assign each of these individuals a census wealth index by taking the first principal component of the 13 assets present in the census data. This list is similar to the DHS asset list, but excludes data on motorcycles and rooms in the household. As with the DHS data, the principal component analysis (PCA) eigenvectors are computed separately for each country. Finally, we compute the average census wealth index over all households within each second administrative unit, the smallest unit that is consistently available across countries. Of the 1,003 census units, 979 have households with wealth information and also contain a 2.4-km tile with a centroid inside the unit.

Fig. 3C shows a scatterplot of these 979 administrative units, sized by population. The x axis indicates the average wealth of each administrative unit, according to the census (calculated as the mean first principal component across all households in the unit). The y axis indicates the average predicted RWI of the administrative unit, calculated by taking the population-weighted mean RWI of all grid cells within the unit. The population-weighted regression line R² = 0.72 (obtained when pooling the 979 admin-2 regions from all 15 countries). SI Appendix, Fig. S4 disaggregates Fig. 3C by country, showing the relationship between census-based wealth and RWI across the administrative units of each country. The average population-weighted R² across the 15 countries is 0.86 (SI Appendix, Table S3).

High-Resolution Validation with Independently Collected Microdata from Togo, Nigeria, and Kenya.

We further validate the accuracy of the ML estimates at the finest possible spatial resolution by comparing them to three independently collected household surveys in Togo, Nigeria, and Kenya. In each case, we obtain the original survey data for all households, as well as the exact GPS coordinates of each surveyed household. As with the census data, none of these datasets were used to train the ML model; they thus provide an independent and objective assessment of the accuracy and validity of our new estimates.

Togo.

As part of the 2018 to 2019 Enquete Harmonizee sur les Conditions de Vie des Menages (EHCVM), the government of Togo conducted a nationally representative household survey with 6,172 households.^†† A key advantage of these data is that, in addition to observing a wealth index for each household (calculated as the first principal component of roughly 20 asset-related questions), we observe each household’s exact geocoordinates (Fig. 4A). The 6,172 households are located in 922 unique 2.4-km grid cells (which correspond to 260 unique cantons, the smallest administrative unit in Togo), of the 9,770 total grid cells in the country. We also note that there is nothing Togo specific in how the ML model is trained: We simply use the estimates generated by the final model that is trained using spatially stratified cross-validation from all 56 countries with DHS data (Fig. 1).

Fig. 4A shows the approximate location of each of the households surveyed in the EHCVM. Fig. 4B compares, for each of the 922 grid cells with surveyed households, the average wealth of all households in each grid cell as calculated from the EHCVM (x axis) to the estimated RWI of the grid cell, which is displayed on the y axis (R² = 0.76). Fig. 4C presents an analogous analysis for each of the 260 cantons in Togo, where the x axis indicates the average EHCVM wealth of all households in the canton and the y axis indicates the average RWI for each canton, calculated as population-weighted mean of all cells within the canton (R² = 0.84).

Nigeria.

During the 2018 to 2019 Nigerian Living Standards Survey (NLSS), Nigeria’s National Bureau of Statistics, in collaboration with the World Bank, conducted a nationally representative household survey with 22,104 households (Fig. 4D). The survey excluded Borno State due to security concerns (see https://www.nigerianstat.gov.ng/nada/index.php/catalog/64). Like the EHCVM in Togo, the NLSS in Nigeria contains a wealth index for each household and each household’s exact geocoordinates. The 22,104 households are located in 2,446 unique 2.4-km grid cells. We compare the NLSS microdata, which were never used to train the model, to the final estimates of the ML model.

Fig. 4D shows the approximate location of each of the households surveyed in the NLSS. Fig. 4E compares, for each of the 2,446 grid cells with surveyed households, the average wealth of all households in the grid cell as calculated from the NLSS to the estimated RWI of the grid cell (R² = 0.50). Fig. 4F presents an analogous analysis for each of Nigeria’s 774 Local Government Areas (R² = 0.71).

Kenya.

We also validate the accuracy of the grid-cell RWI estimates using GPS-enabled survey data collected in the Kenyan counties of Kilifi and Bomet (Fig. 4G). These data were collected by GiveDirectly, a nonprofit organization that provides unconditional cash transfers to poor households. When GiveDirectly works in a village, they typically conduct a socioeconomic survey with every household in the village. The survey includes a standardized set of 10 questions that form the basis for a poverty probability index (PPI) (https://www.povertyindex.org/country/kenya), which GiveDirectly uses to determine which households are eligible to receive cash transfers. GiveDirectly also records the exact geocoordinates of each household that they survey (Fig. 4G).

Fig. 4I compares estimates of microregional wealth based on GiveDirectly’s household PPI census to estimates of wealth based on the ML model. We calculate the average PPI score of each 2.4-km grid cell by taking the mean of the PPI scores of all households in the grid cell. We compare this to the predicted RWI from the ML model. Across the 44 grid cells shown in Fig. 4H (10 from region 1, 26 from region 2, and 8 from region 3), the predicted RWI explains 21% of the variation in PPI (Pearson’s r = 0.46). Within each region, the correlation between PPI and RWI ranges from 0.41 to 0.78.

While the ML model explains less of the variation in Kenya than it does in Togo, Nigeria, or the 15 census countries, this is a much more stringent test. This is because the comparison is being done across 44 spatially proximate units (Fig. 4H) in three small and relatively homogenous villages. Within these villages, there is less variation in wealth than there is across an entire country (the variance in RWI across the 44 cells is 0.05; across all of Kenya the variance is 0.10). Our other tests—and indeed all prior work of which we are aware—measure R² across entire countries. The Kenya test is also handicapped by the fact that the Kenyan PPI is not strictly a wealth index, containing questions about education, consumption, and housing materials. Measures of wealth and poverty are quite sensitive to the measurement instrument used. For instance, Filmer and Pritchett (37) find that, even within a single survey, the Spearman rank correlation between an asset index and a measure of consumption expenditures ranges from 0.43 (in Pakistan) to 0.64 (in Nepal). The analysis in Fig. 4I compares estimates of microregional wealth, based on variation within single villages, to independently collected household survey data where the exact location of each surveyed household is known. We therefore find it encouraging that the predicted RWI roughly separates wealthier from poorer neighborhoods within these small regions.

Model Accuracy in High-Income Nations.

The primary intent of the model is to produce estimates of wealth in LMICs, and it is from LMICs that we source all of the ground-truth data used to train the model. For completeness, we assess the performance of the model’s predictions in high-income nations. This comparison is imperfect, because high-income nations do not typically collect asset-based wealth indexes, which is what the ML model is trained to estimate. Instead, we compare the absolute wealth estimates (AWEs) of the ML model (see below for details on how these are constructed) to independently produced data on regional gross domestic product per capita (GDPpc) from 30 member nations of the Organization for Economic Cooperation and Development (OECD). These data are collected by the National Statistical Offices of each respective country, through the network of delegates participating in the Working Party on Territorial Indicators.^‡‡

In each country, we obtain the OECD’s estimate of the average GDPpc of each “small” Territorial Level (TL)3 region.^§§ We separately calculate the AWE of each region by taking the population-weighted average AWE of all 2.4-km grid cells in the region. SI Appendix, Fig. S5A shows a scatterplot of these 1,540 administrative units, sized by population, where the x axis indicates the OECD-based measure of wealth of the administrative unit and the y axis indicates the population-weighted average predicted AWE of the administrative unit. SI Appendix, Fig. S5B shows the accuracy of the model in each of the 30 countries. The average population-weighted R² across the 30 countries is 0.50; the population-weighted regression line R² = 0.59 (obtained when pooling the 1,540 regions from all 30 countries). We note that the AWE values are generally larger than the OECD estimates of GDPpc (the slope of the regression line in SI Appendix, Fig. S5A is 1.35). This is likely due to the fact that the GDPpc estimates used to construct the AWE (sourced from the World Bank) are consistently higher than the GDPpc estimates sourced from the OECD. This comparison is made in SI Appendix, Fig. S5C, where we compare, for the 30 OECD nations, the relationship between the World Bank estimate of GDPpc and the average regional GDPpc based on OECD data (the slope of the regression line in SI Appendix, Fig. S5C is 1.66).

Estimates of Model Error.

In many applied settings, it is important to have not just a point estimate of the wealth of a particular location, but also an understanding of the uncertainty associated with each point estimate. We are encouraged by the fact that we do not find evidence that the model performs any worse in poorer regions (SI Appendix, Fig. S13), as occurs with nightlights data (17).

Disaggregating this error, we find that model error is lower when the target country is near many countries with ground-truth data used to train the model and when there are many training observations nearby. This can be seen in SI Appendix, Table S4, where we estimate the error of each individual 2.4-km location l by fitting a linear regression of the absolute value of the model’s residual at l (in the locations with ground-truth data) on observable characteristics of l. We selected a broad set of observable characteristics that include all of the features used in the predictive model (with the exception of the imagery-based features), how much ground-truth training data were available near the spatial unit (such as the distance to the nearest DHS cluster), and country-level characteristics (such as average GDP per capita and continent dummy variables). We then regress the absolute model error, in RWI units, of grid cell l on l’s vector of observable characteristics. We show the correlates of model error in SI Appendix, Table S4, column 1.

To better understand the sensitivity of these error estimates, we reestimate the results in column 1 of SI Appendix, Table S4 using different subsets of available predictors. Columns 2 and 3 of SI Appendix, Table S4 indicate that while the point estimates β depend somewhat on the other variables included in the regression, the qualitative patterns are the same. More importantly, we observe that the actual error estimates (for any given location l) are not very sensitive to the variables included in the model. For instance, SI Appendix, Fig. S15 compares the error predicted by the model in column 1 of (x axis) against the error predicted by the two alternative specifications in columns 2 and 3 of SI Appendix, Table S4. SI Appendix, Fig. S15A shows the correlation between the median error of a country under the original specification and the median error of a country using a different specification that also includes the 100 satellite imagery features as predictors (r = 0.770). SI Appendix, Fig. S15B shows the correlation between the median country error under the original model and a model that includes only the set of features that were not used to estimate RWI (r = 0.773).

More broadly, SI Appendix, Figs. S6 and S14 indicate that models trained with data from a single country perform best when applied to countries with similar characteristics. To construct SI Appendix, Fig. S14, we calculate the cosine similarity between all pairs of countries based on the country-level attributes listed in SI Appendix, Table S4. (i.e., area, population, island, landlocked, distance to the closest country with DHS, number of neighboring countries with DHS, GDP per capita, and Gini coefficient). We then show, for different thresholds of dissimilarity d, the average test error across all countries c when the model is trained on countries at least d dissimilar to c. For instance, when d = 0.1, the model for each country c is trained only on countries at least distance 0.1 from c.

An advantage of modeling error with a linear regression is that the resulting coefficients can be readily interpreted, as we have done above. It is possible, however, that such a simple model might not predict model error as well as a more flexible nonlinear model. For this reason, we test a machine-learning approach to predicting the absolute residuals from the wealth prediction model. In particular, SI Appendix, Fig. S16 shows the results from using three different methods for cross-validation to predict the absolute value of the model’s residual at location l. SI Appendix, Fig. S16A shows the distribution of R² values across the 56 DHS countries, using a linear regression with all of the regressors shown in SI Appendix, Table S4, column 1. SI Appendix, Fig. S16B shows the results obtained when a gradient-boosted regression tree is used instead. SI Appendix, Fig. S17 indicates the feature importances for the gradient-boosting model of prediction error.

We observe little difference in the predictive accuracy of the linear model and gradient-boosted decision tree. We also make this comparison more directly in SI Appendix, Fig. S15C, which plots the median error of the linear model for each country (x axis) against the median error of the gradient-boosting model for the same country (r = 0.541). More generally, this analysis indicates that it is more difficult to predict model error than it is to predict ground-truth wealth. This is expected, since model error is itself based on the residual of a predictive model; unless that original model was misspecified, its residuals should be hard to predict.

Our objective in constructing the microestimates of model error is to provide policymakers and other users with a sense of where the model is accurate and where it is not. Thus, SI Appendix, Fig. S3B provides a granular map of expected model error produced using the linear model described in SI Appendix, Table S4, column 1. The raw data used to produce SI Appendix, Fig. S3B are available for download from http://www.povertymaps.net. We also provide country-level summary statistics of model error in SI Appendix, Table S5 (i.e., the mean, median, and SD of estimated model error in each country), to provide policymakers in specific countries with at-a-glance estimates of model performance.

Absolute Wealth Estimates.

The predictive models are trained to estimate the RWI of each 2.4-km grid cell. The RWI indicates the wealth of that location relative to other locations within the same country. However, certain practical applications require a measure of the absolute wealth of a region that can be more directly compared from one country to another.

To provide a rough estimate of the absolute per capita wealth of each grid cell, we use the technique proposed by Hruschka et al. (47) to convert a country’s relative wealth distribution to a distribution of per-capita GDP. This method relies on three parameters to define the shape of the wealth distribution: the mean GDP per capita, as a measure of the central tendency (GDP_c); the Gini coefficient, as a measure of dispersion (Gini_c); and a combination of the Pareto and log-normal distributions that are used to estimate skewness. Specifically, our AWE of a grid cell i in country c is defined by

$$AW{E}_{ic}=\mathit{ran}{k}_{ic}*\frac{GD{P}_c}{\frac{1}{n}{\displaystyle \sum _{j}I}CD{F}_c(\mathit{ran}{k}_j)},$$

where rank_ic is the rank of each grid cell’s RWI (relative to other cells in c), GDP_c is the mean wealth per capita of c, and ICDF_c is the inverse cumulative distribution of wealth, which is parameterized exactly following Hruschka et al. (47).^¶¶ We collect indicators of each country’s Gini coefficient and mean per capita GDP from the sources listed in SI Appendix, Table S6, and use it to produce the AWEs shown in SI Appendix, Fig. S3A.

This conversion requires strong parametric assumptions about the national distribution of wealth based on information about the average wealth and wealth inequality in each country. These assumptions are not justified in many countries, particularly where Gini estimates are unreliable, or when the ICDF approximation is a poor fit. Thus, the AWE estimates should be treated with more caution than the RWI estimates, which were carefully validated with several different sources of independent survey data.

SI Appendix, Fig. S18 shows the global distribution of (predicted) absolute wealth, as derived from the relative wealth index using the above procedure. SI Appendix, Fig. S18 compares the predicted wealth distribution based on our method to the global income distribution in 2013, as independently estimated by Hellebrandt and Mauro (48) using household income surveys for more than 100 countries that were collected through the Luxembourg Income Study. As expected, the average wealth distribution, which is a measure of per capita GDP, is uniformly higher than the estimated income distribution, which reflects actual family incomes (i.e., total economic output does not translate directly to better family outcomes).

Targeting Simulations.

We simulate a scenario in which an antipoverty program administrator has a fixed budget to distribute to a country’s population. Following Ravallion (30) and Elbers et al. (2), we assume that the program will be geographically targeted and that all individuals within targeted regions will receive the same transfer. Our analysis compares the performance of different approaches to geographic targeting in Togo and Nigeria. Performance is evaluated using recent nationally representative household survey data collected in each country.

In Table 1, A and C, the row labeled “Tile targeting” simulates geographic targeting using the high-resolution ML estimates, where cash is transferred to households located in the poorest 2.4-km tiles of the country; the “Canton targeting” and “Ward targeting” rows simulate distribution to the households located in the poorest administrative units of the country (the canton is the smallest administrative unit in Togo and the ward is the smallest administrative unit in Nigeria), where the wealth of the administrative unit is calculated as the population-weighted average of the RWI of all tiles in that unit. Column 1 indicates the number of unique spatial units in each country; column 2 simply indicates that every spatial unit (tile or canton/ward) has a corresponding wealth estimate. Column 3 reports the R² of a regression of the ground-truth wealth of each household (i.e., “true wealth”) and the estimate of the wealth of the spatial unit in which that household is located (i.e., “predicted wealth”), calculated at the household level using weighted least-squares regression using household weights from the EHCVM (in Togo) or NLSS (in Nigeria). In columns 4 and 5 in Table 1, we assume that the government has a fixed budget that allows it to target 25% or 50% of the population and uses that budget to target the k poorest administrative units (where k is set to ensure that the budget constraint is respected—in instances where including one additional spatial unit would imply that more than 25% or 50% of households would receive benefits, households from that region are randomly selected to ensure that exactly 25% or 50% of households receive benefits). We consider the “true poor” to be the 25% or 50% of households in the ground-truth survey with the lowest household asset index and report the accuracy of each geographic targeting approach in providing benefits to those true poor.

For comparison, in Table 1, B and D simulate alternative geographic targeting approaches that a policymaker might rely on in the absence of comprehensive household-level data on poverty status. These simulations assume that the policymaker does not have access to the ML microestimates of RWI or the ground-truth data from the EHCVM/NLSS that are used to evaluate their allocation decisions. Instead, the policymaker designs a geographic targeting policy based on the most recent DHS survey, which was conducted in 2013 to 2014 in Togo and in 2018 in Nigeria.

Each row in Table 1, B and D corresponds to targeting at a different level of geographic aggregation. For instance, the row labeled “Prefecture targeting” in Table 1, B assumes that the program will be targeted at the prefecture level, the second-level administrative region in Togo, such that either all households in the prefecture will receive benefits or none will. Subsequent rows allow for targeting at smaller geographic units. The columns in Table 1, B are organized similarly to Table 1, A. Note, however, that it is no longer the case that each spatial unit will necessarily have a “predicted wealth” value. For instance, the Canton targeting row in Table 1, B (column 2) indicates that only 185 cantons have one or more surveyed households in the most recent DHS (i.e., only 47.8% of all cantons). In Table 1, column 3, the “predicted wealth” of each household is defined as the average wealth of households in that region, as calculated from the most recent DHS. In subsequent columns, the targeting mechanism selects the k predicted poorest administrative units, based on the average DHS wealth of households in that region.

The targeting simulations highlight three main results. First, and echoing previous results, the ML estimates are accurate at estimating household wealth (Table 1, column 3). Table 1 is based on two countries with recent DHS data and thus provides a conservative estimate of the gains from using the ML estimates for geographic targeting. Many LMICs do not have a recent nationally representative household survey available; for such countries, these microestimates create options for geographic targeting that might otherwise not exist.

Second, the ML estimates allow for geographic targeting at a level of spatial resolution that would not be possible with traditional survey-based data. For logistical reasons, many geographically targeted programs will be tied to administrative regions; it may simply not be possible to target benefits at the tile level. For such programs, we find that admin-region targeting based on the ML estimates performs similarly to admin-region targeting based on recent nationally representative household surveys (i.e., the comparison of the last row of Table 1, A or C to the last row of Table 1, B or D). This is important because the ML estimates can be used to construct accurate estimates of the wealth of 100% of administrative units. By contrast, the DHS surveyed households in only 185 (47.8%) cantons in Togo and only 1,218 (13.8%) wards in Nigeria—see SI Appendix, Fig. S19 for a map of the surveyed and unsurveyed regions. Thus, a geographic targeting approach relying on the DHS data alone would either require implementation at a larger administrative unit or require some other form of imputation into unsurveyed regions (as is the case in Table 1, B and D)—both of which adjustments reduce the effectiveness of geographic targeting (2, 30, 31).

Third, the microestimates create an option to geographically target very small units, which in turn produces gains in targeting performance. The gains to disaggregation are most evident in column 3 of Table 1, which highlights how targeting at the tile level increases accuracy relative to the other targeting options that provide 100% coverage. While subregional targeting is not common, recent programs have demonstrated how mobile money can be used to deliver cash transfers directly to beneficiaries, which may increase the scope for this type of approach (1, 15).

Finally, we note that the above discussion compares universal geographic targeting using the ML estimates to universal geographic targeting using recent DHS data, such that all individuals in a targeted region receive uniform benefits. In practice, most real-world programs are more nuanced and rely on additional targeting criteria (such as proxy means tests and participatory wealth rankings) to determine program eligibility. These additional criteria would be expected to increase the performance of all methods listed in Table 1; we do not simulate those changes to better highlight the gains from geographic disaggregation.

Data Availability

The main datasets of population wealth estimates produced in this study are publicly available at https://data.humdata.org/dataset/relative-wealth-index (27). The data used to construct these estimates are available from public online repositories, publicly available upon registration at https://www.dhsprogram.com/ (35) and not publicly available because of restrictions by the data provider. A detailed table of data sources and availability is provided in SI Appendix, Table S2. The code used for these analyses is publicly available online at https://github.com/g-chi/global-poverty. Our repository excludes the pretrained CNN used to extract features from satellite imagery, which is considered propriety information of Facebook. This CNN is based on code available at https://github.com/facebookresearch/WSL-Images (41), which should produce similar results.