A connectivity-constrained computational account of topographic organization in primate high-level visual cortex

Significance

We introduce the Interactive Topographic Network (ITN), a computational framework for modeling cortical organization of high-level vision. Through simulations of ITN models, we demonstrate that the topographic clustering of domains in primate inferotemporal cortex may arise from the demands of visual recognition under biological constraints on the wiring cost and modulatory sign of neuronal connections. The learned organization of the model is highly specialized but not fully modular, capturing many of the properties of organization in higher-order primates. Our work is significant for cognitive neuroscience, by providing a domain-general developmental account of topographic functional specialization, and for computational neuroscience, by demonstrating how well-known biological details can be incorporated into neural network models to account for empirical findings.

Abstract

Inferotemporal (IT) cortex in humans and other primates is topographically organized, containing multiple hierarchically organized areas selective for particular domains, such as faces and scenes. This organization is commonly viewed in terms of evolved domain-specific visual mechanisms. Here, we develop an alternative, domain-general and developmental account of IT cortical organization. The account is instantiated in interactive topographic networks (ITNs), a class of computational models in which a hierarchy of model IT areas, subject to biologically plausible connectivity-based constraints, learns high-level visual representations optimized for multiple domains. We find that minimizing a wiring cost on spatially organized feedforward and lateral connections, alongside realistic constraints on the sign of neuronal connectivity within model IT, results in a hierarchical, topographic organization. This organization replicates a number of key properties of primate IT cortex, including the presence of domain-selective spatial clusters preferentially involved in the representation of faces, objects, and scenes; columnar responses across separate excitatory and inhibitory units; and generic spatial organization whereby the response correlation of pairs of units falls off with their distance. We thus argue that topographic domain selectivity is an emergent property of a visual system optimized to maximize behavioral performance under generic connectivity-based constraints.

Inferotemporal (IT) cortex subserves higher-order visual abilities in primates, including the visual recognition of objects and faces. By adulthood in humans, IT cortex, and ventral temporal cortex more generally, contains substantial functional topographic organization, including the presence of domain-selective spatial clusters in reliable spatial locations, including clusters for faces (1–3), objects (4), buildings and scenes (5, 6), and words (7). Similar domain-level topographic properties have been found in rhesus macaque monkeys, including multiple regions of clustered face selectivity (8–10). Intriguingly, this selectivity is encompassed in a larger-scale “mosaic” of category selectivity, in which areas of category selectivity themselves have further columnar clustering within them (11–13), and moreover, category selectivity appears to exist as clusters within general dimensions of object space (14) spatially organized to smoothly map neuronal correlations over space (15), pointing to more general principles of organization beyond the domain level. In line with this idea, human IT cortex also exhibits larger-scale organization for properties such as animacy and real-world size (16, 17), and midlevel features characteristic of these properties and domains have been shown to account well for patterns of high-level visual selectivity (18). How these domain-level and more general facets of functional organization arise, how they are related, and whether and in what ways they rely on innate specification and/or experience-based developmental processes remain contentious.

Recent work has demonstrated that the neural basis of face recognition depends crucially on experience, given that deprivation of face viewing in juvenile macaque monkeys prevents the emergence of face-selective regions (19). Relatedly, the absence of exposure to written forms through reading acquisition precludes the emergence of word-selective regions (20, 21). That there exists clustered neural response selectivity for evolutionarily new visual categories such as written words offers further evidence that the topographic development of the human visual system has a critical experience-dependent component (22, 23). In contrast with a system in which innate mechanisms are determined through natural selection, this experiential plasticity permits the tuning of the visual system based on the most frequent and important visual stimuli that are actually encountered, thereby enabling greater flexibility for ongoing adaptation across the lifespan.

There is considerable computational evidence that experience-dependent neural plasticity can account for the response properties of the visual system at the single-neuron level. Classic work demonstrated that the statistics of natural images are sufficient for learning V1-like localized edge tuning within a sparse coding framework (24, 25). More recently, deep convolutional neural networks (DCNNs) trained on image classification have been successful in accounting for the tuning of neurons in V1, V2, V4, and IT in a hierarchically consistent manner, where deeper layers of the DCNN map onto later layers of the anatomical hierarchy (26, 27).

Above the single-neuron level, considerable prior work has demonstrated that topographic organization in V1 may emerge from self-organizing, input-driven mechanisms (28–34) (for review, see ref. 35). For example, the pinwheel architecture of spatially repeating smooth orientation selectivity overlaid with global retinotopy has been shown to be well accounted for by self-organizing maps (SOMs) (31, 32, 36).

One notable application of an SOM to modeling high-level visual cortex by Cowell and Cottrell (37) demonstrated stronger topographic clustering for faces compared to other object categories (e.g., chairs, shoes), suggesting that the greater topographic clustering of faces in IT is due to greater within-category similarity among faces compared to these other categories. This work provides a strong case for domain-general developmental principles underlying cortical topography in IT, but at least two important issues remain unaddressed. First, rather than supporting only discrimination of face from nonface categories (as in ref. 37), face representations in humans (and likely nonhuman primates, although see ref. 38) must support the more difficult and fine-grained task of individuation; this task requires a “spreading transformation” of representations for different face identities (39, 40), which could alter the feature space and its topographic mapping and necessitate a more domain-specialized representation than that examined by ref. 37. Second, rather than a single face-selective area, IT cortex actually contains multiple hierarchically organized face-selective regions with preferential interconnectivity (41). Generally, SOMs are not well equipped to explain such hierarchical topographic interactions, as they are designed to map a feature space into a topographic embedding, but not to transform the feature space hierarchically in the way needed to untangle invariant visual object representation from the statistics of natural images (42). This suggests that SOMs are an incomplete model of topographic development in cortical networks.

An alternative approach to studying topographic organization involves incorporating distance-dependent constraints on neural computation within more general neural network models (43–46). Of particular interest is a hierarchical neural network developed by Jacobs and Jordan (45) in which error-driven learning was augmented with a spatial loss function penalizing large weights to a greater degree on longer versus shorter connections. This model was shown to develop topographic organization for “what” versus “where” information when trained with spatially segregated output units for the two tasks. Closely related work by Plaut and Behrmann (47) demonstrated that a similarly spatially constrained model with biased demands on input (e.g., retinotopy) and output (e.g., left-lateralized language) could account for the organization of domain-specific areas in IT cortex, such as the foveal bias for words and faces, leftward lateralization of words, and rightward lateralization of faces (48–50).

However, to date, none of these structurally biased neural network models have been applied to large-scale sets of naturalistic images, the statistics of which are thought to organize high-level visual representations in IT cortex (51), and the topography in these models (45, 47) has been analyzed at a relatively coarse level. Nonetheless, this early work raises the possibility that the application of distance-dependent constraints in a deep neural architecture trained on natural images might provide a more comprehensive account of topographic organization in IT.

Along these lines, Lee et al. (15) have recently modeled the topography of IT cortex with topographic deep artificial neural networks (TDANNs) that are trained on a large set of natural images using a correlation-based layout that explicitly encourages units within a layer of the network to be spatially nearer to units with correlated responses and farther from units with uncorrelated or anticorrelated responses. As a result, the TDANN developed face-selective topography that corresponded well with data from macaque monkeys. However, this approach imposes topographic functional organization on the network based on measured functional responses, rather than deriving it from realistic principles of cortical structure and function, such as constraints on connectivity. Moreover, like the SOM, the TDANN can explain only within-area topographic organization and not spatial relationships between areas, such as the stream-like organization of multiple stages of IT cortex (3, 52) and their embedding in a network coupled with upstream and downstream cortical areas (48). Thus, the question remains whether such basic structural principles can account for the topographic organization of IT.

In the current work, we combined the approaches of task-optimized DCNN modeling (15, 51) with flexible connectivity-constrained architectures (45, 47) to develop a hierarchical model of topographic organization in IT cortex. We implemented a bias toward local connectivity through minimization of an explicit wiring cost function (45) alongside a task performance cost function. Intriguingly, we observed that this pressure on local connectivity was, on its own, insufficient to drive substantial topographic organization in our model. This led us to explore two neurobiological constraints on the sign of connectivity—strictly excitatory feedforward connectivity and the separation of excitation and inhibition—with the result that both, and particularly, excitatory feedforward connectivity, provided a powerful further inductive bias for developing topographic organization when combined with a bias toward local connectivity. Our results begin to shed light on the factors underlying hierarchical topographic organization in the primate visual system.

Materials and Methods

The Interactive Topographic Network

We introduce the interactive topographic network (ITN), a framework for computational modeling of high-level visual cortex, and specifically its functional topographic organization. ITN models are defined as neural network models that are 1) optimized to perform naturalistic tasks (following ref. 53) and 2) connectivity constrained in a biologically plausible manner to give rise to functional organization (extending previous work by refs. 45 and 47). In this work, we introduce a form of ITN that is divided into three components: an encoder that approximates early visual cortex, interactive topography (IT) layers that approximate inferotemporal cortex, and a readout mechanism for one or more downstream tasks. The goal of the encoder is to extract general visual features that describe the visual world along dimensions that support a broad range of downstream readout tasks. However, our main modeling focus is on the IT layers, which consist of a series of pairs of recurrent layers that are subject to biological constraints. For computational simplicity, such constraints are not modeled in the encoder (but see Discussion for future directions).

Encoder Architecture and Training

We used a ResNet-50 (54) encoder to allow the ITN to extract deep and predictive features of the trained inputs. The encoder is pretrained on equal-sized subsets of faces, objects, and scenes from the VGGFace2 (55), ImageNet (56), and Places365 (57) datasets, respectively, matched in terms of total training images. We reused the same subsets of faces and objects as in ref. 58, and an additional scene domain was constructed to match the other two domains in total images. An initial learning rate of 0.01 was used, and this learning rate was decayed five times by a factor of 10 upon plateau of the validation error; after the fifth learning rate decay, the next validation error plateau determined the end of training. Stochastic gradient descent with momentum ($\rho =0.9$) and l2 weight decay ($\lambda =0.0001$) was used, with batch size of 256 on a single graphics processing unit (GPU).

Recurrent Neural Network Formulation of IT

Our model of IT extends the standard discrete-time recurrent neural network (RNN) formulation common in computational neuroscience (59). We begin with the continuous-time dynamics of units in an RNN layer, where ${\mathit{x}}^{(a)}$ is the vector of preactivation activities in area a of IT, ${\mathit{r}}^{(a)}$ is the vector of postactivation activities in area a, ${\mathit{b}}^{(a)}$ is the vector of baseline activities in area a, τ is the scalar neuronal time constant, and $W^{(a,b)}$ is the matrix of weights from area a to area b:

$$\tau \frac{d{\mathit{x}}_t^{(a)}}{dt}=-{\mathit{x}}_t^{(a)}+W^{(a,a)}{\mathit{r}}_t^{(a)}+W^{(a-1,a)}{\mathit{r}}_t^{(a-1)}+{\mathit{b}}^{(a)}$$ [1]

where the activation function ${\mathit{r}}_t^{(a)}={[{\mathit{x}}_t^{(a)}]}_{+}$ is positive rectification, also called a rectified linear unit (ReLU). Applying the Euler method to integrate this first-order ordinary differential equation, with time-step size $\mathrm{\Delta }t$, and substituting $\alpha =\frac{\mathrm{\Delta }t}{\tau }$, yields the discrete-time update:

$${\mathit{x}}_t^{(a)}=(1-\alpha ){\mathit{x}}_{t-1}^{(a)}+\alpha \left(W^{(a,a)}{\mathit{r}}_{t-1}^{(a)}+W^{(a-1,a)}{\mathit{r}}_{t-1}^{(a-1)}+{\mathit{b}}^{(a)}\right).$$ [2]

When training models with separate excitatory and inhibitory units, we noted that training could be extremely unstable and typically required some mechanism for achieving stability. To this end, we adopted layer normalization (60), without the trainable scaling parameter that is sometimes used (see ref. 60 for more details). We found layer normalization to be extremely effective in stabilizing models and encouraging well-distributed activations (SI Appendix, Fig. S38). Where $\mu (\mathit{x})$ is the mean of x, and $\sigma (\mathit{x})$ is the SD of x, and b is the learned bias term (moved outside of the layer normalization), the layer-normalized activities are given as

$$\begin{array}{l}{\mathit{z}}_t=\frac{{\mathit{x}}_t-\mu ({\mathit{x}}_{\mathit{t}})}{\sigma ({\mathit{x}}_{\mathit{t}})}+\mathit{b}\\ {\mathit{r}}_t\prime ={[{\mathit{z}}_t]}_{+}.\end{array}$$

Incorporating layer normalization into our update equation yields the final update equation:

$${\mathit{x}}_t^{(a)}=(1-\alpha ){\mathit{z}}_{t-1}^{(a)}+\alpha \left(W^{(a,a)}{\mathit{r}}_{t-1}^{\prime (a)}+W^{(a-1,a)}{\mathit{r}}_{t-1}^{\prime (a-1)}\right).$$ [3]

Extending the Standard RNN Framework with Biological Constraints

Here, we outline the major biological constraints implemented in this work.

Spatial organization

An essential aspect of an ITN model is that each IT layer has a spatial organization (15). We chose to model layers as square grids, with each layer of the hierarchy of equal size (typically, a grid size length of 32, corresponding to a layer of 1,024 units). We normalize the coordinates to lie in the range [0,1]. Each unit thus has a unique (x, y) coordinate that will be used to determine the distance-dependent network topology. In general, the specific choices about map spatial arrangement are not critical to the predictions of the model, but they can potentially be manipulated in certain ways in the service of other theoretical goals.

Spatial connectivity costs

We impose distance-dependent constraints on connectivity through a cost on longer connections throughout training. This basic formulation of the loss was introduced by Jacobs and Jordan (45) as a way to induce spatially organized task specialization and was shown to do so in a simple neural network model trained on small-scale tasks. To our knowledge, no other research has examined this loss in modern deep-learning architectures trained on natural images. We use a simple modification of the original loss function, using the squared Euclidean distance ${\left({\mathcal{D}}_{i,j}\right)}^2=\left|\right|{\mathit{r}}_i-{\mathit{r}}_{\mathit{j}}|{|}_2^2$ [in place of ${\left({\mathcal{D}}_{i,j}\right)}^{10}=\left|\right|{\mathit{r}}_i-{\mathit{r}}_{\mathit{j}}|{|}_{10}^{10}$ distance (45)]. By using the squared distance, we penalize longer connections disproportionally compared to shorter connections. The spatial loss on connections between areas a and b, ${\mathcal{L}}_w^{(a,b)}$, is given by

$${\mathcal{L}}_w^{(a,b)}={\displaystyle \sum _{i,j}\frac{{\left({\mathcal{D}}_{ij}^{(a,b)}\right)}^2{\left(W_{ij}^{(a,b)}\right)}^2}{1+{\left(W_{ij}^{(a,b)}\right)}^2}}.$$ [4]

The total spatial loss is the sum of the area-to-area spatial losses ${\mathcal{L}}_w={\displaystyle {\sum }_{a,b}{\mathcal{L}}_w^{(a,b)}}$ and is added to the task-based loss as $\mathcal{L}={\mathcal{L}}_t+{\lambda }_w{\mathcal{L}}_w$, on which gradient descent is performed. Additionally, in contrast to ref. 45, we choose a single λ_w parameter, rather than varying it throughout training. For each architectural variant, we chose the λ_w that maximized a metric of generic topographic organization (T_g, Eq. 7).

Connection noise

To approximate axon-specific variability in instantaneous firing rate (61), we apply multiplicative noise on the individual connections between neurons that is uniform over distance and layers. In practice, we find that connection noise helps to regularize the activations in the network, encouraging a more distributed representation that aids the formation of topography across a range of models (see SI Appendix, Fig. S39 for evidence that it is not absolutely necessary). Noise is sampled independently from a Gaussian distribution $\mathcal{N}$ centered at 0 with variance ${\sigma }^2$ at each time step of each trial and is squashed by a sigmoidal function $S(x)=\frac{2}{1+e^{-x}}$, ensuring that the sign of each weight is not changed and each magnitude does not change by more than 100%. Thus, the noisy weight matrix $W_n^{(a,b)}$ from area a to area b on a given trial and time step is

$$W_n^{(a,b)}=S\left(\mathcal{N}(0,\sigma )\right)*W^{(a,b)}.$$ [5]

Sign-based restrictions on neuronal connectivity

Standard neural networks gloss over a key detail of neuronal morphology—that single neurons obey Dale’s law, whereby all of their outgoing connections are either excitatory or inhibitory (ignoring modulatory neurons and other special, rare cases) (59). We employ this principle within our framework by replacing the single sheet of unconstrained neurons with parallel sheets of excitatory (E) and inhibitory (I) neurons. The second sign-based restriction we implement is that between-area interactions are carried out predominantly by excitatory pyramidal neurons. Thus, we restrict between-area feedforward connectivity to originate from the excitatory neurons only. In the main model, both E and I neurons receive feedforward inputs.

IT Architecture and Training

The main ITN model consists of three IT layers (posterior IT [pIT], central IT [cIT], and anterior IT [aIT]) with separate E and I populations and feedforward connections sent only by E units. To facilitate training many models with fewer computational demands, the model is trained using a fixed pretrained ResNet-50 encoder on smaller subsets of faces, objects, and scenes. Specifically, we created image subsets equal to the size of the popular CIFAR-100 dataset but at higher image resolution, containing 100 categories each with 500 training images and 100 validation images, resized to 112 × 112 pixels. Thus, the combined dataset contained 300 categories with 150,000 training images and 30,000 validation images. The same learning-rate schedule as used for training the encoder was used. Stochastic gradient descent with momentum ($\rho =0.9$) was used, with batch size of 1,024 on a single GPU. In the main model, we used spatial regularization with ${\lambda }_w=0.05$, without additional weight decay on IT connections.

IT Model Variants

To better understand the relative importance of different aspects of model design that contribute to the development of topographic organization, we examine a variety of IT model variants containing different subsets of implemented constraints (see Fig. 6). Some of these models do not use separate populations of E and I units, but still restrict feedforward connectivity to be excitatory. In this case, we simply restrict the feedforward weights to be positive, despite the same neuron having both positive and negative lateral connections. In another case, separate populations of E and I units are both allowed to send feedforward projections. In another class of variants, we remove learned lateral connections entirely. These models are trained for a single time step, and the only recurrent computation is that of a single pass of layer normalization. Finally, we explore a range of spatial regularization strengths.

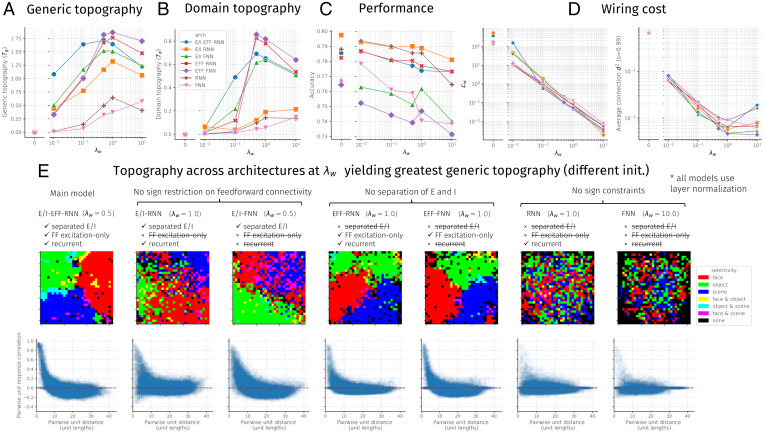
Fig. 6.

Topographic organization, performance, and wiring cost as a function of spatial regularization strength (λ_w) and architectural constraints. Seven architectures were tested, sweeping all unique variations of models containing or not containing separate excitation and inhibition (E/I), excitatory-only feedforward connectivity (EFF), and learned lateral/recurrent connections (RNN vs. FNN); see D for a model-by-model constraint breakdown. Note that all models contained a minimal form of recurrence induced by the layer normalization operation. (A) Generic topographic organization summary statistic (Eq. 7). (B) Domain-level topographic organization summary statistic (Eq. 6). (C) Final accuracy on validation images. (D) Two measures of wiring cost: (Left) L_w (Eq. 4) and (Right) $L_{w,u}$ (Eq. 8). (E) Domain-level and generic topographic organization visualizations for each architecture using the tuned value of λ_w that maximized T_g. Each model was tested using a different random initialization from the one used to tune λ_w.

Analyses of Trained Models

After training, the responses in IT layers are probed to investigate emergent task specialization and its topographic organization. We use three main approaches.

Mass-univariate analyses

The first analytic approach is the simple mass-univariate approach, in which each unit is analyzed separately for its mean response to each stimulus domain (objects, faces, scenes), using untrained validation images from the same categories used in training. In addition to computing the mean response to each domain, we compute selectivity, a ubiquitous metric used in neuroscience, to analyze how responsive a unit is to one domain compared to all others. We compare the responses of each domain versus the others using a two-tailed t test, and given the test statistic t, the significance value p of the test, and the sign of the test statistic $s=\mathit{sign}(t)$, we compute the selectivity as $-s\hspace{0.17em}\text{log}(p)$.

Searchlight decoding analysis

The second analysis approach is the multivariate searchlight analysis commonly used in functional MRI (fMRI) (62), in which a pool of units is selected in a (circular) spatial window around each unit, and the accuracy for discriminating between different categories (e.g., hammer vs. screwdriver) in each domain (e.g., objects) is computed using the activations of only that pool of units; the mean accuracy value is assigned to the center unit, and the process is repeated for all units.

Lesion analysis

To assess the causal role of certain units in the performance of specific tasks, we adopt a lesioning approach in which the activities of lesioned units are set to 0 at each time step. This effectively removes them from processing, allowing the network’s dynamics to unfold independently of these units. The effect of a lesion is measured by computing the accuracy following the lesion and relating that to the baseline accuracy.

The first type of lesion we perform is a spatial or focal lesion in which a circular neighborhood of size p × n units is selected, where p is the fraction of units selected and n is the total number of units in the area where the lesion is performed. The lesion is centered on a unit $u_{i,j}$ either randomly or according to the peak of a specific metric such as selectivity. To lesion spatial neighborhoods corresponding to regions of high domain selectivity, we take the selectivity map, perform spatial smoothing, and select the unit u of peak smoothed selectivity.

The second type of lesion sorts units according to a given selectivity metric irrespective of their spatial location. In this analysis, the p × n most selective units are chosen for a given lesion. This is done separately for the selectivity of each domain, as in the focal lesions. When the topography is smooth and the regions approximately circular, the selectivity-ordered and focal lesions yield similar results. However, to the extent that the topography is not perfectly smooth or circular, the selectivity-ordered lesion may knock out a more relevant set of units for a given task.

Distance-dependent response correlation

We calculate the correlations of the responses of all pairs of units as a function of distance between them. Response correlation is computed for a given time step over a large number of images, either from all domains or from each domain separately.

Topographic organization summary statistics

We compute two metrics of topographic organization—one indexing generic organization and the other, domain-level organization. The domain-level topography statistic T_d is a measure of how much the alignment of domain-level selectivity vectors between pairs of units falls off with distance. For a given layer l, cell type c, and neuron i, let us consider a three-dimensional (3D) vector of selectivity values for each domain ${\mathit{s}}_i$. Using the dot product ${\mathit{s}}_i·{\mathit{s}}_j$ between selectivity vectors of $m=\left(\begin{array}{c}p\\ 2\end{array}\right)$ pairs of neurons (to allow for magnitude effects), standardized over all neuron pairs as $z(·)$, and assuming l and c are held constant, the domain-topography statistic T_d is then given as

$$T_d=\frac{1}{m}{\displaystyle \sum _{i,j}^p\frac{z({\mathit{s}}_i·{\mathit{s}}_j)}{{\mathcal{D}}_{i,j}}}.$$ [6]

The standardization ensures that the statistic is not inflated for poorly trained networks with uniformly high correlation values across unit pairs. Similarly, the generic topography statistic is a measure of how much pairwise response correlation falls off with distance. For a given layer l, cell type c, and neuron i, let us consider a n-D vector of responses over n images ${\mathit{s}}_i$. The statistic T_g is then given as

$$T_g=\frac{1}{m}{\displaystyle \sum _{i,j}^p\frac{z(r({\mathit{a}}_i,{\mathit{a}}_j))}{{\mathcal{D}}_{i,j}}}.$$ [7]

In this paper, we plot the T_g and T_d values averaged over layers and cell types. In SI Appendix, we additionally plot values per layer and cell type.

Analyzing spatial costs of trained networks

To understand the wiring cost of certain trained models, we analyze the spatial cost of a network, as given by Eq. 4, as a function of architectural parameters such as the spatial regularization strength λ_w. In one analysis, we analyze only the feedforward spatial cost, which simply requires summing spatial costs over pairs of areas a and b where $a\ne b$. Similarly, to analyze only the recurrent spatial cost, we can sum spatial cost over pairs of areas a and b where a = b.

Unweighted spatial cost of sparsified networks

While wiring cost in an artificial neural network should depend to some extent on the strength of connections—stronger connections may require greater myelination, and strong connections in an artificial neural network may correspond to a larger number of synapses in a biological neural network—there is another notion of wiring cost whereby it depends only on whether or not two neurons are connected. This notion of wiring costs has been commonly applied to the study of cortical areal layout and early visual cortical maps (31, 63–65). Moreover, the analysis of binary connectivity in thresholded networks is also common in graph-theoretic analysis of brain data (66). To analyze this notion of wiring costs, we pruned our trained models to a desired connection sparsity level s, setting to 0 the $n\times m\times s$ connections with the smallest magnitude, where n and m are the number of units in areas a and b. Sparsity was enforced globally within IT and from IT to readout, rather than individually for each set of connections. We then analyzed an unweighted wiring cost ${\mathcal{L}}_{w,u}^{(a,b)}$ that computes the mean of squared Euclidean distance values between connected units i and j in areas a and b, given that (a, b) are in the set of connected areas C:

$${\mathcal{L}}_{w,u}^{(a,b)}=\frac{1}{n\hspace{0.17em}m\hspace{0.17em}(1-s)}{\displaystyle \sum _{i,j}{\left({\mathcal{D}}_{ij}^{(a,b)}\right)}^2}\left(W_{ij}^{(a,b)}\ne 0\right).$$ [8]

Results

A Connectivity-Constrained Model of Ventral Temporal Cortex Produces Hierarchical, Domain-Selective Response Topography

We first present the results of simulations of a specific ITN model (Fig. 1A), which we refer to as the main model or “E/I-EFF-RNN,” to indicate that it possesses separate neurons responsible for excitation and inhibition (E/I), a restriction that feedforward connections are strictly excitatory (EFF), and temporally recurrent processing is mediated through learned lateral connections (RNN). These three factors—in addition to the strength of the wiring cost penalty λ_w—will be of interest later as we uncover the key ingredients of developing topography. Additionally, this model uses a ResNet-50 encoder that is pretrained on a large dataset including several categories from the domains of objects, faces, and scenes (each domain matched in total training images) and, following pretraining, is used as a feature extractor that provides input to a three-area IT containing separate pIT, cIT, and aIT areas. The main model used a spatial cost parameter ${\lambda }_w=0.5$ that was chosen to maximize a metric of domain-level organization (see Fig. 6).

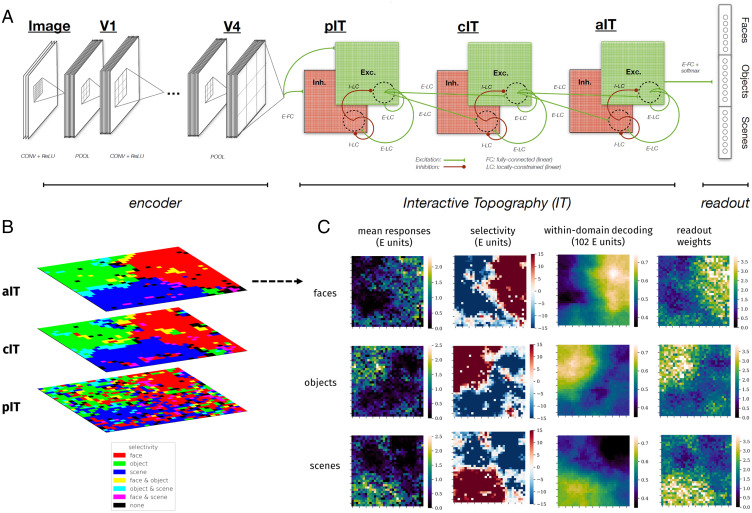
Fig. 1.

The interactive topographic network produces hierarchical domain-level organization. (A) Diagram of the ITN. An ITN model consists of three components: an encoder that approximates early visual processing prior to inferotemporal cortex, the IT areas that approximate inferotemporal cortex, and the readout mechanism for tasks such as object, scene, and face recognition. The architecture of each component is flexible. For example, a four-layer simple convolutional network or a deep 50-layer ResNet can be used as the encoder; whereas the former facilitates end-to-end training along with a temporally precise IT model, the latter supports better learning of the features that discriminate among trained categories. In this work, topographic organization is restricted to the IT layers. Shown is the main version of the ITN containing three constraints: a spatial connectivity cost pressuring local connectivity, separation of neurons with excitatory and inhibitory influences, and the restriction that all between-area connections are sent by the excitatory neurons. The final IT layer projects to the category readout layer containing one localist unit per learned category, here shown organized into three learned domains. (Note that this organization is merely visual and does not indicate any architectural segregation in the model.) (B) Domain selectivity at each level of the IT hierarchy. Selectivity is computed separately for each domain and then binarized by including all units corresponding to P < 0.001. Each domain is assigned a color channel to plot all selectivities simultaneously. Note that a unit can have zero, one, or two selective domains, but not three, as indicated in the color key. (C) Detailed investigation of domain-level topography in aIT. Each heatmap plots a metric for each unit in aIT. Left column shows the mean domain response for each domain, Center Left column shows domain selectivity, Center Right column shows the within-domain searchlight decoding accuracy, and Right column shows the mean of weights of a given aIT unit into the readout categories of a given domain.

After training, the model performed well on each domain, reaching a classification accuracy of 86.4% on the face domain, 81.8% on the object domain, and 65.9% on the scene domain (SI Appendix, Fig. S1). Performance differences across domains are unlikely to be an artifact of the specific architecture as they can be seen across a variety of DCNNs, reflecting the intrinsic difficulty of each task given the variability within and between categories of each domain for the given image sets.

As can be seen in Fig. 1B, the trained model exhibits domain-level topographic organization that is hierarchically linked across corresponding sectors of each layer. This result reflects the fact that the distance-dependent constraints on feedforward connectivity pressured units that have minimal between-area distances to learn a similar tuning, which means that each layer is roughly overlapping in its respective (separate) 2D topography. The topographic organization gets somewhat smoother moving from pIT to cIT, most likely because units in cIT and aIT (but not pIT) have local feedforward receptive fields and thus greater constraint on local cooperation. Further quantification of topographic organization in each layer can be found in SI Appendix, Fig. S6. Overall, the presence of domain-level topography—but not its particular spatial arrangement—was robust to variation elicited by random initialization of model parameters (SI Appendix, Fig. S23) (67).

We next scrutinized the topography in aIT, where there are very smooth domain-level responses, and where we can directly compare responses with those of the recognition readout mechanism. We computed mean domain responses, plotted in Fig. 1 C, Left column, and domain selectivity, plotted in Fig. 1 C, Center Left column, which demonstrates corresponding topographic organization. We confirmed the functional significance of response topography by conducting a searchlight analysis inspired by multivariate approaches to analyzing fMRI data (62). We used searchlights containing the 10% (102) nearest units. The results of this analysis, shown in Fig. 1 C, Center Right column, revealed topographic organization of information for discriminating between categories of each domain that is strongly correlated with the domain selectivity maps for each domain (all $P\text{s}<0.0001$). Importantly, every searchlight contained information substantially above chance level for discriminating within each domain, pointing to partially distributed information despite topographic domain selectivity, in line with human and macaque neurophysiology (68, 69) (see SI Appendix, Fig. S3 for comparisons of searchlight decoding accuracy for each unit across domains).

To further confirm the functional significance of the topographic organization, we analyzed the spatial organization of readout weights from aIT to the localist category readout layer. We evaluated whether each domain placed more weight in reading out from the units for which there was greater selectivity, by calculating the mean domain response weight for each unit, averaged over classes in each domain. This produced a map for each domain, shown in Fig. 1 C, Right column. We find a large positive correlation between the mean readout weight and the mean response for each domain (all rs > 0.7, all $P\text{s}<0.0001$), further demonstrating the functional significance of the response topography.

Excitatory and Inhibitory Units Operate as Functional Columns

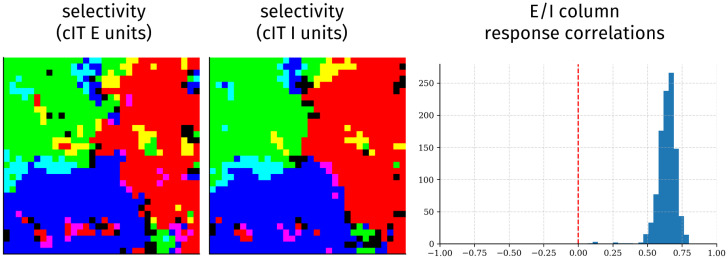
In the main ITN model, the E cells serve as the principal neurons that exclusively project to downstream areas—thus, we have focused entirely on the E cells. The I cells, in contrast, play a local role in processing, receiving inputs from and sending outputs to both E and I cells in the same cortical area. As all the neurons are subject to the same spatial constraint, we predicted that E and I neurons would have similar functional topographic organization. We show the topography of response selectivity of E and I neurons in area cIT in Fig. 2. The neuron types demonstrate clearly similar functional topography, which we quantify at the columnar level of a pair of E and I units in the same location. We find that such E-I columns have highly correlated activity, implying specific functional coupling, as has been demonstrated in ferret visual cortex (70) and in cortical columns more generally (71). Inhibitory neurons in aIT yielded sparser selectivity and therefore weaker, but similar, coupling with E units (SI Appendix, Fig. S11). One reason I units in aIT may have sparser responses is that the network discovers that it can reduce inhibitory weights (and thereby spatial costs) here, as aIT units project onto readout units subject to a squashing softmax nonlinearity. E/I columnar organization was not found in a model trained without the spatial constraint (SI Appendix, Fig. S12).

Fig. 2.

E and I cells act as functional columns. Shown are selectivity of cIT E units (Left) and I units (Center) for each domain (colored as in Fig. 1B) and histograms (Right) of response correlations between colocalized E and I units over all images.

Effects of Lesions Indicate Strong Yet Graded Domain-Level Specialization

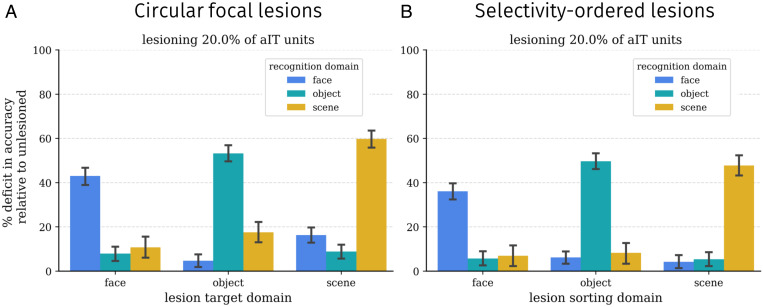
We next performed a series of “lesion” analyses in the model to compare with neuropsychological data on face and object recognition (72–74). First, we performed focal lesions. To simulate the impairment of patients with maximally specific deficits, we centered circular focal lesions of various sizes at the center of (smoothed) domain selectivity. Performance following each lesion was measured separately for each domain.

A subset of results of this lesion analysis using a medium-sized lesion is shown in Fig. 3A, with complete results in SI Appendix, Fig. S2. These focal lesions centered on each domain lead to an especially severe deficit in recognition for that domain and milder but significant deficits for the other domains as well. For such lesions, the deficit is significant for all domains (all Ps < 0.05) and significantly stronger for recognition of the target domain (all Ps < 0.05).

Fig. 3.

Lesion results in the ITN model. Each plot shows the relative effects of a set of medium-sized lesions (20% of aIT units) on recognition performance for each domain, relative to the performance on the same domain in the undamaged model. Error bars show bootstrapped 95% confidence intervals over trials; thus, the statistical significance of a given lesion can be assessed by determining whether the confidence interval includes 0. (A) Damage from circular focal lesions centered on the peak of smoothed selectivity for each domain. (Left) Results for a variety of lesion sizes. (B) Damage from selectivity-ordered lesions for each domain.

Are these more general effects of circumscribed lesions on nonpreferred domains the result of imperfect (patchy) or noncircular topographic organization of an underlying modular organization? To answer this question, we performed selectivity-ordered lesions, in which units were sorted by their selectivity for a given domain and selected according to their sorting index. Again, a subset of results is shown in Fig. 3B with complete results across a broader range of lesion sizes shown in SI Appendix, Fig. S2. The effects of damage in this case are similar to those for focal lesions, with greater damage to the domain on which sorting was performed and smaller but significant deficits to other domains (all Ps < 0.05). This suggests that some but not all of the damage to the nonpreferred domain induced by focal lesions may be due to imperfect or noncircular topographic functional organization. Importantly, these more distributed effects of lesions indicate that the functional organization, while highly specialized, is not strictly modular; damage to those units purported to be a part of a given module (e.g., for face recognition) nevertheless affects object recognition (albeit to a weaker degree). SI Appendix, Figs. S3–S5 provide additional data on the nature of domain specialization in the network.

Domain Selectivity Exists within a Broader Organization Similar to That of Primate IT Cortex

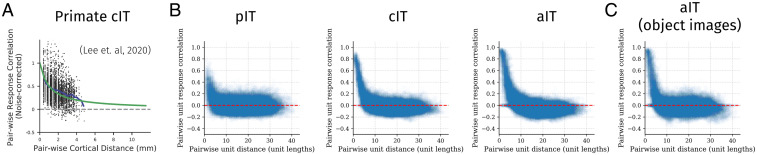
Previous empirical research has demonstrated that the response correlations between pairs of neurons fall off smoothly with increasing distance between the neurons (15, 75), as shown in Fig. 4A. As discussed, this finding is the basis of TDANN models that explicitly fits the spatial layout of units to this relationship (15). We explored whether this relationship emerged naturally in our network due to its constrained connectivity, in line with the emergence of domain-selective topography. We thus computed the correlations among pairs of unit activations across images as a function of the distance between the units in each area. As shown in Fig. 4B, there is, indeed, a smooth decay of response correlations with distance, matching the qualitative trend in the empirical data.

Fig. 4.

Generic topographic organization beyond domain selectivity emerges through task optimization under biologically plausible constraints on connectivity. (A) Distance-dependent response correlation in macaque IT (reproduced from ref. 15, which is licensed under CC BY-NC-ND 4.0 [https://creativecommons.org/licenses/by-nc-nd/4.0/]). (B) Distance-dependent response correlation in the excitatory cells of each layer, using images from all three domains (objects, faces, scenes). (C) Distance-dependent response correlation in aIT using images from the object domain only, highlighting within-domain generic functional organization.

This result is not simply due to differences between domains, as it is also found when examining responses to images within each domain separately (shown for objects in Fig. 4C). Along with previous results (15), our findings suggest that the domain-level topography may simply be a large-scale manifestation of a more general representational topography in which the information represented by neighboring units is more similar than that represented by more distal units. Our results demonstrate that this organization can arise under explicit wiring length and sign-based constraints on connectivity.

Generic Organization Encompasses Interpretable Domain-Level and Subdomain-Level Organization

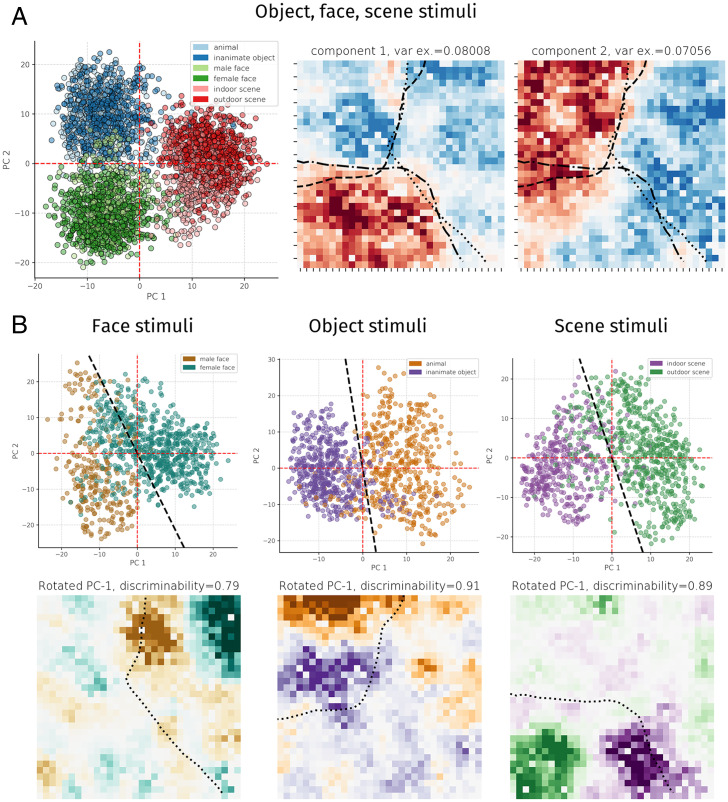
Recently, Bao et al. (14) provided evidence that IT cortex contains a map of object space that corresponds well to the first two principal components (PCs) of high-level visual representations in an ImageNet-trained convolutional neural network and that clusters in this object space corresponded to topographic clusters in IT cortex, including face-selective areas. We asked whether our network displayed a similar relationship. Similarly, we found that each domain lies in weakly overlapping clusters in the subspace spanned by the first two PCs of aIT activations (hereafter PC1-PC2 space), where the first PC mostly separated faces and scenes, and the second PC separated objects from faces and scenes (Fig. 5 A, Left). When we visualized the weights of these two PCs, we found that they were topographically organized (Fig. 5 B, Right) and corresponded well to the large-scale domain structure inherent to aIT (see contour lines and Fig. 1). Notably, relatively little within-domain clustering was seen along the first two PCs, and higher dimensions were less interpretable (SI Appendix, Fig. S20), and so, to seek finer-grained organization, we opted to visualize the principal components of activations to each domain separately, shown in Fig. 5B. For each domain, we determined a within-domain attribute that might induce further representational—and thus, topographic—distinctions; we labeled whether the faces were male or female, whether objects were animate or inanimate, and whether scenes were indoors or outdoors. The PC1–PC2 space of each domain appeared to discriminate each attribute well but not necessarily exactly along either component, so we fitted a logistic regression over the first two PCs to extract a line (2D hyperplane) in PC1 to PC2 space that best discriminated between exemplars of each attribute type [i.e., $y(x)=w_1\times P{C}_1(x)+w_2\times P{C}_2(x)$]; this led to discriminability of 0.84 for gender, 0.92 for animacy, and 0.87 for scenes. We then visualized the topographic weights from aIT onto these discriminating projections, revealing striking topographic organization. In each case, there was an ON-OFF weight pattern localized within the sector of domain selectivity, along with further, weaker weight outside this sector—for example, orange-colored weight contributing to the animate object attribute within the face-selective cluster (Fig. 5 B, Bottom Center)—indicating graded contributions of nonselective units. A complementary clustering analysis of each domain yielded similar results, whereby categories with different attributes clustered spatially (SI Appendix, Figs. S8–S10).

Fig. 5.

Principal components analysis of activations. A plots the PC1 to PC2 space and PC1 and PC2 component weights across images from all three domains. Dashed lines on component weight plots show the contour of selectivity for each domain, using selectivity maps smoothed with a local averaging kernel (5% nearest units) corresponding to significance P < 0.001. B plots the PC1 to PC2 space for responses to each domain separately and the weight visualization of a rotated axis in PC1 to PC2 space that maximized the discriminability of images according to a given subdomain attribute (gender for faces, animacy for objects, and indoor/outdoor for scenes). Dashed lines show selectivity for the domain of interest, using selectivity maps smoothed with a local averaging kernel (5% nearest units) corresponding to significance P < 0.001.

Sign-Based Constraints Combine with Wiring Length Constraints to Produce Topographic Organization

Having established that the main ITN architecture produces a host of empirically grounded topographic organizational phenomena, we next performed a constraint-removal analysis to determine which constraints—in addition to the bias toward local connectivity—are necessary for the development of topographic organization. We varied three binary constraints: whether between-area feedforward connections were excitatory only (EFF), whether the model employed separate E and I unit populations within each area (E/I), and whether the model contained lateral (recurrent) connections within each area (RNN vs. FNN [feedforward neural network]). We thus constructed seven architectures (the I units in the E/I-EFF-FNN model would exert no effect, making the E/I-EFF-FNN model equivalent to the EFF-FNN model). Each of these architectures was trained across a log-spaced range of λ_w values, and the generic topography, domain-level topography, performance, and wiring cost were analyzed (Fig. 6). For each architecture, we selected an optimal λ_w, chosen to maximize the measure of generic topography (Eq. 7) averaged over layers and cell types, trained an additional instance of the architecture with this λ_w, and visualized the learned topography, shown in Fig. 6E. We found that models without sign constraints (RNN, FNN) produced only weak topography, uncharacteristic of primate IT cortex. In contrast, models with separate excitation and inhibition (E/I-RNN, E/I-FNN) produced somewhat greater topographic organization, and models with strictly excitatory feedforward connectivity (EFF-RNN, EFF-FNN) produced topographic organization equivalent to that of the main model (E/I-EFF-RNN). Moreover, temporal recurrence, mediated through learned lateral connections, was not necessary to develop topography. In terms of performance, we found that the accuracy of the various recurrent models was very similar, with a very small advantage for models in which feedforward connectivity was not constrained to be excitatory. In contrast, accuracy for the feedforward models was reduced more substantially (>4 percentage points), pointing to a performance benefit of the recurrent connections. Moreover, while wiring cost (next section) was determined much more by λ_w than architecture (Fig. 6D), we found that, for the same λ_w across variants, the variants that developed clear domain-level organization had the smallest wiring cost (SI Appendix, Fig. S36).

Finally, we found that an identical set of models that did not employ layer normalization typically was too unstable to train, and those models in the set that did train performed worse and exhibited weaker topography (SI Appendix, Fig. S38 and associated text in SI Appendix). The broad but untuned effect of layer normalization thus appears to both stabilize activity and introduce a global competition that contributes to topographic organization.

Overall, these results demonstrate the importance of sign-based constraints for developing topography in the ITN framework and highlight that several model variants can produce topographic organization and be used for different purposes, depending on the level of detail desired. More detailed analyses for these variants are available in SI Appendix, Figs. S25–S32.

Networks Can Reduce Spatial Costs While Maintaining Performance by Increasing Topographic Organization

The optimization problem of Eq. 4 explicitly works to both maximize visual recognition performance through a task-based loss term ${\mathcal{L}}_t$ and minimize overall wiring cost through a connection-based loss term ${\mathcal{L}}_w$ that scales with the square of connection distance. To what extent does minimizing the wiring cost term compromise performance? To answer this question, we computed wiring costs for each architecture and λ_w discussed in the previous section. We computed wiring cost in two ways. The first way is by using the ${\mathcal{L}}_w$ term, which takes into account both the length and strength of connections. The second way is inspired by the wiring cost minimization framework (64), which takes into account only the length of connections, assuming sparse connectivity. To compute this wiring cost ${\mathcal{L}}_{w,u}$, we sparsified the network to contain only the 1% strongest connections (sparsity = 0.99) and took the averaged squared distance of remaining connections (65) (Eq. 8); this sparsification introduces minimal performance deficits in the main ITN model (SI Appendix, Fig. S7). The results, shown in Fig. 6D, demonstrate that increasing the wiring cost penalty λ_w by an order of magnitude decreased the first spatial cost ${\mathcal{L}}_w$ by roughly an order of magnitude. Precisely, for the main architecture, the log-log plot in Fig. 6 D, Left revealed a power-law relationship of the form $y=A{x}^m$, where $m=-1.24$ (P < 0.001). The unweighted wiring cost $L_{w,u}$ similarly decays roughly linearly on the log-log plot up to ${\lambda }_w=0.1$, after which $L_{w,u}$ saturates and then rises for increasing values of λ_w. Thus, an intermediate value of λ_w appears sufficient to drive the network toward preferentially local connectivity, and further increasing λ_w may minimize further the optimization term ${\mathcal{L}}_w$ through other means, such as by further shrinking small long-range weights and reducing participation at the grid boundaries where mean connection lengths are longest (SI Appendix, Fig. S6). In contrast to the wiring costs, the final classification performance was only marginally affected by λ_w (for the main model: log-log slope $m=-0.0016$, P < 0.001, explained variance $r^2=0.582$; fit was not significantly better than log-linear regression, $m=-0.0028$, P < 0.001, explained variance $r^2=0.583$). Finally, increasing the wiring cost penalty gradually resulted in the emergence of domain-selective topographic organization, along with generic topographic organization indexed by distance-dependent pairwise response correlations (Fig. 6 A and B and SI Appendix, Fig. S6). Thus, models with a large wiring cost penalty perform similarly to models with unconstrained connectivity but achieve very small wiring cost, through the development of topographic functional organization.

Discussion

Is IT cortex a collection of independent, possibly hard-wired domain-specific modules or a more general-purpose, interactive, and plastic system? A central goal of the current work was to determine whether seemingly domain-specific organization can emerge naturally from domain-general constraints. The simulations we report demonstrate that many of the key findings thought to support a modular view of separable, innately specified mechanisms for the recognition of different high-level domains (faces, objects, scenes) can be accounted for within a learning-based account operating under generic connectivity constraints (23, 37, 76). By simulating a biologically plausible ITN model of IT without domain-specific innate structure, we found that we can “let the structure emerge” (77, 78). Specifically, we observed that the model developed largely domain-selective spatial clusters that contain preferential information for each domain and that, when lesioned, produced largely (but not purely) specific deficits.

The Equivalence of Domain-General and Domain-Specific Organization

Beyond domain-level spatially clustered organization, the model exhibited a more generic form of topographic organization, whereby nearby units had more correlated responses over images compared to more distant units, a relationship that has been demonstrated in macaque IT cortex (15, 79). In concert with other modeling work (15) that pressured neurons to obey this relationship as a proxy for wiring cost, our work suggests that this generic spatial functional relationship appears to both underlie domain-level organization and emerge from wiring cost minimization. Moreover, we found that the principal components of image space were mapped across each area of model IT, as in macaque IT (14). That many of the hallmarks of domain specificity can be simulated in a domain-general experiential account, and such domain-level organization exists within a more generic organization, gives credence to domain-general accounts that accommodate learned specialization (50, 80).

The Importance of Sign-Based Constraints alongside a Minimal Wiring Constraint

Importantly, wiring cost and multitask optimization (i.e., object, face, and scene image recognition), by themselves, were not sufficient to produce substantial topographic organization (Fig. 6 and SI Appendix, Fig. S32). However, we found that two well-known biological details—excitatory-only between-area communication and separate excitatory and inhibitory neural populations—could induce greater topographic organization in the context of wiring cost and task optimization. Notably, locally biased excitatory feedforward connectivity provides an inductive bias that neighboring units should have positively correlated response properties, without specifying how correlated they should be. As widespread correlation impairs representational capacity, the network is encouraged to learn in a fashion whereby pairwise correlation of neural representations decays with distance, a hallmark of topographic organization (15, 75). Models with separate excitatory and inhibitory neurons—but no restriction on which neurons sent feedforward connections—produced greater topography relative to non–sign-constrained models, but weaker topography than models with the feedforward excitation restriction. Interestingly, the feedforward E/I variant (E/I-FNN) produced stronger topographic organization than the recurrent variant (E/I-RNN). Finally, future work examining other tasks (81, 82) and architectures (83–86) that place greater functional demands on lateral connectivity may find that local connectivity constraints would make a greater contribution to topographic organization in the absence of sign-based constraints.

Comparison with Other Topographic Algorithms

The SOM (36) and other algorithms applied to early visual cortex topographic organization (28, 30) each implement a form of local cooperation alongside broader competition. Specifically, in the SOM, global competition is implemented by selecting a winning unit on each trial and suppressing the responses of all other units, and local cooperation is mediated through Hebbian learning scaled by a Gaussian neighborhood around the winning unit. While the main ITN model is quite different from the SOM—employing error-driven rather than Hebbian learning, optimized rather than fixed lateral weights and receptive field sizes, and hierarchical organization—one of the simple ITN variants can be seen as conceptually similar to the SOM, and this may provide insight into the minimal components of topographic development in ITN models. Specifically, we found that a feedforward model employing local excitatory-only between-area connections and lateral connectivity limited to the layer normalization operation (EFF-FNN) was capable of producing many of the hallmarks of topographic organization in the main model (Fig. 6 and SI Appendix, Fig. S31). In EFF-ITN models, including this variant, the local excitatory feedforward connections (SI Appendix, Fig. S10) implement a form of local cooperation, ensuring that neighboring units are positively correlated; the layer normalization operation then implements a global competition by attempting to convert the distribution of preactivations to a standard normal distribution, which leads to sparser activity following rectification (the degree of which can be controlled by each unit’s bias term) and ensures that units represent different aspects of the feature space. Thus, layer normalization implements both competition and interactivity that, when combined with the local representational cooperation induced by local excitatory feedforward connections, leads to a smooth topographic organization whereby the unit feature tuning is systematically more similar for nearby units than for farther units. In recurrent ITN models, such as the main model, the learned lateral connections can adapt this competition and interactivity, allowing for increased performance (Fig. 6C). Moreover, these learned lateral connections may contribute to competition through learned broad inhibition (SI Appendix, Fig. S17).

Despite some conceptual similarities, there are some distinct advantages to ITNs relative to SOMs and other previous topographic mapping algorithms. First, ITNs are naturally hierarchical, allowing for multiple interacting levels of topographically organized representations, rather than assuming a single feature space to be arranged in a single topographic map. This allows the ITN to account for the presence of multiple domain-selective regions arranged in a stream from earlier to later parts of IT (1, 3, 87, 88) and (in future work) to incorporate connectivity with upstream and downstream areas to IT. Second, and relatedly, the connectivity constraints of the ITN can be incorporated into generic task-optimized neural networks, without requiring separate Hebbian updates to topographically organize the feature space following development of the feature space (as in the SOM), yielding a functional rather than purely organizational role for lateral connections. Finally, the ITN framework is very flexible, allowing for future research to examine different encoders, different IT architectures and topologies including more detailed modeling of neuronal circuitry, and different task training environments and readout mechanisms, yielding promise for a variety of future directions.

Limitations and Future Directions

The current work addresses only the topographic organization of high-level representations, since the connectivity constraints were not applied within the encoder model of early and midlevel vision. Modeling topographic organization in convolutional layers is a particular challenge for the ITN framework, as doing so over both retinotopic location and stimulus features—well-known organizing principles of early visual cortex—would necessitate that each channel have potentially different connections with other channels across different retinotopic positions, precluding the convolution. In point of fact, feature tuning in the brain is not actually uniform across the visual field (89, 90), and thus relaxing the convolution assumption has merits for advancing visual computational neuroscience and would enable more detailed connectivity-based topographic modeling of early and midlevel visual areas. It is now clear that convolution is not strictly required—fully connected visual “transformer” layers using multiplicative attentional interactions (91, 92) have recently been shown to reach high performance without convolution. These architectures, and other biologically plausible variants, thus serve as an exciting opportunity to examine topographic organization from connectivity-based constraints.

Relatedly, despite its strength in explaining hierarchical topographic organization owing to between-area spatial constraints, the ITN is not yet able to satisfactorily explain certain aspects of hierarchical representational transformation—specifically, increasing invariance to 3D rotation (14)—in contrast to the earlier convolutional layers of the encoder (SI Appendix, Figs. S13 and S14). This is related to the need to use nonconvolutional layers in model IT, rather than a result of the wiring or sign-based constraints, as an RNN-ITN model with λ = 0 shows the same plateau of representational invariance in the ITN layers (SI Appendix, Fig. S15). Thus, our work should be seen as a demonstration that within- and between-area connectivity constraints can give rise to within- and between-area topographic organization, but future research will need to bridge the gap to jointly explain the increasing invariance commonly seen in standard convolutional neural networks. This again points to the critical need for future work to extend the ITN framework to more powerful computational architectures, training environments, and learning rules (93), rather than relegating this computational power to a distinct encoder.

We also discovered some differences between the overarching representational space of the ITN models and primate IT. Namely, while the main ITN trained to recognize categories from three domains (faces, objects, and scenes) mapped these domains smoothly, the representational space elicited by a set of artificial object stimuli was less cleanly topographically organized (SI Appendix, Fig. S20A). In contrast, an alternative ITN model trained only on ImageNet (general results shown in SI Appendix, Figs. S18 and S19) mapped these objects in a smoother fashion more similar to primate IT (SI Appendix, Fig. S20B) (14). However, such a model cannot account for human expertise in face recognition (SI Appendix, Fig. S18B). Thus, each image set is limited in its ability to fully explain the empirical data. Future work employing more naturalistic datasets in which faces appear in the context of individuals in scenes alongside demands for individuation may lead to the development of representations that can more fully capture both the large-scale organization and behavioral demands of primate vision. We also found that a weaker spatial penalty resulted in less patchy topography for images outside the distribution of training images, such as the stimuli of ref. 14 (SI Appendix, Fig. S22). Thus, a more detailed comparison of how well different ITN models quantitatively and qualitatively explain IT cortex is an exciting line for future research.

While our work advanced biological plausibility beyond previous works, by incorporating wiring constraints, the separation of excitation and inhibition, and between-area excitatory connectivity, additional biological details are likely to be important to the computation and organization of the visual cortex. Future work may seek to consider incorporating details such as E/I neuron ratio, E/I balance, variability in neuronal time constants, divisive vs. subtractive inhibitory cell types, etc. Notably, the layer normalization operation is similar to divisive normalization and its effects in activity stabilization and global untuned inhibition might be modeled in a biologically plausible fashion in future work.

Finally, we focused on constraints local to the IT circuit, demonstrating that they can give rise to the presence of biologically realistic domain-level clusters and global generic organization. But in humans and nonhuman primates, domain-selective regions do not merely exist, but exist in consistent locations across individuals of a given species (3, 19, 48, 94, 95), albeit with modest yet reliable individual variability (96). The retinotopic organization of upstream early visual cortical areas is thought to encourage foveally biased cortex to support face representations and peripherally biased cortex to support scene representations (47, 97), and connectivity biases with downstream nonvisual areas are thought to play a further role in shaping the global organization of domain-selective areas in IT (47, 98–102). These biases, such as left-hemispheric language biases, other more fine-grained patterning of connections with domain-relevant downstream areas (i.e., socially responsive areas for faces, memory areas for scenes, motor areas for manipulable objects), and cross-modal map alignment (23, 80), should be explored in future work to understand better the factors underlying IT organization both within and between hemispheres. We hypothesize that modeling long-range connectivity-based constraints with regions external to IT (46, 47, 103) in an extended ITN architecture containing two hemispheres will give rise to reliable within- and between-hemisphere patterns of areal localization. Given that different initializations and architectural variants can yield interesting individual representational differences in deep-learning models (67), we expect that a systematic study of architectural variation in ITN models could lead to successful quantitative accounting of individual differences in human cortical topography and representation.

Conclusion

The interactive topographic network framework demonstrates that generic connectivity constraints can produce the central aspects of topographic organization in primate visual cortex. Extensions of the approach hold promise in accounting for the systematic localization of domain specialization both within and between hemispheres.

Data Availability

Code to reproduce our results and to develop and test new ITN models is available at https://www.github.com/viscog-cmu/ITN. Simulation results have been deposited in Kilthub (https://doi.org/10.1184/R1/17131319).

Change History

November 23, 2022: The Acknowledgments section has been updated to recognize funding.