Time-frequency analysis methods and their application in developmental EEG data

Abstract

EEG provides a rich measure of brain activity that can be characterized as neuronal oscillations. However, most developmental EEG work to date has focused on analyzing EEG data as Event-Related Potentials (ERPs) or power based on the Fourier transform. While these measures have been productive, they do not leverage all the information contained within the EEG signal. Namely, ERP analyses ignore non-phase-locked signals and Fourier-based power analyses ignore temporal information. Time-frequency analyses can better characterize the oscillations contained in the EEG data. By separating power and phase information across different frequencies, time-frequency measures provide a closer interpretation of the neurophysiological mechanisms, facilitate translation across neurophysiology disciplines, and capture processes not observed by ERP or Fourier-based analyses (e.g., connectivity). Despite their unique contributions, a literature review of this journal reveals that time-frequency analyses of EEG are yet to be embraced by the developmental cognitive neuroscience field. This manuscript presents a conceptual introduction to time-frequency analyses for developmental researchers. To facilitate the use of time-frequency analyses, we include a tutorial of accessible scripts, based on Cohen (2014), to calculate time-frequency power (signal strength), inter-trial phase synchrony (signal consistency), and two types of phase-based connectivity (inter-channel phase synchrony and weighted phase lag index).

Electroencephalography (EEG) is an established and practical tool for studying brain function, psychology, and psychiatry across development. Most developmental EEG work to date has focused on Event-Related Potentials (ERP) analyses or power analyses based on the Fourier transform. Although these measures have proven fruitful, they do not utilize all the information contained within the EEG signal. Namely, ERP analyses ignore non-phase-locked signals and Fourier-based power analyses ignore temporal information. Time-frequency (TF) analyses can better characterize the temporal dynamics of three of the features of oscillations contained in the EEG data: frequency, power, and phase. As such, time frequency measures provide a closer interpretation of the neurophysiological mechanisms and provide a link to multiple disciplines of neurophysiology (e.g., single-cell recordings, nonhuman animal work, intracranial EEG, and MEG). Time frequency computations can be both computationally intensive and intimidating to researchers who are beginning to characterize more aspects of the EEG signal. The goal of this paper is to provide a comprehensive and understandable tutorial and automated, but easily customizable, Matlab scripts to calculate TF power, inter-trial phase synchrony (ITPS) and two types of phase synchrony, inter-channel phase synchrony (ICPS) and weighted phase lag index (wPLI), for developmental EEG researchers.

We start by providing a theoretical overview of TF analyses, highlighting its advantages over other commonly used methods (e.g., ERPs and Fourier-based power). The goal of this first section is to provide the reader with the motivations behind TF analyses and a conceptual understanding of the main TF measures. In the following section, we cover how to estimate TF measures, including their mathematical definitions and how to use the publicly available code. After discussing the motivations and how to estimate TF measures, we discuss the limitations and the practical challenges of applying TF analyses for developmental data. Finally, we illustrate how to perform TF analyses with the code provided by using a dataset of adolescents.

1. Why time-frequency analyses?

Throughout the lifespan, from infancy to adulthood, EEG can be collected in laboratory and mobile environments (e.g., at home or in schools) at relatively low costs while maintaining excellent temporal resolution and being fairly robust to movement and noise, compared to other neuroimaging modalities. In the last several decades, EEG has been utilized to study the development of cognition, socioemotional abilities, and psychopathology. Historically, partly due to limitations in computational power, most EEG studies focused on ERP or Fourier-based power analyses. For example, we identified 177 empirical articles published in the journal Developmental Cognitive Neuroscience between 2011 and June of 2021 that examined EEG by searching for “EEG” in the journal’s search bar on the website and screening out studies that only mentioned EEG or were review articles. Of those 177 empirical articles, ~77% used ERPs, ~15% examined Fourier-based power, and ~4% used TF, and ~4% used other methods like signal complexity (e.g., entropy), frequency tagging (e.g., steady state visually evoked potentials), or microstates analyses. This quick search illustrates that even though TF analyses have been available to the EEG research community for several years (Delorme and Makeig, 2004), are widely used in the cognitive neuroscience literature, and there have been previous calls for the benefits of TF analyses on developmental EEG data (Maguire and Abel, 2013), TF analysis as an EEG method is still rarely used. Moreover, this review demonstrates that most studies in the developmental cognitive neuroscience field rely on ERPs and Fourier-based power.

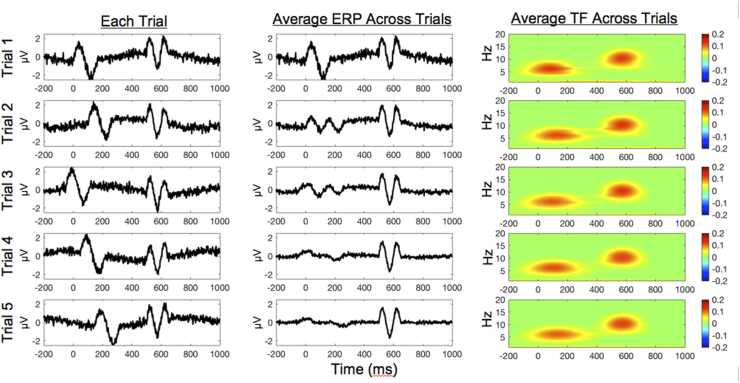
While ERPs and Fourier-based power are informative and have provided important insight to our understanding of the development of psychological phenomena, ERPs and Fourier-based power do not fully leverage all of the information in the EEG signal. ERP analyses assume that the component of interest is temporally synchronous across trials, only focusing on neural activity that is time-locked to the event of interest and disregarding signals that are not synchronized across trials (Luck, 2014). For example, as illustrated in Fig. 1, imagine you have two ERPs, one at 0 ms and the other at 500 ms. If these components vary slightly in their latency across trials (i.e., are not temporally consistent across trials) like the first component at 0 ms, the activity will be lost as noise as we average trials. In contrast, the second component at 500 ms is perfectly synchronous across trials and clearly retained when we average across trials. Although our example is clearly hypothetical, the assumption that brain responses are temporally synchronous across trials is not always met and is particularly questionable when examining developmental processes. For example, in a longitudinal sample of children, DuPuis and colleagues (2015) found that temporal consistency across trials increased with age from 5 to 9 years, partly explaining the age-related differences observed in the ERPs. Other studies have also found that the latency of brain responses significantly varied from trial-to-trial across development – with more trial-to-trial variability earlier in development (Gavin et al., 2019). Consequently, it is especially important to consider this variability when examining ERP in developmental populations, especially when comparing ERPs across age.

Fig. 1.

ERP and TF analysis comparison. On the left column, the figure shows a simulated EEG signal across five trials. The trials were simulated to have a non-phased-locked 6 Hz response around 0 ms and a phase-locked 10 Hz response around 500 ms. The middle column shows the average ERP of each trial and all previous trials. The third column is the average TF power of each trial and all previous trials.

2. Brain activity as oscillations

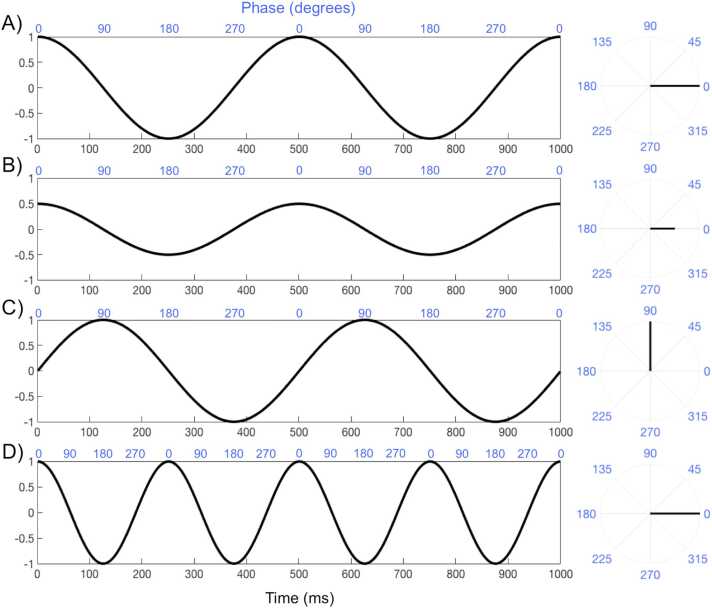
One possibility is to consider brain activity as oscillations, rather than as deflections in voltage at a specific time (i.e., ERPs). Characterizing EEG as oscillations has the advantage that brain activity can be characterized as several independent measures, such as frequency, amplitude, and phase. The frequency of an oscillation captures the number of full oscillations per unit time, usually one second, and is measured in Hertz (Hz). In Fig. 2A, we show a sine wave that completes two full cycles per second, so it has a frequency of 2 Hz. In contrast, the sine wave shown in Fig. 2D is oscillating faster, completing four cycles per second, having a frequency of 4 Hz. The other characteristic of these sine waves is that they cycle from 1 to − 1 around 0. This range or height of the oscillation represents the amplitude, which is the distance between the point of equilibrium and the highest and lowest points, so the waves shown in Fig. 2A and Fig. 2D both have an amplitude of 1. On the other hand, the oscillation shown in Fig. 2B has the same frequency as Fig. 2A, but smaller amplitude of 0.5.

Fig. 2.

Characteristics of oscillations. The left column shows the oscillations across time. The phase of oscillations is measured in degrees with 360 degrees, representing a full cycle of the oscillation. The phase is indicated by the blue numbers and also illustrated on the right column using a circular representation of the oscillations by using polar plots. A) Illustrates a 2 Hz sine wave with an amplitude of 1; B) Shows a 2 Hz sine wave with an amplitude of 0.5; C) Depicts the same sine wave as A, but with a different phase; D) Shows a 4 Hz sine wave with an amplitude of 1.

Finally, we can characterize an oscillation with respect to its phase. Phase is the position on the oscillation at a specific time (usually 0). In this way, we can use phase to estimate the alignment of the oscillations relative to a specific time, event, or other oscillations. For example, the waves in Figs. 2A and 2B have the same frequency and phase (i.e., they are perfectly aligned), such that both start at the peak of the oscillation. These are often referred to as “phased-locked” signals. On the other hand, Fig. 2C shows a wave identical to Fig. 2A, but it is shifted, starting at its equilibrium or zero. In other words, relative to the other oscillations (Figs. 2A and 2B), it is one quarter through its cycle so it is in a different phase of the oscillation. Phase is formally measured in degrees with 360 degrees, representing a full cycle of the oscillation. This is illustrated on the right column of Fig. 2 using polar plots. As shown in Fig. 2, the sine wave shown in Fig. 2C is 90 degrees (or ¼ of 360 degrees) compared to the waves shown in Figs. 2A and 2B. These signals, shifted in phase compared to each other, are often referred to as “non-phased locked” signals. Another example of non-phase locked signals is the component at time 0 ms on Fig. 1, which would not be captured by ERPs.

Now that we covered the basics of oscillations, we can highlight how these measures can be used to characterize brain activity. The most common way oscillations are used to characterize brain activity is by using the Fourier transform to measure the amount of activity in a given frequency. This approach is done by convolving sine waves at different frequencies with the EEG data to measure their amplitude at a given frequency. The activity or energy of the signal at a given frequency is commonly measured as power, which is the amplitude squared. Importantly, this measure of power at each frequency includes non-phase locked signals. However, it assumes that the signal is stationary, losing the rich temporal information embedded in the EEG signal. Moreover, when the signal is not stationary, the Fourier transform loses precision (Cohen, 2014). Except for resting state paradigms or short-time windows (hundreds of a second), this assumption is likely violated as psychophysiological processes change across time because of external and internal processes. Going back to our example on Fig. 1, if we think of our ERP components as oscillations, a Fourier-based analysis (not shown) would reveal increased power around 6 Hz and around 10 Hz, which are the frequencies in which the components at 0 and 500 ms occur, respectively. However, Fourier-based analyses would not be able to indicate when in the trials 6 Hz and 10 Hz increases in power occur. Thus, it is of interest to examine measures that capture phase and non-phase locked signals as well as how these signals change across time. Finally, Fourier-based analyses are rarely used to examine the phase of the signal in developmental studies.

TF analyses measure the dynamic changes in amplitude and phase of neural oscillations across different frequencies. By differentiating between amplitude and phase information, both phase-locked and non-phase-locked signals can be studied in relation to an event of interest. For example, returning to Fig. 1, we have a 6 Hz non-phase locked oscillation at 0 ms that is not captured by ERPs, but is clearly observed in the TF representation as an increase in signal strength or power at 6 Hz between 0 and 200 ms. Similarly, TF analyses capture the 10 Hz phase-locked oscillation at 500 ms as an increase in power at that time and frequency. As a separate measure, TF analyses also provide an estimate of the phase across time for a given frequency. This phase information can be examined for its consistency or synchronicity across trials. This measure is commonly referred to as inter-trial phase synchrony (ITPS; but also as inter-trial phase clustering or phase-locking value). In our example in Fig. 1, the non-phase locked component at 6 Hz yields an ITPS value of ~.23 from 0 to 200 ms. In contrast, the phase-locked component at 10 Hz results in an ITPS of 1.0, indicating perfect phase consistency across trials. In addition to examining the consistency of phase oscillations across trials (ITPS), TF analyses can also examine the consistency of phase oscillations across different electrodes across trials or time. This measure is often interpreted as a measure of connectivity between electrodes and is called inter-channel phase synchrony (ICPS). We will discuss ICPS in detail below, but conceptually (and mathematically), it is similar to ITPS. The difference is that ICPS is examined between two electrodes, while ITPS is calculated within the same electrode.

3. Benefits of TF analyses

A major strength of TF analyses over other EEG methods is their interpretability. Because neuronal oscillations are a fundamental property of the brain (Buzsaki, 2004), TF measures provide more direct information regarding the neurophysiological mechanisms underlying the processes captured by the EEG data. This also provides a link to multiple disciplines of neurophysiology (e.g., single-cell recordings, nonhuman animal work, intracranial EEG, and MEG). For example, by using TF analyses, it is possible to study shared processes across species like neural responses to errors – as TF analyses reveal similar brain responses in similar frequency and timing between humans, non-human primates, and rodents (Narayanan et al., 2013, Tsujimoto et al., 2006, Womelsdorf et al., 2010).

Because TF analyses provide separate measures of signal strength (power), phase consistency across trials (ITPS), and connectivity (ICPS), they may provide unique insight into the development of neurocognitive processes. For example, emerging evidence suggests that TF analyses are able to capture developmental changes when they are not evident when using traditional approaches like ERPs. For example, Bowers et al. (2018) and Morales et al. (2021) did not observe age-related differences in using ERPs, but observed age-related increases in both the strength (power), consistency (ITPS), and connectivity (ICPS) of the neural responses to feedback and error processing, respectively. These results suggest that TF analyses, by distinguishing between power and phase information at specific frequencies, may be more sensitive to detect developmental changes. Moreover, even if age-related changes in ERPs are observed, TF analyses may also help provide a more nuanced understanding of the developmental processes underlying the developmental changes observed with ERPs (Bishop et al., 2011, DuPuis et al., 2015). For instance, in a prospective study in early childhood, an ERP component in response to errors showed increases in amplitude from ages 5–7 years. Importantly when examining the same data with TF analyses, phase synchrony, but not power, mediated the developmental changes observed in the ERPs (DuPuis et al., 2015), implying that age-related increases in the signal consistency, rather than signal strength (power), underlay the age changes observed in this ERP. A recent study further supported this conclusion by measuring the trial‐to‐trial latency variability in the ERP by using an Adaptive Woody technique finding that variability significantly decreases across age (7–25 years). Moreover, adjusting for the trial‐to‐trial latency variability reduced the age-related difference initially observed in the ERP (Gavin et al., 2019). Together these studies illustrate the importance of examining signal strength (power) and consistency (ITPS) separately, as these separate signal components are confounded in ERPs.

Finally, there are several processes that can only be captured by using TF as they do not generate clear ERP components. They can also be captured with Fourier-based power, but this may miss important temporal dynamics. One example of such processes is an EEG measure to capture activity of the mirror neuron system, called mu desynchronization (Fox et al., 2016). Mu rhythm reflects EEG activity occurring in the alpha range (~8 −13 Hz in adults and ~6 −9 Hz in infants and children) over the motor cortex (i.e., C3 and C4) that decreases in amplitude when an individual executes or observes an action. For example, in a sample of infants, Debnath et al. (2019) found mu desynchronization when executing and observing actions. Importantly, the mu desynchronization during action observation was only present for movement onset and was not observable for movement completion, which even showed some mu synchronization. Using a Fourier transform over a traditional, larger time window (e.g., 500–1000 ms) would have likely missed these crucial dynamics; however, TF analyses are better suited to capture the brain’s dynamics on a finer timescale. As a further illustration of the advantage of TF analyses, in the same study, the phase information was leveraged to examine the connectivity between different brain regions. Results showed increased connectivity between the visual and motor cortex during action observation, compared to connectivity between other brain areas, providing further evidence of mirror neuron system activity when infants observed others’ actions.

In sum, TF analyses have several notable advantages over the most commonly used ways of analyzing EEG data in developmental cognitive neuroscience: ERPs and Fourier-based power. In the next section, we discuss more details on how to compute TF analyses.

4. Computing TF analyses

4.1. Convolution

The main operation behind TF analyses is called convolution. Convolution is a procedure that involves combining two signals to produce another signal that captures the aspects that are common or shared between the two original signals. In this way, convolution can be conceptualized as a measure of the similarity between two signals. Mathematically, the first step of convolution involves computing the dot product between two signals. The dot product involves multiplying two signals, element by element, and then summing all their products:

$$\mathit{Dot}{\mathit{Product}}_{\mathit{ab}}=\sum _{i=1}^n{a}_i{b}_i$$

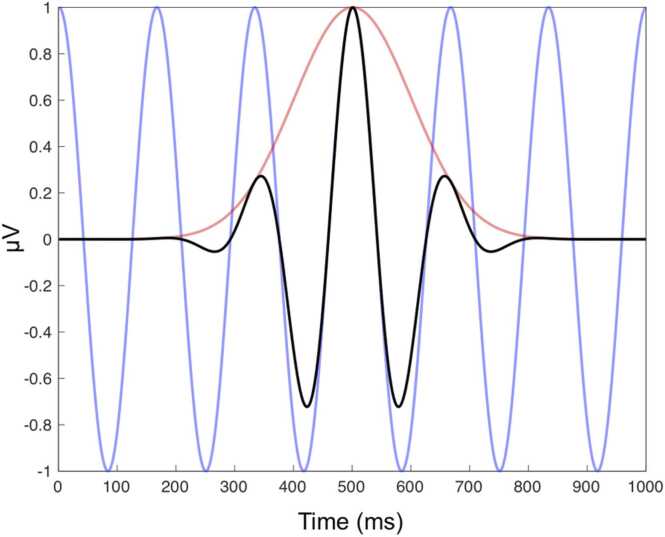
Where a is the first signal, for TF analyses this would be the EEG signal, and b is the second signal, for TF analyses this would be a signal with a predefined/known function, called the kernel. For Fourier-based analyses, the kernel used is a sine wave. Because sine waves are constant over time, Fourier-based analyses are not able to provide time information and just provide frequency information. For TF analyses, rather than using a sine wave, a time-varying sine wave is used. These time-varying sine waves are called wavelets and are an oscillation whose amplitude starts at zero, increases, and then decreases. The most commonly used wavelets are called Morlet or Gabor wavelets. Morlet wavelets are the combination of a sine wave and a Gaussian window. Namely, it is not tapered at the center and it is symmetrically filtered/dampened. An example of a Morlet wavelet and its relation to a sine wave and a Gaussian window is shown in Fig. 3.

Fig. 3.

Example of Morlet wavelet and its relation to sine waves. A 6 Hz sine wave (blue) is convolved with a Gaussian filter (red), which produces a Morlet wavelet (black). (For interpretation of the references to colour in this figure, the reader is referred to the web version of this article.)

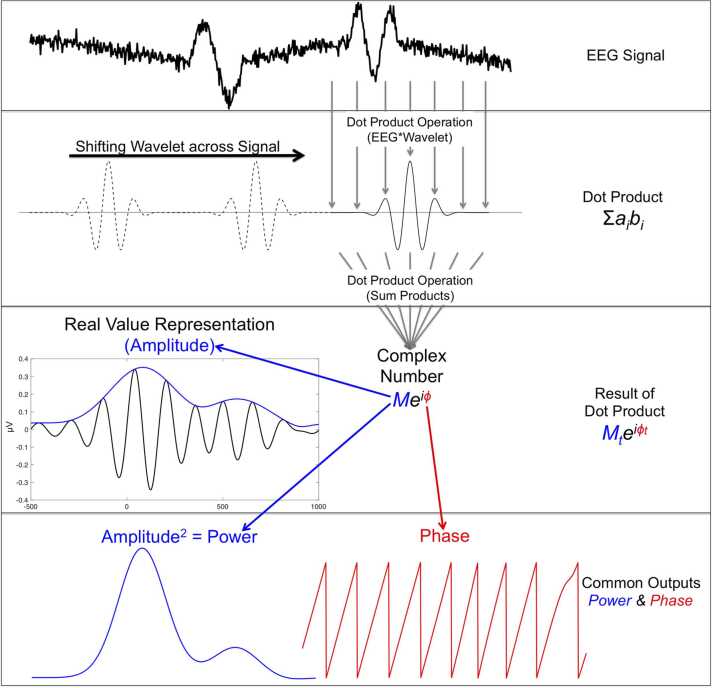
Convolution involves performing the dot product repeatedly over time. As shown in Fig. 4, this is performed by sliding/shifting the wavelet across the EEG signal. The result of convolution is a new time series that captures the similarity between the EEG and the wavelet of interest. For example, in Fig. 4, we convolve the first trial from Fig. 1 and a 6 Hz wavelet, capturing all the 6 Hz oscillations, which are greater around 0 ms. For TF analyses, convolution is actually performed using complex Morlet wavelets. The reason they are called “complex” is because they are composed of a real and an imaginary component. Because the main goal of the current article is an accessible introduction to TF analyses to developmental psychologists or neuroscientists, we will not cover in the detail complex numbers here – interested readers can find more in-depth explanations in Cohen (2014). For the purposes of this article, the main thing to know about complex numbers is that by utilizing both the real and imaginary components, it is possible to independently measure the amplitude of the oscillations as well as their phase. In this way, convolving the EEG signal and a complex Morlet wavelet produces a time series of complex numbers. Mathematically, the convolution process can be characterized by the following formula:

$$M_{\mathit{tf}}{e}^{i{\varphi }_{\mathit{tf}}}$$

Where M corresponds to amplitude, $\varphi$ indicates the angle of the phase, e is the base of the natural logarithm, and i is the imaginary unit. Moreover, all of the terms have subscript t, to indicate that this is applied across time as the wavelet is shifted across the EEG signal, creating a time series at frequency f. Fig. 4, illustrates the convolution process and how this is done repeatedly, obtaining the amplitude (M) and phase ($\varphi$) for each time point. Although we illustrate the convolution procedure with a 6 Hz wavelet, the process can be repeated with wavelets of different characteristics (e.g., different frequencies), allowing researchers to capture the amplitude and phase information of the EEG signal across time and frequencies. Thus, it is important to carefully select the characteristics of the wavelets, which can be done by defining different parameters (see below). Now that we have covered convolution as a fundamental operation of TF analyses, we can discuss the main outcomes of TF analyses: power and phase synchrony.

Fig. 4.

Convolution with complex Morlet wavelet to measure amplitude and phase of oscillations across time for each frequency. The EEG signal is convolved with a complex Morlet wavelet using the dot product (element-by-element multiplication and summing the products), creating a complex number. This process is repeated across the signal by shifting the wavelet across the signal, yielding a time series of complex numbers. These complex numbers contain information about the amplitude (M) and phase ($\varphi$) of the oscillations for each time point. This process can be repeated with wavelets of different characteristics like different frequencies to capture the amplitude and phase information of the EEG signal across time and frequencies.

4.2. Time frequency power

Examining TF power is one of the most common ways that researchers employ TF analyses. Developmental researchers have utilized TF power analyses to link a variety of TF dynamics to cognitive and affective processes including auditory discrimination (Bishop et al., 2011), conflict and error processing (Buzzell et al., 2019, 2020), social rejection (Morales et al., 2019), processing others actions (Debnath et al., 2019, Meyer et al., 2020), learning and cognitive engagement (Begus and Bonawitz, 2020, Meyer et al., 2019), as well as reward processing (Bowers et al., 2018, Nelson et al., 2018). In order to measure the temporal dynamics of TF power over a period of time in different frequency bands, researchers utilize the convolution procedure previously described, also called time-frequency decomposition, to isolate the amplitude of the signal at each time and frequency. The amplitude is usually squared as a measure of power (μV²; Fig. 4). This measure of TF power captures the amount of energy or the signal strength at a specific time and frequency. The TF decomposition from each trial is then averaged together to reveal the amount of total power. Included in total power are both phase locked and non-phase locked activity. Phase locked activity is also called evoked power and non-phase locked activity is also referred to as induced power. Although it is possible to separate these forms of power, analyzing total power is the most common way TF analyses are used.

After averaging over trials to compute total power, there are several potential confounding factors when interpreting these values of “raw” total power. First, raw total power values are heavily influenced by outside factors like skull thickness, electrical activity in the recording location, and cortical anatomy. Similarly, raw total power values are affected by underlying background neural activity that is occurring regardless of event-related activity (e.g., increased background activity could lead to what seems like increased event-related activity). Also, raw total power values can only be positive, as they are the squared amplitude, creating a skewed distribution. Finally, the nature of the frequency power spectrum, with lower frequencies having higher levels of power and higher frequencies having lower levels of power, makes comparing low frequency and high frequency activity difficult. To rectify some of these issues, researchers generally use the decibel conversion below to baseline normalize raw total power values:

$${\mathit{dB}}_{\mathit{tf}}=10*\mathit{log}10(\frac{{\mathit{Activity}}_{\mathit{tf}}}{{\mathit{Baseline}\mathit{Activity}}_f})$$

Where the average activity across trials at time t and frequency f is divided by the average activity over the baseline period at frequency f, log10 transformed, and multiplied by 10, producing decibels (dB). After baseline normalization, all activity will be on the same scale and any activity common to the average baseline time period will be removed, allowing for TF power to be interpreted as levels of activity relative to the baseline period; thus, the baseline time period should be carefully selected by the researcher, as there are several factors to consider.

Ideally, the baseline period would be as long as the event of interest to provide a comparable time period, cancel out any potential random fluctuations in activity, and thus, provide a robust and representative measure of pre-stimulus activity. However, because of the brain activity is rapidly changing and there are no time periods in which the brain is “at rest,” having a long baseline could lead to the inclusion of other cognitive processes (e.g., a child adapting from the previous trials or getting distracted). Moreover, and particularly relevant to developmental data, having a longer baseline period creates longer epochs, which will likely lead to higher rates of trials being rejected because of artifact contamination. Finally, a baseline that is further away from the event of interest will make it less comparable due to cognitive changes and differences in signal drift. Because of this, using a time period that is 10–20% of the overall epoch duration is recommended (Luck, 2014). Because in most cases epochs range from 1.5 to 2 s, commonly used baseline windows are 200–400 ms. However, this is not a strict rule. It is important to consider the most appropriate time for a specific study (e.g., it is better to use 100 ms that are particularly suited to serve as a baseline period than 400 ms that are contaminated by previous events). When unsure, it is recommended to examine different baseline periods and examine activity of the baseline period to ensure that it is the most appropriate (Cohen, 2014, Luck, 2014).

A final point of consideration for TF analyses, compared to ERPs, is that baseline windows for TF analyses should usually stop before the start of the event of interest. This is because of temporal smearing (see Section 5 below). As such, TF analyses often use a few hundred milliseconds and ends prior to the event of interest – usually time zero (e.g., −300 to −100 ms). Moreover, it is often not necessary for the baseline to have its own epoch – unless the study design does not have the baseline right before the event of interest. In that case, the baseline condition should ideally have a similar length to the epoch of interest. It is important to keep in mind these considerations about choosing a baseline not only when analyzing the EEG data, but also when designing the study to ensure an appropriate baseline time window. Finally, while decibel conversion is a common type of baseline normalization, there are other methods, which may be useful, including percent change or z-scored baseline normalization (see Cohen, 2014 for more details).

Traditional baseline-normalized time frequency calculations are commonly displayed in a time by frequency plot, in which power is color coded with warmer colors to indicate more power and cooler colors to indicate less power. An example of these plots was shown on the rightmost column of Fig. 1, illustrating how power changes at different frequencies over the time period of interest. Additionally, results can be displayed in a topographic plot that shows where on the scalp power at a certain time and frequency is maximal over the electrode montage.

4.3. Phase synchrony

The other main outcome of TF analyses is the phase information of the EEG signal. As with power, the phase information can be captured for each time point at different frequencies. This phase measure provides information about the timing of the oscillations at a specific frequency and can be examined across trials to capture how consistent or synchronous the phase of the oscillations is across trials (e.g., does the oscillation rise and fall at the same time across trials; Fig. 2). This measure is often called phase synchrony, but is also known in the literature by a variety of names such as coherence, phase clustering, and phase locking – to name a few. Phase synchrony can be estimated by averaging the phase angle values across trials. However, phase angles cannot be simply averaged like an ERP or TF power because phase angles are circular, rather than linear. Due to this circular distribution, the average of the phase angle differences is computed via vector math, in which phase angles are represented in a complex plane with real and imaginary components (for more details see Cohen et al., 2014). The resulting vector is a value between 0 and 1 with a lower value representing less consistency and a higher value indicating greater consistency.

4.3.1. Inter-trial phase synchrony (ITPS)

One manner in which phase synchrony can be applied in TF analyses is inter-trial phase synchrony (ITPS) or inter-trial coherence. ITPS is a measure of phase consistency at a specific time and frequency when examined across trials. Generally, event-related EEG paradigms include multiple trials of various types or conditions that are time-locked to a specific event of interest (e.g., presentation of a stimulus or a participant’s response). ITPS captures the consistency of the EEG activity to the event of interest at a specific time and frequency – with higher ITPS values reflecting more consistency (1 = perfect consistency) and decreased ITPS representing closer to random phase alignment time-locked to events of interest (0 = random phases at that time–frequency point across trials). Mathematically, ITPS is calculated using the following equation:

$$\mathit{ITPS}=\left|\frac{1}{n}*\sum _{x=1}^n{e}^{i{\varphi }_{\mathit{tf}}}\right|$$

which represents the average of the phase angle ($\varphi$) vectors of n trials on trial x at timepoint t and frequency f. Developmental researchers have used ITPS to examine the consistency of the brain responses to specific events to examine error processing (DuPuis et al., 2015, Gavin et al., 2019, Morales et al., 2021), reward processing (Bowers et al., 2018), and auditory discrimination (Bishop et al., 2011). Across studies and event types, results often show that signal consistency increases with age. The mechanisms behind these increases in consistency are unclear, but they have been interpreted as increased variations in the timing of the activation and the coordination of various sensory and motor neural circuits (Gavin et al., 2019) as well as variability in the neural representations of the stimuli (Buss et al., 2006, Buss et al., 2009).

One important caveat is that, in instances with largely different numbers of trials between conditions or participants, ITPS estimates can be biased. Specifically, for the instances that have fewer trials, ITPS estimates can be artificially inflated for that condition/participant (Cohen, 2014). Thus, it is useful to employ a strategy that equates the number of trials across conditions. For example, a subsampling procedure selects an amount of trials at random and calculates the phase synchrony measure for that random subsample of trials. This procedure is then repeated for a specified number of subsamples. By using this subsampling approach, conditions with unequal numbers of trials can be equated to reduce the inflated estimates of phase synchrony measures for conditions with fewer trials. Moreover, to further mitigate the impact of unequal numbers of trials and to isolate the events of interest (e.g., responses to a stimulus or action), it is also possible to perform a baseline correction similar to the one done for ERPs. This is done by subtracting the average ITPS during the baseline (e.g., −300 to −100 ms relative to the event of interest) time window from the rest of the epoch.

4.3.2. Phase synchrony as a measure of connectivity

In addition to ITPS, phase synchrony can be examined across channels as an indicator of the consistency in the phase of the signals for a given frequency. This measure has been interpreted as a measure of connectivity between different electrodes across the scalp (Cavanagh et al., 2009). The rationale behind this interpretation is that brain areas communicate with each other by using synchronized neural oscillations (Fries et al., 2005, Singer, 1999). Developmental researchers have used this measure to examine the connectivity in the Mu (alpha) band between visual areas and motor areas to study infant’s processing of others’ actions (Debnath et al., 2019) as well as connectivity between medial prefrontal cortex and lateral prefrontal cortex to study cognitive control (Bowers et al., 2021, Buzzell et al., 2019).

Quantifying inter-channel phase synchrony (ICPS) is similar to ITPS, but rather than examining consistency of phase across trials, ICPS calculates phase synchrony between different channels. Thus, ICPS uses similar phase angle vector math as ITPS. The formula for ICPS is similar to ITPS, but rather than estimating the average phase vectors across trials, the average of the phase angle differences between two channels is calculated. If the phase angles from the two channels fluctuate synchronously over time, their difference will be constant, producing ICPS values close to 1. In contrast, if the phase angles from the two channels fluctuate randomly to one another over time, their difference will be highly variable, producing ICPS values close to 0. The ICPS measure is formalized in the following equation:

$$\mathit{ICPS}=\left|\frac{1}{n}*\sum _{x=1}^n{e}^{i\left[{\varphi }_{\mathit{jtf}}-{\varphi }_{\mathit{ktf}}\right]}\right|$$

which represents the average of the phase angle ($\varphi$) differences between channel j and channel k of n trials on trial x at timepoint t and frequency f.

One limitation to EEG analyses between electrodes is the poor spatial resolution of EEG. Due to volume conduction, signals generated by one source can propagate to different areas of the scalp and readings recorded at one location on the scalp have activity from multiple generators. However, there are some transformations or filters that can be applied to the EEG signal to mitigate volume conduction. For example, current source density or a Laplacian transform works to attenuate broadly-distributed (e.g., diffusely synchronized) activity, which would be indicative of volume conduction (Tenke and Kayser, 2012). In order to calculate ICPS with a greater degree of spatial specificity, these transformations must be applied to the data before ICPS is calculated. Importantly, these transformations require a certain number of electrodes to be accurate and should not be used for a low-density electrode montage (e.g., < 64 channels).

An alternative to using a data transformation prior to ICPS calculation is to use a different algorithm called weighted phase lag index (wPLI). The phase lag index (PLI) measures lags or leads of the phase between two different electrodes (or clusters). The PLI mathematical formula discards phase differences of 0 or 180 degrees (see Fig. 2), which are most likely caused by volume conduction, by averaging the sign of the estimated phase difference. However, using PLI risks missing true instantaneous interactions (Cohen, 2015). In contrast, wPLI weights the magnitude of the lag instead of removing all 0 or 180 degree phase difference (for the mathematical details of this measure, see Vinck et al., 2011), de-weighting estimates that are likely due to volume conduction, becoming less sensitive to noise, and showing a more reliable relationship with true phase consistency. Thus, while it does not completely mitigate concerns about volume conduction, wPLI does reduce concerns about volume conduction and the necessity of a spatial transform. In the developmental cognitive neuroscience literature, studies have recently used wPLI as a measure of connectivity in relation to parenting quality (Perone and Gartstein, 2019), physical growth (Xie et al., 2019), cognitive development (Xie et al., 2019), and neurodevelopmental disorders like autism (Haartsen et al., 2019, Orekhova et al., 2014) and attention deficit hyperactivity disorder (Debnath et al., 2021).

These phase-based measures of connectivity (ICPS and wPLI) can be calculated between every electrode on the head, called “all-to-all connectivity.” Conversely, if the researcher has an a priori hypothesis about connectivity between two specific regions, ICPS and wPLI can be calculated from one seed electrode to the other electrodes of interest, called “seed-based connectivity.” All-to-all methods can be computationally intensive, especially with high-density electrode montages. Furthermore, connectivity matrices (e.g., from all-to-all connectivity) can be subsequently examined using network and graph theory metrics, providing a characterization of the overall network. For example, developmental researchers have utilized such methods to characterize the development of attention networks in infancy (Xie et al., 2018) or resting state networks across childhood (Miskovic et al., 2015).

Finally, in addition to quantifying ICPS and wPLI over trials, these phase-based measures can be estimated for each trial averaging over time – known as connectivity over time rather than over trials (Cohen, 2014). As discussed in the sections above, ICPS/wPLI over trials results in a frequency by time matrix so the researcher can see periods of increased or decreased ICPS/wPLI over the time period of interest at each channel of interest. Alternatively, ICPS/wPLI over time results in a frequency by trials matrix, which removes the time dimension, but allows the researchers to examine connectivity (ICPS/wPLI) over an entire epoch changes per trial. For example, Colomer et al. (2021) utilized ICPS over time to examine functional connectivity between visual and motor brain areas during action observation and how this connectivity varies as a function of infants’ previous experiences.

These different TF frequency measures are summarized in Table 1, in which we provide their mathematical and conceptual definition as well as studies that have used them with developmental populations.

Table 1.

Summary of Time-Frequency Measures.

Measure	Formula	Definition	Example Studies
TF Power	$\mathit{TF\; Power}=\frac{1}{n}*\sum _{x=1}^n{\left(M_{\mathit{tf}}\right)}^2$	Signal strength at a specific time and frequency	(Bishop et al., 2011, Bowers et al., 2018, Buzzell et al., 2020, Morales et al., 2019, Nelson et al., 2018)
ITPS	$I\mathit{TPS}=\left|\frac{1}{n}*\sum _{x=1}^n{e}^{{i\varphi }_{\mathit{tf}}}\right|$	Phase consistency at a specific time and frequency examined across trials	(Bishop et al., 2011, Bowers et al., 2018, DuPuis et al., 2015, Gavin et al., 2019, Morales et al., 2021)
ICPS	$\mathit{IC}\mathit{PS}=\left|\frac{1}{n}*\sum _{x=1}^n{e}^{i\left[{\varphi }_{\mathit{jtf}}-{\varphi }_{\mathit{ktf}}\right]}\right|$	Phase consistency at a specific time and frequency examined across a pair of electrodes or clusters	(Bowers et al., 2021, Buzzell et al., 2019, Debnath et al., 2019, Morales et al., 2021)
wPLI	$\mathit{wPLI}=\left|\frac{\sum _{x=1}^n\left|\mathit{Imag}\left[{\mathit{e}}^{i\left({\varphi }_{\mathit{jtf}}-{\varphi }_{\mathit{ktf}}\right)}\right]\right|\mathit{sgn}\left(\mathit{Imag}\left[{\mathit{e}}^{i\left({\varphi }_{\mathit{jtf}}-{\varphi }_{\mathit{ktf}}\right)}\right]\right)}{\sum _{x=1}^n\left|\mathit{Imag}\left[{\mathit{e}}^{i\left({\varphi }_{\mathit{jtf}}-{\varphi }_{\mathit{ktf}}\right)}\right]\right|}\right|$	Phase consistency at a specific time and frequency examined across a pair of electrodes or clusters that minimizes activity likely due to volume conduction	(Debnath et al., 2021, Haartsen et al., 2019, Perone and Gartstein, 2019, Orekhova et al., 2014, Xie et al., 2019)

5. Challenges and Limitations of TF Analyses

TF measures are extremely informative as they allow for investigating time, frequency, phase and power dynamics of neural oscillations. However, calculating these measures does have some challenges and limitations. First, on a practical note, the computation of these different characteristics of the neural signal can be both computationally intensive and time consuming, especially compared to other EEG analyses like ERPs or Fourier-based power. We recommend using a high-powered computer or high-performance computing cluster to run these analyses in order to ensure enough memory and computing power. Additionally, the code creates large multidimensional matrices for each participant and condition that must be stored for later plotting and analyses (see below for down sampling suggestions to alleviate this concern).

Another challenge is that TF analysis yields a large number of measures, creating a multiple comparisons problem. One way to overcome this challenge is to use the existing literature to define a priori the different regions of interest (e.g., scalp locations, time periods, or frequency bands). However, at times, this can be difficult, especially with developmental data, which may not produce the same pattern of results as expected based on adult data. For example, the frequency bands commonly used in adults might be different for infants and children (Marshall et al., 2002). Another approach to alleviate this problem is to use non-parametric cluster-based approaches to account for the dependencies between sample points across topography, time, and frequencies, while at the same time controlling for the family-wise error rate (Maris and Oostenveld, 2007). Importantly, this approach is data driven and can be done for a condition contrast or for a relation with an individual difference measure of choice (see FieldTrip’s online documentation). Another approach is to use dimension reduction techniques like principal component analyses to characterize the time-frequency information into a subset of parameters that capture meaningful activity (Bernat et al., 2005).

Another limitation of TF analyses is the trade-off between frequency and time. In general, TF analyses that use the wavelet transform, as described in this article, represent lower frequencies with higher frequency resolution and lower/coarser time resolution. The reverse is true for higher frequencies, such that frequency resolution is coarser and time resolution is higher. This can potentially lead to some low frequency neural processes that are close in time to be smeared together, making it hard to dissociate them (e.g., distinguish pre- and post-event dynamics). To ameliorate this issue, it is possible to use a different kind of time-frequency decomposition like Cohen's class reduced interference distributions, which yields uniformly high resolution in both time and frequency (Bernat et al., 2005). For example, Buzzell and colleagues (2019) used this approach together with TF principal component analyses to distinguish between pre- and post-response theta power dynamics.

Another important issue to consider when examining time-frequency analyses is the nature of the oscillations. In the current manuscript, we have assumed that neuronal oscillations have a sinusoidal shape. Although this is a reasonable assumption for EEG data (Cohen, 2019), brain oscillations might not be shaped exactly like sine waves (Cole and Voytek, 2017) and there are instances in which this may lead to spurious results, especially when examining coupling across frequencies (Donoghue et al., 2021). Another assumption of brain activity as described in the current manuscript is that oscillations are relatively stable and continuous across trials, rather than occurring in bursts. Recent evidence suggests that brain activity, especially at higher frequencies like beta and gamma (>15 Hz), might occur in bursts rather than as sustained oscillations (Jones, 2016, Sherman et al., 2016). However, when these brief periods of activity are averaged across trials, they might appear as sustained oscillations. A solution is to examine trial-by-trial activity to ensure that the interpretation of averaged power is supported. For a more detailed discussion of these assumptions, along with recent recommendations and solutions, see Donoghue and colleagues (2021).

Because TF measures are relatively newer in developmental cognitive neuroscience research, fewer standards exist (e.g., minimum trials). Pediatric and clinical populations pose a unique challenge because participants are not always able to sit still or pay attention for the length of time needed to collect the optimal number of trials. Current work is beginning to examine the robustness of TF measures in developmental populations and the minimum number of trials needed to observe the effect of interest and reach acceptable internal consistency reliability (Morales et al., 2021). Initial findings from a study of 4- to 9-year-olds’ responses to errors found that TF measures and ERPs required a similar number of trials to observe an effect of interest – in this case error vs. correct contrasts. Effect sizes increased with the number of trials and age (for measures that showed age-related effects). However, for this specific contrast (error vs. correct) ERP and TF measures showed large effect sizes with only 4–12 trials. This suggests that to detect error-related effects using TF or ERP measures, a large number of trials might not be as practically relevant as the age of the participants. Importantly, the number of trials needed to detect a significant difference between conditions depends on the effect of interest. Future studies should examine other psychological phenomena, as error-related effects might be particularly robust.

For reliability, TF measures required similar numbers of trials as ERPs to achieve acceptable internal consistency reliability (≥0.60), ranging from 8 to over 32 trials depending on the measure, condition of interest, and age of the participant. In general, younger participants, measures related to correct responses (compared to errors), and phase-based measures (ITPS and ICPS) need more trials to achieve acceptable reliability (Morales et al., 2021). Similarly, in a longitudinal examination of children’s responses to errors from Kindergarten to second grade (5–7 years), signal strength (power) showed high levels of stability across the three assessments – stronger than ERPs, which displayed low-to-moderate stability, and phase-based measures, which did not show stability across development (DuPuis et al., 2015). Together, these results suggest that signal consistency and connectivity measures may require more trials than ERP and TF power measures.

The number of trials required to obtain a reliable signal per condition poses an important challenge to developmental EEG, especially investigations interested in individual differences. However, this challenge is not unique to TF measures and likely impacts any type of event-related EEG data similarly, as for most TF investigations the epoch length can be similar to ERPs (e.g., 1500–2000 ms, except when examining 1-Hz delta; see above). Even in the adult literature, which likely deals with higher signal-to-noise data than developmental data, it is commonly recommended to use over 40 trials per condition for both ERPs and TF measures (Cohen, 2014, Luck, 2014). Future studies should develop processing algorithms that effectively remove artifacts to maximize the data collected and use experimental paradigms that yield high signal-to-noise measures. Moreover, developmental EEG researchers could utilize a multi-session approach recently employed in other neuroimaging modalities (e.g., fMRI; Ellis et al., 2020), in which the same participant is repeatedly assessed in a short period of time to provide enough data in each condition of interest. Finally, it is important to emphasize that these are initial investigations regarding the reliability of TF measures in developmental populations and have only focused on error monitoring. Even the limited evidence highlights that reliability depends on several factors (e.g., age, condition, and measure). Because of this, researchers must examine the psychometric properties of TF measures calculated in their own data and be cognizant of potential nuances of TF psychometrics for different tasks, different ages, and different populations. For this, there are emerging publicly available tools to assist and encourage each EEG study to examine and report the reliability for their specific measures (Clayson and Miller, 2017, Morales et al., 2021, Parsons, 2021).

6. Computing TF using Matlab

TF measures can be computed using a variety of software, including both script-based and GUI-based programs like FieldTrip (Oostenveld et al., 2011) and EEGLAB (Delorme and Makeig, 2004) – both of which have excellent tutorials on their respective websites. We chose to implement our TF analysis script in Matlab, so that the user can both easily edit the code for their specific needs, unlike a GUI, and to eliminate any type of “black box” feel as our script allows a novice user to see exactly how the code manipulates data. Our scripts utilize the EEGLAB data format, are largely based on Cohen (2014), and can be accessed here: osf.io/taed5.

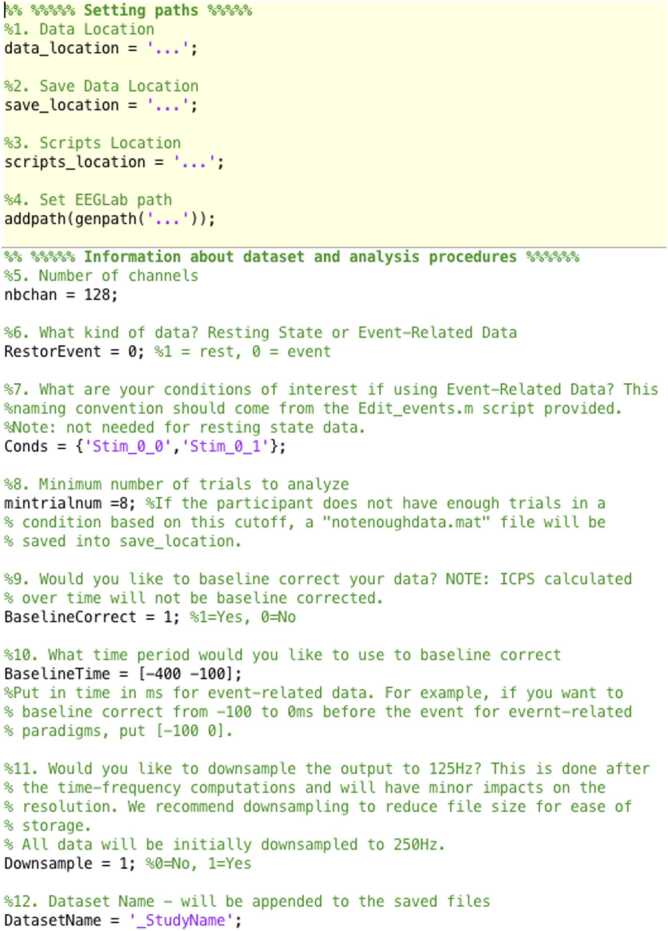
The input to the code should be cleaned and epoched data. These TF scripts can analyze both resting state and event-related data. The initial TF analysis script (MainScript_Calculate_TF_ITPS_ICPS.m) includes a variety of settings and parameters for the researcher to choose from. As shown in Fig. 5, the scripts begin with the user inputting the paths indicating 1) the data_location path to folders that contain the data to be analyzed, 2) the save_location path to the folder in which they would like the data to be saved, 3) the scripts_location path to the location of the scripts, and 4) the path to the location of EEGLAB (see EEGLAB’s documentation for how to install this toolbox).

Fig. 5.

Settings and dataset information to be input by the researcher for the first script called “MainScript_Calculate_TF_ITPS_ICPS.m.”.

Next, the user inputs some information about the dataset and analysis procedures (Fig. 5). The researcher inserts the number of channels (nbchan) and whether it is resting or event-related data (RestorEvent). If resting state data has multiple conditions (e.g., eyes open vs. eyes closed), we recommend inputting that data as event-related. If the paradigm contains multiple conditions, the researcher will also need to designate the names of each condition (Conds). For ease, we are also providing a script (Edit_events.m) that will re-label the events of interest in the naming convention needed to run these scripts. The researcher will also need to indicate the minimum number of trials the participant must have in a condition order to be analyzed (mintrialnum). If one of the conditions for the participant does not meet this threshold, a blank file named “notenoughdata.mat” will be saved for that participant and the script will skip to the next participant in the list. Here, the researchers also input whether they would like the data to be baseline corrected (BaselineCorrect) and the time period of the baseline period to use.

The researcher also will decide whether they would like the data to be downsampled. Data will automatically be downsampled to 250 Hz at the beginning of the scripts to reduce file sizes and computation time; however, if the researcher would like to further downsample the data after TF computations to 125 Hz to reduce file size and storage space, without losing substantial resolution, they can choose to downsample again. We recommend downsampling to 125 Hz after TF decomposition especially for datasets with many conditions and/or a large sample size. Finally, the researcher can choose to append an extension of a study identifier to the final filenames.

Next, the researcher must determine the parameters for the TF analyses (Fig. 6). First, the user will need to decide the lowest frequency to analyze. This decision is influenced by a few factors including a priori bands of interest and the length of the epoch. For example, if low frequencies like delta (1–4 Hz) are not of interest, then there is no need to analyze down to 1 Hz. However, if delta is of interest, the epoch needs to be long enough to have a few cycles of activity. It is recommended that the data have at least 3 full cycles of the lowest frequency to be analyzed (Cohen, 2014). Second, the user will also choose the highest frequency to analyze. Again, this will be influenced by a priori hypotheses about particular frequency bands, but also must stay below the Nyquist frequency (½ of the sampling rate). For example, if the highest frequency to be analyzed is the alpha frequency band (8–13 Hz), then it may be computationally unnecessary to analyze much higher than that frequency of interest.

Fig. 6.

Settings and parameters for TF power, ITPS, and ICPS/wPLI calculations to be input by the researcher for the MainScript_Calculate_TF_ITPS_ICPS.m script.

Third, the researcher needs to decide on the resolution between frequencies or how many frequency bins should be in between the lowest and highest frequency. This resolution will depend on the precision needed for the analyses. For example, if interested in larger frequency bands (e.g., 4–8 Hz), frequency bins of 0.5 Hz should be sufficient and allows for the researcher to create larger frequency bands (e.g., 4–8 Hz or 4–7 Hz) to investigate either based on literature or data patterns. The frequency resolution is also important for plotting. Twenty to thirty frequency bins should be sufficient to flexibly create frequency bands but also maintain adequate resolution for plotting (Cohen, 2014). Finally, the researcher needs to establish the number of cycles included in the wavelet, which roughly equates to the width of the wavelet. The width of the wavelet influences both the temporal and frequency precisions. More cycles increases frequency precision, while fewer cycles lead to increased temporal precision. A common approach, which is implemented in this Matlab code, is to start with fewer cycles at lower frequencies and gradually increase the number of cycles as frequency increases. This strategy increases temporal precision at lower frequencies and strengthens frequency precision at higher frequencies, balancing both temporal and frequency precision.

Finally, the researcher will set parameters for phase-based analyses (Fig. 6). First, they will determine if they would like to compute or skip ITPS. The researcher will also decide whether they would like to use the subsampling procedure to equate number of trials if their conditions have different numbers of trials. For subsampling, they will also need to decide 1) how many trials to randomly sample on each subsample and 2) the number of subsamples. In choosing these parameters, we encourage the researcher to make sure that they choose numbers that will make it likely that all of the data are being used. For example, if there are 300 trials in one condition, but only 5 trials are being pulled in each of 10 subsamples, a lot of data are being left out. After subsampling procedures are set, the user will determine whether or not they would like to compute or skip ICPS/wPLI calculations. If they would like to do this, they decide whether they would like to compute ICPS or wPLI. Note again that if ICPS is chosen, we recommend doing a CSD or Laplacian transform to the data. The researcher also needs to determine whether ICPS/wPLI should be computed over time or over trials. Because over time analyses eliminate the time dimension, baseline correction and downsampling are not completed for over time analyses. The researcher can also choose if they would like to compute ICPS/wPLI between all electrodes (all-to-all) or between a seed electrode and other specific electrodes (seed-based). If the seed-based approach is chosen, then both a seed and the other specific electrodes need to be indicated. Generally, all-to-all analyses are more common in a resting state analysis and seed-based analyses are more useful for a priori hypotheses for event-related designs. The all-to-all analyses, especially if subsampling procedures are being used, require powerful computers or servers to run. Running that analysis on a regular desktop computer may error out due to a lack of Matlab memory. Finally, the researcher needs to use a regular expression (e.g., sequence of characters that a search index will use) for the script to find the files of interest in the data location path and create a list of the subjects to loop through. With these settings and parameters chosen, the MainScript_Calculate_TF_ITPS_ICPS.m script will calculate the measures of interest using the timefreq.m, ITPS.m, ICPS.m, and wPLI.m scripts and save Matlab (.mat) files with final measures for each condition and subject.

In addition to the scripts to calculate the various TF measures, we are also providing two other scripts. One script (Edit_events.m) will ensure that events/flags in the EEG file for different conditions are labeled in a way that will be easily read into the scripts. This script should be run on all of the epoched files before they are run through the Main Script. Second, after the TF scripts calculate the appropriate measures, a final script called Compiling_and_plotting.m will create a matrix that compiles the frequency by time by channel data for all subjects and conditions. This matrix is then used by the script to plot TF surfaces and topographic plots for each condition averaged over all subjects.

The Compiling_and_plotting.m script requires the researcher to again input some information (Fig. 7). First, the researcher will input three paths: 1) the data_location path, which should lead to the folder that contains the.mat files for each subject and condition calculated by the Main Script, 2) the save_location path, which should lead to the folder where researchers want the compiled data to be saved, and 3) add the path to the location of EEGLAB. Next, the researcher designates whether the data was resting or event-related, the names of the conditions as named in the Edit_events.m script, and the generic names of the conditions. The researcher will also indicate specifics about the TF calculations based on what was performed by the Main Script. First, they will choose whether their TF data was baseline corrected (TF_bln). They will also indicate whether they chose to calculate ITPS, ICPS, or wPLI (ITPS_calc, ICPS_calc, or wPLI_calc) and whether they chose to baseline correct those measures (ITPS_bln, ICPS_bln, and wPLI_bln). Finally, they will indicate if they chose to downsample their data.

Fig. 7.

Settings, dataset information, and plotting parameters to be input by the researcher for the Compiling_and_plotting.m script.

Finally, the researcher will make some decisions regarding plotting parameters (Fig. 7) for both surface plots (i.e., time by frequency) and scalp topography plots (TF measure values over scalp locations based on channel montage). They will need to choose what time window (time_window_surface) will be plotted on the x-axis of the surface plot. Generally, this time window should encompass time both before the event of interest and after the event of interest. They also need to choose what frequency window (freq_window_surface) should be plotted on the y-axis of the surface plot. The choices of the time window and frequency window allow for the researcher to customize their plots to illustrate the effects of interest. Additionally, the researcher will need to decide which electrode (or cluster of electrodes) they would like to plot the surface for. If multiple electrodes are chosen, the script will average the TF surface over all of the listed electrodes. They will need to do this separately for TF (chans2plot_TF), ITPS (chans2plot_ITPS), and ICPS/wPLI (chans2plot_ICPSwpli). In order to plot all-to-all ICPS or wPLI in a similar manner, the researcher will have to choose a seed electrode (Seed). When plotting surface plots ICPS or wPLI, the researcher should only plot non-seed electrodes.

In addition to parameters for surface plots, the researcher will set a few parameters for scalp topography plots. Again, the researcher will need to input the time window (time_window_for_topo) and frequency window (freq_window_for_topo) to be plotted in the scalp topography. While the surface plots generally include a larger time and frequency window (e.g., the entire epoch and 1–30 Hz), scalp topographies generally zoom in on the time period and frequency band of the specific event of interest (e.g., 0–100 ms and 4–8 Hz).

7. Examples

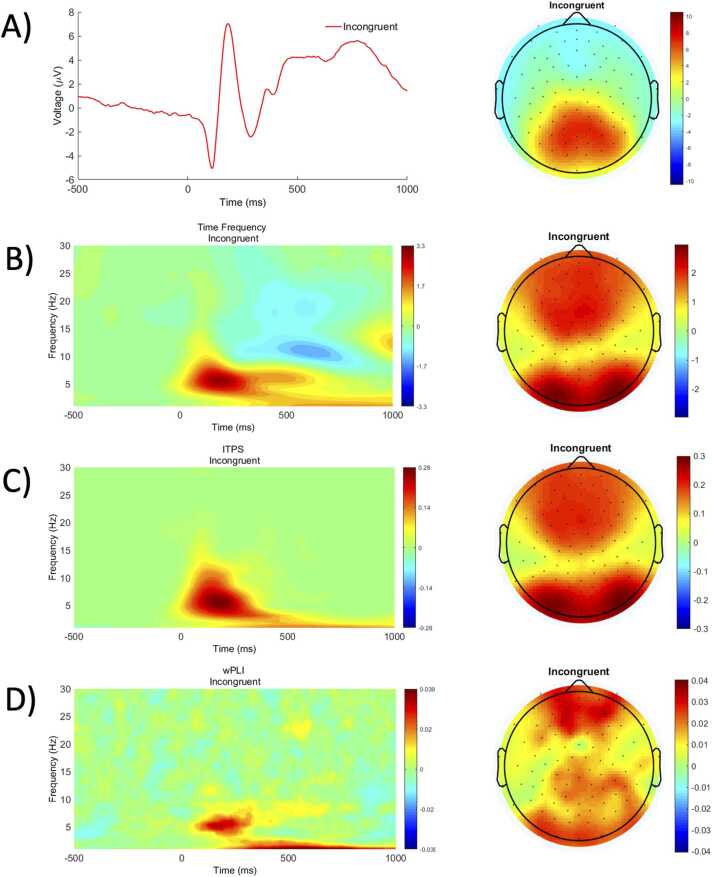
Next, we will illustrate the output of our TF processing scripts with TF surface plots and topographic plots from a study of reward’s influence on cognitive control in adolescent males using a rewarded cued flanker paradigm (Bowers et al., 2021). For the purposes of this illustration, we will focus on stimulus-locked data from incongruent stimuli in 25 male children (Mean age = 10.55, SD = 1.10, Range = 9.08 −13.92). Parental consent and child assent was obtained for all participants. All data were preprocessed using the Maryland analysis of developmental EEG (MADE) pipeline (Debnath et al., 2020, Leach et al., 2020) – see Bowers et al. (2021) for more details.

In the stimulus-locked ERP plot (Fig. 8A), there is a clear negative deflection around 300 ms over the frontocentral areas, indicating the presence of the N2. The TF power (Fig. 8B) and ITPS (Fig. 8C) surfaces for the incongruent condition display elevated theta (4–8 Hz) from about 0–400 ms. Examining how theta (4–8 Hz) power and ITPS are distributed across the scalp, we see increased signal strength (power) and consistency (ITPS) in fronto-central and occipital regions. As an example of connectivity, we used seed-based wPLI with a fronto-central seed (electrode E6). Results show increased connectivity in theta from 0 to 300 ms. Notably, the scalp topography looks somewhat different because these plots are in relation to the seed of interest (E6). Thus, the pattern observed likely represents increased bilateral connectivity (wPLI) to frontal regions in the incongruent condition.

Fig. 8.

A) ERP plot and scalp topography of 230–350 ms surrounding the N2 for the incongruent condition. B) Time frequency surface plots and scalp topographies (4–8 Hz from 0 to 300 ms) for stimulus-locked TF power in the incongruent condition. C) Time frequency surface plots and scalp topographies (4–8 Hz from 0 to 300 ms) for stimulus-locked ITPS in the incongruent condition. D) wPLI surface plots and scalp topographies for the congruent and incongruent stimulus-locked activity. The surface plots depict an average of wPLI values from seed E6 to electrodes E24, E27, and E23. The scalp topographies also depict wPLI values from seed E6 at 4–8 Hz from 0 to 300 ms.

8. Conclusions

The present manuscript provides an introduction to TF analyses, highlighting the unique contributions of this approach to the study of developmental cognitive neuroscience, particularly over the more traditionally used approaches such ERPs and Fourier-based power. ERP analyses ignore non-phase-locked signals and Fourier-based power approaches ignore temporal information. TF analyses dissociate the power and phase information contained in the EEG data at specific frequencies providing a more comprehensive characterization of the EEG signal. By reviewing the emerging studies using TF analyses of developmental EEG data, we underscore the potential of these analyses to increase our understanding of developmental processes. We also discuss the challenges and future directions of TF methods. Finally, in order to promote the use of TF analyses by the developmental cognitive neuroscience community, we provide an approachable tutorial of Matlab scripts, based on Cohen (2014), to calculate the mostly widely used TF measures on a sample of adolescents.

Funding

SM was supported by grants from the National Institutes of Health (U01MH093349-09S1, PI of parent grant: Dr. Nathan Fox; and UH3OD023279, PI: Dr. Amy J. Elliott). MEB was supported by the William Hodos Dissertation Assistantship through the Neuroscience and Cognitive Science Program at the University of Maryland.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data Availability

The data and code used in the manuscript can be found here: https://osf.io/taed5/.