Gene surfing of underdominant alleles promotes formation of hybrid zones

Abstract

The distribution of genetic diversity over geographical space has long been investigated in population genetics and serves as a useful tool to understand evolution and history of populations. Within some species or across regions of contact between two species, there are instances where there is no apparent ecological determinant of sharp changes in allele frequencies or divergence. To further understand these patterns of spatial genetic structure and potential species divergence, we model the establishment of clines that occur due to the surfing of underdominant alleles during range expansions. We provide analytical approximations for the fixation probability of underdominant alleles at expansion fronts and demonstrate that gene surfing can lead to clines in one-dimensional range expansions. We extend these results to multiple loci via a mixture of analytical theory and individual-based simulations. We study the interaction between the strength of selection against heterozygotes, migration rates, and local recombination rates on the formation of stable hybrid zones. Clines created by surfing at different loci can attract each other and align after expansion, if they are sufficiently close in space and in terms of recombination distance. Our findings suggest that range expansions can set the stage for parapatric speciation due to the alignment of multiple selective clines, even in the absence of ecologically divergent selection.

This article is part of the theme issue ‘Species' ranges in the face of changing environments (part I)’.

1. Introduction

In diploid organisms, dominance of mutations is a crucial aspect determining fitness of heterozygous individuals. Dominance can modulate the evolutionary fate of mutations [1,2] and can lead to interesting phenomena, such as pseudo-overdominance [3] or heterosis [4]. The degree of dominance is difficult to predict [5], and in some cases the fitness of heterozygotes is higher (overdominance) or lower (underdominance) than fitness of either homozygote. Underdominant mutations only express their deleterious effects in heterozygotes, making these mutations the simplest form of incompatibilities between different lineages. These mutations thus play an important role in maintaining stable range edges between diverged lineages via the formation of hybrid zones [6] and are also often involved in reproductive isolation and speciation [7].

It is commonly assumed that hybrid zones form as a result of (secondary) contact between two different species. However, less studied and perhaps less expected to occur, is a case at the other end of the spectrum of speciation: differentiation over a continuous species range. The formation of a hybrid zone without ecological forces changing over space seems improbable, yet there are observed instances of such differentiation occurring; for example, in systems with isolation by distance there may be observed geographical regions of distinct change in genetic makeup, such as in the greenish warbler where distinct genetic clusters within the species range have been shown to exist [8]. In panmictic populations, Barton & De Cara [9] have shown that underdominant mutations can combine with other pre- or postzygotic incompatibilities and may therefore play an important role in the evolution of strong reproductive isolation and speciation.

While Barton & De Cara [9] studied the interaction of pre-existing incompatibilities by assuming some form of frequency dependence that keeps allele frequencies constant, a critical unresolved question is how underdominant mutations can establish within populations despite their selective disadvantage while rare. In large populations, underdominant mutations with appreciable fitness effects should not be able to reach high frequencies because they experience a form of positive frequency-dependent selection: they are selected against while rare and positively selected only when they pass a certain frequency threshold. Wright [10, p. 552] argued that fixation of underdominant mutations is unlikely ‘except in a species in which there are numerous isolated populations that pass through phases of extreme reduction of numbers’. He further argued that metapopulations with local extinction and recolonization events in subpopulations are the most favourable scenario for the evolution and local fixation of underdominant mutations. This has led to a series of influential theoretical papers investigating the role of metapopulation dynamics on the establishment of underdominant mutations, such as chromosomal inversions [11,12]. There is, however, another important and common demographic scenario that may strongly facilitate the establishment of clines in allele frequency of underdominant mutations across space: spatial range expansion.

Species range expansions are known to create a phenomenon of allele surfing, allowing for the accumulation of fixed genetic diversity at range edges [13,14]. This process can impact selected and neutral variants, and has been studied extensively, particularly in regards to expansion load and deleterious variants [15–21]. Another scenario less investigated, however, is the dynamics of underdominant alleles which confer heterozygote disadvantage. During a range expansion, strong drift at the expansion front can allow underdominant mutations to cross the threshold below which they would otherwise be selected against in their heterozygous state. A cline in allele frequencies for underdominant mutations may readily establish across the landscape. In spatially extended populations with limited gene flow, underdominant mutations can form stable clines [22], and may also combine with other incompatibilities [7,23]. If multiple such clines coincide at the same spatial location, linkage disequilibrium between the different loci will reinforce the barrier to gene flow created by underdominant mutations [24,25]. Slatkin [25] also studied how linkage disequilibrium can attract clines at different loci despite spatially heterogeneous selection that would keep clines apart under free recombination. A recent mathematical analysis has shown that even without environmental variation that keeps clines aligned or close to each other in space, clines that coincide spatially will remain together indefinitely at a stable equilibrium [26].

In this paper, we investigate if clines in underdominant alleles can form due to allele surfing and whether clines at different loci may align in space to reinforce reproductive barriers, contributing to observed patterns of genetic diversity over space. We investigate the conditions under which range expansion can result in the establishment of such incompatibilities as well as which conditions might lead to stable hybrid zones, setting the stage for reproductive isolation and parapatric speciation.

2. Methods and results

(a) . The model

We model the evolutionary dynamics of allele frequencies at the front of a one-dimensional range expansion, using a discrete-space serial founder event model [27]. Demes are arranged as a one-dimensional array and each deme has a carrying capacity of K individuals. We label adjacent demes by 1, 2, 3, …, n. Initially, only a subset of demes is colonized, and all other demes are empty. The expansion front at time t is the most recently colonized deme, and we call its position d_f(t). Individuals are diploid and monoecious, and we consider a single locus with two alleles denoted a and A. Let p denote the frequency of the mutant allele A at the expansion front, that is in deme d_f. Note that the dependence on t is omitted for the sake of simplicity. We consider a simple model of symmetric underdominance which holds across all loci: the relative fitness of genotypes is given by w_aa = 1, w_aA = 1 − s, w_AA = 1, where 0 < s < 1.

A key simplifying assumption in our model is that we model the colonization of new demes as discrete founder events occurring every T generations (e.g. [14,20]). When the deme currently at the expansion front reaches carrying capacity, a propagule of size F is placed into the next empty deme d_f(t) + 1. The population then grows exponentially for T generations until the new deme’s carrying capacity is reached. The time T corresponds to the inverse of the expansion speed and depends on the size of the propagule and the growth rate of the population at the expansion front. The size of the propagule is determined by the dispersal rate m of individuals such that F = K m/2. The factor 1/2 is due to the fact that individuals migrate to each of the two neighbouring demes with the same probability. During the growth phase, migration is ignored. Assuming exponential growth at rate ρ = log(R), where R is the geometric growth rate, this yields T = log(2/m)/ρ [14]. This model is a good approximation to range expansions with continuous gene flow when growth rates are larger than migration rates [14]. We also consider the case where ρ is so large that a deme grows to carrying capacity within a single generation T = 1, independently of the number of founders F.

(i) . Fixation probability of underdominant mutations

Before we examine the serial founder event model, we consider a single panmictic population of constant size N. In electronic supplementary material, appendix A, we use diffusion approximations to derive a formula for the fixation probability of underdominant mutations. The fixation probability of a mutation with frequency p₀ at the expansion front is:

$$p_{\mathrm{fix}}\approx \frac{({\mathrm{e}}^{-2(1/3(2p_0-1)s)p_{0}N}-1)}{({\mathrm{e}}^{-2(1/3(2p_0-1)s)N}-1)}.$$ 2.1

This approximation generalizes the strong selection approximation of Lande [28] to arbitrary selection coefficients. Electronic supplementary material, figure S1 shows the fixation probability as a function of the initial frequency and for various combinations of parameters. Comparison between our analytical results and stochastic simulations shows an excellent fit between theory and simulations. Underdominant mutations are selected against as long as the initial frequency is less than 0.5, and positively selected for when initial frequencies are larger than 0.5. In electronic supplementary material, appendix A, we also present an approximation for the asymmetric case where the derived allele is beneficial when homozygous, that is w_AA = 1 + z > w_aa = 1, with z being the selection coefficient for the homozygous AA genotype. Then the critical initial frequency at which the direction of selection changes is given by s/(2 s + z) < 0.5 (see electronic supplementary material, figure S1b–d). This illustrates that underdominant mutations are especially prone to gene surfing because large allele frequency fluctuations at the expansion front can change the direction of selection acting on the variant and hence drive them to local fixation. A curious and related observation is that the formula for underdominant mutations introduced as a single copy has the same shape as that of co-dominant mutations, but with an additional factor 1/3 in front of the selection coefficient. In other words, the strength of selection against rare underdominant mutations is reduced by 1/3 as compared to co-dominant deleterious mutations.

(ii) . Fixation probability at the expansion front

We next calculate the probability that a mutation goes to fixation at the expansion front in a serial founder event model. In electronic supplementary material, appendix A, we argue that we can approximate the fixation probability at the expansion front by replacing s with sT and N_e with the number of founders F in equation (2.1). The intuitive justification for this approximation is that the action of selection over T generations is very similar to a single generation of selection but with a stronger selection coefficient sT. Furthermore, the amount of drift during founder events is the main source of stochasticity and we ignore drift during the growth phase, so we can replace N_e with F. Our formula allows us to consider the fate of mutations present at an arbitrary initial frequency p₀ in a founding population. Figure 1 compares this approximation as a function of the initial frequency of the mutation with results from individual-based simulations showing that our approximation works very well. In particular, we see that only the compound parameter sT matters. If sT ≪ 1 the mutation behaves as if it is neutral and the fixation probability is approximately 1/F. Thus, for rapidly expanding populations (that is, small values of T), selection is inefficient and mutations will readily surf if they appear at the expansion front. If in addition the number of founders F is small, the probability of surfing becomes very large as it approaches the neutral fixation probability 1/F.

Figure 1.

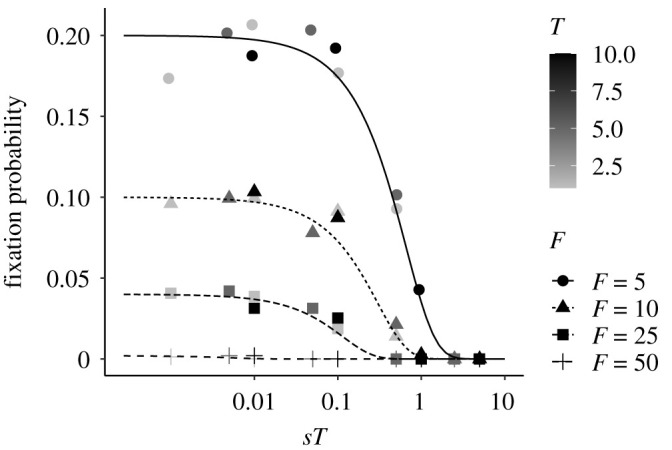
Fixation probability of an underdominant, beneficial mutation in a serial founder effect model. F is the number of founders, T the time between founding events and s the strength of selection. Points indicate results from individual-based simulations while lines show the analytic approximation.

(b) . Surfing can lead to stable clines in simulations

In spatially structured populations, locally fixed deleterious mutations will eventually be purged when gene flow reintroduces genotypes from locations where the mutation is not fixed. Underdominant mutations, however, can be maintained over long time periods if they establish locally because the joint action of selection and gene flow against heterozygotes leads to stable clines in deterministic models without genetic drift [6]. This has an important consequence: while the establishment of mutation load during range expansions is generally a transient phenomenon, surfing of underdominant mutations can lead to long-lasting clines and so-called hybrid zones.

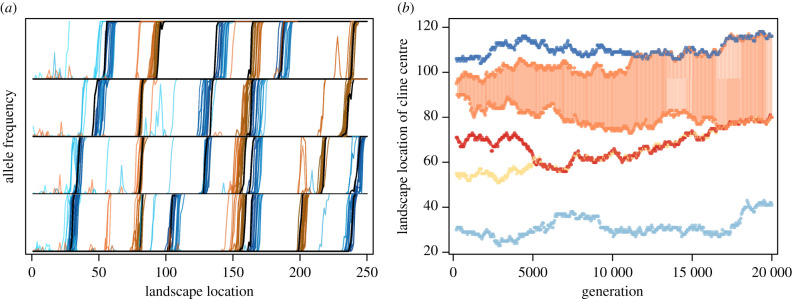
We use forward-time, individual-based simulations in SLiM v. 3.4 [29] to further investigate the formation of such clines due to gene surfing. Using a non-Wright-Fisher model (see SLiM manual), we generate a linear landscape of 250 demes with carrying capacity K = 25 per deme. We initialize the population in one end deme and allow expansion to proceed across empty space via a stepping stone model of migration with m = 0.1. This results in a realized expansion speed of 0.302 demes per generation, which corresponds to T = 1/0.302 ≈ 3.3 generations in our serial founder event model. These parameter combinations (high migration, small population sizes) approach a more continuous-space landscape model, and can thus be seen as complementary to our discrete-space serial founder event model. SLiM input scripts are available on github (https://github.com/kjgilbert/UnderdominantSurfing) for exact details of simulation parameters and settings. Underdominant alleles enter the population as random new mutations (genome-wide mutation rate U = 0.05, genome size of 100 kb, and per-bp mutation rate μ = 5e⁻⁷) with heterozygotes for single locus mutants having a relative fitness of 0.9. Figure 2a shows that clines in underdominant allele frequency do establish during range expansions. Figure 2 also shows that multiple clines coincide spatially, suggesting that clines do not evolve independently but may either form simultaneously during a simultaneous surfing event, or move over space after formation until cline centres coincide for multiple loci. In the former case, if the mutant alleles surf together, it is straightforward to understand that the clines will coincide in geographical space. Simultaneous surfing requires that the mutations fall on the same genomic background or that recombination is sufficiently high so as to prevent interference between the surfing of one underdominant allele on one genomic background versus another. However, we can also see that simultaneous surfing is not always the case and that clines do move over space to eventually later coincide. From the earlier generation snapshots (lighter colours) in figure 2, we can see several loci which initially formed non-coinciding clines and over time moved to the same geographical location by the final generation (black lines).

Figure 2.

The formation (a) and movement (b) of clines for underdominant alleles during a range expansion. In (a), a single replicate simulation for cases with a mutation rate is shown as an example for the formation of clines in allele frequency of underdominant mutations via allele surfing. Twenty-six loci which established stable clines (black lines) in this replicate are shown and separated onto rows only to visually distinguish aligned clines in the same location on the landscape. Each coloured line is a snapshot in time of the allele frequency at a given locus starting at t = 100 for the lightest colours of blue or orange and progressing each 100 generations to darker colours and eventually the black lines at t = 2000. In earlier generations, the dynamics of the underdominant alleles can be seen in some cases before the surfing event has increased the allele frequency to 1. In (b), a single replicate simulation is shown for cases with manually introduced underdominant alleles. These simulations contain only 5 loci, conditioned on each of these loci forming a cline. The movement of these clines is then examined over space for 20 000 generations to investigate the alignment of clines in space. Each colour is the location of a cline centre for a given locus (five colours), and the orange locus with shading between it has formed two clines, with the underdominant mutation as a fixed homozygote in the space between the two clines. (Online version in colour.)

(c) . Clines at different loci can align spatially

To further investigate the movement and interaction of clines through space, we next conduct a set of simulations where the underdominant alleles are manually introduced into the population at a set number of generations apart, always at the range edge, for simulation efficiency. These simulations are conditioned on the mutant underdominant allele at every locus being retained in the population (i.e. simulations where an underdominant allele is lost from the entire population are discarded and rerun). Figure 2b shows one replicate simulation with five such manually introduced underdominant loci that have surfed and formed six clines. The centre of each of these clines is measured as the deme where allele frequency is closest to 0.5 (because clines are steep, as can be seen in figure 2a, there is a +/ − 1 deme margin of the exact deme centre), and the position of these centres is tracked over space through time. Because we want to examine the movement of clines over space, migration was increased to m = 0.25 and carrying capacity per deme was instead K = 50. Note that increasing migration rates and population sizes also makes clines wider [30] when compared with the parameters used in figure 2a. The five mutations enter the population at generations t = 50, 85, 120, 155 and 190, and their movement is then tracked from generation 200 onward. We observe that the clines do drift randomly over space, and when they happen to approach each other, once they reach a critical distance apart, they couple together in space and remain coupled for the remainder of the simulation (figure 2). We also observe that in the fourth (orange) locus, the underdominant allele has surfed past the 0.5 allele frequency threshold but not yet fixed locally, allowing for subsequent strong drift to remove the allele at the range front creating a second cline in frequency from 1 to 0, since eventually behind the expanding front the initial allele does reach fixation. This locus thus forms two clines in space with homozygous mutants residing between them (shaded orange area in figure 2b). These six initial clines at five loci drift over space and eventually align at several loci resulting in three multi-locus clines across the landscape after the simulation has completed. The critical distance between cline centres before coupling of clines is quite small, given the steepness of these clines, with uncoupled cline centres never reaching closer than four demes apart, out of 20 replicate simulations of five loci each (electronic supplementary material, figure S2).

(d) . When do clines attract each other?

To investigate the conditions for when clines will align spatially after their formation at different loci we introduce a deterministic model [31]. Our goal is to model the dynamics of clines in the wake of the expansion wave or after the expansion has ended. We therefore ignore genetic drift and use a two-locus model of migration, selection and recombination in one-dimensional continuous space. We use the following fitness scheme for two-locus genotypes:

	aa	aA	AA
bb	1	1 − s	1
bB	1 − s	(1 − s)2	1 − s
BB	1	1 − s	1

We denote the frequency of haplotype ij by p_ij, i ∈ a, A, j ∈ b, B. The marginal fitness of haplotype ij is given by $w_{ij}=\sum _{kl}{w}_{ij,kl}\hspace{0.17em}{p}_{kl}$, and the mean fitness of the population is given by $\overline{w}=\sum _{ij}{w}_{ij}\hspace{0.17em}{p}_{ij}$. The temporal evolution of the haplotype frequencies is then given by

$$\frac{\mathrm{\partial }}{\mathrm{\partial }t}{p}_{ij}(x,t)=d\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}{p}_{ij}(x,t)+(w_{ij}-\overline{w})p_{ij}+r{\eta }_{ij}D,$$ 2.2

where D = p_ab p_AB − p_aB p_Ab is a measure for linkage disequilibrium. The parameter d is the diffusion term describing the variance in the displacement of offspring from the origin of their parents, and r measures the strength of recombination. Furthermore, η_ab = η_AB = −1 and η_aB = η_Ab = 1. We can simplify the system of differential equations by re-scaling its parameters. We use the natural spatial scale $x_0=\sqrt{d/s}$ introduced by Slatkin [25] and re-scale time by τ₀ = 1/s. Dividing both sides of the equation by s we can write

$$\frac{\mathrm{\partial }}{\mathrm{\partial }(t/{\tau }_0)}{p}_{ij}(x,t)=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{(x/x_0)}^2}{p}_{ij}(x,t)+\frac{1}{s}(\overline{w}-w_{ij})p_{ij}+\frac{r}{s}{\eta }_{ij}D.$$

If we re-scale time and space accordingly with t ← t/τ₀ and x ← x/x₀ the equation becomes

$$\frac{\mathrm{\partial }}{\mathrm{\partial }t}{p}_{ij}(x,t)=\frac{{\mathrm{\partial }}^2}{\mathrm{\partial }{x}^2}{p}_{ij}(x,t)+\frac{1}{s}(\overline{w}-w_{ij})p_{ij}+\frac{r}{s}{\eta }_{ij}D.$$

At first order, the fitness difference between the haplotype ij and the mean fitness is proportional to s, so that the second term of the right-hand side is independent of s. For r = 0, the equation is thus dimensionless, and for r > 0 we can introduce another re-scaled parameter, r/s (the inverse of the coupling coefficient introduced by Barton [24]), that measures the strength of recombination relative to selection.

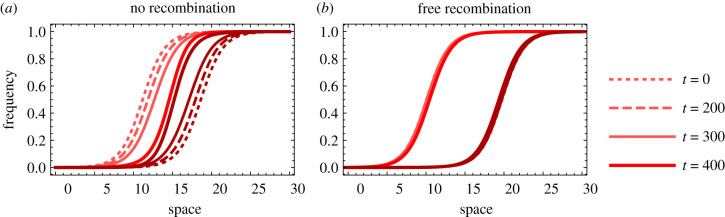
Figure 3 shows an example for numerical solutions of this system of partial differential equations. The spatial width of a cline is proportional to $x_0=\sqrt{d/s}$, in agreement with the fact that dispersal tends to homogenize allele frequencies across the cline whereas selection tends to remove unfit heterozygotes from the population and steepen the cline [6]. We find that two clines at different loci will tend to spatially align quickly in the absence of recombination (figure 3a) but move towards each other only very slowly if recombination is strong (figure 3b). To better understand why clines attract each other in our model, we also observe that linkage disequilibrium is formed in the region where clines overlap (electronic supplementary material, figures S3 and S4). It has been shown that linkage disequilibrium between underdominant alleles at different loci modulates indirect selection on local allele frequencies [6,23,25], which can lead to shifts in cline position in spatially heterogeneous models [25] and affect the shape of spatially coinciding clines [6]. In our spatially homogeneous model, linkage disequilibrium creates a fitness advantage for both the a and B alleles in the central region (see electronic supplementary material, figure S3 for a detailed explanation in terms of haplotype frequencies), inducing movement of the A cline to the right and the B cline to the left. When recombination is sufficiently strong, linkage disequilibrium is mitigated (electronic supplementary material, figure S4), and the fitness advantage of the alleles between the clines is reduced, leading to slower movement of the clines.

Figure 3.

Temporal evolution of two clines at two different loci and spatial locations. Parameter values: s = 0.1, d = 0.05 and r = 0 (a) and r = 0.5 (b). (Online version in colour.)

Figure 4 investigates the time it takes until two clines spatially align as a function of their initial distance, the selection intensity, the diffusion parameter, and the recombination rate. We find that clines will always couple, but over longer time spans when recombination is higher or the initial distance between clines is greater. The time it takes for clines to spatially align increases exponentially with increasing re-scaled initial distance (for a given r and a given s). Furthermore, for a given re-scaled initial distance, the time it takes for the clines to align is inversely proportional to the selection coefficient s, and the strength of attraction also rapidly declines if the re-scaled recombination rate r/s increases.

Figure 4.

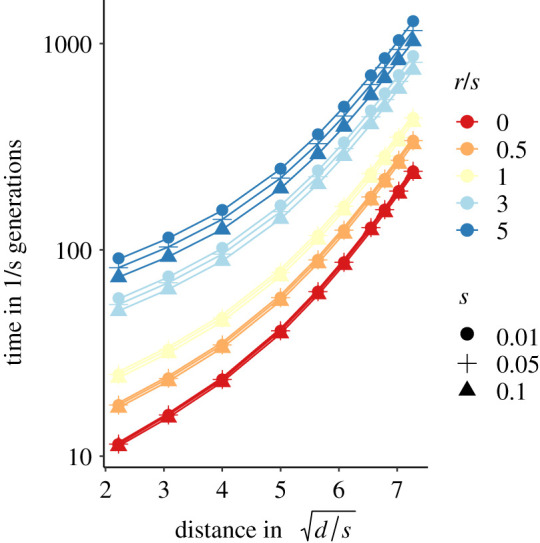
Time until clines coincide spatially, as a function of the re-scaled initial distance. The clines are initially vertical, i.e. the space is divided into three compartments where only one haplotype is present: ab to the left, Ab in the centre and AB to the right. s is selection, r is recombination and d is the diffusion parameter (see main text). (Online version in colour.)

The patterns described above result because the clines described by our differential equations have an infinite spatial width, therefore even when they are far apart, there is always a partial overlap eventually leading to alignment of the clines. Our differential equations ignore genetic drift, creating important differences in behaviour when compared with finite-sized populations. For finite populations, drift makes the width of a cline finite and proportional to the characteristic length x₀ [30]. Here, we use another method to estimate this width. We make the approximation that the differential equation correctly describes clines in finite populations for frequencies in the range [ε, 1 − ε], and that outside of this range the allele is either fixed or lost. We take ε = 1/2K, expressing the fact that genetic drift dominates when a single copy of the allele is present in the deme. For a carrying capacity K = 50, we find that the effective spatial extent of a cline is $\mathrm{\Delta }=9.2\sqrt{m/2s}$ demes, where m is the migration rate of the discrete space model. If the clines are separated by a distance larger than Δ they do not overlap, and consequently they will not attract each other. If they are closer than Δ, they will potentially attract each other if selection is strong but recombination is weak, as observed in figure 4. For the parameters investigated in our forward simulations (figure 2a, m = 0.1, hs = 0.1), we expect a critical distance of Δ = 10 demes between clines below which we would expect attraction and eventual cline alignment to occur. We observe, however, that many clines reach closer distances without aligning (e.g. see electronic supplementary material, figure S2), indicating that genetic drift plays an important role even at close distances. This is sensible because with slight overlap between clines linkage disequilibrium will be weak and hence drift will outweigh indirect selection impacting movement of clines.

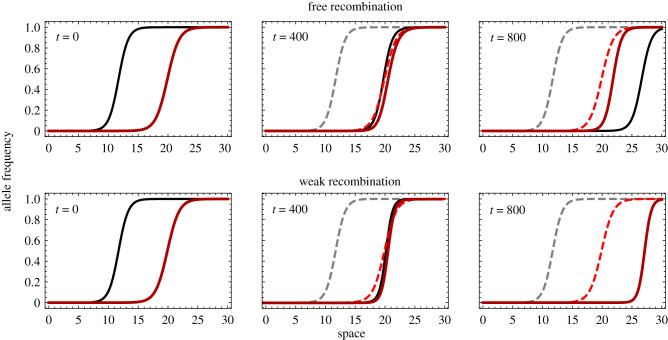
So far we have only considered clines that are neutral in the sense that both homozygotes have the same fitness. Figure 5 shows an example with one neutral cline (solid red lines) and a cline where the derived homozygote has a lower fitness than the wild-type (solid black lines). Thus, one cline moves towards the other one due to the selective advantage of the wild-type homozygotes. With strong recombination (r = 0.5, top panels) we find that the clines move past each other without much interaction. If the two clines are tightly linked (r = 0.01, bottom panels) we find that the two clines align and remain spatially aligned as they travel through space together. This suggests that the ‘travelling wave’ solution of equation (2.2), where both clines travel together indefinitely, disappears for some critical r > 0 (see also [26] for a stability analysis of spatially coinciding clines).

Figure 5.

Temporal evolution of two clines at two different loci, red versus black, and spatial locations. At one locus (solid black lines) derived homozygotes have fitness 1 − s_A such that the cline moves through space from left to right (dashed lines indicate the original location of the clines while solid lines track the current location of clines at the time point indicated). Parameter values: s = 0.1, m = 0.05, s_A = −0.05 and r = 0.5 (top row) and r = 0.01 (bottom row). (Online version in colour.)

3. Discussion

In this study, we have examined a little-studied phenomenon: the surfing of underdominant alleles during range expansion and the subsequent movement over space of clines in allele frequencies established during surfing events. We derived the probability that underdominant mutations successfully establish at the expansion front in a serial founder event model (figure 1). Unlike deleterious mutations that can lead to a transient increase in mutation load in recently colonized areas [14], underdominant mutations will be maintained in the form of clines after a surfing event (figure 2). Using individual-based simulations and mathematical modelling, we have shown that once clines of disadvantageous heterozygotes form, clines can align in space due to differences in fitness on different genomic backgrounds and have the potential to combine as double (or more) heterozygotes. Our results show that the spatial alignment of clines is a stable state, corroborating theoretical results on the local stability of already aligned multi-locus clines [24–26].

We have identified two main factors determining whether and how fast clines will spatially align: (i) clines need to be sufficiently close in space and (ii) the recombination distance between the two clines needs to be sufficiently low (see figures 3 and 4). An intuitive interpretation of these results is that clines will only attract each other if there is a spatial overlap of unfit single-locus heterozygotes such that unfit double heterozygotes are produced (see electronic supplementary material, figure S3). When this overlap occurs, clines will move towards each other since the double homozygotes to either side of both clines are more fit than the single heterozygotes interior to the two overlapping clines. In the absence of recombination, once double heterozygotes are formed, they cannot be broken apart so selection cannot remove these genotypes at the cline centre and a steep cline exists of low fitness as selection maintains double homozygotes on either side. Under high recombination, however, single heterozygotes are continually formed. Selection acts less strongly against single heterozygotes since they have higher fitness than double heterozygotes, explaining the slower movement and eventual alignment of clines in the presence of recombination (as well as the slightly wider region of space exhibiting lower fitness; see electronic supplementary material, figure S3). The strength of selection has opposing effects on the spatial alignment of clines. Strong selection makes clines steeper (by decreasing the spatial scale $\sqrt{d/s}$), such that they become less likely to overlap. But strong selection also reduces the efficacy of recombination in creating fitter genotypes because multi-locus heterozygotes are efficiently removed from the population which renders recombination ineffective. The resulting linkage disequilibrium in turn increases the strength of attraction of clines.

There are several important caveats and future directions to pursue related to our results. First, because our analytical model is based on diffusion in space, clines will always overlap and thus our model always predicts that clines will eventually merge (figure 4). However, in finite populations, clines will not extend indefinitely and genetic drift will play a larger role. We observe this when examining the movement of clines in our forward simulations (figure 2b) and from the smaller observed critical distance (electronic supplementary material, figure S2) below which two clines are predicted to merge, which is sensible as drift should reduce cline width when compared with deterministic expectations [30]. Second, we modelled simple single mutations that confer heterozygote disadvantage, yet there are a wide range of genomic or environmental scenarios that can cause heterozygote disadvantage as well as potential epistatic interactions. It would be interesting to extend our model to include epistatic interactions between mutations, such as Dobzhansky–Muller incompatibilities (DMIs) which could also establish and form clines during range expansions [32]. Genomic inversions may be the most prevalent example where heterozygotes are disfavoured due to the suppression of recombination in the inverted region [33]. Polymorphism, and even ancient persistence, of inversions is widely observed in species across the globe [34,35]. Our model provides one potential explanation for the existence of such clines in inversion frequencies. We have also ignored the role of epistatic interactions between mutations at different loci. Our results suggest that any fitness landscape where multi-locus heterozygotes suffer a disproportionate fitness disadvantage as compared to single-locus heterozygotes should hasten the spatial alignment of underdominant clines.

Further investigation in several areas would prove fruitful in understanding the generation of fixed differences across continuous species ranges. We have not examined the role of long-distance dispersal, which has previously exhibited the creation of fixed differences across the landscape during range expansions [36], and which in our case could also be of interest since rare long-distance dispersers might establish underdominant alleles much like a surfing event does. We have not investigated in depth the impact of unbalanced fitness between homozygotes in our model. Our clines, if alone, would remain stable and only fluctuate over space due to genetic drift. However, if either the derived or ancestral homozygotes are more fit than the other (with heterozygotes still being least fit), such clines would move over space after they have formed due to selection, until the less fit allele is purged from the population (figure 5). Furthermore, if the fitness advantage is confined to a certain region of the species range, the movement of the cline will stop at some point and form a stable tension zone [6,23]. Intriguingly, our model shows that if such moving clines merge with a neutral non-moving cline, these two clines will continue to travel together when recombination is sufficiently weak (figure 5). This suggests that underdominant alleles that confer a fitness advantage as homozygotes in a region of a species range, or beneficial alleles that are linked to underdominant alleles, may move through space and collect neutral clines that would otherwise not move, reinforcing genetic differentiation across aligned clines. This is closely related to the idea that any cline determined by environmental change (and thus of fixed position) would tend to trap underdominant clines [6,23].

The role of range expansions on the establishment and subsequent alignment of clines in space has important ramifications, since over evolutionary timescales such clines will be expected to couple with more clines and reinforce more strongly any reproductive barrier one cline already imposes ([7], see also [26]). It will be fruitful to pursue empirical investigations into the prevalence of underdominance in regions of partial reproductive isolation across species ranges. Since heterozygote disadvantage does not necessitate genetic underpinnings, even the ‘surfing’ of cultural behaviour, such as learned birdsong, could equally contribute to regions of heterozygote disadvantage arising during range expansions. These phenomena could potentially play a large role in the process of speciation as pre- and post-zygotic barriers are reinforced at a localized area within a species range. Our results are also relevant to conservation and management decisions, since a continuously distributed species could exist across a constant environment without locally adapting within populations, yet populations may still exhibit genetic differences across a multi-locus cline barrier that arose during historic range expansions of the species. Such a scenario would necessitate management of individually differentiated populations spread over continuous space.

Data accessibility

This article has no additional data.

Authors' contributions

A.M., K.J.G. and S.P. conceived the project. A.M. and S.P. performed the mathematical analysis. K.J.G. performed simulations. A.M., K.J.G. and S.P. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

K.J.G. was funded by Swiss National Science Foundation Ambizione grant no. PZ00P3_185952.