Generalized Equations for Predicting Percent Body Fat from Anthropometric Measures Using a Criterion Five-Compartment Model

Abstract

Introduction:

Anthropometric-based equations are used to estimate percent body fat (%BF) when laboratory methods are impractical or not available. However, because these equations are often derived from two-compartment models, they are prone to error because of the assumptions regarding fat-free mass composition. The purpose of this study was to develop a new anthropometric-based equation for the prediction of%BF, using a five-compartment (5C) model as the criterion measure.

Methods:

A sample of healthy adults (52.2% female; age, 18 to 69 yr; body mass index, 15.7 to 49.5 kg·m⁻²) completed hydrostatic weighing, dual-energy x-ray absorptiometry, and bioimpedance spectroscopy measurements for calculation of 5C %BF (%BF_5C), as well as skinfolds and circumferences. %BF_5C was regressed on anthropometric measures using hierarchical variable selection in a random sample of subjects (n = 279). The resulting equation was cross-validated in the remaining participants (n = 78). New model performance was also compared with several common anthropometric-based equations.

Results:

The new equation [%BF_New = 6.083 + (0.143 × SS_new) − (12.058 × sex) − (0.150 × age) − (0.233 × body mass index) + (0.256 × waist) + (0.162 × sex × age)] explained a significant proportion of variance in %BF_5C (R² = 0.775, SEE = 4.0%). Predictors included sum of skinfolds (SS_new, midaxillary, triceps, and thigh) and waist circumference. The new equation cross-validated well against %BF_5C when compared with other existing equations, producing a large intraclass correlation coefficient (0.90), small mean bias and limits of agreement (0.4% ± 8.6%), and small measures of error (SEE = 2.5%).

Conclusions:

%BF_New improved on previous anthropometric-based equations, providing better overall agreement and less error in %BF estimation. The equation described in this study may provide an accurate estimate of %BF_5C in healthy adults when measurement is not practical.

Multicompartment models are the preferred criterion method in body composition research due to their ability to account for interindividual variations in fat-free mass (FFM). However, because multicompartment models are often restricted to research settings, assessment methods in sport science and field settings are often based on simpler models which employ assumptions regarding FFM composition (e.g., 73% hydration) and thus lead to substantial error in percent body fat (%BF) when violated (1,2). For example, height and circumference-based equations including body adiposity index (BAI) and relative fat mass (RFM) have been validated using dual-energy x-ray absorptiometry (DXA) in various adult populations (3,4). In addition, body mass index (BMI) has been used in conjunction with sex, age, and race to predict %BF determined via hydrostatic weighing (5). Although these methods are simple to administer, they have been shown to overestimate %BF between 2.4% and 7.8% in healthy adults when compared with multicompartment models (6,7).

Skinfold-based assessments of body composition expand upon basic anthropometric methods by quantifying the thickness of subcutaneous fat at various sites across the body. Although some tests include up to 10 measurement sites, as few as three have been shown to provide similar estimates in %BF (8,9). Popular equations like those of Jackson and Pollock (10,11) use the sum of skinfold thicknesses to estimate body density, which can then be incorporated into a two-compartment (2C) model (1,12) to determine %BF. Similar to the BAI, RFM, and BMI techniques, however, these skinfold equations are subject to errors arising from variations in FFM constituents. Although skinfolds improve upon simpler methods, body density conversion formulas have been shown to produce substantial error in %BF estimation across various populations (13-15).

Researchers have worked to improve upon previous skinfold-based methods by utilizing criterion four-compartment (4C) models for equation development. For instance, Peterson et al. (16) and Evans et al. (8) each developed equations in samples of healthy adults while using a criterion 4C model. Nonetheless, the new skinfold equations outlined by these authors have potential issues: 1) Peterson et al. used a limited criterion 4C model developed from a sample of 10 young (<25 yr) army soldiers (17) and 2) Evans et al. derived and validated their equation in a sample of division 1 collegiate athletes. Despite high internal validity, the applicability of equations to a general population is limited. In addition, the integration of various anthropometric-based measures was not completed, which raises the possibility of developing a new and improved equation that is more comprehensive.

Considering the importance of body composition assessment to the health sciences, accurate equations based on a precise measure of %BF should be available to health and fitness professionals. Practitioners, including sports training staff, dietitians, and trainers, often assess %BF to gauge the efficacy of training and nutrition interventions. Given the limitations of current field techniques and the inaccessibility of laboratory methods to many professionals, there is a need for an improved anthropometric equation that can be applied to the general adult population. Therefore, the purpose of this study was to 1) develop a more valid anthropometric-based body fat equation, and 2) cross-validate the new anthropometric equation and previous circumference-, BMI-, and skinfold-based body fat equations against a criterion five-compartment (5C) model in a sample of healthy adults.

METHODS

Participants

Descriptive characteristics of the participants are presented in Table 1. Persons were considered eligible if they were between the ages of 18 and 90 yr and apparently healthy. Those with cardiac, pulmonary, or metabolic conditions were excluded, as were women who were pregnant, pregnant within the previous 12 months, or currently lactating. All participants were informed of study procedures and provided written informed consent before testing. The university’s institutional review board reviewed and approved all testing procedures.

TABLE 1.

Descriptive characteristics of participants in the development and cross-validation cohorts.

	Development			Cross-validation
Variable	Total (N = 279)	Males (n = 125)	Females (n = 154)	Total (N =78)	Males (n = 46)	Females (n = 32)
Age (yr)	26.0 ± 11.0	26.5 ± 11.8	25.2 ± 9.3	25.2 ± 9.5	26.2 ± 10.1	23.7 ± 8.6
Height (cm)	171.0 ± 9.2	178.6 ± 6.4	164.8 ± 6.0	173.9 ± 9.4	178.7 ± 7.5	166.8 ± 7.0
Weight (kg)	73.7 ± 17.9	84.1 ± 6.2	65.3 ± 14.5	78.6 ± 14.7	86.6 ± 11.5	67.1 ± 10.7
BMI (kg·m−2)	25.1 ± 5.2	26.4 ± 4.7	24.1 ± 5.3	25.9 ± 3.7	27.1 ± 3.5	24.1 ± 3.3
Body fat (%)	22.9 ± 8.4	17.1 ± 6.6	27.6 ± 6.5	21.5 ± 7.7	18.3 ± 6.6	26.2 ± 6.8
Ethnicity/race (%)
White	83.2	83.2	83.1	88.5	89.1	87.5
African American/Black	9.2	8.8	9.7	6.4	6.5	6.3
Asian	2.2	1.6	2.6	1.3	0.0	3.1
Hispanic/Latino	2.2	2.4	1.9	2.5	2.2	3.1
Other/not reported	3.2	4.0	2.6	1.3	2.2	0.0

Body fat determined by the 5C model.

Testing Protocol

Testing occurred during a single visit to the University’s Exercise Physiology Laboratory. Participants were instructed to adhere to the following pretesting guidelines: abstain from alcohol and exercise for 24 h; abstain from food and caffeine for 8 to 12 h; abstain from drinking water for ≥2 h. Hydration was assessed via urine specific gravity (USG) using a refractometer (Atago SUR-NE, Atago Corp Ltd., Tokyo, Japan) to ensure adequate hydration before testing; USG values <1.030 were required for participation (18). Participants exceeding this threshold were asked to reschedule their testing time for another day. Shoes, jewelry, and any metallic objects were removed before body composition assessments.

Anthropometrics

Standing height was measured to the nearest 0.1 centimeter using a stadiometer (SECA 213, Seca Ltd., Hamburg, Germany). Body mass (BM) was measured to the nearest 0.1 kg using a digital scale (Tanita BWB-800; Tanita Corporation, Tokyo, Japan). Skinfold thicknesses were measured using a Lange caliper (Beta Technology Incorporated, Cambridge, MA) at seven sites (chest, axilla, subscapular, triceps, suprailium, abdominal, and thigh) as described by Jackson and Pollock (19). Skinfolds were taken in duplicate on the right side of the body, with a third measurement taken if measures varied more than 2 mm (20). Waist circumference (at the umbilicus) was measured in duplicate using a spring-loaded measuring tape, with a third measurement taken if the second was not within 5 mm of the first (20). The average of the two closest measurements was recorded for all skinfold and circumference measures.

Body Composition Measurement

Body volume.

Body volume was determined using hydrostatic weighing and residual lung volume as described previously (16,21,22). Hydrostatic weighing was performed by placing participants on a nylon seat harness in a submersion tank with water heated to approximately body temperature. The harness was suspended from a 15-kg scale (Chatillon, Largo, FL). Five to ten trials were performed, and the mean of the three heaviest values were used to calculate body volume. All underwater weights were recorded to the nearest 0.025 kg.

Pulmonary nitrogen concentrations were measured using closed-circuit spirometry. Raw nitrogen concentrations following a maximal exhalation and after a rebreathing period were determined using either a metabolic cart (ParvoMedics; TrueOne 2400 Metabolic Cart, Sandy, UT) or a nitrogen analyzer (VacuMed, Ventura, CA). Residual lung volume was calculated using the technique described by Wilmore (23). A minimum of two trials were performed, and the average of two trials within 0.2 L was used in the calculation of body volume. Agreement analysis in a sample of 34 participants demonstrated that the use of either system for the determination of residual lung volume did not impact within-subject body volume (intraclass correlation coefficient [ICC] = 1.00, P < 0.001; bias ±95% limits of agreement, 0.36 ± 0.52 L) or %BF_5C (ICC = 1.00, P < 0.001; 1.4 ± 0.6 %BF). Body volume was calculated from body mass, underwater mass, and residual lung volume as described by Goldman and Buskirk (24).

Total body water and soft tissue mineral.

Total body water (TBW) was determined using whole-body bioimpedance spectroscopy (Imp™ SFB7, ImpediMed Ltd., Brisbane, Australia). Participants were instructed to lie supine on a padded gurney with arms angled approximately 30 degrees to the torso with legs shoulder-width apart. Before electrode placement, excess hair was removed from the electrode sites. Dual-tab electrodes were placed on the back of the right wrist and top of the right ankle after being cleaned with alcohol (25). Total body water was determined using the right-side whole-body configuration outlined by the manufacturer. The average of the two measurements to the nearest 0.1 liter was used in the body composition calculations. Total body soft tissue mineral (M_S, kg) was calculated from TBW (26):

$$M_S=[0.882(12.9\text{TBW})+37.9]∕1000$$

Total body bone mineral.

Bone mineral content (BMC) was measured using DXA. The DXA was calibrated according to manufacturer guidelines before each use using a standardized calibration block (GE Lunar Prodigy; Software version 14.10.022; GE Lunar Corporation, Madison, WI). Participants were positioned supine on the DXA platform with arms held at the sides and feet secured with Velcro straps around the ankles to prevent movement. Bone mineral content provided by the DXA was converted to total body bone mineral (M_O, kg) using the following equation (22,26):

$$M_O=1.0436\text{BMC}$$

Calculation of %BF

The criterion 5C model %BF (%BF_5C) was determined using the 5C model described by Wang et al. (26). In addition, several existing skinfold-based equations were used to predict %BF for comparison within the cross-validation cohort (Table 2). Body density equations by Jackson and Pollock (10,11), converted to %BF using the Siri equation (12), were selected due to their common use in research and practice. Equations by Evans et al. (8) and Peterson et al. (16) were also selected, since they were developed using multicompartment models as the criterion. Finally, additional anthropometric-based estimates of %BF were calculated using BAI (3), RFM (4), and BMI (5). Outcomes from these equations are referred to as %BF_JP, %BF_Evans, %BF_Peterson, %BF_BAI, %BF_RFM, and %BF_BMI.

TABLE 2.

Equations for the prediction of %BF.

Author (citation)	Equation
Wang 5C/criterion (26)	FM = 2.748 × BV − 0.715 × TBW + 1.129 × M0 + 1.222 × MS − 2.051 × BM %BF5C = (FM/BM) × 100
Jackson and Pollock
Men (10)	$\text{BD}=1.1093800-0.0008267\times {\text{SS}}_1+0.0000016\times {\text{SS}}_1^2-0.0002574\times \text{age}$
Women (11)	$\text{BD}=1.0994921-0.0009929\times {\text{SS}}_2+0.0000023\times {\text{SS}}_2^2-0.0001392\times \text{age}$
Siri (12)	%BFJP = (4.95/BD − 4.50) × 100
Evans et al. (7)	%BFEvans = 8.997 + 0.24658 × SS3 − 6.343 × sex − 1.998 × race
Peterson et al. (16)
Men	$\%{\text{BF}}_{\text{Peterson}}=20.94878+0.1166\times \text{age}-0.11666\times \text{ht (cm)}+0.42696\times {\text{SS}}_4-0.00159\times {\text{SS}}_4^2$
Women	$\%{\text{BF}}_{\text{Peterson}}=22.18945+0.06368\times \text{age}+0.60404\times \text{BMI}-0.14520\times \text{ht (cm)}+0.30919\times {\text{SS}}_4-0.00099562\times {\text{SS}}_4^2$
BAI (3)	%BFBAI = (hip (cm)/ht (m)1.5) − 18
Relative fat mass (4)
Men	%BFRFM = 64 − [20 × (ht (m)/waist (m))]
Women	%BFRFM = 76 − [20 × (ht (m)/waist (m))]
BMI (5)
Men	%BFBMI = − 103.94 + 37.35 × In BMI + 0.14 × age
Women	%BFBMI = − 102.01 + 39.96 × In BMI + 0.14 × age

BD, body density in g·cm³; BM, body mass in kg; BV, body volume in L; ht, height; hip, circumference around the buttocks in cm; FM, fat mass in kg; M_o, osseous bone mineral content in kg; M_S, soft tissue bone mineral in kg; SS_x, sum of skinfolds in mm; waist, circumference around the umbilicus. Equation variables: SS₁, chest, abdomen, thigh; SS₂, triceps, suprailiac, thigh; SS₃, triceps, abdomen, thigh; SS₄, triceps, subscapular, suprailiac, thigh. Sex coded as 0, female; 1, male. Race coded as 0, White; 1, Black.

Selection of Predictor Variables for Inclusion in the Regression Analysis

The potential independent variables in this model were the sum of three and seven skinfolds, the square of the sum of three and seven skinfolds, age, sex, BMI, and waist circumference. Skinfolds were selected as the primary independent variable due to their well-documented association with body density and subcutaneous body fat (8-11,27,28). In addition, three-site skinfold tests are considerably quicker to perform and have been shown to produce comparable results to seven-site tests (8-11). Age, sex, BMI, and waist circumference were included as they have been shown to relate to variation in %BF (5,29-31). Interaction terms between sex and age (sex × age) and sex and waist circumference (sex × waist) were also considered for inclusion, as fat distribution has been shown to change with age and vary between sexes (27,32,33). Because our sample was predominantly White, ethnicity was not included as a factor in this analysis. Further, exploratory analyses revealed no significant differences in body composition metrics between ethnic groups.

Statistical Analysis

Data were managed using Microsoft Excel for Windows (Microsoft Corporation, Redmond, WA). Statistical analyses were completed using SPSS for Windows (Version 25.0; IBM, Somers, NY) and R (R Foundation for Statistical Computing, Vienna, Austria). Based on previous equation validation research (8,10,11,16), the total sample of participants was randomly divided into a development (~75%) and a cross-validation cohort (~25%) using the “select cases” function in SPSS. Standard assumptions for all statistical tests were assessed before analysis. Power analyses (G*Power, version 3.1.9.4, Universität Kiel, Germany) confirmed that adequate statistical power (1 − β = 1.000) was achieved during equation development and cross-validation procedures. All power calculations were conducted using an α level of 0.05.

Model development.

Linear regression was conducted in the development cohort to produce an equation for predicting %BF_5C from the independent variables. The initial model regressed %BF_5C on the sum of skinfolds. Bivariate correlational analyses were used to identify which skinfold sites should be used to define the sum of skinfolds term. Additional variables (age, sex, BMI, waist, and interaction terms) were assessed for linearity with %BF_5C and added to the model using a hierarchical variable selection procedure (34,35) based on previous research. Age and sex were added first, as they have been consistently shown to impact body composition and are included in most existing models (9-11,16,27). Waist circumference and BMI were added next, as they have been used to improve the predictive ability of equations using only skinfolds (9,16). Last added were the interaction terms, in order of the highest correlation coefficient with %BF_5C. Model fit was assessed using adjusted R-squared change. Trending and significant (P < 0.10) variables remained in the model. Nonsignificant variables and those that introduced multicollinearity (variance inflation factor, VIF > 10.0) were removed.

Cross-validation and equation comparison.

New model (%BF_New) performance, as well as %BF_JP, %BF_Evans, %BF_Peterson, %BF_BAI, %BF_RFM, and %BF_BMI were compared to criterion %BF_5C within the cross-validation cohort. Agreement between predicted and %BF_5C was examined using the Bland–Altman method for calculating limits of agreement (bias ±1.96 SD) (36), two-way fixed intraclass correlation coefficient (37,38), and standard error of the estimate (SEE). Significance for all statistical tests was accepted at P < 0.05. Data are presented as mean ± standard deviation (M ± SD) unless otherwise specified. Mean bias, limits of agreement, and SEE are expressed as %BF.

RESULTS

A total of 357 healthy adults completed the study protocol (84.4% White, 52.2% female, age 18 to 69 yr, BMI 15.7 to 49.5 kg·m⁻², %BF_5C 3.1 to 46.1%). All participants were apparently euhydrated (USG, 1.001 to 1.029) at the time of measurement. There were no significant differences in body composition metrics between development (n = 279) and cross-validation (n = 78) groups. Participants in the cross-validation group were slightly taller and heavier than in the developmental group, likely due to a greater proportion of men.

Model development.

All assumptions for multiple linear regression were satisfied. A Durbin-Watson statistic of 1.420 suggests independence of error terms; heteroscedasticity of standardized residuals versus predicted values suggests equality of error variance; normality of standardized residuals was observed graphically and statistically, W(279) = 0.990, P = 0.064. Multicollinearity was not indicated in the model (VIF < 10 for all variables). In addition, all hypothesized predictor variables were correlated (all P < 0.001) with the outcome variable. The strongest combination of skinfolds observed in our sample was the sum of the thigh, triceps, and midaxillary sites (SS_new). Individually, these three sites had the largest associations with %BF_5C (r values between 0.69 and 0.79). When summed, they produced a larger correlation coefficient with %BF_5C than the other sum of skinfolds terms (including the seven-site) so it was included in the development of the new model. Inclusion of quadratic skinfold terms did not enhance model fit.

The interaction term sex–age was significant (P < 0.05), suggesting that the effect of age on %BF was different between the sexes. Older men displayed significantly larger %BF_5C values than younger men (mean difference, 5.5%), whereas older and younger women displayed similar values (mean difference, 0.1%). The term sex × waist was not significant (P = 0.16), indicating that the association between waist circumference and %BF_5C was consistent between men and women. Only the term sex × age was included in the model.

Initial regression analysis showed that SS_new explained 68.7% of the variance in %BF_5C in the development group, which was greater than the other skinfold terms (R² values between 0.59 and 0.65). The addition of sex and age significantly (P < 0.001) increased explained variance to 74.5%, whereas waist and BMI brought it to 76.6%. The interaction term sex × age further increased the explained variance of the model to 77.5%. The final model was significant, F(6, 278) = 160.6, P < 0.001, adjusted R² = 0.775, SEE = 4.0%, and is presented in Table 3 with regression statistics from the model building process. The new equation, along with sex-specific reduced equations, are presented in Table 4.

TABLE 3.

Regression analyses predicting 5C %BF in the developmental cohort (n = 279).

Model	Intercept	Model Coefficients						Adjusted R2	SEE (%)
		SSnew (mm)	Sex	Age (yr)	BMI (kg·m−2)	Waist (cm)	Sex × Age
1	7.810*	0.249*	—	—	—	—	—	0.687	4.73
2	12.433*	0.208*	−4.736*	—	—	—	—	0.745**	4.26
3	12.428*	0.207*	−4.738*	0.000	—	—	—	0.745	4.27
4	10.536*	0.181*	−5.820*	0.001	0.157	—	—	0.747**	4.25
5	3.934*	0.145*	−7.807*	−0.058*	−0.243*	0.255*	—	0.766**	4.09
6	6.083*	0.143*	−12.058*	−0.150*	−0.233*	0.256*	0.162*	0.775**	4.01

SS_new, sum of skinfolds (thigh, midaxillary, triceps); adjusted R², coefficient of determination adjusted for multiple predictors. SEE, standard error of the estimate. Sex is coded as 0 = female, 1 = male.

^*Significant at P < 0.05.

^**Significant R² change (P < 0.05).

TABLE 4.

Final equations for predicting 5C %BF in healthy adults.

Full model

%BFNew = 6.083 + (0.143 × SSnew) − (12.058 × sex) − (0.150 × age) − (0.233 × BMI) + (0.256 × WC) + (0.162 × sex × age)

Reduced models

Male

%BFNew = − 5.975 + (0.143 × SSnew) − (0.312 × Age) − (0.233 × BMI) + (0.256 × WC)

Female

%BFNew = 6.083 + (0.143 × SSnew) − (0.150 × Age) − (0.233 × BMI) + (0.256 × WC)

SS_new, sum of thigh, midaxillary, and triceps skinfolds, in mm; Sex, coded as 0 = female, 1 = male; Age, in years; BMI, body mass index in kg·m⁻²; WC, waist circumference in cm. Note: sex-specific equations were derived by substituting the “sex” variable for either 0 (female) or 1 (male) in the full model and then combining like terms.

Cross-validation and equation comparison.

Cross-validation and comparison statistics are presented in Table 5. Sex-specific comparison statistics are available in Supplemental Digital Content 1 (see Table, Supplemental Digital Content, Comparison statistics between criterion 5C and predicted %BF in the cross-validation cohort by sex, http://links.lww.com/MSS/C389). Standardized residuals for all %BF values were normally distributed according to visual inspection of histograms, Q-Q plots, and the Shapiro–Wilk test of normality (all P > 0.05). Intraclass correlation coefficients were significant (all P < 0.001) across equations, ranging from 0.69 to 0.90. Cohen’s d effect size ranged from small to large, with %BF_Evans and %BF_New producing the smallest effects and %BF_RFM and %BF_BAI producing the largest. %BF_New produced the smallest overall error and narrowest limits of agreement, whereas %BF_BAI was associated with the largest SEE. %BF_BAI also produced the widest limits of agreement compared with the other equations. In addition, %BF_JP, %BF_BAI, and %BF_BMI demonstrated proportional bias as indicated by moderate to strong trends (all P < 0.001) between the difference and average %BF values (Fig. 1).

TABLE 5.

Comparison statistics between criterion 5C and predicted percent body fat in the cross-validation cohort (n =78)

						Limits of Agreement
	Mean ± SD	ICC	d	SEE	Subjective rating of SEE	Bias ± 1.96 SD	Lower	Upper	Trend
Criterion 5C	21.5 ± 7.7
5C-based model
%BFNew	21.8 ± 6.9	0.90*	0.06	2.48	Ideal/excellent	0.4 ± 8.6	−8.2	9.0	−0.19
4C-based models
%BFEvans	21.5 ± 8.6	0.87*	−0.01	3.43	Very good	−0.1 ± 10.8	−10.8	10.7	0.18
%BFPeterson	25.7 ± 6.8	0.87*	0.62	3.02	Very good	4.2 ± 9.5	−5.3	13.7	−0.21
2C-based models
%BFJP	20.5 ± 9.3	0.87*	−0.11	3.62	Good	−1.0 ± 11.4	−12.4	10.4	0.29**
%BFBAI	26.9 ± 3.9	0.69*	0.88	4.44	Fairly good/fair	5.4 ± 11.6	−6.2	17.0	−0.71**
%BFRFM	28.0 ± 7.2	0.88*	0.87	2.95	Excellent/very good	6.5 ± 9.5	−3.0	16.0	−0.11
%BFBMI	24.8 ± 5.9	0.83*	0.49	3.50	Good	3.3 ± 10.2	−6.8	13.5	−0.37**

Bias, mean difference between predicted and criterion body fat percentage; lower, lower limit (bias −1.96 SD); upper, upper limit (bias +1.96 SD); trend, correlation (expressed as Pearson’s r) between the difference and average. Subjective rating of SEE is from Lohman (39).

^*Significant correlation (P < 0.001).

^**Trend is significant (P < 0.01).

FIGURE 1.

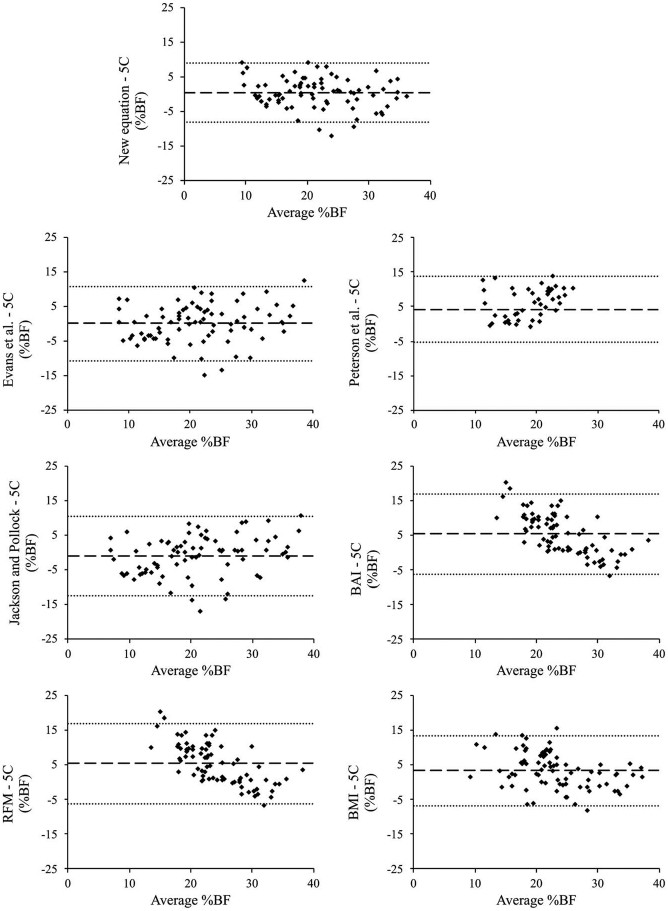
Bland–Altman plots showing predicted versus criterion 5C %BF in the cross-validation cohort (n = 78). Dark center line represents mean bias. Light dotted outer lines represent limits of agreement (bias ±1.96 SD of bias).

DISCUSSION

The current investigation developed and cross-validated a new equation to predict 5C %BF using simple anthropometric measures. The new equation explained more than 75% of the variability in %BF_5C while producing the smallest overall and individual error. Notably, the new equation produced a lower SEE upon cross-validation than equations reported by other authors, who have shown classic 2C-based skinfold equations to produce SEE values ranging from 3.5% to 5.0% (8,40). All equations had strong associations with the criterion 5C model (ICC ≥ 0.69). The circumference-based %BF_BAI and %BF_RFM methods produced the largest effect sizes (d ≥ 0.87) and mean bias, consistently overestimating %BF by 5.4 and 6.5%, respectively. Limits of agreement were comparably large between %BF_JP and %BF_BAI (≥11.4%), indicating a wide range of error in %BF estimation across individuals. In addition, three of the 2C-based models produced significant trends between the difference and the mean axes on the Bland-Altman plots; %BF_JP showed a tendency to overestimate %BF in individuals with higher levels of body fat, whereas %BF_BAI and %BF_BMI appeared to underestimate %BF.

The present study builds upon previous research aimed at developing anthropometric-based equations for the prediction of %BF. Circumference-based BAI and RFM equations were developed in large, diverse samples of participants using (DXA) as the criterion (3,4). Investigations to cross-validate these techniques have shown them to overestimate %BF when compared with reference methods, as well as demonstrate significant proportional bias similar to that observed in the current study (6,41,42). The body density equations of Jackson and Pollock (10,11) were also developed using a criterion 2C model (hydrodensitometry), which can result in significant error in %BF estimation due to the assumptions regarding FFM (12,22). For example, Withers et al. (15) reported that %BF_JP significantly underestimated 4C model %BF in a sample of adults independent of training status, whereas Peterson et al. (16) found %BF_JP to underestimate 4C %BF in healthy women by 6.6%. Similar findings have been reported in samples of college-age adults, with %BF_JP underestimating criterion %BF from 4C (14) and 3C (13) models by 4.8 and 5.0%, respectively. Although the Jackson and Pollock equations produced a smaller mean bias in the current study than those previously mentioned, the wide limits of agreement (>11.0%) suggest large individual error in estimation. In addition, the SEE of %BF_JP produced during cross-validation in our cohort was similar to that reported by Esco et al. (13) when comparing %BF_JP to a criterion 3C model.

As well as improving upon 2C-based equations, %BF_New produced less overall and individual error than other equations developed from a multicompartment criterion. For example, although developed in a sample similar to the current study, %BF_Peterson overestimated criterion %BF by 4.2% upon cross-validation. Nickerson et al. (14) observed a similarly large mean difference, reporting that %BF_Peterson underestimated criterion 4C %BF by 3.1%. This error may be attributable to the criterion 4C model used in Peterson et al. (16), which was developed in a small (n = 10) sample of young soldiers ranging in age from 19 to 24 yr (17). The equation described by Evans et al. (8) used a more general criterion 4C model (43), and expanded on the anthropometric approach by including sex and race as independent variables. Compared with our criterion, %BF_Evans produced the smallest mean difference, underestimating 5C %BF by 0.1%. However, the limits of agreement from %BF_Evans were considerably wider than both %BF_New and %BF_Peterson. In addition, SEE was larger than %BF_New. The error associated with %BF_Evans may be due to limitations arising from their development sample. Evans et al. (8) derived their equation in college athletes who were considerably younger (20.8 ± 2.3 yr) and leaner (14.6% ± 6.5%) than that in the current study, which could limit the ability of %BF_Evans to accurately predict higher %BF. Especially given that our regression analysis found a significant interaction between sex and age, %BF_Evans may be particularly prone to error when predicting %BF in older men.

Although not the explicit purpose of the present study, the interaction effect observed between sex and age clearly showed that %BF increased with age in men, whereas there were no differences observed in women. These findings are similar to those noted by van Der Ploeg et al. (9), who noted that the sum of skinfolds was associated with a higher %BF in older men than younger men. These observations suggest that body composition status may change as age increases, and may be the result of alterations in adipose tissue storage, an increase in skinfold compressibility, or a decrease in skin thickness (9). There could also be hormonal changes associated with age in men that impact body composition more than women, as longitudinal studies have shown that men tend to exhibit poorer changes in body composition (i.e., decreases in FFM and increases in fat mass) than women over time (44,45). This presents unique challenges for the measurement of subcutaneous body fat in older adults and is a topic that should be explored thoroughly in the future.

Despite the strengths of this study, there are several limitations that should be considered. Although our age range is comparable to those reported by other researchers (9,16), the majority of our participants were under the age of 26 which may limit its applicability to older populations. This is particularly important given there is a noticeable decrease in the subcutaneous-to-visceral fat ratio over the lifespan (32,46), which could impact the ability of skinfolds to accurately assess body fat in older subjects (9). In addition, the sample in the current study was predominantly White, so the effect of ethnicity was not included in the regression analysis. Although there were no significant body composition differences between White and non-White participants, interethnic variability in subcutaneous fat distribution, anthropometry, and FFM characteristics has been well-documented (5,29,30,47). Although the new equation accounted for a significant portion of interindividual variation in %BF, its performance in more diverse groups has yet to be established. Specifically, cross-validation in older adults and non-White ethnicities needs to be conducted before its use can be recommended in groups other than those represented in our sample.

The current study described an accurate equation for predicting 5C %BF using simple anthropometric measures in healthy adults. In addition, our analysis revealed a significant interaction between sex and age, suggesting that changes in body composition may occur differently in men and women over time. This unique variable may allow the new equation to capture the disparate effects of aging for which other equations would not be able to account, although this needs to be further investigated. At present, we suggest the equation developed in this study be used by health and fitness professionals to monitor body composition in healthy adults as an alternative to less accurate methods. Because of the sampling limitations discussed previously, caution should be exercised when using this equation in populations other than that described here until additional investigations are completed.