Abstract
Insufficient testing capacity has been a critical bottleneck in the worldwide fight against COVID-19. Optimizing the deployment of limited testing resources has therefore emerged as a keystone problem in pandemic response planning. Here, we use a modified SEIR model to optimize testing strategies under a constraint of limited testing capacity. We define pre-symptomatic, asymptomatic, and symptomatic infected classes, and assume that positively tested individuals are immediately moved into quarantine. We further define two types of testing. Clinical testing focuses only on the symptomatic class. Non-clinical testing detects pre- and asymptomatic individuals from the general population, and a concentration parameter governs the degree to which such testing can be focused on high infection risk individuals. We then solve for the optimal mix of clinical and non-clinical testing as a function of both testing capacity and the concentration parameter. We find that purely clinical testing is optimal at very low testing capacities, supporting early guidance to ration tests for the sickest patients. Additionally, we find that a mix of clinical and non-clinical testing becomes optimal as testing capacity increases. At high but empirically observed testing capacities, a mix of clinical testing and non-clinical testing, even if extremely unfocused, becomes optimal. We further highlight the advantages of early implementation of testing programs, and of combining optimized testing with contact reduction interventions such as lockdowns, social distancing, and masking.
Keywords: COVID-19, Epidemiology, Optimal control, SARS-CoV-2, SEIR model
1. Introduction
The COVID-19 pandemic caught the world off-guard and continues to result in devastating consequences to life, health, and national economies. A key factor hampering global control efforts has been the unanticipated shortage of testing capacity. While testing was clearly problematic early in the pandemic, it remains a critical bottleneck in many parts of the world despite massive efforts to ramp up capacity (Hasell et al., 2020). Extensive testing provides the empirical basis on which to build a robust, scientifically based response strategy (Grassly et al., 2020). Insufficient testing leaves public health authorities with little information on how to coordinate efforts to effectively combat an emerging epidemic. For example, Li et al. (2020) estimated that, early in the COVID-19 outbreak in China, 86% of infections went undocumented, and these unnoticed cases fueled the subsequent global expansion of the disease. Similarly, undetected introductions of the virus coupled with undocumented community transmission facilitated the rapid spread of COVID-19 in New York City (Gonzalez-Reiche et al., 2020). Sustained high-rate testing also plays a crucial role in strategies for safely moving beyond costly and crippling lockdowns (Grassly et al., 2020). Specifically, quick identification and isolation of new infection clusters is critical for managing a disease like COVID-19 before a vaccine is widely available. While other aspects of epidemic response such as vaccine distirbution have been studied from a resource allocation perspective (Zaric and Brandeau, 2001, Hansen and Day, 2011, Emanuel et al., 2020), the optimal allocation of limited testing capacity has, so far, received little attention (Grassly et al., 2020). The limited work that has been done on this topic has emerged recently, with some efforts focusing on using pooled testing as a simple means to stretch limited testing capacity as far as possible (Aragón-Caqueo et al., 2020, de Wolff et al., 2020, Ghosh et al., 2020, Gollier and Gossner, 2020, Jonnerby et al., 2020), while others consider stratified testing strategies focused on high risk groups such as health care workers (Cleevely et al., 2020, Grassly et al., 2020). Mathematical optimization has been applied to the economics of lockdown and quarantine policies (Aldila et al., 2020, Alvarez et al., 2020, Choi and Shim, 2021, Jones et al., 2020, Khatua et al., 2020, Piguillem and Shi, 2020), and to parameter estimation using testing data (Chatzimanolakis et al., 2020), but has not yet been applied comprehensively to resource allocation problems under testing constraints. Faced with insufficient testing capacity, public health agencies advise the prioritization of testing effort via qualitative considerations (Centers for Disease Control and Prevention, 2020). These guidelines base resource allocation decisions on total testing capacity, quality of information gained via contact tracing, current outbreak stage, and other characteristics specific to individual communities (Centers for Disease Control and Prevention, 2020). The proportion of limited testing resources reserved for high priority cases (e.g., highly symptomatic and vulnerable patients, essential healthcare workers) depends in part on the overall degree of sporadic versus clustered versus community-wide transmission (Robert Koch Institute, 2020, WHO, 2020b). While these recommendations provide useful qualitative guidance, quantitative determination of optimal allocation strategies under limited testing is lacking despite its potential to increase testing efficiency. Here, we address the optimal allocation of limited testing capacity with a COVID-19 specific SEIR ordinary differential equation compartmental model that features constrained testing and quarantine. We consider the allocation of testing and health care resources between two broad strategies (Centers for Disease Control and Prevention, 2020, Robert Koch Institute, 2020, WHO, 2020b): 1) clinical testing focused on moderate to severely symptomatic cases, and 2) non-clinical testing designed to detect mildly symptomatic, pre-symptomatic, or fully asymptomatic cases. We further explore how the degree to which non-clinical testing resources can be concentrated on infected individuals (through contact tracing efforts, for example) affects the optimal balance between strategies. For both strategies, we assume that individuals that test positive are immediately moved into quarantine. We first quantify the extent to which an outbreak can be suppressed via optimal testing and quarantine as a function of both testing capacity and non-clinical concentration level. Specifically, we identify strategies that minimize the peak of the infection curve (i.e., “flatten the curve”). We then consider how positive factors like social distancing measures, and detrimental factors such as delays in testing onset affect optimal testing strategies and outbreak controllability. Throughout, we focus our analyses on empirically supported parameter values including realistic testing rates. While many existing COVID-19 SIR-like compartmental models explore the effects of testing with forms of isolation like quarantine or hospitalization, the majority of these studies assume simple linear equations for the rates at which tests are administered and individuals are isolated (Adhikari et al., 2021, Ahmed et al., 2021, Amaku et al., 2021, Choi and Shim, 2021, Dwomoh et al., 2021, Hussain et al., 2021, Ngonghala et al., 2020, Rong et al., 2020, Saldaña et al., 2020, Sturniolo et al., 2021, Tuite et al., 2020, Verma et al., 2020, Youssef et al., 2021). We show (see Sec 2.1.2) that linear models can not fully describe highly limited testing capacity scenarios, and we propose a novel testing model which flexibly accounts for resource-rich and resource-limited settings.
2. Methods
2.1. Model development
We develop a modified SEIR model to determine how limits on the number of tests administered per day influence disease controllability, and to determine how limited resources can be best distributed among compartments in the modeled population. Our study was motivated by the COVID-19 crisis, both in terms of model structure, and in terms of the pressing need to make the most of limited testing capacity. Following other COVID-19 models (Contreras et al., 2020, Hellewell et al., 2020, Kretzschmar et al., 2020, Liu et al., 2020, Piasecki et al., 2020, Rong et al., 2020), we assume two separate infectious categories based on observable symptoms. One, the “symptomatic class,” collects moderate to severely symptomatic cases for which one would typically seek clinical treatment, and the other, the “asymptomatic class,” collects all remaining cases, which may be either properly asymptomatic, or may simply be mild enough that the infected individual does not consider themselves sick or seek clinical treatment. We first develop a baseline disease model without interventions, and then incorporate testing and quarantine control strategies.
2.1.1. Baseline SEIR model
We assume a homogeneously mixed population divided into S susceptible, E exposed, A asymptomatic and infectious, Y symptomatic and infectious, and R recovered classes. Newly infected individuals first enter the exposed class where they are unable to transmit the disease, and after a latent period, will enter the symptomatic or asymptomatic infectious class. For clarity, we take “asymptomatic” to include individuals who will show only mild to no symptoms over the course of the disease. The portion of individuals in the exposed class who eventually transition to the symptomatic class are considered “pre-symptomatic”. Although some evidence suggests that pre-symptomatic individuals can begin transmitting the disease one to several days before showing symptoms (Furukawa et al., 2020, He et al., 2020, Walsh et al., 2020), for simplicity, we assume that only A and Y class individuals are infectious. We further assume no host births or deaths, and that recovered hosts obtain permanent immunity. The model equations are as follows:
| (1a) |
| (1b) |
| (1c) |
| (1d) |
| (1e) |
Here and throughout this paper, over dots denote derivatives with respect to time, and we measure time in units of days. The meaning of each model parameter, and the numerical values used, are given in Table 1 , and a schematic summarizing the flow of infectives through our baseline model is given Fig. 1 . We note that while the recovery time and incubation period can be consistently estimated from data, some parameters in our model are not accurately known. Specifically, the fractions of asymptomatic and symptomatic infectious populations, and , respectively, are highly uncertain parameters, as estimates based on both modeling and clinical data place the truly asymptomatic population anywhere from 1% to 80% of all infections (Furukawa et al., 2020, Walsh et al., 2020, Widders et al., 2020). Focusing on symptomatic individuals, the fractions that are mildly symptomatic versus moderately to severely symptomatic are also uncertain, although some evidence suggests the majority of cases are mild (Liu et al., 2020). Based on these observations, we choose and as baseline values. Studies quantifying viral loads via RT-PCR tests and viral culture studies generally show that asymptomatic individuals are as, or less, infectious than symptomatic individuals (Walsh et al., 2020, Widders et al., 2020), and that more severely symptomatic cases can be associated with higher viral loads (Liu et al., 2020, Walsh et al., 2020, Widders et al., 2020). We therefore assume that the symptomatic transmission probability, , is twice that of the asymptomatic transmission probability, . Finally, we choose the overall values of , and the contact rate, , to yield a basic reproduction number of absent of any testing or quarantine control (see Appendix A for an analytic expression for ). This value falls within the ranges of values suggested by a number of studies (Jiang et al., 2020, Majumder and Mandl, 2020, Rong et al., 2020, Sanche et al., 2020), and may best represent the transmissibility of the alpha variant, which is more infectious than the original COVID-19 strain but less infectious than the more recent delta variant (Hendaus and Jomha, 2021). Note that under our model parameters, in the absence of testing and quarantine, the symptomatic and asymptomatic contributions to are 2.0 and 3.0, respectively.
Table 1.
Model parameter definitions and baseline numerical values used. Values for highly uncertain parameters based on the current literature for which we make an estimate are indicated with an asterisk.
| Parameter | Name | Meaning | Value | Refs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Contact rate | Average number of contacts per individual per unit time | Jiang et al., 2020, Majumder and Mandl, 2020, Rong et al., 2020, Sanche et al., 2020 | |||||||||||||
| Asymptomatic transmission probability | Probability of disease transmission per susceptible-symptomatic contact | Jiang et al., 2020, Majumder and Mandl, 2020, Rong et al., 2020, Sanche et al., 2020 | |||||||||||||
| Symptomatic transmission probability | Probability of disease transmission per susceptible-asymptomatic contact | Liu et al., 2020, Walsh et al., 2020, Widders et al., 2020 | |||||||||||||
| Latent period or incubation period | Time between transmission and onset of infectiousness or symptoms | 5 days | Furukawa et al., 2020, Hellewell et al., 2020, He et al., 2020, Lauer et al., 2020, Rong et al., 2020, Sanche et al., 2020 | ||||||||||||
| Asymptomatic fraction | Fraction of infections which remain mild or asymptomatic | Furukawa et al., 2020, Grassly et al., 2020, Liu et al., 2020, Walsh et al., 2020, Widders et al., 2020 | |||||||||||||
| Severely symptomatic fraction | Fraction of infections which become severe and symptomatic | - | |||||||||||||
| Infectious period | Average time over which infected individuals can actively transmit the virus | 8 days | Walsh et al., 2020, Widders et al., 2020 | ||||||||||||
| Z | Population size | Total number of hosts (assumed fixed) | 50000 | Assumed |
Fig. 1.
Diagram indicating the flow of infectives in our baseline SEIR model (no testing or quarantine control). Upon infection, susceptible individuals S move into the exposed class E where they are neither symptomatic or infectious. A fraction of exposed individuals transition to the asymptomatic infectious class A at rate , and a fraction transition to the symptomatic infectious class Y at rate . Infectious individuals transition to the recovered class R at rate r.
2.1.2. Testing model
To analyze testing and quarantine control strategies operating with testing capacity constraints, we construct a simple model that scales smoothly between extremes of abundant and severely constrained testing resources. This model is governed by the testing capacity, C, and the testing time, . The testing capacity C denotes the maximum achievable per capita testing rate assuming a fixed level of resources. This maximum testing rate represents the limitations of a finite health care infrastructure and finite testing supplies, and we take “increased resources” to mean an increased value of C. The testing time represents the average amount of time required for an individual be tested and obtain results, absent any backlogs or waiting times due to other patients. Time-consuming factors independent of the number of people needing to be tested determine the value of , for example, procrastination, travel time, and test processing times.
Suppose that some sub-population of the total population Z is eligible to be tested at time t, and let denote the rate at which tests are administered and processed for results. We demand that our model for attain two limiting expressions representing “resource-limited” and “testing time-limited” testing regimes as follows:
| (1f) |
The testing time-limited regime represents a high resource availability scenario, where the total testing rate is limited only by the rate at which individuals arrive to be tested and the actual time required for a single test to produce results. Here, the number of tests administered and processed per unit time is simply the average processing rate for an individual test absent of patient backlogs, multiplied by the total patient load . The resource-limited regime represents a low resource availability scenario, where the number of people needing to be tested far exceeds the maximum daily testing capacity. In this regime, tests are administered and processed at the maximum possible rate CZ, independent of the excess patient load. To incorporate this limiting behavior into a testing model, we propose the following simple function for :
| (1g) |
The above expression limits to the testing time-limited regime for small , monotonically increases with , and saturates to the resource-limited regime as approaches . We justify this testing model based on the fact that it exhibits the correct limiting behavior, and that it incorporates the reasonable assumption that the average waiting time required to administer and process a single test increases linearly with the patient load (see Appendix A Eq. (10)).
It is important to note that despite its frequent use in the literature, a simple linear testing rate model , where represents a testing rate parameter, is insufficient for describing resource-limited scenarios. Under a linear model, even if is made to be very small in reflection of testing limitations, the rate at which tests are administered will always increase in proportion with the demand for testing, and this can not describe a resource-limited scenario where the maximum testing rate is capped at a fixed value independent of the testing demand. The linear model is in fact equivalent to our testing model in Eq. (1f) under the testing time-limited regime shown in Eq. (1g), which represents a resource-rich rather than resource-limited scenario.
We note further that the testing rate model in Eq. (1g) can be extended to multiple sub-populations subject to distinct testing capacity constraints. Specifically, suppose two distinct sub-populations and are subject to two distinct testing policies with distinct resource pools limited by the capacities and , respectively. In this scenario, the total rate at which tests are administered to the two populations is given by the following:
| (1h) |
2.1.3. Disease model with resource allocation, testing, and quarantine
We now utilize our testing model to incorporate testing and quarantine into our disease model. We assume that testing resources can be allocated between two control strategies, designated “clinical testing” and “non-clinical testing,” which are applied to individuals based the presence of observable symptoms. Clinical testing applies resources to the moderate to severely symptomatic class . This strategy represents saving resources for hospital and health care facilities to ensure adequate treatment of the most seriously ill individuals. Under a pure clinical testing strategy, individuals are only eligible to be tested if they show severe enough symptoms. Non-clinical testing applies resources to the exposed class and the asymptomatic class , as well as to some portion of the uninfected population. This strategy represents a combination of large scale population monitoring programs, contact tracing and case investigation programs, and testing centers open to the general public. Population monitoring and contact tracing allow individuals unaware of their infection status to be identified, possibly before they become infectious, while testing centers facilitate testing for individuals who have not been reached by population monitoring or contact tracing efforts but who are concerned about potential recent COVID exposures. For both strategies, we assume perfectly accurate tests with no false positives or negatives, and we assume that testing can detect the disease at any point after infection to when the period of infectiousness ends. These assumptions are somewhat optimistic in comparison to real-world testing efficacies (Kucirka et al., 2020, Surkova et al., 2020), and our model thus represents a limit on what can be achieved.
When an infected individual is tested in our model, they will instantly transition to the quarantine class , and will subsequently recover from the disease and transition to the recovered class. We also introduce the “unknown status” class , which is the subset of recovered hosts who did not receive any testing or quarantine, and are therefore unaware that they previously had COVID-19. We assume that recovered individuals who have previously been tested and quarantined will exclude themselves from non-clinical testing due to assumed immunity, and therefore assume that non-clinical testing covers the entirety of the and classes as well as a fraction of the class, where denotes the “concentration parameter.” This parameter provides a simplified means for representing the degree to which modes of non-clinical testing in aggregate are able to concentrate testing resources on infected individuals. Different values are taken to represent different combinations of non-clinical resources jurisdictions may devote to large scale monitoring, contact tracing, and public testing centers, as well the varying efficacies of jurisdictions’ contact tracing efforts. Larger values represent greater efficacies of non-clinical testing in the sense that a greater share of resources are used for quarantining the COVID-19 positive population, and less are “wasted” obtaining negative results. The case represents a strictly random large scale population monitoring program, where non-clinical testing resources are dispersed randomly among the entirety of the population. Non-zero values are obtained from the presence of any influence which compels test-positive rates to be greater than overall prevalence rates obtained by random population sampling, such the information gained through contact tracing allowing resources to be focused away from individuals less likely to be infected, or the fact that public testing centers may be naturally biased towards receiving infected individuals. By “biased,” we mean that individuals with suspected recent exposures or extremely mild symptoms may be more inclined than others to seek testing on their own volition, so testing centers may see a higher proportion of infected individuals during an outbreak as compared to a random population monitoring program. The case represents an impossibly perfect large scale contact tracing and case investigation program, where all non-clinical testing is focused on infected individuals, and testing centers have impossibly perfect omniscience of who is and is not infected. Although and are extreme cases, and is not practically achievable, they place informative bounds on what can be accomplished according to our model.
In Appendix B, we provide a concrete definition of using our testing model. Here, we derive a mathematical expression which shows explicitly the manner in which quantifies non-clinical testing efficacy in terms of non-clinical test-positivity rates and disease prevalence rates. Utilizing this expression, we estimate plausible ranges for real-world testing programs by comparing test-positivity rate data to estimated prevalence rate data. We find to be a generous range of plausible values for testing programs which are not strictly random population sampling, although this is an admittedly rough estimate due to the unavailability of strictly non-clinical testing data, as well as the crude manner in which our model uses to represent the aggregate influence of multiple modes of non-clinical testing. To achieve values greater than , contact tracers would likely require foreknowledge on which secondary contacts of a confirmed case are more likely to be infected, for example, based on factors such as age or the presence of comorbidities. Finally, we acknowledge that our non-clinical testing model makes a simplification in assuming that testing is applied to the entirety of the , and this assumption may be overly generous and unrealistic regarding the reach of contact tracing and testing centers. In Appendix C, we show that relaxing this assumption does not qualitatively change our model or results, and that our central result in Fig. 4 remains entirely unchanged.
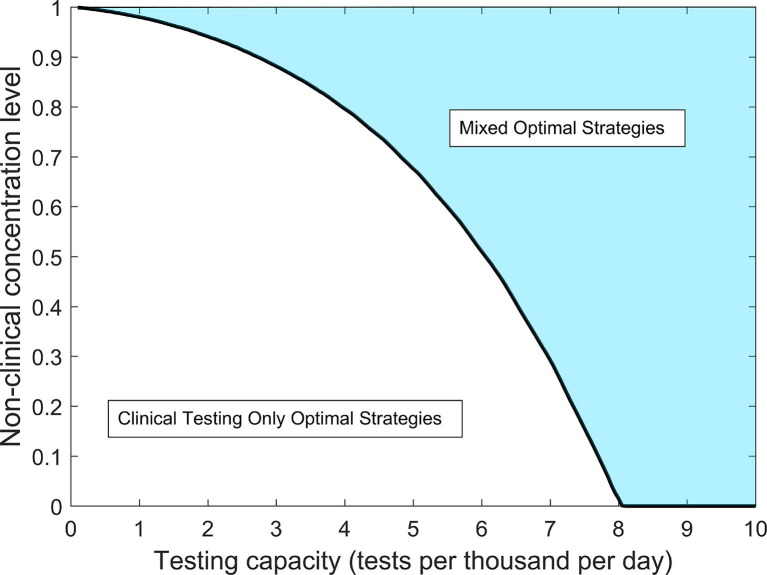
Fig. 4.
Optimal resource allocation strategy regimes for reducing the epidemic peak as a function of testing capacity C and non-clinical testing concentration level . For values within the shaded region, optimal strategies call for sharing resources between a mix of clinical and non-clinical testing. Within the non-shaded region, optimal strategies call for all resources to be focused to clinical testing only. The black curve indicates a critical concentration level threshold which for a given testing capacity, determines whether the optimal strategy will be mixed or clinical testing only.
Suppose that a fraction of the testing capacity C is allocated to non-clinical testing, with the remainder devoted to clinical testing. The parameter denotes the “strategy parameter,” and its value represents a government’s policy for balancing health care resources between reservation for more critical symptomatic cases and for use in contact tracing, testing centers, and surveillance programs. Our modified SEIR model including testing, quarantine, and resource allocation is as follows:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
| (5f) |
| (5g) |
Note that as , Eq. (5d) reduces to Eq. (1d), and as , Eqs. (5b) and (5c) reduce to Eqs. (1b) and (1c), respectively. Additionally, as , all of Eq. (5) reduces to Eq. (1a). In Appendix A, we analyze a closed-form expression for under our full SEIR + testing and quarantine model, and we provide expressions in Eqs. (11) and (12) for average testing waiting times for non-clinical and clinical patients, respectively.
A summary of all control related parameters is given in Table 2 for reference, and a schematic summarizing the flow of infected individuals through our control model is given in Fig. 2. For all simulations, we assume the testing time = 1 day, which is reasonable for an effective testing and processing system lacking patient backlogs. For all other control parameters, we will consider a range of numerical values. Note that for notational simplicity in our model equations, we define C in units of tests per person per day, while actual testing capacities are often reported in units of tests per thousand people per day. To establish clear connections between our results and real-world testing limitations, we too report numerical values for testing capacity in units of tests per thousand per day. Thus, if we report a particular numerical value in per thousand units, the corresponding value in per person units used for numerical simulations is given by .
Table 2.
Testing and quarantine control parameter definitions.
| Parameter | Name | Meaning | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C | Testing capacity | Maximum number of tests able to be administered per day per capita | ||||||||||||||
| Testing time | Average amount of time required for an individual be tested (including procrastination, travel time, processing time, etc.) absent of backlogs or delays due to other patients | |||||||||||||||
| Strategy parameter | Fraction of testing capacity used for non-clinical testing | |||||||||||||||
| Concentration parameter | = fraction of COVID-19 negative population with unknown infection history subjected to non-clinical testing |
Fig. 2.
Diagram indicating the flow of infectives in our SEIR model with testing or quarantine control. Blue arrows represent natural disease transitions, and red arrows represent transitions due to testing and quarantine interventions. Exposed E and asymptomatic infectious A individuals enter the quarantined class Q via non-clinical testing, while symptomatic infectious individuals Y enter quarantine Q via clinical testing. Quarantined individuals are prevented from generating new infections, and enter the recovered class R at the natural recover rate r. Infectious individuals who do not enter the quarantined class also recover at rate r, and subsequently enter the subset U of recovered individuals with unknown infection histories, signifying that they are unaware that they were ever infected with COVID-19.
2.2. Flattening the epidemic peak as a control goal
In accordance with the goal of “flattening the curve” typically communicated by government and health agencies (World Health Organization, 2020a), we simulate our model dynamics to determine if and to what extent appropriately allocated resources can reduce the peak number of infections. First, we calculate optimal resource allocation strategies for reducing the epidemic peak (defined as the maximum value of the sum of the , and Y classes), assuming parameter values in Table 1 and an initial outbreak of one exposed individual as our baseline case. Optimization is executed by numerically integrating the disease dynamics in Eq. (5) and utilizing the fmincon function in MatlabR2017a running the sqp algorithm with as an initial guess. To account for the possibility of multiple local minima, we employ the parallel MultiStart algorithm from Matlab’s global optimization toolbox. Simulations assume specific values for and find optimal and epidemic peak values for all testing capacities in the range (in units of tests per thousand per day). In Appendix A, we consider the alternative optimization goal of minimizing under our combined disease + testing model.
To determine the effects of delays in testing/quarantine policy implementation, as well as the effects of social distancing efforts, we consider alternative scenarios of initial conditions and/or model parameters. We model implementation delays by considering initial conditions equal to the outbreak size after a given number days under our baseline scenario with no testing or quarantine controls. In the case of a 30 day delay, for example, the alternative initial condition is given by , which yields 218 initially infected individuals. To model the effects of social distancing, we reduce to a given fraction of its baseline value. Additionally, we consider the effects of social distancing and implementation delays together. To evaluate the effects of alternative scenarios on optimal control policies, we perform the same optimization procedure as in our baseline case. We provide an in-depth examination of the specific conditions of a 30 day initial testing delay and a 50% reduction of , and also consider a broader range of delays and reductions in less detail.
3. Results
3.1. Optimal resource allocation strategies
We find that, even under extremely limited testing capacities, the epidemic peak can be reduced to the initial outbreak size of 1 infected individual, provided that resources are optimally allocated and that non-clinical resources are sufficiently concentrated on the infected population (Fig. 3a ). Reducing the epidemic peak to the initial outbreak size signifies that disease spread has been effectively suppressed. For a given at low testing capacities, the optimal strategy is to devote all resources to clinical testing, and a minimum threshold capacity exists, above which optimal strategies call for a mix of clinical and non-clinical testing (Fig. 3b). As testing capacity increases above optimal strategies require an increasing share of resources to be devoted to non-clinical testing until a second threshold capacity is reached. The threshold represents the smallest testing capacity for which the outbreak can be suppressed to its initial size with a non-clinical concentration level . For example, at concentration level and tests per thousand per day (Fig. 3b). Table 3 summarizes the threshold capacity definitions and gives numerical values for various values of .
Fig. 3.
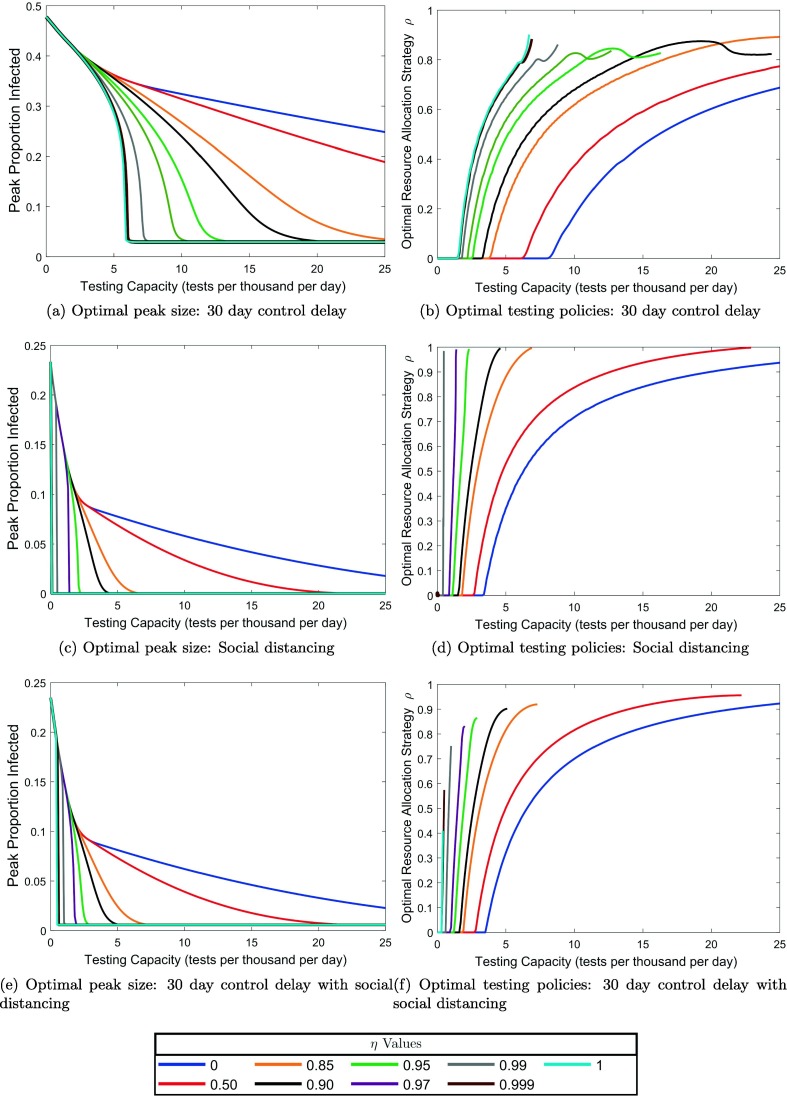
Optimally reduced infected population proportions at the epidemic peak and corresponding optimal values as a function of testing capacity. Note that the peak proportion 0.48 (corresponding to 23882 individuals) at zero testing capacity corresponds to the uncontrolled disease dynamics without a testing or quarantine program. (a) Optimally reduced epidemic peak proportions as a function of testing capacity for the values of non-clinical testing concentration level indicated in the legend. (b) Optimal resource allocation strategies for reducing the epidemic peak as a function of testing capacity. An optimal curve which terminates at a testing capacity below than the maximally considered value 25.0 tests per thousand per day indicates a non-clinical concentration level for which the optimal strategy is not unique at capacities above , and for which the optimal epidemic peak size can be reduced to the initial value of one infected at capacities above . Note that for the idealized omniscient limit , the optimal testing strategy is not unique down to the smallest non-zero testing capacity considered (0.01 tests per thousand per day). Note also that for = 0.85, 0.90, 0.95, and 0.97, the optimal values at appear to be close to 1, but are not actually equal to 1.
Table 3.
Threshold testing capacity definitions and numerical values for the non-clinical concentration levels considered in Fig. 3. Note that critical concentration threshold levels can be inferred from this table from the relationship if and only if . For example, the column indicates that .
| Threshold Capacity | Definition | Numerical Values (tests per thousand per day) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| =0.00 | =0.50 | =0.85 | =0.90 | =0.95 | =0.97 | =0.999 | =1.00 | ||
| Minimal capacity beyond which optimal strategies are mixed | 8.0 | 6.0 | 3.4 | 2.8 | 1.8 | 1.2 | 0.1 | 0.0 | |
| Minimal capacity beyond which optimal strategies reduce epidemic peaks to initial infection levels | 154.0 | 77.0 | 23.1 | 15.4 | 7.6 | 4.6 | 0.2 | 0.0 | |
For testing capacities , the epidemic peak size will always be reduced to 1 as long as at least as much of the total capacity is devoted to clinical and non-clinical testing as is called for by the optimal strategy at . As a result, optimal strategies are not unique when . To see this non-uniqueness explicitly, consider a concentration level , and let denote the optimal strategy parameter at the critical capacity . At this critical capacity, the optimal action is to devote total resources to non-clinical testing and total resources to clinical testing, the result of which reduces the epidemic to the smallest possible value 1. If the testing capacity C exceeds the critical level , one can always allocate at least and total resources to non-clinical and clinical testing, respectively, thereby guaranteeing the epidemic peak to be reduced to 1. The allocation of the remaining resources will therefore be irrelevant, as adding resources to either strategy can not further decrease the peak size beyond the initial infection size. In other words, for a given , if , the epidemic peak will be reduced to 1 whenever is selected such that and . These inequalities imply that any drawn from the interval will reduce that epidemic peak to the minimum possible value, thus showing that the optimal strategy is not unique for .
For a given capacity C, there exists a critical non-clinical concentration value , below which the optimal strategy is clinical testing only, and above which the optimal strategy is mixed (Fig. 3). From the definition of as the minimal capacity below which the optimal strategy is clinical testing only for a given , we have the relation if and only if , and numerical values for at specific C values can therefore be inferred from Table 3. The critical concentration value represents an important practical decision making threshold for public health officials operating under a potentially limited testing capacity C; if is estimated to be below , no testing resources should be diverted away from severely symptomatic individuals, while if is estimated to be above , important resource management decisions should be considered. In Fig. 4, we plot as a function of testing capacity C. Here, the curve defined by divides the plane into two regimes, one where the optimal strategy calls for clinical testing only, one where optimal strategies are a mix of clinical and non-clinical testing. In particular, we find that for tests per thousand per day, . Thus, for testing capacities above , it is always optimal to devote at least some resources to non-clinical testing, even if the non-clinical testing is a simple randomized population sampling program lacking the efficacy of targeted contact tracing efforts.
3.2. Social distancing and delays in testing program implementation
Unsurprisingly, delaying the implementation of a testing program by 30 days has negative impact on optimal peak reduction, with the delay being most detrimental at the lowest testing capacities (cf. Fig. 5, Fig. 5 ). Specifically, a delay of this magnitude makes it impossible to reduce the epidemic peak to its initial value, regardless of the non-clinical concentration level, within the range of testing capacities tests per thousand per day (Fig. 5a). This is not the case for immediate testing program implementation, where the peak can be reduced to its initial value at any non-zero testing capacity given a sufficient concentration level (Fig. 3). Reducing the peak to its initial value is an important control goal, as it is equivalent to the ability to force an immediate downturn in the infection curve upon implementation of testing and quarantine. These results emphasize the need for early implementation of a testing program at the beginning stages of a novel disease epidemic, where resources may be extremely limited as health agencies adjust to the biology of the newly discovered infectious agent.
Fig. 5.
Effects of social distancing and control delays on optimal testing strategies for reducing the epidemic peak. See Fig. 3 for a comparison to our baseline case and an explanation of the meaning of each plot.
Halving the contact rate, which simulates the influence of social distancing, has a strong effect on optimal policies and peak sizes (Fig. 5, Fig. 5). At zero testing capacity (which corresponds to the disease dynamics without testing and quarantine), the epidemic peak reaches a proportion of 0.23, which is approximately half of the no testing peak proportion without social distancing. This finding is not surprising given that we model social distancing by reducing the contact rate by half. Generally, social distancing expands the range of testing capacities over which the peak can be reduced to its initial value for a given non-clinical concentration level. Compare, for example, the curve in Fig. 5c to that of Fig. 3a. We thus conclude that social distancing allows for more effective utilization of limited testing capacities under lower concentration levels. Note that in both the base and socially distanced parameter scenarios, we find no non-zero testing capacities for which the peak can not be suppressed to its initial size for , and therefore no range of testing capacities over which the optimal is unique (Fig. 5, Fig. 3).
Combining the two modulating factors shows that the beneficial effects of social distancing at low testing capacities can counteract some of the detrimental effects of delays in testing implementation (Fig. 5, Fig. 5). Indeed, social distancing reduces the testing capacity range over which implementation delays render epidemic control impossible. This interval is given by tests per thousand per day with 50% contact reduction social distancing (Fig. 5e), as compared to without social distancing (Fig. 5a). For all delays between 1 day and the time of the uncontrolled epidemic peak, 62 days, larger degrees of contact reduction from social distancing yield larger reductions in the range of testing capacities for which the peak can not be reduced to its initial size in the idealized omniscient limit (Fig. 6 ). Note that after day 62, the infection curve turns downward in the uncontrolled model, so for delays greater than 62 days in the controlled model, the epidemic peak value will always be equal to the initial value regardless of testing capacity, and peak reduction is not a useful control goal. Also note that in Fig. 6, the plotted curves begin to turn down around a delay of 50 days due to the fact that in the uncontrolled model, the slope of the epidemic curve begins decrease after about 50 days. This occurs because a smaller intervention force is required to cause an immediate downturn when the infection curve has already started moving towards a downturn on its own. In total, these results emphasize the importance of social distancing during the early resource-limited stages of a novel disease epidemic.
Fig. 6.
Combined effects of social distancing and delays in testing implementation on epidemic controllability. Threshold testing capacities are plotted as a function of implementation delay, where different curves represent different social distancing strengths as percent reduction in the contact rate. For a given implementation delay time, if testing capacity falls below the value indicated by a curve in the figure, the epidemic will not be forced into a downturn upon control implementation despite perfectly omniscient non-clinical testing, assuming the indicated level of social distancing. Plotted curves terminate at a 62 day delay because the uncontrolled epidemic curve peaks and begins to decrease on its own after day 62. Plotted curves begin to decrease after about a 50 day delay because the slope of the uncontrolled epidemic curve begins to decrease after about 50 days.
4. Discussion
The COVID-19 pandemic has exposed a critical lack of capacity for diagnostic testing in an emerging pandemic. Using a modified SEIR model, we explored how distributing a limited amount of testing effort can affect the course of an epidemic when testing is directly coupled to quarantine. The model is tailored to the epidemiology of SARS-CoV-2, and divides infected individuals into symptomatic and non-symptomatic classes, with the latter class including individuals who have been exposed but are not yet infectious as well as those who are infectious but not strongly symptomatic. We further defined clinical testing as that focused exclusively on the symptomatic class, while non-clinical testing is distributed across the rest of the potentially infected population (S, E, A, and U). For a given testing capacity C, our model thus allows us to identify optimal testing policies in terms of the balance between clinical and non-clinical testing, modulated by the strategy parameter, , and the non-clinical concentration parameter . This latter parameter governs the extent to which non-clinical testing is concentrated on infected individuals. We further examined how optimal policies shift as a function of testing capacity. .
Focusing on the goal of maximally reducing the height of the infection curve (i.e., “flattening the curve”), we found that optimal testing is always able to supress the epidemic, provided that testing is implemented at the onset of disease transmission. Clinical testing strategies are generally optimal at low testing capacities. Under some conditions when the testing rate is low, mixed strategies that include a small but finite amount of non-clinical testing are optimal, but only when there is nearly omniscient information with which to focus non-clinical testing on infected individuals. While perfectly omniscient non-clinical testing is unlikely to be achieved in reality, high values are indeed empirically plausible provided that the non-clinical test positivity rate exceeds the prevelance rate in the general population (see Appendix B). These results therefore suggest that testing policies employed in many countries early in the pandemic, which strongly emphasized clinical testing with some additional testing effort aimed at the highest risk individuals (e.g., front-line healthcare workers), were reasonable. Furthermore, we demonstrated that exclusively non-clinical testing is never the optimal strategy. In other words, non-clinical testing plus a small but finite amount of clinical testing will always be better than a purely non-clinical strategy for epidemic peak reduction.
Since the onset of the pandemic, testing capacity has steadily increased throughout much of the world. Our results show that increased testing capacity brings with it a broader range of possibilities for optimizing testing. As testing rate increases, the amount of non-clinical testing concentration required for a mixed strategy to be optimal decreases, with all other factors held constant. At a testing capacity of 8 tests per day per 1000 people, a mixed strategy becomes optimal even when there is no ability or tendency for non-clinical resources to be focused away from uninfected individuals. This testing rate thus defines the minimal testing capacity for which a broad, non-targeted population monitoring program, in conjunction with clinical testing, is optimal. While on the higher end of the realistic range of testing rates, this level of testing has been exceeded in several countries, including Denmark, Iceland, Luxembourg, and United Arab Emirates.
While we have chosen minimizing the height of the peak of the infection curve as a pragmatic and meaningful control goal, we also explored the common approach of minimizing (see Appendix A). A mathematical advantage of minimization is that it leads to closed-form expressions for key threshold parameter values that delimit the conditions under which different testing strategies are optimal. However, we found that for our model, results between these two control goals often differed markedly. Specifically, we identified conditions under which testing policies resulting in still yielded large outbreaks, which suggests limited utility of as a control target. We hypothesize that this phenomenon results from the combination of a finite system size and a finitely small initial condition (see Appendix A). We further note that the choice of control goal can also lead to qualitatively different conclusions about optimal strategies. For example, purely clinical testing strategies are never optimal under minimization, which contrasts sharply with low testing capacity results for peak minimization.
Our results suggest that testing early is critically important to control efforts. Specifically, the range of testing rates that allows full epidemic control is broadest when testing is implemented immediately at the start of an epidemic. A delay of even 30 days is sufficient to significantly narrow the conditions under which the epidemic can be brought to heel. Looking in the other direction, mitigation efforts that lower the effective contact rate, such as lockdowns, social distancing, and mask wearing, significantly facilitate epidemic control, particularly when combined with early testing. Importantly, interventions that reduce the contact rate also lower the threshold testing capacity where uniform random testing of the non-symptomatic population is warranted. These considerations suggest that testing programs should be designed in conjunction with non-pharmaceutical interventions.
Taken together, our results suggest that focusing exclusively or mostly on clinical testing at very low testing capacities is often optimal or close to optimal. As testing capacities increase, which can typically be expected to happen with time since epidemic onset, the options for optimally distributing testing effort also open up. To our knowledge, this possibility has been largely unexplored in the literature. This implies that the main gains to be had by optimizing allocation of testing effort will occur at intermediate testing capacities, where options exist for optimization, but capacity is still limited relative to demand. These considerations further suggest that testing policies should evolve over time, and that time-dependent optimal control (Kirk, 1998, Lenhart and Workman, 2007), which can explicitly account for the dynamics of testing capacity, will be necessary to robustly identify how testing should change through the course of an epidemic. While beyond the scope of the present effort, broadening our approach to consider time-dependent optimal control is a clear next step. Another key direction for future efforts would be to consider optimal allocation of testing effort after relaxing the homogeneous, well-mixed population assumption at the core of compartment-type disease models. Spatially explicit extensions of disease models have been shown to change key quantities such as immunization thresholds (Eisinger and Thulke, 2008), and we expect that introducing spatial heterogeneity would also change the picture for optimal testing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was partially funded by the Center of Advanced Systems Understanding (CASUS) which is financed by Germany’s Federal Ministry of Education and Research (BMBF) and by the Saxon Ministry for Science, Culture and Tourism (SMWK) with tax funds on the basis of the budget approved by the Saxon State Parliament. This work was also partially funded by the Where2Test project, which is financed by SMWK with tax funds on the basis of the budget approved by the Saxon State Parliament.
Appendix A. The basic reproduction number
In this appendix, we provide an analytic expression for our model’s basic reproduction number, , and we demonstrate that reduction is not a reliable metric of control efficacy for epidemic peak reduction. The basic reproduction number is a threshold quantity which determines the stability of a disease-free population with no natural or acquired immunity: small numbers of initial cases will produce large epidemic outbreaks when , and will result in rapid disease die-out when (Diekmann et al., 1990). Intuitively, quantifies the number of secondary cases produced by a typical initial case when interacting with the disease-free state. Because we are able to obtain an analytic expression for , the question of its suitability as a metric for control efficacy is especially prescient; the ability to analytically minimize rather than numerically minimize the peak itself would provide exact expressions and deep mechanistic insight into optimal control strategies if were indeed found to be a reliable metric for control efficacy.
A.1. Analytic expression for
The analytic expression for our model’s basic reproduction number is found utilizing the next-generation matrix method (van and Watmough, 2002). We find that can interpreted as the asymptomatic population fraction multiplied by average number of secondary infectious individuals produced by an asymptomatic case, plus the symptomatic population fraction multiplied by the average number of secondary infectious individuals produced by an symptomatic case:
| (6) |
where
| (7) |
| (8) |
| (9) |
The case corresponds to the uncontrolled model in Eq. (1a), and is a discontinuous function of C at except for the special case . Under uncontrolled conditions, the parameters in Table 1 give , with 3.0 originating from the asymptomatic contribution, and 2.0 originating from the symptomatic contribution. For is a discontinuous function of at and at . Note that these discontinuous limits represent potentially unrealistic extremes of testing policies and non-clinical concentration levels.
A.2. Suitability of as a control metric
To determine if reduction provides a reliable assessment of control efficacy for epidemic peak reduction, we plot the infected population proportion at the epidemic peak as a function of in Fig. 7 . These figures were generated by integrating Eq. (5) for specific C and and all assuming the baseline parameter values and initial condition, and plotting the resulting peak infected proportions against the corresponding values as determined by Eq. (6). These results show clearly that is not a reliable measure of control efficacy for epidemic peak reduction, as there exists several cases where the epidemic peak value increases as decreases. Further, there exist conditions where epidemic peaks are large even though , in apparent contradiction the definition of as a threshold for large epidemic outbreaks. This effect can be seen in for ,and in Fig. 7a, and for and in Fig. 7b. For and curves, large peaks occurring with correspond to values very close but not equal to 1, while for the curve, correspond values very close but not equal to 0.
Fig. 7.
Infected population proportions at the epidemic peak plotted as a function of for testing capacities and tests per thousand per day. Curve colors correspond to the concentration values indicated in the legend. Along each curve, increases from 0 and 1, with the beginning of each curve at indicated by the centers of the black circles ( represents clinical testing only where the concentration parameter is irrelevant, so all curves must coincide). The dashed black lines indicate the uncontrolled peak infected proportion of , and the black x indicates the uncontrolled .
To explain the presence of large outbreaks when , we define the effective testing time, , which represents the average time an individual must wait to be tested given the current backlog of patients. For the basic testing model in Eq. (1g), the effective testing time is defined by , which evaluates to
| (10) |
Extending this definition to our disease model with testing and quarantine in Eq. (5), we find two effective testing times for non-clinical and clinical testing, denoted and , respectively:
| (11) |
| (12) |
These effective testing times represent the average delays for asymptomatic and symptomatic individuals, respectively, in getting tested, receiving results, and moving to quarantine, given the current backlog of patients and tests. and provide measures of non-clinical and clinical control efficiency, respectively, under the current load of infected patients. Specifically, and increase monotonically with the patient load (and are thus equal to the minimal possible testing times when the patient load is negligibly small), so for larger patent loads, a fixed number of resources will move individuals to quarantine at a slower effective per-capita rate. In this sense, lower patient loads allow a given number of resources to be leveraged more efficiently.
We hypothesize that the large outbreaks observed when arise due to a finite system size and a finitely small initial condition size. The threshold property of for outbreak suppression assumes a disease-free equilibrium background state perturbed by a sufficiently small number of initial infected individuals, where “sufficiently small” means small in comparison to the total system size such that the disease dynamics can be well-approximated by linearizing about the disease-free equilibrium. Under disease-free equilibrium conditions, there is no backlog of patients needing to be tested, so the effective testing times in Eqs. (11) and (12) achieve their minimal values, and thus assumes a maximally efficient level of control when assessing outbreak potential. Under the full disease dynamics, however, Eqs. (11) and (12) show that small numbers of initial infectives will produce slightly longer than minimal effective testing times, and that this small increase can become exaggerated when is very close but not equal to 1 or 0. Thus, initial conditions can yield testing efficacies much smaller than those assumed by , sometimes to a degree which allows epidemics to grow even when . In support of our hypothesis, we have found that reducing the initial condition size by a factor of 10 (which corresponds to less than one infected individual) eliminates the effect of large peaks when for all cases pictured in Fig. 7.
Appendix B. The concentration parameter
In this appendix, we provide a definition for the concentration parameter in terms of test-positive and prevalence rates, and use the resulting expression to estimate plausible values from data. To begin, consider the case representing a monitoring program conducted via random population sampling. Let and denote the rates at which positive and negative tests, respectively, are processed and administered under non-clinical testing for :
| (13) |
| (14) |
Let and denote the corresponding respective test-positive and negative rates, defined as the fractions of tests returning positive and negative results:
| (15) |
| (16) |
The above expression show that for , test positive and negative rates are equivalent to the overall disease prevalence and non-prevalence, respectively, within population. This result agrees with the notion that represents a random population sampling, as the test positive rate from a random sample should be an unbiased estimate for disease prevalence. Consider now the case of , and let and denote the rates at which positive and negative tests, respectively, are processed and administered under non-clinical testing:
| (17) |
| (18) |
The corresponding test-positive rate and test-negative rate are given by the following:
| (19) |
| (20) |
Combining the above expressions with Eqs. (15) and (16), we find the following expression for :
| (21) |
Eq. (21) shows that is a measure of the efficacy of a non-clinical testing program’s tendency to focus tests on infected individuals relative to overall prevalence levels. When non-clinical testing performs little to no better than a random sampling program, the test-positive to negative ratio will nearly equal the positive to negative prevalence ratio, so the fraction term in Eq. (21) will be close to one, and will be close to zero. As the ratio of test-positive to negative rates increases beyond the level of positive to negative prevalence, the fraction term decreases in magnitude, and grows larger. When the test-positive to negative ratio becomes much larger than the ratio of positive to negative prevalence, the fraction term in Eq. (21) will be small, and will be close to one. Interestingly, because is constant, Eq. (21) shows that, as a consequence of our model structure, the time-dependencies of the test-positive to negative ratio and the positive to negative prevalence ratio cancel one another.
Substituting the identities and , Eq. (21) gives a mathematical relationship between , the test-positive rate, and the prevalence rate. In Fig. 8a , we plot the test-positive rate as a function of the prevalence rate for a number of values. In our disease + testing model, as the epidemic grows, the point will travel to the rightwards along one of the corresponding curves in Fig. 8a, stop and reverse direction once the epidemic peaks, and eventually approach the origin as the disease dies out.
Fig. 8.
Plots of the non-clinical test-positivity rate as a function of the non-clinical disease prevalence rate according to the relation in Eq. (21), assuming various values of . Fig. 8a exemplifies the degree to which non-zero values increase the test-positivity rate beyond the level of prevalence that would be measured by random population sampling at . Fig. 8b zooms into the ranges of prevalence and test-positivity rates for the entire clinical plus non-clinical population estimated over the first year of the pandemic 2020 in the United States. Test-positive rates are taken from Ritchie et al. (2020), and estimated prevalence rates are taken from Noh and Danuser (2021). Specific values pairs of test-positivity and prevalence values on specific dates in 2020 are indicated by the marks in Fig. 8b.
To properly estimate for a real system, one must acquire test-positive rates and prevalence rates which exclude data from moderate to severely symptomatic cases in clinical settings. To the best of our knowledge, such data are not readily available. As a substitute, we use test-positive and prevalence rates for estimated for the entire infected population in the Untied States over the first year of the pandemic. Test-positive rates are taken from Ritchie et al. (2020), and estimated prevalence rates are taken from Noh and Danuser (2021). Fig. 8b provides a zoomed-in view of the Fig. 8a within the range of values suggested by this data, and we include markers for specific values of test-positivity and prevalence on specific dates. We see that during the initial stages of the pandemic in April 2020, test-positive and prevalence rates give values between 0.95 and 0.90, while in later months, values tend to cluster between 0.75 and 0.85. The higher test-positive to prevalence ratios in April coincide with an extreme lack of testing supplies during the early pandemic when the majority of tests were reserved for the most severe cases. The lower test-postivity to prevalence ratios in later months coincide with initial increases in testing supplies and expanded testing beginning to be available to a wider population. From these considerations, we posit as a reasonable upper bound for a non-clinical testing program including an efficacious contact tracing program. We base this assertion on the idea that one would likely not do better identifying asymptomatic individuals in our model than what the real world achieves in identifying symptomatic individuals. For a lower bound on a non-clinical testing program lacking a random population element (i.e. a program comprised of only contact tracing and testing centers open to individuals concerned with possible exposure), we posit . This is based on Fig. 8a, where we see that for less than 0.50, test-positive rates are only slightly above prevalence rates, and this would not be reasonable for a testing program which does not randomly sample both infected and non-infected individuals.
Appendix C. Limited non-clinical testing access
In this appendix, we consider the effects of limiting the overall population accessible to non-clinical testing. Such limitations may be especially relevant for large values representing extremely efficacious contact tracing programs, as the time and effort required to run such programs may limit the number of individuals able to be reached, and many individuals may not be amenable to participation in such programs. Suppose that a fraction of the non-clinical is accessible by non-clinical testing. Assuming a concentration level , the rate at which positive and negative non-clinical tests are administered and processed, and , respectively, are given by the following.:
| (22) |
| (23) |
The above expressions show that limited non-clinical testing access effectively increases the non-clinical testing time to . Importantly, we see that limited testing access does not change the interpretation of in terms of test-positivity rates and prevalence rates outlined in Appendix B. In Fig. 9 , we plot optimal infected population proportions at the epidemic peak and corresponding allocation strategies for the same values as in Fig. 3, assuming only a fraction of class can be reached by non-clinical testing. Generally, we find that when non-clinical testing has limited access to the population, a larger testing capacity is required to achieve a given level of controllability compared to the full testing access case. Interestingly, we find that the critical threshold testing capacities at which optimal actions become a mix of clinical and non-clinical testing are equivalent to the full testing access case. This occurs because the critical thresholds indicate the points at which the optimal fraction of resources devoted to non-clinical testing switches from 0 to an infinitesimal but non-zero amount, and so the associated non-clinical testing capacities are extremely small, regardless of the size of . Thus, at these thresholds, non-clinical testing is always in the resource limited regime, where and are irrelevant. This implies that our central result Fig. 4 is completely unaffected by limited non-clinical testing access. From these considerations, we conclude that limited non-clinical testing does not considerably change the qualitative aspects of our main analysis.
Fig. 9.
Recreation of Fig. 3 in the main text assuming only a fraction of the non-clinical population can be accessed by non-clinical testing. This assumption is equivalent to increasing the non-clinical testing time equal to . Comparing Fig. 9a to Fig. 3a shows that limited testing access generally requires larger testing capacity to achieve a given level of peak reduction. Comparing Fig. 9b to Fig. 3b shows that for a given value, the threshold testing capacity at which optimal strategies become a mix of clinical and non-clinical testing are equivalent under limited and full. testing access.
References
- Adhikari K., Gautam R., Pokharel A., Uprety K.N., Vaidya N.K. Transmission dynamics of COVID-19 in Nepal: Mathematical model uncovering effective controls. J. Theor. Biol. 2021;521 doi: 10.1016/j.jtbi.2021.110680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmed I., Modu G.U., Yusuf A., Kumam P., Yusuf I. A mathematical model of Coronavirus Disease (COVID-19) containing asymptomatic and symptomatic classes. Results Phys. 2021;21 doi: 10.1016/j.rinp.2020.103776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aldila D., Ndii M.Z., Samiadji B.M. Optimal control on COVID-19 eradication program in indonesia under the effect of community awareness. Math. Biosci. Eng. 2020;17:6355–6389. doi: 10.3934/mbe.2020335. [DOI] [PubMed] [Google Scholar]
- Alvarez, F.E., Argente, D., Lippi, F., 2020. A simple planning problem for COVID-19 lockdown. Working Paper 26981, National Bureau of Economic Research. Series: Working Paper Series
- Amaku M., Covas D.T., Bezerra Coutinho F.A., Azevedo Neto R.S., Struchiner C., Wilder-Smith A., Massad E. Modelling the test, trace and quarantine strategy to control the COVID-19 epidemic in the state of So Paulo, Brazil. Infect. Dis. Model. 2021;6:46–55. doi: 10.1016/j.idm.2020.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aragón-Caqueo D., Fernández-Salinas J., Laroze D. Optimization of group size in pool testing strategy for SARS-CoV-2: A simple mathematical model. J. Med. Virol. 2020;92:1988–1994. doi: 10.1002/jmv.25929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Centers for Disease Control and Prevention, 2020. Interim guidance on developing a COVID-19 case investigation and contact tracing plan. [cited 2020 September 23]. Available from:https://www.cdc.gov/coronavirus/2019-ncov/php/contact-tracing/contact-tracing-plan/overview.html.
- Chatzimanolakis M., Weber P., Arampatzis G., Wlchli D., Karnakov P., Kii I., Papadimitriou C., Koumoutsakos P. medRxiv. Cold Spring Harbor Laboratory Press; 2020. Optimal Testing Strategy for the Identification of COVID-19 Infections. [Google Scholar]
- Choi W., Shim E. Optimal strategies for social distancing and testing to control COVID-19. J. Theor. Biol. 2021;512 doi: 10.1016/j.jtbi.2020.110568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleevely M., Susskind D., Vines D., Vines L., Wills S. A workable strategy for Covid-19 testing: Stratified periodic testing rather than universal random testing. Covid Economics. 2020;8:44. [Google Scholar]
- Contreras S., Villavicencio H.A., Medina-Ortiz D., Biron-Lattes J.P., Olivera-Nappa A. A multi-group SEIRA model for the spread of COVID-19 among heterogeneous populations. Chaos Solitons Fractals. 2020;136 doi: 10.1016/j.chaos.2020.109925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Wolff, T., Pflger, D., Rehme, M., Heuer, J., Bittner, M.-I., 2020. Evaluation of Pool-based Testing Approaches to Enable Population-wide Screening for COVID-19. arXiv:2004.11851 [q-bio, stat]. arXiv: 2004.11851. [DOI] [PMC free article] [PubMed]
- Diekmann O., Heesterbeek J.A.P., Metz J.A.J. On the definition and the computation of the basic reproduction ratio R_0) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- Dwomoh D., Iddi S., Adu B., Aheto J.M., Sedzro K.M., Fobil J., Bosomprah S. Mathematical modeling of COVID-19 infection dynamics in Ghana: Impact evaluation of integrated government and individual level interventions. Infect. Dis. Model. 2021;6:381–397. doi: 10.1016/j.idm.2021.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisinger D., Thulke H.-H. Spatial pattern formation facilitates eradication of infectious diseases. J. Appl. Ecol. 2008;45(2):415–423. doi: 10.1111/j.1365-2664.2007.01439.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emanuel E.J., Persad G., Upshur R., Thome B., Parker M., Glickman A., Zhang C., Boyle C., Smith M., Phillips J.P. Fair allocation of scarce medical resources in the time of Covid-19. N. Engl. J. Med. 2020;382:2049–2055. doi: 10.1056/NEJMsb2005114. [DOI] [PubMed] [Google Scholar]
- Furukawa N.W., Brooks J.T., Sobel J. Evidence supporting transmission of severe acute respiratory syndrome coronavirus 2 while presymptomatic or asymptomatic. Emerg. Infect. Dis. 2020;26 doi: 10.3201/eid2607.201595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh, S., Rajwade, A., Krishna, S., Gopalkrishnan, N., Schaus, T.E., Chakravarthy, A., Varahan, S., Appu, V., Ramakrishnan, R., Ch, S., Jindal, M., Bhupathi, V., Gupta, A., Jain, A., Agarwal, R., Pathak, S., Rehan, M.A., Consul, S., Gupta, Y., Gupta, N., Agarwal, P., Goyal, R., Sagar, V., Ramakrishnan, U., Krishna, S., Yin, P., Palakodeti, D., Gopalkrishnan, M., 2020. Tapestry: A Single-Round Smart Pooling Technique for COVID-19 Testing. preprint, Infectious Diseases (except HIV/AIDS).
- Gollier, C., Gossner, O., 2020. Group testing against Covid-19. Covid Economics, 1(2):32–42. Publisher: CEPR Press.
- Gonzalez-Reiche, A.S., Hernandez, M.M., Sullivan, M.J., Ciferri, B., Alshammary, H., Obla, A., Fabre, S., Kleiner, G., Polanco, J., Khan, Z., Alburquerque, B., van de Guchte, A., Dutta, J., Francoeur, N., Melo, B.S., Oussenko, I., Deikus, G., Soto, J., Sridhar, S.H., Wang, Y.-C., Twyman, K., Kasarskis, A., Altman, D.R., Smith, M., Sebra, R., A’berg, J., Krammer, F., Garca-Sastre, A., Luksza, M., Patel, G., Paniz-Mondolfi, A., Gitman, M., Sordillo, E.M., Simon, V., van Bakel, H., 2020. Introductions and early spread of SARS-CoV-2 in the New York City area. Science, 369:297–301. [DOI] [PMC free article] [PubMed]
- Grassly, N., Pons Salort, M., Parker, E., White, P., Ainslie, K., Baguelin, M., Bhatt, S., Boonyasiri, A., Boyd, O., Brazeau, N., et al., 2020. Report 16: Role of testing in COVID-19 control. Imperial College London.
- Hansen E., Day T. Optimal control of epidemics with limited resources. J. Math. Biol. 2011;62:423–451. doi: 10.1007/s00285-010-0341-0. [DOI] [PubMed] [Google Scholar]
- Hasell J., Mathieu E., Beltekian D., Macdonald B., Giattino C., Ortiz-Ospina E., Roser M., Ritchie H. A cross-country database of covid-19 testing. Scientific Data. 2020;7(1):1–7. doi: 10.1038/s41597-020-00688-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X., Lau E.H.Y., Peng W., Deng X., Wang J., et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020;26:672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Hellewell, J., Gimma, A. amd Bosse, N.I., Jarvis, C.I., Munday, J.D., et al., 2020. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Glob Health, 8:e488 – e496. [DOI] [PMC free article] [PubMed]
- Hendaus, M.A., Jomha, F.A., 2021. Delta variant of COVID-19: A simple explanation. Qatar. Med. J., 2021. [DOI] [PMC free article] [PubMed]
- Hussain, T., Ozair, M., Ali, F., Rehman, S.U., Assiri, T.A., Mahmoud, E.E., 2021. Sensitivity analysis and optimal control of COVID-19 dynamics based on SEIQR model. Results Phys., 22:103956. [DOI] [PMC free article] [PubMed]
- Jiang S., Li Q., Li C., Liu S., Wang T., et al. Mathematical models for devising the optimal SARS-CoV-2 strategy for eradication in China, South Korea, and Italy. J. Transl. Med. 2020;18:345. doi: 10.1186/s12967-020-02513-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones C.J., Philippon T., Venkateswaran V. Series: Working Paper Series. 2020. Optimal mitigation policies in a pandemic: Social distancing and working from home. Working Paper 26984, National Bureau of Economic Research. [Google Scholar]
- Jonnerby, J., Lazos, P., Lock, E., Marmolejo-Cosso, F., Ramsey, C.B., Shukla, M., Sridhar, D., 2020. Maximising the benefits of an acutely limited number of COVID-19 tests. arXiv preprint arXiv:2004.13650.
- Khatua, D., De, A., Kar, S., Samanta, E., Mandal, S.M., 2020. A dynamic optimal control model for SARS-CoV-2 in India. Available at SSRN:https://ssrn.com/abstract=3597498.
- Kirk D.E. Dover Publications Inc; Mineloa, New York: 1998. Optimal Control Theory: An Introduction. [Google Scholar]
- Kretzschmar M.E., Rozhnova G., Bootsma M.C.J., van Boven M., van de Wijgert J.H.H.M., Bonten M.J.M. Impact of delays on effectiveness of contact tracing strategies for COVID-19: A modelling study. Lancet Public Health. 2020;5:E452–E459. doi: 10.1016/S2468-2667(20)30157-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucirka L.M., Lauer S.A., Laeyendecker O., Boon D., Lessler J. Variation in false-negative rate of reverse transcription polymerase chain reaction-based SARS-CoV-2 tests by time since exposure. Ann. Intern. Med. 2020;173:262–267. doi: 10.7326/M20-1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K. The incubation period of coronavirus disease 2019 (COVID-19) from publicaly reported confirmed cases: Estimation and application. Ann. Intern. Med. 2020;172:577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenhart S., Workman J.T. Chapman and Hall/CRC; Boca Raton, Fl: 2007. Optimal Control Applied to Biological Models. [Google Scholar]
- Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Yan L., Wan L., Xiang T., Le A., et al. Viral dynamics in mild and severe cases of COVID-19. Lancet Infectious Diseases. 2020;20:656–657. doi: 10.1016/S1473-3099(20)30232-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Z., Magal P., Seydi O., Webb G. A COVID-19 epidemic model with latency period. Infectious Disease Modell. 2020;5:323–337. doi: 10.1016/j.idm.2020.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majumder M.S., Mandl K.D. Early in the epidemic: Impact of preprints on global discourse about COVID-19 transmissibility. Lancet Global Health. 2020;8:e627–e630. doi: 10.1016/S2214-109X(20)30113-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngonghala C.N., Iboi E., Eikenberry S., Scotch M., MacIntyre C.R., Bonds M.H., Gumel A.B. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel Coronavirus. Math. Biosci. 2020;325 doi: 10.1016/j.mbs.2020.108364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noh J., Danuser G. Estimation of the fraction of COVID-19 infected people in U.S. states and countries worldwide. PLOS ONE. 2021;16(e0246772) doi: 10.1371/journal.pone.0246772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piasecki, T., Mucha, P.B., Rosiska, M., 2020. A new SEIR type model including quarantine effects and its application to analysis of Covid-19 pandemia in Poland in March-April 2020. arXiv:2005.14532 [physics, q-bio]. arXiv: 2005.14532.
- Piguillem F., Shi L. EIEF Working Papers Series 2004, Einaudi Institute for Economics and Finance (EIEF) 2020. Optimal COVID-19 Quarantine and Testing Policies. [Google Scholar]
- Ritchie, H., Mathieu, E., Rods-Guirao, L., Appel, C., Giattino, C., Ortiz-Ospina, E., Haselland, J., Macdonald, B., Beltekian, D., Roser, M., 2020. Coronavirus pandemic (COVID-19). Our World in Data.https://ourworldindata.org/coronavirus.
- Robert Koch Institute, 2020. Nationale teststrategie – wer wird in Deutschland getestet. [cited 2020 September 23]. Available from:https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Teststrategie/Nat-Teststrat.html?nn=13490888.
- Rong X., Yang L., Chu H., Meng F. Effect of delay in diagnosis on transmission of COVID-19. Math. Biosci. Eng. 2020;17:2725–2740. doi: 10.3934/mbe.2020149. [DOI] [PubMed] [Google Scholar]
- Saldaña F., Flores-Arguedas H., Camacho-Gutiérrez J.A., Barradas I. Modeling the transmission dynamics and the impact of the control interventions for the COVID-19 epidemic outbreak. Math. Biosci. Eng. 2020;17:4165–4183. doi: 10.3934/mbe.2020231. [DOI] [PubMed] [Google Scholar]
- Sanche S., Lin Y.T., Xu C., Romero-Severson E., Hengartner N., Ke R. High contagiousness and rapid spead of severe acute respiratory syndrome cornoavirus 2. Emerg. Infect. Dis. 2020;26:1470–1477. doi: 10.3201/eid2607.200282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sturniolo S., Waites W., Colbourn T., Manheim D., Panovska-Griffiths J. Testing, tracing and isolation in compartmental models. PLoS Comput. Biol. 2021;17 doi: 10.1371/journal.pcbi.1008633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surkova, E., Nikolayevskyy, V., Drobniewski, F., 2020. False-positive COVID-19 results: Hidden problems and costs. Lancet Respir Med. [Advance online publication 29 Sept. 2020]. Available from:https://www.thelancet.com/journals/lanres/article/PIIS2213-2600(20)30453-7/fulltext. [DOI] [PMC free article] [PubMed]
- Tuite A.R., Fisman D.N., Greer A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. Can. Med. Assoc. J. 2020;192:E497–E505. doi: 10.1503/cmaj.200476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- Verma V.R., Saini A., Gandhi S., Dash U., Koya S.F. Capacity-need gap in hospital resources for varying mitigation and containment strategies in India in the face of COVID-19 pandemic. Infect. Dis. Model. 2020;5:608–621. doi: 10.1016/j.idm.2020.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh K.A., Jordan K., Clyne B., Rohde D., Drummond L., et al. SARS-CoV-2 detection, viral load and infectivity over the course of an infection. J. Infect. 2020;81:357–371. doi: 10.1016/j.jinf.2020.06.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widders A., Broom A., Broom J. SARS-CoV-2: The viral shedding vs infectivity dilemma. Infection, Disease and Health. 2020;25:210–215. doi: 10.1016/j.idh.2020.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- World Health Organization, 2020a. Coronavirus disease 2019 (COVID-19): WHO Thailand situation report - 19 March 2020. [cited 2020 September 23]. Available from:https://www.who.int/docs/default-source/searo/thailand/2020-03-19-tha-sitrep-26-covid19.pdf?sfvrsn=6f433d5e_2.
- World Health Organization, 2020b. Laboratory testing strategy recommendations for COVID-19. [cited 2020 August 11]. Available from:https://apps.who.int/iris/handle/10665/331509.
- Youssef H., Alghamdi N., Ezzat M.A., El-Bary A.A., Shawky A.M. Study on the SEIQR model and applying the epidemiological rates of COVID-19 epidemic spread in Saudi Arabia. Infect. Dis. Model. 2021;6:678–692. doi: 10.1016/j.idm.2021.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaric G.S., Brandeau M.L. Resource allocation for epidemic control over short time horizons. Math. Biosci. 2001;171(1):33–58. doi: 10.1016/s0025-5564(01)00050-5. [DOI] [PubMed] [Google Scholar]