Abstract
In recent years, there has been an enormous demand for the security of image multimedia in healthcare organizations. Many schemes have been developed for the security preservation of data in e-health systems however the schemes are not adaptive and cannot resist chosen and known-plaintext attacks. In this contribution, we present an adaptive framework aimed at preserving the security and confidentiality of images transmitted through an e-healthcare system. Our scheme utilizes the 3D-chaotic system to generate a keystream which is used to perform 8-bit and 2-bit permutations of the image. We perform pixel diffusion by a key-image generated using the Piecewise Linear Chaotic Map (PWLCM). We calculate an image parameter using the pixels of the image and perform criss-cross diffusion to enhance security. We evaluate the scheme’s performance in terms of histogram analysis, information entropy analysis, statistical analysis, and differential analysis. Using the scheme, we obtain the average Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) values for an image of size 256 × 256 equal to 99.5996 and 33.499 respectively. Furthermore, the average entropy is 7.9971 and the average Peak Signal to Noise Ratio (PSNR) is 7.4756. We further test the scheme on 50 chest X-Ray images of patients having COVID-19 and viral pneumonia and found the average values of variance, PSNR, entropy, and Structural Similarity Index (SSIM) to be 257.6268, 7.7389, 7.9971, and 0.0089 respectively. Furthermore, the scheme generates completely uniform histograms for medical images which reveals that the scheme can resist statistical attacks and can be applied as a security framework in AI-based healthcare.
Keywords: Medical images, Biomedical systems, Privacy, Security, Healthcare, Image Encryption, Big data
Introduction
Present-day healthcare has been remodeled with the advancement in AI, smart communication networks, and IoT-based systems [3]. The IoT framework makes use of different sensors to collect a lot of information about the patient which is transmitted to cloud-based servers and processed by AI-based models as shown in Fig. 1. AI and Big Data analysis is being used increasingly for remote consultation, monitoring, and diagnosis in the e-healthcare system [20]. The application of AI in healthcare often known as Deep medicine entails the use of Deep Learning (DL) and Machine Learning (ML)-based models for automatic image classification, analysis, and segmentation [12, 21]. The AI models are also utilized for personalized medicine, drug development, and the organization of treatment strategies. The AI-based biomedical systems have been able to improve the quality of healthcare service while also decreasing its transmittal time.
Fig. 1.
Architecture of an IoT-based Healthcare with the wireless transference of data for remote diagnosis and consultation
N. S. Nariman et al. [22] present an analysis of the clinical and public health applications of ML and illustrate the critical role of data sharing and privacy. They discuss the different ML strategies like supervised, unsupervised, and reinforcement learning and identify the potential application areas like disease prediction, diagnosis, precision health, epidemic outbreak prediction, and treatment effectiveness, etc. S. K. Mohan et al. [19] propose a cardiovascular disease prediction system using IoT sensors and ML processing techniques. The system obtains health data from smart devices and can classify cardiovascular disease with 88.7% accuracy using the optimized ML techniques. M. P. Belfiore et al. [6] propose an AI-based tool called Thoracic VCAR software for COVID-19 diagnosis. The model can recognize and differentiate the ground glass opacities from consolidation and measures the volume of the affected areas using AI. Several recent works aim at integrating the IoT framework for data collection with the AI-based processing models [10, 25]. The e-healthcare systems transfer the collected medical data over to cloud-based servers through insecure communication channels that lead to security breaches [26, 28]. In the e-health systems, Computer-aided Diagnosis (CAD) is carried out for the treatment of the patient by using medical image analysis and segmentation. The medical details are transferred for remote consultation and the CAD systems are used to assist the healthcare professionals for diagnosis and monitoring of the conditions and formation of a treatment strategy. Z. F. Mohammed et al. [17] present a CAD system for the identification of acute lymphoblastic leukemia (ALL) cells. The cells are classified as normal and abnormal using various feature extraction techniques. Their system can automatically identify ALL cells with 97.45% accuracy. A. A. Abdulla [1] further present a CAD system with improved accuracy of 98.7% employing the Naïve Bayes and k-nearest neighbor classifier techniques.
Often medical images contain personal information and maintenance of their security has become a top area for research. Around 200 million healthcare records have been breached up to the year 2020 as reported by the Health Insurance Portability and Accountability (HIPPA) journal. Unysis report that there has been a 30% increase in cyberattacks with more than 192,000 COVID-19 related breaches taking place per week only in May 2020. Furthermore, IBM calculates the average economic burden incurred per data breach to be around $3.86 million. These statistical details are a motivating factor for researchers to formulate improved cryptosystems that can guarantee the security of sensitive medical data during transmission and storage through an IoT-based healthcare system.
Encryption is the most suitable method to safeguard against security breaches preventing data loss and data leak. Images are a form of unstructured voluminous data containing high redundancy and correlation and cannot be encrypted by the traditional schemes [29]. Many improved encryption techniques have been proposed in the past years based on chaos, compressed sensing, transform theory, and Deoxyribonucleic acid (DNA) encryption. Chaos is a deterministic phenomenon that is extremely contingent on initial conditions. Chaotic systems can be combined with different encryption schemes for the development of strong cryptosystems for image encryption. The chaos-based encryption architecture includes a key generation phase wherein the different chaotic systems are employed to generate a pseudorandom number sequence (PRN) [24]. The scheme includes pixel position permutation and value substitution using the PRN sequence generated by the chaotic maps. There are 1D maps like Chebyshev map and Quadratic map, and higher dimensional maps like Chen’s Hyperchaotic system that can be employed for image security. The higher dimensional maps are complex but have a larger keyspace and are more robust as compared to 1D maps [2]. F. Masood et. al., [15] present a lightweight security framework employing the Henon map, Chen’s Chaotic system, and the Brownian motion. The scheme has been evaluated using histogram analysis, entropy, time, and correlation analysis among others. The 1D chaotic map-based system is simple to implement but can be broken using phase-space estimation schemes. On the other hand, the hyperchaotic systems offer strength but have high computational complexity. Many hybrid schemes that integrate the DNA and chaos-construct schemes have been recently proposed [16]. DNA computing offers minimum power consumption, parallelism, and high storage capacity and is incorporated in many encryption schemes to increase robustness [27].
The purpose of this contribution is to present a security solution for IoT-based healthcare utilizing 3D chaos and PWLCM. The 3D chaotic map is used for PRN generation utilized in the permutation step [11]. We compute an image parameter using the sum of the pixels making the scheme adaptive. The image parameter forms an initial condition for the PWLCM which is used for key image generation [32]. The key image is then XORed with the image sequence to diffuse the pixels. Furthermore, 2-bit (DNA) and 8-bit (pixel) permutation along with crisscross diffusion is performed to increase security [35].
The contributions of the proposed technique are as follows:
The presented technique employs DNA encryption and hybrid chaotic maps like 3D chaotic maps and PWLCM for higher robustness. The scheme performs crisscross diffusion and XOR diffusion using a key image increasing security.
The scheme computes an image parameter which makes the proposed technique adaptive and more resistant to known and chosen-plaintext attacks. The scheme can resist statistical attacks as it generates uniform histograms for medical images that have a non-uniform intensity distribution.
The presented scheme leads to lossless medical data recovery which can facilitate data analysis and diagnosis in an IoT-based healthcare setup.
The rest of our work is formulated as follows. Section 2 summarizes the review of DNA and Chaos encryption schemes as per the recent literature. Section 3 illustrates the preliminaries used in the scheme. Section 4 presents the security model. Results are represented in Sect. 5. Section 6 shows the conclusion of the work.
Literature review
In this section, we discuss some recent literary works of chaos and DNA encryption that have been proposed for image data security. K. Zhan et al. [34] propose an encryption scheme built on a 4D hyperchaotic system and DNA cryptography. The 4D map is iterated to calculate a PRN sequence which is employed to globally disarrange the binary representation of the pixels. They perform DNA addition and complementation to increase the robustness of the scheme. The method has justifiable performance for natural images but generates a non-uniform histogram for medical images. Furthermore, the average NPCR and UACI for a natural image like Lena are 59.7406 and 25.0487 respectively which is much less than the theoretically ideal values revealing weakness towards differential attacks. X. Chai et al. [8] present a medical image encryption scheme that utilizes the PRN sequence generated from the 4D memristive chaotic map to carry out the diffusion and permutation operations. The scheme calculates the SHA-256 value as an initial condition of the 4D map rendering the scheme resistant to known and chosen-plaintext attacks. They use Latin square for pixel permutation and bi-directional adaptive diffusion for increased encryption effect. Their scheme has comparable performance with state-of-the-art schemes.
F. P. An et al. [4] present an encryption scheme using the cyclic encryption technique, chaos scheme, and adaptive wavelet algorithm. The scheme uses the particle swarm optimization (PSO) technique to enhance the adaptivity of the scheme and calculates SHA-1 as an index value for cyclic operation. The scheme has higher keyspace and improved adaptability and can resist chosen plaintext attacks. However, the computational complexity of the scheme is slightly higher than many recent schemes. S. S. Askar et al. [5] propose an image security framework based on the 2D economic map and the logistic map. They illustrate a key generation scheme and make use of logical XOR operation for the diffusion of image pixels. The performance of the scheme is evaluated and it is concluded that the method has a high level of security to prevent any form of attacks. T. Li et al. [14] present a scheme of image encryption employing the logistic and 2D Lorenz maps. The scheme has a large keyspace of 10112 and theoretically ideal NPCR and UACI values. Y. Wan et al. [31] design a 1D chaotic map called LLSS by combining the logistic and sine map equations and the mod operation. The generated map has no period window and completely maps to the range [0, 4] in the bifurcation diagram. They further propose an encryption scheme using the LLSS map, Qi hyperchaotic map, and DNA encryption. The scheme uses the Fibonacci transform and DNA block coding to increase the security strength of the scheme. However, the performance of the abovementioned schemes has not been evaluated on clinical images where there is a high contrast between intensity values. N. Tsafack et al. [30] propose a security module for IoT-based healthcare systems called IoHT. They design an infinite solution map called the trigonometric map and evaluate its performance. This map is designed using the existing chaotic systems like sine, cosine, and logistic map and evaluated using analysis techniques like bifurcation diagram analysis, Lyapunov exponent, and phase portrait analysis. They further propose an encryption scheme utilizing the novel trigonometric map and Mandelbrot set. They evaluate a Hamming distance between the R, G, B components of the image and the PRN sequence computed using the novel trigonometric map. This distance vector is XORed with the PRN sequence to increase the robustness of the scheme. Furthermore, Mandelbrot set is used for confusion operation by providing input to the conditional shift algorithm. The scheme is highly secure for IoHT based systems and can resist many attacks. D. Zareai et al. [33] present an encryption scheme that combines the Arnold cat map, logistic map, and image blocking technique. The blocking technique and Arnold map are used to permute the image pixels and multiple keys are formed to generate a highly secure cryptosystem. However, the schemes based on 1-D maps are vulnerable to attacks like key-space analysis and trajectory estimation algorithms.
The limitations of the reviewed works are as follows:
Most of the reviewed schemes are not adaptive and cannot resist the known and chosen-plaintext attacks.
The NPCR and UACI values for many schemes are below the theoretical maximum values indicating a lower diffusion mechanism. Furthermore, many schemes have a low keyspace and are less key sensitive.
Many techniques do not generate completely uniform histograms for medical images that have a non-uniform intensity distribution and hence cannot resist statistical attacks.
Many schemes lead to lossy recovery of the data making the scheme unacceptable for medical data security required in IoT-based healthcare.
Preliminaries
The 3D chaotic system
The 1D logistic equation is the simplest and most common chaotic system utilized for image encryption as shown in Eq. (1).
| 1 |
where ‘r’ is the parameter of the logistic equation. The system exhibits chaotic behavior where , and 3.57 ≤ r ≤ 4. Hongjuan Liu. et al. [11] proposed the 2D version of the logistic map. In this work, we employ the 3D version of the logistic chaotic map described by P. N. Khade et al. in [13]. The system of equations for a 3D logistic chaotic map is shown in equation set (2). The 3D chaotic system involves cubic and quadratic coupling and can generate highly chaotic sequences.
| 2 |
The final key sequence ‘k1’ is formed by concatenating the individual components as shown in Eq. (3).
| 3 |
| 4 |
where k1 [0, 1] and the decimal representation are shown in Eq. (4), where, k [0, 255]. The 3D chaotic system generates the sequences that together form the sequence k1. This sequence is converted into a decimal form which generates the sequence k used for encryption.
DNA encryption
DNA computing offers tremendous advantages for image encryption which include parallelism, increased capacity for storage, and low power demand [18]. The basic DNA molecule comprises 4 nucleotide bases called Thymine (T), Guanine (G), Cytosine (C), and Adenine (A). As in the digital systems, 0 is taken complementary to 1 the base A is always complementary to T and G to C. There are 24 DNA coding techniques but only 8 follow the complementation rule called the Watson–Crick rule. In this work, we perform DNA also called 2-bit permutation using the index of the PRN sequence generated by the 3D chaotic system. The DNA sequence for an image of size M × N is 4 × M × N. The DNA encoding rules are shown in Table 1.
Table 1.
DNA Encoding Rules
| Rule | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| A | 00 | 00 | 01 | 01 | 10 | 10 | 11 | 11 |
| T | 11 | 11 | 10 | 10 | 01 | 01 | 00 | 00 |
| C | 01 | 10 | 00 | 11 | 00 | 11 | 01 | 10 |
| G | 10 | 01 | 11 | 00 | 11 | 00 | 10 | 01 |
Piecewise Linear Chaotic Map (PWLCM)
The scheme is made adaptive by calculating a parameter ‘P’ from the sum of the pixels of the image as shown in Eq. (5).
| 5 |
where M and N represent the row and column of the image I. The parameter ‘P’ has been calculated for natural and medical test images and is in the range of 0 to 1. This parameter is taken as the initial condition for the PWLCM represented in equation set (6) [32]. This chaotic map is then used to generate the key image as shown in Eq. (7). If the input image is slightly altered the initial condition for PWLCM is changed and the resultant key image is also altered.
| 6 |
where, q ∈ (0, 0.5), ∈ (0, 1), and q = 0.25678900 [32]. The key image is used to perform pixel diffusion using the XOR operation and making it dependent on the parameter ‘P’ increases the strength of the cryptosystem towards chosen plaintext and known-plaintext attacks
| 7 |
where ‘KI’ is the pixel of the key image and l ∈ (0, 1). Pixels computed by the PWLCM are highly random and have a negligible correlation coefficient which is desirable for image encryption as described in [32].
Crisscross diffusion
In this work, we employ the Crisscross diffusion described in the CDCP technique as shown in [35]. The technique makes use of the XOR and mod operation to generate a cipher image block in two phases. The input image is divided into two halves called the upper half (UH) and lower half (LH) and is processed parallelly. The input decimal key sequence generated by the 3D chaotic system is taken as the key for the crisscross diffusion technique. The scheme makes use of an input key-value called The initial value of UH and LH are ′E′ and ′E(MN/2+1)′ respectively and are generated as shown in equation set (8), where MN is the size of the image.
| 8 |
The remaining pixels of the UH and LH of the encrypted image E is simultaneously generated using the equation set (9).
| 9 |
where ′i′ is from index value 2 to MN/2 and ′E(i)′ represents one pixel of the encrypted image E and ′k(i)′ is the corresponding key-value generated by the 3D chaotic system. The final diffused image ‘Z’ is generated by the following set of equations. The initial values of the UH and LH are Z (1) and Z(MN/2 + 1) respectively and are calculated as shown in equation set (10).
| 10 |
The rest of the image pixels are computed by the equations set (11) wherein the pixel values are calculated in a crisscross manner using the bitxor and mod operations.
| 11 |
where j is the index ranging from 2 to MN/2 and ‘Z(j)’ represents one pixel of the final diffused image Z and k(j) is the corresponding key-value generated by the 3D chaotic system.
Proposed method
In this section, we present the proposed security module for medical images transferred and stored in IoT-based healthcare. The input image is converted to its 2-bit DNA sequence form using one of the DNA encoding techniques. The 3D chaotic map is iterated using Eq. (2) and the PRN key sequence is generated by Eq. (4). The DNA sequence is permuted using the index of the key sequence. The decimal equivalent of the permuted DNA sequence is retrieved and its XOR diffusion is done using the key image. The key-image is generated by the PWLCM and the parameter P is calculated from the input image achieved by iterating the Eqs. (5–7). The index of the decimal representation of the PRN generated by the 3D chaos is calculated and employed for the crisscross diffusion of the image. Finally, the pixel permutation is carried out again using the sorted PRN sequence. The image encryption process is shown in Algorithm 1.
Algorithm 2 describes the image decryption process in detail.
Results and discussion
To evaluate the proposed method, we performed many experiments on the grayscale and color natural and medical images. The Windows 10 Operating system has been utilized with MATLAB R2017a (version 9.2.0 538,062). For all the experiments test images are resized to 256 × 256. The medical images have been retrieved from the OPENi image database represented in Fig. 2. For performance comparison purposes, we have taken natural test images as well. It has been demonstrated that the proposed method produces state-of-the-art results for natural and medical images and can be effectively used for an IoT-based healthcare system.
Fig. 2.
Test images (
Source for medical Images: OPENi Database retrieved from https://openi.nlm.nih.gov/index.php/)
Encryption evaluation metrics
The encryption algorithm has been evaluated using histogram analysis, key sensitivity analysis, statistical analysis, and differential analysis. The encryption technique must combat all the attacks like differential attacks, brute-force, and statistical among others. Furthermore, we compare the performance of the scheme with some recent schemes and can conclude that the proposed model is highly secure and implementable.
-
i.
Uniform Histogram and Visual Disguise
Histograms of the images generated by the proposed cryptosystem are completely uniform as shown in Fig. 3. The histogram H of an image is given by the following Eq. (12):
| 12 |
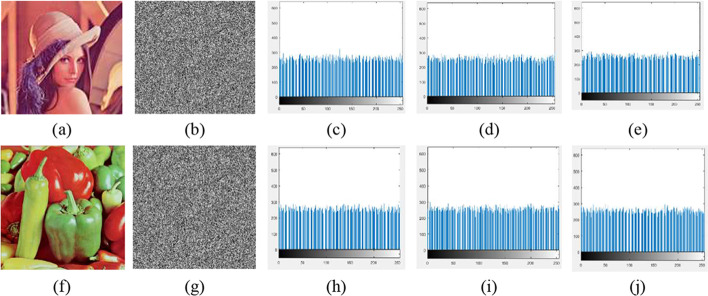
where is the ith intensity value and represents the number of pixels in the image with an intensity value equal to . As shown from Fig. 3 the generated histogram of the encrypted image is uniform and the encrypted image has a high visual disguise. The variance of histograms is also evaluated for the test Lena image to quantitatively evaluate the uniformity of the histogram. The security of the cryptosystem is more when the variance of the histogram is lower. The variance of the histogram of different images is shown in Table 2 and a comparison for the Lena image has been shown in Table 3. The results for the color Lena and Peppers images are shown in Fig. 4.
-
ii.
Correlation Coefficient and PSNR
Fig. 3.
a Plain Images, (b) Encrypted Images (c) Histogram of Encrypted Images
Table 2.
Variance of Histogram of cipher images
| Image (256 × 256) | Variance |
|---|---|
| Lena | 237.2784 |
| Peppers | 256.6196 |
| OPENi1 | 288.5020 |
| OPENi2 | 232.5961 |
| OPENi3 | 215.4039 |
Table 3.
Comparison of variance of the histogram of Lena Image
Fig. 4.
a, f 256 × 256 size Color Lena and Pepper Images, (b, g) Encrypted Images, (c-e, h-j) Histograms of R, G, and B channels of Color Lena and Peppers image respectively
The correlation coefficient (CC) gives a measure of the redundancy of the pixels in the image. The plain image has high redundancy but the encrypted image should have a very low CC value. This will indicate minimum redundancy in the encrypted image. We evaluate the horizontal (C_H), vertical (C_V), and diagonal (C_D) correlation coefficient of plain and encrypted images as shown in Table 4 and comparison in Table 5. The PSNR value for encrypted images should be less than 10 as shown in Table 6. The correlation C has been described as shown in Eq. (13) and PSNR is shown in Eq. (14). The correlation analysis for the Lena image is shown in Fig. 5.
| 13 |
| 14 |
-
iii.
Diffusion Analysis and Information entropy Analysis
Table 4.
Correlation Coefficient of the plain and encrypted images
| Image (256 × 256) | CC of Plain Image | CC of Encrypted Image | ||||
|---|---|---|---|---|---|---|
| C_H | C_V | C_D | C_H | C_V | C_D | |
| Lena | 0.9494 | 0.9667 | 0.9366 | 0.0021 | 0.0099 | 0.0011 |
| Circuit | 0.9757 | 0.9750 | 0.9652 | -0.0054 | -0.0056 | 0.0033 |
| Cameraman | 0.9329 | 0.9566 | 0.9117 | -0.0086 | 0.0024 | -0.0014 |
| Baboon | 0.8710 | 0.8210 | 0.7810 | -0.0040 | -0.0019 | -0.0018 |
| OPENi1 | 0.9159 | 0.9568 | 0.8951 | 5.4731e-04 | 3.2932e-04 | -0.0034 |
| OPENi2 | 0.9911 | 0.9865 | 0.9852 | -0.0025 | -9.4017e-04 | -0.0033 |
| OPENi3 | 0.9670 | 0.9715 | 0.9408 | -0.0017 | -0.0013 | 0.0013 |
| OPENi4 | 0.9803 | 0.9803 | 0.9688 | 0.0048 | -0.0012 | -2.3609e-04 |
Table 5.
Comparison of Correlation Coefficients for Lena Image
| Plain Image | Cipher Image | ||||||
|---|---|---|---|---|---|---|---|
| Lena (256 × 256) | Proposed | X. Chai et al. (2019) [8] | S. S. Askar et al. (2019) [5] | T. Li et al. (2020) [14] | Y. Wan et al. (2020) [31] | J. Ferdush et al. (2021) [9] | |
| C_H | 0.9494 | 0.0021 | 0.0070 | 0.0005 | 0.0044 | 0.0020 | -0.0414 |
| C_V | 0.9667 | 0.0099 | -0.0102 | 0.0017 | 0.0015 | 0.0105 | -0.0342 |
| C_D | 0.9366 | 0.0011 | 0.0030 | -0.0025 | 0.0019 | 0.0019 | 0.1083 |
Table 6.
Comparison of PSNR values
Fig. 5.
Correlation analysis for plain and encrypted Lena image. (a, c) Row, and Column plot of Correlations of the plain Lena image and (b, d) Row, and Column plot of correlations of the encrypted image
For diffusion analysis, we employ the parameters called NPCR and UACI. In the proposed scheme all the images have NPCR and UACI values of more than 99.55% and 33.35% respectively. The mathematical expression for NPCR and UACI have been shown in Eqs. (15) and (16) respectively. The comparison of NPCR and UACI values with state-of-the-art schemes has been shown in Table 7 and Table 8 respectively.
| 15 |
| 16 |
Table 7.
Comparison of NPCR with state-of-the-art schemes
Table 8.
Comparison of UACI values
The information entropy H(R) of the input source R can be seen in Eq. (17).
| 17 |
Here M gives the total symbols . Information entropy is a measure of the randomness of encrypted images. We see that the value of entropy is more than 7.99 as shown in Table 9 and the comparison is shown in Table 10. The scheme is also tested for salt and pepper noise attack and Gaussian noise attack for Lena and Peppers image, the Mean Square Error (MSE) and PSNR values of the decrypted images are shown in Table 11. The results of the colored Lena and Peppers image are shown in Table 12. Furthermore, we have evaluated the scheme on 50 medical images retrieved from the Kaggle platform (kaggle.com/pranavraikokte/covid19-image-dataset/). The dataset contains chest X-ray scans of three classes i.e., normal, covid-19, and viral pneumonia. From the original dataset, we have formed a new dataset containing 50 images with the first 20 images taken each from the Covid-19 and normal classes and the first 10 images taken from the viral pneumonia class. The average values of the evaluation parameters are shown in Table 13.
Table 9.
NPCR, UACI and Entropy values for different Test Image
| Image (256 × 256) | NPCR (%) | UACI (%) | Entropy |
|---|---|---|---|
| Lena | 99.5880 | 33.4059 | 7.9970 |
| Circuit | 99.6216 | 33.5953 | 7.9969 |
| Cameraman | 99.5865 | 33.5306 | 7.9969 |
| Barbara | 99.6201 | 33.5194 | 7.9971 |
| Baboon | 99.6048 | 33.4914 | 7.9971 |
| Aerial | 99.6155 | 33.3924 | 7.9973 |
| Plane | 99.6155 | 33.4624 | 7.9973 |
| Peppers | 99.6063 | 33.5527 | 7.9972 |
| OPENi1 | 99.5880 | 33.6000 | 7.9968 |
| OPENi2 | 99.6002 | 33.4203 | 7.9974 |
| OPENi3 | 99.5573 | 33.3654 | 7.9976 |
| OPENi4 | 99.6155 | 33.5477 | 7.9971 |
| OPENi5 | 99.6063 | 33.5005 | 7.9971 |
| OPENi6 | 99.6063 | 33.6081 | 7.9973 |
| OPENi7 | 99.5743 | 33.4977 | 7.9972 |
| OPENi8 | 99.5911 | 33.4266 | 7.9975 |
| OPENi9 | 99.6109 | 33.5207 | 7.9967 |
| OPENi10 | 99.5850 | 33.5455 | 7.9974 |
Table 10.
Comparison of Entropy values
Table 11.
Noise Attack for Lena Image
| Noise | Proposed scheme | Z. Parvin et al. [23] | |
|---|---|---|---|
| Gaussian noise with variance = 0.01 and mean = 0 | MSE | 131.7695 | 4410.1 |
| PSNR | 9.7566 | 11.7 | |
| Gaussian noise with variance = 0.1 and mean = 0 | MSE | 141.7987 | 5631.4 |
| PSNR | 9.3006 | 10.6 | |
| Salt and Pepper noise with density 0.05 | MSE | 22.4624 | 869.9 |
| PSNR | 18.7001 | 18.7 | |
| Salt and Pepper noise with density 0.1 | MSE | 40.97 | 1829.6 |
| PSNR | 15.8650 | 15.5 | |
Table 12.
Evaluation parameters for colored images
| Parameter | Coloured Lena Image | Coloured Peppers Image | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| PSNR | 7.8704 | 8.6345 | 9.6641 | 9.1158 | 7.6449 | 7.7195 |
| Entropy | 7.9972 | 7.9973 | 7.9973 | 7.9975 | 7.9975 | 7.9976 |
| SSIM | 0.0090 | 0.0091 | 0.0110 | 0.0106 | 0.0069 | 0.0081 |
| C_H | -0.0013 | -0.0072 | -0.0061 | 0.0018 | -0.0023 | -0.0064 |
| C_V | 0.0046 | -0.0033 | -0.0033 | 0.00023 | -0.0004 | 0.0059 |
| C_D | -0.0012 | 0.0016 | 0.0021 | 0.0016 | -0.00022 | 0.00076 |
Table 13.
Average values of the evaluation parameters of 50 medical images
taken from Kaggle platform
| Medical Images | 50 Chest X-ray scans |
|---|---|
| Variance | 257.6268 |
| PSNR | 7.7389 |
| Entropy | 7.9971 |
| SSIM | 0.0089 |
| C_H | 0.0001499 |
| C_V | -0.00007372 |
| C_D | -0.00031538 |
Conclusion
In this work, we present a robust image encryption scheme for the prevention of cyberattacks for IoT-driven e-healthcare systems. The scheme can resist the known and chosen-plaintext attacks as it generates a parameter from the input image pixels. The parameter forms the initial conditions for the chaotic maps and is used for the generation of key images and key sequences used for image confusion and diffusion. The scheme employs DNA encryption and crisscross-diffusion to enhance the level of security provided. The 3D chaotic logistic map is used to generate PRN sequences for 2-bit and 8-bit permutations and as key to the crisscross diffusion mechanism. Furthermore, the parameter from the input image is calculated and taken as the initial condition of the PWLCM. The key image generated with the map is used to diffuse the image pixels and increase security. The scheme is resistant to statistical, entropy, and differential analysis. The average NPCR and UACI values are equal to 99.5996 and 33.499 respectively. The average entropy is 7.9971 and the average Peak Signal to Noise Ratio is 7.4756 which is found to be comparable to most of the state-of-the-art schemes. Furthermore, for the Lena image, the variance of histogram equals 237.2784, and the horizontal, vertical, and diagonal correlations are equal to 0.9494, 0.9667, and 0.9366 respectively. However, the scheme takes around 3.9 s to encrypt an image of size 256 × 256. In the future, we would like to improve the execution time of the scheme by developing an improved chaotic map for the fast generation of highly chaotic key sequences that can produce robust encrypted images.
Acknowledgements
The authors would like to thank the Department of Science and Technology (DST) New Delhi, Government of India for providing financial support under the DST Inspire Fellowship Scheme with reference number DST/INSPIRE/03/2018/000093.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Abdulla AA. 'Efficient computer-aided diagnosis technique for leukemia cancer detection. IET Image Proc. 2020;14(17):4435–4440. doi: 10.1049/iet-ipr.2020.0978. [DOI] [Google Scholar]
- 2.Alghafis A, Munir N, Khan M. An encryption scheme based on chaotic Rabinovich-Fabrikant system and S8 confusion component. Multimed Tools Appl. 2021;80:7967–7985. doi: 10.1007/s11042-020-10142-x. [DOI] [Google Scholar]
- 3.Alshehri F, Muhammad G. A Comprehensive Survey of the Internet of Things (IoT) and AI-Based Smart Healthcare. IEEE Access. 2021;9:3660–3678. doi: 10.1109/ACCESS.2020.3047960. [DOI] [Google Scholar]
- 4.An FP, Liu JE. Image encryption algorithm based on adaptive wavelet chaos. J Sensors. 2019;2019:1–12. doi: 10.1155/2019/2768121. [DOI] [Google Scholar]
- 5.S. S. Askar, A. A. Karawia, A. Al-Khedhairi, F. S. Al-Ammar, “An Algorithm of Image Encryption Using Logistic and Two-Dimensional Chaotic Economic Maps,” Entropy, Vol. 21, no. 44, 2019. [DOI] [PMC free article] [PubMed]
- 6.Belfiore MP, Urraro F, Grassi R, et al. Artificial intelligence to codify lung CT in Covid-19 patients. Radiol Med. 2020;125(5):500–504. doi: 10.1007/s11547-020-01195-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chai X, Gan Z, Yang K, Chen Y, Liu X. An image encryption based on the memristive hyperchaotic system cellular automata and DNA sequence operations. Image Communication. 2017;52:6–19. [Google Scholar]
- 8.Chai X, Zhang J, Gan Z, et al. Medical image encryption algorithm based on Latin square and memristive chaotic system. Multimedia Tools and Applications. 2019;78:35419–35453. doi: 10.1007/s11042-019-08168-x. [DOI] [Google Scholar]
- 9.Ferdush J, Begum M, Uddin MS (2021) Chaotic lightweight cryptosystem for image encryption. Adv Multimed 16. 10.1155/2021/5527295.
- 10.Fouad H, Hassanein AS, Soliman AM, Al-Feel H (2020) Analyzing patient health information based on IoT sensor with AI for improving patient assistance in the future direction,. Measurement 159
- 11.Hossain MB, Rahman MT, Rahman ABMS, Islam S (2014) A new approach of image encryption using 3D chaotic map to enhance the security of multimedia component. 2014 International Conference on Informatics, Electronics & Vision (ICIEV), pp. 1–6. 10.1109/ICIEV.2014.6850856.
- 12.Kaw JA, Loan NA, Parah SA, Muhammad K, Sheikh JA, Bhat GM. A reversible and secure patient information hiding system for IoT driven e-health. Int J Inf Manage. 2019;45:262–275. doi: 10.1016/j.ijinfomgt.2018.09.008. [DOI] [Google Scholar]
- 13.Khade PN, Narnaware M. 3D Chaotic Functions for Image Encryption. International Journal of Computer Science Issues. 2012;9(1):323–328. [Google Scholar]
- 14.Li T, Du B, Liang X. Image Encryption Algorithm Based on Logistic and Two-Dimensional Lorenz. IEEE Access. 2020;8:13792–13805. doi: 10.1109/ACCESS.2020.2966264. [DOI] [Google Scholar]
- 15.Masood F, Driss M, Boulila W et al (2021) A Lightweight Chaos-Based Medical Image Encryption Scheme Using Random Shuffling and XOR Operations. Wireless Pers Commun
- 16.Malik MGA, Bashir Z, Iqbal N, Imtiaz MA. Color Image Encryption Algorithm Based on Hyper-Chaos and DNA Computing. IEEE Access. 2020;8:88093–88107. doi: 10.1109/ACCESS.2020.2990170. [DOI] [Google Scholar]
- 17.Mohammed ZF, Abdulla AA. An efficient CAD system for ALL cell identification from microscopic blood images. Multimed Tools Appl. 2021;80:6355–6368. doi: 10.1007/s11042-020-10066-6. [DOI] [Google Scholar]
- 18.Mohamed HG, ElKamchouchi DH, Moussa KH. A Novel Color Image Encryption Algorithm Based on Hyperchaotic Maps and Mitochondrial DNA Sequences. Entropy. 2020;22(2):158. doi: 10.3390/e22020158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mohan SK, Thirumalai C, Srivastava G (2019) Effective heart disease prediction using hybrid machine learning techniques. IEEE Access
- 20.Muhammad G, Alhamid MF, Long X. Computing and Processing on the Edge: Smart Pathology Detection for Connected Healthcare. IEEE Network. 2019;33(6):44–49. doi: 10.1109/MNET.001.1900045. [DOI] [Google Scholar]
- 21.Muhammad G, Hossain MS, Kumar N. EEG-Based Pathology Detection for Home Health Monitoring. IEEE J Sel Areas Commun. 2021;39(2):603–610. doi: 10.1109/JSAC.2020.3020654. [DOI] [Google Scholar]
- 22.Nariman NS, et al. Artificial Intelligence Transforms the Future of Health Care. Am J Med. 2019;132(7):795–801. doi: 10.1016/j.amjmed.2019.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Parvin Z, Seyedarabi H, Shamsi M. A new secure and sensitive image encryption scheme based on new substitution with chaotic function. Multimed Tools Appl. 2016;75:10631–10648. doi: 10.1007/s11042-014-2115-y. [DOI] [Google Scholar]
- 24.Pourjabbar KA, Habibizad Navin NA, Bidgoli AM et al (2021) A new image encryption scheme based on hybrid chaotic maps. Multimed Tools Appl 80:2753–2772
- 25.Rong G, Mendez A, Assi EB, Zhao B, Sawan M. Artificial Intelligence in Healthcare: Review and Prediction Case Studies. Engineering. 2020;6(3):291–301. doi: 10.1016/j.eng.2019.08.015. [DOI] [Google Scholar]
- 26.Sadek I, Rehman SU, Codjo J, Abdulrazak B (2019) Privacy and security of IoT based healthcare systems: concerns, solutions, and recommendations. In: Pagán J, Mokhtari M, Aloulou H, Abdulrazak B, Cabrera M (eds) How AI impacts urban living and public health. ICOST 2019. Lecture Notes in Computer Science, vol 11862. Springer, Cham
- 27.Sarosh P, Parah SA, Bhat GM, Muhammad K (2021) A security management framework for big data in smart healthcare. Big Data Research25:100225
- 28.Shaw JA, Sethi N, Block BL. Five things every clinician should know about AI ethics in intensive care. Intensive Care Med. 2021;47:157–159. doi: 10.1007/s00134-020-06277-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tariq S, Khan M, Alghafis A, et al. A novel hybrid encryption scheme based on chaotic Lorenz system and logarithmic key generation. Multimed Tools Appl. 2020;79:23507–23529. doi: 10.1007/s11042-020-09134-8. [DOI] [Google Scholar]
- 30.Tsafack N, et al. A New Chaotic Map with Dynamic Analysis and Encryption Application on Internet of Health Things. IEEE Access. 2020;8:137731–137744. doi: 10.1109/ACCESS.2020.3010794. [DOI] [Google Scholar]
- 31.Wan Y, Gu S, Du B. A New Image Encryption Algorithm Based on Composite Chaos and Hyperchaos combined with DNA Coding. Entropy. 2020;22(2):171. doi: 10.3390/e22020171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang X, Liu C. A novel and effective image encryption algorithm based on chaos and DNA encoding. Multimedia Tools Appl. 2017;76(5):1–17. [Google Scholar]
- 33.Zareai D, Balafar M, Derakhshi MRF. A new Grayscale image encryption algorithm composed of logistic mapping, Arnold cat, and image blocking. Multimed Tools Appl. 2021;80:18317–18344. doi: 10.1007/s11042-021-10576-x. [DOI] [Google Scholar]
- 34.K. Zhan, D. Wei, J. Shi, and J. Yu, “Cross-utilizing hyperchaotic and DNA sequences for image encryption,” Journal of Electronic Imaging, Vol. 26, no. 1, 013021, 2017.
- 35.Zhu C, Hu Y, Sun K. New Image Encryption Algorithm Based on Hyperchaotic System and Ciphertext Diffusion in Crisscross Pattern. Journal of Electronics Information & Technology. 2013;34:1735–1743. doi: 10.3724/SP.J.1146.2011.01004. [DOI] [Google Scholar]