Characterizing fenestration size in sodium channel subtypes and their accessibility to inhibitors

Abstract

Voltage-gated sodium channels (Nav) underlie the electrical activity of nerve and muscle cells. Humans have nine different subtypes of these channels, which are the target of small-molecule inhibitors commonly used to treat a range of conditions. Structural studies have identified four lateral fenestrations within the Nav pore module that have been shown to influence Nav pore blocker access during resting-state inhibition. However, the structural differences among the nine subtypes are still unclear. In particular, the dimensions of the four individual fenestrations across the Nav subtypes and their differential accessibility to pore blockers is yet to be characterized. To address this, we applied classical molecular dynamics simulations to study the recently published structures of Nav1.1, Nav1.2, Nav1.4, Nav1.5, and Nav1.7. Although there is significant variability in the bottleneck sizes of the Nav fenestrations, the subtypes follow a common pattern, with wider DI-II and DIII-IV fenestrations, a more restricted DII-III fenestration, and the most restricted DI-IV fenestration. We further identify the key bottleneck residues in each fenestration and show that the motions of aromatic residue sidechains govern the bottleneck radii. Well-tempered metadynamics simulations of Nav1.4 and Nav1.5 in the presence of the pore blocker lidocaine also support the DI-II fenestration being the most likely access route for drugs. Our computational results provide a foundation for future in vitro experiments examining the route of drug access to sodium channels. Understanding the fenestrations and their accessibility to drugs is critical for future analyses of diseases mutations across different sodium channel subtypes, with the potential to inform pharmacological development of resting-state inhibitors and subtype-selective drug design.

Significance

Voltage-gated sodium channels initiate electrical signaling in nerve and muscle tissue. Nine different subtypes are expressed in humans. These are critical targets of drugs for treating pain, epilepsy, and cardiac arrhythmias, but it is unclear whether differential access of drugs to their binding sites could be harnessed to target medications to enter just one sodium channel subtype, reducing side effects. We compare multiple pathways for drug access (fenestrations) in individual subtypes and among subtypes over time to identify likely entry routes. Although fenestration dimensions are variable, one appears most favorable for drug passage in all subtypes, confounding the possibility of subtype-selective drug access.

Introduction

Voltage-gated sodium channels are integral membrane proteins that initiate and propagate the electrical action potential in excitable cells, by selectively allowing influx of sodium ions across the cell membrane in response to depolarization (1,2). To enable this, sodium channels cycle through three functional states (Fig. 1 A): (1) closed or “resting,” when the channel prevents sodium current, occurring at resting membrane potentials; (2) open or “activated,” in which the channel opens to allow sodium current in response to membrane depolarization; and (3) “fast-inactivated,” in which the channel prevents further conduction, although the membrane remains depolarized (2). In addition, there are also several slow inactivated states that can modulate electrical excitability (3). There are nine different eukaryotic sodium channel subtypes with greater than 50% sequence identity in their pore-forming alpha-subunit (4). These subtypes have differential tissue expression, with Nav1.1, Nav1.2, Nav1.3, and Nav1.6 expressed predominantly in the central nervous system; Nav1.4 in skeletal muscle; Nav1.5 in cardiac muscle; and Nav1.7, Nav1.8, and Nav1.9 in peripheral sensory neurons and dorsal root ganglia (5). Sodium channel dysfunction is implicated in a range of neurological and neurodevelopmental disorders depending on which channel subtype is affected. These include epilepsy (6), pathological pain (7), and autism (8), as well as various cardiac arrythmias (9) and skeletal muscle disorders (10).

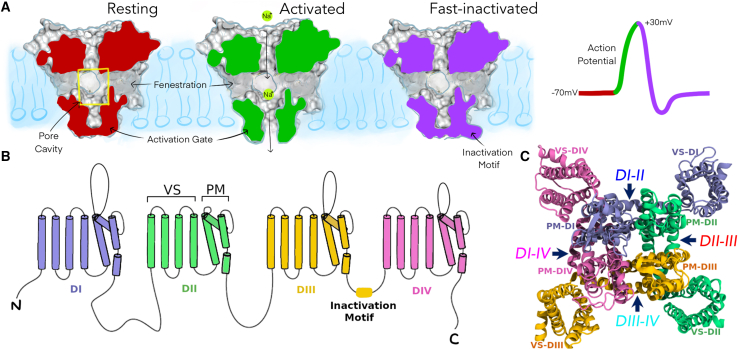
Figure 1.

Overview of voltage-gated sodium channel structure and function. (A) Cut-surface view of a eukaryotic sodium channel pore module (voltage sensors not shown here) in different states during an action potential: resting (red), activated (green), and fast-inactivated (purple); also, highlighting the location of pore cavity (yellow box) and fenestrations. (B) Topology of the pseudotetrameric eukaryotic sodium channel alpha-subunit showing each of the domains (DI-DIV) consisting of six transmembrane helices each (S1-S6). (C) Top-down view of the entire sodium channel depicting the voltage sensors (VS) wrapping around the pore module (PM) in a domain-swapped manner; fenestrations labeled by arrows.

Progress in understanding the molecular basis of sodium channel function has been accelerated by the publication of many cryoelectron microscopy (cryo-EM) structures of both bacterial (11, 12, 13, 14, 15, 16, 17, 18) and eukaryotic (19, 20, 21, 22, 23, 24, 25, 26, 27) sodium channels (see Table S1 for a summary of recent eukaryotic channel structures). These structures all capture the sodium channel’s alpha-subunit, which contains four homologous domains (DI–DIV), with each domain consisting of six transmembrane helices (S1–S6) that encapsulate a central pore. These helices form distinct functional motifs: the four voltage sensors, each made up of S1–S4 helices from each respective domain, and the pore module, composed of S5 and S6 helices from all four domains (Fig. 1 B and C). The four domains are formed by four identical but separate protein subunits in bacterial sodium channels (15), whereas eukaryotic sodium channels are formed by a single pseudotetrameric protein of homologous domains connected via loop sequences (20). Several auxiliary beta-subunits have also been captured in some of the eukaryotic structures (21, 22, 23,27). Despite some structural differences, the general architecture and voltage-sensing and ion-conducting mechanisms are conserved across bacterial and eukaryotic sodium channels. The pore module comprises the P1/P2 helices and selectivity filters at the extracellular region, which permits selective sodium entry over other cations (28). The S6 helices of the pore module encompass the central pore cavity with the base of the S6 helices forming the “activation gate” that opens and closes in response to membrane potential to control the passage of ions into the cytoplasm (29) (Fig. 1 A).

The pore module also features four lateral tunnels known as “fenestrations” that extend orthogonally to the pore axis and provide direct access from the membrane bilayer to the pore interior (Fig. 1 A). These fenestrations were originally hypothesized to exist as access pathways for small hydrophobic drugs to bind in the pore cavity and inhibit the sodium channel (30) and were later confirmed in various bacterial (11,14,17,18) and eukaryotic (21,23,24) sodium channel structures. The fenestrations are often occupied by the tails of lipid molecules in experimental structures suggesting the hydrophobic nature of these tunnels. Each of the four fenestrations is delineated by the interface between S5 and S6 helices of two adjacent pore module domains; hence they can be named DI-II, DII-III, DIII-IV and DI-IV (Fig. 1 C).

Multiple structures have been obtained for some bacterial channels, such as for NavAb from Arcobacter butzleri (12,14,17) and NavMs from Magnetococcus marinus (11,16), which are thought to represent different functional states. In contrast, the eukaryotic cryo-EM structures most likely represent a single functional state, as evidenced by the common structural features of voltage sensor activation, predominantly closed pore, and bound inactivation motif. This is expected, as cryo-EM structures are obtained in the absence of a membrane potential (i.e., 0 mV), where the channel is most likely to have opened and subsequently inactivated. However, the structural asymmetry and presence of detergent molecules in the pore gate in some structures make it difficult to assign a definitive physiological functional state. Conversely, the Periplaneta americana sodium channel NavPas (19) was the only eukaryotic channel to be supposedly captured in resting state, featuring tightly closed fenestrations and pore gate. However, as experimentalists have failed to obtain electrophysiological recordings from the NavPas channel, it is unknown whether this protein is truly representative of a functional sodium channel.

The major class of clinical sodium channel inhibitors are pore blockers. These include anticonvulsant, antiarrhythmic (AA), and local anesthetic drugs, which all share a common pore binding site involving highly conserved residues in the central pore cavity (31, 32, 33). Consequently, these drugs have little to no subtype selectivity and cause unwanted side effects when administered systemically. Thus, there is significant interest in developing inhibitors that target just one of the nine human subtypes. Pore blockers act via two main pathways (30). The use-dependent blocking pathway occurs when the activation gate is open (the channel has been “used”) and the drug passes through the opening from the intracellular space. Alternatively, resting-state block (when the activation gate is still closed) involves the drug partitioning into the hydrophobic membrane bilayer and arriving at its pore binding site, presumably via the fenestrations, without ever entering the cell. After entering the sodium channel pore, these drugs modulate function by either physically occluding the pore cavity to prevent sodium ion passage, or stabilizing the inactivated state, or a combination of both mechanisms (32). This idea is supported by recent cryo-EM structures that depict the binding of the AA drugs flecainide (24), quinidine (25), and propafenone (34) in the pore of Nav1.5.

The structures of eukaryotic channels further demonstrate that the four fenestrations in each protein are nonidentical, with distinct dimensions (20,21,23,24). Moreover, the different structures are not in agreement over which of the four fenestrations is widest or narrowest, and it is not clear if these differences are characteristic to each subtype. However, these structures are static snapshots of the protein, and previous simulation studies of bacterial channels have demonstrated that the small-timescale dynamics of the protein can dramatically alter the dimensions of the fenestrations (35,36). Thus, even a fenestration that appears too small to allow drug entry may intermittently be wide enough for drug access. Indeed, simulations have captured the direct movement of a number of general and local anesthetic compounds through the fenestrations and into the pore in both bacterial channels (37, 38, 39, 40) and a human Nav1.5 (hNav1.5) homology model (41), proving that this route is plausible for drug access. The most direct evidence of drug access through the fenestrations, however, was seen in a mutagenesis experiment of NavAb (42), in which mutation of a key fenestration-lining residue (F203) predicted to enlarge or narrow the fenestration resulted in a corresponding change in the degree of resting-state block exhibited by benzocaine, lidocaine, and flecainide.

Although there is strong evidence that small hydrophobic drugs can access the pore interior through the fenestrations, it is not clear which of the four nonidentical fenestrations of eukaryotic channels the drugs are most likely to pass through. Furthermore, it not known whether there are differences among the subtypes that could generate subtype-selective access of resting-state blockers into the pore. In this study, we capitalize on the recent availability of numerous cryo-EM structures of eukaryotic sodium channel subtypes to address these questions, by conducting molecular dynamics (MD) simulations to characterize the size of the fenestrations, accounting for the flexibility and mobility of the protein. Specifically, we run equilibrium simulations in the absence of drugs to examine the size of the fenestrations and how this fluctuates over time and subsequently run enhanced sampling metadynamics simulations in the presence of the pore-blocking drug lidocaine to directly determine how easily it can pass through each fenestration. In doing so, we identify the amino acid residues that control the fenestration size and directly assess the ease at which lidocaine can pass through each of the four fenestrations in two different subtype structures, Nav1.4 and Nav1.5.

Materials and methods

Protein structures

The voltage-gated sodium channel structures for our study were downloaded from the Protein Data Bank (PDB) (43) for human Nav1.1 (PDB: 7DTD), human Nav1.2 (PDB: 6J8E), human Nav1.4 (hNav1.4; PDB: 6AGF), rat Nav1.5 (rNav1.5; PDB: 6UZ0), human Nav1.7 (PDB: 6J8G), and cockroach NavPas (PDB: 5X0M). Preprocessing of these proteins was required to (1) remove nonprotein ligands and (2) align the molecule to previously membrane-aligned sodium channel structures to ensure correct membrane orientation. FASTA amino acid sequences for the aforementioned Nav subtypes, as well as the hNav1.5 and bacterial NavAb, were obtained from the Uniprot database (44) and aligned using ClustalW (45). Additionally, interdomain sequence alignment of S5, P1, selectivity filter, P2, and S6 was performed using ClustalW to compare sequence similarities among the four Nav domains and with the NavAb template (46). The ALINE program (47) was used to visualize the sequences.

Given the 95% sequence similarity between the rNav1.5 and hNav1.5 subtypes, a homology model of the hNav1.5 was constructed from the 6UZ0 rat structure using the MODELLER 9.24 (48) automodel protocol. Missing loop segments less than 10 amino acids in length were modeled concurrently for hNav1.5. For rNav1.5 and human Nav1.7, MODELLER’s loopmodel function was used to add in the missing amino acids in the local loop region without altering the coordinates of the global protein. In each case, eight models were generated and the best was chosen according to the lowest discrete optimized protein energy value (49) calculated using MODELLER. Larger loop regions with missing structural data (the N-terminus, DI and DIV extracellular loops, I-II and II-III intracellular linkers, and the C-terminus) were not modeled and were simply treated as protein terminations.

Equilibrium MD simulations

Each channel was embedded in a pre-equilibrated 1-palmytoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC) lipid bilayer using PACKMOL-MEMGEN (50). POPC molecules were arranged around the channel in equal concentrations across both leaflets. Box dimensions were flexibly determined using PACKMOL-MEMGEN, ensuring a minimum distance of 10 Å between the protein and the box boundaries. System sizes are provided in Table S2. Systems were then solvated in water molecules and 0.15 M NaCl. Systems were visualized using Visual Molecular Dynamics (VMD) software (51).

Topology and coordinate files were prepared using LEaP (52) with the Amber ff19SB protein forcefield (53), lipid17 forcefield (54), and OPC water (55) and TIP4P/EW ion parameters (56). Subsequently, ParmEd was used to repartition the hydrogen masses of all nonwater molecules to 3.024 Da, in order to accelerate simulations by using a 4 fs time step as opposed to the typical 2 fs time step, which has previously been shown to accurately reproduce protein structure (57,58).

The cryo-EM structures require equilibration before running MD. The protocol (summarized in Table S3) involved (1) minimization, to bring the system to a local energy minimum and eliminate any instances of bad molecular interactions or steric clashes; (2) heating, to gradually increase the system energy to relevant temperatures of 310 K (25°C) over 0.5 ns using the Langevin thermostat (59); and (3) pressurizing, to increase and maintain the pressure of the system at 1 atm for 5 ns using the Monte Carlo barostat (60). During these three steps, the α-carbon atoms of each sodium channel were held under harmonic restraint of 5 kJ/mol to ensure minimal disturbance to the protein structure, while allowing the lipid and water to accommodate to the protein rather than vice versa. Subsequently, the restraints were gradually reduced over a 24 ns time frame, decreasing in five 1 kJ/mol steps from 5 to 1 kJ/mol, then four 0.2 kJ/mol steps from 0.8 to 0.2 kJ/mol, then 0.1 kJ/mol, and finally 0.05 kJ/mol.

Unrestrained production MD was conducted using the GPU implementation of Amber20 (61, 62, 63). Three replicates of each system were run under a constant temperature of 310 K (25°C) (Langevin thermostat), constant pressure of 1 atm using anisotropic periodic boundary conditions (Monte Carlo barostat), and a 4 fs time step. Hydrogen bonds were constrained by SHAKE, and electrostatic interactions were calculated using particle mesh Ewald summation with a real-space cutoff of 10. These equilibrium simulations were run for 500 ns per replicate, totaling 10.5 μs (7 systems × 3 replicates × 500 ns) simulation time across the subtype structures.

Fenestration identification

CAVER 3.0 (64) was used to search for the fenestrations in each 0.1 ns snapshot of each 500 ns replicate for all systems. To do this, Amber trajectories were processed into series of PDB snapshots using cpptraj (65), concomitantly removing water molecules, ions, lipid bilayer, and voltage sensors, leaving only the pore module. Parameters (see Table S4 for exact inputs) for tunnel detection were set on the basis of previous ion channel fenestration studies (36,66). This included using a large spherical probe of 15 Å in radius to determine the exterior shell of the protein and a smaller probe of radius 0.8 Å to identify internal tunnels. The tunnel shapes were approximated using 12 spheres of varying sizes along the tunnel length. The starting point for tunnel calculations was set as the geometric center of the four midpoint residues along each of the S6 helices. Identified tunnels in each frame were then clustered together by relative proximity of each tunnel’s centerline across all snapshots of the simulation. Approximate clustering was used and the clustering threshold was set at 10 Å. “Murtagh matrix size” ranged from 9000 to 12,000 and was adjusted on the basis of computer memory. Bottleneck residues in each frame were also identified by CAVER.

Metadynamics in the presence of lidocaine

The three-dimensional (3D) molecular structure of lidocaine (C₁₄H₂₂N₂O) was obtained from the PubChem database (67) and converted to PDB format using OpenBabel (68). Lidocaine was parameterized using the AnteChamber program (69) with the General Amber Force Field (70). The endpoint of the first replicate of the 500 ns equilibrium run was used as the starting protein structure for subsequent metadynamics runs. To generate the simulations system, lidocaine was positioned randomly within the pore cavity using VMD, ensuring minimal molecular overlaps. The protein was packed in a 125 × 125 × 135 Å box containing POPC membrane using PACKMOL-MEMGEN and equilibrated as above. Collective variables representing polar cylindrical 3D coordinates of the center of mass of lidocaine relative to the protein were chosen for the metadynamics simulations as shown in Fig. S1. To do this, a central pore axis was defined as the vector between the center of mass (COM_top) of 24 P1 α-carbon atoms (6 from each domain) and the center of mass (COM_base) of 24 α-carbon atoms close to the activation gate (3 from S5 and 3 from S6 from each domain). A third reference point (COM_side) made use of 12 of the P1 α-carbon atoms (specifically on DI and DII only). Three positional coordinates of the lidocaine were then used: (1) projection (z) of COM_drug position along this pore axis, measured from the midpoint the vector; (2) perpendicular distance (r) of COM_drug to the pore axis; and (3) the torsion (θ) among COM_side, COM_top, COM_base, and COM_drug. The collective variables z and r were calculated using PLUMED version 2.5 CUSTOM CV using Equations 1 and 2, respectively, and θ was calculated with PLUMED TORSION CV. Restraining bias potentials were used on z and r at ±12 and 18 Å, respectively, using UPPER_WALLS and LOWER_WALLS (force constant of 100).

$$z={\left(b^2-a^2\right)}^{1/2}/c$$ (Equation 1)

and

$$r={[a^2-{\left(c/2-z\right)}^2]}^{1/2}$$ (Equation 2)

where a is the distance between COM_top and COM_drug, b is the distance between COM_base and COM_drug, and c is the distance between COM_top and COM_base

Well-tempered metadynamics (71,72) was implemented to facilitate better convergence, which required setting the initial Gaussian hill height, as well as a bias factor to define the rate at which Gaussian hill heights are reduced. Simulations were run using PLUMED version 2.5 (73, 74, 75) and Amber20. Input files can be accessed on PLUMED-NEST (plumID: 21.048). On the basis of previous literature for protein-ligand systems (40,76) and multiple test runs, we chose an initial height of 1 kJ/mol and a bias factor of 15. The collective variables z, r, and θ were measured over a short 20 ns unbiased run, from which the SDs of 0.44, 0.42, and 0.094 were determined for each variable. Consequently, the approximate Gaussian width (σ) values chosen for metadynamics were 0.5 Å, 0.5 Å, and 0.1 rad, respectively. Finally, a file-based version of multiple interacting walkers metadynamics algorithm (77) was used, which is expected to linearly increase sampling speed relative to number of walkers. This was implemented using nine independent runs on separate GPUs from the same starting coordinates and velocities but with random seed values for the Langevin integrator to ensure simulations diverged. Multiple-walker well-tempered metadynamics was run across nine walkers for each system, with total times of 3000 and 3200 ns for Nav1.4 and Nav1.5, respectively. The free energy surface (FES) was reconstructed using the PLUMED postprocessing tool sum_hills on the accumulated hills potentials from all nine walkers, integrating out either z or θ. To assess convergence, the two-dimensional top-down polar FES was generated at every 100 ns time increment, from which the one-dimensional (1D) free energy profile along each fenestration was plotted. Minimum free energy pathway (MFEP) analysis through each three-dimensional fenestration space was conducted using the MULE package (78). Pathways were subsequently overlayed on the top-down FES, as well as plotted according to the one-dimensional free energy profiles. Frames in which lidocaine was present in each fenestration were identified using cluster analysis of lidocaine, performed using the WMC PhysBio Clustering Tool in VMD with a broad root-mean-square deviation cutoff of 7.2 Å and a selection of all lidocaine-heavy atoms.

Results

Fenestrations adopt a breadth of distinct shapes and dimensions

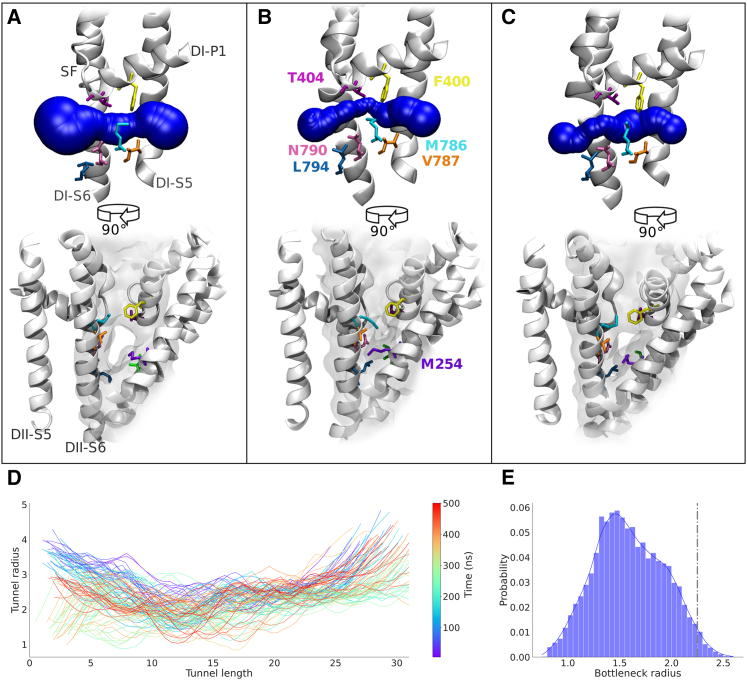
To investigate the dynamic nature of the fenestrations, triplicate 500 ns equilibrium simulations were run on the cryo-EM structures for each of Nav1.1, Nav1.2, Nav.1.4, Nav1.5, and Nav1.7. Although the cryo-EM structures clearly delineate the fenestrations, MD captures the small-timescale fluctuations in the protein that significantly influence their dimensions. As an example of dynamic fenestration behavior, we show the shape of a typical fenestration (DI-II, Nav1.4) in the static cryo-EM structure (Fig. 2 A) adopting a straight and wide state, whereas the two snapshots from equilibrium MD simulations (Fig. 2 B and C) reveal much more restricted and curved fenestration dimensions that fluctuate over time along the entire length of the fenestration (Fig. 2 D). To assess potential drug accessibility, we measure the minimum width of the fenestration (known as the “bottleneck radius”) across simulations. The Nav1.4 DI-II fenestration reaches a maximum possible bottleneck radius of 3.27 Å but is most commonly observed at approximately 1.5 Å, which is skewed lower than the cryo-EM structure bottleneck radius of 2.25 Å (indicated by the dashed line in Fig. 2 E).

Figure 2.

Simulations capture dynamics of fenestration shape and dimensions. Comparison of a representative fenestration, DI-II in Nav1.4, as seen in the cryo-EM structure (A) and two snapshots sampled from the MD simulation (B and C); a transverse view of the fenestration in sphere representation (top) and an axial view from outside the pore module (bottom) depict the bottleneck positions and key fenestration-lining residues. Overall tunnel profile time series (D) shows the changes to fenestration shape over the 500 ns simulation. The range of bottleneck radius sampled across the three replicate simulations is shown as a combined distribution (E); radius of cryo-EM structure indicated by gray dotted line.

Probability distribution of fenestration bottleneck radii is mostly consistent across the eukaryotic Nav subtypes

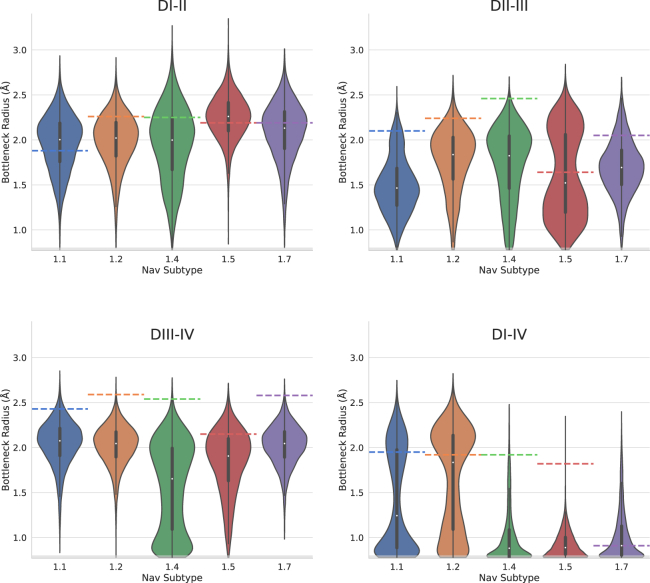
To determine how restricted each fenestration is to drug access, the distributions of bottleneck radii for each fenestration of each Nav subtype are compared in Fig. 3. Overall, all subtype fenestrations display significant variation from their bottleneck radii found in the cryo-EM structures (shown as a dashed line in Fig. 3). The most striking result was that the DI-IV fenestration was the narrowest across the subtypes and in most replicates. Although Nav1.4 features a wide DI-IV fenestration in the cryo-EM structure, our simulations indicate that the narrow state is more likely. However, discrepancies do appear in Nav1.1, where one of the replicates remains wider, and Nav1.2, where two out three replicates favor the wide position (Fig. S4). Of all four fenestrations, DI-II demonstrates the greatest maximum bottleneck radius and the most normally distributed around a radius greater than 2 Å across all Nav subtypes. DIII-IV displays a comparable bottleneck width and in some cases the highest average bottleneck radius. Therefore DI-II and DIII-IV are potentially equally accessible to drug entry. Last, the DII-III fenestration appears to be most variable in its bottleneck radius distribution, with significant difference between Nav1.7 compared with Nav1.2 and Nav1.4. Furthermore, variation within some of the subtypes (especially Nav1.5) between highly open and more occluded fenestration states is indicated by the bimodal distribution.

Figure 3.

Distributions of fenestration bottleneck radius for each fenestration and each human Nav subtype. Data from all three replicates of equilibrium MD simulations were combined to produce the overall bottleneck distributions for each fenestration (DI-II, DII-III, DIII-IV, and DI-IV) of Nav1.1 (blue), Nav1.2 (orange), Nav1.4 (green), Nav1.5 (red), and Nav1.7 (purple). Colored horizontal dashed lines indicate the bottleneck radius of each fenestration in the starting structures of each Nav subtype.

For Nav1.5, we can generalize that DI-II has the largest maximum and average bottleneck radii, suggesting that this is the most likely route for drug entry; followed by DIII-IV with a lower maximum bottleneck radius; then DII-III, which averages to a lower bottleneck radius; and finally DI-IV, which is unlikely to allow drug accessibility. Nav1.7, on the other hand, is more tightly distributed around an open state in DIII-IV than DI-II or DII-III. Intriguingly, Nav1.1 and Nav1.2 have the potential to be least restricted in the DI-IV fenestration as seen in the bimodal distributions, but we can more confidently conclude the openness of DIII-IV given the consistency between replicates distributed around a mean greater than 2 Å (Fig. S4).

Lipid tail molecules were also observed to extend into all fenestrations across the subtypes (an example for degree of hNav1.5 lipid occupancy is shown in Fig. S9). Overall, lipids extended further and more consistently into fenestrations DI-II and DIII-IV, which featured wider bottleneck radii.

Fenestration bottleneck radius converges over time but not between replicates

To assess reproducibility of our equilibrium simulations we ran three replicates of each Nav subtype. Furthermore, to determine how long it takes for the bottleneck radii to stabilize, we assessed the running average for the bottleneck radius of each fenestration over the course of each simulation (Fig. S3). In most replicates, the running averages maintain roughly constant values after 250 ns. Thus, 500 ns of equilibrium simulation would be sufficient to sample the accessible range of fenestration sizes and converge the bottleneck radii distributions.

However, regarding the reproducibility of the bottleneck radius distributions for each of the fenestrations, although the individual simulations appear to converge, there is a significant amount of interreplicate variability (Fig. S4). This suggests structural differences arise between the replicates and that the slow movement between these structural states occurs outside the 500 ns time frame. Particularly, distinct bimodal distributions are represented in DII-III of Nav1.5 and DI-IV of Nav1.1/Nav1.2, suggesting that there are two dominant bottleneck conformations. Some replicates capture transitions between the two conformations, whereas other replicates only show the bottleneck fluctuating around a single state. Given this, we cannot accurately quantify the relative probability of each bottleneck state in these cases. As Nav1.4 had the greatest discrepancy between replicates across fenestrations DI-II, DII-III, and DIII-IV, we extended simulations until 2 μs to assess whether we would observe congruency in bottleneck radius distributions. This was not the case, as the distributions across the three replicates remained distinct even after lengthy simulation (Fig. S12), which suggests large conformational differences between the replicates that are unlikely to converge within current time frames.

Bottleneck residues are predominantly hydrophobic amino acids located on S6

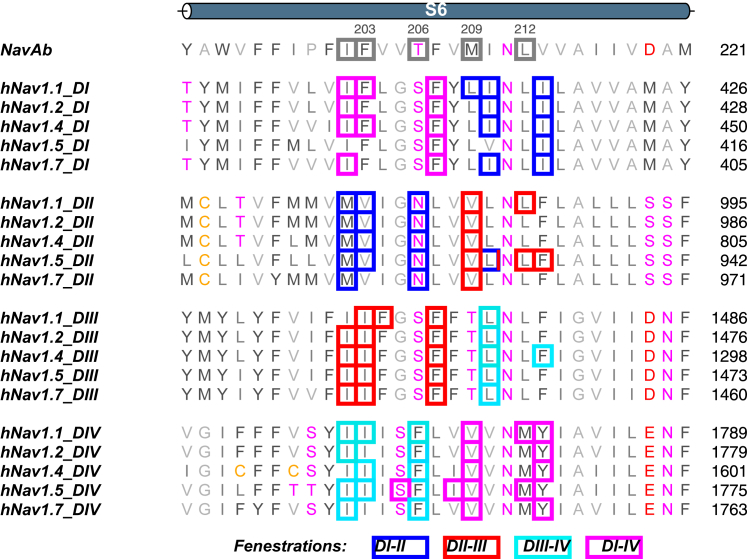
To evaluate the physical features within the fenestrations that are likely to influence drug accessibility, we analyzed the six most identified bottleneck residues across each replicate (Fig. S5). Bottleneck residues for each fenestration are predominantly found on S6, with some identified on the P1 and S5 helices (Fig. S6). Overall, the positions of these bottleneck residues, appear to be found in congruent helical backbone positions across fenestrations and subtypes. Bottleneck residues identified within the upper half of each S6 (positions 10, 11, and 14/15) participate in the fenestration on one side of the domain, whereas residues on the latter portion of S6 (positions 17/18 and 21) line the fenestration on the other side (Fig. 4). A curious pattern is that DI and DIII bottlenecks fall in identically aligned positions (positions 15 and 18), whereas DII and DIV bottleneck residues are located in an off-by-one upstream position (positions 14 and 17). Whether this is inherent to the S6 structural configuration in eukaryotic channels or a manifestation of possible inactivated state asymmetry is unclear.

Figure 4.

Fenestration bottleneck residues on S6. Sequence alignment of S6 helices by domain and subtype (aligned to NavAb), highlighting the conserved position of hydrophobic bottleneck residues in the four fenestrations. Bottleneck forming residues are contained in a box whose color represents the fenestration which they line (blue, DI-II; red, DII-III; cyan, DIII-IV; magenta, DI-IV). The 29 residues of S6 numbered sequentially in the top row to aid in identifying common positions between subtypes. Bottleneck residues on the upper and lower portion of S6DIII line different fenestrations.

Bulky, mobile sidechains are responsible for bottleneck radii variability

Aromatic sidechains are most likely to restrict bottleneck regions, as they are bulkier. Immediately evident is that the lack of aromatic residues on the S6 helix within residues lining the DI-II fenestration (Fig. 4), which potentially explains the openness of this fenestration across all subtypes. The greater variability of the fenestration widths seen for DII-III and DI-IV can also be ascribed to specific phenylalanine residues as detailed below.

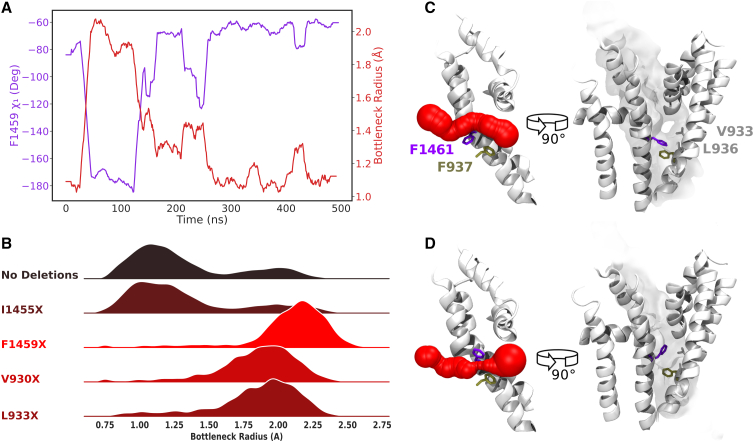
Interestingly, it is not the residues at position 11 (analogous to F203 in NavAb as described in the literature) but rather residues at position 14 or 15 (T206/F207 in NavAb) that are most responsible for bottlenecking the eukaryotic fenestrations. The phenylalanine in position 15 (F₁₅) of S6DI and S6DIII was consistently identified across Nav subtypes to be bottlenecking the DI-IV and DII-III, respectively, and accounts for most of the bimodal behavior seen in the bottleneck radii. From analysis of bottleneck residue sidechain dihedrals, it is evident that the mobility of the F₁₅ sidechain correlates strongly with bottleneck narrowing and widening across subtypes. To demonstrate this, we show the effect of F1459 (F₁₅ of S6DIII) mobility in the bottleneck radius distribution of DII-III for hNav1.5 in Fig. 5 A (similar results for F414 in DI-IV of Nav1.2 are shown in Fig. S7). The downward configuration (χ₁ = −175°) creates the wide fenestration detected above F1459 (Fig. 5 C), whereas the up-oriented conformation (χ₁ = −75°) of the aromatic sidechain creates a restricted bottleneck below the residue (Fig. 5 D). To further substantiate the impact of F₁₅ on fenestration restriction, the sidechains of individual residues were deleted one by one from trajectories and the fenestration sizes reanalyzed. Deletion of F1459 (Fig. 5 B) creates a constantly wide fenestration, eliminating the narrow bottleneck radius state. Although deletion of the V930 side chain also significantly widens the fenestration, this sidechain does not display significant mobility. This indicates V930 limits the size of the fenestration but does not move to open and close it in the same way as F1459.

Figure 5.

F1459 (in the 15th position on S6) is responsible for gating the DII-III fenestration of hNav1.5. Chi1(χ₁) dihedral angle of F1459 (purple) plotted alongside bottleneck radius (red) over time with a moving average window of 20 ns (A); bottleneck radius distributions resultant from individual sidechain deletions of bottleneck residues (B) showed that deletion of the F₁₅ aromatic sidechain had a profound effect on creating a consistently wide bottleneck radius; representative snapshots for F1459 being in the “down” configuration resulting in a wide fenestration bottleneck radius (C); compared with F1459 being in the “up” configuration, resulting in a narrowed fenestration bottleneck radius (D).

Bottlenecks can occur in varied locations along the length of the fenestration (as seen when comparing Fig. 2 B and C). Given the tilted orientation of helices, the medial bottleneck residues (located on S6 and P1) generally form a smaller ring and therefore are more likely to be responsible for the bottleneck. However, in some cases, the more lateral S5 residues may form a pronounced bottleneck in the outer portion of the fenestration. In fenestrations DIII-IV, the phenylalanine bottleneck residue occurs at position 14 (F₁₄, Fig. 4); however, its sidechain movements are less correlated with the bottleneck radius because of the occurrence of another bottleneck at the tryptophan residue on DIII-S5 (equivalent to F141 in NavAb). For example, in Nav1.4 (Fig. S8), the relationship between motion of this residue (W1171) and DIII-IV bottleneck radius is more significant than that of the F₁₄ residue (F1586).

Metadynamics simulations indicate most accessible fenestrations for lidocaine

To directly test the ease at which a sodium channel inhibitor can pass through each fenestration, we conducted metadynamics simulations, in which a neutral lidocaine molecule (C₁₄H₂₂N₂O) is encouraged to sample the central cavity and fenestrations of two human subtypes. We chose two subtypes, Nav1.4 and Nav1.5, because they had distinct bottleneck radius distributions during equilibrium runs, to run two independent instances of metadynamics, using nine walkers each time. From this, the FES for lidocaine’s position relative to the channel is determined. The choice of studying Nav1.4 also allowed us to compare lidocaine binding site locations shown by the FES with those identified in previous replica exchange simulations (79).

To assess the convergence of the free energies we track the evolution of 1D free energy profiles along the length of each metadynamics simulations (Fig. S11). Although it is difficult to reach absolute convergence, simulations were stopped once each fenestration had been completely sampled more than once and the 1D profiles were showing reduced fluctuations in the location of the minima (Fig. S11). The pore module root-mean-square deviation shows varying degrees of structural deviations among the walkers, but with values less than 3 Å, we can consider that the protein structure is not significantly altered by the accumulating metadynamics potential.

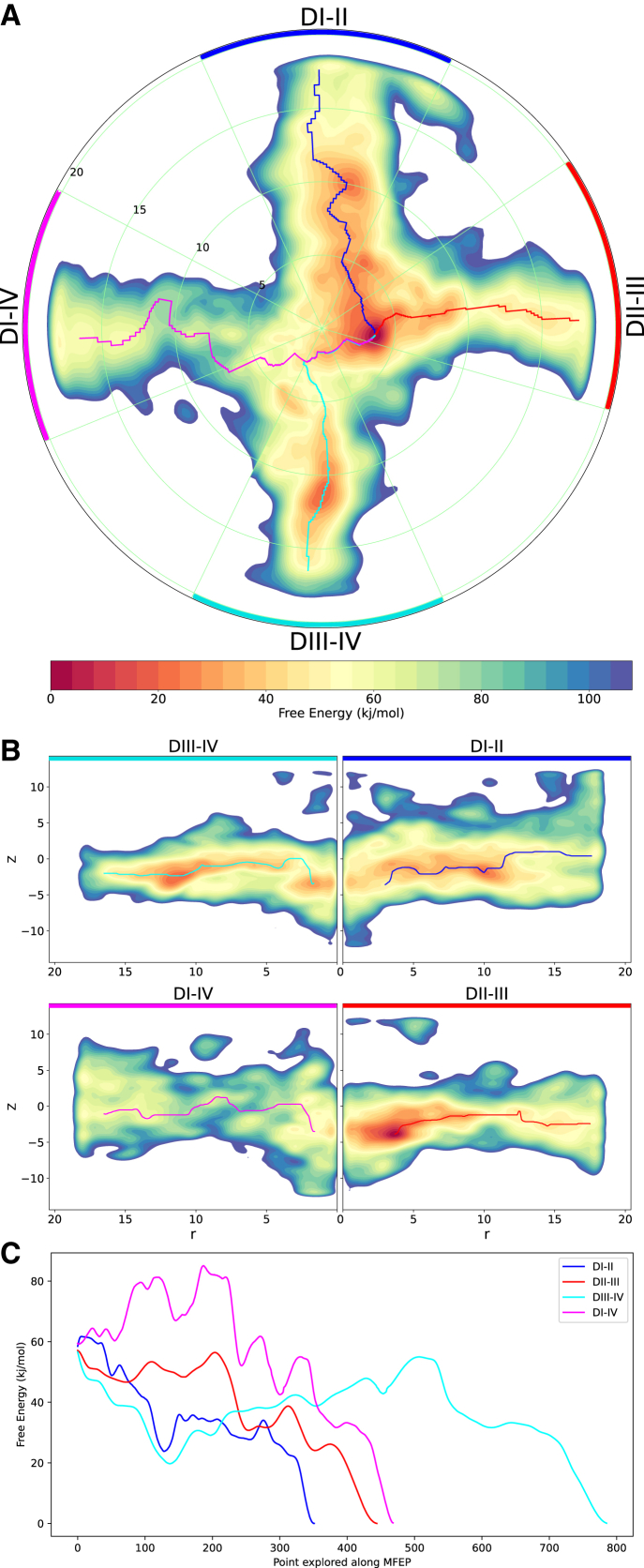
Congruent with findings from equilibrium simulations in which the DI-II fenestration was the widest and DI-IV was the narrowest, the metadynamics runs on Nav1.4 substantiate that DI-II is favorable to lidocaine passage, whereas DI-IV is not. Despite the deepest free energy minimum for Nav1.4 occurring in the pore cavity at the DII-III opening, the MFEP throughout the DII-III fenestration fluctuates around a free energy value of 50–60 kJ/mol (Fig. 6, red). In contrast, the steep downward trend of the MFEP profile via DI-II (Fig. 6, blue) suggests that DI-II is more favorable to lidocaine entry. DIII-IV also appears to be a possible energetically favorable route within the fenestration itself, but lidocaine faces a significant energy barrier, climbing from approximately 20 to 55 kJ/mol, in order to reach the binding site (Fig. 6, cyan). The F₁₅ bottleneck residues identified on S6 in DII-III and DI-IV (shown in Fig. 5) correspond to positions of approximately r = 10 Å on the FES at these two fenestrations, suggesting the physical obstruction of aromatic sidechains makes these regions adverse to lidocaine occupation. Overall, the most favorable pathway would appear to be via the DI-II fenestration in accessing the most likely binding site at the DII-III opening. The positions of the energy minima in Fig. 6 A closely reflect our previous simulations of inhibitors in hNav1.4 (79) in which the neutral compound favorably resides at the opening of the DII-III fenestration but can also occupy a range of alternative positions, including near the S6 helix of DIV (near fenestration DIII-IV).

Figure 6.

Accessibility of Nav1.4 fenestrations. The two-dimensional (2D) FES of lidocaine’s occupancy within the pore cavity and fenestrations of Nav1.4, reconstructed from the hills potentials deposited during metadynamics simulations, where warmer/darker red colors indicate energetically favorable regions and cooler/darker blue regions represent significant barriers to lidocaine. (A) Top-down polar view of the FES (obtained by integrating out z, keeping r and θ) with the MFEP through fenestrations DI-II, DII-III, DIII-IV, and DI-IV, colored blue, red, cyan, and magenta, respectively, ending at the minimum free energy binding site at the mouth of DII-III. (B) Four transverse views of each individual fenestration extending radially from the central pore axis at r = 0 (obtained by integrating out θ, keeping z and r, using 50° segments of the 3D FES for each corresponding fenestration, as indicated in (A) with DI-II spanning the blue segment, DII-III spanning the red, DIII-IV spanning the cyan, and DI-IV spanning the magenta); MFEPs also mapped along relevant sections of the transverse fenestration axes. (C) Free energy value along the MFEPs along each fenestration, colored accordingly, showing the most favorable pathway along fenestration DI-II.

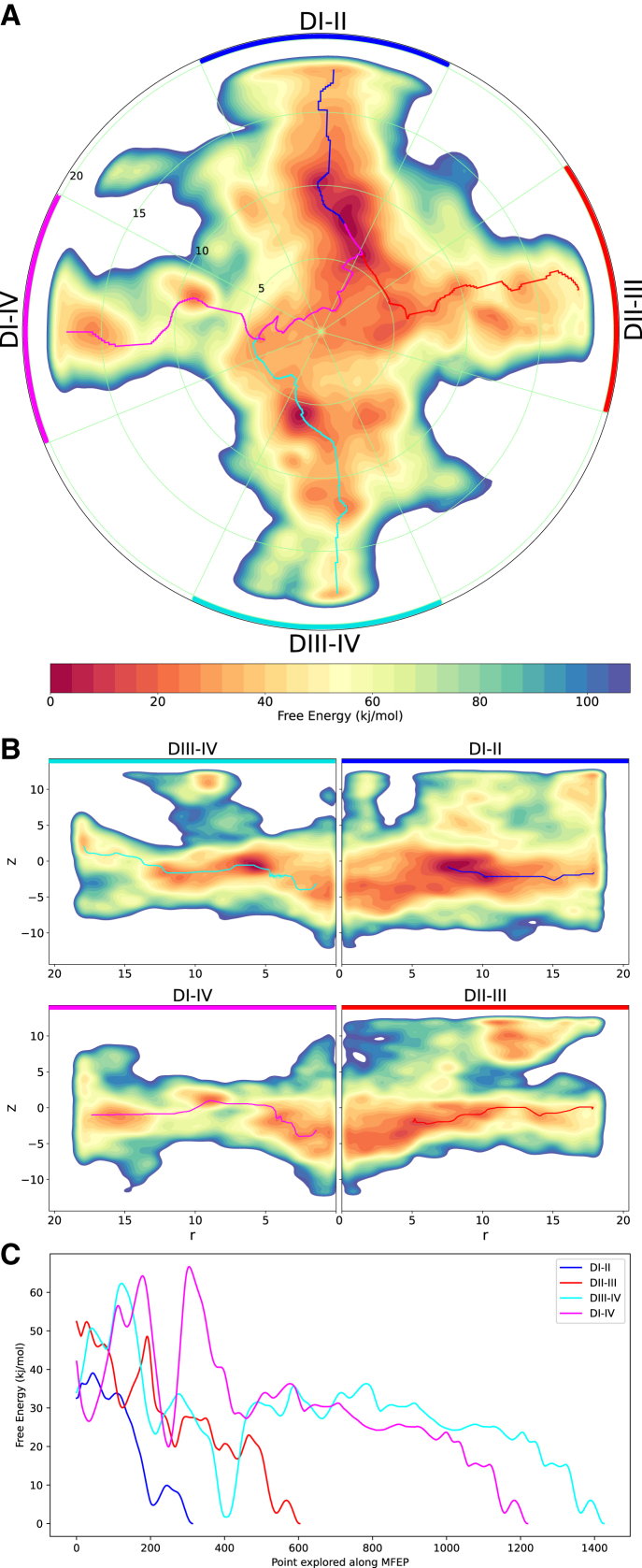
The FES for Nav1.5 also highlights the possible lidocaine entry pathways along the DI-II and DIII-IV fenestrations and significant energy barriers along DII-III and DI-IV, similar to what is seen for Nav1.4. The DI-II fenestration has the MFEP (Fig. 7 C) with the smallest free energy barriers (less than 5 kJ/mol) and therefore represents the most probable entrance route of lidocaine to the pore. In comparison, the MFEP along fenestrations DII-III and DIII-IV indicate much larger barriers (about 20 kJ/mol), suggesting that they are alternative lidocaine access pathways but less favorable than DI-II. Two potential binding sites for lidocaine are represented by energy minima in the FES. One is at the opening to the DIII-IV fenestration in which the drug has a well-defined orientation and tightly clustered positions. In this position, the aromatic group of lidocaine appears to be interacting with F1760 on S6 of DIV, which accords with mutagenesis experiments in rat Nav1.4 (32,80) and previous simulation studies (41,79,81), indicating the importance of the conserved phenylalanine in S6DIV in binding various pore blockers. A second, broader site, featuring the minimum energy site, is at the entrance to the DI-II fenestration in which lidocaine has less well defined orientations.

Figure 7.

Accessibility of Nav1.5 fenestrations. The 2D FES of lidocaine’s occupancy within the pore cavity and fenestrations of Nav1.5, reconstructed from the hills potentials deposited during metadynamics simulations. (A) The top-down polar view (obtained by integrating out z, keeping r and θ) with the MFEP through each fenestration, colored blue, red, cyan, and magenta, ending at the minimum free energy binding site at the mouth of DI-II (note that the last section of the cyan and red pathways overlap with the magenta line). (B) Transverse views of each fenestration extending radially from the central pore axis (obtained by integrating out θ, keeping z and r, for each corresponding fenestration segment, spanning 50°, as depicted in A); MFEPs also mapped along relevant sections of the transverse fenestration axes. (C) Free energy value along the MFEPs, colored according to each fenestration, also showing the most favorable pathway along fenestration DI-II.

In contrast to Nav1.4, the FES for Nav1.5 demonstrates lidocaine occupying extracellular positions above the fenestrations, between the P1 and P2 helices of adjacent domains (Fig. 7 B), specifically above three fenestrations: between P1DI and P2DII, P1DII and P2DIII, and P1DIII and P2DIV. The presence of stable positions above the fenestrations suggests alternative pathways for lidocaine to enter the pore without partitioning into the lipid bilayer. Previous flooding simulations (41) show that passing via P1DIII and P2DIV is a feasible route. However, we find a large energy barrier of ∼30 kJ/mol to move from these positions between the P1 and P2 helices into the pore, suggesting that it is an unfavorable route into the channel. The pathway between P1DI and P2DII into the pore cavity offers a lower energy alternative. However, despite evidence for these routes, our simulations suggest that the lateral entry from the membrane is much more likely (especially via DI-II), as neutral lidocaine has previously been shown to spontaneously partition into the bilayer (81).

Discussion

The four lateral fenestrations are a critical feature in the sodium channel pore module, thought to allow antagonist entry to the central cavity and facilitate resting-state inhibition. Given the nonidentical eukaryotic sodium channel domains, the four interdomain fenestrations are expected to be structurally different. Our study compared the physical characteristics of each fenestration within several eukaryotic Nav subtypes to determine the differences between their bottleneck dimensions and thus provide indication of the likely route for resting-state block accessibility. Additionally, comparisons were made among the Nav subtypes to determine the feasibility of achieving subtype-selective drug entry.

Analyzing the physical dimensions of each of the four eukaryotic fenestrations from equilibrium simulations, we found a lack of tetrameric symmetry, in stark contrast to bacterial channels (36). Furthermore, we demonstrate that the static structures of subtypes are not entirely representative of the average fenestration dimensions obtained when the protein is mobile. Overall, our results indicate that the DI-IV fenestration is the most unlikely route for small-molecule entry into the cavity, being the narrowest in most equilibrium simulations of the subtypes and evidently restrictive to lidocaine entry in both hNav1.4 and hNav1.5 from metadynamics simulations. However, the variability seen in some replicates prevents completely disregarding this fenestration as a possible access route. Fenestrations DI-II and DIII-IV are generally the widest and most accessible to drugs across most subtypes. DII-III has a greater degree of variability but may be more accessible in some subtypes. The metadynamics simulations reinforce these conclusions, particularly the favorable access via DI-II. Interestingly, the FES of Nav1.5 shows alternative pathways to the canonical fenestrations, that is, between the P1 and adjacent P2 helices. However, such pathways were not identified in Nav1.4, which can be attributed to interdomain structural differences in the two structures. Additionally, the different positions of pore binding sites identified suggest that these two structures represent slightly different inactivated pore conformations, which can be attributed to the auxiliary structures and ligands bound. That is, the Nav1.4 starting structure (PDB: 6AGF) features the β1 subunit bound above VSD-III, and the Nav1.5 structure used (PDB: 6UZ0) features flecainide bound within the central cavity. As studies have proposed that beta-subunits modulate voltage dependence (82) and AA drug binding stabilizes certain voltage sensor conformations (83), there may be structural effects in our simulations, although the β1-subunit and flecainide were removed at the start.

The main question we wanted to address in this study is whether there are differences in the physical characteristics of the fenestrations between the Nav subtypes that could be exploited to develop subtype-selective inhibitors on the basis of their accessibility to the pore. The overall trend in our simulations is that physical bottleneck radii across the subtypes differs only subtly, suggesting that subtype-selective accessibility is unlikely. Although we see differences in the preferred lidocaine binding site in our metadynamics simulations in Nav1.4 and Nav1.5 (Figs. 6 and 7), these results still demonstrate that lidocaine is likely to enter both channel subtypes via similar routes (namely, DI-II and potentially DIII-IV) and that the channels are unlikely to be selectively targeted by differences in accessibility to tonic blocking drugs. Although important for ruling out routes for drug development, this is not entirely surprising given that there are no known pore-blocking compounds with subtype-selective resting-state block. The caveat to our results is that metadynamics simulations were performed with lidocaine, a recognized non-subtype-selective sodium channel inhibitor. Our study does demonstrate, however, that metadynamics is a valid approach for verifying the subtype-selective drug access of future newly discovered compounds.

The equilibrium simulations of five different human Nav subtypes show significant variability in the distributions of fenestration bottleneck radius over time and between replicates. Specifically, the bottleneck radii of the fenestrations are governed by the small-timescale motions of hydrophobic residue sidechains. We identified key bottleneck residues within each fenestration, most notably located at the 15th position along the S6 helix (F₁₅), that control most of this variability. This residue seems to play a similar role to F203 identified in NavAb, which has been shown to (1) display distinct rotamer conformations that influence the fenestration opening (35) and (2) significantly alter resting-state block when mutated (42). Thus, mutations to F₁₅ across DII-III and DI-IV fenestrations could have implications on resting-state block. Furthermore, we identified other hydrophobic residues in key positions on S5 and S6 to have significant effect on the bottleneck, providing a practicable starting point for mutagenesis in eukaryotic sodium channel subtypes to restrict or widen fenestrations, with the experimental goal of respectively decreasing or increasing resting-state block.

A recent study (84) generated a 4-fold tryptophan mutant across the four fenestrations of hNav1.4 in order to occlude their drug accessibility. However, they were unable to reproduce reduced resting-state block using lidocaine or flecainide (as had been shown by Gamal El-Din et al. (42) in their NavAb mutagenesis experiment). This suggests that the four hNav1.4 mutations, DI-F432W, DII-V787W, DIII-I1280W, and DIV-I1583W, did not sufficiently occlude the fenestrations. Applying our present results, we would suggest that DI-F436 and DIII-F1284 (in S6 position 15), and possibly DII-N790 and DIV-F1586 (in S6 position 14), could be better mutation candidates to facilitate more complete fenestration occlusion in Nav1.4. Combined with experimental verification, we can better understand the most effectual bottleneck residues across subtypes, thus informing our molecular understanding of the complex interplay between Nav fenestration mutations and drug block.

Our simulations were conducted using eukaryotic sodium channel structures that were available at the time, and unfortunately, all these structures most likely represent inactivated states of the channel. Obviously, the use of resting state structures would be more accurate for simulating resting-state block. To address this limitation, we also characterized the fenestrations of the eukaryotic cockroach channel NavPas (19). All the fenestrations are tightly closed except for DIII-IV (Fig. S4), although it remains unclear if NavPas forms a functional sodium channel. Structures of the bacterial NavAb do indicate that the fenestration dimensions can change with functional state (12,85). Furthermore, we now have open (34) and intermediate-open (86) structures of rNav1.5 suggesting that slight pore conformation changes are coupled with the fenestration dimensions. Together this raises the possibility that the resting state of human channels may display different fenestration dimensions compared with the structures analyzed here, and it is plausible that DIII-IV could be the most likely route of resting-state drug access as in the NavPas case, but this remains to be determined. Nevertheless, hydrophobic access and binding of lidocaine during the inactivated state could contribute to overall use-dependent block, and similarly, during the open pore state. Thus, close investigation of the fenestrations in all channel conformations is warranted.

A prominent structural observation from our simulations is the distinct helix kinking occurring at the midpoint of S6 which appears to be restrictive at the level of the fenestrations. Kinking at this position has previously been identified as an important component of ion channel gating (87,88). Our metadynamics simulations further support this, showing that S6DII distortion resulted in DI-II widening when lidocaine was present in this fenestration. Furthermore, the bottleneck radius distributions for all fenestrations were right shifted when analyzing the bottleneck radii across the entire metadynamics simulation, and when accounting for the frames in which lidocaine was clustered within each individual fenestration, the widening effect of lidocaine was even more apparent (Fig. S10). This is reminiscent of a previous finding (39) in which the bottleneck radius of NavAb was also enlarged in the presence of benzocaine. Each of the four S6 helices appear to bend to different degrees; notably, S6DIV has reduced bending capacity compared with the other domains. Previous theories (12,89) suggest that the glycine and small polar residue at the midpoint of S6s in DI, DII and DIII acts as a flexible hinge that confers faster activation kinetics across these three domains, while DIV lags behind because of absence of this glycine. The stability of S6DIV potentially explains the lesser variability in bottleneck radius across DI-IV and DIII-IV fenestrations with one rigid helix, in comparison with DI-II and DII-III that are bounded by two flexible S6 helices. Thus, further quantification of how S6 distortion affects fenestration bottlenecks is warranted to understand the impact on drug accessibility, particularly in the case of larger compounds and their capacity to fit in the fenestrations. Furthermore, interactions between inhibitors and residues near the bending region could play a role in stabilizing specific functional states of the channel.

Some bottleneck residues found in our study are at the site of disease-causing mutations. For example, among the more than 1500 epileptogenic mutations that have been discovered in Nav1.1 (90), we identified 16 of the fenestration bottleneck residues as having one or more missense (and in one case deletion) mutations with disease relevance to Dravet’s syndrome or intractable childhood epilepsy with generalized tonic-clonic seizures as listed in Table S6. These bottleneck residue mutations were found across all fenestrations. Theoretically, as Nav1.1 occurs predominantly in inhibitory interneurons and SCN1A epileptogenic mutations are primarily loss of function (91), sodium channel antagonism that excludes Nav1.1 would be valuable for epilepsy treatment. Although pore blockers may not currently be subtype selective, they may be “disease-mutant selective.” Patients with phenylalanine mutations (e.g., I1770F in Dravet’s syndrome) could have better responses to pore blockers, as Nav1.1 channels are potentially less affected by resting-state block because of decreased hydrophobic drug entry via the DII-III fenestration. Thus, these patients could demonstrate less interneuron inhibition, which favorably tips the excitatory-inhibitory balance in the brain to decrease seizures. Conversely, the intractable childhood epilepsy with generalized tonic-clonic seizures mutation V983A, could detrimentally increase accessibility of pore blockers via DII-III, causing greater interneuron inhibition, leading to epileptogenic hyperexcitability.

Although our study focused on the physical dimensions of the fenestrations, the chemical nature of the fenestration residues would also be highly relevant to drug access. For example, mutation from a residue with a hydrophobic sidechain to significantly bulkier negatively charged sidechain, A1429D in DIII-IV, would be interesting to study with respect to drug accessibility and binding, especially for protonated compounds. Simulating such disease mutations would be a viable approach to mechanistically understanding how mutations in the fenestrations could implicate selective drug accessibility and ultimately affect therapeutic potency.

Author contributions

E.T. designed the research, performed the simulations and analysis, and wrote the paper. B.C. designed the research, supervised the simulations and analysis, and wrote the paper.

Editor: Chris Chipot.