Revealing Weak Dimensional Confinement Effects in Excitonic Silver/Bismuth Double Perovskites

Abstract

Lead-free perovskites are attracting increasing interest as nontoxic materials for advanced optoelectronic applications. Here, we report on a family of silver/bismuth bromide double perovskites with lower dimensionality obtained by incorporating phenethylammonium (PEA) as an organic spacer, leading to the realization of two-dimensional double perovskites in the form of (PEA)₄AgBiBr₈ (n = 1) and the first reported (PEA)₂CsAgBiBr₇ (n = 2). In contrast to the situation prevailing in lead halide perovskites, we find a rather weak influence of electronic and dielectric confinement on the photophysics of the lead-free double perovskites, with both the 3D Cs₂AgBiBr₆ and the 2D n = 1 and n = 2 materials being dominated by strong excitonic effects. The large measured Stokes shift is explained by the inherent soft character of the double-perovskite lattices, rather than by the often-invoked band to band indirect recombination. We discuss the implications of these results for the use of double perovskites in light-emitting applications.

Introduction

The flexible crystal structure and ionic nature of hybrid halide perovskites (HPs) allow for incredible tuning of their structural and electronic properties through rational design, including reducing their dimensionality by cation engineering.¹ This is obtained by the addition of bulky organic ligands during the synthesis, which break the three-dimensional (3D) perovskite structure into separated inorganic layers, hence creating 2-dimensional (2D) systems, also defined as low-dimensional perovskites (LDPs).¹ LDPs are currently attracting significant attention for their use in efficient and stable solar cells and light-emitting devices but have also been explored for phototransistors and spintronics.^2,3 However, while the chemical adaptability of the organic part has been widely investigated,⁴⁻⁶ much less attention has been paid to the inorganic metal–halide backbone. Most investigated LDPs are lead-based compounds, leaving room for the design and exploration of other nontoxic LDP systems, leveraging the toxicity issue.⁷⁻¹⁰ Exploring lead-free HP compounds and tuning their dimensionality can hence open up new and interesting research directions. In this regard, to date, much attention has been devoted to double perovskites of the form A₂MM′X₆;¹¹ with Cs₂AgBiBr₆ representing the workhorse material, due to its easy processability, environmental stability, and optical absorption in the visible range.¹² Cs₂AgBiX₆ incorporates the mildly toxic metal bismuth¹³ (Bi³⁺) and monovalent silver (Ag⁺) into the perovskite lattice with a rock-salt ordering.^12,14−16 Such lead-free double perovskites have been essentially investigated for photovoltaics (PVs),¹⁷ with a reported power conversion efficiency (PCE) of 2.84%.¹⁸ The limited PCE has been attributed to the short diffusion length of the photogenerated charge carriers, as induced by the large trap density in the devices,¹⁹ its indirect band gap, and intermediate electron and hole effective masses (as large as 0.6, 3 times larger than those of lead-based compounds).¹⁵ In addition, recent studies have suggested an intrinsic excitonic character for this compound, with theoretical estimates of electron–hole binding energy ranging from 170 meV²⁰ to 340 meV.²¹ In contrast, excitonic properties are generally of interest for light emission, as the strong electron–hole interaction results in enhanced radiative recombination mechanisms, supporting their extended application beyond PV, in light-emitting diodes,^22,23 photodetectors,^24,25 and lasers,^26,27 to name a few. In this context, it is important to recall that light emission from the 3D Cs₂AgBiBr₆ has been observed,^{12,14,15,20,28} despite its native indirect band gap, usually hindering radiative recombination pathways. Light emission from this material is also characterized by broad lines (full width half-maximum, fwhm, of 400 meV)²⁹ and Stokes shifts almost reaching 1 eV,³⁰ which strongly contrast with narrow (fwhm 20–35 meV)³¹ and weakly Stokes shifted (40 meV)³² emissions typical of 3D lead-HP, thus opening the door to the integration of these materials in white color emitter devices.³³⁻³⁵

Similarly to their lead-based counterparts, double perovskites are open to dimensional confinement via the incorporation of bulky organic spacers. However, only a few examples have been reported^28,36 thus far, limited to silver/bismuth n = 1 (BA)₄AgBiBr₈ and n = 2 (BA)₂CsAgBiBr₇ compounds, with butylammonium (BA) as the organic spacer and n indicating the number of inorganic layers defining the system dimensionality. 5,5′-Diylbis(aminoethyl)[2,2′-bithiophene] has also been used as an organic spacer (AE2T) in the [AE2T]₂AgBiI₈ perovskite.³⁶ In both cases, a transition from an indirect to- a direct band structure was evidenced from first-principles calculations, on going from thicker n > 1 layered systems to the thinnest n = 1 nanostructures, consisting of an inorganic AgBiBr₈ layer with a thickness of just one [MX]₆ octahedron.

In this work, we synthesize—to the best of our knowledge for the first time—single crystals and thin films of LDPs in the form of n = 1 (PEA)₄AgBiBr₈ and n = 2 (PEA)₂CsAgBiBr₇ double perovskites, containing phenylethylammonium (PEA) as an organic spacer. We report thorough experimental and theoretical characterization of the structural organization, optical absorption, and emission properties, aiming to extend the body of experiments related to this class of materials and to clarify their unique photophysical properties. It is worth noting that, while the n = 1 compound of this series has been reported in the literature by Wang and co-workers³⁷ and very recently by Schmitz and co-workers,³⁸ the n = 2 compound is novel. Overall, our investigations show that the optical absorption is weakly influenced by spatial confinement. Remarkably, we observe light emission from both the n = 1 and n = 2 compounds, regardless of the direct/indirect character of the band structure.²⁸ A clear Stokes-shifted emission is found. First-principles simulations disentangle the relative contributions to the Stokes shift of indirect band to band recombination versus charge trapping via electron–phonon coupling. The emerging picture from the joint experimental and theoretical study reveals that the layered AgBi-HPs behave differently from layered lead-based HPs and conventional semiconductors.

Results and Discussion

Material Structure

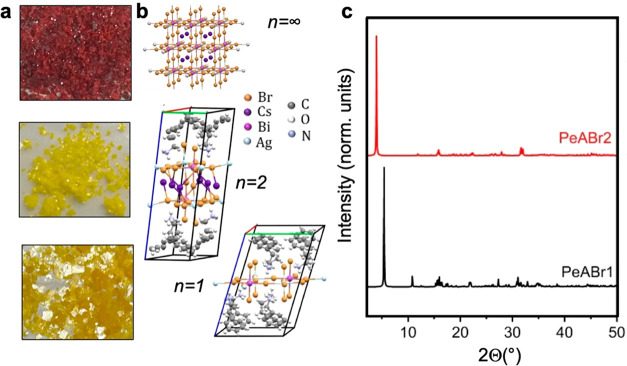
Single crystals and thin films of n = 1 (PEA)₄AgBiBr₈ and n = 2 (PEA)₂CsAgBiBr₇ double perovskites, named PeABr1 and PeABr2 in the following, have been prepared using the slow crystallization method (see Experimental Methods), resulting in yellow platelike single crystals 3 × 3 × 0.2 mm³ in size, as shown in Figure 1a. Crystalline structures, as resolved from single-crystal X-ray diffraction (XRD), are shown in Figure 1b, with the corresponding space group and lattice parameters being collected in Table 1. Corresponding XRD data along with SEM images of PeABr1 and PeABr2 thin films are reported in the Supporting Information. The parental 3D Cs₂AgBiBr₆ (n = ∞) double perovskite has also been synthesized and characterized, for reference. The crystal structures of PeABr1 and PeABr2 belong to the low-symmetric P1̅ triclinic lattice, consistent with similar findings reported for phenylethylammonium-incorporated lead–bromine-based perovskite compounds.³⁹⁻⁴² We may thus speculate that this specific organic spacer experiences significant orientational and conformational disorder, in comparison to butylammonium, hence resulting in reduced crystalline symmetry. The lowest angle reflection in Figure 1c is associated with the interplanar stacking (001) direction, which shifts from 5.397 to 3.945° on going from the n = 1 (PeABr1) to the n = 2 (PeABr2) system, reflecting the increased thickness of the inorganic frame. Finally, we anticipate that the n = 1 compound features cell doubling within the inorganic plane: that is, it contains four metal sites (two silver and two bismuth) per inorganic plane, per cell. This fact may have important consequences in the definition of the direct/indirect character of the band gap, as we shall discuss in the next section.

Figure 1.

(a, b) Single crystals and crystal structures for 3D Cs₂AgBiBr₆ (n = ∞) halide perovskites and layered PeABr2 (n = 2) and PeABr1 (n = 1) compounds, respectively, as refined from XRD measurements; (c) XRD patterns for PeABr2 (n = 2) and PeABr1 (n = 1) compounds.

Table 1. Derived Crystallographic Data of the (PEA)₄AgBiBr₈ and (PEA)₂CsAgBiBr₇ Single Crystals Compared to Those of the Reference Cs₂AgBiBr₆.

	PeABr1 → (PEA)4AgBiBr8	PeABr2 → (PEA)2CsAgBiBr7	Cs2AgBiBr6
space group	triclinic (P1̅)	triclinic (P1̅)	cubic (Fm3̅m)
chemical units	2	2	4
lattice params
a (Å)	11.5184	7.9591	11.2499
b (Å)	11.6000	8.0394	11.2499
c (Å)	17.3679	22.6161	11.2499
α (deg)	106.624	97.634	90
β (deg)	100.528	93.818	90
γ (deg)	90.203	90.2700	90

Apart from the detailed lattice symmetry and parameters, lead-free perovskites feature very specific structural distortions in comparison to their lead halide analogues. These are discussed in Table 2 for our new PeABr1 and PeABr2 layered compounds, as well as for previously reported BA₄AgBiBr₈ and BA₂CsAgBiBr₇ (named BABr1 and BABr2 in the following; butylammonium = BA)²⁸ and for lead bromine layered perovskites (either containing BA or phenylethylammonium = PEA, as a spacer). For n = 1 PEA₂PbBr₄, several structures have been reported experimentally,³⁹⁻⁴² but we focus here only on those from refs (39 and 41), as they do not feature disorder in the octahedral tilting. The structural distortions considered, as depicted in Figure 2, consist of (i) the octahedral rotation pattern, as measured by the β and δ angles proposed by Pedesseau et al.,⁴³ (ii) the Jahn–Teller distortion of the [MX]₆ octahedra, as described here by the ratio between the average of the metal–halide bond lengths in the apical and equatorial directions (MX_ap/MX_eq), and (iii) the off-centering of the metal from the plane of the equatorial halides (d_m). Note that widely exploited octahedral elongation (λ_oct) and angle variance (σ_oct) may provide information about the specific octahedral distortions in perovskites,⁴⁴ in relation to Jahn–Teller deformations and off-centering, in principle. However, we verified that these are not as informative as the descriptors proposed in (ii) and (iii), at least for the layered compounds investigated here (see the Supporting Information).

Table 2. Comparison of the Structural Distortions from the Archetypal Perovskite Structure in Lead and Silver/Bismuth Double Perovskite Compounds^a.

compound	CCDC no.	β (deg)	metal	δ (deg)	MXap/MXeq (Å)	dm (Å)
Thickness n = 1
BA2PbBr4	1521054	154.8		6.3	1.005	0.00
	1945905	152.9		5.5	1.010	0.00
PEA2PbBr4	754094	150.8–152.1		2.9–3.5	1.012	0.20
	1903529	151.1–152.2		2.8–3.2	1.012–1.014	0.17
BA4AgBiBr8	1814979	159.3–160.2	Ag	4.2	0.895	0.00
			Bi	5.6	1.016	0.00
PEA4AgBiBr8b	2088920	158.6–159.1	Ag	3.4–3.9	0.880	0.07
			Bi	3.9	1.012	0.03
Thickness n = 2
BA2CsPb2Br7	1945912	151.9–157.0		1.2–7.3	1.005	0.09
BA2CsAgBiBr7	1814799	161.0–171.7	Ag	3.4–10.3	1.029	0.50
			Bi	3.7–8.5	1.008	0.05
	1814800	163.9–178.9	Ag	5.3–7.4	0.982	0.38
			Bi	4.0–8.8	1.001	0.03
PEA2CsAgBiBr7b	2088919	163.9–167.6	Ag	1.5–7.5	1.002	0.42
			Bi	1.5–7.5	1.003	0.02

^aAbbreviations: BA, butylammonium; PEA, phenylethylammonium. Analyses were carried out on the crystalline structures deposited with the Cambridge Crystallographic Data Center, with the corresponding CCDC reference reported. For a detailed description of the considered distortions, vide infra.

^bThis work.

Figure 2.

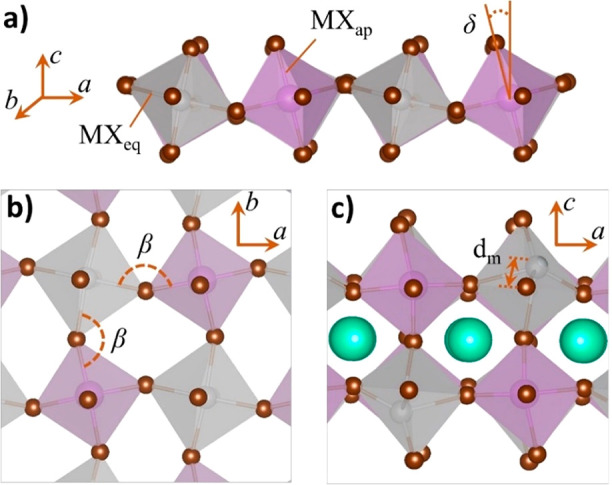
(a) Lateral and (b) top views of a lead-free double perovskite octahedral structure of n = 1 thickness displaying the β and δ tilted angles. (c) Lateral view of an n = 2 perovskite representing the off-centering of the metal from the plane of the equatorial halides.

Both lead-based and silver/bismuth double perovskites show large deviations of the M–Br–M′ valence angles from linearity, hence indicating considerable octahedral rotations, especially along the perpendicular direction with respect to the inorganic plane (β). Similar findings have been reported for lead-based systems, where an increase of the octahedral tilting was correlated to the electronic properties, in terms of both the band gap opening^43,45 and an increase in the charge carrier effective masses.⁴⁶ Similarly, both systems are sensitive to the Jahn–Teller effect but with a very peculiar trend in double perovskites, in comparison to lead-based systems. In the latter, in fact, elongation of the lead–apical halide bond length was reported, while in the former, opposite distortions take place for the Ag/Bi metal site, experiencing a shrinking/elongation of the apical metal–halide bonds, respectively.

Special attention is needed in discussing the off-centering of the metal site, as contradicting evidences have already been reported for well-known lead-based n = 1 compounds, with BA and PEA incorporating layered perovskites showing null and 0.17–0.20 Å off-centering, respectively. This fact, however, should be properly correlated to space group symmetry assignment for these two compounds.⁴⁷ Indeed, for the BA-incorporated lead perovskite, metal atoms reside in the Wyckoff position a of the corresponding space group (Pbca), inherently not allowing for off-centering of the metal, while for the PEA-incorporated lead perovskite the low crystalline symmetry relaxes any constraint for the off-centering. Similarly, the appearance of metal off-centering in the n = 2 BA-incorporated lead bromine perovskite in Table 2 should be considered in relation to the displacement of the metal ion from high-symmetry Wickoff positions, hence allowing for small (0.1 Å) off-centering. For n = 1 double perovskites, very small, metal-dependent off-centering is observed, which is genuine, considering the space group symmetry of this system. Finally, in the n = 2 layered double perovskite we find minimal off-centering of bismuth and huge off-centering of silver, at the same time, for both our newly reported PEA-incorporated double perovskites and previously reported BA-incorporated double perovskites.²⁸ This large off-centering is therefore a peculiar structural marker for silver/bismuth double perovskites with n = 2 thickness, whose origin remains still unclear, as it cannot be fully explained either in terms of pseudo Jahn–Teller effects or in terms of strong electrostatic repulsion between silver and bismuth cations.²⁸

UV–Vis Absorption and Electronic Properties

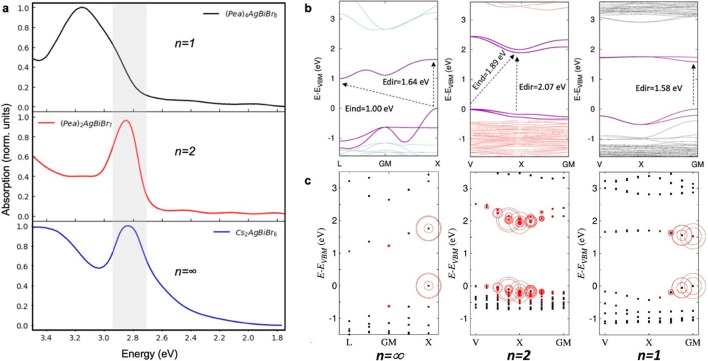
In Figure 3a, we report the UV–vis absorption spectra of our newly synthesized PeABr1 and PeABr2 compounds and of the 3D reference Cs₂AgBiBr₆ double perovskite, as measured on thin films at room temperature. All of the spectra show a well-defined absorption band at low energy, with fwhms of a few hundreds of meV, followed by continuous absorption at higher energy. The low-energy absorption feature is measured to be 3.1, 2.9, and 2.85 eV for PeABr1, PeABr2, and 3D, respectively, closely paralleling the corresponding signatures measured in layered BABr1 and BABr2 and 3D double-perovskite compounds, reported by Connor and co-workers (3.0, 2.85, and 2.75 eV, respectively).²⁸ The close energetics for the absorption in the presence of two different organic spacers (BA and PEA) once more confirms the negligible contribution of this constituent on the optical properties of LDPs, as related to the formation of a type I interface between the inorganic and the organic components, with the band gap of the former being embedded into that of the latter. This may be not the case in the presence of π-conjugated organic cations, as for the bithiophene-incorporated n = 1 [AE2T]₂AgBiI₈ perovskite reported in ref (36). For this material, in fact, the absorption onset was measured to be around 2 eV, that is ∼1 eV red-shifted with respect to that reported in Figure 3a for PeABr1. On the other hand, this red shift in absorption in [AE2T]₂AgBiI₈ cannot be ascribed solely to the formation of type II heterointerface, that is, the intercalation of the HOMO or the LUMO of the organic spacer into the band gap of the inorganic structure, as also the halide substitution from Br to I is expected to close the band gap, following the destabilization of the outer s and p orbitals of the latter halide. DFT calculations from ref (36) indeed pointed out halide substitution as being solely responsible for the aforementioned absorption red shift, with the electronic interface of the [AE2T]₂AgBiI₈ being at the very limit of type IIb (HOMO of the organic close in energy with the top of the valence band of the inorganic). Figure 3a also highlights the limited role of spatial confinement on the optical absorption properties of these double-perovskite compounds, with the measured red shift of the absorption going from the n = 1 to the n = 2 compound and finally to the 3D reference material being limited to only 150 and 250 meV, respectively. For the sake of comparison, the red shift measured in lead-based layered HP compounds corresponding to the same dimensional reduction amounts to 400 meV and to 1 eV, respectively.⁴⁸ From this comparison, one may naïvely classify quantum confinement effects on the optical absorption properties of lead-based and layered double perovskites in two different regimes, a strong one and a weak one, respectively. Note in fact that the effect of quantum confinement on the optical absorption properties of layered double perovskites saturates very quickly, with the n = 2 compound showing almost the same absorption properties as the parental 3D system.

Figure 3.

(a) UV–vis absorption spectra of PeABr1, PeABr2, and 3D Cs₂AgBiBr₆ double perovskites measured on thin films at room temperature. (b) Corresponding band structures as obtained from DFT simulations, based on the standard PBE exchange-correlation functional, including SOC. (c) Weighted contributions in the reciprocal space to the lowest energy, dipole-allowed excited state for the investigated compounds, as obtained from an ab initio solution of the Bethe–Salpeter equation.

To clarify the role of spatial confinement, we conducted electronic structure calculations for these newly reported systems, as well as for the reference 3D Cs₂AgBiBr₆. We first performed periodic density functional theory (DFT) simulations adopting the PBE exchange-correlation functional, including spin–orbit coupling (SOC). We relaxed the atomic positions of the investigated compounds, keeping the cell parameters fixed, and evaluated the corresponding band structures. A detailed description of the computational protocol is reported in Computational Methods. Our results closely parallel those previously reported for butylammonium layered Ag/Bi bromine double perovskites,²⁸ with the frontier orbitals being associated with the inorganic frame. The electronic structure of the widely studied 3D Cs₂AgBiBr₆ compound in Figure 3b is indirect, with the valence band maximum/conduction band minimum located at the X/L high-symmetry points of the Fm3̅m first Brillouin zone, roughly corresponding to the metal–halide–metal and to the metal–cesium–metal directions, respectively. For the sake of reference, the first Brillouin zones for the Fm3̅m and P1̅ space groups⁴⁹ and the correlation between high-symmetry points in the reciprocal space and corresponding directions in the real space are graphically depicted in the Supporting Information. The layered n = 2 PeABr2 double perovskite also shows an indirect band gap (Figure 3b) with valence and conduction band edges located at the V and X points of the Brillouin zone, the first corresponding to the metal–halide–metal direction and the second roughly corresponding to the in-plane projection of the metal–cesium–metal direction. The n = 1 PeABr1 compound, instead, shows a direct band gap at Γ (Figure 3b), but this result should be considered in light of the previously mentioned in-plane cell doubling. In other words, a reduced model for PeABr1 containing only one silver/bismuth pair per cell/plane may still present an indirect band structure, with the valence and conduction band edges being located in different points of the Brillouin zone and then folding back to the center of the Brilloun zone as a result of the doubling of the cell. To check this point, we designed a reduced model for PeABr1 with only one silver and bismuth atom per cell and computed the corresponding band structure; we still found a direct band gap at Γ (see the Supporting Information). Hence, this result rules out band folding, demonstrating that the n = 1 PeABr1 double perovskite is a genuine direct semiconductor, in striking contrast with the n = 2 PeABr2 and 3D Cs₂AgBiBr₆ analogues. This indirect-to-direct transition when the thickness of the [MX]₆ octahedral structure is decreased is not new, as was already pointed out for butylammonium-containing BABr1 and BABr2 systems reported by Connor and co-workers,²⁸ and is also consistent with the direct band gap structure reported for [AE2T]₂AgBiI₈ perovskite by Jana and co-workers.³⁶ The reason behind this unusual change in the electronic structure still has to be clarified, as it is potentially due to the involvement of d orbitals for the metal sites.⁵⁰ Symmetry analyses are ongoing to shed light on this point.⁵¹

Direct band gaps computed using a standard GGA (PBE) exchange-correlation functional including SOC amount to 1.87, 2.06, and 1.58 eV for 3D Cs₂AgBiBr₆, PeABr2 and PeABr1, respectively, and hence do not reproduce the observed blue shift of the optical absorption with the decrease in the thickness of the perovskite frame, as expected from the corresponding increasing quantum confinement. Standard DFT approximations such as GGA are well-known to fail in quantitatively reproducing the experimental band gaps of semiconductors,⁵² though they usually provide correct trends for a set of analogous compounds, as in the case of 3D pure⁵³ and mixed HPs⁵⁴ or in the case of n-variable layered lead HPs.⁴⁸ To clarify this unexpected failure of the standard DFT, we therefore resorted to more accurate hybrid DFT calculations, employing the PBE0 exchange-correlation functional, obtaining band gaps in slightly better agreement with experiment (3.17, 3.36, and 3.02 eV for 3D, PeABr2, and PeABr1, respectively) but still not reproducing the trend associated with the quantum confinement. We therefore speculate that the experimental absorptions in Figure 3a are not solely related to the band gap of the materials but also reflect a more complicated underlying physics, where excitonic effects may play a role (as we will show below) but also where thermal effects, such as phonon-induced band gap renormalization, may be important.⁵⁵

In the pivotal works by Volonakis¹⁵ and Slavney,¹² great effort was devoted to explain the optical properties of 3D Cs₂AgBiBr₆ double perovskites, in connection with their indirect electronic structure. However, the consensus is currently shifting toward the assignment of the low-energy absorption signature in Figure 3a to a stable exciton, that is, to the formation of a strongly bounded electron–hole pair, upon light absorption. This assignment therefore places double perovskites under a different light, in comparison to 3D lead-based perovskites, for which exciton binding energy estimates as small as 16 meV have been reported in the literature,^56,57 with excitonic features in the absorption spectrum becoming evident only at low temperature.⁵⁸ Excitonic effects in lead-based HP instead arise from quantum confinement, as in the case of 2D nanoarchitectures, where breaking the perovskite motif into atomically thin perovskite sheets (and unavoidable dielectric contrast between the organic and the inorganic components⁵⁹) gives rise to binding energies as large as 450 meV for the thinnest n = 1 layered lead iodide perovskites.⁵⁹ In contrast, recent theoretical estimates of the exciton binding energy for the lead-free Cs₂AgBiBr₆ reference compound amounted to 104,⁶⁰ 170,²⁰ and 340 meV,²¹ therefore raising the question about the role of quantum confinement in materials already featuring such strong excitonic character in 3D. To address this point, we first extracted qualitative estimates of the exciton binding energy for the investigated 3D and layered double perovskite material, from a Tauc plot and Elliot fit of the corresponding absorption spectrum, similarly to ref (68) (see the Supporting Information). The resulting exciton binding energies for n = 1, n = 2, and 3D materials amount to 270, 220, and 150 meV, respectively. The discrepancy between our estimate for the 3D material and a previous estimate by Kentsch et al. (268 meV) mainly arises from the red-shifted band gap measured here.⁶⁸ Notice, however, that estimates from this phenomenological approach should be taken with care, as the broad figure at 2.85 eV may hide several excitonic features (vide infra), as also suggested from previous theoretical calculations.²⁰ We then assessed excited-state properties by performing an ab initio solution of the Bethe–Salpeter equation (BSE; see details discussed in Computational Methods). Since the cost of these calculations for the full models in Figure 1b would be prohibitive, we proceeded to substitute the organic component with Cs atoms, then recalculating the band structure at the PBE+SOC level of theory and performing ab initio simulations of the BSE, with the results being shown in Figure 3c. Our simulations confirm the exciton character for the 3D Cs₂AgBiBr₆ double perovskite, with the lowest energy dipole-allowed excited state mainly corresponding to a direct transition at the X point of the Brillouin zone. The corresponding exciton binding energy, as estimated from the difference between the excited state energy and the band-to-band transition X, amounts to 240 meV, hence falling into the range of previous BSE calculations reported in the literature,^20,21,60 with differences that may arise from the use of different lattice parameters and details of the computational setup. Our DFT/BSE calculations also shed some light on the origin of the broad experimental signature at around 2.85 eV. In fact, when correcting our BSE excited states via a scissor operator, to overcome the aforementioned limitation by standard DFT in reproducing experimental band gaps, we find that this signature is not just ascribed to one excitonic resonance but also results from the convolution of several resonances, with the final broadening being related to the energy differences between individual excitons, in addition to the ubiquitous thermal electron–phonon coupling effect. This is by itself an interesting change in perspective, in comparison to the conventional picture that implicitly considers only one excitonic feature and further stresses the limitation in estimating the exciton binding energy via simplified approaches such as Tauc plots and Elliot fitting.

For layered PeABr2 and PeABr1, we find the lowest energy dipole-allowed excited state associated with a direct transition at the X and Γ points of the Brillouin zone, respectively. Computed binding energies amount to 280 and 150 meV, respectively, but these are likely affected by the different screening of the Cs atoms, in comparison to the native organic PeA spacers.⁵⁹ Similarly, this incorrect dielectric screening also likely influences the detailed energetics of the lowest energy excitons predicted for the n = 1 and n = 2 perovskites. We therefore prefer to avoid performing an assignment of the lowest excitonic feature of these materials, on the basis of the resonances predicted by our BSE simulations, as was done for the 3D material. Note that, while the excitonic character of the 3D Cs₂AgBiBr₆ material is currently well established,^{20,21,30,60,61,68} some doubts arise from recent studies focused on the thinnest n = 1 double-perovskite structure. Adopting accurate hybrid DFT+SOC calculations, in fact, Jana and co-workers computed a band-to-band transition for n = 1 [AE2T]₂AgBiI₈ in good agreement with the experimental absorption onset, hence indicating rather negligible excitonic effects.³⁶ This fact, however, comes in contrast with the general understanding of enhanced many-body effects with quantum confinement,⁵⁹ therefore calling for future investigations.

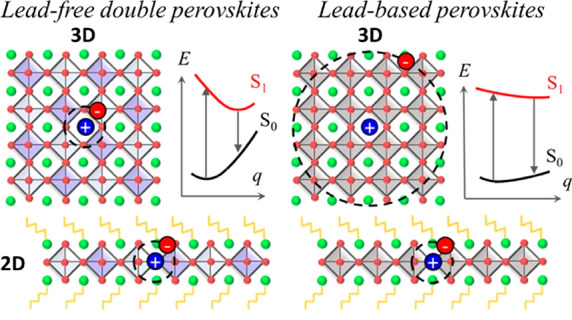
In this framework, it becomes evident that quantum confinement has limited influence on the optical absorption properties of these double perovskites in comparison to lead-based systems, likely because of their native excitonic character. Indeed, the photogenerated electron–hole pairs experience spatial localization arising from reciprocal Coulombic interactions already in the 3D network, with very recent theoretical estimates of an exciton radius of 6 Å,²⁰ which is comparable to the dimensional confinement for the thinnest n = 1 PeABr₁ compound. As a result, photogenerated charges are inherently localized in the lattice of these double-perovskite materials, resulting in an overall weak influence associated with dimensional confinement (becoming evident only for the thinnest n = 1 compound).

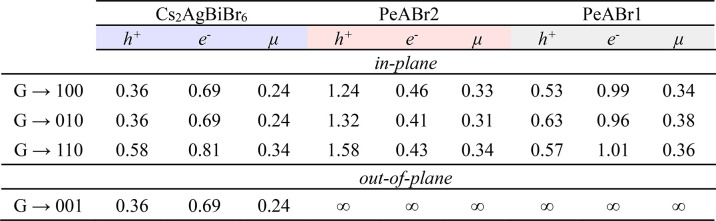
As a final note, from the electronic band structures in Figure 3b, we estimate the diagonal component of the charge carrier effective mass tensor for our three compounds (see Table 3). Estimates for the 3D material are close to those of previous reports,¹⁵ with effective masses for holes/electrons 2/4 times larger than the corresponding values in 3D lead-based HPs.⁶⁰ The reason behind these (relatively) large carrier effective masses has to be sought in the narrow band dispersions computed for these materials, as already pointed out in refs (28 and 36). Dimensional confinement obviously affects the out-of-plane transport properties of double-perovskite compounds, with infinite effective masses along the stacking ⟨001⟩ direction. Interestingly, electron and hole effective masses do not show a monotonic dependence with respect to the thickness of the inorganic frame. We speculate that these trends are strictly related to the detailed structural distortions discussed in Table 2.

Table 3. Calculated Hole (h⁺), Electron (e^–), and Reduced (μ) Effective Masses for Cs₂AgBiBr₆, PeABr2, and PeABr1 along the In-Plane ((100), (010), and (110)) and Out-of-Plane (001) Directions^a.

^aHere G is used to designate the point of the reciprocal space where the band edge is located.

Photoluminescence (PL) of Thin Films of Lead-Free 3D Compared to That of LDPs

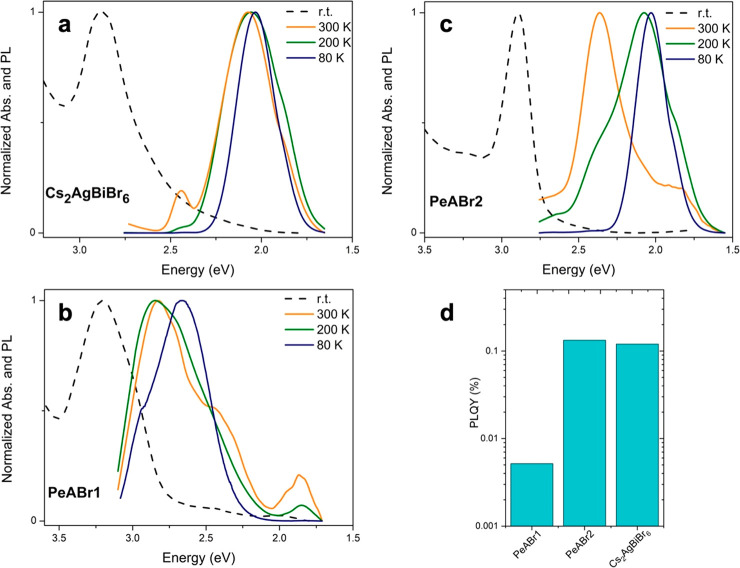
After discussing the absorption properties of our PeABr1 and PeABr2 double perovskites, we move to analyzing their emission properties. In Figure 4a–c, we report photoluminescence (PL) spectra of our newly reported layered double perovskites together with that of the reference Cs₂AgBiBr₆ perovskite, as measured on thin films at room temperature, at 200 K and at 80 K. For the 3D Cs₂AgBiBr₆ material, we were able to measure light emission (although with small a emission efficiency; vide infra). The PL spectrum matches previous reports well,³³ showing one broadened feature (FHWM = 400 meV) centered at ca. 2.1 eV, hence characterized by a Stokes shift as large as 750 meV with respect to the absorption. Very weak PL is observed also for the layered PeABr1 (n = 1) compound (Figure 4b), characterized again by a broadened line shape and a large Stokes shift (250 meV), in agreement with previous measurements on BABr1.²⁸

Figure 4.

(a–c) Photoluminescence spectra of Cs₂AgBiBr₆ (a), PeABr1 (b), and PeABr2 (c), as measured on thin films at 80 K and at 300 K. The dashed lines indicate the UV–vis absorption spectra at the corresponding temperature. (d) PL quantum-yield measurement at room temperature.

For the first time, we also observe light emission from the PeABr2 (n = 2) compound (Figure 4c), characterized again by a broadened line shape and a large Stokes shift (500 meV). Previous investigations on butylammonium-incorporated n = 2 double perovskite in fact highlighted suppressed light emission from this compound, potentially because of poor control over phase purity.²⁸ Still, it is worth stressing, once more, the broad line shape and the large Stokes shift observed for all the investigated double-perovskite compounds, which strongly contrasts with the narrow and weakly Stokes shifted emission of 3D and layered 2D lead-based HPs.^31,62

We also measured the PL quantum yield (PLQY) at room temperature on thin films of our layered compounds and of the reference Cs₂AgBiBr₆ using an integrating sphere, as shown Figure 4d. Measured room-temperature efficiencies are overall quite small, ranging between 0.01 and 0.1%, as a function of the material, where the error of ca. 10^–4 guarantees a proper comparison between the different materials. Still, although modest, the emission efficiencies reported for our samples in Figure 3d should not discourage the exploration of double perovskites for light-emitting applications. Indeed, as the scope of this work was not to report highly efficient materials, film morphologies (grain size and improvement of the substrate coverage) and thicknesses were not optimized and surface treatments were not introduced, all factors that leave great possibilities for serious improvements in the overall emission efficiency. The most striking result from PLQY in Figure 4d is related to the trend of the emission efficiency with respect to the band structure of the three reported compounds, with larger PLQY being associated with indirect semiconductors. This fact is clearly unexpected, as the emission from an indirect band gap semiconductor is a second-order perturbation phenomenon that requires simultaneous phonon emission or absorption to conserve the total momentum, therefore being intrinsically less effective in comparison to direct-gap emission.

Explaining the PL Mechanism in 3D and Layered 2D Double-Perovskite Compound

From Figure 4, it immediately appears that the emissive properties of the investigated double-perovskite compounds are inherently more complicated than those of long-established lead-based perovskite systems, where large Stokes shifts and broadened and temperature-dependent line shapes go together with the reported direct/indirect transition in the band gap, as a function of the material thickness. In an effort to obtain a global picture for the emissive properties of both the 3D compound and its layered analogues, we recall the two different mechanisms that have been invoked thus far: (i) intervalley radiative band-to-band recombination⁶³ and (ii) a self-trapping process due to the coupling of the exciton with lattice vibrations (also called intrinsic self-trapping).⁶⁴⁻⁶⁶ In the following, we will discuss these two mechanisms, extending the discussion to the layered PeABr1 and PeABr2 compounds in light of the results reported in the previous sections. The shift is visible only in the normalized spectra, while it is highly depressed in the non-normalized data that we report in Figure S11 in the Supporting Information.

Intervalley Recombination

On consideration of an indirect semiconductor, the generation of an electron–hole pair due to light absorption is ideally followed by the relaxation of one or both charge carriers in different high-symmetry points of the corresponding Brillouin zone. In this case, light emission is shifted with respect to the absorption, by the difference between the direct and the indirect gap, with phonon absorption or emission ensuring total momentum conservation. In this framework, it was noted for the 3D reference Cs₂AgBiBr₆ perovskite that the 700 meV energy difference between the calculated direct band gap at X and the indirect band gap from L → X (Figure 3b) is in semiquantitative agreement with the measured Stokes shift (800 meV).²¹ Indirect recombination is, however, a second-order process and therefore likely inefficient, hence contrasting with the PL reported in Figure 4a. Nevertheless, this is not always the case, with reports of PL external quantum efficiency for textured silicon wafers being on the order of 6% at room temperature.⁶⁷

Even so, we note that while the present argument would hold for the case of a 3D double perovskite, it already does not parallel the case of the n = 2 layered system, with the computed energy difference between the direct and indirect band gaps (18 meV) now being much smaller than the measured Stokes shift (around 500 meV at room temperature). Finally, the intervalley recombination argument totally fails in describing the case of the n = 1 layered compound, which has direct band gap at Γ (Figure 3b) but still shows sizable red-shifted emission, with a Stokes shift ranging from 250 to 450 meV with temperature. We further stress that the measured PLQYs for the different materials in Figure 4d anticorrelates with respect to the computed direct/indirect character of the band structure, with more effective emission being associated with indirect semiconductors. Overall, we conclude that either the intervalley recombination is not responsible for the Stokes shift observed in these 3D and layered double-perovskite compounds or the mechanism at the basis of the Stokes shift is different for the 3D material and its layered analogues, with the former supporting intervalley recombination while the latter presenting different relaxation mechanisms for the photogenerated charge carriers (vide infra).

Self-Trapping Due to Lattice Vibrations

The photogeneration of free carriers or of electron–hole pairs may instead result in perturbation of the electronic forces holding the crystal lattice together. In this case, after the vertical excitation takes place in the equilibrium configuration of the ground state, the lattice relaxes toward a new equilibrium configuration associated with the photogenerated excited state. The magnitude of this geometric relaxation effect depends on the softness of the lattice together with the strength of the electron–phonon interaction. For 3D Cs₂AgBiBr₆ double perovskites, a large Fröhlich coupling constant^30,68 (γ_LO = 228 meV³⁰) and Huang–Rhys factor (S = 11.7⁶⁴) have been reported thus far, hence suggesting strong relaxation via Fröhlich phonon coupling and deformation of potential coupling mechanisms, respectively. These findings contrast again with the case of both 3D and layered lead-based HPs, where several investigations point toward weak coupling between the electronic structure and the lattice. For 3D MAPbI₃, Wright and co-workers have estimated couplings on the order of 12 meV between the electronic structure and longitudinal optical phonons, with a total Frölich coupling constant ranging between 40 and 61 meV for formammidinium lead iodide and bromide, respectively.⁶⁹ Similar findings have also been reported for layered 2D butylammonium and phenylethylammonium lead iodide perovskites, with Thouin and co-workers highlighting a total electron–phonon coupling of around 45 meV within the deformation of potential mechanism,⁶² which compares well with the overall small Stokes shift measured in these compounds.

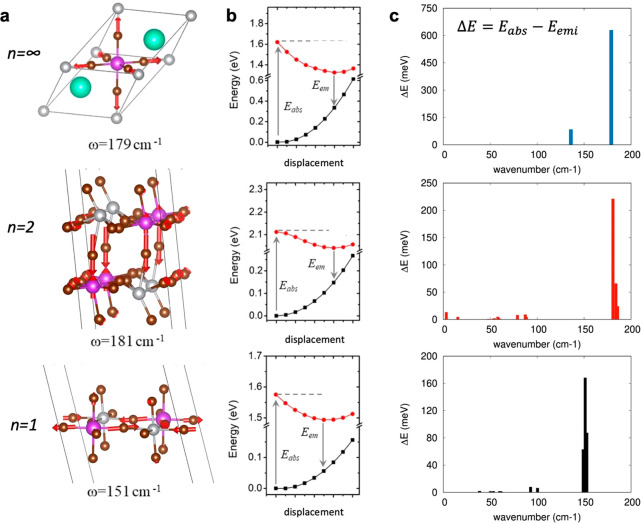
To investigate self-trapping as a potential mechanism related to the Stokes-shifted emission in double-perovskite materials, we first performed Raman measurements for both the layered and 3D compounds (Figure 5). Our results for the 3D material parallel those from Zelewski and co-workers,⁶⁴ with the Raman spectrum dominated by one peak at 180 cm^–1 and another peak at around 75 cm^–1, the former being assigned to the total-symmetric breathing mode of the [MX]₆ octahedron while the second is assigned to a T_2g irreducible representation. These authors also found a Raman-active feature at 139 cm^–1, which in Figure 5 is hidden behind the broadened line shape of the dominating peak at 180 cm^–1. The spectra of our newly reported PeABr1 and PeABr2 materials are similar to that of the parental 3D compound, with one dominating signal around 150–180 cm^–1 and two weaker signals at 75 and 140 cm^–1. It is worth noting that the frequency of the main peak associated with the [MX]₆ breathing mode is modulated by the thickness of the inorganic frame, shifting toward larger frequencies for the thicker PeABr2 and Cs₂AgBiBr₆ materials. However, as in the case of optical absorption, the blue shift of this signal rapidly saturates with the thickness of the perovskite layer, with PeABr2 and Cs₂AgBiBr₆ both falling at 180 cm^–1.

Figure 5.

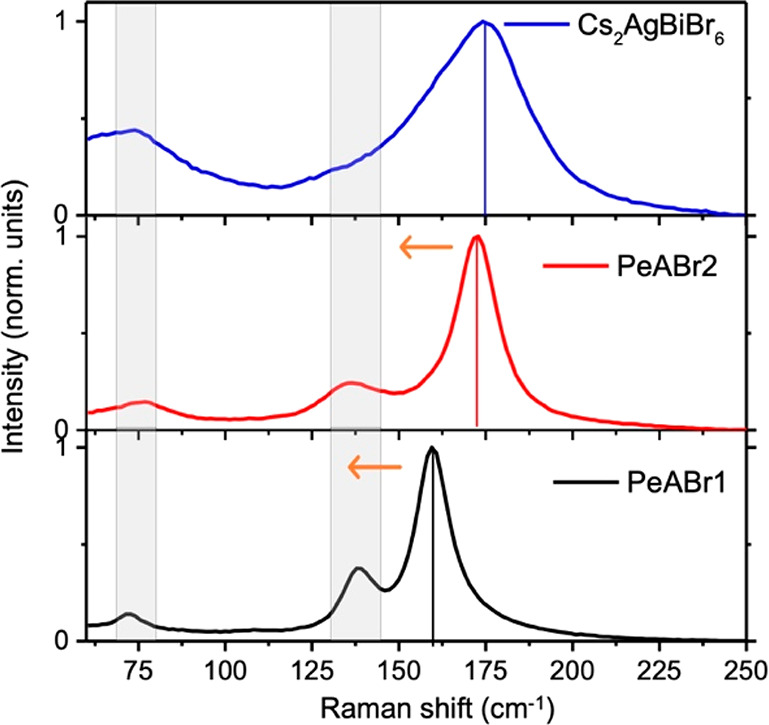
Raman spectra measured on thin films of the 3D Cs₂AgBiBr₆ double perovskite and layered PeABr2 (n = 2) and PeABr1 (n = 1) compounds. Measurements were performed at room temperature using a 532 nm laser.

Raman-active vibrations, such as those in Figure 5, may interact with the electronic structure via the deformation of potential mechanism,⁷⁰ mediating the structural relaxation from the ground-state equilibrium structure (departure structure following vertical excitation, as related to the Franck–Condon principle) to the equilibrium structure in the excited state. To investigate along this line, we performed electronic structure simulations in the same spirit of what was proposed by Thouin et al. for lead-based layered systems,⁶² by Zelewski et al. for Cs₂AgBiBr₆ double perovskite,⁶⁴ and by Luo et al. for Cs₂AgInCl₆ double perovskite.³³ Namely, we computed the normal modes of vibrations at the center of the Brillouin zone, for both the 3D and the layered double-perovskite compounds and we then explored the ground- and lowest-excited state potential energy surfaces (PES) along the computed normal modes (all details are reported in Computational Methods). The PES of the ground state is routinely obtained from DFT snapshots performed by distorting the crystal structure along each normal mode. For the lowest excited state, instead, excitonic effects highlighted in Figure 3c complicate the estimation of the corresponding PES, as the distortion along the normal modes may affect also the exciton binding energy, in addition to the expected influence on the single particle band gap. While the latter contribution is promptly accessible from DFT calculations, the potential variation of the exciton binding energy requires more involved computational schemes (such as the ab initio solution BSE reported in Figure 3c), which on the other hand becomes very cumbersome, considering the need of exploring multiple structures. We then first assumed that the exciton binding energy is not influenced by the structural distortion along the various normal modes and remains constant. The corresponding ground and lowest excited state PES for the Cs₂AgBiBr₆ compound along the dominating Raman mode at 179 cm^—1 is reported in Figure 6, together with the corresponding structural distortion pattern. Following the deformation of the crystalline structure along the normal mode, the emission energy decreases, and the corresponding Stokes shift increases, because of a stabilization of the excited state accompanied by a destabilization of the ground state; the total energy relaxation ΔE between vertical absorption and emission amounts to 630 meV. Summing up the contributions from the total-symmetric mode and from the degenerate E_g modes computed at 136 cm^–1, we find a total relaxation energy of 795 meV, nicely matching the measured 750 meV Stokes shift.⁶⁸ This result therefore supports self-trapping as a potential mechanism dictating the emission in Cs₂AgBiBr₆ alternative to intervalley recombination. We now come back to the validity of considering constant exciton binding energy, which for Cs₂AgBiBr₆ can be checked by solving the BSE equation along the normal modes at 179 cm^–1 and at 136 cm^–1. The corresponding excited state PESs reported in the Supporting Information, as estimated neglecting and including excitonic effects, closely follow each other (apart from a rigid shift related to a constant exciton binding energy), hence fully justifying the assumption above.

Figure 6.

(a) Displacement pattern for the computed vibrational modes with frequencies closer to the most intense Raman bands in Figure 5. (b) Corresponding ground (black)- and excited-state (red) PESs along the normal mode in (a). The Stokes shift was obtained from the difference between the absorption energy (E_abs) and the emission energy (E_em), with the total relaxation energy ΔE given as E_abs – E_em. (c) Contribution from all vibrational modes to the total relaxation energy ΔE.

In the n = 2 compound, the symmetry reduction from the Fm3̅m to the P1̅ space group results in less defined vibrational displacement patterns, with the intense Raman signal found experimentally associated with the off-centering of bismuth and of the central bromine, as shown in Figure 6a. This mode contributes a ΔE value of 219 meV (see Figure 6b), with the total relaxation energy ΔE from all the vibrational modes (376 meV) semiquantitatively matching the measured Stokes shift (500 meV). For the n = 1 PeABr1 compound, a set of vibrational modes resembling [MX]₆ octahedral breathing is found, with that in Figure 6a featuring a ΔE value of 168 meV. Also in this case, the total relaxation energy obtained on summing the contributions from all the vibrational modes amounts to 343 meV, in reasonably good agreement with the measured Stokes shift of 250 meV. The full list of computed vibrational frequencies and corresponding ΔE values is reported in the Supporting Information. Note that the verification of potential oscillations of the exciton binding energy in layered compounds may be ideally applied but is complicated here by the need to substitute the organic spacers with Cs atoms, as required to make the BSE simulations computationally affordable. For the n = 2 perovskite, in fact, the difference in the excited-state PESs evaluated with and without exciton effects clearly indicates a variable exciton binding energy along the normal mode at 181 cm^–1 (see the Supporting Information). However, this result should be considered in light of the lack of dielectric contrast, associated with the different polarizability of Cs atoms in comparison to the actual PeA spacer.⁵⁹ For the n = 1 case, instead, even the ground state PES (see the Supporting Information) differs from that reported in Figure 6, hence indicating that the organic spacer plays an important role in dictating the energetics of the system, at least along the selected normal mode.

Discussion and Conclusions

We have designed novel 2D layered double-HP compounds incorporating phenylethylammonium as an organic spacer, namely, n = 1 (PEA)₄AgBiBr₈ and n = 2 (PEA)₂CsAgBiBr₇, with XRD measurements confirming the formation of the targeted layered perovskite structure. While the n = 1 compound was reported in very recent literature,³⁸ the n = 2 compound, incorporating PEA, is reported here for the first time. Optical spectroscopic measurements confirm the limited effect of quantum confinement in tuning the optical absorption wavelength of these materials, with a blue shift from the 3D reference to the thinnest layered n = 1 compound that amounts to only ca. 250 meV. On the other hand, our PL measurements reveal emission not only from the n = 1 but also from the n = 2 material, hence demonstrating the general capability of the AgBiBr₆ network to emit light, irrespective of the degree of quantum confinement, although with limited efficiency, at least in the case of our nonoptimized thin films. Most notably, the light-emission efficiency is found to anticorrelate with the nature of the band gap: that is, the indirect 3D and n = 2 perovskites are more emissive.

In an effort to provide a global rationale to these findings, we performed atomistic simulations, which first confirmed the likely formation of excitons not only in the spatially confined 2D materials but also in the parental 3D Cs₂AgBiBr₆ lattice.^20,21 Most important, first-principles calculations also demonstrate the inherently “soft” character of the double-perovskite lattice and the substantial ionic reorganization upon photoexcitation. In this framework, the inherent excitonic character of the double perovskites explains the overall limited influence of quantum confinement on their corresponding optical absorption, as the primary photogenerated species are strongly bound and have spatially confined electron–hole pairs, thus being far less sensitive to dimensional confinement effects. The large measured Stokes shift is in accordance with the picture prevailing in organics, where massive lattice reorganization occurs around the photogenerated excitons. This strongly contrasts with respect to the case of 3D lead-based halide perovskites, where lattice relaxation effects have been demonstrated to be much smaller.^60,61,67 The emerging picture is therefore that, in spite of sharing the same crystal structure as lead-based halide perovskites, double-perovskite semiconductors resemble more closely traditional organic semiconductors, for which (i) the optical response is dominated by stable electron–hole excitonic pairs rather than by free charges, both for the bulk 3D phase and for dimensionally confined analogues, and (ii) the exciton formation is followed by a large local structural reorganization, as described by the Holstein excitonic model.^80,81 The formation of excitons upon photoexcitation and the consequent large local structural reorganization dominate the optical response.

We believe the present work represents a leap forward in understanding the electronic and optical properties of double HPs and will motivate further studies, from both the experimental and theoretical sides, with the aim of pushing these materials into nontoxic, high-impact optoelectronic applications. In particular, from a technological innovation perspective, the present findings point out the inherent limitations of double perovskites for display applications. This is due to the limited color tunability of the emitted light via quantum confinement and large broadening, which are intrinsic material properties. On the other hand, these findings encourage the exploitation of double perovskites as white-light emitters. From a materials design perspective, the present findings also show that the current conceptual strategy of substituting the metal site while keeping the perovskite structure may induce important modifications of the optical and electronic properties of the targeted material, going well beyond the single particle band structure and direct/indirect gap character.

Experimental Methods

Single-Crystal Formation

To obtain PeABr1 single crystals, phenylethylamine bromide (PeABr, 2 mmol), bismuth bromide (BiBr₃, 0.5 mmol), and silver bromide (AgBr, 0.5 mmol) were dissolved in 4 mL of hydrobromic acid (HBr) at 100 °C. For PeABr2, phenylethylamine bromide (PeABr, 1 mmol), bismuth bromide (BiBr₃, 0.5 mmol), silver bromide (AgBr, 0.5 mmol), and cesium bromide (CsBr, 0.4 mmol) were dissolved in 4 mL of hydrobromic acid (HBr) at 100 °C. The solution was saturated and kept at 100 °C for 1 h until all compounds were dissolved. The single crystals were prepared by growing from a saturated aqueous HBr solution by cooling the solution at a cooling rate of 3 °C/h. The as-obtained yellow crystals were filtered, and after filtration, the crystals were washed with diethyl ether and dried in a vacuum oven at room temperature overnight.

Thin-Film Preparation

The solutions for the thin films were prepared by dissolving the starting materials BiBr₃, AgBr, and PeABr in DMF for n = 1 (PeABr1) and in DMSO for n = 2 (PeABr2) with the addition of CsBr and a final concentration of 0.5 mol/L. Thin films were prepared by spin-coating deposition, using a two-step program, first at 500 rpm for 30 s and second at 5000 rpm for 60 s. All films were then annealed at 100 °C for 4 min (see images of the resulting films in Figure S1b for PeABr2 and Figure S1c for PeABr1), with the SEM images showing the particles of the new materials to have a needle shape. The XRD diffractogram is presented in Figure S1, showing the main reflectances (001), (002), and (003) at low angles matching with the single-crystal XRD data reported in Figure 1c. In agreement, a peak shift appears to lower diffraction angles on going from n = 1 to n = 2.

X-ray Diffraction (XRD) Measurements

Samples were investigated with X-ray diffraction at room temperature (prepared thin films) and at 260 K (single crystals). Powder XRD was carried out using a Bruker D8 Advance diffractometer equipped with a Lynxeye XE detector, using a nonmonochromated (Kα) Cu source in a Bragg–Brentano geometry, between 10 and 70° 2θ. Single-crystal diffraction was performed on a Bruker D8 Venture diffractometer, equipped with a Photon 100 detector, using Mo Kα radiation. Samples were not cooled below 260 K due to the potential of crystal cracking or phase transformation. Diffraction data were reduced to correct with Apex 3 and the associated tools; crystal structures were solved with ShelXT and refined with ShelXL using Olex2. The refinements were stabilized using restraints where necessary. Crystallographic data were deposited with the Cambridge Crystallographic Data Centre and correspond to the following codes: PEA₄AgBiBr₈ (2088920) and PEA₂CsAgBiBr₇ (2088919).

Photoluminescence/Absorption: Room and Low Temperature

Steady-state absorption spectra were acquired with a Perkin-Elmer Lambda 950s UV/vis spectrophotometer using an integrating sphere to account for optical losses outside of the active layer. Photoluminescence spectra of the perovskite thin films were measured and recorded using a Fluorolog3-22 spectrofluorometer. The spectra were recorded upon excitation at 450 nm.

Absolute Photoluminescence

Excitation for the PL measurements was performed with a 445 nm continuous wave laser (Insaneware) through an optical fiber into an integrating sphere. A second optical fiber was used from the output of the integrating sphere to an Andor SR393i-B spectrometer equipped with a silicon charge-coupled-device camera (DU420A-BR-DD, iDus). The system was calibrated by using a calibrated halogen lamp with specified spectral irradiance, which was shone into the integrating sphere. A spectral correction factor was established to match the spectral output of the detector with the calibrated spectral irradiance of the lamp. The spectral photon density was obtained from the corrected detector signal (spectral irradiance) by division through the photon energy (hf) and the photon numbers of the excitation and emission obtained from numerical integration using Matlab. For the PLQY we have used the same density of photons absorbed, retrieved from the absorption coefficient from the absorption spectra of each sample at 445 nm (by applying the Lambert–Beer law). The spot area on the sample was around 1 cm². This enabled us to take into consideration the density of photons absorbed by the material and an exact comparative analysis among the different samples.

Raman Measurements

The micro Raman system is based on an optical microscope (Renishaw microscope, equipped with 5×, 20×, 50×, and 100× short- and long-working-distance microscope objectives) used to focus the excitation light and collect it in a backscattering configuration, a monochromator, a notch filter system, and a charge-coupled detector. The sample was mounted on a translation stage of a Leica microscope. The excitation used consisted of a diode laser at 532 nm. The system was calibrated against the 520.5 cm^–1 line of an internal silicon wafer. The spectra were registered in the 60–300 cm^–1 range, which is particularly sensitive to the metal-halide modes. The final data were averaged over 10 accumulations in order to maximize the signal to noise ratio. The measurements were conducted at room temperature and in air. The laser power intensity was kept on the order of 300 W/cm² in order to avoid any sample degradation effects.

Computational Methods

Ground-State DFT Simulations

Periodic boundary electronic-structure simulations were performed within the plane-wave/pseudopotential framework, as implemented in the Quantum-Espresso suite.⁷¹ Relaxation of the atomic positions (with cell parameters fixed to the experimental values) and single-point band structure calculations were performed byadopting the Perdew–Burke–Ernzerhof (PBE) functional,⁷² along with a 60 Ry cutoff for the plane-wave expansion and norm-conserving pseudopotentials. D2 Grimme corrections⁷³ were included in atomic relaxations, to account for van der Waals interactions, which are expected to play a role in determining the packing of the organic spacer. Spin–orbit coupling (SOC) was included for band structure calculations, as it is known to be especially relevant for the states in the vicinity of the CB edge due to the splitting of the j = 1/2 and j = 3/2 total angular momenta of the 6p Bi states.^15,28 Automatic sampling of the first Brillouin zone was adopted with the Monkhorst–Pack scheme, with 10 × 10 × 10 and 4 × 4 × 1 grids for the 3D and layered 2D compounds, respectively (the less dense sampling being associated with the plane-stacking direction).

Additional hybrid DFT calculations were performed by adopting the PBE0 exchange-correlation functional for an accurate estimation of the single-particle band gaps. These were performed byemploying the VASP code, adopting a coarser 2 × 2 × 1 sampling of the Brillouin zone and a smaller value of the plane-wave cutoff of 50 Ry, in view of the immense computational hurdle associated with the use of hybrid DFT.

Excited-State Properties

The excited-state properties of the studied compounds have been investigated by solving the model Bethe–Salpeter equation^74,75 (mBSE) as it is implemented in the VASP 6.1.0 package. A plane-wave cutoff of 44 Ry (600 eV) and projected augmented wave method (PAW) PPs were used, with SOC fully included. The BSE calculations were solved within the Tamm–Dancoff approximation (TDA).⁷⁶ We used a total of 64 k-points in the Monkhorst–Pack scheme⁷⁷ for the three materials, which is translated in k-samplings of 4 × 4 × 4 for the bulk and 8 × 8 × 1 for the layered systems. While for the bulk this k-sampling assured the convergence of the results,^14,21 in the case of the layered double perovskites, we adopted a reciprocal space partition similar to that used in a former work done with layered lead HPs.⁷⁸ A total number of 1120 bands was used in our calculations, which ensured the presence of empty states up to 40 eV above the VBM. We employed 20 occupied and 10 unoccupied states in the computation of the dielectric function, due to the presence of a large number of valence bands in the vicinity of the edge.

Vibrational Properties and Electron–Phonon Interactions in the Deformation of Potential Mechanism

Normal modes of vibration were obtained by the finite-displacement method adopting the PHONOPY program to generate the displaced structures and to collect the results for the evaluation of the Hessian,⁷⁹ while the Quantum Espresso suite software⁷¹ was used for the explicit evaluation of the forces and energies. The real-space Hessian was evaluated on a 2 × 2 × 2 supercell of the conventional cell of the 3D Cs₂AgBiBr₆ double perovskites (320 atoms, similar to what was done in ref (21)) and on 2 × 2 × 1 supercells of the cells of PeABr1 and PeABr2 (752 and 416 atoms, respectively). DFT self-consistent-field calculations were therefore performed by adopting the PBE exchange-correlation functional, along with ultrasoft pseudopotentials and plane-wave/electron density cutoffs of 25/200. All calculations were performed at the Γ point of the Brillouin zone, imposing an accurate convergence threshold of 10^–9 Ry, as was required to obtain accurate forces.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.1c00429.

• Additional experimental data (XRD, SEM, PL) and additional computational analyses (PDF)

Author Contributions

^∇ M.P. and V.D.-C. contributed equally to the paper.

The authors declare no competing financial interest.