Spectral parameterization for studying neurodevelopment: How and why

Abstract

A growing body of literature suggests that the explicit parameterization of neural power spectra is important for the appropriate physiological interpretation of periodic and aperiodic electroencephalogram (EEG) activity. In this paper, we discuss why parameterization is an imperative step for developmental cognitive neuroscientists interested in cognition and behavior across the lifespan, as well as how parameterization can be readily accomplished with an automated spectral parameterization (“specparam”) algorithm (Donoghue et al., 2020a). We provide annotated code for power spectral parameterization, via specparam, in Jupyter Notebook and R Studio. We then apply this algorithm to EEG data in childhood (N = 60; M_age = 9.97, SD = 0.95) to illustrate its utility for developmental cognitive neuroscientists. Ultimately, the explicit parameterization of EEG power spectra may help us refine our understanding of how dynamic neural communication contributes to normative and aberrant cognition across the lifespan. Data and annotated analysis code for this manuscript are available on GitHub as a supplement to the open-access specparam toolbox.

Highlights

• •Electroencephalogram (EEG) is comprised of periodic and aperiodic activity.
• •Specparam is an open-access toolbox that disentangles power spectral features.
• •We provide a step-by-step guide to using specparam in Jupyter Notebook and R Studio.
• •This method may foster new insight into cognition from infancy through old age.

1. Parameterizing neural power spectra: developmental considerations

Dynamic neural communication is essential to cognitive development. Neurophysiological signals consist of periodic (putative oscillations) and aperiodic (exponent, offset) components that are dynamic and physiologically distinct, and are thought to reflect neural communication (Donoghue et al., 2020a, He, 2014, Voytek and Knight, 2015). The inherent overlap of periodic and aperiodic components necessitates quantification that separates the signal to ensure that the observed neural activity is attributed to the appropriate physiological mechanism. Many canonical analysis approaches, such as analyzing pre-defined oscillation bands, may conflate, bias, and misrepresent these different components. As a result, developmental cognitive neuroscientists may be less likely to isolate and understand the mechanisms driving constructs of interests over time.

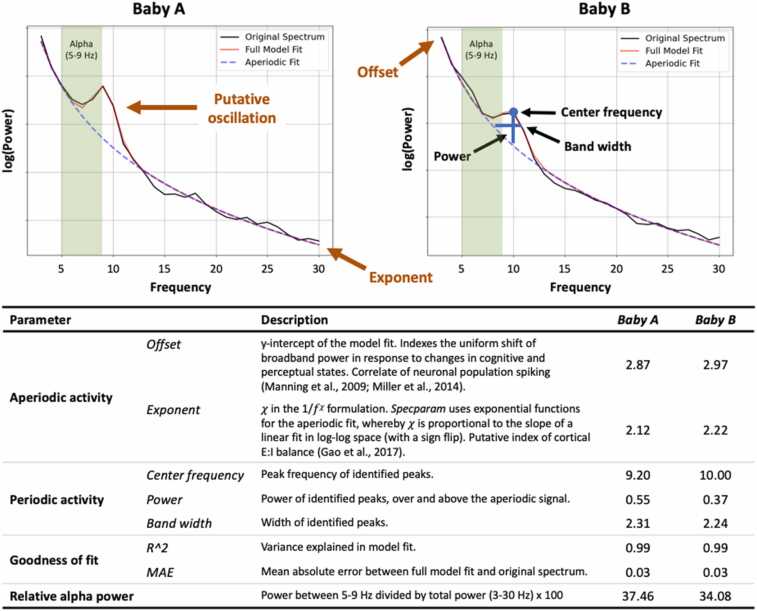
An example illustrating the importance of explicit parameterization can be seen in Fig. 1. In this case, Baby A and Baby B, both approximately 18-months of age, exhibit alpha activity during a resting baseline recording. Using a traditional (non-parameterized) approach based on the canonical alpha frequency band (5–9 Hz in infants), we may conclude that the Baby B has lower relative alpha power compared to the Baby A, when in fact the difference is in peak frequency. It is worth noting that the canonical frequency band may not appropriately capture alpha activity for these infants, as peak frequency of the putative alpha oscillation for both Baby A and Baby B falls outside the commonly-used frequency range. In addition, using the traditional approach, it is unclear whether these infants differ in regards to aperiodic activity, which could conflate estimates of the periodic activity (Donoghue et al., 2020b, He et al., 2019). This inaccurate information could then be used to predict a behavioral outcome (e.g., lower alpha power is associated with less fearfulness), ultimately obscuring real brain-behavior associations because we failed to take a valid measurement of periodic activity.

Fig. 1.

Periodic and aperiodic power spectral components can differ between individuals, exemplified here by two 18-month old infants who differ in alpha activity. EEG data were recorded at central midline (Cz) during a resting baseline. Algorithm settings were set as: peak width limits: [2,8]; max number of peaks: 6; minimum peak height: 0.05; peak threshold: 2; aperiodic mode: fixed. Power spectra were parameterized across the frequency range 3–30 Hz. Relative alpha power is expressed as the percentage of power in the canonical frequency band for this age group (5–9 Hz) relative to total power across frequencies (3–30 Hz).

Instead, a more appropriate conclusion based on parameterized power spectral data is that Baby B had a higher alpha center frequency, suggesting relatively more cortical maturation (Marshall et al., 2002), as well as a slightly larger aperiodic offset and exponent relative to Baby A. On the other hand, Baby A exhibited more alpha power during the resting baseline relative to Baby B. Without explicit parameterization of power spectral features, rich physiological information on key indicators of normative and aberrant neurodevelopment may be lost.

With this need in mind, Donoghue et al. (2020a) introduced an automated method for parameterizing neural power spectra to disentangle periodic and aperiodic spectral features. This spectral parameterization (“specparam”) algorithm1 fits components of power spectral densities (PSDs) in an efficient and physiologically-informed manner, while remaining agnostic to predefined canonical frequency bands.

In this paper, we provide a step-by-step tutorial to showcase the utility of parameterizing electroencephalogram (EEG) power spectra via specparam in pediatric samples. Moreover, we discuss the importance of spectral parameterization for advancing the field of developmental cognitive neuroscience, emphasizing the role of the aperiodic signal in biasing the measurement of putative oscillations. Many of our examples focus on normative aging and neurodevelopmental disorders to highlight the utility of careful parameterization of neural power spectra across the lifespan. We do not intend to comprehensively describe developmental research on oscillatory neural activity, but instead select examples that illustrate key interpretive questions about the role of periodic versus aperiodic activity. Indeed, growing interest in the aperiodic exponent has shown that it is a physiologically distinct spectral component with important links to development and psychopathology in its own right (e.g., Molina et al., 2020; Tran et al., 2020). Data and annotated analysis code are available on GitHub (https://github.com/fooof-tools/DevelopmentalDemo) as a supplement to the open-access specparam toolbox (Donoghue et al., 2020a). The specparam website includes detailed information about the algorithm and its many utilities (https://specparam-tools.github.io).

1.1. Aperiodic activity

Aperiodic activity refers to the arrhythmic component of neural field data, such as the EEG signal, which contributes power across all frequencies (He, 2014, Freeman and Zhai, 2009). Explicit parameterization of the aperiodic signal has challenged prevailing assumptions regarding the physiological underpinnings of cognitive and behavioral health and dysfunction by showing how aperiodic activity uniquely relates to cognitive, developmental, and clinical measures of interest (González-Villar et al., 2017, He et al., 2019, Molina et al., 2020, Robertson et al., 2019, Tran et al., 2020).

Aperiodic activity is characterized by an exponential decrease in power across increasing frequencies that follows approximately a 1/f distribution. This “1/f-like” characteristic can be described by two parameters: the aperiodic ‘offset’, which describes the broadband offset of the spectrum and the aperiodic exponent, defined as the $\chi$ in the 1/$f^{\chi }$ formulation, which describes the pattern of power across frequencies (Donoghue et al., 2020a). Animal and computational models have proposed that the aperiodic exponent may be a noninvasive index of the balance of excitation and inhibition (E:I) in cortical circuits (Gao et al., 2017). In this case, a smaller exponent reflects a broadband flattening of the PSD, signifying a shift away from cortical inhibition (E > I), while a larger exponent indicates the opposite pattern of activation (E < I). Practically, emerging evidence suggests that the aperiodic exponent systematically relates to perceptual and cognitive behaviors, such as working memory performance (Donoghue et al., 2020a; Podvalny et al., 2015; Waschke et al., 2020).

1.1.1. Aperiodic exponent and normative aging

Converging evidence suggests that the aperiodic exponent decreases with age, and may account for a normative redistribution of spectral power from lower to higher frequencies over time (He et al., 2019). In adulthood, older individuals consistently display flatter PSDs (smaller exponents and less cortical inhibition) relative to their younger peers (Tran et al., 2020, Waschke et al., 2017, Voytek et al., 2015). A similar pattern emerges when considering adults and children, with older individuals (23–58 years old) showing flatter PSDs compared to school-aged children (5–10 years old) (He et al., 2019).

Only two studies to date have examined the aperiodic exponent in infancy. Using cross-sectional data, Karalunas et al. (2021) observed that exponents were smaller (flatter PSDs) in adolescents relative to infants. Using longitudinal data, Schaworonkow and Voytek (2021) observed a progressive flattening of power spectra among infants across the first months of life. Psychometrically, the exponent has been shown to have high internal consistency in infancy and adolescence (Karalunas et al., 2021), as well as good test-retest reliability in adulthood (Pathania et al., 2021) and among children with autism spectrum disorder (Levin et al., 2020). While studies suggest good signal reliability, it is important to note that it would be difficult to compare aperiodic parameters across participants when different recording systems are used, or in different environments, due to the fact that measurement noise is also often 1/f in nature (He et al., 2010, Miller et al., 2009). Together, findings to date indicate that the exponent is a reliable neural signature that decreases in an approximately linear manner across development, possibly contributing to age-related changes in cognitive function (e.g., Tran et al., 2020).

1.1.2. Aperiodic exponent and neurodevelopmental disorders

Crucially, the exponent may offer insight into a physiological mechanism that contributes to disrupted information processing among neurodevelopmental disorders, chiefly, attention deficit/hyperactivity disorder (ADHD) (Ostlund et al., 2021, Robertson et al., 2019), autism (Levin et al., 2020), schizophrenia (Molina et al., 2020), and Fragile X Syndrome (Wilkinson and Nelson, 2021). For instance, the balance of excitatory (glutamatergic) and inhibitory (GABAergic) influences appears critical for attention control, and has thus been implicated as a putative mechanism contributing to ADHD (Mamiya et al., 2021). Clinical and animal models point to altered GABAergic and glutamatergic activity among individuals with ADHD (Edden et al., 2012, Hammerness et al., 2012; Zimmermann et al., 2015), indicating that E:I imbalance in cortical circuits may be a core dysfunction for this population (Mamiya et al., 2021). Findings from Ostlund et al. (2021) lend support for this hypothesis, showing that adolescents (11–17 years old) with ADHD had smaller exponents (flatter PSDs), compared to their typically-developing peers. This flattening suggests an atypical E:I balance in developing cortical circuits, namely, a shift away from cortical inhibition.

Though promising, a recent study from Robertson et al. (2019) with younger children (3–7 years old) found the opposite pattern: children with ADHD had larger exponents compared to their typically-developing peers. In addition, larger exponents were only characteristic of children who were stimulant medication-naïve. This group had larger exponents (steeper PSDs) compared to both typically-developing peers and children with ADHD who were prescribed stimulant medication but had undergone a 24-hour medication washout prior to the EEG recording. Findings raised at least two major questions: (1) is the power spectrum among children with ADHD steeper or flatter compared to children without ADHD? and (2) are the patterns dependent on stimulant treatment history?

To reconcile inconsistent findings, Karalunas et al. (2021) examined the aperiodic exponents of infants (M_weeks = 6.08, SD = 1.67) and adolescents (11–17 years old) at high familial risk for, or currently diagnosed with, ADHD, respectively, in relation to their typically-developing peers.2 Compared to their same-aged typically-developing peers, adolescents with ADHD had smaller exponents, but effects were moderated by lifetime history of stimulant treatment. Specifically, only adolescents with ADHD and no history of stimulant treatment had smaller exponents than their typically-developing peers. In addition, during infancy high familial risk for ADHD was associated with larger exponents. These results mirror discrepant findings reported by Robertson et al. (2019) and Ostlund et al. (2021), pointing to a potential developmental effect among children at-risk for ADHD, which may help understand symptom and functional trajectories.

To this end, Karalunas and colleagues posited that neurodevelopmental risk for ADHD may be characterized by a differential rate in the normative broadband flattening of neural power spectra across development. This pattern may be normalized with pharmacological intervention (e.g., methylphenidate medications such as Ritalin; Pertermann et al., 2019), given that results were specific to medication-naïve children (Karalunas et al., 2021, Robertson et al., 2019; see Molina et al., 2020 for E:I normalization among individuals with schizophrenia), and is consistent with changes in GABA and glutamate concentrations for individuals with ADHD across the lifespan (Mamiya et al., 2021). This provocative hypothesis warrants further examination in longitudinal samples, and motivates the importance of applying analyses such as spectral parameterization in developmental samples in order to differentiate periodic and aperiodic activity and understand their relations to behaviors of interest.

1.1.3. Aperiodic offset

The offset—an aperiodic parameter that indexes the uniform shift of broadband power in response to changes in cognitive and perceptual states—has received relatively less attention than the exponent, despite being a correlate of neuronal population spiking (Manning et al., 2009, Miller et al., 2014) and the blood oxygenated level dependent (BOLD) signal from functional magnetic resonance imaging (fMRI) (Winawer et al., 2013). The offset parameter has shown fair test-retest reliability among typically-developing children as well as children with autism (Levin et al., 2020). Developmentally, He et al. (2019) have shown that the aperiodic offset is smaller in adults relative to children. These authors also found that the offset is negatively correlated with age in childhood, an effect that was marginal among adults. Overall, these results are consistent with other neurophysiological findings showing age-related reductions in broadband power (e.g., Gómez et al., 2017; Rodríguez-Martínez et al., 2017). To this end, medication-naïve young children with ADHD have larger offsets compared to their typically-developing peers and stimulant-treated children with ADHD who underwent a 24-hour medication washout (Robertson et al., 2019), consistent with the neurodevelopmental nature of the disorder.

It is important to note that any exponent change, if it rotates the spectrum around a non-zero frequency, will also lead to a change in offset. Thus, the offset and exponent are often highly correlated.

1.2. Periodic activity

Periodic activity refers to the rhythmic component of the EEG signal that rises above the aperiodic exponent, indexing putative neural oscillations, visible as peaks in the power spectrum (Buzsaki et al., 2013). The distribution of power across frequencies is traditionally divided into fixed frequency bands that, in adults, are typically approximately defined as delta (0.1–4 Hz), theta (4–8 Hz), alpha (8–13 Hz), beta (13–30 Hz), and gamma (30–80 Hz) (Pernet et al., 2020). It is worth noting that studies vary in their definition of the frequency range over which the canonical bands are estimated, particularly when considering pediatric samples, raising practical challenges for comparing results between studies.

Across the lifespan, band-limited power is an established correlate of cognition, emotionality, and behavior. Since research on band-limited power in childhood has been discussed extensively, a comprehensive review of this literature is beyond the scope of this paper (see e.g., Saby and Marshall, 2012 for review). The frequency ranges that define these narrow bands shift with age (e.g., Marshall et al., 2002). More specifically, with advancing age, power in the lower frequency range (< 20 Hz) tends to decrease, whereas power in the higher frequencies range (> 40 Hz) tends to increase. Recent evidence suggests that this age-related redistribution of power may reflect normative change in aperiodic activity with aging (Donoghue et al., 2020a, He et al., 2019, Tran et al., 2020), observed as a broadband “see-saw” rotation of the power spectrum as a result of changes in the aperiodic signal (Voytek and Knight, 2015).

Notably, few studies have explicitly parameterized the neural power spectra to account for aperiodic activity, which may bias estimations of narrowband power, consequently affecting physiological interpretations of cognition and behavior in childhood. The importance of this issue is exemplified in a recent study by Donoghue et al. (2020b), who examined whether band ratio measures (e.g., theta/beta, theta/alpha) were conflated by the aperiodic signal. Historically, researchers have used band ratio measures to understand individual differences in development, cognition, and psychopathology risk (e.g., Loo and Makeig, 2012). The suggestion is that an increased theta/beta ratio reflects more subcortical (relative to cortical) involvement, which may impede inhibitory control (e.g., Angelidis et al., 2016). Thus, theta/beta and other low/high frequency ratio measures have been of interest in neurodevelopmental disorders, such as ADHD, where inhibitory control is impaired. However, using real and simulated EEG data, Donoghue et al. (2020b) demonstrated that band ratio measures, particularly the theta/beta ratio, were conflated with the aperiodic signal. These findings raise questions regarding the utility of band ratio measures specifically, as well as the interpretability of band-limited power estimates that do not account for aperiodic activity more broadly. The conflating of periodic and aperiodic activity may also help explain why research findings for theta/beta and similar metrics in ADHD have been equivocal at best (Arns et al., 2013, Loo and Arns, 2015, Loo et al., 2013), and help answer calls for alternative ways to quantify differences in the power spectrum in these clinical groups (Saad et al., 2018).

With this in mind, recent studies have begun to explore whether aperiodic-adjusted power measures change over development. Comparing children (5–10 years old) and adults (23–58 years old), He et al. (2019) replicated power differences in delta, theta, beta, and gamma activity that have been reported in prior studies. These findings suggest that neuronal activity within each canonical frequency band changes as a function of cortical maturation, which permits researchers to draw conclusions about how cognitive and behavioral correlates of these neural signatures may change across the lifespan. However, after accounting for the aperiodic signal, age-related increases in power were only observed in the canonical beta band, with adults exhibiting relatively greater peak beta power compared to children (He et al., 2019). These results lend support to the suggestion that the aperiodic signal conflates age-related changes in spectral power, and raise questions as to whether narrowband changes in cortical activity (calculated via standard methods) do in fact underpin observed age-related changes in cognition and behavior. Further investigation into the development of aperiodic-adjusted power, center frequency, and bandwidth of putative oscillations is necessary to clarify their role in cognitive and behavioral functioning across the lifespan.

Notably, whereas neural oscillations are an interesting and important feature of neural activity (Buzsaki et al., 2013), including in development (Saby and Marshall, 2012, Cellier et al., 2021), the presence of aperiodic activity and the complex properties of oscillatory activity requires care when estimating. As with the spectral parameterization approach described here, we direct the reader to Donoghue et al. (2021) for a detailed discussion of necessary considerations for detecting neural oscillations. For example, in the spectral domain, prominent rhythmic components in a time series will be reflected as a peak of power at the corresponding frequency. However, the reverse inference is not necessarily true–a peak in the spectral domain may reflect a harmonic of a non-sinusoidal rhythm. For example, a 10 Hz mu wave may exhibit a harmonic peak at 20 Hz in the spectrum despite there being no corresponding 20 Hz rhythmic activity. While we focus on spectral domain measures and representations here, we also note that specparam can be used in conjunction with time-domain analyses approaches which can provide alternate and complementary approaches to detecting the oscillatory activity, and examining oscillatory features such as waveform shape (e.g., Jones, 2016; Cole and Voytek, 2019).

2. A practical guide for using the specparam algorithm

Here, we briefly describe the specparam algorithm, along with considerations for the model fitting process. We then provide a step-by-step guide to fitting individual and group power spectra via specparam in Jupyter Notebook and R Studio, respectively. We selected these two programs due to their ease of use and familiarity among developmental cognitive neuroscientists for data analysis and visualization. Using real data from children, we fit the same individual and group power spectra in both programs. We direct the reader to Donoghue et al. (2020a) for information on algorithm performance with real and simulated EEG/MEG data. Although not discussed in this paper, a Matlab wrapper is available on the specparam website as well.

We recommend that users interested in this tutorial download the full code and data from the GitHub repository and follow the instructions in the ReadMe document when setting up their environment. Please check the repository for this project periodically for updates related to, among other things, future version releases and improvements in functionality.

2.1. Specparam algorithm

2.1.1. Model parameters

In specparam, PSDs are treated as a linear combination of aperiodic activity (in log-log space) and oscillatory peaks (individually modeled with a Gaussian) that rise above the aperiodic signal. The aperiodic component is initially fit across the observed frequency range and then removed from the raw PSD. The residual activity is iteratively fit as Gaussian functions and removed, up to a predefined noise threshold. Fitted oscillatory peaks are removed from the raw PSD, at which point aperiodic activity is re-fit. Lastly, the fit EEG signals are combined and goodness of fit assessed (Donoghue et al., 2020a). In the end, the algorithm provides information on periodic and aperiodic components of the EEG power spectra. Periodic parameters include center frequency (mean of the Gaussian), aperiodic-adjusted power (distance between Gaussian peak and aperiodic fit), and bandwidth (2 SD of the fitted Gaussian). Aperiodic parameters include the offset (y-intercept of model fit) and exponent ($\chi$ in the 1/$f^{\chi }$ model fit).

Specparam also provides two “goodness of fit” measures that describe how well the algorithm fit the data – R^2 and Mean Absolute Error (MAE), representing the explained variance and total error of the model fit, respectively. It is important that users evaluate model fit before interpreting data. We recommend including descriptive information for the goodness of fit parameters when reporting results to give other researchers a sense of the quality of the model fits. These measures can be used for quality control, for example, as a way to identify outlier spectra that are not well fit. Indeed, high error and low r-squared may reflect a poor fitting model, whereas exceptionally low error and high r-squared may reflect a model that is overfit. Though helpful, it is important to keep in mind that the model fitting process is not designed to directly optimize these goodness of fit measures, that is, provide low error and high r-squared. Rather, the algorithm aims to measure the aperiodic and periodic components in the most parsimonious manner. This optimization approach may at times result in over- or underfitting of power spectra. Further recommendations for reducing over- and underfitting are available on the specparam website.

2.1.2. Model fit settings

An overview of key parameterization settings for the fitting algorithm is presented in Table 1. One important consideration is whether to fit the aperiodic signal with a bend, or “knee” (aperiodic_mode, default = ‘fixed’), a common spectral feature in broad frequency ranges (see e.g., Miller et al., 2009) that might reflect the electrophysiological timescale of the underlying neural population activity (Gao et al., 2020). In specparam, the aperiodic signal is modeled as:

L = b – log(k +Fχ)

where b is the broadband offset, χ is the exponent, k is the ‘knee’ parameter, and F is a vector of input frequencies. We recommend that a user visually inspect spectral data across a broad frequency range to see if the putative aperiodic signal appears approximately linear (in log-log space). The ‘fixed’ mode (k = 0) is the default because the PSD is likely approximately linear over smaller frequency ranges (e.g., 3–35 Hz). Fitting with a knee may perform sub-optimally in ambiguous cases (where the data may or may not have a knee), or if no knee is present. The ‘fixed’ mode will not fit the data well if there is a clear knee in the power spectrum; in this case, use the ‘knee’ mode.

Table 1.

Brief overview of key settings for the specparam algorithm.

Setting	Units	Default	Description
peak_width_limits	Hz	[0.5, 12]	Limits on the bandwidth of extracted peaks.
max_n_peaks		infinite	Maximum number of peaks that can be extracted.
peak_threshold	Standard deviations	2	Threshold above which a data point must pass to be considered a candidate peak.
min_peak_height	Power	0	Minimum height, above aperiodic fit, that a peak must have to be extracted in the initial fit stage.
aperiodic_mode		‘fixed’	The mode for fitting the aperiodic component, i.e., fitting with or without a ‘knee’ parameter.

Another important consideration is whether to adjust the relative threshold for detecting peaks (peak_threshold, default = 2 standard deviations). In most cases, the default setting will be sufficient for identifying peaks above the aperiodic signal. The specparam algorithm allows a user to adjust a number of other parameterization settings as well, including limits on the possible bandwidth of extracted peaks (peak_width_limits), the maximum number of peaks (max_n_peaks), and minimum height above the aperiodic signal that a peak must be to be extracted in the initial fit (min_peak_height). A full description of all possible setting options can be found at the specparam website.

We suggest that researchers report their algorithm settings to aid the interpretation of results and support replication in future studies with related populations. Here, we provide a template methods report:

The specparam algorithm (version X.X.X) was used to parameterize EEG power spectra. Algorithm settings were set as: peak width limits: XX; max number of peaks: XX; minimum peak height: XX; peak threshold: XX; and aperiodic mode: XX. Power spectra were parameterized across the frequency range XX to XX Hz.

Code to access required settings from the specparam model object is provided on the specparam website (see https://fooof-tools.github.io/fooof/reference.html).

2.1.3. A data-driven approach to tune model fitting

There is no one-size-fits-all recommendation for specparam algorithm settings. The default settings are general settings that can accommodate different recording modalities, data quality, and frequency ranges, but often need some tuning to individual datasets and may result in over- or underfitting if care is not taken. In general, small changes in the algorithm settings tend to have minimal influence on model fits overall when broadly appropriate settings have been applied. We suggest applying a data-driven approach to tune model fitting for optimal performance, while taking into account your expectations about periodic and aperiodic activity given the data, the question of interest, and prior findings. To this end, a recommended workflow may include the following steps: (1) test model fit on a subsample of the data, selecting algorithm settings based on prior findings and a priori expectations; (2) adjust algorithm settings (e.g., frequency range, peak threshold) as needed; (3) fit power spectra of full sample with selected settings; and (4) assess model goodness of fit metrics, including cases of over- or underfitting. If the algorithm settings produce problematic model fitting for the full sample, a researcher may consider going back and adjusting algorithm settings as needed.

We provide two options for evaluating the appropriateness of algorithm settings based on a subset of the data in the 02-GroupPSDs.ipynb and 03-R_GroupPSDs.Rmd scripts. In the first option, a user can efficiently fit a model for each participant in the identified subsample. Each model result is saved out for further consideration. Algorithm settings can be adjusted based on inspection of individual model fits. Alternatively, a user can fit two group models based on the subsample of data, with different algorithm settings for each model object. Group model results are saved out for further consideration. Code is also available to check possible over- or underfitting once initial algorithm settings have been selected and a group model object has been fit. This code loops through all model objects and extracts fits that are either above (underfitting) or below (overfitting) a specific error threshold. The reports for potentially problematic models are saved out for further examination.

It is worth noting that researchers differ in the number and location of electrode channels in their analysis of aperiodic activity. The spatial origin of aperiodic activity is not thought to be confined to a specific brain area. With this in mind, it may be helpful to plot the spatial topography of aperiodic activity across the scalp to support selection of channels for analysis. This information can be assessed in conjunction with a priori hypotheses regarding the task-dependent topographical distribution of aperiodic activity. Reporting the spatial topography of aperiodic activity will be particularly useful when examining resting-state EEG among pediatric samples, given spatial heterogeneity inherent in neurophysiology across development (e.g., Cellier et al., 2021), and can inform future developmental research.

2.2. Spectral parameterization in Jupyter Notebook

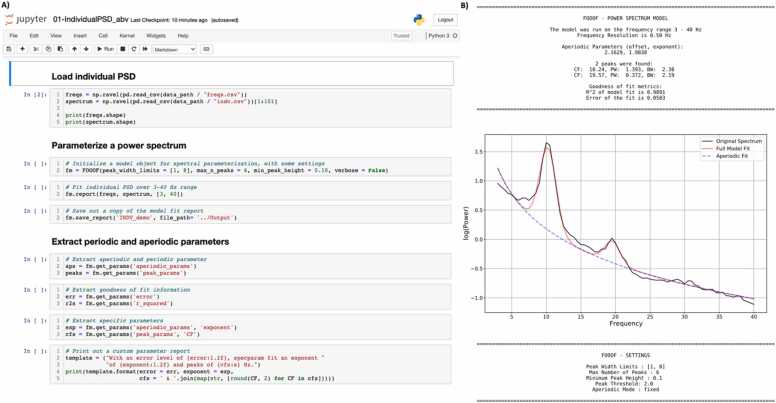
Jupyter notebooks are an open-source interface for interactive coding, allowing for integrating code, outputs, and markdown descriptions in order to develop and apply computational workflows. Jupyter notebooks support multiple programming languages, including Python and R. The Jupyter project also includes Jupyter lab, a platform for organizing and interacting with code scripts, data files, notebooks, and code outputs. Once the spectral parameterization module is installed, Jupyter notebooks can be used to run and visualize spectral parameterizations. Instructions for installing Jupyter Notebook are provided in the Supplement and in the README file in the Python folder on the GitHub repository. The following tutorial to fit a single power spectrum in Jupyter Notebook is based on a shortened version of the 01-IndividualPSD.ipynb script provided on GitHub, which we present in Fig. 2A.

Fig. 2.

Abbreviated version of the 01-IndividualPSD.ipynb script for parameterizing individual power spectrum using specparam in Jupyter Notebook (A). See the GitHub repository for full annotated script. Results of the specparam fitting of EEG data from a single child, recorded during an eyes-closed resting state, is presented in B. CF = center frequency of identified peak. PW = power of identified peak above the aperiodic signal. BW = band width of identified peak.

2.2.1. Load libraries

Install the requirements document from the GitHub repository (pip install -r requirements.txt) and specparam (see specparam website for up-to-date installation information) via the pip function in the Terminal. These installations include all Python libraries necessary for spectral parameterization. Next, launch Jupyter Notebook, navigate to the folder with the 01-IndividualPSD.ipynb script, and open the script.

2.2.2. Load data

Set the working directory to the Data folder (data_path = Path(‘./Data/’)). Load the two CSV files that contain a vector of frequencies (“freqs.csv”) and a power by frequency matrix (“indv.csv”). It is worth noting that in the provided script we use the read_csv function from pandas and the ravel function from numpy to read in the CSV files and then flatten the data into one-dimensional arrays, respectively. Adjustments may be necessary if data are in a different format (see specparam website for examples using NPY files).

2.2.3. Fit model

The next step is to define the spectral parameterization object. Algorithm settings were set as: peak width limits: [1,8]; max number of peaks: 6; minimum peak height: 0.10; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 3–40 Hz. The model is then fit using the report function from specparam, which fits the model and plots the results, creating the output seen in Fig. 2B. Model fit information can also be saved out, in this case as a PDF file.

2.2.4. Store and print parameters

Lastly, we extract and store model fit information. Example code for printing various model parameters is presented in Fig. 2A, including code for a custom parameter report. We store parameters from the model fit as objects for subsequent analyses and save the results as a JSON file. Additional data processing and visualization functions are described in the full 01-IndividualPSD.ipynb script and on the specparam website. In the 01-IndividualPSD.ipynb script, we also provide code for those who prefer to save Python results as a CSV file and read them into R separately for additional data analysis.

2.3. Spectral parameterization in R Studio

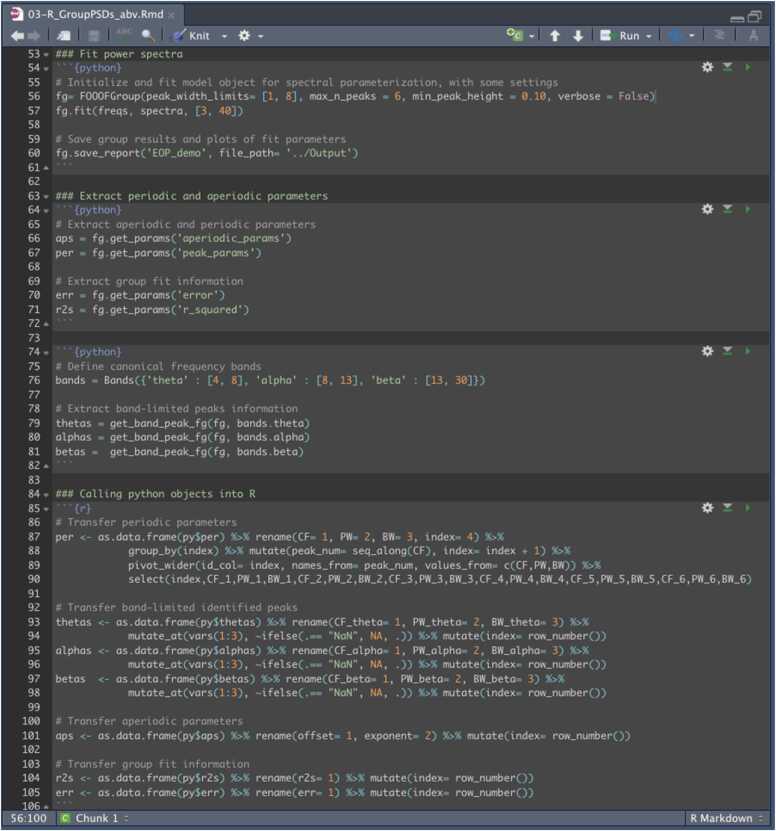
To facilitate integration of power spectral parameterization into analysis pipelines among researchers who prefer R, we provide code to run Python through R Studio using the reticulate package (Ushey et al., 2020). The provided code allows a user to execute core features of specparam, namely, parameterization and visualization of individual and group power spectra. We provide code for using Python in R Markdown to support users interested in incorporating code from both languages into their data processing pipeline (see reticulate website for processing via the console). The following tutorial for fitting group power spectra in R Studio is based on a shortened version of the 03-R_GroupPSDs.Rmd script provided on GitHub, which we present in Fig. 3.

Fig. 3.

Abbreviated version of the 03-R_groupPSDs.Rmd script that parameterizes multiple power spectra using specparam in R Studio. See the GitHub repository for full annotated script.

It is worthwhile to take time to ensure that the preferred Python version is being called in R—this is the most common issue users report when accessing Python in R Studio. Detailed instructions for setting up Python in R Studio are provided in the Supplement and in the README file in the R folder on the GitHub repository. The use of an older version of R or R Studio is another common issue. It may be necessary to update R and/or R Studio to newer versions in order to use the reticulate package and, by extension, the install_miniconda function.

2.3.1. Load libraries

Open the 03-R_groupPSDs.Rmd file in R Studio to analyze group power spectra (Fig. 3). We list a few necessary packages at the beginning of the provided script, namely, tidyverse (Wickham et al., 2019), gridExtra (Auguie, 2017), psych (Revelle, 2021), and magick (Ooms, 2021). Load the reticulate package as well. Next, load the required Python libraries. It is important to note that a user must include the code chunk delimiter ```{python} in order to interface with Python. An example of this is shown on line 54 in Fig. 3.

2.3.2. Load data

Load the two CSV files that contain a vector of frequencies (“freqs.csv”) and a power by frequency matrix (“eop.csv”). It is often helpful to check the shape of these objects to ensure that they are appropriate for the specparam algorithm. Namely, check that the column number from freqs matches with the row number from spectra.

2.3.3. Fit model

The next step is to define the spectral parameterization object (line 56). Algorithm settings were set as: peak width limits: [1,8]; max number of peaks: 6; minimum peak height: 0.10; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 3–40 Hz. The model is then fit using the fit function (line 57). Model fit results can be output, in this case as a PDF file.

2.3.4. Extract periodic and aperiodic parameters

Store model fit and aperiodic parameters to Python objects for subsequent analyses (lines 66–71). In regards to periodic parameters, we used the Bands function from specparam to identify peaks that occurred within a specific frequency range following spectral parameterization. This approach may be useful if comparing aperiodic-adjusted periodic activity to prior work on band-limited power (see e.g., He et al., 2019). Using the get_bands_peak_fg function, store periodic peak parameters that occur in the newly defined frequency bands as Python objects.

2.3.5. Transfer to R data frames

Call Python objects into an R workspace using the py$ command in a code chunk with the ```{r} chunk delimiter. For example, in Fig. 3, we define a variable with theta peak parameters (“thetas”) within a Python code chunk (line 79) that we call into an R code chunk as a data frame (lines 93–94). We create an R variable that binds together key variables from our original dataset (e.g., participant ID) with periodic, aperiodic, and model fit parameters into a single data frame. This data frame can be saved out as a CSV file. A user may now analyze and visualize aperiodic-adjusted power spectral data in R.

2.3.6. Additional features

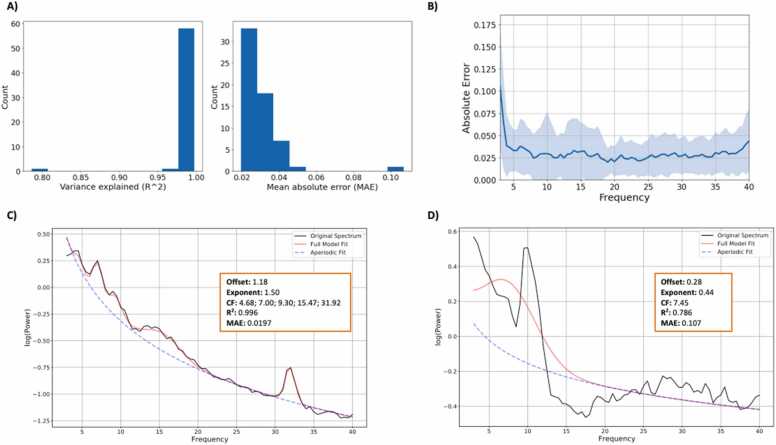
We include code for additional features that may aid a user with tuning the specparam algorithm, some of which we demonstrate in Fig. 4.

Fig. 4.

Histograms for variance explained (R^2) and mean absolute error (MAE) for the full sample, recorded during an eyes-open resting state (A). Mean error per frequency, as well as standard deviation in error per frequency (blue shading), are presented in B. In this condition, the 3 Hz bin had the highest mean error and largest standard deviation in error, suggesting possible misfit at the lower end of the examined frequency range. Further consideration about specparam settings may be needed. C and D depict two fit models that were flagged as potentially being overfit (MAE < 0.025) and underfit (MAE > 0.100), respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Based on the goodness of fit metrics presented in Fig. 4A, specparam fit the data recorded during an eyes-open resting state relatively well, with the exception of one potential outlier. The average R^2 was 0.99 (SD = 0.03, range = 0.786–0.998). The average MAE was 0.03 (SD = 0.01, range = 0.019–0.107). Grand averaged MAE is presented in Fig. 4B; error appears low across frequencies, except around 3 Hz. Overall, this pattern indicates that the model fit parameters were largely appropriate across the examined frequency range, although additional consideration on whether to parameterize beginning at 3 Hz may be warranted.

Fig. 4C and D depict two fit models that were flagged as potentially over- (MAE < 0.025) and underfit (MAE > 0.100), respectively. There is no strict guideline as to what constitutes “bad” MAE values; relevant MAE depends on the scale and noisiness (smoothness) of the data. Based on visual inspection of Fig. 4C, the identified peaks appear reasonable, and the aperiodic fit does not appear to be fitting random noise in the data. The model fit presented in Fig. 4D, however, does not appear to be fitting the original spectrum well, with the original data going above and below the fit line across the examined frequency range. In this case, we may exclude this participant from subsequent analyses. In practice, participant exclusion should be informed by expectations about the data quality given the task, sample, and published research with comparable samples, particularly for young children.

3. Illustrative example

This illustrative example was conducted in R Studio using the 04-R_ExampleAnalysis.Rmd script provided on the GitHub repository. We tested whether power spectral features differed as a function of behavioral inhibition, a temperament trait characterized by distress to novelty, particularly if social in nature (Fox et al., 2001, Pérez-Edgar and Fox, 2018). Behavioral inhibition is associated with a three- to four-fold increased risk for social anxiety (Fox et al., 2001, Clauss and Blackford, 2012). However, not every behaviorally inhibited child goes on to develop anxiety (Degnan and Fox, 2007). Prior work has examined frontal alpha asymmetry as a neural marker that may explain this heterogeneity in risk trajectories, suggesting that behavioral inhibition in tandem with greater right frontal alpha asymmetry may lead to higher risk for anxiety and socioemotional difficulties (Hane et al., 2008, Henderson et al., 2001). As such, we also examined the association between frontal alpha asymmetry calculated using the traditional method (i.e., no explicit parameterization of aperiodic activity) and via specparam to illustrate the unique relations that can be derived from disentangling contributors to the EEG signal (see Supplemental Information).

3.1. Method

Example data come from a subsample of children (N = 60, M_age = 9.97 years, SD = 0.95; 55% female) recruited from central Pennsylvania for a study on behavioral inhibition and affect-biased attention. Descriptions of recruitment procedures and sample characteristics are published elsewhere (Liu et al., 2019, Liu et al., 2018, Thai et al., 2016). Children and their parents provided assent and consent, respectively, for participation at the initial laboratory visit.

3.1.1. EEG collection and preprocessing

EEG was recorded using a 128-channel geodesic sensor net (Electrical Geodesic Inc., Eugene, Oregon) during four 1-minute blocks. Children were instructed to keep their eyes open (EO) for two of the blocks, and closed (EC) for the other two blocks; blocks alternated between conditions (EO, EC, EO, EC). EEG data were sampled at 1000 Hz and referenced online to the central midline electrode (Cz). Impedances were kept below 50 k$\Omega$ while recording. EEG data were preprocessed using the Maryland Analysis of Developmental EEG (MADE) pipeline (Debnath et al., 2020). Power spectra were estimated in 0.5 Hz increments from 1 to 50 Hz using Welch’s method with a hamming window (50% overlap) in Matlab 2021a for each participant at each available electrode site. Although we chose to estimate the power spectral density using Welch’s method, other approaches, such as multitapers, can be used. The decision for which method to use depends somewhat on the characteristics of the data, and the intended purpose. Multitapering, for example, can provide less biased spectral estimates, especially for noisier, shorter time windows. Furthermore, the choice of which parameters to use when using Welch’s method (window size, window overlap), can influence spectral estimates. Therefore, it is advisable to examine the robustness of the results to different spectral estimation methods.

Note that Matlab does not need to be used for this step, and all spectral analyses can be performed in Python using the MNE or neurodsp packages (Cole et al., 2019, Gramfort, 2013). Children from the larger sample with usable EEG in the EC and EO conditions were semi-randomly selected for the current analyses, only ensuring that half were behaviorally inhibited and half non-inhibited (see Supplemental Information for description of EEG preprocessing and subsample selection). Analyses for the illustrative example were limited to data from the EC condition.

3.1.2. Tuning the specparam algorithm

The specparam algorithm (version 1.0) was used to parameterize EEG power spectra. For illustrative purposes, we will consider results from models fit with different algorithm settings. In practice, we suggest that algorithm settings be informed by published results from similar samples, taking into account expectations about periodic and aperiodic activity given the data and question of interest. Model #1 algorithm settings were set as: peak width limits: [2,5]; max number of peaks: 4; minimum peak height: 0.05; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 2–20 Hz. Model #2 algorithm settings were set as: peak width limits: [1,8]; max number of peaks: 6; minimum peak height: 0.10; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 3–40 Hz.

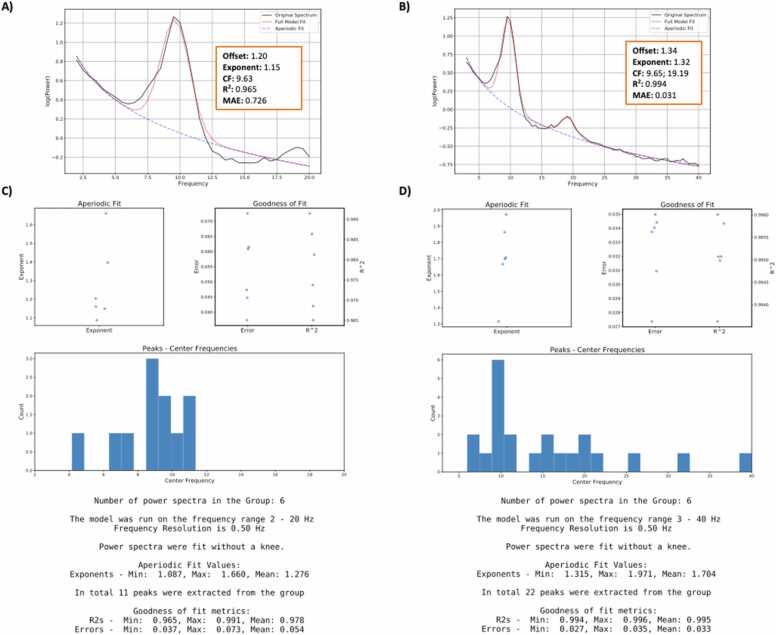
Results from model fits using different settings on a randomly selected 10% subset of the data (n = 6) are presented in Fig. 5. Parameterized power spectra from the same individual using different algorithm settings are presented in Fig. 5A and B. Although both model fits identified a peak at ~9.65 Hz, algorithm settings for model #1 resulted in a relatively poorer fit compared to model #2, as indicated by the goodness of fit metrics. Parameterized power spectra for the full subset of data are presented in Fig. 5C and D. Overall, the goodness of fit measures appear relatively better in Fig. 5D compared to C. This difference is likely due to identified peaks at ~20 Hz range present in Fig. 5D that are not captured in C as a result of the smaller examined frequency range. As a general guideline, it is recommended to choose frequency ranges that are not in the middle of peak ranges, as is the case with model #1. Based on model fit results from the subset of participants, and our expectations of periodic and aperiodic parameters in this sample, we chose to fit the group power spectra with algorithm settings from model #2.

Fig. 5.

Spectral parameterization using different algorithm settings on a randomly sampled subset of the data (n = 6), recorded during an eye-closed resting state. Parameterized power spectra from the same individual are presented in A and B, demonstrating a participant-level assessment of model fit. Subgroup model fit results are presented in C and D. Algorithm settings for models fit for A and C were set as: peak width limits: [2,5]; max number of peaks: 4; minimum peak height: 0.05; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 2–20 Hz. Algorithm settings for models fit in B and D were set as: peak width limits: [1,8]; max number of peaks: 6; minimum peak height: 0.10; aperiodic mode: fixed; default settings otherwise. Power spectra were parameterized across the frequency range 3–40 Hz.

Visual inspection of error across examined frequencies indicated that the algorithm fit the data relatively well. There were no instances of underfitting, defined as MAE > 0.100, when considering data from the full sample. There was one instance of potential overfitting (MAE = 0.199, R^2 = 0.996), defined here as MAE < 0.020. After additional consideration, we decided that the identified peaks and aperiodic fit were reasonable. This participant was retained for subsequent analyses.

The selected algorithm settings were used to fit power spectra for behaviorally inhibited and non-behaviorally inhibited children separately (Table 2, Fig. 6, Fig. 7).

Table 2.

Sample characteristics, periodic and aperiodic activity by BI status.

	BI		BN		95% CI
	N	Mean (SD)	N	Mean (SD)
Age (years)	30	10.00 (0.95)	30	9.93 (0.98)	[−0.43, 0.57]
Female		47%		63%
BIQ	30		30
Total		128.00 (20.49)		78.22 (19.92)	[39.34, 60.23]
Social Novelty		70.23 (10.28)		38.78 (11.32)	[25.86, 37.04]
Aperiodic	30		30
Offset		1.62 (0.28)		1.54 (0.24)	[−0.06, 0.21]
Exponent		1.69 (0.22)		1.67 (0.18)	[−0.09, 0.12]
Periodic
Theta (4–8 Hz)	9		16
Center frequency		6.65 (0.89)		7.06 (0.46)
Power		0.21 (0.06)		0.37 (0.13)
Band width		1.28 (0.31)		1.49 (0.35)
Alpha (8–13 Hz)	29		30
Center frequency		10.03 (0.80)		9.50 (0.51)	[0.18, 0.88]
Power		1.19 (0.27)		0.98 (0.30)	[0.06, 0.36]
Band width		2.04 (1.01)		1.91 (0.54)	[−0.29, 0.55]
Beta (13–30 Hz)	28		27
Center frequency		18.09 (2.72)		17.43 (2.09)	[−0.65, 1.98]
Power		0.33 (0.16)		0.26 (0.11)	[−0.01, 0.14]
Band width		4.71 (2.10)		3.99 (1.89)	[−0.36, 1.80]
Model fitting
R^2		0.99 (0.01)		0.99 (< 0.01)	[< −0.01, < 0.01]
MAE		0.04 (0.02)		0.03 (0.01)	[< 0.01, 0.01]

Note: Periodic activity group comparisons were limited to alpha and beta due to a small number of children exhibiting activity in the theta band after accounting for the aperiodic signal. BI = behaviorally inhibited. BN = non-behaviorally inhibited. BIQ = Behavioral Inhibition Questionnaire. Participants were categorized as BI if BIQ total score was $\ge$ 119 and/or social novelty score $\ge$ 60. R^2 = variance explained in specparam model fit. MAE = mean absolute error in specparam model fit.

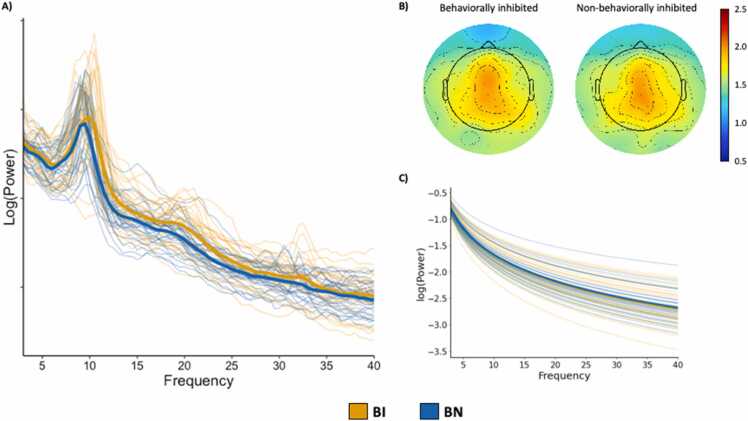
Fig. 6.

Individual and grand averaged fitted power spectra for behaviorally inhibited (BI; orange) and non-behaviorally inhibited (BN; blue) children, recorded during an eyes-closed resting state, are presented in A. The spatial topography of the aperiodic exponent across the scalp for BI (left) and BN (right) children is presented in B. The aperiodic fits by group, controlling for offset, are presented in C. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

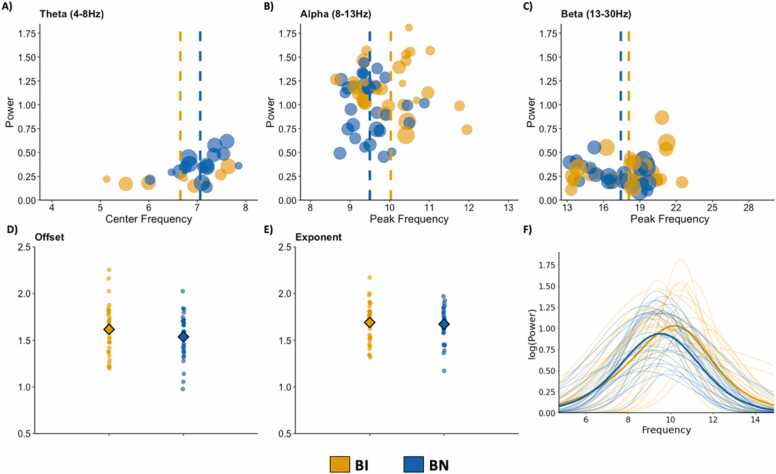
Fig. 7.

EEG measures for behaviorally inhibited (BI; orange) and non-behaviorally inhibited (BN; blue) children. Aperiodic-adjusted activity in the theta (A), alpha (B), and beta (C) canonical frequency bands, as well as the aperiodic offset (D) and exponent (E), for BI and BN children during an eyes-closed resting state. Dot size in plots A-C reflects the band width of the identified peaks. Vertical lines in plots A–C and diamonds in plots D,E reflect group mean values. Reconstructed aperiodic-adjusted alpha peaks are presented in F. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.1.3. Measures

Behavioral inhibition was measured using the Behavioral Inhibition Questionnaire (Bishop et al., 2003), a 30-item parent-report questionnaire that assesses a child’s behavior in response to social and situational novelty. We examined BI as a categorical variable (total score 119 and/or social novelty score 60), classifying a child as behaviorally inhibited (BI; n = 30) or non-behaviorally inhibited (BN; n = 30) (Broeren and Muris, 2009, Fu et al., 2017, Poole et al., 2020).

Absolute power was calculated as spectral power averaged within the alpha (8–13 Hz) and beta (13–30 Hz) frequency ranges. Total power was calculated as spectral power averaged across all frequencies (3–40 Hz). Absolute power in each frequency band was divided by total power and then multiplied by 100 to create relative alpha and beta power.

3.2. Results

Descriptive information is presented in Table 2. Specparam model mean squared error (MAE) was significantly higher for BI children (M = 0.04, SD = 0.02) compared to BN children (M = 0.03, SD = 0.01), t = 2.26, p = .03. Specparam model variance explained (R^2) did not differ between BI children (M = 0.99, SD = 0.01) and BN children (M = 0.99, SD < 0.01), t = −1.79, p = .08. A plot depicting the overlap between averaged raw and specparam-estimated power spectra is provided in the Supplemental Information.

Aperiodic fits, as well as the spatial topography of the aperiodic exponent across the scalp, are presented for each group in Fig. 6. BI children did not differ from their BN peers in regards to their offsets (t = 1.18, p = .24; Fig. 7D) or exponents (t = 0.34, p = .73; Fig. 7E). Group comparisons were limited to alpha and beta activity. BI and BN children differed in regards to alpha center frequency (t = 3.01, p = .004) and power (t = 2.83, p = .006), but not bandwidth (t = 0.64, p = .52). That is, BI children had a higher peak frequency and more aperiodic-adjusted power in the canonical alpha band compared to BN children (Fig. 7B). Alpha peaks are reconstructed in Fig. 7F. BI and BN children did not differ in regards to beta center frequency (t = 1.01, p = .32). Neither beta power (t = 1.66, p = .10) nor bandwidth (t = 1.34, p = .19) differed between the groups. When considering behavioral inhibition as a continuous variable, total BIQ scores were significantly associated with alpha center frequency (r = 0.44, p < .001) and aperiodic-adjusted power (r = 0.33, p = .01). Results indicate that more behavioral inhibition is related to higher center frequency and more aperiodic-adjusted power in the canonical alpha band, complementing results from the analysis of BI as a categorical variable. When applying traditional methods, BI and BN children differed in regards to relative alpha power (t = 2.21, p = .03), but not relative beta power (t = −0.10, p = .92). Once again, BI children were shown to have more alpha power compared to BN children.

3.3. Discussion

As expected, using traditional approaches for deriving frequency band measures, children with BI had higher relative alpha power but not higher beta power. However, these approaches leave the cause of these differences unclear. In contrast, by explicitly parameterizing the EEG power spectrum, we observed unique patterns of neural activation among BI children and their non-inhibited peers. Specifically, we found that alpha peak frequency and aperiodic-adjusted power during the eyes-closed resting state were higher for BI children relative to their BN counterparts. Thus, while alpha differences were present using both approaches, specparam clarifies that this is due to differences in peak frequency, which is not apparent using the traditional approach. Moreover, by parameterizing the power spectra, we can ascertain that the observed difference is driven by differences in periodic power, not the aperiodic signal. Recent work has shown that alpha peak frequency and power increase when visual input is restricted (Webster and Ro, 2020), a pattern of neural activation associated with an introspective cognitive state, a reduction in cognitive engagement, and decreased autonomic arousal (Barry et al., 2009, Haegens et al., 2014, Ray and Cole, 1985a, Ray and Cole, 1985b).

Notably, less than half of the children in our illustrative example exhibited power above the aperiodic signal in the canonical theta band, lending credence to the necessity for spectral parameterization prior to interpretation of band-limited power. It is possible that the lack of observed peaks within this canonical band may be attributed to very-low-power oscillations or rare bursts of oscillatory activity. In this case, specparam could be used in conjunction with time-domain analyses approaches to, among other things, quantify burst features over a short time window (see e.g., Jones, 2016, and Cole and Voytek, 2019) in order to confirm whether oscillatory activity is in fact completely absent (Donoghue et al., 2021).

It is important to note that other methods for measuring periodic and aperiodic activity are available. One conceptually similar method is a time-domain rhythm detection algorithm called extended Better Oscillation Detector (eBOSC) which can be used to identify rhythmicity (relative to arrhythmic activity) at the single-trial level (Kosciessa et al., 2020). The eBOSC algorithm uses a 1/f fit in order to detect bursts of oscillatory activity over and above the aperiodic component, which may be useful for time-resolved analyses focused on periodic activity. Another related measure is irregular-resampling auto-spectral analysis (IRASA), which decomposes time series to extract the 1/f activity (Wen & Liu, 2016). However, neither of these tools fully parameterizes the periodic and aperiodic parameters as done in specparam, which offers an algorithm and user-friendly tool measuring multiple spectral features together. Further comparisons of spectral parameterization to other approaches are described in Donoghue et al. (2020a).

Overall, the examples and results indicate that greater attention to power spectral parameterization is warranted when considering electrophysiological signatures among pediatric samples. Both periodic and aperiodic features are dynamic both within and between subjects, with systematic variation across age, requiring methods that explicitly consider and measure both components, such as specparam. This spectral parameterization approach can also be used and combined with other methodological considerations for analyzing neural oscillations (Donoghue et al., 2021), and best practice recommendations for analyzing and reporting EEG/MEG data in research (Pernet et al., 2020) and clinical (Babiloni et al., 2020) contexts.

4. Conclusions

In this paper, we discussed why developmental cognitive neuroscientists should parameterize power spectral data, and demonstrated how this can be accomplished via specparam, in Jupyter Notebook and R Studio. Many of the studies discussed used specparam to parameterize neural power spectra, often during resting baseline EEG recordings (e.g., Levin et al., 2020; Robertson et al., 2019), underscoring the applicability of the specparam algorithm for typically-developing and clinical pediatric samples. Results from the illustrative example lend additional support for this idea, demonstrating how specparam can be applied to EEG data to answer crucial questions regarding periodic and aperiodic activity differences between groups of children. By explicitly parameterizing power spectral features, developmental cognitive neuroscientists may further clarify how dynamic neural communication contributes to normative and aberrant cognition, from infancy through old age.

Declaration of Competing Interest

No conflicts of interest to declare.

Appendix A. Supplementary material

Supplementary material

.