Multiple timescales in bacterial growth homeostasis

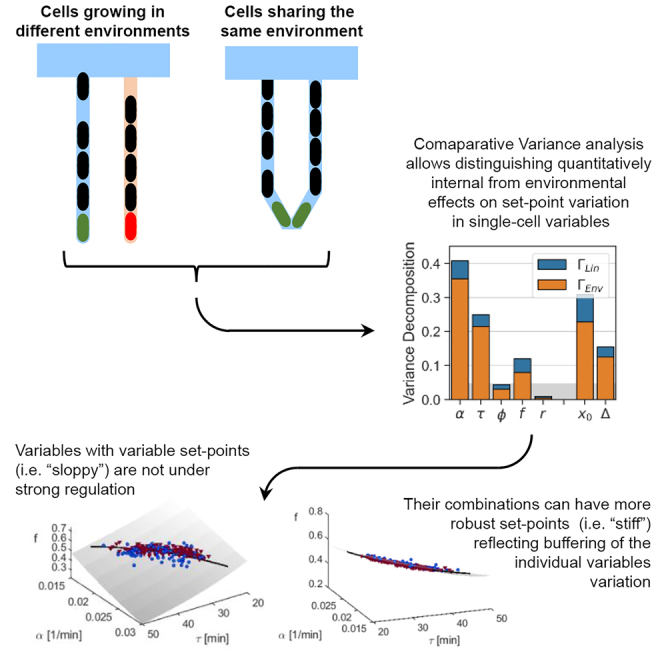
Summary

In balanced exponential growth, bacteria maintain many properties statistically stable for a long time: cell size, cell cycle time, and more. As these are strongly coupled variables, it is not a-priori obvious which are directly regulated and which are stabilized through interactions. Here, we address this problem by separating timescales in bacterial single-cell dynamics. Disentangling homeostatic set points from fluctuations around them reveals that some variables, such as growth-rate, cell size and cycle time, are “sloppy” with highly volatile set points. Quantifying the relative contribution of environmental and internal sources, we find that sloppiness is primarily driven by the environment. Other variables such as fold-change define “stiff” combinations of coupled variables with robust set points. These results are manifested geometrically as a control manifold in the space of variables: set points span a wide range of values within the manifold, whereas out-of-manifold deviations are constrained. Our work offers a generalizable data-driven approach for identifying control variables in a multidimensional system.

Graphical abstract

Highlights

• •Temporal averaging over lineages disentangles homeostatic set points from noise
• •The environment is revealed as the dominant source of set point variability
• •Cellular variable set points exhibit a range of behaviors from sloppy to stiff
• •Geometry of homeostatic control manifold is identified in cellular variable space

Microbiology; Systems biology

Introduction

Microbial cells are variable in every property that can be measured: size, shape, protein content, metabolic fluxes, and more. A clonal cell population is a complex stochastic and nonlinear dynamical system in which cells grow and divide, perpetuating their properties on to the next generation; they interact with their environment as well as with nearby cells. Nevertheless, despite this complexity and variability, a microbial cell population can maintain balanced growth for extended times. In balanced growth, homeostasis keeps the distributions of many phenotypic variables, such as cell size, cycle time, and protein content, stable over time–defining a steady state of the system.

Bacterial homeostasis has been the focus of significant research efforts for decades. How is cell size regulated to maintain its stable distribution? How is growth coordinated with cell cycle events, such as division? These and related questions are central in bacterial physiology. The current work reveals that bacterial homeostasis mechanisms span multiple timescales and tie together variables that display a hierarchy of sensitivities to the environment, suggesting principles that might be general to such systems.

Recent years have seen renewed interest in the classic problem of bacterial growth homeostasis (Jun et al. 2018; Meunier et al. 2021). Following the development of single-cell measurement techniques (Rosenthal et al. 2017), in particular microfluidic single-cell trapping devices (Wu and Dekker 2016) that utilize perfusion to maintain a stable chemical environment, quantitative data could be obtained on different bacterial properties over extended time periods. These data allow mapping distributions of phenotypic variables and correlations among them with unprecedented precision (Campos et al. 2014; Taheri-Araghi et al. 2015; Brenner et al. 2015; Tanouchi et al., 2015; Grilli et al. 2018). Correlation patterns in these data were studied extensively, and have been interpreted in the framework of stochastic models. Such models usually assume that cells homeostatically regulate certain properties, e.g., cell size or growth-rate; this allows for comparing and assessing different models for regulation strategy (Osella et al. 2014; Amir 2014; Sauls et al. 2016; Nordholt et al. 2020).

The accumulation of single cell data has revealed strong coupling between different phenotypic variables. This strong coupling obscures which variables are actually under regulation, and which are constrained as a result of interactions; an unbiased approach to test this question is desirable. Recent progress in this direction using multivariate linear regression revealed that multiple coordinated mechanisms could be involved in cell size regulation (Kohram et al. 2021). Nevertheless, a holistic data-driven approach is still not well developed. In particular, homeostasis mechanisms are often assumed to operate within a single cell-cycle time, and correlations are thus examined at the timescale of a single cell-cycle; for example, correlations between initial and final size in a cycle, or added size over a cycle and its time duration. It is nevertheless possible that homeostasis mechanisms also act on longer timescales. In support of this possibility, recent work revealed that bacterial cellular properties exhibit memory patterns that can extend up to ∼ 10 generations (Susman et al. 2018; Vashistha et al. 2021). Therefore, long-term correlations between the different phenotypic variables should also be examined to identify possible slow homeostasis mechanisms.

In this work, we characterize bacterial growth homeostasis by studying the sensitivity of phenotypic variables to both extracellular (environmental) and intracellular (cellular compositions) perturbations, and by examining correlations among them at different timescales. To this end, we distinguish between a homeostatic set point, empirically estimated as a time-averaged quantity along an individual lineage, and temporal fluctuations around this set point. The rationale behind our approach is that tightly controlled variables are expected to exhibit robust set points that are insensitive to perturbations. In contrast, less controlled variables – ones which may be stable because of interactions, but under less stringent direct regulation – may still have homeostatic set points, but those will be more sensitive and vary with perturbations. This approach is inspired by the concept of robustness in engineering theory that was widely applied to biology in the context of metabolic and biochemical regulation systems (Savageau 1971; Fell 1992; Stelling et al., 2004). To apply a similar approach to bacterial growth and division, we develop an analysis framework that quantifies the robustness of set points for an array of cellular variables against perturbations. Because of the large number of parameters that determine the environment (e.g., growth medium components, temperature, pH, and growth region geometry), one cannot easily quantify these perturbations in a set of experiments. Instead, we utilize uncontrolled variation across measurements performed under nominally identical conditions to reveal the sensitivity of different cellular variables. We analyze data obtained from the recently developed sisters machine microfluidic device (Vashistha et al. 2021), which allows us to track two cells trapped next to each other as they grow and divide for tens of generations. Unrelated cells growing in close proximity to each other in the same trap are subject to the same environment, which allows us to disentangle effects of lineage history from microenvironment and to quantify their influence on the set point variation. This in turn enables us to disentangle the relative sensitivity to the two types of perturbations.

Our results reveal that homeostatic set points generally vary among individual lineages. We find that environmental perturbations are a crucial driver of this variation, while perhaps surprisingly, the internal cell-state (or cellular composition) that depends on lineage history, contributes only a small fraction. Despite the uncontrolled nature of environmental perturbations, a qualitatively consistent behavior of cellular variables emerges: the different variables span a broad range of sensitivities to the environment, with a well-defined repeatable hierarchy among them. This hierarchy of sensitivities portrays a multivariable connected system, forming a cascade of coupling levels that protects some variables from perturbations more than others, a property reminiscent of a sloppy system (Daniels et al. 2008; Braun 2020). In such a system, some variables can vary over a large range (“sloppy” variables), whereas others must be kept tightly controlled (“stiff” variables), to maintain functionality.

Importantly, we find that some sloppy variables covary with one another in a simple and logical way over long timescales. Such correlations suggest the existence of long-term homeostatic mechanisms that extend over multiple cell-cycles. In the space of growth-rate, generation time, and division ratio, (α, τ, f), we identify a control variable hierarchically composed of the sloppier variables, and predict if that homeostatic set points will adhere to a manifold defined by: r = fe^ατ = 1, while occupying a large region inside the manifold. This prediction is verified in the entire set of experiments analyzed. These results suggest that long-term growth and division homeostasis is characterized by a ”set-manifold” rather than a set point. Directions on the surface of this manifold are flexible to change with perturbations, while the direction perpendicular to it is stiff. Cell-size is found to be a sloppy variable, but does not covary with any of the growth and division variables over long times. Well-known correlations reported previously are recovered on a cycle-by-cycle basis, and their significance in connection to long-term homeostasis is discussed.

Results

Separating short and long timescale contributions to variance

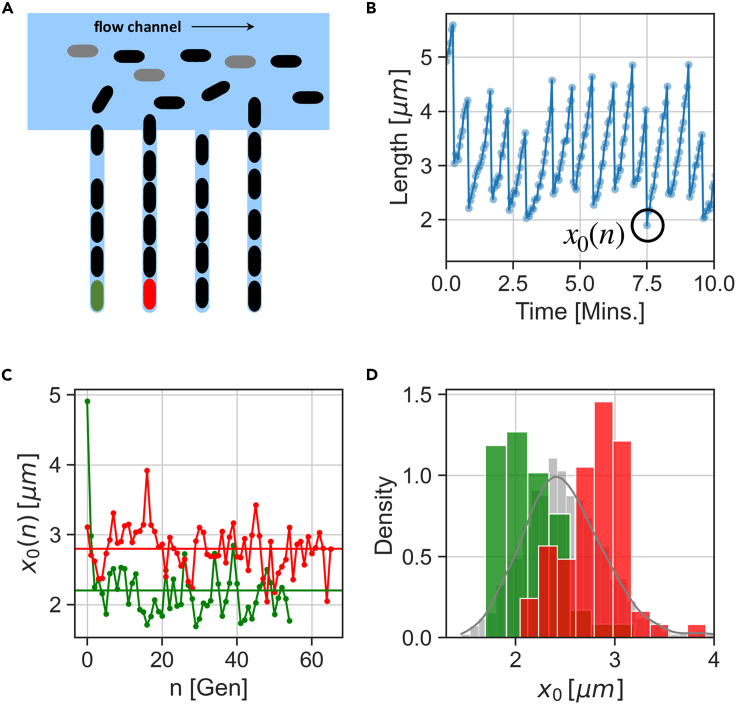
In recent years, microfluidic devices have proven to be a powerful experimental tool in characterizing single cell physiology. In particular, trapping single cells in various geometries in a device allowing continuous flow of nutrients has opened a window on the long-term monitoring of single cells as they divide and form lineages. Experimental parameters such as temperature and pH can be carefully monitored and the experiments are considered very highly controlled. Figure 1A illustrates the device known as the mother machine, where single lineages are trapped and followed over time (Wang et al., 2010; Brenner et al. 2015). Figure 1B presents a portion of a time series extracted from mother machine movies, where cell length is measured as a proxy of cell size, because its width remains mostly constant. It is seen that the cell length increases almost exponentially over time within the cell cycle and then abruptly divides to start the next cycle.

Figure 1.

Short-term and long-term variability in single cell data

(A) E. coli cells are trapped in the channels of a mother machine, and can be followed for many growth and division cycles, while medium flows through the device.

(B) Images from the microfluidic device are analyzed to provide time traces of cell length in the trap vs time. Smooth accumulation and sharp divisions are clearly seen.

(C) Initial size x₀(n) from each cycle n vs. generation number, marked on the trace in (B). Data from two separate traps are shown in red and green. Lineages remain distinct over dozens of generations.

(D) Collecting the initial sizes x₀ from all generations in each of the traces in (C), gives a distribution (corresponding color). Collecting data from all traps in the same experiment, the gray distribution represents the pooled ensemble.

A lot has been learnt about cell physiology, thanks to such experiments. However, despite the efforts to control the environment, some measurements do not exhibit the same statistics in repeated experiments with nominally identical external conditions. For comparison, recall that distributions of cell size and highly expressed proteins collapse onto a universal shape after scaling, over a broad range and with very high accuracy, demonstrating the precision of statistical measurements over populations and over time (Salman et al. 2012; Brenner et al. 2015). In contrast, in physical units these variables exhibit a persistent individuality among lineages measured in different traps (Susman et al. 2018; Kohram et al. 2021). This individuality is apparently well beyond experimental error, but its origins remain unclear.

To illustrate this effect over longer times, Figure 1C shows cell size measured at the start of each cell cycle, x₀(n) (the initial point from the nth cycle, see Figure1B). The two traces from the same experiment exhibit fluctuations for a long time, but also a difference in their temporal average that persists over dozens of division cycles. Collecting the histogram of initial size over all cycles in each trace n = 1, 2, ...N, reveals that their distributions are distinct (Figure 1D, colored distributions). For the entire collection of traces in the experiment, a pooled distribution of the data gives the overall statistics (Figure 1D, gray distribution).

To quantify this effect, we note that for any observable z, the variance across the pooled ensemble is a sum of variations in the set point $\overline{z}$ among traps, and temporal fluctuations δz around each trap-specific set point:

$${\sigma }^2\left(z\right)={\sigma }^2\left(\overline{z}\right)+⟨{\sigma }^2\left(\delta z\right)⟩\text{.}$$ (Equation 1)

We can write the same equation using the law of total variance, which enables further generalization later on. A time-series in a single trap is a subset of the pooled ensemble that is conditioned on a particular trap, with this notation,

$${\sigma }^2\left(z\right)={\sigma }^2\left(\overline{z|\text{trap}}\right)+⟨{\sigma }^2\left(z|\text{trap}\right){⟩}_{\text{trap}}\text{.}$$ (Equation 2)

Here $\overline{z|\text{trap}}$ is the average conditioned on the trap, and $⟨\cdot {⟩}_{\text{trap}}$ denotes the averaging over all traps. A similar decomposition of variance was previously developed to disentangle contributions to gene expression variation and to protein concentrations in growing cells (Bowsher and Peter S., 2012; Lin and Amir 2021).

Lineages are statistically equivalent, if their temporal averages are all the same and the first term in Equations (1 and 2) vanishes (or, for a finite data-set, is negligible relative to the total variance). If we view single lineages as realizations of a dynamical system, then with borrowed terminology, this term reflects weak ergodicity breaking. Indeed, normalized by the total variance, it has been suggested as an ergodicity breaking parameter (He et al. 2008; Meroz and Sokolov 2015), quantifying what fraction of the variance comes from differences among time-averages. In our context we define the trap-conditioned variance fraction

$${\text{Γ}}_{\text{trap}}\left(z\right)=\frac{{\sigma }^2\left(\overline{z}\right)}{{\sigma }^2\left(z\right)}\text{,}$$ (Equation 3)

a parameter in the range [0, 1]. Figure 2 presents an artificial illustration of three groups of time series, each group with the same overall (pooled) mean and variance, but different ${\text{Γ}}_{\text{trap}}$. For ${\text{Γ}}_{\text{trap}}=0$ (Figure 2 left panel), all traces mix with one another through the measurements and have the same average. The variance in this case is contributed only from fluctuations around this average (the “ergodic” limit). At the other extreme for ${\text{Γ}}_{\text{trap}}\approx 1$ (Figure 2 right panel), variance comes mainly from distinct averages among traps and very little from fluctuations around them. Time series are then seen to center around different means. ${\text{Γ}}_{\text{trap}}=0.6$ (Figure 2 middle panel) is an intermediate case with the two terms contributing to the total variance.

Figure 2.

Quantifying the contribution of set point variability to total variance (illustration)

In each panel, the pooled ensemble has zero mean and unit variance, holding fixed the sum of the two contributions to variance. However, the segregation of time traces illustrates an increasing contribution of set-point variance, corresponding to an increase in the value of ${\text{Γ}}_{\text{trap}}$ from left to right

Sloppy and stiff variables in trapped bacteria

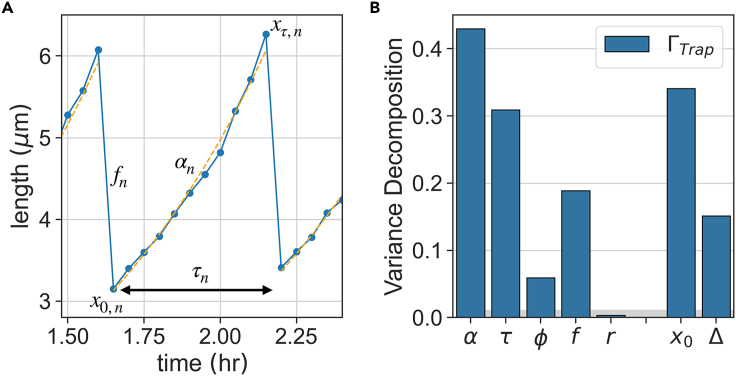
We apply our analysis first to cell size traces measured in a mother machine, in which the MG1655 Escherichia coli (E. coli) bacteria were grown in LB medium (rich complex medium) at 32° C. These data were previously published in (Susman et al. 2018). From cell size traces, several different coarse-grained variables of growth and division can be estimated per cycle; they are illustrated in Figure 3A. One may identify the two time/rate variables in each cycle, the interdivision (or generation) time τ and the exponential growth-rate α. Although growth deviates from an exact exponential when measured carefully (Kohram et al. 2021; Nordholt et al. 2020; Vashistha et al. 2021), the best fit exponential rate is still a useful approximation for the continuous accumulation over the cell cycle and will be used in what follows. Cell size is characterized by its length x₀ at the start and x_τ at the end of each cycle, as well as their difference Δ = x_τ-x₀. In addition, we define several relative dimensionless size variables, to which we also apply the variance decomposition: the logarithmic fold-growth per cycle ϕ = ατ = ln(x_τ/x₀), the fold-decrease at division f(n) = x₀(n) /x_τ(n-1), and the total fold change in cell size over an entire cycle r = f(n) e^ϕ(n) = x_τ(n) / x_τ(n-1). The last two connect consecutive cell cycles, cycle n - 1 to cycle n. We note that this is not a set of independent variables; on the contrary, some are clearly combinations of others. Such coarse-grained variables have been extensively analyzed in previous work, with statistics estimated over pooled ensembles (Robert et al., 2014; Soifer et al., 2016; Sauls et al. 2016; Grilli et al. 2017).

Figure 3.

Sloppy and stiff variables in trapped bacteria

(A) Illustration of the main phenotypic variables in a cell cycle. Presented for one cycle are the initial size x₀, final size at division x_τ, exponential growth-rate α, interdivision time τ, and division ratio $f=\frac{x_0\left(n\right)}{x_{\tau }\left(n-1\right)}$, relating the current cycle n to the previous one n - 1. The log-fold growth is ϕ = ατ, added length Δ = x_τ - x_0, and size ratio $r=f{e}^{\varphi }$.

(B) Variance decomposition conditioned on trap: ${\text{Γ}}_{\text{trap}}$ for all variables, estimated from a set of mother machine experiments performed under identical conditions. Vertical bar heights are the fraction of variance contributed from different set points among traps, whereas the remaining fraction complementing to 1 represents the contribution of temporal fluctuations. The gray horizontal bar is the noise level (finite size sampling effect) estimated by running the same analysis on artificial lineages drawn at random from the pooled ensemble (see STAR Methods, Quantification and Statistical Analysis).

We estimated ${\text{Γ}}_{\text{trap}}$ for each of the variables from a large set of mother machine measurements; the results are plotted as bars in Figure 3B. The remaining fraction (complementing the bar heights to 1) represents the contribution of temporal fluctuations around individual trap-conditioned time average. Finite-size sampling effects that were estimated from a set of artificial lineages with the same global statistical properties is depicted as a control (gray baseline; see STAR Methods, Quantification and Statistical Analysis).

Growth-rate α shows the largest trap-dependent variance, with more than 0.4 of its total variance contributed from differences in temporal averages among traces. Generation time τ is also significant with ${\text{Γ}}_{\text{trap}}\approx 0.3$. Interestingly, their product - logarithmic fold growth ϕ - shows a markedly smaller value of ${\text{Γ}}_{\text{trap}}$, indicating that its average is more strongly regulated across traps. Division fraction f has a surprisingly non-negligible contribution ($\approx 0.2$), suggesting that single cells can maintain a division fraction different from 1/2 consistently across many cycles. The product r = fe^ϕ shows a smaller value of ${\text{Γ}}_{\text{trap}}$ than each one of its factors, and moreover, even smaller than the noise level. The initial size x₀ (as well as x_τ (not shown)) show significant values of ${\text{Γ}}_{\text{trap}}$, but their difference Δ somehow buffers this variability. These observations hint to nontrivial correlations of variables across time in each trace, as will be discussed in detail below.

Sensitivity to environment underlies sloppy set points

Before addressing the relationships between variables, we first ask: what is the source of the variability among individual trap averages? Possible sources can be broadly categorized into two types: internal and environmental. Internal sources reflect the cellular composition, lineage history, epigenetic memory, and any hidden internal variables that are at least partly inherited across divisions (for example, age of the cell at the beginning of the measurement). Environmental factors include variation in physical variables such as channel width and temperature, as well as local biochemical variation in the growth medium. Mother machine data cannot distinguish between these two sources, because two separate traps differ by both lineage and environment.

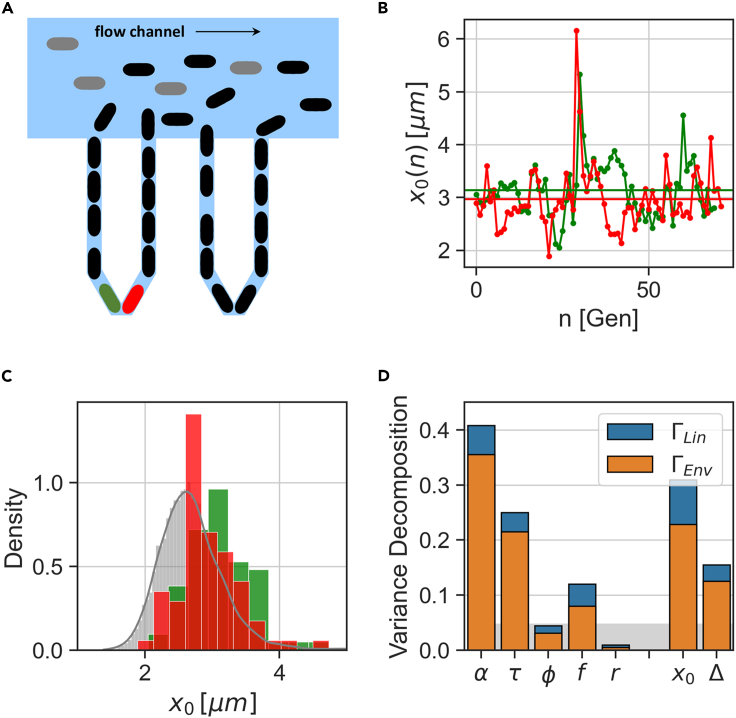
We utilize the experimental design of the sisters machine to follow two lineages in each channel of a single trap, which start growing at roughly the same time (Vashistha et al. 2021). In this new device, depicted in Figure 4A, two neighboring traps of the mother machine are combined at their closed end via a V-shaped connection of the same dimension as the original traps. This in turn allows us to track two cells, each of which is trapped at one side of the V-shaped tip, as they both grow and divide for tens of generations while sharing the same microenvironment. In a recent study, this device was used to track lineages stemming from two sister cells – “sister lineages” – revealing the divergence between two sisters after their separation, and thus quantitatively determining the cellular memory of the different variables (Vashistha et al., 2021). Here we examine pairs of unrelated lineages having flown into both sides of the same trap and grown in parallel in that trap – “neighbor lineages”. To allow a fair comparison with the previous section, we used previously published data (Vashistha et al., 2021) of cell-size dynamics measured in MG1655 E. coli as before, grown under the same conditions detailed earlier, i.e., in LB medium at 32°C. Examples of neighbor lineage size measurements are presented in Figure 4B, and the distributions of x₀(n) for both traces in Figure 4C. Note that the traces are more similar to one another, and the distributions of the neighbor lineages measured in the same trap are closer to one another than those of different traps (Figure 1D). Because each trap now includes two separate lineages with different histories and internal cell-states but with a shared environment, the variance conditioned on the trap in Equation 2, now has two components: the temporal fluctuations of each lineage about its own average, and the deviation of each lineage average from the trap average. We use this here to refine our variance decomposition, and thus obtain three components contributing to the total variance: temporal fluctuations, physical trap, and lineage identity within the trap (see STAR Methods). We find that ${\text{Γ}}_{\text{trap}}$ splits into two terms, ${\text{Γ}}_{\text{trap}}={\text{Γ}}_{\text{env}}+{\text{Γ}}_{\text{lin}}.$

Figure 4.

Sisters machine data separates internal from environmental contributions to variance

(A) Two neighboring lineages of E. coli cells grow at the V-shaped bottom of the sisters machine trap, such that they share the same environment but have different lineage histories.

(B) Initial cell size vs generation number for two neighbor cells growing in the same trap (marked red and green in (A)).

(C) Collecting data along the green and red traces results in corresponding initial cell size distribution; pooling all data from the experiment results in the gray pooled ensemble distribution.

(D) Variance decomposition conditioned on trap microenvironment (orange) and on lineage identity (blue), computed from a set of sisters machine experiments. The remaining fraction complementing to 1 represents the contribution of temporal fluctuations. The gray vertical bar is the noise level (finite size sampling effect) estimated by running the same analysis on artificial lineages drawn at random from the pooled ensemble (see STAR Methods).

Figure 4D depicts this decomposition with the two fractions ${\text{Γ}}_{\text{env}},{\text{Γ}}_{\text{lin}}$ marked by orange and blue, respectively. As before, the remaining fraction complementing to one is the contribution of temporal fluctuations around individual lineage averages. For most variables, the contribution of lineage individuality is approximately 2-5% (blue part of bars). With the exception of r, the trap environment is the major source of conditioned variance to all variables in the set of experiments analyzed (orange portion of bars).

Comparison of Figures 3B and 4D provides an important test for the generality of our results: disregarding the internal decomposition into two sources (two colors) in Figure 4D, the total bar heights representing ${\text{Γ}}_{\text{trap}}$ should be similar. Recall that the datasets are taken from two different microfluidic machines; although nominal conditions are the same, in each pooled ensemble the collection of traces is characterized by an uncontrolled variability in environments - everything that is beyond the experimenter’s control (for further dependence on experiments and the effect of pooling see Figure S1). Therefore, it is not surprising that the results are not quantitatively identical. However, a considerable similarity is observed in the values of ${\text{Γ}}_{\text{trap}}+{\text{Γ}}_{\text{lin}}$ between the two setups for all variables. More importantly, an even higher level of repeatability is seen in the relative behavior of the different phenotypic variables. It appears that some are regulated more tightly around a well conserved set point, which is robust to both environmental and internal variability; most pronounced are the variables ϕ and r. In contrast, growth-rate, inter-division time, and size variables have a significant fraction of their variance contributed from different time averages, suggesting they are sensitive to perturbations and regulated only locally around different set points. For further comparison, Figures S2, S3 show the same analysis for previously published results covering two bacterial strains (Wang et al., 2010) and a range of temperatures (Tanouchi et al., 2015). Important features of our results are shared by these data as well.

We next return to the correlations that arise among set points , and their implications on growth and division homeostasis.

Long-term homeostatic correlations in growth and division

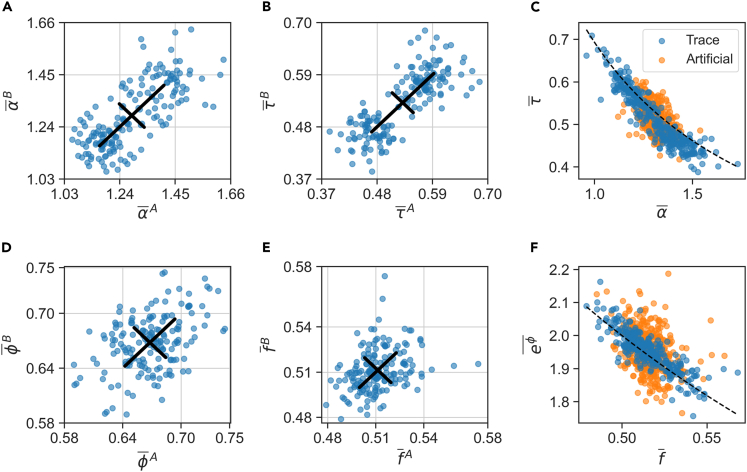
The large contribution of microenvironment to the variance of growth-rate α, as seen in Figures 3B and 4D, indicates that it fluctuates around distinct set-points in different traps. A direct way to visualize this environment dependence is to examine the time averaged growth-rate of two neighbor-lineages grown in the same trap in the sisters machine; Figure 5A shows that they are indeed correlated. The diagonal spread of points represents the range across traps, and is larger than the off-diagonal spread representing variation between one lineage and its neighbor in the same trap. Neighbor cells are correlated only in their set points and not in the fast fluctuations around them (Figures S7, S8), indicating that the effect of the environment has a long timescale, closer to the lineage length than to the single cell cycle time. A qualitatively similar picture emerges for interdivision time, as shown in Figure 5B.

Figure 5.

Covariation of sloppy homeostatic set points

(A and B) Sloppy variables α, τ display a range of homeostatic set points (time averages). Scatter plots for two neighboring lineages in the same microfluidic trap: (A) Exponential growth-rate α, Pearson $\rho =0.74$; (B) generation time τ, $\rho =0.8$. The set points are primarily sensitive to the environment (diagonal spread), and less so to lineage history (off-diagonal spread). Black lines are standard deviations in the two directions.

(C) Within each lineage, set points strongly covary (blue circles; $\rho =-0.9$) and lie close to the line $\overline{\alpha }\overline{\tau }=\text{ln}2$ (dashed black). Orange circles show averages of per-cycle variables over arbitrary groups of the same sizes as lineages (artificial lineages; $\rho =-0.42$).

(D) Scatter plot of fold-growth set points ϕ for neighbor cells, Pearson $\rho =0.43$.

(E) Scatter plot of division fraction set points $\overline{f}$ for neighbor cells, Pearson $\rho =0.33$.

(F) Same presentation as in C, for the variables $\overline{f}$ and $\overline{e^{\varphi }}$. The dashed black line is $\overline{f}\overline{e^{\varphi }}=1$; $\rho =-0.84$ for temporal averages, $\rho =-0.38$ for artificial averages. For a full matrix of set point scatter plots for pairs of variables between neighbor lineages, see Figure S7

By common intuition, homeostasis requires no drift in growth and division across time. With symmetric cell division, this would dictate that cells roughly double their size over the cell-cycle. This in turn requires the set-points of growth-rate and interdivision time to be correlated within each lineage, so that $\overline{\alpha }\overline{\tau }\approx \text{ln}2$; Figure 5C (blue circles) shows that indeed the set points are located along this expected line (black dashed line).

Correlations between growth-rate and interdivision time were previously reported over short times, on a cycle-by-cycle basis (Grilli et al. 2018; Panlilio et al. 2021). Typically such correlations are inferred from a large number of data points, each representing a single cell-cycle from the pooled ensemble, thus making up a noisy cloud; in our experiments, this set of points has a Pearson correlation coefficient of $\rho =\frac{\text{cov}\left(\alpha ,\tau \right)}{{\sigma }_{\alpha }{\sigma }_{\tau }}=-0.52$ (averages and standard deviations computed over pooled ensemble). Had the per-cycle correlations been the only mechanisms at play, correlation between averaged values would reflect a merely statistical effect: they would remain qualitatively the same as the per-cycle correlations, with a possible decreased magnitude because of the smaller dynamic range after averaging. This effect is depicted in Figure 5C by the orange symbols, where arbitrary finite samples from the pooled ensemble were averaged (artificial lineage averages; see STAR Methods for details, $\rho =-0.42$). In contrast, averaging over time in single lineages, we find that the correlation coefficient is dramatically increased, reflecting the large range of distinct and correlated time-averages (blue circles; $\rho =-0.9$).

How can we tease out the contribution of short-term vs. long-term effects to the correlation? Similar to the variance, the covariance between two variables decomposes linearly: $\text{cov}\left(\alpha ,\tau \right)=\text{cov}\left(\overline{\alpha },\overline{\tau }\right)+⟨\text{cov}\left(\delta \alpha ,\delta \tau \right)⟩$. The first term describes the contribution of set point covariance, and the second term describes fluctuation covariance. To obtain a dimensionless measure, we normalize the covariance by the pooled-ensemble standard deviations; this results in a decomposition of the total Pearson correlation coefficient into two terms, neither of which are themselves Pearson correlation coefficients because of their normalization. Nevertheless, this decomposition quantifies the relative contributions coming from long-term and short-term effects (see STAR Methods for details). We find that the total $\rho =-0.52$ decomposes into - 0.28 from long-term and - 0.24 from short-term covariance. This implies that α and τ are negatively correlated on both long (multiple cycles) and short (single cycle) timescales. Note that the high value of $\rho \left(\overline{\alpha },\overline{\tau }\right)=-0.9$ between time averages appears when normalizing correctly by their respective standard deviations $\sigma \left(\overline{\alpha }\right),\sigma \left(\overline{\tau }\right)$, which takes into account the limited dynamic range of time averages (see STAR Methods).

Similar to this analysis for α, τ, covariance decomposition can be carried out for all pairs of variables; the results are presented in Figure S4. Although the correlation between α and τ was found to have contributions from both long and short timescales, this is not the case for all pairs (as discussed in more detail below). We note that in general, despite numeric differences between components of the covariance and Pearson correlation coefficients, the two measures are mostly qualitatively consistent (Figure S4 compared to Figure S5).

As the set points of α, τ lie close to the line of constant product, it is of interest to examine next the product itself: $\overline{\alpha \tau }=\overline{\varphi }$, which is the logarithmic fold-growth in cell size per cycle. This variable is also affected by the trap environment, but to a lesser extent (Figure 5D). The range across different microenvironments is now more similar to the range between neighbors in the same trap; the scatter plot is close to circular. This is just a different way of expressing the smaller relative contribution of trap environment to total variance in ϕ compared to α and τ, which was seen in Figures 3B and 4D. A similar behavior is also displayed by the fraction f, shown in Figure 5E, showing again that this variable keeps its set point more consistent among individual traps.

Applying the no-drift criterion to ϕ, f suggests that deviations from doubling of cell size over the cycle (namely from e^ϕ = 2, or ϕ = ln2) might be compensated by deviation from exactly symmetric division (f = 1/2. Indeed, Figure 5F shows that set points of division ratio and fold-growth are correlated and lie along the line $\overline{f}\overline{e^{\varphi }}=1$. This result is somewhat surprising, as f exhibits the smallest CV among phenotypic variables, and is often considered irrelevant to growth homeostasis. However, a recent study showed that on short timescales f does correlate with the growth rate in the following cell cycle: the smaller-fraction daughter cell was found to grow faster than its larger sister (Kohram et al. 2021; Vashistha et al. 2021).

Examining the decomposition of cov (ϕ, f) into short and long timescales (Figure S4), we find that the largest contribution comes from short-term fluctuations around the set point, approximately $80\text{\%}$. This mostly reflects the small dynamic range of averages $\overline{\varphi },\overline{f}$, relative to the range of per-cycle fluctuations. After normalizing by their respective standard deviations, we find that the time-averages have a high Pearson correlation coefficient, $\rho \left(\overline{\varphi },\overline{f}\right)=-0.8$.

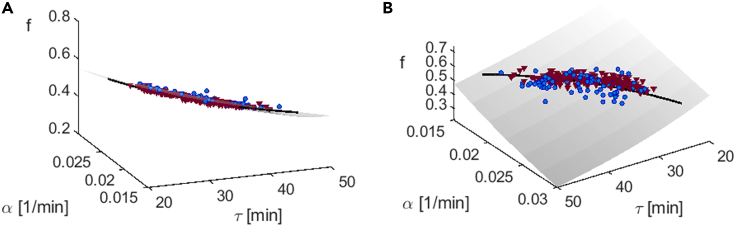
The product of $f\cdot e^{\varphi }=r$ makes up the ratio between cell sizes over a full cycle. Looking back at Figures 3B and 4D we recall that this variable is the tightest of all, holding a strict set point whose contribution to variance is even smaller than the noise level. We interpret this to imply that over long times this variable is tightly regulated to maintain an absolute constant set point, despite variability of its factors. Taken together, these results point to a two-level hierarchy among phenotypic variables: although the set points of α, τ are free to drift with changes in the environment, their product ϕ is more constrained; at the next level, this product is coupled to the division fraction variable f, and their product is in turn even more strongly buffered from perturbations. These processes take place on long timescales of many generations and are revealed by averaging individual traces over sufficiently long time. Looking in the three dimensional space (α, τ, f), Figure 6 shows that the lineage set points adhere to the manifold r (α, τ, f) = fe^ατ = 1 (Figure 6A, side view of manifold); the spread perpendicular to this manifold represents the variability in set points of r, which is precisely its (negligible) conditioned variance in Figures 3B and 4D. In contrast, the variables that make up the combination r span a significant range inside this manifold (Figure 6B, front view of manifold). Most points are close to the line ατ = 1n2; those that deviate are still on the manifold, with values of f removed away from 1/2 to compensate and hold r still close to 1. The three-dimensional structure of the data can be better appreciated through a rotating video (Video S1).

Figure 6.

Homeostasis attractor manifold, two views. Homeostatic set points (temporal averages) of lineages from mother machine experiments (blue circles) and from sisters machine experiments (violet triangles), both grown in LB medium at ${32}^{\circ }$.

(A) Side view, emphasizing the small variability in the direction perpendicular to the manifold.

(B) Front view emphasizing the spread within the manifold, in the vicinity of ατ = 1n2 (black line). In both panels, gray manifold represents r (α, τ, f) = fe^ατ = 1

Video S1. Rotating homeostatic attractor manifold, related to Figure 6

The manifold depicted in Figure 6 is shown rotating around its axis, to highlight the three-dimensional structure of the data. Measured points are seen to spread throughout the manifold but remain close to it.

Cell size variables

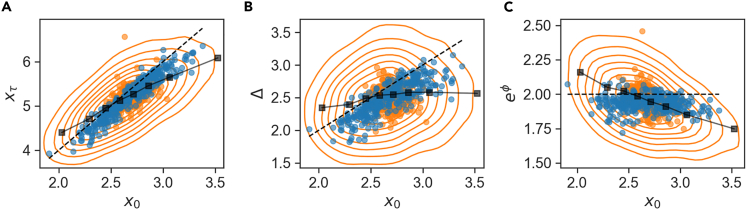
As seen in Figure 3, size variables x₀ and Δ show a significant conditioned variance, indicating sloppy set points across trap environments. This extends and quantifies the results of Susman et al. 2018. The different measures of cell size exhibit long-term correlations among themselves that follow from general intuitive homeostasis arguments. For example, assuming approximately symmetric division, one must have on average $\overline{x_{\tau }}\approx 2\overline{x_0}$. Figure 7A shows that measured lineage time-averages keep this relation to a good approximation (blue circles, with the black dashed line showing the expected relation). This highlights the stability of cell-size homeostasis across time, concomitant with a broad range of size set points maintained in individual lineages - from 2 to 3.5 μm. We compare this to previously studied correlations between per-cycle data over the pooled ensemble, plotted as orange contours in Figure 7A. Interestingly, these show a different positive relation, with a slope closer to 1: $x_{\tau }\approx x_0$ (orange contours). This relation also characterizes the binned per-cycle data (black squares) and their averages over artificial lineages (orange circles), consistent with previous publications, where size progression over a cycle was approximated by a linear map with a slope close to 1 (Amir 2014; Soifer et al., 2016; Tanouchi et al., 2015).

Figure 7.

Cell size correlations over long and short timescales

(A–C)Correlations between initial size and (A) size at division, (B) added size, and (C) fold growth. The orange contours represent percentiles 20 to 80 of the pooled ensemble per-cycle data, black squares are the same data after binning. Blue and orange dots are the averages of real and artificial lineages, respectively. Black dashed lines represent expected relations from general considerations of long-term homeostasis: x_τ = 2x₀ (A), Δ = x₀ (B), e^φ = x_τ/x₀ = 2. The Pearson correlation coefficients for the pooled ensemble, artificial and lineage set points respectively are: 0.61, 0.64, and 0.95 for (A), 0.1, 0.17, and 0.82 for (B) and - 0.43, -.0.35, and - 0.11 for (C).

In terms of the added size Δ = x_τ - x₀, the difference in correlation slopes found in Figure 7A is now transformed into a qualitatively different behavior of pooled vs. time-averaged data. Figure 7B shows that the average values follow approximately $\text{Δ}\approx x_0$ (blue circles with expected black dashed line), consistent with 7A. In contrast, the pooled data shows no correlation between Δ and x₀ – the well-known adder correlation pattern, reported in several types of bacteria (Sauls et al. 2016; Soifer et al., 2016; Willis and Huang, 2017; Yu et al., 2017; Eun et al., 2018). Adder correlations are seen also in the binned data and in averages over artificial lineages (black squares and orange circles, respectively), but not in the time averages (blue circles). Here, we see our first example of qualitatively different correlations between the same phenotypic variables on the short and long timescales (there will be more below). How do such qualitative differences come about?

Figure 7C might provide a clue to answer this question. Previous work has shown that the adder correlation – the independence of added volume on initial size – is equivalent to a negative correlation between fold-growth and initial size (for a derivation see Appendix in Susman et al. 2018). Such negative correlation was reported several times in previous work (Amir 2014; Taheri-Araghi et al. 2015; Brenner et al. 2015; Grilli et al. 2018; Susman et al. 2018). Indeed we observe it in the pooled data (orange contours in Figure 7C), also after binning (black squares) and averaging over artificial lineages (orange circles). However, when averaging over lineages, this correlation is lost; the set points of x₀ and fold-growth e^ϕ (blue circles), show no significant correlation ($\rho =-0.11$). From examining the figure, it can be appreciated that, relative to the range of single-cycle value (contours), $\overline{e^{\varphi }}$ is a stiff variable that spans a narrow range across lineages, whereas $\overline{x_0}$ spans almost the entire range. Therefore, it seems that the lack of correlation over long times is in this case related to the large differences in range of set points between the sloppy cell-size and the stiff fold-change. The residual variability in the set point of e^ϕ is not significantly correlated with that of x₀.

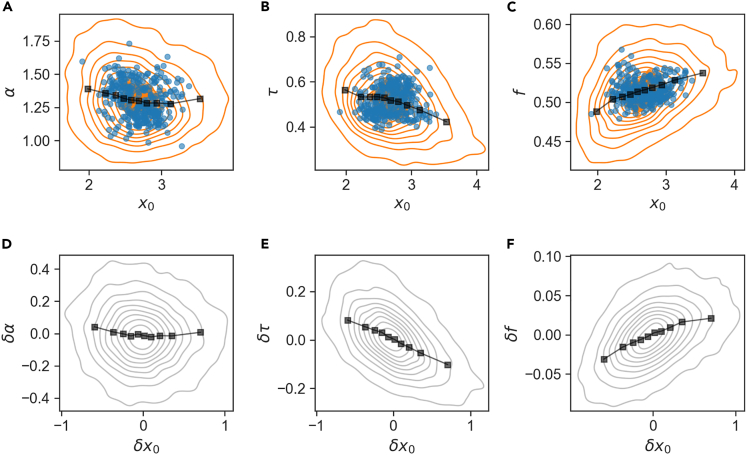
More generally, however, set points of cell-size variables are not significantly correlated with any of the growth variables (α, τ, f) over long timescales, as seen in Figure 8 (A, B, and C blue circles); the correlation is small despite the fact that there is no dramatic difference in the sloppiness of the variables. In fact, long-term homeostasis does not require the connection of size to growth set points: the intuitive arguments on relations between growth variables invoked above (e.g., $\alpha \tau \approx \text{ln}2$), are indifferent to the cell size itself and only refer to relative sizes. Similarly, homeostatic relations between cell size variables themselves (such as $x_{\tau }\approx 2x_0$), can hold for any absolute size and do not contain reference to temporal variables or to division. Therefore, correlations between size and growth/division variables represent specific and short-term mechanisms within the cell cycle. Indeed, recent work points to specific processes such as protein accumulation to threshold for completion of discrete cycle events that underlie such correlations (Si et al. 2020; Nordholt et al. 2020; Kohram et al. 2021). Taking into account that lineages maintain distinct homeostatic set points, we expect such mechanisms to operate on deviations of the variables from their local set point and to be seen most clearly when set points are subtracted. The bottom row in Figure 8 illustrates these short-term correlations: for each variable, the lineage-specific set point is subtracted and correlations are plotted over the pooled ensemble. As expected, we find that compared to the original pooled data (Figure 8, top row), correlations are enhanced when the confounding effect of different set-points is removed. For example, although $\rho \left(x_0,\tau \right)=-0.3$, in relative variables $\rho \left(\delta x_0,\delta \tau \right)=-0.4$.

Figure 8.

Correlations between cell size and growth/division variables

Top: contour plots of correlation between pooled per-cycle variables in physical units (orange contours; $\rho =-0.12,-0.3,-0.37$ for A, B, C, respectively), their binned values (black square) and time averages (blue circles; $\rho =-0.19,-0.1,-0.11$). Bottom: Correlations between fast temporal fluctuations, where lineage set points (long term averages) have been subtracted, sharpen the top row correlations ($\rho =-.05$, - .49, 0.44 for D, E, F.). Gray contours: pooled data for relative variables, black squares: binned data

In a similar approach, all pairs of phenotypic variables were divided into their time-averages and relative variables, and the Pearson correlations between them examined separately. The results, which complement those of the covariance partitioning (Figure S4), are summarized in Figures S5 and S6. Some correlations stem from a simple mathematical dependence, for example $\rho \left(\varphi ,\tau \right)$ reflects the fact that these variables are proportional to one another; others highlight the separate contributions of long and short timescales in the coupling between different variables.

Persistent and anti-persistent temporal fluctuations

The previous analysis suggests that short-term processes over a single cell-cycle are best seen in relative variables, after subtracting the lineage-dependent time average. Correlations over the ensemble are generally sharpened, as the confounding effect of pooling together variables with different averages is removed. However, the correlations across the ensemble still do not tell the whole story – we next focus on the dynamic aspect of the temporal fluctuations.

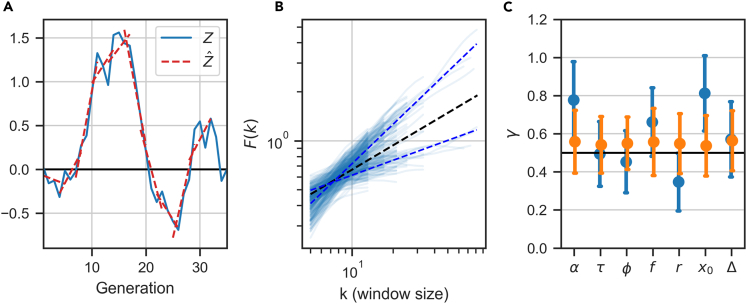
It is often assumed that if a quantity fluctuates, it accumulates error and can cause instability; this intuition comes from independent fluctuations, and is not necessarily the case in the presence of correlations. We use Detrended Fluctuation Analysis (DFA) to measure the degree to which fluctuations of a variable δz_n accumulate (Peng et al. 1995). Given a time-series of fluctuations in a lineage of length N, let $Z={\sum }_{n=1}^N\delta z_n$ be the cumulative sum. If the fluctuations were independent, they would accumulate like a random walk. DFA estimates the standard deviation of fluctuations F(k) around linear approximations of Z in windows of size k, as a function of window size (see STAR Methods). This quantity generally increases with k as a power law, $F\left(k\right)\propto k^{\gamma }$; $\gamma \simeq 0.5$ corresponds to a sequence of independent variables, 0.5 < γ < 1 corresponds to a positive correlation between consecutive steps (a persistent signal), and γ < 0.5 corresponds to a negative correlation between consecutive steps (anti-persistent).

Figure 9 shows the results of this analysis applied to the different phenotypic variables. Figure 9A depicts the outline of the calculation, whereas 9B shows the scaling of F (k) with window size k. For initial size x₀, the scaling is approximately ∼ k^0.8 whereas for ϕ the power is smaller than 1/2. For all phenotypic variables considered, the scaling power is plotted in 9C, together with the control estimation of shuffled lineages; all of these show a power of 1/2 as expected from uncorrelated variables.

Figure 9.

Persistence of phenotypic variables

(A) An illustration of the normalized cumulative sum (blue solid line) and its linear approximation for windows of size k = 5 (red dotted line). F (k) will estimate the standard deviation around the linear fits as a function of window size (see STAR Methods).

(B) Standard deviation of the fluctuations F (k) as a function of window size k for each lineage separately (light blue lines) and averaged over all lineages (dotted blue lines), showing an approximate power law scaling $F\left(k\right)\propto k^{\gamma }$. Top line: x₀, with power γ = 0.81; bottom line: r, with γ = 0.3. The black dotted line illustrates $F\left(k\right)\propto k^{0.5}$, expected for temporally independent fluctuations.

(C) Mean and standard deviation of the scaling exponents for each variable in individual lineages from all mother and sisters machine data (blue symbols). Orange symbols show the same analysis for lineages with shuffled generation order. See Figure S9 for the same analysis on publicly available datasets

The first conclusion from Figure 9C is that the phenotypic variables behave differently from one another also in the temporal aspects of their fluctuations around set points. Moreover, we find that there is an approximate correspondence between sloppiness of set point and accumulation of fluctuations. Extreme examples are cell-size variables and growth-rate, which exhibit super-diffusive scaling γ > 1/2 indicating persistent fluctuations, and correspondingly flexible set points. In contrast r has a very small power of $\approx 0.3$, suggesting it is anti-persistent, and correspondingly a tightly regulated set point. These results indicate the different nature of each cellular variable, which is reflected by its various statistical properties on both long and short timescales.

Discussion

The biological cell is a complex system with a vast number of microscopic degrees of freedom. At the mesoscopic scale, multiple phenotypic variables are dynamically coupled to one another. How gene expression, metabolism, growth, division, and other cell cycle events coordinate to give rise to growth homeostasis over extended time is a fundamental question in biology; even for simple cells such as bacteria, much remains to be understood.

A central challenge when interpreting homeostasis in a multidimensional system is to identify which variables are regulated and which are constrained as a byproduct of interactions. Here, we addressed this question by developing a framework that decouples homeostatic set points from temporal fluctuations around them. Given long enough single-cell measurements, the homeostatic set points can be estimated by the temporal average of each variable. We propose that tightly regulated variables will have robust set points that are buffered from environmental and other perturbations. Other, less regulated variables – while still possibly maintaining homeostasis in the sense of stable distributions – will exhibit a higher sensitivity to environmental changes, reflected by their set points moving around with perturbations.

Our analysis relies on single-cell measurements from trapped E. coli in two types of microfluidic devices. Using the law of total variance and conditioning of data on individual traps, we separated the contribution of set point variation from temporal fluctuations to the total variance. Examining a collection of phenotypic variables, we found a broad range of behaviors, from highly flexible set points that can move up to 30 - 40% of their values, to tightly controlled ones that vary at the level of sampling error or below (Figure 3B). Making use of the recently developed sisters machine, we could assign fractions of the conditioned variance to lineage history separately from the effect of microenvironment. All variables showed a similar sensitivity to lineage history, about 2 - 5% of the total variance; see Figure 4D. This component can be mediated by noise in expression of metabolic enzymes; previous work has demonstrated that such noise can induce metabolic variability that manifests in growth-rate (Labhsetwar et al. 2013; Nikolic et al., 2017). However, this is only a minor contribution to the total variance, leaving the larger portion to the effect of the trap environment. Thus, the graded conditioned variance of different cellular phenotypic variables reflects their wide range of sensitivities with respect to the environment.

The uniqueness of a microfluidic trap is defined in terms of several parameters such as temperature, medium composition, physical dimensions, and perfusion rate. Although most studies routinely pool all data from experiments performed in the same controlled conditions, the limitations of repeatability across experiments was recently highlighted (Yang et al. 2018; Kohram et al. 2021). In the present study, we actually utilized the non-repeatability of trap environments to learn something qualitative about the cell itself. Although we do not have control over the environmental perturbations, we can compare the behavior of different variables and how they co-vary. The qualitative picture arising from the variance decomposition is consistent across several datasets that we have examined. The measurements in Figures 3B and 4D are taken from two different microfluidic devices; Figure S1 shows the effect of pooling together different traps and different experiments, whereas Figures S2 and S3 apply our analysis to publicly available data from other labs. We find that the quantitative values of conditioned variance vary substantially between datasets, but most qualitative observations made in this paper are robust. Future research might extend these comparisons and study different medium conditions and different bacterial species within the same framework.

Examining the correlations between the set points of different variables, we found a pattern indicating a hierarchy of buffering. Time variables – growth-rate and generation time – have sloppy set points, that negatively covary with one another. Their product, logarithmic fold-growth, already buffers some of the external perturbations and exhibits a more robust set point; it is itself negatively correlated with division fraction. Finally, the product of fold-growth and fold-division defines the most protected variable – cell size ratio across consecutive cycles – which is almost perfectly buffered from all types of perturbations, at noise level or below. Based on this picture we predicted that set points are confined to a manifold in the three-dimensional space (α, τ, f); this prediction was verified to high precision by a large set of data.

Our results suggest that, at the mesoscopic scale, phenotypic cellular variables exhibit a hierarchy of sloppiness - the hallmark of a “sloppy system” (Daniels et al. 2008). We have explicitly identified combinations that become increasingly stiff and finally make up a control variable that is highly buffered from perturbations. Keeping this control variable in check is sufficient to ensure the system's functionality, namely, growth and division homeostasis. From a geometric point of view, this implies that homeostasis does not have a well-defined set point but rather a “set manifold”, with different lineages maintaining homeostasis around points scattered inside the manifold. In this view, in-manifold variables define null directions along which changes in time-averaged values do not alter functionality. A similar concept was developed for motor control, specifically for the control of muscles by neural activity, where certain directions in the high-dimensional space of neural activity did not alter the muscle output and were therefore termed “output-null” directions (in contrast to “output-potent” ones, see (Kaufman et al. 2014)). Another biological context where similar concepts were developed is neural excitability, where sensitivity was investigated in parameter space of the Hodgkin-Huxley equations (Ori et al. 2018). There, stiff parameter combinations were identified, which define a continuous region supporting different neuronal functional behaviors: excitable, non-excitable, and oscillatory.

The resulting structure of sloppy and stiff directions with respect to functionality has far-reaching consequences and continues to be investigated (Transtrum et al. 2015). In the context of excitability, it was argued that slow feedback processes at the molecular scale enable adaptive maintenance of system functionality amidst variation in components (Ori et al. 2018). In motor learning, the significance of null-directions was implicated in acquiring new capabilities while keeping functional structures intact (Perich et al. 2018). Indication of a possible analogous role for our system is suggested by recent results on transitions between external conditions (Panlilio et al. 2021); this intriguing possibility calls for further investigation.

The fact that some lineage set points in Figure 6 are not at f = 1/2 but still on the homeostatic manifold, suggests that division fraction can participate in growth and division homeostasis. Our results show that it is strongly coupled to fold-growth such that the two are compensated, though we cannot distinguish which variable actively follows which. Recent results showed that, on the short-timescale of a single cell-cycle, growth rate compensates for the preceding fraction (Kohram et al. 2021; Vashistha et al. 2021); on the long-timescale of many generations, further investigations are needed to decipher the mechanisms involved. Biologically, a set point for division which is consistently different from 1/2 might be an artifact of the trapping apparatus; the breaking of symmetry between daughter cell trajectories can reflect e.g., aging, because we follow the old-pole cell throughout the experiment, or a geometrical constraint, because the mother cell is confined at the bottom of the trap. Clearly, in a dividing population tree, following any particular lineage is arbitrary and division is expected to be symmetric for a long time. Nevertheless, our results demonstrate that division fraction has the capacity to contribute to homeostasis – or to be compensated for – when needed. They also highlight the gap that still remains between our understanding of a trapped lineage and of a population.

The high precision of the homeostatic manifold (Figure 6) suggests that long-term growth and division homeostasis takes place without size control. However in the short-term, cell size clearly couples to growth within a cell-cycle. For example, recent work has shown that certain discrete events related to division depend on threshold accumulation of specific proteins, whose production is in turn dependent on cell size (Nordholt et al. 2020; Panlilio et al. 2021; Si et al. 2020). In other publications growth-rate was reported to compensate, within a single cycle, for noise that occurs at division (Vashistha et al. 2021; Nordholt et al. 2020; Kohram et al. 2021). Such coupling induces correlations between cell size and effective per-cycle variables, e.g., division time and growth-rate; however, these could be an indirect consequence of basic biophysical size-dependent events rather than a regulation mechanism aimed at controlling cell size itself. In support of this view, we found that cell size is a sloppy variable that exhibits a flexible set point, such that different lineages sustain homeostasis around different average cell sizes. Relative to the stiffest variable r, its set point spans a range ∼ 250 times larger. The short-timescale mechanisms involving cell size are possibly separate from the long-term ones that couple the homeostatic set points to one another. Further work is required to test this hypothesis, as well as to decipher the underlying mechanisms on the long timescales.

Our work offers a general methodology for analyzing homeostasis in a multidimensional system from ensembles of temporal data, to reveal tightly controlled variables without prior assumptions. This approach can be widely used and is already being tested in other contexts. Applied to bacterial growth and division, our results taken together highlight the multiple-timescale and multivariable nature of bacterial homeostasis. As more high-quality data that extends over long times accumulate, a future challenge is to test the generality of these observations to other cell populations that maintain stable growth and division.

Limitations of the study

A limitation of our study is the use of uncontrolled environmental variation among traps in microfluidic devices. This is particularly apparent when comparing analysis of data taken from different labs: because measures for keeping the environment stable may differ between labs (for example, incubator for temperature control, etc.), the quantitative range of variability is different depending on details of the experimental system. Further comparative studies on different datasets will help in identifying the common features and those which are strongly dependent on experiment design.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and virus strains
MG1655 E. coli	E. coli Genetic Resources at Yale, CGSC	CGSC#: 6300
Deposited data
Mother machine lineages	Susman et al., Proc. Natl. Acad. Sci. USA 115 (25) 2018.	https://www.pnas.org/content/115/25/E5679.short
Sisters machine lineages	Harsh Vashistha, Maryam Kohram, Hanna Salman, eLife 10:e64779 (2021).	https://elifesciences.org/articles/64779
Recombinant DNA
pZA3R-GFP	Lutz & Bujard, Nucleic Acids Research 25 (6) 1997.	https://academic.oup.com/nar/article/25/6/1203/1197243
Software and algorithms
MATLAB	MathWorks	N/A
ImageJ	Schneider et al., Nature Methods (9) 671–675 2012.	https://imagej.nih.gov/ij/, https://www.nature.com/articles/nmeth.2089
TLM-Tracker	Klein et al., Bioinformatics 28, 2012.	https://europepmc.org/article/med/22772947
Analysis programs	Gitub page for this project	https://github.com/astawsky/Multiple-Timescales-in-Bacterial-Growth-Homeostasis

Resource availability

Lead contact

Further information and requests should be directed to and will be fulfilled by the lead contact. Naama Brenner (nbrenner@technion.ac.il).

Materials availability

This study did not generate new unique reagents.

Experimental model and subject details

This study analyzes experimental data that were previously published. All experimental details are presented in the references as pointed to in the main text and figures.

Methods details

Data processing

Raw movies of dividing bacteria are analyzed to produce time-series of cell length inside microfluidic channels. To detect a division event from the length measurements, we calculated the difference between cell length at consecutive time-points and set a difference threshold that, if passed, means that a division event has most likely occurred. Having identified and verified these division events, we fit an exponential curve to the length measurements in each cycle, whose exponent is the growth-rate and whose intercept is the initial size of the cycle. Other phenotypic variables are derived accordingly (see Figure 3A). The measurements are of high precision and low noise-level, and results are independent of precise definitions; for example, fold-growth can be defined alternatively as ϕ = ατ or 1n (xτ/x₀) with very similar results. Filamentation events were removed from the data by excluding cycles that contain variables 3 standard deviations away from the mean (using single-lineage statistics). Analysis was done in Python and the code is available at our repository on github: https://github.com/astawsky/Multiple-Timescales-in-Bacterial-Growth-Homeostasis.git.

Three-way variance decomposition

For neighbor lineages in a single sisters machine trap, the phenotypic variable z can be expressed as the sum of the trap average $\overline{z}$, deviation of lineage-average from trap-average Δz, and lineage-specific temporal fluctuations δz. Thus at cycle n of the time series,

$$z_n=\overline{z}+\Delta z+\delta z_n\text{.}$$

Specifically if the two lineages A, B grow in the same trap whose total average $\overline{z}$, then for lineage A $\Delta z=\left({\overline{z}}^A-\overline{z}\right)$ and similarly for B. average to zero over the two neighboring lineages A, B, and δz averages to zero over time in each lineage, causing the cross-terms to vanish from the total variance:

$${\sigma }^2\left(z\right)={\sigma }^2\left(\overline{z}\right)+⟨{\sigma }^2\left(\text{Δ}z\right){⟩}_{\text{traps}}+⟨⟨{\sigma }^2\left(\delta z\right)⟩{⟩}_{\text{lin},\text{traps}}={\sigma }^2\left(\overline{z}\right)+{⟨\frac{1}{2}{\left({\overline{z}}^A-\overline{z}\right)}^2+\frac{1}{2}{\left({\overline{z}}^B-\overline{z}\right)}^2⟩}_{\text{traps}}+{⟨\frac{1}{2}\sum _n\left\{{\left(z_n^A-{\overline{z}}^A\right)}^2+{\left(z_n^B-{\overline{z}}^B\right)}^2\right\}⟩}_{\text{traps}}$$

This expression is developed for the case of two lineages of equal lengths. In the more general case, averaging over lineages takes into account the number of cell-cycles in each one with the appropriate weight factor. Using the notation of the law of total variance, and conditioning on groups of events (same lineage, same trap etc), we find the general formula

$${\sigma }^2\left(z\right)={\sigma }^2\left(\overline{z|\text{env}}\right)+⟨{\sigma }^2\left(\left(\overline{z|\text{lin}}\right)|\text{env}\right){⟩}_{\text{env}}+⟨{\sigma }^2\left(z|\text{lin},\text{env}\right){⟩}_{\text{lin},\text{env}}$$ (Equation 4)

Here, the three terms describe the contribution to total variance of trap environment, individual lineages given the environment, and fluctuations within individual lineages around their average. Normalizing by the total variance we find that.

Covariance decomposition

Our variance decomposition for single trapped lineages, specifies how much of the pooled ensemble variance comes from long and short timescales:

$${\sigma }^2\left(z\right)={\sigma }^2\left(\overline{z}\right)+⟨{\sigma }^2\left(\delta z\right)⟩\Rightarrow 1={\text{Γ}}_{trap}+\frac{⟨{\sigma }^2\left(\delta z\right)⟩}{{\sigma }^2\left(z\right)}$$

Where z is phenotypic variable in a single trapped lineage, $z=\overline{z}+\delta z$. If we generalize this equation to the covariance between two phenotypic variables we get:

$$\text{cov}\left(z,y\right)=\text{cov}\left(\overline{z},\overline{y}\right)+⟨\text{cov}\left(\delta z,\delta y\right)⟩\Rightarrow \rho \left(z,y\right)=\frac{\text{cov}\left(\overline{z},\overline{y}\right)}{\sigma \left(z\right)\sigma \left(y\right)}+\frac{⟨\text{cov}\left(\delta z,\delta y\right)⟩}{\sigma \left(z\right)\sigma \left(y\right)}.$$

It is important to emphasize that neither component on the r.h.s.is itself a Pearson correlation, because they are normalized by the pooled standard deviations. In contrast, Pearson coefficients are normalized by their corresponding standard deviations:

$$\rho \left(\overline{z},\overline{y}\right)=\frac{\text{cov}\left(\overline{z},\overline{y}\right)}{\sigma \left(\overline{z}\right)\sigma \left(\overline{y}\right)}\rho \left(\delta z,\delta y\right)=\frac{\text{cov}\left(\delta z,\delta y\right)}{\sigma \left(\delta z\right)\sigma \left(\delta y\right)}.$$

For example, we find cov (α, τ) = -.0083; with the standard deviations of the pooled ensemble σ (α) = 0.222, σ (τ) = 0.131 and the standard deviations of the time-averages themselves $\sigma \left(\overline{\alpha }\right)=0.138,\sigma \left(\overline{\tau }\right)=0.065$, we find

$$\frac{\text{cov}\left(\overline{\alpha },\overline{\tau }\right)}{\sigma \left(\overline{\alpha }\right)\sigma \left(\overline{\tau }\right)}=-0.9,\text{while}\frac{\text{cov}\left(\overline{\alpha },\overline{\tau }\right)}{\sigma \left(\alpha \right)\sigma \left(\tau \right)}=-0.52.$$

Figure S4 presents the covariance decomposition for all pairs of phenotypic variables in the sisters machine data-set.

Detrended Fluctuation Analysis (DFA)

We follow Peng et al. (1995) to characterize the accumulation of fluctuations in a time-series. For a window of a fixed number of cycles k inside the lineage containing N cycles let $\hat{Z}[n:n+k]$ be the least-squares linear regression to the Z [n : n + k] points found inside each window. This line approximates the trend inside the window, and the root-mean-squared deviation of the data around the line is the detrended fluctuation:

$$F\left(k\right)=\sqrt{\frac{1}{N-k-1}{\sum _{n=1}^{N-k-1}\left(Z\left[n:n+k\right]-\hat{Z}\left[n:n+k\right]\right)}^2}$$

For $k\in \left[5,\lfloor \frac{N}{2}\rfloor \right]$, we fit via a least squares linear regression on the log-log graph of F (k) vs. k. In general $F\left(k\right)\propto k^{\gamma }$, where γ is the scaling exponent and tells us how the phenotypic variables of subsequent cycles are correlated. The window sizes increase in steps of 4 until the maximum window size and there is a 3 generation-gap between two windows of the same size. If a lineage has less than three windows sizes we can use to approximate the scaling exponent γ, we discard this lineage.

The need to use a detrended analysis to measure persistence comes from the fact that phenotypic variables in some lineages have a monotonic trend, and are therefore non-stationary In this case, traditional spectral analyses such as the Hurst exponent, autocorrelation function and Fourier transform give slightly incorrect scaling because homeostasis is now around a linear trend, possibly imposed at least in part by a changing micro-environment. For lineages that do not have a trend, the results for DFA and the previously mentioned analyses are equivalent (Peng et al. 1995).

Quantification and statistical analysis

Artificial lineages for statistical baseline

To estimate the statistical effect of finite sampling, we create for each experiment a set of artificial lineages with the same statistics as the measured ones – number of traces and number of generations in each trace. The phenotypic variables are drawn at random from the pooled ensemble and therefore averaging over artificial lineages represents only the statistical effect of averaging over arbitrary finite groups of variables from the pool. This artificial data-set helps to assess the finite-size effects that emerge from the averaging procedure itself, without any temporal information in the actual lineages across time.

Published: February 18, 2022

Data and code availability

• •This paper analyzes published, publicly available data. The accession numbers for the datasets are listed in the key resources table.
• •All original code is available at https://github.com/astawsky/Multiple-Timescales-in-Bacterial-Growth-Homeostasis and is publicly available as of the date of publication.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contacts upon request.