Multi-task learning based structured sparse canonical correlation analysis for brain imaging genetics

Abstract

The advances in technologies for acquiring brain imaging and high-throughput genetic data allow the researcher to access a large amount of multi-modal data. Although the sparse canonical correlation analysis is a powerful bi-multivariate association analysis technique for feature selection, we are still facing major challenges in integrating multi-modal imaging genetic data and yielding biologically meaningful interpretation of imaging genetic findings. In this study, we propose a novel multi-task learning based structured sparse canonical correlation analysis (MTS2CCA) to deliver interpretable results and improve integration in imaging genetics studies. We perform comparative studies with state-of-the-art competing methods on both simulation and real imaging genetic data. On the simulation data, our proposed model has achieved the best performance in terms of canonical correlation coefficients, estimation accuracy, and feature selection accuracy. On the real imaging genetic data, our proposed model has revealed promising features of single-nucleotide polymorphisms and brain regions related to sleep. The identified features can be used to improve clinical score prediction using promising imaging genetic biomarkers. An interesting future direction is to apply our model to additional neurological or psychiatric cohorts such as patients with Alzheimer’s or Parkinson’s disease to demonstrate the generalizability of our method.

1. Introduction

Brain imaging genetics is a data science field focused on integrative analysis of neuroimaging and genetic data (Shen and Thompson, 2020). One widely studied problem in brain imaging genetics is to perform association analysis for identifying genetic variations, such as single nucleotide polymorphisms (SNPs) and copy number of variations (CNVs), which are highly correlated with brain imaging phenotypes, such as cortical thickness, volume, and brain connectivity. These findings can provide valuable insights into the genetic and neurobiological mechanisms of the brain and subsequently aid the investigation of their impact on the normal and disordered brain function and behavior.

The advances of technologies for acquiring brain imaging and high-throughput genetic data allow the researchers to access multi-modal and high dimensional data (Jack Jr et al., 2008; Shen and Thompson, 2020). The multi-view representation learning models, such as canonical correlation analysis (CCA) and parallel independent component analysis (PICA), have been widely used for solving the imaging genetics association problem (Chi et al., 2013; Witten et al., 2009; Pearlson et al., 2015). These models have the advantage of explaining the representation better and capturing more meaningful biomarkers compared with the penalized regression model. One pitfall of the CCA model is the high risk for overfitting due to the high dimensionality of the data. To overcome this challenge, various kinds of regularization methods were applied to the CCA model to simplify model complexity, incorporate biologically meaningful structure, and reduce the risk for overfitting (Du et al., 2014, 2019; Hardoon and Shawe-Taylor, 2011; Kim et al., 2019).

Recently, many researchers have developed and applied several regularization methods and constraints on the CCA model to identify relevant biomarkers and associations and simplify model complexity. For example, the sparse CCA (SCCA) was proposed for detecting sparse bi-multivariate associations by adopting l₁ regularization (i.e., Lasso penalty) (Chi et al., 2013; Witten et al., 2009; Hardoon and Shawe-Taylor, 2011). The group Lasso regularization was employed to encourage group structure information (Yan et al., 2014; Du et al., 2014). Graph-constrained Elastic Net (GraphNet) regularization was applied to the CCA model to incorporate prior biological knowledge (i.e., brain network or correlation structure) (Kim et al., 2019; Du et al., 2016). Some studies extended the fundamental SCCA model to multi-view SCCA (mSCCA) to handle more than two datasets, where SCCA was performed simultaneously for each pair of datasets (Witten and Tibshirani, 2009).

The multi-task learning framework has also been introduced into the CCA model to incorporate multi-modal brain imaging (Du et al., 2019). Despite their success in a few brain imaging genetics applications, these integrative models are still facing several limitations. First, most of them are applicable only to the case of two views, such as association analysis between single modal imaging and genetic data. Second, it remains a challenge to obtain biologically interpretable findings because markers are obtained from the canonical loadings that are computed to maximize the correlation between two datasets.

In this paper, we propose multi-task learning based structured sparse canonical correlation analysis (MTS2CCA) model to 1) incorporate complementary multi-modal imaging information, 2) embrace rather than ignore meaningful biological structures (e.g., linkage disequilibrium [LD] block, pathway, and brain network) and 3) identify relevant biomarkers. Our scientific contributions are summarized as follows.

1. To integrate complementary multi-modal imaging data, we extend the multi-task learning based CCA model. We aim to discover sparse and discriminative shared representation across the multi-modal imaging data.

2. By employing the GraphNet penalty, we incorporate the biologically meaningful structures with the multi-task learning based CCA model. The estimated canonical loadings are constrained by biological structures, which improves model interpretability.

3. We develop an efficient iteratively reweighted algorithm via alternating optimization to solve the problem and prove its convergence theoretically.

4. We perform experiments on both simulation and real data to demonstrate the effectiveness and clinical benefits of the proposed model over the competing algorithms.

The rest of this paper is organized as follows. In Section 2, we describe our proposed model (i.e., MTS2CCA) and an efficient algorithm for solving the proposed model. In Section 3, we present the experimental results on simulation and real imaging genetics data and provide a brief discussion about experimental results. In Section 4, we summarize and describe the potential implications of the study.

2. Methodology

We use the boldface lowercase letter to denote a vector and the boldface uppercase letter to denote a matrix. For matrix X, its i-th row and j-th column are denoted by xⁱ and x_j respectively, x_i denotes the i-th elements in vector x, X_i denoted the i-th matrix, and X_i,j denotes the (i, j)-th element of matrix X.

2.1. Sparse canonical correlation analysis (SCCA)

Let $\mathit{X}\in {\mathcal{R}}^{n\times p}$ and $\mathit{Y}\in {\mathcal{R}}^{n\times q}$ represent the data matrices, where X denotes the genetic data with p variables and Y denotes imaging data with q variables on n subjects. The fundamental SCCA is defined as follows.

$$\begin{gathered} \underset{\mathit{u},\mathit{v}}{\min }-{\mathit{u}}^{\top }{\mathit{X}}^{\top }\mathit{Y}\mathit{v} \\ \text{s.t.}\Vert \mathit{X}\mathit{u}{\Vert }_2^2=1,\Vert \mathit{Y}\mathit{v}{\Vert }_2^2=1,P(\mathit{u})\le c_1,P(\mathit{v})\le c_2, \end{gathered}$$ (1)

where u and v are the canonical loading vectors and P(u) and P(v) are the penalty functions. The goal is to find u and v that maximize the correlation between the genetic feature representation, Xu, and the imaging feature representation, Yv, under one or more constraints. Various kinds of regularization methods have been studied in the literature, such as Lasso, group Lasso, and GraphNet penalty (Chi et al., 2013; Du et al., 2014; Kim et al., 2019; Yan et al., 2014; Du et al., 2016).

2.2. Multi-task based Structured sparse canonical correlation analysis (MTS2CCA)

In this section, we present an algorithm for performing multi-task bi-multivariate imaging genetics association analysis. Let $X\in {\mathcal{R}}^{n\times p}$ and $Y_k\in {\mathcal{R}}^{n\times q}(k=1,\dots ,K)$ represent the data matrices, where X corresponds to the genetic data with p variables on n subjects, Y_k corresponds to the imaging data with q imaging measurements, and K denotes the number of imaging modalities (i.e., tasks). Let $\mathit{U}=\left[{\mathit{u}}_1,{\mathit{u}}_2,\dots ,{\mathit{u}}_k\right]\in {\mathcal{R}}^{p\times K}$ and $\mathit{V}=\left[{\mathit{v}}_1,{\mathit{v}}_2,\dots ,{\mathit{v}}_k\right]\in {\mathcal{R}}^{q\times K}$ be the canonical weight matrices of X and Y, respectively. We propose a multi-task learning based structured sparse canonical correlation analysis (MTS2CCA) model defined as follows.

$$\begin{gathered} \underset{{\mathit{u}}_k,{\mathit{v}}_k}{\min }\sum _{k=1}^K-{\mathit{u}}_k^{\top }{\mathit{X}}^{\top }{\mathit{Y}}_k{\mathit{v}}_k \\ s\text{.}t\text{.}\Vert \mathit{X}\mathit{u}{\Vert }_2^2=1,{\Vert {\mathit{Y}}_k{\mathit{v}}_k\Vert }_2^2=1,\mathrm{\Psi }(\mathit{U})\le a_1,\mathrm{\Psi }(\mathit{V})\le a_2, \\ \mathrm{\Omega }(\mathit{U})\le b_1,\mathrm{\Omega }(\mathit{V})\le b_2,\forall k, \end{gathered}$$ (2)

where Ψ and Ω are the penalty functions to control sparsity and incorporate meaningful biological structures (e.g., LD blocks and brain connectivity), as described in Sections 2.2.1 and 2.2.2. We propose MTS2CCA for the following reasons. First, the multi-task framework is an efficient and robust approach to learn different imaging modalities together (Nie et al., 2010). By applying l_2,1-norm regularization on both canonical weight matrices (i.e., U and V), the model can learn multiple imaging genetics association pairs simultaneously. This helps the model identifying common genetic markers associated with multi-modal imaging measurements in the same brain region. Second, the GraphNet penalty encourages the related elements in the canonical loading vector to be similar based on prior network information (Grosenick et al., 2013; Kim et al., 2019; Du et al., 2016). Thus, we employ the GraphNet penalty to incorporate the prior network information (e.g., LD blocks and brain connectivity). This encourages the model to learn canonical weights based on the network structure to identify meaningful imaging and genetic biomarkers.

2.2.1. Common feature selection across different modalities

Generally, imaging measurements from different modalities are extracted using a common coordinate space (e.g., Montreal Neurological Institute [MNI] space) and a single brain atlas (e.g., Automated Anatomical Label [AAL] atlas and Human Connectome Project’s Multi-Modal Parcellation [HCP-MMP] atlas). Although each imaging modality may capture a distinct brain phenotype, these multi-modal measures have close relathionships due to structal-functional coupling. For example, many studies reported that the structural network could provide the backbone of the functional network and the structural-functional network coupling was associated with higher-order cognitive processes (Baum et al., 2020; Mišić and Sporns, 2016; Kim et al., 2021). Thus, we propose an algorithm that employs the l₂-norm on all the multi-modal measurements for each region to handle co-linearity, and then applies the l₁-norm to select relevant regions. The formulation of l_2,1-norm penalty is defined as follows:

$$\begin{gathered} \mathrm{\Omega }(\mathit{U})=\Vert \mathit{U}{\Vert }_{2,1}=\sum _{i=1}^p\sqrt{\sum _{k=1}^K{\left(U_{i,k}\right)}^2}, \\ \mathrm{\Omega }(\mathit{V})=\Vert \mathit{V}{\Vert }_{2,1}=\sum _{j=1}^q\sqrt{\sum _{k=1}^K{\left(V_{j,k}\right)}^2}. \end{gathered}$$ (3)

Thus, in this work, we apply an l_2,1-norm penalty on the imaging canonical weight matrix (i.e., V) to select common features considering multi-modal imaging measurements. We also apply the penalty on the genetic canonical weight matrix (i.e., U) to learn and select genetic components corresponding to each imaging modality.

2.2.2. Network structure guided feature selection

The l_2,1-norm penalty performs feature selection at the region level, meaning that all the multi-modal features for a given region tend to be selected or deselected together. It is not designed to model prior knowledge about the brain and genome. To overcome this problem, we propose to use a GraphNet penalty to integrate the meaningful biological structures in the brain and genome (Du et al., 2016; Kim et al., 2019; Yan et al., 2014). Many researchers demonstrated that the SNPs and brain imaging features could be modeled using meaningful network structures in the brain and genome (Shen and Thompson, 2020; Hariri and Weinberger, 2003). These comprehensive network data can help to improve the identification of meaningful biomarkers in each modality. Thus, we introduce a GraphNet penalty to embrace this information, defined as follows:

$$\begin{gathered} \psi (\mathit{U})=\Vert \mathit{U}{\Vert }_{gn}=\sum _{k=1}^K{\mathit{u}}_k^{\top }{\mathit{L}}_{\mathit{u}}{\mathit{u}}_k, \\ \psi (\mathit{V})=\Vert \mathit{V}{\Vert }_{gn}=\sum _{k=1}^K{\mathit{v}}_k^{\top }{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k, \end{gathered}$$ (4)

where the matrices L_u and $L_{v_k}$ are the graph Laplacians of the network structure in the genome and multi-model brain imaging, respectively. The graph Laplacian is defined as L = D–A, where D is the degree matrix of the network A (e.g., LD matrix and brain network). This regularization encourages the weights or coefficients to be equal or similar for nodes when they have high connectivity in the network.

In this work, we employ biologically meaningful structures in the form of a graph or network. In the genomic domain, we employ the LD measures computed from 1,000 genome project datasets to create the genetic network, where the edges are weighted by the r-squared values between two SNPs and the nodes are the SNPs. In the neuroimaging domain, we employ group-level functional or structural connectivity computed from the Human Connectome Project (HCP) dataset to form the brain network. The group-level structural connectivity is computed by applying the distance-dependent consensus thresholds based group-representative network model (Betzel et al., 2019b) and the averaged functional connectivity is used as group-level functional connectivity. The detailed procedures for obtaining individual functional and structural connectivity are presented in Section 3.3.1. Our goal is to learn canonical weights based on these networks to identify biologically meaningful biomarkers.

2.3. The Optimization algorithm for MTS2CCA

In this section, we propose an alternating iterative reweighted method to obtain U and V in Eq. 2. In order to solve the Eq. 2, we modify the loss function to

$$\begin{gathered} \underset{\mathit{U},\mathit{V}}{\min }\sum _{k=1}^K\Vert \mathit{X}{\mathit{u}}_k-{\mathit{Y}}_k{\mathit{v}}_k{\Vert }_2^2 \\ s\text{.}t\text{.\hspace{0.22em}}\Vert \mathit{X}{\mathit{u}}_k{\Vert }_2^2=1,\Vert {\mathit{Y}}_k{\mathit{v}}_k{\Vert }_2^2=1,\Vert \mathit{U}{\Vert }_{gn}\le a_1,\Vert \mathit{V}{\Vert }_{gn}\le a_2, \\ \Vert \mathit{U}{\Vert }_{2,1}\le b_1,\Vert \mathit{V}{\Vert }_{2,1}\le b_2,\forall i, \end{gathered}$$ (5)

which is equivalent to the original problem in Eq. 2 due to ${\Vert X{\mathit{u}}_k\Vert }_2^2=1$ and ${\Vert {\mathit{Y}}_k{\mathit{v}}_k\Vert }_2^2=1$. Then, we can rewrite its Lagrangian as follows:

$$\begin{gathered} \mathcal{L}(\mathit{U},\mathit{V})=\sum _{k=1}^K[{\Vert \mathit{X}{\mathit{u}}_k-{\mathit{Y}}_k{\mathit{v}}_k\Vert }_2^2+{\lambda }_1{\mathit{u}}_k^{\top }{\mathit{L}}_{\mathit{u}}{\mathit{u}}_i+{\lambda }_2{\mathit{v}}_k^{\top }{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k+ \\ {\gamma }_1{\Vert \mathit{X}{\mathit{u}}_k\Vert }_2^2+{\gamma }_2{\Vert {\mathit{Y}}_k{\mathit{v}}_k\Vert }_2^2]+{\beta }_1\Vert \mathit{U}{\Vert }_{2,1}+{\beta }_2\Vert \mathit{V}{\Vert }_{2,1} \end{gathered}$$ (6)

where β₁, β₂, γ₁, γ₂, λ₁, and λ₂ are tuning parameters. The problem in Eq. 6 is difficult to solve since its non-convex loss function and non-smooth penalty functions. Fortunately, the non-smooth penalties (i.e., l_2,1 norms of U and V) can be approximated as smooth penalty (defined as ${\sum }_{i=1}^p\sqrt{{\mathit{u}}^{i^{\top }}{\mathit{u}}^i+\zeta }$. Non-convex loss function can be solved using alternatively iterative re-weighted algorithm, since it is convex in U with V fixed, and v_k with those remaining $v_{k^{\prime }}\left(k\ne k^{\prime }\right)$ and U fixed.

2.3.1. Updating U

We first solve U with V fixed by minimizing Eq. 7 as follows.

$$\sum _{k=1}^K\left[{\Vert \mathit{X}{\mathit{u}}_k-{\mathit{Y}}_k{\mathit{v}}_k\Vert }_2^2+{\lambda }_1{\mathit{u}}_k^{\top }{\mathit{L}}_{\mathit{u}}{\mathit{u}}_k+{\gamma }_1{\Vert \mathit{X}{\mathit{u}}_k\Vert }_2^2\right]+{\beta }_1\Vert \mathit{U}{\Vert }_{2,1}.$$ (7)

We take the derivative of $\mathcal{L}(\mathit{U},\mathit{V})$ with respect to U and let it be 0. Then, we can rewrite the problem as follows:

$$2{\mathit{X}}^{\top }\mathit{X}\mathit{U}-2{\mathit{X}}^{\top }\mathit{Y}+2{\gamma }_1{\mathit{X}}^{\top }\mathit{X}\mathit{U}+2{\lambda }_1{\mathit{L}}_{\mathit{u}}\mathit{U}+2{\beta }_1{\mathit{D}}_1\mathit{U}=\mathbf{0},$$ (8)

where $\mathit{Y}=\left[\begin{array}{llll}{\mathit{Y}}_1{\mathit{v}}_1\hfill & {\mathit{Y}}_2{\mathit{v}}_2\hfill & \dots \hfill & {\mathit{Y}}_k{\mathit{v}}_k\hfill \end{array}\right]$, 2D₁U is the subgradient of U_2,1, and D₁ is a diagonal matrix with i-th diagonal element as (D1)_i,i = 1/(2||uⁱ||2)(i ∈ [1, p]). Note that D₁ is constructed based on the estimation of U at the previous iteration and is thus known at the current iteration. Thus, we can derive

$${\mathit{X}}^{\top }\mathit{X}U+{\gamma }_1{\mathit{X}}^{\top }\mathit{X}U+{\lambda }_1{\mathit{L}}_u\mathit{U}+{\beta }_1{\mathit{D}}_1\mathit{U}={\mathit{X}}^T\mathit{Y},$$ (9)

and further

$$\mathit{U}={\left({\mathit{X}}^T\mathit{X}+{\gamma }_1{\mathit{X}}^T\mathit{X}+{\lambda }_1{\mathit{L}}_u+{\beta }_1{\mathit{D}}_1\right)}^{-1}{\mathit{X}}^T\mathit{Y}.$$ (10)

2.3.2. Updating V

We solve individual v_k by fixing those remaining $v_{k^{\prime }}\left(k\ne k^{\prime }\right)$ and U. We take the derivative of $\mathcal{L}(\mathit{U},\mathit{V})$ with respect to v_k and let it be 0. Then, we can rewrite the problem as follows:

$$2{\mathit{Y}}_k^{\top }{\mathit{Y}}_k{\mathit{v}}_k-2{\mathit{Y}}_k^{\top }\mathit{X}{\mathit{u}}_k+2{\gamma }_2{\mathit{Y}}_k^{\top }{\mathit{Y}}_k{\mathit{v}}_k+2{\lambda }_2{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k+2{\beta }_2{\mathit{D}}_2{\mathit{v}}_k=\mathbf{0}.$$ (11)

We can derive

$${\mathit{Y}}_k^{\top }{\mathit{Y}}_k{\mathit{v}}_k+{\gamma }_2{\mathit{Y}}_k^{\top }{\mathit{Y}}_k{\mathit{v}}_k+{\lambda }_2{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k+{\beta }_2{\mathit{D}}_2{\mathit{v}}_k={\mathit{Y}}_k^{\top }\mathit{X}{\mathit{u}}_k,$$ (12)

and further

$${\mathit{v}}_k={\left({\mathit{Y}}_k^{\top }{\mathit{Y}}_k+{\gamma }_2{\mathit{Y}}_k^{\top }{\mathit{Y}}_k+{\lambda }_2{\mathit{L}}_{v_k}+{\beta }_2{\mathit{D}}_2\right)}^{-1}{\mathit{Y}}_k^{\top }\mathit{X}{\mathit{u}}_k.$$ (13)

where D₂ denotes a diagonal matrix with j-th diagonal element as (D2)_jj = 1/(2||v^j||2)(j ∈ [1, q]). Therefore, each v_k can be solved alternatively through an iterative algorithm. We present the pseudo-code in Algorithm 1.

2.4. Convergence analysis

In this section, we prove that the objective function of Eq. 6 is non-increasing in Algorithm 1. First, we consider the following lemma:

Lemma 1:

For any nonzero vectors $a,b\in {\mathcal{R}}^k$, the following inequality holds:

$$\Vert a{\Vert }_2-\frac{\Vert a{\Vert }_2^2}{2\Vert b{\Vert }_2}\le \Vert b{\Vert }_2-\frac{\Vert b{\Vert }_2^2}{2\Vert b{\Vert }_2}.$$ (14)

Proof:

Obviously, arithmetic–geometric mean inequality holds: $\left(\Vert a{\Vert }_2+\Vert b{\Vert }_2\right)/2\ge \sqrt{\Vert a{\Vert }_2\Vert b{\Vert }_2}$. We can derive

$$\begin{gathered} \Vert \mathit{a}{\Vert }_2+\Vert \mathit{b}{\Vert }_2-2\sqrt{\Vert \mathit{a}{\Vert }_2\Vert \mathit{b}{\Vert }_2}\ge 0 \\ \Rightarrow \Vert \mathit{a}{\Vert }_2^2+\Vert \mathit{b}{\Vert }_2^2-2\Vert \mathit{a}{\Vert }_2\Vert \mathit{b}{\Vert }_2\ge 0 \\ \Rightarrow 2\Vert \mathit{a}{\Vert }_2\Vert \mathit{b}{\Vert }_2-\Vert \mathit{a}{\Vert }_2^2\le \Vert \mathit{b}{\Vert }_2^2 \\ \Rightarrow \Vert \mathit{a}{\Vert }_2-\frac{\Vert \mathit{a}{\Vert }_2^2}{2\Vert \mathit{b}{\Vert }_2}\le \Vert \mathit{b}{\Vert }_2-\frac{\Vert \mathit{b}{\Vert }_2^2}{2\Vert \mathit{b}{\Vert }_2}. \end{gathered}$$ (15)

Theorem 1:

Algorithm 1 monotonically decreases the objective of Eq. 6 in each iteration until the algorithm converges.

Proof:

In order to prove theorem 1, we apply alternating iterative re-weighted method to solve minimization problem in Eq. 6. In the t-th iteration, the update U can be computed by minimizing the problem in Eq. 7 as follows:

$$\begin{gathered} {\mathit{U}}^{(t+1)}=\underset{U}{\min }\sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{\top }{\mathit{L}}_u\mathit{U}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{\top }{\mathit{X}}^{\top }\mathit{X}U\right)+{\beta }_1\mathit{Tr}\left({\mathit{U}}^{\top }{\mathit{D}}_1^{(t)}\mathit{U}\right). \end{gathered}$$ (16)

Since U^(t+1) is the optimal solution of Eq. 7, the following inequality holds:

$$\begin{gathered} \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{L}}_u{\mathit{U}}^{(t+1)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t+1)}\right)+{\beta }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{D}}_1^{(t)}{\mathit{U}}^{(t+1)}\right) \\ \le \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{\mathit{L}}_u{\mathit{U}}^{(t)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t)}\right)+{\beta }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{\mathit{D}}_1^{(t)}{\mathit{U}}^{(t)}\right). \end{gathered}$$ (17)

By substituting ${\mathbf{D}}_1^{(t)}$ by definition, following inequality holds:

$$\begin{gathered} \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{L}}_u{\mathit{U}}^{(t+1)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t+1)}\right)+{\beta }_1\sum _{\ell =1}^p\frac{{\Vert {\mathit{u}}^{{\ell }^{(t+1)}}\Vert }_2^2}{2{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2} \\ \le \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{(t)}{\mathit{L}}_u{\mathit{U}}^{(t)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t)}\right)+{\beta }_1\sum _{\ell =1}^p\frac{{\Vert {\mathit{u}}^{\ell (t)}\Vert }_2^2}{2{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2}. \end{gathered}$$ (18)

By substituting a and b in Eq. 15 with ${\mathit{u}}^{{\ell }^{(t+1)}}$ and ${\mathit{u}}^{{\ell }^{(t)}}$ respectively, we can derive

$$\sum _{\ell =1}^p{\Vert {\mathit{u}}^{{\ell }^{(t+1)}}\Vert }_2-\sum _{\ell =1}^p\frac{{\Vert {\mathit{u}}^{{\ell }^{(t+1)}}\Vert }_2^2}{2{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2}\le \sum _{\ell =1}^p{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2-\sum _{\ell =1}^p\frac{{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2^2}{2{\Vert {\mathit{u}}^{\ell (t)}\Vert }_2}.$$ (19)

By summing Eq. 18 and Eq. 19 on both sides, we obtain

$$\begin{gathered} \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{L}}_u{\mathit{U}}^{(t+1)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t+1)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t+1)}\right)+{\beta }_1\sum _{\ell =1}^p{\Vert {\mathit{u}}^{{\ell }^{(t+1)}}\Vert }_2 \\ \le \sum _{k=1}^K{\Vert \mathit{X}{\mathit{u}}_k^{(t)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{L}_u{\mathit{U}}^{(t)}\right) \\ +{\gamma }_1\mathit{Tr}\left({\mathit{U}}^{{(t)}^{\top }}{\mathit{X}}^{\top }\mathit{X}{\mathit{U}}^{(t)}\right)+{\beta }_1\sum _{\ell =1}^p{\Vert {\mathit{u}}^{{\ell }^{(t)}}\Vert }_2. \end{gathered}$$ (20)

We can rewrite

$$\begin{gathered} \sum _{k=1}^K[{\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2+{\lambda }_1{\mathit{u}}_k^{(t+1)}{L}_{\mathit{u}}{\mathit{u}}_k^{(t+1)}+ \\ {\gamma }_1{\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}\Vert }_2^2]+{\beta }_1{\Vert {\mathit{U}}^{(t+1)}\Vert }_{2,1}\le \sum _{k=1}^K[{\Vert \mathit{X}{\mathit{u}}_k^{(t)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}\Vert }_2^2 \\ +{\lambda }_1{\mathit{u}}_k^{{(t)}^{\top }}{\mathit{L}}_u{\mathit{u}}_k^{(t)}+{\gamma }_1{\Vert \mathit{X}{\mathit{u}}_k^{(t)}\Vert }_2^2]+{\beta }_1{\Vert {\mathit{U}}^{(t)}\Vert }_{2,1}. \end{gathered}$$ (21)

The objective value of the problem in Eq. 7 monotonically decreases in each iteration regarding updating U. Similarly, we can hold the following inequality.

$$\begin{gathered} \sum _{k=1}^K[\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}{\Vert }_2^2+{\lambda }_2{\mathit{v}}_k^{{(t+1)}^{\top }}{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k^{(t+1)}+ \\ {\gamma }_2\Vert {\mathit{Y}}_k{\mathit{v}}_k^{(t+1)}{\Vert }_2^2]+{\beta }_2\Vert {\mathit{V}}^{(t+1)}{\Vert }_{2,1}\le \sum _{k=1}^K[\Vert \mathit{X}{\mathit{u}}_k^{(t+1)}-{\mathit{Y}}_k{\mathit{v}}_k^{(t)}{\Vert }_2^2 \\ +{\lambda }_2{\mathit{v}}_k^{{(t)}^{\top }}{\mathit{L}}_{{\mathit{v}}_k}{\mathit{v}}_k^{(t)}+{\gamma }_2\Vert {\mathit{Y}}_k{\mathit{v}}_k^{(t)}{\Vert }_2^2]+{\beta }_2\Vert {\mathit{V}}^{(t)}{\Vert }_{2,1}. \end{gathered}$$ (22)

From 21–22, it follows that Algorithm 1 monotonically decreases the objective of the problem in Eq. 6 in each iteration and the objective function of problem 6 is bounded from below (by e.g., zero), Algorithm 1 will converge to a local optimum solution to problem 6. Moreover, according to (Bezdek and Hathaway, 2002, 2003), the rate of convergence is linear.

3. Results and discussion

3.1. Benchmarks and experimental setups

We applied and compared our model with several state-of-the-art CCA models to demonstrate the strengths of the proposed model. Many researchers have successfully adopted multi-modal brain imaging data into canonical correlation analysis. We carefully choose five related methods for comparison: 1) sparse canonical correlation analysis (SCCA) (Chi et al., 2013), 2) multi-task learning based sparse canonical correlation analysis (MTSCCA) (Xu et al., 2019), 3) multi-task learning based group sparse canonical correlation analysis (MTGSCCA) (Du et al., 2019), 4) joint-connectivity-based sparse canonical correlation analysis (JCBSCCA) (Kim et al., 2019), and 5) tensor based canonical correlation analysis (TCCA) (Min et al., 2019).

• The standard SCCA is applied to discover the association between two datasets. It learns only a single canonical weight thus cannot fully estimate from different modalities simultaneously.

• MTSCCA studies bi-multivariate association with l_2,1-norm to discover compact and discriminative representation for multiple modalities. The; _2,1-norm enables the model to select variables in the canonical loadings and learn a common canonical representation that keeps consistent with the most canonical variables from each modality. However, it is limited to incorporate biological knowledge or structure.

• MTGSCCA is an extension of the MTSCCA by combining group l_2,1-norm and l_2,1-norm to incorporate group information. Although group l_2,1 regularization enables us to take into consideration the group structure, it is challenging to incorporate weighted overlapped prior knowledge based on group l_2,1-norm.

• JCBSCCA employs GraphNet penalty and fused lasso to incorporate prior knowledge and handle a multi-modal dataset. However, the fused lasso is limited to incorporated three or more neuroimaging modalities and difficult to optimize the objective function efficiently.

• TCCA enables the identification of a relationship between two tensors with fewer parameters. However, it is limited to handle multi-modal datasets and obtain optimal hyperparameters.

The single-task CCA models were performed with concatenated multi-modal imaging measurements (i.e., TCCA and SCCA). The performances of these models were evaluated on the simulation data in terms of the correlation, feature selection accuracy, and estimation accuracy. In addition, we applied the proposed model to the real imaging genetics data to demonstrate its clinical benefits and interpretability.

We apply nested five-fold cross valication strategy to examine the performance of the models. In the outer loop, the dataset is split into five different folds. The model is trained and tested in the cross-validate fashion where four of them are used as the training set and one of them is used as the testing set. In the inner loop, we train and tune hyper-parameters using cross-validation fashion on the training set. All parameters (e.g., λ₁, λ₂, β₁, β₂, γ₁, and γ₂) are jointly tuned by five-fold cross validation, defined as follows:

$$\mathit{C}V=\frac{1}{5}\sum _{i=1}^{5}corr\left({\mathit{X}}_i{\mathit{u}}_{-i},{\mathit{Y}}_i{\mathit{v}}_{-i}\right),$$ (23)

where X_i and Y_i denoted the i-th subset of the dataset (validation set); u_−i and v_−i denoted the estimated loading vectors from the dataset except for the i-th subset (train set, X_−i, and Y_−i). We tuned the parameters via a grid search with the following finite set: [0.01, 0.1, 1, 10, 100]. The optimal parameters were obtained by maximizing CV in Eq. 23 for training set in inner loop. Once the optimal hyper-parameters were determined, we trained the model with these parameters on the training set and then applied it into the testing set in the outer loop to generate the final results.

3.2. Simulation study

In this section, we present the comparison results on the simulation data to evaluate the potential power of the proposed MTS2CCA model. We measure the training and testing canonical correlation coefficients (CCCs) to evaluate the generalizability of the model. Additionally, we measure angle between estimated loading vector and ground truth vector to evalute estimation accuracy, and area under the curve (AUC) between ground truth vector and estimated loading vector to evalute feaure selection accuracy.

3.2.1. Simulation setup

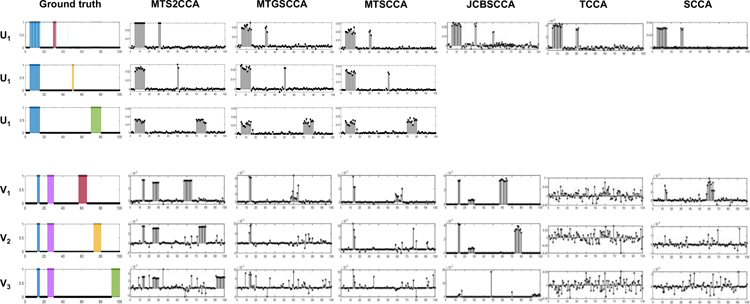
We generate two sets of simulation data using a generative model described in (Min et al., 2019). Fig. 1 shows the ground truth signal vectors U and V. The simulation data X is generated with a true signal vector U, and the simulation data Y_k are generated with true signal vectors V_k. For each data, we generate three different association patterns, such as modality-common, modality-specific, and network driven association patterns. For modality-common association, we set the association between X and Y_k(k = 1, 2, 3), where the blue variables in Fig. 1-(a) and (b) (variables a and A) have a high correlation. Modality-specific association patterns were generated between X and Y_k(k = 1, 2, 3) pairs, where the red, yellow, green variables U and V have associations (variables b and B, c and C, d and D in Fig. 1). For network-driven association, we set a association based on pre-defined network structure, where the structure have a connectivity between sparse sets of variable in Y_k(k = 1, 2, 3). In Fig. 1, blue and purple variable in V have a high correlation (variable A and F in Fig. 1).

Fig. 1:

Ground truth signal vectors of simulation data. Sub-figure-(a) and (b) present ground truth signals and association patterns in U and V, respectively. In simulation data, we generate modality-common (variables a and A), modality-specific (variables b and B, c and C, and d and D), and network-driven association pattern (variable A and F).

To evaluate the performance of methods, we simulate low-dimensional and high-dimensional problem, Data 1 and 2. In Data 1, we generate the simulation data X and Y_i with true signal vectors U and V_i respectively, where p = q = 100 and n = 1,000. Fig. 2-(a) shows the ground truth signals U and V_i. In Data 2, we generate the simulation data X and Y_i with true signal vectors U and V_i respectively, where p = q = 300 and n = 100. Fig. 2-(b) shows the ground truth signals U and V_i. The samples were generated with different true correlation levels: true CCC between X and Y₁ is 0.9, true CCC between X and Y₂ is 0.6, and true CCC between X and Y₃ is 0.3.

Fig. 2:

The estimated canonical loading vectors on simulation data. The first column corresponds to the ground truth signal, where blue, red, yellow, and purple signals represent different association patterns. The remaining columns present estimated canonical loading vectors of SCCA models: MTS2CCA, MTGSCCA, MTSCCA, JCBSCCA, TCCA, and SCCA, respectively. For MTS2CCA, MTGSCCA, and MTSCCA, the first three rows present u₁, u₂, and u₃, respectively. Only u is presented for JCBSCCA, TCCA, and SCCA. The remaining rows present canonical loading vectors v₁, v₂, and v₃.

3.2.2. Simulation results

We first compared the training and testing performances in terms of CCC in Table 1. All methods generally performed well when true CCC was high (X vs. Y₁). The multi-task CCA models, including MTS2CCA, MTGSCCA, MTSCCA, and JCBSCCA, outperformed single task CCA models, when true CCC was medium (X vs. Y₂). When true CCC was extremely low (X vs. Y₃), the proposed model outperformed all the competing methods. Although we observed the SCCA showed the highest training and testing CCC between X vs. Y₁, the performance differences with other competing methods were very small. These results suggested that the multi-task learning strategy had an improved ability to identify the associations among three or more views of data, and worked especially better for a low canonical correlation setup.

Table 1:

The canonical correlation coefficients on simulation data. The training and testing canonical correlation coefficients (mean ± std) of nested five-fold cross-validation were reported. For each model, the canonical correlation coefficients of multi-modal associations were presented in separate rows.

Methods		Training canonical correlation coefficients						Testing canonical correlation coefficients
		fold 1	fold 2	fold 3	fold 4	fold 5	mean ± std	fold 1	fold 2	fold 3	fold 4	fold 5	mean ± std
MTS2CCA	X vs. Y1	0.906	0.906	0.913	0.912	0.909	0.909±0.003	0.890	0.893	0.861	0.851	0.892	0.877±0.020
	X vs. Y2	0.621	0.639	0.623	0.605	0.642	0.626±0.015	0.505	0.381	0.487	0.471	0.457	0.461±0.048
	X vs. Y3	0.414	0.392	0.383	0.402	0.422	0.403±0.016	0.227	0.167	0.100	0.040	0.105	0.128±0.071
MTGSCCA	X vs. Y1	0.907	0.905	0.903	0.905	0.904	0.905±0.001	0.902	0.848	0.854	0.856	0.883	0.869±0.023
	X vs. Y2	0.625	0.653	0.626	0.608	0.627	0.628±0.016	0.474	0.374	0.501	0.544	0.412	0.461±0.068
	X vs. Y3	0.389	0.396	0.399	0.430	0.406	0.404±0.016	0.181	0.142	0.040	0.005	0.169	0.107±0.079
MTSCCA	X vs. Y1	0.909	0.897	0.900	0.910	0.901	0.903±0.006	0.855	0.887	0.871	0.850	0.887	0.870±0.018
	X vs. Y2	0.628	0.628	0.618	0.628	0.613	0.623±0.007	0.474	0.487	0.455	0.468	0.481	0.473±0.012
	X vs. Y3	0.377	0.393	0.383	0.411	0.422	0.397±0.019	0.116	0.060	0.144	0.161	0.066	0.110±0.045
JCBSCCA	X vs. Y1	0.765	0.754	0.806	0.764	0.798	0.777±0.023	0.781	0.685	0.774	0.731	0.792	0.753±0.044
	X vs. Y2	0.539	0.528	0.542	0.515	0.525	0.530±0.011	0.389	0.397	0.415	0.411	0.371	0.397±0.018
	X vs. Y3	0.320	0.293	0.207	0.266	0.252	0.268±0.043	−0.004	0.009	0.038	0.069	0.066	0.036±0.033
TCCA	X vs. Y1	0.903	0.883	0.904	0.900	0.893	0.897±0.009	0.845	0.861	0.857	0.817	0.879	0.852±0.023
	X vs. Y2	0.130	0.149	0.117	0.144	0.179	0.144±0.023	0.086	−0.007	0.042	0.035	0.223	0.076±0.089
	X vs. Y3	0.130	0.121	−0.001	0.081	0.151	0.097±0.060	−0.041	−0.071	−0.043	−0.151	−0.069	0.075±0.045
SCCA	X vs. Y1	0.917	0.910	0.919	0.914	0.909	0.914±0.004	0.853	0.898	0.866	0.893	0.901	0.882±0.021
	X vs. Y2	0.117	0.118	0.120	0.048	0.113	0.103±0.031	0.037	0.031	0.047	−0.022	0.090	0.037±0.040
	X vs. Y3	0.031	0.099	0.036	0.026	0.102	0.059±0.038	0.016	−0.149	0.123	−0.070	0.007	−0.015±0.102

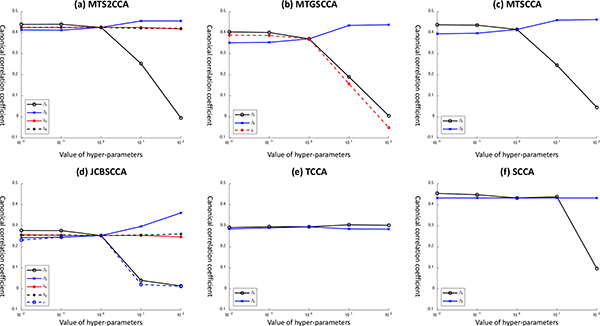
In addition, we compared the parameter sensitivity of models. We measured the CCC by varying the parameter from 0.01 to 100 with a scale factor of 10 and fixing the remaining parameters to 1 for simplicity. As shown in Fig. 3, for all methods except TCCA, CCC curves appear stable and insensitive to β₁, which controls the sparsity for dataset X. However, CCC curves drop from 100 or higher for β₂, which controls the sparsity for dataset Y. CCC curves are stable and insensitive to both β₁ and β₂ in TCCA. For MTS2CCA and JCBSCCA, CCC curves appear to be stable and insensitive to λ₁ and λ₂, where it controls the level of incorporating network information for both dataset X and Y. For MTGSCCA, CCC curves drop while λ increases; λ controls the level of incorporating group structure for dataset X. These findings indicate that the CCA with GraphNet penalty is more stable to incorporate prior knowledge than GroupLasso. Both CCA with l_2,1 regularizer and FusedLasso are sensitive for multi-modal data integration setup.

Fig. 3:

Parameter sensitivitiy of CCA models. We measured the CCC by varying the parameter from 0.01 to 100 with a scale factor of 10 and fixing the remaining parameters to 1 for simplicity.

The estimated u_k and v_k were plotted in Fig. 2. For the MTS2CCA, MTGSCCA, and MTSCCA, the estimated u_k (k=1,2,3) were plotted in the first three rows of Fig. 2. For the JCBSCCA, TCCA, and SCCA, The estimated u was plotted. For all methods, three estimated v_k (k=1,2,3) were plotted in the last three rows of Fig. 2. To compare the estimation accuracy of the model, we measured the cosine similarity between estimated canonical loading vector $\tilde{u}$ and ground truth signal u. The cosine similarity was defined as cose $(u,\tilde{u})=\langle u,\tilde{u}\rangle /\Vert u{\Vert }_2\Vert \tilde{u}{\Vert }_2$. We observed that the proposed model showed the best estimation accuracy for all canonical loading weights compared with competing methods, as shown in Table 3. Specifically, we observed that the proposed model and JCBSCCA performed better than MTGSCCA and MTSCCA in terms of angle of V. In Fig. 2, the proposed model and JCBSCCA showed the ability to identify the correct location of the network association signals. This demonstrated that the GraphNet penalty could help with association discovery from predefined network structure.

Table 3:

The estimation accuracy on simulation data. The cosine similarity between estimated loading vector and ground truth is presented in each row. The best values are shown in bold text.

	MTS2CCA	MTGSCCA	MTSCCA	JCBSCCA	TCCA	SCCA
u 1	0.999	0.999	0.999	0.990	0.997	0.999
u 2	0.991	0.991	0.991	0.983	0.726	0.136
u 3	0.966	0.962	0.963	0.819	0.549	0.071
v 1	0.990	0.782	0.768	0.919	0.394	0.741
v 2	0.968	0.708	0.685	0.986	0.032	0.042
v 3	0.610	0.449	0.449	0.174	0.034	0.032

In addition, we evaluated the feature selection accuracy of the various CCA models by calculating the area under the curve (AUC). The results showed that the multi-task CCA models performed better than single-task CCA models for detecting the signals. Specifically, the multi-task CCA model was robust to the low correlation level, while SCCA and TCCA were not. The multi-task CCA models with GraphNet penalty (e.g., MTS2CCA and JCBSCCA) performed slightly better than those without GrapnNet penalty, especially on detecting network-driven association signals as shown in Fig 2. This indicated that owing to the multi-task learning framework and GraphNet regularization, the feature selection accuracy for bi-multivariate association can be improved.

The computation time and memory consumption for each method are shown in Table 4 and 5, respectively. We measured the computation time using a machine with a single 3.6-GHz octa-core Intel i9 CPU and 32-GB memory. There was no significant difference between these methods, except TCCA. In addition, SCCA consumes the least memory usage (3.77MB) and TCCA consumes the most memory usage (14.60MB). Except TCCA and SCCA, there is no significant difference in memory usage between the methods. Despite complex constraints in the model, the empirical study on the simulation data demonstrated the effectiveness and efficiency of the proposed algorithm.

Table 4:

The computation time and memory usage comparison on simulation data. The computation time (mean ± std seconds) was measured during the model training. The memory usage (mean ± std mega bytes) is measured during the model training.

	MTS2CCA	MTGSCCA	MTSCCA	JCBSCCA	TCCA	SCCA
Time	0.042 ± 0.019	0.045 ± 0.026	0.041 ± 0.018	0.115 ± 0.253	5.782 ± 1.769	0.041 ± 0.025
Memory	4.68 ± 0.69	4.67 ± 0.17	4.67 ± 0.11	4.66 ± 0.18	14.60 ± 7.74	3.77 ± 0.68

Table 5:

Demographic information.

Participant characteristics
Number of Subjects	291
Gender(M/F)	144/147
Age (year, mean±std)	28.63 ± 3.67
Education (year, mean±std)	15.15 ± 1.62

3.3. Results on real imaging genetics data

We present our results on real imaging genetics data, where the proposed model has been applied and compared with six state-of-the-art CCA models, including MTGSCCA, MTSCCA, JCBSCCA, TCCA, and SCCA. The multi-modal neuroimaging data and genotyping data were obtained from the HCP database. We evaluated the CCA model performances and their predictive powers using the identified imaging and genetic feature representations for the studied outcome of interest. In addition, we performed neurosynth meta-analysis and gene enrichment analysis to functionally annotate the selected brain regions and genetic variants and provide biological interpretation.

3.3.1. Dataset

In this study, we collected the neuroimaging data, including resting-state functional magnetic resonance imaging (rs-fMRI) and diffusion-weighted MRI (dMRI), and the genotyping data of 291 participants from the HCP database (Van Essen et al., 2013). This HCP subset includes participants who are genetically unrelated and non-Hispanic and have full demographic information. Table 5 shows the participant characteristics.

Brain connectivity toolbox (BCT) was employed to extract connectivity measurement (i.e., degree centrality) from functional and structural connectivity (Rubinov and Sporns, 2010). For each subject, preprocessed rs-fMRI and dMRI data were obtained from the HCP database. For rs-MRI data, the functional connectivity matrix was calculated by Pearson’s correlation analysis between the two different brain regions. The HCP-MMP atlas, which is the most detailed cortical in-vivo parcellations with 360 regions, was used as nodes of the connectivity (Glasser et al., 2016). For dMRI data, the FSL software was used to construct the structural connectivity (Smith et al., 2004). The HCP database provided the preprocessed dMRI, which estimated the fiber orientation using FSL’s multi-shell spherical deconvolution toolbox (bedpostx) (Jbabdi et al., 2012). We performed probtrackX to estimate fiber streamlines and mapped onto the 360 regions of HCP-MMP to build the structural connectivity matrix (Behrens et al., 2003). The degree centrality was then obtained by applying BCT on each connectivity matrix. We applied the distance-dependent consensus thresholding method to generate the average group-level connectivity network, and this network was used as the GraphNet constraint of the neuroimaging data in our model (Betzel et al., 2019a).

The genotyping data released by HCP was obtained from the dbGAP website, under phs001364.v1.p1 (Mailman et al., 2007). Illumina Multi-Ethic Global Array (MEGA) SNP-array was used for genotyping 1,580,642 SNPs data for all subjects. The quality of genotyping data was controlled using the following condition: SNPs with a minor allele frequency < 1%, Hardy–Weinberg equilibrium < 10⁻⁶, or genotype missing rate > 5% were excluded. The associations between mental ability measures (e.g., DSM-5 depression score and anxiety score) and SNPs were assessed by performing GWAS using the PLINK software (Purcell et al., 2007), where we employed a linear regression model adjusting sex, age, and education as covariates. We obtained 981 candidate SNPs significantly related to mental ability measurements (p-value < 0.0005). These findings were used for the subsequent analyses. In addition, we computed LD matrix based on 1,000 genome project and used it as GraphNet constraints of genotyping data in our model (Clarke et al., 2017).

3.3.2. Multi-task imaging genetics associations

We evaluate the proposed model in terms of CCC for the multi-task imaging genetics association, including the association between the SNPs and fMRI (SNP-fMRI) and the association between the SNPs and dMRI (SNP-dMRI). Tables 6 and 7 show training and testing CCCs of multi-task imaging genetic associations computed from various state-of-the-art CCA models. For SNP-fMRI association, MTS2CCA, MTGSCCA, MTSCCA, and JCBSCCA showed excellent training CCCs and relatively good testing CCCs compared with TCCA and SCCA. For SNP-dMRI association, MTS2CCA, MTGSCCA, MTSCCA, JCBSCCA, and SCCA showed excellent training CCCs and relatively good testing CCCs compared with TCCA. Overall, we observed that MTS2CCA showed the highest testing CCCs on both SNP-dMRI (0.689 ± 0.011 of training and 0.236 ± 0.060 of testing CCCs) and SNP-fMRI tasks (0.738 ± 0.017 of training and 0.295 ± 0.105 of testing CCCs). For single-task CCA model, we compared the model using concatenated multi-modal imaging measurements (i.e., TCCA and SCCA) to pair-wise model (i.e., TCCA-p and SCCA-p). We observed overfitted CCCs both SCCA and TCCA in pair-wise analysis. Specifically, we observed that SCCA was overfitted both SNP-fMRI association (i.e., 0.976 ± 0.037 of training and 0.120 ± 0.175 of testing CCCs) and SNP-dMRI association (0.855 ± 0.045 of training and 0.122 ± 0.135 of testing CCCs). For TCCA, we observed overfitted CCCs on both SNP-fMRI association (i.e., 0.986 ± 0.013 of training and 0.201 ± 0.100 of testing CCCs) and SNP-dMRI association (0.949 ± 0.041 of training and −0.048 ± 0.060 of testing CCCs). This indicated that the multi-task learning strategy and graphnet constraint showed the ability to improve multi-task bi-multivariate association on real imaging genetics applications.

Table 6:

The canonical correlation coefficients between fMRI and SNP. The training and testing canonical correlation coefficients (mean ± std) of five-fold cross-validation were reported. The best values are shown in bold text.

Methods	Training canonical correlation coefficients						Testing canonical correlation coefficients
	fold 1	fold 2	fold 3	fold 4	fold 5	mean±std	fold 1	fold 2	fold 3	fold 4	fold 5	mean±std
MTS2CCA	0.718	0.745	0.762	0.735	0.729	0.738±0.017	0.327	0.110	0.367	0.354	0.320	0.295±0.105
MTGSCCA	0.907	0.821	0.842	0.960	0.895	0.874±0.054	0.315	0.022	0.319	0.317	0.240	0.243±0.128
MTSCCA	0.884	0.895	0.959	0.949	0.901	0.901±0.034	0.256	0.014	0.323	0.294	0.238	0.225±0.122
JCBSCCA	0.662	0.587	0.674	0.631	0.658	0.658±0.035	0.270	−0.121	0.356	0.253	0.267	0.205±0.187
TCCA	0.381	0.572	0.584	0.171	0.431	0.428±0.168	0.155	−0.159	−0.049	−0.187	−0.085	−0.065±0.135
SCCA	0.362	0.445	0.503	0.430	0.439	0.436±0.050	−0.051	0.019	0.025	0.130	0.050	0.034±0.065

Table 7:

The canonical correlation coefficients between dMRI and SNP. The training and testing canonical correlation coefficients (mean±std) of five-fold cross-validation were reported. The best values are shown in bold text.

Methods	Training canonical correlation coefficients						Testing canonical correlation coefficients
	fold 1	fold 2	fold 3	fold 4	fold 5	mean ± std	fold 1	fold 2	fold 3	fold 4	fold 5	mean ± std
MTS2CCA	0.686	0.698	0.686	0.701	0.672	0.689±0.011	0.238	0.200	0.277	0.157	0.307	0.236±0.060
MTGSCCA	0.795	0.815	0.953	0.857	0.838	0.852±0.061	0.220	0.225	0.204	0.146	0.324	0.224±0.064
MTSCCA	0.857	0.878	0.953	0.928	0.879	0.899±0.040	0.216	0.198	0.210	0.113	0.281	0.204±0.060
JCBCCA	0.653	0.554	0.607	0.629	0.606	0.610±0.037	0.200	0.222	0.296	0.178	0.229	0.225±0.044
TCCA	0.840	0.677	0.646	0.918	0.776	0.771±0.113	0.091	0.049	0.083	0.018	0.057	0.060±0.029
SCCA	0.620	0.574	0.663	0.600	0.536	0.599±0.042	0.158	0.363	0.186	0.144	0.266	0.223±0.091

3.3.3. Multi-task imaging genetics integration and its clinical benefits

We applied the proposed model to integrate imaging genetic data and evaluated its clinical benefits by predicting behavioral score using the imaging and genetics feature representations learned from the model. As mental disorders, such as depression and anxiety, are associated with sleep disturbances, we show the clinical benefits of the model by predicting the Pittsburgh sleep quality index (PSQI) scores. The multivariate linear regression model was used for predicting the PSQI score, where the imaging genetics feature representations were considered as the predictors, PSQI score was considered as the response variable, and sex, age, and education were considered as covariates. In addition, we compared our model with state-of-arts regression-based model (i.e., the deep collaborative learning (DCL) model) to demonstrate generalized ability of model without target phenotypes (Hu et al., 2019). The nested five-fold cross-validation was employed to examine the prediction performance. The prediction performance of the model was evaluated using root-mean-square error (RMSE) and Pearson’s correlation coefficient (CC) between the actual and predicted scores.

As shown in Table 8, the proposed model outperformed three multi-task CCA models as well as single-task CCA models, in terms of RMSE and CC. The prediction model using feature representation from the proposed model yielded the highest CC of 0.292±0.092 and the lowest RMSE of 2.654±0.307 between the actual and predicted PSQI scores. The model with feature representation from DCL yielded the second-highest CC of 0.274±0.083 with the RMSE of 2.874±0.491, and the model with MTGSCCA took the third place (i.e., CC of 0.214±0.111 with the RMSE of 2.719±0.328). In addition, the prediction model using all genetics and imaging data (i.e., 981 SNPs, 360 ROIs from fMRI and dMRI) yielded 13.97±1.46 of RMSE and −0.01±0.10 of CC, the model using genetic data (981 SNPs) alone obtained 11.38±1.68 of RMSE and −0.09±0.14, the model using dMRI (360 ROIs from dMRI) alone obtained 16.37±5.12 of RMSE and 0.02±0.18 of CC, and the model using fMRI (360 ROIs from fMRI) alone obtained 13.97±1.46 of RMSE and −0.01±010 of CC.

Table 8:

The comparison of prediction performance. The prediction performance was reported in terms of the root-mean-squared error (RMSE) and correlation coefficients (r) between actual and predicted scores. The values were reported as format of mean ± standard deviation (std).

Methods		fold1	fold2	fold3	fold4	fold5	Mean ± std
MTS2CCA	r	0.183	0.350	0.417	0.260	0.252	0.292±0.092
	RMSE	3.105	2.490	2.828	2.492	2.355	2.654±0.307
MTGSCCA	r	0.044	0.243	0.352	0.196	0.237	0.214±0.111
	RMSE	3.193	2.575	2.913	2.527	2.388	2.719±0.328
MTSCCA	r	−0.088	0.256	0.350	0.176	0.174	0.174±0.163
	RMSE	3.322	2.567	2.913	2.536	2.484	2.764±0.355
JCBSCCA	r	0.102	0.166	0.354	0.270	0.165	0.212±0.100
	RMSE	3.122	2.616	2.982	2.481	2.454	2.731±0.303
TCCA	r	0.307	0.290	0.079	0.091	0.217	0.197±0.108
	RMSE	3.043	2.593	3.099	2.568	2.369	2.734±0.320
SCCA	r	−0.151	0.155	0.130	0.210	0.037	0.076±0.141
	RMSE	3.304	2.621	3.153	2.524	2.557	2.832±0.368
DCL	r	0.166	0.369	0.334	0.285	0.217	0.274±0.083
	RMSE	3.471	2.615	3.317	2.623	2.344	2.874±0.491

3.3.4. Interpretation of selected imaging markers

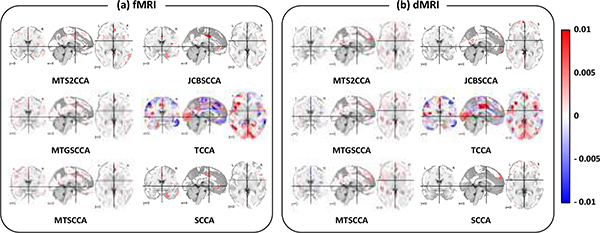
The estimated imaging canonical loading vectors for each modality (i.e., fMRI and dMRI) from the CCA models are shown in Fig. 4. In our analysis, the identified biomarkers based on nested five-fold cross validation were slightly different in different cross validation trials. In order to select stable markers, we averaged the loading vectors across the five folds. Specifically, we have trained and tuned the hyperparameters with four folds of datasets (i.e., training and validation sets) and applied it on the remaining fold (i.e., testing set) to identify biomarkers. The cross validation process is then repeated 5 times, with each of the 5 partitions used exactly once as the testing data. The five results from these cross validation trials can then be averaged to produce a single estimation. Finally, we ignored weights less than 0.00005 to make estimation stable.

Fig. 4:

The identified imaging biomarkers. Sub-figures (a) and (b) visualized averaged canonical loading maps for fMRI and dMRI, respectively.

We found that 231 out of 360 regions are overlapped between identified ROIs from fMRI and dMRI. In addition, 21 regions are identified from dMRI and 17 regions are identified from fMRI. Table 9 shows the top ten most significant ROIs from dMRI and fMRI. Among these top findings, there are in total 16 ROIs associated with SNPs; and 7 out of 23 ROIs (i.e., L_471_ROI, L_47m_ROI, L_9m_ROI, R_10v_ROI, R_23d_ROI, R_47m_ROI, R_a24_ROI) are subregions of the posterior-multimodal network. Four ROIs (i.e., L_DVT_ROI, L_LO3_ROI, L_V3B_ROI, R_LO2_ROI) are subregions of the visual network, two ROIs (i.e., L_a24pr_ROI and R_FOP3_ROI) are subregions of the cingulo-opercular network, and R_PHT_ROI, RIFJa_ROI, and R_OFC_ROI are subregion of language, default mode, and frontoparietal network, respectively.

Table 9:

Top 10 regions from fMRI and dMRI associated with SNPs. The canonical weight of fMRI and dMRI are reported. The network is annotated to the each ROI according to the Cole-Anticevic Brain-side Network (Ji et al., 2019).

ROI	Network	fMRI	dMRI	ROI	Network	fMRI	dMRI
L_DVT_ROI	Visual1	0.005	0.004	R_OFC_ROI	Frontoparietal	0.004
L_LO3_ROI	Visual2		0.007	L_47l_ROI	Posterior-Multimodal		0.005
L_V3B_ROI	Visual2	0.004		L_47m_ROI	Posterior-Multimodal		0.008
R_LO2_ROI	Visual2	0.003		L_9m_ROI	Posterior-Multimodal		0.007
L_a24pr_ROI	Cingulo-Opercular	0.008	0.004	R_10v_ROI	Posterior-Multimodal		0.004
R_FOP3_ROI	Cingulo-Opercular	0.004		R_23d_ROI	Posterior-Multimodal	0.005
R_PHT_ROI	Language	0.004		R_47m_ROI	Posterior-Multimodal		0.004
R_IFJa_ROI	Default	0.026	0.011	R_a24_ROI	Posterior-Multimodal	0.006	0.006

For both fMRI and dMRI, corpus callosum and prefrontal cortex are top markers contributing to the association for all models. To biologically interpret the complicated activation patterns, we also conducted a Neurosynth meta-analysis to decode the results (Gorgolewski et al., 2015; Yarkoni et al., 2011). Neurosynth is a platform designed to identify the topics associated with the brain activation maps. The top five Neurosynth topics and their CCs between the estimated canonical loading vector and the topic loading are shown in Tables 10 and 11. The topics related to anatomical terminology were excluded.

Table 10:

Neurosynth meta analysis of identified fMRI features map. Top five Neurosynth topics and its correlation coefficient (r) were reported.

Rank	Topic	r	Rank	Topic	r	Rank	Topic	r
1	Cognitive control	0.116	1	Deficit hyperactivity	0.078	1	Deficit hyperactivity	0.079
2	Pain	0.061	2	Attention deficit	0.075	2	Attention deficit	0.076
3	Demands	0.056	3	Cognitive control	0.068	3	Education	0.067
4	Deficit hyperactivity	0.047	4	Education	0.066	4	Pain	0.063
5	Remembering	0.043	5	Pain	0.060	5	Remembering	0.062
	(a) MTS2CCA			(b) MTGSCCA			(c) MTSCCA
Rank	Topic	r	Rank	Topic	r	Rank	Topic	r
1	Response inhibition	0.095	1	Sentence	0.085	1	Cognitive control	0.069
2	Cognitive control	0.085	2	Words	0.083	2	Tactile	0.057
3	Hand	0.060	3	Lexical	0.083	3	Morphology	0.055
4	Pain	0.057	4	Verb	0.075	4	Genes	0.055
5	Inhibition	0.050	5	Syntactic	0.073	5	Mentalizing	0.052
	(d) JCBSCCA			(e) TCCA			(f) SCCA

Table 11:

Neurosynth meta analysis of identified dMRI features map. Top five Neurosynth topics and its correlation coefficient (r) were reported.

Rank	Topic	r	Rank	Topic	r	Rank	Topic	r
1	Social	0.193	1	Social	0.129	1	Social	0.135
2	Moral	0.158	2	Moral	0.096	2	Sentences	0.108
3	Evaluation	0.126	3	Sentences	0.086	3	Comprehension	0.107
4	Mental states	0.119	4	Comprehension	0.083	4	Sentence	0.099
5	Mentalizing	0.109	5	Linguistic	0.083	4	Language	0.096
	(a) MTS2CCA			(b) MTGSCCA			(c) MTSCCA
Rank	Topic	r	Rank	Topic	r	Rank	Topic	r
1	Naturalistic	0.094	1	Demands	0.078	1	Social	0.229
2	Videos	0.087	2	Phonological	0.068	2	Moral	0.204
3	Social	0.075	3	Sighted	0.067	3	Mental states	0.173
4	Vision	0.073	4	Intensity	0.067	4	Evaluation	0.156
4	Button	0.0	4	Word	0.066	4	Mentalizing	0.149
	(d) JCBSCCA			(e) TCCA			(f) SCCA

For fMRI, we found that the anterior cingulate cortex, anterior insula cortex, inferior frontal cortex, and parahippocampal gyrus were top regions contributing to maximizing the canonical correlation, as shown in Fig. 4. We observed that cognitive control, pain, demands, deficit hyperactivity, and remembering were top-five Neurosynth topics related to our findings with the highest CC, as shown in Table 10. For the dMRI, we found that the medial prefrontal cortex, dorsomedial prefrontal cortex, ventromedial prefrontal cortex, and cingulate cortex were regions contributing to maximizing the canonical correlation. These regions were associated with the topics, including social, moral, evolution, mental states, and mentalizing, and they showed the second-highest CC, as shown in Table 11. The metabolism in the medial prefrontal and the anterior cingulate cortex is affected by sleep deprivation and depression (Wu et al., 2001). Many human and animal studies have demonstrated that the cingulate and insular cortex are highly associated with pain-related perception, such as psychological and social pain, which affect insomnia (Talbot et al., 1991; Rainville et al., 1997; Narita et al., 2011). These results indicated that the proposed model could identify biologically meaningful imaging biomarkers related to sleep.

3.3.5. Interpretation of selected genetic markers

Besides the selected imaging biomarkers, the model selected informative genetic variants associated with each imaging modality, except for JCBSCCA, TCCA, and SCCA. To select stable markers, we averaged trained canonical loading vectors from the five-folds and the variables with a weight less than 0.00005 were ignored to make results stable, as described in the section 3.3.4. We observed that MTS2CCA selected 262 and 285 SNPs associated with fMRI and dMRI, respectively. The full list of identified genetic variants from the CCA models, including MTS2CCA, MTGSCCA, MTSCCA, JCBSCCA, TCCA, and SCCA, are shown in Supplementary Table S1. Except for TCCA, all methods obtained similar sparsity (i.e., 262 and 285 SNPs for MTS2CCA, 332 and 345 SNPs for MTGSCCA, 363 and 387 SNPs for MTSCCA, 217 SNPs for JCBSCCA, and 310 SNPs for SCCA).

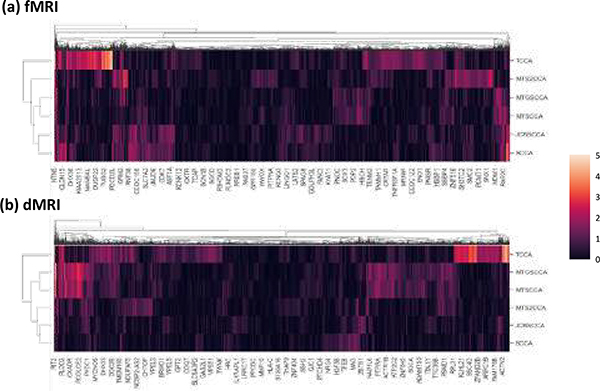
To help interpret our results, we identify genes whose expression levels are spatially correlated to genetic effects map through computing their Pearson’s correlation coefficients. In detail, our analysis generate genetic and imaging canonical loading vectors (i.e., U and V). The imaging canonical loading vector, called genetic effect map, denoted genetic effects on brain imaging traits (e.g. fMRI and dMRI). The preprocessed gene expression data of 10,027 genes were collected from the Allen Human Brain Atlas (AHBA) (Hawrylycz et al., 2012; Arnatkevičiūtė et al., 2019). We identify genes whose expression levels are spatially correlated to genetic effects map through computing their Pearson’s correlation coefficients. Then, we explore the overlapping gene between identified genetic variants of the CCA model (i.e. genetic canonical loading) and significant gene whose expression levels are spatially correlated to genetic effects map.

In Fig. 5, we observed that 1,576 genes were correlated (p < 0.05) with imaging canonical loading map obtained from MTS2CCA, and there were 17 overlapped genes. The detailed list of overlapped genes is shown in Table 12. For the competing models, we observed that 16 out of 1,815 genes were overlapped using MTGSCCA, 15 out of 1,556 genes were overlapped using the MTSCCA, 9 out of 987 genes were overlapped using JCBSCCA, 40 out of 4,560 genes were overlapped using TCCA, and 9 out of 1,028 genes were overlapped using SCCA.

Fig. 5:

The genetic-gene expression association results. The heatmap showed the correlation between the 10,027 gene expression map and the imaging canonical loading map. Sub-figures (a) and (b) corresponded to the genetic-gene expression association of fMRI and dMRI canonical loading maps, respectively. The y-axis presented the different CCA models, including MTS2CCA, MTGSCCA, MTSCCA, JCBSCCA, TCCA, and SCCA, and the x-axis presented 10,027 genes. The randomly selected gene symbols were labeled due to limited space. A value in the heatmap is color-coded according to the −log10 of the P-value.

Table 12:

The identified overlapped genes of MTS2CCA. The gene overlapped between identified genetic variants of MTS2CCA, and the gene-expression correlation results were reported. The correlation coefficients r between the AHBA gene expression map and identified imaging feature map was presented.

	Gene symbol	r		Gene symbol	r
fMRI	FARP1	−0.120	dMRI	DLGAP1	0.183
	TNFRSF21	0.156		KDM4C	−0.123
dMRI	RPL18A	0.123		FBXO25	0.135
	RPS6KA2	−0.118		KIAA1217	0.174
	RXRA	−0.119		SPSB1	−0.131
	SLC12A2	−0.122		PRICKLE2	0.142
	SRPK2	0.136		JAZF1	0.126
	TUSC3	0.141		TIMM23	0.159
	NRIP1	0.131

Gene enrichment analysis was conducted using overlapped genes using Enrichr (Chen et al., 2013; Kuleshov et al., 2016) based on the KEGG2019 human database. The lists of the enriched pathway are summarized in Tables 13 and 14. Several studies found that poor sleep quality and short sleep duration were associated with high risk for several types of cancer (e.g., thyroid, prostate, and breast) (Phipps et al., 2016; Mogavero et al., 2020). An electroencephalographic study demonstrated the decrease of associative synaptic long-term potentiation after sleep deprivation in human (Kuhn et al., 2016). A microarray study demonstrated that the dysregulation of adipocytokine signaling pathway was related to the depressive-like behaviors in rat and correlated with the depressive and anxiety symptoms in human (Wilhelm et al., 2013). These studies collectively support our findings that the identified brain regions are associated with executive functions and further provide the rationale for constructing structural-enriched functional networks.

Table 13:

Gene enrichment analysis of the overlapped gene for fMRI using MTS2CCA. P-value was computed from the Fisher exact test. Combined score was computed by taking the log of the p-value from the Fisher exact test and multiplying that by the z-score of the deviation from the expected rank.

Rank	Pathway name	p-value	q-value	Odd ratio	Combined score
1	Cytokine-cytokine receptor interaction	0.029	1	34.01	120.21

Table 14:

Gene enrichment analysis of the overlapped gene for dMRI using MTS2CCA.

Rank	Pathway name	p-value	q-value	Odd ratio	Combined score
1	Thyroid cancer	0.027	1	36.04	129.63
2	N-Glycan biosynthesis	0.037	1	26.67	88.01
3	Vibrio cholerae infection	0.037	1	26.67	88.01
4	Non-small cell lung cancer	0.048	1	20.20	61.18
5	Long-term potentiation	0.049	1	19.90	59.98
6	Adipocytokine signaling pathway	0.050	1	19.32	57.68
7	Bile secretion	0.052	1	18.52	54.51
8	PPAR signaling pathway	0.054	1	18.02	53.56
9	Salivary secretion	0.065	1	14.81	40.40
10	Small cell lung cancer	0.067	1	14.31	38.64

This study has several limitations. The first one is the sample size (i.e., 291 participants). We collected neuroimaging and genotyping data from the HCP database, and included only genetically unrelated non-Hispanic participants with full demographic information. In GWAS analysis, our sample size (i.e., 291 samples) is much smaller than the number of SNPs (e.g., 1,580,642 SNPs), leading to an overfitting risk for machine learning models. Hence, to reduce false discoveries, the candidate SNPs should be further confirmed with independent replications and meta analysis summary statistics from different cohorts. Another issue is that we use Pearson’s correlation analysis to interpret genetic results. However, its expressive power may be limited to capture the underlying association between genetic effect map and gene expression patterns. One interesting direction could be to explore different and improved mapping strategies. Expanding to a model, like fully connected neural network, has the potential to capture complex associations. Another interesting direction could be confirmed with densely parcelled atlas and voxel-level and possibly with candidate gene expression, instead of 10K genes, related with clinical outcomes.

4. Conclusions

The advances in technologies for acquiring brain imaging and high-throughput genetic data allow the researchers to access a large amount of multi-modal data. Although the sparse canonical correlation analysis is a powerful bi-multivariate association analysis technique for feature selection, we are still facing major challenges in integrating multi-modal imaging genetic data and yielding biologically meaningful interpretation of imaging genetic findings.

In this study, we have proposed a novel multi-task learning based structured sparse canonical correlation analysis (MTS2CCA) to deliver interpretable results and improve integration in imaging genetics studies. We have tested our algorithm on both simulation and real imaging genetics data. For the simulation data, we demonstrated that the proposed model outperformed several state-of-the-art competing methods in terms of identification of stronger canonical correlations, estimation accuracy, and feature selection accuracy. In addition, MTS2CCA has succeeded in identifying an association pattern generated from predefined network structures.

For real data, we have demonstrated the clinical benefits of the proposed model using the SNP, dMRI, and fMRI data from a real imaging genetics cohort. MTS2CCA outperformed all the competing models with higher canonical correlation coefficient and better predictive performance estimating PSQI scores. Identified imaging markers of MTS2CCA were associated with cognitive function, depression, and sleep deprivation. Additionally, identified genetic markers of MTS2CCA were related to sleep quality and sleep duration. These promising results demonstrated that the proposed multi-task learning based SCCA framework could provide a powerful tool for analyzing brain imaging genetics data and yielding biologically meaningful findings.

Table 2:

The feature selection accuracy on simulation data. The AUC between estimated loading vector and ground truth was reported. The best values are shown in bold text.

	MTS2CCA	MTGSCCA	MTSCCA	JCBSCCA	TCCA	SCCA
u 1	1.000	1.000	1.000	1.000	1.000	1.000
u 2	1.000	1.000	1.000	1.000	0.981	0.642
u 3	1.000	1.000	1.000	0.991	0.850	0.519
v 1	1.000	0.812	0.816	1.000	0.767	0.811
v 2	0.980	0.775	0.761	0.969	0.455	0.436
v 3	0.931	0.730	0.757	0.848	0.431	0.525