Cerebral vascular strains in dynamic head impact using an upgraded model with brain material property heterogeneity

Abstract

Cerebral vascular injury (CVI) is a frequent consequence of traumatic brain injury but has often been neglected. Substantial experimental work exists on vascular material properties and failure/subfailure thresholds. However, little is known about vascular in vivo loading conditions in dynamic head impact, which is necessary to investigate the risk, severity, and extent of CVI. In this study, we resort to the Worcester Head Injury Model (WHIM) V2.1 for investigation. The model embeds the cerebral vasculature network and is further upgraded to incorporate brain material property heterogeneity based on magnetic resonance elastography. The brain material property is calibrated to match with the previously validated anisotropic V1.0 version in terms of whole-brain strains against six experimental datasets of a wide range of blunt impact conditions. The upgraded WHIM is finally used to simulate five representative real-world head impacts drawn from contact sports and automotive crashes. We find that peak strains in veins are considerably higher than those in arteries and that peak circumferential strains are also higher than peak axial strains. For a typical concussive head impact, cerebral vascular axial strains reach the lowest reported yield strain of ~7–8%. For severe automotive impacts, axial strains could reach ~20%, which is on the order of the lowest reported ultimate failure strain of ~24%. These results suggest in vivo mechanical loading conditions of the cerebral vasculature (excluding bridging veins not assessed here) due to rapid head rotation are at the lower end of failure/subfailure thresholds established from ex vivo experiments. This study provides some first insight into the risk, severity, and extent of CVI in real-world head impacts.

1. Introduction

Traumatic brain injury (TBI) remains a devastating health issue across the world (Hyder et al., 2007; Thomas R. Frieden, Debra Houry, 2015). Understandably, injury to the brain neural tissue has been of fundamental concern in numerous TBI-related investigations (Madhukar and Ostoja-Starzewski, 2019; Morrison et al., 2011; Yang et al., 2006). Nonetheless, injury to the cerebral vasculature is also a frequent consequence that plays a significant role in patient outcome (Kenney et al., 2016; Monson et al., 2019). However, the risk of cerebral vascular injury (CVI) has often been neglected (Salehi et al., 2017). The cerebral vasculature delivers oxygen and nutrients to the brain through arteries and drains metabolic products via veins to maintain the brain health (Iadecola, 2017). In patients with fatal brain injury, acute hematoma frequently occurs (Graham, 1996). In less severe and non-hemorrhagic head trauma, pathophysiological alteration of cerebral blood flow is common (Armonda et al., 2006; DeWitt and Prough, 2009, 2003). The dysfunction of the vasculature would expose neural tissue to less regulated composition of blood that can disrupt the homeostasis of the central nervous system (Daneman and Prat, 2015). Even subfailure deformation of cerebral vessels can cause cellular damage of the vascular wall (Ohkawa et al., 1996) and leads to persistent vessel softening (Bell et al., 2015).

Similar to TBI, CVI or dysfunction of the cerebral vasculature is thought to be initiated through mechanical forces imparted on the blood vessels during head impact (Monson et al., 2019). Therefore, there has been substantial work aimed at determining cerebral vessel mechanical properties and loading responses using human and animal vessel samples. These include large-deformation properties of arteries and veins (Monson et al., 2003), bridging vein failure (Famaey et al., 2015), the effect of overstretch on vessel compliance in both axial and circumferential loading conditions (Bell et al., 2015; Converse and Monson, 2021; Maher et al., 2012; Weisbecker et al., 2012), cerebral vessel mechanical and failure properties (Nye et al., 2017), as well as acute blood-brain-barrier breakdown in microvessels (Maikos and Shreiber, 2007). Bridging vein–superior sagittal sinus units from fresh adult cadavers were also axially stretched until failure under a range of strain rate conditions to determine biomechanical parameters such as the yield and ultimate strain (Delye et al., 2006; Monea et al., 2014; Monson et al., 2005). These experimental studies establish an important foundation of cerebral blood vessel biomechanical behaviors.

Nevertheless, despite the prominence of CVI and significant efforts charactering vessel biomechanical properties, little is known about the biomechanical loading conditions that in vivo cerebral vessels experience during an actual head impact (Monson et al., 2019). Without this information, it is not possible to assess the risk, severity, or extent of CVI in dynamic head impact by comparing with vessel failure or subfailure thresholds. Directly measuring vessel strains in an intact brain during impact seems impossible at present, due to limitations in technology and physical inaccessibility to the tissue in a live human brain. In this study, therefore, we resort to a computational head injury model for investigation.

The latest anisotropic Worcester Head Injury Model (WHIM) V2.0 is used for this task. This model has been upgraded from the earlier anisotropic version V1.0 (Zhao and Ji, 2019a) by embedding cerebral vasculature obtained from arterial and veinous probabilistic atlases (Bernier et al., 2018) into a re-meshed brain via affine registration to reach strain convergence (Zhao and Ji, 2020a). With material properties of fresh human cerebral arteries and veins chosen to represent average behaviors in dynamic tests (Monson et al., 2003), brain tissue peak strains can be lowered by ~20–36% in regions where major arteries reside due to blood vessel stiffening effect. The previous anisotropic V1.0 model has been validated against a wide-range of experimental data representing high-, mid-rate cadaveric impacts and in vivo loading conditions, achieving a peak strain ratio between model simulation and experimental counterpart of 0.94±0.30 based on 12 cadaveric impacts (Zhao and Ji, 2020b). A peak strain ratio of 1.00±0.00 would be “perfect”, albeit errors from experimental data, themselves, should not be ignored. Nevertheless, the V2.0 model has not been calibrated, which is necessary given its higher mesh density and the inclusion of vasculature that would compete for an overall increased (Zhao and Ji, 2019b) and locally decreased (Zhao and Ji, 2020a) strain, respectively, relative to the baseline V1.0 model. This would lead to uncertainty in how the V2.0 model compares against experimental strains.

In addition, there has been report of brain material property heterogeneity in stiffness found from magnetic resonance elastography (MRE) in live humans (Hiscox et al., 2020), which is being incorporated into head injury models (Giudice et al., 2021; Madhukar and Ostoja-Starzewski, 2020). Brain regional tissue property heterogeneity is also observed in other ex vivo tests at injury-relevant rates (Finan et al., 2017; Forte et al., 2017; Jin et al., 2013) and quasi-static conditions (Budday et al., 2017). The MRE data are obtained under small strain and strain rate conditions and may not directly reflect large-strain/strain rate behaviors relevant to injury (Bayly et al., 2021). Nonetheless, this is currently the only dataset available to inform voxel-wise property heterogeneity of the whole brain, which is necessary for computational head injury model development.

Therefore, this study has two primary goals. First, we further upgrade the WHIM by incorporating MRE-derived material property heterogeneity and then calibrate the model to match strains relative to the previously validated baseline V1.0 model. Although the anisotropic WHIM V1.0 incorporates anisotropy—stiffness differences due to white matter fiber directional dispersion—it uses the same initial (and equivalently, long-term) shear modulus for the entire brain, including both the white matter and gray matter. It does not yet incorporate voxel- or elementwise tissue stiffness heterogeneity.

After model upgrade, as a second goal, we use it to investigate cerebral vascular strains in real-world head impacts with a range of documented brain injury severities. These investigations are expected to advance our understanding of in vivo loading conditions of cerebral vasculature in real-world head impacts, which is currently lacking. In addition, the upgraded WHIM, which will be referred to as anisotropic WHIM V2.1 hereafter, will enable investigations of CVI in the future. Previous studies have focused on bridging vein rupture (Franklyn et al., 2005; Kapeliotis et al., 2019; Migueis et al., 2019) but not injury to the cerebral vasculature network. Similarly, when studies incorporate vasculature network, they focus on strain of the brain rather than that of the vasculature, itself (Ho and Kleiven, 2007; Zhang et al., 2002; Zhao and Ji, 2020a). In contrast, here we use an upgraded head injury model to investigate strains in cerebral vasculature network under a range of blunt impact conditions.

2. Materials and Methods

The anisotropic Worcester Head Injury Model V2.0 (Fig. 1) has been upgraded from the earlier V1.0 version with a higher mesh density (202.8 k hexahedral elements and 227.4 k nodes for the brain, vs. 55.1 k and 56.6 k, respectively, with the corresponding average brain mesh size of 1.8 mm vs. 3.3 mm, respectively (Ji et al., 2015)) to reach strain response convergence (Zhao and Ji, 2019b). The upgraded model uses the same whole-brain tractography to define anisotropy of the white matter (Zhao and Ji, 2019a), which also embeds 440.0 k triangular surface membrane elements and 221.1 k nodes for the cerebral vasculature, including arteries and veins/sinuses (Zhao and Ji, 2020a). The vessels are modeled as hollow tubes by assuming a tied boundary condition relative to surrounding tissues and the dural surface through the embedded element method. The vessel wall thickness is uniformly set to either 0.5 mm for major arteries, or 0.1 mm for minor arteries and veins/sinuses. No pressurized blood or pre-tension of vessels prior to impact simulation are considered.

Fig. 1.

The anisotropic Worcester Head Injury Model (WHIM) V2.0, showing the brain mesh (a), direction-encoded elementwise fiber orientations (b), and major (dark red) and minor (light red) arteries as well as veins and sinuses (blue) (c). The upgraded V2.1 model has identical brain and vascular meshes after incorporating MRE-derived material property heterogeneity.

The detailed material properties for the brain (Zhao and Ji, 2019a) and vasculatures (Zhao and Ji, 2020a) are summarized in Table 1. Of note, the vasculature from the probability imaging atlases (Bernier et al., 2018) does not explicitly include bridging veins, which precluded evaluation of their strains in this study. The following sections describe details of model incorporation of brain material property heterogeneity from MRE and further property calibration. In addition, procedures of deriving cerebral vascular centerlines and calculating vessel axial and circumferential strains are also described.

Table 1.

Summary of baseline material properties for the brain (Holzapfel-Gasser-Ogden model) and vasculature (3^rd-order Ogden model). μ_i, α_i, G₀, G_∞, K, k_i, κ, g_i, τ_i are material property parameters defined in previous publications (Zhao and Ji, 2020a, 2019a). In the upgraded V2.1 model, the G₀ value for each brain element is further adjusted according to MRE-derived heterogeneity map, and the co-dependent G₀, G_∞, and k₁ values are doubled after calibration.

Parameter	Brain	Parameter	Artery	Vein
Density (kg/m3)	1040	Density (kg/m3)	1040	1040
G0 (Pa)	2673.23	μ1 (MPa)	−1491.30	−129.81
G∞ (Pa)	895.53	α 1	−1.48	1.19
K (MPa)	219	μ2 (MPa)	739.21	67.08
k1 (Pa)	25459 for white matter, 0 for gray matter	α 2	−0.95	1.72
k 2	0	μ3 (MPa)	752.40	63.17
κ	Depending on FA * values	α 3	−2.03	0.62
g 1	0.6521	Poisson’s ratio	0.48	0.48
g 2	0.0129
τ 1	0.0067
τ 2	0.0747

^*FA: Fractional anisotropy.

2.1. WHIM V2.1 material property heterogeneity

The MRE dataset reports a voxel-wise normalized viscoelastic shear moduli map of the brain averaged from 134 healthy, young adults (78F/56M; 18–35 years) (Hiscox et al., 2020). The image atlas has an isotropic image resolution of 2 mm and is given in the MNI152 standard structural template within the spatial coordinates of the ICBM-152 (Mori et al., 2008). This allowed co-registering with WHIM V2.0 mesh by using the corresponding high-resolution images (isotropic resolution of 2 mm) used to develop the model (Ji et al., 2015) with the same established techniques (Zhao et al., 2017; Zhao and Ji, 2020a). The stiffness values of each brain mesh element were then determined by averaging those of the corresponding enclosing voxels (as determined by voxel centroids). Some stiffness values were found to be quite low (e.g., <1000 Pa) due to artifacts, edge effects, and the inclusion of cerebral spinal fluid (CSF) (Giudice et al., 2021). Similarly, therefore, we empirically capped the lowest possible stiffness value to 1000 Pa, which is the generally accepted long-term modulus of the brain (Chatelin et al., 2010). Figure 2 reports histograms of the elementwise MRE stiffness values and ratios relative to the baseline initial shear modulus of the anisotropic WHIM V1.0 (G₀ of 2673.23 Pa (Zhao and Ji, 2019a)).

Fig. 2.

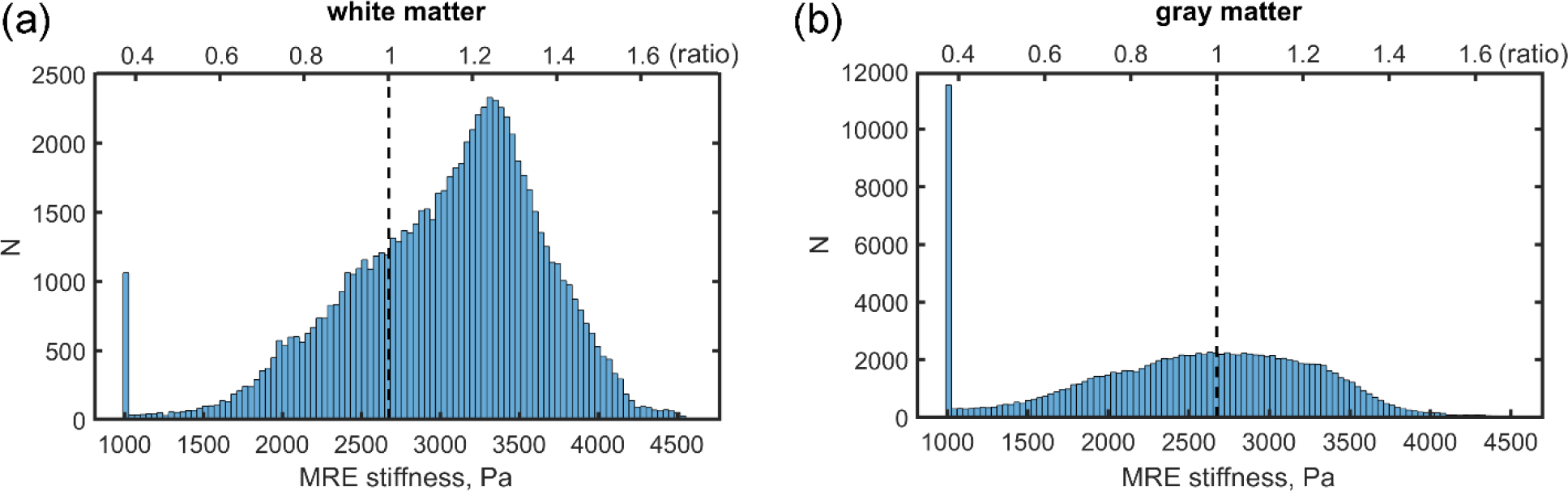
Histogram distributions (with 100 bins) of MRE stiffness values in the (a) white matter (defined elementwise) and (b) gray matter (limited to 100 bins), along with their corresponding ratios relative to G₀ of 2673.23 Pa adopted in the anisotropic WHIM V1.0 model for reference. The stiffness values of a large portion of the gray matter elements (b) are capped at the lower end of the spectrum.

Ideally, an elementwise material property definition would maximize the use of the MRE stiffness information. However, this was not feasible due to the large element number (~203 k) that prevented Abaqus to even launch the simulation job. Therefore, we chose to implement elementwise property definition only for the white matter (~81.3 k elements), given its elementwise anisotropy already defined (Zhao and Ji, 2019a). For the gray matter (~122.1 k elements), however, we limited the number of discretized MRE stiffness values to 100 bins (Fig. 2). Figure 3 shows elementwise stiffness ratios (relative to baseline G₀) on three representative mesh planes. Lower stiffness values were generally found around the brain surface, with larger values mostly occurring in the central white matter regions.

Fig. 3.

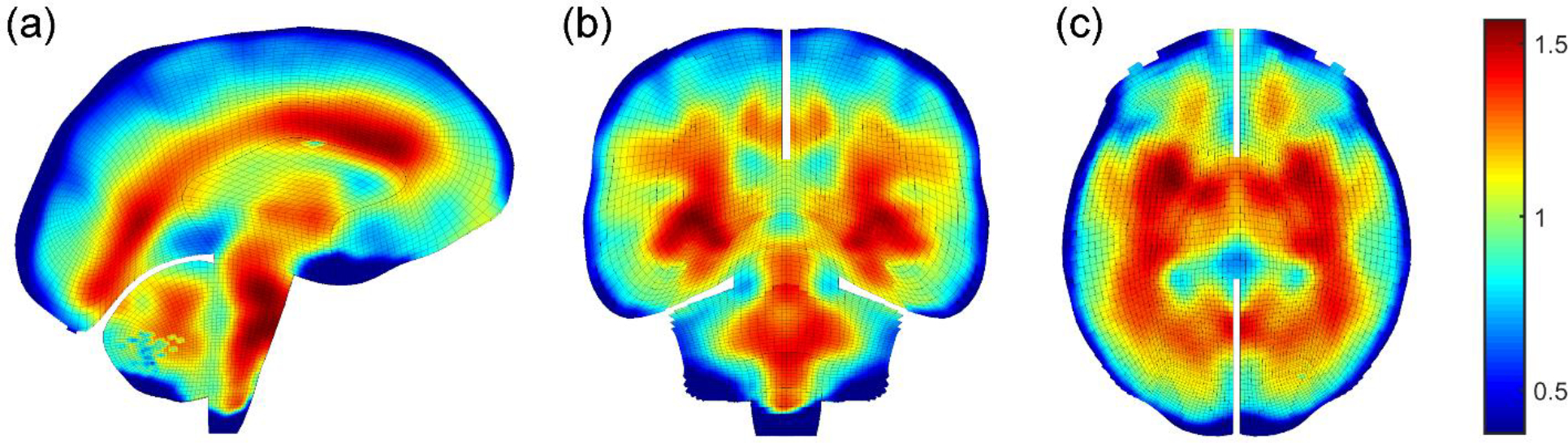
Elementwise stiffness ratios relative to the baseline G₀ on a (a) sagittal, (b) coronal, and (c) axial plane based on MRE (images rendered by a ~4 mm slab of brain meshes). Material properties for the anisotropic white matter elements (~81.3 k) are defined elementwise, while those for the isotropic gray matter (~122.1 k) are defined by 100 discrete sets (Fig. 2).

2.2. WHIM V2.1 material property calibration

Compared to the baseline anisotropic WHIM V1.0, the V2.0 model has a much higher brain mesh resolution (202.8 k vs. 5.5 k), which would increase strain (Zhao and Ji, 2019b). In contrast, stiffening from cerebral vasculatures would decrease strain in local regions (Zhao and Ji, 2020a). Therefore, the two competing factors would lead to some uncertainty in strain over- or underestimation relative to the V1.0 baseline model. Further, the newly incorporated MRE material property heterogeneity (Fig. 2 and Fig. 3) is expected to further alter strain distribution, which would exacerbate strain uncertainty relative to the already-validated baseline WHIM V1.0. The baseline model has achieved a peak strain ratio (simulations vs. experiments) of 0.94±0.30 in terms of marker-based strains averaged from 12 high- and mid-rate cadaveric impacts, with a slight underestimation relative to a “perfect” ratio of 1.00±0.30 (albeit errors from experimental data, themselves, should not be ignored). In addition, it also compares reasonably well to in vivo brain strains from 4 live human tests of rotation and extension (Zhao and Ji, 2020b).

Given these considerations, we first used the material properties from baseline anisotropic WHIM V1.0 (Zhao and Ji, 2019a) to simulate six representative experiments, including 2 high-rate cadaveric impacts, 2 mid-rate impacts simulating head rotations in contact sports, and 2 in vivo head rotation/extension tests (Table 2). They represent a wide range of head impact severities and motion modes, and are a subset of the previously used experimental validation datasets (Zhao and Ji, 2020b). Their resulting peak maximum principal strains (MPS) were then compared to their baseline counterparts using linear regression slopes based on MPS resampled on the same grid. The slope magnitudes, k, would inform how the properties should be scaled across the brain while maintaining the same relative stiffness ratios (Fig. 3).

Table 2.

Summary of linear regression slope and Pearson correlation coeffícient (the latter in parentheses, all with p < 0.001) between cumulative peak MPS relative to those from the anisotropic WHIM VI.0 model when using the baseline brain material properties or by scaling up G₀/G_∞ by 2 or 4 times. Six experimental datasets were selected for comparison, including 2 high-rate cadaveric impacts, 2 mid-rate cadaveric impacts, and 2 in vivo loading conditions.

Scaling ratio	C288-t3	C380-t4	NDTA-t4	Vrot20dt30	Knutsen et al.	Lu et al.
Baseline	1.61 (0.62)	1.32 (0.20)	1.19 (0.60)	1.55 (0.35)	1.37 (0.65)	1.47 (0.49)
2	1.50 (0.34)	1.14 (0.23)	1.01 (0.47)	0.94 (0.48)	0.91 (0.68)	1.19 (0.43)
4 a	1.42	0.95	0.59	0.65	0.53	0.89

^aOnly linear regression slopes were reported, as the brain was obviously over-stiff relative to the baseline for the majority of cases when scaled by 4 times.

The baseline material properties led to strain overestimation for all six datasets (Fig. 4). Uniformly scaling G₀ (and equivalently, G_∞) by 2 led to largely comparable strains relative to the anisotropic WHIM V1.0 for most cases as their linear regression slopes are mostly around 1.0 (Fig. 4; Table 2). An exception was C288-t3 that had a regression slope of ~1.5, where large strains in the inferior region of the brainstem were also evident. Compared to the baseline, WHIM V2.0 and V2.1 models significantly altered strain distribution, with Pearson correlation coefficients ranging from 0.20 to 0.68 (all with p<0.001).

Fig. 4.

Cross-sectional views of cumulative peak MPS of WHIM V2.1 (left), the baseline WHIM V2.0 (middle), and the anisotropic WHIM V1.0 (right) for four cadaveric impacts and two in vivo motions.

2.3. WHIM V2.1 validation

For consistency with previous work (Zhao and Ji, 2020b), we used the “triad” approach (Zhou et al., 2018) to define triangular elements for the two high-rate cases (C288-t3 and C380-t4). For mid-rate case NDTA-t4, the largest triangle from the 12 NDTs was used to assess strain, as this was least sensitive to marker displacement errors (Zhao et al., 2021). For Vrot20dt30, only one triangle was formed from the three markers (Zhao and Ji, 2020b). For all cases, marker displacement trajectories from either the experiment or simulation were applied to the homologous markers to calculate maximum principal strain (MPS) at every time frame. This ensured appropriate strain comparison. For the two in vivo cases, area fractions of above-threshold strains or peak strains from model simulations were compared to the experimental findings, as conducted previously (Zhao and Ji, 2020b).

2.4. Cerebral vasculature centerlines

Calculating cerebral vascular strains requires first extracting the vessel centerlines. There are a variety of techniques available based on either medical images (e.g., through iterative removal of vessel boundary voxels (Schneider et al., 2015; Starzynski et al., 2015), and recently, via deep learning (Tetteh et al., 2020)), point clouds for relatively simple objects (Kurlin, 2015; Tagliasacchi et al., 2009), or surface meshes (e.g., through curve skeleton and mesh contraction (Au et al., 2008; Wang et al., 2012)). Given that the vasculature meshes were already available from probabilistic image atlases after removal of minor arteries and veins, here we chose to apply a simple and intuitive approach based on vasculature surface meshes to further extract vessel centerlines.

The method starts with the observation that vessel geometry is cylindrical tube-like and its cross-section with respect to a plane perpendicular to the centerline can be approximated by a circle in a 3D space (Wei et al., 2018). This inspired us to generate vessel cross-sections by sweeping through the brain volume using a plane perpendicular to one of the three major anatomical axes at a step size of 1 mm. The resulting cross-sections were then individually fitted into a circle using a least squares minimization procedure. The fitted circles were discarded, if the fitting residual root mean squared error was greater than an empirical threshold of 1 mm, because of either (1) the plane significantly deviated from the plane perpendicular to the vessel centerline; and (2) the cross-section was geometrically complex that cannot be fitted into a circle. When the plane was not perpendicular to the vessel centerline, the resulting cross-section would be expected to be approximately an ellipse. When it was fitted into a circle instead (for simplicity and fitting robustness due to the fewer number of parameters needed), the center point would remain the same for generating centerlines.

This process was repeated along the three anatomical axes so that vessel cross-sections failed in circle fittings along one direction (e.g., when the fitting plane deviated too much from the plane that is perpendicular to the vessel centerline) can be successfully fitted when intersecting with another orthogonal plane. This is illustrated with an example in Fig. 5. Vessel centerlines were then created by iteratively connecting the center points immediately before, at, and immediately after the current plane, if their projections had a distance less than an empirical threshold of 1 mm to ensure centerline continuity. Since the process was repeated along the three anatomical axes, some vessels or portions of the vessels could yield multiple copies of essentially the same centerlines. The duplications were removed by a point-based distance thresholding (of 1 mm). The resulting artery and vein centerlines (Fig. 6) were finally used for subsequent strain analysis.

Fig. 5.

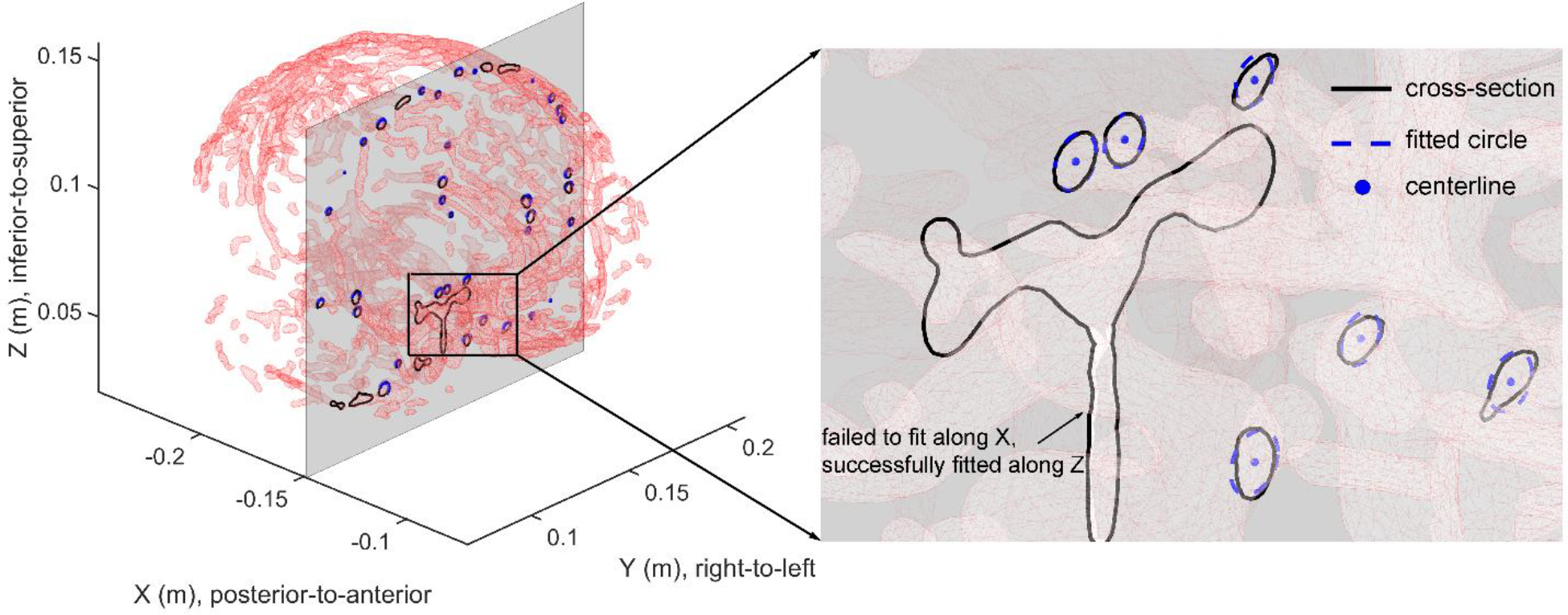
Illustration of vessel centerline extraction based on triangulated vessel surface meshes along the X direction of the arteries (same for the veins). Vessel cross-sections on a given plane are first identified, and each is individually fitted into a circle. Those with large residual errors are discarded and will be fitted along another orthogonal direction (e.g., the basilar artery (BA) in the inset is successfully fitted along the Z axis in X-Y planes). The fitted circles appear as ellipses due to an oblique viewing angle.

Fig. 6.

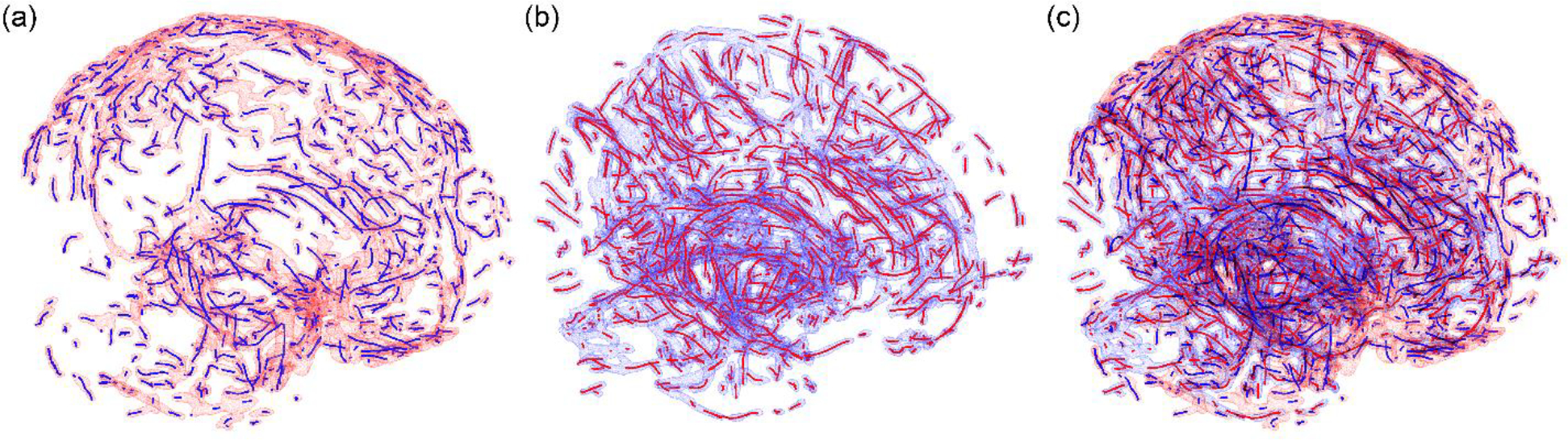
Centerlines for the arteries (a; blue lines with red surfaces) and veins (b; red lines with blue surfaces) are combined into the same space (c). Some vessel discontinuity exists due to threshold-related vessel removal from the probabilistic image atlases (Zhao and Ji, 2020a) and failed circle fitting at vessel junctions. In total, there are 5.3 k centerline sampling points for arteries and 7.9 k for veins, respectively, with an approximate point-to-point distance of 1 mm.

2.5. Cerebral vascular strains

Both axial and circumferential strains were evaluated. The former measure strains along the vessel centerline longitudinal direction, which are analogous to white matter fiber strains along white matter tractography. Therefore, techniques to calculate white matter fiber strains are readily applicable. Most studies employ a strain tensor projection method because strains are already available from model simulation (Giordano and Kleiven, 2014; Ji et al., 2015; Knutsen et al., 2020; Li et al., 2020; Sahoo et al., 2016). Due to large rotation of the head in impact, it is important to use the current, rather than the initial, undeformed tissue orientation for strain tensor projection, as recognized (Zhou et al., 2021). This can be conveniently achieved by first transforming the strain tensor into the global coordinate system before projecting along the initial configuration, which would avoid the need for a separate and cumbersome tracking of tissue orientation (Zhou et al., 2021). Nevertheless, localizing the enclosing element for each sampling point (either white matter fiber or vessel centerline as in this study) remains necessary, which is not trivial (Ji et al., 2015).

In this study, we adopted an alternative post-processing strategy for local strain calculation directly based on displacement, without strain tensor projection or its associated complication. For axial strain along vessel centerlines, 1D linear elements were first formed by two adjacent sampling points along the vessel centerlines. Their displacements in the global coordinate system were next interpolated from the surrounding brain nodal displacements. The updated sampling point locations were then used to calculate element length and stretch/strain relative to the undeformed configuration prior to the start of simulation. Peak longitudinal engineering strain was finally determined as the maximum strain over simulated impact duration.

For circumferential strain along the vessel perimeter, cross-sections perpendicular to vessel centerlines were first obtained. Cross-sectional points were then used to determine the deformed and undeformed configurations from interpolation of surrounding nodal displacements. At each time frame, cross-sectional points were then used to fit into circles. Similarly, only those with fitting residual errors less than 1 mm were retained. Circumferential engineering strains were determined as the relative change in circle circumference, from which the peak value over the impact duration was finally obtained.

2.6. Real-world impact simulations

There is paucity of well-documented impact cases with vascular injury as well as biomechanical impact acceleration profiles necessary to drive model simulation. In this study, we selected a pair of reconstructed concussive and non-injury impacts from the National Football League for analysis (‘Case077HD02’ and ‘Case077HD01’, respectively (Sanchez et al., 2018)). They were expected to provide typical cerebral vascular strains in contact sports.

In addition, three automotive head impacts were also employed (Franklyn et al., 2005). These impacts had an Abbreviated Injury Scale (AIS) equal to or greater than 4. Two of the cases had documented haematoma (AIS 5 and AIS multiple; Table 3). All cases also had skull fracture documented. However, the reported head linear and rotational acceleration profiles from crash reconstruction only allowed assuming the skull to be a rigid body so that to apply the acceleration profiles to the head center of gravity as model input. The necessity and implications of using acceleration profiles as model input have been discussed extensively (Franklyn et al., 2005). Table 3 summarizes the five impacts simulated in this study.

Table 3.

Summary of five head impacts and documented injury drawn from reconstructed American football and automotive crashes used in this study, including their corresponding peak linear/rotational acceleration (a_lin and a_rot, respectively) and peak rotational velocity (v_rot).

Case #	Description of documented head/brain injury	Peak alin (g)	Peak arot (krad/s2)	Peak vrot (rad/s)
NFL 0017	No injury	39.8	3.1	30.4
NFL 0018	Concussion	95.6	7.4	53.4
AIS 4	Fracture of the right petrous pyramid and suspected fracture of the left petrous pyramid GCS=11 at scene (not codeable in presence of other head injuries) (AIS 4).	680.1	27.9	30.5
AIS 5	Bilateral extradural haematoma (temporal) (AIS 5); Temporal lobe contusion (AIS 3); GCS = 3 at scene (not codeable when in presence of other head injuries); Bilateral temporal bone fracture (AIS 3); Bilateral sphenoid bone fracture (AIS 3).	218.7	12.7	103.7
AIS multiple	Right inferior frontal lobe extradural haematoma (14 mm); Right anterior temporal lobe subdural haematoma (9 mm); Cerebral swelling with partial effacement of some basal cisterns; Right inferior cortical contusions associated with a 5 mm midline shift to the left; Comminuted fracture right orbital roof extending into the greater wing of the sphenoid bone and involving the right optic foramen, fracture right lamina papyracea, right nasal bone; Traumatic right optic neuropathy with optic atrophy (no vision right eye on discharge); Pneumocephalus (according to AIS rules, not coded as it was a result of another injury); Right VI cranial nerve palsy; Severe right side trismus (lockjaw).	294.6	24.4	39.3

2.7. Data analysis

The upgraded WHIM V2.1 was compared against the four cadaveric impacts in terms of marker-based strain, and against the two in vivo cases in terms of area fractions of strains above a range of thresholds (Knutsen et al., 2014) or peak strains in selected anatomical regions (Lu et al., 2019).

The validated WHIM V2.1 was then used to simulate five real-world impacts. Their resulting cerebral vascular engineering strains were reported for the arteries and veins, and in terms of peak axial and circumferential strains, respectively. They were assessed at the 95^th percentile level to mitigate any numerical artefacts. In addition, fractions of vessels (based on centerline sampling points) above two empirically chosen strain thresholds of 0.1 and 0.2 were also reported.

All impact simulations were executed on a Linux computer (Intel Xeon E5–2698 with 256 GB memory). A typical impact of 100 ms required ~6 hours for simulation with Abaqus/Explicit (double precision). All data analyses were conducted in MATLAB (R2020a; MathWorks, Natick, MA). Statistical significance was defined at the 0.05 level.

3. Results

3.1. WHIM V2.1 validation performance

Fig. 7 reports marker-based strains from the validated WHIM V2.1, as compared to the anisotropic WHIM V1.0 and experiment. For further comparison, relative brain-skull displacements for case C288-t3 are shown in the Supplementary Data (Fig. S1). Fig. 8 reports the area-fractions of an in vivo head axial rotation and regional peak strains for a head extension test.

Fig. 7.

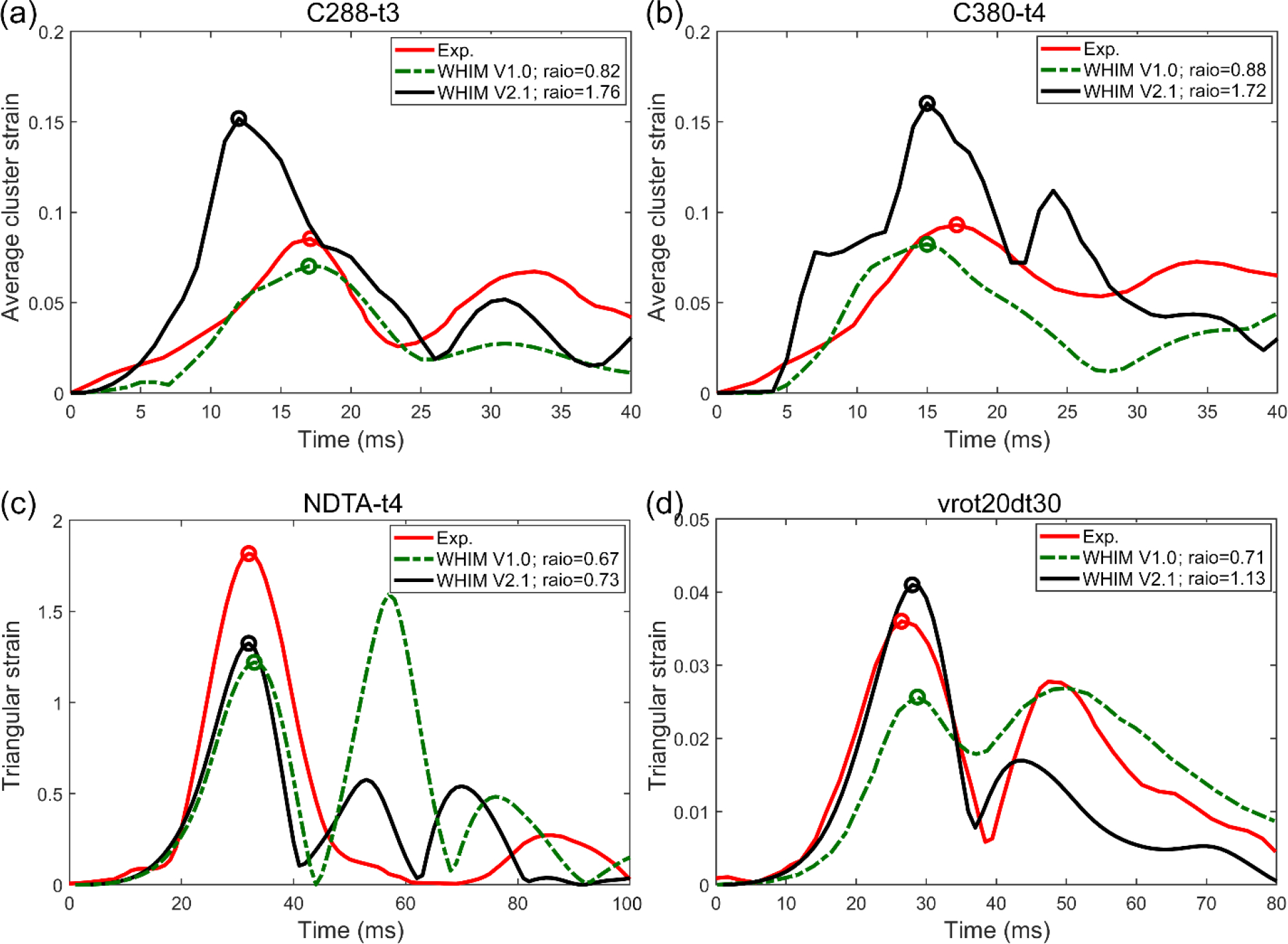
Comparison of marker-based strains from WHIM 2.1 and anisotropic V1.0 against experimental counterparts from cadaveric impacts. For C288-t3 and C380-t4 (a and b, respectively), marker-based MPS are averaged from a number of triangular elements, as previously adopted (Zhao and Ji, 2020b; Zhou et al., 2018). For NTDA-t4 and Vrot20dt30 (c and d, respectively), MPS of a single triangular element is compared (Zhao and Ji, 2020b). Ratios of the first major peaks against experimental strains (circles) are also reported.

Fig. 8.

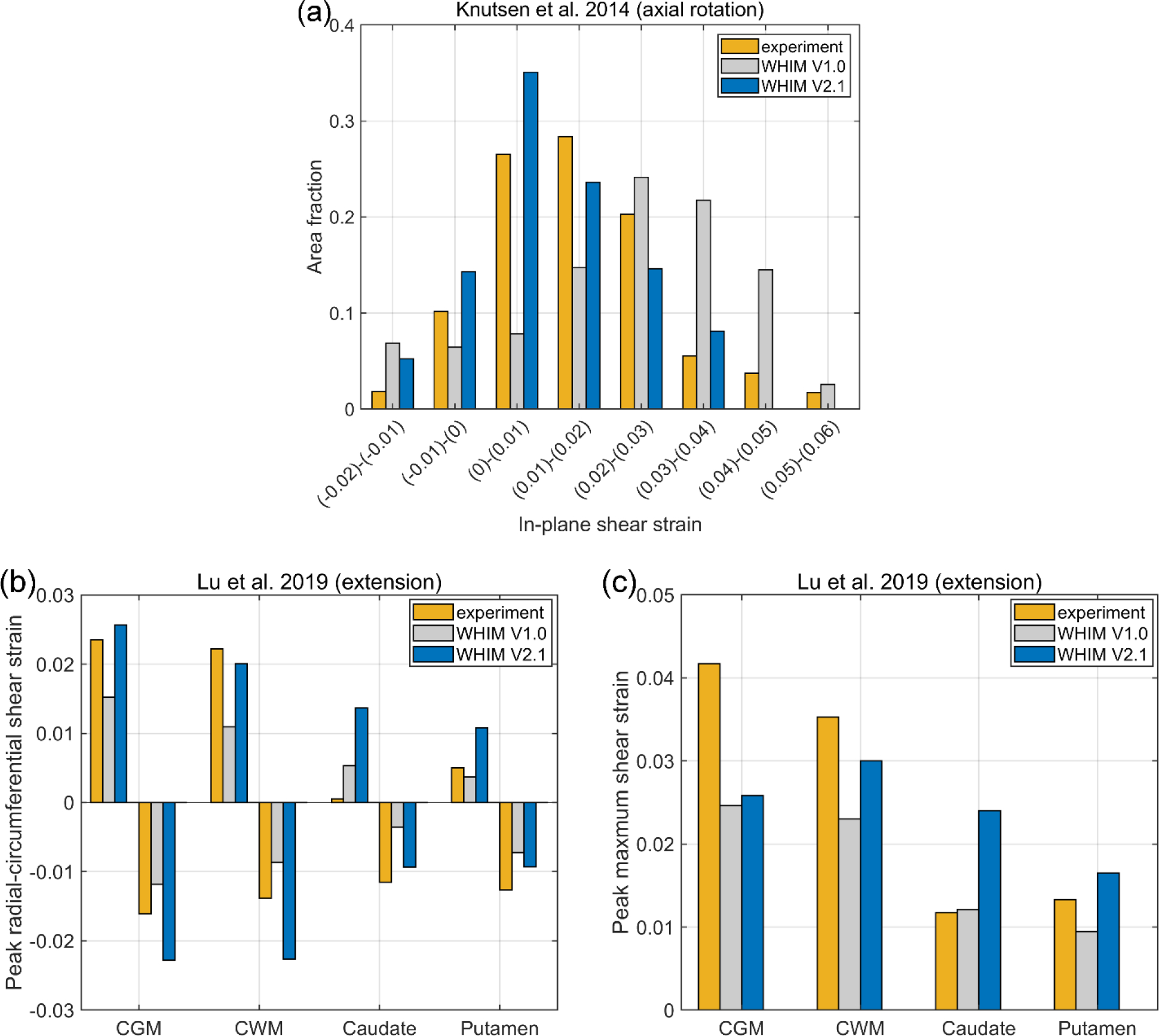
Comparison of in vivo strains from WHIM V2.1 and V1.0 against experimental counterparts. Area fractions of above-threshold strains for an axial head rotation (a) and peak radial-circumferential (b) and maximum shear (c) strains for a head extension test.

3.2. Cerebral Vascular Strains

Table 4 summarizes the peak axial and circumferential strains for arteries and veins, along with the percentage of their centerline sampling points experiencing strains above two thresholds. In general, peak axial strains in veins were considerably higher than those in arteries by 77.7±41.4% (range of 35.7–137%). In addition, peak circumferential strains in veins were also higher than those in arteries by 49.5±18.1% (range of 31.5–76.1%). Point-wise peak axial and circumferential strains were highly and statistically correlated, for both arteries and veins (p<0.001). This suggests that if one strain measure is high, the other strain measure is also high. Fig. 9 illustrates the distribution of peak axial/circumferential strains in arteries and veins for two selected impact cases.

Table 4.

Summary of artery and vein peak axial and circumferential strains (ε_axial and ε_circ, respectively; assessed at the 95^th percentile level), as well as the percentage of vessel (based on the fitted centerline sampling points) experiencing strains above 0.1 and 0.2 (reported in parentheses).

	Artery εaxial	Artery εcirc	Vein εaxial	Vein εcirc
NFL/0017 (no injury)	0.014 (0.0%; 0.0%)	0.038 (0.07%; 0.0%)	0.019 (0.0%; 0.0%)	0.05 (0.22%; 0.0%)
NFL/0018 (concussion)	0.035 (0.04%; 0.0%)	0.089 (3.4%; 0.02%)	0.071 (1.4%; 0.0%)	0.142 (18.3%; 0.79%)
0002 (AIS 4)	0.112 (6.3%; 0.3%)	0.139 (11.9%; 1%)	0.168 (21.4; 2.8%)	0.196 (32.0%; 4.6%)
0003 (AIS 5)	0.057 (0.9%; 0.03%)	0.113 (10.9%; 0.9%)	0.135 (7.4%; 0.4%)	0.199 (29.1%; 4.8%)
0004 (AIS multiple)	0.083 (3.2%; 0.2%)	0.156 (12.9%; 2.3%)	0.20 (20.6%; 5.0%)	0.212 (32.7%; 6.1%)

Fig. 9.

Illustration of peak artery/vein axial and circumferential strains for two representative impact cases (top: concussive NFL case; bottom: AIS multiple automotive impact). Note the different color-bar scales. For both cases, peak vein circumferential strains are the highest and include a larger number of vessels over larger regions that are above the threshold.

4. Discussion

In this study, we incorporated brain material property heterogeneity measured from MRE into the latest anisotropic Worcester Head Injury Model (WHIM). We then re-calibrated the brain properties to achieve comparable strains relative to the previously validated V1.0 baseline model when simulating a wide range of impact severities. This approach allowed consistency between the different WHIM versions in injury investigation. We then applied the upgraded V2.1 model to evaluate cerebral vascular strains in five head impacts, with severity ranging from no injury, concussion, to severe brain injury.

4.1. Material property heterogeneity

Incorporation of MRE-based heterogeneity significantly altered brain train distribution (Fig. 4), with Pearson correlation coefficients ranging from 0.23 to 0.68 (Table 2). This also led to some strain discontinuity, which was amplified when aggregating across time to yield peak strains. This was evident in the sub-cortical areas (Fig. 4a) where changes in stiffness values were the greatest (Fig. 3). The altered strain distribution may have significant implications when concurrently using strains in multiple regions for injury prediction (Wu et al., 2020), which merits further investigation. Nevertheless, some artefacts and incomplete sampling in the MRE data (Giudice et al., 2021) especially around brain boundaries led to local high strains that may not be realistic (e.g., brainstem near the foramen magnum for C288-t3; Fig. 3 and Fig. 4).

In addition, it must be recognized that the MRE-derived heterogeneity was measured at strain and strain rate levels far below injury, with an assumption of a linear displacement vs. strain relationship (Hiscox et al., 2020). Therefore, there are some inherent uncertainties about its applicability under injury-level loading conditions as the relationship becomes nonlinear and depends on both the strain magnitude and rate (hyperelasticity and viscoelasticity, respectively) (Bayly et al., 2021; Giudice et al., 2021). Retaining voxel- or elementwise stiffness ratios rather than directly using the absolute MRE stiffness values allows calibrating a single baseline material constant to satisfy model validation requirement. However, it does not eliminate the uncertainty in its applicability for injury-relevant, more severe impacts in the real world. Thus, it remains an open question how best to implement MRE-based heterogeneity for brain injury models (Bayly et al., 2021).

4.2. Material property calibration and model validation

The previous (isotropic and anisotropic) WHIM V1.0 already achieved a reasonable validation performance across a wide-range of blunt impact conditions (e.g., average simulation vs. experiment peak strain ratio of 0.94±0.30 from 12 cadaveric impacts (Zhao and Ji, 2020b)). Therefore, we calibrated brain material properties of the upgraded WHIM V2.1 by matching whole-brain strains relative to the previous anisotropic WHIM V1.0. This was similarly conducted when calibrating anisotropic WHIM V1.0 material properties to match with the earlier isotropic V1.0 model (Zhao and Ji, 2019a), which maximized the consistency between different WHIMs. We did not calibrate the properties by maximizing the commonly used CORrelation and Analysis (CORA) (Giudice et al., 2021; Miller et al., 2016) because this metric is ineffective in discriminating model validation performances (Zhao and Ji, 2020b) (more below).

Doubling the baseline G₀ value across the brain yielded largely comparable whole-brain strains for mid-rate cadaveric experiments and in vivo datasets (Fig. 4 and Table 2). However, the model overestimated for a high-rate impact (C288-t3; predominantly sagittal rotation) relative to the anisotropic V1.0 model (Fig. 4), which was consistent with its overestimation in marker-based strain (Fig. 7a, also for the other high-rate impact, C380-t4; Fig. 7b). This suggests that the brain’s time-varying shear modulus, G_t, at the corresponding loading rate (~3–4 ms; Table 2), was relatively low. This was also evident when comparing the relative brain-skull displacements for the 7 NDT markers, where displacements in the anterior-posterior direction for some markers were notably larger for this sagittal head rotation (Fig. S1 in the Supplementary Data). It is possible to further adjust the brain’s viscoelasticity g_i and τ_i values so that to increase G_t to improve the match for this high rate impact while maintaining comparable responses for lower severity cases (Zhao et al., 2018). However, there are a few concerns and obstacles to resolve before such an attempt.

First, marker-based strains from high-rate cadaveric experiments are particularly sensitive to marker displacement errors. In fact, with an assumed ±10% random error and ±2 ms synchronization error, they provide few or no “useable” elements for model strain validation (Zhao et al., 2021). Therefore, unless sufficient confidence is ascertained, it may be ill-advised to further calibrate the brain material properties at this stage to match with marker-based strain for the two high-rate experiments. In contrast, the two mid-rate experiments are less sensitive to marker displacement errors, especially when the element size is large to minimize error propagation from marker displacements. Based on the two mid-rate experiments, V2.1 achieved an average peak strain magnitude ratio of 0.93, which was an improvement relative to the V1.0 model (of 0.69, albeit limited to two cases here; Fig. 7c and d). In addition, the V2.1 model appeared to slightly improve the match relative to in vivo strains, particularly for the axial rotation (Fig. 8).

Second, it is necessary to further investigate the implications of artefacts and incomplete sampling of MRE-derived heterogeneity on brain strains in order to develop a mitigation strategy. It may also be advised to investigate the sensitivity of the elementwise stiffness ratios on brain strains to understand their significance on strain distribution, e.g., by halving or doubling the stiffness ratios, as well as the significance of the number of unique stiffness sets (e.g., limited to 10 for the entire brain (Giudice et al., 2021) vs. elementwise for the white matter and 100 bins for the gray matter in this work). These studies are important to understand how best to utilize the MRE data acquired under in vivo conditions for injury-relevant applications (Bayly et al., 2021).

Third, while model validation is transitioning from marker displacement-based assessment to strain-based evaluation (Zhao et al., 2021; Zhao and Ji, 2020b; Zhou et al., 2019, 2018), it remains an ongoing effort to develop an effective and objective approach to evaluate the validation performance (Giordano and Kleiven, 2016; Zhao et al., 2021; Zhao and Ji, 2020b). Different models with a similar CORA score can produce 2–3 times different whole brain strains (Zhao and Ji, 2020b). Thus, this metric is ineffective in discriminating head injury models for simulating whole-brain strains often used for injury analysis.

Fourth, there is also ongoing effort to develop a more robust strain-based model validation strategy. For consistency with our recent study (Zhao and Ji, 2020b), we have used the previous “triad” (Hardy et al., 2007; Zhou et al., 2018) approach to calculate average MPS of a number of triangular elements for marker-based strain evaluation (for cases C288-t3 and C380-t4; Fig. 7a and b). However, the aggregated average MPS may not be effective in revealing the details of model-experiment mismatch. A recent “generalized marker-based strain” systematically samples volumetric, surface, and linear 1D strains among markers using a deterministic and non-overlapping manner (Zhao et al., 2021; Zhao and Ji, 2020b). In particular, exhaustive linear 1D elements may have some advantages to ensure unambiguous validation not attainable from directionally insensitive maximum principal or shear strains (Zhao et al., 2021; Zhao and Ji, 2020b). Nevertheless, marker displacement errors could propagate into strain, and it may be necessary to pre-screen the marker-based elements to achieve a balance between larger elements for smaller strain errors and smaller elements for greater resolution in spatial sampling (Zhao et al., 2021).

Given these considerations, we chose to leave further potential material property calibration and more extensive validations into the future. This would also maintain an appropriate scope of work in the current study. Strain overestimation for high-rate impacts (e.g., impulse of head rotational acceleration <5 ms with peak rotational acceleration >10 krad/s²; Table 2), if one chooses to trust their experimental marker-based strains, suggests that cerebral vascular strains for the three automotive head impacts (Table 3) may have been overestimated. However, this would strengthen the notion that rotation-induced cerebral vascular strains in typical real-world head impacts are towards the lower end of ex vivo vessel experimental strains (further discussed below).

4.3. Cerebral vascular strains

A primary purpose of the study was to evaluate cerebral vascular strains in real-world head impacts. It was not surprising that both peak strains and above-threshold percentages were higher for impacts of higher kinematics and of more severe brain injuries (Table 4 and Fig. 9). Nevertheless, we also found that veins sustained higher strains than arteries for both strain measures, and that circumferential strains were higher than axial strains for both arteries and veins as well. Since both veins and arteries were distributed across the brain, including the cortical and subcortical regions as well as deep in the brain, the higher veinous strain was likely, in part, due to the lower moduli of veins compared to those of arteries (Monson et al., 2003) as adopted in the model (Table 1) (Zhao and Ji, 2020a). In addition, veinous wall thickness was thinner (of 0.1 mm) than major arteries (of 0.5 mm; 0.1 mm for minor arteries) (Zhao and Ji, 2020a). These factors led to locally reduced stiffening in veins compared to arteries, and conversely, higher strains.

The simulated peak axial strains for severe automotive crashes (~20%; Table 4) have reached the experimental yield and ultimate strains for cerebral vessels. At low/moderate rates relevant to most blunt impacts (<100 s⁻¹), yield strain of ~8% and ultimate strain of ~24% were reported for bridging vein-superior sagittal sinus complex harvested from fresh adult cadavers, which increased to ~17% and ~34% at higher rates (100–200 s⁻¹) (Monea et al., 2014). These reports were similar to another study at low rates (18% and 25% for yield and ultimate strain, respectively (Delye et al., 2006)). In addition, (Monson et al., 2005) also found the average yield and ultimate strains to be as low as 25% and 27% for autopsy cortical arteries under quasi-static loading conditions. For the automotive impacts, up to 5% of the veins experienced axial strains greater than 20%. Even for the NFL concussive case (corresponding to mild injury), axial strain in veins reached 7.1%, which was similar to the lowest reported yield strain of ~8% at a moderate rate (Monea et al., 2014). About 1.4% of the veins experienced axial strains larger than 10%. For the non-injury case, no significant vessel strains were predicted.

For vessels experiencing subfailure overstretch (e.g., >20% for arteries harvested from adult ewes), persistent vessel softening would occur (Bell et al., 2015) that may alter the vessel function following the initial injury/sub-injury. Nevertheless, the simulated cerebral vascular strains did not exceed the higher end of the reported ultimate strain of ~50% (Lee and Haut, 1989; Monea et al., 2014; Monson et al., 2005). Collectively, these results provide context of the level of cerebral vessel loading conditions in vivo in typical blunt head impacts and the likelihood of acute failure and subfailure.

Finally, while the current leading theory of vascular injury is driven by vessel axial strain (Famaey et al., 2015; Monson et al., 2019), cerebral vessels do experience circumferential strains as well. In fact, they were found to be even higher than axial strains in general, for both arteries and veins (Table 4). For peak axial and circumferential strains obtained at the same vessel sampling locations, Pearson correlation tests suggest that the two normally distributed values were highly and statistically correlated, for both arteries and veins (p<0.001). Unfortunately, experimental data on failure and subfailure thresholds of circumferential strains do not seem to exist, which precluded further comparison with model simulation results in this study.

5. Limitations and conclusion

In addition to limitations associated with vasculature modeling assumptions (Zhao and Ji, 2020a), imperfect centerline extractions, and others related to MRE-derived heterogeneity discussed previously, there are other limitations worthy of note. First, all impact acceleration profiles were reconstructed, and there were inherent reconstruction errors (Franklyn et al., 2005; Sanchez et al., 2018). For the three severe automotive head impacts, detailed injury analyses including contusion, diffuse axonal injury, and acute subdural haematoma (ASDH) due to bridging vein rupture were previously conducted using two head injury models (Franklyn et al., 2005). This was not performed here as that was not the purpose of the current study. The provided acceleration loading conditions also did not allow using a deformable skull to simulate skull fracture, which is usually the cause for epidural haematoma (Franklyn et al., 2005).

In addition, the WHIM does not yet include bridging veins, which did not allow assessing the likelihood of ASDH due to bridging vein rupture. Most state-of-the-art head injury models still lack a biofidelic representation of the bridging veins (Famaey et al., 2015), albeit significant improvements are emerging that include realistic geometry of local bridging veins to model their damage behavior (Migueis et al., 2019). Finally, this study did not include impact cases of moderate or serious (AIS 2 and AIS 3, respectively) brain injuries, due to the lack of appropriate impact and injury data. Nevertheless, vessel strains from these intermediate impact severities are anticipated to be within the ranges established from the current study.

Notwithstanding these limitations, this study offers some first insight into the in vivo loading conditions of the cerebral vasculature network under a range of impact severities. Head rotation-induced cerebral strains (excluding those of the bridging veins as they were not assessed here) are typically at or below the lowest reported failure and subfailure thresholds measured from ex vivo experiments. These results bridge the gap between ex vivo experimental studies on vessel mechanical behaviors and the risk, severity, and extent of CVI in real-world head impacts.

Highlights:

• First study to investigate human brain in vivo cerebral vascular strains in dynamic head impact

• In vivo cerebral vascular strains are at the lower end of failure/subfailure ex vivo thresholds

• Further upgraded the Worcester Head Injury Model (WHIM) with brain material property heterogeneity

• The WHIM is re-calibrated and re-validated for future investigations of brain and cerebral vascular injuries