Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2022 Jan 7;7(3):2661–2670. doi: 10.1021/acsomega.1c05027

Exploration of the Mechanism of the Dimerization of Hydroxymethylsilanetriol Using Electronic Structure Methods

Khaoula Maghrebi †,‡, Safa Gam †,‡, Bechir Hammami †,§, Atheer Alsadiri §, Manef Abderrabba ‡, Sabri Messaoudi †,‡,§,*
PMCID: PMC8792941  PMID: 35097264

Abstract

graphic file with name ao1c05027_0007.jpg

Hydroxymethylsilanetriol undergoes condensation reactions to form new structures with an organic part in the formed bridges. As a first step to explore the formation of these bridges, we studied the corresponding mechanisms using simple models and theoretical methods. Three mechanisms were studied for the formation of dimers of hydroxymethylsilanetriol with bridges: Si–O–C–Si, Si–O–Si, and Si–C–O–C–Si. Energies are calculated using M06/6–311+G(d,p) single-point calculations on B3LYP-optimized geometries in solution and including B3LYP thermodynamic corrections. The first mechanism for the formation of the Si–O–C–Si bridge consists of one step. The second mechanism for the formation of the Si–O–Si bridge consists of two steps. The barrier for the last mechanism for the formation of the Si–C–O–C–Si bridge is too high and cannot occur at room temperature. The energy barriers are 31.8, 27.6, and 65.9 kcal mol–1 for the first, second, and third mechanisms, respectively. When adding one explicit water molecule, these energies are 25.9, 22.9, and 80.3 kcal mol–1, respectively. The first and second mechanisms can occur at room temperature, which is in agreement with the experimental results.

Introduction

Silicates are the predominant substance of the earth’s crust.1 Over the last decade, silica nanoparticles have been used in varied applications, including ceramics, pharmaceuticals, catalysis, chromatography, imaging, and electronic packaging and in the synthesis of multifunctional nanocomposites.2−4

For years, research has been dedicated to the preparation of hybrid organic–inorganic structures. The wide diversity of organic molecules in combination with silicon-based polymers or alkoxysilanes allowed preparation of many hybrid materials used in different fields.5 The use of precursors already carrying an organic part and a mineral part allows obtaining advantageous properties and can lead to new mechanisms of condensation.

Silanetriols having the general formula RSi(OH)3 (R = organic substituent) are a particular class of complexes that combines the properties of silicic acid with those of organosilicon structures. Silanetriols can form siloxane bonds through condensation reactions.

Arkles et al.1 used the precursors hydroxymethyltriethoxysilane and hydroxymethyltrimethoxysilane to form hydroxymethylsilanetriol, HOCH2Si(OH)3. They used spectroscopy techniques to identify its structures in the presence of water. Hydroxymethylsilanetriol is similar to silicic acid, which has four hydroxyl groups and differs only by a methylene group.1 With similar properties to the latter, it can go through condensation reactions related to sol–gel processing techniques leading to organosilicate compounds. The sol–gel process is a widely used method to synthesize a wide selection of materials. Its main application is on silicate materials, which can be synthesized with great homogeneity and purity under relatively mild conditions.6,7 The organosilicate structures derived from hydroxymethylsilanetriol can be converted to silicon dioxide at relatively low temperatures.1

During drying, hydroxmethylsilanetriol-derived gels have less stress cracking than conventional tetraethoxysilane. It was proposed that the Si–O–C bond equilibration during this process contributes to stress relief.

Even though a large number of theoretical7−16 and experimental studies1,17−19 on the mechanisms of silicate condensation have been reported, to our knowledge, there is no theoretical study of the mechanisms of condensation of hydroxymethylsilanetriol with different properties due to the presence of an organic part that leads to different products with Si–O–Si, Si–O–C–Si, and Si–C–O–C–Si bonds.

To achieve this goal, density functional calculations using a solvation model were performed to determine the different reactant compounds, transition states, intermediates, and products for the condensation mechanisms of hydroxymethylsilanetriol.

We compared our findings with the available experimental 29Si NMR observations presented by Arkles et al.1

Results and Discussion

Arkles et al.1 followed the condensation reaction of hydroxymethylsilanetriol experimentally using various spectroscopic techniques.29Si NMR was used in the analysis of the hydrolysis reaction. They proposed that the obtained products were the simple monomer hydroxymethylsilanetriol and siloxane-bridged, silmethyleneoxide-bridged, and mixed bridged oligomeric condensates. The NMR of the hydrolysis reaction was different from tetraethoxysilane hydrolysis, showing that there is no loss of the hydroxymethylene group. This 29Si NMR study of hydrolysis was performed by mixing a sample of 50% of hydroxymethyltriethoxysilane with an equal volume of water, leading to hydroxymethylsilanetriol and the different condensation products.1 Thus, the solvent used in this work was water.

As a first step to explore the formation of these products, we studied the corresponding formation mechanisms using simple models and theoretical methods. The mechanisms that lead to products with Si–O–Si, Si–O–C–Si, and Si–C–O–C–Si bonds were studied theoretically. All of the optimized geometrical structures of the critical points (transition structures, reactants, and products) were performed using a DFT method at the B3LYP level of theory with the standard 6-31+G(d) basis set and the continuum solvation model SMD. Reaction energies and barriers in the solvent phase were computed at different levels of theory B3LYP/6-31+G(d) and M06/6-311+G(d,p)//B3LYP/6-31+G(d).

Study of the First Mechanism of Dimerization (D1): Formation of Dimer D1 (Si–O–C–Si)

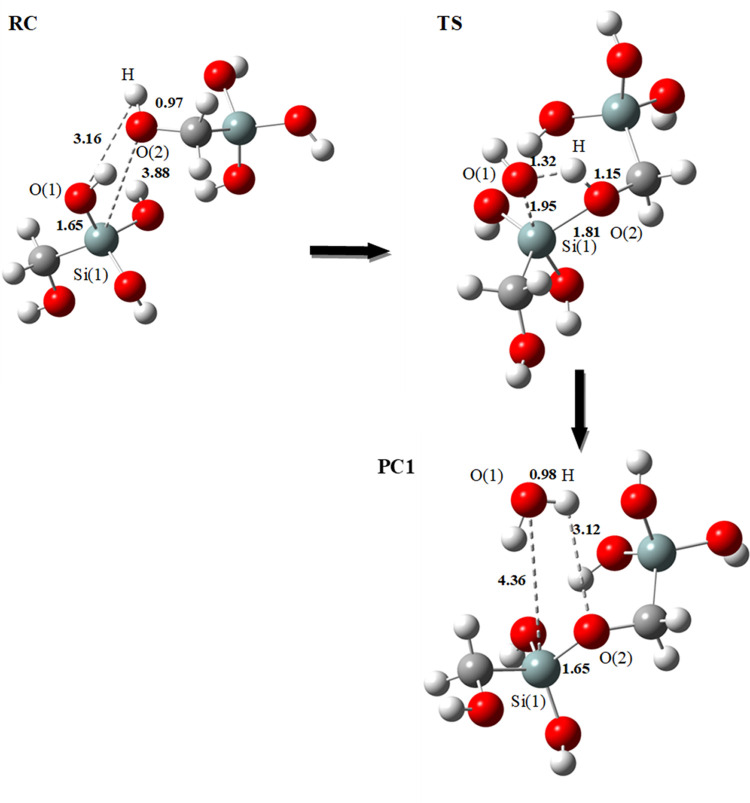
We first began by studying the formation of dimer D1. The formation of this dimer passes through a reaction of oxolation. The optimized model structures of the condensation of HOCH2Si(OH)3 are presented in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Optimized geometrical structures for the first mechanism of dimerization: formation of dimer D1 (Si–O–C–Si) at the B3LYP/6-31+G(d) level using the SMD solvation model. Bond lengths are in angstrom (Å); RC: reactant complex, TS: transition state, and PC: product complex.

The reaction begins with the nucleophilic attack of hydroxide (C–O(2)–H) of the first monomer on the Si(1) atom of the second monomer [O(2) on Si(1)] to form a transition state (TS) that has a four-membered ring [Si(1)–O(1)–H–O(2)]. The four atoms Si(1), O(1), H, and O(2) are in the same plane. The nucleophile (O(2)–H) is coordinated with the atom Si(1) with a distance of 3.88 Å (Figure 1: RC). This transition state (Figure 1: TS) is formed by a bridge (Si–O–C–Si) (O(2) is bound to Si(1) with a distance equal to 1.81 Å).

The hydrogen migrates to O(1) to form a water molecule. We note that the formation of a hydrogen bond between [O(2), H, and O(1)] occurs during the transfer of the proton. The [O(2)–H] bond distance is elongated to 1.15 Å (from 0.97 Å in the reactant complex (RC)), and the [Si(1)–O(1)] bond is also stretched to 1.95 Å (from 1.65 Å in the reactant complex (RC)). The distance [O(1)–H] is shortened to 1.32 Å (from 3.16 Å), and the[Si(1)–O(2)] bond is reduced to 1.81 Å (from 3.88 Å). This transition state leads to a complex involving dimer D1 with the departure of a H2O molecule (Figure 1: PC1).

The reaction energy between the reactant complex (RC) and the product complex (PC1) is ΔE = 2.1 kcal mol–1 (ΔG = 2.6 kcal mol–1) at B3LYP/6-31+G(d) and ΔE = 0.6 kcal mol–1 (ΔG = 1.0 kcal mol–1) at M06/6-311+G(d,p)//B3LYP/6–31+G(d) (Table 1 and Figure 4). It is noted that the reactive complex (RC) is more stable than the product complex (PC1). The reaction remains possible because the energy gap between the reactants and the product remains low.

Table 1. Relative Electronic Energy ΔE and Relative Gibbs free Energies ΔG Using the SMD Solvation Model at Different Levels of Theory for the Mechanisms of Dimerization (kcal mol–1).

B3LYP/6–31+G(d)
 M06/6–311+G(d,p)// B3LYP/6–31+G(d)
  ΔE ΔG ΔE ΔG
Mechanism (D1) (Si–O–C–Si)
RC 0.0 0.0 0.0 0.0
TS 33.2 34.3 30.7 31.8
PC1 2.1 2.6 0.6 1.0
Mechanism (D2) (Si–O–Si)
RC 0.0 0.0 0.0 0.0
TS1 27.0 29.5 25.1 27.6
IM 9.2 17.2 7.1 15.1
TS2 10.3 18.4 7.7 15.8
PC2 –8.4 –3.9 –8.2 –3.7
Mechanism (D3) (Si–C–O–C–Si)
RC 0.0 0.0 0.0 0.0
TS 68.0 65.1 68.7 65.9
PC3 –0.7 –2.3 –2.2 –3.8
Open in a new tab

Figure 4.

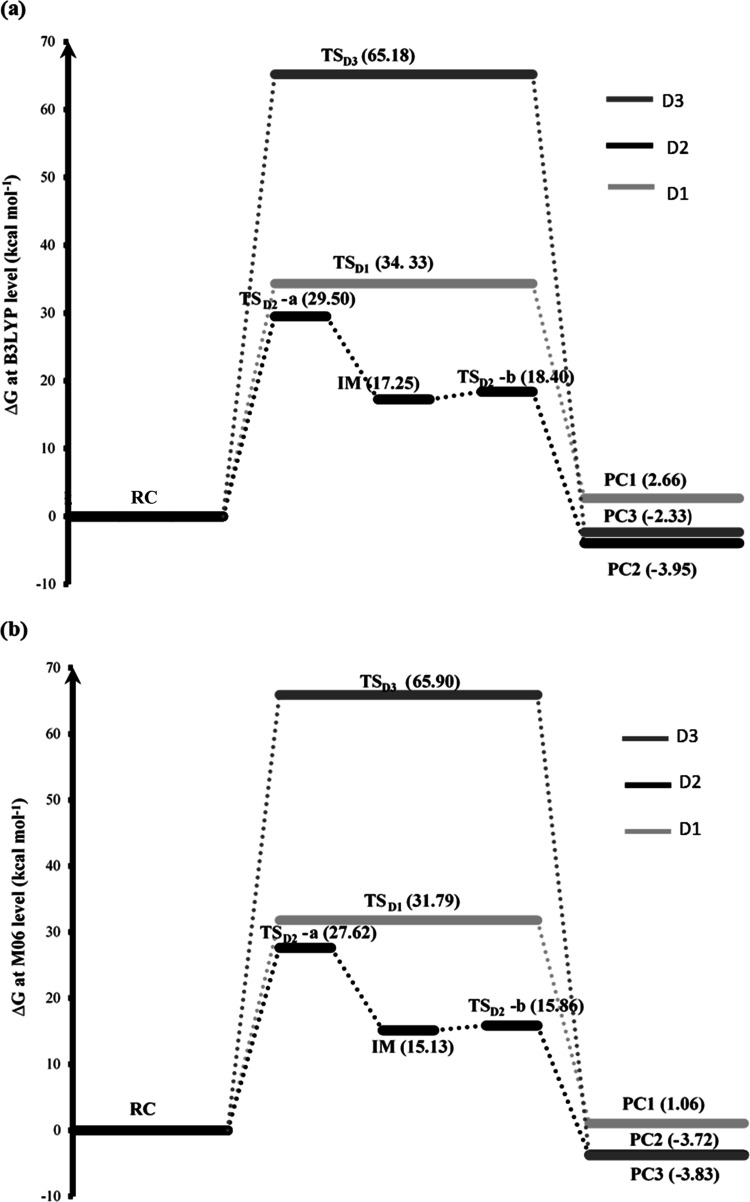
Figure 4

Open in a new tab

Free energy profiles of the dimerization of hydroxymethylsilanetriol: (a) free energy profiles at the B3LYP level using the SMD model and (b) free energy profiles at the (M06/6-311+G(d,p)//B3LYP/6-31+G(d)) level, including B3LYP thermodynamic corrections and using the SMD solvation model.

By studying the energy profiles of the dimerization reaction of two monomers leading to the formation of dimer D1, the energy barrier between the transition state (TS) and the reactive complex (RC) is found to be 33.2 kcal mol–1 (ΔG‡ =34.3 kcal mol–1) at B3LYP and for M06/B3LYP, ΔE‡ is of the order of 30.7 kcal mol–1(ΔG‡ = 31.8 kcal mol–1).

Study of the Second Mechanism of Dimerization (D2): Formation of Dimer D2 (Si–O–Si)

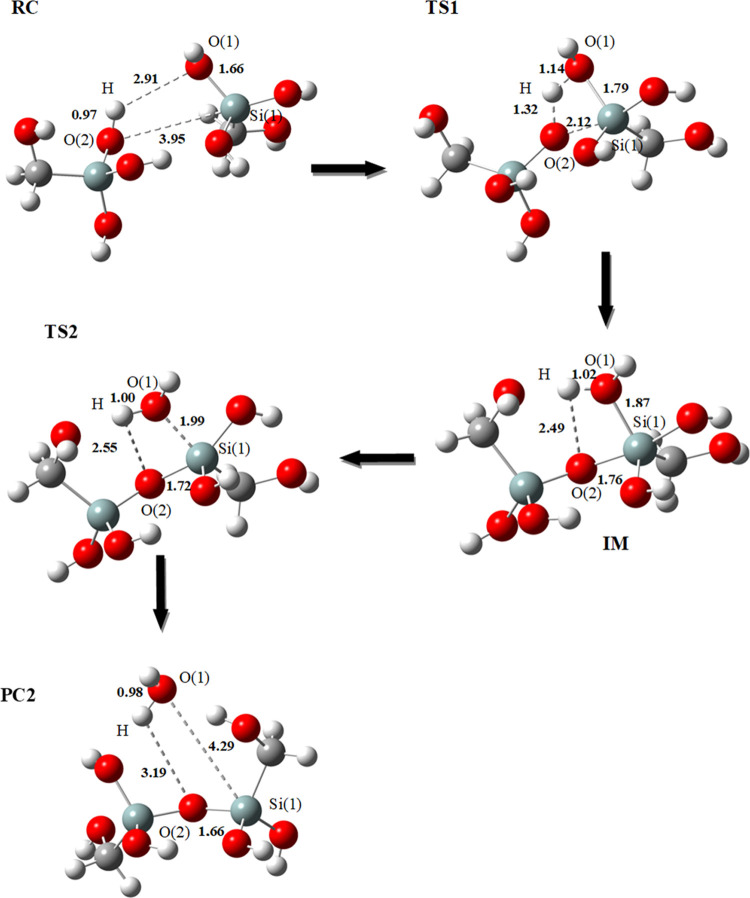
The formation of dimer D2 also passes through a reaction of oxolation. The formation of the dimer D2 passes through two transition states and a single intermediate. The structures optimized by our calculations are presented in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Optimized geometrical structures for the second mechanism of dimerization: formation of dimer D2 (Si–O–Si) at the B3LYP/6-31+G(d) level using the SMD solvation model. Bond lengths are in angstrom (Å); RC: reactant complex, TS: transition state, and PC: product complex.

In this case, the reaction proceeds by the nucleophilic attack of the hydroxide (O(2)–H) bonded to the Si atom of the first monomer on the Si(1) atom of the second monomer [O(2) on Si(1)], passing through a first transition state (TS1) that has a four-membered ring [Si(1)–O(1)–H–O(2)]. The nucleophile (O(2)H) is coordinated to Si(1) with a distance of 3.95 Å.

In this transition state (Figure 2:TS1), the distance [Si(1)–O(2)] is reduced to 2.12 Å from 3.95 Å present in the reactant complex (RC). This transition state leads to an intermediate (IM) formed by a bridge (Si–O–Si), where the Si(1) is pentacoordinate. O(2) is bonded to Si(1) with a distance equal to 1.76 Å. The hydrogen atom “H” migrates to O(1) to form a molecule of water.

In the second transition state (Figure 2:TS2), the distance [O(2)–H] is elongated to 2.55 Å (from 2.49 Å in the intermediate (IM)) and the distance [O(1)–H] is reduced to 1.00 Å (from 1.02 Å in the (IM)). The [Si(1)–O(2)] bond is shortened to 1.72 Å (from 1.76 Å in the (IM)). The length of the bond [Si(1)–O(1)] is 0.12 Å longer than that of the intermediate (IM), which eventually leads to the total separation of the water molecule and makes it possible to obtain the final product (Figure 2: PC2).

It is observed that the product complex (PC2) is more stable than the reactive complex (RC), and the difference between them is of the order of ΔE = −8.4 kcal mol–1 (ΔG = −3.9 kcal mol–1) at B3LYP/6-31+G(d) and about ΔE = −8.2 kcal mol–1 (ΔG = −3.7 kcal mol–1) at M06/6-311+G(d,p)//B3LYP/6–31+G(d) (Table 1 and Figure 4).

By analyzing the energy profiles of the condensation reaction of the two monomers leading to the formation of dimer D2, the energy barrier between the first transition state (TS1) and the reactive complex (RC) is found to be equal to 27 kcal mol–1(ΔG‡ = 29.5 kcal mol–1) in B3LYP and for B3LYP/M06, it is of the order of 25.1 kcal mol–1 (ΔG‡ = 27.6 kcal mol–1).

Study of the Third Mechanism of Dimerization (D3): Formation of Dimer D3 (Si–C–O–C–Si)

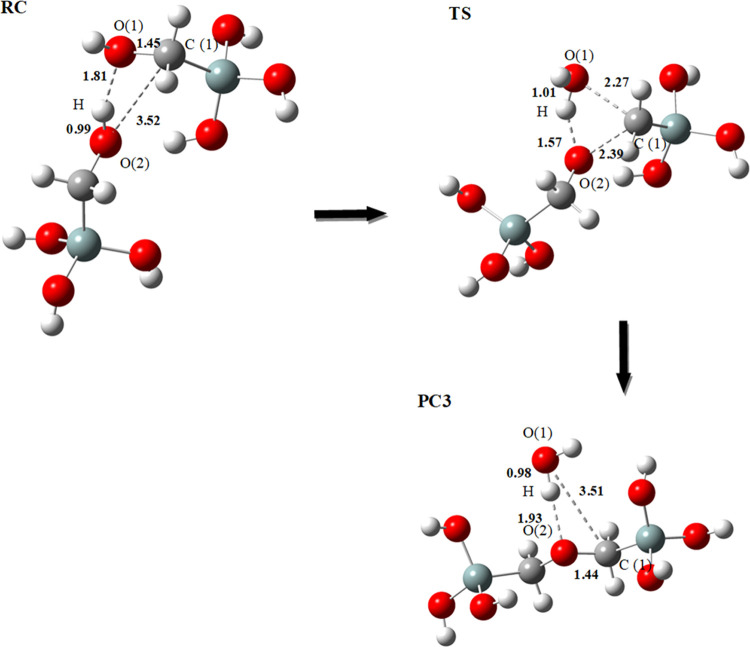
We proposed a third mechanism for the dimerization of hydroxymethylsilanetriol, leading to the formation of dimer D3 with a C–O–C bridge using the same calculation methods presented previously. This dimer has not been identified experimentally. Figure 3 shows the details of this reaction path.

Figure 3.

Figure 3

Open in a new tab

Optimized geometrical structures for the third mechanism of dimerization: formation of dimer D3 (Si–C–O–C–Si) at the B3LYP/6-31+G(d) level using the SMD solvation model. Bond lengths are in angstrom (Å); RC: reactant complex, TS: transition state, and PC: product complex.

The reaction proceeds by the nucleophilic attack of the hydroxide (O(2)–H) bonded to the carbon “C” of the first monomer on the C(1) atom of the second monomer [O(2) on C(1)]. The complex reactant turns into the product via a transition state with hydrogen transfer. After “H” transfer, the water fragment leaves the molecule to form the dimer D3.

The reaction energy between the reactant complex (RC) and the product complex (PC3) is ΔE = −0.7 kcal mol–1 (ΔG = −2.3 kcal mol–1) at B3LYP/6-31+G(d) and ΔE = −2.2 kcal mol–1 (ΔG = −3.8 kcal mol–1) at M06/6-311+G(d,p)//B3LYP/6–31+G(d) (Table 1 and Figure 4). It is observed that the product complex (PC3) is more stable than the reactive complex (RC).

In our study, the activation energy of this reaction is very high, of the order of 65 kcal mol–1 (Table 1and Figure 4), which may explain why in the experimental results1 this compound was not observed.

We showed theoretically that it is very difficult (expensive from an energy point of view) to form the dimer D3 during the condensation reaction of hydroxymethylsilanetriol.

Comparison between the Different Pathways of Condensation and the Effect of Adding an Explicit Water Molecule

Free energy profiles of the different pathways of the dimerization of hydroxymethylsilanetriol at two different levels of theory are summarized in Figure 4. The activation energy of the third mechanism that we proposed for the dimerization of hydroxymethylsilanetriol is very high, of the order of 65 kcal mol–1. It cannot be observed at room temperature, which is in agreement with the experimental results.

It is noted that the energy barriers calculated with B3LYP/6-31+G(d) and M06/6-311+G(d,p)//B3LYP/6-31+G(d) are different. For the two possible mechanisms of condensation leading to the formation of both dimers D1 and D2, the activation barriers calculated by M06/B3LYP are lower than those computed by B3LYP.

The results with the B3LYP level show that the formation of dimer D2 is more favorable since it gives us the lowest energy barrier. The barrier energy of the second dimerization mechanism to obtain compound D2 is lower by 6.2 kcal mol–1 (Table 1) than that of the first mechanism leading to the formation of dimer D1. Similarly, for free energies, the difference between the two activation barriers is equal to 4.8 kcal mol–1 (Table 1 and Figure 4a) in favor of the formation of dimer D2. The second level of calculation with M06/B3LYP (Table 1 and Figure 4b) confirms that the second dimerization mechanism is more favorable. It is found that the dimerization reaction leading to the formation of dimer D1 is more expensive from an energy point of view.

The Becke three-parameter Lee–Yang–Parr functional (B3LYP)20−22 is a hybrid gradient approximation. M0623 is a meta-hybrid generalized gradient approximation functional parameterized for systems with noncovalent interactions. M06 gives better performance than B3LYP for main-group thermochemistry, barrier heights, and noncovalent interactions.24 The computational model with the basis sets we used was validated by Lu et al.25 for the theoretical study of the reaction mechanisms and the determination of barrier heights of complexes with organic compounds.

We calculated with the same level of theory using M06-D3 with empirical dispersion D3, the D3 version of Grimme’s dispersion.26 The determinant step free energy barriers with M06-D3 are 31.6, 27.5, and 65.8 kcal mol–1 for D1, D2, and D3, respectively. They are 31.8, 27.6, and 65.9 kcal mol–1, respectively, with M06 functional. The free reaction energies with M06-D3 are 0.9, −3.8, and −4.0 kcal mol–1, respectively. They are 1.0, −3.7, and −3.8 kcal mol–1, respectively, with M06 functional. These relative calculated energies with empirical dispersion D3 give the same relative order of activation barriers for the rate-limiting step and relative order of reaction energies of each studied mechanism with M06.

Finally, by comparing the two possible reaction paths studied, it is concluded that the formation of a Si–O–Si bridge (dimer D2) is more energetically favorable than the formation of a Si–O–C–Si bridge (dimer D1).

The only available experimental results for the studied structures were NMR results,1 which showed that the observed structures are the reactant, PC1, and PC2. Our calculated results show that the most stable structures are those observed experimentally. The product PC1 is 1.06 kcal mol–1 higher in energy than the reactants, and the product PC2 is −3.72 kcal mol–1 lower in energy than the reactants. The relative energies suggest that different proportions of these species are present at room temperature, and the presence of reactants can be the result of the reverse reaction from product PC1. For the most preponderant compound PC2, we calculated the chemical shifts of 29Si with the same level of theory and obtained the values −48.7 and −50.2 ppm, and they are in the range of chemical shifts observed experimentally.1

Mcintosh27 showed that the energy condensation barrier of the two monomers Si(OH)4 is 157.3 kJ mol–1 (37.60 kcal mol–1) at the temperature T = 300 K with the same calculation method we used (DFT/B3LYP/6-31+G(d)) but using a different solvation model that is the CPCM (conductor-like polarizable continuum). Previous theoretical studies showed that the barrier to this process is found in the range of 129–189 kJ mol–1.7,11,27−29 A simple comparison of these energies with the two energetic barriers we obtained for D1 and D2 suggests that these reactions have comparable energy barriers.

When using different explicit models, the same study shows that the energy differences are smaller than the large differences we have between D3 and other mechanisms. Thus, we suggest that it will not change qualitatively our conclusions. The addition of a water molecule leads to three new mechanisms, D1′, D2′, and D3′. The energies at M06/6-311+G(d,p)//B3LYP/6-31+G(d) are presented in Table 2.

Table 2. Relative Gibbs Free Energies ΔG Using the SMD Solvation Model at M06/6-311+G(d,p)//B3LYP/6-31+G(d) for the Mechanisms of Dimerization with One Water Molecule (D1′, D2′, and D3′) (kcal mol–1)a.

  D1′ D2′ D3′
R 0.0 0.0 0.0
TS1 21.8 21.4 80.3
I 20.7 19.7  
TS2 25.9 22.9  
P 0.5 –1.1 –1.4
Open in a new tab
a

The transition states for the determinant steps for D1′, D2′, and D3′ are presented in Figure 5.

The addition of one water molecule contributes to the lowering of the energy barriers for D1 and D2 but does not change qualitatively the order between the different mechanisms. The energy barriers are now 25.9 and 22.9 kcal mol–1 for the first and second mechanisms, respectively. The third mechanism has now a higher energy barrier of 80.3 kcal mol–1.

Our results found that the introduction of the hydroxymethylene group can contribute to condensation through two mechanisms (D1) and (D2), with energy barriers and energy reactions that can occur at room temperature. These results can be used to predict physical and mechanical properties of formed gels. Our theoretical calculations correlate with the experimental propositions of Arkles et al.1

Mulliken charges for the three pathways are presented in Tables 3, 4, and 5. For the most favorable pathway, we show a notable charge separation in TS1D2 by charges of 1.28 and −0.88 on Si1 and O2 atoms, respectively (Table 4). These charges in TSD1 were 1.29 and −0.46 on Si1 and O2 atoms, respectively (Table 3). The charges on the reactant RCD2 were 1.33 on Si1 and −0.66 on O2. The charges in reactant RCD1 were 1.17 on Si1 and −0.42 on O2. This shows evidence for more charge separation in TS1D2 and contributes to the differences in the energies.

Table 3. Mulliken Atomic Charges/Atomic Charges Using the Natural Population Analysis of the Reactants, Transition States, and Products for (D1).

M06/6-311+G(d,p)//B3LYP/6–31+G(d)
solvent = water
atomic charges
structuresa Si1 O1 O2 H
RC 1.17/2.20 –0.61/–1.15 –0.42/–0.80 0.34/0.52
TS 1.29/2.13 –0.64/–1.09 –0.46/–0.87 0.39/0.55
PC 1.19/2.22 –0.71/–1.03 –0.47/–0.96 0.38/0.51
Open in a new tab
a

Refer to Figure 1 for atom labeling: RC (reactant complex), TS (transition state), and PC (product complex).

Table 4. Mulliken Atomic Charges/Atomic Charges Using the Natural Population Analysis of the Reactants, Transition States, Intermediates, and Products for (D2).

M06/6-311+G(d,p)//B3LYP/6–31+G(d)
solvent = water
atomic charges
structuresa Si1 O1 O2 H
RC 1.33/2.19 –0.66/–1.13 –0.66/–1.13 0.36/0.53
TS1 1.28/2.17 –0.62/–1.01 –0.88/–1.28 0.44/0.56
IM 1.23/2.16 –0.67/–0.95 –0.74/–1.30 0.52/0.56
TS2 1.05/2.19 –0.62/–0.96 –0.70/–1.29 0.45/0.55
PC 1.25/2.22 –0.68/–1.01 –0.84/–1.28 0.37/0.52
Open in a new tab
a

Refer to Figure 2 for atom labeling: RC (reactant complex), TS (transition state), IM (intermediates), and PC (product complex).

Table 5. Mulliken Atomic Charges/Atomic Charges Using the Natural Population Analysis of the Reactants, Transition States, and Products for (D3).

M06/6-311+G(d,p)//B3LYP/6–31+G(d)
solvent = water
atomic charges
structuresa C1 O1 O2 H
RC –0.69/–0.51 –0.45/–0.81 –0.53/–0.82 0.41/0.52
TS –0.58/–0.41 –0.54/–0.92 –0.72/–0.87 0.40/0.53
PC –0.69/–0.51 –0.68/–1.02 –0.31/–0.66 0.36/0.50
Open in a new tab
a

Refer to Figure 3 for atom labeling: RC (reactant complex), TS (transition state), and PC (product complex).

The reactions D1 and D2 begin with the nucleophilic attack on the Si atom. Negatively charged nucleophiles are more reactive than less charged nucleophiles. If we have a strong nucleophile with a relatively more negative charge than the Si atom, the reaction will happen faster.

We have also calculated the charges with the “natural population analysis” (NPA) (Tables 3, 4, and 5). This method has been developed to calculate atomic charges and orbital populations of molecular wave functions in general atomic orbital basis sets. The natural analysis is an alternative to the conventional Mulliken population analysis and seems to exhibit improved numerical stability and better describe the electron distribution in compounds of high ionic character, such as those containing metal atoms.30 The NPA charge on O2 in TS1D2 is −1.28 and in TSD1 is −0.87 (Table 4). The NPA charge on Si1 in TS1D2 is 2.17 and in TSD1 is 2.13. This supports the fact that the nucleophilic attack is facilitated in TS1D2.

We notice for TSD3 that the charges on C1 (−0.58) and O2 (−0.72) (Table 5) are both negative, whereas the charge separation between Si1 and O2 in D1 and D2 is important (Tables 3 and 4). In TSD3, the NPA charges on C1 and O2 are respectively −0.41 and −0.87. When adding a water molecule for D3, the mechanism is done in one step, whereas for D1 and D2, we have two steps in the mechanism in the presence of the additional water molecule. This can affect the energy of the mechanism in a different way.

The SMD continuum solvation model is based on the quantum mechanical charge density of a solute molecule interacting with a continuum description of the solvent. The solvent is not represented explicitly but rather as a dielectric medium with surface tension at the solute–solvent boundary. This limitation can change the effect of the solvent on the solute.

When adding a water molecule (Figure 5), the charge separation in TS2D2′ becomes more important with a charge of 1.21 on Si1 and a charge of −1.07 on O2, which can contribute more in the modification of energy values.

Figure 5.

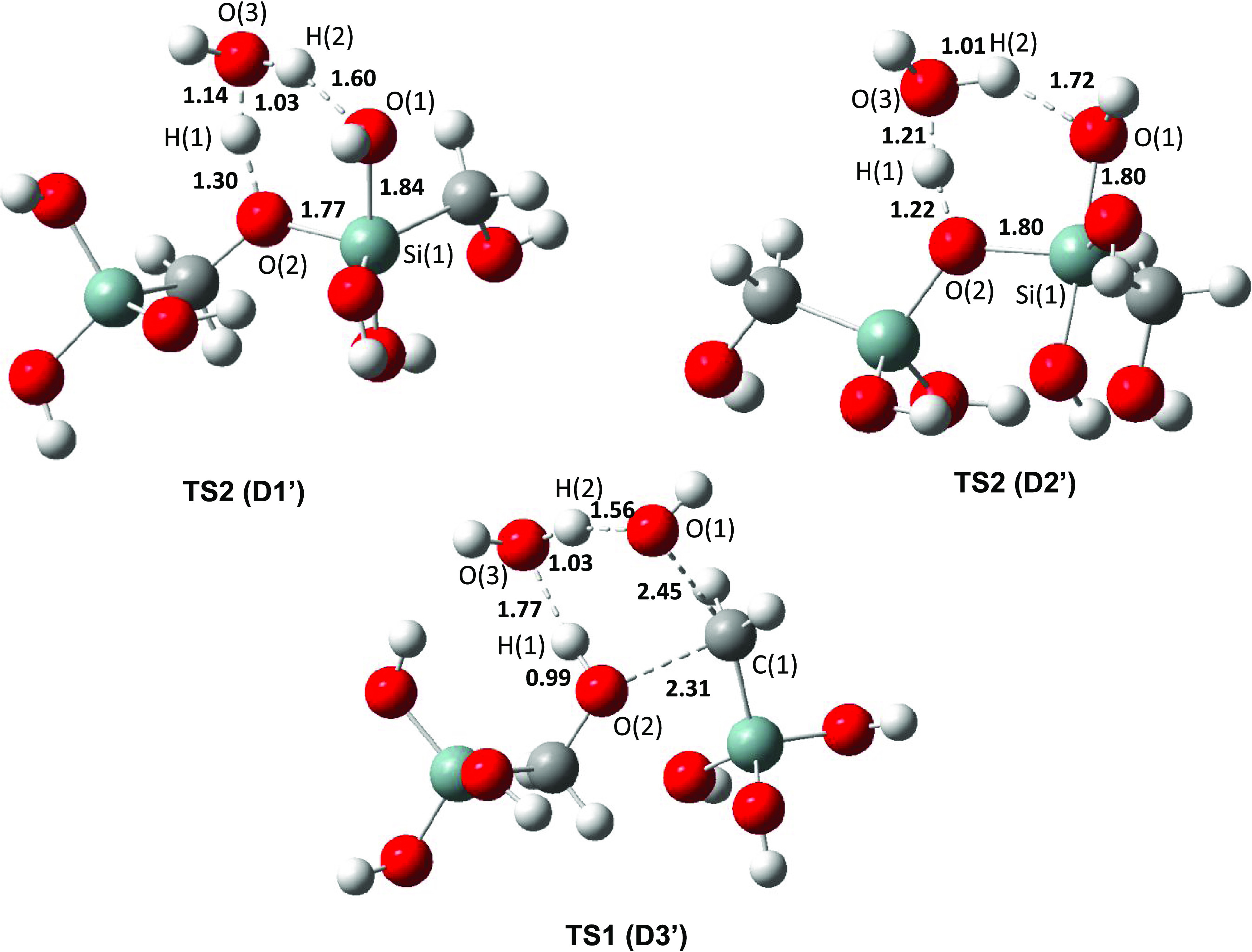
Figure 5

Open in a new tab

Transition states for the determinant steps for the mechanisms of dimerization with one water molecule (D1′, D2′, and D3′). Bond lengths are in angstrom (Å).

This suggests that charge separation can be more important when a second water molecule is added and this can reduce the energy. Many different positions can be taken by the second water molecule, and the different configurations can be studied in future work.

As suggested experimentally,26 hydroxmethylsilanetriol-derived gels were subject to less stress cracking during drying than conventional tetraethoxysilane-derived gels, suggesting that the Si–O–C bond equilibration during drying provides a mechanism for stress relief. Our pathways give insight into the formation and energetics of the different bridges and particularly into the formation of the Si–O–C bridge that contributes to the interesting properties of the obtained products.

We suggest that our theoretical study, which gives to our knowledge for the first time the detailed mechanisms and the corresponding energies for the formation of Si–C–O–Si and Si–C–O–C–Si bridges, can give the parameters for molecular mechanics to simulate larger systems and thus to understand the properties of the extended products.

Conclusions

Hydroxymethylsilanetriol can give new structures through condensation due to the presence of the organic groups in the formed bridges. We studied theoretically the different mechanisms that can lead to a dimer of hydroxymethylsilanetriol using simple models. Three mechanisms were considered in the creation of dimers with bridges: Si–O–C–Si, Si–O–Si, and Si–C–O–C–Si. A theoretical study has been performed using the DFT method with an implicit solvation model (SMD). In this approach, we optimized the geometry of stationary states at the B3LYP level of theory with the standard 6-31+G(d) basis set and single-point calculations at M06/6-311+G(d,p)//B3LYP/6-31+G(d) with B3LYP thermal corrections.

The first mechanism (D1) consists of one step with the nucleophilic attack of hydroxide bonded to carbon of the first monomer on the Si atom of the second monomer. The second mechanism consists of two steps, the first where the reaction proceeds by the nucleophilic attack of the hydroxide bonded to the Si atom of the first monomer on the Si atom of the second monomer to form an intermediate with one water molecule attached, which is separated from the complex in the second step. The third mechanism’s energy barrier is too high and cannot occur at room temperature. When we compare the two possible reaction paths, it is shown that the energy barrier for the formation of a Si–O–Si bridge (dimer D2) is more energetically favorable than that for the formation of a Si–O–C–Si bridge (dimer D1). The energy barriers of the two possible mechanisms (D1 and D2) are ranging from 27 to 32 kcal mol–1. When adding one explicit water molecule, the energies are 25.9, 22.9, and 80.3 kcal mol–1 for the first, second, and third mechanisms, respectively, which proves that both reactions D1 and D2 can take place at room temperature. This is in agreement with experimental results.

Computational Methods

Quantum mechanical calculations were achieved using the Gaussian 09 software package.31

We used in all of the calculations density functional theory (DFT), with the B3LYP20,21,32 hybrid exchange–correlation functional. The B3LYP method has been reported to offer excellent descriptions of various reaction profiles and particularly of structures, heats of reaction, and vibrational properties of various systems.7,11,27

The basis set used was all-electron type 6-31+G(d). We checked all stationary geometries by frequency calculations, yielding only positive eigenvalues for minima and only one negative eigenvalue for transition states. Transition states were confirmed to match to the desired transformation by determination of the intrinsic reaction coordinate (IRC).33,34 The geometries from the IRC pathway were optimized to find the corresponding reactant complex (RC) and product complex (PC).

Solvation was included using solvation model density (SMD).35 Geometry optimization was calculated with the B3LYP/6-31+G(d) basis set and SMD solvation model (solvent = water). Frequency analysis was used to obtain the thermodynamic energy corrections at this level.

To obtain higher accuracy, single-point energies of the optimized geometries were calculated at the M06/6-311+G(d,p) level of theory with the SMD model. The basis set includes a polarization function for hydrogen, which is involved in the reaction. The M0623,36 functional has been proven to be highly effective with large basis sets.37−41 It considers dispersion forces.42 The M06 functional showed an error of 0.63 kcal mol–1 for noncovalent interaction energies.24

Throughout this study, the energies were determined using the formula25

graphic file with name ao1c05027_m001.jpg 1

where Gsolv is defined as the solvate Gibbs free energy, Gcorr is defined as the thermal correction of Gibbs free energy from the B3LYP-optimized geometry, and Esolv is defined as the single-point M06 SCF energy.

Acknowledgments

The authors are grateful to the Tunisian Ministry of Higher Education and Scientific Research for financial support.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c05027.

  • Cartesian coordinates and energies of important stationary points (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c05027_si_001.pdf (135.6KB, pdf)

References

  1. Arkles B.; King K.; Pannell K. Hydroxymethylsilanetriol – A Simple Analog of Silicic Acid. Silicon 2013, 5, 187–197. 10.1007/s12633-013-9146-2. [DOI] [Google Scholar]
  2. Mestanza S. N. M.; Ribeiro A. O.; Ribeiro C. S. d. S.; Giunta G.; Ribera A. Study of the influence of dynamics variables on the growth of silica nanoparticles. Inorg. Nano-Met. Chem. 2017, 47, 824–829. 10.1080/15533174.2016.1212226. [DOI] [Google Scholar]
  3. Wu S.-H.; Mou C.-Y.; Lin H.-P. Synthesis of mesoporous silica nanoparticles. Chem. Soc. Rev. 2013, 42, 3862–3875. 10.1039/c3cs35405a. [DOI] [PubMed] [Google Scholar]
  4. Wagner T.; Haffer S.; Weinberger C.; Klaus D.; Tiemann M. Mesoporous materials as gas sensors. Chem. Soc. Rev. 2013, 42, 4036–4053. 10.1039/C2CS35379B. [DOI] [PubMed] [Google Scholar]
  5. Hellali T.; Hafidh A.; Etteyeb N.; Touati F.; Hamzaoui A. H.; Somrani S. New silica-based hybrid materials (Nouveaux matériaux hybrides à base de silicium). Phosphorus, Sulfur Silicon Relat. Elem. 2017, 192, 1018–1026. 10.1080/10426507.2017.1315423. [DOI] [Google Scholar]
  6. Hench L. L.; West J. K. The sol-gel process. Chem. Rev. 1990, 90, 33–72. 10.1021/cr00099a003. [DOI] [Google Scholar]
  7. Henschel H.; Schneider A. M.; Prosenc M. H. Initial Steps of the Sol–Gel Process: Modeling Silicate Condensation in Basic Medium. Chem. Mater. 2010, 22, 5105–5111. 10.1021/cm100401f. [DOI] [Google Scholar]
  8. Kudo T.; Gordon M. S. Theoretical Studies of the Mechanism for the Synthesis of Silsesquioxanes. 1. Hydrolysis and Initial Condensation. J. Am. Chem. Soc. 1998, 120, 11432–11438. 10.1021/ja980943k. [DOI] [Google Scholar]
  9. Pereira J. C. G.; Catlow C. R. A.; Price G. D. Ab Initio Studies of Silica-Based Clusters. Part I. Energies and Conformations of Simple Clusters. J. Phys. Chem. A 1999, 103, 3252–3267. 10.1021/jp982866l. [DOI] [Google Scholar]
  10. Mora-Fonz M. J.; Catlow C. R. A.; Lewis D. W. Oligomerization and Cyclization Processes in the Nucleation of Microporous Silicas. Angew. Chem., Int. Ed. 2005, 44, 3082–3086. 10.1002/anie.200462524. [DOI] [PubMed] [Google Scholar]
  11. Trinh T. T.; Jansen A. P. J.; van Santen R. A. Mechanism of Oligomerization Reactions of Silica. J. Phys. Chem. B 2006, 110, 23099–23106. 10.1021/jp063670l. [DOI] [PubMed] [Google Scholar]
  12. Trinh T. T.; Jansen A. P. J.; van Santen R. A.; Jan Meijer E. The role of water in silicate oligomerization reaction. Phys. Chem. Chem. Phys. 2009, 11, 5092–5099. 10.1039/b819817a. [DOI] [PubMed] [Google Scholar]
  13. Moqadam M.; Riccardi E.; Trinh T. T.; Åstrand P.-O.; Erp T. S. v. A test on reactive force fields for the study of silica dimerization reactions. J. Chem. Phys. 2015, 143, 184113 10.1063/1.4935179. [DOI] [PubMed] [Google Scholar]
  14. Moqadam M.; Riccardi E.; Trinh T. T.; Lervik A.; van Erp T. S. Rare event simulations reveal subtle key steps in aqueous silicate condensation. Phys. Chem. Chem. Phys. 2017, 19, 13361–13371. 10.1039/C7CP01268C. [DOI] [PubMed] [Google Scholar]
  15. Mora-Fonz M. J.; Catlow C. R. A.; Lewis D. W. Modeling Aqueous Silica Chemistry in Alkali Media. J. Phys. Chem. C 2007, 111, 18155–18158. 10.1021/jp077153u. [DOI] [Google Scholar]
  16. Xiao Y.; Lasaga A. C. Ab initio quantum mechanical studies of the kinetics and mechanisms of quartz dissolution: OH– catalysis. Geochim. Cosmochim. Acta 1996, 60, 2283–2295. 10.1016/0016-7037(96)00101-9. [DOI] [Google Scholar]
  17. Pelster S. A.; Schrader W.; Schüth F. Monitoring Temporal Evolution of Silicate Species during Hydrolysis and Condensation of Silicates Using Mass Spectrometry. J. Am. Chem. Soc. 2006, 128, 4310–4317. 10.1021/ja057423r. [DOI] [PubMed] [Google Scholar]
  18. Kinrade S. D.; Swaddle T. W. Silicon-29 NMR studies of aqueous silicate solutions. 2. Transverse silicon-29 relaxation and the kinetics and mechanism of silicate polymerization. Inorg. Chem. 1988, 27, 4259–4264. 10.1021/ic00296a035. [DOI] [Google Scholar]
  19. Zerda T. W.; Hoang G. Effect of solvents on the hydrolysis reaction of tetramethyl orthosilicate. Chem. Mater. 1990, 2, 372–376. 10.1021/cm00010a012. [DOI] [Google Scholar]
  20. Becke A. D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
  21. Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  22. Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. A 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
  23. Zhao Y.; Truhlar D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. 10.1007/s00214-007-0310-x. [DOI] [Google Scholar]
  24. Zhao Y.; Truhlar D. G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. 10.1021/ar700111a. [DOI] [PubMed] [Google Scholar]
  25. Lu Q.-Q.; Yu H.-Z.; Fu Y. Computational Study of Formic Acid Dehydrogenation Catalyzed by AlIII–Bis(imino)pyridine. Chem. - Eur. J. 2016, 22, 4584–4591. 10.1002/chem.201504573. [DOI] [PubMed] [Google Scholar]
  26. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  27. McIntosh G. J. A theoretical kinetic model of the temperature and pH dependent dimerization of orthosilicic acid in aqueous solution. Phys. Chem. Chem. Phys. 2012, 14, 996–1013. 10.1039/C1CP22273B. [DOI] [PubMed] [Google Scholar]
  28. Schaffer C. L.; Thomson K. T. Density Functional Theory Investigation into Structure and Reactivity of Prenucleation Silica Species. J. Phys. Chem. C 2008, 112, 12653–12662. 10.1021/jp066534p. [DOI] [Google Scholar]
  29. Pereira J. C. G.; Catlow C. R. A.; Pereira J. C. G.; Price G. D. Silica condensation reaction: an ab initio study. Chem. Commun. 1998, 13, 1387–1388. 10.1039/a801816b. [DOI] [Google Scholar]
  30. Reed A. E.; Weinstock R. B.; Weinhold F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. 10.1063/1.449486. [DOI] [Google Scholar]
  31. Frisch M.; Trucks G.; Schlegel H.; Scuseria G.; Robb M.; Cheeseman J.; Scalmani G.; Barone V.; Mennucci B.; Petersson G.. Gaussian 09, Revision D. 01; Gaussian: Wallingford, CT, 2009. [Google Scholar]
  32. Miehlich B.; Savin A.; Stoll H.; Preuss H. Results obtained with the correlation energy density functionals of becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. 10.1016/0009-2614(89)87234-3. [DOI] [Google Scholar]
  33. Gonzalez C.; Schlegel H. B. An improved algorithm for reaction path following. J. Chem. Phys. 1989, 90, 2154–2161. 10.1063/1.456010. [DOI] [Google Scholar]
  34. Fukui K. The path of chemical reactions - the IRC approach. Acc. Chem. Res. 1981, 14, 363–368. 10.1021/ar00072a001. [DOI] [Google Scholar]
  35. Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
  36. Zhao Y.; Truhlar D. G. Benchmark Energetic Data in a Model System for Grubbs II Metathesis Catalysis and Their Use for the Development, Assessment, and Validation of Electronic Structure Methods. J. Chem. Theory Comput. 2009, 5, 324–333. 10.1021/ct800386d. [DOI] [PubMed] [Google Scholar]
  37. Huang G.; Kalek M.; Liao R.-Z.; Himo F. Mechanism, reactivity, and selectivity of the iridium-catalyzed C(sp3)-H borylation of chlorosilanes. Chem. Sci. 2015, 6, 1735–1746. 10.1039/C4SC01592D. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. He G.; Wu L.; Bai W.; Chen J.; Sung H. H. Y.; Williams I. D.; Lin Z.; Jia G. Synthesis and Reactivities of Polyhydrido Osmium Arylsilyl Complexes Prepared from OsH3Cl(PPh3)3. Organometallics 2017, 36, 3729–3738. 10.1021/acs.organomet.7b00512. [DOI] [Google Scholar]
  39. LeBlanc L. M.; Boyd R. J.; Burnell D. J. Density Functional Theory Study of BF3-Mediated Additions of Enols and [(Trimethylsilyl)oxy]alkenes to an Oxyallyl Cation: Homologous Mukaiyama Reactions. J. Phys. Chem. A 2015, 119, 6714–6722. 10.1021/acs.jpca.5b03003. [DOI] [PubMed] [Google Scholar]
  40. Han S.-M.; Wang X.; Miao S.; Yu Z.-Y.; Liu T. Mechanistic study on ligand-controlled copper-catalyzed regiodivergent silacarboxylation of allenes with carbon dioxide and silylborane. RSC Adv. 2017, 7, 29035–29041. 10.1039/C7RA03723F. [DOI] [Google Scholar]
  41. Karmel C.; Li B.; Hartwig J. F. Rhodium-Catalyzed Regioselective Silylation of Alkyl C–H Bonds for the Synthesis of 1,4-Diols. J. Am. Chem. Soc. 2018, 140, 1460–1470. 10.1021/jacs.7b11964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kozuch S.; Martin J. M. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. 10.1021/ct301064t. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c05027_si_001.pdf (135.6KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES