Abstract
The gas–liquid contact area can be increased by the gas–liquid swirl flow, and the heat and mass transfer efficiency between gas and liquid can be enhanced by the gas–liquid swirl flow. The gas hydrate formation can be promoted by the swirl flow. The swirl flow can ensure the safety of the natural gas hydrate slurry. The flow pattern and conversion law of gas–liquid swirl with a twist tape should be investigated, and numerical simulation has been carried out by using the Reynolds stress model and the level set model. As a result, four different flow patterns are obtained, namely, swirl-stratified flow, swirl bubble flow, swirl slug flow, and swirl annular flow. The influence of gas–liquid-phase velocity on the flow pattern is investigated. The drag force generated by the two-phase slip velocity can change the gas form. At the same time, the flow pattern at different positions of the pipe will also change because of the attenuation of the swirl flow. Finally, the flow pattern map of the gas–liquid swirl flow is accomplished, and it is compared with the Mandhane flow pattern map. The flow boundary of the swirl bubble flow and the swirl annular flow is predicted.
Introduction
The gas–liquid swirl flow is a complex and variable flow process with a tangential velocity in addition to the annular and radial velocities compared to flat flow. In recent years, swirl flow has become more and more widely used in technical fields such as pipe transportation, combustion technology, cyclone separation, and so forth. Therefore, the study of swirl flow patterns and their conversion laws is of great practical significance. Investigations of swirl flow patterns and pressure drop are necessary to develop the safe operation of oil and gas industries.1−3
Many scholars from various countries have studied flow patterns, and they obtained some classic flow pattern maps such as the Baker flow pattern map,4 the Mandhane flow pattern map,5 the Taitel flow pattern map,6 the Weisman flow pattern map,7 the Hewitt flow pattern map,8 the Weisman flow pattern map,9 and the Barnea flow pattern map.10−13 However, investigations on the flow pattern of a gas–liquid swirl flow are less.
Zhou et al.14 (2014) used the coupled level set and volume of fluid (CLSVOF) method to investigate the effect of the swirl parameter and the swirl angle of the rectangular swirl pipe on the flow transition boundary and plotted the flow pattern maps of different swirl diameters and different swirl angles. Wang et al.15 (2013) studied the gas–liquid swirl flow pattern with impeller rotation and analyzed the influence of the different blade area and angle convection to the pattern. Dai et al.16 (2014) studied the gas–liquid swirl flow pattern with the surfactant. The effect of SDBS on the transition boundary of the swirl annular flow, the swirl agglomerate flow, and the swirl dispersion flow had been investigated. Cai et al.17 (2016) studied the gas–liquid swirl flow pattern and pressure drop and obtained the flow pattern map and compared with the Taitel vertical pipe flow pattern to find that the screw swirl channel in the annular flow region increases, while that in the intermittent flow region decreases. Liu et al.18 (2016) investigated the flow characteristics of the slug flow in a horizontally placed rectangular section swirl channel. It was found that the gravity and centrifugal force had an effect on the development of the liquid film and gave the law of liquid film change at different times. Liu et al.19 (2014) used the Reynolds stress model (RSM) and the volume of fluid (VOF) model to simulate the gas–liquid flow pattern in the pipe. Numerical simulation is reliable, and different flow patterns are simulated. The simulation results are similar to the Mandhane flow pattern map. Cui et al.20 (2018) studied the boiling gas–liquid flow pattern and pressure drop with R134a, and the layered wave flow, intermittent flow, and annular flow were obtained. Subhashini and Nigam21 (2008) investigated the effect of volume fraction of gas on the flow pattern. The stratified flow, the slug flow, the plug flow, the wave flow, and the agitation flow were obtained. The flow pattern map was obtained, and the empirical relationship between the stratified flow, the transition zone, and the turbulent void fraction was established on the basis of the experimental results. Liu et al.22 (2015) studied the gas–liquid flow characteristics in a vertical swirl rectangular channel with high-speed flow visualization. They had drawn the flow pattern map of the swirl rectangular channel and investigated the evolution process of the flow pattern at different positions of the swirl rectangular channel. Fabio and Gherhardt23 (2012) studied the gas–liquid flow with a twist tape, and the five types of flow patterns were stratified flow, intermittent flow, annular stratified flow, annular flow, and plug flow. A new method to predict the pressure drop of the gas–liquid two-phase swirl flow was proposed. Wang et al.24 (2019) investigated the effect of the surfactant on swirl flow, and the surfactant flow pattern of the gas–liquid swirl flow was the swirl linear flow, the swirl wave stratified flow, the swirl axial flow, and the swirl dispersed flow. The influence of flow pattern, volume fraction of gas, vane size, surfactant, and flow velocity on pressure drop was obtained. Wang et al.25−28 (2012) studied the gas–liquid flow patterns and the flow pattern transition boundary. Liu et al.29,30 (2019) studied the axial development of the gas–liquid annular swirl flow in a vertical pipe. The flow patterns, void fraction, and pressure drop were investigated with the visualization experiment. An axial flow separator with working principle and separation efficiency was studied numerically.31 The research status of swirl flow is shown in Table.1.
Table 1. Research Status of the Swirl Flow Pattern Numerical Simulation.
| author | model and method | research content |
|---|---|---|
| Zhou et al.14 | CLSVOF method | the influence of the swirl diameter and the helix angle of the rectangular swirl pipe on the flow transition boundary |
| Wang et al.15 | experimental study | the gas–liquid two-phase swirl flow pattern with impeller rotation |
| Liu et al.19 | RSM and VOF model | the gas–liquid two-phase flow pattern of an ordinary straight pipe |
| Cui et al.20 | numerical simulation | the boiling gas–liquid two-phase flow pattern and the pressure drop characteristics |
| Fabio and Gherhardt23 | experimental study | the gas–liquid two-phase flow with a twist tape |
In this paper, the numerical simulation of the gas–liquid two-phase swirl flow pattern with a twist tape is carried out by using the RSM model and the level set model under the VOF method to provide guidance for predicting the transition of flow patterns at various locations of the gas–liquid two-phase swirl flow pattern and swirl flow attenuation at different flow velocities.
Simulation Scheme
Governing Equation
The level set model under the VOF method is used for simulation. This is a numerical method widely used for interface tracking of two-phase flow problems with complex interfaces. The model has the characteristics of accurately estimating the curvature of the interface and the bending effect caused by surface tension.
Continuity equation
| 1 |
Momentum equation
| 2 |
In the formula, ρ(φ) is the density of the mixed phase, P is the pressure, and μ(φ) is the dynamic viscosity of the mixed phase.
CLSVOF Model Equation
In this paper, the level set model based on the VOF method is adopted, which is widely used to track the interface of the two-phase flow with a complex interface. The VOF method has the advantage of preserving volume conservation, but it is difficult to describe the interface curvature accurately. The level set model can accurately estimate the bending effect caused by the interface curvature and surface tension, but it cannot guarantee the conservation of volume. Therefore, the CLSVOF model proposed by combining the advantages of both can accurately describe the change of flow pattern of gas–liquid two-phase swirl flow.
The volume rate equation of the VOF model
| 3 |
In the formula, t is the time, ν is
the
fluid velocity, αq is the volume rate of the q-phase
fluid, and 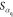 is the source
term, here zero. The main
item volume rate constraint is as follows
is the source
term, here zero. The main
item volume rate constraint is as follows
| 4 |
The level set equation is
| 5 |
 |
6 |
In the formula, φ is the distance function, x is the position vector, and d is the shortest distance of the point x interface at time t.
VOF governing equation
| 7 |
CLVOF combines the level set model with the VOF model by defining a function (level set function) to replace the function in the VOF method to characterize the gas–liquid interface.
Level set equation
 |
8 |
where ϕ is the level set function (distance function) and d is the shortest distance from the point in t time to the interface.
Its alternative is as follows
| 9 |
The Heaviside function smoothed is introduced
 |
10 |
where H(ϕ) is the Heaviside function, ε = 1.5d, d is the minimum size of the grid.
The density and viscosity after smoothing are
| 11 |
| 12 |
Turbulence Equation
The RSM model eliminates the shortcomings of the isotropic eddy viscosity hypothesis, and it can better reflect the changes of the complex two-phase flow turbulence. The governing equations are as follows
| 13 |
where
| 14 |
| 15 |
| 16 |
| 17 |
where C1 and C2 are constants; u′ is the pulsation rate; φ is the source term; ε is the dissipative term; K is the turbulent kinetic energy term; υt is the turbulent viscosity; x is the axial distance; σk is a constant; Ω is a constant; i is a constant; j = 1, 2, and 3; k is a constant; and m = 1, 2, and 3.
Physical Model
The twisted tape is used as the spinning device, and its physical model is shown in Figure 1. The diameter of the horizontal pipe is 25 mm and the length is 2500 mm. The pipe can be divided into two front and rear pipe sections, the front pipe section includes a twist tape structure, and the twist tape is provided at the entrance. The twist tape L1 = 400 mm, the twist rate of the twist tape is 6.2, and the rear pipe section L2 = 2100 mm. Figure 2 shows the model meshing diagram. The unstructured grid is used to encrypt the twist tape and the grid at the edge of the pipe. The bottom layer has a thickness of 0.2 mm and is encrypted by a rate of 1.1. The rest are divided by volume mesh with a grid spacing of 3 mm. The calculation uses a Cartesian coordinate system. The coordinate origin is located at the center of the pipe entrance, and the y-axis is the flow direction. It flows from the left to the right, and the negative direction of the z-axis is the direction of gravity.
Figure 1.
Diagram of the physical model.
Figure 2.
Partition diagram of the model meshing.
There is a significant difference between the swirl flow and the normal flow. The current twist tape images do not show swirl flow well. A three-dimensional picture of the twist tape is drawn according to the readers’ comments, which can better show the characteristics of the twist tape. The twist tape is shown in Figure 3. The twist rate Y is 6.2. The twist rate Y is related to H and B. The calculation formula of the twist tape is as follows
| 18 |
Figure 3.

Schematic diagram of the twist tape.
Solution Method and Boundary Conditions
The simulated medium uses air and water; it is calculated using the non-steady state, and the time step is 2 × 10–4 s. The turbulence model uses the RSM model. The multi-phase flow model adopts the level set model in the VOF method. The convergence condition is defined as the residual value < 10–6. In addition, under the condition of satisfying convergence, in order to improve the accuracy, the second-order upwind style is adopted for the pressure equation, the momentum equation, the turbulent kinetic energy equation, and the turbulent diffusivity equation; the volume fraction equation is implicitly solved by the implicit time format, and the pressure–velocity coupling adopts the PISO algorithm.
The inlet boundary condition is the mass flow inlet and the outlet is the free outlet. The direction of gravity is in the negative direction of the z-axis, and the gravitational acceleration is 9.81 m/s2. The pressure reference point is set at the center of the pipe outlet, and the reference pressure is 0 Pa. The turbulence intensity of the incoming flow is set according to the set gas–liquid mass flow velocity, assuming that the volume fraction of each phase at the inlet is evenly distributed, and the wall surface adopts a non-slip wall condition.
Grid Independence Verification
In order to minimize the amount of calculation based on the accuracy, the number of grids is verified independently. Under the same experimental conditions, a grid of about 1 × 106–5 × 106 was taken for simulation. The average annular flow velocity at the same cross section of the pipe and the tangential flow velocity are compared. The results are shown in Figures 4 and 5. At the same section of the pipe, a detection point was set every 0.1 m to calculate the average axial flow velocity and tangential flow velocity for comparison. The apparent flow velocity of the inlet fluid was 3 m/s, and the torsion rate was 6.2. The axial velocity increases with the increase of the mesh number, and the tangential velocity decreases continuously; however, when the number of meshes reaches 3.7 × 106 or more, the influence of the number of meshes on Ub and Uθ is very small. Therefore, after considering the calculation efficiency and the accuracy of the result, the grid with the number of meshes of about 4 × 106 is finally selected as the grid for the final simulation experiment.
Figure 4.
Axial velocity as a function of the number of grids.
Figure 5.
Tangential velocity as a function of the number of grids.
Experimental Verification by Numerical Methods
The reliability of the calculation model should be verified, and the simulation results were compared with the experimental results32 (Chang et al., 2017). The test pipe section adopts a fully transparent plexiglass pipe with a length of 2000 mm and an inner diameter of 25 mm, and a twist tape with a length of 400 mm is placed at the front of the pipe. The test medium was distilled water, and the liquid-phase flow velocity was from 0 to 3 m/s. The simulated pressure drop is compared with the experimental data, and the result is shown in Figure 6, and the error between the numerical simulation data and the experimental data is less than 10%. The instability of the experimental measurement and the error of the simulation calculation should be considered, and it shows that the model is reliable.
Figure 6.

Results of experimental verification.
Results and Discussion
In this simulation, four flow patterns were obtained, which were the swirl-stratified flow, the swirl bubble flow, the swirl slug flow, and the swirl annular flow. The following is a comparison of several flow patterns of experimental photographs and simulation results, and the characteristics of each flow pattern are analyzed.
Swirl-Stratified Flow
As shown in Figure 7, it is found that the flow pattern is characterized in that the gas is in the upper part of the pipe and the liquid phase is in the lower part. Fluctuations may occur at the gas–liquid-phase interface and will stabilize after full development, especially when the swirl flow is almost completely attenuated. The flow pattern mainly appears in the case where the gas superficial velocity is high, and the liquid superficial velocity is very low, as shown in Figure 8a at the whole pipe section 0–2.5 m, or the second half of the swirl flow attenuation of the pipe with a higher flow velocity of the gas–liquid conversion phase, as shown in Figure 9a, at the rear pipe section 1–2.5 m. It is found from Figures 8b and 9b that in the strong swirl flow section, the tangential shear force generated by the swirl flow causes disturbance at the fluid interface and is wavy. Then, the swirl flow is attenuated, and the stratified flow tends to be stable. It is found from Figure 8c that since the liquid superficial velocity is small and the centrifugal force is less than gravity, the liquid is mainly concentrated on the bottom of the pipe or on the twist tape. It is found from Figure 9c that as the swirl flow is attenuated in the rear pipe section, the gas begins to rise by buoyancy, and the centrifugal force of the liquid is less than the gravity begins to sink. This is also the flow pattern from the annular flow to the stratified flow conversion section. The disturbance between the gas and liquid interface is the largest. Therefore, the fluctuations are large, and the liquid surface thickness is high.
Figure 7.

Experimental diagram of the swirl-stratified flow.
Figure 8.
Phase distribution diagram at Vl = 0.1 m/s and Vg = 1 m/s.
Figure 9.
Phase distribution diagram at Vl = 0.1 m/s and Vg = 4 m/s.
Swirl Bubble Flow
As shown in Figure 10, it is found that the flow pattern is characterized by the fact that the gas phase exists in the liquid phase in the form of smaller bubbles and moves in a swirl form around the central axis of the pipe, and the bubble spacing is relatively uniform. When this type of flow occurs, the liquid-phase flow velocity is much larger than the gas-phase flow velocity. The flow pattern mainly occurs in the first half of the pipe with a lower gas-phase flow velocity and a higher liquid-phase flow, as shown in Figure 11a, and the first half of the pipe is 0.5 to 0.8 m. Whereas the rear pipe section has a high gas-phase flow velocity and a high liquid-phase flow velocity, as shown in Figure 12a, and the second half of the pipe is 1.3 to 2.5 m. The flow pattern is judged by the appearance of a continuous, more evenly distributed bubble. It is found from Figure 11b that the bubble advances in a clear swirl axis manner. At the beginning, since the liquid-phase density is much larger than the gas phase, the centrifugal acceleration is large, and the liquid phase is pulled outside. The centrifugal force of the gas phase is small, so it is concentrated in the center of the pipe and advances in a swirl axis manner. With the advancing of the two-phase fluid, the initial swirling intensity is small due to the small gas–liquid superficial velocity, and the swirl flow intensity decreases with the increase of the moving distance after leaving the twisted band segment. Therefore, the buoyancy of the gas is gradually greater than the centrifugal force, and the bubble starts to rise and eventually converge on the top of the pipe. It is found from Figure 12b that the gas–liquid superficial velocity is large and the initial swirl flow intensity is strong, and the gas phase is always concentrated at the annular center of the pipe. At the same time, since the liquid velocity is much larger than the gas velocity, and the gas phase is divided into bubbles in the action of the liquid phase and the tangential force, and as the distance increases, the smaller bubbles converge to become relatively large bubbles, and the bubble spacing increases.
Figure 10.

Experimental diagram of the swirl bubble flow.
Figure 11.
Phase distribution diagram at Vl = 1 m/s and Vg = 0.1 m/s.
Figure 12.
Phase distribution diagram at Vl = 10 m/s and Vg = 1 m/s.
Swirl Slug Flow
As shown in Figure 13, it is found that the gas moves in the liquid phase in the form of mass or large bubbles and moves annularly forward in the swirl manner. The condition of this flow pattern is when the liquid superficial velocity is large and the gas-phase velocity is not too large. As shown in Figure 14a,b, the gas phase mainly exists in the form of mass immediately after the twist tape section and advances in a substantially twisted swirl manner. This is because the liquid superficial velocity is greater than the gas phase, but the phase difference is smaller than that of the bubble flow. Therefore, the drag force can only divide the gas into larger blocks and cannot be further divided into smaller bubbles. At the same time, due to the swirl flow, the air mass is twisted into a swirl block shape, and as the swirl flow is attenuated, the twisted spin mode and the swirl advancement mode of the gas phase itself become smaller and smaller, the air mass diameter becomes larger, and the buoyancy of the bubble is gradually larger than the centrifugal force causes the air mass to start to rise slowly. Comparing Figures 14b and 15b, it is observed that as the liquid superficial velocity increases, the annular air mass in the front pipe section is more slender, the air mass divided in the rear pipe section is smaller, and the gas–liquid superficial velocity is higher. The large swirl flow is strong, so the air mass is still concentrated at the axis of the pipe.
Figure 13.

Experimental diagram of the swirl slug flow.
Figure 14.
Phase distribution diagram at Vl = 2 m/s and Vg = 1 m/s.
Figure 15.
Phase distribution diagram at Vl = 4 m/s and Vg = 1 m/s.
Swirl Annular Flow
As shown in Figure 16, it is found that the gas is mainly concentrated in the form of a continuous phase at the axis of the pipe and advances in a small swirl manner, and the liquid is mainly distributed on the wall surface of the pipe. The condition in which the flow pattern occurs is when the liquid-phase velocity is not large and the gas-phase velocity is large. As shown in Figure 17a, the front pipe is 0–1.2 m and the whole pipe is as shown in Figure 18a. Comparing Figure 17b with Figure 18b, it is found that as the liquid superficial velocity increases, the occurrence area of the swirl annular flow also increases, and the swirl flow diameter also becomes larger. It is found from Figures 17c and 18c that the liquid phase in the initial stage where the swirl flow intensity is strong is more evenly distributed around the pipe wall. As the intensity of the swirl flow decreases, the liquid phase is increased by the gravity on the lower side of the pipe; at the same time, due to the large gas superficial velocity, the swirl flow is not completely attenuated, so the liquid will accumulate on the same side as the twist tape, and the film thickness is increased.
Figure 16.

Experimental diagram of the swirl annular flow.
Figure 17.
Phase distribution diagram at Vl = 1 m/s and Vg = 6 m/s.
Figure 18.
Phase distribution diagram at Vl = 1 m/s and Vg = 10 m/s.
Influence Factor Analysis
Effect of Gas Superficial Velocity on Flow Patterns
It is found from Table 2 that when the liquid superficial velocity is constant and the gas superficial velocity is gradually increased to 8 m/s, a swirl-stratified flow occurs in the rear pipe section. In addition, the greater the flow velocity, the later the position of the swirl-stratified flow occurs. This is because the swirl flow intensity gradually increases with the increase of the gas flow velocity. Because of the large difference in gas–liquid density, the liquid phase is subjected to strong centrifugal force, so the liquid phase is smashed onto the wall surface. With the increase of the distance, the swirl flow intensity gradually decreases, and the liquid is gradually absorbed by the centrifugal force. Therefore, the liquid phase is deposited at the bottom of the pipe, and the gas phase floats on the top of the pipe to form a stratified flow. In the first half of the pipe, as the gas superficial velocity increases, the flow pattern transitions from the swirl bubble flow to the swirl mass flow and finally becomes a swirl annular flow. The most frequently occurring is the swirl annular flow. The reason is that when the gas-phase flow velocity is much smaller than the liquid-phase flow velocity, the gas phase is split into small bubbles due to the drag of the velocity slip liquid relative to the gas phase, and a tangential force is generated due to the action of the swirl flow. Therefore, a swirl bubble flow occurs. With the increase of the gas-phase flow velocity, the slip velocity between the gas and liquid phases decreases, and the drag liquid of the liquid relative to the gas phase decreases, so the gas phase mainly appears in a lump-like manner. As the gas phase continues to increase, the gas superficial velocity is greater than the liquid superficial velocity, so the gas produces drag force relative to the liquid phase, and the gas phase exists in a continuous manner, and the tension between the liquid phases is much larger than the gas phase and is not easily divided into small droplets. The liquid phase is mainly entangled around the pipe wall to form a liquid film under the action of centrifugal force. Only when the gas superficial velocity is much greater than the liquid superficial velocity, the liquid phase can be uniformly dispersed around the pipe wall in the form of large droplets.
Table 2. Simulation Results of the Influence of Gas Superficial Velocity on the Flow Pattern.
| the superficial velocity (liquid) m/s | the superficial velocity (gas) m/s | the position of the swirl bubble flow m | the position of the swirl slug flow m | the position of the swirl annular flow m | the position of the swirl-stratified flow m |
|---|---|---|---|---|---|
| 1 | 0.1 | 0–0.6 | 0.6–2.5 | ||
| 1 | 0–0.6 | 0.6–2.5 | |||
| 2 | 0–0.8 | 0.8–2.5 | |||
| 4 | 0–0.9 | 0.9–2.5 | |||
| 6 | 0–1.0 | 1.0–2.5 | |||
| 8 | 0–1.1 | 1.1–2.5 | |||
| 10 | 0–2.5 |
Effect of Liquid Superficial Velocity on the Flow Pattern
It is found from Table 3 that when the gas superficial velocity is constant, the position of the swirl-stratified flow appears in the second half of the pipe more and more as the liquid superficial velocity increases. When the liquid superficial velocity is 4 m/s, the rear pipe segment does not show a swirl-stratified flow again. In the front part of the pipe, as the liquid superficial velocity increases, the flow pattern transitions from the swirl-stratified flow to the swirl slug flow, and finally the swirl bubble flow occurs. The reason for this flow pattern conversion is that when the liquid superficial velocity is lower than the gas superficial velocity, and the gas–liquid two-phase velocity is small, the initial swirl flow intensity is small, and the centrifugal force generated by the liquid is much smaller than the liquid gravity. At the same time, the drag of the gas relative to the liquid phase is small, which is not enough to overcome the indicated tension of the liquid phase, so the liquid deposit forms a stratified flow at the bottom of the pipe. When the liquid superficial velocity is increased, the liquid generates the drag force relative to the gas phase. Since the gas-phase tension is small, the gas phase is easily pulled by the liquid phase to become a mass or a bubble dispersion in the liquid phase. The greater the gas–liquid-phase velocity slip difference, the stronger the drag force of the gas phase, the slender the gas phase is pulled, the smaller the bubble generated when the drag force is greater than the gas surface tension, and finally the swirl slug flow is converted into the swirl bubble flow. Unlike the bubble flow at low flow velocity, at this time, due to the large swirl flow intensity, the bubbles are almost always concentrated at the axis of the pipe, and the bubble itself is more intense in spin.
Table 3. Simulation Results of the Influence of Liquid Superficial Velocity on the Flow Pattern.
| the superficial velocity (gas) m/s | the superficial velocity (liquid) m/s | the position of the swirl bubble flow m | the position of the swirl slug flow m | the position of the swirl annular flow m | the position of the swirl-stratified flow m |
|---|---|---|---|---|---|
| 1 | 0.1 | 0–2.5 | |||
| 1 | 0–0.6 | 0.6–2.5 | |||
| 2 | 0–1.2 | 1.2–2.5 | |||
| 4 | 0–2.5 | ||||
| 6 | 0–2.5 | ||||
| 8 | 1.3–2.5 | 0–1.3 | |||
| 10 | 1.0–2.5 | 0–1.0 |
Diagram of the Flow Pattern
Since the gas–liquid swirl two-phase flow pattern is related to the swirling intensity, the flow pattern at different positions of the pipe will also change with the attenuation of the swirl flow intensity. In order to compare with the classic Mandhane flow diagram, the flow pattern is drawn from the main flow pattern at the strong swirl flow position (0.4–0.8 m in the pipe), as Figure 19 shows the simulated gas–liquid two-phase swirl flow pattern with the twist tape and Figure 20 shows the classic Mandhane flow pattern diagram. The author believes that the existence of the gas phase in the gas–liquid two-phase flow is mainly related to the gas–liquid two-phase slip velocity. For an ordinary straight pipe flow, when the liquid-phase flow velocity is greater than the gas-phase flow velocity, a drag force is generated. When the drag force is not greater than the surface tension of the interface, the gas phase appears similarly as a continuous elastic or annular flow. With the increase of the slip velocity rate, the drag begins to be greater than the surface tension, and the gas bomb begins to be shredded and converted into a mass or a block. When the slip rate is large, the gas is torn into a large number of small bubbles. However, compared with the ordinary straight pipe gas–liquid two-phase flow, the swirl flow also has a tangential velocity, which generates a centrifugal force due to the tangential velocity and a shear force at the gas–liquid interface. It is precisely that the gas–liquid two-phase swirl flow pattern is different from the ordinary straight pipe flow.
Figure 19.
Flow pattern diagram of a gas–liquid two-phase swirl flow.
Figure 20.
Flow pattern diagram of Mandhane.
Figures 19 and 20 were compared to find the following:
-
a
The boundary of the stratified flow to the bubble flow is advanced. This is because the liquid-phase flow velocity is larger than the gas phase when the bubble flow occurs, and the gas phase has a large slip velocity rate. The gas phase is subjected to a large annular drag force, and the gas phase is easily broken. At the same time, due to the existence of the tangential force, the gas phase which has been elongated in the annular direction is more likely to be further shredded by the tangential force in the radial direction. The combination of the two effects makes the transition boundary advanced. At the same time, the bubbles appear in a regular swirl shape and move forward.
-
b
The boundary of the slug flow (air elastic flow) to the annular (annular) flow is advanced. The annular flow in the ordinary straight pipe flow is mainly due to the large gas superficial velocity and the small gas-phase velocity, so the liquid phase is impacted by the gas phase to the pipe wall surface. In the swirl gas–liquid two-phase flow, when the gas–liquid slip velocity rate is not large, the gas phase mainly exists in the liquid phase in a continuous manner, and the gas phase is subjected to centrifugal force due to the existence of the tangential velocity. Since the liquid-phase density is much larger than the gas phase, the liquid phase is easily smashed to the side wall, and the gas phase is easily concentrated in the axis of the pipe to make the occurrence of the annular flow advance.
-
c
There is no slug flow in the strong swirl flow zone, and the occurrence of slug flow tends to cause the change of pipe pressure, so that the vibration of the pipe has a great influence on the safe operation of the pipe. Therefore, the swirl flow can be used to avoid the appearance of this flow pattern. The main reason why this flow pattern does not appear is that the gas–liquid two phases move along the axis, and there is a tangential motion in the cross section due to the action of the twist tape. The liquid density is greater than the gas density, and because the centrifugal force is gradually thrown to the inner wall of the pipe, in addition, when the swirl flow intensity is strong, the gas phase is concentrated on the axis of the pipe. Due to the tangential velocity, the gas phase will produce a cut in the liquid phase. Because of the force, the gas–liquid interface wave is weakened, so that the liquid phase does not block, so there is no slug flow.
Conclusions
The RSM model and the level set model under the VOF method is adopted, and the numerical simulation of the gas–liquid two-phase swirl flow of the horizontal pipe with the twist tape is carried out to obtain the following conclusions.
-
a
The simulations show that the four main flow patterns are the swirl-stratified flow, the swirl bubble flow, the swirl slug flow, and the swirl annular flow. In addition, the experimental results show that the model is suitable for the simulation of the gas–liquid two-phase swirl flow. The flow characteristics of the swirl gas–liquid two-phase flow are introduced.
-
b
The gas–liquid two-phase slip velocity rate is the main reason that affects the form of gas phase. When the liquid phase is much larger than the gas-phase velocity, the gas phase is broken by the liquid phase. When the liquid-phase velocity is large, the gas phase is divided into a mass, or a long bubble, when the liquid-phase velocity is small or the phase difference is not large, the drag force cannot overcome the tension, and the gas phase exists in the liquid phase in the form of a continuous phase.
-
c
The flow pattern transformation law of the gas–liquid two-phase flow with different gas–liquid superficial velocities is studied. It is found that the gas–liquid two-phase flow pattern is also related to the strength of the swirl flow. When the gas–liquid superficial velocity is large, the swirl flow attenuation is slower, and the influence of the swirl flow of the fluid is more obvious. With the moving distance increases, the slug will appear and transform to the bubble flow. When the gas–liquid superficial velocity is small, the swirl flow intensity is small and the attenuation is rapid. In addition, with the moving distance, the bubble flow, the slug flow, and the annular flow may be converted into the stratified flow.
-
d
According to the simulation results, the gas–liquid two-phase swirl flow pattern of the horizontal pipe is drawn and compared with the flow pattern diagram of Mandhane. It is found that the bubble flow occurs in advance, which is mainly due to the tangential velocity. There is also a tangential force in the direction that makes the gas phase more easily divided into small bubbles. The occurrence condition of the annular flow is also advanced, mainly because the centrifugal force generated by the tangential velocity causes the liquid phase to be smashed to the side wall.
-
e
The simulation results show that there is no slug flow in the strong swirl flow, which is important to the pipe safety operation.
Acknowledgments
This work was supported by the National Nature Science Foundation of China (no. 51574045), the CNPC Innovation Foundation(no. 2020D-5007-0211), the Changzhou Applied Basic Research Project (no. CJ20200085), and the Opening Fund of Jiangsu Key Laboratory of Oil-gas Storage and Transportation Technology(no. CDYQCY202105).
Glossary
Nomenclature
- RSM
Reynolds stress model
- VOF
volume of fluid
- CLSVOF
coupled level set and volume of fluid
- PISO
pressure implicit split operator
The authors declare no competing financial interest.
Notes
The data presented in this study are available on request from the corresponding author.
References
- Manglik R. M.; Bergles A. E. Swirl flow heat transfer and pressure drop with twisted-tape inserts. Adv. Heat Transfer 2003, 36, 183–266. 10.1016/s0065-2717(02)80007-7. [DOI] [Google Scholar]
- Guo L. J.Two Phase Multiphase Flow Mechanics; Xi’an Jiaotong University Press: Xi’an, 2002; pp 1–16. [Google Scholar]
- Chen X. J.; Chen L. X.. Gas-Liquid Two Phase Flow and Heat Transfer Basis; Science Press: Beijing, 1995; pp 1–10. [Google Scholar]
- Baker O. Simulations flow of oil and gas. Oil Gas J. 1954, 26, 185–190. [Google Scholar]
- Mandhane J. M.; Gregory G. A.; Aziz K. A flow pattern map for gas-liquid flow in horizontal pipes. Int. J. Multiphase Flow 1974, 1, 537–553. 10.1016/0301-9322(74)90006-8. [DOI] [Google Scholar]
- Taitel Y.; Dukler A. E. A model for predicting flow regime transitions in horizontal and near horizontal gas liquid flow. AIChE J. 1976, 22, 47–55. 10.1002/aic.690220105. [DOI] [Google Scholar]
- Weisman J.; Duncan D.; Gibson J.; Crawford T. The effect of fluid properties and pipe diameter on two-phase flow patterns in horizontal lines. Int. J. Multiphase Flow 1979, 5, 437–462. 10.1016/0301-9322(79)90031-4. [DOI] [Google Scholar]
- Hewitt G.; Roberts D.. Studies of two-phase flow patterns by simultaneous X-ray and flash photography; UKAEA Report, 1969; p 2159.
- Weisman J.; Kang S. Y. Flow pattern transitions in vertical and upwardly inclined lines. Int. J. Multiphase Flow 1981, 7, 271–291. 10.1016/0301-9322(81)90022-7. [DOI] [Google Scholar]
- Barnea D.; Shoham O.; Taitel Y.; Dukler A. E. Flow pattern transition for gas-liquid flow in horizontal and inclined pipes: comparison of experimental date with theory. Int. J. Multiphase Flow 1980, 6, 217–225. 10.1016/0301-9322(80)90012-9. [DOI] [Google Scholar]
- Barnea D.; Shoham O.; Taitel Y. Flow pattern transitions for down-ward inclined two-phase flow: Horizontal to vertical. Chem. Eng. Sci. 1982, 37, 735–740. 10.1016/0009-2509(82)85033-1. [DOI] [Google Scholar]
- Barnea D.; Shoham O.; Taitel Y.; Dukler A. E. Gas-liquid flow in inclined pipes: flow pattern transitions for upward flow. Chem. Eng. Sci. 1985, 40, 131–136. 10.1016/0009-2509(85)85053-3. [DOI] [Google Scholar]
- Barnea D. A Unified model for predicting flow pattern transition for whole ranges of pipe inclinations. Int. J. Multiphase Flow 1987, 13, 1–12. 10.1016/0301-9322(87)90002-4. [DOI] [Google Scholar]
- Zhou Y. L.; Zhang L. Y. Numerical Simulation of Gas-Liquid Two-Phase Flow Pattern Conversion in a Rectangular Section of a Swirl Pipe. J. Chem. Ind. Eng. 2014, 65, 4767–4774. [Google Scholar]
- Wang S. L.; Rao Y. C.; Wu Y. X.; Wang X. B. Experimental study on gas-liquid two-phase swirl flow in horizontal pipe. J. Exp. Mech. 2013, 28, 77–86. [Google Scholar]
- Dai Y.; Rao Y. C.; Wang S. L.; Dai W. J.; Chang K. Experimental study on gas-liquid two-phase swirl flow in horizontal pipe under degradable surfactant system. J. Exp. Mech. 2016, 31, 134–140. [Google Scholar]
- Cai B.; Xia G. D.; Yang G.; Liu X. F.; Wang Z. P. Study on Flow Pattern and Pressure Drop Characteristics of Gas-Liquid Two-Phase Flow in Screw Channel. J. Eng. Therm. 2016, 37, 1690–4774. [Google Scholar]
- Liu X. F.; Xia G. D.; Yang G. Experimental study on the slug flow in a swirl channel with rectangular cross section. J. Chem. Ind. Eng. 2016, 37, 1690–4774. [Google Scholar]
- Liu S. L.; Cai W. H.; Li F. C. Numerical Simulation of Flow Pattern and Heat Transfer Characteristics of Vapor-Liquid Two-Phase Flow in Horizontal Pipe. J. Eng. Therm. 2014, 46, 57–64. [Google Scholar]
- Cui W. Z.; Li L. J.; Xin M. D.; Jen T. C. An experimental study of flow pattern and pressure drop for flow boiling inside microfinned helically coiled pipe. Int. J. Heat Mass Transfer 2018, 51, 169–175. 10.1016/j.ijheatmasstransfer.2007.04.014. [DOI] [Google Scholar]
- Subhashini V.; Nigam K. Experimental investigation of void fraction and flow patternsin coiled flow inverter. Chem. Eng. Process. 2008, 47, 1281–1291. 10.1016/j.cep.2007.04.008. [DOI] [Google Scholar]
- Liu X. F.; Xia G. D.; Yang G. Experimental study on the characteristics of air-water two-phase flow in vertical helical rectangular channel. Int. J. Multiphase Flow 2015, 73, 227–237. 10.1016/j.ijmultiphaseflow.2015.03.012. [DOI] [Google Scholar]
- Fabio T. K.; Gherhardt R. Two-phase flow patterns and pressure drop inside horizontal pipes containing twisted-tape inserts. Int. J. Multiphase Flow 2012, 47, 50–65. 10.1016/j.ijmultiphaseflow.2012.07.003. [DOI] [Google Scholar]
- Wang S.; Ding B.; Rao Y.; Chen F. Study on the influence of coconut oil on flow pattern and pressure drop of two-phase swirl flow. RSC Adv. 2019, 9, 32644–32655. 10.1039/c9ra05369g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S. L.; Rao Y. C.; Wu Y. X.; Wang X. B. Experimental research on gasliquid two-phase spiral flow in horizontal pipe. China Pet. Process. Petrochem. Technol. 2012, 14, 24–32. [Google Scholar]
- Wang S. L.; Rao Y. C.; Wei M. J.; Zhang L.; Ma W. J. Experimental study on pressure drop of gas-liquid two-phase swirl flow in horizontal pipe. Sci. Technol. Eng. 2013, 28, 77–86. [Google Scholar]
- Wang S. L.; Rao Y. C.; Wu Y. X.; Zhou S. D.; Sun L. Experimental study on gas-liquid spiral flow with twisted types. J. Hydrodyn. 2013, 28, 105–110. [Google Scholar]
- Li J. M.; Wang S. L.; Rao Y. C.; Zhao S. H.; Zhang Y. F.; Wang L. Effect of Surfactants on Flow Characteristics of Gas-Liquid Two-Phase Spiral Pipe Flow. J. Hydrodyn. 2015, 30, 18–23. [Google Scholar]
- Liu W.; Lv X.; Bai B. Axial development of air–water annular flow with swirl in a vertical pipe. Int. J. Multiphase Flow 2020, 124, 103165. 10.1016/j.ijmultiphaseflow.2019.103165. [DOI] [Google Scholar]
- Liu W.; Lv X.; Bai B. The effect of swirl on transition from churn flow to annular flow in an intermediate diameter pipe. Exp. Therm. Fluid Sci. 2019, 109, 109861. 10.1016/j.expthermflusci.2019.109861. [DOI] [Google Scholar]
- Cai B.; Wang J.; Sun L.; Zhang N.; Yan C. Experimental study and numerical optimization on a vane-type separator for bubble separation in TMSR. Prog. Nucl. Energy 2014, 74, 1–13. 10.1016/j.pnucene.2014.02.007. [DOI] [Google Scholar]
- Ling Y.; Zhang H. B.; Pan Y. X.; Wang Q.; Shang Z. P. Study on the pressure drop characteristics of swirl flow in horizontal and inclined pipes. Procedia Environ. Sci. Eng. Manag. 2018, 45, 105–109. 10.5220/0007558501700177. [DOI] [Google Scholar]

















