Augmented Inverse Probability Weighting and the Double Robustness Property

Abstract

This article discusses the augmented inverse propensity weighted (AIPW) estimator as an estimator for average treatment effects. The AIPW combines both the properties of the regression-based estimator and the inverse probability weighted (IPW) estimator and is therefore a “doubly robust” method in that it requires only either the propensity or outcome model to be correctly specified but not both. Even though this estimator has been known for years, it is rarely used in practice. After explaining the estimator and proving the double robustness property, I conduct a simulation study to compare the AIPW efficiency with IPW and regression under different scenarios of misspecification. In 2 real-world examples, I provide a step-by-step guide on implementing the AIPW estimator in practice. I show that it is an easily usable method that extends the IPW to reduce variability and improve estimation accuracy.

Highlights.

• • Average treatment effects are often estimated by regression or inverse probability weighting methods, but both are vulnerable to bias.

• • The augmented inverse probability weighted estimator is an easy-to-use method for average treatment effects that can be less biased because of the double robustness property.

Estimating treatment effects is central to health economic practice to evaluate policy interventions and medical trials. Ideally, the effects caused by treatments are investigated in experiments that randomly assign individuals to treatment or control, thereby ensuring that comparable groups are compared under competing treatments, but many experiments with humans are infeasible or unethical. ¹ Therefore, most analyses rely on observational data.

In this article, I discuss an estimator for average treatment effects (ATEs) known as the augmented inverse propensity weighted (AIPW) estimator. Although the AIPW has been known for 20 y, most analyses in health and social sciences rely on the traditional inverse propensity weighted (IPW) estimator or the regression estimator. ²

The AIPW estimator involves 2 basic steps: first, fitting a propensity score model (i.e., the estimated probability of treatment assignment conditional on observed baseline characteristics), and second, fitting 2 models that estimate the outcome under treatment and control conditions. Each outcome is then weighted by the propensity score from the previous step to produce a weighted average of the 2 outcome models.

I illustrate that the AIPW estimator has a property called “double robustness,” meaning that it is consistent (i.e., it converges in probability to the true value of the parameter) for the ATE if either the propensity score model or the outcome model is correctly specified. ³ To demonstrate the accuracy of the AIPW estimator for the ATE, I conduct a Monte Carlo simulation study to compare it to the IPW estimator and a regression estimator and provide real-world examples on how to apply it. I show that this is an easy-to-use estimator that can be more accurate under different scenarios of misspecification (i.e., when treatment assignment or outcome model are uncertain).

Causal Effects Framework

Throughout this article, I will stick to the causal effects framework established by Neyman ⁴ and Rubin. ⁵ Suppose $N$ individuals, indexed by $n=1,\dots ,N$ and randomly sampled from some population, a binary treatment assignment $A\in \{0,1\}$ , ${\mathit{X}}_n$ a set of observed covariates, and $Y_n$ a continuous outcome. In this setting, $Y_n^{(1)}$ is the outcome that we would observe if individual $n$ had received treatment and $Y_n^{(0)}$ otherwise. These quantities are often referred to as the “potential” outcomes, given that we never observe both $Y_n^{(1)}$ and $Y_n^{(0)}$ for the same individual:

$$Y_n^{(A_n)}=(\begin{array}{cc}{Y}_n^{(1)}& \mathrm{if}{A}_n=1\\ Y_n^{(0)}& \mathrm{if}{A}_n=0.\end{array}$$

In other words, for a binary cause with 2 causal states and associated potential outcome variables $Y_n^{(1)}$ and $Y_n^{(0)}$ , a corresponding causal exposure variable, $A_n$ , is specified that takes on 2 values: $A_n$ is equal to 1 for members of the population who are exposed to the treatment state and equal to 0 for members of the population who are exposed to the control state. Exposure to the alternative causal states is decided through a specific mechanism, usually an individual’s decision to join one state or another, an outside actor’s decision to assign individuals to one state or another, a planned random allocation carried out by an investigator, or any combination of these alternatives. ⁶ The causal effect of the treatment can be represented by the difference in potential outcomes, $Y^{(1)}-Y^{(0)}$ . We assume that the actual observed outcome is connected to the potential outcomes through

$$Y_n=Y_n^{(1)}{A}_n+Y_n^{(0)}(1-A_n).$$

This equation implies that one can never observe the potential outcome under the treatment state for those observed in the control state, and one can never observe the potential outcome under the control state for those observed in the treatment state. The fact that we are missing either $Y_n^{(1)}$ or $Y_n^{(0)}$ for every observation is sometimes called the “fundamental problem of causal inference.”^7,8

The probability distribution of $Y_n^{(A_n)}$ represents how outcomes in the population would turn out if everyone received treatment ( $A=1$ ) or control ( $A=0$ ), with means $\mathbb{E}\left[Y_n^{(1)}\right]$ and $\mathbb{E}\left[Y_n^{(0)}\right]$ , respectively.

Because calculating individual-level causal effects is usually difficult, we concentrate on estimating carefully described aggregate causal effects. Where the difference in possible outcomes is used to describe the individual-level causal effect, aggregate causal effects are usually defined as averages of these individual-level effects. The broadest possible average effect is the ATE in the population as a whole. To have a causal interpretation for the ATE,

$${\tau }_{\mathrm{ATE}}=\mathbb{E}[Y_n^1-Y_n^0],$$

we need to require restrictions on the data-generating distribution. First, we assume that the stable unit treatment value assumption (SUTVA) ⁹ holds, such that the treatment status of a given individual does not affect the potential outcomes of any other individual. It is a basic assumption of causal effect stability that can often be enforced through careful study design. ¹⁰ See Morgan and Winship ⁶ for examples of possible violations of the SUTVA assumption.

Second, we assume exchangeability (also called “ignorability,”“exogeneity,”“unconfoundedness,” or “selection on observables”) given $\mathit{X}$ , that is, all causes of both the treatment and the outcome have been measured:

$$\{Y_n^{(1)},Y_n^{(0)}\}\perp \perp A_n|{\mathit{X}}_n,$$ (1)

where the symbol ⊥⊥ denotes statistical independence. This assumption implies that the missing outcome information for the counterfactual treatment status for a given individual can be recovered using individuals with similar observed characteristics. In other words, under exchangeability, the actual exposure does not predict the counterfactual outcome, ¹¹ and controlling for X makes the treatment unconfounded. Exchangeability means that treatment decisions (or assignments) are not based on what the outcomes might be under various scenarios for treatment. If we undertake to assess the effect of some treatment, we need to make sure that any response differences between the treated and the control group are due to the treatment itself and not to some intrinsic differences between the groups that are unrelated to the treatment.^6,11

An important third assumption is positivity (or overlap), that is, every individual has a positive nonzero probability of receiving treatment,

$$0<\mathbb{P}(A_n=1|{\mathit{X}}_n)<1.$$ (2)

Equation 1 allows for the identificaiton of treatment effect parameters by conditioning on $X$ ,

$$\mathbb{E}[Y^{(1)}-Y^{(0)}|X]=C(X)=\mathbb{E}[Y|A=1,X]-\mathbb{E}[Y|A=0,X],$$

and together with Equation 2 implies

$${\tau }_{\mathrm{ATE}}=\mathbb{E}[\mathbb{E}[Y|A=1,X]-\mathbb{E}[Y|A=0,X]].$$ (3)

The violation of any of these assumptions means causal effects will not be identifiable,^7,12 meaning estimates will be biased for the “true” ATE.

Under SUTVA, the ATE represents the difference in average outcomes induced by shifting the entire population from no treatment (i.e., control) to treatment, ¹³ but researchers often aim to estimate ATE after accounting for a set of individuals’ characteristics, $X$ . This means that when we average over all possible values of $X$ , we get

$$\begin{array}{c}\mathbb{E}\left[\mathbb{E}[Y|A=1,X]\right]=\mathbb{E}\left[\mathbb{E}[Y^{(1)}|A=1,X]\right]\hfill \\ =\mathbb{E}\left[\mathbb{E}[Y^{(1)}|X]\right]\hfill \\ =\mathbb{E}\left[Y^{(1)}\right],\hfill \end{array}$$

and similarly, $\mathbb{E}\left[\mathbb{E}[Y|A=0,X]\right]=\mathbb{E}\left[Y^{(0)}\right]$ .

Estimating the Treatment Effect

Traditional causal estimation relies on either fitting a model for the outcome conditional on the treatment and confounding covariates (often called modeling the response surface [RSM]ⁱ or modeling the treatment assignment mechanism). ¹⁴ Models to fit the response surface include regression models but also more advanced models from the machine-learning literature.^15,16 According to Equation 3, if we define $\mathbb{E}[Y|A_n=1,{\mathit{X}}_n=x]=f(1,x)$ and $\mathbb{E}[Y|A_n=0,{\mathit{X}}_n=x]=f(0,x)$ , we get the formula for the treatment effect:

$${\tau }_{\mathrm{ATE}}=\mathbb{E}[f(1,X)-f(0,X)],$$

and all approaches that can flexibly estimate $f$ yield the following estimator of the ATE:

$${\hat{\tau }}_{\mathrm{ATE}}^{\mathrm{RSM}}=\frac{1}{N}\sum _{1=n}^N(\hat{f}(1,X_n)-\hat{f}(0,X_n)).$$

This is the empirical analog of Equation 3, and it relies on the same assumptions (Equation 1 and Equation 2). It is also equivalent to estimating the contrast function $C(X)$ at each of the observed data points:

$${\hat{C}}_{\mathrm{RSM}}(X_n)=\hat{f}(1,X_n)-\hat{f}(0,X_n).$$

These outcome models are basically used to estimate a contrast between what would happen if every observation were put in the control group and what would happen if every observation were put in the treatment group. ¹⁷

However, modeling the response surface has a major disadvantage: it requires that the postulated model $f$ is correct, that is, $f$ must capture the true relationship between $Y$ , $A$ , and $\mathit{X}$ . For example, regression analysis cannot reliably adjust for differences in observed covariates when there are substantial differences in the distribution of these covariates in the 2 groups. ¹⁸ Estimation over such nonoverlapping ranges may massively underestimate the uncertainty in this estimator. ¹⁹

For these reasons, researchers opted for methods that model treatment assignment instead of (regression) models for the outcome. ²⁰ IPW removes confounding by creating a “pseudo-population” in which the treatment is independent of the measured confounders. ²¹ When we define the propensity score as the conditional probability of receiving treatment given covariate values,

$$e(X)=\mathbb{E}[A=1|X],$$

we can rewrite the treatment effect as

$${\tau }_{\mathrm{ATE}}=\mathbb{E}[\frac{\mathrm{AY}}{e(X)}-\frac{(1-A)Y}{1-e(X)}].$$ (4)

See Appendix A.

Again, the IPW estimator can be obtained by the contrast function

$${\hat{C}}_{\mathrm{IPW}}(X_n)=\frac{A_n{Y}_n}{\hat{e}(X_n)}-\frac{(1-A_n)Y_n}{1-\hat{e}(X_n)},$$

and the IPW estimator for the ATE is

$${\hat{\tau }}_{\mathrm{ATE}}^{\mathrm{IPW}}=\frac{1}{N}\sum _{n=1}^N(\frac{A_n{Y}_n}{\hat{e}(X_n)}-\frac{(1-A_n)Y_n}{1-\hat{e}(X_n)}).$$

The fundamental difference between modeling the response surface and approaches using propensity scores (including IPW) is that the former models the relationship between a covariate and the outcome, whereas the latter models the relationship between the covariate and the treatment assignment. The IPW estimator is constructed by estimating each individual’s propensity score and then weighting the observation for that individual by the inverse of this estimated probability. That is, participants in the treatment condition receive a weight of $1/\hat{e}(X_n)$ , and participants in the control condition receive a weight of $1/(1-\hat{e}(X_n))$ . Because of the exchangeability assumption, we can generate an unbiased estimate of every potential outcome by reweighting each sample by the inverse probability of that sample receiving the treatment we observed.

If the propensity score is known, then this IPW estimator is unbiased. Therefore, $e(x)$ must be the true propensity score for this estimator to be consistent. ²² In addition, the IPW has poor small sample size properties when the propensity score gets close to 0 or 1. For example, a unit that receives treatment and very low propensity scores (i.e., is highly unlikely to receive the treatment based on the observed covariates) will provide extreme contributions to the estimate.

AIPW Estimator

For these reasons, the IPW estimator has been improved to combine information about the probability of treatment and predictive information about the outcome variable. Robins et al. ¹⁷ augmented the IPW by a weighted average of the outcome model, called the augmented inverse propensity weighted (AIPW) estimator:

$$\begin{array}{c}{\hat{C}}_{\mathrm{AIPW}}(X_n)=(\underset{\mathrm{IPW}}{\underbrace{\frac{A_n{Y}_n}{e(X_n)}}}-\underset{\mathrm{Augmentation}}{\underbrace{\frac{A_n-e(X_n)}{e(X_n)}f(1,X_n)}})\hfill \\ \multicolumn{1}{c}{-(\underset{\mathrm{IPW}}{\underbrace{\frac{(1-A_n)Y_n}{1-e(X_n)}}}-\underset{\mathrm{Augmentation}}{\underbrace{\frac{A_n-e(X_n)}{1-e(X_n)}f(0,X_n)}}),}\\ {\hat{\tau }}_{\mathrm{ATE}}^{\mathrm{AIPW}}=\frac{1}{N}\sum _{n=1}^N{\hat{C}}_{\mathrm{AIPW}}(X_n).\hfill \end{array}$$

This AIPW is called “doubly robust” because it is consistent as long as either the treatment assignment mechanism or the outcome model is correctly specified. If, for example, the propensity score $e(X_n)$ does a very good job of estimating whether or not the patient will receive the treatment of interest, then $A_n-e(X_n)$ will go to 0 in expectation and AIPW will simplify to the IPW estimator. In the same way, if the propensity score is inaccurate, the estimator reduces to the RSM model. See Appendix B for detailed proofs. If both RSM and propensity score are replaced with their true counterparts, the augmentation term again has expectation zero.

The AIPW is more flexible in that it does not require the same set of covariates $X_n$ to be used in both the propensity score model and the response surface model. The only requirement is that conditional ignorability holds given $X_n$ . In addition, ${\hat{C}}_{\mathrm{AIPW}}$ can be shown to be asymptotically normally distributed, and valid standard errors can be derived by an empirical sandwich estimator^23,24 or bootstrapping,^20,25 It is easy to see that this method augments the IPW to reduce variability and improve estimate efficiency while holding the same assumptions as the IPW. The only drawback of this estimator is that one must estimate a propensity score model and 2 response surface (e.g., regression) models (1 for treatment and 1 for control).

Monte Carlo Simulation

In a simulation study, I compared the performance of the 3 ATE estimators described above: 1) the doubly robust AIPW estimator, 2) the IPW estimator, and 3) the ATE estimator based on RSM using regression. All the data sets in the simulation feature 5 variables (similar to Glynn and Quinn ²⁰ ): 3 covariates $X_1,X_2,X_3$ , binary treatment status $A$ , and continuous outcome $Y$ . I drew $X_1,X_2$ , and $X_3$ from standard normal distributions and treatment status $A$ from a Bernoulli distribution, where the probabilities of $A=1$ were dependent on the realized $X_1,X_2$ through the standard normal distribution function $\Phi (·)$ , $\mathrm{Pr}(A=1|X)=\Phi (X_1+X_2+0.4X_1{X}_2)$ . The interaction term adds a small degree of confounding. After $X_1,X_2,X_3$ , and $A$ were generated, I drew the outcome variable $Y$ from a normal distribution with a mean that depends on $X_2,X_3$ , and $A$ and a constant variance of one, $Y~\mathcal{N}(1·A+X_2+X_3,1)$ . Using this specification, the true treatment effect is exactly 1. Note that the treatment assignment depends on $X_1$ and $X_2$ , whereas the outcome depends on $X_2$ , $X_3$ , and $A$ . This means that adjusting for $X_2$ is sufficient to produce a consistent estimate of the ATE of $A$ on $Y$ . ²⁶

I defined 3 settings to compare the accuracy of AIPW, IPW, and RSM to estimate the treatment effect: 1) both propensity score and response surface are correctly specified; 2) the propensity score is correct, but the response surface is not; and 3) the propensity score is incorrect but the response surface is correctly specified. The incorrect propensity score is a logistic regression estimate of $A~X_1$ (leaving out the confounder $X_2$ ), whereas the incorrect response surface model for the outcome estimated $Y~X_3$ (again leaving out $X_2$ ) using linear regression. I further defined a setting with low number of observations ( $N=300$ ) and one with a high number of observations ( $N=5000$ ). All Monte Carlo experiments were repeated 1000 times.

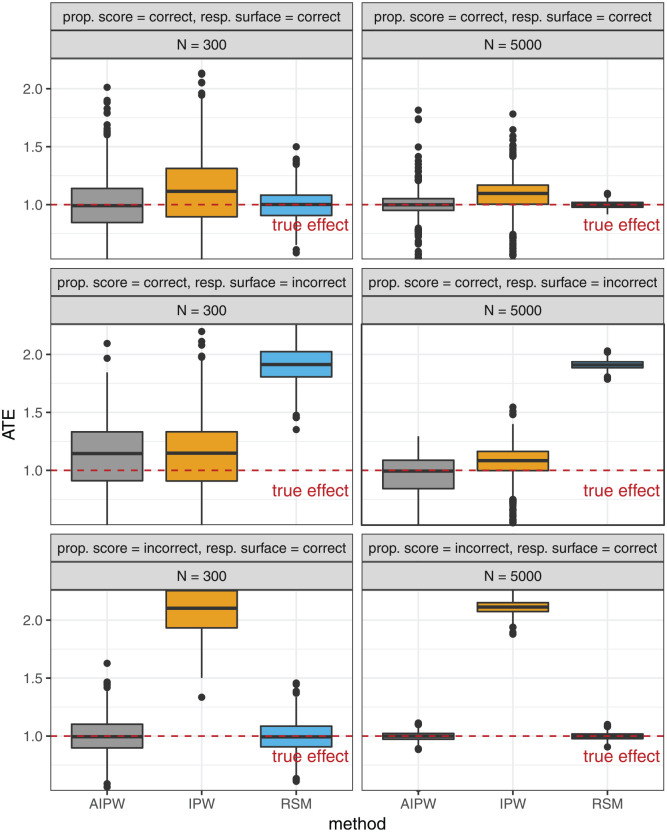
Figure 1 presents the results of the Monte Carlo simulation study. The general pattern is that only the AIPW provides unbiased estimates across all settings. In the setting in which both propensity score and outcome response surface model are consistent, all 3 estimators, AIPW, IPW, and RSM, estimate the ATE very accurately. Here, RSM provides the least variation around the true effect, followed by AIPW. In the setting in which the response surface is incorrectly specified, RSM estimates are severly biased, as expected. AIPW and IPW are unbiased here. In the third setting with incorrectly specified propensity score, IPW is biased while AIPW and RSM remain intact. In all settings, we see a finite sample size effect as $N$ increases from 300 to 5000, producing more accurate ATE estimates.

Figure 1.

Box plot results of the simulation study to compare the accuracy of augmented inverse propensity weighted, inverse probability weighted, and response surface estimators for the average treatment effect, based on 1000 repetitions in each panel. The dashed red line marks the true treatment effect of 1.0.

Application

In this section, I will walk through 2 examples on how to calculate the AIPW in a real-world setting. The first example uses data from the RAND Health Insurance Experiment (HIE). Because these data are based on a randomized experiment, they avoid many problems such as the exchangeability assumptions that observational data have. However, this simple example nicely illustrates that under such “perfect” conditions, AIPW, IPW, and RSM produce similar results. The second example uses data from the National Health Interview Survey (NHIS) to show how the AIPW can be robust to misspecification.

Both examples are implemented in the R programming language, ²⁷ but the AIPW estimator is also available in, for example, the teffects aipw function in STATA and as an option for the causaltrt function in SAS. For simplicity, these examples include a continuous outcome (see Chernozhukov et al. ²⁸ for a discussion of binary outcomes). The R code is also available as an online supplement that additionally illustrates how to calculate bootstrap confidence intervals.

The RAND HIE

In this example, I calculate the AIPW estimator using data from the RAND HIE. This US study ran from 1974 to 1982 and measured health care costs, among other outcomes, of people randomly assigned to 1 of 14 different health insurance plans. The HIE was motivated primarily by an interest to assess the impact of health insurance on health care costs and health. In a very ambitious attempt, the investigators tried to answer whether free medical care led to better health and lower costs than insurance plans that require the patient to shoulder part of the cost. Participants did not have to pay insurance premiums, although there were a number of cost-sharing clauses in the policies, resulting in significant variations in the amount of insurance they provided. The most generous plan offered free comprehensive treatment, whereas 6 “catastrophic coverage” plans at the other end of the insurance spectrum required families to pay 95% of their health care costs. All other plans were in between these extremes with different amounts of co-payment and coverage. Because of the many small treatment groups spread over 14 insurance plans, most analyses start by grouping subjects who were assigned to similar HIE plans together. ²⁹

Here, I provide a very simplified analysis to measure the causal effect of a “free” plan versus a “catastrophic” coverage plan on total medical costs. As illustrated, the outcome of interest is total medical spending over 1 y, and I include 5 covariates in the analysis (age, sex, race, education, and number of chronic diseases). First, I load the HIE data (available in the R package sampleSelection) and clean the data set:

The next step is to calculate the propensity score $e(X)$ and the response surface model, together with $f(1,X)$ and $f(0,X)$ . For simplicity, I use the same covariates in both propensity model and regression.

Finally, I can easily calculate the AIPW using a custom function:

This results in an estimate of US $78.31 increased medical spending for participants in the “free” health insurance plan over a year. For comparison, I calculate the IPW estimator and the response surface model based on linear regression:

I get estimates of 78.18 for IPW and 77.52 for the response surface model. All results are very close, and one can be somewhat sure that both the propensity model and outcome response surface model are correctly specified. This is expected because this example is a randomized experiment in which the risk of misspecification is low.

NHIS 2009

The NHIS is an annual survey of the US population with detailed information on health and health insurance. The research question in this example is whether having health insurance is associated with better health. For that, I used an index that ranges from 1 to 5, where 5 indicates excellent health and 1 poor health as the outcome of interest. This index is based on self-reports. For simplicity, I restrict to a sample of married 2009 NHIS respondents between 26 and 59 y old who may or may not be insured. Available covariates include age, sex, education, family size, employment status, and household income. The first step is loading and cleaning the data:

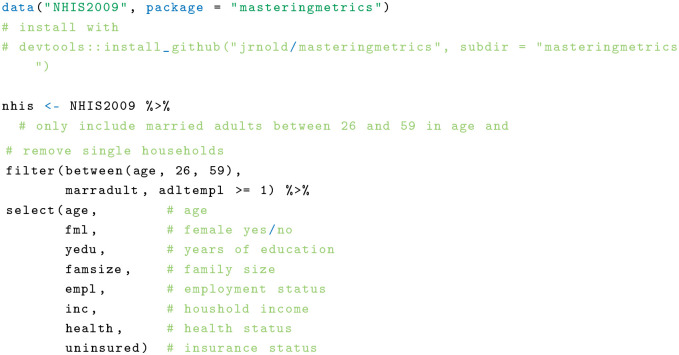
I then calculate the propensity score. As in the previous example, I include all available covariates in the propensity score model:

Then I calculate the regression estimates,

and lastly the AIPW estimator using the previously defined function:

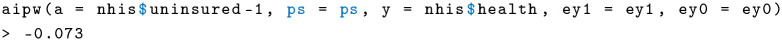
I get an estimate of −0.073, meaning that the absence of health insurance has a slightly negative effect on self-reported health. Compare this with the response surface estimator using regression:

The regression estimate of −0.044 is slightly higher than the AIPW but still very close. Finally, I calculate the IPW for comparison:

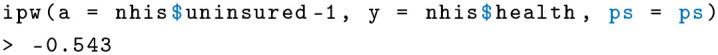
The IPW estimate of −0.543 is significantly lower than the previous 2 estimates of AIPW and RSM. What does this mean? It could hint that the IPW estimator is actually biased in this case. The IPW relies solely on the propensity score. Note that to calculate the propensity score, I regressed insurance status on age, sex, education, family size, employment status, and income. The reason this is problematic is because employment status might be reversely causated with insurance; having insurance can be a consequence of being employed. In addition, timing is important. Control covariates should generally be measured before the treatment variable (here, insurance status), so they cannot be changed by the treatment. ²⁹ This is unproblematic for age, sex, and probably education, but income and employment status may be on direct or intermediate causal pathways of insurance status. This is less of an issue in the RSM model with health status as the outcome because the health variable is determined at the time of the survey. This example shows that misspecifications are often difficult to detect, but the AIPW estimate is consistent in such a case.

Discussion and Conclusion

In this article, I have illustrated the AIPW estimator, an extension of the traditional IPW estimator. The most interesting property is that AIPW is “doubly robust” in that it will be consistent for the ATE whenever either the propensity model is correctly specified or the outcome response surface models are correctly specified. This has the advantage that the AIPW can provide more reliable results in a complicated real-world setting where treatment assignment process and outcome model are uncertain.

A simulation showed that the AIPW performs about as well as the IPW or RSW under fully correct specifications. However, the AIPW estimator is more accurate when either IPW or RSM is misspecified. This is by no means a comprehensive simulation study, but it seems reasonable that applied researchers should consider the AIPW estimator for the ATE when the specification is partially deficient.

Two examples using real data showed that the AIPW is easy to calculate in practice and can be more robust when the propensity score model may be misspecified. However, it is often difficult to specify the 2 key pieces of the AIPW estimator: the propensity score model and the response surface model. For the propensity model, it is generally wise to choose adjustment covariates that both remove bias and produce maximal overlap between the distributions of the estimated propensity scores for the treated and control units. ²⁰ Because the AIPW estimator weights observations in accordance with their observed similary, the propensity score distributions do not need to be perfectly congruent but sufficient overlap is important. ³⁰ Conversely, the set of adjustment covariates for the response surface model should be sufficient to control bias and minimize residual variance. In simulations, Glynn and Quinn ²⁰ found that using a minimally sufficient set of adjustment covariates for the propensity score model and a maximally sufficient set of adjustment covariates for the response surface model can result in lower sampling variability for the AIPW estimator.

Of course, in many situations, the causal process of the data generation is unclear. In such settings, the proper specification decisions are much less clear, and one could use, for example, causal diagrams ³¹ to identify sets of covariates that can be adjusted for to remove bias. However, in situations in which the researcher has a plausible idea of both contextual factors that motivate treatment assignment and important adjustment covariates for the outcome, this can lead to very sophisticated AIPW estimators. For example, in an analysis by Scott, ³⁰ the author was able to derive key factors for treatment assignment from the literature and at the same time could choose completely different covariates for the outcome model.

It is important to note that even though the AIPW estimator has many advantages, it can still be biased because of unobserved factors that affect both treatment and outcome. In situations in which both propensity score model and response surface model for the outcome are incorrectly specified, its performance might be poor. These limitations, however, are universal drawbacks of using observational data and affect all methods estimating treatment effects.

There is some evidence that the doubly robust estimator can be less efficient than the maximum likelihood estimator with a correctly specified model. ²³ Thus, there is a tradeoff to consider between potentially reducing bias at the expense of precision. It is generally advisable to compare effect estimates of several models to rule out possible biases and misspecifications. Still, the AIPW estimator comes at little additional cost but with much greater reliability. Recent research explores how doubly robust effect estimates can be combined with machine learning. Such approaches allow machine learning to be used to weaken parametric modeling assumptions.^28,32,33

Appendix A

Proof for Equation 4

$$\begin{array}{c}\mathbb{E}[Y_n^1-Y_n^0|{\mathit{X}}_n=x]=\hfill \\ =\mathbb{E}[\frac{Y_n^1}{e(x)}e(x)-\frac{Y_n^0}{1-e(x)}(1-e(x))|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\frac{Y_n^1}{e(x)}\mathbb{E}[A|X=x]-\frac{Y_n^0}{1-e(x)}(1-\mathbb{E}[A|X=x])|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\frac{Y_n^1}{e(x)}\mathbb{E}[A|Y_n^1,X=x]-\frac{Y_n^0}{1-e(x)}(1-\mathbb{E}[A|Y_n^0,X=x])|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\mathbb{E}[\frac{Y_n^{1}A}{e(x)}|Y_n^1,X=x]-\mathbb{E}[\frac{Y_n^0(1-A_n)}{1-e(x)}|Y_n^0,X=x]|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\mathbb{E}[\frac{A(Y_n^{1}A+Y_n^0\stackrel{=0}{\overbrace{A(1-A)}})}{e(x)}|Y_n^1,X=x]-\mathbb{E}[\frac{\stackrel{=0}{\overbrace{Y_n^{1}A-Y_n^1{A}^2}}+Y_n^0-Y_n^{0}A\stackrel{=0}{\overbrace{-Y_n^{0}A+Y_n^0{A}^2}}}{1-e(x)}|Y_n^0,X=x]|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\mathbb{E}[\frac{A(Y_n^{1}A+Y_n^0(1-A))}{e(x)}|Y_n^1,X=x]-\mathbb{E}[\frac{(1-A)(Y_n^{1}A+Y_n^0(1-A))}{1-e(x)}|Y_n^0,X=x]|{\mathit{X}}_n=x]\hfill \\ =\mathbb{E}[\frac{\mathrm{AY}}{e(x)}-\frac{(1-A)Y}{1-e(x)}|\mathit{X}=x].\hfill \end{array}$$

Appendix B

Double Robustness of the AIPW Estimator

Only the $Y^{(1)}$ case is shown, but it is an analog for $Y^{(0)}$ .

Scenario 1: The propensity score model is correct, $e(X)=\mathbb{E}[A|X]=\mathbb{E}[A|Y^{(1)},X]$ , but the response surface model is incorrect, $f(1,X)\ne \mathbb{E}[Y|A=1,X]$ .

$$\begin{array}{c}\mathbb{E}[\frac{A-e(X)}{e(X)}{Y}^{(1)}-f(1,X)]\hfill \\ =\mathbb{E}[\mathbb{E}[\frac{A-e(X)}{e(X)}(Y^{(1)}-f(1,X))|Y^{(1)},X]]\hfill \\ =\mathbb{E}[(Y^{(1)}-f(1,X))\mathbb{E}[\frac{A-e(X)}{e(X)}|Y^{(1)},X]]\hfill \\ =\mathbb{E}[(Y^{(1)}-f(1,X))\frac{\mathbb{E}[A|Y^{(1)},X]-e(X)}{e(X)}]\hfill \\ =\mathbb{E}[(Y^{(1)}-f(1,X))\frac{\mathbb{E}[A|X]-e(X)}{e(X)}]\hfill \\ =\mathbb{E}[(Y^{(1)}-f(1,X))\stackrel{=0}{\overbrace{\frac{e(X)-e(X)}{e(X)}}}]\hfill \\ =0.\hfill \end{array}$$

Scenario 2: The propensity score model is incorrect, $e(X)\ne \mathbb{E}[A|X]=\mathbb{E}[A|Y^{(1)},X]$ , but the response surface model is correct, $f(1,X)=\mathbb{E}[Y|A=1,X]$ .

$$\begin{array}{cc}\multicolumn{1}{c}{\mathbb{E}[\frac{A-e(X)}{e(X)}}& Y^{(1)}-\mathbb{E}[Y|A=1,X]]\hfill \\ =\mathbb{E}[\mathbb{E}[\frac{A-e(X)}{e(X)}(Y^{(1)}-\mathbb{E}[Y|A=1,X])|A,X]]\hfill \\ =\mathbb{E}[\frac{A-e(X)}{e(X)}\mathbb{E}[Y^{(1)}-\mathbb{E}[Y|A=1,X]|A,X]]\hfill \\ =\mathbb{E}[\frac{A-e(X)}{e(X)}(\mathbb{E}[Y^{(1)}|A,X]-\mathbb{E}[Y|A=1,X])]\hfill \\ =\mathbb{E}[\frac{A-e(X)}{e(X)}\stackrel{=0}{\overbrace{(\mathbb{E}[Y^{(1)}|X]-\mathbb{E}[Y^{(1)}|X])}}]\hfill \\ =0.\hfill \end{array}$$