Global analysis of within-host SARS-CoV-2/HIV coinfection model with latency

Abstract

The coronavirus disease 2019 (COVID-19) is a respiratory disease caused by a virus called the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). In this paper, we analyze a within-host SARS-CoV-2/HIV coinfection model. The model is made up of eight ordinary differential equations. These equations describe the interactions between healthy epithelial cells, latently infected epithelial cells, productively infected epithelial cells, SARS-CoV-2 particles, healthy CD$4^{+}$ T cells, latently infected CD$4^{+}$ T cells, productively infected CD$4^{+}$ T cells, and HIV particles. We confirm that the solutions of the developed model are bounded and nonnegative. We calculate the different steady states of the model and derive their existence conditions. We choose appropriate Lyapunov functions to show the global stability of all steady states. We execute some numerical simulations to assist the theoretical contributions. Based on our results, weak CD$4^{+}$ T cell immunity in SARS-CoV-2/HIV coinfected patients causes an increase in the concentrations of productively infected epithelial cells and SARS-CoV-2 particles. This may lead to severe SARS-CoV-2 infection in HIV patients. This result agrees with many studies that discussed the high risk of severe infection and death in HIV patients when they get SARS-CoV-2 infection. On the other hand, increasing the death rate of infected epithelial cells during the latency period can reduce the severity of SARS-CoV-2 infection in HIV patients. More studies are needed to understand the dynamics of SARS-CoV-2/HIV coinfection and find better ways to treat this vulnerable group of patients.

Introduction

The coronavirus disease 2019 (COVID-19) is a new epidemic that emerged in China in late 2019. It is a respiratory disease ascribed to a virus called the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). According to COVID-19 weekly epidemiological update of October 13, 2021, by the World Health Organization (WHO) [1], the cumulative number of confirmed cases reported globally exceeded 237 million and the total number of deaths reached over 4.8 million [1]. The number of new weekly COVID-19 cases has showed a decline since late August 2021 in most countries of the world [1]. SARS-CoV-2/HIV coinfection has become a concern especially in HIV patients who are not receiving antiretroviral therapy (ART) or have low CD$4^{+}$ T cell counts [2, 3]. As there were approximately 37.7 million people living with HIV at the end of 2020 [4], understanding SARS-CoV-2/HIV coinfection should take a special attention.

SARS-CoV-2 is an RNA virus and it is a member of the Coronaviridae family [5]. It binds to the angiotensin-converting enzyme 2 (ACE2) receptor of epithelial cells [5, 6]. The principal target of SARS-CoV-2 is the alveolar epithelial type 2 cells of the lungs [7]. ACE2 is also expressed in many organs like the kidney, liver, and heart [8]. SARS-CoV-2 is mainly transmitted through respiratory droplets which carry virus particles [9]. Many COVID-19 therapies are being clinically tested to evaluate their effectiveness and safety [10]. The U.S. Food and Drug Administration (FDA) has approved the antiviral drug Veklury to treat COVID-19 in adults and some pediatric patients who need hospitalization [10]. There are seven vaccines approved for use by WHO: Pfizer/BioNTech, Moderna, Janssen(Johnson & Johnson), Oxford/AstraZeneca, Serum Institute of India, Sinpharm (Beijing), and Sinovac [11].

On the other hand, HIV is a member of RNA lentiviruses [9]. The principal receptor of HIV is CD4 receptor [6, 9]. CD4 is expressed in different immune cells like CD$4^{+}$ T cells, macrophages, and dendritic cells [6]. Nevertheless, CD$4^{+}$ T cells are the primary target of HIV. CD$4^{+}$ T cells help other immune cells like CD$8^{+}$ T cells and B cells in fighting against viral infections [12]. Targeting CD$4^{+}$ T cells by HIV causes a reduction in the number of these cells. Therefore, the body of HIV patient becomes susceptible to other viral infections [13]. HIV is transmitted through blood or sexual contact [6]. Antiretroviral therapy (ART) is used to treat HIV infection, which reduces the viral load and prevents the development to the acquired immunodeficiency syndrome (AIDS) [14]. Notably, no HIV vaccines have been approved yet [6].

The first case of SARS-CoV-2/HIV coinfection was reported for a 61-year-old man from China [9]. Other coinfection cases were reported in Spain, Italy, and the USA [9]. The most typical symptoms of coinfection were fever, cough, and shortness of breath [9]. It has been found that HIV patients are more likely to experience severe COVID-19 when infected [3]. The risk of severe infection increases further in HIV patients who do not receive antiretroviral therapy or have low CD$4^{+}$ T cell counts [3, 15]. Furthermore, the severity risk increases in the presence of other comorbidities like hypertension, diabetes, respiratory disease, cardiovascular disease, and chronic kidney disease [3, 16, 17]. Based on WHO recommendations [18], many COVID-19 vaccines are safe for people living with HIV.

Mathematical modeling has been considered a significant tool for studying and investigating viral infections. HIV within-host models have received great attention and lead to the significant results. These models were formulated using ordinary differential equations (ODEs) [19–23], delay differential equations (DDEs) [24–27], partial differential equations (PDEs) [28–31], delay partial differential equations (DPDEs) [13, 32–34], and fractional differential equations (FDEs) [35, 36]. These models exhibit mainly the interactions between HIV, uninfected CD$4^{+}$ T cells, different types of infected CD$4^{+}$ T cells, and the immune system.

However, very few models have studied so far to investigate the dynamics of SARS-CoV-2 within the human body. For example, Li et al. [37] formulated a within-host ODE model to characterize the interactions between uninfected epithelial cells, infected epithelial cells, and SARS-CoV-2 particles. Du and Yuan [38] analyzed a similar model with taking into consideration the effect of antiviral drugs which prevent either infection or the production of SARS-CoV-2 particles. Al Agha et al. [7] used a within-host DDE to depict the effect of SARS-CoV-2 infection on cancer patients and the impact of infection on immune responses. Pinky and Dobrovolny [39] established a within-host model to study SARS-CoV-2 coinfection with other viruses like influenza A virus and human rhinovirus. Fadai et al. [40] proposed an ODE model with the assumption that uninfected epithelial cells follow logistic growth.

To the best of our knowledge, no within-host SARS-CoV-2/HIV models have been studied so far. However, it is worth mentioning that Bellomo et al. [41, 42] studied the within-host dynamics of SARS-CoV-2 within a multiscale approach and the mathematical theory of active particles. The multiscale approach accounts for the interaction of different spatial scales where the dynamics at the high scale of individuals depends on the dynamics at the microscopic scale. Microscopic scale is determined by the competition between virus particles and the immune cells. Thus, the multiscale approach can be used to predict the time evolution of the number of healthy, infected, recovered, and dead individuals. Nevertheless, in this paper we concentrate on the interactions at the microscopic scale of coinfection between SARS-CoV-2 and HIV. Coinfection models are needed to help understand the dynamics of SARS-CoV-2 infection in HIV patients and the role of the immune system, to support medical research, and to find better ways to treat this vulnerable group of patients. In this paper, we establish a within-host model of SARS-CoV-2/HIV coinfection. For this model, we (i) demonstrate that all solutions are bounded and nonnegative, (ii) calculate all steady-state solutions and the corresponding conditions of their existence, (iii) show the global stability of the steady states, (iv) execute some numerical simulations to enhance the results of computations, (v) discuss the effect of low concentration of CD$4^{+}$ T cells on coinfected patients, (vi) test the impact of latency on the number of SARS-CoV-2 particles and HIV particles, and (vii) suggest some possible future works.

The paper is organized as follows. Section 2 describes the model under consideration. Section 3 shows that all solutions are bounded and greater than or equal zero. In addition, it lists all steady states with the positivity conditions of their components. Section 4 proves the global stability of all steady states computed in Sect. 3. Section 5 displays some numerical simulations. Finally, Sect. 6 discusses the results with some suggestions for future works.

SARS-CoV-2/HIV coinfection model with latency

This section describes the model intended to be studied in this paper. The proposed model takes the form

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\dot{X}=\rho -d_{1}X-\eta VX,\hfill \\ \dot{N}=\eta VX-(k+d_2)N,\hfill \\ \dot{Y}=kN-d_{3}Y-\mu YS,\hfill \\ \dot{V}=aY-d_{4}V,\hfill \\ \dot{S}=\xi +uYS-d_{5}S-\theta HS,\hfill \\ \dot{T}=(1-b)\theta HS-(\alpha +d_6)T,\hfill \\ \dot{W}=b\theta HS+\alpha T-d_{7}W,\hfill \\ \dot{H}=\lambda W-d_{8}H,\hfill \end{array}\right)\end{array}$$ 1

where $(X,N,Y,V,S,T,W,H)=(X(t),N(t),Y(t),V(t),S(t),T(t),W(t),H(t))$ denote the concentrations of uninfected epithelial cells, latently infected epithelial cells, actively infected epithelial cells, free SARS-CoV-2 particles, uninfected CD$4^{+}$ T cells, latently infected CD$4^{+}$ T cells, actively infected CD$4^{+}$ T cells, and free HIV particles at time t. Epithelial cells are produced from a source at a constant rate $\rho$, die at rate $d_{1}X$, and get infected by SARS-CoV-2 at rate $\eta VX$. Latently infected epithelial cells proliferate at rate $\eta VX$, turn into active infected cells at rate kN, and die at rate $d_{2}N$. Actively infected epithelial cells die at rate $d_{3}Y$ and are indirectly eliminated by CD$4^{+}$ T cells at rate $\mu YS$. SARS-CoV-2 particles are produced from infected cells at rate aY and die at rate $d_{4}V$. Uninfected CD$4^{+}$ T cells are produced at a constant rate $\xi$, stimulated by infected epithelial cells at rate uYS, die at rate $d_{5}S$, and get infected by HIV at rate $\theta HS$. A fraction $b\in [0,1]$ of new infected CD$4^{+}$ T cells will be active and the rest $1-b$ will be latent. Latently infected CD$4^{+}$ T cells are transmitted into active cells at rate $\alpha T$ and die at a natural death rate $d_{6}T$. Actively infected CD$4^{+}$ T cells die at a natural death rate $d_{7}W$. HIV particles are produced by infected cells at rate $\lambda W$ and die at rate $d_{8}H$. The descriptions of the different parameters are summarized in Table 1.

Table 1.

Values of parameters of model (1)

Par.	Description	Value	References
$\rho$	Recruitment rate of uninfected epithelial cells	0.02241	[43]
$d_1$	Death rate constant of uninfected epithelial cells	${10}^{-3}$	[43]
$\eta$	Infection rate constant of epithelial cells	Varied	–
k	Transmission rate constant of latently infected epithelial cells into active cells	4.08	[39]
$d_2$	Death rate constant of latently infected epithelial cells	${10}^{-3}$	[39]
$d_3$	Death rate constant of actively infected epithelial cells	0.11	[43]
$\mu$	Indirect killing rate constant of CD$4^{+}$ T cells	Varied	–
a	Production rate constant of SARS-CoV-2 by actively infected epithelial cells	0.24	[43]
$d_4$	Death rate constant of free SARS-CoV-2 particles	Varied	–
$\xi$	Recruitment rate of uninfected CD$4^{+}$ T cells	10	[21]
u	Stimulation rate constant of CD$4^{+}$ T cells	0.1	[44]
$d_5$	Death rate constant of uninfected CD$4^{+}$ T cells	0.01	[45]
$\theta$	Infection rate constant of CD$4^{+}$ T cells	Varied	–
$\alpha$	Transmission rate constant of latently infected CD$4^{+}$ T cells into active cells	0.2	[46]
$d_6$	Death rate constant of latently infected CD$4^{+}$ T cells	0.02	[46]
b	A fraction of newly infected CD$4^{+}$ T cells that become active	0.7	[46]
$d_7$	Death rate constant of actively infected CD$4^{+}$ T cells	0.5	[47]
$\lambda$	Production rate constant of HIV by actively infected cells	5	[48]
$d_8$	Death rate constant of free HIV particles	2	[48]

Basic properties

This section verifies the nonnegativity and boundedness of solutions of model (1). Moreover, it calculates all possible steady states with the associated threshold conditions.

Nonnegativity and boundedness

We define a compact set

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathrm{\Theta }=& \left\{\left(X,N,Y,V,S,T,W,H\right)\in {\mathbb{R}}_{\ge 0}^8:0\le X\left(t\right),N\left(t\right),Y\left(t\right)\le {\mathrm{\Omega }}_1\right),\hfill \\ \hfill & \left(0\le V\left(t\right)\le {\mathrm{\Omega }}_2,0\le S\left(t\right),T\left(t\right),W\left(t\right)\le {\mathrm{\Omega }}_3,0\le H\left(t\right)\le {\mathrm{\Omega }}_4\right\},\hfill \end{array}\end{array}$$

where ${\mathrm{\Omega }}_j>0$, $j=1,\dots ,4$.

Proposition 1

The set $\mathrm{\Theta }$ is positively invariant for model (1).

Proof

From model (1), we have

$$\begin{array}{c}\hfill \begin{array}{c}{\left(\dot{X}\right|}_{X=0}=\rho >0,\\ {\left(\dot{N}\right|}_{N=0}=\eta VX\ge 0\text{for all}V,X\ge 0,\\ {\left(\dot{Y}\right|}_{Y=0}=kN\ge 0\text{for all}N\ge 0,\\ {\left(\dot{V}\right|}_{V=0}=aY\ge 0\text{for all}Y\ge 0,\\ {\left(\dot{S}\right|}_{S=0}=\xi >0,\\ {\left(\dot{T}\right|}_{T=0}=(1-b)\theta HS\ge 0\text{for all}H,S\ge 0,\\ {\left(\dot{W}\right|}_{W=0}=b\theta HS+\alpha T\ge 0\text{for all}H,S,T\ge 0,\\ {\left(\dot{H}\right|}_{H=0}=\lambda W\ge 0\text{for all}W\ge 0.\\ \end{array}\end{array}$$

Thus, we get $(X(t),N(t),Y(t),V(t),S(t),T(t),W(t),H(t))\in {\mathbb{R}}_{\ge 0}^8$ for all $t\ge 0$ when $(X(0),N(0),Y(0),V(0),S(0),T(0),$$W(0),H(0))\in {\mathbb{R}}_{\ge 0}^8$.

To prove the boundedness of all state variables, we define

$$\begin{array}{c}\hfill \mathrm{\Psi }(t)=X+N+Y+\frac{d_3}{2a}V+\frac{\mu }{u}\left(S+T+W\right)+\frac{\mu d_7}{2u\lambda }H.\end{array}$$

Then, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \dot{\mathrm{\Psi }}(t)& =\rho +\frac{\mu }{u}\xi -d_{1}X-d_{2}N-\frac{d_3}{2}Y-\frac{d_3{d}_4}{2a}V-\frac{\mu d_5}{u}S-\frac{\mu d_6}{u}T-\frac{\mu d_7}{2u}W-\frac{\mu d_7{d}_8}{2u\lambda }H\hfill \\ \hfill & \le \left(\rho +\frac{\mu }{u}\xi \right)-\varphi \left[X+N+Y+\frac{d_3}{2a}V+\frac{\mu }{u}\left(S+T+W\right)+\frac{\mu d_7}{2u\lambda }H\right]\hfill \\ \hfill & =\left(\rho +\frac{\mu }{u}\xi \right)-\varphi \mathrm{\Psi }(t),\hfill \end{array}\end{array}$$

where $\varphi =min\left\{d_1,d_2,{\displaystyle \frac{d_3}{2}},d_4,d_5,d_6,{\displaystyle \frac{d_7}{2}},d_8\right\}$. It follows that

$$\begin{array}{c}\hfill \mathrm{\Psi }(t)\le e^{-\varphi t}\left(\mathrm{\Psi }(0)-\frac{\rho +\frac{\mu }{u}\xi }{\varphi }\right)+\frac{\rho +\frac{\mu }{u}\xi }{\varphi }.\end{array}$$

Hence, $0\le \mathrm{\Psi }\left(t\right)\le {\mathrm{\Omega }}_1$ if $\mathrm{\Psi }\left(0\right)\le {\mathrm{\Omega }}_1$ for $t\ge 0$, where ${\mathrm{\Omega }}_1={\displaystyle \frac{\rho +\frac{\mu }{u}\xi }{\varphi }}$. As X, N, Y, V, S, T, W and H are nonnegative, we have $0\le X\left(t\right),N\left(t\right),Y\left(t\right)\le {\mathrm{\Omega }}_1,$ $0\le V\left(t\right)\le {\mathrm{\Omega }}_2$, $0\le S\left(t\right),T\left(t\right),W\left(t\right)\le {\mathrm{\Omega }}_3$, $0\le H\left(t\right)\le {\mathrm{\Omega }}_4$ if $X\left(0\right)+N\left(0\right)+Y\left(0\right)+{\displaystyle \frac{d_3}{2a}}V\left(0\right)+{\displaystyle \frac{\mu }{u}}\left(S\left(0\right)+T\left(0\right)+W\left(0\right)\right)+{\displaystyle \frac{\mu d_7}{2u\lambda }}H\left(0\right)\le {\mathrm{\Omega }}_1$, where ${\mathrm{\Omega }}_2={\displaystyle \frac{2a}{d_3}}{\mathrm{\Omega }}_1$, ${\mathrm{\Omega }}_3={\displaystyle \frac{u}{\mu }}{\mathrm{\Omega }}_1$, and ${\mathrm{\Omega }}_4={\displaystyle \frac{2u\lambda }{\mu d_7}}{\mathrm{\Omega }}_1$. This shows that the set $\mathrm{\Theta }$ is positively invariant. $\square$

Steady states

In this subsection, we calculate all possible steady states of model (1) and conclude the threshold conditions that cover the existence of these steady states.

To compute the steady states of the model we solve the following system of algebraic equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}0=\rho -d_{1}X-\eta VX,\hfill \\ 0=\eta VX-(k+d_2)N,\hfill \\ 0=kN-d_{3}Y-\mu YS,\hfill \\ 0=aY-d_{4}V,\hfill \\ 0=\xi +uYS-d_{5}S-\theta HS,\hfill \\ 0=(1-b)\theta HS-(\alpha +d_6)T,\hfill \\ 0=b\theta HS+\alpha T-d_{7}W,\hfill \\ 0=\lambda W-d_{8}H.\hfill \end{array}\right)\end{array}$$

We find that model (1) has four steady states:

• (i)The uninfected steady state ${\mathrm{\Delta }}_0(X_0,0,0,0,S_0,0,0,0)$, where $X_0={\displaystyle \frac{\rho }{d_1}}$and $S_0={\displaystyle \frac{\xi }{d_5}}$.
• (ii)
  The single HIV-infection steady state ${\mathrm{\Delta }}_H(X_1,0,0,0,S_1,T_1,W_1,H_1)$, where

  $$\begin{array}{cc}\hfill X_1& =\frac{\rho }{d1}=X_0,S_1=\frac{d_7{d}_8\left(d_6+\alpha \right)}{\theta \lambda \left(\alpha +d_{6}b\right)}=\frac{S_0}{R_1},\hfill \\ \hfill T_1& =\left(1-b\right)\left(\frac{\xi }{d_6+\alpha }-\frac{d_5{d}_7{d}_8}{\theta \lambda \left(\alpha +d_{6}b\right)}\right)=\frac{d_5{d}_7{d}_8\left(1-b\right)}{\theta \lambda \left(\alpha +d_{6}b\right)}(R_1-1),\hfill \\ \hfill W_1& =-\frac{d_5{d}_8}{\theta \lambda }+\frac{\xi \left(\alpha +d_{6}b\right)}{d_7\left(d_6+\alpha \right)}=\frac{d_5{d}_8}{\theta \lambda }(R_1-1),H_1=-\frac{d_5}{\theta }+\frac{\lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)}=\frac{d_5}{\theta }(R_1-1),\hfill \end{array}$$

  where $R_1={\displaystyle \frac{\xi \theta \lambda \left(\alpha +d_{6}b\right)}{d_5{d}_7{d}_8\left(d_6+\alpha \right)}}$. Here, $R_1$ is the basic reproduction number of HIV infection. It determines the establishment of HIV infection in the body. We see that $X_1$ and $S_1$ are always positive, while $T_1$, $W_1$ and $H_1$ are positive if $R_1>1$. Therefore, ${\mathrm{\Delta }}_H$ exists when $R_1>1$.
• (iii)
  The single SARS-CoV-2–infection steady state ${\mathrm{\Delta }}_V(X_2,N_2,Y_2,V_2,S_2,0,0,0)$, where

  $$\begin{array}{c}\hfill Y_2=\frac{d_4{V}_2}{a},S_2=\frac{\xi }{d_5-u{Y}_2},X_2=\frac{(k+d_2)(Y_2{d}_3+S_2{Y}_2\mu )}{k\eta V_2},N_2=\frac{Y_2{d}_3+S_2{Y}_2\mu }{k},\end{array}$$ 2

  and $V_2$ satisfies the following equation:

  $$\begin{array}{c}\hfill \frac{P_1{V_2}^2+P_2{V}_2+P_3}{ak\eta (a{d}_5-u{d}_{4}V)}=0,\end{array}$$ 3

  where

  $$\begin{array}{c}\hfill \left\{\begin{array}{c}{P}_1=u{d}_4^2\eta d_3(k+d_2),\hfill \\ P_2=u{d}_1{d}_4^2{d}_3(k+d_2)-a{d}_5{d}_4\eta d_3(k+d_2)-a{d}_4\eta \mu \xi (k+d_2)-au{d}_4\eta \rho k,\hfill \\ P_3=-a{d}_1{d}_5{d}_4{d}_3(k+d_2)-a{d}_1{d}_4\mu \xi (k+d_2)+a^2{d}_5\eta \rho k.\hfill \end{array}\right)\end{array}$$

  Now we show that there exists a positive root for Eq. (3). We define a function G(V) as

  $$\begin{array}{c}\hfill \mathrm{G}(\mathrm{V})=\frac{P_1{V}^2+P_{2}V+P_3}{ak\eta (a{d}_5-u{d}_{4}V)}.\end{array}$$

  We have

  $$\begin{array}{c}\hfill G(0)=\frac{-a{d}_1{d}_5{d}_4{d}_3(k+d_2)-a{d}_1{d}_4\mu \xi (k+d_2)+a^2{d}_5\eta \rho k}{a^2{d}_5\eta k}=\frac{(k+d_2)(d_1{d}_5{d}_4{d}_3+d_1{d}_4\mu \xi )}{a{d}_5\eta k}(R_2-1),\end{array}$$

  where $R_2={\displaystyle \frac{a{d}_5\eta \rho k}{d_1{d}_4(k+d_2)(d_5{d}_3+\mu \xi )}}$. This implies that $G(0)>0$ when $R_2>1$. Moreover, we find that

  $$\begin{array}{c}\hfill \underset{V\to {{\displaystyle \frac{a{d}_5}{u{d}_4}}}^{-}}{lim}G(V)=-\infty .\end{array}$$

  It follows that there exists $0<V_2<{\displaystyle \frac{a{d}_5}{u{d}_4}}$ such that $G(V_2)=0$. From Eq. (2) we get $Y_2>0,$ $S_2>0$, $X_2>0$ and $N_2>0$. As a result, ${\mathrm{\Delta }}_V$ exists when $R_2>1$. The parameter $R_2$ is the basic reproduction number of SARS-CoV-2 infection. It determines the establishment of SARS-CoV-2 infection in the body.
• (iv)
  The SARS-CoV-2/HIV coinfection steady state ${\mathrm{\Delta }}_{\mathit{VH}}(X_3,N_3,Y_3,V_3,S_3,W_3,H_3)$, where

  $$\begin{array}{cc}& X_3=\frac{d_4(k+d_2)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}{ak\eta \theta \lambda \left(\alpha +d_{6}b\right)}\text{,}\hfill \\ \hfill & N_3=-\frac{d_1{d}_4\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}{ak\eta \theta \lambda \left(\alpha +d_{6}b\right)}+\frac{\rho }{k+d_2},\hfill \\ \hfill & Y_3=-\frac{d_1{d}_4}{a\eta }+\frac{\theta \lambda \rho k\left(\alpha +d_{6}b\right)}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\text{,}\hfill \\ \hfill & V_3=-\frac{d_1}{\eta }+\frac{ak\theta \lambda \rho \left(\alpha +d_{6}b\right)}{d_4\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\text{,}\hfill \\ \hfill & S_3=\frac{d_7{d}_8\left(d_6+\alpha \right)}{\theta \lambda \left(\alpha +d_{6}b\right)}\text{,}\hfill \\ \hfill & T_3=\frac{d_7{d}_8\left(1-b\right)\left(d_1{d}_{4}u+a{d}_5\eta \right)}{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}\hfill \\ \hfill & \times \left[\frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u},\left(\frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}+\frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\right),-,1\right],\hfill \\ \hfill & W_3=\frac{d_8\left(a\eta d_5+d_1{d}_{4}u\right)}{a\eta \theta \lambda }\hfill \\ \hfill & \times \left[\frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u},\left(\frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}+\frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\right),-,1\right],\hfill \\ \hfill & H_3=\frac{a\eta d_5+d_1{d}_{4}u}{a\eta \theta }\hfill \\ \hfill & \times \left[\frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u},\left(\frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}+\frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\right),-,1\right].\hfill \end{array}$$

  It follows that $T_3>0$, $W_3>0$ and $H_3>0$ only when ${\displaystyle \frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u}}$ $\left({\displaystyle \frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}},+,{\displaystyle \frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}}\right)>1$. On the other hand, $N_3>0$, $Y_3>0$ and $V_3>0$ only when ${\displaystyle \frac{a\eta \theta \lambda \rho k\left(\alpha +d_{6}b\right)}{d_1{d}_4\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}}>1$. Thus, we can rewrite the components of ${\mathrm{\Delta }}_{\mathit{VH}}$ as

  $$\begin{array}{cc}\hfill X_3& =\frac{X_0}{R_4}\text{,}{N}_3=\frac{d_1{d}_4\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}{a\eta \theta \lambda k\left(\alpha +d_{6}b\right)}\left(R_4-1\right),\hfill \\ \hfill Y_3& =\frac{d_1{d}_4}{a\eta }\left(R_4-1\right)\text{,}{V}_3=\frac{d_1}{\eta }\left(R_4-1\right),\hfill \\ \hfill S_3& =\frac{d_7{d}_8\left(d_6+\alpha \right)}{\theta \lambda \left(\alpha +d_{6}b\right)}\text{,}{T}_3=\frac{d_7{d}_8\left(1-b\right)\left(d_1{d}_{4}u+a{d}_5\eta \right)}{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}\left(R_3-1\right),\hfill \\ \hfill W_3& =\frac{d_8\left(a\eta d_5+d_1{d}_{4}u\right)}{a\eta \theta \lambda }\left(R_3-1\right)\text{,}{H}_3=\frac{a\eta d_5+d_1{d}_{4}u}{a\eta \theta }\left(R_3-1\right),\hfill \end{array}$$

  where

  $$\begin{array}{cc}\hfill R_3& =\frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u}\left(\frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}+\frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\right)\text{,}\hfill \\ \hfill R_4& =\frac{a\eta \theta \lambda \rho k\left(\alpha +d_{6}b\right)}{d_1{d}_4\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}.\hfill \end{array}$$

  Therefore, ${\mathrm{\Delta }}_{\mathit{VH}}$ exists when $R_3>1$ and $R_4>1$. At this point, $R_3$ and $R_4$ are threshold numbers that determine the occurrence of SARS-CoV-2/HIV coinfection.

All steady states of model (1) and their existence conditions are summarized in Table 2.

Table 2.

Steady states of model (1) and their existence conditions

Steady state	Definition	Existence conditions
${\mathrm{\Delta }}_0=(X_0,0,0,0,S_0,0,0,0)$	Uninfected steady state	None
${\mathrm{\Delta }}_H=(X_1,0,0,0,S_1,T_1,W_1,H_1)$	Single HIV–infection steady state	$R_1>1$
${\mathrm{\Delta }}_V=\left(X_2,N_2,Y_2,V_2,S_2,0,0,0\right)$	Single SARS-CoV-2–infection steady state	$R_2>1$
${\mathrm{\Delta }}_{\mathit{VH}}=\left(X_3,N_3,Y_3,V_3,S_3,T_3,W_3,H_3\right)$	SARS-CoV-2/HIV coinfection steady state	$R_3>1$ and $R_4>1$

The four threshold parameters are given as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{R}_1=\frac{\xi \theta \lambda \left(\alpha +d_{6}b\right)}{d_5{d}_7{d}_8\left(d_6+\alpha \right)},\hfill \\ R_2=\frac{a{d}_5\eta \rho k}{d_1{d}_4(k+d_2)(d_5{d}_3+\mu \xi )},\hfill \\ R_3=\frac{a\eta \theta \lambda \left(\alpha +d_{6}b\right)}{a\eta d_5+d_1{d}_{4}u}\left(\frac{\xi }{d_7{d}_8\left(d_6+\alpha \right)}+\frac{u\rho k}{\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}\right),\hfill \\ R_4=\frac{a\eta \theta \lambda \rho k\left(\alpha +d_{6}b\right)}{d_1{d}_4\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}.\hfill \end{array}\right)\end{array}$$

Global stability of steady states

In this section, we prove the global asymptotic stability of all steady states by constructing Lyapunov functions following the method presented in [49]. We define $F(\nu )=\nu -1-ln\nu$. We will use the arithmetic–geometric mean inequality

$$\begin{array}{c}\hfill \frac{1}{n}\sum _{i=1}^n{\chi }_i\ge \sqrt[n]{\underset{i=1}{\overset{n}{\mathrm{\Pi }}}{\chi }_i},{\chi }_i\ge 0,i=1,2,\dots \end{array}$$

which yields

$$\begin{array}{cc}& \frac{S_j}{S}+\frac{S{W}_{j}H}{S_{j}W{H}_j}+\frac{W{H}_j}{W_{j}H}\ge 3,j=1,3,\hfill \end{array}$$ 4

$$\begin{array}{cc}& \frac{S_j}{S}+\frac{S{T}_{j}H}{S_{j}T{H}_j}+\frac{W{H}_j}{W_{j}H}+\frac{T{W}_j}{T_{j}W}\ge 4,j=1,3,\hfill \end{array}$$ 5

$$\begin{array}{cc}& \frac{X_j}{X}+\frac{X{N}_{j}V}{X_{j}N{V}_j}+\frac{Y{V}_j}{Y_{j}V}+\frac{N{Y}_j}{N_{j}Y}\ge 4,j=2,3.\hfill \end{array}$$ 6

Theorem 1

If $R_1\le 1$ and $R_2\le 1$, then ${\mathrm{\Delta }}_0$ is globally asymptotically stable (G.A.S).

Proof

Construct a Lyapunov function ${\vartheta }_0(X,N,Y,V,S,T,W,H)$ as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\vartheta }_0& =X_{0}F\left(\frac{X}{X_0}\right)+N+\frac{k+d_2}{k}Y+\frac{\eta X_0}{d_4}V+\frac{\mu (k+d_2)}{\mathit{uk}}{S}_{0}F\left(\frac{S}{S_0}\right)+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}T\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}W+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}H.\hfill \end{array}\end{array}$$

Clearly, ${\vartheta }_0(X,N,Y,V,S,T,W,H)>0$ for all $X,N,Y,V,S,T,W,H>0$, and ${\vartheta }_0(X_0,0,0,0,S_0,0,0,0)=0$. By calculating ${\displaystyle \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}}$ along the solutions of model (1), we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}& =\left(1-\frac{X_0}{X}\right)\dot{X}+\dot{N}+\frac{k+d_2}{k}\dot{Y}+\frac{\eta X_0}{d_4}\dot{V}+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_0}{S}\right)\dot{S}+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\dot{T}\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\dot{W}+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\dot{H}\hfill \\ \hfill & =\left(1-\frac{X_0}{X}\right)\left(\rho -d_{1}X-\eta VX\right)+[\eta VX-\left(k+d_2\right)N]+\frac{k+d_2}{k}\left(kN-d_{3}Y-\mu YS\right)+\frac{\eta X_0}{d_4}\left(aY-d_{4}V\right)\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_0}{S}\right)\left(\xi +uYS-d_{5}S-\theta HS\right)+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}[\left(1-b\right)\theta HS-\left(\alpha +d_6\right)T]\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(b\theta HS+\alpha T-d_{7}W\right)+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(\lambda W-d_{8}H\right).\hfill \end{array}\end{array}$$

Using $\rho =d_1{X}_0$ and $\xi =d_5{S}_0$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}& =-\frac{d_1}{X}{\left(X-X_0\right)}^2-\eta VX+\eta V{X}_0+\eta VX-\left(k+d_2\right)N+\left(k+d_2\right)N-\frac{k+d_2}{k}{d}_{3}Y-\frac{k+d_2}{k}\mu YS\hfill \\ \hfill & +\frac{\eta X_0}{d_4}aY-\eta X_{0}V-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_0\right)}^2+\frac{k+d_2}{k}\mu YS-\frac{k+d_2}{k}\mu Y{S}_0-\frac{\mu (k+d_2)}{\mathit{uk}}\theta HS\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\theta S_{0}H+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(\alpha +d_6\right)T\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\alpha T-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_{7}W\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_{7}W-\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_{8}H\hfill \\ \hfill & =-\frac{d_1}{X}{\left(X-X_0\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_0\right)}^2+\left(\frac{\eta X_0}{d_4}a-\frac{k+d_2}{k}{d}_3-\frac{k+d_2}{k}\mu S_0\right)Y\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\left(\theta S_0-\frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}\right)H\hfill \\ \hfill & =-\frac{d_1}{X}{\left(X-X_0\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_0\right)}^2+\frac{(k+d_2)\left(d_5{d}_3+\mu \xi \right)}{k{d}_5}\left(\frac{a{d}_5\eta \rho k}{d_1{d}_4(k+d_2)(d_5{d}_3+\mu \xi )}-1\right)Y\hfill \\ \hfill & +\frac{\mu d_7{d}_8(k+d_2)(d_6+\alpha )}{\lambda ku(\alpha +d_{6}b)}\left(\frac{\xi \theta \lambda \left(\alpha +d_{6}b\right)}{d_5{d}_7{d}_8\left(d_6+\alpha \right)}-1\right)H\hfill \\ \hfill & =-\frac{d_1}{X}{\left(X-X_0\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_0\right)}^2+\frac{(k+d_2)\left(d_5{d}_3+\mu \xi \right)}{k{d}_5}\left(R_2-1\right)Y\hfill \\ \hfill & +\frac{\mu d_7{d}_8(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(R_1-1\right)H.\hfill \end{array}\end{array}$$

As $R_1\le 1$ and $R_2\le 1$, we get ${\displaystyle \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}}\le 0$ for all $X,N,Y,V,S,T,W,H>0$ and ${\displaystyle \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}}=0$ when $X=X_0$, $S=S_0$ and $Y=H=0$. Define ${\mathrm{{\rm Y}}}_0=\left\{\left(X,N,Y,V,S,T,W,H\right):{\displaystyle \frac{\mathrm{d}{\vartheta }_0}{\mathrm{d}t}}=0\right\}$ and let ${\mathrm{{\rm Y}}}_0^{{}^{\prime }}$ be the largest invariant subset of ${\mathrm{{\rm Y}}}_0$. The solutions of model (1) converge to ${\mathrm{{\rm Y}}}_0^{{}^{\prime }}$. The set ${\mathrm{{\rm Y}}}_0^{{}^{\prime }}$ includes elements with $X=X_0$, $S=S_0$ and $Y=H=0$, and hence $\dot{Y}=\dot{H}=0$. The third and last equations of model (1) yield

$$\begin{array}{c}\hfill 0=\dot{Y}=kN,\\ \hfill 0=\dot{H}=\lambda W.\end{array}$$

Thus, $N(t)=W(t)=0$ for all t. The second and seventh equations give

$$\begin{array}{cc}\hfill 0=& \dot{N}=\eta V{X}_0,\hfill \\ \hfill 0=& \dot{W}=\alpha T.\hfill \end{array}$$

Thus, $V(t)=T(t)=0$ for all t. Therefore, ${\mathrm{{\rm Y}}}_0^{{}^{\prime }}=\left\{{\mathrm{\Delta }}_0\right\}$ and by applying Lyapunov–LaSalle asymptotic stability theorem [50–52] we get that ${\mathrm{\Delta }}_0$ is G.A.S. $\square$

Theorem 2

If $R_1>1$ and $R_4\le 1$, then ${\mathrm{\Delta }}_H$ is globally asymptotically stable (G.A.S).

Proof

Define a Lyapunov function ${\vartheta }_1(X,N,Y,V,S,T,W,H)$ as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\vartheta }_1& =X_{1}F\left(\frac{X}{X_1}\right)+N+\frac{k+d_2}{k}Y+\frac{\eta X_1}{d_4}V+\frac{\mu (k+d_2)}{\mathit{uk}}{S}_{1}F\left(\frac{S}{S_1}\right)+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}{T}_{1}F\left(\frac{T}{T_1}\right)\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{W}_{1}F\left(\frac{W}{W_1}\right)+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{H}_{1}F\left(\frac{H}{H_1}\right).\hfill \end{array}\end{array}$$

By differentiating ${\vartheta }_1$, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_1}{\mathrm{d}t}& =\left(1-\frac{X_1}{X}\right)\dot{X}+\dot{N}+\frac{k+d_2}{k}\dot{Y}+\frac{\eta X_1}{d_4}\dot{V}+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_1}{S}\right)\dot{S}+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-\frac{T_1}{T}\right)\dot{T}\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(1-\frac{W_1}{W}\right)\dot{W}+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(1-\frac{H_1}{H}\right)\dot{H}\hfill \\ \hfill & =\left(1-\frac{X_1}{X}\right)\left(\rho -d_{1}X-\eta VX\right)+[\eta VX-\left(k+d_2\right)N]+\frac{k+d_2}{k}\left(kN-d_{3}Y-\mu YS\right)+\frac{\eta X_1}{d_4}\left(aY-d_{4}V\right)\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_1}{S}\right)\left(\xi +uYS-d_{5}S-\theta HS\right)+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-\frac{T_1}{T}\right)[\left(1-b\right)\theta HS-\left(\alpha +d_6\right)T]\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(1-\frac{W_1}{W}\right)\left(b\theta HS+\alpha T-d_{7}W\right)+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(1-\frac{H_1}{H}\right)\left(\lambda W-d_{8}H\right)\hfill \\ \hfill & =\left(1-\frac{X_1}{X}\right)\left(\rho -d_{1}X\right)+\eta V{X}_1-\frac{k+d_2}{k}{d}_{3}Y+\frac{\eta X_1}{d_4}aY-\eta V{X}_1+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_1}{S}\right)\left(\xi -d_{5}S\right)\hfill \\ \hfill & -\frac{k+d_2}{k}\mu Y{S}_1-\frac{\mu (k+d_2)}{\mathit{uk}}\theta HS+\frac{\mu (k+d_2)}{\mathit{uk}}\theta H{S}_1+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS\frac{T_1}{T}-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(\alpha +d_6\right)T+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(\alpha +d_6\right)T_1\hfill \\ \hfill & +\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS\frac{W_1}{W}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\alpha T\hfill \\ \hfill & -\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\alpha T\frac{W_1}{W}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_7{W}_1-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_{7}W\frac{H_1}{H}\hfill \\ \hfill & -\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_{8}H+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_8{H}_1.\hfill \end{array}\end{array}$$

Using steady-state conditions for ${\mathrm{\Delta }}_H$, we get

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\rho =d_1{X}_1,\hfill \\ \xi =d_5{S}_1+\theta H_1{S}_1,\hfill \\ \left(1-b\right)\theta H_1{S}_1=\left(\alpha +d_6\right)T_1,\hfill \\ b\theta H_1{S}_1=d_7{W}_1-\alpha T_1,\hfill \\ \lambda W_1=d_8{H}_1.\hfill \end{array}\right)\end{array}$$

Then, we obtain

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_1}{\mathrm{d}t}=& -\frac{d_1}{X}{\left(X-X_1\right)}^2+\left(\frac{\eta X_1}{d_4}a-\frac{k+d_2}{k}{d}_3-\frac{k+d_2}{k}\mu S_1\right)Y-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_1\right)}^2\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_1{S}_1-\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_1{S}_1\frac{S_1}{S_1}+\frac{\mu (k+d_2)}{\mathit{uk}}\theta H{S}_1-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS\frac{T_1}{T}\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS\frac{W_1}{W}\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\frac{T{W}_1}{T_{1}W}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_1{S}_1+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\hfill \\ \hfill & -\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_1{S}_1\frac{W{H}_1}{W_{1}H}-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\frac{W{H}_1}{W_{1}H}-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H{S}_1\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H{S}_1+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_1{S}_1+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\hfill \\ \hfill =& -\frac{d_1}{X}{\left(X-X_1\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_1\right)}^2+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_1{S}_1\left(2-\frac{S{W}_{1}H}{S_{1}W{H}_1}-\frac{W{H}_1}{W_{1}H}\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\left(3-\frac{S{T}_{1}H}{S_{1}T{H}_1}-\frac{T{W}_1}{T_{1}W}-\frac{W{H}_1}{W_{1}H}\right)+\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_1{S}_1\left(1-\frac{S_1}{S}\right)\hfill \\ \hfill & +\frac{(k+d_2)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}{k\theta \lambda \left(\alpha +d_{6}b\right)}\left(\frac{a\eta \theta \lambda \rho k\left(\alpha +d_{6}b\right)}{d_1{d}_4\left(k+d_2\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}-1\right)Y\hfill \\ \hfill =& -\frac{d_1}{X}{\left(X-X_1\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_1\right)}^2+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_1{S}_1\left(3-\frac{S_1}{S}-\frac{S{W}_{1}H}{S_{1}W{H}_1}-\frac{W{H}_1}{W_{1}H}\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_1{S}_1\left(4-\frac{S_1}{S}-\frac{S{T}_{1}H}{S_{1}T{H}_1}-\frac{T{W}_1}{T_{1}W}-\frac{W{H}_1}{W_{1}H}\right)\hfill \\ \hfill & +\frac{(k+d_2)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}{k\theta \lambda \left(\alpha +d_{6}b\right)}\left(R_4-1\right)Y.\hfill \end{array}$$

As $R_4\le 1$ and according to inequalities (4) and (5), we get ${\displaystyle \frac{\mathrm{d}{\vartheta }_1}{\mathrm{d}t}}\le 0$ for all $X,N,Y,V,S,T,W,H>0$. Moreover, ${\displaystyle \frac{\mathrm{d}{\vartheta }_1}{\mathrm{d}t}}=0$ when $X=X_1$, $S=S_1$, $T=T_1$, $W=W_1$, $H=H_1$ and $Y=0$. The solutions of model (1) converge to ${\mathrm{{\rm Y}}}_1^{{}^{\prime }}$ the largest invariant subset of ${\mathrm{{\rm Y}}}_1=\left\{\left(X,N,Y,V,S,T,W,H\right):{\displaystyle \frac{\mathrm{d}{\vartheta }_1}{\mathrm{d}t}}=0\right\}$. The set ${\mathrm{{\rm Y}}}_1^{{}^{\prime }}$ includes $Y=0$, and then $\dot{Y}=0$. The third equation of model (1) implies that

$$\begin{array}{c}\hfill 0=\dot{Y}=kN,\end{array}$$

which yields $N(t)=0$ for all t. We get from the second equation that

$$\begin{array}{c}\hfill 0=\dot{N}=\eta V{X}_1,\end{array}$$

which yields $V(t)=0$ for all t. Hence, ${\mathrm{{\rm Y}}}_1^{{}^{\prime }}=\left\{{\mathrm{\Delta }}_H\right\}$ and ${\mathrm{\Delta }}_H$ is G.A.S using Lyapunov–LaSalle asymptotic stability theorem. $\square$

Theorem 3

If $R_2>1$ and $R_3\le 1$, then ${\mathrm{\Delta }}_V$ is globally asymptotically stable (G.A.S).

Proof

Define a Lyapunov function ${\vartheta }_2(X,N,Y,V,S,T,W,H)$ as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\vartheta }_2& =X_{2}F\left(\frac{X}{X_2}\right)+N_{2}F\left(\frac{N}{N_2}\right)+\frac{k+d_2}{k}{Y}_{2}F\left(\frac{Y}{Y_2}\right)+\frac{\eta X_2}{d_4}{V}_{2}F\left(\frac{V}{V_2}\right)+\frac{\mu (k+d_2)}{\mathit{uk}}{S}_{2}F\left(\frac{S}{S_2}\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}T+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}W+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}H.\hfill \end{array}\end{array}$$

By differentiating ${\vartheta }_2$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_2}{\mathrm{d}t}& =\left(1-\frac{X_2}{X}\right)\dot{X}+\left(1-\frac{N_2}{N}\right)\dot{N}+\frac{k+d_2}{k}\left(1-\frac{Y_2}{Y}\right)\dot{Y}+\frac{\eta X_2}{d_4}\left(1-\frac{V_2}{V}\right)\dot{V}+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_1}{S}\right)\dot{S}\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\dot{T}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\dot{W}+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\dot{H}\hfill \\ \hfill & =\left(1-\frac{X_2}{X}\right)\left(\rho -d_{1}X-\eta VX\right)+\left(1-\frac{N_2}{N}\right)\left[\eta VX-\left(k+d_2\right)N\right]+\frac{k+d_2}{k}\left(1-\frac{Y_2}{Y}\right)\left(kN-d_{3}Y-\mu YS\right)\hfill \\ \hfill & +\frac{\eta X_2}{d_4}\left(1-\frac{V_2}{V}\right)\left(aY-d_{4}V\right)+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_2}{S}\right)\left(\xi +uYS-d_{5}S-\theta HS\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left[\left(1-b\right)\theta HS-\left(\alpha +d_6\right)T\right]+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(b\theta HS+\alpha T-d_{7}W\right)\hfill \\ \hfill & +\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(\lambda W-d_{8}H\right)\hfill \\ \hfill & =\left(1-\frac{X_2}{X}\right)\left(\rho -d_{1}X\right)-\eta VX\frac{N_2}{N}+\left(k+d_2\right)N_2-\left(k+d_2\right)N\frac{Y_2}{Y}-\frac{k+d_2}{k}{d}_{3}Y+\frac{k+d_2}{k}{d}_3{Y}_2\hfill \\ \hfill & +\frac{k+d_2}{k}\mu Y_{2}S+\frac{\eta X_2}{d_4}aY-\frac{\eta X_2}{d_4}aY\frac{V_2}{V}+\eta V_2{X}_2+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_2}{S}\right)\left(\xi -d_{5}S\right)-\frac{k+d_2}{k}\mu Y{S}_2\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\theta S_{2}H-\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_{8}H.\hfill \end{array}\end{array}$$

By using the steady-state conditions for ${\mathrm{\Delta }}_V$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\rho =d_1{X}_2+\eta V_2{X}_2,\hfill \\ \eta V_2{X}_2=(k+d_2)N_2,\hfill \\ k{N}_2=d_3{Y}_2+\mu Y_2{S}_2,\hfill \\ a{Y}_2=d_4{V}_2,\hfill \\ \xi =d_5{S}_2-u{Y}_2{S}_2,\hfill \end{array}\right)\end{array}$$

we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_2}{\mathrm{d}t}& =-\frac{d_1}{X}{\left(X-X_2\right)}^2+\eta V_2{X}_2-\eta V_2{X}_2\frac{X_2}{X}-\eta VX\frac{N_2}{N}+\eta V_2{X}_2+\left(\frac{\eta X_2}{d_4}a-\frac{k+d_2}{k}{d}_3-\frac{k+d_2}{k}\mu S_2\right)Y\hfill \\ \hfill & -\eta V_2{X}_2\frac{N{Y}_2}{N_{2}Y}+\eta V_2{X}_2-\frac{k+d_2}{k}\mu Y_2{S}_2+\frac{k+d_2}{k}\mu Y_{2}S-\eta V_2{X}_2\frac{Y{V}_2}{Y_{2}V}+\eta V_2{X}_2\hfill \\ \hfill & -\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_2\right)}^2-\frac{k+d_2}{k}\mu Y_2{S}_2+\frac{k+d_2}{k}\mu Y_2{S}_2\frac{S_2}{S}+\frac{\mu (k+d_2)}{\mathit{uk}}\left(\theta S_2-\frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}\right)H\hfill \\ \hfill & =-\frac{d_1}{X}{\left(X-X_2\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_2\right)}^2-\frac{k+d_2}{k}\mu Y_2{S}_2\left(2-\frac{S_2}{S}-\frac{S}{S_2}\right)\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\left(\theta S_2-\frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}\right)H+\eta V_2{X}_2\left(4-\frac{X_2}{X}-\frac{X{N}_{2}V}{X_{2}N{V}_2}-\frac{N{Y}_2}{N_{2}Y}-\frac{Y{V}_2}{Y_{2}V}\right)\hfill \\ \hfill & =-\frac{d_1}{X}{\left(X-X_2\right)}^2-\frac{\mu \xi (k+d_2)}{ukS{S}_2}{\left(S-S_2\right)}^2+\frac{\mu (k+d_2)}{\mathit{uk}}\left(\theta S_2-\frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}\right)H\hfill \\ \hfill & +\eta V_2{X}_2\left(4-\frac{X_2}{X}-\frac{X{N}_{2}V}{X_{2}N{V}_2}-\frac{N{Y}_2}{N_{2}Y}-\frac{Y{V}_2}{Y_{2}V}\right).\hfill \end{array}\end{array}$$

Hence, if $R_3\le 1$, then ${\mathrm{\Delta }}_{\mathit{VH}}$ does not exist since $H_3\le 0$, $W_3\le 0$ and $T_3\le 0$. This implies that

$$\begin{array}{cc}& \dot{H}(t)=\lambda W-d_{8}H\le 0,\hfill \\ \hfill & \dot{W}(t)=b\theta HS+\alpha T-d_{7}W\le 0,\hfill \\ \hfill & \dot{T}(t)=(1-b)\theta HS-(\alpha +d_6)T\le 0.\hfill \end{array}$$

It follows that $\theta S-{\displaystyle \frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}}\le 0$ for all $H>0$. Thus, $\theta S_2-{\displaystyle \frac{d_7{d}_8(d_6+\alpha )}{\lambda (\alpha +d_{6}b)}}\le 0$ and by using inequality (6), we get ${\displaystyle \frac{\mathrm{d}{\vartheta }_2}{\mathrm{d}t}}\le 0$ for all $X,N,Y,V,S,T,W,H>0$ with equality holding when $X=X_2$, $S=S_2$, $N=N_2$, $Y=Y_2$, $V=V_2$ and $H=0$. The solutions of model (1) converge to ${\mathrm{{\rm Y}}}_2^{{}^{\prime }}$, the largest invariant subset of ${\mathrm{{\rm Y}}}_2=\left\{\left(X,N,Y,V,S,T,W,H\right):{\displaystyle \frac{\mathrm{d}{\vartheta }_2}{\mathrm{d}t}}=0\right\}$. ${\mathrm{{\rm Y}}}_2^{{}^{\prime }}$ contains elements with $H=0$, and then $\dot{H}=0$. Using the last equation of model (1), we obtain

$$\begin{array}{c}\hfill 0=\dot{H}=\lambda W,\end{array}$$

which gives $W(t)=0$ for all t. Using the seventh equation of model (1), we obtain

$$\begin{array}{c}\hfill 0=\dot{W}=\alpha T,\end{array}$$

which gives $T(t)=0$ for all t. Therefore, ${\mathrm{{\rm Y}}}_2^{{}^{\prime }}=\left\{{\mathrm{\Delta }}_V\right\}$ and by applying Lyapunov–LaSalle asymptotic stability theorem we get that ${\mathrm{\Delta }}_V$ is G.A.S. $\square$

Theorem 4

If $R_4>1$ and $1<R_3\le 1+{\displaystyle \frac{a\eta \theta \lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)(a\eta d_5+d_1{d}_{4}u)}}$, then ${\mathrm{\Delta }}_{\mathit{VH}}$ is globally asymptotically stable (G.A.S).

Proof

Define a Lyapunov function ${\vartheta }_3(X,N,Y,V,S,T,W,H)$ as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\vartheta }_3& =X_{3}F\left(\frac{X}{X_3}\right)+N_{3}F\left(\frac{N}{N_3}\right)+\frac{k+d_2}{k}{Y}_{3}F\left(\frac{Y}{Y_3}\right)+\frac{\eta X_3}{d_4}{V}_{3}F\left(\frac{V}{V_3}\right)+\frac{\mu (k+d_2)}{\mathit{uk}}{S}_{3}F\left(\frac{S}{S_3}\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}{T}_{3}F\left(\frac{T}{T_3}\right)+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{W}_{3}F\left(\frac{W}{W_3}\right)+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{H}_{3}F\left(\frac{H}{H_3}\right).\hfill \end{array}\end{array}$$

Differentiating ${\vartheta }_3$ with respect to t gives

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_3}{\mathrm{d}t}& =\left(1-\frac{X_3}{X}\right)\dot{X}+\left(1-\frac{N_3}{N}\right)\dot{N}+\frac{k+d_2}{k}\left(1-\frac{Y_3}{Y}\right)\dot{Y}+\frac{\eta X_3}{d_4}\left(1-\frac{V_3}{V}\right)\dot{V}+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_3}{S}\right)\dot{S}\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-\frac{T_3}{T}\right)\dot{T}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(1-\frac{W_3}{W}\right)\dot{W}+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(1-\frac{H_3}{H}\right)\dot{H}\hfill \\ \hfill & =\left(1-\frac{X_3}{X}\right)\left(\rho -d_{1}X-\eta VX\right)+\left(1-\frac{N_3}{N}\right)\left[\eta VX-\left(k+d_2\right)N\right]+\frac{k+d_2}{k}\left(1-\frac{Y_3}{Y}\right)\left(kN-d_{3}Y-\mu YS\right)\hfill \\ \hfill & +\frac{\eta X_3}{d_4}\left(1-\frac{V_3}{V}\right)\left(aY-d_{4}V\right)+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_3}{S}\right)\left(\xi +uYS-d_{5}S-\theta HS\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-\frac{T_3}{T}\right)\left[\left(1-b\right)\theta HS-\left(\alpha +d_6\right)T\right]+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\left(1-\frac{W_3}{W}\right)\left(b\theta HS+\alpha T-d_{7}W\right)\hfill \\ \hfill & +\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}\left(1-\frac{H_3}{H}\right)\left(\lambda W-d_{8}H\right)\hfill \\ \hfill & =\left(1-\frac{X_3}{X}\right)\left(\rho -d_{1}X\right)-\eta VX\frac{N_3}{N}+(k+d_2)N_3-\left(k+d_2\right)N\frac{Y_3}{Y}-\frac{k+d_2}{k}{d}_{3}Y+\frac{k+d_2}{k}{d}_3{Y}_3\hfill \\ \hfill & +\frac{k+d_2}{k}\mu Y_{3}S+\frac{\eta X_3}{d_4}aY-\frac{\eta X_3}{d_4}aY\frac{V_3}{V}+\eta V_3{X}_3+\frac{\mu (k+d_2)}{\mathit{uk}}\left(1-\frac{S_3}{S}\right)\left(\xi -d_{5}S\right)-\frac{k+d_2}{k}\mu Y{S}_3\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\theta H{S}_3-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS\frac{T_3}{T}+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(\alpha +d_6\right)T_3\hfill \\ \hfill & -\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS\frac{W_3}{W}-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}\alpha T\frac{W_3}{W}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_7{W}_3\hfill \\ \hfill & -\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}{d}_{7}W\frac{H_3}{H}-\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_{8}H+\frac{\mu d_7(k+d_2)(d_6+\alpha )}{\lambda uk(\alpha +d_{6}b)}{d}_8{H}_3.\hfill \end{array}\end{array}$$

By using the steady-state conditions of ${\mathrm{\Delta }}_{\mathit{VH}}$

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\rho =d_1{X}_3+\eta V_3{X}_3,\hfill \\ \eta V_3{X}_3=(k+d_2)N_3,\hfill \\ k{N}_3=d_3{Y}_3+\mu Y_3{S}_3,\hfill \\ a{Y}_3=d_4{V}_3,\hfill \\ \xi =d_5{S}_3+\theta H_3{S}_3-u{Y}_3{S}_3,\hfill \\ \left(1-b\right)\theta H_3{S}_3=\left(\alpha +d_6\right)T_3,\hfill \\ b\theta H_3{S}_3=d_7{W}_3-\alpha T_3,\hfill \\ \lambda W_3=d_8{H}_3,\hfill \end{array}\right)\end{array}$$

we get

$$\begin{array}{cc}\hfill \frac{\mathrm{d}{\vartheta }_3}{\mathrm{d}t}=& -\frac{d_1}{X}{\left(X-X_3\right)}^2+\eta V_3{X}_3-\eta V_3{X}_3\frac{X_3}{X}-\eta VX\frac{N_3}{N}+\eta V_3{X}_3+\left(\frac{\eta X_3}{d_4}a-\frac{k+d_2}{k}{d}_3-\frac{k+d_2}{k}\mu S_3\right)Y\hfill \\ \hfill & -\eta V_3{X}_3\frac{N{Y}_3}{N_{3}Y}+\eta V_3{X}_3-\frac{k+d_2}{k}\mu Y_3{S}_3+\frac{k+d_2}{k}\mu Y_{3}S-\eta V_3{X}_3\frac{Y{V}_3}{Y_{3}V}+\eta V_3{X}_3-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_3\right)}^2\hfill \\ \hfill & +\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_3{S}_3-\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_3{S}_3\frac{S_3}{S}-\frac{k+d_2}{k}\mu Y_3{S}_3+\frac{k+d_2}{k}\mu Y_3{S}_3\frac{S_3}{S}+\frac{\mu (k+d_2)}{\mathit{uk}}\theta H{S}_3\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta HS\frac{T_3}{T}+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta HS\frac{W_3}{W}\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\frac{T{W}_3}{T_{3}W}+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_3{S}_3+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\hfill \\ \hfill & -\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_3{S}_3\frac{W{H}_3}{W_{3}H}-\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\frac{W{H}_3}{W_{3}H}-\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H{S}_3\hfill \\ \hfill & -\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H{S}_3+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_3{S}_3+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\hfill \\ \hfill =& -\frac{d_1}{X}{\left(X-X_3\right)}^2-\frac{\mu d_5(k+d_2)}{\mathit{ukS}}{\left(S-S_3\right)}^2-\frac{k+d_2}{k}\mu Y_3{S}_3\left(2-\frac{S_3}{S}-\frac{S}{S_3}\right)+\frac{\mu (k+d_2)}{\mathit{uk}}\theta H_3{S}_3\left(1-\frac{S_3}{S}\right)\hfill \\ \hfill & +\eta V_3{X}_3\left(4-\frac{X_3}{X}-\frac{X{N}_{3}V}{X_{3}N{V}_3}-\frac{N{Y}_3}{N_{3}Y}-\frac{Y{V}_3}{Y_{3}V}\right)+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_3{S}_3\left(2-\frac{S{W}_{3}H}{S_{3}W{H}_3}-\frac{W{H}_3}{W_{3}H}\right)\hfill \\ \hfill & +\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\left(3-\frac{S{T}_{3}H}{S_{3}T{H}_3}-\frac{T{W}_3}{T_{3}W}-\frac{W{H}_3}{W_{3}H}\right)\hfill \\ \hfill =& -\frac{d_1}{X}{\left(X-X_3\right)}^2+\frac{\mu \alpha (k+d_2)}{uk(\alpha +d_{6}b)}\left(1-b\right)\theta H_3{S}_3\left(4-\frac{S_3}{S}-\frac{S{T}_{3}H}{S_{3}T{H}_3}-\frac{T{W}_3}{T_{3}W}-\frac{W{H}_3}{W_{3}H}\right)\hfill \\ \hfill & +\eta V_3{X}_3\left(4-\frac{X_3}{X}-\frac{X{N}_{3}V}{X_{3}N{V}_3}-\frac{N{Y}_3}{N_{3}Y}-\frac{Y{V}_3}{Y_{3}V}\right)+\frac{\mu (k+d_2)(d_6+\alpha )}{uk(\alpha +d_{6}b)}b\theta H_3{S}_3\left(3-\frac{S_3}{S}-\frac{S{W}_{3}H}{S_{3}W{H}_3}-\frac{W{H}_3}{W_{3}H}\right)\hfill \\ \hfill & +\frac{\mu (k+d_2)(u{d}_1{d}_4+a{d}_5\eta )}{a\eta ukS}{\left(S-S_3\right)}^2\left(\frac{a\eta \theta \lambda u\rho k\left(\alpha +d_{6}b\right)}{\left(k+d_2\right)\left(a\eta d_5+d_1{d}_{4}u\right)\left[d_3\theta \lambda \left(\alpha +d_{6}b\right)+\mu d_7{d}_8\left(d_6+\alpha \right)\right]}-1\right).\hfill \end{array}$$

Since $1<R_3\le 1+{\displaystyle \frac{a\eta \theta \lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)(a\eta d_5+d_1{d}_{4}u)}}$ and using inequalities (4), (5) and (6) we get ${\displaystyle \frac{\mathrm{d}{\vartheta }_3}{\mathrm{d}t}}\le 0$ for all $X,N,Y,V,S,T,W,H>0$. Moreover, ${\displaystyle \frac{\mathrm{d}{\vartheta }_3}{\mathrm{d}t}}=0$ when $X=X_3$, $S=S_3$, $N=N_3$, $Y=Y_3$, $V=V_3$, $T=T_3$, $W=W_3$ and $H=H_3$. The solutions of model (1) converge to ${\mathrm{{\rm Y}}}_3^{{}^{\prime }}$ the largest invariant subset of ${\mathrm{{\rm Y}}}_3=\left\{\left(X,N,Y,V,S,T,W,H\right):{\displaystyle \frac{\mathrm{d}{\vartheta }_3}{\mathrm{d}t}}=0\right\}$. Hence, ${\mathrm{{\rm Y}}}_3^{{}^{\prime }}=\left\{{\mathrm{\Delta }}_{\mathit{VH}}\right\}$ and ${\mathrm{\Delta }}_{\mathit{VH}}$ is G.A.S using Lyapunov–LaSalle asymptotic stability theorem. $\square$

The global stability conditions of all steady states are summarized in Table 3.

Table 3.

Global stability conditions of the steady states of model (1)

Steady state	Global stability conditions
${\mathrm{\Delta }}_0=(X_0,0,0,0,S_0,0,0,0)$	$R_1\le 1$ and $R_2\le 1$
${\mathrm{\Delta }}_H=(X_1,0,0,0,S_1,T_1,W_1,H_1)$	$R_1>1$ and $R_4\le 1$
${\mathrm{\Delta }}_V=\left(X_2,N_2,Y_2,V_2,S_2,0,0,0\right)$	$R_2>1$ and $R_3\le 1$
${\mathrm{\Delta }}_{\mathit{VH}}=\left(X_3,N_3,Y_3,V_3,S_3,T_3,W_3,H_3\right)$	$R_4>1$ and $1<R_3\le 1+{\displaystyle \frac{a\eta \theta \lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)(a\eta d_5+d_1{d}_{4}u)}}$

Numerical simulations

This section presents some numerical simulations to assist the results obtained in the previous parts. In addition, it shows the impact of low number of CD$4^{+}$ T cells on SARS-CoV-2/HIV coinfection. Furthermore, it illustrates the effect of death rates during the latency periods on viral loads. To achieve these goals, we consider three sets of initial conditions as follows:

Set 1 $X(0)=5$, $N(0)=0.0001$, $Y(0)=0.0002$, $V(0)=0.0003$, $S(0)=100$, $T(0)=5$, $W(0)=10$, $H(0)=15$.

Set 2 $X(0)=10$, $N(0)=0.001$, $Y(0)=0.002$, $V(0)=0.003$, $S(0)=200$, $T(0)=10$, $W(0)=15$, $H(0)=20$.

Set 3 $X(0)=15$, $N(0)=0.002$, $Y(0)=0.003$, $V(0)=0.004$, $S(0)=300$, $T(0)=15$, $W(0)=20$, $H(0)=25$.

The selection of these values is optional. Furthermore, it is divided into three sets to ensure that the global stability of the steady states is not affected by the choice of initial conditions. We use the MATLAB solver ode45 to solve system (1). According to the global stability of the steady states ${\mathrm{\Delta }}_0$, ${\mathrm{\Delta }}_H$, ${\mathrm{\Delta }}_V$, and ${\mathrm{\Delta }}_{\mathit{VH}}$ in Theorems 1–4, we split the simulations into four cases. In these cases, we vary the values of $\eta$, $\mu$, $d_4$, and $\theta$ of model (1). The values of all other parameters are fixed and listed in Table 1. The four cases are given as follows:

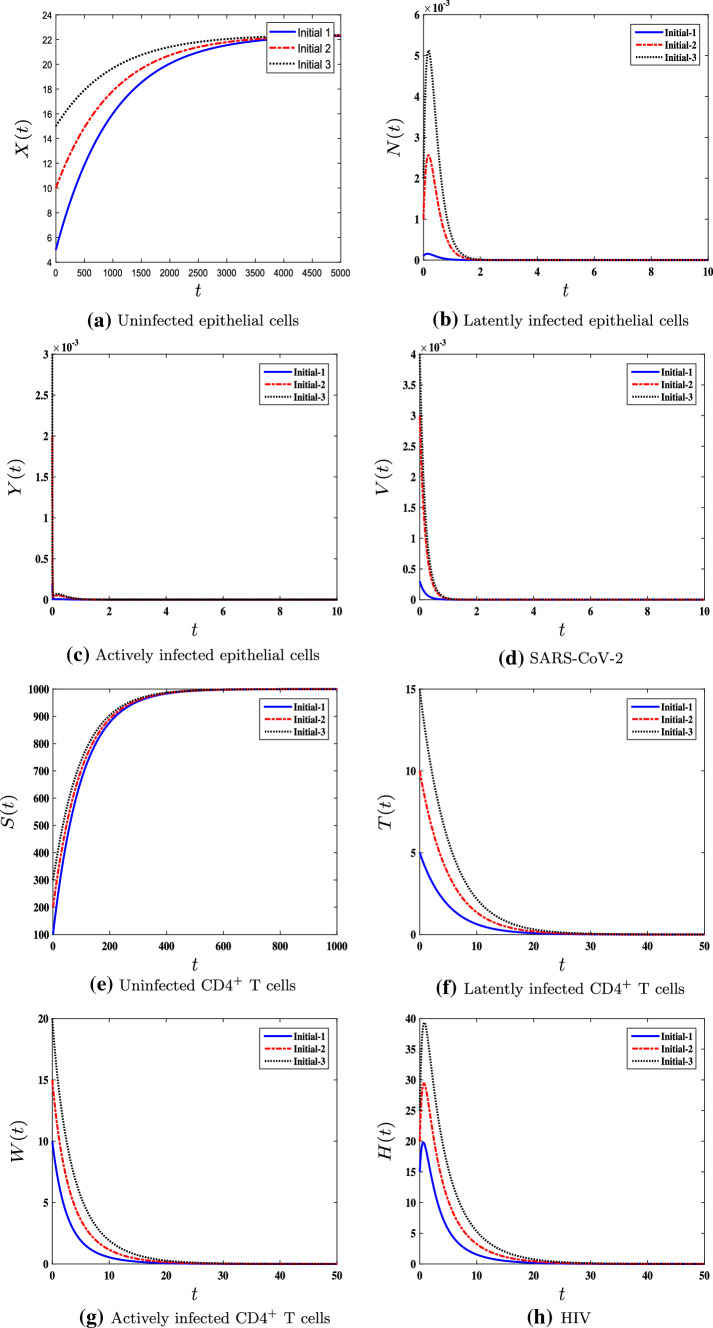
• (i)We take $\eta =0.9$, $\mu =1$, $d_4=5.36$, and $\theta =0.0001$. The thresholds in this case are given by $R_1=0.4864<1$ and $R_2=9.03\times {10}^{-4}<1$. In harmony with Theorem 1, the steady state ${\mathrm{\Delta }}_0=(22.41,0,0,0,1000,0,0,0)$ is G.A.S (see Fig. 1). This is an optimal situation when the person does not have neither SARS-CoV-2 infection nor HIV infection.
• (ii)We choose $\eta =0.55$, $\mu =1$, $d_4=5.36$, and $\theta =0.0016$. This provides us with $R_1=7.7818>1$ and $R_4=0.0043<1$. According to Theorem 2, the steady state ${\mathrm{\Delta }}_H=(22.41,0,0,0,128.505,11.88,16.95,42.39)$ is G.A.S (see Fig. 2). This point represents the case when a person has HIV infection with low CD$4^{+}$ T cell counts, while SARS-CoV-2 infection is not detected.
• (iii)We select $\eta =2.9$, $\mu =0.02$, $d_4=0.03$, and $\theta =0.0001$. This gives $R_2=25.8471>1$ and $R_3=0.4916<1$. In this case, the solutions globally converge to the steady state ${\mathrm{\Delta }}_V=(0.876,0.0053,0.0011,0.0085,1010.71,0,0,0)$. This result agrees with Theorem 3 and is displayed in Fig. 3. This case represents a person with SARS-CoV-2 infection, but he does not have HIV disease.
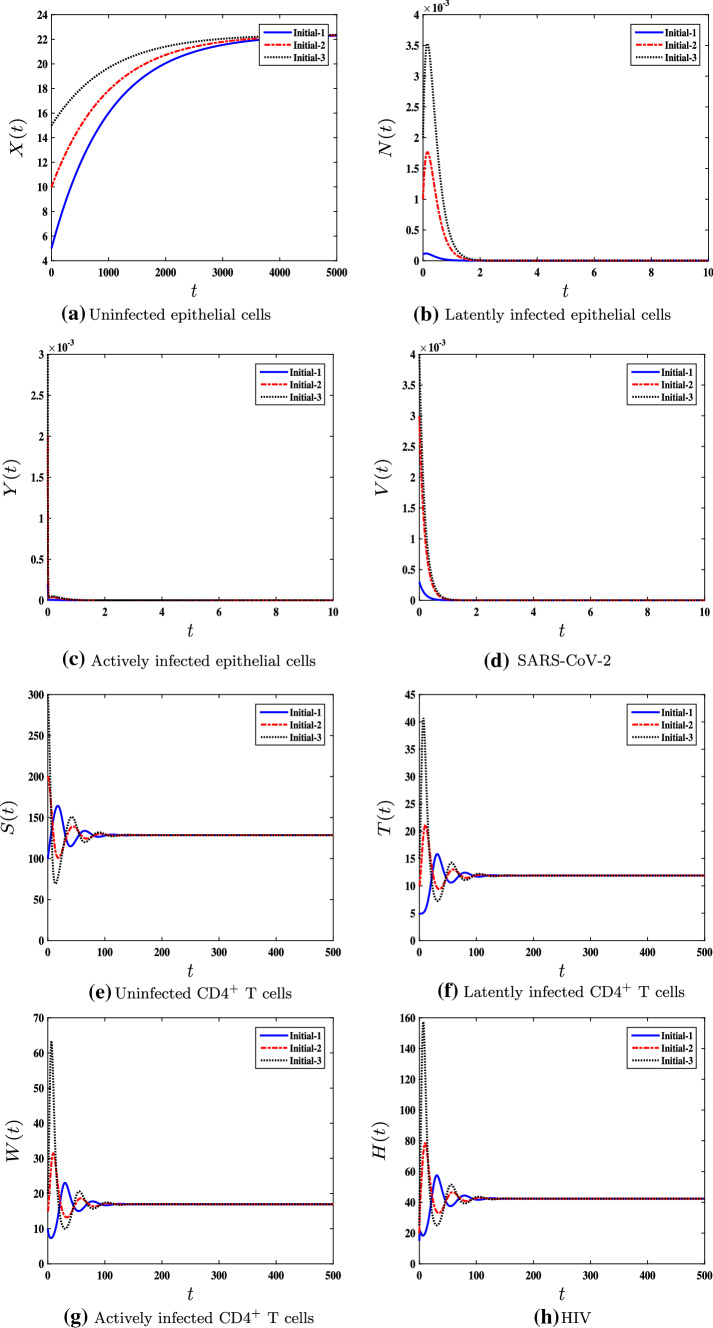
• (iv)We consider $\eta =2.9$, $\mu =0.02$, $d_4=0.1$, and $\theta =0.0016$. This implies that $R_3=7.8541>1$, $R_3<1+{\displaystyle \frac{a\eta \theta \lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)(a\eta d_5+d_1{d}_{4}u)}}=8.7707$, and $R_4=58.1828>1$. In harmony with Theorem 4, the steady state ${\mathrm{\Delta }}_{\mathit{VH}}=(0.385,0.0054,0.0082,0.02,128.505,12.028,17.16,42.89)$ is G.A.S (see Fig. 4). In this situation, SARS-CoV-2/HIV coinfection occurs, where an HIV patient gets infected with COVID-19. CD$4^{+}$ T cells are stimulated to eliminate SARS-CoV-2 infection from the body. Nevertheless, if the patient has low CD$4^{+}$ T cell counts, the clearance of SARS-CoV-2 may not be achieved. This can lead to severe infection and death.
  For further verification of the asymptotic stability of ${\mathrm{\Delta }}_{\mathit{VH}}$, we calculate the Jacobian matrix of model (1) at the steady state $\mathrm{\Delta }=(X,N,Y,V,S,T,W,H)$ as

  $$\begin{array}{c}\hfill \mathcal{J}(\mathrm{\Delta })=\left[\begin{array}{cccccccc}-d_1-\eta V& 0& 0& -\eta X& 0& 0& 0& 0\\ \eta V& -k-d_2& 0& \eta X& 0& 0& 0& 0\\ 0& k& -d_3-\mu S& 0& -\mu Y& 0& 0& 0\\ 0& 0& a& -d_4& 0& 0& 0& 0\\ 0& 0& uS& 0& uY-d_5-\theta H& 0& 0& -\theta S\\ 0& 0& 0& 0& (1-b)\theta H& -d_6-\alpha & 0& (1-b)\theta S\\ 0& 0& 0& 0& b\theta H& \alpha & -d_7& b\theta S\\ 0& 0& 0& 0& 0& 0& \lambda & -d_8\end{array}\right].\end{array}$$

  Next, we calculate the eigenvalues ${\mathcal{L}}_j$ ($j=1,2,\dots ,8$) of the Jacobian matrix at all possible steady states. For asymptotic stability of ${\mathrm{\Delta }}_{\mathit{VH}}$, we need to prove that

  $$\begin{array}{c}\hfill \text{Re}({\mathcal{L}}_j)<0,\text{for all}j=1,2,\dots ,8,\end{array}$$

  and all other steady states have eigenvalues with positive real parts. The computations are organized in Table 4.

Fig. 1.

The numerical simulations of model (1) for $\eta =0.9$, $\mu =1$, $d_4=5.36$, and $\theta =0.0001$ with three different sets of initial conditions. The uninfected steady state ${\mathrm{\Delta }}_0=(22.41,0,0,0,1000,0,0,0)$ is G.A.S

Fig. 2.

The numerical simulations of model (1) for $\eta =0.55$, $\mu =1$, $d_4=5.36$, and $\theta =0.0016$ with three different sets of initial conditions. The single HIV–infection steady state ${\mathrm{\Delta }}_H=(22.41,0,0,0,128.505,11.88,16.95,42.39)$ is G.A.S

Fig. 3.

The numerical simulations of model (1) for $\eta =2.9$, $\mu =0.02$, $d_4=0.03$, and $\theta =0.0001$ with three different sets of initial conditions. The single SARS-CoV-2–infection steady state ${\mathrm{\Delta }}_V=(0.876,0.0053,0.0011,0.0085,1010.71,0,0,0)$ is G.A.S

Fig. 4.

The numerical simulations of model (1) for $\eta =2.9$, $\mu =0.02$, $\delta =0.1$, and $\theta =0.0016$ with three different sets of initial conditions. The SARS-CoV-2/HIV coinfection steady state ${\mathrm{\Delta }}_{\mathit{VH}}=(0.385,0.0054,0.0082,0.02,128.505,12.028,17.16,42.89)$ is G.A.S

Table 4.

Local stability of the steady state ${\mathrm{\Delta }}_{\mathit{VH}}$

Case	The steady sates	Re(${\mathcal{L}}_j$), $j=1,2,\dots 8$	Stability
(iv)	${\mathrm{\Delta }}_0=(22.41,0,0,0,1000,0,0,0)$	(− 19.907, − 4.94688, − 3.70454, 1.29544, 0.562873, − 0.310899, − 0.01, − 0.001)	Unstable
	${\mathrm{\Delta }}_H=(22.41,0,0,0,128.505,11.88,16.95,42.39)$	(− 4.46776, − 4.46776, − 2.37868, 2.07443 , − 0.340978, − 0.0390795, − 0.0390795, − 0.001)	Unstable
	${\mathrm{\Delta }}_V=(2.918,0.005,00096,0.0023,1009.69,0,0,0)$	(− 20.2784, − 4.20655, − 3.71538, 1.30623, − 0.310848, − 0.00380659, − 0.00380659, − 0.00987671)	Unstable
	${\mathrm{\Delta }}_{\mathit{VH}}=(0.385,0.0054,0.0082,0.02,128.505,12.03,17.16,42.89)$	(− 3.81897, − 3.04464, − 2.3788, − 0.340867, − 0.0395697, − 0.0395697, − 0.0273365, − 0.0273365)	Stable

The effect of the CD$4^{+}$ T cells killing rate

To check the impact of changing the value of $\mu$ on the stability of model (1), we take the same values used in case (iv) ($\eta =2.9$, $d_4=0.1$, and $\theta =0.0016$) with increasing the value of $\mu$ from 0.02 to 1.5. It follows that $R_1=7.7818>1$ and $R_4=0.8085<1$. Thus, the steady state ${\mathrm{\Delta }}_H=(22.41,0,0,0,128.505,11.88,16.95,42.39)$ is G.A.S. Mathematically, increasing the value of $\mu$ switches the value of $R_4$ from $R_4=58.183>1$ to $R_4=0.8085<1$. This means that there is a bifurcation at $R_4=1$. Accordingly, the steady state ${\mathrm{\Delta }}_{\mathit{VH}}$ becomes unstable and ${\mathrm{\Delta }}_H$ becomes G.A.S.

In addition, to characterize the effect of increasing or decreasing the value of $\mu$ on the number of actively infected epithelial cells and SARS-CoV-2 particles, we examine case (iv) with different values of $\mu$ (Fig. 5). We find out that decreasing the value of $\mu$ increases the concentration of actively infected epithelial cells and, accordingly, the concentration of SARS-CoV-2 particles is increased. On the other hand, increasing the value of $\mu$ decreases SARS-CoV-2 viral load.

Fig. 5.

The effect of decreasing $\mu$ on the concentrations of SARS-CoV-2 particles V(t). The parameters considered are $\eta =2.9$, $d_4=0.1$, and $\theta =0.0016$ with initial conditions $(X(0),N(0),Y(0),V(0),S(0),T(0),W(0),H(0))=\left(5,,,0.0001,,,0.0002,,,0.0003,,,100,,,5,,,10,,,15\right)$

Biologically, these results imply that high killing rate $\mu$ of CD$4^{+}$ T cells is needed to remove SARS-CoV-2 from the body of HIV patient. Conversely, low killing rates can cause severe SARS-CoV-2 infection for HIV patient.

The effect of latency

To see the effect of the eclipse phase on the production of SARS-CoV-2 particles, we take the same values considered in case (iv) with increasing the value of $d_2$. We observe from Fig. 6a that increasing the death rate of latently infected epithelial cells decreases the concentration of SARS-CoV-2 particles in coinfected patients. Similarly, increasing the death rate ($d_6$) of latently infected CD$4^{+}$ T cells decreases the density of HIV particles (See Fig. 6b). Thus, the death rates during the latency periods can have a strong impact on the viral loads.

Fig. 6.

The effect of increasing the death rates during the latency periods on SARS-CoV-2 and HIV particles. The parameters considered are $\eta =2.9$, $\mu =0.02$, and $\theta =0.0016$ with initial conditions $(X(0),N(0),Y(0),V(0),S(0),T(0),W(0),H(0))=\left(5,,,0.0001,,,0.0002,,,0.0003,,\right)\left(100,,,5,,,10,,,15\right)$

Discussion

In this paper, we developed a within-host SARS-CoV-2/HIV coinfection model that investigates the interactions between eight components: uninfected epithelial cells, latently infected epithelial cells, productively infected epithelial cells, SARS-CoV-2 particles, uninfected CD$4^{+}$ T cells, latently infected CD$4^{+}$ T cells, productively infected CD$4^{+}$ T cells, and HIV particles. The model has four steady states as the following:

1. The uninfected steady state ${\mathrm{\Delta }}_0$ always exists. It is G.A.S when $R_1\le 1$ and $R_2\le 1$. This represents the healthy state when the person does not suffer from neither SARS-CoV-2 infection nor HIV infection.

2. The HIV infection steady state ${\mathrm{\Delta }}_H$ is defined if $R_1>1$, and it is G.A.S if $R_4\le 1$. This represents the case of a patient carrying only HIV infection.

3. The SARS-CoV-2–infection steady state ${\mathrm{\Delta }}_V$ is defined if $R_2>1$, and it is G.A.S if $R_3\le 1$. This represents the case of a patient carrying only SARS-CoV-2 infection.

4. The SARS-CoV-2/HIV coinfection steady state ${\mathrm{\Delta }}_{\mathit{VH}}$ is defined and G.A.S if $R_4>1$ and $1<R_3\le 1+{\displaystyle \frac{a\eta \theta \lambda \xi \left(\alpha +d_{6}b\right)}{d_7{d}_8\left(d_6+\alpha \right)(a\eta d_5+d_1{d}_{4}u)}}$. This case simulates the occurrence of SARS-CoV-2 infection in HIV patients.

The numerical results are totally compatible with the theoretical results. We found that decreasing the killing rate ($\mu$) of CD$4^{+}$ T cells increases the concentrations of both productively infected epithelial cells and SARS-CoV-2 particles. This implies that low CD$4^{+}$ T cell counts can increase the severity of SARS-CoV-2 infection in HIV patients. This result comes in agreement with many results that discussed that HIV patients with low CD$4^{+}$ T cell counts or who do not receive ART are at higher risk of death when they get infected by SARS-CoV-2. In addition, we observed that increasing the death rate ($d_2$) of infected epithelial cells during the latency period decreases SARS-CoV-2 viral load in the body. Increasing $d_2$ means that more cells will die in the eclipse phase before converting into productively infected cells. This can have a positive effect on reducing the severity of SARS-CoV-2 infection in HIV patients. Comparing with previous studies, the model considered in this work is the first model that takes into consideration the coinfection of HIV with SAR-CoV-2. The results obtained in this paper can be examined and used to (i) understand SARS-CoV-2/HIV coinfection, (ii) estimate the values of the parameters that are needed to clear SARS-CoV-infection from the body of HIV patient, (iii) test the effect of increasing the killing rate ($\mu$) on SARS-CoV-2 viral load, and (iv) examine the effect of death rates during the latency periods on the concentrations of viral particles. The main limitation of this work is that we did not use real data due to its unavailability. Therefore, these results can be examined when more data become available.

The model studied in this paper can be improved by considering the effect of time delays that are associated with many biological processes. Furthermore, adding the effect of treatments may lead to the important results that can help to find treatments for this group of patients. In addition, the coinfection dynamics of SARS-CoV-2 and HIV can be studied within a multiscale approach [41, 42] which can provide a deeper understanding and help develop vaccines and antiviral therapies. Finally, the results can be developed by using real data to find an accurate estimation of the parameters of model (1).

Declarations

Conflict of interest

The authors declare that they have no conflict of interest.