Differentiable Biology: Using Deep Learning for Biophysics-Based and Data-Driven Modeling of Molecular Mechanisms

Abstract

Deep learning using neural networks relies on a class of machine learnable models constructed using “differentiable programs.” These programs can combine mathematical equations specific to a particular domain of natural science with general-purpose machine-learnable components trained on experimental data. Such programs are having a growing impact on molecular and cellular biology. In this Perspective, we describe an emerging “differentiable biology” in which phenomena ranging from the small and specific (e.g. one experimental assay) to the broad and complex (e.g. protein folding) can be modeled effectively and efficiently, often by exploiting knowledge about basic natural phenomena to overcome the limitations of sparse, incomplete, and noisy data. By distilling differentiable biology into a small set of conceptual primitives and illustrative vignettes, we show how it can help address long-standing challenges in integrating multi-modal data from diverse experiments across biological scales. This promises to benefit fields as diverse as biophysics and functional genomics.

Machine learning (ML) (and its applications in artificial intelligence; AI) has undergone dramatic changes over the past decade, led by rapid advances in differentiable programming. The development of better algorithms, introduction of more powerful computers, and increased data availability have allowed neural networks to transform one ML subfield after another. What began as deep learning has now evolved into a broader class of learnable models, often termed “differentiable programs” (where differentiable literally means functions with defined derivatives). Like traditional mathematical or computational models from physics and chemistry, differentiable programs can be specified in part using logic or equations particular to the problem under investigation. Unlike traditional models, which are commonly parameterized using a handful of fitted variables (often having physical meanings), differentiable programs can have millions or even billions of variables as part of their neural networks. Training involves learning these parameters. “End-to-end differentiable” programs have the important feature that they can be jointly optimized from input to output to achieve a desired behavior; in current practice they frequently comprise neural networks but they need not do so.

The emergence of differentiable programming has been driven by four interrelated developments in basic science and software engineering: better pattern recognizers, the rise of bespoke (fit-to-purpose) modelling, joint optimization, and robust automatic differentiation frameworks and programming interfaces (e.g., TensorFlow¹, PyTorch² and JAX³). In this Perspective, we discuss how ML models that incorporate biological and chemical knowledge have the potential to overcome limitations commonly encountered when modeling sparse, incomplete, and noisy experimental data. We distill the essential features of differentiable programming into conceptual primitives and use two illustrative vignettes to show how these primitives can be leveraged to solve a range of biologically significant problems. The vignettes cover the small and specific (e.g., one experimental assay) and the broad and general (e.g., protein folding). Taking stock of “differentiable biology”, we consider its implications for functional genomics and “multi-omic” biology, and how the long-standing challenges in data integration might be addressed by differentiable programming. We conclude with outstanding challenges and a description of new frontiers in ML, arguing that the full impact of end-to-end differentiable biology has yet to be realized.

Four Key Developments

Pattern Recognizers

The first and most visible development in differentiable programming is the emergence of powerful algorithms for processing (“recognizing”) sensory inputs such as images and speech. Deep neural networks are central to the success of these algorithms. Neural networks were first formulated decades ago, subjected subsequently to intensive study and then largely dismissed; their widespread adoption in the last decade represents a dramatic and important shift for the ML field⁴. Prior to the emergence of deep learning, which was made possible by faster processors and better optimization techniques, supervised ML relied heavily on convex functions, a simpler class of mathematical functions than neural networks. Convex functions have a single global minimum that is reachable by moving in the direction of descent irrespective of where the function is evaluated. The use of deep neural networks⁴ has yielded a dramatic advance in the expressivity of ML algorithms: they need no longer be convex. When combined with large amounts of data, this has made it possible to generate hierarchical representations of data and capture the gestalt of vision and sound, in some cases with super-human performance⁵.

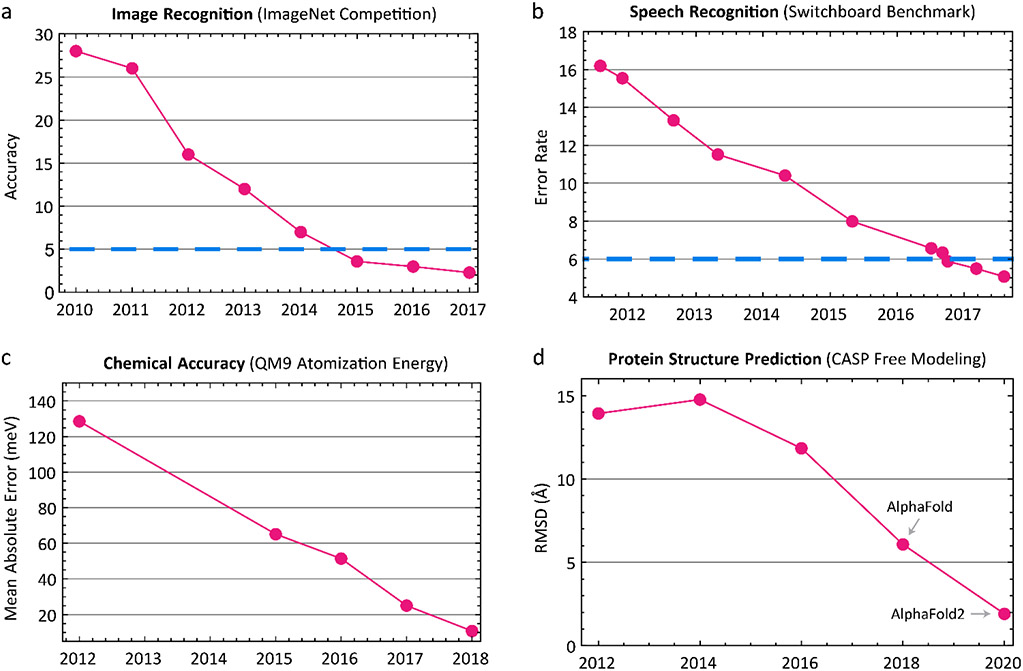
Deep learning is sometimes dismissed in a biological context as mere pattern recognition⁶ (a viewpoint challenged below) but pattern recognition has long been a holy grail of AI and is itself valuable in biomedicine⁷. Moreover, recent and rapid progress in pattern recognition is historically unprecedented: as recently as 2011 the classification error for image recognition (measured by the difference between labels such as cat, flower, etc. assigned by humans and machines using ImageNet⁸ data) was >25%; by 2016 that figure had fallen to ~3%⁸ (Figure 1). This is below the error for a single human trained to distinguish ImageNet classes and therefore represents super-human performance⁸. In speech recognition, the error rate for the Switchboard Corpus⁹, long stalled at ~30%, fell to 5% in 2017, similar to human transcribers¹⁰. These well-known examples illustrate the degree to which pattern recognition has thoroughly changed our expectation of what is possible in AI, with biomedical applications in fields as diverse as ophthalmology^11-13 and digital pathology^14,15.

Figure 1: Deep Learning Revolution.

Improvements in prediction accuracy driven by deep learning over the last decade in (a) image recognition tasks⁸, (b) speech recognition^9,10, (c) quantum chemical calculations¹⁶², and (d) protein structure prediction¹⁶³. Human baselines based on expert curators are shown as dashed blue lines.

AI subfields that tackle cognition, such as symbolic systems, planning, and optimization have also benefited from advances in pattern recognition, in many cases bringing wider attention to under-appreciated advances: with the sudden advent of robust pattern recognizers, there is an opportunity to exploit an untapped reservoir of classical AI research. For example, the AlphaGo game playing agent¹⁶ fused the classical AI approach of Monte Carlo Tree Search¹⁷ with neural networks. Similarly, robotics, which has long been resistant to machine learning, is now benefiting from greatly improved vision systems¹⁸. Once classical AI systems are given the ability to process sensory inputs, they gain the ability to perform a variety of complex real-world tasks including relational reasoning¹⁹.

Bespoke Modelling

The application of ML to scientific problems has been accompanied by the emergence of bespoke ML models designed to capture salient aspects of a specific physical or chemical process. Bespoke models contrast with general purpose ML algorithms such as support vector machines²⁰ or random forests²¹ by encoding prior knowledge about the structure of input data. Ideally, this is accomplished using general-purpose abstractions that deemphasize complex feature engineering in favor of architecture engineering. In feature engineering, transformations are made on primary inputs to extract information judged to be relevant based on past experience; such transformations often involve complex and potentially opaque data “pre-processing”. In architecture engineering the emphasis is on incorporating high-level aspects of the phenomenon being modeled in the design of the learning systems itself. This can involve fundamental concepts such as translational or rotational invariance of molecules in solution, the known chemistry of polypeptide backbones, and established relationships between data types of measurement methods.

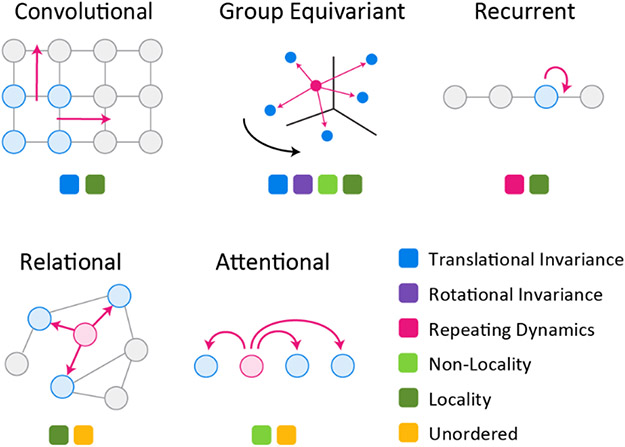
A simple example is provided by convolutional networks²² that assume translational equivariance in an image (Figure 2). Convolutional networks are effective in this setting because they reuse the same set of parameters, and hence the same pattern recognition components, across a receptive field. Bespoke models can also encode priors that facilitate the learning process, for example by including hierarchy in the organization of neural networks²³ to capture short and long-range interactions in the inputs. A model that generates image captions provides an early example²⁴ (circa 2015): visual and text-processing neural networks were paired so that one processes an image and the other a caption. During training, the joint model learned a latent representation that captured both the visual and textual aspects of inputs; the latent representation is subsequently used to generate new captions conditioned on unseen images. Bespoke models are now commonplace²⁵ and can be constructed using reusable templates and libraries of interoperable building blocks, creating a rich ecosystem for innovation.

Figure 2: Neural Network Primitives.

A powerful set of neural network building blocks makes it possible to build learnable models that encode a variety of inductive priors. Convolutional networks model regular grids such as images or sequences, inducing local structure and limited forms of spatial invariance such as indifference to shifts in images. They are generalized by group-equivariant networks that operate on arbitrary point clouds and induce local and global structure as well as more general spatial invariances including rotational and translational shifts, important in molecular applications. Recurrent networks model sequences with repeating dynamics such as time series, music, or the actions of a computational agent. Relational or graph networks reflect highly structured objects with rich interrelationships such as phylogenetic trees. Attention networks on the other hand essentially assume no underlying structure and are capable of inferring arbitrarily complex relationships, including long-range interactions that have historically been difficult to capture with conventional mathematical models. This ability has been crucial to the development of accurate methods for protein structure prediction. These primitives can be combined to yield even more complex combinations, for example group-equivariant attentional networks⁷⁴.

Joint Optimization of Differentiable Systems

By exclusively using mathematically differentiable functions as building blocks, differentiable models can be jointly optimized, from input to output, using backpropagation²². Joint optimization ensures that all model parameters are tuned simultaneously to optimize global behavior. Regardless of how complex a model becomes, the same backpropagation algorithm can be used. In contrast, earlier generations of ML algorithms typically involved many separate components, each of which needed to be optimized independently. Updating such algorithms is technically demanding and jointly optimized models are not only simpler, they are also more performant and robust. The power of end-to-end differentiable models has spurred renewed interest in first-order numerical optimization²⁶, a class of simple optimization techniques that have proven to be the most effective for deep models.²⁷ Their continued development and elucidation has led to resurgent interest in the theory of nonconvex optimization^28-30 as well as new techniques³¹ that have made training deep differentiable models relatively routine.

Automatic Differentiation Frameworks

A fourth advance in differentiable programming is the wide-spread availability of industrial-quality software tools known as automatic differentiation (autodiff) frameworks; these include TensorFlow¹,PyTorch² and JAX³ among others. Using autodiff frameworks it is possible to use a few lines of code in a high-level programming interface such as Keras³² (which runs on top of TensorFlow) to combine off-the-shelf neural network building blocks with custom mathematical transformations. Crucially, it is necessary to specify only the “forward” view of a model, i.e., the direct relationship between inputs and outputs. Autodiff frameworks automatically compute the “backward” pass, which specifies how changes in parameter values affect model input-output relationships. These are precisely the derivatives used during training. Autodiff frameworks greatly simplify the practical task of model construction, making computation of derivatives a programming detail rather than the purview of a specialized branch of computer science. Modern autodiff frameworks come preloaded with a variety of ready-to-use neural network and mathematical operations, a suite of optimization algorithms for fitting parameters to data, and continuously updated documentation. The existence of a few widely used frameworks promotes model reuse and has democratized bespoke model building, making it possible for a large community of scientists to contribute. Democratization is potential cause for concern because subtle errors can still be made. Ideally, greater transparency in model formulation, which is enhanced by the use of high-level languages and common frameworks, will make it easier to document and error-check new applications of ML.

Primitives for a Differentiable Biology

In the biological context, differentiable programming provides primitives for tackling three conceptually distinct classes of information: biological patterns, physical and phenomenological priors, and experimental and data acquisition priors. Priors constrain the space of possible models and enable use of smaller datasets. The most useful and defensible priors are those based on well-understood features of physical and chemical systems, such as the range of allowable bond angles in a polypeptide chain³³. Priors can be interspersed with pattern recognizers that learn from data mappings that are too complex or poorly understood to be modeled explicitly.

Biological Patterns

As a class, pattern recognizers are the most mature differentiable programming tools. They have been used to learn essential aspects the retinal fundus,¹¹ identify and segment cell boundaries in crowded environments such as tissues,³⁴ and predict new cell states from multiplexed immunofluorescence images³⁵. The complexity of a pattern recognizer is often determined by the structure of the inputs. Images represented by 2D grids of pixels having fixed dimensions (e.g. images collected by conventional electronic cameras) are among the simplest inputs and they exhibit shift invariance, which can be used as a prior in model training via data augmentation.³⁶ “Images” need not be restricted to visual patterns. For example, intra-protein contact maps encoding residue co-evolution have been used as inputs to convolutional neural networks (CNNs) to predict protein structure^37-40. Generalizing 2D grids to higher dimensions, e.g., by discretizing 3D space into equal-sized cubes, has yielded pattern recognizers that can operate on high molecular weight macromolecules to predict protein functions^41,42 and the affinity of protein-drug complexes^43,44. Some of the features learned by these models are human-interpretable but some are not, due to their size, complexity, or counter-intuitive nature, but neural networks are still able to learn them.

Variable-sized grids whose dimensions vary with the input data, such as one-dimensional grids comprising DNA sequences of varying length, represent another step up in complexity. For example, the patterns underpinning transcription factor binding motifs in DNA have long eluded a simple probabilistic code⁴⁵, but convolutional neural networks have modelled them with success^46,47. Trees and other types of graphs, which can represent phylogenies, interaction networks and molecules, vary not only in length but in structure and can be learned using graph convolutional networks (GCNs).⁴⁸ GCNs have been used to learn mappings from molecules to protein-binding affinities⁴⁴ and to perform in silico chemical retrosynthesis⁴⁹. In all of these cases, the key advantages of neural networks are their ability to recognize multi-way interactions occurring at both small and large scales.

While most contemporary ML applications focus on the relationship between complex inputs such as protein structure and simple outputs such as binding affinity, differentiable programming allows for richer input-output mappings. For example, we have developed an end to end differentiable “ recurrent geometric network” (RGN) that learns protein structure directly from sequence, taking a variable-length protein sequence as input and generating a variable-sized set of atomic coordinates as output³³. More recently, AlphaFold2 developed by Google’s sister company DeepMind, uses an end-to-end differentiable system to predict single domain protein structures with accuracy approaching that of experimental methods such as crystallography (Figure 1).^50,51 The ability to generate complex outputs (e.g., 3D folded proteins) from simple inputs (primary sequence) demonstrates one significant advantage of differentiable programs vis-à-vis conventional ML methods used for regression and classification. The latter are limited to narrow ranges of simple outputs types, most commonly categorical variables or real-valued scalars.

Phenomenological Priors

ML research in biology increasingly incorporates prior knowledge about structure, chemistry, and evolution into differentiable programs (Figure 3a). Prior information can range in scope and generality from enumeration of genes or proteins and their interactions⁵² to fundamental biophysics, including features of space itself.⁵³ For example, interactions within and between macromolecules are translationally and rotationally invariant and this can be formalized by generalizing CNNs from fixed grids (which have no guarantee of rotational invariance) to mathematical objects known as Lie groups⁵⁴ which capture rotational symmetry in three (or higher) dimensions. In modeling protein-protein interaction (PPI) networks, protein folding, and similarly complex biological phenomena, the incorporation of such priors makes it easier to capture distance-dependent physical interactions (e.g., rotationally-invariant electrostatic forces). Recent progress in equivariant networks on Lie groups has been swift⁵⁵, including applications in molecular sciences⁵⁶ - most prominently protein folding - but the problem and attendant approaches remain far from solved. When such approaches become broadly deployable, they may prove to be as consequential for molecular systems as convolutional networks have been for image data: the analogy here is between shift invariance and rotational symmetry (in practice there are subtleties even within shift invariance, e.g., local vs. global invariance⁵⁷).

Figure 3: Differentiable Programming Fuses Principles-based and Data-driven Modeling.

(a) Three types of primitives underlie the emerging field of differentiable biology: (i) biological pattern recognizers that perform mappings too complex to be interpretable, such as predicting the DNA binding motif of a transcription factor from its structure, (ii) phenomenological priors that encode existing biological knowledge, such as known signaling pathways, and (iii) data priors that capture the data acquisition process, for example the physical process underlying mass spectrometry. (b) In conventional modeling, principles-based and data-driven approaches are used largely independently. Differentiable programming makes it impossible to build bespoke systems that intermingle the two types of approaches in a manner that best reflects the desired modeling task.

A valuable aspect of bespoke ML models in biomedical applications is that they can incorporate detailed information on the structural and chemical properties of macromolecules. For example, due to divergent and convergent evolution, many proteins utilize similar structural features for binding other biomolecules^58-60. These features constitute the vocabulary of protein binding surfaces and, once learned, can be reused across domain families to increase predictive power. Phenomenological priors formalized mathematically force models to distill interactions across a protein family to a compact set of binding surfaces, or to prefer that evolutionarily-related proteins share binding partners. Pursuing this line of reasoning, we recently developed a model⁶¹ for predicting the ligands of peptide-binding domains (PBDs) involved in signal transduction (e.g., Src Homology 2 and 3 domains). We incorporated the concept of shared and reused binding surfaces by sharing energy potentials across PBD families, implicitly creating an energetic lingua franca for this type of macromolecular interaction. Energy potentials were learned, not prescribed (only the notion of reuse was assumed) and were found to improve model accuracy, particularly in data poor domains. Incidentally, our PBD-ligand interaction model⁶¹ was fully differentiable but did not make use of neural networks. Models incorporating geometrically-aware neural networks and the concept of binding surface reuse are also showing promise^59,62. A related approach, based on the simple idea that a protein’s active site uses the same set of atoms to bind diverse small molecules resulted in substantial advances in predicting protein-ligand interactions⁶³.

When modeling biological networks, yet more specialized priors are possible. For example, joint modeling of transcriptional, proteomic, and phospho-proteomic time series data can be enhanced by imposing time separation between phospho-signaling and transcriptional regulation, as the former often occurs on a more rapid time scale than the latter, or by encouraging signaling cascades to terminate on a transcriptional change (which is implicitly another form of time-scale separation). Such high-level knowledge can be combined with molecular data on specific signaling pathways (e.g., the structure of the MAPK kinase cascade) or transcription factor binding motifs (Figure 3b). In such a hypothetical model, the matrix of all possible protein-protein and protein-DNA interactions would be inferred, with some interacting pairs already pre-determined (e.g., from the literature or focused experimentation), and some merely encouraged or discouraged based on knowledge of the archetypical interactions they represent.

Data Priors

Most modeling in biology involves analysis of incomplete, noisy, and heterogeneous data. Incorporating priors that account for the data generation process are needed to minimize the effects of error and fuse disparate data types. Data normalization is another process that is ad hoc to a problematic degree. Data process invariably include adjustable parameters that are fit heuristically, typically one step at a time. Differentiable programming offers a fundamentally different approach: adjustable parameters can be optimized within a broader problem framework that involves evaluation of a hypothesis or prediction of outcome (e.g., cell state). Parameters of both the experimental and computational aspects of the model can then be jointly fit to maximize predictive power. Few examples of such joint learning have appeared, but pre-processing steps for microscopy-based imaging (e.g., image segmentation⁶⁴ and classification⁶⁵) already incorporate learning elements. This is not a “glamorous” application of ML but it will prove to be one of the more consequential areas for differentiable programming if it can make y the connection between data and models more accurate, robust and informative.

Random error is present in all real-world data and most molecular measurements are also subject to poorly understood systematic error. Physics-based error modeling is common in structural biology and high-resolution optical microscopy, domains in which enough is known about the measurement process and the range of expected physical phenomena that many types of uncertainty can be quantified and modelled. While this approach is in principle transferable to other biological assays,^66,67 sophisticated error models are relatively rare in biomedical research, usually because the underlying physical processes are not sufficiently understood. In this case, simple parametrizations of the error may be possible, e.g., when normalizing high-throughput RNA-seq measurements. However, the approach can be extended to describing the physical processes underpinning experimental assays. This is important when the biophysical quantity being sought, such as a disassociation constant, derives from an indirect measurement. For example, experimental characterization of protein-protein affinity involves a variety of analytical methods that measure different physical parameters (e.g., on or off rates, equilibrium binding, heat emitted or required for binding, inhibition of activity, competition between substrates, etc.) Both simple and complex equations exist to describe the relationship between experimental observables and underlying biophysical parameters and these equations can be incorporated into differentiable programs. Backpropagating through these equations during optimization makes it possible to estimate unknown parameters in a robust manner, because the optimization is jointly accounting for all aspects of the model. Even when simple analytical formulas are unavailable, recent progress in incorporating ordinary differential equation solvers within neural networks⁶⁸ suggests the feasibility of encoding elementary mass action rate laws as differential equations within differentiable programs⁶⁹.

Illustrative Vignettes

To illustrate the concepts described above we consider two situations in which the building blocks of end-to-end differentiable biology are combined to address complex and significant research questions. The first vignette illustrates how prior biological knowledge can be reflected in the architecture of a bespoke ML model; the second focuses on data homogenization in the context of protein-protein interactions.

Protein Structure Prediction

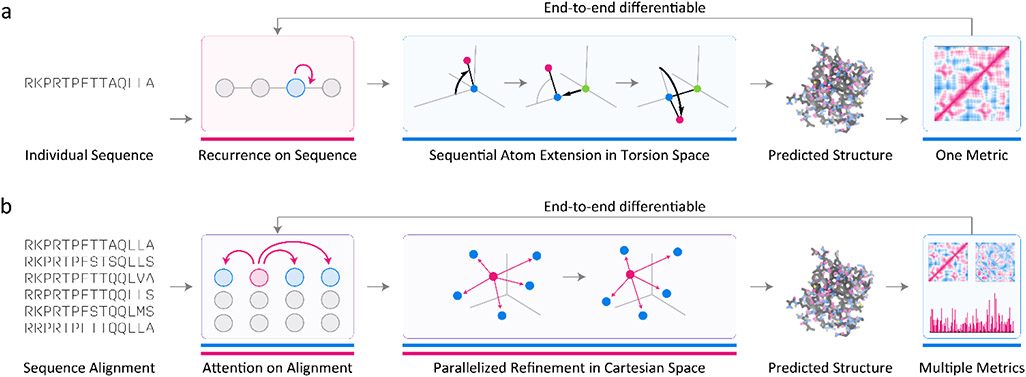
The goal of protein structure prediction is to construct models that maps protein sequence (a variable-length string of discrete symbols) to the tertiary structure of the protein (variable-length sequence of 3D coordinates). Recent ML-based approaches make use of both phenomenological priors and pattern recognizers. In principle, off-the-shelf pattern recognizers such as recurrent neural networks can perform this mapping but in practice, achieving high performance has required leveraging features of protein geometry learned from 70 years of solving and analyzing protein structures (Figure 4a).^33,51,70 For example, the knowledge that protein backbones are covalently bonded polypeptide chains with nearly fixed bond lengths and angles but sequence-dependent torsion angles⁷¹.

Figure 4: Protein Structure Prediction Vignette.

(a) A minimal end-to-end differentiable system³³ for protein structure prediction accepts a variable-length protein sequence and processes it recurrently, implicitly learning sequence-torsion patterns (pink underlines indicate purely data-driven processes that do not rely on prior knowledge). These learned patterns are then converted sequentially into 3D coordinates using known (fixed) equations for converting sequences of torsion angles to Cartesian coordinates (blue underlines indicate purely knowledge-based processes that do not utilize learning.) After the final structure is produced, a rotationally- and translationally-invariant error metric computes its deviation from an experimental structure, feeding this information back into the learning loop. (b) A more advanced system for protein structure prediction, based on reported features of AlphaFold2, would accept multiple sequence alignments of protein sequences, using attention to reason over individual sequences and residues in the alignment. Based on learned sequence-structure patterns, an initial set of 3D coordinates are predicted then refined using attention mechanisms that operate directly on the 3D structure and that are equivariant to both translations and rotations. The predicted structure is then assessed using multiple error metrics which are fed back into the learning loop.

There exists a one-to-one mapping between torsion angles and 3D coordinates using known (differentiable) mathematical transformations⁷². To predict a 3D structure, it is sufficient to predict torsion angles from the amino acid sequence and optimize model parameters to maximize agreement between predicted and known angles. Fixing bond lengths and angles is a seemingly simple addition to an ML model but it has an important effect on learning efficiency and accuracy and it also helps ensure that local protein geometry is almost always correct.

Unfortunately, a purely local approach of this type—trained and judged exclusively by the accuracy of predicted torsion angles—performs poorly because minor local errors accumulate to generate large errors at the level of a complete protein. A better approach involves conversion of local torsion angles to 3D protein coordinates as part of the modelling process itself using parameters that maximize agreement between predicted and known coordinates from the Protein Data Bank. Here too we are faced with a choice. The simplest loss function penalizes deviations between predicted and known coordinates, e.g., by averaging the sum of their differences. However, this is not translationally or rotationally invariant. A loss function that is defined in terms of distances, for example one that averages the sum of differences of inter-atom distances between predicted and known structures, circumvents this problem.

Designing a custom loss function also permits more sophisticated treatments of protein structure data, which frequently suffers from missing (disordered) side-chain atoms and stretches of sequence, in large part because unstructured domains are integral to protein function. Eliminating such proteins from consideration reduces the amount of training data by up to 50% and may also bias it. A custom loss function can ignore unresolved atoms or residues, penalizing only well-resolved parts of structures, making available for training all but a dozen of the ~100,000 unique structures in the Protein Data Bank⁷³ (Figure 4a).³³ The approach can be adapted to predict structures from individual protein sequences, without using any explicit co-evolutionary information, a valuable capability for protein design.⁵³

More generally, the use of chemical and geometric that has historically been a key advantage of physics-based modeling is now available in a data-driven, learnable setting. This was leveraged in AlphaFold2⁵¹ which uses specialized forms of (Transformer-based) attention^74,75 to reason over multiple protein sequence alignments, thereby implicitly learning the idea of co-evolution and perhaps also phylogeny.⁷⁶ Transformers have the ability to learn from local and remote features, a powerful capability in structure prediction in which residues distant in the primary sequence interact directly in the folded protein to stabilize it. AlphaFold2 also refines protein structures in 3D space in a rotationally and translationally-invariant matter, leveraging recent efforts in differentiable programming to add features of physical space as constraints (Figure 4b). This has led to the speculation that attention and symmetry are essential features of AlphaFold2, explaining its remarkable performance.⁵⁰ We anticipate that it will be possible to add other aspects of protein chemistry in future years, further increasing the performance of ML algorithms while also making them more interpretable.

Homogenizing Protein-Protein Interaction Data

We illustrate the use of differentiable programs for data fusion with a model that learns protein-protein interaction (PPI) affinities from diverse types of experimental data collected using different methods at different times (Figure 5). The sheer diversity of PPIs, particularly those involving peptide-binding domains such PDZ domains⁷⁷ and their peptidic ligands, makes it highly unlikely that more than a small fraction of affinities can all be ascertained experimentally. Instead we must work from distinct types of information (we discuss four below), each incomplete and involving a different measurement method. “Quantitative binding data” involve direct measurement using quantitative biophysical methods such as surface plasmon resonance (SPR), isothermal titration calorimetry (ITC), or peptide arrays. These are the most quantitative but limited types of data. A second source of data are acquired from cell extracts using affinity purification mass spectrometry^78,79 (pull-down assays) or in vivo using yeast two-hybrid assays⁸⁰ (“high throughput binding data”). These data cover an increasing proportion of the proteome but are neither direct (two proteins that pull down together can both bind a third protein) nor particularly quantitative. A third type of data involves functional interactions inferred from genetic or over-expression studies⁸¹; these data are numerous but the least direct. A fourth type of data comprises high-resolution co-complex structures of individual PPIs to use for training or validation of biophysical hypotheses inferred by ML.

Figure 5: Protein-Protein Interaction Vignette.

An integrated system for data homogenization and prediction of protein-protein binding affinity is illustrated. The system accepts sequences of two proteins (top) that are fed to a learned energy model to quantitatively predict their disassociation rate. To train the model, multiple data types with varying degrees of precision, directness, and physical characterization are used (bottom). Depending on the data type, a different data homogenizer (D.H.) is used to bring all data modalities into congruence. For quantitative data, conventional double-sided loss functions are used to train the model whenever its predictions deviate from the ground truth. For binary data, one-sided and potentially learnable loss functions are used (see main text) to only penalize predictions that are clearly in conflict with the ground truth. The entire model, including the parameters of the energy model and the data homogenizers, is trained jointly using an inner loop for the energy model and an outer loop for the data homogenizers to ensure correct training behavior. A key assumption of the model is that the number of distinct experimental conditions and assays is substantially smaller than the number of distinct data points (right). Otherwise, the model is non-identifiable. Throughout the illustration green indicates raw data, blue indicates terms coming from principles-based modeling, and pink indicates learnable quantities.

Our goal is to use the entirety of available data to create a model that predicts equilibrium association constants (K_a) of as many PPIs as possible using a differentiable model with two components: (i) an energy function that maps inputs (pairs of protein sequences) to predicted K_a and (ii) a set of data homogenizers that map raw experimental data to a form that can be compared to predicted K_a values; the latter is relevant to the current discussion on data fusion. We start with a key assumption: namely that the number of distinct experimental conditions or assay types is much smaller than the number of individual measurements and that we know which assay gave rise to each data point. We begin by homogenizing quantitative binding data from methods for which the same set of equations maps a measured value to K_a; we allow for variation in scaling and other parameters by permitting the mapping equations to have different and unknown parameter values. The entire model is then jointly optimized so that parameters in the data homogenizers maximize the performance of the energy function (used to predict PPI affinities). A more complex version of this scenario, in which experiments are different but still describable by known equations (e.g., ITC vs. SPR) are handled with assay-specific transformation equations.

Homogenization is more difficult when the relationship between biophysical parameters and measured features are not describable in equations known a priori (e.g., if it is unknown whether binding data involve competition between substrates). If we assume that at least one member of a family of equations can map raw values to reported affinities, the homogenizer can be constructed to draw from the family of equations as needed, for example by formalizing the mapping as a convex mixture of equations whose weights are penalized using a sparsemax⁸² penalty. Alternatively, a general purpose map such as a Gaussian process⁸³ can be used with range and monotonicity constraints that reflect universal aspects of protein-protein binding biophysics without assuming a specific functional form for the conversion of measured values to binding constants.

In the foregoing examples, the model can be optimized by penalizing deviation between predicted and data-derived K_a values on a continuous landscape of parameter values because the data-derived quantities have precise values. This is not true for binary interactions obtained from high-throughput binding data. These data typically involve a call of binding or not binding based on a statistical test. It is reasonable to assume that positive PPIs have a K_a higher than some presumed but unknown threshold, but the absence of interaction may or may not be interpretable in biophysical terms (it might reflect either a true absence of binding or a technical error in the measurement). Direct comparison between predicted K_a values and binary data is therefore not possible, but binary data can be used by estimating detection thresholds. To accomplish this we define a loss function that penalizes predictions in which the K_a is below the positive threshold for positive PPIs and when applicable, above the negative threshold for negative PPIs; in other cases, no penalty is imposed. This results in a one-sided loss function for binary (high-throughput) data and a two-sided loss for quantitative data. If the detection thresholds are unknown but can be assumed to be fixed within any given assay or experimental condition, they can be treated as parameters and fit jointly with the rest of the model.

The last class of data to consider involves indirect interactions, which in extant PPI databases covers a large variety of possible assays including epistatic genetic interactions, patterns of gene or protein co-expression across tissue or cell types, and evolutionary conservation. While a positive score does not demonstrate physical interaction between proteins, it is positively correlated with it. We formulate this transformation process as a binary assessment of interaction with a single unknown positive threshold. Predicting low affinities for indirect PPIs is not penalized, but predicting high affinities is encouraged. The (learned) detection threshold depends on the strength of the statistical correlation and is therefore correct only in expectation, not for individual measurements. If the correlation is high however, the model may be able to extract meaningful information. On the other hand, if the correlation is low, the learned threshold will get set to a very high number, in which case no information is extracted and the model is unaffected.

A key feature of the approaches described above is that parameters of the data homogenizer are learned jointly with those of the energy function. This runs the danger of unwanted interaction between the parameters used to homogenize data and those being learned by the energy function, leading to degenerate solutions in which performance is misleadingly high simply because all homogenization parameters are set to zero. To avoid such problems, constraints must be imposed on the data homogenizer: parameters must be non-zero and fall within meaningful ranges based on prior knowledge (for example single-domain PPI affinities will fall in the nanomolar to micromolar range). More generally, a hierarchical approach to learning the two sets of parameters (sometimes called “meta learning”) is usually the most robust. In this case, an inner backpropagation loop fits parameters of the energy potential to a training set while an outer backpropagation loop fits parameters of the data homogenizers to a validation set, and the entirety of the process is assessed through a second validation set. Such metaparameter fitting has been successfully used in other applications^84,85. Under these circumstances two validation sets are needed to avoid overfitting. As is true in all ML applications, careful selection of training, test, and validation datasets is important.

Differentiable Programming as a Framework for Functional Genomics

The last decade has seen a dramatic increase large datasets characterizing whole genomes, transcriptomes, metabolomes, and proteomes and new technologies are extending this to differences in space (e.g., spatial transcriptomics)⁸⁶ and time⁸⁷. The analysis of such functional genomic data aims to better understand cell signaling, development and disease but dramatic increases in instrumentation and data have not, in general, been matched by commensurate increases in our understanding of biological systems. This gap stems in part from the lack of analytical frameworks to integrate different data types, make use of complex and irregular prior knowledge, and extract useful insights from the resulting mixture. Differentiable programming promises to provide much needed new tools.

Integrating Multi-Omic Data

By definition, multi-omic biology involves multiple types of data, typically spanning different classes of biological entities (e.g., mRNA and protein abundance) and different ways of measuring the same entity (e.g., RNA sequencing vs. microarrays). In principle, such data provide rich and complementary views of a biological system but they are typically related in complex ways (e.g., mRNA is used to generate proteins but the levels of the two are not well correlated)⁸⁸ and involve incongruous quantities that are not directly comparable (e.g., protein expression vs. gene amplification). When tackling such data, off-the-shelf ML methods face three major obstacles that cannot be simultaneously resolved: generation of interpretable models, capture of epistatic or multi-step causal effects, and incorporation of prior knowledge. For example, the most interpretable models for identifying the molecular origins of differential drug responses in cell lines ^89,90 are linear regressions mapping multiple input features, e.g., gene expression levels to drug response. The relative weighting of input features is often used to score a gene’s importance⁹¹ but what does it mean when the weight associated with a mutation in one gene is twice as large that associated with the expression level of a second gene? Biological mechanism is necessarily obfuscated in such approaches in an attempt to achieve data fusion. Furthermore, linear models do not capture epistasis in the input space, such as the combined effects of having a mutant allele and a change in expression of the same gene. Off-the-shelf nonlinear models, such as deep neural networks, make a different tradeoff. By virtue of their nonlinearity, they can capture complex epistatic effects but they are less interpretable: it is difficult to know what a weighted mixture of gene expression and allelic variants means in a mechanistic sense, and even less so when this mixture has been non-linearly transformed. Finally, in both linear and nonlinear models, the use of prior knowledge is largely restricted to feature engineering (or feature selection), for example using gene set enrichment analysis (GSEA), in which genes previously observed to co-vary are used to reduce the dimensionality of a dataset involving many genes or proteins into a smaller set of grouped features.⁹¹ Unfortunately, this type of feature engineering cannot capture the richness and nuance of accumulated biological knowledge and it is itself often hard to understand.

One way to combine different data types while incorporating prior knowledge, and – ideally – revealing causality is to use mechanistic models such as systems of ordinary differential equations (ODEs) and related formalisms grounded in chemical reaction theory. A key advantage of these models is that they are both interpretable and executable.⁹² However, while conventional ML-based approaches are in a sense too flexible, since they allow ad hoc integration of disparate quantities, ODE-type models suffer from the opposite problem of being time consuming to create and have difficulty incorporating diverse types of data without careful pre-processing into a common set of units (e.g., molecules per cell). We propose that differentiable programming serve as a bridge between the ML and ODE paradigms. Differentiable programs have the ability to incorporate mechanistic models, including ODE models based on reaction theory, with black box pattern recognizers: ODE solvers can themselves be made differentiable and optimized through within existing autodiff frameworks⁶⁸. In fact, development of new ODE-based primitives is a very active area of ML research⁹³. Pattern recognizers can also be used to tackle aspects of a problem that are too complex to be modelled mechanistically, or whose details are irrelevant to the mechanistic question under study, while maintaining a mechanistic approach to the salient aspects of a problem. Integration of ML and ODE frameworks allows for joint optimization of all aspects of the model by backpropagating through the dynamic simulation itself. For example, training an ML model to predict protein stability and binding affinity based on genetic variation would conventionally be done separately from optimization of an ODE model whose parameters are products of the former. Training of a joint model can also capture emergent properties of the system not explicitly encoded in its parameters⁶⁹.

The ability to mix and match model components based on different mathematical formalisms facilitates integration of prior knowledge in a far deeper way than traditional feature engineering, which largely involves pre-processing of input data. Differentiable programming enables knowledge incorporation at multiple levels of abstraction. At the most basic level, well established properties about biological systems can be “hard coded” into differentiable programs, for example known transcription factor binding sites in a model of transcriptional regulation. These models can be parameterized in a way such that they are partially learned, e.g., for transcription factors with unknown motifs, and partially fixed based on biological data⁹⁴. A prior might also impose time-scale separation between regulatory factors, model discrete events in time with recurrent architectures,⁹⁵ or sample rate parameters from a probability distribution based on known enzymology⁹⁶. Facilitating this, so-called probabilistic programming extensions have emerged for essentially all major autodiff frameworks^97,98, allowing probabilistic primitives to be stochastically backpropagated through during model optimization. Finally, prior knowledge can be reflected in the learning process, such as “curriculum learning” techniques in which easier to fit data points are presented early in training to learn simpler patterns before more complex data are learned compositionally.

Integrating Irregularly Shaped Data

A parallel challenge is the irregular nature (incompleteness) of most biological data. One common scenario involves joint learning from data sets that were generated independently with a focus on similar but not identical questions. In this scenario “inputs” are likely to vary with the data set, for example the subset of genes whose expression levels have been measured, as will the “outputs” —e.g., IC₅₀ or fraction of cells killed for the effects of drug perturbation.⁹⁹ One approach to combining such data is to consider only quantities and measurement methods that are common to all data sets, but this results in loss of usable data. Implicitly, a tradeoff is being made between the number of data points retained and the richness and diversity of measurements being utilized for each data point. Differentiable programming can help integrate irregularly shaped and partially overlapping data sets despite limitations in data imputation techniques¹⁰⁰ through the use of learned latent spaces. In this approach raw input features are mapped to rich internal latent spaces with the ability to extract complex multi-way interactions (i.e., epistatic effects) between raw input features.

For regularly shaped data a single latent space is typically used. With irregularly shaped data, the key concept is creation of a compositional latent space made up of subspaces shared between data sets. For example, if two data sets measure the levels of partially overlapping sets of proteins, three latent spaces can be learned; one for the shared proteins and two for the proteins unique to each data set. Predictions based on inputs present in either data set can then be based on a composite latent space formed by stitching together the shared latent space with a data set-specific one. When multiple data sets are used, with more complex overlapping patterns, correspondingly more complex arrangements of latent spaces can be constructed. In this way, information sharing is enabled at a granular level; latent representations of input features common to all data sets are learned using all data sets, maximizing data utilization, while representations of input features specific to individual data sets are only used in making predictions for these data sets, maximizing the breadth of input feature utilization. On the output side, missing data can be generally treated as described in the protein structure vignette: for any given data point, custom loss functions are constructed to ignore contributions that arise from components of the output that are unavailable, while retaining contributions that arise from available components. This approach also serves to maximize information utilization at the level of model output or prediction.

Recent and Upcoming Developments

Self-supervised Representation Learning

Automatic learning of useful representations of input data is a defining characteristic of deep learning and marks the shift from feature engineering to architecture engineering. Most representation learning is done implicitly within a supervised learning framework in which the prediction task drives pattern recognizers to identify aspects of the input most relevant for accurate prediction. This requires inputs and labelled outputs (corresponding to the prediction task), which can be difficult to obtain. Self-supervised learning is an alternative approach for learning that does not require labelled outputs, unlocking the potential of very large unlabeled data¹⁰¹. It relies on artificial learning tasks, for example the imputation of randomly masked regions in the input, which, when combined with the information bottleneck present in learnable models having limited parameters, induces models to be compressive, i.e., to identify recurrent input patterns that efficiently capture the data. We and others have used self-supervised learning to induce representations of protein sequence from very large sequence databases^102-106, and once learned, applied them to unrelated downstream tasks, including protein design¹⁰⁷ and prediction of protein structure^53,108 and function^109-111. Similarly, learning representations for sets of homologous proteins found in multiple sequence alignments¹¹² was used as an auxiliary learning task in AlphaFold2⁵¹. Beyond protein sequences, the structures of organic chemical compounds represent a massive source of unlabeled data¹¹³, and self-supervised learning approaches are now being applied in chemical applications^114-118, including protein-ligand binding.

Generators

Generative models, the most prominent of which are generative adversarial networks¹¹⁹ variational autoencoders¹²⁰, normalizing flows¹²¹, and diffusion models¹²², use neural networks to learn a generative model of data: that is, a model able to generate new data points. These approaches have garnered headlines due to the ultra-realistic quality of the images they can synthesize for use in computer-animated film and deepfakes.¹²³ Such models have also found applications in biology and chemistry, including generation of new molecules^124-126 and macromolecular sequences^127-129, and imputation of RNA-seq data¹³⁰. A key feature of generative methods is the ability to capture higher-order correlations within individual samples, for example the consistency of gender or skin color across a face, overcoming the problem of blurry samples caused by implicit averaging in maximum likelihood models. This capability can be useful for biological systems with missing or unknown elements, potentially including biological networks, for which it is desirable to generate specific instantiations of a network (e.g., physiologically relevant combinations of correlated protein concentrations) as opposed to averaged network states that do not reflect the ground truth of any individual cell or cell type.

Simulators

Simulators can be used to generate synthetic data as a substitute for real data when training ML models and can even be integrated within differentiable programs as fixed or learnable components. Simulators also find application in testing models, by direct analogy with other types of synthetic data. Examples of the first approach include realistic simulated driving environments (e.g., games) for training autonomous vehicles¹³¹, and highly accurate quantum chemistry models, such as coupled clusters and density functional theory¹³², used to generate synthetic data for training neural network-based force fields^133,134. Such models can predict molecular properties at nearly the same accuracy as the high-level theories but with orders of magnitude less computation time¹³⁵. While differences between real and synthetic data can be difficult to bridge, as no simulation can perfectly replicate reality, there have been many impressive successes, particularly in robotics¹³⁶.

Examples of the second approach include so-called inverse graphics applications in which simulated 3D worlds are visualized using a differentiable rendering engine and augmented with neural networks that learn a mapping from rendered 2D images back to the underlying 3D structures¹³⁷. In protein folding, the method of contrastive divergence¹³⁸ has been used to fold small proteins using a (non-learnable) molecular dynamics simulator coupled to a learnable forcefield¹³⁹, and more recently, differentiable and learnable Langevin dynamics simulators have been coupled to a learnable energy-based model to do the same^74,140,141. The incorporation of simulations within a learning framework enables the inference of much richer objects, including for example the trajectory of protein motion or the kinetics of molecular binding events.

Probabilistic Programs

Bayesian models are particularly useful for capturing uncertainty; they include Bayesian nonparametric¹⁴² approaches that capture models with a potentially infinite number of parameters. With the rise of deep learning, hybrid approaches combining neural networks with Bayesian modeling have proliferated¹⁴³. Moreover, the advent of autodiff frameworks with probabilistic programming capabilities such as TensorFlow Probability⁹⁷ and Pyro⁹⁸ have made it easier to build bespoke probabilistic models. Such frameworks combine the best of probabilistic programming, i.e., a concise way of constructing Bayesian models having complex interdependencies between random variables, with modern neural networks, using stochastic generalizations of automatic differentiation. Such models will likely play an important role in capturing uncertainty and causality of measurements and natural phenomena in the future.

Non-Differentiable Learning

This perspective focuses on end-to-end differentiable modelling in biology because differentiable programming has shown the greatest promise in building bespoke models of complex natural phenomena. However, just as convexity ultimately proved to be an overly limiting constraint on learnable mathematical models, it may well be that differentiability will prove to be similarly limiting, especially in applications involving discrete reasoning. Many old and new approaches to learning go beyond differentiable programming, including ones dating back to the genesis of the AI field. One of the most promising current directions is reinforcement learning¹⁴⁴, which involves learning agents that perform actions in real or simulated environments. Training of such agents often, but not always, involves discrete non-differentiable actions. Reinforcement learning, when combined with differentiable pattern recognizers, has proven effective in simulated environments such as game playing^145,146, as well as in burgeoning applications in chemistry such as organic synthesis^49,147 and RNA design¹⁴⁸. We expect that as these methods mature and migrate to real-world applications, their importance in the life sciences will continue to grow.

Obstacles and Opportunities

Several challenges remain before end-to-end differentiable programming will be broadly adopted in biomedicine. First, the steps that comprise the “art” of modeling, from formulating a problem, mathematically encoding the correct priors, building pattern recognizers, and selecting training, test and validation data do not yet permit automation. The need for scientific intuition and data wrangling remain unchanged. Second, many entities in biological systems, including molecules, networks, and dynamical reactions, are structurally richer than the data types used in most contemporary ML research, particularly in large corporations, resulting in a need for more algorithmic development of differentiable programming frameworks. Data availability is a challenge as are labelled datasets for supervised learning. However, deep learning can be as data efficient as so-called shallow approaches¹⁴⁹ and bespoke differentiable models are more, rather than less, data efficient than conventional ML models because they use prior knowledge to extract more information from data. Mathematical machinery for representing complex input modalities such as graph neural networks^150,151 also makes more data types available for learning.

The requirement that all model components be made differentiable can be difficult to reconcile with the fundamentally discrete nature of biological entities such as DNA and protein sequence, particularly in a generative context in which algorithms are tasked with designing new biological constructs. Recently, ML researchers have made major strides in inventing differentiable versions of discrete concepts including sentences¹⁵² and mathematical statements¹⁵³, computational data structures such as stacks, queues, and lists¹⁵⁴, computational processes such as sorting¹⁵⁵, recursion¹⁵⁶, and arithmetic logic units¹⁵⁷ as well as physical objects such as molecules¹⁵⁸. Further development of differentiable primitives is a general challenge in ML with major implications for natural science.

As computing demands continue to grow, in some cases exponentially¹⁵⁹ a large gap has appeared between resources available to academic and industrial labs. For academia to remain meaningfully competitive in ML, particularly with large-scale models, renewed national or multi-institutional investments in computing power and software engineering must be made, by direct analogy with the efforts that have made traditional supercomputing widely available. We believe that this is a worthwhile investment for governments and corporations because academic research remains essential in undergraduate and graduate education and is published and available for reproduction and improvement. There is no guarantee that this will also be true of industrial research.

There is legitimate concern that ML models can be difficult to understand and this has given rise to calls for “intelligible” or “interpretable” ML models and systems.¹⁶⁰. Interpretability in the context of models typically revolves around our ability to understand the relationship between inputs and outputs.¹⁶¹ A problem arises because presence of large numbers of learned parameters in differentiable programs obscures their meaning. In some clinical applications this might not be an issue, but the goal of most scientific research is not just to predict outcomes from a set of inputs but to generalize conclusions in terms of physical and chemical principles. However, the incorporation of physical principles in differentiable models not only improves performance, it also increases intelligibility.

In conclusion, differentiable programming and other forms of deep learning are growing rapidly in sophistication and scope and they promise to accelerate research in multiple areas of experimental and molecular biology – not just protein structure prediction. Bespoke differentiable models are well suited to fragmentary, confounded and noisy data. In general, they are not displacing a previous generation of mechanistic or physics-based models but instead merging with such models while also tackling a wealth of topics that have historically proven computationally intractable.