Skip to main content
PMC home page
PLOS ONE logoLink to PLOS ONE
. 2022 Jan 27;17(1):e0262291. doi: 10.1371/journal.pone.0262291

Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver disease

François Destrempes 1, Marc Gesnik 1, Boris Chayer 1, Marie-Hélène Roy-Cardinal 1, Damien Olivié 2,3, Jeanne-Marie Giard 4, Giada Sebastiani 5, Bich N Nguyen 6,7, Guy Cloutier 1,2,8,*,#, An Tang 2,3,9,*,#
Editor: Omar Sultan Al-Kadi10
PMCID: PMC8794185  PMID: 35085294

Abstract

Objective

To develop a quantitative ultrasound (QUS)- and elastography-based model to improve classification of steatosis grade, inflammation grade, and fibrosis stage in patients with chronic liver disease in comparison with shear wave elastography alone, using histopathology as the reference standard.

Methods

This ancillary study to a prospective institutional review-board approved study included 82 patients with non-alcoholic fatty liver disease, chronic hepatitis B or C virus, or autoimmune hepatitis. Elastography measurements, homodyned K-distribution parametric maps, and total attenuation coefficient slope were recorded. Random forests classification and bootstrapping were used to identify combinations of parameters that provided the highest diagnostic accuracy. Receiver operating characteristic (ROC) curves were computed.

Results

For classification of steatosis grade S0 vs. S1-3, S0-1 vs. S2-3, S0-2 vs. S3, area under the receiver operating characteristic curve (AUC) were respectively 0.60, 0.63, and 0.62 with elasticity alone, and 0.90, 0.81, and 0.78 with the best tested model combining QUS and elastography features. For classification of inflammation grade A0 vs. A1-3, A0-1 vs. A2-3, A0-2 vs. A3, AUCs were respectively 0.56, 0.62, and 0.64 with elasticity alone, and 0.75, 0.68, and 0.69 with the best model. For classification of liver fibrosis stage F0 vs. F1-4, F0-1 vs. F2-4, F0-2 vs. F3-4, F0-3 vs. F4, AUCs were respectively 0.66, 0.77, 0.72, and 0.74 with elasticity alone, and 0.72, 0.77, 0.77, and 0.75 with the best model.

Conclusion

Random forest models incorporating QUS and shear wave elastography increased the classification accuracy of liver steatosis, inflammation, and fibrosis when compared to shear wave elastography alone.

Introduction

Chronic liver disease (CLD) is one of the top ten leading causes of death in the United States [1]. Nonalcoholic fatty liver disease (NAFLD) is the most common cause of CLD, affecting up to one third of the adult Western population [2]. It has a substantial burden due to the incidence and prevalence, and its impact on longevity and quality of life [3]. NAFLD is characterized by vacuoles of fat and may lead to nonalcoholic steatohepatitis (NASH), which is characterized by inflammation. All causes of CLD may evolve to liver fibrosis, a scarring process, which may progress to cirrhosis and liver failure. Although liver biopsy is the established reference standard for classification of steatosis grade, inflammation grade, and fibrosis stage, it has several limitations including cost, sampling error, and procedure-related morbidity and mortality [4].

The noninvasiveness, wide availability, innovative technical developments, and cost-effectiveness of ultrasound constitute key advantages for management of patients with CLD. Medical ultrasound has traditionally been used to diagnose diseases based on B-mode (structures) and Doppler-mode (flow) images. More recently, elastography techniques, which assess stiffness, tissue strain or viscoelasticity, provide the highest diagnostic performance for staging of liver fibrosis [5–7]. Over the past 5 decades, quantitative ultrasound (QUS) imaging techniques have been developed to analyze constructive and destructive interferences between echoes to characterize tissue microstructure below the typical resolution of ultrasound scanners, based on spectral analysis of radiofrequency signals or statistical properties of the echo envelope [8]. In earlier clinical studies, QUS controlled attenuation [9–11], which is related to ultrasound energy loss in tissues, and backscatter coefficient [12] provided promising results for grading liver steatosis. More recently, several studies have proposed traditional machine learning [13–16] or deep learning [17–19] techniques combined with shear wave elastography to improve the staging of liver fibrosis. The homodyned-K distribution has also been proposed to model the ultrasound echo envelope in the context of liver steatosis and steatohepatitis [12, 20–22], since its parameters are related to cell density, tissue echogenicity, and tissue microstructure.

Considering the high disease prevalence, there is a need for noninvasive imaging and classification of CLD. The purpose of this study was to develop a combined QUS and elastography-based model to improve classification of steatosis grade, inflammation grade, and fibrosis stage in comparison with elastography alone, using histopathology as the reference standard. We privileged the random forests machine learning strategy to identify combination of imaging features providing the highest classification accuracy for a given training dataset [21].

Materials and methods

Study design and subjects

This is a retrospective, cross-sectional ancillary study to an imaging trial (ClinicalTrials.gov Identifier No. NCT02044523). This study was approved by the institutional review board of the two participating institutions, Centre hospitalier de l’Université de Montréal and McGill University Health Centre. All patients gave written informed consent.

The prior cross-sectional imaging trial compared diagnostic accuracy of ultrasound-based and magnetic resonance-based elastography techniques using liver biopsy as the reference standard [6]. For this ancillary study, QUS and elastography measurements were used to develop models for classification of steatosis grade, inflammation grade, and fibrosis stage.

Between October 2014 and September 2018, consecutive adult subjects were enrolled if a liver biopsy was scheduled as part of their clinical standard of care. Ninety-one subjects recruited at hepatology clinics of the two participating institutions underwent QUS. Subjects were excluded from this ancillary study if: (a) images were not acquired with the probe assigned to the study protocol (n = 2); (b) the underlying pathology did not meet eligibility criteria due to ethanol consumption (n = 2), drug-induced hepatitis (n = 1), sarcoidosis (n = 1), cholestasis (n = 1), or no biopsy was performed (n = 2). Characteristics of 82 subjects included in this study are described in Table 1. Among the 82 included subjects, the underlying pathology was CLD attributable to NAFLD (n = 6), NASH (n = 38), hepatitis B virus (n = 2), hepatitis C virus (n = 13), autoimmune hepatitis (n = 16), or mixed causes (n = 7). Consecutive eligible participants were included.

Table 1. Characteristics in 82 patients.

Characteristic Data
Sex
 Male 42 (51%)
 Female 40 (49%)
Age (y)
 Mean ± SD (range) 56 ± 12 (23–78)
BMI (kg/m2)
 Mean ± SD (range) 30.0 ± 5.8 (17–45)
 < 25 16 (20%)
 ≥ 25 and < 30 23 (28%)
 ≥ 30 and < 40 39 (47%)
 ≥ 40 4 (5%)
Racial category
 White 62 (76%)
 Black 4 (5%)
 Asian 2 (2%)
 American Indian 2 (2%)
 Hawaiian or Pacific Islander 1 (1%)
 N/A 11 (14%)
Diabetes 27 (33%)
Hypertension 32 (39%)
Laboratory tests: Mean ± SD (range)
 AST (U/L) 56 ± 55 (14–319)
 ALT (U/L) 75 ± 81 (13–473)
 GGT (U/L) 77 ± 93 (10–464)
 Platelet count (x 109/L) 201 ± 66 (87–383)
 Total bilirubin (μmol/L) 12.5 ± 5.0 (4.5–28.5)
 Prothrombin time (%) 99.3 ± 7.8 (83–120)
 Alkaline phosphatase (U/L) 76 ± 36 (32–217)
 Albumin (g/L) 41.2 ± 6.4 (31–79)
 Cholesterol (mmol/L) 4.6 ± 1.0 (2.9–7.0)
Biopsy length (mm)
 Mean ± SD (range) 20.1 ± 5.1 (10–30)
Fibrosis stage
 F0 (none) 12 (14%)
 F1 (perisinusoidal or periportal) 13 (16%)
 F2 (periportal and presence of septa) 18 (22%)
 F3 (numerous septa without cirrhosis) 13 (16%)
 F4 (cirrhosis) 26 (32%)
Inflammation activity grade
 A0 (none) 8 (10%)
 A1 (negligible) 39 (47%)
 A2 (moderate) 27 (33%)
 A3 (severe) 8 (10%)
Steatosis grade
 S0 (<5% hepatocytes involved) 29 (35%)
 S1 (5%-33% hepatocytes involved) 22 (27%)
 S2 (33%-66% hepatocytes involved) 15 (18%)
 S3 (>66% hepatocytes involved) 16 (20%)
Iron
 0 59 (72%)
 1 13 (16%)
 2 2 (2%)
 3 0 (0%)
 4 0 (0%)
 N/A 8 (10%)
Open in a new tab

Numbers in parentheses are percentages, unless otherwise specified.

SD = standard deviation, BMI = body mass index, AST = aspartate aminotransferase, ALT = alanine aminotransferase, GGT = gamma-glutamyl transpeptidase.

For each of steatosis or inflammation grade and fibrosis stage, classification tasks obtained from splitting the dataset into two classes based on the grade (4 values) or stage (5 values), viewed as ordinal variables, were assessed. Thus, we considered 3 steatosis and inflammation classification tasks, and 4 fibrosis classification tasks.

Ultrasound imaging

Ultrasound images were acquired with a clinical scanner (Acuson S2000 or S3000, Siemens Healthineers) using a convex probe (4C1). Patients were required to fast at least 4 hours prior to the examination. They were scanned in dorsal decubitus with their right arm in maximal abduction. Required standard intercostal B-mode images included: (1) the right liver lobe and right kidney, (2) right liver lobe at the level of the right portal vein, and (3) hepatic veins. A 3-second cine-loop of radiofrequency (RF) signals of the right liver lobe in a plane without major vessels was recorded for subsequent QUS post-processing.

Ultrasound shear wave elastography

Point shear wave elastography (pSWE) was performed with the same convex probe according to guidelines [23]. The median shear wave velocity (expressed in m/s) of 10 valid measurements (obtained in 20 repetitions or less) was used as a surrogate biomarker of liver stiffness. Reliability of measurements was based on the success rate and an interquartile range to the median (IQR/M) < 30% as per European Federation of Societies for Ultrasound in Medicine and Biology (EFSUMB) guidelines and Recommendations on the Clinical Use of Liver Ultrasound Elastography [23].

Preliminary post-processing

Echo envelope of RF data was computed based on Hilbert’s transform, after having compensated for time gain compensation settings. The first 30 images of uncompressed and unfiltered echo envelopes of RF signals were analyzed. A region of interest (ROI) was manually delineated in the first image of the cineloop and then propagated automatically to subsequent images. A pre-classification of pixels (pixels’ labeling) within the ROI of all frames was estimated [24], according to the statistical distribution of the echo envelope.

Quantitative ultrasound analysis

A sliding window of 78 x 12 pixels, corresponding to about 3 mm along both axial and lateral axes, was swept across the ROI by steps of 4 x 1 pixels. For each window, only pixels with same label as the central pixel were used for homodyned K-distribution (HKD) parameters’ estimation [24], so that the hypothesis of a single distribution was met locally (as opposed to a mixture of a few distributions), thus allowing for application of the XU estimation method of the HKD parameters [25]. Notice that the HK distribution was proposed as a general model for echo envelope distribution, with the advantage of a physical interpretation of its parameters [24]. These QUS maps comprised the normalized mean intensity μn (mean intensity divided by the maximal intensity within ROI) [26]; the reciprocal 1/α of the scatterer clustering parameter α, which is an indicator of density and homogeneity in fluctuations of acoustical impedance [1]; the coherent-to-diffuse signal ratio k [27] and the diffuse-to-total signal power ratio 1/(k +1) [1], both of which are QUS biomarkers of structure within scatterers’ spatial organization [24]. Notice that k represents the coherent-to-diffuse signal power ratio, not to be confused with parameter k above. For each parametric map, mean value and inter-quartile range (IQR) within the ROI were computed, and median values over the 30 frames yielded two QUS features per map [21]. Thus, 8 HKD features were produced for each acquisition: (mean and IQR features) x (4 parametric maps). Means and maxima were winsorized to avoid spurious outliers [28].

The total acoustical attenuation due to layers of fat that could be present in patients with obesity might be a confounder for HKD parameters. Therefore, the total attenuation coefficient slope (ACS) was estimated, based on spectral Gaussian fit method [8], and its median value over 30 frames was output as an QUS feature, in addition to HKD parameters. Combination of total attenuation with statistical features was shown to improve classification performance [29], and this is an alternative to estimating HKD parameters directly on the echo envelope compensated for total attenuation.

Lastly, the local ACS was estimated as a further QUS biomarker. Estimation was based on a hybrid state-of-the-art method [30]. For both total and local attenuation estimation methods, a calibrated reference phantom (model 117GU-101, CIRS, Norfolk, VA) was used to compensate for acquisition settings [8]. In total, 11 features were extracted from each acquisition of radiofrequency data.

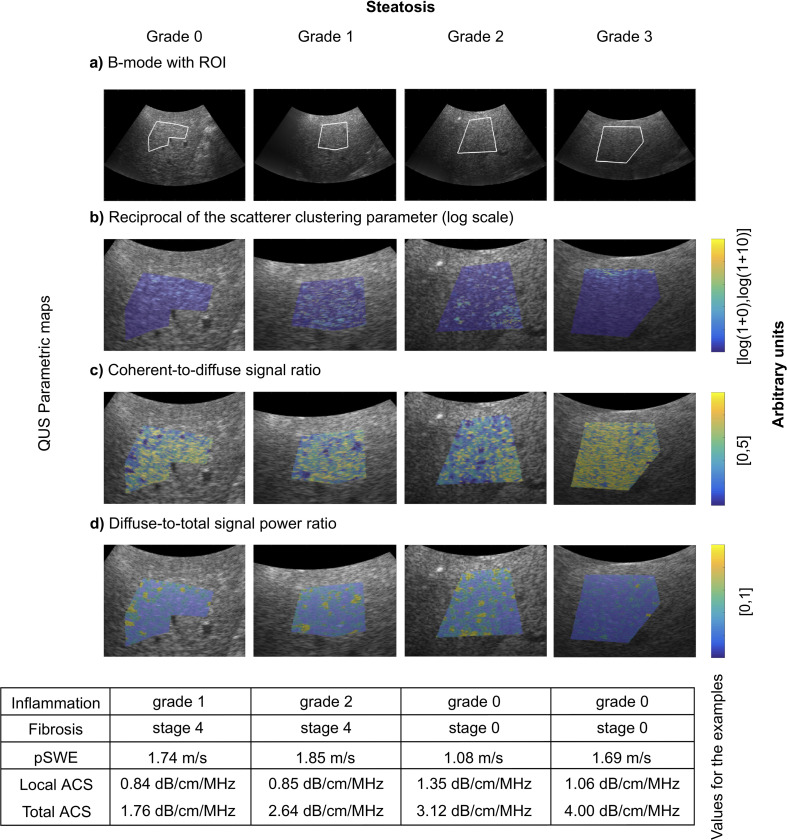
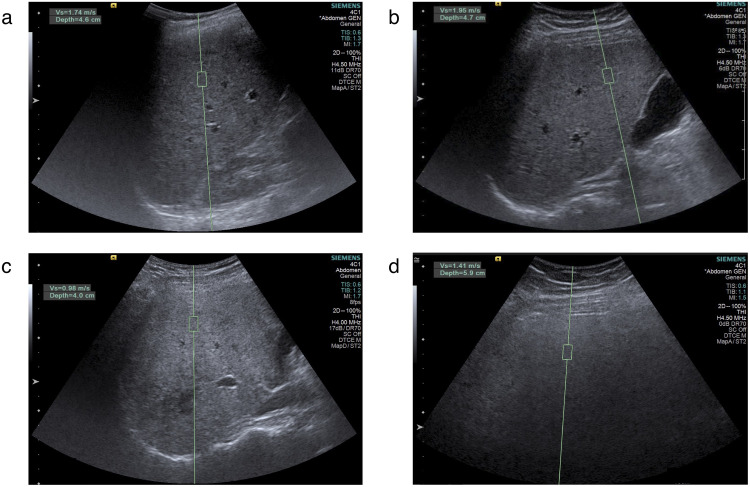
B-mode images with overlaid parametric maps of QUS features in 4 representative patients are shown in Fig 1. Point shear wave elastography images in the same patients are shown in Fig 2. Custom programs for QUS computations were implemented in C++ language and Matlab R2018a software (MathWorks).

Fig 1. Examples of histopathology-proven steatosis grades.

Fig 1

Open in a new tab

From left to right with histopathology-proven steatosis grades: 1) 62-year-old man with hepatitis B virus with steatosis grade 0; 2) 62-year-old man with NASH and hepatitis B virus with steatosis grade S1; 3) 38-year-old man with NASH with steatosis grade S2; and 4) 69-year-old woman with NASH with steatosis grade S3. Displayed images: (A) Representative B-mode acquired in the right liver lobe and corresponding QUS parametric maps (zoomed in on ROIs) illustrating (B) reciprocal of scatterer clustering parameter (log scale), (C) coherent-to-diffuse signal ratio, and (D) diffuse-to-total signal power ratio. Yellow indicates higher values, whilst dark blue values indicate lower values. In the table are reported the inflammation grade and the fibrosis stage, as well as the corresponding point shear wave elasticity (pSWE), and local and total attenuation coefficient slopes (ACS).

Fig 2. Examples of point shear wave elastography (pSWE) measurements.

Fig 2

Open in a new tab

pSWE measurements in 4 different patients: (A) steatosis grade S0, (B) steatosis grade S1, (C) steatosis grade S2, and (D) steatosis grade S3. Green rectangles indicate regions of interest where measurements are performed.

Histopathology analysis

Liver biopsies were performed by percutaneous approach with 16-G or 18-G core needles. Specimens were stained with hematoxylin and eosin and centrally scored by a hepatopathologist. Steatosis was graded according to the proportion of hepatocytes with macrovesicles of fat according to the NASH Clinical Research Network (CRN) scoring system, where S0: < 5%, S1: 5–33%, S2: 33–66%, and S3 > 66%. Inflammation was graded according to the level of lobular inflammation with the NASH CRN system for patients with NAFLD or NASH, and according to the severity of inflammation with the METAVIR scoring system for patients with autoimmune or chronic hepatitis, where A0: no foci, A1: < 2 foci per 200x field, A2: 2–4 foci per 200x field, and A3: > 4 foci per 200x field. Fibrosis was staged according to the distribution and severity of fibrosis and level of architectural modeling with the METAVIR scoring system for patients with autoimmune hepatitis or hepatitis B or C infection, and according to the NASH CRN for patients with NAFLD or NASH. Fibrosis stages F1A, F1B, and F1C in the NASH CRN system were pooled into stage F1.

Machine learning model and features selection

Classification tasks were performed with random forests [31]. This statistical learning approach is suitable in the case of relatively small data sets, as random forests avoid over-fitting (i.e., that would be based on too many trees—see Theorem 1.2 and the remark thereafter in [31]), and have very few hyper-parameters to be tuned; i.e., input features and maximum number of terminal nodes (MNTNs) in each tree. For classification purposes, we used 1000 trees and let MNTN vary from 2 to 20 by steps of 2. Selection of features was performed with G-mean as a recommended evaluation index in the case of imbalanced data set [32]. Random forests used for feature selection comprised 3000 trees. The 10 combinations of 4 features or less among all 11 features that obtained highest G-mean were selected, together with any other combination with same G-mean values in case of ties. Notice that random forests do not perform pruning on trees [33] and that Gini index is used at each node to determine the best split [34]. The number of variables randomly selected at each node is the default one; i.e., the square root of the total number of variables (one or two candidates per node in the context of this study since we used one to four features for classification).

Features selection was performed by testing all possible combinations of 1 to 4 features (there are 561 such combinations) as follows. Each combination of features was considered as the input of its own random forest consisting of 3000 trees. A random forest was trained for each of these combinations of features on the whole dataset. As a measure of potential quality of a given combination of features that was quick to compute (unlike an AUC obtained from several bootstraps), the G-mean was computed based on the sensitivity and specificity obtained on the whole dataset. The 10 combinations of 4 features or less among all 11 features that obtained highest G-mean were selected, together with any other combination with same G-mean values in case of ties. Further assessment of the 10 (or more) selected combinations of features was then performed based on AUCs estimated with the 0.638+ bootstrap method. See S1 Table for AUCs obtained with 0.638+ bootstrap method for each of the 11 features taken individually. For inflammation grade 0 vs. ≥ 1, the AUC of total attenuation was within the AUC’s 95% CI corresponding to the best tested combination of features. For inflammation grade A0-1 vs. A2- = 3, the AUC of parameter k was within the corresponding AUC’s 95% CI. For fibrosis stage F0 vs. F1-4, F0-1 vs. F2-4, or F0-3 vs. 4, the AUCs of parameter pSWE were within the corresponding 95% CIs corresponding to the best combinations of features. For all other classification tasks, none of the best performing individual features were within the corresponding AUC’s 95% CI of the best tested combination of features. S2 Table presents ANOVA tests and post-hoc multiple comparisons when applicable for each of these features. AUCs obtained with 0.638+ bootstrap method in the case where all features were taken as input of random forests are presented in S3 Table. The resulting AUCs all fell off below the AUC’s 95% CI of the corresponding best tested combinations of features.

ROC curves were obtained using stratified sampling, akin to varying the loss function used at the learning phase according to the sensitivity aimed at [35]. This may explain the non-monotonicity appearing in some of the reported ROC curves, as the dataset was imbalanced for some of the dichotomous classification tasks. We did not apply post-processing algorithms on the reported ROC curves.

Evaluation of classification performance

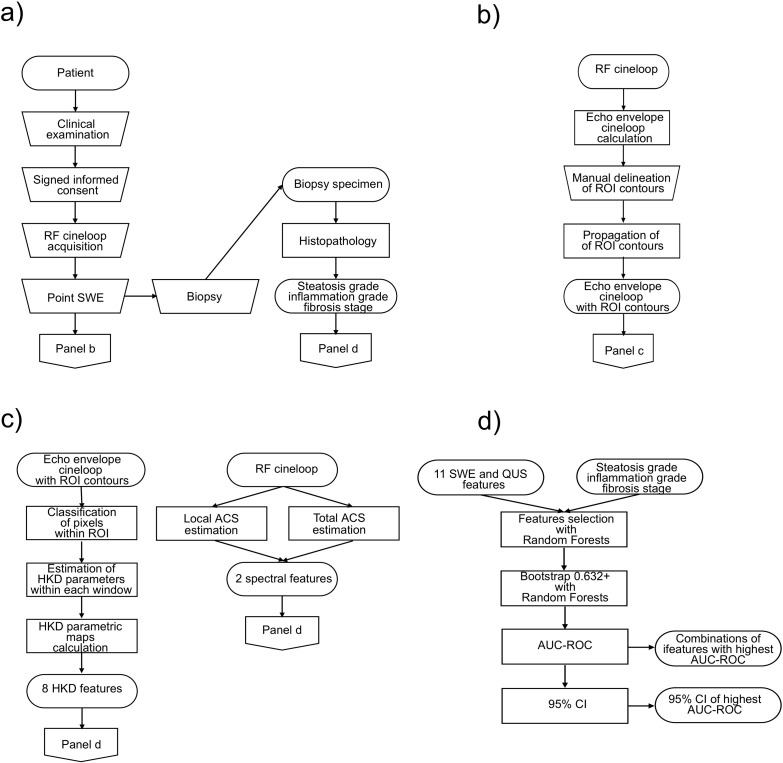
Classification performance was evaluated with the 0.632+ bootstrap method [36]. This method, which is recommended when sample size is too small for allowing training-validation-test set split, combines the leave-one-out bootstrap error and the training error with adaptive weights, thus avoiding over-estimation of the generalization error by the former and under-estimation by the latter. Receiver operating characteristic (ROC) curves were estimated by considering stratified resampling of the dataset with proportion of one class varying from 0 to 1 by steps of 1/40. One thousand bootstraps were generated for each stratification proportion, and for each bootstrap, classification errors were evaluated only on data not belonging to the bootstrap. The area under receiver operating characteristic curves (AUC-ROC) were then computed with the trapezoidal method for each previously selected combination of features and each value of MNTN. Combination of features and corresponding MNTN with highest AUC-ROC was selected as best model among tested ones for a given classification task. The jackknife method [37] was used to generate a sample of ROC-AUCs, from which a 95% confidence interval (CI) could be estimated based on percentiles. For each classification task, the point with maximal Youden index on the ROC curve of its best model was computed, and corresponding sensitivity and specificity were reported. The flow chart of the full post-processing pipeline is presented in Fig 3.

Fig 3. Flow chart of the post-processing pipeline.

Fig 3

Open in a new tab

(A) Clinical examination, recruitment with signed informed consent, research data acquisitions, biopsy and histology. (B) Calculation of the echo envelope of radiofrequency (RF) cineloops, manual delineation of a region-of-interest (ROI) contours in one frame, and propagation of contours along all frames of the cineloop. (C) Calculation of quantitative ultrasound (QUS) features. (D) Machine learning with random forests based on 11 features and gold standards: selection of 10 combinations of 4 features or less with highest G-mean (features selection), calculation of AUC-ROC on these combinations (0.632+ bootstrap), and estimation of the 95% CI for the features combination with highest AUC-ROC.

Blinding

Sonographers performing ultrasound examinations were blinded to histopathological results. The hepatopathologist was blinded to ultrasound results.

Statistical analysis

To evaluate relationships between single features and liver steatosis, inflammation, and fibrosis, features were further analyzed with univariate ordinal logistic regressions. Steatosis grade, inflammation grade, and fibrosis stage were considered in turn as response, and any of the features appearing within the best combinations for the corresponding classification task was considered as single predictor. Coefficients of these regressions were reported, together with P-values, after Holm-Bonferroni correction.

To test for association between histopathological components (steatosis, inflammation, and fibrosis), viewed as categorical variables, contingency tables for pairs of these variables were computed, and Pearson’s chi-square tests were performed based on corresponding tables. P-values were reported, after Holm-Bonferroni correction.

Statistical analyses were performed with software R (version 3.2.5, 2016; R Foundation for Statistical Computing). For proportional odds logistic regressions (also called ordinal logistic regressions), we have used the function “polr” of the package “MASS” [38, 39] usable with the software R. The raw p-values were obtained with the function “pnorm” based on the statistics t output by the function“polr”. The Holm-Bonferroni correction on p-values was then computed according to the algorithm introduced in [40]. Machine learning and regression analyses used the package “randomForest” (version 4.6–12, 2015) [41] and “MASS” (version 7.3–45, 2015) [42], respectively.

Results

Study database

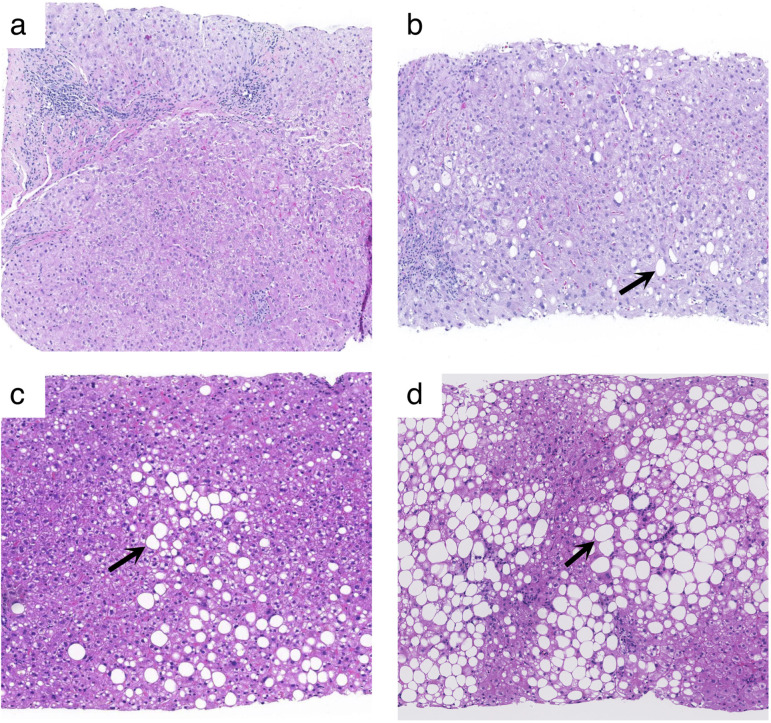
Table 1 indicates the sample size of each group determined by histopathology: 29, 22, 15, and 16 patients for steatosis grades S0, S1, S2 and S3, respectively; 8, 39, 27, and 8 patients for inflammation grades A0, A1, A2 and A3, respectively; and 12, 13, 18, 13, and 26 patients for fibrosis stages F0, F1, F2, F3, and F4, respectively. Examples of representative histopathology images are presented in Fig 4. Dataset is provided in S4 Table.

Fig 4. Examples of histopathology slides.

Fig 4

Open in a new tab

Hematoxylin and eosin-stained images (10x magnification) in 4 different patients corresponding to those shown in Fig 1 above: (A) steatosis grade S0, (B) steatosis grade S1, (C) steatosis grade S2, and (D) steatosis grade S3. Representative vacuoles of macrovesicular steatosis are indicated by arrows.

Machine learning model and features selection

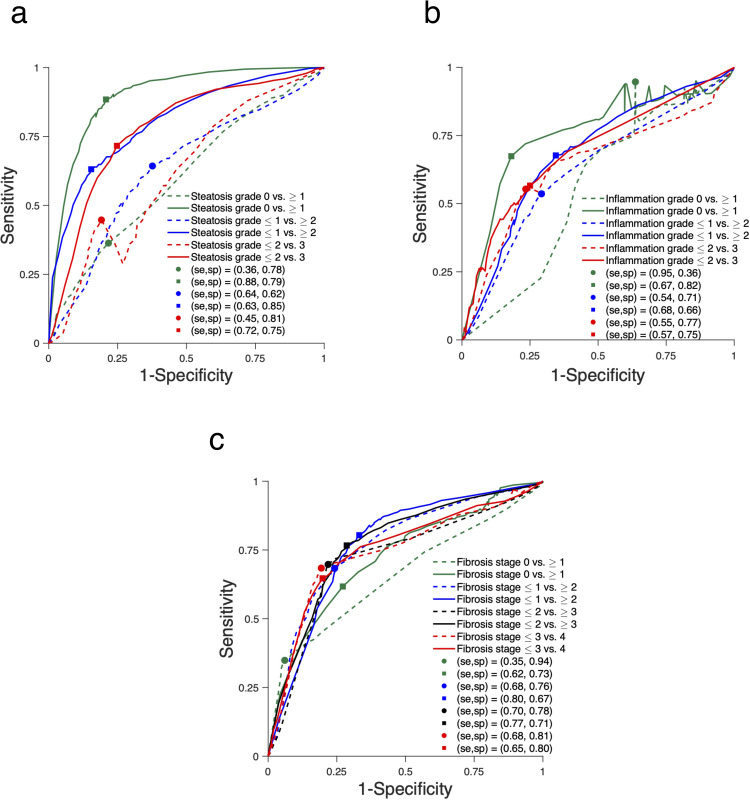
In Table 2, combination of QUS features and/or elasticity providing the highest AUC-ROC is reported for each classification task. AUCs obtained with elasticity alone were improved by combining QUS and elastography features, for each classification task, except for fibrosis stage ≤ 1 vs. ≥ 2. Improvements were most substantial for steatosis grade (25%-50% in AUC) and for classification of inflammation 0 vs. ≥ 1 (34% in AUC). For the six other dichotomous tasks, improvement was less than 10% in AUC, despite the fact that for five of them, QUS features were combined with shear-wave elasticity.

Table 2. Accuracy of shear wave elasticity alone and in combination with quantitative ultrasound (QUS) features for classification of steatosis, inflammation, and fibrosis.

Pathological features Groups Size AUC-ROC AUC-ROC Parameters
pSWE only Multi-parameter
Steatosis S0 vs. S1-3 29/53 0.60 (0.59–0.61) 0.90 (0.89–0.91) k IQR + 1/(k + 1) IQR + Local ACS
S0-1 vs. S2-3 51/31 0.63 (0.62–0.66) 0.81 (0.80–0.83) k IQR + pSWE + Local ACS
S0-2 vs. S3 66/16 0.62 (0.60–0.64) 0.78 (0.77–0.79) k Mean + μn Mean + Local ACS
Inflammation A0 vs. A1-3 8/74 0.56 (0.54–0.60) 0.75 (0.73–0.76) Total ACS
A0-1 vs. A2-3 47/35 0.62 (0.61–0.64) 0.68 (0.67–0.71) k Mean
A0-2 vs. A3 74/8 0.64 (0.60–0.65) 0.69 (0.66–0.71) pSWE + 1/α IQR
Fibrosis F0 vs. F1-4 12/70 0.66 (0.64–0.69) 0.72 (0.69–0.74) pSWE + k Mean +1/(k + 1) Mean
F0-1 vs. F2-4 25/57 0.77 (0.76–0.78) 0.77 (0.76–0.80) pSWE + μn IQR + k IQR + 1/(k + 1) IQR
F0-2 vs. F3-4 43/39 0.72 (0.72–0.74) 0.77 (0.76–0.79) pSWE + μn IQR +1/(k + 1) IQR
F0-3 vs. F4 56/26 0.74 (0.73–0.75) 0.75 (0.74–0.77) pSWE + μn IQR +1/(k + 1) IQR + Total ACS
Open in a new tab

ACS = attenuation coefficient slope. AUC-ROC = area under the receiver operating characteristic curve. Numbers in parentheses are 95% confidence intervals. size = N/M, where N = number of cases (out of 82 patients) such that pathological feature ≤ x (= 0, 1, 2, or 3) and M = 82 –N; pSWE = point shear wave elasticity; μn = mean intensity normalized by its maximal value; 1/α = reciprocal of the scatterer clustering parameter; k = coherent-to-diffuse signal ratio; 1/(k + 1) = diffuse-to-total signal power ratio; IQR = inter-quartile range.

Classification tasks performance

Table 2 also provides AUC-ROC and its 95% confidence interval, for each classification task obtained with shear wave elasticity only, or with best combination of QUS and elastography features. For classification of steatosis grades S0 vs. S1-3, S0-1 vs. S2-3, S0-2 vs. S3, AUCs were 0.60, 0.63, 0.62, respectively, with elasticity alone, and were 0.90, 0.81, and 0.78, respectively, with the best tested combination of features. For classification of inflammation grades A0 vs. A1-3, A0-1 vs. A2-3, A0-2 vs. A3, AUCs were respectively 0.56, 0.62, and 0.64 with elasticity alone, and raised up to 0.75, 0.68, and 0.69, respectively, with the best selected combination of features. For classification of liver fibrosis stages F0 vs. F1-4, F0-1 vs. F2-4, F0-2 vs. F3-4, F0-3 vs. F4, elasticity alone yielded AUCs of 0.66, 0.77, 0.72, and 0.74, respectively, whereas best tested combinations of features gave AUCs of 0.72, 0.77, 0.77, and 0.75.

From Table 2, one observes that local ACS is the only common parameter in the best combinations of parameters for the three dichotomous classifications tasks of steatosis grade. Moreover, the three dichotomous classification tasks of the inflammation grade have no common parameters. For the four dichotomous classification tasks of the fibrosis stage, point shear wave elasticity is the only common parameter. However, except for the task F0 vs. F1-4, for which the best combination of parameters was pSWE, μn mean and 1/(k + 1) mean, there were three common parameters: pSWE, μn IQR and 1/(k + 1) IQR.

The importance values, viewed as mean decrease in accuracy, of each of the parameters within the combinations of parameters appearing in Table 2 are reported in S5 Table, based on the R package “randomForest”.

ROC curves for combination of elastography and QUS features with highest ROC-AUC for classification of steatosis, inflammation, and fibrosis are shown in Fig 5.

Fig 5. Receiver operating characteristic (ROC) curves.

Fig 5

Open in a new tab

ROC curves obtained with elastography (dashed lines) and the combinations of QUS and elasticity features (solid lines) with highest AUC-ROC for the classification of (A) steatosis grade S0 vs. S1-3, S0-1 vs. S2-3, S0-2 vs. S3, (B) inflammation grade A0 vs. A1-3, A0-1 vs. A2-3, A0-2 vs. A3, and (C) fibrosis stage F0 vs. F1-4, F0-1 vs. F2-4, F0-2 vs. F3-4, F0-3 vs. F4. Sensitivity and specificity at optimal Youden index are displayed for each ROC curve.

For sake of comparison, we present in S5 Table in Supplemental Materials the ROC-ACUs obtained with the support vector machine (SVM) model on the same combinations of parameters that are appearing in Table 2. For this purpose, we used the R package “e1071” (version 1.7–9, 2021) [43]. The kernel for projection of data in higher dimensional space was the radial basis function (RBF) of degree 3 with parameter “γ” equal to the reciprocal of the number of parameters (default values in the package). The ROC curves were produced with class weights of the form (p/N(0), (1-p)/N(1)), where N(0) and N(1) represent the number of elements in the two groups of a given dichotomous classification task, letting p vary from 0 to 1. As the cost C related to the soft margin of SVM has an impact on accuracy, powers of 2 (with exponent varying from 0 to 10) were tested with the 0.632+ bootstrap method, and the best obtained values are reported in S6 Table. In cases where the best AUC was obtained with C = 210, we tested further powers of 2 until decrease in ACU. Finer tuning may have been desirable for some classification tasks, notably for inflammation grade, but we did not pursue this task. As the number of hyper-parameters to be tuned for SVM is larger than for RF, further tuning of the SVM model might require a grid search on a validation set in the case of a larger sample size.

Ordinal relation between steatosis, inflammation or fibrosis and QUS/pSWE features

Ordinal logistic regressions revealed significant ordinal relations (adopting a confidence level of 0.05) between steatosis grade and mean value (within the segmented ROI) of the normalized mean intensity μn (p = 0.0039), mean value and IQR of the coherent-to-diffuse signal ratio k (p = 0.0029 and 0.029, respectively), and the local ACS (p < 0.001). There was also a significant relation between the fibrosis stage and shear wave elasticity (p = 0.0011). See Table 3 for standard deviations of regression coefficients.

Table 3. Coefficients (with 95% confidence intervals in parentheses) of ordinal logistic regressions with the steatosis grade, or the inflammation grade, or the fibrosis stage as responses, and with features appearing in Table 1, as single predictors.
Pathological features pSWE μn Mean μn IQR 1/α IQR k Mean k IQR 1/(k + 1) Mean 1/(k + 1) IQR Total ACS. Local ACS.
Steatosis -0.80 (-1.44, -0.23) -0.033 (-0.052, -0.016) — — 2.84 (1.46, 4.47) 1.65 (0.67, 2.83) — -5.39 (-25.13, 12.90) — 9.75 (6.31, 13.71)
p = 0.097 p = 0.0039 p = 0.0027 p = 0.029 p = 1.0 p < 0.001
Inflammation 0.82 (0.23, 1.43) — — -11.12 (-24.54, 1.95) -0.95 (-2.12, 0.20) — — — -0.28(-0.78, 0.20) —
p = 0.083 p = 0.76 p = 0.75 p = 1.0
Fibrosis 1.50 (0.82, 2.29) — -0.0009 (-0.0112, 0.0095) — -1.08 (-2.24, 0.01) -0.57 (-1.42, 0.25) 7.99 (0.59, 15.93) 9.90 (-6.78, 28.36) -0.05 (-0.52, 0.40) —
p = 0.0011 p = 0.86 p = 0.51 p = 1.0 p = 0.39 p = 1.0 p = 1.0
Open in a new tab

ACS = attenuation coefficient slope. AUC-ROC = area under the receiver operating characteristic curve. Numbers in parentheses are 95% confidence intervals. pSWE = point shear wave elasticity; μn = mean intensity normalized by its maximal value; 1/α = reciprocal of the scatterer clustering parameter; k = coherent-to-diffuse signal ratio; 1/(k + 1) = diffuse-to-total signal power ratio; IQR = inter-quartile range. Holm-Bonferroni correction was applied to p-values. A positive coefficient indicates an increasing ordinal relation between the predictor and the response.

Categorical association between steatosis, inflammation, and fibrosis

There was an association between inflammation grade and fibrosis stage (p = 0.010) but not between steatosis and inflammation grades (p = 0.57), nor between steatosis grade and fibrosis stage (p = 0.97).

Discussion

This study revealed that a machine learning approach combining QUS features with elasticity provides a higher accuracy than elasticity alone for the classification of steatosis, inflammation, and fibrosis in patients with CLD. Ultrasound-based elastography techniques provide high accuracy for staging liver fibrosis [44, 45]. However, performance is limited in the case of steatosis and inflammation, which may coexist with fibrosis and confound liver stiffness [21, 46]. It has been reported that liver steatosis decreases liver stiffness in mixed steatohepatitis condition [6, 46, 47], and that inflammation, through a combination of hepatocellular ballooning, aggregation of macrophages, and edema, increases liver stiffness [6, 48–51].

Steatosis grades were best classified by a combination of QUS parameters (including coherent-to-diffuse signal ratio, local attenuation coefficient slope, mean intensity normalized by its maximal value, and shear wave elasticity). Multi-parametric approaches provided good to excellent classification accuracy: 0.90 for steatosis grades S0 vs. 1–3, 0.81 for grades S0-1 vs. S2-3, and 0.78 for grades S0-2 vs. S3. Based on coefficients of proportional odds logistic regressions, the local ACS tended to increase with steatosis grade, as expected to occur with an increase in fat content, in agreement with Goshal et al. [12]. Related to the increase in local ACS, a trend of decrease in normalized intensity (μn) was observed. On the other hand, the backscatter coefficient, which is related to the intensity itself (μ), has been reported to be positively correlated with steatosis grade [52]. Moreover, as noted in Zhou et al. [22], an increase in fat content (i.e., fat-infiltrated hepatocytes with nuclei pushed to the cell periphery) is expected to yield an increase in the coherent component of the analytic ultrasound signal. The observed trend was indeed an increase in the average coherent-to-diffuse signal ratio with steatosis grade. There was also a corresponding trend for the IQR of this parameter. Features that did not perform well as stand-alone features could nonetheless improve classification performance when combined with other features, although this makes physical interpretation of their contribution more difficult to analyze. Our proposed method compares favorably with recent results reported by Moret et al. for two state-of-the-art techniques: hepatorenal index ratio with AUCs of 0.90 for S0 vs. S1-3, 0.78 for S0-1 vs. S2-3, and 0.73 for S0-2 vs. S3 and controlled attenuation parameter (CAP) with AUCs of 0.93 for S0 vs. S1-3, 0.76 for S0-1 vs. S2-3, and 0.70 for S0-2 vs. S3 [53].

Inflammation grades were best classified by QUS and elastography features (including total attenuation coefficient slope, coherent-to-diffuse signal ratio, point shear wave elasticity, and reciprocal of the scatterer clustering parameter). Multi-parametric approaches provided AUCs ranging from 0.68 to 0.75, significantly higher than elastography alone, which provided AUCs ranging from 0.56 to 0.64. There was no significant ordinal relation between inflammation grade and any features retained in the 3 binary inflammation classification tasks. However, pSWE was somewhat related to inflammation grade with a P value of 0.083. This trend of increase in stiffness with inflammation is consistent with reported results in an animal study [47].

Fibrosis staging with pSWE alone provided rather low performance for classification of fibrosis stages F0 vs. F1-4 and moderate performance ranging from 0.72 to 0.77 for fibrosis stages F0-1 vs. F2-4, F0-2 vs. F3-4, and F0-3 vs. 4. We believe that the coexistence of confounding factors in a heterogeneous disease population may explain the lower AUCs of pSWE in detecting advanced fibrosis, whereas many prior studies on elastography focused on populations with only one disease. Nonetheless, the combination with QUS parameters (coherent-to-diffuse signal ratio, diffuse-to-total signal power ratio, mean intensity normalized by its maximal value, and total attenuation) could further improve the classification accuracy, leading to AUCs in the range of 0.72 to 0.77 for all dichotomization schemes. Among features that were retained for the 4 binary fibrosis classification tasks, pSWE presented an ordinal relation with fibrosis stage. The observed trend of increase in stiffness with fibrosis stage is consistent with the multivariate analysis reported in Kazemirad et al. [47]. Recent works by Brattain et al, Durot et al., Kagadis et al., showed that fibrosis classification accuracy could be further improved, with AUCs in the range of 0.93 to 0.99, by using machine learning techniques such as automated image quality assessment and ROI selection [54], support vector machines [16] and deep learning techniques applied on shear wave elastography data [19].

These results confirm that using machine learning to select the best combination of QUS and elastography parameters may significantly improve classification of steatosis, inflammation, and fibrosis in patients with CLD in comparison with elastography alone. Such a comprehensive approach is critical to reduce or alleviate the need for liver biopsy because these histological components coexist and may have confounding effects on liver stiffness. Of note, our study found associations between inflammation grade and fibrosis stage. Therefore, a multi-parametric approach was required to account for the stiffness-increasing effect of inflammation and fibrosis.

Notice that for some of the classification tasks, distinct combinations of features yielded the same AUC, up to two decimals: steatosis grade S0 vs. S1-3, with QUS features combined with pSWE; steatosis grade S0-2 vs. S3, also with QUS features only; fibrosis stage F0-1 vs. ≥ F2-4, fibrosis stage F0-2 vs. F3-4 and fibrosis stage F0-3 vs. F4, also with QUS features combined with pSWE. In particular, in all cases where the best combination of features comprised pSWE, none of the tested combinations of QUS features only were as good.

Limitations

The sample size was limited to 82 patients with various causes of CLD. However, this pilot study constitutes a proof of concept indicating that incorporating QUS and elastography increases the classification study, a line of work that should be investigated in larger studies with a single etiology such as NAFLD. We did not assess iron overload, another histological feature encountered in some causes of CLD. While there is currently no ultrasound-based technique for assessment of iron overload, this remains a relatively uncommon clinical problem encountered in select populations with hemochromatosis and transfusional hemosiderosis that can be detected by blood tests and quantitated by magnetic resonance imaging [55]. Another limitation was the lack of assessment of biliary disease. Similarly, biliary disease can be suspected on the basis of cholestatic enzymes and assessed by magnetic resonance cholangiopancreatography when relevant. Ultrasound images were acquired with two clinical scanner models which could have introduced variability. Finally, our dataset was imbalanced with few positive cases for steatosis grades S0-2 vs. S3 (66 vs. 16) and inflammation grades A0-2 vs. A3 (74 vs. 8), and with few negative cases for inflammation grades A0 vs. A1-3 (8 vs. 74) and fibrosis stages F0 vs. F1-4 (12 vs. 70). However, we have used the G-mean as metric for features selection, which is recommended in the case of imbalanced datasets. Moreover, in that context, AUC under the Precision-Recall curve (PRC) has been suggested as alternative metric to AUC-ROC [56]. We have verified that AUC-PRCs were higher for combinations of features than with pSWE stand-alone, albeit further assessment in future studies would require larger sample size. Further assessment would be required on a larger data set in a target population of patients with NAFLD or NASH, in particular to assess more precisely the impact of each of the proposed QUS features in the considered dichotomous tasks. Future work could include clinical variables, such as body mass index, to take into account variability in patient’s health conditions, at the classifier’s training step. Furthermore, other machine learning models than random forests could be assessed on a larger database.

Conclusions

In conclusion, this ancillary study to a prospective imaging trial revealed that a machine learning model based on random forests could select combinations of QUS features and shear wave elastography stiffness that improved the classification accuracy of three key histological features of CLD (steatosis, inflammation, and fibrosis) over that of elastography alone. Future research should validate this approach in human cohorts with NAFLD, a highly prevalent cause of CLD.

Supporting information

S1 Table. Accuracy of pSWE and QUS features.

Accuracy of each of the eleven features alone and for the best combination of features for classification of steatosis, inflammation, and fibrosis. The best combination depends on the classification task; see Table 2.

(DOCX)

Click here for additional data file. (41.8KB, docx)
S2 Table. ANOVA tests and post-hoc multiple comparisons when applicable for each of these features.

Anova (AOV) test if Shapiro-Wilk (S-W) test succeeded (p-value > 1) or else Kruskal-Wallis (K-S) tests with post-hoc multiple comparison tests with Bonferroni-Holm adjustment of p-values, based on t-test in the former case, or Wilcoxon rank sum test in the latter case.

(DOCX)

Click here for additional data file. (39.9KB, docx)
S3 Table. Accuracy of all eleven features obtained with 0.638+ bootstrap method.

All features taken as input to random forests and of the best combination of features for classification of steatosis, inflammation, and fibrosis. The best combination of features depends on the classification task; see Table 2.

(DOCX)

Click here for additional data file. (38.8KB, docx)
S4 Table. Dataset.

Dataset contains patient identification from 1 to 82 (ID), steatosis grade (Steatosis), inflammation grade (Inflammation), fibrosis stage (Fibrosis), point shear wave elasticity (pSWE), μn = mean intensity normalized by its maximal value (munMean), 1/α = reciprocal of the scatterer clustering parameter (ialphaMean), k = coherent-to-diffuse signal ratio (kMean), 1/(k + 1) = diffuse-to-total signal power ratio (ikappaMean), mean intensity normalized by its maximal value inter-quartile range (munIQR), reciprocal of the scatterer clustering parameter inter-quartile range (ialphaIQR), coherent-to-diffuse signal ratio inter-quartile range (kIQR), diffuse-to-total signal power ratio inter-quartile range (ikappaIQR),total attenuation coefficient slope (TotalACS), local attenuation coefficient slope (LocalACS).

(XLSX)

Click here for additional data file. (19.5KB, xlsx)
S5 Table. Importance of each parameter within the multi-parameter combinations appearing in Table 2 for the various dichotomous classification tasks.

The reported importance is represented by the mean decrease in accuracy, where a higher value corresponds to a higher importance.

(DOCX)

Click here for additional data file. (41.5KB, docx)
S6 Table. Accuracy of shear wave elasticity alone and in combination with quantitative ultrasound (QUS) features for classification of steatosis, inflammation, and fibrosis, based on support vector machine (SVM) models.

The same combinations of parameters as in Table 2 were tested with SVM. The parameter γ of radial basis functions (RBF) was set to the reciprocal of the number of parameters (default value with R package “e1071”); the degree of RBFs was the default value 3; the cost C was varied according to powers of 2 for each combination of parameters and the best resulting AUC-ROC is reported.

(DOCX)

Click here for additional data file. (40.6KB, docx)

Acknowledgments

We thank Mrs. Assia Belblidia, Mrs. Catherine Huet, and Mr. Walid El Abyad for their assistance in patient enrollment. ACUSON S2000 and S3000 ultrasound systems were lent by Siemens Healthineers.

Abbreviations

ACS

attenuation coefficient slope

AUC

area under the receiver operating characteristic curve

CLD

chronic liver disease

CRN

Clinical Research Network

HKD

homodyned K-distribution

IQR

inter-quartile range

MNTN

maximum number of terminal nodes

NAFLD

nonalcoholic fatty liver disease

NASH

nonalcoholic steatohepatitis

pSWE

point shear wave elastography

QUS

quantitative ultrasound

ROC

receiver operating characteristic

ROI

region of interest

Data Availability

All relevant data are within the paper and its Supporting Information files.

Funding Statement

This work was supported by grants from the Canadian Institutes of Health Research (CIHR)-Institute of Nutrition, Metabolism and Diabetes (INMD) (CIHR-INMD #273738 and #301520, https://cihr-irsc.gc.ca/) to AT. This work was also supported by Junior 1 and Junior 2 Clinical Research Scholarships from the Fonds de recherche du Québec en Santé (FRQS, https://frq.gouv.qc.ca/en/) and Fondation de l'Association des radiologistes du Québec (FARQ) (FRQS-FARQ #26993 and #34939 to AT; and by a Junior 1 Clinical Research Scholarships from FRQS (#27127) and research salary from McGill University to GS. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

  • 1.Kim WR, Brown RS Jr., Terrault NA, El-Serag H. Burden of liver disease in the United States: summary of a workshop. Hepatology (Baltimore, Md. 2002;36(1):227–42. Epub 2002/06/27. doi: S0270913902000265 [pii] doi: 10.1053/jhep.2002.34734 . [DOI] [PubMed] [Google Scholar]
  • 2.Younossi ZM, Koenig AB, Abdelatif D, Fazel Y, Henry L, Wymer M. Global epidemiology of nonalcoholic fatty liver disease-Meta-analytic assessment of prevalence, incidence, and outcomes. Hepatology (Baltimore, Md. 2016;64(1):73–84. Epub 2015/12/29. doi: 10.1002/hep.28431 . [DOI] [PubMed] [Google Scholar]
  • 3.Lima PH, Fan B, Berube J, Cerny M, Olivie D, Giard JM, et al. Cost-Utility Analysis of Imaging for Surveillance and Diagnosis of Hepatocellular Carcinoma. AJR Am J Roentgenol. 2019:1–9. Epub 2019/04/18. doi: 10.2214/AJR.18.20341 . [DOI] [PubMed] [Google Scholar]
  • 4.Ratziu V, Charlotte F, Heurtier A, Gombert S, Giral P, Bruckert E, et al. Sampling variability of liver biopsy in nonalcoholic fatty liver disease. Gastroenterology. 2005;128(7):1898–906. doi: 10.1053/j.gastro.2005.03.084 . [DOI] [PubMed] [Google Scholar]
  • 5.Petitclerc L, Sebastiani G, Gilbert G, Cloutier G, Tang A. Liver fibrosis: Review of current imaging and MRI quantification techniques. J Magn Reson Imaging. 2017;45(5):1276–95. doi: 10.1002/jmri.25550 . [DOI] [PubMed] [Google Scholar]
  • 6.Lefebvre T, Wartelle-Bladou C, Wong P, Sebastiani G, Giard JM, Castel H, et al. Prospective comparison of transient, point shear wave, and magnetic resonance elastography for staging liver fibrosis. Eur Radiol. 2019;29(12):6477–88. Epub 2019/07/07. doi: 10.1007/s00330-019-06331-4 . [DOI] [PubMed] [Google Scholar]
  • 7.Gatos I, Drazinos P, Yarmenitis S, Theotokas I, Zoumpoulis PS. Comparison of Sound Touch Elastography, Shear Wave Elastography and Vibration-Controlled Transient Elastography in Chronic Liver Disease Assessment using Liver Biopsy as the "Reference Standard". Ultrasound Med Biol. 2020;46(4):959–71. Epub 2020/01/28. doi: 10.1016/j.ultrasmedbio.2019.12.016 . [DOI] [PubMed] [Google Scholar]
  • 8.Mamou J, Oelze ML. Quantitative Ultrasound in Soft Tissues: Springer; 2013. Oct. 9 2013. [Google Scholar]
  • 9.Myers RP, Pollett A, Kirsch R, Pomier-Layrargues G, Beaton M, Levstik M, et al. Controlled Attenuation Parameter (CAP): a noninvasive method for the detection of hepatic steatosis based on transient elastography. Liver Int. 2012;32(6):902–10. doi: 10.1111/j.1478-3231.2012.02781.x . [DOI] [PubMed] [Google Scholar]
  • 10.Sasso M, Miette V, Sandrin L, Beaugrand M. The controlled attenuation parameter (CAP): a novel tool for the non-invasive evaluation of steatosis using Fibroscan. Clinics and research in hepatology and gastroenterology. 2012;36(1):13–20. doi: 10.1016/j.clinre.2011.08.001 . [DOI] [PubMed] [Google Scholar]
  • 11.Yilmaz Y, Yesil A, Gerin F, Ergelen R, Akin H, Celikel CA, et al. Detection of hepatic steatosis using the controlled attenuation parameter: a comparative study with liver biopsy. Scand J Gastroenterol. 2014;49(5):611–6. doi: 10.3109/00365521.2014.881548 . [DOI] [PubMed] [Google Scholar]
  • 12.Ghoshal G, Lavarello RJ, Kemmerer JP, Miller RJ, Oelze ML. Ex vivo study of quantitative ultrasound parameters in fatty rabbit livers. Ultrasound Med Biol. 2012;38(12):2238–48. doi: 10.1016/j.ultrasmedbio.2012.08.010 ; PubMed Central PMCID: PMC3640816. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Stoean R, Stoean C, Lupsor M, Stefanescu H, Badea R. Evolutionary-driven support vector machines for determining the degree of liver fibrosis in chronic hepatitis C. Artif Intell Med. 2011;51(1):53–65. Epub 2010/08/03. doi: 10.1016/j.artmed.2010.06.002 . [DOI] [PubMed] [Google Scholar]
  • 14.Gatos I, Tsantis S, Spiliopoulos S, Karnabatidis D, Theotokas I, Zoumpoulis P, et al. A new computer aided diagnosis system for evaluation of chronic liver disease with ultrasound shear wave elastography imaging. Med Phys. 2016;43(3):1428–36. Epub 2016/03/05. doi: 10.1118/1.4942383 . [DOI] [PubMed] [Google Scholar]
  • 15.Gatos I, Tsantis S, Spiliopoulos S, Karnabatidis D, Theotokas I, Zoumpoulis P, et al. A Machine-Learning Algorithm Toward Color Analysis for Chronic Liver Disease Classification, Employing Ultrasound Shear Wave Elastography. Ultrasound Med Biol. 2017;43(9):1797–810. Epub 2017/06/22. doi: 10.1016/j.ultrasmedbio.2017.05.002 . [DOI] [PubMed] [Google Scholar]
  • 16.Durot I, Akhbardeh A, Sagreiya H, Loening AM, Rubin DL. A New Multimodel Machine Learning Framework to Improve Hepatic Fibrosis Grading Using Ultrasound Elastography Systems from Different Vendors. Ultrasound Med Biol. 2020;46(1):26–33. Epub 2019/10/16. doi: 10.1016/j.ultrasmedbio.2019.09.004 ; PubMed Central PMCID: PMC6879839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Wang K, Lu X, Zhou H, Gao Y, Zheng J, Tong M, et al. Deep learning Radiomics of shear wave elastography significantly improved diagnostic performance for assessing liver fibrosis in chronic hepatitis B: a prospective multicentre study. Gut. 2019;68(4):729–41. Epub 2018/05/08. doi: 10.1136/gutjnl-2018-316204 ; PubMed Central PMCID: PMC6580779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Gatos I, Tsantis S, Spiliopoulos S, Karnabatidis D, Theotokas I, Zoumpoulis P, et al. Temporal stability assessment in shear wave elasticity images validated by deep learning neural network for chronic liver disease fibrosis stage assessment. Med Phys. 2019;46(5):2298–309. Epub 2019/04/01. doi: 10.1002/mp.13521 . [DOI] [PubMed] [Google Scholar]
  • 19.Kagadis GC, Drazinos P, Gatos I, Tsantis S, Papadimitroulas P, Spiliopoulos S, et al. Deep learning networks on chronic liver disease assessment with fine-tuning of shear wave elastography image sequences. Phys Med Biol. 2020;65(21):215027. Epub 2020/10/02. doi: 10.1088/1361-6560/abae06 . [DOI] [PubMed] [Google Scholar]
  • 20.Fang J, Zhou Z, Chang NF, Wan YL, Tsui PH. Ultrasound parametric imaging of hepatic steatosis using the homodyned-K distribution: An animal study. Ultrasonics. 2018;87:91–102. Epub 2018/02/25. doi: 10.1016/j.ultras.2018.02.015 . [DOI] [PubMed] [Google Scholar]
  • 21.Tang A, Destrempes F, Kazemirad S, Garcia-Duitama J, Nguyen BN, Cloutier G. Quantitative ultrasound and machine learning for assessment of steatohepatitis in a rat model. Eur Radiol. 2019;29(5):2175–84. Epub 2018/12/19. doi: 10.1007/s00330-018-5915-z . [DOI] [PubMed] [Google Scholar]
  • 22.Zhou Z, Fang J, Cristea A, Lin YH, Tsai YW, Wan YL, et al. Value of homodyned K distribution in ultrasound parametric imaging of hepatic steatosis: An animal study. Ultrasonics. 2019;101:106001. Epub 2019/09/11. doi: 10.1016/j.ultras.2019.106001 . [DOI] [PubMed] [Google Scholar]
  • 23.Dietrich CF, Bamber J, Berzigotti A, Bota S, Cantisani V, Castera L, et al. EFSUMB Guidelines and Recommendations on the Clinical Use of Liver Ultrasound Elastography, Update 2017 (Long Version). Ultraschall Med. 2017;38(4):e16–e47. Epub 2017/04/14. doi: 10.1055/s-0043-103952 . [DOI] [PubMed] [Google Scholar]
  • 24.Destrempes F, Emilie F, Yu F, Cloutier G. Unifying concepts of statistical and spectralquantitative ultrasound techniques. IEEE Trans Med Imaging. 2016;35:488–500. Epub 2015/09/29. doi: 10.1109/TMI.2015.2479455 . [DOI] [PubMed] [Google Scholar]
  • 25.Destrempes F, Poree J, Cloutier G. Estimation Method of the Homodyned K-Distribution Based on the Mean Intensity and Two Log-Moments. SIAM journal on imaging sciences. 2013;6(3):1499–530. Epub 2014/05/06. doi: 10.1137/120875727 ; PubMed Central PMCID: PMC4008482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Trop I, Destrempes F, El Khoury M, Robidoux A, Gaboury L, Allard L, et al. The Added Value of Statistical Modeling of Backscatter Properties in the Management of Breast Lesions at US. Radiology. 2015;275(3):666–74. doi: 10.1148/radiol.14140318 . [DOI] [PubMed] [Google Scholar]
  • 27.Dutt V, Greenleaf JF. Ultrasound echo envelope analysis using a homodyned K distribution signal model. Ultrason Imaging. 1994;16(4):265–87. Epub 1994/10/01. doi: 10.1177/016173469401600404 [DOI] [PubMed] [Google Scholar]
  • 28.Wilcox RR. Introduction to Robust Estimation and Hypothesis Testing. Oxford, UK: Academic Press; 2011. [Google Scholar]
  • 29.Sheet D, Karamalis A, Eslami A, Noel P, Chatterjee J, Ray AK, et al. Joint learning of ultrasonic backscattering statistical physics and signal confidence primal for characterizing atherosclerotic plaques using intravascular ultrasound. Med Image Anal. 2014;18(1):103–17. Epub 2013/11/05. doi: 10.1016/j.media.2013.10.002 . [DOI] [PubMed] [Google Scholar]
  • 30.Bigelow TA, Labyed Y. Attenuation compensation and estimation. In: J. M, Oelze ML, editors. Quantitative ultrasound in soft tissues. Springer Dordrecht Heildelberg New York London; 2013. p. 75–6. [Google Scholar]
  • 31.Breiman L. Random forests. Machine learning. 2001;45(1):5–32. [Google Scholar]
  • 32.He H, Garcia EA. Learning from imbalanced data. IEEE Transactions on knowledge and data engineering. 2009;21(9):1263–84. [Google Scholar]
  • 33.Breiman L. Manual on setting up, using, and understanding random forests v3. 1. Statistics Department University of California Berkeley, CA, USA. 2002;1:58. [Google Scholar]
  • 34.Cutler A, Cutler DR, Stevens JR. Random forests. Springer, editor. Boston, MA2012. 157–75 p. [Google Scholar]
  • 35.Woods K, Bowyer KW. Generating ROC curves for artificial neural networks. IEEE Trans Med Imaging. 1997;16(3):329–37. Epub 1997/06/01. doi: 10.1109/42.585767 . [DOI] [PubMed] [Google Scholar]
  • 36.Hastie T, Tibshirani R, Friedman J. The elements of statistical learning: data mining, inference and prediction. Springer-Velag New York Berlin Heldelberg. 2001;27(2):83–5. [Google Scholar]
  • 37.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837–45. [PubMed] [Google Scholar]
  • 38.Venables WN, Ripley BD. Modern applied statistics with S-PLUS: Springer Science & Business Media; 2013. [Google Scholar]
  • 39.https://cran.r-project.org/web/packages/MASS/MASS.pdf [last accessed 14/12/2020].
  • 40.Holm S. A simple sequentially rejective multiple test procedure. Scandinavian journal of statistics. 1979:65–70. [Google Scholar]
  • 41.Breiman L, Cutler A. Package ‘randomForest”. Version 4.6–12. October 7, 2015. Available from: https://www.stat.berkeley.edu/~breiman/RandomForests/.
  • 42.Venables W, Ripley B. Modern applied statistics (Fourth S., editor) New York. ISBN 0-387-95457-0.: Springer; 2002. [Google Scholar]
  • 43.Meyer D, Dimitriadou E, Hornik K, Weingessel A, Leisch F, Chang CC, et al. Package ‘e1071’. Version 1.7–9. September 16, 2021. [Google Scholar]
  • 44.Tang A, Cloutier G, Szeverenyi NM, Sirlin CB. Ultrasound Elastography and MR Elastography for Assessing Liver Fibrosis: Part 1, Principles and Techniques. AJR Am J Roentgenol. 2015;205(1):22–32. doi: 10.2214/AJR.15.14552 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Tang A, Cloutier G, Szeverenyi NM, Sirlin CB. Ultrasound Elastography and MR Elastography for Assessing Liver Fibrosis: Part 2, Diagnostic Performance, Confounders, and Future Directions. AJR Am J Roentgenol. 2015;205(1):33–40. doi: 10.2214/AJR.15.14553 . [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Yoneda M, Suzuki K, Kato S, Fujita K, Nozaki Y, Hosono K, et al. Nonalcoholic fatty liver disease: US-based acoustic radiation force impulse elastography. Radiology. 2010;256(2):640–7. Epub 2010/06/10. doi: radiol.10091662 [pii] doi: 10.1148/radiol.10091662 . [DOI] [PubMed] [Google Scholar]
  • 47.Kazemirad S, Zhang E, Nguyen BN, Bodson-Clermont P, Destrempes F, Trudel D, et al. Detection of Steatohepatitis in a Rat Model by Using Spectroscopic Shear-Wave US Elastography. Radiology. 2017;282(3):726–33. Epub 2016/08/12. doi: 10.1148/radiol.2016160308 . [DOI] [PubMed] [Google Scholar]
  • 48.Iredale JP. Models of liver fibrosis: exploring the dynamic nature of inflammation and repair in a solid organ. Journal of Clinical Investigation. 2007;117(3):539–48. doi: 10.1172/jci30542 PubMed PMID: PMC1804370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Zeng X, Xu C, He D, Zhang H, Xia J, Shi D, et al. Influence of Hepatic Inflammation on FibroScan Findings in Diagnosing Fibrosis in Patients with Chronic Hepatitis B. Ultrasound in medicine & biology. 2015;41(6):1538–44. Epub 2015/03/01. doi: 10.1016/j.ultrasmedbio.2015.01.011 . [DOI] [PubMed] [Google Scholar]
  • 50.Dong D-R, Hao M-N, Li C, Peng ZE, Liu XIA, Wang G-P, et al. Acoustic radiation force impulse elastography, FibroScan(®), Forns’ index and their combination in the assessment of liver fibrosis in patients with chronic hepatitis B, and the impact of inflammatory activity and steatosis on these diagnostic methods. Molecular Medicine Reports. 2015;11(6):4174–82. doi: 10.3892/mmr.2015.3299 PubMed PMID: PMC4394958. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Chen J, Talwalkar JA, Yin M, Glaser KJ, Sanderson SO, Ehman RL. Early detection of nonalcoholic steatohepatitis in patients with nonalcoholic fatty liver disease by using MR elastography. Radiology. 2011;259(3):749–56. doi: 10.1148/radiol.11101942 PubMed PMID: PMC3099044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Han A, Zhang YN, Boehringer AS, Montes V, Andre MP, Erdman JW Jr., et al. Assessment of Hepatic Steatosis in Nonalcoholic Fatty Liver Disease by Using Quantitative US. Radiology. 2020;295(1):106–13. Epub 2020/02/06. doi: 10.1148/radiol.2020191152 ; PubMed Central PMCID: PMC7104700. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Moret A, Boursier J, Houssel Debry P, Riou J, Crouan A, Dubois M, et al. Evaluation of the Hepatorenal B-Mode Ratio and the "Controlled Attenuation Parameter" for the Detection and Grading of Steatosis. Ultraschall Med. 2020. Epub 2020/09/30. doi: 10.1055/a-1233-2290 . [DOI] [PubMed] [Google Scholar]
  • 54.Brattain LJ, Ozturk A, Telfer BA, Dhyani M, Grajo JR, Samir AE. Image Processing Pipeline for Liver Fibrosis Classification Using Ultrasound Shear Wave Elastography. Ultrasound Med Biol. 2020;46(10):2667–76. Epub 2020/07/06. doi: 10.1016/j.ultrasmedbio.2020.05.016 ; PubMed Central PMCID: PMC7483774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Labranche R, Gilbert G, Cerny M, Vu K-N, Soulières D, Olivié D, et al. Liver Iron Quantification with MR Imaging: A Primer for Radiologists. RadioGraphics. 2018;38(2):392–412. Epub 2018/03/13. doi: 10.1148/rg.2018170079 . [DOI] [PubMed] [Google Scholar]
  • 56.Davis J, Goadrich M, editors. The relationship between Precision-Recall and ROC curves. Proceedings of the 23rd international conference on Machine learning; 2006: ACM.

Decision Letter 0

Omar Sultan Al-Kadi

13 Aug 2021

PONE-D-21-21119

Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver disease

PLOS ONE

Dear Dr. Tang,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Sep 27 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

  • A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.

  • A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.

  • An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Omar Sultan Al-Kadi, PhD

Academic Editor

PLOS ONE

 Journal Requirements: When submitting your revision, we need you to address these additional requirements. 1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf 2. Thank you for stating the following in the Acknowledgments Section of your manuscript: [We thank Mrs. Assia Belblidia, Mrs. Catherine Huet, and Mr. Walid El Abyad for their assistance in patient enrollment. ACUSON S2000 and S3000 ultrasound systems were lent by Siemens Healthineers. This work was supported by grants from the Canadian Institutes of Health Research (CIHR)-Institute of Nutrition, Metabolism and Diabetes (INMD) (CIHR-INMD #273738 and #301520) and Fonds de recherche du Québec en Santé (FRQS) and Fondation de l'Association des radiologistes du Québec (FARQ) Clinical Research Scholarship – Junior 1 and 2 Salary Award (FRQS-FARQ #26993 and #34939) to An Tang. Junior 1 Salary Award from FRQS (#27127) and research salary from McGill University to Giada Sebastiani.] We note that you have provided funding information that is not currently declared in your Funding Statement. However, funding information should not appear in the Acknowledgments section or other areas of your manuscript. We will only publish funding information present in the Funding Statement section of the online submission form. Please remove any funding-related text from the manuscript and let us know how you would like to update your Funding Statement. Currently, your Funding Statement reads as follows:  [This work was supported by grants from the Canadian Institutes of Health Research (CIHR)-Institute of Nutrition, Metabolism and Diabetes (INMD) (CIHR-INMD #273738 and #301520, https://cihr-irsc.gc.ca/) to AT.  This work was also supported by Junior 1 and Junior 2 Clinical Research Scholarships from the Fonds de recherche du Québec en Santé (FRQS, https://frq.gouv.qc.ca/en/) and Fondation de l'Association des radiologistes du Québec (FARQ) (FRQS-FARQ #26993 and #34939 to AT; and by a Junior 1 Clinical Research Scholarships from FRQS (#27127) and research salary from McGill University to GS.] Please include your amended statements within your cover letter; we will change the online submission form on your behalf. 3. Thank you for stating the following in your Competing Interests section:  [No]. Please complete your Competing Interests on the online submission form to state any Competing Interests. If you have no competing interests, please state "The authors have declared that no competing interests exist.", as detailed online in our guide for authors at http://journals.plos.org/plosone/s/submit-now  This information should be included in your cover letter; we will change the online submission form on your behalf. 4. Please include captions for your Supporting Information files at the end of your manuscript, and update any in-text citations to match accordingly. Please see our Supporting Information guidelines for more information: http://journals.plos.org/plosone/s/supporting-information. 

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

Reviewer #3: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: A very nicely structured paper. I have some suggestions that may help the authors to improve the paper.

--Lines 186-192. It's not clear how these parameters were generated. I would suggest clarifying this section

-- NASH-CRN system uses 1a, 1b and 1c. Did you pool these values as 1 and merged with the rest of the group? (METAVIR for other etiologies).

--Using two different ultrasound models (S2000 and S3000) could cause variability. I would suggest adding this factor to the limitations.

--I would suggest annotating Fig3 and showing the areas with fibrosis, inflammation and steatosis.

--I would suggest providing some images from the pSWE exams.

--I would suggest using NAS scores and performing analysis if available.

Thank you for considering my recommendations.

Reviewer #2: General Comments:

This study presents a machine learning method for assessing chronic liver disease (CLD) diagnostic parameters (fibrosis, steatosis, inflammation) through ultrasound (US) B-Mode and Elastographic information provided by ultrasound imaging. The study has some merits as the combination of information of fibrosis, steatosis and inflammation for CLD assessment has not yet been evaluated. Also, the statistical analysis of the Results provided is good and properly written. Its novelty is limited to this combination though, as the algorithms used are already known and used widely in the literature. Its flow is sometimes confusing as many aspects referred for the first time are explained in other, later parts of the manuscript. Furthermore, the manuscript has some major flaws that should be considered before publication.

Non-Specific Comments:

1. The study’s text flow is sometimes confusing as many aspects referred for the first time are explained in other, later parts of the manuscript. For example, the histological information section containing Metavir Classification systems for fibrosis and inflammation (activity) should be earlier in the manuscript as there are points that stage-grade information is shown that are unknown to the non-expert reader, and are not explained. For a large part of the manuscript it is not clear whether the Metavir or Ishak classification system is used. Also, Table 2 should be transferred in the Results section as it is early in the Methods section.

2. The stage-grade notation is a little confusing as usually, in the literature, there is a capital letter ahead of stage-grade number e.g. F≥F2 for fibrosis, S≥S1 for steatosis and A≥A3 for inflammation. Please provide clearer stage-grade class representation.

3. The Introduction section needs many additions regarding existing literature. Only clinical information of the CLD is mentioned and minimal information is given on the non-invasive approaches (clinical or A.I. based) for CLD assessment. Many elastographic variants exist (MR- and US-based) that present variable performances in clinical and A.I. related studies that are completely absent on this study. Also, no information is given on other A.I. related works on CLD assessment. What is their performance? Their performance should be discussed in comparison with the literature.

a. Indicative works (much more exist) that the Authors should include and discuss are:

i. Gatos, I., Tsantis, S., et al, (2016), A new computer aided diagnosis system for evaluation of chronic liver disease with ultrasound shear wave elastography imaging. Med. Phys., 43: 1428–1436. doi:10.1118/1.4942383

ii. Gatos, I., Tsantis, S., et al, (2017), A Machine-Learning Algorithm Toward Color Analysis for Chronic Liver Disease Classification, Employing Ultrasound Shear Wave Elastography, Ultrasound in Medicine and Biology, Volume 43, Issue 9, 1797 – 1810. doi:10.1016/j.ultrasmedbio.2017.05.002

iii. Gatos, I., Tsantis, S., et al, (2019), Temporal stability assessment in shear wave elasticity images validated by deep learning neural network for chronic liver disease fibrosis stage assessment. Med. Phys., 46(5): 2298-2309. doi:10.1002/mp.13521

iv. Gatos, I., Drazinos, P., et al, (2020), Comparison of Sound Touch Elastography, Shear Wave Elastography and Vibration-Controlled Transient Elastography in Chronic Liver Disease Assessment using Liver Biopsy as the "Reference Standard". Ultrasound in Medicine and Biology, 46(4):959-971. doi:10.1016/j.ultrasmedbio.2019.12.016.

v. Kagadis, G.C., Drazinos, P., et al, (2020), Deep learning networks on chronic liver disease assessment with fine-tuning of shear wave elastography image sequences. Phys. Med. Biol. 65 215027

vi. Stoean R, Stoean C, Lupsor M, Stefanescu H and Badea R 2011 Evolutionary-driven support vector machines for determining the degree of liver fibrosis in chronic hepatitis C Artif. Intell. Med. 51 53–65

vii. Wang K et al 2019 Deep learning radiomics of shear wave elastography significantly improved diagnostic performance for assessing liver fibrosis in chronic hepatitis B: a prospective multicentre study Gut 68 729–41

viii. Meng D, Zhang L, Cao G, Cao W, Zhang G and Hu B 2017 Liver fibrosis classification based on transfer learning and FCNet for ultrasound images IEEE Access 5 5804–10

ix. Durot I, Akhbardeh A, Sagreiya H, Loening A M and Rubin D L 2020 A new multimodel machine learning framework to improve hepatic fibrosis grading using ultrasound elastography systems from different vendors Ultrasound Med. Biol. 46 26–33

4. The Methods section has also issues as:

a. The Authors compare plain pSWE measurement with all the information processed in the proposed machine learning scheme that is somewhat irrelevant or, at least, should be just complementary. The authors should compare the proposed algorithm’s estimation with the combination of information given by the pSWE measurement and the US B-Mode image by an expert clinician or by other analysis.

b. Only binary class differentiation is presented. Although this is not a major limitation as other class combinations (e.g. ternary or full) may be evaluated due to small sample in certain classes, some could be realized as they may contain significant clinical information (e.g. Mild Fibrosis vs. Significant Fibrosis vs. Cirrhosis, or in other words, F0-F1 vs. F2-F3 vs. F4).

c. No splitting of data (e.g. 70% training to 30% validation) is provided resulting in no estimation of the robustness of the results.

5. The Discussion section is incomplete in terms of comparison with relevant clinical and technical works in the literature that is also absent in the Introduction. That being said, the proposed method shows relatively low performance scores (~0.70-0.80) for fibrosis, steatosis and inflammation. Compared to the literature for fibrosis, these are much lower, especially for the proposed scheme to other machine learning schemes. If the proposed scheme’s performance on CLD assessment is inferior to other A.I. variants processing US imaging information, why should it be published? Regarding Steatosis comparison with other popular parameters in the literature as the Hepatorenal Index (HRI) or the Controlled Attenuation Parameter (CAP) is absent. Regarding inflammation, other studies have discussed that elastography in general, provides no significant clinical information. Is this study’s result a confirmation on this aspect? Please discuss and compare with literature. Also, as there are studies in the literature having deep learning implementations on visualized elastography (e.g. Supersonic’s SWE) with far better results, why should a machine learning scheme such as this be preferred? Please also discuss.

Specific Comments:

1. Page 9, Abstract: “This ancillary study to a prospective institutional review-board approved study included 82 patients with non-alcoholic fatty liver disease, chronic hepatitis B or C virus, or autoimmune hepatitis.”

Bad English here. Also, there are some aspects that are unclear. For example, the use of the word «prospective» when in the Methods section you mention that this is a retrospective study. Also, i don’t understand the «ancillary» part that this study fulfills and is mentioned also in the Methods section. Please explain.

Reviewer #3: This paper presented a machine learning method that used QUS and pSWE to classify steatosis grade, inflammation grade, and fibrosis stage in the CLD patient population. Histopathology was used as the gold standard. Results indicated that the addition of QUS was superior than using SWE alone.

The paper was clearly written and easy to follow. The topic is of interest to the medical ultrasound community.

A few comments below:

1. One major weakness of the paper is that only Random Forrest (RF) was used. There is no other machine learning method to compare the RF results against to. It’s well known in the SWE community that due to the current challenge of high variability in SWE acquisition and measurement, SWE alone is not a reliable measurement for inflammation, fibrosis and steatosis grading. Due to the reason above, it is almost expected that combining QUS and SWE will result in improved assessment, therefore without additional method(s) to compare against it is difficult to understand the efficacy of the RF method presented here.

Recommend adding at least one additional machine learning method.

2. As we can see from Table 2, the parameters chosen for each of the binary classification tasks vary. This begs the question of how practical this RF-based method is. Furthermore, it’s perceivable that with addition of new data in the future, the parameters will change, which means that the results presented here are far from conclusive.

3. Minor comment: some of the text in the manuscript is in bold. Unclear if it follows any particular pattern. Recommend removing or cleaning up the bold formatting.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2022 Jan 27;17(1):e0262291. doi: 10.1371/journal.pone.0262291.r002

Author response to Decision Letter 0

20 Sep 2021

Please refer to the Response to Reviewers.docx document which is formatted to facilitate differentiation between reviewers' comments, responses, and modifications to the manuscript, figures, and supporting information.

Attachment

Submitted filename: Response to Reviewers.docx

Click here for additional data file. (59.9KB, docx)

Decision Letter 1

Omar Sultan Al-Kadi

26 Oct 2021

PONE-D-21-21119R1Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver diseasePLOS ONE

Dear Dr. Tang,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

Please submit your revised manuscript by Dec 10 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

  • A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.

  • A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.

  • An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: https://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols. Additionally, PLOS ONE offers an option for publishing peer-reviewed Lab Protocol articles, which describe protocols hosted on protocols.io. Read more information on sharing protocols at https://plos.org/protocols?utm_medium=editorial-email&utm_source=authorletters&utm_campaign=protocols.

We look forward to receiving your revised manuscript.

Kind regards,

Omar Sultan Al-Kadi, PhD

Academic Editor

PLOS ONE

Journal Requirements:

Please review your reference list to ensure that it is complete and correct. If you have cited papers that have been retracted, please include the rationale for doing so in the manuscript text, or remove these references and replace them with relevant current references. Any changes to the reference list should be mentioned in the rebuttal letter that accompanies your revised manuscript. If you need to cite a retracted article, indicate the article’s retracted status in the References list and also include a citation and full reference for the retraction notice.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: All comments have been addressed

Reviewer #3: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

Reviewer #3: Yes

**********

6. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Thank you for addressing my comments. I do not have any further suggestions. Congratulations

As a minor note. The authors may consider adding this paper to their discussion as well (PMID: 32622685)

Reviewer #2: (No Response)

Reviewer #3: This paper presented an ML-based method, specifically Random Forest (RF), to classify three important grades for the CLD population: steatosis, inflammation, and fibrosis. Feature sets of QUS and pSWE combind were compared against pSWE alone. When tested on a dataset of 82 patient, RF on combined feature sets outperformed pSWE alone.

The paper is clearly written and easy to follow. The dataset description is thorough, the experiment setup is clear, the results can be easily understood.

Major comments:

1. The selected feature set is different for each classification tasks. What are the overlapping features among these classification tasks?

2. RF can also rank the weights of the selected features. Which features carry more weights? This is helpful to understand, because it can help interpret the ML results further.

3. One of the biggest limitations of the paper, as mentioned in the discussion, is that only RF is presented. SVM has been reported by other papers, it would be helpful to see how the RF classifier compares against SVM given the feature sets used.

Minor comments:

1. The font size is different at a number of locations, e.g., Line 279, 281, 302, 343, 526, etc.

2. Figures appear blurry, but that could be the result of how the pdf is generated.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

Reviewer #3: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

Decision Letter 2

Omar Sultan Al-Kadi

21 Dec 2021

Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver disease

PONE-D-21-21119R2

Dear Dr. Tang,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

Kind regards,

Omar Sultan Al-Kadi, PhD

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

**********

6. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: Thank you for addressing my comments. The manuscript looks great.

I do not have any further suggestions. Thank you.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Acceptance letter

Omar Sultan Al-Kadi

14 Jan 2022

PONE-D-21-21119R2

Quantitative ultrasound, elastography, and machine learning for assessment of steatosis, inflammation, and fibrosis in chronic liver disease

Dear Dr. Tang:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Omar Sultan Al-Kadi

Academic Editor

PLOS ONE

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Supplementary Materials

    S1 Table. Accuracy of pSWE and QUS features.

    Accuracy of each of the eleven features alone and for the best combination of features for classification of steatosis, inflammation, and fibrosis. The best combination depends on the classification task; see Table 2.

    (DOCX)

    Click here for additional data file. (41.8KB, docx)
    S2 Table. ANOVA tests and post-hoc multiple comparisons when applicable for each of these features.

    Anova (AOV) test if Shapiro-Wilk (S-W) test succeeded (p-value > 1) or else Kruskal-Wallis (K-S) tests with post-hoc multiple comparison tests with Bonferroni-Holm adjustment of p-values, based on t-test in the former case, or Wilcoxon rank sum test in the latter case.

    (DOCX)

    Click here for additional data file. (39.9KB, docx)
    S3 Table. Accuracy of all eleven features obtained with 0.638+ bootstrap method.

    All features taken as input to random forests and of the best combination of features for classification of steatosis, inflammation, and fibrosis. The best combination of features depends on the classification task; see Table 2.

    (DOCX)

    Click here for additional data file. (38.8KB, docx)
    S4 Table. Dataset.

    Dataset contains patient identification from 1 to 82 (ID), steatosis grade (Steatosis), inflammation grade (Inflammation), fibrosis stage (Fibrosis), point shear wave elasticity (pSWE), μn = mean intensity normalized by its maximal value (munMean), 1/α = reciprocal of the scatterer clustering parameter (ialphaMean), k = coherent-to-diffuse signal ratio (kMean), 1/(k + 1) = diffuse-to-total signal power ratio (ikappaMean), mean intensity normalized by its maximal value inter-quartile range (munIQR), reciprocal of the scatterer clustering parameter inter-quartile range (ialphaIQR), coherent-to-diffuse signal ratio inter-quartile range (kIQR), diffuse-to-total signal power ratio inter-quartile range (ikappaIQR),total attenuation coefficient slope (TotalACS), local attenuation coefficient slope (LocalACS).

    (XLSX)

    Click here for additional data file. (19.5KB, xlsx)
    S5 Table. Importance of each parameter within the multi-parameter combinations appearing in Table 2 for the various dichotomous classification tasks.

    The reported importance is represented by the mean decrease in accuracy, where a higher value corresponds to a higher importance.

    (DOCX)

    Click here for additional data file. (41.5KB, docx)
    S6 Table. Accuracy of shear wave elasticity alone and in combination with quantitative ultrasound (QUS) features for classification of steatosis, inflammation, and fibrosis, based on support vector machine (SVM) models.

    The same combinations of parameters as in Table 2 were tested with SVM. The parameter γ of radial basis functions (RBF) was set to the reciprocal of the number of parameters (default value with R package “e1071”); the degree of RBFs was the default value 3; the cost C was varied according to powers of 2 for each combination of parameters and the best resulting AUC-ROC is reported.

    (DOCX)

    Click here for additional data file. (40.6KB, docx)
    Attachment

    Submitted filename: Response to Reviewers.docx

    Click here for additional data file. (59.9KB, docx)
    Attachment

    Submitted filename: Response to Reviewers.docx

    Click here for additional data file. (46.7KB, docx)

    Data Availability Statement

    All relevant data are within the paper and its Supporting Information files.

    Articles from PLoS ONE are provided here courtesy of PLOS

    RESOURCES