Machine learning prediction of antibody aggregation and viscosity for high concentration formulation development of protein therapeutics

ABSTRACT

Machine learning has been recently used to predict therapeutic antibody aggregation rates and viscosity at high concentrations (150 mg/ml). These works focused on commercially available antibodies, which may have been optimized for stability. In this study, we measured accelerated aggregation rates at 45°C and viscosity at 150 mg/ml for 20 preclinical and clinical-stage antibodies. Features obtained from molecular dynamics simulations of the full-length antibody and sequences were used for machine learning model construction. We found a k-nearest neighbors regression model with two features, spatial positive charge map on the CDRH2 and solvent-accessible surface area of hydrophobic residues on the variable fragment, gives the best performance for predicting antibody aggregation rates (r = 0.89). For the viscosity classification model, the model with the highest accuracy is a logistic regression model with two features, spatial negative charge map on the heavy chain variable region and spatial negative charge map on the light chain variable region. The accuracy and the area under precision recall curve of the classification model from validation tests are 0.86 and 0.70, respectively. In addition, we combined data from another 27 commercial mAbs to develop a viscosity predictive model. The best model is a logistic regression model with two features, number of hydrophobic residues on the light chain variable region and net charges on the light chain variable region. The accuracy and the area under precision recall curve of the classification model are 0.85 and 0.6, respectively. The aggregation rates and viscosity models can be used to predict antibody stability to facilitate pharmaceutical development.

Introduction

In recent years, high concentration antibody formulations have been developed for low-volume, subcutaneous administration of therapeutic antibodies and the industry is moving toward convenient, patient-centric dosing schemes that enable at-home delivery.¹ The developability properties of monoclonal antibodies (mAbs), such as low aggregation propensity and low viscosity, are essential to new drug development.^2–4 However, the stability profiles of antibodies at high concentrations are difficult to assess during early-stage discovery and candidate screening due to the limited number of molecules for which sequence, biophysical property data, and sufficient material are available. Therefore, development of predictive tools that can evaluate the developability of high concentration antibody formulation as early as possible in the discovery/development process is desired.

Computational tools have been applied to identify drug-like antibodies that have favorable stability.⁴ For viscosity prediction, Sharma et al. found that viscosity is highly correlated with variable fragment (Fv) net charge and charge symmetry and weakly correlated with hydrophobicity.⁵ Based on these three parameters, a linear equation was proposed to calculate viscosity at 180 mg/ml (pH 5.5 and 200 mM arginine-HCl).⁵ Spatial charge map (SCM) is another viscosity predictive tool calculated by molecular dynamics (MD) simulation that accounts for the exposed surface-negative charge distribution on the Fv region.⁶ Tomer et al. proposed an equation to predict the concentration-dependent viscosity curves using charges on the heavy and light chain variable regions and the hinge region and the hydrophobic surface area of full-length antibody.⁷ The comparison of these viscosity prediction tools is summarized in a recent review paper.⁸ Recently, a machine learning model based on 27 mAbs was proposed to predict antibody viscosity at 150 mg/ml.⁹ This machine learning model implements the decision tree (DT) classification method that includes two features of mAbs, net charge and high viscosity index (HVI). In addition, a coarse-grained model combined with hydrodynamic calculations and HVI-derived parameters were developed to predict viscosity at different concentrations.¹⁰ For aggregation, there are several in silico models for predicting solubility/protein aggregation rates, such as Camsol,¹¹ Solubis,¹² and developability index (DI),¹³ or identifying aggregation-prone regions, such as ANuPP,¹⁴ Aggrescan 3D,¹⁵ and spatial aggregation propensity (SAP).¹⁶ The aggregation rate tools predict the kinetic rate of proteins. The aggregation-prone regions identify specific sequences that induce aggregation, which can guide protein engineering to reduce the aggregation. Furthermore, machine learning has been applied to predict antibody amyloidogenesis (classification)^17–20 and protein aggregation kinetics (regression)^21,22 based on the sequence features. Antibody amyloidogenesis is of great concern for diseases in humans, but has limited application in the development of therapeutic proteins.²³ Moreover, a machine learning-based model that was trained on 21 mAbs was developed to predict therapeutic antibody aggregation rates at 150 mg/ml using structural-based features extracted from MD simulations.²⁴

The molecular origin of antibody aggregation and viscosity remains unclear, but hydrophobicity and charge are considered to be the two major driving forces.^23,25 Recent studies that evaluated the aggregation and viscosity of 21 mAbs showed no overlap between those with high aggregation rates and those with high viscosity,^9,24 indicating that the underlying mechanisms of aggregation and viscosity are different. Machine learning provides a great tool to find the most relevant features for aggregation and viscosity, respectively. Previous machine learning research on predicting antibody aggregation rates and viscosity used data derived from commercial mAbs, which may have gone through molecule and/or formulation optimization for stability.^9,24 Although predictive models could be applied to mAbs in early development, such studies have not been previously reported. In this work, we measured the aggregation rates and viscosity at 150 mg/ml of 20 preclinical and clinical stage mAbs. The molecules used for this study were from a subset of preclinical/clinical stage assets that were accessible from a material generation and technology development program, with the intellectual property approved for publication purposes. Machine learning regression methods such as linear regression, support vector regression (SVR) and k-nearest neighbors (KNN) regression were applied to predict antibody aggregation rates using features obtained from MD simulations of the full-length antibody. Moreover, machine learning classification methods such as logistic regression (LR), support vector machine (SVM), KNN classification, and DT classification were implemented to predict low and high viscosity with a threshold value of 30 cP. In addition to the 20 preclinical and clinical stage mAbs in this work, we included 27 commercial mAbs from our previous work to expand the training and testing dataset. From this work, we provide here the best machine learning models as aggregation and viscosity predictive tools for antibody development.

Results

Accelerated aggregation rates

An accelerated stability study at 45°C was performed to measure aggregation of 20 mAbs in a 20 mM histidine-HCl buffer, pH 6.0 at 150 mg/mL for 2 weeks. The onset temperature (Tonset) of the first thermal transition melting temperature (Tm1) for the 20 mAbs were experimentally measured as > 50°C by differential scanning calorimetry (Table S1). Therefore, this thermal stress condition should enable an accelerated screening approach to screen the propensity for mAb aggregation, without directly imparting conformational unfolding due to storage temperature. The rate of aggregation per week is reported in Figure 1 and Table S2. Five mAbs had aggregation rates over 3% per week (mAb1, mAb3, mAb9, mAb11, and mAb20).

Figure 1.

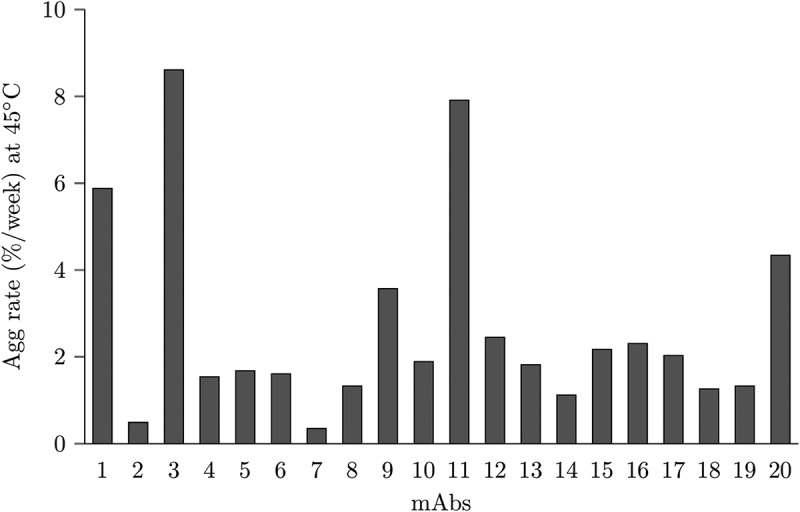
Aggregation rates of all 20 mAbs studied in this work.

Machine learning and feature selection for preclinical and clinical stage antibody aggregation rates.

We applied a machine learning protocol developed from our previous work²⁴ to predict antibody aggregation. Thirty-five structural descriptors, including solvent-accessible surface area of hydrophobic residues (SASA_phobic), solvent-accessible surface area of hydrophilic residues (SASA_philic), SAP, spatial negative charge map (SCM_neg) and spatial positive charge map (SCM_pos) on the complementarity-determining region (CDR) loops and Fv region, were used for feature selection and model building (Table 1). Surface-exposed hydrophobicity, charge patches and area have been found to correlate with antibody aggregation,^13,16,24 although the detailed mechanisms remain unknown. These could have compound effects for aggregation; therefore, all the relevant features were included for selection.

Table 1.

List of mAb properties and domains for feature selection of antibody aggregation rate. The CDR definitions are based on Chothia numbering. The feature properties are obtained from dynamic average of MD trajectories. In total, there are 35 features for selection

Feature list (mAb properties (5) x domains (7) = 35)
mAb properties	description		domains	description
Solvent accessible surface area of hydrophobic residues (SASA_phobic)	Calculated by VMD		CDRH1	H26-H32
Solvent accessible surface area of hydrophilic residues (SASA_philic)	Calculated by VMD		CDRH2	H52-H56
Spatial aggregation propensity (SAP)	In-house program		CDRH3	H95-H102
Spatial negative charge map (SCM_neg)	In-house program		CDRL1	L24-L34
Spatial positive charge map (SCM_pos)	In-house program		CDRL2	L50-L56
			CDRL3	L89-L97
			Fv	H1-H113 + L1-L107

After the preprocessing step, four features were removed because of a high correlation (r > 0.8) with other features shown in the Supporting Information (aggregation_feature_correlation_SI.xlsx). These are SAP_pos_L2, SAP_pos_L3, SASA_phobic_H1, and SASA_phobic_L1. Exhaustive one-feature and two-feature combinations using different regression models were performed to select high-performance features based on mean square error (MSE). The MSE are averaged from 100 randomly generated fourfold cross-validation sets. Table 2 lists the top 5 one-feature and two-feature combinations using linear regression, SVR and KNN models; the complete list is in the Supporting Information (aggregation_exhaustive_SI.xlsx). For the linear model, the best one-feature is SCM_neg_H2 (MSE = 5.04), and the best two-feature combination is SCM_neg_H2 and SASA_phobic_H3 (MSE = 4.81). For the SVR model, the best one-feature is SCM_pos_H2 (MSE = 4.96), and the best two-feature combination is SCM_pos_H2 and SASA_phobic_Fv (MSE = 4.12). For the KNN model, the best one-feature and two-feature combinations are the same as that for the SVR model; however, the MSE, which are 4.35 and 3.37, respectively, are much better. Overall, the KNN model is the best for predicting aggregation rates.

Table 2.

Mean squared error (MSE) of the top five one-feature and two-feature combinations of the linear regression, support vector regression (SVR) and k-nearest neighbors regression (KNN) models for predicting aggregation rates. There are 20 mAbs in this study. The MSE are averaged from 100 randomly generated fourfold cross-validation sets

	One-feature	MSE	Two-features		MSE
	SCM_neg_H2	5.04	SCM_neg_H2	SASA_phobic_H3	4.81
	SAP_pos_H1	5.31	SCM_neg_H2	SASA_philic_L3	4.97
Linear	SASA_phobic_H3	5.49	SAP_pos_L1	SCM_neg_H2	5.08
	SCM_neg_H1	5.66	SCM_neg_H1	SASA_phobic_H3	5.19
	SASA_philic_L3	5.70	SCM_neg_H2	SCM_pos_L1	5.23
	SCM_pos_H2	4.96	SCM_pos_H2	SASA_phobic_Fv	4.12
	SCM_neg_H2	5.14	SAP_pos_L1	SCM_pos_H2	4.68
SVR	SCM_pos_L3	5.43	SAP_pos_L1	SCM_neg_H2	4.89
	SASA_phobic_Fv	5.44	SAP_pos_Fv	SASA_phobic_Fv	4.90
	SAP_pos_L1	5.46	SCM_pos_H2	SCM_pos_L3	4.90
	SCM_pos_H2	4.35	SCM_pos_H2	SASA_phobic_Fv	3.37
	SCM_pos_L3	4.97	SAP_pos_L1	SCM_pos_H2	3.80
KNN	SCM_neg_H1	5.35	SCM_neg_H1	SCM_pos_H2	3.97
	SCM_pos_H1	5.59	SCM_pos_H2	SASA_philic_L3	4.21
	SAP_pos_Fv	5.65	SCM_pos_L3	SASA_philic_L1	4.73

Cross-validation for aggregation rate models

The performance of different regression models is evaluated by the leave-out-one-cross-validation (LOOCV) method. Figure 2 illustrates the linear correlation coefficients of the experimental aggregation rates and predicted rates using the best two-feature combination from the three regression models. If the correlation coefficients of LOOCV is similar to that using the whole dataset, it indicates the predictive models can be applied in predictive models for new datasets. The correlation coefficients and root mean square errors (RMSE) of the linear regression model using all 20 data and LOOCV are 0.54 and 1.88 (%/week) and 0.38 and 2.15 (%/week), respectively. The correlation coefficients and RMSE of the SVR model using all 20 data and LOOCV are 0.88 and 1.71 (%/week) and 0.69 and 1.99 (%/week), respectively. The correlation coefficients of the KNN model using all 20 data and LOOCV are 0.89 and 1.07 (%/week) and 0.79 and 1.50 (%/week), respectively. In addition, Table 3 shows the bootstrapping results of the best two-feature combinations for the three regression models. The values of correlation coefficients (0.54, 0.88, 0.89) and RMSE (1.88, 1.71, 1.07) of the regression equations using all 20 data fall within the range of standard deviation obtained from the bootstrap method (r = 0.56 ± 0.12, 0.87 ± 0.07, 0.90 ± 0.07 and RMSE 1.72 ± 0.42, 1.52 ± 0.29, 0.89 ± 0.22) for the linear, SVR and KNN models, respectively. Overall, the KNN model gives the best result for predicting antibody aggregation rates from the validation testing.

Figure 2.

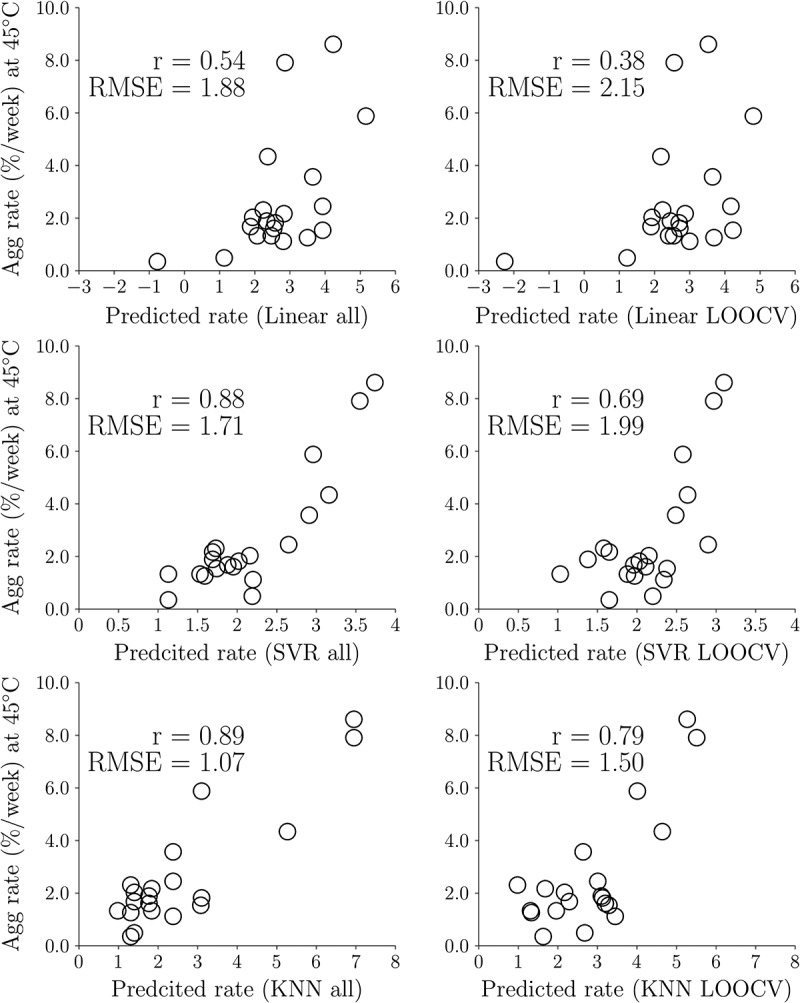
Correlation coefficients for the best two-feature linear, support vector regression (SVR) and k-nearest neighbors (KNN) regression models trained using all 20 data and LOOCV. The features for the linear regression model are SCM_neg_H2 and SASA_phobic_H3. The features for the SVR and KNN models are both SCM_pos_H2 and SASA_phobic_Fv.

Table 3.

Bootstrapping of the best two-feature combinations for the Linear, SVR and KNN regression models. In bootstrapping, the 20 data from the original dataset were randomly sampled with replacement. The regression models were generated 100 times and average value of the regression coefficients (r), RMSE and their standard deviations were calculated

	Two-features		r	RMSE
Linear	SCM_neg_H2	SASA_phobic_H3	0.56 ± 0.12	1.72 ± 0.42
SVR	SCM_pos_H2	SASA_phobic_Fv	0.87 ± 0.07	1.52 ± 0.29
KNN	SCM_pos_H2	SASA_phobic_Fv	0.90 ± 0.07	0.89 ± 0.22

Predictive models for aggregation rates

The best model for predicting aggregation rates for preclinical and clinical antibodies is the KNN model with two features, SCM_pos_H2 and SASA_phobic_Fv. Unlike linear models whose parameters are constants, the parameters for the KNN models depend on the values of the training and testing data. It is nontrivial to show the KNN models in a concise form. Therefore, the input data for the 20 antibodies are provided in the Supporting Information (aggregation_features_SI.csv) for constructing the models, which can be used to predict the aggregation rates of new antibodies. Note that we limited the models to two features so as not to overfit.

Viscosity and diffusion interaction coefficients measurements

The viscosity measurements were conducted from 80 to 250 mg/mL at multiple shear rates depending on the mAbs tested. For mAbs that exhibit shear thinning effect, the viscosity is extrapolated to zero-shear rate at different concentrations. Figure 3 depicts the viscosity interpolated at 150 mg/ml for the 20 mAbs in this study. Six mAbs exhibit high viscosity (> 30 cP), including mAb10, mAb12, mAb13, mAb14, mAb16 and mAb20. In addition, Figure 4 plots the relationship between viscosity and diffusion interaction coefficients (kD). Five high viscosity mAbs have kD values < −5 mL/g (mAb10, mAb12, mAb13, mAb16, and mAb20). Interestingly, mAb8, which has the most negative kD value (−36 mL/g), only exhibits moderate viscosity (16.07 cP) at 150 mg/mL.

Figure 3.

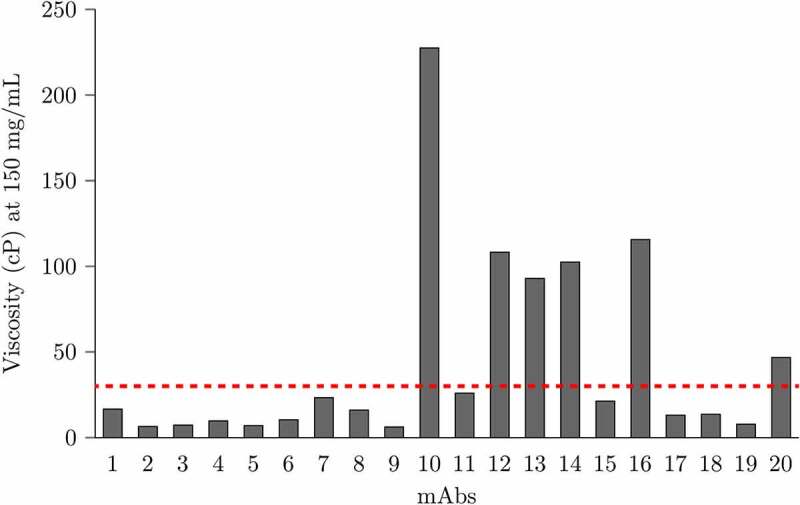
Viscosity at 150 mg/mL at pH 6.0 in histidine buffer of all 20 mAbs studied in this work. The red dashed line indicates the low/high viscosity cutoff (30 cP). A histogram showing the experimental viscosity at 150 mg/ml of 20 mAbs. The viscosity of mAb10, mAb12, mAb13, mAb14, mAb16 and mAb20 are above the high viscosity threshold 30 cP.

Figure 4.

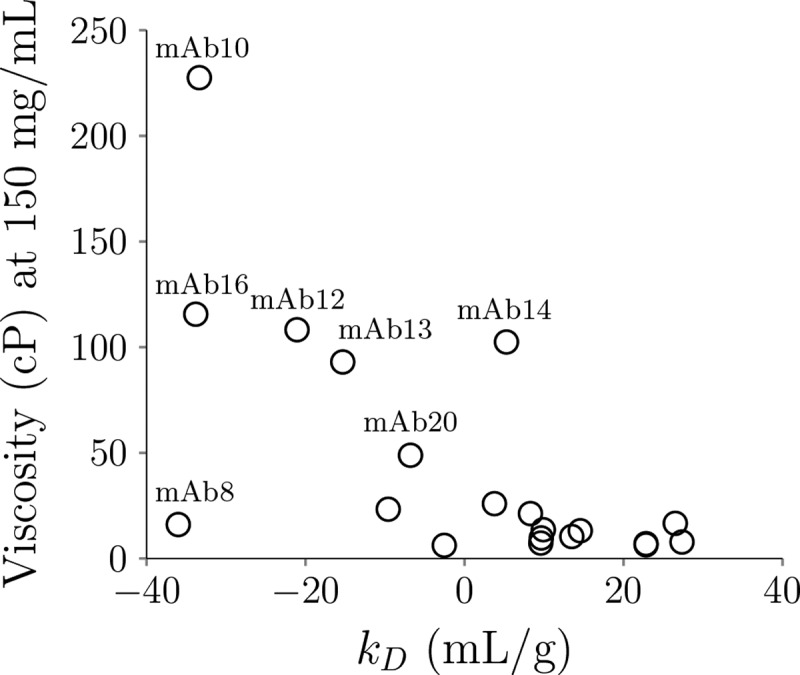
The relationship of viscosity at 150 mg/ml with the diffusion interaction coefficients (kD) for the 20 mAbs in this study. Open circles showing the viscosity on the y-axis and kD on the x-axis. Five high viscosity mAbs have kD values < −5 mL/g (mAb10, mAb12, mAb13, mAb16 and mAb20).

Previous viscosity predictive models

SCM scores and a decision tree model have been applied to predict or classify antibody viscosity.^6,9 These two approaches are used to predict viscosity of the 20 mAbs in this study, as shown in Table 4. The high viscosity for the predicted models is defined as SCM_neg_Fv > 1000, 12< mAb_chg<32 and HVI > 17.3 for the SCM model⁶ and the machine learning model,⁸ respectively. Assuming the high and low viscosity are positive and negative cases, respectively, the accuracy for the SCM model is 0.60 and the precision, recall and F1-score for the SCM model are 0.38, 0.50 and 0.43, respectively. The accuracy for the decision tree model is 0.55. The precision, recall and F1-score for the decision tree model are 0.20, 0.17 and 0.18, respectively. It should be noted that the mAb_chg criterion was 12< mAb_chg<34 in the previous work.⁹ In this study, the upper-bound charge is modified to 32 because there were no low viscosity data that have mAb_chg equal to 32 in the previous study. The new criterion does not affect the performance of the previous dataset, but can correctly predict mAb4 and mAb17 as low viscosity mAbs in this work. Based on these metrics, the SCM model predicts better than that of the decision tree model for the 20 datasets. The performance of the decision tree model for the preclinical and clinical-stage antibody data is worse than that of the commercially available antibody data reported elsewhere.² Because the decision tree model was trained using the commercial antibody, which have different molecular origins compared to the clinical-stage antibody. Therefore, it does not generalize well to the clinical-stage antibody data.

Table 4.

Viscosity classification accuracy (ACC) of the 20 mAbs in this study using the SCM score and the machine learning model from a previous work. Predicted and experimental high viscosity are shaded in gray. The high viscosity is defined as SCM_neg_Fv > 1000, 12< mAb_chg<32 and HVI>17.3, and Vis_exp > 30 cP, respectively. Correct predictions are labeled as 1, and wrong predictions are labeled as 0

	SCM_neg_Fv	mAb_chg	HVI	Vis_exp (150 mg/ml)		SCM_pred	ML_pred
mAb1	772.7	28	14.60	16.64		1	1
mAb2	1214.6	20	15.56	6.49		0	1
mAb3	869	28	17.02	7.30		1	1
mAb4	870	32	23.38	9.72		1	1
mAb5	1055	24	19.74	7.03		0	0
mAb6	507.6	28	14.98	10.41		1	1
mAb7	1010.2	26	16.09	23.33		0	1
mAb8	2156.2	4	12.45	16.07		0	1
mAb9	808.1	12	10.04	6.23		1	1
mAb10	667.5	24	16.74	227.54		0	0
mAb11	987.2	24	18.26	25.95		1	0
mAb12	767	30	13.79	108.25		0	0
mAb13	1089.1	22	20.18	93.00		1	1
mAb14	993.9	24	17.11	102.46		0	0
mAb15	993.6	26	20.6	21.26		1	0
mAb16	1151.8	18	16.45	115.60		1	0
mAb17	763	32	22.52	13.14		1	1
mAb18	886.9	24	12.72	13.63		1	1
mAb19	1294.7	26	22.47	7.80		0	0
mAb20	1292.7	20	16.59	48.86		1	0
					ACC (%)	60	55

Machine learning and feature selection for preclinical and clinical stage antibody viscosity

Commercially available antibodies are likely to have gone through stability optimization processes prior to lead candidate molecule selection. Some unstable molecular regions may have been removed. Using data on these marketed mAbs for model training is not ideal for predicting preclinical and clinical-stage antibody viscosity. In this study, the machine learning protocol we previously proposed was applied to develop new predictive models for the preclinical and clinical stage mAb data. These molecules include 18 IgG1 and 2 IgG4P isotypes, with an even distribution of lambda and kappa light chains (Table S1). Five of them have high viscosity (>30 cP) at 150 mg/ml. The commercial mAb dataset include 21 IgG1, 4 IgG2 and 2 IgG4 isotype mAbs, with 1 lambda and 26 kappa light-chain molecules.⁹ Six of them have high viscosity at 150 mg/ml. The decision tree model trained from the imbalanced number of kappa and lambda light chains for the commercial mAbs could be the reason for low accuracy when predicting the preclinical/clinical stage molecules, which contain 10 IgG1 mAbs with lambda light chain (Table 4). Additionally, comparing the molecular descriptors of commercial and early-stage mAbs, we found SAP_pos_Fv is statistically different between these two groups (Table S3), which may have gone through different screening and optimization procedures. These are the rationales for developing new predictive models for the preclinical/clinical stage mAbs.

Table 5 lists the 35 features used for selection and model construction. These features include the number of hydrophobic residues (N_phobic), the number of hydrophilic residues (N_philic), the number of positive residues (N_pos), the number of negative residues (N_neg), net charges, charge symmetric parameter (CSP), SAP, SCM_neg, SCM_pos, and HVI on all or some of the heavy chain variable region (VH), light chain variable region (VL), Fv and mAb domains. Four different classification algorithms (LR, SVM, KNN and DT) were used to select features and evaluate model performance using exhaustive one-feature and two-feature combinations. The model performance is evaluated by accuracy (ACC) and the area under precision-recall curve (AUPRC). The ACC and AUPRC are averaged from 100 randomly generated 4-fold cross-validation sets.

Table 5.

List of mAb properties and domains for feature selection of antibody viscosity. The structural features (SAP, SCM pos and SCM neg) are obtained from dynamic average of MD trajectories. Other features are extracted from antibody sequences. Charge symmetry parameters are calculated for Fv and mAb domains (2). High viscosity index is calculated for Fv domain (1). The remaining properties are calculated for VH, VL, Fv and mAb domains (8x4 = 32). In total, there are 35 features for selection

Feature list
mAb properties	description		domains	description
Number of hydrophobic residues (N_phobic)	A,F,I,L,M,P,V,W		VH	H1-H113
Number of hydrophilic residues (N_philic)	S,T,N,Q,Y,K,R,H,D,E		VL	L1-L107
Number of positive residues (N_pos)	K,R,H		Fv	H1-H113 + L1-L107
Number of negative residues (N_neg)	D,E		mAb	Full length
Net charges	Calculated by PROPKA3
Charge symmetric parameter (CSP)	Product of heavy and light chain charge
Spatial aggregation propensity (SAP)	In-house program
Spatial positive charge map (SCM_pos)	In-house program
Spatial negative charge map (SCM_neg)	In-house program
High viscosity index (HVI)	In-house program

Table 6 summarizes the classification results for different models. The complete list is in the Supporting Information (viscosity_exhaustive_SI.xlsx). The ACC and AUPRC for the baseline model are 0.70 and 0.30, respectively. The ACC and AUPRC of the best one-feature combinations for the four classification models range from 0.73 to 0.79 and from 0.47 to 0.59, respectively, showing slight improvement compared to that of the baseline model. However, the ACC and AUPRC of the best two-feature combinations for the four models range from 0.83 to 0.86 and from 0.64 to 0.74, respectively, which are significantly better than that of the baseline model.

Table 6.

Accuracy (ACC) and area under the precision-recall curve (AUPRC) of the top five one-feature and two-feature combinations of the logistic regression (LR), support vector machine (SVM), k-nearest neighbors (KNN) and decision tree (DT) models for classifying low/high viscosity. There are 20 mAbs in this study. The ACC and AUPRC are averaged from 100 randomly generated 4-fold cross-validation sets. The baseline ACC is 0.70 and the baseline AUPRC is 0.30

	One-feature	ACC	AUPRC	Two-features		ACC	AUPRC
	N_neg_VH	0.79	0.57	SCM_neg_VH	SCM_neg_VL	0.86	0.70
	SCM_neg_VL	0.77	0.54	N_neg_VH	SCM_neg_VL	0.84	0.68
LR	net charges_VH	0.78	0.53	N_neg_VH	net charges_VL	0.83	0.67
	N_neg_VL	0.77	0.51	SCM_neg_VL	SCM_pos_VH	0.83	0.66
	net charges_VL	0.74	0.48	net charges_VH	net charges_VL	0.81	0.65
	N_neg_VH	0.76	0.47	N_philic_VH	SAP_pos_VL	0.82	0.64
	net charges_VH	0.74	0.46	N_philic_Fv	SAP_pos_VL	0.82	0.63
SVM	SCM_neg_VL	0.72	0.45	N_philic_Fv	N_neg_VH	0.82	0.60
	mAbCSP	0.74	0.37	N_phobic_VL	N_neg_VH	0.82	0.60
	N_neg_VL	0.70	0.34	N_philic_VH	N_neg_VH	0.81	0.58
	HVI	0.76	0.59	N_pos_VL	N_neg_VH	0.83	0.66
	SAP_pos_VL	0.82	0.65	N_philic_Fv	FvCSP	0.82	0.64
KNN	SCM_neg_VL	0.74	0.52	N_pos_VL	net charges_VH	0.83	0.64
	net charges_VH	0.78	0.51	SCM_neg_VH	SCM_neg_VL	0.82	0.62
	N_neg_VH	0.78	0.5	N_philic_VH	FvCSP	0.76	0.62
	SAP_pos_VL	0.73	0.52	N_phobic_VL	SAP_pos_VL	0.84	0.74
	net charges_VH	0.77	0.51	N_neg_Fv	SCM_pos_VL	0.78	0.60
DT	N_neg_mAb	0.79	0.51	N_neg_mAb	net charges_VL	0.77	0.60
	SCM_pos_VL	0.75	0.49	N_neg_mAb	SCM_neg_VL	0.76	0.58
	N_neg_VH	0.76	0.49	N_phobic_VL	net charges_VH	0.79	0.56

Predictive models for preclinical and clinical stage antibody viscosity

The predictive models for the LR and DT models based on the 20 preclinical and clinical-stage antibodies are provided to classify low/high viscosity for new data. The high viscosity threshold is above 30 cP. The LR model is

$$\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}:-1.1\ast \mathrm{S}\mathrm{C}\mathrm{M}\mathrm{\_}\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{\_}\mathrm{V}\mathrm{H}+1.3\ast \mathrm{S}\mathrm{C}\mathrm{M}\mathrm{\_}\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{\_}\mathrm{V}\mathrm{L}-0.86>0$$

The features need to be scaled by their means and standard deviations. The mean and standard deviation for SCM_neg_VH are 540.81 and 241.47, respectively. The mean and standard deviation for SCM_neg_VL are 466.72 and 155.21, respectively. If the predictive model is greater than 0, it is predicted to be high viscosity. Moreover, the DT model is

$$\left\{\begin{array}{c}Lowviscosity:SAP\mathrm{\_}pos\mathrm{\_}VL\le 38.05\\ \left\{\begin{array}{c}Lowviscosity:SAP\mathrm{\_}pos\mathrm{\_}VL38.05andN\mathrm{\_}phobic\mathrm{\_}VL39.50\\ Highviscosity:SAP\mathrm{\_}pos\mathrm{\_}VL38.05andN\mathrm{\_}phobic\mathrm{\_}VL\le 39.50\end{array}\right.\end{array}\right.$$

The feature values are not scaled. The predictive models for SVM and KNN can be obtained by training the 20 mAb data using the corresponding best two-feature combinations in the Supporting Information (viscosity_features_SI.csv).

Machine learning and feature selection for combined preclinical and clinical stage and commercial antibody viscosity

One of the major challenges in applying machine learning to predict antibody stability at high concentration is developing robust models with a limited amount of data. In previous work, our group has trained a viscosity classification model using 27 commercial mAbs.⁹ In this study, the viscosity of 20 preclinical and clinical stage mAbs were measured in a similar solution condition as that of the previous work (histidine/histidine-HCl buffer at pH 6.0, without surfactant and other excipients). A Chinese hamster ovary expression system used to produce the material and, following purification, the starting monomer purity was >95%. In both studies, the viscosity was measured at 18–20°C by VROC Initium viscometer at multiple shear rates. For the 27 commercial mAbs, non-Newtonian effects were assumed. In this study, we found non-Newtonian effects for low viscosity mAbs were negligible, but significant for high viscosity mAbs. For high viscosity mAbs, viscosity was extrapolated to zero-shear rate.

In order to expand the data size, we combined the two datasets for machine learning training. In total, there are 47 data that cover preclinical, clinical and commercial mAbs. The same protocol and features were used as those for the 20 preclinical and clinical mAbs described previously. Table 7 shows the top 5 one-feature and two-feature combinations for different classification models. The complete list is in the Supporting Information (viscosity_exhaustive_combined_SI.xlsx). The ACC and AUPRC for the baseline model are 0.74 and 0.26, respectively. The best one-feature for the LR, SVM and DT models are the same, mAbCSP, which have the same ACC (0.81) and similar AUPRC (0.47 to 0.49). Similarly, the best two-feature combinations for the LR, SVM and DT models are also the same, N_phobic_VL and net charges_VL (ACC = 0.83 to 0.85 and AUPRC = 0.53 to 0.60). On the other hand, the best one-feature for the KNN model is net charges_mAb (ACC = 0.78; AUPRC = 0.47). The best two-feature combination for the KNN model is N_neg_Fv and net charges_VL (ACC = 0.85; AUPRC = 0.57).

Table 7.

Accuracy (ACC) and area under the precision-recall curve (AUPRC) of the top five one-feature and two-feature combinations of the logistic regression (LR), support vector machine (SVM), k-nearest neighbors and decision tree (DT) models for classifying low/high viscosity. There are 20 mAbs in this study plus 27 mAbs from the literature. The ACC and AUPRC are averaged from 100 randomly generated 4-fold cross-validation sets. The baseline ACC is 0.74 and the baseline AUPRC is 0.26

	One-feature	ACC	AUPRC	Two-features		ACC	AUPRC
	mAbCSP	0.81	0.49	N_phobic_VL	net charges_VL	0.85	0.60
	net charges_VL	0.76	0.39	N_phobic_VL	mAbCSP	0.85	0.58
LR	N_neg_VL	0.77	0.37	net charges_VL	HVI	0.84	0.56
	FvCSP	0.76	0.36	N_phobic_Fv	net charges_VL	0.84	0.56
	N_pos_VL	0.75	0.35	N_phobic_mAb	net charges_VL	0.83	0.55
	mAbCSP	0.81	0.47	N_phobic_VL	net charges_VL	0.83	0.53
	net charges_mAb	0.77	0.37	N_philic_mAb	mAbCSP	0.83	0.51
SVM	net charges_VL	0.76	0.37	net charges_mAb	mAbCSP	0.83	0.50
	N_pos_VL	0.73	0.29	N_neg_VH	net charges_mAb	0.82	0.49
	net charges_VH	0.75	0.28	net charges_VL	net charges_mAb	0.82	0.49
	net charges_mAb	0.78	0.47	N_neg_Fv	net charges_VL	0.85	0.57
	N_phobic_VH	0.77	0.42	net charges_VL	net charges_mAb	0.82	0.53
KNN	net charges_VL	0.78	0.42	net charges_VH	net charges_mAb	0.82	0.53
	mAbCSP	0.76	0.41	N_philic_VL	net charges_VL	0.82	0.53
	SAP_pos_VL	0.73	0.39	mAbCSP	HVI	0.80	0.53
	mAbCSP	0.81	0.47	N_phobic_VL	net charges_VL	0.85	0.57
	SAP_pos_mAb	0.75	0.41	net charges_VL	net charges_mAb	0.84	0.56
DT	net charges_mAb	0.75	0.40	N_philic_VL	net charges_VL	0.84	0.54
	net charges_VL	0.76	0.39	SAP_pos_mAb	FvCSP	0.78	0.48
	net charges_VH	0.76	0.35	SCM_pos_VL	mAbCSP	0.80	0.48

Predictive models for antibody viscosity from combined datasets

The predictive models for the LR and DT models using the 20 preclinical and clinical stage and the 27 commercial antibodies are provided to classify low/high viscosity for new data. The LR predictive model is

$$\mathrm{H}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{t}\mathrm{y}:-0.72\ast \mathrm{N}\mathrm{\_}\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{c}\mathrm{\_}\mathrm{V}\mathrm{L}-1.17\ast \mathrm{n}\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{s}\mathrm{\_}\mathrm{V}\mathrm{L}-1.19>0$$

The features need to be scaled by their means and standard deviations. The mean and standard deviation for N_phobic_VL are 37.91 and 2.70, respectively. The mean and standard deviation for net charges_VL are 0.64 and 1.93, respectively.

The DT predictive model is

$$\begin{array}{c}Lowviscosity:netcharges\mathrm{\_}VL>-0.50\\ \begin{array}{c}Lowviscosity:netcharges\mathrm{\_}VL\le -0.50andN\mathrm{\_}phobic\mathrm{\_}VL>38.0\\ Highviscosity:netcharges\mathrm{\_}VL\le -0.50andN\mathrm{\_}phobic\mathrm{\_}VL\le 38.0\end{array}\end{array}$$

Similarly, these feature values are unscaled. In addition, the predictive models for SVM and KNN can be constructed by training the 47 mAb data using the best two-feature combination in the Supporting Information (viscosity_features_combined_SI.csv).

Discussion

In this study, we measured the aggregation rates and viscosity of 20 preclinical and clinical stage mAbs at high concentration. Antibodies having the top 5 highest aggregation rates are mAb1, mAb3, mAb9 and mAb11 and mAb20, and the top 5 highest viscosity are mAb10, mAb12, mAb13, mAb14 and mAb16. Interestingly, these groups of mAbs do not overlap, suggesting that the driving forces for antibody aggregation and viscosity may be different.

Antibody self-association is considered to promote high viscosity.²⁶ Diffusion interaction coefficients (kD) are commonly used to measure protein–protein interactions, although their relationship to predict viscosity remains controversial.^27,28 Figure 4 shows that most high viscosity mAbs have large negative kD values; however, mAb8, which has the most negative kD value exhibits low viscosity. From the SCM score in Table 4, mAb8 has the highest SCM score, indicating strong electrostatic interactions due to negative charge patches on the Fv region, which supports the experimental kD measurement. Kingsbury et al. recently found that antibody solutions that have large negative kD values could exhibit either high viscosity or high opalescence.²⁷ We found that mAb8 also exhibits high solution opalescence, which agrees with the previous finding. Although kD or the SCM score cannot distinguish high viscosity and high opalescence, they are still good indicators for poor stability.

The protocol and machine learning features described in this paper are built on our previous works.^6,9,16,24 Because of the limited availability of high concentration therapeutic antibody aggregation and viscosity data, it is of great value to evaluate the performance of existing models and improve the predictive models using larger datasets.

We applied machine learning to predict the antibody aggregation rates at 45°C in a 20 mM histidine-HCl buffer, pH 6.0 at 150 mg/mL based on 20 preclinical and clinical stage mAbs. It is worth noting that the ranking of aggregation tendency may differ and the accelerated thermal stress conditions may not always correlate to real-time stability at the intended storage conditions. This may be due to differences in the molecular origins of degradation pathways, impacting the physicochemical stability and resulting in conformational changes of the protein structure.^29–31 The accelerated stability condition described here provides a screening approach to assess the propensity for aggregation, especially in a controlled matrix (i.e., base buffer, with no stabilizing excipients). Of course, the approach that we present here can be used to parameterize the model at any conditions. In previous work, we developed an aggregation rate model at 40°C in a 10 mM histidine-HCl buffer, pH 6.0 at 150 mg/mL based on 21 commercial antibodies.²⁴ Although the solution conditions (buffer and pH) are similar for the two datasets, the difference in the temperature makes the aggregation rates very different even for the same antibody (data not shown). As such, the previous model may not be directly applicable to the data at 45°C. Therefore, new models were built using a similar protocol as the previous work.²⁴ In this study, we found the best aggregation rates model is the KNN model, which agrees with our previous work.²⁴ The best two-feature combination of the KNN model is SCM_pos_H2 and SASA_phobic_Fv. Hydrophobicity has been used to predict antibody aggregation in earlier works.^13,16 In addition, in our previous work, we also found SCM_pos is an important feature for the antibody aggregation rate. It should be noted that SCM includes a distance cutoff of 10 Å, so SCM_pos_H2 does not mean only the positive charges on the CDRH2 region are important. Residues surrounding CDRH2 should be also considered.

It has been suggested that, due to their complex nature, mAb degradation pathways may or may not follow Arrhenius behavior/kinetics. Therefore, expanding this approach to extrapolate to real-time storage for predicting shelf-life considerations could be difficult. Recently, Kuzman et al. and Gentiluomo et al. have shown some potential for predicting long-term shelf-life stability when using non-linear machine learning models.^32,33 This, however, also leads to some challenges when assuming first-order kinetics of proteins that may be susceptible to different degradation pathways that may affect chemical and physical stability upon exposure to thermal stress.³⁴ Therefore, the accelerated stability and real-time stability measurements are different approaches. Of course, long-term data could easily be used to train our model using our methodology.

Two sets of antibody viscosity data for 47 mAbs in total were used for training and testing. In this study, the viscosity of 20 preclinical and clinical stage mAbs were measured. In our previous study, the viscosities of 27 commercial antibodies were measured. We performed a blind test by using the ML model, trained from the 27 commercial antibodies, to predict the 20 investigational antibodies in this study (Table 4), and the results were not satisfactory. Because of the limited dataset, training on a subset of data is prone to find features not the most relevant for viscosity. In order to generalize our predictive models, we decided to combine both datasets for the ML algorithms to capture the common features. The experimental conditions are very similar (pH = 6.0 in 10–20 mM histidine-HCl buffer at 18–20°C), and for binary classification, slight viscosity variation from equipment setup and operation do not change the overall low/high viscosity categories. The DT model obtained from the commercial mAbs were applied to predict preclinical and clinical stage mAb data. The accuracy was only 0.55, indicating that the underlying mechanism of the preclinical and clinical mAbs could be different from the marketed mAbs so that the DT model does not capture these features. By using the same protocol, new predictive models based on the 20 new data were developed. The performance for these classification models is similar (ACC = 0.82 to 0.86; AUPRC = 0.64 to 0.74), although the best two-feature combination for each model varies. Conversely, the best LR, SVR and DT models for the combined 47 datasets share the same one-feature and two-feature combinations. As the number of datasets increases, only the most important feature combinations are selected despite the statistical models implemented. The best two features are N_phobic_VL and net charges_VL. Both hydrophobicity and net charges are reported to be related to antibody viscosity. The machine learning models provide a quantitative relationship to connect them with antibody viscosity. These two features are sequence-based descriptors, which can be implemented very efficiently. Why only the VL regions matter to the viscosity prediction is still unknown. More data are needed to validate these models.

Although there are some public databases for antibody aggregation and protein aggregation kinetics such as CPAD 2.0,³⁵ these data focus primarily on amyloid aggregates. These amyloid aggregates are related to immunogenicity in animal models, but are of limited utility for pharmaceutical proteins.²³ Currently, there is no public database available for therapeutic antibody aggregation rates and viscosity at high concentrations. Data from published literature could be performed in different solution conditions (pH, buffers, excipients, and protein concentrations), but very often the sequence information is not available. This is one of the major challenges for applying machine learning to predict antibody stability. In addition, because high concentration antibodies are expensive to produce, it is not feasible to obtain a large number from one source with sufficient amount of data for machine learning applications. Combining the datasets from different sources with proper pre-experimental designs as performed in this study is a possible solution.

Materials and methods

Protein preparation

The 20 mAbs used for this study were internally manufactured at AstraZeneca (Gaithersburg, MD) and consisted of a combination of 18 IgG1and 2 IgG4P subclass mAbs (Table S1). The protein solutions were obtained as bulk Drug Substance, in a molecule-respective, non-surfactant containing, formulation buffer. The starting monomer purity for each mAb was >95% as measured by high-performance size exclusion chromatography (HPSEC; Agilent Technologies Santa Clara, CA) using a TSK-Gel G3000SWXL HPLC column (Tosoh Bioscience LLC, Montgomeryville, PA) and mobile phase comprised of 0.1 M sodium phosphate dibasic anhydrous, 0.1 M sodium sulfate, and 0.05 M sodium azide at pH 6.8 with 250 µg protein injection. The mAbs solutions were individually buffer exchanged into a formulation buffer of 20 mM histidine-HCl at pH 6.0 using 10 K MWCO Slide-A-Lyzer dialysis cassette (Thermo Scientific). Dialysis was performed overnight with multiple buffer exchanges at a minimum buffer-to-protein solution ratio of 1000:1. The dialyzed product was tested to meet the appropriate pH and osmolality requirements. The samples were then concentrated using Amicon Ultra-4 Centrifugal Filter units with 10 K MWCO (EMD Millipore, Merck KGaA, Darmstadt, Germany) to a target concentration of 150 mg/mL. Total protein was measured using a UV-vis spectrophotometer (Trinean DropSense 96, Unchained Labs Pleasanton, CA) with respective mAb experimentally determined extinction coefficients and corrected for density when necessary.

Measurement of accelerated aggregation rates

Samples were 0.22 µm filtered (PVDF membrane, EMD Millipore, Merck KGaA, Darmstadt, Germany) and aseptically hand filled into 2 R glass vials (Std Type 1, USP; Schott) with rubber stoppers (13 mm chlorobutyl, Diakyo/West Pharmaceutical Services) and aluminum overseals (13 mm, West Pharmaceutical Services). Samples were placed in a temperature and humidity-controlled incubation chamber with setpoints of 45°C and 75% relative humidity. The vials were aseptically sampled on 2-day intervals for a total duration of 2 weeks. The pulled samples were prepared for HPSEC analysis by diluting to 10 mg/mL with 0.2 µm filtered formulation buffer and 250 µg of protein injected (similar to method described above). The rate of aggregation was determined using linear regression of the total content of aggregates over the timecourse of the stability study (Table S2).

Measurements of viscosity

Viscosity was measured at multiple concentrations (3–6 concentrations each construct) ranging from 80 mg/mL to 250 mg/mL dependent on mAb sample; all samples included at least one measurement of concentrations >150 mg/mL aside from mAb 11, which was measured at a highest concentration of 142 mg/mL due to material constraints. All mAb samples were formulated in 20 mM histidine-HCl buffer at pH 6.0. Prior to concentration and viscosity measurement, samples were passed through a 0.45 µm filter. Concentration was determined using the UV-vis spectrophotometry method described above.

Using a VROC Initium viscometer (Rheosense, San Ramon, CA), viscosities were determined at multiple shear rates between 300 and 50,000 s⁻¹ with a B05 or E02 measuring chip where appropriate to ensure optimal pressure across the sensor array of the chip. Approximate zero shear viscosity for each sample exhibiting shear thinning was estimated through extrapolation of measured viscosities across multiple shear rates. The viscosity at 150 mg/mL was then interpolated by a best fit equation of natural log of viscosity vs concentration for each construct.

Measurements of diffusion interaction parameters

The diffusion interaction parameter (k_D) was calculated using measurements obtained from experimental diffusion coefficient as a function of total protein concentration (DynaPro Plate Reader II -Wyatt, Santa Barbara, CA). Protein samples were equilibrated to room temperature and titrations were prepared at 2, 4, 6, 8, and 10 mg/mL in formulation buffer (20 mM histidine-HCl, pH 6.0) and filtered using a 0.22 um syringe filter. Using a low volume 384-well plate (Corning, Tewksbury, MA), samples were meticulously aliquot in triplicate (35 µL each). A run method protocol was written using the Dynamics software package (Wyatt, Santa Barbara, CA; version 7.1.9.3) to analyze samples at 25°C using an 830-nm laser and the sample acquisitions were set to 5 seconds, with 10 total acquisitions collected for each sample run. Correction factors such as viscosity and refractive index were also provided prior to sample analysis. The data was exported to excel and plots created to determine the slope and y-intercept for the diffusion coefficient versus total protein concentration. The k_D was subsequently calculated by taking the ratio of the slope and the y-intercept values.

Computational modeling of mAbs

The mAb molecules were constructed following the protocol proposed by Brandt et al.³⁶ Briefly, the structure of antigen-binding fragment (Fab) region was superimposed on a template structure obtained from the KOL/Padlan structure.^37,38 The immunoglobulin G1 (IgG1) template was obtained from the KOL/Padlan structure. For IgG4 models, the Fc regions (PDB: 4C54) were superimposed on the KOL/Padlan IgG1 structure. The Fab structure was retrieved from either available crystal structures or homology model built from RosettaAntibody.^39–41 Disulfide bridges were carefully matched to the respective isotypes. The glycosylation pattern for each mAb was modeled according to available literature data. For mAbs without literature data on the glycosylation pattern, the G₀F glycosylation pattern was chosen.

Molecular dynamics simulations

Molecular dynamics simulations were performed using all-atom structures with explicit solvent using the TIP3P water model.⁴² Simulation boxes were set up using visual MD to place a single antibody in a water box extending 12 Å beyond the protein surface.⁴³ Simulations were performed at 300 K and 1 atm in the NPT ensemble, using the NAMD software package and the CHARMM36m force field.^44–46 The system pH was set to 6.0 to match the experimental pH by adjusting the protonation states of histidine residues using the PROPKA3 protocol.⁴⁷ Electrostatic interactions were treated with the Particle Mesh Ewald (PME) method and van der Waals interactions were calculated using a switching distance of 10 Å and a cutoff of 12 Å.⁴⁸ The integration time step was set to 2 fs. Each mAb system was pre-equilibrated for 10 ns, followed by 50 ns production runs.

Feature selection for aggregation rates and viscosity

Based on a previous study, structural features obtained from MD simulations were extracted for building regression models for aggregation rates.²⁴ Table 1 lists the features used for aggregation rates in this work. We included structural features such as SASA_phobic, SASA_philic, SAP and SCM_neg and SCM_pos covering 6 CDR and 1 Fv regions for selection.²⁴ In total, there are 35 features (see supporting information: aggregation_features_SI.csv for details). They were calculated from averaging 50 ns MD trajectories. The 50 ns simulation is long enough to obtain converged feature values, but may not capture large conformational change of antibodies. In the preprocessing step, highly correlated features (correlation coefficient > 0.8) were filtered to keep only one of them from each pair. The features for viscosity classification contain both structural and sequence descriptors (Table 5) as described previously.⁹ In total, there are 35 features (see Supporting Information: viscosity_features_SI.csv for details).

For each machine learning method described in the next section, exhaustive feature selection for one-feature and two-features were performed to search for the best feature combinations using the exhaustive feature selector tool from mlxtend library.⁴⁹ The best feature combinations for the regression models were selected based on their mean squared errors. The best feature combinations for the classification models were selected based on their AUPRC. AUPRC was chosen because the dataset contains an imbalanced number of high and low viscosity antibodies.

Machine learning methods for aggregation rates and viscosity

All the machine learning methods were implemented using the scikit-learn library.⁵⁰ The protocols follow our previous works.^9,24 Briefly, different regression models were used for aggregation rates including linear regression (linear_model.LinearRegression()), nearest neighbors regression (neighbors.KNeighborsRegressor()) and support vector regression (svm.SVR()). For viscosity classification, logistic regression (linear_model.LogisticRegression()), support vector machine (linear_model.svm()), nearest neighbors classification (neighbors.KNeighborsClassifier()) and decision tree classification (tree.DecisionTreeClassifier()) models were employed. The functions utilized from the scikit-learn library were specified in the parentheses. The default parameters were used for all functions, except the number of neighbors in the KNN models is 3 and the maximum depth in the DT models is 2.

Funding Statement

The author(s) reported there is no funding associated with the work featured in this article.

Abbreviations

CDRcomplementarity-determining region

CDRH1 the first complementarity-determining region of the heavy chain

CDRH2 the second complementarity-determining region of the heavy chain

CDRH3 the third complementarity-determining region of the heavy chain

CDRL1 the first complementarity-determining region of the light chain

CDRL2 the second complementarity-determining region of the light chain

CDRL3 the third complementarity-determining region of the light chain

CSP charge symmetric parameter

DT decision tree

Fv variable fragment

HVI high viscosity index

IgG1 immunoglobulin G1

KNNk- nearest neighbors

LOOCV Leave-out-one-cross-validation

LR logistic regression

mAbs monoclonal antibodies

MD molecular dynamics

MSE mean square error

N_negnumber of negative residues

N_philicnumber of hydrophilic residues

N_phobicnumber of hydrophobic residues

N_posnumber of positive residues

RMSE root mean square error

SAP spatial aggregation propensity

SASA solvent-accessible surface area

SCM spatial charge map

SVM support vector machine

SVR support vector regression

Tonsetonset temperate

Tm1 first thermal transition melting temperature

VHheavy chain variable region

VLlight chain variable region

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary material

Supplemental data for this article can be accessed on the publisher’s website