Synchronous inhibitory pathways create both efficiency and diversity in the retina

Significance

Complex connections in neural circuits make it difficult to quantitatively assign even the most basic neural computations to the actions of specific neurons. Retinal ganglion cells are most sensitive to changes in intensity across space and over time. This property, caused by a region known as the receptive field surround, improves information transmission about natural scenes. We dynamically manipulated individual interneurons to directly measure their effect on retinal receptive fields, finding that two inhibitory neuron types, horizontal cells and amacrine cells, synchronously create the same contribution to the receptive field surround at different spatial scales. By analyzing large populations of ganglion cells, we show that this arrangement increases diversity in retinal signaling while preserving maximal information transmission about natural scenes.

Abstract

Sensory receptive fields combine features that originate in different neural pathways. Retinal ganglion cell receptive fields compute intensity changes across space and time using a peripheral region known as the surround, a property that improves information transmission about natural scenes. The visual features that construct this fundamental property have not been quantitatively assigned to specific interneurons. Here, we describe a generalizable approach using simultaneous intracellular and multielectrode recording to directly measure and manipulate the sensory feature conveyed by a neural pathway to a downstream neuron. By directly controlling the gain of individual interneurons in the circuit, we show that rather than transmitting different temporal features, inhibitory horizontal cells and linear amacrine cells synchronously create the linear surround at different spatial scales and that these two components fully account for the surround. By analyzing a large population of ganglion cells, we observe substantial diversity in the relative contribution of amacrine and horizontal cell visual features while still allowing individual cells to increase information transmission under the statistics of natural scenes. Established theories of efficient coding have shown that optimal information transmission under natural scenes allows a diverse set of receptive fields. Our results give a mechanism for this theory, showing how distinct neural pathways synthesize a sensory computation and how this architecture both generates computational diversity and achieves the objective of high information transmission.

The interconnected architecture of the nervous system makes it a challenge to understand the circuit origin of neural computations and the functional advantages of those circuits. Despite new recording and neurostimulation techniques (1, 2), even widely studied computations such as the sensory receptive fields of retinal ganglion cells and orientation selective cells in the visual cortex have not been quantitatively assigned to their neural components (3–5).

The linear receptive field represents the average sensory feature conveyed by a neuron to the next stage of processing and is a compact summary of the cell’s neural code. Although ganglion cells have numerous nonlinear properties of adaptation and selectivity for different types of stimuli involving motion and other visual features (6, 7), the linear receptive field is the most widely studied property of sensory neurons. As such, it has led to an understanding of how the nervous system represents sensory stimuli in neural populations (8) and how the receptive field surround increases the efficiency of information transmission (9, 10).

Linear computations pose an added difficulty in establishing the mechanisms that generate the neural code, as neural pathways that carry the same signals and are summed without distortion cannot be separately identified without a selective way to perturb each component. Both horizontal and amacrine cells are thought to contribute to the ganglion cell receptive field surround, as indicated by current injection into horizontal cells (11, 12), and pharmacological experiments on amacrine cells, although these latter studies have yielded conflicting results (13–15). In addition, several studies have removed the function of the horizontal cell population by genetic or chemogenetic manipulations, concluding that they contribute to the receptive field surround (16–19). However, these studies using slow manipulations leave room for compensatory effects that can occur on timescales as short as seconds to minutes. Other results from our previous work show that to accurately measure the computational effect of an interneuron, it is necessary to dynamically perturb an interneuron in a way that matches the visually driven responses experienced by the interneuron (20). Consequently, the spatiotemporal features contributed by horizontal and amacrine cells to the ganglion cell linear receptive field have not been directly and quantitively measured, and the functional benefits of utilizing such an architecture with two distinct components are not understood.

Here, we use an approach to directly and quantitatively measure the contribution of an interneuron to a neural computation in a circuit. Using simultaneous intracellular recording and extracellular multielectrode recording, we inject patterns of current that amplify or cancel visually driven membrane potential fluctuations produced by a particular visual stimulus, thus changing the gain of the effect of the interneuron on the circuit (20). We extend this previous analysis by then calculating how ganglion cell receptive fields are affected by this manipulation, thereby directly measuring the spatiotemporal visual feature that individual interneurons contribute to the ganglion cell receptive field. We find, unexpectedly, that horizontal and sustained amacrine cells contribute temporally synchronous visual features to the ganglion cell surround at two different spatial scales. Importantly, these two components fully account for the diversity of measured linear receptive field surrounds across the ganglion cell population, indicating that although other amacrine classes may also contribute to the linear surround, this contribution is largely redundant to the two components we directly measure here. These other amacrine cells likely contribute to nonlinear properties of the receptive field in other ways.

We then addressed the theoretical question of why the ganglion cell surround would benefit from synchronous receptive fields at narrow and wide spatial scales. It has previously been shown that the center-surround structure optimizes information transmission about natural scenes in homogeneous and nonhomogeneous populations (9, 10, 21, 22). Even though there are substantial nonlinearities in the retina, these theories nonetheless do successfully predict the linear receptive fields of ganglion cells. This implies that the functional pressures that lead to the extensive nonlinearities have an effect that is neutral to the linear receptive field and that theoretical questions related to the linear receptive field can be addressed separately from those relating to nonlinearities.

We analyzed more than a thousand ganglion cell receptive fields and find that the ganglion cell population is diverse in terms of the weighting of the horizontal cell versus amacrine cell (broad versus narrow) spatial surround but highly constrained in terms of the overall relative weighting of center versus surround. Well-known theories of efficient coding have shown that there are multiple possible solutions to the problem of how receptive fields can contribute to the increase in information transmission under the statistics of natural scenes (9, 10). It has also been proposed that diverse receptive fields can increase information transmission among the neural population and allow for other objectives to be achieved, such as the detection of specific visual features (8, 22–24). Our results show a mechanism for how both optimal information transmission and diversity can be generated. Receptive field surrounds created by interneurons of different spatial scales create diversity in the population while preserving optimal information transmission.

Results

Amacrine and Horizontal Cells Convey Synchronous Visual Features that Match the Ganglion Cell Surround.

We first sought to directly measure the spatiotemporal contributions of individual interneurons to the linear ganglion cell receptive field. The sensory feature C_x,t, contributed by an interneuron to a downstream neuron, is created in two stages—first, the transformation from the stimulus to the interneuron, which is the interneuron’s own spatiotemporal receptive field, F_x,t, and second, the transformation G_t between the interneuron and the downstream neuron in its projective field (25, 26) (Fig. 1A). The combined effect of these two functions has rarely, if ever, been measured, and thus, the contributions of individual interneurons are largely unknown. We measured the receptive field component, C^(a), contributed by single sustained amacrine cells. These cells are narrow-field cells with receptive field centers of <200 μm, comprising multiple amacrine cell types that have linear flash responses with little rectification (Fig. 1D) (20, 26) as well as an inhibitory receptive field surround as measured with a white noise stimulus. To measure the receptive field component conveyed by sustained amacrine cells to the ganglion cell receptive field, we presented a one-dimensional spatiotemporal stimulus consisting of randomly flickering lines. An amacrine cell was recorded intracellularly, and a population of ganglion cells was recorded simultaneously with a multielectrode array. Most cells recorded in this configuration were fast off-type ganglion cells consisting of two cell types, adapting and sensitizing cells. Both of these form independent mosaics in the salamander (27), and so we focused our initial analyses on these ganglion cell types. We first averaged the amacrine cell’s receptive field across space, yielding $F_t^{(a)}$ (Figs. 1 B–D and 2A). Next, while presenting the same visual stimulus, we computed the temporal filter, $G_t^{\left(a\right)}$, describing the transmission from amacrine to ganglion cell by injecting white noise current for 300 s into the amacrine cell and correlating that current with the recorded ganglion cell spikes. This transmission filter $G_t^{(a)}$ had a monophasic negative peak (Fig. 2B), indicating that the amacrine cell was inhibitory (20).

Fig. 1.

Components of a linear receptive field. (A) Schematic of a hypothetical linear neuron that receives input from multiple neural pathways. The response of each interneuron a⁽ⁱ⁾ is the convolution of the stimulus and its particular linear spatiotemporal filter $F_{x,t}^{\left(i\right)}$, $a^{\left(i\right)}$ = $F_{x,t}^{\left(i\right)}*s_{x,t}$, where * indicates a convolution. The response of the neuron b is the sum of the outputs of $a_t^{\left(i\right)}$, each filtered through a transmission filter $G_t^{\left(i\right)}$, such that $b={{\displaystyle \sum }}_i{G}_t^{\left(i\right)}*a_t^{\left(i\right)}={{\displaystyle \sum }}_i{G}_t^{\left(i\right)}*F_{x,t}^{\left(i\right)}*s_{x,t}$. The visual feature C⁽ⁱ⁾ contributed by each interneuron a_i is a combination of the neural pathways leading into and out of a_i (blue bold lines for one interneuron), i.e., a convolution of the spatiotemporal filter F⁽ⁱ⁾ from the stimulus to interneuron a_i and the temporal filter G⁽ⁱ⁾ from a_i to b. (B) Experimental arrangement showing simultaneous intracellular and multielectrode recording. (C) (Top) One-dimensional spatiotemporal receptive field of a fast off-type retinal ganglion cell. (Bottom) Spatial average of receptive field surround (blue), center (red), and total receptive field (black). At the first (negative) peak of the total receptive field, the spatial surround is still zero, indicating that the first peak derives mostly from the spatial center. Similarly, at the second (positive) peak of the total receptive field, the spatial center has returned to zero, indicating that the second peak derives mostly from the spatial surround. (D) (Top) One-dimensional receptive field of a sustained off-type amacrine cell. (Bottom) Flash response from a sustained off-type amacrine with corresponding scale bar (black) and normalized superimposed responses from 31 different sustained off-type amacrine cells (gray). (E) One-dimensional receptive field of a horizontal cell.

Fig. 2.

Synchronous visual features from inhibitory pathways at different spatial scales. (A) Spatial average of an amacrine cell, $\langle F_{x,t}^{\left(a\right)}\rangle { }_x=F_t^{\left(a\right)}$, and horizontal cell. (B) (Left) Transmission filter $G_t^{\left(a\right)}$ between amacrine and ganglion cell computed from white noise current injection in the presence of the flickering lines visual stimulus to place the ganglion cell in a similar state of adaptation as in the control condition. (Right) The transmission filter $G_t^{\left(h\right)}$ for a horizontal cell. (C) (Left) The visual feature $C_t^{\left(a\right)}$ conveyed by the amacrine cell, computed as the convolution between $F_t^{\left(a\right)}$ and $G_t^{\left(a\right)}$, corrected for the membrane time constant, compared with that of the ganglion cell surround computed by spatially averaging the region that lay outside the receptive field center. (Right) The same for a horizontal cell and different ganglion cell. (D) Histogram of correlation coefficients between the time course of predicted interneuron transmission and the time course of the ganglion cell surround, computed separately for each cell pair. (E) Spatial one-dimensional receptive field of amacrine and horizontal cells. (F) The strength of transmission between amacrine cells (Left) or horizontal cells (Right) and ganglion cells computed from the average slope of a nonlinearity computed during white noise current injection into the interneuron. The nonlinearity was taken from an LN model computed between each cell pair during current injection (20). Values show the decay constant of an exponential fit. (G) Amacrine and horizontal cell population predictions estimated by convolving the interneuron receptive fields with their appropriate spatial transmission filters, compared to retinal ganglion cell receptive field spatial surrounds estimated from the linear receptive field model in Fig. 3C. (H) Histogram of the sizes of a population of linear amacrine and horizontal cells, measured as 1 SD of a Gaussian fit.

We then estimated the temporal feature conveyed by the amacrine cell to the ganglion cell as $C_t^{(a)}=F_t^{(a)}*G_t^{(a)}$, convolving the amacrine cell temporal receptive field $F_t^{(a)}$ with the amacrine-to-ganglion cell transmission filter $G_t^{(a)}$, correcting for a double contribution of the amacrine cell membrane time constant (see Methods) (20). The visual feature $C_t^{(a)}$ conveyed by this amacrine cell to the ganglion cell was an increase in light intensity with a latency of ∼120 ms.

We found that $C_t^{(a)}$ matched very closely the time course of the ganglion cell spatial surround (Fig. 2C). The correlation coefficient computed across time for each cell pair was, on average, 0.81 ± 0.02 (Fig. 2D; n = 21 cell pairs), similar to the measured variation within the ganglion cell surround itself, computed between the two opposite sides of the ganglion cell surround (r = 0.83 ± 0.03).

The same analysis was then performed with horizontal cells rather than amacrine cells (Fig. 2 A–D). Although one might expect that different interneurons with different temporal kernels would convey different temporal features, we instead found that the visual feature contributed by a horizontal cell to ganglion cells, $C_t^{(h)}$, also matched the time course of the ganglion cell surround for each cell pair (r = 0.81 ± 0.04, n = 18 cell pairs). Thus, the visual features conveyed through the distinct neural pathways of amacrine and horizontal cells were synchronous in time and closely matched the time course of the ganglion cell receptive field surround.

Narrow-Field Amacrine and Horizontal Cells Convey Visual Features at Different Spatial Scales.

From our measurements of the effects of a single horizontal or amacrine cell, we estimated the spatial receptive field components $C_x^{(\left\{a\right\})}$ and $C_x^{(\left\{h\right\})}$ contributed by amacrine and horizontal cell populations to a single ganglion cell. Because each cell type tiles the retina in space (28), the spatial weighting from one amacrine cell to many ganglion cells is the same as many amacrine cells to a single ganglion cell. More formally, the spatial weighting deriving from the divergence of one amacrine cell’s projective field (26)—equivalent to the amacrine-to-ganglion cell point spread function—is equivalent to the spatial weighting, $G_x^{(\left\{a\right\})}$, deriving from the convergence of many amacrine cells to one ganglion cell. We measured the projective field of interneurons from white noise current injection by computing a linear–nonlinear (LN) model from the injected current to the firing rate of each ganglion cell (20). The slope of the firing rate nonlinearity was taken as the strength of the connection between each cell pair. Although measurements of the projective field were based on fast off-type ganglion cells, we recorded a small number of other types of ganglion cells, and the effects on these cells were consistent with a similarly sized projective field (SI Appendix, Fig. 1B). We convolved the spatial receptive field (Fig. 2E) of each interneuron class with its measured projective field (Fig. 2F) to estimate the spatial visual feature conveyed by a population of amacrine or horizontal cells to a single ganglion cell (Fig. 2G), indicating that the effect of the population was to increase the size of the amacrine cell visual feature by 31% and the size of the horizontal cell visual feature by 17%. The receptive field component conveyed by the amacrine cell population on average had a smaller half-maximal width (332 ± 75 μm SD) than that of horizontal cells (740 ± 139 μm SD), with the surround sizes of ganglion cells falling in a range in between (Fig. 2 G and H). We concluded that amacrine and horizontal cells conveyed the same temporal feature at different spatial scales that spanned the range of sizes of ganglion cell receptive field surrounds.

Dynamic Perturbation Shows that Amacrine and Horizontal Cells Create the Ganglion Cell Surround.

The above analysis relied on a linear model of the transformations from stimulus to interneuron to ganglion cell and furthermore assumes that the interneuron’s effects were the same under perturbation by white noise current injection as during visual input. To measure the interneuron’s contribution without these assumptions, we designed a direct causal test to measure whether the interneuron’s timed visual responses specifically generated the ganglion cell surround.

We first used a full-field visual stimulus to measure the temporal receptive field of the ganglion cell. To directly test whether amacrine transmission contributed to the ganglion cell temporal surround, we amplified or diminished the amacrine cell’s visually driven voltage fluctuations (Fig. 3A). We first recorded ganglion cell and amacrine cell responses to visual stimuli alone without current, then played back timed current that either amplified or diminished the voltage fluctuations of the interneuron while repeating the visual stimulus. Current amplitudes were chosen so that they were estimated to maintain the membrane potential within a physiological range (∼10 mV SD) given a measurement of membrane conductance and time constant using steady pulses of current (20). This record-and-playback method perturbed the cell only at the times of the visually driven response, avoiding potential off-target effects created by mistimed perturbations.

Fig. 3.

Direct causal measurements of the visual feature conveyed by an interneuron. (A) Schematic of experiment recording the membrane potential response of an amacrine cell. The visual stimulus was then repeated along with current injection timed to either amplify or diminish the amacrine cell’s visually driven membrane potential fluctuations (see Methods). (B) (Left) Normalized visual sensitivity (in dimensionless units) to a uniform visual stimulus computed in the control condition, with amacrine transmission amplified, and with amacrine transmission diminished. Filters were scaled in amplitude so that all sensitivity was represented in the filter (see Methods). (Right) Average change in visual sensitivity (n = 14 cell pairs) computed as the difference in filter between the amplified and diminished conditions, along with the average control temporal filter. Curves were stretched in time so that their control negative and positive peaks aligned. Shaded region shows mean ± SEM. (C) Spatial average of a one-dimensional spatiotemporal receptive field averaged over twenty ganglion cells, along with the average time course of the spatial surround. Curves were stretched in time so that their control negative and positive peaks aligned. As in Fig. 1C, the second peak of the total receptive field (the temporal center) derives mostly from the spatial surround. (D) Amplitude of the surround compared for conditions when amacrine transmission was amplified or diminished (n = 6 amacrine cells and 31 ganglion cells). Black symbols indicate amacrine–ganglion cell pairs for which a monophasic or biphasic transmission filter could be computed from the separate protocol of white noise current injection (Fig. 1). Gray symbols indicate those symbols for which the transmission filter was composed only of noise. (E) One-dimensional spatiotemporal receptive field of an amacrine cell. (F) Change in linear receptive field averaged across five ganglion cells when the amacrine cell’s output was amplified (Right) or diminished (Left) using record and playback. Ganglion cells were chosen whose receptive fields overlapped that of the amacrine cell. Results are shown for a single amacrine cell (n = 5 ganglion cells). (G) Spatial amplitude of the amacrine cell receptive field (black) compared with the difference in visual sensitivity across a population of ganglion cells between when amacrine cell fluctuations were amplified or diminished (green) (10 amacrine cells and 70 ganglion cell pairs). A Gaussian fit to the average amacrine cell receptive field had an SD of 56 μm, smaller than the total region of visual sensitivity resulting from summed ganglion cell receptive fields, which was 336 μm. Spatial extent of recorded ganglion cells shown in gray. All curves normalized by their maximum value for ease of spatial comparison. (H–J) Same as panels E to G for horizontal cells (3 horizontal cells and 18 ganglion cells). A Gaussian fit to the average horizontal cell receptive field had an SD of 283 μm, smaller than the total region of visual sensitivity of the measured ganglion cell population, which was 363 μm.

Amplifying the amacrine cell’s output increased the amplitude of the ganglion cell temporal surround, with only a very small change in the sensitivity of the temporal center, which is the first (negative) peak. Conversely, canceling the amacrine cell’s visually driven voltage fluctuations in some cases caused the ganglion cell’s temporal surround to nearly disappear, whereas the effect on the first peak was minor. The average time course of this change for the uniform field stimulus was similar to the time course of the spatial surround measured separately using spatiotemporal white noise (Fig. 3 B and C). Although the change in temporal receptive field from a uniform field stimulus sums over the spatial center and surround of the cell, the first peak in the ganglion cell temporal receptive field receives little contribution from the spatial surround, and the second opposing peak is almost exclusively comprised by the spatial surround (Figs. 1C and 3C). These results show causally that the visual feature conveyed by amacrine cells is used to construct the ganglion cell temporal surround.

The above results imply that a linear amacrine cell contributes a temporal visual feature equal to its own linear receptive field filtered through a temporal synaptic delay. We tested this idea for a spatial stimulus by mapping the receptive fields of amacrine and ganglion cells with a one-dimensional white noise stimulus and then amplifying or diminishing the voltage fluctuations of the amacrine cell. We then measured the change in ganglion cell receptive fields summed across the ganglion cell population. Comparing the amacrine amplified and diminished conditions showed that the ganglion cell population experienced a localized reduction in sensitivity that spatially matched the amacrine cell’s own receptive field (Fig. 3 E–G). This demonstrates causally that amacrine cells contribute their own receptive field to construct the ganglion cell receptive field. Note that this result is not guaranteed and that nonlinearities such as a multiplicative interaction between neural pathways could potentially cause an interneuron to deliver a visual feature that is the combination of its own receptive field and other pathways (SI Appendix, Fig. 2 and SI Appendix), although that is not the case here.

Similar experiments using the record and playback technique applied to horizontal cells altered the spatiotemporal receptive field of ganglion cells. As with amacrine cells, the change in sensitivity across the ganglion cell population matched the larger horizontal cell spatial receptive field (Fig. 3 H–J). Thus, the visual feature comprising the ganglion cell surround was not an average of differently timed contributions from separate interneuron pathways. Instead, two distinct pathways contributed the same temporal feature that matched the final ganglion cell surround, yet at different spatial scales.

Sustained Amacrine Cells and Horizontal Cells Account for the Ganglion Cell Receptive Field Surround.

To assess whether we have accounted for the main components that generate the ganglion cell receptive field surround, we modeled the ganglion cell receptive field as a linear combination of the measured average visual features contributed by horizontal and amacrine cells, as well as an excitatory central region (Fig. 4A). This model captured 93 ± 0.3% (n = 1,382) of the variance of measured ganglion cell receptive fields, indicating that we have accounted for the main receptive field components that create the linear surround (SI Appendix, Fig. 3 D and E).

Fig. 4.

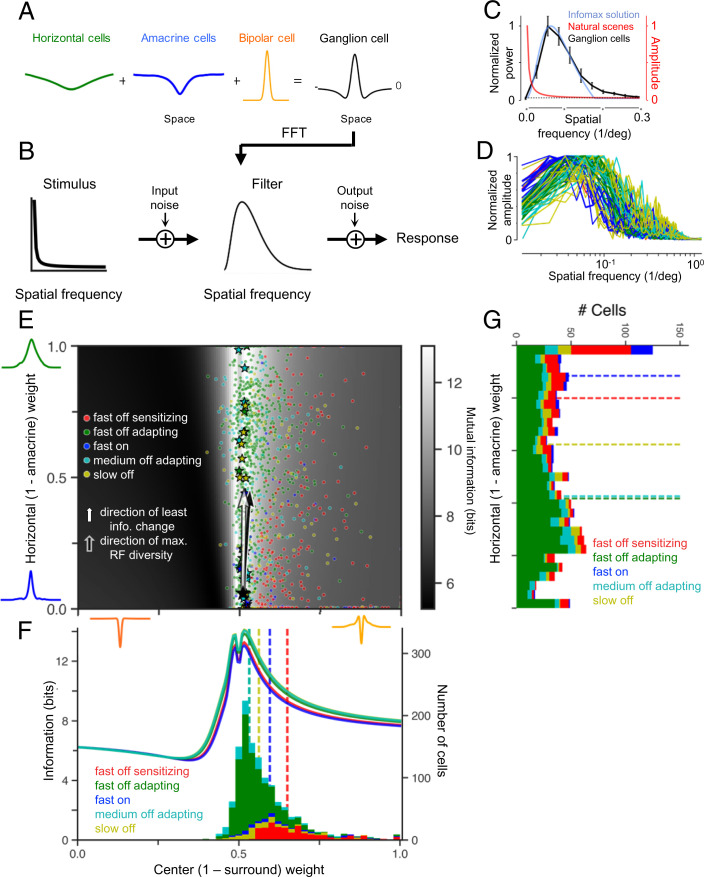
Horizontal and amacrine cell contributions create diverse retinal ganglion cell receptive fields that maximize information transmission. (A) Ganglion cell linear receptive field modeled as a linear combination of horizontal and amacrine cell populations, together with a Gaussian center. (B) Schematic diagram of framework considered for theoretical analysis of information transmission, with a signal corrupted by input noise such as photon noise or photoreceptor noise, then filtered through a spatial filter, then further corrupted by output noise such as spiking variability. (C) Normalized power spectra of the average retinal ganglion cell receptive field (n = 13, black) and the linear filter that maximizes information about natural scenes (blue), together with the amplitude spectrum of natural scenes (red). (D) Example retinal ganglion cell receptive fields in the frequency domain, colored by cell type. (E) Grayscale map shows the information fitness landscape, computed as the mutual information between natural scenes and the output of linear receptive field models as a function of different horizontal and amacrine weightings (ordinate) and different excitatory center contributions (abscissa). Colored symbols indicate 1,354 ganglion cell receptive fields of different cell types, 772 fast off adapting, 217 fast off sensitizing, 159 medium off, 58 fast on, and 148 slow off, parameterized by the model in A, and stars are the examples in D. Large black star at the origin of the two vectors indicates the single ideal receptive field, which lies on the ridge of near-optimal information transmission. Light arrow indicates the direction of least information loss with respect to the ideal receptive field. Dark arrow indicates the direction of largest variation of ganglion cell receptive fields, computed using principal components analysis. (F) Information transmission for different cell types as a function of receptive field center weight. Different cell types have slightly different curves because the measured noise level for each cell type was used to constrain the total SNR (see Methods). Curves show information transmission at an interneuron weighting of 0.5 horizontal cell weight, which is a horizontal slice through the grayscale image in (E). Stacked histograms show the number of cells with receptive fields at each center weighting. Dotted lines denote the medians of the distributions. The slight trough at equal center-surround weighting (0.5) reflects the loss of information when the mean intensity is completely rejected. (G) Distribution of different cell types as a function of amacrine–horizontal cell weighting. Dotted lines show the median weighting for each cell type. FFT, fast Fourier transform; RF, receptive field.

This accounting worked equally well for multiple ganglion cell types, indicating that the receptive field features conveyed by horizontal cells, which contribute to all ganglion cell types, and narrow-field sustained off-type amacrine cells, which have a diffuse arborization and target multiple types of bipolar and ganglion cells, are sufficient to explain the shape of the linear receptive field surround. Note that it is acknowledged that part of the signal deriving from a horizontal cell does flow through amacrine cells. However, we know from retinal circuitry that the two cells generate distinct receptive field components because they do act in part in parallel (Fig. 1A), and regardless of the circuit path, the effects of the different interneurons on the linear receptive field sum (Fig. 3). The finding that horizontal and sustained amacrine cells together account for the ganglion cell receptive field surround does not rule out contributions of other amacrine cells to the linear receptive field. However, we can conclude that these other linear receptive field contributions are largely redundant to the ones we describe from sustained amacrine and horizontal cells, and so, theoretical questions as to the benefits of this combined construction of the receptive field do not rely on the complete identification of all amacrine cell types that contribute.

Both Amacrine and Horizontal Cells Create Near-Optimal Surrounds.

What is the advantage of having two interneuron pathways conveying the same temporal visual feature at different spatial scales to the ganglion cell linear receptive field? Previous analyses on ganglion cell receptive fields indicate that among possible linear receptive fields, the observed receptive fields approximately maximize information transmission given the statistics of natural visual images (9, 21, 29). It is also known that there is not only a single solution to the problem of optimal information transmission and that a diversity of receptive field shapes could achieve the goal of maximizing information (9, 21). We considered a simple linear model of a receptive field transmitting information about a natural stimulus with added noise (Fig. 4 A and B) and used a classical approach of information theory (see Methods) (9, 10) to compute the ideal receptive field under the natural scene statistics. Such models have been successful at explaining the spatial frequency content of the ganglion cell receptive field as optimizing information transmission about natural scenes (9, 10), although the localized center-surround structure can be further derived by including a static nonlinearity in the optimization (29). Our analysis confirmed previous claims that the average ganglion cell receptive field in the spatial frequency domain matched the ideal receptive field (Fig. 4C; SI Appendix, Fig. 3 A–C), with the presence of the surround corresponding to the reduction of sensitivity at the lowest frequencies. Yet ganglion cells have different receptive field shapes (Fig. 4D) (28–30) to support different functional roles such asymmetric receptive fields in direction selectivity (31) or selecting for particular speeds of motion (32). Furthermore, it has been proposed that diverse receptive fields and neural responses reduce correlations and increase the information transmission capacity of a neural population (8, 22–24, 33–36).

From our model combining a center, horizontal, and amacrine cell components (Fig. 4A), the shape of ganglion cell linear receptive fields can be summarized by two values, the relative horizontal cell/narrow-field amacrine cell weighting and the relative strength of center and surround (Fig. 4E), thus defining a two-dimensional (2D) space. Using measured noise in fast off ganglion cells, and photoreceptor noise estimates based on the previously measured mean vesicle release rate (see Methods), we computed the information transmitted by every possible receptive field shape in this 2D space. With respect to the axis of amacrine cell–horizontal cell weighting, this analysis revealed that around the single optimal receptive field was not simply a point, but an extended ridge of receptive field shapes with near-optimal information transmission. This near-optimal region was highly sensitive to the weight of the surround, with information being maximized when the center weight slightly exceeded that of the surround, but the surround size, as controlled by the relative horizontal and amacrine cell weight, had little effect on information transmission (Fig. 4E). Thus, so long as the center-surround weighting is maintained, the horizontal and amacrine contribution can change the receptive field shape without impacting information transmission.

Horizontal and Amacrine Cells Create Diverse Near-Optimal Surrounds.

When we examined the actual receptive fields of over 1,300 ganglion cells, their receptive fields closely approximated this ridge of near-optimal transmission. The cell population had a tightly constrained center-surround ratio, which matched the expected theoretical values (Fig. 4 E and F). Yet the sizes of receptive field surrounds were diverse, ranging from having surrounds matching the horizontal cell feature with no amacrine contribution to those with only an amacrine contribution (Fig. 4 E and G). Individual cell types had different median values of amacrine contribution yet varied broadly within cell type. Although some cell types had weaker surrounds than the optimal value, cell types with higher noise systematically had weaker surrounds, consistent with theories of information maximization (SI Appendix, Fig. 3 F and G) (9). Within this landscape, we computed the direction of greatest variation of receptive field shape across the ganglion cell population and found that it was nearly identical to the direction of least loss of information transmission, differing by approximately two degrees (Fig. 4E). This correspondence between the theoretical landscape information and the diversity of ganglion cell receptive fields indicates that by adding an additional inhibitory pathway that contributes to the surround, receptive field diversity has been generated in a direction of neutral impact to information transmission in single cells. Consistent with previous theories showing that there are different solutions to the problem of optimal information transmission under natural scenes, our results give a mechanism for those theories, showing how diverse receptive fields can be generated that nonetheless achieve the goal of optimal information transmission.

It is unknown how this relative weighting of amacrine and horizontal cell input are separately controlled to achieve an overall balance of center and surround. However, because the horizontal cell component is present in the amacrine cell’s own inhibitory surround and then the amacrine cell receptive field is subtracted through inhibition, it is plausible that adding a greater weighting of amacrine cells automatically cancels the wider horizontal cell contribution (SI Appendix, Fig. 4). This effect would change the shape of the receptive field surround without changing the relative weighting of center and surround.

Discussion

These results offer a quantitative and theoretical explanation as to how and why two inhibitory pathways generate the ganglion cell classical receptive field. Our analysis quantitatively accounts for the measured optimal linear receptive fields of ganglion cells and explains the origin and benefits of their observed diversity.

We have taken two complementary experimental approaches to determine the contribution of an interneuron to the computation of a circuit. The first involved measuring the transformation between the circuit’s input and the interneuron and the transformation between the interneuron and circuit output and then inferring the composition of those two functions as the total effect of the interneuron (Fig. 2). This process involved mathematical modeling of the cell’s input and output and the relationship between the cell’s effects and other processing in the circuit, effectively testing the hypothesis that the model is correct. The second approach of record and playback effectively turns up or down the gain of a neural pathway (Fig. 3), allowing a measurement of its effects whether or not a specific model exists of that effect. It is important to note that this dynamic perturbation matched to the fluctuations of the cell differs from simply activating a neuron or blocking its activity, which generates a signal or a change in mean activity that is unrelated to the signal experienced by the cell. Because the method of record and playback, or alternatively a real-time dynamic clamp (37), requires no prior hypothesis of a cell’s effects, this approach is a flexible method to study the contribution of a cell to a neural function.

Although the question of what receptive field properties are optimal has been studied (9, 21, 29, 38), little attention has been given to how neural circuits should generate those receptive fields. It has been shown that splitting nonlinear neural pathways into different cell types with different thresholds can increase information transmission (34, 35). However, each of the two pathways deviates substantially from the optimal position of a single threshold, effectively yielding an improved solution with two differing pathways, each of which are suboptimal if considered alone. For linear receptive fields, an ideal solution for a single cell type has been shown (9) and diverse receptive fields can increase information transmission among a neural population (8, 22–24), but it was not considered previously how this diversity competes with the information conveyed by a single receptive field type. It appears that the constraint to optimize information transmission for single cells, maintaining a nearly balanced center and surround, still allows information in the population to be increased by generating diversity in spatial properties neutral to the center-surround ratio.

It has been proposed that diverse receptive fields can increase information transmission among the neural population (8, 22–24). This can be understood as differences in receptive field shapes reducing redundancy between cell types in the same way that the surround reduces redundancy between neighboring cells of the same type. Our examination of ganglion cell receptive fields shows that the retina has found this solution. This arrangement could allow the higher brain to read out signals from populations of different sizes with high efficiency. For example, one brain region might receive input from only direction selective cells to drive oculomotor responses, and another region could integrate information from multiple cell types encoding for example direction of motion and fine textures.

Because sustained amacrine cells and horizontal cells conveyed a different spatial feature with the same temporal properties, we did not study the effect of temporal diversity. However, space and time have a similar power spectrum under natural scenes and simply represent different directions in stimulus space. Both ganglion cells and transient amacrine cells do have diverse temporal receptive fields, and we expect a similar benefit for temporal diversity that may arise in part from other amacrine types.

An additional potential benefit of distinct linear signals is the ability to adjust the strength of these components based on the recent stimulus statistics. It is known that the surround strength changes with the mean luminance (39), consistent with the theoretical principle that weaker surrounds are more optimal when the noise is very high (10). The strength of amacrine cell input can also change depending on illumination (14), and thus, the two pathways of amacrine and horizontal cell input may serve an additional function as a mechanism to change the shape of the receptive field. It will be important to conduct further studies under different adaptation states.

Our analysis of information transmission focuses on single cells, but because the analysis is in terms of the spatial frequency content, it is effectively considering a population of cells of the same type that tiles the retina. The diversity that we observe exists within single cell types (Fig. 4 E–G) as well as across cell types. Within a cell type, we see that added diversity can occur even if all single cells are near optimal. For multiple cell types, when multiple cells are present at the same location and thus are potentially redundant, the effect of this added diversity is unknown. One would expect that the diversity that maintains the center-surround ratio as we observe would increase information across the population of different cell types by decorrelating the different populations while preserving information in single cell types.

Clearly, other factors will also influence the encoding properties of ganglion cells, such as eye movements (40), which have been shown to whiten the stimulus, changing its statistics, as well as other biological functions such as the detection of ethologically important features such as edges or small objects. It is less well understood, however, how these different influences combine jointly to influence the receptive field and information transmission. However, it is known that if one optimizes the effects of the linear receptive field alone, the receptive field that maximizes information transmission closely matches those of retinal ganglion cells, including how those receptive fields change at difference luminance levels. This suggests that one can consider the influence of the linear receptive field on information transmission—the question we address—as a separable question from the influence of complex nonlinearities on information transmission. This conclusion has been further confirmed by the optimizing linear receptive fields along with simple static nonlinearities, an optimization that can further increase information transmission (41) and can result in a localized receptive field but does not affect the spatial frequency content of the linear receptive fields that we have analyzed (29). In addition, one can infer that more complex nonlinearities are also neutral to the linear receptive field, as ganglion cells that have typical center-surround receptive fields also have additional properties such as direction selectivity, nonlinear subunits, or object motion sensitivity (42), and this functional diversity improves information transmission across the population (43). In addition to maximizing information transmission about past stimuli, conveying information that specifically predicts future stimuli is an important other factor that will influence the neural code (44). Taken together, it is likely that given the statistics of natural scenes along with eye movements, optimization of the linear receptive field along with complex nonlinear properties serve multiple simultaneous functions, including increasing information transmission, conserving energy, and selecting for ethological features.

Our direct approach to analyzing an interneuron’s contribution to a neural function can also be applied to more complex nonlinear computations, as well as to other stimulus modalities and optogenetic perturbations. Critical to this process will be to both record from a neuron and perturb it in order to avoid misinterpretations that arise from optogenetic perturbation alone (45). In the case of retinal receptive fields, this approach reveals how multiple interneuron pathways in the retina’s parallel and layered circuitry maintain an efficient representation across diverse neural populations.

Methods

Visual Stimuli.

Stimuli were projected from a video monitor at a photopic mean intensity of 10 mW/m² and were drawn from a Gaussian distribution unless otherwise noted. The contrast of stimuli is defined as SD of the intensity distribution divided by the mean ranged from 10 to 35%.

Simultaneous Intracellular and Multielectrode Recording.

Methods for simultaneous intracellular and extracellular recording using a 60-electrode array in the intact salamander retina were as described (20). Briefly, intracellular electrodes (150 to 250 MΩ) were used for either recording or current injection in bridge mode. To compute the temporal receptive field component contributed by an amacrine or horizontal cell, we computed a visual filter F_t as the spatial average of the spatiotemporal receptive field F_x,t between the visual stimulus and the interneuron membrane potential. We then computed a transmission filter G_t between white noise current injected into the cell and ganglion cell spikes. We used this estimate based on steady current pulses because the high resistance of electrodes prevented accurate measurement of membrane potential during time-varying current injection. The amplitude of current was 0.5 nA SD for amacrine cells and 0.5 to 1.0 nA SD for horizontal cells. To compute the predicted transmission C_t for a neural pathway as a composition of F_t and G_t, because F_t was computed between the stimulus and interneuron membrane potential but G_t was computed from injected current, we corrected for the double contribution of the amacrine cell membrane time constant τ by deconvolving with the function $e^{\raisebox{1ex}{$-t$}\!\left/ \!\raisebox{-1ex}{$\text{τ}$}\right.}$ as previously described (20).

For record-and-playback experiments, to amplify or diminish the fluctuations of an interneuron, first, the membrane potential fluctuations were recorded without current, and an exponential function representing the membrane time constant of the cell was measured (SI Appendix, Fig. 1A). The recorded membrane potential fluctuations were then deconvolved by the exponential function, creating a current sequence that, when filtered according to the membrane time constant, was predicted to match the measured voltage response. With cells that have slower membrane potential fluctuations such as sustained amacrine and horizontal cells, this procedure is not highly sensitive to an accurate measurement of the membrane time constant (20). To amplify the cell’s voltage fluctuations, the visual stimulus s(t) was repeated while injecting the current I_a(t) synchronized with the visual stimulus so as to make both depolarizations and hyperpolarizations larger. The SD of the current was set to 500 pA for amacrine cells and 750 pA for horizontal cells. To diminish the cell’s voltage fluctuations, s(t) was repeated while injecting the current −I_a(t), thus partially canceling the cell’s visual input. This allowed us to compare two opposite perturbations of the input.

Sustained off-type amacrine cells likely comprise multiple cell types, most of which have a narrow receptive field (<200 μm) and were identified by their sustained linear flash responses, the presence of an inhibitory surround, and their inhibitory transmission to off-type ganglion cells (Figs. 1D and 2B) (20). Approximately 60% (32 of 52) of amacrine cells encountered in recordings for this study were sustained off-type cells. Horizontal cells were identified by their lack of receptive field surround, linear response, and a receptive field center that exceeded 200 μm in diameter. Ganglion cells were classified by a white noise stimulus as described (27). Fast off-type ganglion cells include two distinct cell types, adapting and sensitizing, that form independent mosaics, but here they were analyzed together unless otherwise noted.

Linear Model of Visual Responses and Interneuron Transmission.

Linear models of visual responses and of amacrine and horizontal cell transmission were computed as described using the standard method of reverse correlation (20). Stimulus frames were updated every 30 ms. For current injection, the stimulus, i(τ), was white noise current (bandwidth of 0 to 50 Hz). In the model, the stimulus was convolved with a linear temporal filter, F_t = F(t), which was computed as the time reverse of the spike-triggered average current stimulus such that

$$\mathit{h}\left(\mathit{t}\right)={{\displaystyle \int }}^{\text{}}\mathit{F}\left(\mathit{t}-\text{τ}\right)\mathit{i}\left(\text{τ}\right)\mathit{d}\text{τ}\mathit{.}$$ [1]

To compare the absolute sensitivity in spatial and temporal regions of the receptive field between conditions, all sensitivity was placed in the linear filter. To do this, the linear filter was extended to an LN model by computing a static nonlinearity N(h) that captured the threshold and average sensitivity of the cell. The nonlinearity was then scaled along the input axis in the condition of current injection so that N(h) was the same as in the control condition, and the linear filter was scaled in amplitude (along the vertical axis) by the same factor (46). This procedure left the overall LN model the same but placed all sensitivity in the linear filter.

Spatiotemporal receptive fields were measured using reverse correlation (47) of the firing rate or membrane potential response with a visual stimulus consisting of independently modulated 100-μm squares or 50-μm wide bars. Filters were not normalized by the power spectrum of the stimulus, but given that there was little temporal or spatial variation of filters nearing the highest frequencies of the stimuli, we would not expect this normalization to make a significant difference.

Optimal Receptive Fields.

The ideal spatial linear ganglion cell receptive field was taken to be one that maximizes information transmission about natural scenes. We solved for this optimal receptive field in the frequency domain assuming a constraint on the ganglion cell response variance, using the method of Atick and Redlich (9). This problem can be reformulated as minimizing redundancy, min_F C(Y) − λI(X; Y), where I(X; Y) is the mutual information between the retina’s visual input X and ganglion cell response Y, C(⋅) is the channel capacity or upper bound on the information the optimized linear receptive field F can transmit, and λ is a Lagrange multiplier introduced for the optimization (9, 21). The response Y = F(X + N_in) + N_out, where N_in is the input noise in the retinal circuit prior to the ganglion cell and N_out is the output noise that corrupts the ganglion cell response after the stimulus is filtered by the linear receptive field. The capacity is fixed by our measurements of the signal-to-noise ratio (SNR), and our goal was to find a filter F that causes information to equal this capacity. Constraining the receptive field F to be linear and spatially symmetric and making a Gaussian approximation assumption on the visual stimulus XF, the optimal ganglion cell receptive field F can be computed explicitly. The amplitude spectrum F = F(ω) of the spatial receptive field was solved previously (9) as being

$$F=\frac{S_0}{2N_{in}^{2}S}\left(1+\sqrt{\frac{2\text{λ}{N}_{in}^2}{S_0}}\right)-\frac{1}{N_{in}^2},$$ [2]

where ω is spatial frequency, S₀(ω) is the power spectrum of the visual input X, and $S\left(\text{ω}\right)=S_0\left(\text{ω}\right)+N_{in}^2\left(\text{ω}\right)$ is the power spectrum of the signal + noise input the ganglion cell receives. In this equation, the term $S_0/2N_{in}^{2}S$ places less power in the filter in a frequency bin in which the noise is large compared to the signal, whereas the term $\sqrt{2\text{λ}{N}_{in}^2/S_0}$ decreases power in the filter in which the stimulus has high power and thus has a whitening effect. The constant Lagrange multiplier λ is solved through an optimization process to satisfy the following previously derived expression (9),

$${{\displaystyle \int }}^{\text{}}d\omega \text{log}\left(\sqrt{\frac{S_0}{2\lambda N_{in}^2}}+\sqrt{1+\frac{S_0}{2\lambda N_{in}^2}}\right)=\frac{1}{2}{{\displaystyle \int }}^{\text{}}d\omega \text{log}\left(\frac{S\left(N_{in}^2+N_{\mathit{out}}^2\right)}{N_{in}^2\left(S+N_{\mathit{out}}^2\right)}\right).$$ [3]

The spatial receptive field F that maximizes information transmission depends only on the signal power spectrum and the input and output noise amplitude spectra. For all optimal receptive fields in this paper, we used the average power spectrum of natural images obtained from a database (48) and fixed the input and output noise to be Gaussian white noise. We constrained the total SNR var(X)/var(XN_in + N_out) to match the average SNR estimated from the trial-to-trial variability of 28 fast off ganglion cells simultaneously recorded in response to a repeated 35% contrast natural scenes sequence. The SNR in these experiments was measured by dividing the variance of each trial, averaged over all trials, by the variance across trials averaged across time. The relevant cone photoreceptor noise occurs prior to spatial filtering by horizontal cells and includes photoreceptor vesicle release. To estimate the SNR, we assumed a mean vesicle release rate (49) of 750 s⁻¹, Poisson noise, and a 100-ms integration time, meaning that in one integration time, an average of 75 vesicles are released. We then computed the SNR as a function of the temporal contrast of a Gaussian stimulus, defined as the SD divided by the mean intensity (SI Appendix, Fig. 3 A and B). An average contrast value of 30% previously reported for natural scenes (50), corresponds to an SNR of ∼7. An additional source of noise is likely to arise from phototransduction (51), but according to computations of how information transmission changes over a range of SNR values (SI Appendix, Fig. 3G), this is likely not to have a qualitative impact on the conclusions here.

To investigate the contributions of the horizontal cell and linear, or sustained, amacrine cell populations, C_{h} and C_{a}, to the ganglion cell linear receptive field, we convolved the average amacrine cell spatial receptive field $F_x^{(a)}$ with the amacrine cell projective field $G_x^{\left(a\right)}$ and similarly convolved the horizontal cell receptive and projective fields and $F_x^{(h)}$ and $G_x^{\left(h\right)}$ (Fig. 1D), respectively. This convolution represents the spatial weighting of the horizontal and amacrine population contributions to a given ganglion cell, assuming that both interneuron and ganglion cell populations tile the retina.

To explore how well horizontal or amacrine cell populations alone could contribute to a ganglion cell surround that maximizes information, we modeled the ganglion cell spatial receptive field as the linear combination αB_μ,σ + (1 − α)(ηC_{h} + (1 − η)C_{a}), where α ∈ [0, 1] represents the relative weight between center and surround and η ∈ [0, 1] represents the relative weight between horizontal and amacrine contributions. For the amacrine-only surround, η = 0, and for the horizontal-only surround, η = 1. The center contribution B_σ is a Gaussian in which both the mean μ and SD σ are jointly fitted with η, α. Two parameters allowed for a spatial offset of the horizontal and amacrine receptive field components to account for the observation that center and surround were not always perfectly concentric. When fitting individual retinal ganglion cells (Fig. 4 C–G), parameters were refitted for each cell. The information landscape in Fig. 4E did not change qualitatively when σ was chosen to be the average center width of the five different retinal ganglion cell types.

To enforce that the weights η and α were between 0 and 1 and also maintain a smooth gradient for optimization, η and α were defined as η = θ(η′) and α = θ(α′), where θ() is a sigmoidal function with a range between 0 and 1. The alternate parameters η′ and α′ were then optimized. We verified using simulated data that the fitting procedure could recover weights η and α that were exactly 0 or 1.

Data Availability

Electrophysiological recordings data have been deposited in GitHub: (https://github.com/baccuslab/surround-components).