Ultrafast end-to-end protein structure prediction enables high-throughput exploration of uncharacterized proteins

Significance

We present a deep learning-based predictor of protein tertiary structure that uses only a multiple sequence alignment (MSA) as input. To date, most emphasis has been on the accuracy of such deep learning methods, but here we show that accurate structure prediction is also possible in very short timeframes (a few hundred milliseconds). In our method, the backbone coordinates of the target protein are output directly from the neural network, which makes the predictor extremely fast. As a demonstration, we generated over 1.3 million models of uncharacterized proteins in the BFD, a large sequence database including many metagenomic sequences. Our results showcase the utility of ultrafast and accurate tertiary structure prediction in rapidly exploring the “dark space” of proteins.

Abstract

Deep learning-based prediction of protein structure usually begins by constructing a multiple sequence alignment (MSA) containing homologs of the target protein. The most successful approaches combine large feature sets derived from MSAs, and considerable computational effort is spent deriving these input features. We present a method that greatly reduces the amount of preprocessing required for a target MSA, while producing main chain coordinates as a direct output of a deep neural network. The network makes use of just three recurrent networks and a stack of residual convolutional layers, making the predictor very fast to run, and easy to install and use. Our approach constructs a directly learned representation of the sequences in an MSA, starting from a one-hot encoding of the sequences. When supplemented with an approximate precision matrix, the learned representation can be used to produce structural models of comparable or greater accuracy as compared to our original DMPfold method, while requiring less than a second to produce a typical model. This level of accuracy and speed allows very large-scale three-dimensional modeling of proteins on minimal hardware, and we demonstrate this by producing models for over 1.3 million uncharacterized regions of proteins extracted from the BFD sequence clusters. After constructing an initial set of approximate models, we select a confident subset of over 30,000 models for further refinement and analysis, revealing putative novel protein folds. We also provide updated models for over 5,000 Pfam families studied in the original DMPfold paper.

Analysis of amino acid residue covariation in deep multiple sequence alignments (MSAs) has revealed that covarying residues in proteins are frequently found to be close together in the tertiary structure. This principle has been successfully exploited for predicting interresidue contacts by a variety of methods. Notable among these are the family of methods based on direct-coupling analysis (DCA) (1–3) and, more recently, a number of methods based on deep learning. The latter have produced increasingly precise predictions of interresidue contacts in recent years (4–6) and have also been adapted to output probabilistic predictions of the distance between the residues in contact, either as a probability distribution (7–10) or as real values (11–13). These predictions are usually made by models that operate on precomputed features derived from an MSA, such as covariance and/or precision matrices, contact predictions from DCA-based methods, together with other features such as predicted secondary structure labels and sequence profiles. This approach, though effective, requires that these features be precomputed, which can in some cases be a time-consuming process and can sometimes take longer than the rest of the prediction pipeline combined. Additionally, it does not allow the neural network model to utilize all the information that might be available in the sequence alignment, as a model trained on derived features is limited to using the information available in those handpicked features.

A key difficulty in using MSAs directly as input to a neural network is the fact that an MSA for a target sequence can have arbitrarily many sequences in it. To date, only a few published methods attempt to use an encoding of the MSA itself as the input to a neural network-based predictor of protein structural features. In rawMSA (14), the difficulty of embedding MSAs of arbitrary depth was addressed by training separate convolutional networks using predetermined maximum MSA depths. Recently, we demonstrated that a system of recurrent neural network (RNN) layers can be used to process MSAs of arbitrary size (15). A handful of subsequent studies have also demonstrated that directly processing MSAs in a neural network can be effective for predicting structural features such as interresidue contacts or distances. In the MSA Transformer (16), the neural network model exploits the equivalence of aligned positions in the MSA in order to derive embeddings via a tied row attention framework. These embeddings are shown to be useful for producing accurate predictions of interresidue contacts in a number of proteins. The process of end-to-end differentiable coordinate generation for protein structures, where atomic coordinates are produced as a direct output of a neural network, was first demonstrated in the Recurrent Geometric Network (17), which takes as input an amino acid sequence and a position-specific substitution matrix (PSSM) for the sequence family. Another end-to-end method, NEMO (18), combines a neural network representation of a forcefield with a coarse-grained Langevin dynamics simulator to derive structures, starting from a sequence and PSSM. More recently, RoseTTAFold (31) and AlphaFold2 (26) employed direct embeddings of an input MSA to directly output atomic coordinates for a protein structure, with the latter producing models of unprecedented accuracy in many cases.

A number of studies have applied recent advances in protein structure prediction to model large sets of protein sequences with unknown structures, such as Pfam families (9, 19–22) or proteins from a minimal genome (23). These efforts have been limited, though, by the computational cost of running more than a few thousand predictions in a reasonable time frame. This has prevented structural annotations from keeping pace with the vast increase in sequence data now available as a result of metagenomic sequencing efforts. These large sequence collections present unique opportunities for discovery of proteins with potentially novel folds and/or novel functionality, and therefore, the development of rapid, accurate methods for predicting protein structures from sequence information alone is highly desirable.

In this paper, we develop a deep neural network-based method for predicting protein structures directly from MSAs in an end-to-end-differentiable fashion, building on methods we trialed in CASP14 (15). Our method produces coordinates of backbone atoms as a direct output of the neural network model, further saving time over model generation approaches used previously, and also provides a predicted confidence in the output coordinates. Using this method, we model protein sequences from the BFD (24, 25), a clustered collection of over 2.2 billion sequences assembled from a number of metagenomic sequencing efforts as well as sequences from UniProt. We have attempted to leverage this collection of sequences to derive structural annotations for the protein families represented therein.

We show that despite the relatively simple composition of the input feature set, we are able to obtain predictions of comparable or better accuracy than DMPfold1 (9) while taking under a second to a few minutes to produce one structure on readily available hardware. DMPfold2 is thus fast enough to run at unprecedented scale, and we apply it to over 1.3 million subsequences without detectable templates extracted from the BFD, generating over 30,000 confident models, and using these to explore the structural content of the dark protein space in the BFD. We show how such an approach can be used to find otherwise undetectable homologs and aid in function prediction, along with finding a number of novel folds. We also provide updated models for Pfam families whose structures were predicted in the original DMPfold1 study (9).

Results

Tertiary Structure Model Accuracy on CASP13 Domains.

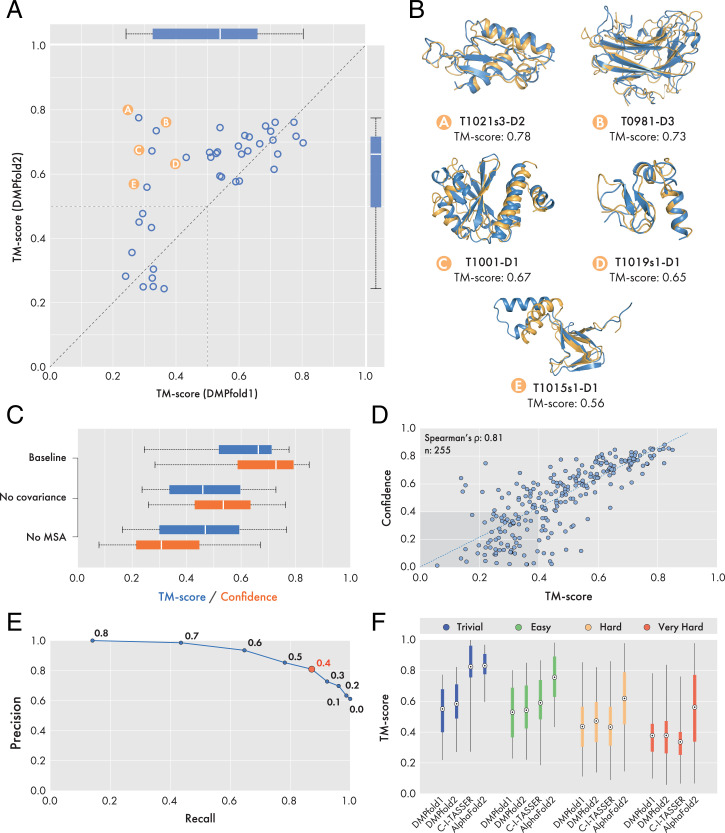
As an evaluation of the effectiveness of the DMPfold2 end-to-end model building procedure, we built three-dimensional (3D) models of 39 FM and FM/TBM domains from the CASP13 experiment. Comparison against models generated using DMPfold1 (Fig. 1A and SI Appendix, Table S1) shows that DMPfold2 produces more accurate structure models for these domains; five examples are shown in Fig. 1B. DMPfold2 is able to fold 30 domains to a TM-score of 0.5 or greater, as compared to 26 for DMPfold1. The mean TM-score is 0.590 for DMPfold2 and 0.531 for DMPfold1.

Fig. 1.

Results obtained on CASP13 domains and Pfam families. (A) Comparison of TM-scores obtained by DMPfold2 and DMPfold1 on 39 CASP13 FM and FM/TBM domains. Detailed model accuracy data for each target can be found in SI Appendix, Table S1. A dashed line of unit slope is drawn, as well as segments demarcating the TM-score ≥ 0.5 regions of the plot. Overall, DMPfold2 end-to-end achieves comparable or greater model accuracy than DMPfold1. (B) Five CASP13 domains could be folded correctly (TM-score > 0.5) by the end-to-end procedure but not by DMPfold1. Models and native structures are shown in orange and blue respectively. (C) Effect of ablating covariance or MSA features on DMPfold2 performance. Results compare TM-scores and confidence scores on 39 CASP13 domains. Ablating either the covariance features or the MSA embeddings results in a pronounced drop in predictive accuracy. (D) Scatterplot comparing TM-scores and confidence scores of 255 Pfam models generated by DMPfold2. (E) Precision-recall curve generated from data shown in D. Values next to data points represent the confidence score threshold used for binary classification. A maximal precision, recall and F1-score is achieved using a threshold of 0.4 (red datapoint). (F) Comparison of DMPfold1, DMPfold2, C-I-TASSER and AlphaFold2 predictive accuracy on a subset of 221 targets from the Pfam dataset. Pfam targets were subdivided into four difficulty classes as reported in Ref. 22. The marker at the center of each boxplot represents the mean TM-score obtained.

We also used the CASP13 domains to assess the impact of ablating either the MSA embedding or covariance features input to the DMPfold2 neural network. The results in Fig. 1C show that both of these features contribute substantially to the accuracy of the predictions, and that the reduced predictive accuracy upon ablation of either feature type also results in a drop in confidence in the predictions. Additionally, predictions with the baseline network using all input features appear to be robust to MSAs of varying quality (measured using effective sequence counts and gap fraction; SI Appendix, Fig. S2).

Pfam Models.

We produced updated models for 5,193 Pfam families, using the same MSAs as used in the original DMPfold1 paper (9). A subset of 255 Pfam families have since had representative models made available. Using this subset, we found a strong positive correlation between predicted confidence and TM-scores to the ground-truth structures (Fig. 1D). We also determined that a confidence threshold of 0.4 could be used in a binary classification manner to dichotomize models into those likely to have a TM-score greater or less than 0.4. The appropriate confidence threshold value was determined by selecting the value at which precision, recall and the F1-score was maximized and therefore minimizing type I and type II errors (Fig. 1E and SI Appendix, Table S2). Of the remaining 4,938 Pfam families without representative structures, ∼60% of the models generated (2,950 models) were at a confidence score of 0.4 or greater, with the majority of these high-confidence models representing targets between 50 and 200 residues in length (SI Appendix, Fig. S3 A and B). Using a confidence threshold of 0.4 as a binary classifier affords a precision of 0.87, thus we estimate that ∼2,600 of these models will have a true TM-score of 0.4 or greater.

As a benchmarking exercise, we compared the models of a common subset of 221 Pfam families generated by DMPfold2 to those generated by DMPfold1 (9), C-I-TASSER (22), and AlphaFold2 (26), calculating the TM-score of each model to a PDB entry assigned to the equivalent family (Fig. 1F and SI Appendix, Fig. S4). We additionally subdivided targets based on their LOMETS classification (22) into trivial, easy, hard, and very hard categories. A table of mean TM-scores achieved by each method in each difficulty category can be found in SI Appendix, Table S3. From our analysis, it can be seen that DMPfold2 outperforms DMPfold1 in all difficulty classes, in terms of the mean TM-score achieved for each category (Fig. 1F and SI Appendix, Fig. S4). DMPfold2 further outperforms C-I-TASSER in the hard and very hard categories but underperforms in trivial and easy cases. Examples of six targets belonging to the very hard category are shown in SI Appendix, Fig. S3C. The lower performance of our method on easy and trivial targets can be attributed to the fact that DMPfold2 does not make explicit use of template information, whereas C-I-TASSER does. The architecture of DMPfold2 does allow for distance information from templates to be added as an input to the ResNet section, replacing the distance map derived from the output coordinates (see Neural Network Model), though this was not done during the training process. We are currently investigating methods for explicitly supplying template information during the prediction process. Finally, it can also be seen that AlphaFold2 outperforms all other methods for all difficulty classes, with the exception of trivial targets, where it achieves a similar mean TM-score as C-I-TASSER (Fig. 1F and SI Appendix, Table S3).

BFD Modeling Experiments.

We modeled 1,333,242 subsequences from the BFD not matching conserved families in the Pfam or CATH-Gene3D HMM libraries using one iteration of DMPfold2. Given that around 86% of these subsequences were fewer than 300 residues in length, most will correspond to single domains, and a single pass through the DMPfold2 neural networks will provide a rough idea of the distribution of folds present, following which we can select a subset of promising models for further refinement and analysis. A summary of key metrics on the set of 1.3 million models appears in SI Appendix, Fig. S5. Although the vast majority of the models are predicted to have a confidence score of less than 0.4, most of these low-confidence models correspond to target sequences that are either very short, and/or whose MSAs have very few sequences (SI Appendix, Fig. S5). Additionally, for some fraction of these targets, domain boundaries may not have been correctly parsed, as our subsequence filtering procedures were based only on sequence profile HMM similarity.

From the initial set of 1,333,242 models, we focused on a subset of 33,548 models predicted by DMPfold2 to have a confidence score of 0.4 or greater (see Materials and Methods). Our reasoning for not choosing a stricter cutoff was that it should be possible to refine some fraction of these models using the iterative prediction mode of DMPfold2. The majority of these targets are also predicted to be ordered according to IUPred, with 79% of sequences having 80% or more residues predicted as ordered. A comparison of per-residue confidence scores and IUPred scores shows that residues confidently predicted as ordered (IUPred score ≤ 0.3) or disordered (IUPred score ≥ 0.7) show distinct distributions of confidence scores, with residues strongly predicted to be disordered showing low DMPfold2 confidence scores on average (Fig. 2C).

Fig. 2.

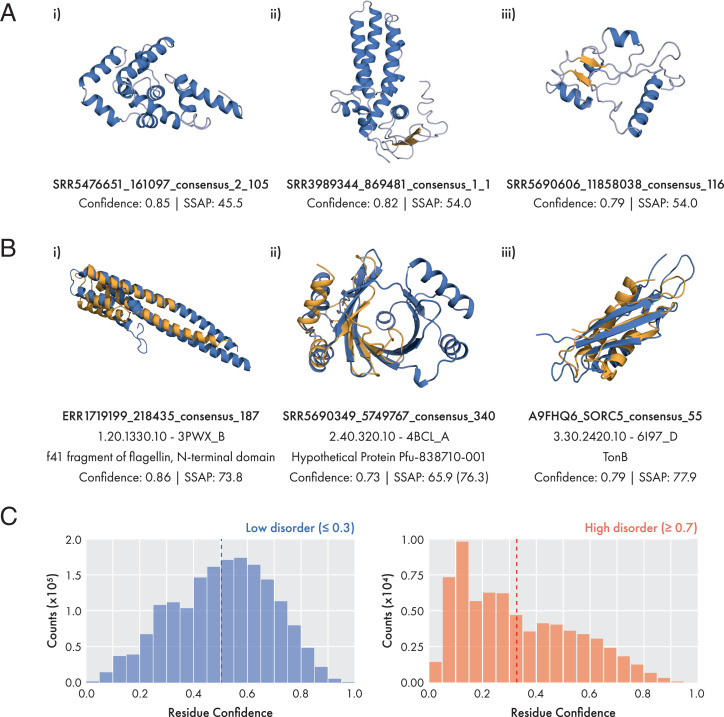
Examples of BFD models generated by DMPfold2. (A) Potential novel folds identified from 225 remodeled BFD targets. Structures shown are high-confidence models with a SSAP score (57, 58) of less than 70 to the most similar structure in the PDB representative set. Models are generated from recomputed BFD alignments using the 10-iteration end-to-end procedure. Helices and sheets are colored in blue and orange respectively. (B) Examples of BFD proteins matched to CATH topology classes with a single homologous superfamily. In these cases it is likely that the target protein shares function with other members of the superfamily. Models and native structures are shown in orange and blue respectively. For target b-ii), the value in parentheses represents the SSAP score if aligned to only half of the template. (C) Confidence distributions for residues with low (blue) or high (red) disorder. Residue disorder was predicted for a sample of 33,000 BFD models using IUPred. Residues with low or high disorder were classified using a IUPred-predicted disorder score of 0.3 or lower, or 0.7 or higher, respectively. Dashed lines indicate the mean of the distribution at 0.504 for low disorder residues, and 0.327 for high disorder residues.

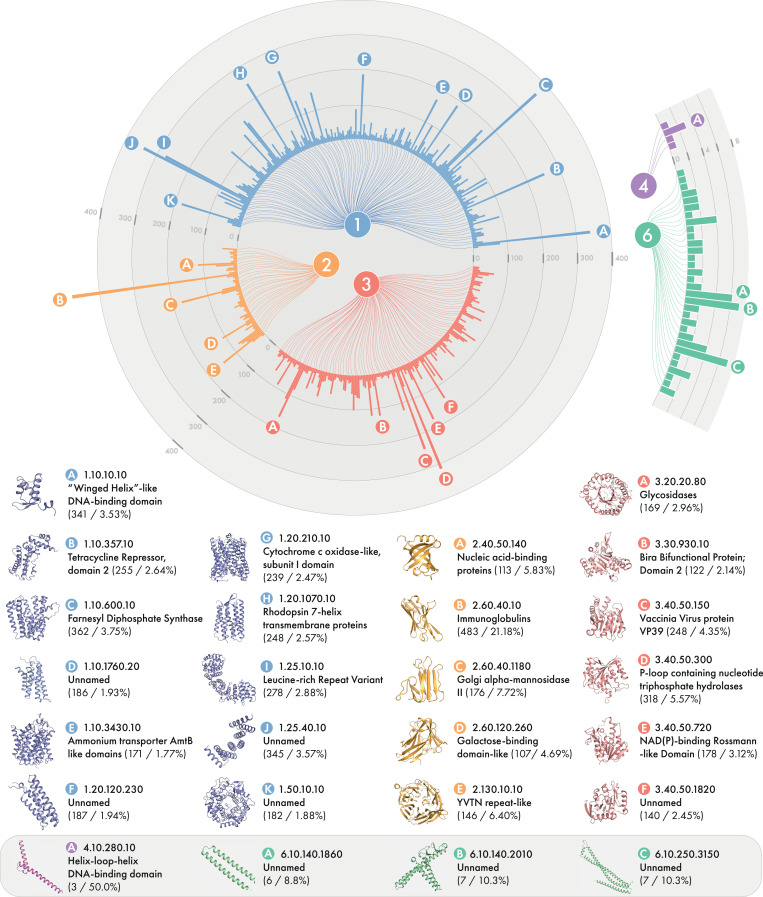
We also assessed this set of models for similarity to existing CATH families. Overall, we were able to assign 23,495 models to 2,394 CATH superfamilies on the basis of structural similarity (SI Appendix, Table S5), suggesting that the predictions are correct at the fold level. Fig. 3 shows the distribution of these models and their folds. The large fraction of models with a similar structure in the PDB despite most sequences with templates being eliminated shows the value of de novo protein structure prediction for mapping sequences to the existing fold space and inferring homology. Indeed, most targets in the FM category at CASP do match a known fold, even though the template is not found with sequence-based searching (27). As in our study of Pfam with DMPfold1, we do find a number of confident models that do not match structures in the PDB and likely represent novel folds.

Fig. 3.

Distribution of BFD models assigned to CATH superfamilies. Data represent the number of models assigned to each class and superfamily from CATH. The values under each superfamily name represents the number of models assigned to that superfamily and as a percentage of total models assigned to that class. Superfamilies with fewer than 10 models assigned for class 1 to 3 were omitted for clarity (211/945, 54/451, and 154/962 shown, respectively).

Iterative refinement of medium-to-high-confidence models.

A total of 225 targets with medium-to-high confidence models were chosen and MSAs and models were rebuilt for these targets by searching against the BFD. We compared the models built using the original MSAs extracted from the BFD against those built afresh using the trimmed consensus sequences as a query, with DMPfold2 running either 1 or 10 iterations. The results in SI Appendix, Fig. S6 demonstrate that regardless of the MSA used, the iterative updates to the coordinates output by DMPfold2 result in improved confidence scores as well as greater secondary structure content. Concomitantly, a larger fraction of the models are found to have a hit to the PDB with a TM-score of 0.5 or greater. These results show the benefit of iterative structure refinement, but also demonstrate that model quality can usually be improved by generating a fresh MSA for the subsequence of interest rather than merely extracting a region of the original BFD MSA for a longer sequence family. A number of targets were identified as potentially having a novel fold, based on comparison to the PDB with TM-align. Three of these models are shown in Fig. 2A.

Template detection and function prediction using modeled structures.

An additional experiment was run to assess whether the DMPfold2 models can be used for detection of distantly related proteins that may otherwise be missed by state of the art HMM-HMM comparison tools such as HHsearch. We used the BFD sub-MSAs for the 33,548 modeled sequences as queries to search the PDB70 database using HHsearch. Thirty-one percent have at least one hit in the PDB70 database at an E-value threshold of 1.0. At an E-value threshold of 0.001, only 12% of the queries retrieve significant hits despite 83% having a model that matches a structure in the PDB. This illustrates the value of tertiary structure models in retrieving structural templates: assuming that the DMPfold2 models are correct at the fold level, the TM-align search against the PDB reveals that these models are structurally similar to existing PDB entries, whereas an HMM-HMM comparison would miss these templates. Of course, this principle has been well understood for some time and is the basis of protein threading (28, 29), but the ease and speed with which a rough candidate model can be generated for a query sequence has the potential to accelerate and improve the sensitivity of structural template searches.

In some cases it is possible to speculate about the function of modeled sequences by matching the model to structures of known function (30). Three examples are shown in Fig. 2B of models that match CATH superfamilies that are the only superfamily in the respective CATH topology type. In these cases it is likely that the sequences share a function with other members of the matched superfamily. This approach to assigning function will become more applicable as protein structure prediction methods improve and more experimental structure data becomes available.

Discussion

Recent successes in applying deep learning to protein structure prediction have mostly relied on the use of large, precomputed feature sets as inputs to the deep learning model. Here, we show that it is possible to directly process a MSA into a learned representation that is effective for predicting structural features in proteins. Structural models built using DMPfold2 are more accurate on average than those from DMPfold1. It is expected that allowing the network to access all the information in a raw MSA, rather than just pairwise frequency information, for example, enables it to extract richer information that can be used for more accurate prediction of structural features. Although the best performance is obtained when using the learned MSA representation alongside an on-the-fly computed precision matrix, the work in this study opens up the possibility of using just the MSA representation itself as the sole input to the ResNet for predicting protein structure, though that will probably require using methods with better ability to deal with very long-range dependencies (see paragraph 5 of this section), as some groups have recently done (16, 26, 31). It also enables lines of work that were prohibitive with large feature sets (such as those used in DMPfold1) due to the time and storage requirements of using those features.

The idea of end-to-end de novo prediction (17, 18) has certainly been tantalizing, in that a 3D model can be produced in a fraction of a second compared to the hours or days needed previously. So far, however, most published end-to-end methods have not been able to produce models comparable to the state of the art in de novo prediction, mainly because they have not effectively exploited covariation data as inputs. DMPfold2 is able to produce main chain coordinates of comparable or greater accuracy as compared to DMPfold1, while taking very little time to produce each model. This allows quick validation of de novo predictions before full modeling is carried out or could be combined with a refinement method to almost completely replace the whole 3D modeling pipeline. We showcased this approach by applying DMPfold2 to sequence families from the BFD, and even using a relatively coarse-grained approach, we were able to predict structures with plausible topologies for tens of thousands of uncharacterized protein domains, including some with potentially novel folds. We also showed that the modeling process can be used to identify fold-level similarity to existing PDB entries, where such similarity would otherwise have been missed by a purely sequence-based comparison.

During the preparation of our manuscript, two papers describing successful protein structure prediction using MSA embeddings were published. The RoseTTAFold method employs direct embeddings of MSAs to produce distance restraints, as well as to produce coordinates directly (31). This method employs a three-track attention-based neural network model inspired by DeepMind’s AlphaFold2 system, which produced excellent results in CASP14. AlphaFold2 (26) employs a number of novel neural network modules that are specialized for producing representations of MSAs and protein structures, beginning from a direct embedding of the input MSA and target sequence. In comparison to these methods, DMPfold2 produces models in much less time (SI Appendix, Fig. S7), making it suitable for use at a very large scale. Although DMPfold2’s models are not as accurate, they are still of sufficient accuracy to allow for easy identification of potentially interesting targets from very large datasets that can then be modeled using slower and more accurate modeling tools.

There are many interesting potential applications for nearly instant tertiary structure modeling methods based on direct embedding of MSAs. One example would be to visualize changes to the final 3D model as the input sequences in the MSA are changed, essentially in real time. Assuming that the confidence scores predicted by the neural network are an accurate indication of accuracy of the predicted structure, one could envision optimizing the MSA in a way that maximizes the neural network’s confidence in the structure, for example by removing sequences that disrupt covariation or other signals that the neural network uses to make its prediction. Changes in predicted model confidence could also be used in iterated HMM-HMM searches or clustering procedures to identify profile drift, which would in theory manifest as a drop in predicted model confidence upon incorporating additional sequence hits in the MSA. Predicted structures could also be used as enhancements to existing HMM libraries, similar to the manner in which secondary structure predictions have been used in the past (32). They could also be used to predict domain boundaries in large sequence libraries.

We are continuing to develop neural network architectures for end-to-end structure prediction. In DMPfold2, the use of two gated recurrent networks to embed the input MSA is clearly effective but was something of a design compromise in that RNNs are relatively fast to train, but have known limitations in terms of the limits of modeling long-range dependencies in sequences. In theory, gated RNNs are able to avoid the problems of vanishing gradients when modeling long sequences, but in practice, dependencies beyond a window of a few hundred sequence positions are poorly modeled. For this reason we used two GRU networks, one to embed in the vertical (sequence number) and one in the horizontal (residue number) direction so that the number of time steps that each GRU would need to model would be limited by either the lengths of typical protein domains or the depths of typical MSAs. For MSAs with longer sequences or with many more homologous sequences, even gated RNNs will start to become ineffective. We are currently investigating alternative means of embedding MSAs, such as the use of models based on new efficient Transformer architectures (33), which are far more memory-efficient than the original Transformer (34) due to avoiding the calculation of large self-attention matrices over the length of the sequences. Standard Transformer models have already been used to embed unaligned protein sequences (35–37), but the most efficient Transformer models released in the last year are now capable of handling sequence lengths even in the millions, and so this suggests that a single deep Transformer model with a compressed self-attention mechanism could, in principle, embed a whole MSA in one go by essentially treating it as a single sequence. Current experiments along these lines are promising.

Overall, we have demonstrated that the idea of embedding whole MSAs into a linear representation using standard language modeling approaches can enable the efficient generation of 3D structures directly from sequence data. This approach enables structural models to be built on a far larger scale than was previously possible. In methodological terms, being able to directly link individual amino acids in an MSA to the outputs of the network, many structural bioinformatics applications could be made easier, e.g., modeling variant effects or protein design. At the very least, these direct MSA embedding methods make de novo protein structure prediction methods far more efficient and easier to use.

Materials and Methods

Datasets for Training and Evaluation.

Training was conducted on a mixture of both chains and domains, comprising 31,159 domains from the V4.2 CATH (38) s35 representative set of domains and 6,742 full length chains from the original DMPfold1 training set. A set of 300 chains were held out from training to use as a validation set to monitor convergence. MSAs for each training example in the CATH s35 set were created using 3 iterations of HHblits v3.0b3 (39) using the UniClust30 (October 2017) database, with an E-value threshold of 0.001 and minimum coverage of 50%.

We tested the effectiveness of our method on a set of 39 domains from the CASP13 experiment, categorized as either FM or FM/TBM by the CASP13 assessors. MSAs were built using HHblits (39) by first searching the UniRef30 database (2020_06 release), then using the MSA thus obtained as a query for a further HHblits search against the BFD.

Neural Network Model.

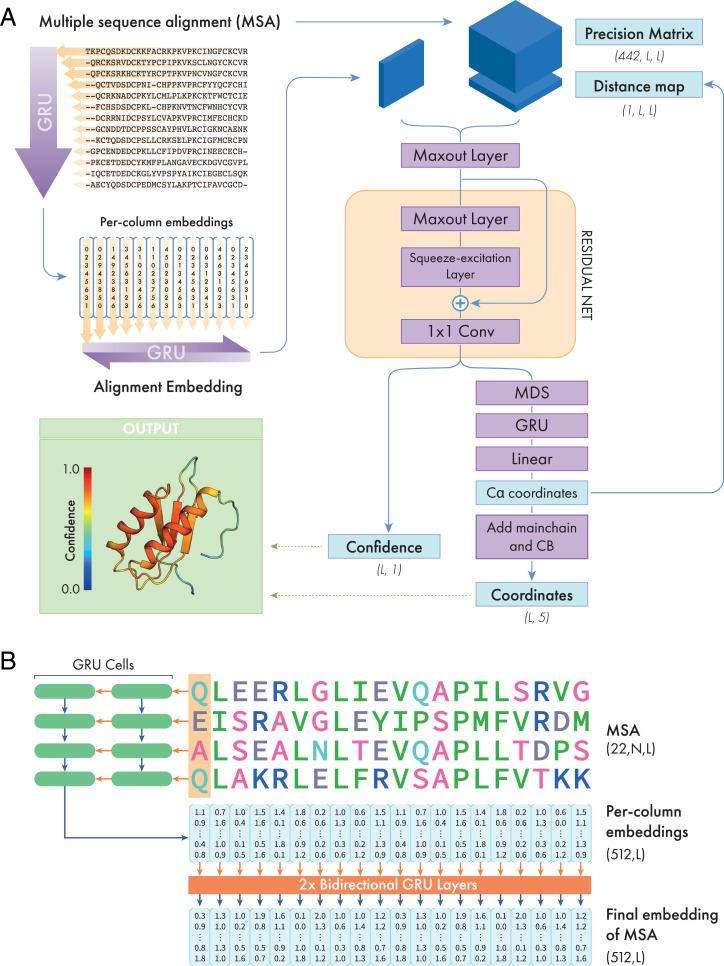
A schematic representation of the DMPfold2 architecture is shown in Fig. 4A, and the MSA embedding procedure is shown in Fig. 4B. We used a system of gated recurrent unit (GRU) layers to process and embed the input MSA and output a feature map with 256 × L values, where L is the length of the target sequence. Starting from a 22-dimensional one-hot encoding of each residue in each sequence in the MSA, a stack of 2 GRU layers scans individual columns in the MSA in the vertical direction. The hidden state of these layers is a vector of fixed size (512 in our case), and the hidden state at the end of the vertical scan is used as a fixed-length representation of the information in each column of the MSA. The per-column representations are then passed to another stack of 2 bidirectional GRU layers with 256 hidden units, producing final embeddings for each column of 2 × 256 values. These embeddings are striped vertically and horizontally [similar to the manner in which per-residue features are prepared for use by 2D convolutional layers (4, 5)], and combined with a fast approximation of a precision matrix, calculated using the “fast_dca” algorithm from trRosetta (10). These features are then used as input to a convolutional Maxout layer to reduce the number of channels to 128, followed by a series of 16 residual blocks, each composed of one Maxout layer (40) and one squeeze-excitation layer (41) each.

Fig. 4.

Schematic representation of the DMPfold2 neural net. (A) The input multiple sequence alignment (MSA) is processed into a learned embedding, as shown in detail in B. This embedding is combined with a precision matrix calculated from the MSA and fed to a convolutional Maxout layer to reduce its dimensionality, before being fed to a series of 16 residual neural net (ResNet) blocks. Each block is composed of a convolutional Maxout layer and a Squeeze-excitation layer. The outputs from the network are collected as the outputs of a 2D convolutional layer with 1 × 1 filter, and are a combination of different structural features, represented in the right-hand column. All outputs from the network are predicted jointly. (B) Details of the MSA embedding section. The MSA is represented by a one-hot encoding of 22 residue types (including gaps and unknown residues). First, the residues in a single column of the MSA are treated as timesteps and fed as input to a stack of two Gated Recurrent Unit (GRU) network layers. The final hidden state of the second GRU, obtained after processing the whole column of the MSA, is used as an embedding of the information in that column. The process is then repeated for the remaining columns in the MSA, producing a separate embedding for each MSA column. Finally, these per-column embeddings are used as inputs to a stack of 2 bidirectional GRU layers that produces an embedding of all sequences and columns in the MSA. The dimensions of the input tensor and embeddings are shown in parentheses.

As we first showed with DMPfold1 (9), iteration of the prediction process, where the final model is fed back in as an input to the network, can result in significant improvements in model quality. We note that a similar strategy also proved effective in AlphaFold2. DMPfold2 also allows iterations, where the output coordinate set can be used as a seed for second and subsequent passes through the network. To allow this, the ResNet incorporates an extra input feature channel carrying pairwise Cα distances from an existing 3D structure, which can all be set to a constant of −1 to indicate no distances are to be considered, i.e., during the first pass. Such a setup also allows for this distance information to be provided from other sources such as templates, though we did not train the network in this way and no explicit template information was used for any of the predictions made in this work.

The final stages of the network implement end-to-end prediction of coordinates from the output embeddings of the ResNet as shown in Fig. 4A. A two-channel 1 × 1 convolutional layer is used to project the ResNet embeddings into two channels, one for the output Cα-Cα distance map, the other to represent confidence estimates for each pair distance. The distance outputs from this layer are converted to a real-value distance matrix $\mathit{D}$ by first averaging the upper and lower triangles of the matrix and taking absolute values to ensure that the distance matrix is positive-definite and symmetric. This matrix is projected to 3D Cα coordinates using classical multidimensional scaling (MDS) (42). In MDS, the following (Gram) matrix is defined for the predicted distance matrix $\mathit{D}$:

$${\mathit{M}}_{ij} = \frac{{\mathit{D}}_{1j}^2+{\mathit{D}}_{i1}^2-{\mathit{D}}_{ij}^2}{2}$$

The eigendecomposition $\mathit{M}=\mathit{US}{\mathit{U}}^T$ is then calculated, where $\mathit{X}\mathbf{ }\mathbf{=}\mathbf{ }\mathit{U}\sqrt{\mathbf{S}}$ gives the coordinates of the points. Note that if a distance map can be fully embedded in 3D space there will only be 3 nonzero eigenvalues of $\mathit{M}$ , but this is not necessarily the case for the real-valued distance matrix predicted by the network. Coordinates corresponding to the largest 8 eigenvalues were therefore calculated and the rest discarded. Potential problems with MDS are that there are no learnable elements, and the procedure can arbitrarily produce mirror images of the coordinate set, and so there is no way for the network to learn to modify the coordinates, for example to correct chirality issues. Therefore, a “learnable MDS” module was implemented simply by feeding the 8-dimensional output from the MDS step, concatenated with the original biGRU embedding of the MSA, through a final 2-layer bidirectional GRU recurrent network (256 weights per hidden layer), with 520 input channels and a final fully connected layer with 512 inputs and 3 outputs (representing the final Cα coordinates). During training with a rigid body coordinate loss, as opposed to a distance-based loss, this final network is able to learn to automatically transform the output coordinates for any structures mirrored by the multidimensional scaling process, without manual intervention.

After the network predicts Cα coordinates, a simple coordinate refinement module attempts to correct “obvious” issues with the model. Cα atoms adjacent in sequence are moved to a target distance of 3.78 Å and all Cα-Cα distances are moved to a minimum of 3.0 Å according to a harmonic potential for 100 steps. Backbone N, C, and O atoms and Cβ atoms are then added using a geometric procedure based on the “catomain” routine from the DRAGON method (43). Suppose that v₋₁ is the vector from a Cα to the previous Cα in the sequence, v₊₁ is the vector from a Cα to the next Cα in the sequence, m₋₁ is the midpoint between a Cα and the previous Cα in the sequence, and x_α is the normalized vector cross product of v₋₁ and v₊₁. The coordinates C_N of N, C_C of the previous residue C and C_O of the previous residue O are then given by the following:

$${\mathit{C}}_{\mathbf{N}}= {\mathit{m}}_{\mathbf{-}\mathbf{1}}- {\mathit{v}}_{\mathbf{-}\mathbf{1}}/8\mathbf{ }+ {\mathit{x}}_{\mathbf{\alpha }}/4$$

$${\mathit{C}}_{\mathbf{C}}={\mathit{m}}_{\mathbf{-}\mathbf{1}}+{\mathit{v}}_{\mathbf{-}\mathbf{1}}/8\mathbf{ }- {\mathit{x}}_{\mathbf{\alpha }}/2$$

$${\mathit{C}}_{\mathbf{O}}={\mathit{m}}_{\mathbf{-}\mathbf{1}}- \mathrm{1.8}·{\mathit{x}}_{\mathit{\alpha }}$$

If v_N is the vector from N to Cα in a residue, v_C is the vector from C to Cα in a residue, v_β is the normalized sum of v_N and v_C, x_β is the normalized vector cross product of v_N and v_C, and C_α is the coordinates of Cα, then the coordinates C_β of Cβ are given by the following:

$$\text{θ} = \text{π/2} -{ \text{sin}}^{-1}\left(1/\sqrt{3}\right)$$

$${\mathit{C}}_{\mathbf{\beta }}={\mathit{C}}_{\mathbf{\alpha }}+ 1.5·\text{cos}\left(\theta \right)\text{·}{\mathit{v}}_{\mathbf{\beta }}+ 1.5·\text{sin}\left(\theta \right)\text{·}{\mathit{x}}_{\mathbf{\beta }}$$

Special considerations are required for the terminal residues, with details available in the source code. No further atom-level optimization or refinement of the structure was attempted in any of the results shown, though it would be easy to add side chains to these models and refine the models further, at the expense of losing the end-to-end characteristics of the method.

In its iterative mode, the DMPfold2 network allows a recurrent processing of the final model. In this mode, predicted Cα coordinates are used to calculate a distance matrix and this matrix is fed back to the ResNet layer as an additional input channel (Fig. 4). Together with the dynamic computational graph construction used by PyTorch, this enables us to train the network with the iterations included. During training, the number of allowed iterations was varied between 0 and 5 due to the accumulated gradients and GPU memory limitations (see next section), but during inference any number of iterations can be requested as no gradient information is needed. The final model returned after iteration is the model which has the highest overall confidence as judged by one output channel of the ResNet.

Training Procedures.

The DMPfold2 neural network was implemented using PyTorch (44) and trained using the Adam optimizer (45). An initial learning rate of 0.0003 was used, a dropout probability of 0.1 was used for the recurrent network layers, and dropout 0.2 used in the convolutional layers. For data augmentation, at each epoch each alignment in the training set is subsampled as follows:

• a)Random rows from the alignment are selected, up to a maximum of 1,000, though always including the target sequence in the first row.
• b)Alignments with >350 columns (residues) are randomly cropped to that maximum length to fit within available GPU memory, and the target coordinates are similarly cropped to match.

As a loss function, we opted for TM-score (46) rather than RMSD. This choice of loss function reduced the effects of bad model outliers and kept both the model loss and confidence scores to be normalized to the range [0,1]. Confidence values are output per residue, which allows confidently modeled segments of the model to be distinguished from less confidently modeled segments.

To reduce the memory footprint of the model and to include the iterative portion of the prediction pipeline during training, we made use of automatic mixed-precision training and gradient checkpointing. The number of iterations included was initially varied between a minimum of 0 (single forward pass with no iteration) and a maximum of 3 iterations. This limit was increased to 5 during further fine-tuning training runs.

Effects of Ablations and MSA Quality on Predictive Accuracy.

In order to better understand the contribution of the MSA embedding and covariance-based features on predictive accuracy, we carried out ablation experiments by removing each of these features as described as follows. In addition, we evaluated the performance of the baseline DMPfold2 model, using all features, on MSAs of varying effective sequence count (N_eff) and gap fraction. We used the same CASP13 domain MSAs obtained in Datasets for Training and Evaluation for these experiments, as these had an informative range of N_eff and gap fraction values.

Ablation of MSA embedding.

This variant of the DMPfold2 network has access to the covariance features of the MSA when these can be calculated, but is only allowed to embed the target sequence using the MSA embedding network (Fig. 4B and Neural Network Model).

Ablation of covariance features.

In this variant, the network has access to the complete MSA embedding, but the covariance features are all set to zero.

Effect of MSA quality.

We assessed the TM-scores and confidence values obtained by DMPfold2 on MSAs with a range of N_eff and gap fractions. Effective sequence counts were calculated as the number of sequence clusters returned by CD-HIT (47) using a sequence identity threshold of 62% (48). Gap fraction was calculated as the number of gaps in the alignment divided by the number of positions (number of residues multiplied by number of sequences).

Modeling Pfam Families.

In the original DMPfold1 publication (9), we generated models for a set of 5,214 Pfam families for which no structural annotation was available. Models were generated for 5,193 of these families, using DMPfold2 and the same alignments as those used for DMPfold1. Some target sequences contained nonstandard amino acids and were excluded.

Experimental structures have since been made available for 255 of these families. To assess the accuracy of our models, we calculated the TM-score between the 255 Pfam families annotated in this study and their respective PDB representatives. We additionally compared the accuracy of our models with those produced by DMPfold1 (9), C-I-TASSER (22), and AlphaFold2 (26). In this comparison, 221 Pfam models generated by each of the four methods were compared to the same reference PDB chain via TM-align (normalized by the length of the modeled protein). 34 targets were excluded from this analysis due to either not having been modeled in the original DMPfold1 publication (24 targets), or because they overlapped with the AlphaFold2 training set (12 targets). Targets were additionally subdivided according to their predicted difficulties reported in the C-I-TASSER (22). It is also important to note that the representative PDBs of the 255 families did not overlap with the DMPfold2 training set. These results were also used to evaluate the confidence scores predicted by DMPfold2, and to choose a threshold value of the confidence measure that maximizes the F1 score for binary classification. This threshold value was found to be 0.4 (Fig. 1E and SI Appendix, Table S2), and was used to identify promising models in the BFD modeling experiments.

Modeling Protein Domains from the BFD.

Extraction of subalignments from the BFD.

The consensus sequences from each MSA in the BFD were extracted and scanned against the Pfam (49) and CATH-Gene3D (38, 50) HMM libraries using hmmscan (51) in order to filter out regions corresponding to well-characterized protein families. Unmatched subsequences at least 30 residues long were then used to extract the corresponding (sub)MSAs from the BFD alignments, discarding rows in the resulting subalignment comprising only gap characters. The resulting set of 1,333,242 MSAs were used as the inputs for the modeling runs.

Generation and evaluation of end-to-end-predicted models.

We ran DMPfold2 using one iteration in order to obtain a first set of models. Because the BFD subalignments vary greatly in terms of quality and coverage, we opted to use a quick modeling sweep of the MSAs in order to identify promising candidates that might benefit from several iterations of the modeling procedure. In total, we generated 1,333,242 models from the BFD alignments by running one iteration of DMPfold2. From each model, we recorded model descriptors including: the number of target residues (nres), alignment depth, predicted confidence, radius of gyration (Rg) and 8-class secondary structure assignments via DSSP (52). Given that reasonable runtimes could be obtained even without the use of GPUs, all structure models were generated on a CPU cluster using ∼200 to 400 CPU cores over the course of approximately 3 weeks.

Of the 1,333,242 models, 48,625 models (3.65%) corresponded to single- or double-helix structures. We identified these models using the criteria that such models must consist of only one or two helices (composed of at least 50% of residues) and have a Rg/nres ratio of greater than 0.28 or 0.18, respectively. These criteria were manually calibrated from a sample of generated models. The Rg/nres ratio describes the average contribution of each residue toward the model Rg, and can be helpful for identifying single/double helices with partially malformed secondary structure.

Next, from the remaining 1,284,617 models, 33,548 (2.61%) were found to have a network-predicted confidence score of 0.4 or greater. These targets were scanned for disorder using IUPred (53, 54). To assess the similarity of these models to known folds, we compared each model to a representative set of PDB chains formed by clustering all protein chains in the PDB with 30+ residues at 30% sequence identity. The closest match by TM-score calculated using TM-align (55) normalized over the length of the modeled protein was recorded, meaning that models could register a match to part of a larger domain. To assign CATH superfamilies, any CATH domains present in the closest matched PDB chains were extracted using BioStructures.jl (56), and the TM-score was calculated with TM-align between the modeled protein and the CATH domain. The model was assigned to the superfamily if the largest TM-score was greater than 0.5. A visual summary of the entire model filtering workflow can be found in SI Appendix, Fig. S1.

Iterative refinement of medium-to-high-confidence models.

A total of 225 models with a variety of predicted confidence scores were taken from the initial set of 1.3M models. We rebuilt MSAs for this set using HHblits searching against the BFD and modeled them using either 1 or 10 iterations of DMPfold2 modeling. For a baseline, we also used the same MSAs used in the first modeling sweep with either 1 or 10 iterations of DMPfold2 to evaluate the effect of rebuilding MSAs and including more iterations during modeling. We assessed the refined models in terms of their predicted confidence scores, secondary structure content, and similarity to PDB entries. Secondary structure content was assessed as the fraction of residues having a DSSP-assigned code corresponding to secondary structures. Models were compared to a representative set of PDB chains as described previously and potential novel folds were identified as those with a largest TM-score of less than 0.5.

Data Availability

The DMPfold2 source code and trained neural network weights are available at https://www.github.com/psipred/DMPfold2 under the terms of the GPLv3 free software license. Protein structures predicted from the BFD and Pfam are available via the UCL Research Data Repository (https://doi.org/10.5522/04/14979990) (59). Training scripts and data are also available via these repositories.