Probing molecular crowding in compressed tissues with Brillouin light scattering

Significance

Volume regulation is key in maintaining important tissue functions, such as growth or healing. In this process, the role of efflux of cellular fluids is difficult to capture due to the lack of apt technologies. Here, we use a tool based on Brillouin light scattering (BLS) that uses the interaction of a laser light with inherent picosecond timescale density fluctuations in the sample. We induced gradual volume decrease in multicellular spheroids using osmotic perturbations. BLS revealed a nonlinear increase of the tissue compressibility due to the subsequent increased biopolymer crowding within the cells. Our findings should inspire research regarding volume regulation and cellular crowding in tissues and stimulate the emergence of models for cell mechanics at short timescales.

Abstract

Volume regulation is key in maintaining important tissue functions, such as growth or healing. This is achieved by modulation of active contractility as well as water efflux that changes molecular crowding within individual cells. Local sensors have been developed to monitor stresses or forces in model tissues, but these approaches do not capture the contribution of liquid flows to volume regulation. Here, we use a tool based on Brillouin light scattering (BLS) that uses the interaction of a laser light with inherent picosecond timescale density fluctuations in the sample. To investigate volume variations, we induced osmotic perturbations with a polysaccharide osmolyte, Dextran (Dx), and compress cells locally within multicellular spheroids (MCSs). During osmotic compressions, we observe an increase in the BLS frequency shift that reflects local variations in the compressibility. To elucidate these data, we propose a model based on a mixing law that describes the increase of molecular crowding upon reduction of the intracellular fluids. Comparison with the data suggests a nonlinear increase of the compressibility due to the dense crowding that induces hydrodynamic interactions between the cellular polymers.

Volume regulation is key in maintaining important tissue functions, such as embryogenesis or wound healing (1). Perturbation of volume homeostasis, by external forces applied to the tissue or abnormal regulation, has also been associated with the development of degenerative diseases, such as cancer (2). Coordinated modulation of active contractility, membrane tension, and cell–cell and cell–extracellular matrix junctions are known to drive cell shape and volume. For this reason, a large body of research has been devoted to the implementation of local sensors to monitor stresses or forces in model tissues during hyperosmotic shocks (3, 4). Such approaches focus on stiffness regulation, but they cannot capture the role of water efflux that changes molecular crowding within individual cells and can impact cell fate (5) and induce cytoplasm phase separation (6) or colloidal glass-like transition (7).

In recent years, a new quantitative microscopy based on Brillouin light scattering (BLS) has been proposed that uses the interaction of a laser light with picosecond timescale density fluctuations in the sample (8). BLS has been successfully used for mechanical phenotyping and imaging with a contrast based on the stiffness (9), but its relevance from a physiological standpoint remains debated due to the ultrashort timescales involved. Since the probing mechanism involves coupling of photons to longitudinal phonons, variations in the scattering spectra can be interpreted as the response of the sample to an infinitesimal uniaxial compression and formally described by the longitudinal modulus M. In an idealized two-phase biological sample, variations of M would be driven in part by the polymer meshwork but also—and this feature separates BLS from classical microrheology approaches—by the compressibility and the dynamics of the liquid phase (10).

Usually discarded, this unique feature was used to interrogate the liquid-to-solid transition in stress granules related to amyotrophic lateral sclerosis diseases (11). However, an investigation of hydrogels also recently suggested that water content should play an important role in the response in biological materials (12). In tissues, the respective contributions of the stiffness of the elastic network and of the liquid phase remain unclear. To elucidate this question and investigate its implication in volume control, we induced osmotic perturbations in order to compress isotropically multicellular tissues. We demonstrate that volume changes due to water efflux at the cellular level dominate the BLS response. Comparison of the data with a model based on a mixing law suggests that the increase of molecular crowding upon reduction of the intracellular fluids leads to a nonlinear acoustic behavior due to hydrodynamic interactions within the cells.

Results

Volume Control in Multicellular Spheroids with Osmotic Shocks.

To investigate volume regulation in three-dimensional (3D) clusters, we engineered multicellular spheroids (MCSs) from the spontaneous aggregation of the colorectal carcinoma cell line HCT116. In contrast to single-cell experiments, such a model allows for the analysis of the volume regulation by both intracellular spaces and intercellular spaces (ICSs). One of the difficulties of analyzing volume changes in mammalian cells is that compression can be followed by a regulatory volume increase driven by ion channels and pumps (13). To circumvent this difficulty, we imposed isotropic osmotic compressions using solutions containing Dextran (Dx) molecules that do not lead to regulatory volume increase (SI Appendix, Fig. S2) (14).

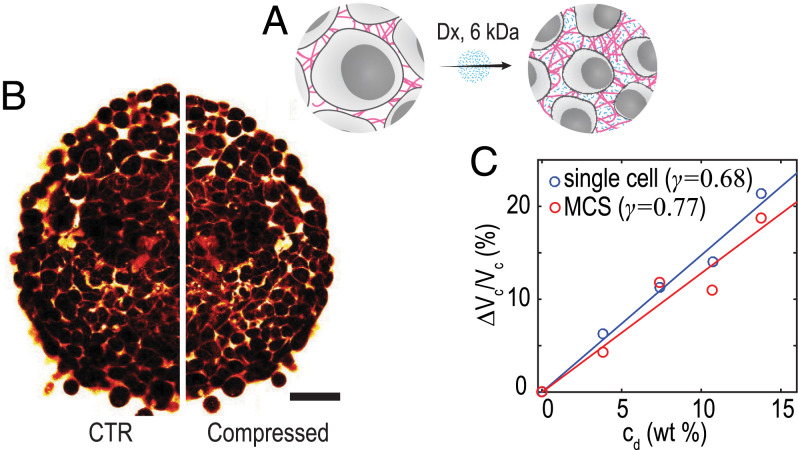
Dx is a type of biocompatible glucose polymer that generates osmotic pressures depending on its molecular weight and concentration. We take advantage of the selective compression method described in ref. 15. Briefly, 6-kDa Dx molecules can diffuse throughout the ICS and thus, only apply a local osmotic pressure to the cell within the MCS. This mechanism of compression is sketched in Fig. 1A.

Fig. 1.

(A) Schematic representation of the isotropic osmotic compression by Dx. (B) Two-photon images of MCS captured before and after shocks with 6 kDa Dx. (Scale bar: 100 µm.) (C) Variation of single-cell volume vs. Dx concentration measured by FXm on single cells (blue markers and line fit) and determined from MCS volume variations (red markers and line fit) (SI Appendix, Note 1).

As an illustration of the impact of osmotic compression by Dx on the structure of MCS, we placed MCSs in between two plates separated by $\sim 70$ µm and labeled the ICS with a fluorescent dye (tissue confiner is discussed in Materials and Methods); the reduced thickness of the sample allows two-photon microscopy in a two-dimensional (2D)–like configuration. Fig. 1B shows the images obtained before and after the shock with 6 kDa Dx. The two-photon images clearly show a reduction of both the MCS and cell volumes, consistent with the literature (15). To quantify this observation, we plot the MCS volume determined from the white light images recorded on the BLS microscope during the shocks in Fig. 1C (n = 40, N = 2) (SI Appendix, Note 1). We observe a linear dependence of the normalized MCS volume change with increasing Dx concentration c_d,

$$\mathrm{\Delta }{V}_c/V_c=\left(V_c^0-V_c\right)/V_c=c_d/\gamma ,$$ [1]

with $V_c^0$ the initial volume and $\gamma =0.77$ obtained from the best fit to the data.

To quantify the contribution of cell compression to this volume reduction, we measured the volume variation in single cells during shocks for different Dx concentrations using the fluorescence exclusion microscopy (FXm) (Materials and Methods). Briefly, HCT116 cells were suspended in a medium supplemented with a fluorescent dye that does not cross the cell membrane, and they were inserted in a microfluidic chamber with a fixed height. Fluorescence is excluded from the cells, leading to a decrease in total fluorescence, proportional to cell volume (16). Images obtained in epifluorescence microscopy with a large depth of field allow for integrating intensity over the whole chamber height ($\sim 20$ µm). This signal is integrated over the cell-projected area to calculate cell volume (17). Here, we also observe a linear dependence of the normalized increment in cell volume with increasing Dx concentration. Using Eq. 1 to fit these data yields $\gamma =0.68$. This γ value is close to that found from the MCS volume, demonstrating that cell compression is the main source of volume variation during osmotic compressions with small Dx molecules.

Brillouin Spectroscopy Reveals Cell Compression.

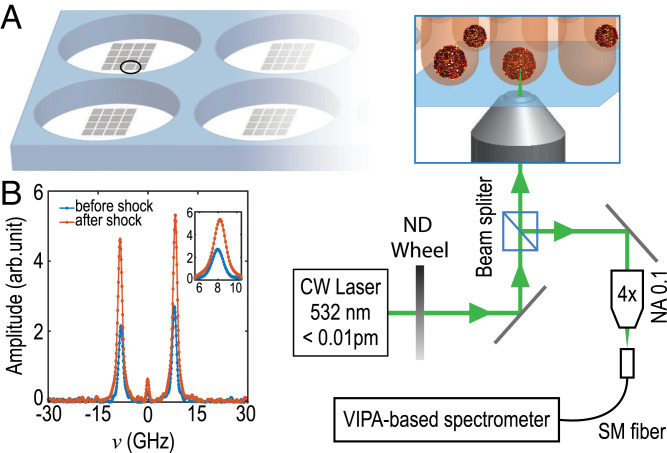
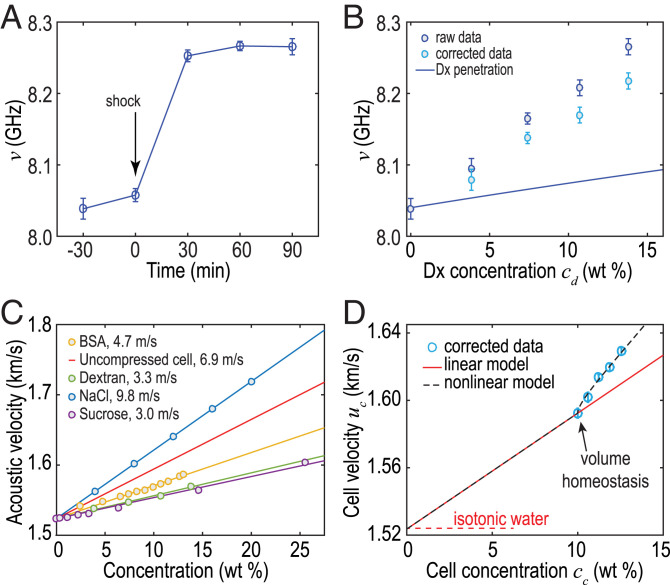
To implement Brillouin spectroscopy with a high throughput, we engineered patterns of hundreds of agarose-based microwells (Materials and Methods), each of them containing one MCS, as is sketched in Fig. 2A. Such a custom-made plate is placed in an inverted microscope equipped with an environmental chamber. We focus a laser beam at the center of the MCS and collect the backscattered light with a $20\times$ objective lens that gives a scattering volume of $\sim 5\times 17$ µm. We analyze the spectrum of the backscattered light using a virtually imaged phase array (VIPA)-based spectrometer (18). We show in Fig. 2B the typical spectra obtained before and after shocks. We plot the BLS frequency shift ν as a function of time in Fig. 3A (n = 40, N = 2) during shocks with Dx molecules at 160 g/L. We observe a significant increase of the BLS shift ν after the shock that stabilizes after $\sim 30$ min.

Fig. 2.

(A) Schematic of microstructured wells for MCS; the virtually imaged phase array (VIPA)-based Brillouin spectrometer is coupled with a microscope. (B) Typical spectrum obtained at the center of an MCS before and after the shock. (Inset) Zoomed-in view of the anti-Stokes shift. SM, single mode. NA, numerical aperture; ND, neutral density; CW, continuous wave.

Fig. 3.

(A) BLS frequency shift during osmotic compressions vs. time after shock for Dx solutions at 160 g/L. (B) Brillouin shift before (dark blue; raw data) and after subtraction (light blue) of the contribution of the penetration of small Dx molecules vs. Dx concentration. The solid line indicates the sole contribution of Dx penetration. (C) Velocity increment measured for different solutions (results for NaCl are from ref. 18). (D) Sound velocity in cells u_c vs. cell concentration (blue markers; corrected to remove the contribution of Dx penetration as in B). Black lines show the predictions by the linear (solid) and nonlinear (dashed) models. BSA, bovine serum albumin.

Although a similar increase in ν has been observed on single cells (8), its origin remains debated. Assuming that the refractive index and mass density are not significantly affected by the osmotic conditions, it was initially proposed that such an increase was due to structural changes (8). Recent studies, however, suggested that water content—or volume—should also play an important role (12). In order to clarify this possible contribution in MCS, we imposed osmotic compressions at increasing pressures p using solutions containing increasing concentrations of Dx. We first plot in Fig. 3B the BLS shift ν_small vs. osmolyte concentration c_d. We observe a largely linear increase in ν_small, but this variation also includes an artifactual increase due to the replacement of the intercellular fluids by Dx solutions with a higher refractive index, sound velocity, and mass density. In order to isolate the contribution of cell compression, we correct for this effect using a mixing law model.

We describe the MCS as the spatial average of cellular and intercellular compartments with a volume fraction of cells $\varphi =0.9$ (15). The ICS is initially considered to behave as an isotonic solution (1% sodium chloride) but is replaced by the small Dx molecules that can penetrate into the ICS. Since the Brillouin shift ν depends on the refractive index n, mass density ρ, and longitudinal modulus M (or equivalently, sound velocity $u=\sqrt{M/\rho }$), it is necessary to define these quantities for the ICS. We consider the variations in refractive index $\mathrm{\Delta }{n}_i=\alpha \mathrm{\Delta }{c}_d$ and mass density $\mathrm{\Delta }{\rho }_i=\xi \mathrm{\Delta }{c}_d$, with classical values $\alpha =0.0019$ and $\xi =3.75$ kg/m³ found in the literature (19, 20). We determined the velocity increment, $\mathrm{\Delta }{u}_i={\beta }_i\mathrm{\Delta }{c}_d$, from the frequency shift measured in Dx solutions of relevant concentrations and found ${\beta }_i=2.5$ m/s at 37 ${}^{°}$C. To validate this result, we compared it with several reference solutions (sucrose, NaCl, and bovine serum albumin) (Fig. 3C). As expected, the value for Dx is close to that of sucrose. From these values, we evaluate the average u, ρ, and n values for the MCS using standard mixing laws (Materials and Methods) and determine the artifactual frequency increase, ν^artefact, due to the penetration of the Dx molecules. We plot the corrected frequency, ${\nu }^{\mathit{corr}}=\nu -{\nu }^{\mathit{artefact}}$, in Fig. 3B as well as the prediction for ν^artefact (Fig. 3B, solid line). We observe a smaller corrected frequency shift that represents the sole contribution of the compressed cells.

Modeling a Crowding-Induced Nonlinear Acoustic Behavior.

One may postulate that the increase in ν arises from the increased solute concentration within the compressed cells. To integrate cell volume in a predictive model for tissue compression, we refine our previous description and model the cells as a dilute suspension of proteins and ions with an initial concentration $c_c^0=10$ wt %, as measured on a similar cell line (17, 21). During the osmotic shock, we assume a constant dry mass, so the decrease in cell volume $\mathrm{\Delta }{V}_c$ is accompanied by an increase in the concentration $\mathrm{\Delta }{c}_c=c_c^0\mathrm{\Delta }{V}_c/(V_c-\mathrm{\Delta }{V}_c)$ within the cells. Since we have measured the normalized increment in cell volume $\mathrm{\Delta }{V}_c/V_c$ (Eq. 1 and Fig. 1C), we can simply write

$$\mathrm{\Delta }{c}_c=c_c^0\frac{c_d}{\gamma -c_d}.$$ [2]

Since α and ξ are largely independent of the type of molecule (19, 20), we can express the increase in refractive index $\mathrm{\Delta }{n}_c=\alpha \mathrm{\Delta }{c}_c$ and mass density ${\rho }_c=\xi \mathrm{\Delta }{c}_c$, as we did for the ICS. However, because there is a greater dependence of the velocity increment, as exemplified by the values measured in several biorelevant fluids (Fig. 3C), we need to determine the velocity increment in cells, $\mathrm{\Delta }{u}_c$.

As observed in Fig. 3C, the velocity increment in dilute polymer solutions is near linear as can be approximated by Wood’s formula based on the additivity of compressibilities (22). As a first approach, we thus use

$$\mathrm{\Delta }{u}_c/\mathrm{\Delta }{c}_c={\beta }_c^0,$$ [3]

and we determine ${\beta }_c^0$ by fitting the frequency shift before the shock ($\mathrm{\Delta }{c}_c=0$). We find a velocity increment, ${\beta }_c^0=6.9$ m/s, that lies in between solutions of proteins (e.g., bovine serum albumin [BSA]) and ions (e.g., NaCl), providing a plausible value for cells within a tissue (the red line in Fig. 3C). Implementing this modeling of the cells in the model based on the spatial average of cellular and intercellular compartments we described previously, we predict the frequency shift resulting from cell compression. For ease of comparison of the modeling with the data, we convert Dx concentration to cell concentration using Eq. 2. We then convert ν to a cell velocity using the mixing laws for the refractive index and velocity (SI Appendix, Note 2). We plot u_c vs. c_c in Fig. 3D (markers) and compare with the prediction (Fig. 3D, solid line). We observe a cell velocity of $\sim 1,594$ m/s before the shock, in good agreement with values obtained for single cells by acoustic microscopy at similar frequencies (23–25). Interestingly, we see that we cannot describe the full frequency shift, clarifying that a phenomenon additional to the variation in cell volume is at work.

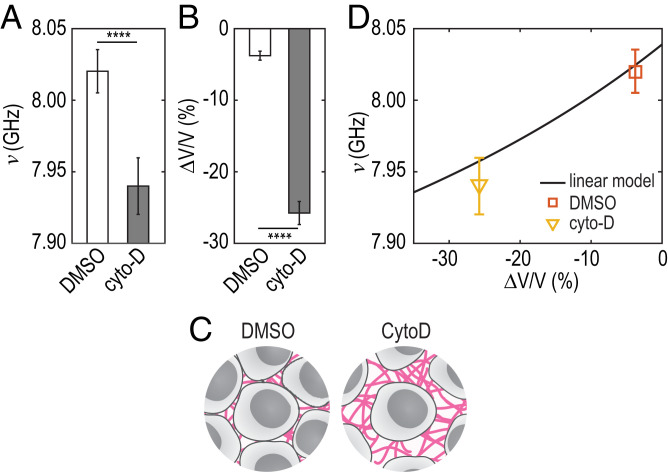
To investigate a possible contribution of a structural change due to cytoskeleton remodeling, we inhibit actin polymerization with cytochalasin D (cytoD) (Materials and Methods). We plot the BLS frequency shift ν mock treated with dimethyl sulfoxide (DMSO) and treated with cytoD in Fig. 4A (n = 40, N = 2). We observe a significant decrease of the BLS shift ν after actin depolymerization (P < 0.0001), as has been observed at the single-cell scale (8). We also determined the MCS volume from the projected area in bright-field imaging. We observed a significant increase in volume ($\sim 25$ %, leading to negative $\mathrm{\Delta }V$ values) upon actin depolymerization (n = 8, P < 0.0001) (Fig. 4B). This volume increase most probably arises from an increase of the ICS since actin depolymerization with cytoD does not affect cellular volume, as is sketched in Fig. 4C (26). We plot in Fig. 4D the prediction from the model we presented earlier (Fig. 4D, plain line) and the cytoD/DMSO data points. We see that such an increase in MCS volume can entirely explain the observed decrease in ν. This result indicates that a possible cytoskeleton remodeling has negligible influence on the frequency shift.

Fig. 4.

(A) Frequency shift and (B) normalized volume measured in the agarose microwells measured on MCS treated with DMSO or cytoD. ${}^{****}P<0.0001$, unpaired two-tailed t test. (C) Schematic representation of the compression by cytoD. (D) Frequency shift predicted by the linear model (solid line) vs. volume change of MCS treated with DMSO (square) and cytoD (triangle).

Increase of sound velocity with increasing solute concentration can be well described by the volume average of the compressibilities in colloidal suspensions (27) or emulsions (28). In biological solutions containing polymers and ions, however, intermolecular interactions (e.g., hydrogen bonds or dipole interactions) can lead to correlation of volume fluctuation of adjacent molecules, often resulting in a deviation from such classical description (29). For this reason, a power law is usually preferred:

$$\mathrm{\Delta }{u}_c/\mathrm{\Delta }{c}_c={\beta }_c^0+{\beta }_c^1{\left(\mathrm{\Delta }{c}_c-c_c^0\right)}^{\tau },$$ [4]

where ${\beta }_c^1=9.1$ m/s is determined by the best fit to the data and $\tau =0.5$ as is used in electrolytic solutions (30). We observe excellent agreement in Fig. 3D (dashed line). This comparison strongly suggests that the observed increase in ν arises from a nonlinear acoustic behavior due to the increased crowding within the cells inside the MCS.

Discussion

In conclusion, we have shown that BLS can monitor locally—without any label—the impact of tissue compression. This methodology is a powerful noncontact, label-free, and high-throughput alternative to microinjected stress sensors (3, 4) and opens up possibilities to investigate the role of cell volume during various cellular events (17) at the tissue scale and down to the single-cell scale. It should also find applications for the investigation of local pressure in small animals during development (31). Constant improving of spectrometers, both in terms of sensitivity and speed, and implementation of BLS-compatible endoscopes and adaptive optics should also allow medical translation in the near future.

The velocity increment in cells, ${\beta }_c=6.9$ m/s, is three orders of magnitude larger than the refractive index increment, $\alpha =0.0019$. BLS is therefore exquisitely sensitive to changes in the sound velocity with changes in cell volume (or solute concentration within them). We have observed a clear deviation of the data from the classical mixing law model based on the volume average of the compressibilities. We have proposed a model that accounts for a nonlinear increase of the sound velocity with decreasing cell volume.

This simple empirical approach captures the main features of our data and suggests that the dense crowding in the cells induces correlated fluctuations of the cellular polymers. Similar observations have been made in hydrogels, where the emergence of such nonlinear acoustic behavior has been attributed to a stiffening of the elastic frame composed by the intercellular components (32). The exact nature of such interactions requires more in-depth exploration of the complexity of multicellular systems and the development of more refined theoretical acoustic descriptions. In particular, it seems important to investigate the possible effect of active volume regulations that might occur at short timescales with different osmolytes and for an extended range of volumes.

Such sensitivity of the sound velocity has been used to probe protein transitions (33), binding events (34), or hydration (35) at the macroscale using ultrasonic frequencies. The ability of BLS to produce such data at hypersonic frequencies at the single-cell scale should allow for investigating structural arrests or phase separations during protein condensation. We also anticipate that our results should stimulate the emergence of models for cell mechanics at short timescales and expand the range of application of BLS to the life sciences.

Materials and Methods

Cell Culture and Reagents.

HCT116 colorectal carcinoma (CCL-247) adenocarcinoma cell lines were purchased from the American Type Culture Collection. Cells were cultured in Dulbecco’s Modified Eagle Medium (DMEM) supplemented with 10% fetal bovine serum (FBS; PAN Biotech), 1× penicillin/streptomycin (P/S), and glutamax (Life Technologies) at 37 ${}^{°}$C under a 5% CO₂ atmosphere. All cells were used at low passage numbers, subconfluently cultured, and plated at 10⁴ cells per cm². MCSs for BLS imaging were obtained by seeding the cells onto the homemade agarose microwells and grown for 4 to 5 d in culture medium.

FXm for Single-Cell Volume Measurements.

Cell volumes were obtained using FXm as detailed in refs. 16 and 17. Briefly, cells were incubated in polydimethylsiloxane (PDMS) with medium supplemented with a fluorescent dye coupled to small (10-kDa) Dx molecules to prevent entry into cells. Fluorescence is thus excluded by the cells, and volume is obtained by integrating the fluorescence intensity over the cell. Chips for volume measurements of single cells were made by pouring a mixture (1:10) of PDMS elastomer and curing agent (Sylgard 184) onto a brass master and cured at 80 ${}^{°}$C for at least of 2 h. Inlets and outlets were created with a 3-mm biopsy puncher. Chips were prepared a few days ahead of the experiment, bonded with oxygen plasma for 30 s, warmed up at 80 ${}^{°}$C for 3 min, incubated with Poly-l-lysine (Sigma) for 30 min to 1 h, washed first with phosphate-buffered saline (PBS) then washed with dH₂ O, dried, and stored sealed with a paraffin film. The chips can be stored up to 10 d. The chambers were washed with PBS before cell injection.

Imaging started within 10 min after cell injection in order to prevent adhesion and thus, cells response to the shear stress generated by medium exchange. Acquisition was performed at 37 ${}^{°}$C in CO₂ independent medium (Life Technologies) supplemented with 1 g/L Alexa647 Dx (10 kDa; Thermo Fischer Scientific) on an epifluorescence microscope (Leica DMi8) with a 10× objective (numerical aperture (NA) 0.3).

Tissue Confiner Experiments.

Spheroids were harvested 4 or 5 d after cell seeding and injected in the 2D confiner microsystem using an MFCS pressure controller (Fluigent). Spheroids rested from 2 to 5 h to relax in the microsystem at 37 ${}^{°}$C in CO₂ independent medium. Before two-photon imaging, medium supplemented with 2 g/L fluorescein isothiocyanate-Dx (10 kDa; Sigma Aldrich) was injected to label the ICS. Medium exchange was performed manually using large inlets ($>1$ mm) during two-photon acquisition. Images were recorded at 37 ${}^{°}$C on a Nikon C1 two-photon microscope coupled with a femtosecond laser at 780 nm with a 40× water-immersion objective (NA 1.10).

The chip was made by pouring PDMS elastomere and curing agent (1:10) on a mold and cured for at least 2 h. Molds were made using the classical photolithography technique. Chips were bonded to glass coverslips with 30 s oxygen plasma. Immediately after bonding, a solution of PLL-g-PEG (SuSoS) at 1 g/L was injected and incubated for 30 min in humid atmosphere to prevent cell surface adhesion during the experiment. The chips were washed with dH₂O, dried, and sealed with a paraffin film. They can be stored up to 1 wk and washed with PBS prior to spheroid injection.

Agarose Microwells Molding.

A solution of 4% (wt/vol) agarose (Sigma Aldrich) in distilled water was prepared by autoclaving at 120 ${}^{°}$C for 15 min. The agarose solution was deposited on the prewarmed PDMS molds (placed on a hot plate at 78 ${}^{°}$C for standard agarose) and covered with silanized coverslips. Then, the mold and coverslip were removed from the hot plate and left to jellify at reach room temperature for 10 min. PDMS molds were removed, and the coverslips with the agarose microwells were glued to homemade bottomless six-well plates using biocompatible Norland optical adhesives (NOA81; Norland Products).

Molds Fabrication.

For the agarose microwells and FXm experiments, master molds were fabricated on brass substrate with a micromilling machine (MiniMill/3; Minitech) using a flat or ball-nose milling cutter (Dixi Polytool). Height profiles and surface roughness were measured with a vertical scanning interferometric profilometer (Brucker). The 3D mold design and tool paths were generated using Autodesk Inventor Professional software (Autodesk).

Molds for spheroid confinement were made with classical soft lithography techniques. PDMS molds for agarose molding are countermolds obtained from brass master molds.

Osmotic Compressions.

We induced osmotic perturbations with a polysaccharide osmolyte, Dx (6 kDa), at different concentrations (40, 80, 120, and 160 g/L). The solutions were prepared by diluting Dx powder from Leuconostoc mesenteroides (Sigma Aldrich) into CO₂ independent imaging medium (DMEM supplemented with glutamax, 10% FBS, 1× P/S, and 20 mM hydroxyethyl piperazineethanesulfonic acid; Life Technologies). Culture medium was replaced by imaging medium for at least 10 min to equilibrate before adding the compression solutions. For easier comparison, the concentrations are expressed in units of solute concentrations to [weight percentage]. For BLS imaging, we changed the culture medium by fresh culture 30 min before the shock and verified that the BLS frequency shift was not changing upon renewing culture medium.

Brillouin Spectroscopy.

BLS is an inelastic process (36) arising with creation (Stokes process) or annihilation (anti-Stokes process) of acoustic phonons in the medium. The resulting spectra consist of peaks shifted by frequencies $\pm \nu$ (the + and –signs correspond to the anti-Stokes and Stokes contributions, respectively) relative to the frequency of the incident laser light (Fig. 2 shows a typical spectrum). The Brillouin frequency shift, ν, is defined by the following relations (37):

$$\nu =2nu/\lambda ,$$ [5]

where n is the refractive index, $u=\sqrt{M/\rho }$ is the acoustic velocity (with M the elastic modulus and ρ the density), and λ the laser wavelength (18). We used a 532-nm single-mode continuous wave laser with a spectral line width $<0.01$ pm (Spectra-Physics Excelsior-532; 15 mW measured at the sample). The laser is coupled to an inverted life science microscope (Nikon Eclipse Ti2-U) to focus and collect the backscattered light with the same objective lens ($20\times$, NA 0.35). We chose a lens with a low numerical aperture to avoid broadening of the Brillouin spectrum (38). The direction of the output beam is collected by an objective lens ($4\times$, NA 0.10) into a single-mode fiber (1 m, 400 to 680 nm, core diameter 3 µm) connected to a Brillouin spectrometer as shown in Fig. 2. The VIPA-based spectrometer (Light Machinery; Hyperfine HF-8999-532) is based on a 3.37-mm-thick VIPA etalon (30 GHz, 500 to 600 nm) and is equipped with two double-pass air-spaced etalons to increase the contrast to about 120 dB. The fiber is directly connected to the built-in connector of the spectrometer. The free spectral range of the VIPA used in our work is 30 GHz, corresponding to a sampling interval of 0.11 GHz. To ensure perfect control of the sample, the microscope is enclosed in an environmental chamber to maintain a constant temperature (37 ${}^{°}$C) and 5% CO₂ level. For the BLS measurements of MCS under osmotic shocks, we changed the culture medium at $\text{time}=0$ min and then added the Dx solutions after measurements of $\text{time}=30$ min. For each condition, we probed 20 MCS.

Data Availability

Raw data and associated treatments have been deposited in Zenodo (DOI: 10.5281/zenodo.5773601) (39).