Regional Gas Transport During Conventional and Oscillatory Ventilation Assessed by Xenon-Enhanced Computed Tomography

Abstract

Enhanced intrapulmonary gas transport enables oscillatory ventilation modalities to support gas exchange using extremely low tidal volumes at high frequencies. However, it is unknown whether gas transport rates can be improved by combining multiple frequencies of oscillation simultaneously. The goal of this study was to investigate distributed gas transport in vivo during multi-frequency oscillatory ventilation (MFOV) as compared with conventional mechanical ventilation (CMV) or high-frequency oscillatory ventilation (HFOV). We hypothesized that MFOV would result in more uniform rates of gas transport compared to HFOV, measured using contrast-enhanced CT imaging during wash-in of xenon gas. In 13 pigs, xenon wash-in equilibration rates were comparable between CMV and MFOV, but 21 to 39% slower for HFOV. By contrast, the root-mean-square delivered volume was lowest for MFOV, increased by 70% during HFOV and 365% during CMV. Overall gas transport heterogeneity was similar across all modalities, but gravitational gradients and regional patchiness of specific ventilation contributed to regional ventilation heterogeneity, depending on ventilator modality. We conclude that MFOV combines benefits of low lung stretch, similar to HFOV, but with fast rates of gas transport, similar to CMV.

INTRODUCTION

Multi-frequency oscillatory ventilation (MFOV) has been proposed as an alternative modality of mechanical ventilation that delivers to the patient airway opening multiple sinusoidal pressure and flow oscillations at different frequencies delivered simultaneously ^13,23. Compared to conventional mechanical ventilation (CMV) and high-frequency oscillatory ventilation (HFOV), which use a single breathing or oscillatory frequency, MFOV may provide enhanced gas transport, reduced strain heterogeneity, and lung protection ^18,19. A previous study in premature surfactant-deficient lambs demonstrated a benefit of MFOV over HFOV for maintaining a lower oxygenation index and a lower ventilatory cost function ²³. The theorized mechanism of benefit for MFOV is improved regional ventilation-to-perfusion matching, due to the frequency-dependence of distributed flows throughout the lung. Such features in a lung-protective, oscillatory waveform may be highly desirable in the acute respiratory distress syndrome (ARDS).

During CMV, respiratory flows at low frequencies are distributed primarily according to regional lung compliance, and gas transport is dominated by bulk advection of fresh gas directly into alveolar spaces via the conducting airways ⁴². Thus the alveolar concentration of any individual gas species would be expected to equilibrate faster in lung regions with relatively higher compliance and lower regional deadspace ^7,30, at least for a specified blood solubility and cardiac output. This typically occurs in the dorsal lung regions of a supine subject, which exhibit lower end-expiratory inflation level and higher compliance due to the hydrostatic weight of the lung and mediastinal contents ^12,20,22. During HFOV, the distribution of regional flow in the lung becomes increasingly dependent on airway resistance, gas inertia, and asymmetrical airway network branching ^5,17. Gas transport is not dominated by bulk advection at high frequencies, but rather depends on a variety of mechanisms contributing to intrapulmonary mixing ^4,32,37,41. The transport of gases from any particular lung region to the airway opening may depend on regional ventilation distribution more strongly during CMV compared to HFOV ^28,39. Such regional differences in gas exchange will depend on the frequency of ventilation ¹⁷, making MFOV ideally suited for the mechanically heterogeneous lung.

The goal of this study was to investigate the effect of MFOV on distributed gas transport in vivo, as compared with CMV or HFOV. Xenon (Xe), a dense noble gas, has been used extensively as a tracer gas or contrast agent for x-ray computed tomography (CT) ^21,26. Inspired xenon distributes throughout the lung and increases CT voxel value wherever xenon concentration is elevated, providing image contrast for quantitative analysis of regional ventilation distribution ^27,28,30. In this study, we hypothesized that MFOV would result in more uniform rates of gas transport compared to HFOV, measured using xenon-enhanced CT imaging (XeCT). To test this hypothesis, we performed a randomized, crossover trial in pigs receiving CMV, single-frequency HFOV, and MFOV during XeCT. Some of the results of this study have been previously reported in the form of an abstract ¹⁶.

MATERIALS AND METHODS

Animal Preparation

All experimental procedures were approved by the University of Iowa Institutional Animal Care and Use Committee. Another study of respiratory mechanics and structural dynamics was previously published using data collected from a subset of the subjects used in this study ¹³. Thirteen porcine subjects were used in this study, weighing 9 to 13 kg. Following intramuscular injection of 2.2 mg kg⁻¹ telazol, 1.1 mg kg⁻¹ ketamine, and 1.1 mg kg⁻¹ xylazine, deep sedation was maintained throughout surgical procedures using inhaled isoflurane. Each subject was intubated and mechanically ventilated using a Uni-Vent Eagle Model 754 (Impact Instrumentation, West Caldwell, NJ). End-tidal capnography, peripheral oxygen saturation, and electrocardiogram waveforms were obtained using a Philips patient monitor equipped with the M3001A measurement module (Philips Healthcare, Andover, MA). Surgical incision into the neck was performed to allow placement of central venous and arterial lines, as well as relocation of the endotracheal tube into an incision in the trachea inferior to the larynx. Endotracheal tubes were manually shortened prior to tracheostomy, to reduce apparatus deadspace. Following completion of surgical procedures, subjects were transported to the CT scanner. Inhaled isoflurane was discontinued, and sedation was maintained using an intravenous infusion of propofol at 7 to 9 mg kg⁻¹ hr⁻¹. Subjects were paralyzed during experimental ventilation and imaging procedures with intermittent doses of 1 mg kg⁻¹ rocuronium.

Mechanical Ventilation

Subjects were mechanically ventilated using a FabianHFO hybrid oscillator/ventilator (Acutronic Medical Systems AG, Switzerland). A compressed gas cylinder containing a 20%-80% oxygen-xenon mixture was connected by a 3-way ball valve in parallel with the pressurized medical air supply. Figure 1 shows a schematic of the apparatus for xenon delivery during mechanical ventilation. Each subject was mechanically ventilated with CMV, HFOV, and MFOV in randomized order over 30-minute intervals. For all modalities, mean airway pressure (${\bar{P}}_{\text{aw}}$) was set via the ventilator interface at 12 cmH₂O, with fractional inspired oxygen (F_iO₂) at 40% for consistency with 40%-60% oxygen-xenon use during imaging. Control of ${\bar{P}}_{\text{aw}}$ during CMV was achieved via positive end-expiratory pressure (PEEP). CMV was delivered at rates between 20 to 32 min⁻¹ (0.33 to 0.53 Hz), with driving pressure 13 cmH₂O and inspiratory:expiratory time ratio 1:2. HFOV was delivered at 5 Hz, with peak-to-peak (or peak-to-trough) pressure amplitude approximately 50 cmH₂O. MFOV was delivered using a combination of 5, 10, 15, and 20 Hz superimposed oscillations ²³, with peak-to-peak pressure amplitude approximately 84 cmH₂O. Ventilator driving pressure or pressure amplitudes were adjusted to maintain arterial CO₂ tension (P_aCO₂) between 30 to 60 mmHg. Each 30-minute experimental ventilation interval was followed by arterial blood gas analysis and a XeCT scan sequence, without interrupting mechanical ventilation. Between each experimental ventilation interval, a 15-minute ventilation wash-out interval using CMV was conducted to restore baseline mechanical and physiological state.

Figure 1.

(A) Schematic of xenon delivery using a ventilator/oscillator with a three-way valve used to switch gas supplies between air and xenon-oxygen mixtures. After switching the valve without disrupting ventilation, xenon concentration [Xe] in the lung gradually increases (B). The rise in [Xe] is assumed to produce a proportional rise in CT density within lung voxels. CT scans are synchronized with the ventilator to acquire scans at the same phase of ventilation or oscillation, with irregular intervals throughout xenon wash-in. Specific ventilation is estimated by the reciprocal of the time constant of an exponential regression to [Xe] during xenon wash-in.

Ventilatory cost function (V_C) was defined as the product of mean squared delivered volume ($V_{\text{rms}}^2$) and arterial carbon dioxide tension (P_aCO₂) divided by body weight (Wt) ²³:

$$V_{\mathrm{C}}=\frac{V_{\text{rms}}^2\cdot P_{\mathrm{a}}{\text{CO}}_2}{\text{Wt}}$$ (1)

with V_rms computed as:

$$V_{\text{rms}}=\sqrt{\underset{0}{\overset{\Delta t}{\int }}[V(t)-\overline{V}{]}^2\mathrm{d}t}$$ (2)

where V(t) denotes the volume waveform measured at the airway opening, Δt is the duration of sampling (i.e., either 1 breath during CMV, or 1 second during HFOV and MFOV), and $\overline{V}$ is the mean of the volume waveform. The use of V_rms enables comparison between single-frequency modalities, which are typically described by a single tidal volume, and MFOV, which is described by a distinct volume amplitude at each frequency ^13,23.

Image Acquisition

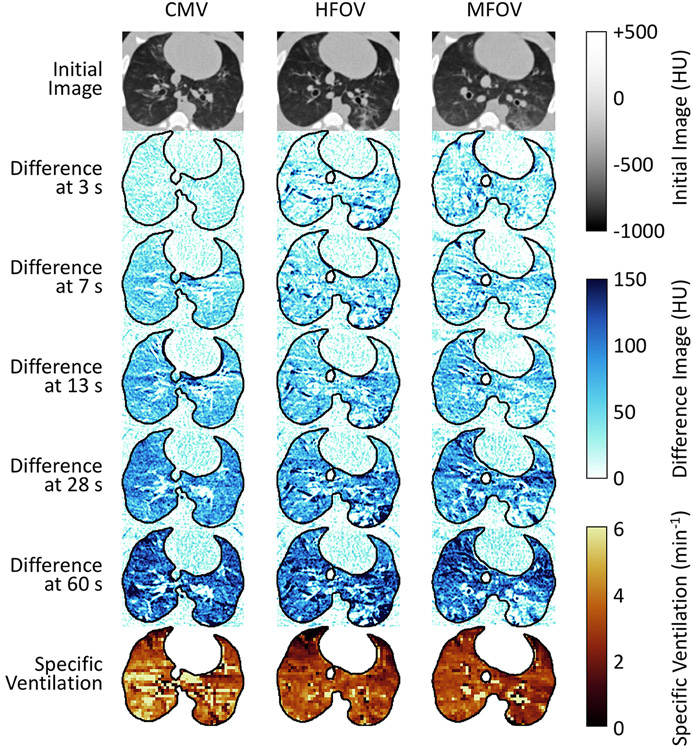
CT scans were acquired using a Siemens SOMATOM Force (Forchheim, Germany) in an axial scanning mode, with 5.76 cm of axial coverage (0.6 mm slice thickness, 96 slices) and 17 cm field of view (0.3 mm in-plane spatial resolution). Subjects were scanned at 70 kVp tube voltage and 200 mA tube current, with 250 ms scanner rotation period. Each scan sequence was initiated immediately following the changeover of gas supply from an approximately 40%-60% oxygen-nitrogen mixture to a 40%-60% oxygen-xenon mixture ²⁸. XeCT scan sequences were timed to acquire a series of images at the same phase of the ventilatory cycle over a wash-in duration of approximately 60 seconds ²⁸. Scans during conventional mechanical ventilation were acquired once per breath, i.e., at the same rate as mechanical ventilation. Scans during high-frequency and multi-frequency oscillatory ventilation were acquired at 1-second intervals over the first 40 seconds, followed by 2-second intervals over the last 20 seconds, for a total of 51 images. Figure 2 shows several images taken from a sequence acquired in one subject during xenon wash-in, as well as the resulting specific ventilation image. Supplemental Video 1 provides an animation of the changes in CT image intensity during the xenon wash-in.

Figure 2.

Representative subject exhibiting changes in CT voxel value during xenon wash-in (0.3 mm spatial resolution), with a few example scan timings indicated at left. Specific ventilation images characterize the rate constant of xenon gas equilibration obtained by exponential regression (2.4 mm spatial resolution). Ventilation modalities were conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV).

Image Processing

Each image in the XeCT image sequence was denoted I_n(x), where n indexes the number of images in the sequence 0 through N – 1, and x is a vector representing 3-dimensional spatial position. Each image was associated with a corresponding elasped time t_n since initial image acquisition. The first image in the sequence was denoted I₀(x) with t₀ = 0 seconds. The acquisition times for each scan were selected to coincide consistently with the same phase of the mechanical ventilation cycle. However, asynchronous cardiogenic motion presented a source of structural misalignment throughout the XeCT image sequence ¹⁴. To compensate for this extraneous motion, each image I_n(x) was warped by pairwise deformable image registration using I₀(x) as the reference or “fixed” image ²⁴. Thus, each deformed image I_n→0(x) contained voxel intensities from I_n(x), but was structurally aligned with I₀(x). Supplemental Figure 1 shows an example of nonrespiratory motion in an image sequence, which produced large fluctuations in CT density that were reduced following image registration. The resulting deformed images were then downsampled to 2.4 mm isotropic resolution to mitigate effects of imaging noise ^28,30. The time-varying intensity within each voxel was fit to an exponential model using nonlinear regression:

$$\widehat{I}(\mathit{x},t)=D_0(\mathit{x})+[D_{\infty }(\mathit{x})-D_0(\mathit{x})]\cdot [1-e^{-t∕\tau (\mathit{x})}]$$ (3)

where D₀(x), D_∞(x), and τ(x) are the regionally varying initial intensities, equilibrium intensities, and time constants of equilibration, respectively ³⁵. Assuming that temporal variations in regional image intensity within co-registered images are due solely to temporal variations in regional xenon concentration, then τ(x) can also be considered the regional xenon equilibration time constant. Values for D₀(x), D_∞(x), and τ(x) were computed at each spatial location x using a nonlinear gradient descent technique (MATLAB, Natick, MA) to minimize the sum of squared differences between model-predicted intensities $\widehat{I}(\mathit{x},t_n)$ and measured intensities I_n→0(x). Regional specific ventilation $s\stackrel{.}{V}(\mathit{x})$ was computed by the reciprocal of the regional time constant τ(x), such that $s\stackrel{.}{V}(\mathit{x})$ also represents the regional rate constant of xenon equilibration ³⁴. Supplemental Figure 2 shows an example of $s\stackrel{.}{V}(\mathit{x})$ in transverse sections for one subject, with varying degrees of downsampling prior to τ(x) estimation. Voxels corresponding to spatial positions within the lungs were identified by an automated segmentation algorithm using a deep convolutional neural network ^10,11. A single lung mask M(x) was generated for each XeCT image sequence based on the reference image I₀(x). Voxels within 7.2 mm of the image boundaries along the rostral-caudal axis were excluded from the mask, due to potential registration artifacts caused by motion of lung tissue into or out of the axial field of view. Voxels with negligible aeration in the reference image (i.e., I₀(x) ≥ −300 HU) were also excluded ³⁰.

Distributed specific ventilation was assessed by the median and quartile coefficient of dispersion of $s\stackrel{.}{V}(\mathit{x})$ within each subject. Coefficient of dispersion, defined as half the difference between the 75^th and 25^th percentiles divided by their average, was used as a measure of overall specific ventilation spatial heterogeneity ². The mean and coefficient of variation were also considered. Spatial gradients of specific ventilation were assessed along three principal axes: ventral-dorsal ${\stackrel{\rightharpoonup }{x}}_{\text{VD}}$, right-left ${\stackrel{\rightharpoonup }{x}}_{\text{RL}}$, and rostral-caudal ${\stackrel{\rightharpoonup }{x}}_{\text{RC}}$. The spatial gradients g_VD, g_RL, and g_RC were determined as the slopes computed by linear regression of $s\stackrel{.}{V}(\mathit{x})$ with respect to position along each principal axis. A least-median-of-squares regression was used for robustness against non-normal distributions of data about the regression line ³³. Figure 3 shows an example of voxel-wise linear regressions for $s\stackrel{.}{V}(\mathit{x})$ along the dorsal-ventral axis in one subject.

Figure 3.

Sagittal sections of a CT scan from one representative subject during conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Downsampled lung voxels are colored according to specific ventilation. Histograms show counts of voxels binned according to both specific ventilation and spatial position with respect to the dorsal-ventral axis. Solid lines represent least-median-of-squares linear regression of specific ventilation in the dorsal-ventral direction.

Regional patchiness of $s\stackrel{.}{V}(\mathit{x})$ was assessed by two techniques relying on recursive subdivision of regions-of-interest within the lung mask: octree and supervoxel decomposition. Both methods were initiallized with a single region of interest (ROI) containing the entire lung mask. At each recursive step, an ROI was designated for subdivision into multiple new ROIs if the standard deviation of voxel values contained within was greater than a fixed threshold. The threshold value for $s\stackrel{.}{V}$ standard deviation in this study was chosen empirically to be 1.3 min⁻¹, to produce nontrivial distributions of ROI size (i.e., either failing to partition even once, or decomposing the entire region into the smallest possible size ROIs). Octree decomposition, a three-dimensional extension of quadtree decomposition, was used to partition each ROI into eight octants according to bisecting coronal, sagittal, and transverse planes ²⁹. Supervoxel decomposition was used to partition each ROI into two new ROIs by a weighted k-means clustering of voxels according to intensity similarity and spatial proximity ⁶. Recursive subdivision was continued until all ROIs either contained below-threshold values of $s\stackrel{.}{V}$ standard deviation, or were too small to be further partitioned. The threshold value for minimum ROI size in this study was chosen to be 0.2% of the lung mask to avoid decomposing to ROIs into individual voxels. Regional patchiness was then quantified by the mean ROI volume ${\bar{V}}_{\text{ROI}}$ as a fraction of the lung mask.

Statistical Tests

A non-parametric Friedman test of ranks was performed for each imaging outcome (i.e., $s\stackrel{.}{V}$ median, $s\stackrel{.}{V}$ coefficient of dispersion, g_VD, g_RL, g_RC, and ${\bar{V}}_{\text{ROI}}$) to test for significant effects of ventilation modality and intersubject variability at the 0.05 significance level. A non-parametric Skillings-Mack test was performed (rather than the Friedman test) for each gas exchange outcome (i.e., V_rms·Wt⁻¹, P_aO₂, P_aCO₂, pH, and V_C), due to missing data for one subject ³⁶. Wilcoxon signed-rank post hoc tests were used for all pairwise comparisons. Additionally, for each ventilation modality, a Wilcoxon signed-rank test was used to test for non-zero means of each spatial gradient (i.e., g_VD, g_RL, and g_RC) at the 0.05 significance level.

RESULTS

Figure 2 shows an example of $s\stackrel{.}{V}$ in transverse sections for one subject during CMV, HFOV, and MFOV (animated sequence of difference images during xenon wash-in is available in Supplemental Video 1). Supplemental Figure 3 shows pressure waveforms measured by the ventilator at the proximal end of the endotracheal tube throughout five cycles of periodic mechanical ventilation. Ventilator settings for mean pressure were constant across all modalities to maintain consistent lung volumes during ventilation and imaging. Note that pressure amplitudes at the endotracheal tube were greatly increased during HFOV and MFOV with some negative pressure excursions, typical features of oscillatory ventilation. Table 1 provides a summary of gas exchange parameters following 30 minutes of mechanical ventilation. Ventilatory cost function (V_C) was defined as the product of mean squared delivered volume and arterial carbon dioxide tension divided by body weight ²³. The use of root-mean-squared volume enables comparison between single-frequency modalities, which are typically described by a single tidal volume, and MFOV, which is described by a distinct volume amplitude at each frequency ^13,23. Note that only 12 subjects are represented for CMV in Table 1 because arterial blood gas could not be collected for one subject following the 30-minute CMV period.

Table 1.

Gas exchange data from arterial blood gas samples after 30 minutes of mechanical ventilation with 40% inspired oxygen and 12 cmH₂O mean airway pressure. Statistical comparisons using Skillings-Mack non-parametric tests and Wilcoxon signed-rank post hoc tests are shown. Bold text indicates significance at the 0.05 level.

Modality	N sub	Vrms·Wt−1 (mL kg−1)	PaO2 (mmHg)	PaCO2 (mmHg)	pH	VC (mL2 mmHg g−1)
CMV	12	3.21 ± 0.65	192.8 ± 32.7	40.6 ± 5.3	7.49 ± 0.05	4.33 ± 1.32
HFOV	13	1.19 ± 0.27	201.7 ± 16.8	43.2 ± 9.5	7.46 ± 0.11	0.63 ± 0.20
MFOV	13	0.69 ± 0.16	190.2 ± 18.9	50.2 ± 14.5	7.40 ± 0.12	0.24 ± 0.07
Statistics		Vrms·Wt−1	PaO2	PaCO2	pH	V C
Effect of Subject		0.067	0.374	0.014	0.018	0.335
Effect of Modality		< 0.001	0.331	0.004	0.014	< 0.001
CMV vs. HFOV		< 0.001		0.424	0.583	< 0.001
CMV vs. MFOV		< 0.001		0.009	0.016	< 0.001
MFOV vs. HFOV		< 0.001		0.022	0.033	< 0.001

CMV = conventional mechanical ventilation; HFOV = high-frequency oscillatory ventilation; MFOV = multi-frequency oscillatory ventilation; N_sub = number of subjects; V_rms = root-mean-square volume (mL); Wt = body weight (kg); P_aO₂ = partial pressure of oxygen in arterial blood (mmHg); P_aCO₂ = partial pressure of carbon dioxide in arterial blood (mmHg); V_C = ventilatory cost function (mL² mmHg g⁻¹).

Figure 4 shows a comparison of specific ventilation median and coefficient of dispersion across subjects during CMV, HFOV, and MFOV with a fixed isotropic image resolution of 2.4 mm. A non-parametric Friedman test reported a significant effect of ventilation modality for $s\stackrel{.}{V}$ median (p < 0.05). The $s\stackrel{.}{V}$ median during HFOV was 39% lower compared to CMV (p < 0.001) and 21% lower compared to MFOV (p < 0.05), but the $s\stackrel{.}{V}$ median was not significantly different between CMV and MFOV (p = 0.09). No statistical differences were found for the $s\stackrel{.}{V}$ cofficient of dispersion. For comparison across multiple isotropic image resolutions see Supplemental Figure 2 showing example transverse sections of specific ventilation, and Supplemental Figures 4 and 5 showing summaries of specific ventilation median and mean, respectively.

Figure 4.

Box-and-whisker plots showing the minimum, maximum, and quartiles across subjects of specific ventilation median (A) and quartile coefficient of dispersion (B) for each subject, grouped by ventilation modality: conventional mechanical ventilation (CMV), high-frequency oscillatory ventilation (HFOV), and multi-frequency oscillatory ventilation (MFOV). Higher specific ventilation implies faster turnover of alveolar gas with fresh gas; higher coefficient of dispersion implies more heterogeneity of specific ventilation throughout the lung. Voxel size was 2.4 mm isotropic. Significant differences between group medians are indicated by * for p < 0.05 and ** for p < 0.001.

Supplemental Figures 6 and 7 show comparisons of specific ventilation spatial gradients. At a fixed isotropic image resolution of 2.4 mm, a non-parametric Friedman test reported no significant effect of ventilation modality for differences in any of the three principal directions. Non-parametric signed-rank tests revealed significantly non-zero gradients in the ventral-dorsal direction for all ventilation modalities (p < 0.001). The median values across all subjects of $s\stackrel{.}{V}$ ventral-dorsal gradient (and gradient normalized by $s\stackrel{.}{V}$ median) were 0.34, 0.23, and 0.23 min⁻¹ cm⁻¹ (1.18, 1.04, 0.96 % cm⁻¹) during CMV, HFOV, and MFOV, respectively. There were significantly non-zero gradients in the rostral-caudal direction for CMV only (p < 0.05) and in the left-right direction for HFOV only (p < 0.05), however the median gradient (and normalized gradient) values in these cases were only 0.09 and 0.02 min⁻¹ cm⁻¹ (0.29 and 0.10 % cm⁻¹), respectively.

Supplemental Table 1 provides statistical comparisons at multiple isotropic image resolution levels from 0.6 to 4.8 mm. Most of the statistically significant effects reported in this study at the 2.4 mm resolution were consistent across the range of image resolutions examined, particularly $s\stackrel{.}{V}$ median, mean, and ventral-dorsal gradient. Note that all image-based ventilation measures were estimated by exponential regression of voxel values (Equation 3) after downsampling each individual volumetric image, as opposed to simply downsampling the resulting $s\stackrel{.}{V}$ itself.

Figure 5 shows a comparison of regional $s\stackrel{.}{V}$ patchiness using recursive octree or supervoxel decomposition to obtain multiple ROIs with internally consistent voxel values. Each ROI represents a contiguous region of increased or reduced $s\stackrel{.}{V}$ relative to the neighboring regions. The distribution of ROI sizes therefore provides quantification of the size scale of regional ventilation heterogeneity. Mean ROI volumes were consistently smaller using the octree technique compared to the supervoxel technique. A non-parametric Friedman test reported a significant effect of ventilation modality for mean ROI volume using either octree (p < 0.01) or supervoxel (p < 0.01) decomposition. HFOV resulted in larger mean ROI volume compared to CMV (p < 0.01) and MFOV (p < 0.001), but mean ROI volume was not significantly different between CMV and MFOV (octree: p = 0.893, supervoxel: p = 0.735).

Figure 5.

Box-and-whisker plots showing the minimum, maximum, and quartiles across subjects of specific ventilation mean cluster volume after recursive supervoxel (A) or octree (B) decomposition, grouped by ventilation modality. Voxel size was 2.4 mm isotropic. Significant differences between group medians are indicated by * for p < 0.01 and ** for p < 0.001. Two-dimensional transverse slices and three-dimensional perspective renderings of clusters are shown for a representative subject, with randomized colors.

DISCUSSION

This exploratory study of oscillatory ventilation and gas transport in porcine subjects revealed several key findings in comparisons between oscillatory modalities and conventional mechanical ventilation. First, xenon equilibration rates (assessed by $s\stackrel{.}{V}$ median or mean) were comparable between CMV and MFOV, but slower for HFOV. Thus, with considerably smaller regional volume changes, MFOV was able to mimic gas exchange rates similar to CMV and significantly faster than HFOV. The median time duration required for xenon concentration to reach 99.3% of its equilibrium value (i.e., occurring after a duration of $5\cdot s{\stackrel{.}{V}}^{-1}$) was 139 seconds during HFOV, compared to 109 seconds during MFOV or 84 seconds during CMV. Thus any sudden changes in gas composition, e.g., due to fractional inspired oxygen or bias flow, influence patient blood gas content more rapidly during MFOV and CMV compared to HFOV. Similarly to a previous study of gas exchange during MFOV in premature surfactant-deficient lambs ²³, MFOV produced a substantial reduction in ventilatory cost function compared to HFOV, indicating greater ventilatory efficiency with lower lung stretch.

Second, overall gas transport heterogeneity (assessed by $s\stackrel{.}{V}$ coefficient of dispersion) was not significantly different across ventilatory modality. By contrast, spatial gradients in the ventral-dorsal direction—aligned with the gravitational field—were significantly non-zero for all modalities. Thus the dependent regions of the lung exhibited the fastest rates of xenon equilibration regardless of modality. However, the ventral-dorsal $s\stackrel{.}{V}$ gradient magnitude tended to be lower during oscillatory modalities compared to CMV, although this difference was not statistically significant. In addition, our analysis of regional $s\stackrel{.}{V}$ patchiness demonstrated clustering of $s\stackrel{.}{V}$ with larger sizes during HFOV compared to CMV and MFOV. This large-scale spatial clustering during HFOV likely reflects lower $s\stackrel{.}{V}$ mean compared to CMV and MFOV, despite similar total $s\stackrel{.}{V}$ coefficient of variation. Smaller mean cluster volumes during CMV and MFOV implies reduced large-scale patchiness, i.e., a reduced tendency to develop large, contiguous regions of relatively increased or reduced ventilation. During CMV, the tendency for higher ventral-dorsal gradient may have also contributed to smaller cluster sizes: large spatial gradients may be a source of increased variance within each cluster, requiring further decomposition into smaller clusters to achieve internally consistent voxel values within each cluster.

The major results of this study were consistent despite repeated analyses at multiple image resolutions. Image analysis without downsampling affords enhanced spatial resolution at the expense of increased susceptibility to noise. Variability in voxel value throughout the XeCT image sequence may arise from a variety of unintended sources, including misalignment of regional structures between images, imperfect synchronization between image acquisition and ventilation, and CT imaging noise within each image. Spatial averaging of voxel values at each time point mitigates the influence of noise sources on estimation of regional time constants and $s\stackrel{.}{V}$ ³⁵. Nevertheless, group-wise differences in the primary outcomes of this study ($s\stackrel{.}{V}$ median, coefficient of dispersion, and spatial gradients) were robust to the choice of spatial resolution. Measurements of regional $s\stackrel{.}{V}$ patchiness using recursive octree and supervoxel decomposition were only performed at the 2.4 mm image resolution level due to susceptibility of these techniques to noise and regional variability.

These findings support the conclusions of previous imaging studies revealing reduced gravitational dependence of $s\stackrel{.}{V}$ during HFOV compared to CMV ^28,43, although the difference was not statistically significant in this study. Mulreany et al. suggested that the discrepancy in XeCT-derived $s\stackrel{.}{V}$ gravitational dependence between CMV and HFOV indicates a decoupling of regional ventilation and mechanics during HFOV ²⁸. By contrast, Reinhardt et al. demonstrated strong correlation between XeCT-derived measurements of $s\stackrel{.}{V}$ and regional volumetric strain obtained by respiratory-gated image registration during CMV ³⁰. However, this correlation may weaken during HFOV due to fundamental differences in determinants of flow distribution ^1,39 and mechanisms of gas transport ^17,32. Such differences may be exacerbated by heterogeneous mechanical properties throughout the lungs, depending on the oscillation frequency ^1,38. Reduced tidal volume and enhanced intrapulmonary mixing during HFOV lead to reduced correlation between regional strain and ventilation, whereas ventilation during CMV occurs predominantly by bulk advection of fresh gas into the alveolar spaces ^4,17,41. By comparison, the MFOV waveforms used in this study consisted of frequencies between 5 to 20 Hz, and therefore may rely on intrapulmonary mixing similarly to HFOV. However, MFOV was found to produce greater $s\stackrel{.}{V}$ median than HFOV, indicating advantageous gas transport achieved by the use of the additional frequency components in the ventilator waveform.

Several studies using positron emission tomography with nitrogen-13 tracer gas found enhanced ventilation in the basal regions of canine lungs during HFOV at frequencies of 3 and 6 Hz compared to either CMV or 9 Hz HFOV ^40,43. We found no evidence of rostral-caudal gradients in $s\stackrel{.}{V}$ during HFOV or MFOV. There was a significantly non-zero $s\stackrel{.}{V}$ gradient in the rostral-caudal direction observed during CMV yet with a relatively small magnitude. The lack of apical-basal gradients of $s\stackrel{.}{V}$ observed in this study may be a consequence of the limited axial field of view. We report results over only 43.2 mm of axial coverage—compared to 80 mm in Yamada et al. ⁴³—as a result of CT scanning in axial mode for high temporal resolution, and excluding 7.2 mm at the edges of the image following image registration. Slight differences in tidal volume and frequency may also contribute to variability in fresh gas ventilation of alveolar spaces, which dramatically alters the regional specific ventilation ⁴⁰. There may also be differences in ventilation distribution across different species and subject sizes: 10.3 kg pigs in this study vs. 16.2 kg dogs in Yamada et al. ⁴³. Mulreany et al. did not observe apical-basal $s\stackrel{.}{V}$ gradients in 19.2 kg dogs using XeCT over 128 mm of axial coverage ²⁸.

Limitations

An important limitation of this study is the single-frequency HFOV waveform against which MFOV was compared. Our HFOV waveform consisted of a single frequency at 5 Hz, whereas our MFOV waveform included frequencies up to 20 Hz. It is therefore possible that differences in measured outcomes during MFOV may be attributed to the use of higher frequencies above 5 Hz, the effect of combining multiple frequencies, or both factors together. Higher frequencies during HFOV are associated with reduced pressure amplitudes in the lung periphery but also increased regional heterogeneity ^8,25,44, depending on characteristics of lung mechanical impedance such as the resonant and corner frequencies ¹⁵. Thus regional flow heterogeneity (and gas exchange heterogeneity) at a specific frequency may be disadvantageous during HFOV, yet potentially advantageous during MFOV when it is combined with other complementary frequencies ¹⁸. Healthy pigs of this size exhibit typical resonant frequencies of about 6 to 7 Hz ¹³, slightly higher than the 5 Hz frequency used in our HFOV waveform. However our MFOV waveform included additional higher frequencies up to 20 Hz, which may have resulted in increased frequency-dependent flow heterogeneity. Further investigation across a wider range of HFOV and MFOV frequencies may distinguish which waveform characteristics determine the most efficacious gas exchange and lung protective characteristics.

Dual-energy CT scanning was not used in this study, but may provide enhanced signal-to-noise ratio for quantification of regional xenon concentration ⁹. With conventional single-energy CT, changes in xenon concentration are assessed by changes in Hounsfield units, which may also be affected by changes in regional aeration due to inflation, deflation, atelectasis, cardiogenic motion, etc. These extraneous signals were compensated in this study by respiratory gating and image registration, but might be further mitigated using dual-energy CT.

The size and arrangement of dead space may affect regional gas transport rates and specific ventilation in different ways depending on the ventilation modality ⁴. In this study, the dead space was minimized by placing a shortened endotracheal tube via tracheostomy. It is difficult to predict whether the relative differences in gas transport rates observed in this study would persist given standard endotracheal tube lengths and positioning. Furthermore the effects of varying dead space on gas transport rates during MFOV are yet unknown.

Another important limitation of XeCT imaging is the over three-fold increased density of 60%-40% xenon-oxygen gas mixtures compared to air or air-oxygen mixtures. Dense gas mixtures may tend to distribute preferentially towards dependent lung regions at low flow rates, following the gravitational field ⁹. Furthermore, dense gas mixtures result in reduced lung resonant frequency (i.e., the frequency maximizing the ratio of volume to pressure amplitudes) ^3,31. Since frequency-dependent flow heterogeneity increases above resonance ^8,17, the use of xenon during HFOV may result in relatively more flow heterogeneity compared to ventilation with the same frequency and dry air. Therefore regional gas transport rates during xenon wash-in may be altered during ventilation with air-oxygen mixtures. The addition of helium to the gas mixture (e.g., 40%-40%-20% helium-xenon-oxygen) may partially compensate for the high-density xenon gas. However, such mixtures may still be two-fold more dense than dry air ⁹. Although these limitations warrant caution when extrapolating these results to ventilation using the same settings with dry air, the relative differences between each modality (i.e., CMV, HFOV, and MFOV) may still be preserved.

CONCLUSION

Xenon wash-in equilibration rates were comparable between conventional mechanical ventilation and multi-frequency oscillatory ventilation, but 21% to 39% slower for high-frequency oscillatory ventilation. By contrast, the root-mean-square delivered volume was lowest for MFOV, increased by 70% during HFOV and 365% during CMV. Overall gas transport heterogeneity was similar across all modalities, but gravitational gradients and regional patchiness of specific ventilation may contribute to regional ventilation heterogeneity depending on ventilator modality. Thus MFOV combines key benefits of low lung stretch, similar to high-frequency oscillatory ventilation, with fast rates of gas transport, similar to conventional mechanical ventilation. Such features may be highly desirable across many etiologies from acute respiratory failure presenting with heterogeneous changes in lung mechanics.

ABBREVIATIONS

CMV

Conventional mechanical ventilation

CO₂

Carbon dioxide

CT

Computed tomography

HFOV

High-frequency oscillatory ventilation

HU

Hounsfield units

MFOV

Multi-frequency oscillatory ventilation

ROI

Region of interest

XeCT

Xenon contrast-enhanced computed tomography

[Xe]

Xenon concentration

GLOSSARY OF TERMS

D ₀

Model-predicted CT density at scan sequence initiation (HU)

D _∞

Model-predicted CT density at final equilibrium state (HU)

F_iO₂

Fraction of oxygen in inspired gas (%)

g _RC

Spatial gradient of specific ventilation, rostral-caudal direction (min⁻¹ cm⁻¹)

g _RL

Spatial gradient of specific ventilation, right-left direction (min⁻¹ cm⁻¹)

g _VD

Spatial gradient of specific ventilation, ventral-dorsal direction (min⁻¹ cm⁻¹)

I

Volumetric CT density image (HU)

I _n→0

Result of deforming the n^th image to align structures with the initial image (HU)

ΔI

Difference in CT density relative to initial time point (HU)

$\widehat{I}$

Model-predicted CT density image (HU)

M

Lung segmentation mask

n

Image index in xenon wash-in sequence

N

Number of images in xenon wash-in sequence

${\bar{P}}_{\text{aw}}$

Mean airway pressure (cmH₂O)

P_aCO₂

Partial pressure of carbon dioxide in arterial blood (mmHg)

P _a O ₂

Partial pressure of oxygen in arterial blood (mmHg)

$s\stackrel{.}{V}$

Specific ventilation (min⁻¹)

t

Time (s)

T

Time duration of the ventilatory cycle (s)

V

Volume (mL)

$\overline{V}$

Time-averaged volume over the ventilatory cycle (mL)

V _rms

Root-mean-square volume (mL)

${\bar{V}}_{\text{ROI}}$

Mean cluster size after recursive octree or supervoxel decomposition (mL)

V _C

Ventilatory cost function (mL² mmHg g⁻¹)

Wt

Body weight (g)

x

Vector of 3-dimensional spatial coordinates (cm)

${\stackrel{\rightharpoonup }{x}}_{\text{RC}}$

Spatial axis corresponding to the rostral-caudal direction

${\stackrel{\rightharpoonup }{x}}_{\text{RL}}$

Spatial axis corresponding to the right-left direction

${\stackrel{\rightharpoonup }{x}}_{\text{VD}}$

Spatial axis corresponding to the ventral-dorsal direction

τ

Model-predicted time constant of regional xenon equilibration (min)