Stomatal closure during water deficit is controlled by below-ground hydraulics

Abstract

Background and Aims

Stomatal closure allows plants to promptly respond to water shortage. Although the coordination between stomatal regulation, leaf and xylem hydraulics has been extensively investigated, the impact of below-ground hydraulics on stomatal regulation remains unknown.

Methods

We used a novel root pressure chamber to measure, during soil drying, the relation between transpiration rate (E) and leaf xylem water pressure (ψ_leaf-x) in tomato shoots grafted onto two contrasting rootstocks, a long and a short one. In parallel, we also measured the E(ψ_leaf-x) relation without pressurization. A soil–plant hydraulic model was used to reproduce the measurements. We hypothesize that (1) stomata close when the E(ψ_leaf-x) relation becomes non-linear and (2) non-linearity occurs at higher soil water contents and lower transpiration rates in short-rooted plants.

Key Results

The E(ψ_leaf-x) relation was linear in wet conditions and became non-linear as the soil dried. Changing below-ground traits (i.e. root system) significantly affected the E(ψ_leaf-x) relation during soil drying. Plants with shorter root systems required larger gradients in soil water pressure to sustain the same transpiration rate and exhibited an earlier non-linearity and stomatal closure.

Conclusions

We conclude that, during soil drying, stomatal regulation is controlled by below-ground hydraulics in a predictable way. The model suggests that the loss of hydraulic conductivity occurred in soil. These results prove that stomatal regulation is intimately tied to root and soil hydraulic conductances.

INTRODUCTION

Stomata regulate the exchange of carbon and water between the atmosphere and vegetation (Hetherington and Woodward 2003; Wolz et al., 2017; Buckley, 2019; Deans et al., 2020). Stomatal regulation provides a key survival feature to terrestrial vegetation under unfavourable conditions, preventing an excessive drop in water pressure and minimizing the risk of xylem cavitation upon drought (Martin-StPaul et al., 2017; Choat et al., 2018; Grossiord et al., 2020). Despite the importance of this regulation, the mechanisms by which edaphic stress impacts transpiration and stomatal regulation remain elusive.

Stomatal regulation has been extensively studied in relation to xylem vulnerability (Scoffoni et al., 2014; Sperry and Love, 2015; Bartlett et al., 2016; Wolf et al., 2016; Anderegg et al., 2017; Henry et al., 2019; Eller et al., 2020). However, other hydraulic limitations occur along the soil–plant continuum before xylem cavitation (Scoffoni et al., 2017; Huber et al., 2019; Corso et al., 2020; Albuquerque et al., 2020), especially below ground (Rodriguez‐Dominguez and Brodribb, 2020; Carminati and Javaux, 2020; Abdalla et al., 2021). For instance, Rodriguez-Dominguez and Brodribb (2020) have recently shown that, in olive trees, the root–soil interface represented the largest hydraulic resistance to water flow. In a follow-up study, Bourbia et al. (2021) showed that stomata close concomitantly with the decline in root hydraulic conductivity in both herbaceous and woody species. Abdalla et al. (2021) demonstrated that an increase in soil–root hydraulic resistance was the main driver of stomatal closure in tomato. Carminati and Javaux (2020), by means of a soil–plant hydraulic model and a meta-analysis, showed that the loss of soil conductivity, rather than xylem, constrains transpiration. They proposed that stomata close at the onset of hydraulic limitation, i.e. when the relation between transpiration and leaf water potential becomes non-linear (Sperry and Love, 2015; Carminati and Javaux, 2020; see Fig. 1 for details of the main hypothesis). In other words, the loss in soil hydraulic conductance entails severe gradients in soil matric potential around roots, which cause an excessive drop in leaf water pressure to sustain a tiny increment in transpiration. Hence, the relation between stomatal conductance and leaf water potential should be soil- and root-specific (Carminati and Javaux, 2020).

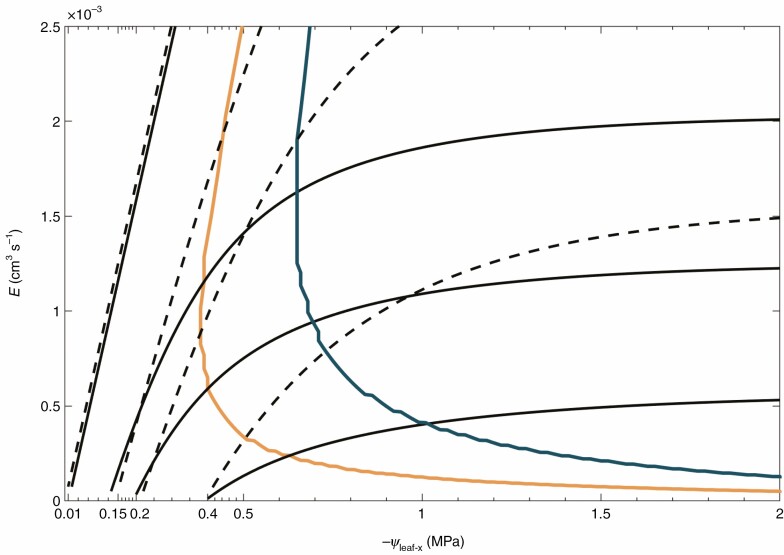
Fig. 1.

Hypothesis: reduction in root length causes an earlier drop in soil hydraulic conductance and an earlier stomatal closure. Relation between transpiration (E) and leaf xylem pressure (ψ_leaf-x) as simulated by a model of water flow across the soil, the root system and along the xylem, including the non-linearity of their hydraulic conductances (Carminati and Javaux, 2020). The model hypothesizes that stomata close at the onset of hydraulic limitation (stress onset line, SOL), which is defined as the point at which the slope of $E({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}})$ reaches 50 % of its maximum (see Materials and methods and Supplementary Data Table S2). $E({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}})$ relations were simulated at soil matric potentials of −0.01, −0.15 −0.2 and −0.4 MPa. Plants with a short root system (solid black lines and orange SOL) require larger gradients in soil matric potential around their roots, which results in a marked non-linearity in $E({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}})$ compared with plants with a long root system (dashed lines and blue SOL). Consequently, stomatal closure occurs at less negative ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$ for plants with short root systems (orange line for the short and blue line for the long root system).

Despite the advances in conceptual and modelling work linking stomatal regulation to soil–plant hydraulics (Sperry and Love, 2015; Wang et al., 2020), there is no conclusive experimental proof that stomatal closure is driven by the loss in below-ground hydraulic conductances (i.e. contrasting root system or soil textures). Previous modelling studies explained midday stomatal closure by the reduction in below-ground hydraulic conductance (Williams et al., 2001; Fisher et al., 2006; Lier et al., 2013). However, these modelling exercises still require experimental validations. Gollan et al. (1985, 1986) compared stomatal behaviour of pressurized and unpressurized plants, and showed that stomata close in dry soil conditions even though the shoots were kept turgid. However, Gollan and co-authors did not attempt to link stomatal closure to the onset of the hydraulic non-linearity. We have recently provided the first systematic experimentation to test stomatal sensitivity to the hydraulic non-linearity (Abdalla et al., 2021). We showed that stomatal closure was concomitant with the onset of the non-linearity in E(ψ_leaf-x)-relation (Abdalla et al., 2021). In this study, we ask the following question: do changes in below-ground traits (i.e. contrasting root system) impact the E(ψ_leaf-x) relation during soil drying?

We experimentally tested the hypothesis that below-ground hydraulics, i.e. soil, root and/or their interface, determine the relation between stomatal conductance and leaf water potential. We measured leaf xylem water pressure (ψ_leaf-x) and transpiration rate (E) in tomato shoots grafted onto two contrasting rootstocks, a short and a long one. To sustain the same transpiration rate, the short root system would require a larger water flow per root surface, and thus larger gradients in soil matric potential (Fig. 1). Therefore, plants with a shorter root system should exhibit a more marked non-linearity in the E(ψ_leaf-x) relation and should close stomata at less negative leaf water pressures (Fig. 1). Alternatively, the larger root system might attenuate the drop in leaf water pressure because of its larger hydraulic capacitance; i.e. not only the ability to conduct water but also the capacity to store water might affect stomatal regulation.

We employed a root pressure chamber designed by Passioura (1980) and implemented by Gollan et al. (1986) and recently by Cai et al. (2020a) to measure the soil–plant hydraulic conductance during soil drying. This method makes it possible to explore the non-linear part of the E(ψ_leaf-x) relation. Additionally, we measured transpiration, leaf water pressure (refers to the hydrostatic component of leaf water potential) and root water content during soil drying. The soil–plant hydraulic model of Carminati and Javaux (2020) was used to reproduce and interpret the data.

MATERIALS AND METHODS

Plant preparation

Two tomato varieties with contrasting root lengths were used as rootstocks; Lycopersicon hirsutum and a hybrid of L. hirsutum and the wild tomato L. pimpinellifolium were used as long- and short-rooted plants, respectively. Scions from Solanum lycopersicum L. (M82 variety) were grafted onto these two rootstocks. Seeds were provided by Rootility (Israel). Seeds were sown in polyvinyl chloride (PVC) columns 30 cm in height and 10 cm in diameter. The columns had five holes with a diameter of 5 mm on the side to facilitate soil moisture content measurements. The PVC columns were topped (using a silicon rubber glue; Teroson, Henkeln, Germany) with a 0.8-cm-thick aluminium plate that had a centred hole 1.4 cm in diameter.

Plants were grafted ~1 week after germination when their stem diameters were matching (Notaguchi et al., 2020). Immediately after grafting, plants were placed inside a chamber at ~95 % relative humidity and 200 µmol m⁻² s⁻¹ photosynthetic photon flux density (PPFD) for 4 d to avoid scion desiccation (Rosskopf et al., 2018). Thereafter, plants were placed in a climate-controlled room with a day/night temperature of 28/18 °C, a day/night relative humidity of 57/65 %, 14-h photoperiod and PPFD of 600 µmol m⁻² s⁻¹ during the daytime (Luxmeter PCE-174, Meschede, Germany).

After 12 d, plants were moved to the laboratory and sealed at the collar using glue (Uhu Plus Endfest 300, Bühl, Germany). During the experiments, leaves were imaged to determine leaf area (LA; cm²) using ImageJ 1.50e (http://imagej.nih.gov/ij). After the experiments, roots were washed and root length was measured using WinRihzo (Regent Instruments, Canada). Supplementary Data Fig. S1 shows root length and leaf area.

Soil preparation

A sandy loam soil was used in the experiments. Quartz sand and loamy soil were sieved through a 1-mm sieve. The sieved substrates were mixed in the ratio of 62.5 % loamy soil and 37.5 % quartz sand. The soil water content (θ [cm³ cm⁻³]) was measured using a time-domain refractometer (TDR) (E-Test, Lublin, Poland). The hydraulic properties of the soil mixture were determined via a Hyprop system (UMS, Munich, Germany), which implemented the evaporation method. The water retention curve and the unsaturated hydraulic conductivity were fitted using the Peters–Durner–Iden (PDI) model (Peters et al., 2015). The corresponding parameters were estimated by fitting the measured soil matric potential and solving the Richards equation.

Transpiration and leaf xylem water pressure measurements

We used a novel root pressure chamber system (RPCS) to simultaneously measure transpiration (E) and leaf xylem water pressure (ψ_leaf-x) within an intact plant (Cai et al., 2020a). The construction and calibration of the RPCS were recently described in Cai et al. (2020b). Briefly, RPCS is composed of a pressure chamber topped with a cuvette and a control unit. Four groups of light-emitting diode (LED) lamps were vertically attached to the cuvette. The lamps provided PPFD that ranged adjustably from 0 to 1000 µmol m⁻² s⁻¹. We altered E by changing PPFD, and the latter was measured via a fixed radiometric sensor (Gamma Scientific, San Diego, USA). A constant airflow passed through the cuvette (8.25 L min⁻¹) and a fan was used to stir the air inside. Combined temperature–humidity sensors (Galltec-Mela, Bondorf, Germany) continuously measured the temperature and the relative humidity of the inward and the outward air. We determined E by multiplying the airflow by the difference between the outward and the inward humidity. Canopy conductance was calculated as g_c = (E/LA)/(VPD/P_atm) according to Jarvis and McNaughton (1986), where VPD is vapour pressure deficit and P_atm is atmospheric pressure.

The basic principle of the method was to balance the negative water pressure inside the plant by applying a pneumatic pressure to the soil and root system, thereby bringing water inside the leaf xylem to atmospheric pressure (Passioura, 1980; Carminati et al., 2017; Cai et al., 2020a) (Supplementary Data Fig. S2). The applied pressure (balancing pressure; P) is numerically equal to leaf xylem tension before pressurization (Passioura, 1980). A meniscus system was connected to a leaf cut to evaluate the stability of the droplet. We determined ψ_leaf-x when the meniscus was stable for ~10 min (Cai et al., 2020a).

To measure E(ψ_leaf-x) relation, plants were positioned inside the RPCS, with the column inside the pressure chamber and the shoot inside the cuvette. We modified E by gradually increasing PPFD from 0 to 200, 400, 600, 800 and 1000 µmol m⁻² s⁻¹. Simultaneously, the corresponding ψ_leaf-x was determined at each PPFD. Additionally, E was also measured without pressurization at 1000 µmol m⁻² s⁻¹. Canopy conductance (g_c [mol m² s⁻¹]) was calculated from E without pressurization. Each plant was measured for several days during soil drying (Supplementary Data Fig. S3 and Table S1).

In parallel, we measured ψ_leaf-x at the highest E for unpressurized plants using a leaf pressure chamber (Soil Moisture Equipment Corp., Santa Barbara, CA, USA) as described in Scholander et al. (1965). These measurements were utilized to assess ψ_leaf-x values obtained from pressurized plants at the same values of E and θ (Abdalla et al., 2021).

Osmotic potential

Leaf osmotic potential was measured using a vapour pressure osmometer (VAPRO, Wescore). Xylem sap was collected from a leaf cut using a 10-μL pipette after applying 0.1 MPa more than the balancing pressure. Leaf osmotic potential was measured at different soil matric potentials during soil drying. Soil osmotic potential was measured when the soil was saturated.

Root hydraulic capacitance

Root hydraulic capacitance was obtained by measuring the root water content at decreasing soil matric potentials. Plants from both rootstock genotypes were grown in the sandy loam. When individuals reached targeted soil matric potential, plants were left overnight inside a humid chamber (relative humidity ≈100 %) to allow soil and roots to equilibrate to the same water pressure. Roots were carefully removed from the soil and were gently shaken to remove any attached soil, and initial fresh weight was measured. Root dry weight was obtained after drying the roots for 24 h at 105 °C. The difference between fresh and dry weights of the roots was divided by their dry weight at different soil matric potentials to calculate root hydraulic capacitance (see eqn 15).

Soil–plant hydraulic model

We used a soil–plant hydraulic model to simulate the water flow in the soil–plant continuum and fit the measured E(ψ_leaf-x) relation. Water flow was modelled through a series of resistances across the soil, across the soil–root interface, across the root to the root xylem, and along the xylem. We briefly describe the model here.

The Buckingham–Darcy law, ignoring gravity, was used to describe the radial water flow in soil towards the root surface:

$${\displaystyle \begin{array}{l}{\displaystyle q=-K_{\mathrm{s}}\left({\psi }_{\mathrm{m}}\right)\frac{\mathrm{\partial }{\psi }_{\mathrm{m}}}{\mathrm{\partial }r}}\end{array}}$$ (1)

where q is the water flux (cm s⁻¹), K_s is the soil hydraulic conductivity, which is a function of the soil matric potential ${\psi }_{\mathrm{m}}$ (hPa), r is the radial distance (cm) and $\mathrm{\partial }{\psi }_{\mathrm{m}}/\mathrm{\partial }r$is the gradient in matric potential. Note that when the soil matric potential is expressed in unit heads (cm, 1 hPa ≈ 1 cm), K_s has units of cm s⁻¹. We use this unit throughout the text when describing soil water flow.

The boundary conditions were expressed as follows:

$${\displaystyle \begin{array}{l}{\displaystyle q(r_0)=\frac{E}{2\pi r_{0}L}}\end{array}}$$ (2)

$${\displaystyle \begin{array}{l}{\displaystyle q(r_{\mathrm{b}})=0}\end{array}}$$ (3)

where r₀ and r_b are the root radius and the exterior radius of soil around the root (cm), E is the transpiration rate (cm³ s⁻¹) and L is the root length active in water uptake (cm); r_b is determined by L and the volume of the column V (cm³), according to:

$${\displaystyle \begin{array}{l}{\displaystyle r_{\mathrm{b}}=\sqrt{\frac{V}{\pi L}}}\end{array}}$$ (4)

We parameterized K_s according to the Brooks and Corey model:

$${\displaystyle \begin{array}{l}{\displaystyle K_{\mathrm{s}}({\psi }_{\mathrm{m}})=K_{\mathrm{s}\mathrm{a}\mathrm{t}}{\left(\frac{{\psi }_{\mathrm{m}}}{{\psi }_0}\right)}^{\tau }}\end{array}}$$ (5)

where K_sat is the saturated hydraulic conductivity of the soil (cm s⁻¹), ${\psi }_0$ is the soil air entry value (cm) and $\tau$ is a fitting parameter (−). We obtained the parameters for eqn (5) by matching the PDI and Brooks and Corey models (Abdalla et al., 2021). According to de Jong van Lier et al. (2008), and assuming a steady-rate behaviour for the water flow in the soil, the radial geometry of water flow could be reformulated using the matric flux potential (Ф, cm² s⁻¹):

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{\Phi }(\psi )={\displaystyle \underset{-\mathrm{\infty }}{{\displaystyle \stackrel{{\psi }_{\mathrm{m}}}{\int }}}}K(x)\mathrm{d}x}\end{array}}$$ (6)

The solution of eqn (6) describes the matric flux potential at the outer boundary r = r_b:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{\Phi }}_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}=\frac{k_{\mathrm{s}\mathrm{a}\mathrm{t}}.{{\psi }_{\mathrm{m}}}^{1-\tau }.{{\psi }_0}^{-\tau }}{1-\tau }}\end{array}}$$ (7)

where ${\mathrm{\Phi }}_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$ is the matric flux potential in the bulk soil (cm² s⁻¹) corresponding to the measured bulk soil matric potential $({\psi }_{\mathrm{m}})$. Meanwhile, the radial flow could be described by combing eqns (1, 5 and 6) as:

$${\displaystyle \begin{array}{l}{\displaystyle q=-\frac{\mathrm{\partial }\varnothing ({\psi }_{\mathrm{m}})}{\mathrm{\partial }r}}\end{array}}$$ (8)

We obtain the flux boundary condition at the soil–root interface, ${\mathrm{\Phi }}_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$ (cm² s⁻¹), by combining eqns (5 and 6) and the radial Richards equation (Schröder et al., 2009):

$${\displaystyle \begin{array}{ll}{\displaystyle {\mathrm{\Phi }}_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}=}& -\frac{E}{2\pi L}(\frac{1}{2}-r_{\mathrm{b}}^2\frac{\ln \left(r_{\mathrm{b}}/r_0\right)}{r_{\mathrm{b}}^2-r_0^2})\\ & +\frac{k_{\mathrm{s}\mathrm{a}\mathrm{t}}\cdot {{\psi }_{\mathrm{m}}}^{1-\tau }\cdot {{\psi }_0}^{-\tau }}{1-\tau }\end{array}}$$ (9)

The water flow in the root is given by

$${\displaystyle \begin{array}{l}{\displaystyle E=-K_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}({\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{x}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{m}}-{\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}})}\end{array}}$$ (10)

where E is the water flow in the root equal to the transpiration rate (cm³ s⁻¹), ${\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$ is the water potential at the root–soil interface (here converted to MPa, 1 MPa ≈ 10⁴ cm), ${\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{x}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{m}}$ is the water potential at the xylem collar (MPa) and $K_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}$ (cm³ s⁻¹ MPa⁻¹) is the root hydraulic conductance. Note that differences in osmotic potential between soil and root xylem can occur and affect the driving force of water flow across the root–soil interface. Therefore, ${\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$ and ${\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{x}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{m}}$ are the sum of their respective matric/hydrostatic potentials and osmotic potentials. Doing so, we assume that the reflection coefficient of the root is 1. The difference between leaf and soil osmotic potential is equal to the measured difference between soil matric potential and leaf xylem pressure when water flow is negligible (Cai et al., 2020a).

We assume no further change in osmotic potential along the xylem. The xylem conductance, K_x (cm³ s⁻¹ MPa⁻¹), which includes the effect of cavitation, is given by:

$${\displaystyle \begin{array}{l}{\displaystyle K_{\mathrm{x}}=K_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}{\left(\frac{{\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}}{{\psi }_{0\mathrm{x}}}\right)}^{-{\tau }_{\mathrm{x}}}}\end{array}}$$ (11)

where ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{~}\text{-}\mathrm{x}}$ is the leaf xylem pressure (MPa), ${\psi }_{0\mathrm{x}}$ is the xylem pressure (MPa) at which K_x drops and ${\tau }_{\mathrm{x}}$ is a fitting parameter (−) that determines the rate of this drop.

The plant conductance, K_plant (cm³ s⁻¹ MPa⁻¹), is given by the harmonic mean of K_root and K_x:

$${\displaystyle \begin{array}{l}{\displaystyle \frac{1}{K_{\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{n}\mathrm{t}}}=\frac{1}{K_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}}+\frac{1}{K_{\mathrm{x}}}}\end{array}}$$ (12)

The leaf matric flux potential is calculated as:

$${\displaystyle \begin{array}{l}{\displaystyle {\mathrm{\Phi }}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}=-E+{\mathrm{\Phi }}_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{x}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{m}}}\end{array}}$$ (13)

Leaf xylem pressure ${{\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}}}_{\text{~}\text{-}x}$ is calculated by inserting K_x into eqn (6) and combining eqns (11 and 13):

$${\displaystyle \begin{array}{l}{\displaystyle {\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\mathrm{\_}\mathrm{x}}={({\psi }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}\mathrm{\_}\mathrm{x}\mathrm{y}\mathrm{l}\mathrm{e}\mathrm{m}}^{1-{\tau }_{\mathrm{x}}}-\frac{E({\tau }_{\mathrm{x}}-1)}{{\psi }_{0\mathrm{x}}^{{\tau }_x}{K}_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}})}^{\frac{1}{1-{\tau }_{\mathrm{x}}}}}\end{array}}$$ (14)

Note that the unit of the matric flux potentials in eqn (13) differs from those of eqn (9) because soil and xylem hydraulic conductivities have different units.

Data were firstly fitted for each day of measurements (i.e. at each measured soil water content) individually to estimate K_root, L and the offset between soil matric potential and leaf xylem pressure. Inverse simulations revealed that L increased as soil dries (reported and discussed later). Therefore, we conducted direct simulations for each group of plants allowing the parameter L to vary during soil drying. We obtained K_root from individual simulations by fitting the linear part of the E(ψ_leaf-x) relation, which was constant during soil drying (Abdalla et al., 2021).

The onset of hydraulic limitation is defined as the point at which the slope of E(ψ_leaf-x) reaches 50 % of its maximum (the soil matric potential being kept constant: soil isolines) (Carminati and Javaux, 2020). Note that the 50 % is rather arbitrary and indeed a value between 40 and 60 % would give the same shape of the stress onset line (SOL). The maximum slope of E(ψ_leaf-x) at any given soil matric potential is at null transpiration; i.e. the slope of E(ψ_leaf-x) decreases with increasing E (Carminati and Javaux, 2020).

The model was used (1) to predict the onset of hydraulic limitation and compare it with measurements of transpiration reduction, and (2) to test whether the decline of E(ψ_leaf-x) is explained by the loss of soil hydraulic conductivity for the two root systems.

Soil–plant hydraulic model including root capacitance

The model above assumed that all water transpired was taken up from the soil (no changes in root water content) and that the change in soil water content during one measurement cycle was negligible. The calculated E(ψ_leaf-x) lines were referred to as soil isolines. The consequence of these assumptions was tested by including measurements of root capacitance and soil drying in the model. We examined to what extent root capacitance attenuates the decline in soil and leaf water potential during one measurement cycle consisting of increasing transpiration rates over a period of ~6 h. The rationale is that root capacitance diminishes the water uptake from the soil. This leads to more water remaining in the soil and a less negative leaf water potential to sustain transpiration.

Root capacitance and soil drying were modelled during one exemplary measurement cycle. The relation between root water content and water potential was obtained by fitting the measured gravimetric root water content θ_g, defined as weight of water in the root divided by root dry weight. The volumetric root water content θ_root was calculated based on densities of water and roots ${\rho }_{{\mathrm{H}}_2{\mathrm{O}}_{}}$ and ${\rho }_{\mathrm{w}\mathrm{e}\mathrm{t}}$:

$${\displaystyle \begin{array}{l}{\displaystyle {\theta }_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}={\theta }_{\mathrm{g}}\ast \frac{{\rho }_{\mathrm{w}\mathrm{e}\mathrm{t}}}{{\rho }_{{\mathrm{H}}_2\mathrm{O}}}}\end{array}}$$ (15)

where ^ρ_wet is the dry root weight divided by the volume of the wet root. The water flow resulting from root shrinkage is the time derivative of the root water volume. This flow was subtracted from the transpiration rate to obtain the root water uptake. To do so, soil matric potential and root water content were estimated for each time step. We simulated two scenarios: (1) soil drying but no root capacitance; and (2) soil drying and root capacitance. The two scenarios were compared with two isolines calculated using the steady-state soil–plant hydraulic model described in the paragraph above (no root capacitance and no changes in soil water content). We calculated one isoline corresponding to the soil matric potential at the beginning of the measurement cycle (fitted to the first two points) and one soil isoline corresponding to the soil matric potential at the end of the measurement cycle (fitted with the last measurement).

Statistical analysis

We used a mixed model to analyse the influence of root system, soil water content, PPFD and their interactions on E using analysis of variance. Replicates were taken as random factors and the remaining parameters were taken as fixed factors. Furthermore, we tested the values of stomatal closure in E(ψ_leaf-x) of the two rootstocks using analysis of covariance. MATLAB 2019a (9.6.0., Mathworks^®) was used to perform the statistical analysis.

RESULTS AND DISCUSSION

Tomato plants were grafted on two contrasting root systems to evaluate the impact of root length on soil–plant hydraulic conductance and stomatal regulation during soil drying. The length of the two root systems differed by a factor of 3 (P < 0.05), whereas root diameter and leaf area were similar (P > 0.05; Supplementary Data Fig. S1).

The relationship between transpiration rates (E) and leaf xylem water pressure (ψ_leaf-x) varied between the two root systems (Fig. 2). E(ψ_leaf-x) was linear in wet soils (θ ≥ 0.15), with the slope being equal to the plant hydraulic conductance. The relation became non-linear as the soil dried (Fig. 2). The long root system sustained higher E during soil drying, while a more marked non-linearity in E(ψ_leaf-x) appeared in the short root system at relatively high ψ_leaf-x and soil water content (θ). Longer roots ensured the linearity of E(ψ_leaf-x) for a broader range of E and θ.

Fig. 2.

Measured relation between transpiration (E) and leaf xylem pressure (${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$) in tomato plants grafted onto (A) a short root system and (B) a long root system during soil drying (θ: soil water content [cm³ cm⁻³], N = 6).

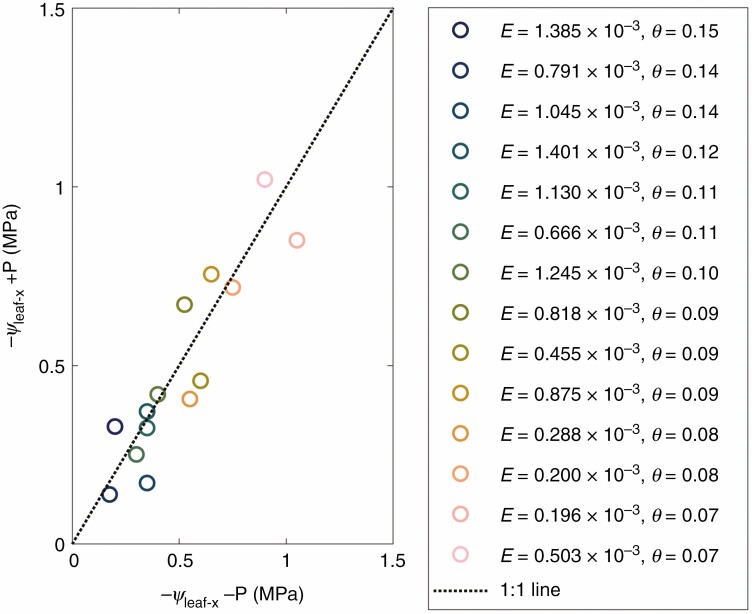
The ψ_leaf-x of pressurized and unpressurized plants, for the same values of E and θ, matched well (Fig. 3, r² = 0.81). This result demonstrates that the total hydraulic conductances of pressurized and unpressurized plants were similar, which is consistent with Abdalla et al. (2021). Note that pressurization maintained the water pressure in the xylem equal to the atmospheric pressure and hence cavitation did not occur during the measurements. Additionally, pressurized plants had a turgid shoot, whose conductivity is likely to have remained constant during the measurements. The latter is in line with the finding of Skelton et al. (2017), who showed a decline in leaf hydraulic conductance when leaf water potential dropped beyond −1.28 MPa in tomato. Further, we used roots of L. hirsutum and its hybrid with the wild tomato L. pimpinellifolium, which might potentially have more resistant xylem. Therefore, the non-linearity of E(ψ_leaf-x) must have been caused by a decline in the below-ground hydraulic conductivity, either in the soil, in the root system or at their interface.

Fig. 3.

Leaf xylem pressure $({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}})$ in pressurized (+P) and unpressurized (−P) tomato plants at the same soil water content (θ [cm³ cm⁻³]) and transpiration rate (E [cm³ s⁻¹]). The ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$ of pressurized plants was measured by the RPCS, while ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$ of unpressurized plants was measured with a Scholander leaf pressure chamber (N = 6). The ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$ of pressurized and unpressurized plants, for the same values of E and θ, matched well (r² = 0.81).

The E(ψ_leaf-x) and E(ψ_soil) relations were well reproduced by the soil–plant hydraulic model of Carminati and Javaux (2020) (black lines in Fig. 4A–D). The model calculates the water potential gradients across the soil–plant continuum based on the measured transpiration rates, soil water content and soil hydraulic properties (see the Materials and methods section and Supplementary Data Table S2 for details of the model description and parameters). The fitting parameters were the root length active in root water uptake L, which was allowed to vary with soil drying, root conductance K_root, and xylem water pressure at which xylem conductivity drops. The latter was set to −1.5 MPa, which is the most negative value measured in the experiments, and thus does not affect the simulations. This choice was based on the observation that pressurized and non-pressurized plants had the same hydraulic conductance, which means that cavitation did not affect the plant hydraulic conductance. The model reproduced well the experimental observation that a more marked non-linearity in the E(ψ_leaf-x) relation occurred in the short root system (Fig. 4E).

Fig. 4.

Relation between transpiration rate (E) and leaf xylem pressure $({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}})$ (A, C) as well as predawn leaf xylem pressure $({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}\text{-}\mathrm{P}\mathrm{D}})$ as proxy of soil matric potential $({\psi }_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}})$ (B, D), for the short (A, B) and long (C, D) root systems. The measurements (open symbols) were well reproduced by the model (black lines) at different soil water contents (different colours). The relation shifted from linear to non-linear during soil drying. The red line marks the onset of non-linearity (SOL). The red squares in (A–D) are the measured transpiration rates during soil drying in unpressurized plants (short root system, r² = 0.74, 0.72; long root system, r² = 0.82, 0.78 from leaf and soil views, respectively). (E) Onset of hydraulic limitation (SOL) for long-rooted (blue line) and short-rooted plants (orange line) match well the reduction in transpiration (blue and orange open symbols, respectively). The reduction in transpiration of long- and short-rooted plants was significantly different (P < 0.001; Supplementary Data Fig. S4), with the shorter root system reducing transpiration at less negative ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$. (F) Canopy conductance (g_c) as a function of ${\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{-}\mathrm{x}}$ for the short-rooted (orange open symbols) and long-rooted plants (blue open symbols). The slope and the intercept of the linear fit were used for the analysis of covariance, which showed a significant difference in stomatal closure between the two root systems (P < 0.01).

The measurements of soil and leaf xylem osmotic potential are consistent with the offset between soil matric potential and predawn leaf xylem pressure. Soil osmotic potential was around −0.02 MPa at soil saturation. This supports the interpretation that the offset was caused by the difference in osmotic potentials. No visible differences were observed between the osmotic potentials of the two root systems, possibly also due to the variability in the measurements (Fig. 5A).

Fig. 5.

(A) Model predictions of the leaf xylem osmotic potential matched the direct measurements of leaf osmotic potential in both root systems (as indicated in the key) during soil drying. (B) Active root length (L) as a function of soil matric potential $({\psi }_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}})$ for short-rooted and long-rooted plants (as indicated in the key). Longer-rooted plants had more active roots, especially in the dry range of ${\psi }_{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$. (C) The difference between root fresh and dry weight was divided by dry weight to obtain root shrinkage. Root water content decreased exponentially as soil matric potential declined.

The simulations predict the active root length L as a function of the ψ_soil (Fig. 5B). The simulated active root length L was greater in the plants with the long root system. The explanation is that a longer root length requires a lower flow rate of water at the root–soil interface and smaller gradients in soil matric potential to sustain the same transpiration rate. The simulations support the hypothesis that the non-linearity in the E(ψ_leaf-x) relation is mainly caused by soil hydraulics. Interestingly, active root length increased as the soil dried, which might be a mechanism to compensate limited fluxes per root segment. The increase in L during soil drying was also observed in maize (Cai et al., 2021) and might reflect root hydraulic adjustment to soil drying. However, L has to be interpreted with caution; L is a fitting parameter and might reflect oversimplification of the plant–soil hydraulic model, such as the representation of the root system with a single root and the assumption that the rhizosphere has the same hydraulic conductivity as the bulk soil.

An alternative explanation of the better ability of the long root system to sustain transpiration during soil drying could be the effect of root capacitance. We investigated the effect of root capacitance by including in the simulations the measured decrease in root water content at decreasing soil matric potential (Fig. 5C). The simulated trajectories of plants with and without root capacitance (green and pink) were very close, indicating that root capacitance had a minor contribution to E(ψ_leaf-x) (Fig. 6). By contrast, the decrease in soil water content during a measurement cycle had significant effects. To understand the effect of decreasing soil water content during a measurement cycle, we plotted the soil isolines at the initial and final stages (orange and blue) of the measurement cycle using the steady-state model. The two isolines perfectly envelop the measurements using a root length of 4000 cm, which is 2.5 times longer than the value estimated using a single line to simulate all points of the measurement cycle (L = 1496 cm). The difference in L shows the problems in using the isolines to fit the data and interpret L as the active root length. The isoline would predict a shorter root length than the actual value, and this mismatch is caused by neglecting the decrease in soil water content. In contrast, the potential role of root capacitance in buffering the decline of soil and leaf water potentials was negligible. However, the choice against specific model simplifications (root shrinkage, rapid soil drying) must match with the research questions addressed. For example, to predict the onset of non-linearity, the classical model approach with soil isolines (solid black line in Fig. 6) is acceptable. However, to reproduce the leaf water potential measurements and properly estimate the active root length, simulations should include the role of soil drying. In summary, the model simulations reinforce the explanation that the drop in soil conductivity is the main cause of non-linearity in the soil–plant system.

Fig. 6.

Relation between transpiration rate (E) and leaf xylem pressure $({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{~}\text{-}\mathrm{x}})$ for one exemplary measurement cycle (θ = 0.1045). Different model simulations were compared regarding their explanatory values. The measurements were well captured by a single soil isoline fitted to all data points (as indicated in the key) using the steady-state soil–plant hydraulic model. To understand the effect of decreasing soil water content during the measurement cycle, we plotted the soil isolines at the initial (θ_i = 0.1045) and final (θ_j = 0.0874) soil water content of the measurement cycle using the steady-state model but with different fitting parameters (L and $K_{\mathrm{r}\mathrm{o}\mathrm{o}\mathrm{t}}$) compared with the single soil isoline. The simulated trajectories with and without root capacitance were very close, indicating that root capacitance had a minor contribution to the $E({\psi }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{f}\text{~}\text{-}\mathrm{x}})$ relation. Both trajectories reproduced the measurements very well.

The onset of hydraulic non-linearity (SOL) was defined as the point when the slope of E(ψ_leaf-x) decreased down to 50 % of its maximum (Carminati and Javaux, 2020). The SOL matches well with the transpiration rate of unpressurized plants (Fig. 4A–E). This supports the idea that stomata close when the relation between transpiration rate and leaf water potential becomes non-linear, as hypothesized by Sperry and Love (2015) and Carminati and Javaux (2020).

The measured E(ψ_leaf-x) relation as well as the SOL of the long and short root systems differed (Fig. 4E), which supports our hypothesis (Fig. 1). Analysis of covariance shows that stomatal closure was significantly different between the two root systems without pressurization (P < 0.001, Fig. 4F; Supplementary Data Fig. S4 and Tables S3 and S4). Plants with a short root system reached 50 % transpiration at ψ_leaf-x = −0.3 MPa compared with ψ_leaf-x = −0.5 MPa with the long root system (Fig. 4E).

Taken together, the measured relations between transpiration rate and leaf water pressure proved that stomata close at the onset of hydraulic non-linearity, as hypothesized in previous models (Sperry and Love, 2015; Carminati and Javaux, 2020). Additionally, the measurements show that a decrease in root length induces an earlier non-linearity in the soil–plant hydraulic conductance and triggers an earlier stomatal closure, which supports our hypothesis (Fig. 1).

We conclude that the relation between stomatal conductance and leaf water potential is affected by root length and below-ground hydraulics, particularly soil hydraulic conductance. This finding has important implications for understanding and predicting the response of transpiration to drought. So far, the current trend puts the focus on the coordination between stomatal closure and xylem vulnerability (Wolf et al., 2016; Anderegg et al., 2017; Henry et al., 2019; Eller et al., 2020). However, to properly predict stomatal closure and understand its relation to soil–plant hydraulics, root length, root and soil hydraulic conductivities are essential. Our results show a tied link between soil hydraulic conductivity, active root length and stomatal conductance, and the coordination between these variables is central in predicting the ability of plants to cope with water shortage. Further research would be needed to explore variations between plant species growing in contrasting soil textures and climatic conditions.

SUPPLEMENTARY DATA

Supplementary data are available at Annals of Botany online and consist of the following. Figure S1: root length and leaf area of tomato plants grafted onto two root systems. Figure S2: the root pressure chamber system used to measure the relation between transpiration and leaf xylem water pressure. Figure S3: transpiration rate of plants with short and long root systems during soil drying. Figure S4: linear fit of the E(ψ_leaf-x) relation measured in unpressurized plants with the two root systems. Table S1: analysis of variance for the influence of different factors on the transpiration rate under plant pressurization. Table S2: parameters used in the model. Table S3: coefficient estimates for stomatal closure E(ψ_leaf-x) in the two rootstocks in terms of the slope and the intercept. Table S4: analysis of variance to identify the significant difference between the slope and the intercept of E(ψ_leaf-x).

FUNDING

The doctoral position of M.A. was funded by Deutscher Akademischer Austauschdienst (DAAD, the German Academic Exchange Servic). The position of G.C. was founded by Bundesministeriums für Bildung und Forschung (BMBF, the Federal Ministry of Education and Research), Project 02WIL1489 (Deutsch-Israelische Wassertechnologie-Kooperation).