Abstract
The mechanics of most soft tissues in the human body are determined by the organization of their collagen fibers. Predicting how mechanics will change during growth and remodeling of those tissues requires constitutive laws that account for the density and dispersion of collagen fibers. Post-infarction scar in the heart, a mechanically and structurally complex material, does not yet have a validated fiber-based constitutive model. In this study, we tested four different constitutive laws employing exponential or polynomial strain-energy functions and accounting for either mean fiber orientation alone or the details of the fiber distribution about that mean. We quantified the goodness of fit of each law to mechanical testing data from 6-week-old myocardial scar in the rat using both sum of squared error (SSE) and the Akaike Information Criterion (AIC) to account for differences in the number of material parameters within the constitutive laws. We then compared their ability to prospectively predict the mechanics of independent myocardial scar samples from other time points during healing. Our analysis suggests that a constitutive law with a polynomial form that incorporates detailed information about collagen fiber distribution using a structure tensor provides excellent fits with just two parameters and reasonable predictions of myocardial scar mechanics from measured structure alone in scars containing sufficiently high collagen content.
Keywords: Myocardial Scar, Constitutive Law, Mechanics, Collagen, Fiber Based Material, Stress
Introduction
Nearly every soft tissue in the human body is supported by collagen fibers, and their mechanical behavior is often highly dependent on the organization of those fibers [1]. Material laws that predict the mechanics of fiber-reinforced tissues have become increasingly important tools in creating models to design new therapies, guide clinical decisions, and evaluate novel treatments for a number of pathologies. One important area where a validated structure-based material law is still needed is post-infarction scar tissue in the heart. In a developing myocardial scar, collagen area fraction increases steadily for up to 6 weeks following infarction, producing a concurrent increase in scar stiffness. In canine and porcine ligation models that develop highly aligned myocardial scar, mechanical tests have shown the tissue to be highly anisotropic, suggesting that collagen structure plays a dominant role in determining mechanics [2, 3]. Those mechanics are a critical determinant of post-infarction heart function, infarct rupture, and other serious complications [3–5]. Our group has created agent-based models that predict evolving scar structure during healing and changes in response to interventions [6–8]. However, to date it has not been possible to use these predictions of scar structure to anticipate how the mechanical properties of the scar will evolve under various conditions, because there is no validated constitutive model that can predict infarct scar mechanics based solely on measured or model-predicted collagen fiber structure. The primary goal of this study was to develop such a constitutive equation.
In the last several decades, many constitutive models have been developed for fiber-reinforced soft tissues such as arteries and myocardium that, like infarct scar, are loaded in biaxial tension in vivo. Some of these laws assume that strain energy and stresses are exponential functions of strain [9, 10], while others assume polynomial dependence on invariants of the Right Cauchy-Green deformation tensor [11, 12]. Within each of these groups, some models only account for the mean orientation of the reinforcing fibers [9, 11], while others incorporate more comprehensive information about the distribution of the fibers about that mean [10, 12, 13]. However, the vast majority of modeling and experimental studies on myocardial scar have focused on the mechanical properties of the scar without attempting to relate those mechanical properties to the underlying structure. Much of the work in this area has been conducted by Guccione and co-workers, who have use finite-element models of the infarcted left ventricle to explore the impact of various surgical therapies [14–16]. These studies used an exponential, anisotropic strain energy function originally developed by Guccione for canine myocardium [9], and scaled the overall stiffness of the material using a multiplication factor (c1 in Eq. 4 below) to simulate scarring. Some studies also used fitted material parameters from biaxial testing, but again without directly relating those parameters to measured collagen structure [17, 18]. Wenk and co-workers extended the approach of Guccione et al. by fitting material parameters and mean fiber direction in finite-element models to match measured strains, but did not measure structure. Gupta et al. [19], Sirry et al. [20], and Brazile et al. [21] all published biaxial test data on myocardial infarct scar without attempting to quantitatively relate those mechanical properties to the underlying structure.
We previously developed a version of the Guccione constitutive law that employed measured fiber distributions to calculate several of the coefficients [10], but never validated the ability of that formulation to capture scar mechanics in samples with known structure. In part this was due to the fact that our later studies of rat infarcts revealed scars resulting from the standard rat ligation model of myocardial infarction to be structurally and mechanically isotropic [2] rather than anisotropic as assumed by the Costa formulation and observed in other animal models [1]. More recently, using surgical reinforcement to direct collagen alignment in healing scars, we were able to create, biaxially test, and histologically characterize a population of post-infarction scars that varied widely in both collagen concentration and measured degree of collagen fiber alignment [8]. Here, we take advantage of this new dataset to compare the ability of the Guccione and Costa exponential formulations – as well as two new polynomial forms that account for either mean fiber orientation or measured fiber distributions – to capture the mechanics measured in biaxial tests while incorporating information on measured collagen fiber structure. We then test whether constitutive parameters identified by fitting tests on 6-week samples can be extrapolated to predict the mechanics of scars from other time points based on structure alone.
Methods
Collection of Mechanical and Histological Data
Previously, we created infarcts in male Sprague-Dawley rats via occlusion of the left anterior descending coronary artery, as described by Caggiano et al. [8]. Some of the infarcts were allowed to heal naturally, while others were reinforced circumferentially with a Dacron patch sewn under tension across the infarcted area. 36 infarcts were harvested and mechanically tested 1, 3, or 6 weeks following infarction. Animals were anesthetized with 3% isoflurane, intubated, and ventilated with oxygen and 2.5–3% isoflurane. The chest was opened via a midline sternotomy, and the heart was arrested via retrograde perfusion with cold BDM in PBS and removed. While still submerged in BDM, the scar and surrounding region were isolated from the rest of the myocardium, trimmed to a 5mm x 5mm square, speckled using powdered graphite, and mounted onto a BioTester using the tissue rakes provided (CellScale Biomaterials Testing, ON, Canada) so that the test region consisted entirely of scar with any small amounts of remaining myocardium located outside the rakes. The sample was mounted with its circumferential axis aligned in the X direction and longitudinal axis aligned in the Y direction of the tester. The sample was subjected to seven displacement-controlled test protocols spanning a range of ratios of circumferential to longitudinal stretch. For each scar, these test protocols included a strip uniaxial test in both the X and Y direction as well as an equibiaxial test. The remaining four ratios of X and Y stretch were included in order to obtain a more comprehensive dataset regarding behavior under a range of biaxial loading conditions. Each test consisted of ten cycles at strain rates of 1%/s, with the loading portion of the last cycle used for analysis. Of the 36 infarcts that were mechanically tested at 1, 3, and 6 weeks post-MI, we were able to obtain complete datasets with appropriate strain-tracking and approximately 15% peak biaxial stretch for all seven stretch protocols in 28. Of these scars, 2 were excluded from the study using a criterion based on the maximum value of |F12 or F21| ≤ 0.02. We focused on the remaining 26 scars in the present study. Sample thickness was measured at nine evenly spaced locations using a laser displacement sensor. Scars were then fixed in 10% formalin and sectioned transmurally at a thickness of 7 μm. Sections were stained with picrosirius red for structural analysis of the collagen using circularly polarized light under 10x magnification as described previously [2, 8, 22]. The structural analysis was performed at three to four evenly spaced depths within each tissue sample to ensure scar transmurality and assess consistency of alignment through the thickness. At each depth, the histologic section was imaged in 9 different regions covering most or all of the area subjected to mechanical testing. As described in more detail previously [2], custom software was used to threshold multiple images acquired with different filters in order to differentiate collagen from the surrounding space and tissue. Collagen area fraction (CAF) was computed as the fraction of collagen to non-collagen tissue pixels. Collagen alignment was quantified by using an intensity gradient detection algorithm within 40×40 pixel subregions, and thousands of these subregion fiber angles were used to represent the collagen fiber distribution in the sample. Mean vector length (MVL) was calculated from these fiber angle distributions to quantify the strength of the overall alignment by representing each angle as a unit vector, averaging their components to determine a mean vector, and then computing its length. Values of MVL range from 0 for randomly aligned fibers to 1 for perfect alignment. To account for any transmural variations in these quantities, fiber distributions from each section were normalized by area fraction, averaged across all transmural depths for each sample, and then the final CAF and MVL were computed from the average distribution for the entire scar.
Experimental Mechanics
Components of the deformation tensor F were calculated for each sample using strain tracking software developed by the Barocas Lab at the University of Minnesota. The full displacement tracking code can be found at http://license.umn.edu/technologies/20130022_robust-image-correlation-based-strain-calcu-lator-for-tissue-systems (free license for academic users). Cauchy stresses for each test were calculated using the measured forces and undeformed area as proposed by Fomovsky [2]:
| (1) |
| (2) |
| (3) |
where f1 and f2 are the measured forces, A1 and A2 are the undeformed areas (length time thickness) of the central region gripped by the rakes, and t11 and t22 are Cauchy stresses in the circumferential and longitudinal directions. Samples with high shear deformation (F12 or F21 values > 2%) were excluded from the study to minimize error related to the fact that the CellScale biaxial tester measures axial forces along each test direction but not transverse (shear) forces.
Material Laws
Measured stretches and Cauchy stresses were then fitted using four different material laws. The first material law was a Fung-type exponential law derived by Guccione et al. [9] and adapted for dog myocardium by Costa et al.[10]:
| (4) |
| (5) |
where E11, E22, and E33 are the fiber, crossfiber, and radial strains, and cj are material constants. This law assumes uniform average fiber alignment along the x1 direction. In this study, we will refer to this law as the Guccione material law. We adapted the second law, referred to here as the Polynomial material law, from a polynomial formulation derived for myocardium by Humphrey et al. [11] based on the invariants I1 and I4 of the right Cauchy-Green deformation tensor C:
| (6) |
| (7) |
where N is a unit vector along the average fiber direction. The original publication by Humphrey et al. used constant-invariant tests to determine a functional form for myocardium that included several polynomial terms. Here, we attempted to keep the number of terms as low as possible by including a single term for each invariant and choosing an exponent for the I4 term by trial-and-error to match the overall curvature of the measured stress-strain data in preliminary fitting trials for a subset of the 6-week samples.
In contrast to the first two material laws, Costa et al. [10] computed most material coefficients by assuming that fibers can bear stress only along their axes and summing components of squared fiber strain over n fibers with orientations αj relative to the mean fiber direction x1:
| (8) |
| (9) |
| (10) |
Finally, we derived a variant of the Humphrey law that incorporates the structure tensor H and invariant I4* introduced by Holzapfel et al., computed from a distribution of n fibers represented by unit vectors Nj [12, 23]:
| (11) |
where,
| (12) |
which we will refer to here as the Polynomial-Structural material law.
Parameter Fitting and Comparison
Stresses from each of the 6-week scar samples were fitted using a parameter sweep across a wide range of material constants in increments of 10 to narrow the solution space, followed by a second, smaller parameter sweep in increments of 1 to minimize the total sum of squared error (SSE) between the experimentally obtained stresses and computed stresses for each test condition. These fits were performed for every material law on each 6-week scar, yielding a single best-fit set of material parameters for each animal. Since comparing SSE does not take the number of material parameters into account, the Akaike Information Criterion (AIC) was also calculated for each fit using the SSE value and number of parameters. We used the specific form of the AIC employed for a similar comparison of constitutive laws for myocardium by Schmidt et al. and Burnham et al. [24], based on prior work by Akaike [25, 26]. The AIC incorporates terms for both goodness of fit and model complexity:
| (13) |
where Ω is the objective function across a vector of all material parameters ϑ (= SSE for our implementation), N is the number of data points, and K is the number of estimable regression parameters ( = the number of material constants for our implementation).
Experimental Validation
Finally, we evaluated whether the material constants which most affect fiber strain could be used to predict mechanics of scars taken from earlier time points during healing. For each law, we plotted the values of the parameter that should theoretically reflect primarily the contributions of the collagen fibers (c2 in Guccione, Polynomial, and Polynomial-Structural, c3 in Costa) against collagen area fraction to test whether they were correlated as expected (i.e., increasing collagen density should produce higher stiffness reflected in a higher coefficient value). For the laws where there was a significant correlation (Polynomial and Polynomial-Structural), we then extrapolated the linear fit to predict values of the fiber-related parameter c2 for six 3-week scars (3 patched, 3 control), and six 1-week scars (3 patched, 3 control) based on their known collagen area fraction. We predicted the stress-stretch response of each 1-week and 3-week sample using the interpolated value of c2 and the average c1 value from the 6-week scars, and compared the predicted stresses to the experimentally determined Cauchy stresses using total SSE.
Results
Scar Alignment
As described previously by Caggiano et al. [8], uniaxial surgical reinforcement with a Dacron patch produced scars with highly aligned collagen, while non-reinforced infarcts formed scars with low alignment (Fig. 1). In that study, alignment in the patch group was significantly different from random at all time points, while the unpatched group showed no significant alignment at any time point. The samples employed in the present study displayed considerable variation in the collagen area fraction, which ranged from 10–70% across all of the scars (Fig. 2). These samples also displayed highly variable degrees of collagen alignment, with the metric mean vector length (MVL) ranging from near 0 (completely random) to more than 0.8 (strong alignment, maximum possible value is 1.0).
Fig. 1.

Representative images of picrosirius red-stained scar samples 1, 3, and 6 weeks after myocardial infarction. A,C,E: In the group with no patch, scars had dense, straight fibers with no preferred direction of collagen alignment. B,D,F: In the patch group, collagen had similar density at each time point but with a clear and strong alignment
Fig. 2.
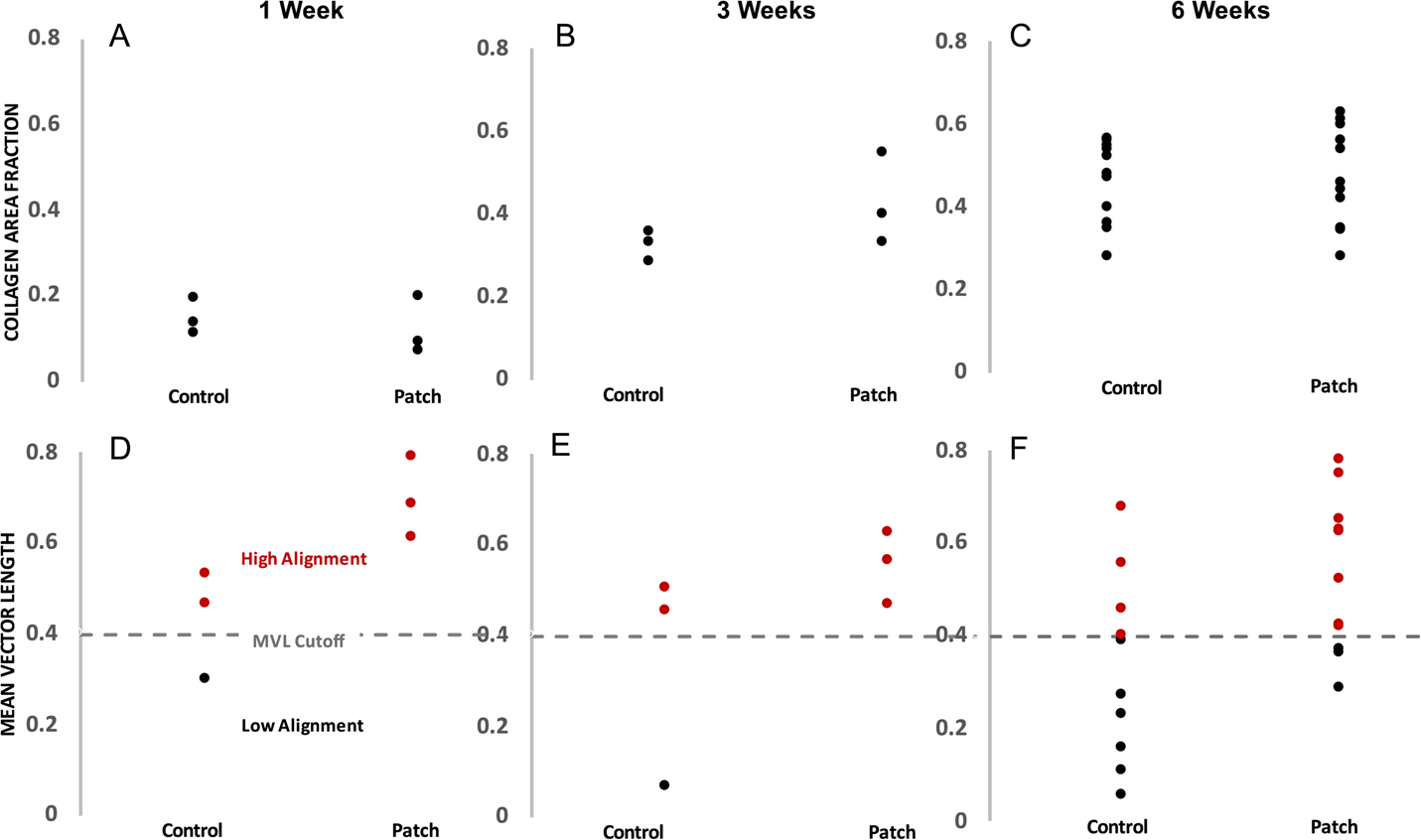
Quantification of infarct collagen density (A,B,C: collagen area fraction) and strength of collagen alignment (D,E,F: mean vector length) at 1,3, and 6 weeks post-MI in the nonpatch and patch groups. Collagen area fraction varied by nearly 60% across groups but was not impacted by the presence of the patch. There was also a large spread in the resulting collagen alignment strength, and overall the patch animals had more scars with very highly aligned collagen than the nonpatch group. Red dots represent scars with highly aligned collagen and black dots represent scars with poorly aligned collagen
Scar Mechanics
In order to study scar mechanical behavior across a wide range of biaxial stretch conditions, we stretched scars using seven biaxial displacement conditions which included both strip-uniaxial and equibiaxial tests. Deformation and was tracked in the central region of the sample to avoid clamping effects at the rakes (Fig. 3a,b). Strain tracking analysis determined the deformation gradient at each grid square across the middle of the sample for each timepoint of the test. Examination of the deformation gradient F along the two primary test axes showed that the tests covered a wide range of stretch combinations (Fig. 3c).
Fig. 3.
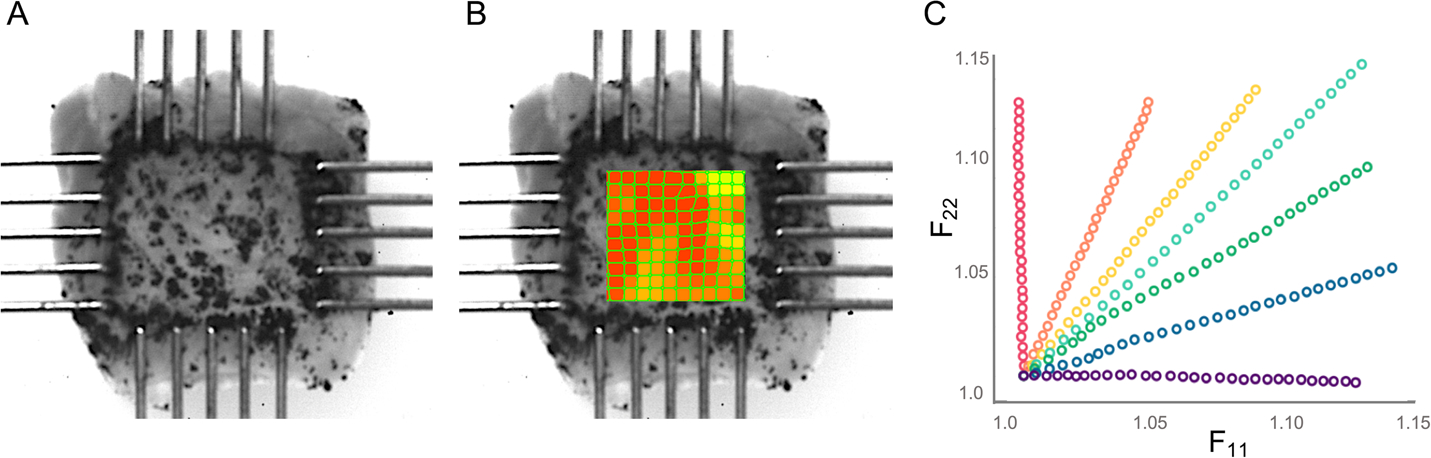
Example images of scar mechanical loading with strain and deformation tracking. A: Samples cut to ~ 5mm x 5mm were speckled and loaded onto rakes for mechanical testing. Strain was calculated in the center of the sample using digital image correlation software (B), and the deformation F values in the direction of the two loading axes were examined (C) to ensure samples were subjected to a wide range of stretch combinations and a maximum stretch of approximately 15%. Red dots indicate data for a near-uniaxial stretch in the x2 (longitudinal) direction, purple indicates data for a near-uniaxial stretch in the x1 (circumferential) direction, and other colors indicate combinations of x1 and x2 stretch
Figure 3 and subsequent figures that present data from multiple stretch protocols use a common color scheme, with red dots or lines indicating data and fits for a near-uniaxial stretch in the x2 (longitudinal) direction, purple indicating data and fits for a near-uniaxial stretch in the x1 (circumferential) direction, and other colors indicating combinations of x1 and x2 stretch. In order to directly compare the goodness of fit of our models to our experimental data, for each constitutive law, we calculated the total SSE in fitted vs. actual stress components T11 and T22 across all test protocols for each animal. The Guccione and Polynomial constitutive laws predicted stress in the fiber direction reasonably well but were unable to capture mechanical behavior in the crossfiber direction for samples with low fiber alignment (Fig. 4). This resulted in a high SSE for these constitutive laws overall, particularly in samples with low alignment (Fig. 5a). Overall, the Polynomial-Structural constitutive law had the lowest average SSE (Fig. 5a). Because it had the lowest number of material parameters, it also had the lowest average AIC (Fig. 5b). The Costa and Polynomial-Structural laws better captured the mechanical behavior in both the fiber and crossfiber direction across samples with different levels of fiber alignment, and the Polynomial-Structural law displayed the lowest relative variation in the best-fit material parameters across samples (Table 1).
Fig. 4.
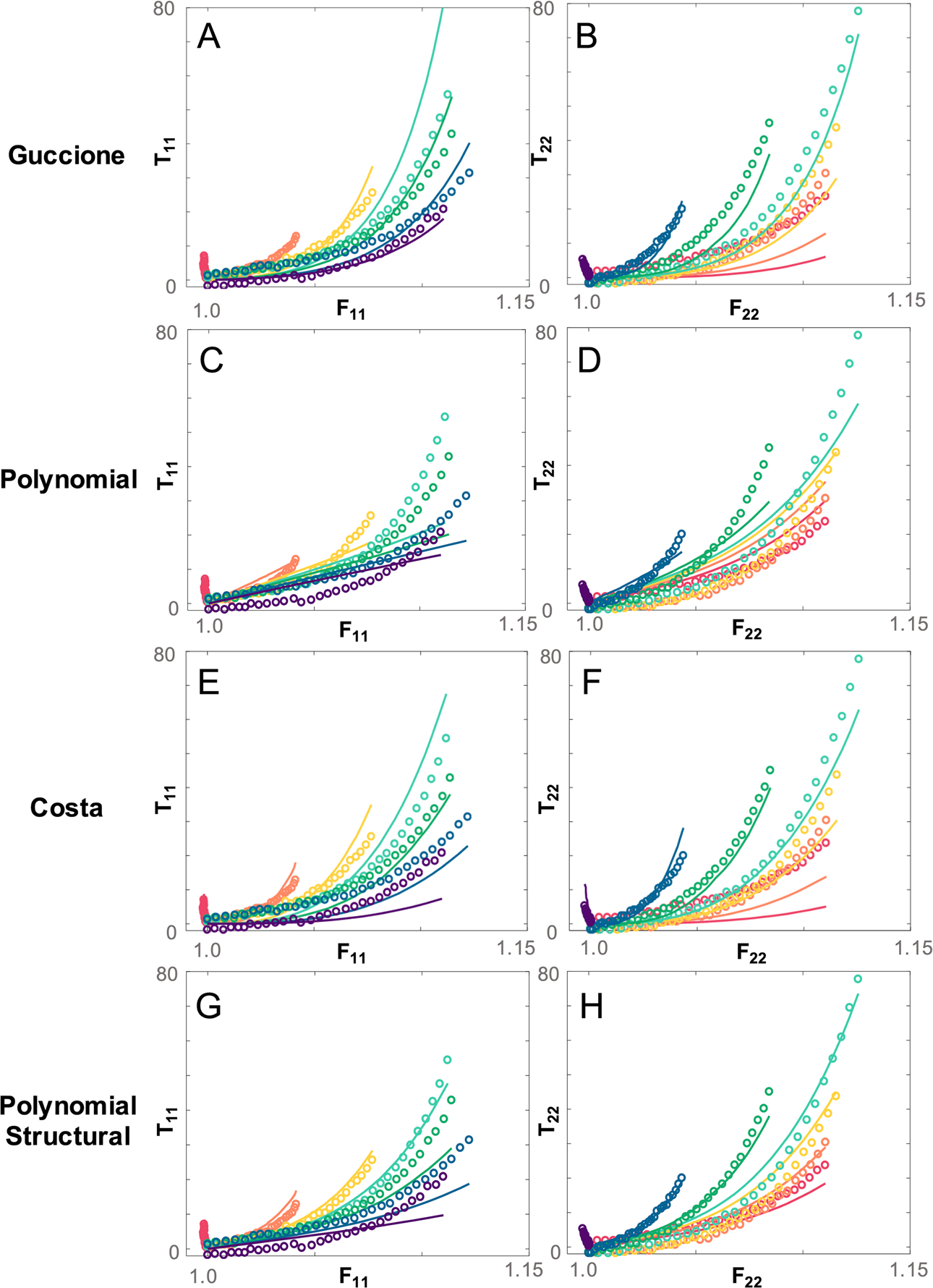
Example comparison of fits to data from one 6 week scar using each of the fiber-based constitutive laws. Fits to both fiber stress T22 and cross-fiber stress T11 are shown. The exponential form of the Guccione law (A,B) results in a discrepancy between the shape of the experimental and fitted stress response in both directions. The Polynomial law predicts fiber stress well (C,D) but is unable to capture cross-fiber stress. The Costa law (E,F) fits the data well using the full fiber distribution but, like the Guccione law, is unable to capture the shape of the full stress response. Overall, the Polynomial Structural law does a better job of predicting the stress response magnitude and shape in both directions (G,H). Red dots or lines indicate data and fits for a near-uniaxial stretch in the x2 (longitudinal) direction, purple indicate data and fits for a near-uniaxial stretch in the x1 (circumferential) direction, and other colors indicate combinations of x1 and x2 stretch
Fig. 5.
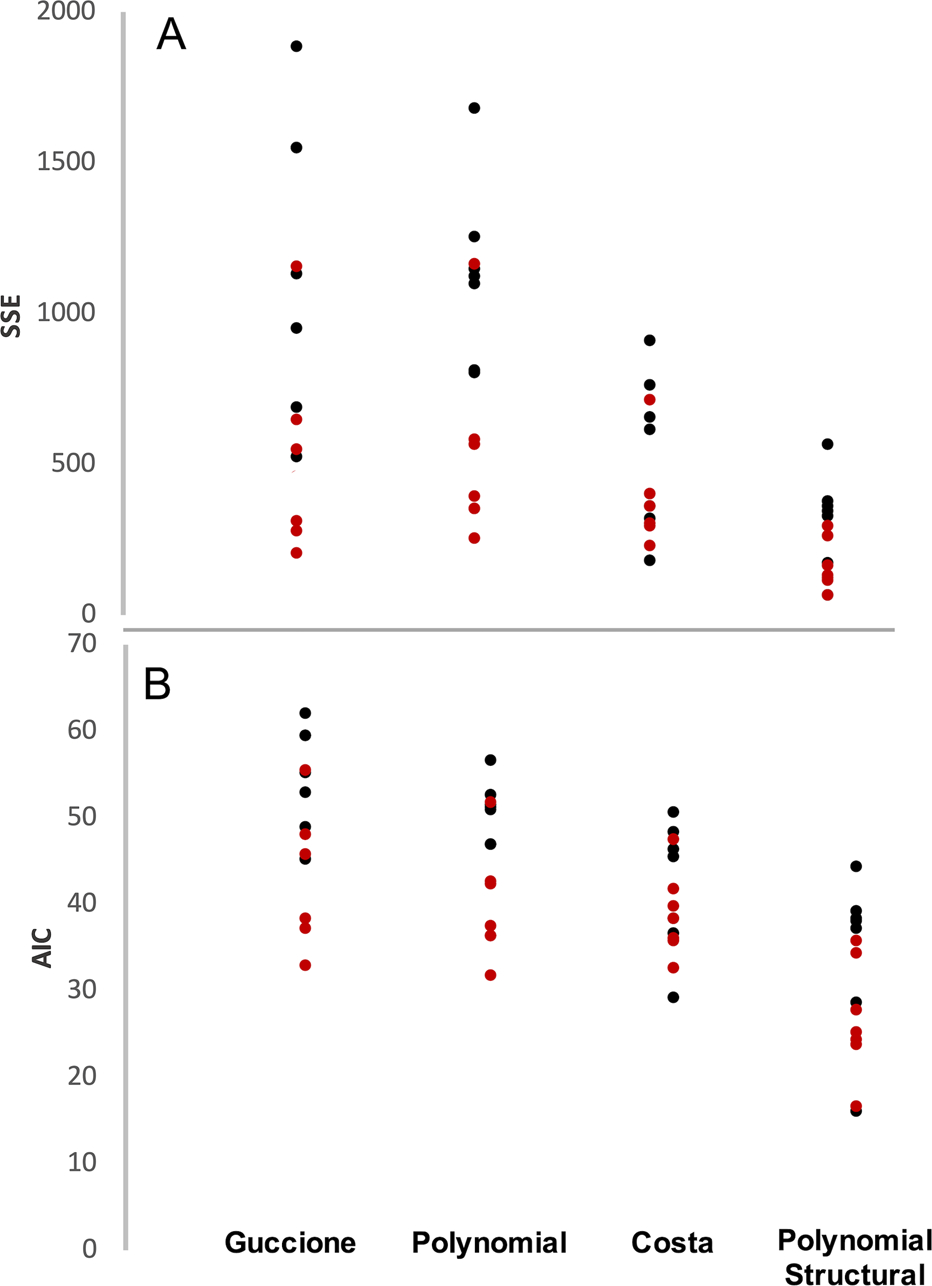
Total SSE (A) and AIC (B) for each scar compared across all four constitutive laws. Total SSE is lowest overall for the Costa and Polynomial Structural laws, which both include information about the distribution of the collagen fibers rather than just their mean orientation. This trend continues in the AIC comparison, which accounts for the number of material parameters in each law. The Polynomial Structural law still maintains the best score overall. Red dots represent scars with highly aligned collagen and black dots represent scars with poorly aligned collagen. Red dots represent scars with highly aligned collagen and black dots represent scars with poorly aligned collagen
Table 1.
Mean and standard deviation for each material parameter across all 6 week infarcts
| Guccione | Polynomial | Costa | Polynomial Structural | |
|---|---|---|---|---|
|
| ||||
| c 1 | 100 ± 42 | 9 ± 7 | 60 ± 45 | 6 ± 3 |
| c 2 | 106 ± 119 | 287 ± 189 | 5 ± 3 | 481 ± 66 |
| c 3 | 4 ± 3 | - | 7 ± 7 | - |
| c 4 | 8 ± 8 | - | - | - |
Material Law Validation
Finally, we tested whether any of the constitutive laws examined here could make reasonable predictions of the mechanics of independent 1-week and 3-week post-MI scars once calibrated using the 6-week fits. By design, each law contained one parameter that should encapsulate most of the contributions of the collagen fibers (c2 in Guccione, Polynomial, and Polynomial-Structural, c3 in Costa). When we plotted these parameters against collagen area fraction for all 6-week scars, the Polynomial and Polynomial-Structural showed a significant correlation, with increasing collagen density associated with a higher coefficient value (Fig. 6). By contrast, there was no significant correlation between CAF and the material parameters for Guccione and Costa, indicating that it would not be possible to reliably predict parameter values for a new sample based on area fraction alone (Fig. 6).
Fig. 6.
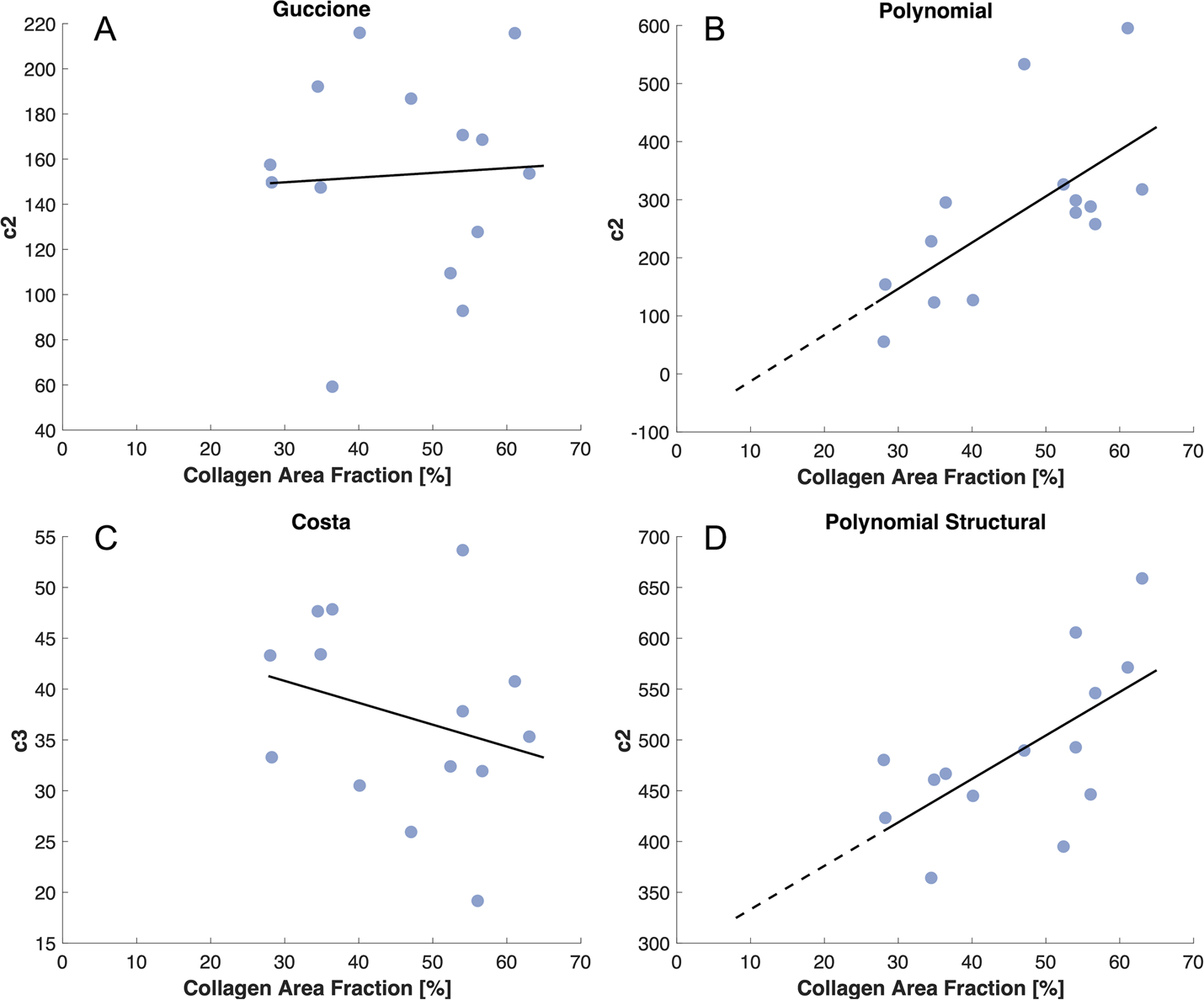
The relationship between collagen area fraction and the parameter values most associated with the contributions of the collagen fibers across all 6-week scars. A linear regression was used to determine which relationships were statistically significant (solid line). A,C: The correlation from the exponential material laws was not significant. B,D: The correlation from the polynomial material laws was significant; therefore, these lines were extrapolated through the range of collagen area fraction from other time points (dotted line) and used to estimate the corresponding fiber parameters for those scars
Next, we extrapolated the linear fits to the 6-week data, and used the measured collagen area fractions for each 1-week and 3-week sample to estimate their c2 terms. We assumed that c1 values for all 1-week and 3-week samples were equal to the mean fitted c1 value from the 6-week scars. Remarkably, this simplistic approach predicted stresses of the right order of magnitude for all samples (Fig. 7). Consistent with the 6-week fitting results, the Polynomial law provided good predictions in the fiber direction for the equibiaxial tests (Fig. 7B,F) while underpredicting the curvature in the cross-fiber direction as well as the spread of the curves across the different test protocols. By contrast, the Polynomial-Structural law captured the major trends in the stress-stretch curves at 3 weeks (Fig. 7G,H), although it performed less well at 1 week. Total SSE for the predicted compared to measured stresses across 6 samples at each time point confirmed that the Polynomial-Structural law performed quite well at 3 weeks, less well at 1 week, and better than the Polynomial law in nearly all samples (Fig. 8). Comparing the SSE values for the 3-week predictions in Figure 8 to those for the 6-week fits in Figure 5 reveals that prospective predictions using the Polynomial-Structural law had errors of the same magnitude as brute-force best fits using the Guccione and Polynomial laws, and twice as large as direct fits using the Polynomial-Structural law.
Fig. 7.
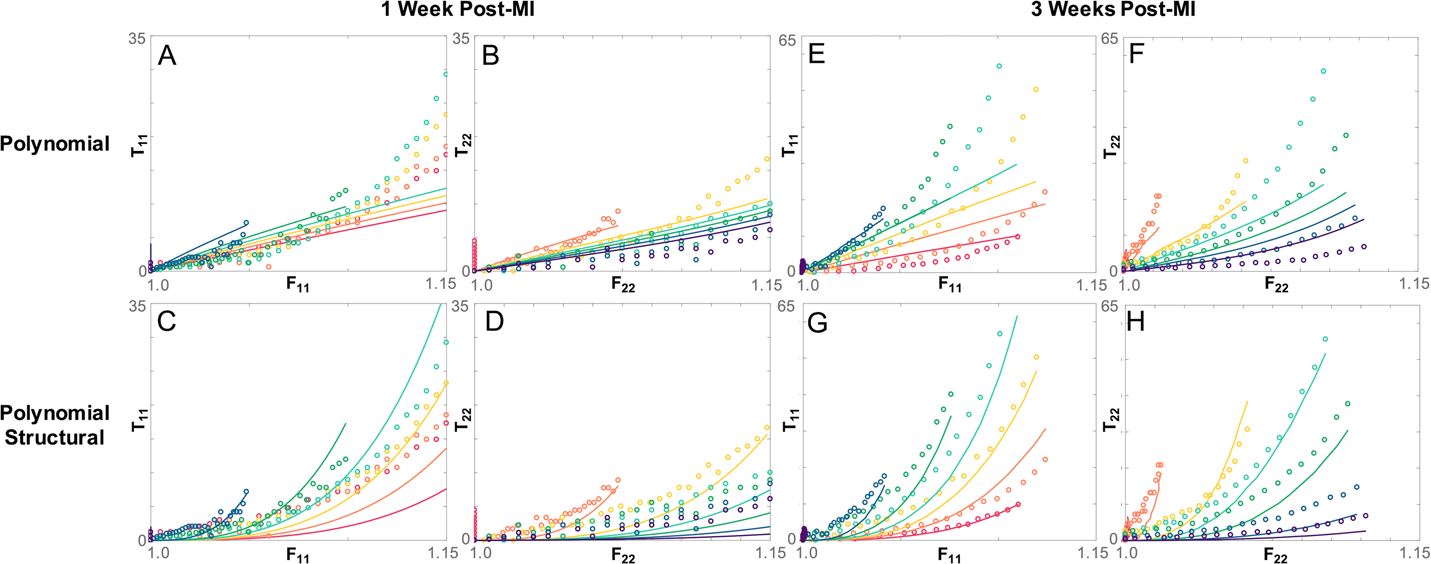
Example comparison of predicted stresses calculated using the fitted fiber parameter c2 and the polynomial based constitutive laws (lines) vs experimentally determined Cauchy stress (dots) in a scar 1 week post-MI (A-D) and a scar 3 weeks post-MI (E-H). Fits to both fiber stress T22 and cross-fiber stress T11 are shown. The Polynomial law predicts some of the fiber stress behavior (B,F) but is unable to capture cross-fiber stress at both time points (A,E). The Polynomial-Structural law is able to predict the fiber stress (C,G), and cross-fiber stress (E,G) behavior more accurately at both timepoints
Fig. 8.
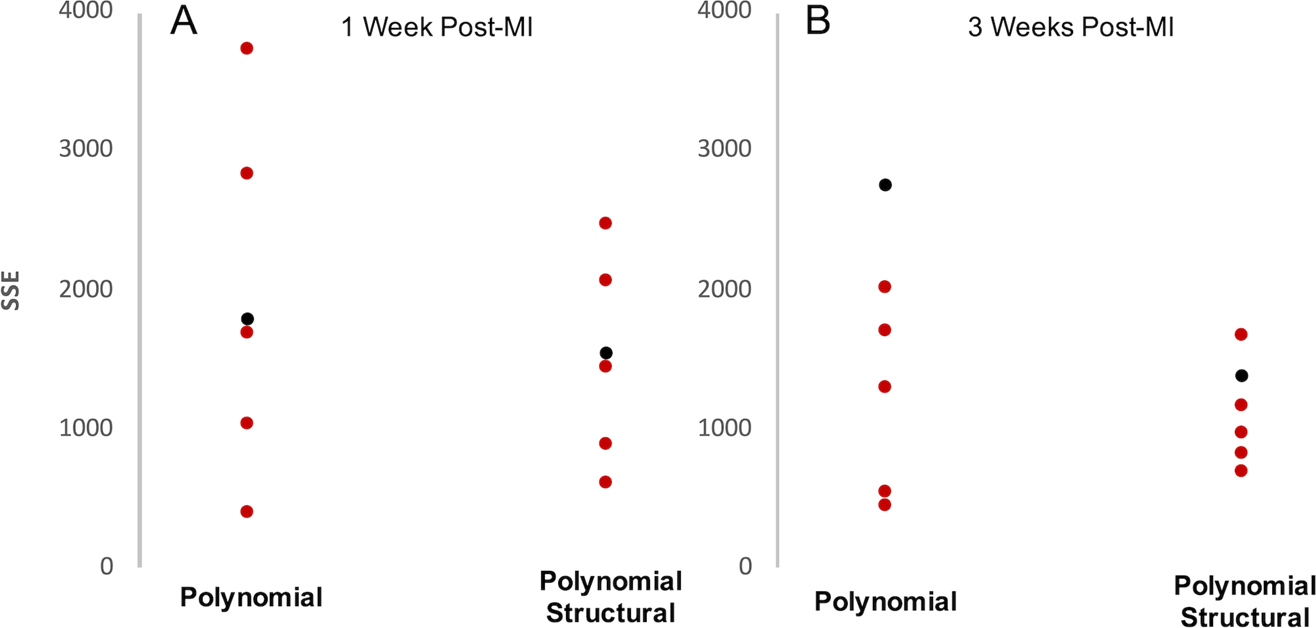
Total SSE for stresses predicted using the Polynomial and Polynomial-Structural law vs measured Cauchy stresses at 1 week (A) and 3 weeks (B) post-MI. Six samples were used (3 patch, 3 control) from each time point. Red dots represent samples with high alignment and black dots represent samples with poor alignment. Total SSE is lower on average and less varied at both time points using the Polynomial-Structural law. Red dots represent scars with highly aligned collagen and black dots represent scars with poorly aligned collagen
Discussion
The Impact of Predicting Scar Mechanics
Following myocardial infarction, damaged muscle is replaced by a collagen-rich scar, and the mechanics of that healing scar are such an important determinant of patient outcomes [3, 27]. The structure of that scar is in turn determined in large part by regional mechanics [7, 8]. A number of proposed therapies such as surgical reinforcement, injection of biomaterials, and treatment with tissue-engineered patches disrupt this interplay between structure and mechanics [8, 28–30]. Computational models that could predict how scar healing will evolve following such interventions would be a valuable tool for anticipating their impact and optimizing their design. Our group has created agent-based models that predict evolving scar structure during healing and changes in response to interventions [6–8]; here, we sought to identify a constitutive equation that we could use to make reasonable predictions of mechanical properties of scars based on based on measured or model-predicted collagen density and fiber orientation.
In this study, we took advantage of a dataset generated previously in our laboratory in which we measured scar structure and mechanics in post-infarction scars with a much wider range of collagen alignments than is typical for infarcts healing without intervention [8]. We chose four constitutive laws representing common forms of fiber-based constitutive laws, two exponential forms that were previously employed for myocardium or myocardial scar and two novel polynomial laws based on previous work in myocardium and other cardiovascular tissues. Notably, these four material laws incorporated varying degrees of structural detail. We first assessed their ability to fit observed mechanics in 6-week post-infarction scars across a wide range of planar biaxial stretch combinations while incorporating measured sample-specific scar structure, and then tested their ability to predict the mechanics of samples from other time points during healing based on measured scar structure alone. We found that the novel Polynomial-Structural formulation proposed here provided excellent fits to measured stress-stretch data with only 2 free parameters, and provided reasonable predictions of the behavior of independent samples from different time points in healing based on their structure alone.
Constitutive Law Fitting
The variants of the Guccione and Polynomial laws tested here did not fit our 6-week scar data well because they account for the mean fiber orientation of each sample but not for the distribution of fibers about that mean, which can be quite broad in healing myocardial scar. While such laws have been employed for myocardial scar, both the Guccione law [9] and the polynomial form proposed by Humphrey [11] that motivated our Polynomial formulation were originally developed for passive myocardium, where there is a clear mean fiber orientation in any transmural plane, with limited variation about that mean. Thus, it is not surprising that these constitutive laws performed less well for samples that demonstrated a wide range of fiber alignment. Consistent with this interpretation, laws incorporating information on the distribution of collagen fibers (Costa and Polynomial-Structural) better fit mechanical behavior across 6-week samples with very different levels of fiber alignment. The fact that the samples tested were from a study where fiber structure was intentionally perturbed, producing a much wider range of fiber alignments than was present in prior animal studies on healing infarcts, improved our ability to discriminate between the formulations compared here.
Comparison of the fits from the Costa and the Polynomial-Structural laws also suggests that a polynomial function may better capture the mechanical behavior of myocardial scar at expected in-vivo levels of stretch compared to a Fung-type exponential. In some respects this comparison is unfair – we chose the power of the I4 term in the polynomial strain-energy functions based on preliminary fits to data from a small number of samples, while the form of the Guccione and Costa laws was taken directly from prior publications. Thus, it may be possible to formulate other exponential strain-energy functions that would perform better. However, the polynomial formulations also displayed several other potential advantages over their exponential counterparts. First, they required only 2 coefficients to provide fits with similar error to exponential counterparts with 3 or 4 parameters. Second, the fitted parameters for the polynomial laws showed more consistency across samples; for example, the average value for the fitted c2 parameter in the Polynomial-Structural law was 481±66 (SD/mean = 0.137), while the relative standard deviations for the coefficients in the Costa law were all 0.6 or greater. This finding likely reflects a known weakness of exponential strain energy functions of the type employed here: many different combinations of the c1 scaling parameter and the other parameters inside the exponent can produce very similar curves, making reliable parameter estimation difficult. Finally, as discussed below, the polynomial laws tested here showed the expected relationship between collagen content and the coefficient multiplying the term that accounts for the mechanical contribution of the fibers (Fig. 6), making it possible to estimate material parameters for new samples based on their measured collagen area fractions alone.
Material Law Validation
Our ultimate goal in pursuing this study was to devise a procedure for making reasonable estimates of scar mechanical properties based on structure alone. This would allow us to run coupled simulations linking an agent-based model that predicts how scar structure will evolve given regional mechanics to a finite-element model that predicts how global and regional left ventricular mechanics will evolve as scar structure changes. Predicting mechanics of a soft tissue based on structure alone is an ambitious goal that has generally proved elusive. One of the more successful studies in this regard was by Sacks [31], who used a single equi-biaxial test to calibrate the overall stiffness of a constitutive law that incorporated measured fiber distributions, then predicted mechanical responses to other, non-equibiaxial test protocols. Yet even this study used one protocol from each sample to calibrate the coefficients.
By contrast, we attempted to predict the mechanics of 1-week and 3-week scar samples based solely on their measured collagen fiber structure and coefficients we determined from our 6-week fits. By design, three of the constitutive equations examined here (all except Guccione) included one coefficient multiplying an isotropic term representing non-collagenous material in the scar and another term intended to scale the contributions of the collagen fibers (c2 in the Polynomial and Polynomial-Structural Laws, c3 in Costa). If these laws performed as designed, we reasoned that these ‘fiber’ terms should be proportional to collagen area fraction (CAF), and that a fit to this relationship could be used to estimate values for new samples based on their CAF alone. Somewhat surprisingly, the c3 coefficient in the Costa law displayed no significant correlation with CAF for our 6-week samples; thus, we did not attempt to perform predictions for other time points using this law. However, prospective prediction with the Polynomial-Structural law based on measured collagen structure alone worked remarkably well for samples tested 3 weeks post-MI, with errors about half of what we achieved using a full parameter optimization at 6 weeks and similar to the 6-week best fits using the Guccione or Polynomial laws. This approach was less accurate at 1 week, likely due to the fact that collagen density is much lower and the mechanics of the scar are likely more heavily impacted by factors such as necrotic myocytes and edema. However, the approach presented here appears very promising for time points after the first couple of weeks, when collagen clearly dominates the mechanics. Consistent with our 6-week fitting results, the Polynomial law was much less effective at predicting the mechanical response in the cross-fiber direction due to its assumption of uniform fiber alignment. Overall, our results suggest that the Holzapfel-type Polynomial-Structural law presented here is a promising framework for incorporating measured fiber structure in simulations of myocardial scar mechanics, because it fit data from samples with a wide range of different structures quite well despite having only two free parameters and was able to predict mechanics from independent samples even at a different time point in healing (3 weeks) using only information about their collagen fiber structure.
Limitations and Sources of Error
The biggest uncertainty in this work is the inability of our test device to measure shear forces perpendicular to the text axes. We tested samples along the in-vivo circumferential and longitudinal directions, and most of our highly aligned samples had a preferred fiber direction close to longitudinal. However, in samples where fibers are aligned obliquely to the text axes, the inability to measure shear forces can produce significant errors in stress calculations and fits. We attempted to mitigate this problem by excluding samples with shear deformation exceeding 2% from the study, but since most of the scars did not exhibit perfect fiber alignment in the direction of loading, our results may have been slightly affected by the presence of shear stress.
Additionally, most structure-based formulations for collagenous tissues assume that collagen fibers resist tension beyond a certain recruitment stretch but offer little resistance to compression. Accordingly, Holzapfel, Ogden, and coworkers have recommended computing fiber stretches and excluding fibers experiencing compression when employing their structure-tensor-based invariants. We did not perform this exclusion because we were computing strain energies for biaxial stretch protocols where normal stretches in the plane containing the fibers were ≥1 and shear deformations were negligible, ensuring that all fibers experienced stretches ≥1. However, when applying the Polynomial-Structural law in other settings such as a finite-element model of an in vivo infarct, it may be necessary to identify and exclude fibers experiencing compression.
Acknowledgements
This work was supported by National Institutes of Health grants R01 HL-116449 and R01 EB-137755.
Footnotes
Conflicts of interest The authors have no relevant financial or non-financial interests to disclose.
Ethics approval All experiments were approved by the University of Virginia Institutional Animal Care and Use Committee
Consent to participate Not applicable
Consent for publication Not applicable
Availability of data Not applicable
Code availability Not applicable
References
- 1.Holmes JW, Nuñez JA, Covell JW: Functional implications of myocardial scar structure. Am. J. Physiol. - Hear. Circ. Physiol 272, (1997). 10.1152/ajpheart.1997.272.5.h2123 [DOI] [PubMed] [Google Scholar]
- 2.Fomovsky GM, Holmes JW: Evolution of scar structure, mechanics, and ventricular function after myocardial infarction in the rat. Am. J. Physiol. Heart Circ. Physiol 298, H221–8 (2010). 10.1152/ajpheart.00495.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Richardson W, SA C, Quinn T, Holmes JW: Physiological Implications of Myocardial Scar Structure. 5, 1877–1909 (2016). 10.1002/cphy.c140067.Physiological [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Richardson WJ, Holmes JW: Why Is Infarct Expansion Such an Elusive Therapeutic Target? J. Cardiovasc. Transl. Res 8, 421–430 (2015). 10.1007/s12265-015-9652-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Weir RAP, McMurray JJV, Velazquez EJ: Epidemiology of Heart Failure and Left Ventricular Systolic Dysfunction after Acute Myocardial Infarction: Prevalence, Clinical Characteristics, and Prognostic Importance. Am. J. Cardiol 97, 13–25 (2006). 10.1016/j.amjcard.2006.03.005 [DOI] [PubMed] [Google Scholar]
- 6.Rouillard AD, Holmes JW: Coupled agent-based and finite-element models for predicting scar structure following myocardial infarction. Prog. Biophys. Mol. Biol 115, 235–243 (2014). 10.1016/j.pbiomolbio.2014.06.010 [DOI] [PubMed] [Google Scholar]
- 7.Fomovsky GM, Rouillard AD, Holmes JW: Regional mechanics determine collagen fiber structure in healing myocardial infarcts. J. Mol. Cell. Cardiol 52, 1083–1090 (2012). 10.1016/j.yjmcc.2012.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Caggiano LR, Lee J, Holmes JW: Surgical reinforcement alters collagen alignment and turnover in healing myocardial infarcts. Am. J. Physiol. Circ. Physiol 315, 1041–1050 (2018). 10.1152/ajpheart.00088.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guccione J, Mcculloch A, Waldman L: Passive material properties of intact ventricular myocardium determined from a cylindrical model. J. Biomech. Eng 118, 262 (1996). 10.1115/1.2795971 [DOI] [PubMed] [Google Scholar]
- 10.Costa KD, Holmes JW, McCulloch AD: Modelling cardiac mechanical properties. Philos. Trans. A. Math. Phys. Eng. Sci 359, 1233–1250 (2001) [Google Scholar]
- 11.Humphrey J, Strumpf R, Yin F: Determination of a Constitutive Relation for Passive Myocardium: I. A New Functional Form. J. Biomech. Eng 112, 333–339 (1990) [DOI] [PubMed] [Google Scholar]
- 12.Holzapfel GA, Ogden RW: Constitutive modelling of passive myocardium: A structurally based framework for material characterization. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci 367, 3445–3475 (2009). 10.1098/rsta.2009.0091 [DOI] [PubMed] [Google Scholar]
- 13.Billiar KL, Sacks MS: Biaxial Mechanical Properties of the Native and Glutaraldehyde-Treated Aortic Valve Cusp: Part II—A Structural Constitutive Model. J. Biomech. Eng 122, 327–335 (2000). 10.1115/1.1287158 [DOI] [PubMed] [Google Scholar]
- 14.Guccione JM, Moonly SM, Moustakidis P, Costa KD, Moulton MJ, Ratcliffe MB, Pasque MK: Mechanism underlying mechanical dysfunction in the border zone of left ventricular aneurysm: A finite element model study. Ann. Thorac. Surg 71, 654–662 (2001). 10.1016/S0003-4975(00)02338-9 [DOI] [PubMed] [Google Scholar]
- 15.Dang ABC, Guccione JM, Zhang P, Wallace AW, Gorman RC, Gorman JH, Ratcliffe MB: Effect of ventricular size and patch stiffness in surgical anterior ventricular restoration: A finite element model study. Ann. Thorac. Surg 79, 185–193 (2005). 10.1016/j.athoracsur.2004.06.007 [DOI] [PubMed] [Google Scholar]
- 16.Sun K, Stander N, Jhun CS, Zhang Z, Suzuki T, Wang GY, Saeed M, Wallace AW, Tseng EE, Baker AJ, Saloner D, Einstein DR, Ratcliffe MB, Guccione JM: A computationally efficient formal optimization of regional myocardial contractility in a sheep with left ventricular aneurysm. J. Biomech. Eng 131, 1–10 (2009). 10.1115/1.3148464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Walker JC, Ratcliffe MB, Zhang P, Wallace AW, Fata B, Hsu EW, Saloner D, Guccione JM: MRI-based finite-element analysis of left ventricular aneurysm. Am. J. Physiol. - Hear. Circ. Physiol 289, 692–700 (2005). 10.1152/ajpheart.01226.2004 [DOI] [PubMed] [Google Scholar]
- 18.Wall ST, Walker JC, Healy KE, Ratcliffe MB, Guccione JM: Theoretical impact of the injection of material into the myocardium: A finite element model simulation. Circulation. 114, 2627–2635 (2006). 10.1161/CIRCULATIONAHA.106.657270 [DOI] [PubMed] [Google Scholar]
- 19.Gupta KB, Ratcliffe MB, Fallert MA, Edmunds LH, Bogen DK: Changes in passive mechanical stiffness of myocardial tissue with aneurysm formation. Circulation. 89, 2315–2326 (1994). 10.1161/01.CIR.89.5.2315 [DOI] [PubMed] [Google Scholar]
- 20.Sirry MS, Butler JR, Patnaik SS, Brazile B, Bertucci R, Claude A, McLaughlin R, Davies NH, Liao J, Franz T: Infarcted rat myocardium: Data from biaxial tensile and uniaxial compressive testing and analysis of collagen fibre orientation. Data Br. 8, 1338–1343 (2016). 10.1016/j.dib.2016.08.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Brazile BL, Butler JR, Patnaik SS, Claude A, Prabhu R, Williams LN, Perez KL, Nguyen KT, Zhang G, Bajona P, Peltz M, Yang Y, Hong Y, Liao J: Biomechanical properties of acellular scar ECM during the acute to chronic stages of myocardial infarction. J. Mech. Behav. Biomed. Mater 116, 104342 (2021). 10.1016/j.jmbbm.2021.104342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Whittaker P, Kloner RA, Boughner DR, Pickering JG: Quantitative assessment of myocardial collagen with picrosirius red staining and circularly polarized light. Basic Res. Cardiol 89, 397–410 (1994). 10.1007/BF00788278 [DOI] [PubMed] [Google Scholar]
- 23.Gasser TC, Ogden RW, Holzapfel GA: Hyperelastic modelling of arterial layers with distributed collagen fibre orientations. J. R. Soc. Interface 3, 15–35 (2006). 10.1098/rsif.2005.0073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schmid H, Nash MP, Young AA, Hunter PJ: Myocardial material parameter estimation - A comparative study for simple shear. J. Biomech. Eng 128, 742–750 (2006). 10.1115/1.2244576 [DOI] [PubMed] [Google Scholar]
- 25.Akaike H: Information Theory and an Extension of the Maximum Likelihood Principle. In: Parzen E, Tanabe K, and Kitagawa G (eds.) Selected Papers of Hirotugu Akaike. pp. 267–281. Springer; New York, New York, NY: (1973) [Google Scholar]
- 26.Akaike H: A new look at the statistical model identification. IEEE Trans. Automat. Contr 19, 716–723 (1974). 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
- 27.Holmes JW, Borg TK, Covell JW: Structure and Mechanics of Healing Myocardial Infarcts. Annu. Rev. Biomed. Eng 7, 223–253 (2005). 10.1146/annurev.bioeng.7.060804.100453 [DOI] [PubMed] [Google Scholar]
- 28.Fomovsky GM, Clark SA, Parker KM, Ailawadi G, Holmes JW: Anisotropic reinforcement of acute anteroapical infarcts improves pump function. Circ. Hear. Fail 5, 515–522 (2012). 10.1161/CIRCHEARTFAILURE.111.965731 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Holmes JW, Laksman Z, Gepstein L: Making better scar: Emerging approaches for modifying mechanical and electrical properties following infarction and ablation. Prog. Biophys. Mol. Biol 120, 134–148 (2016). 10.1016/j.pbiomolbio.2015.11.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Clarke SA, Richardson WJ, Holmes JW: Modifying the mechanics of healing infarcts: Is better the enemy of good? J. Mol. Cell. Cardiol 93, 115–124 (2016). 10.1016/j.yjmcc.2015.11.028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sacks MS: Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. J. Biomech. Eng 125, 280–287 (2003). 10.1115/1.1544508 [DOI] [PubMed] [Google Scholar]


