Synthetic dimension band structures on a Si CMOS photonic platform

Abstract

Synthetic dimensions, which simulate spatial coordinates using nonspatial degrees of freedom, are drawing interest in topological science and other fields for modeling higher-dimensional phenomena on simple structures. We present the first realization of a synthetic frequency dimension on a silicon ring resonator integrated photonic device fabricated using a CMOS process. We confirm that its coupled modes correspond to a one-dimensional tight-binding model through acquisition of up to 280-GHz bandwidth optical frequency comb-like spectra and by measuring synthetic band structures. Furthermore, we realized two types of gauge potentials along the frequency dimension and probed their effects through the associated band structures. An electric field analog was produced via modulation detuning, whereas effective magnetic fields were induced using synchronized nearest- and second nearest–neighbor couplings. Creation of coupled mode lattices and two effective forces on a monolithic Si CMOS device represents a key step toward wider adoption of topological principles.

An integrated Si photonic device hosts a synthetic frequency dimension lattice with intersite coupling and two effective forces.

INTRODUCTION

The concept of dimensionality has become a central fixture in diverse fields of contemporary physics and technology in past years. While inquiries into lower-dimensional materials and structures have been fruitful, rapid advances in topology science have uncovered a further abundance of potentially useful phenomena beyond the three spatial dimensions available in the world around us. Recently, the concept of a synthetic dimension has emerged, with which high-dimensional structures can be hosted on low-dimensional platforms by harnessing nonspatial degrees of freedom as either a substitute or a complement for geometrical ones (1). Owing to the flexibility in tuning both the amplitude and the phase of intersite couplings along the synthetic dimension, the approach has become an important ingredient in realizing various topological lattice models ever since it was pioneered in ultracold atomic gases (2, 3).

Optics and photonics have also become fields in which simulation of various condensed matter phenomena and topological effects is drawing considerable attention (4). This interest is owed to the versatility of photonics as a powerful platform for investigation of questions in fundamental science, as well as to the promise of novel applications that topological effects hold for the realization of next-generation photonic devices. Examples of their notable functionalities and properties resilient to imperfections include robust transmission lines (5–8), reflection-free sharply bent waveguides (9–11), or stable laser cavities (12, 13). Here, in addition, synthetic dimensions have made it possible to exploit higher-dimensional concepts in lower-dimensional devices with reduced complexity, as well as driving critical device functionalities such as on-chip optical isolation (14). Harnessing states along the internal degrees of freedom of a photon as a substitute for or a supplement to a geometrical dimension creates a way of accessing advanced phenomena such as realizing photonic topological insulators (15), higher-order multipole moments (16), Anderson localization (17), higher-dimension quantum Hall effect (14), and photonic Weyl points (18).

Past realizations of photonic synthetic dimensions include orbital angular momentum, polarization, delay between pulses, and, in particular, frequency of light (19). In constructing a synthetic space, optical frequency is an attractive variable because it can be practicably partitioned into a lattice by using conveniently equidistant ring resonator modes and because of its relevance to important applications in frequency translation and spectral shaping of light. Very recently, the first experimental realization of a synthetic frequency dimension was demonstrated using a macroscale optical fiber loop (20), and later, a synthetic Hall ladder was realized by harnessing the direction of propagation within a ring as an additional dimension (21). However, to enable robust platforms for researching complex multidimensional effects and creating practical optical devices, it is vital to miniaturize and transfer photonic realizations of synthetic dimensions into a monolithically integrated format. Early efforts toward this goal involved modeling thin-film lithium niobate electro-optic frequency combs as a multidimensional tight-binding lattice (22). However, using a more scalable silicon photonic chip platform would provide a considerable advancement because, on one hand, it would allow photonics with synthetic dimensions to benefit from the mature and sophisticated complementary metal-oxide semiconductor (CMOS) commercial fabrication toolbox and, on the other, create the means for multidimensional topological phenomena to be introduced into innovative device applications.

We report the realization of a synthetic frequency dimension on a Si CMOS platform by using a custom dynamically modulated integrated ring resonator cavity design. By driving the resonator at its free-spectral range (FSR) rate of Ω_R = 20.4 GHz, a frequency lattice spanning a 280-GHz bandwidth was established, and sideband intensity enhancement was observed. The equidistant ring modes and periodic modulation of the cavity respectively represent lattice sites and their coupling mechanism and, hence, could be mapped to a one-dimensional (1D) tight-binding model. By detecting the time-resolved transmittance during modulation at the FSR rate, we were able to experimentally measure the band structure involving a synthetic frequency dimension in an integrated photonic device. Furthermore, we demonstrate an ability to engineer intersite couplings and induce nonreciprocity through photonic gauge potentials. By respectively using FSR-detuned modulation frequencies or multiple modulation signals, we were able to attain time-resolved demonstrations of band structures indicative of behaviors analogous to effective electric and magnetic field effects for photons.

We suggest that these CMOS process–fabricated ring resonator devices—supporting an extensive frequency dimension with versatile and reconfigurable coupling mechanisms, as well as two synthetic forces—can act as robust building blocks for scalable integrated circuits with nontrivial topology. The inherent perturbation resilience of integrated devices allows to greatly extend the complexity of multidimensional physical systems accessible for photonic simulation, pursued for answering fundamental questions in physics. In addition, the three orders of magnitude increase in synthetic dimension process rates, resulting from device miniaturization, represents a qualitative leap in the realization of innovative device prototypes toward, for example, efficient optical computing and quantum information processing.

RESULTS

Device design

Our approach to producing a lattice of coupled states along a synthetic frequency dimension involves the use of a ring resonator (20, 22). Provided the waveguiding medium comprising the cavity exhibits near-zero group velocity dispersion in the relevant spectral region, it supports a spectrally equidistant sequence of states inherently akin to a 1D lattice. Coupling between different states can be induced using appropriately selected perturbation mechanisms, which, for photonic devices, can be generalized as either extrinsic modulation, which is the approach chosen here, or self-induced nonlinear effects (19). Last, artificial electric and magnetic fields for shaping photon flow can be produced through modulation of the coupling constants between different states along a dimension, be it synthetic (20, 23) or conventional (24).

A schematic of our Si CMOS platform–compatible ring resonator equipped with an in-cavity phase modulator is provided in Fig. 1A. It was designed to have an approximately 20-GHz FSR that could be bridged with reasonable efficiency using electronic modulation at radio frequencies (RF), thereby ensuring coupling between adjacent modes. This necessitates a total cavity circumference of l ≈ 4.1 mm, which is a substantial reduction in form factor compared to previous demonstrations using 13.5-m-length optical fiber loops (20). Management of optical propagation losses is a key aspect of the device, as observation of frequency lattice effects is contingent on photon decay lifetime being maximized relative to the lattice hopping rate. To mitigate internal loss in the resonator, the majority of its passive optical path was established in a 3-μm-wide multimode, operating as quasi-single mode, waveguide. Single mode 400-nm-wide waveguides were nevertheless used where optical confinement was needed, such as for waveguide bends and input/output coupling sections. Cavity modulation was applied using a p-n doped rib waveguide phase shifter segment, which was limited to a 155-μm length to minimize losses. Optical input and output for the device was performed in the add/drop configuration in the weak coupling condition.

Fig. 1. Ring resonator design.

(A) Schematic of the custom modulator-equipped ring resonator cavity design for the implementation of a synthetic frequency dimension. (B) Detailed drop-port transmittance spectrum in the λ = 1550 nm region spanning a 12-FSR interval with an approximately 20.4-GHz mode spacing, highlighted in inset (C) survey spectrum of the device throughout the telecommunication C-band.

Cavity characterization

Ring resonators were fabricated by using commercial CMOS foundry services using a 200-mm-diameter silicon-on-insulator wafer process (device micrographs and design details are provided in note S1). Experimental transmittance spectra, plotted in Fig. 1B, revealed that ring resonators exhibited equidistant mode spacing of 20.4 GHz, close to the specified 20-GHz FSR value, and an approximately 10-dB extinction spectrum owing to the weak coupling regime. Furthermore, as depicted in Fig. 1C, the spectral distribution remained notably consistent throughout the telecommunication C-band wavelength region. Around the λ = 1550 nm wavelength region, the loaded cavity had a quality factor of Q = 42,000, which corresponds to a photon decay rate of 2γ = 4.5 GHz, with dissipation primarily attributable to insertion losses in the p-n modulator section.

For a ring resonator to operate as a lattice along a frequency dimension, a coupling mechanism for photons to translate between different modes has to be induced through an external time-dependent perturbation of the dielectric properties of the cavity at a rate equal to (or a fraction of) an optical round-trip period (14). The most straightforward way of achieving this involves dynamical modulation of the ring resonator at its FSR frequency. In practice, this means ensuring that modulation sidebands overlap with adjacent ring modes. Optical output spectrum in Fig. 2A illustrates an optimized case for our device, in which one of its resonances is pumped (spectral position is indicated by the red line) while the cavity is continuously driven by an FSR-matched Ω_R = 20.4 GHz RF signal.

Fig. 2. Modulated cavity response.

(A) Optical output spectrum of a ring cavity under on-resonance 10-dBm optical excitation and FSR-matched 20.4-GHz frequency and 20-dBm power RF modulation. Orange bars represent an effective 1D tight-binding model with a 1.46 loss/coupling strength ratio. (B) Dependence of sideband peak spectral power density on modulating RF power. (C) Overlapping modulation spectra as 15-dBm power RF signal is swept over the 0- to 40-GHz range. The dashed line illustrates the ring cavity transmittance spectral function. OSA, optical spectrum analyzer.

Modulated device spectra reveal that the mode m under external laser excitation couples to the first nearest FSR modes (m ± 1), but this coupling also cascades to modes further down the lattice (m ± 2, m ± 3 …). It is evident that cavity losses are sufficiently low for cascaded frequency conversion to generate comb lines at a notable distance from the pump laser wavelength. The Si ring resonator device proved capable of hosting a long synthetic frequency dimension of up to 14 coupled modes spanning a 280-GHz bandwidth, as can be seen in Fig. 2B. This span is primarily determined by in-cavity optical losses, whereas the bandwidth over which the innate waveguide dispersion allows for constructive interference needed for cascaded frequency conversion (25) is much larger than the approximately Δλ ≈ 1.5-nm lattice length, and hence is not a primary factor in determining modulated ring resonator response.

A direct demonstration of electrically induced coupling between adjacent modes is provided in Fig. 2C, where overlapping optical output spectra are plotted as modulation frequency is swept from 0 to 40 GHz in 1-GHz increments. As the modulation sidebands approach a 20.4-GHz FSR spacing, they become resonantly enhanced (26), and this increase of their spectral intensity follows the ring cavity transmittance function. Furthermore, the modulation enhancement response was notable at 2 × FSR 40.8 GHz and 3 × FSR 61.2 GHz RF frequencies, indicating that the electrical bandwidth of the p-n junction phase shifter segment is sufficiently high to enable up to the third-nearest-neighbor mode coupling.

Mapping to the 1D tight-binding model

Our device can be interpreted as a tight-binding lattice model, in which particles localized at specific sites can hop to neighboring ones at a certain rate. The model Hamiltonian, which simulates the behavior of our system in the presence of nearest- and next-nearest-neighbor hopping, is

$$H={\sum }_m{\mathrm{\epsilon }}_m{\widehat{b}}_m^{†}{\widehat{b}}_m-{\sum }_m(J_1{\widehat{b}}_m^{†}{\widehat{b}}_{m+1}+e^{i\mathrm{\varphi }}{J}_2 {\widehat{b}}_m^{†}{\widehat{b}}_{m+2}+H.c.)$$ (1)

where ${\widehat{b}}_m^{†}$ denotes a bosonic particle creation operator at a site indexed by an integer m, ε_m represents the position-dependent on-site potential, and J₁ and e^iϕJ₂ are the nearest- and next-nearest-neighbor hopping amplitudes. We allowed the next-nearest-neighbor hopping to take a complex value with phase ϕ, which will later allow us to tune the effective magnetic field present in the synthetic ladder. The position dependence of the on-site potential, ε_m, on the other hand, will allow us to introduce an effective electric field.

A realistic situation in a photonic system has to consider optical driving and continual energy leakage (14). These losses can be taken into consideration by way of a mode-dependent loss rate γ_m, and they are balanced by the continuous injection of monochromatic light at a rate f_m(t) = f_me^−iωt. It has been demonstrated that the cavity field expectation value ${\mathrm{\beta }}_m(t)\equiv \langle {\widehat{b}}_m(t)\rangle e^{-i\mathrm{\omega }t}$ evolves according to the equation of motion (27)

$$\begin{array}{cc}\hfill i\frac{\mathrm{\partial }}{\mathrm{\partial }t}{\mathrm{\beta }}_m=& ({\mathrm{\epsilon }}_m-\mathrm{\omega }) {\mathrm{\beta }}_m-J_1{\mathrm{\beta }}_{m+1}-J_1{\mathrm{\beta }}_{m-1}\hfill \\ & -e^{i\mathrm{\varphi }}{J}_2 {\mathrm{\beta }}_{m+2}-e^{-i\mathrm{\varphi }}{J}_2 {\mathrm{\beta }}_{m-2}-i{\mathrm{\gamma }}_m{\mathrm{\beta }}_m+f_m\hfill \end{array}$$ (2)

Assuming a steady state, Eq. 2 can adequately simulate the frequency synthetic dimension lattice in Fig. 2A, and the result corresponding to a γ/J₁ ≈ 1.46 loss to coupling strength ratio condition has been plotted against the experimental spectrum using orange bars. Deviations from symmetry in the experimentally measured optical output are attributable to influence of effective refractive index dispersion in the Si ring cavity.

One of the primary advantages of using the synthetic frequency dimension approach for lattice simulations is that, since intermode coupling is induced via an externally applied perturbation mechanism, various models can be realized with relative ease by altering the applied modulation pattern. Optical output spectra in Fig. 3 (A and B) show the steady-state response of the microring device under RF modulations of the form V(t) = V₀cos(Ωt) at frequencies Ω = 20.4 and 2Ω = 40.8 GHz, resonantly matched respectively one or two FSR spans. As illustrated in the inset sketches, these two cases correspond to different tight-binding lattice coupling configurations. Figure 3A relates to a basic nearest neighbor–coupled tight-binding model, whereas Fig. 3B shows the equivalent of a next nearest neighbor–coupled tight-binding model in which the available states are divided between two 1D sublattices (only one of which is optically pumped). This, in addition to the ability to tune the coupling strength by changing modulation voltage, provides marked versatility to synthetic dimension devices compared to geometrical space resonant cavity array counterparts, in which both coupling configuration and strength would be fixed during fabrication.

Fig. 3. Band structure measurements.

Optical output spectra of a microring device under on-resonance FSR-matched (A) 20.4-GHz frequency 12-dBm power and (B) 40.8-GHz frequency 20-dBm power RF modulation. Insets show sketches of corresponding tight-binding lattice models. Synthetic frequency dimension bands at different on-resonance modulation powers for (C) FSR 20.4 GHz and (D) 2 × FSR 40.8 GHz. Rightmost is the weak modulation case, and the mode coupling strength J_η (GHz) increases toward the left. Superimposed plots are the dispersion curve of 1D tight-binding model, ε_k = 2J_ηcoskΩ fits.

Band structure measurements

Experimentally measured band structures for the synthetic 1D tight-binding model with nearest-neighbor coupling at different modulation strength conditions are shown in Fig. 3C. They were acquired using the method pioneered by Dutt et al. (20) for macroscale fiber loop cavities (details of the measurement setup and procedure used are provided in note S2). Because modulated ring resonator modes spaced along the frequency axis comprise a direct space, its corresponding reciprocal quasi-momentum axis k is equivalent to time. Here, the Brillouin zone corresponds to a single T = 50 ps time scale optical round trip inside the ring resonator device. When modulation frequency Ω is matched to the FSR frequency Ω_R, RF oscillation period is likewise equal to the duration of the round trip in a ring cavity. Laser detuning Δω is equivalent to the energy axis, and here, it is scanned over a three-FSR range, revealing the same number of Floquet bands. The dispersion relation for a 1D tight-binding model in case of resonant modulation is given by the simple periodic function

$${\mathrm{\epsilon }}_k=2J_{\mathrm{\eta }}\text{cos}(k{\mathrm{\eta }\mathrm{\Omega }}_R)$$ (3)

where J_η is the mode coupling strength over distance η, k is the quasi-momentum, and Ω_R is the modulation frequency. Fits of this dependence are overlaid onto the experimental band structures in Fig. 3 and show good agreement. The nearest-neighbor mode coupling strength parameter derived from this fitting could be set from zero (flat bands) up to J₁ = 0.864 GHz when maximal 20-dBm RF power was used. While the value of J₁ was somewhat lower than the 2γ = 4.5 GHz loss rate in the modulator-equipped Si ring cavity, evidenced by considerable width of the Floquet bands and characterized by a γ/J₁ ≈ 2.6 loss to coupling strength ratio, it nevertheless permitted temporally resolved band structure observations.

In the case of a 1D tight-binding model with next-nearest adjacent mode coupling, dispersion relations, shown in Fig. 3D, exhibit two modulation periods within an optical round-trip delimited Brillouin zone. As this configuration requires the application of an RF signal at Ω = 40.8 GHz spanning over a 2 × FSR range, modulation efficiency was lower because of finite bandwidth of the device. However, at maximum RF power, 1D tight-binding dispersion relation fitting-derived coupling strength parameter was J₂ = 0.452 GHz and clearly resolvable in experiment. Similar measurements conducted using Ω = 61.2 GHz 3 × FSR modulation for J₃ were less conclusive because of experimental limitations and are outlined in note S3.

Demonstration of an effective electric field

To fully exploit the synthetic dimension in integrated optical systems, it is not sufficient to merely establish a coupled lattice model for photons. Another essential component is a way to control photon transport in given lattices. In condensed matter systems, this can be achieved by application of gauge potentials in the form of electric and magnetic fields. While photons do not couple to these fields, an equivalent behavior can be produced by engineering the on-site energy of each site and the hopping phase the particles accumulate as they translate over a sequence of lattice sites either in real or synthetic space (14). This principle can be leveraged to both induce and exert control over a variety of quantum walk phenomena in the optical domain (28–30).

A prominent example of an effective gauge potential in a synthetic dimension involves the induction of Bloch oscillations (31, 32). For a frequency lattice, it requires merely selecting the modulation frequency Ω to be slightly yet appreciably different from the resonant mode spacing Ω_R (all experimental data presented up to this point operated at the Ω = Ω_R condition). When modulation frequency is detuned by ΔΩ so that Ω = Ω_R – ΔΩ, keeping in mind the equivalence between k and t, Eq. 3 can be rewritten

$${\mathrm{\epsilon }}_k(t)=2J_1\text{cos}(k[{\mathrm{\Omega }}_{\mathrm{R}}-\mathrm{\Delta }\mathrm{\Omega }])=2J_1\text{cos}(k{\mathrm{\Omega }}_{\mathrm{R}}-\mathrm{\Delta }\mathrm{\Omega }·t)$$ (4)

This means that a ring resonator cavity modulated at a frequency shifted from an FSR value by a small magnitude is analogous to synthetic frequency dimension 1D tight-binding lattice under a constant force, as sketched in Fig. 4A. Its band structure, while still with a Brillouin zone set by one optical cavity round trip, drifts over time along the k axis at a rate proportional to the frequency detuning magnitude ΔΩ, as illustrated in Fig. 4B. In experimental practice, this means that the band structure acquisitions become dependent on laser wavelength scanning rate, and hence can be considered dynamic. Very recently, the first experimental demonstration of these dynamic acquisitions using a 10-m-circumference optical fiber loop setup was reported by Li et al. (23).

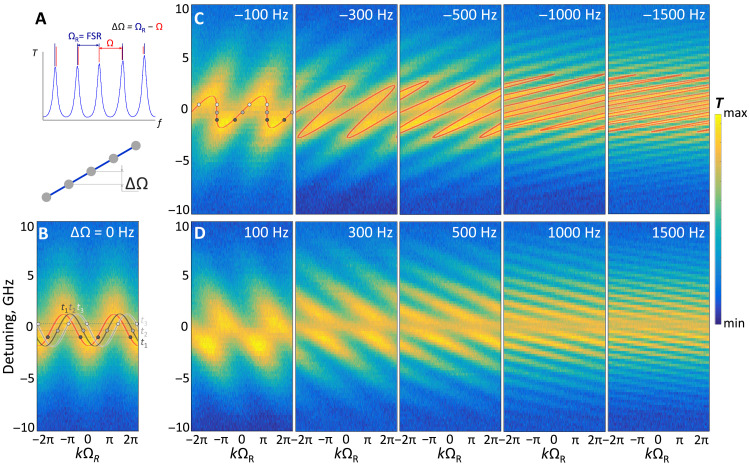
Fig. 4. Experimental measurement of dynamic band structures.

(A) Illustration of the relationship between ring resonator spectrum, resonant optical round-trip FSR frequency Ω_R, and the modulation frequency Ω, shifted from resonance by ΔΩ. Diagram below shows how this system relates to a 1D tight-binding model of a photon under an effective force. (B) Static on-resonance band structure, spanning over two Brillouin zones for clarity. When modulation is off-resonance, bands gradually shift over time along the k axis, so that transmittance acquisitions at different optical frequencies at times t₁, t₂, and t₃ generate a dynamic trajectory as plotted in the first panel of (C). Experimentally measured band structures with different (C) negative and (D) positive modulation frequency detuning from Ω_R = 20.4 GHz values. RF modulation power was P_RF = 13 dBm, which produced an estimated J₁ = 0.61 GHz coupling strength. Trajectories drawn in red are guides for the eye.

The dynamic band structures acquired on our integrated Si ring resonator under detuned modulation conditions are provided in Fig. 4 (C and D). Compared to the static case Ω = Ω_R in Fig. 4B, detuning introduces a time-dependent phase component proportional to frequency difference ΔΩ. It manifests as trajectories produced by the interplay of band structure drift along the quasi-momentum axis due to a constant synthetic force and the rate at which the energy axis is scanned. Furthermore, these trajectories become inverted along the k axis when modulation offset ΔΩ sign is reversed. At ΔΩ = ±100 Hz, corresponding to a situation where Ω and Ω_R frequencies are close enough that their beating rate is comparable to experimental time-resolved 2D transmittance spectral acquisition duration available in our setup, band structures merely appear distorted because of continuous drift. However, at ΔΩ = ±300 Hz and beyond, the drift becomes rapid enough for several Brillouin zone periods to be covered during a single acquisition and band splitting becomes apparent. While the fine structure of individual split bands is somewhat obscured by the considerable ring resonance linewidths in our device, simulated trajectories in Fig. 4C show a good match between experiment and theory. Therefore, this experiment exhibited all the key behaviors expected in a 1D tight-binding model lattice system under constant force.

Demonstration of an effective magnetic field

The photonic analog of a magnetic field has been proposed in real space, which leads to an optical analog of the quantum spin Hall effect without time-reversal symmetry breaking (6) and with temporal modulation by way of which this reciprocity is broken (24). Feasibility of engineering such an effective gauge potential in a synthetic frequency space has been shown by applying dual-tone modulation with controllable strength and relative phase (20). Realizing such a perturbation scheme in our integrated Si photonic device involves the simultaneous application of synchronized Ω_R = 20.4 GHz and 2Ω_R = 40.8 GHz frequency signals, resulting in a modulation voltage of the form V_m(t) = V_Ωcos(Ω_Rt + ϕ) + V_2Ωcos2Ω_Rt, where ϕ is a phase offset introduced using a tunable RF delay component.

As illustrated in the top inset of Fig. 5, this dual-tone modulation induces simultaneous nearest- and second-nearest-neighbor 1D tight-binding lattice couplings. This partitions the ring resonator modes into forming a quasi-2D triangular ladder lattice configuration with an alternating magnetic flux. An effective gauge potential effect can be observed through experimental band structures provided in Fig. 5, where a single FSR spectral span and one Brillouin zone are highlighted for clarity. Each of the depicted plots represents a different phase offset ϕ, and hence a different effective gauge potential. Conversely, the modulation powers of Ω_R = 20.4 GHz and 2Ω_R = 40.8 GHz RF signals where fixed to 12 and 20 dBm to partly compensate for diminishing device response toward higher frequencies. Dispersion relations for this synthetic dimension 1D tight-binding model coupling configuration can be modeled using the equation

$${\mathrm{\epsilon }}_k=2J_1\text{cos}(k{\mathrm{\Omega }}_R+\mathrm{\varphi })+2J_2\text{cos}(k2{\mathrm{\Omega }}_R)$$ (5)

where J₁ and J₂ are coupling strength parameters for adjacent and next-nearest modes, respectively. Fitting of Eq. 5 to the experimental data, depicted as solid curves overlaying color plots in Fig. 5, shows a robust agreement between model and measurement. On the basis of the fits, aforementioned RF modulation powers yield coupling strength values J₁ = 0.367 GHz and J₂ = 0.260 GHz, resulting in a J₂/J₁ ≈ 0.6 ratio.

Fig. 5. Experimental measurement of nonreciprocal band structures.

Band-structure engineering using nearest-neighbor coupling (20.4 GHz), long-range hopping (40.8 GHz), and a synthetic magnetic field (φ) when coupling strength ratio J₂/J₁ ≈ 0.6 is maintained constant. Variation of 20.4-GHz modulation phase delay φ induces gradual band structure changes. The phase delay increases from left to right. Superimposed blue and red plots are the Lorentzian center frequency and ε_k = 2J₂·cosk2Ω_R + 2J_1·cos(kΩ_R + φ) fits, respectively, and inset illustrates the applicable quasi-2D tight-binding model.

The key feature of the synthetic approach is the flexibility afforded to band structure engineering through control of both coupling strength and gauge potential ϕ. We observed that when ϕ ≠ 0, π, the band structure is no longer symmetric about k = 0. This asymmetric band structure is a clear signature of time-reversal symmetry breaking (14, 20). As the relative phase approaches ϕ ≈ π, this nonreciprocity is removed, and the band structure becomes equivalent to the ϕ ≈ 0 case with a π Brillouin zone shift. The system ultimately returns to its initial state at ϕ = 2π. We thereby demonstrate how full control over a magnetic field analogous gauge potential can be achieved in an integrated Si photonic device.

DISCUSSION

We presented and experimentally characterized the first realization of an integrated synthetic frequency dimension device on a Si CMOS platform. The ring resonator, equipped with an in-cavity phase shifter, exhibited an Ω_R = 20.4 GHz FSR and was capable of supporting a 1D tight-binding model–equivalent lattice of up to 14 coupled states spanning a 280-GHz bandwidth. Further confirmation of this model’s applicability was made by way of time-resolved band structure acquisitions. In addition, two types of photonic gauge potentials, namely, equivalents of electric and magnetic forces, have been demonstrated on our Si device platform through their effects on the aforementioned band structures. This work opens the path to harnessing the mature and highly scalable silicon integrated photonics fabrication infrastructure to tackle pressing challenges in quantum simulation and topology science. The high integration density attainable on the Si CMOS platform is poised to greatly increase the level of complexity of lattice models that can be realized on a chip, and to even pursue applications for designing optical devices such as isolators (14), or enacting arbitrary linear transformations of photon frequencies (33) by using integrated cavities analogous to the one presented here as a foundational building block.

Despite a long list of advantages, which includes high integration density, low cost, and a leading level of standardization, the most notable challenge of using a silicon device platform is optical loss that limits the range of observable emergent lattice phenomena through photon decay. The monolithically integrated device presented here has losses that are among the lowest achievable for a contemporary CMOS process with wide quasi–single mode waveguides exhibiting transmittance similar to those achieved using etchless fabrication approaches (34). However, some further optimization is possible with respect to phase shifter design, for instance, by harnessing silicon-polymer hybrid modulator technology (35). Recent advances in hybrid-integrated semiconductor optical amplifier components show remarkable promise as a method for compensating in-cavity losses (36). Furthermore, optical gain would enable the investigation of non-Hermitian topology in both real and synthetic dimensions (37) and greatly expand the wealth of accessible physical phenomena. Some restrictions on the attainable lattice models are also due to limited bandwidth of available measurement equipment, with up to approximately 65-GHz frequency signal generators and photodetectors capable of inducing up to third or fourth-adjacent neighbor coupling between resonant modes for rings with practical FSRs.

Promising avenues for further investigation include the creation of more complex integrated device lattice models in the synthetic frequency dimension, such as a Su-Schrieffer-Heeger configuration (16), or creating an effectively 2D tight-binding lattice in a modulated 1D array of rings (14). Harnessing gauge potentials in the frequency dimension is particularly promising, as it would pave the way for the creation of previously unattainable frequency converters (32). Conversely, development of the synthetic dimension framework will be fruitful for further understanding of cascaded photonic phenomena, such as for rapid yet comprehensive characterization of optical frequency comb signals (38). The inherent flexibility and reconfigurability of the synthetic dimension approach makes it complementary with analogous static lattices in real space and is expected to enable innovative devices that circumvent the 2D constraints imposed by planar integrated photonics and that could model phenomena beyond three dimensions.

MATERIALS AND METHODS

Steady-state characterization

Transmittance spectra were acquired using a telecom wavelength Santec TSL-550 excitation laser source with up to 12-dBm power output, and an Advantest Q8221 optical multipower meter was used for drop-port output detection. Light was coupled into and out of the silicon-on-insulator device edge coupler mode converters via lensed fibers. Optical spectra under RF modulation were detected using an Advantest Q8384 optical spectrum analyzer. RF driving of ring resonator devices was done using continuous wave sinusoidal signals with frequencies from 1 to 61.2 GHz and output powers ranging from −20 to 20 dBm, supplied by a Rohde & Schwarz SMA100B generator. The maximum optical excitation and RF modulation powers that can be applied are limited respectively to 10 and 20 dBm by the onsets of nonlinear responses, which manifest as spectral distortions because of excessive cavity heating. Electronic interfacing with the modulator metal contact pads on the integrated device was conducted using a G-S-G 3-point RF probe.

Band structure measurements

Since the reciprocal space of a synthetic frequency dimension corresponds to time, measurement of dispersion relationships of such a system involves temporally resolved acquisitions of optical power in the ring cavity. This was done by monitoring the device drop-port output using an Agilent Infinium DCA-J 86100C oscilloscope with an up to 50-GHz RF detector module. Before that, optical-to-electronic signal conversion was performed using an Anritsu MN4765B optical receiver module with an up to 65-GHz bandwidth. Optical excitation laser was a Santec TSL-550 device operating at a 10-dBm power and wavelength in the vicinity of λ = 1550 nm. Device output signal strength attainable for the carrier frequency was around −15 dBm, and the first sidebands were −9 dB below that. Therefore, the optical signal was amplified using a low-noise Alnair Labs LNA-220-C erbium-doped fiber amplifier, which supplied up to 20 dB of amplification, and an Alnair Labs CVF-220CL tunable band-pass filter (BPF) to suppress the amplified spontaneous emission noise. The BPF that was set to a moderately broad Δλ_BPF = 2 nm pass band to allow scanning of the probing laser over a several-FSR wavelength range without sideband clipping. The electronic portion of the setup is composed of a set of RF generators phase locked using their internal 10-MHz clocks. In the basic 1D tight-binding model case, a Rohde & Schwarz SMA100B RF source was used for driving the ring resonator device, and a lower-frequency Anritsu MG3692B generator supplied an Ω_R/10 trigger to the oscilloscope. More complex simultaneous nearest- and next-nearest mode coupling configurations were induced by using additional phase-locked HP 83640B RF generators, and their outputs were combined using a Midwest Microwave MFR 34078 up to 40-GHz bandwidth 3-dB power splitter/directional coupler. Relative phase of FSR and 2 × FSR modulation waveforms could be adjusted using a PE8253 controllable delay element connected to the 20.4-GHz frequency input branch. The measurement proceeded by automatically scanning the input laser wavelength in Δλ = 5-pm increments and acquiring time-resolved transmittance output oscilloscope traces over a set optical frequency detuning range. All of these traces are collected and arranged in sequence to compile a 2D transmittance plot, directly related to the synthetic frequency dimension band structure of the system. A schematic and additional explanations of the measurement setup and procedure are provided in note S2.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S6

Table S1