Distortion-Free Diffusion Imaging Using Self-Navigated Cartesian Echo-Planar Time Resolved Acquisition and Joint Magnitude and Phase Constrained Reconstruction

Abstract

Echo-planar time resolved imaging (EPTI) is an effective approach for acquiring high-quality distortion-free images with a multi-shot EPI (ms-EPI) readout. As with traditional ms-EPI acquisitions, inter-shot phase variations present a main challenge when incorporating EPTI into a diffusion-prepared pulse sequence. The aim of this study is to develop a self-navigated Cartesian EPTI-based (scEPTI) acquisition together with a magnitude and phase constrained reconstruction for distortion-free diffusion imaging. A self-navigated Cartesian EPTI-based diffusion-prepared pulse sequence is designed. The different phase components in EPTI diffusion signal are analyzed and an approach to synthesize a fully phase-matched navigator for the inter-shot phase correction is demonstrated. Lastly, EPTI contains richer magnitude and phase information than conventional ms-EPI, such as the magnitude and phase correlation along the temporal dimension. The potential of these magnitude and phase correlations to enhance the reconstruction is explored. The reconstruction results with and without phase matching and with and without phase or magnitude constraints are compared. Compared with reconstruction without phase matching, the proposed phase matching method can improve the accuracy of inter-shot phase correction and reduce signal corruption in the final diffusion images. Magnitude constraints further improve image quality by suppressing the background noise and thereby increasing SNR, while phase constraints can mitigate possible image blurring from adding magnitude constraints. The high-quality distortion-free diffusion images and simultaneous diffusion-relaxometry imaging capacity provided by the proposed EPTI design represent a highly valuable tool for both clinical and neuroscientific assessments of tissue microstructure.

I. Introduction

DIFFUSION MRI (dMRI) is an important imaging tool for neuroscience studies that enables fiber tracking and tissue microstructure assessments [1], [2]. Currently, single-shot EPI (ss-EPI) is the most widely used sequence for diffusion imaging, which is fast and insensitive to motion [3]. Unfortunately, ss-EPI has a relatively low sampling bandwidth along the phase-encoding (PE) direction and long echo train, which makes it prone to B0 inhomogeneity induced image deformation and ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ decay induced blurring. Parallel imaging (PI) [4], [5] can be used to partially alleviate these problems, but the ability of PI is limited by the extra SNR loss and potential aliasing artifacts at high reduction factors.

Multi-shot EPI (ms-EPI) is another strategy to mitigate the distortion and blurring problem [6]-[11]. Multi-shot EPI divides the full k-space acquisition into several shots/segments, thus increasing the effective sampling bandwidth and reducing the total echo train length in each shot/segment. The increased sampling bandwidth will reduce the image distortion, while a shorter echo train can alleviate the image blurring. However, ms-EPI has a number of challenges associated with it. First, multi-shot EPI can only reduce the image distortion and blurring (depending on the number of shots) but not fully remove them. Second, under the presence of strong diffusion gradients, physiological motion (such as cerebrospinal fluid (CSF) pulsation) can cause severe phase variations among different shots. Such phase variations must be corrected before combining different shots, otherwise severe artifacts will appear in the final image [6]-[11]. Lastly, ms-EPI lengthens the scan time because of the need for multiple acquisitions.

Recently, there has been a growing interest in developing distortion-free EPI acquisitions. An underlying principle of the distortion-free EPI technique is that if all k_y lines can be acquired at the same echo time (TE), the B₀ inhomogeneity will induce the same phase across all k_y lines and thus there will be no distortion. The initial implementation of this assumption is termed echo-planar spectroscopic imaging (EPSI) [12]. In EPSI, only one k_y line is acquired in each acquisition at a certain TE and the acquisition is repeated N_y times to accomplish a fully sampled k-space, where N_y is the number of k_y lines. Although initially proposed for spectroscopic imaging, theoretically EPSI is feasible for structural imaging, i.e., individual images with different ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ contrast can be reconstructed from the EPSI acquisition. However, EPSI is not commonly adopted as a technique for distortion-free structural imaging, mainly due to the prohibitively long scan time, i.e., a typical MR image contains >100 k_y lines and therefore a fully sampled EPSI would prolong the scan time by >100 times compared to ss-EPI.

Another strategy similar to EPSI is the point spread function encoded EPI (PSF-EPI) [13], [14]. In PSF-EPI, the acquisition resembles conventional 3D EPI but replaces the k_z encoding with a second k_y encoding, termed “PSF encoding”. After an inverse Fourier transform of the PSF-EPI 3D k-space (k_x-k_y-k_psf), the PSF of each voxel can be estimated. Then if the 3D image is projected to x-psf plane, a distortion-free image will be generated. However, like EPSI, fully sampled PSF-EPI requires lengthy scan time compared with ss-EPI.

Numerous efforts have been made to effectively accelerate EPSI and PSF-EPI. In PSF-EPI, many existing optimized under-sampling strategies for conventional 3D acquisition can be directly extended to PSF-EPI, such as the reduced FOV and controlled aliasing in parallel imaging (CAIPI) techniques [13], [14]. An effective method to accelerate EPSI is echo-planar time resolved imaging (EPTI) [15]-[18]. Different from PSF-EPI, in EPSI/EPTI, the acquired data are handled in k_x-k_y-t space, in which optimized sampling trajectories, such as spatiotemporal CAIPI [15], [18]-[20] can be used. There also exists rich data correlations in EPTI that can facilitate high acceleration. For example, theoretically the magnitude images of EPTI at different TEs follow a mixed T₂ and ${\mathrm{T}}_2^{\ast }$ relaxation. Such magnitude correlations can be jointly used with the coil sensitivity map to achieve high acceleration factors in EPSI [19], [20] or EPTI [15]-[18], [21].

As with other multi-shot EPI acquisitions, inter-shot phase variations represent a main challenge when incorporating PSF-EPI and/or EPTI into diffusion imaging. In conventional multi-shot diffusion imaging, the inter-shot phase variation can be recorded with an internal or external navigator and then corrected with specific algorithms [6]-[11]. Similar methods can be extended to PSF-EPI and EPTI. In PSF-EPI, each shot traverses the k-space center, so the central k-space of each shot can be extracted as an internal navigator (i.e., PSF-EPI is self-navigated) [13], [14]. However, the initial implementation of EPTI (Fig. 1a) [15] is not self-navigated, since not all the shots traverse the center of k-space, which will require an external navigator and thus decrease the acquisition efficiency. A previous study has shown that non-Cartesian PROPELLER sampling [22] can be combined with EPTI (termed “PEPTIDE”) to enable the self-navigating capacity while not decrease the acquisition efficiency, providing motion-robust distortion-free diffusion and relaxometry imaging [16], [17].

Fig. 1.

Data sampling trajectories (shown in k_y-t domain) of (a) the initial EPTI, (b) the self-navigated Cartesian-based EPTI (scEPTI) and (c) the fully sampled time resolved calibration scan. In (b), the sampling during the rewinding gradient is denoted with blue dashed lines. R_pe, R_shot and different TEs (TE_sh1, TE_sh2 and TE_sh3) are schematically defined in (b). Note that the values of R_pe and R_shot here are only for conceptual demonstrations.

The inter-shot phase correction procedure of EPTI is similar to but might be more complex than conventional ms-EPI. EPTI diffusion signal contains more phase components (coil sensitivity, B₀ inhomogeneity induced phase, motion induced phase during diffusion encoding), thus requiring delicate processing to ensure a fully phase-matched navigator before correction. Moreover, as described above, EPTI contains rich magnitude and phase correlations. These correlations might be used as new priors to improve the reconstruction efficacy of EPTI-based diffusion imaging.

In this study, we aim to propose a new EPTI acquisition and reconstruction strategy for distortion-free diffusion imaging. Different from the non-Cartesian PROPELLER sampling in the reported PEPTIDE technique, we develop a self-navigated Cartesian EPTI-based diffusion acquisition sequence, termed scEPTI. Then we develop a phase matched navigator synthesization approach to improve the accuracy of the inter-shot phase correction. Finally, we explore the extensive spatiotemporal magnitude and phase correlations in the scEPTI acquisition to boost the signal-to-noise ratio (SNR) and contrast-to-noise ratio (CNR) of the final diffusion images. The reconstruction results with and without phase matching and with and without phase or magnitude constraints are compared to demonstrate the efficacy of the proposed scEPTI acquisition and reconstruction method.

II. Theory

In this section, we will first introduce our newly proposed scEPTI-based diffusion acquisition sequence. Then we will review phase matching in multi-shot diffusion reconstruction and illustrate how to implement it in the proposed scEPTI-based diffusion imaging. Finally, we will introduce the magnitude and phase correlations in EPTI-based diffusion imaging and how to exploit them in the reconstruction.

A. Self-Navigated Cartesian EPTI-Based Diffusion Acquisition Sequence

The sampling trajectories of the initial EPTI and the newly designed scEPTI are shown in Fig. 1a and 1b, respectively. The sequence diagram of the new scEPTI is displayed in Supplementary Fig. s1.

The self-navigated EPTI is implemented by introducing a rewinding gradient when k_y reaches k_y,max (Supplementary Fig. s1). With the rewinding gradient, the sampling trajectory will be reversed back to −k_y,max and then move towards k_y,max again until the end of the readout. There are two highlights of scEPTI (Fig. 1b). First, the TEs of different shots (marked in Fig. 1b) locate at different time points and do not change linearly with shot indices. Second, the sampling during the rewinding gradient does not lie on a single k_y line as the conventional EPI readout. In this study, we simply discard the sampling points during the rewinding gradient and denote them with hollow circles in Fig. 1b.

Two under-sampling factors are defined in scEPTI (Fig. 1b): R_pe is the k_y step in each shot to adjust the sampling locations and R_shot is the step of the starting k_y location between two shots for acceleration. Fig. 1b shows an example with R_pe = 1, R_shot = 4, 3 shots in total (N_shot = 3), no partial Fourier (PF) in k_y or t dimension (PF_pe = 1, PF_shot = 1).

B. Review of Phase Matching in Joint Multi-Shot Diffusion Reconstruction

In diffusion imaging, the k-space signal can be modeled as:

$$\begin{gathered} d_{\text{diff},i,j}({\mathbf{k}}_i) \\ ={\int }_{\mathbb{R}}^2{\rho }_{\text{diff}}(\mathbf{r})E_{\text{diff},i}(\mathbf{r})E_{{\mathrm{B}}_0}(\mathbf{r})\times s_j(\mathbf{r})e^{-\mathbb{i}2\pi {\mathbf{k}}_i^T\mathbf{r}}d\mathbf{r}, \end{gathered}$$ (1)

where d_{diff,i, j} is the diffusion k-space data of shot i and coil j, ρ_diff is the diffusion magnitude, E_diff,i is the exponential of physiological motion induced phase φ_diff,i in shot i, e.g., ${\mathrm{E}}_{\text{diff},i}=e^{\mathbb{i}{\phi }_{\text{diff},i}}$, s_j is the sensitivity map of coil j, E_B0 is the exponential of B₀ inhomogeneity induced phase φ_B0, $\mathbf{r}\in {\mathbb{R}}^2$ is the image space, k_i is the sampled k-space in shot i, ${\mathbf{k}}_i^T$ is the transpose of k_i, i ∈ [1, N_shot] and j ∈ [1, N_ch] are the indices for shot and coil, respectively. In this study, unless otherwise specified, we use both E and φ to represent the same phase term indiscriminately. E is mainly used in the equation derivations, while φ is used in phase map related descriptions.

The calibration scan is a non-diffusion-encoded acquisition (“b = 0 scan”), which can be formulated as

$$d_{\mathrm{b}0,j}(\mathbf{k})={\int }_{\mathbb{R}}^2{\rho }_{\mathrm{b}0}(\mathbf{r})E_{{\mathrm{B}}_0}(\mathbf{r})s_j(\mathbf{r})e^{-\mathbb{i}2\pi {\mathbf{k}}^T\mathbf{r}}d\mathbf{r},$$ (2)

where d_b0,j is the b = 0 k-space data at coil j and ρ_b0 is b = 0 magnitude. In this study “b = 0” and “b0” represent the image without diffusion encoding, whereas “B₀” means the main magnetic field. Other symbols have the same meaning as in (1).

From (1) and (2), we can see that there is an extra phase E_diff,i in the diffusion signal, compared with the calibration data. This is not problematic when using the conventional PI reconstruction, since we can take ρ_diff (r) E_diff,i (r) as a whole. However, such a phase difference can be problematic in reconstruction that utilizes phase priors, such as the joint multi-shot diffusion reconstruction [6]-[11].

In multi-shot diffusion imaging, a joint reconstruction is commonly used to recover the missing data in each shot [6]-[11], i.e., when reconstructing a certain shot, the sampled data from other shots will also be used. The joint reconstruction requires that both the coil sensitivity s_j and inter-shot phase variation φ_diff,i to be known, since φ_diff,i varies across different shots. However, φ_diff,i is missing in the calibration data in (2), which prohibits the joint reconstruction of all the shots.

Phase matching can be an effective way to overcome the phase discrepancy in multi-shot diffusion reconstruction. Specifically, in multi-shot diffusion imaging, a navigator is either acquired with an extra scan or recovered from each under-sampled shot, which comprises of both φ_diff,i and s_j [6]-[11]. For example, in multiplexed sensitivity-encoding (MUSE) [8], each shot is first roughly reconstructed using conventional PI (only requires s_j), and then a phase matched navigator is synthesized by extracting the phase of the roughly recovered shot, which comprise both φ_diff,i and s_j. Subsequently, a joint multi-shot reconstruction can be performed.

C. Phase Matching in EPTI-Based Diffusion Imaging

From the sampling trajectory of scEPTI (Fig. 1b), it can be seen that each shot in the new EPTI is equivalent to a traditionally under-sampled EPI. After a conventional PI reconstruction, the central k-space (the grey region in Fig. 1b) of each shot can be extracted and then used as navigator, which contains the physiological motion induced phase φ_diff, the coil sensitivity s and the B₀ inhomogeneity induced phase φ_B0. Now we rewrite the diffusion model (1) for a single voxel in the image domain of the “diffusion navigator”,

$$c_{\text{nav}\_\text{diff},i,j}={\rho }_{\text{nav}\_\text{diff},i}{E}_{\text{nav}\_\text{diff},i}{E}_{{\mathrm{B}}_0,i}{s}_j.$$ (3)

where c_{nav_diff,i,j} is the complex diffusion navigator image of shot i and coil j, ρ_{nav_diff,i} is the magnitude of the diffusion navigator in shot i, E_{nav_diff,i} (i.e., φ_{nav_diff,i}) is the motion induced phase in shot i, s_j is the sensitivity map of coil j, E_B0,i (i.e., φ_B0,i) is the B₀ inhomogeneity induced phase in shot i.

As mentioned in II.A, the TE of each shot in scEPTI is different, so ρ_{nav_diff,i} and φ_B0,i also vary in different shots. An example of the diffusion navigator magnitude image is shown in Fig. 2a, with TE marked on the top of each column. TE of the 3^rd shot is the TE of spin echo (TE_SE). The example navigator images are taken from Experiment 2 (4 out of 8 shots are shown), in which PF is used, so TE_SE is not in the central shot.

Fig. 2.

Magnitude images of the (a) diffusion and (b) b = 0 navigators from different shots in Experiment 2 (4 out of 8 shots are shown). (c) B₀ inhomogeneity induced phase map (φ_B0). (d) Motion induced phase map during diffusion encoding (φ_diff). The TE of the spin echo (TE_SE) is not located in the central shot (shot 4 or 5) but in shot 3 due to the using of partial fourier.

The corresponding navigator image without diffusion encoding (“b = 0 navigator”) c_{nav_b0,i,j} only contains s_j and φ_B0,i:

$$c_{\text{nav}\_\mathrm{b}0,i,j}={\rho }_{\text{nav}\_\mathrm{b}0,i}{E}_{{\mathrm{B}}_0,i}{s}_j,$$ (4)

where ρ_{nav_b0,i} is the b = 0 magnitude image of shot i and other symbols have the same meaning as in (3). The example b = 0 navigator magnitude images are shown in Fig. 2b. Different ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ relaxation effects are exhibited in both the b = 0 and diffusion navigators, with the magnitude images displaying different intensity and contrasts.

From (3) and (4), the motion induced phase φ_diff,i in each shot can be extracted from the b = 0 and diffusion navigator:

1. Calculate the magnitude image of the b = 0 and diffusion navigator in each shot, i.e., ρ_{nav_b0,i} and ρ_{nav_diff,i}, using root sum-of-square (rSoS):

   $${\rho }_{\text{nav}\_\mathrm{b}0,i}=\sqrt{{\sum }_{j=1}^{N_{\text{ch}}}\mid c_{\text{nav}\_\mathrm{b}0,i,j}{\mid }^2},$$ (5)

   $${\rho }_{\text{nav}\_\text{diff},i}=\sqrt{{\sum }_{j=1}^{N_{\text{ch}}}\mid c_{\text{nav}\_\text{diff},i,j}{\mid }^2}.$$ (6)
2. Estimate the combination of the coil sensitivity s_j and the B₀ inhomogeneity induced phase φ_B0,i, from the b = 0 navigator:

   $$s_j{E}_{{\mathrm{B}}_0,i}=c_{\text{nav}\_\mathrm{b}0,i,j}∕{\rho }_{\text{nav}\_\mathrm{b}0,i}.$$ (7)
3. Calculate the complex image of the diffusion navigator in each shot, i.e., the combination of the magnitude image ρ_{nav_diff,i} and motion induced phase φ_{nav_diff,i}:

   $$\begin{gathered} {\rho }_{\text{nav}\_\text{diff},i}{E}_{\text{nav}\_\text{diff},i} \\ ={\sum }_{j=1}^{N_{\text{ch}}}\left(c_{\text{nav}\_\text{diff},i,j}(s_j{E}_{{\mathrm{B}}_0,i}{)}^{\ast }\right)∕{\sum }_{j=1}^{N_{\text{ch}}}\left((s_j{E}_{{\mathrm{B}}_0,i})(s_j{E}_{{\mathrm{B}}_0,i}{)}^{\ast }\right), \end{gathered}$$ (8)

   where * is the conjugate operation.
4. Based on (6) and (8), the inter-shot phase variation φ_diff,i can be estimated by dividing the complex image of each shot over its magnitude:

   $$E_{\text{diff},i}=E_{\text{nav}\_\text{diff},i}=({\rho }_{\text{nav}\_\text{diff},i}{E}_{\text{nav}\_\text{diff},i})∕{\rho }_{\text{nav}\_\text{diff},i}.$$ (9)

An example of φ_B0,i and φ_diff,i is shown in Fig. 2c and 2d, respectively. First, it can be seen that the overall variation range of φ_diff,i is larger than φ_B0,i. Second, the local changes of φ_B0,i can be more severe than φ_diff,i, especially in regions with strong susceptibility changes, e.g., the frontal lobe (yellow arrows in the 4^th column).

To recover the full k-space of EPTI (k_x-k_y-t), in addition to the inter-shot phase φ_diff and coil sensitivity s, we also need to estimate the B₀ inhomogeneity induced phases ${\widehat{\phi }}_{{\mathrm{B}}_0}$ at each TE. This is achieved by acquiring an extra low-resolution (along PE direction) time-resolved calibration data, as shown in Fig. 1c, which is a fully sampled EPTI scan, compared to Fig. 1b. No diffusion encoding is added in the calibration scan (“b = 0”). The calibration scan contains the coil sensitivity information s and B₀ inhomogeneity induced phase ${\widehat{\phi }}_{{\mathrm{B}}_0}$ at each TE.

$${\widehat{c}}_{\text{calib}\_\mathrm{b}0,j,k}={\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}{s}_j{\widehat{E}}_{{\mathrm{B}}_0,k},$$ (10)

where ${\widehat{c}}_{\text{calib}\_\mathrm{b}0}$ is the complex b = 0 calibration image, ${\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}$ is the b = 0 image magnitude with all k_y lines at the k^th TE (TE_k), ${\widehat{E}}_{{\mathrm{B}}_0,k}$ is the exponential of B₀ inhomogeneity induced phase at the TE_k, k ∈ [1, N_echo] is the index for echo/TE and other symbols have the same meaning as in (4).

Note that ${\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}$ here differs from ρ_{nav_b0,i} in (4): in ${\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}$, all the k_y lines are acquired at the same TE_k (k is the index for echo/TE and we use “∧” to indicate the TE dependence) and have the same ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ relaxation, whereas ρ_{nav_b0,i} is acquired using traditional EPI (i is the index for shot) and the TE of the central k_y line decides the image contrast. The same difference also exists between ${\widehat{E}}_{{\mathrm{B}}_0,k}$ (i.e., ${\widehat{\phi }}_{{\mathrm{B}}_0,k}$) and E_B0,i (i.e., φ_B0,i), ${\widehat{c}}_{\text{calib}\_\mathrm{b}0,k}$ and c_{nav_b0,i}.

The final “time resolved diffusion calibration data” is synthesized by combining the b = 0 calibration data in (10) with the extracted inter-shot phase maps in (9), namely

$$\begin{gathered} c_{\text{calib}\_\text{diff},i,j,k}=c_{\text{calib}\_\mathrm{b}0,j,k}{E}_{\text{diff},i} \\ ={\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}{s}_j{\widehat{E}}_{{\mathrm{B}}_0,k}{E}_{\text{diff},i}. \end{gathered}$$ (11)

The final diffusion calibration data contains the inter-shot phase variation φ_diff (dependent on the shot index i), sensitivity maps s (dependent on the coil index j) and B₀ inhomogeneity induced phase ${\widehat{\phi }}_{{\mathrm{B}}_0,k}$ (dependent on the TE index k), which is fully matched with the to-be-recovered diffusion EPTI data.

D. Magnitude and Phase Correlation in EPTI-Based Diffusion Imaging

The B₀ inhomogeneity induced phase ${\widehat{\phi }}_{{\mathrm{B}}_0,k}$ in EPTI is linearly proportional to ΔB₀ and ΔTE, where ΔB₀ is the B₀ inhomogeneity and ΔTE is the time difference between a specific TE and TE_SE. TE_SE is a critical point in EPTI. At TE_SE, the spin is fully refocused such that there is no B₀ inhomogeneity induced phase (${\widehat{\phi }}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}=0$). Meanwhile, the magnitude at TE_SE is only affected by T₂ decay (no ${\mathrm{T}}_2^{\ast }$ decay). Before TE_SE, the magnitude follows $1∕T_2-1∕T_2^{\prime }$ decay, while after TE_SE, the magnitude follows $1∕T_2+1∕T_2^{\prime }$ decay, where $1∕T_2^{\prime }=\gamma \Delta {\mathrm{B}}_0$ is the relaxation contribution from ΔB₀ across a voxel and γ is the gyro-magnetic ratio. Quantitative T₂ and ${\mathrm{T}}_2^{\ast }(1∕T_2^{\ast }=1∕T_2+1∕T_2^{\prime })$ maps can be derived by combining the fitting results before and after TE_SE. More details can be found in the initial EPTI paper [15].

In addition to phase information, magnitude represents another important information in diffusion imaging. For example, in a diffusion scan with multiple diffusion encoding directions, the magnitude images from different diffusion encoding directions can be used as a prior to enhance the efficacy of reconstruction, such as PI with sparsity [23], low rank models [9], [24]-[26] and joint reconstruction [10], [27].

In EPTI-based diffusion imaging, the magnitude correlation exists not only among different diffusion encoding directions but also along the temporal dimension (different TEs). Theoretically, the EPTI image magnitude at different TEs follow a mixed T₂ and ${\mathrm{T}}_2^{\ast }$ decay ($1∕T_2-1∕T_2^{\prime }$ or $1∕T_2+1∕T_2^{\prime }$). This relaxometry correlation can be used as a new prior during reconstruction. For example, in conventional EPTI for non-diffusion-encoded imaging, a subspace-based method has been proposed to boost the EPTI reconstruction with magnitude constraints [18], [21]. In this study, we will explore the local low rank (LLR) character of the EPTI magnitude image along the temporal dimension for reconstruction improvement.

In Fig. 3, we graphically illustrate the temporal correlation of the EPTI magnitude and phase with a fully sampled EPTI data. The magnitude and phase images (${\widehat{\phi }}_{{\mathrm{B}}_0}$) from five different TEs are displayed in Fig. 3a and 3b, respectively, with TEs marked on the top. The coil sensitivity maps are estimated from image at TE_SE (third column in Fig. 3).

Fig. 3.

Graphical illustration of the magnitude and phase correlation in EPTI images. Example data are from a fully sampled b = 0 EPTI data with N_echo = 55 and no partial Fourier. (a) The magnitude images and (b) phase maps at 5 representative TEs, with TE₂₈ = TE_SE. (c) The spatial-temporal matrix constructed from magnitude images at different TEs. (d) The evolution curves of singular values at three representative voxels after singular value decomposition (SVD). (e) the unwrapped phase evolution curves for three representative voxels. Strong local low rank (LLR) and phase linearity are observed in the brain parenchyma (voxel 1 and 2) but are absent in the background (voxel 3). In (e), the calibration data centered around TESE (between the dotted lines) will be extracted to estimate the GRAPPA weighting matrix.

As shown in Fig. 3b, at TE_SE, the spin is fully refocused such that ${\widehat{\phi }}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}$ equals 0. If we calculate the phase map from the b = 0 image at TE_SE, the phase only comes from the coil sensitivity. Compared with TE_SE, at other TEs, the influence of the B₀ inhomogeneity becomes more severe on both the magnitude and phase. For example, in the 1^st and 5^th columns in Fig. 3, the strong ${\mathrm{T}}_2^{\ast }$ decay severely degrades the SNR or even causes signal dropout (voxel 1 in Fig. 3a).

To validate the temporal correlation of the magnitude image, we construct a spatial-temporal matrix (Fig. 3c) centered at two example voxels (voxel 1 and 2), as described in [9]. Each column in the matrix represents a local region-of-interest (ROI) centered at voxel 1 or 2, with a predefined block size (10 × 10). The row represents different TEs. Then singular value decomposition (SVD) is carried out and singular values are plotted in Fig. 3d. As shown in Fig. 3d, the singular values in the brain parenchyma (voxel 1 and 2) drop quickly to zeros, indicating strong low-rank property. As a comparison, the same operation is conducted on a background voxel (voxel 3), the singular value decay rate of which is much lower than voxel 1 and 2 (Fig. 3d).

The phase variations of the three voxels are shown in Fig. 3e. The phases of both voxels 1 and 2 vary linearly with TE, except for TEs that are distant from TESE. The slope of voxel 1 is sharper than voxel 2, indicating a more severe B₀ inhomogeneity at voxel 1, which can also be observed from the more severe signal dropout in the magnitude image of voxel 1 in the first and last column. As expected, no strong phase correlation is observed in the background signal (voxel 3).

III. Methods

A. Data Acquisition

In vivo human brain data of four volunteers (4 M, ages 24-30 y/o, with no known neurological conditions) were acquired on a GE 3.0 T Premier MRI scanner (GE Healthcare, Madison, WI), using a 48-channel head coil. One subject was scanned twice (Experiment 1 and 3). All human studies were performed under our local institutional review board (IRB) approval and written consents were obtained before the study. Four experiments were conducted and specific parameters for each scan were listed in Table I.

TABLE I.

Imaging Parameters for Different Scans

Exp. #	Pixel size (mm3)	FOV (mm3)	Matrix size	Slice #	Rpe/Rshot/ Rnet	PFpe/ PFshot	Nshot/ Necho	TESE(ms) /TR(s)	b value (s/mm2)	# b=0/ DWIa	ESP (ms)	Tacq (min:sec)
1	1×1×3	220×220×60	220×220	20	0/1/1	1.0/1.0	220/55	59.7/2.6	--	1/0	1.0	09:36
2	1×1×3	220×220×60	220×220	20	4/22/27.5	0.8/0.8	8/48	63/2.8	1000	1/10	1.0	04:31
3	1×1×3	208×208×60	208×208	20	4/26/34.7	0.75/0.75	6/43	58.1/2.8	1000	1/10	1.0	03:11
4	1×1×3	220×220×60	220×220	20	4/22/27.5	0.8/0.8	8/48	63/2.8	1000	3/30	1.0	12:26
4 (ms-EPI)b	1×1×3	220×220×60	220×220	20	4/--/--	0.8/--	4/--	63/2.8	1000	3/30	1.0	12:32
5	1.5 iso	216×216×60c	144×144	20	4/18/18	1.0/1.0	8/72	86.3/2.8	1000	3/30	0.8	12:26
Calib. 1	1×4×3	220×220×60	220×55	20	0/1/1	1.0/1.0	55/55	59.7/2.6	--	1/0	1.0	02:29
Calib. 2	1×4×3	208×208×60	208×52	20	0/1/1	1.0/1.0	52/52	57.4/2.6	--	1/0	1.0	02:19
Calib. 3	1.5×6×1.5	216×216×60c	144×36	20	0/1/1	1.0/1.0	36/72	62.3/2.6	--	1/0	0.8	01:37

^aThe number of DWIs means either the repetition times for tSNR calculation (Exp. 2 and 3), or the number of all diffusion encoding directions (Exp. 4 and 5). FOV: field-of-view; PF: partial Fourier, TE_SE: TE of the spin echo; ESP: echo spacing time; T_acq: total acquisition time; Calib. 1: time-resolved calibration scan for Exp. 2 and4; Calib. 2: time-resolved calibration scan for Exp. 3; Calib. 3: time-resolved calibration scan for Exp. 5.

^bThe ms-EPI acquisition was repeated once with reversed phase encoding gradient polarity for post distrotion conection with FSL topup and eddy.

^cIn the 1.5 mm isotropic-resolution scan, 1.5 mm gap was used between adjacent slices.

Experiment 1: To seek the optimal singular value threshold in the LLR reconstruction, one subject underwent a fully sampled EPTI scan without diffusion encoding. Data were acquired at 55 TEs (N_echo = 55), with TE_SE located at the 28^th echo (TE_SE = 59.7 ms). Other parameters included: R_pe = 4, R_shot = 1, N_shot = 220, PF_pe = 1 and PF_shot = 1. The acquired data were retrospectively under-sampled to the actual scan setting in Experiment 2, with R_pe = 4, R_shot = 22, N_shot = 8, PF_pe = 0.8 and PF_shot = 0.8. In this study, for clarity, a net acceleration factor R_net is also defined as R_net = R_shot/PF_shot to indicate the total acceleration factor compared with a fully sampled data. Then images were reconstructed following the diffusion reconstruction pipeline in Fig. 4, assuming E_diff,i = 1. Root mean square errors (RMSEs) between the reconstructed images with different LLR thresholds and the fully sampled reference images were calculated. The threshold generating the minimum RMSE was selected as the optimal threshold and used in all the following reconstructions.

Fig. 4.

A flowchart outlining the overall reconstruction steps, including (a) synthesizing the phase-matched diffusion navigator (step 1); (b) GRAPPA-CK reconstruction (step 2), POCS iteration (step 3) and image combination (step 4).

Experiment 2: To evaluate the efficacy of phase matching and magnitude and phase priors, the second subject was scanned in single diffusion encoding direction (b = 1000 s/mm²) with 10 repetitions. Forty-eight echoes (N_echo = 48) were acquired, with TE_SE located at the 17^th echo (TE_SE = 63 ms). Other parameters were: R_pe = 4, R_shot = 22, N_shot = 8, PF_pe = 0.8, PF_shot = 0.8, R_net = 27.5.

Experiment 3: To validate the performance of the proposed reconstruction at a higher acceleration factor, a similar scan as Experiment 2 but with a higher acceleration factor (R_net = 34.7) was conducted. Forty-three echoes (N_echo = 43) were acquired, with TE_SE located at the 14^th echo (TE_SE = 58.1 ms). Other parameters were: R_pe = 4, R_shot = 26, N_shot = 6, PF_pe = 0.75, PF_shot = 0.75, R_net = 34.7. A similar tSNR analysis procedure was conducted as Experiment 2.

Experiment 4: To evaluate the quantitative diffusion metrics with the proposed scEPTI acquisition, one subject was scanned with 30 diffusion encoding directions with b = 1000 s/mm². One b = 0 scan was interlaced among each 10 diffusion volumes for subject bulk motion correction. The scan parameters were the same as Experiment 2. The total scan time was 12:26. For comparison, a conventional 4-shot EPI scans were also conducted, with TE = 63 ms. Other scan parameters of the 4-shot EPI were the same as the scEPTI scan. The 4-shot EPI acquisition was repeated once with reversed phase encoding gradient polarity to allow post distortion and eddy current correction with FSL topup [28] and eddy [29]. The total scan time was 12:32.

Experiment 5: To validate the capacity of the proposed scEPTI acquisition for isotropic resolution imaging and relaxometry imaging, one subject was scanned with 1.5 mm isotropic resolution. A larger number of echoes (N_echo = 72) were acquired to allow a wider TE varying range for T₂ and ${\mathrm{T}}_2^{\ast }$ mapping, with TE_SE located at the 37^th echo (TE_SE = 86.3 ms). Other parameters were: R_pe = 4, R_shot = 18, N_shot = 8, PF_pe = 1.0, PF_shot = 1.0, R_net = 18. 30 diffusion encoding directions with b = 1000 s/mm². One b = 0 scan was interlaced among each 10 diffusion volumes. Other scan parameters were the same as Experiment 4. The total scan time was 12:26.

For each scEPTI scan (Experiment 2 to 4), a fully sampled EPTI (R_pe = 0, R_shot = 1) was acquired as the time-resolved calibration scan (k_x-k_y-t) (Fig. 1c). R_pe = 0 means that in each shot, all echoes were sampled at the same k_y location. As shown in Table I, calibration scan 1 was for Experiment 2 and 4, calibration scan 2 was for Experiment 3 and calibration scan 3 was for Experiment 5. As mentioned in II.E, we only use the central TEs of the calibration data (the region between the two dotted vertical lines in Fig. 3e) to calculate the weighting matrix. The matrix size of the trimmed calibration data is 220 × 55 × 24 (k_x-k_y-t) for Experiment 2 and 4, 208 × 52 × 24 for Experiment 3 and 216 × 36 × 24 for Experiment 5.

Anatomical 2D T₂ fluid-attenuated inversion recovery (FLAIR) or fast spine echo (FSE) images were acquired in each experiment as a distortion-free reference, with the same FOV and resolution as the diffusion scan.

B. Image Reconstruction

Data were reconstructed offline using Matlab 2018b (Mathworks, Natick, MA, USA). After Nyquist ghost correction, data were compressed to 16 channels using geometric coil compression [30] to speed up the reconstruction. The flowchart of the overall reconstruction is shown in Fig. 4, including the following four steps:

1). Synthesize the Phase-Matched Diffusion Navigator:

Each shot was first treated as conventional EPI acquisition (the diagonal line in the k_y-t space in Fig. 1b and s2a) and individually recovered using GRAPPA [5]:

$$d_j(\mathbf{k})={\sum }_{j^{\prime }=1}^{N_{\text{ch}}}\sum \begin{array}{c}\hfill \\ \Delta \mathbf{k}\in {\mathbf{K}}_{2\mathbf{D}}\hfill \end{array}{w}_{2\mathrm{D},j^{\prime }}(\Delta \mathbf{k})d_{j^{\prime }}(\mathbf{k}+\Delta \mathbf{k}),$$ (12)

where k is the k_x-k_y position of the to-be-interpolated data points; (k + Δk) is the k_x-k_y position of the acquired data points within the interpolation kernel (denoted by K_2D); w_2D is the weighting matrix for a specific sampling pattern in the k_x-k_y space (grey region in Supplementary Fig. s2a. No temporal dimension is considered in conventional EPI reconstruction) and calculated from a 4-shot pre-scan using fast low-angle excitation echo-planar technique (FLEET) [31]. The fitting process was the least-square solution of (13), with a standard Tikhonov regularization factor (0.01). The size of interpolation kernel K_2D was 5 × 13 (k_x-k_y). The interpolation procedures of GRAPPA for shot 1 and 2 were shown in Supplementary Fig. s2a for demonstration, with the blue dots denoting the recovered signal. The central k-space (24 k_y lines) of each recovered shot was extracted as the navigator. Then the navigator and the b = 0 time resolved calibration scan were combined to synthesize a phase matched time resolved diffusion navigator, as described in II.C.

2). GRAPPA Reconstruction With Compact Kernel:

The under-sampled diffusion EPTI data were recovered in k-space using GRAPPA with compact kernel (GRAPPA-CK) [6]:

$$\begin{gathered} d_{i,j}(\mathbf{k},t)={\sum }_{i^{\prime }=1}^{N_{\text{shot}}}{\sum }_{j^{\prime }=1}^{N_{\text{ch}}}\sum \begin{array}{c}\hfill \\ (\Delta \mathbf{k},\Delta t)\in {\mathbf{K}}_{3\mathbf{D}}\hfill \end{array}{w}_{3\mathrm{D},i^{\prime },j^{\prime }}(\Delta k,\Delta t) \\ \cdot d_{i^{\prime },j^{\prime }}(\mathbf{k}+\Delta \mathbf{k},t+\Delta t), \end{gathered}$$ (13)

where (k, t) is the k_x-k_y-t position of the to-be-interpolated data points; (k + Δk, t + Δt) is the k_x-k_y-t position of the acquired data points within the interpolation kernel (denoted by K_3D); w_3D is the weighting matrix for a specific sampling pattern in the k_x-k_y-t space (grey region in Supplementary Fig. s2b) and calculated from the synthesized time resolved diffusion navigator, i.e., by sliding the kernel K_3D over the fully-sampled k-space of c_{calib_diff} in (11). The fitting process was the least-square solution of (13), with a standard Tikhonov regularization factor (0.25). In this study, the size of interpolation kernel K_3D was 9 × 9 × 6 (k_x-k_y-t). The interpolation procedure of GRAPPA-CK was shown in Supplementary Fig. s2b, with the red dots denoting the recovered signal. Different from the GRAPPA reconstruction (Supplementary Fig. s2a), the sampled points of all shots were jointly used for the recovery of the target points (e.g., solid and dotted grey arrows in Supplementary Fig. s2b denote the interpolation for two different target points from the same source points but with different weighting coefficients).

3). Magnitude and Phase Constrained Iteration:

After the GRAPPA-CK reconstruction, a full k_x-k_y-t space was recovered for each TE, shot and coil. With inverse Fourier transform, the complex image of each TE, shot and coil (${\widehat{c}}_{i,j,k}$, where i , j and k are the index for shot, coil and TE, respectively) can be recovered. Then the magnitude and phase constraints were applied in a projection onto convex sets (POCS) iteration framework, with details shown in Supplementary Fig. s3 [9], [10], [32]. The magnitude image and phase maps were alternately updated in each POCS iteration.

The phase updating steps included:

1. The coil sensitivity maps s were estimated from the calibration data at TE_SE and kept unchanged. From (5), (7) and (10), s_j can be calculated as:

   $$s_j={\widehat{c}}_{\text{calib}\_\mathrm{b}0,j,{\text{TE}}_{\text{SE}}}∕{\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,{\text{TE}}_{\text{SE}}}.$$ (14)
2. The B₀ inhomogeneity induced phasors ${\widehat{E}}_{{\mathrm{B}}_0,k}$ at each TE were calculated from time resolved b = 0 calibration data and kept unchanged. From (10) and (14)

   $${\widehat{c}}_{\text{calib}\_\mathrm{b}0,k}={\sum }_{j=1}^{N_{\text{ch}}}\left({\widehat{c}}_{\text{calib}\_\mathrm{b}0,j,k}{s}_j^{\ast }\right)∕{\sum }_{j=1}^{N_{\text{ch}}}\left(s_j{s}_j^{\ast }\right),$$ (15)

   and

   $${\widehat{E}}_{{\mathrm{B}}_0,k}={\widehat{c}}_{\text{calib}\_\mathrm{b}0,k}∕{\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k},$$ (16)

   where ${\widehat{c}}_{\text{calib}\_\mathrm{b}0,k}$ and ${\widehat{\rho }}_{\text{calib}\_\mathrm{b}0,k}$ were the complex and magnitude images at TE_k, respectively.
3. The full k-space recovered from GRAPPA-CK was inversely Fourier transformed to calculate the complex images at each TE, shot and coil (${\widehat{c}}_{i,j,k}$). Then the complex images were multiplied by the conjugate of ($s_j{\widehat{E}}_{{\mathrm{B}}_0,k}$) to calculate the complex image at each TE and shot (${\widehat{c}}_{i,k}$):

   $$\begin{gathered} {\widehat{c}}_{i,k}={\sum }_{j=1}^{N_{\text{ch}}}\left({\widehat{c}}_{i,j,k}{\left(s_j{\widehat{E}}_{{\mathrm{B}}_0,k}\right)}^{\ast }\right)∕{\sum }_{j=1}^{N_{\text{ch}}}\left(\left(s_j{\widehat{E}}_{{\mathrm{B}}_0,k}\right) \\ {\left(s_j{\widehat{E}}_{{\mathrm{B}}_0,k}\right)}^{\ast }\right). \end{gathered}$$ (17)

   Then motion induced phasor ${\widehat{E}}_{\text{diff},i,k}$ at each TE and shot was extracted from ${\widehat{c}}_{i,k}$.

   $${\widehat{E}}_{\text{diff},i,k}={\widehat{c}}_{i,k}∕{\widehat{\rho }}_{i,k}.$$ (18)

   For higher SNR purpose, ${\widehat{E}}_{\text{diff},i,k}$ was averaged over 17 TEs around TE_SE to estimate the average E_diff,i of each shot (E_diff,i is only shot dependent).

With E_diff,i the complex images at each TE (${\widehat{c}}_k$) were calculated by combining the complex images ${\widehat{c}}_{i,k}$ from each coil and shot in (17) and the shot combination process was:

$${\widehat{c}}_k={\sum }_{i=1}^{N_{\text{shot}}}\left({\widehat{c}}_{i,k}{E}_{\text{diff},i}^{\ast }\right)∕{\sum }_{i=1}^{N_{\text{shot}}}\left(E_{\text{diff},i}{E}_{\text{diff},i}^{\ast }\right).$$ (19)

All the symbols have the same meaning as in Supplementary Fig. s3. After that, the corresponding magnitude images at each TE (${\widehat{\rho }}_k$) were extracted.

The magnitude updating steps included:

1. A spatial-temporal matrix ∧ of the magnitude image matrix $\widehat{\rho }$ (with ${\widehat{\rho }}_k\in \widehat{\rho }$) was first constructed with a predefined block size (10 × 10), as described in section II.D and Fig. 3c.

2. After SVD of ∧, U ∑ V^H = svd (∧), the τ largest singular values were extracted, i.e.,

   $${\Sigma }_{r,r}^{\text{new}}=\{\begin{array}{cc}{\Sigma }_{r,r}\hfill & \text{if}r\le \tau \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}.$$

   Both ∑ and ∑^new are diagonal matrices with the diagonal elements to be the singular values.

3. The magnitude image was updated by inversing the SVD transform with the τ largest singular values, ∧^new = U ∑^newV^H (H is the Hermitian transpose) and projecting the new spatial-temporal matrix ∧^new back to the image.

In each LLR iteration, we used non-overlapping blocks to construct the spatial-temporal matrix, which can speed up the reconstruction. Random shifts along readout and PE directions were added when constructing those blocks to achieve shift invariance and avoid block-wise artifacts [33].

After the phase and magnitude updates, if the stopping criteria was not reached, the magnitude images at each TE were multiplied by s, ${\widehat{E}}_{{\mathrm{B}}_0}$ and E_diff to synthesize the complex image at each shot, coil and TE. The synthesized complex image was FFT to k-space. The sampled locations in the k-space were resubstituted with the originally acquired data and then the whole k-space was iFFT to get a new complex image at each shot, coil and TE. After that, we repeated the phase and magnitude update steps. The stopping criteria of the POCS iteration was that the image updates between adjacent iterations (defined as ${\Vert {\widehat{\rho }}^{n+1}-{\widehat{\rho }}^n\Vert }_F∕\Vert {\widehat{\rho }}^n{\Vert }_F$, where ${\widehat{\rho }}^n$ is the magnitude image matrix at all TEs in iteration n and ∣∣*∣∣_F is the Frobenius norm) was <1e-2 or the number of iterations reached 100.

4). Image Combination:

The images from different channels and shots were complex averaged to generate the complex images at each TE (as in (17) and (19)), which can be used to study the diffusion and relaxometry properties. If only high-SNR distortion-free diffusion images are desired, images from different TEs can further be combined using rSoS.

C. Image Evaluation

To validate the phase matching theory, we calculated the inter-shot phase variations E_diff in two manners: 1) the phase matching approach described from (5) to (9); 2) the phase mis-matching approach by substituting s_j E_B0,i in (7) with $s_j{\widehat{E}}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}$, which can be calculated from the calibration data at TE_SE. Since the spin is fully refocused at TE_SE, $s_j{\widehat{E}}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}$ only contained the coil sensitivity information (${\widehat{E}}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}=1$) and cannot reflect the B₀ inhomogeneity induced phase in each shot, which causes the phase discrepancy between the final time resolved diffusion navigators and the to-be-recovered EPTI data. We first substituted (7) with

$$s_j{\widehat{E}}_{{\mathrm{B}}_0,{\text{TE}}_{\text{SE}}}={\widehat{c}}_{\text{calib}\_\mathrm{b}0,j,{\text{TE}}_{\text{SE}}}∕{\widehat{\rho }}_{\text{cailb}\_\mathrm{b}0,{\text{TE}}_{\text{SE}}},$$ (20)

and then continued navigator preprocessing as (8) and (9). We compared the reconstruction results between the matched and mismatched navigators.

The efficacy of the POCS iteration framework (Experiment 2 and 3) was then evaluated with three different POCS iterations: 1) without any POCS iteration, 2) only updating magnitude and 3) simultaneously updating magnitude and phase. Both temporal SNR (tSNR) and CNR were used to quantitatively evaluate the efficacy of POCS iterations. Temporal SNR was calculated from the ten repetitions, with $\text{tSNR}=\overline{u}∕\sigma$, where $\overline{u}$ and σ are the mean value and standard deviation of image intensity over different repetitions. CNR between the brainstem and CSF was also calculated, with three manually drawn ROIs in brainstem, adjacent CSF and background. Example ROIs would be given in the results session. First the SNRs of brainstem (SNR_BS) and CSF (SNR_CSF) were calculated as ${\text{SNR}}_{\text{BS}}={\overline{\rho }}_{\text{BS}}∕{\sigma }_{\text{BG}}$ and ${\text{SNR}}_{\text{CSF}}={\overline{\rho }}_{\text{CSF}}∕{\sigma }_{\text{BG}}$, respectively, where ${\overline{\rho }}_{\text{BS}}$ and ${\overline{\rho }}_{\text{CSF}}$ were the mean intensity within brainstem and CSF, σ_BG was the standard deviation of noise in the background. The CNR between brainstem and CSF (CNR_BS-CSF) was calculated as CNR_BS-CSF = SNR_BS–SNR_CSF. Finally, mean CNR_BS-CSF (mCNR_BS-CSF) was calculated by averaging CNR_BS-CSF over the 10 repetitions.

Finally, we compared the quantitative DTI metrics between the distortion-free EPTI acquisitions and conventional ms-EPI acquisitions. Post distortion corrections (topup [28] and eddy [29]) were conducted on the ms-EPI images before DTI analysis. DTI analysis was conducted by using the FMRIB Software Library (FSL) dtifit [34]. To avoid any possible disturbance from the inter-volume subject movement, the ms-EPI and EPTI images were linearly co-registered to the FLAIR or FSE reference using FSL flirt [35], [36]. In experiment 5, T₂ and ${\mathrm{T}}_2^{\ast }$ maps were estimated by least-square fitting using a custom Matlab script.

IV. Results

Supplementary Fig. s4 shows the results of different thresholds in LLR (Experiment 1), with RMSEs marked on the top. The fully sampled reference images, images without LLR and with 4 different thresholds τ are shown, together with the difference between the recovered image and the reference (intensity ×5). Images at two different TE are displayed: TE₁₇ (equal to TE_SE) and TE₄₀ (23 ms after TE_SE). As shown, LLR constraints can greatly improve SNR and reduce the residual artifacts. With a small τ value (τ = 1), the image might be over smoothed, especially in regions with strong susceptibility variations (yellow boxes). With a higher τ value (τ = 5), the residual artifacts might still be present (yellow arrows) as in the image without any LLR constraints. A threshold value of τ = 2 or τ = 3 balances the SNR, residual artifacts and image blurring best. In this study, τ = 3 is selected as the optimized LLR threshold parameter for all reconstructions, which has the minimum RMSE for TE₄₀.

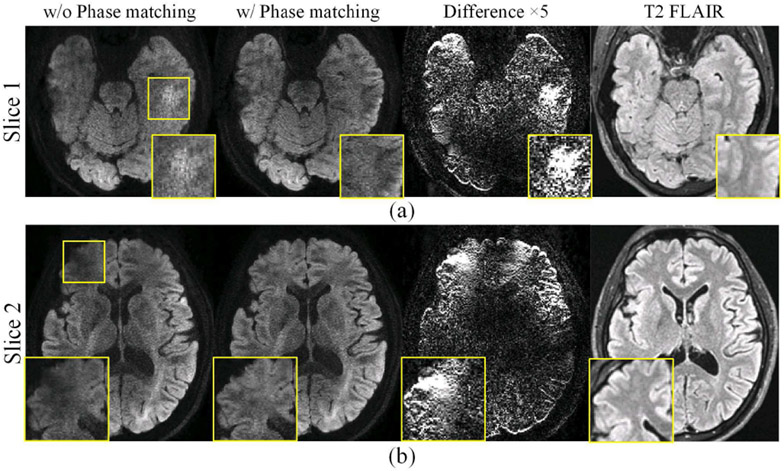
Fig. 5 shows the reconstruction results with and without phase matching when synthesizing the time resolved diffusion navigator. The final combined diffusion images from two slices are shown, together with the different maps between phase matching and mismatching results (intensity ×5) and an anatomical T₂ FLAIR reference image. From the zoomed images (yellow boxes), we can see that structures are corrupted (hyper- or hypo-intensity) without phase matching, whereas they are well recovered when using phase matching.

Fig. 5.

Reconstruction results on (a) slice 1 and (b) slice 2, with and without phase matching when synthesizing navigator. The different maps between phase matching and mismatching results (intensity ×5) and an anatomical T₂ FLAIR image (distortion-free references) are also displayed. Zoomed regions highlight a hyper- (slice 1) and hypo- (slice 2) intensity artifacts when no phase matching is used.

Fig. 6 compares the reconstructed images with different POCS iterations in Experiment 2 (R_net = 27.5). We show the images at two TEs (TE₁₇ = 63 ms and TE₄₀ = 86 ms) and the combined images from all TEs, in which TE₁₇ corresponds to TE_SE. Three ROIs are manually drawn to outline brainstem, adjacent CSF and background (yellow ROIs 1 to 3 in Fig. 6d) for CNR calculation and the corresponding mean CNRs (mCNR) over 10 repetitions are marked on the top of each image. The quantitative tSNR histograms of the brain parenchyma (blue ROI in Fig. 6d) are shown in Fig. 7. From Fig. 6 and 7, the magnitude LLR constraint improves the SNR of the single-TE images. The high-SNR diffusion images at single TE can have the potential for more microstructure studies with simultaneous diffusion and relaxometry imaging. The magnitude LLR does not significantly improve the SNR of the multi-TE combined images. The reason for the difference of SNR improvement in the single-TE and combined images might be that the noise across TEs is correlated after the SVD truncation in LLR. On the contrary, when no LLR is used, the noise is generally independent across different TEs, so the averaging effects are more conspicuous in the combined images. The phase update does not contribute significantly to the SNR improvement but alleviates the image blurring induced by the LLR constraint and thus improves the CNR, especially at the interface of brain parenchyma (brainstem in Fig. 6) and CSF, for both single-TE and multi-TE-combined images.

Fig. 6.

Comparisons among reconstruction with different POCS iterations (Experiment 2): (a) no iteration, (b) only with magnitude LLR, (c) with LLR + phase updates. Images at two TEs (TE₁₇ = 63 ms and TE₄₀ = 86 ms) and the combined images from all TEs are shown. TE17 corresponds to TE_SE, whereas TE₄₀ represents a TE 23ms after TESE. The mean CNRs (mCNR) over 10 repetitions between the brainstem and adjacent CSF are marked on each image. (d) Three ROIs are manually drawn to outline brainstem, adjacent CSF and background (yellow ROIs 1 to 3) and an ROI (blue ROI 4) is manually drawn to outline the whole brain parenchyma on the b = 0 image.

Fig. 7.

The tSNR histograms of image at TE₁₇, TE₄₀ and the combined images in Fig. 6 on the brain parenchyma (blue ROI in Fig. 6d).

Supplementary Fig. s5 and s6 further demonstrate the impacts of magnitude LLR and phase constraints at a higher net acceleration factor (R_net = 34.7) in Experiment 3. The findings are consistent with Fig. 6 and 7, with the magnitude LLR constraint improving SNR (mainly in single-TE images) and phase updates reducing the apparent blurring from LLR constraints, in single-TE and multi-TE-combined images.

Quantitative fractional anisotropy (FA) maps in Experiment 4 are shown in Fig. 8. The results without any iteration and with LLR + phase updates are displayed, together with the difference map between them (difference ×5). We show the results at two TEs (TE₁₇ = 63 ms and TE₄₀ = 86 ms) and the combined results from all TEs. It can be visually observed that the SNR gains in the diffusion images can further contribute to a higher-SNR FA map at single TE, whereas the FA differences from the combined images are minor.

Fig. 8.

Fractional anisotropy (FA) maps: (a) without any iteration and (b) with LLR + phase update. (c) The FA differences (intensity ×5) between (a) and (b). Results include FA maps at two TEs (TE₁₇ = 63 ms and TE₄₀ = 86 ms) and the TE-combined results. Yellow arrows point to a region with potential FA bias at TE₄₀ when no iteration is used.

Fig. 9 compares the mean diffusion images between the scEPTI acquisition and conventional 4-shot EPI (both w/ and w/o topup/eddy distortion correction). In Fig. 9, although ms-EPI alleviates image distortions in most areas, there are still residual artifacts around the temporal lobe (blue and yellow arrows), even with further topup/eddy correction, which are absent in the scEPTI results. Fig. 10 displays FA and color-coded FA (cFA) comparisons between scEPTI and conventional ms-EPI + topup/eddy correction. Much clearer delineations of the optic tract (OPT) and cerebral peduncle (CP) are observed in the scEPTI result (white arrows in the zoomed cFA map), which are visually blurred in the result of conventional 4-shot EPI + topup/eddy correction.

Fig. 9.

Mean diffusion images from conventional 4-shot EPI with (a) blip down, (b) blip up and (c) topup / eddy distortion correction and (d) the proposed scEPTI acquisition. Distortion is still observed in 4-shot EPI (blue and yellow arrows) but removed in scEPTI. (e) An FSE anatomical image is shown as distortion-free reference.

Fig. 10.

(a) FA and (b) color-coded FA (cFA) maps from: conventional 4-shot EPI acquisition + post topup/eddy correction and the proposed scEPTI acquisition. (c) Enlarged brainstem region (yellow box in (a)). Structure details (white arrows) are more clearly depicted using scEPTI. OPT: optic tract, CP: cerebral peduncle.

Fig. 11 displays the 1.5 mm isotropic resolution acquisition results, including b = 0 image, T₂ and ${\mathrm{T}}_2^{\ast }$ maps, mean diffusion image, FA and cFA maps. The high-quality T₂, ${\mathrm{T}}_2^{\ast }$ and FA maps demonstrate the potential of the proposed scEPTI method for simultaneous diffusion and relaxometry imaging. Additionally, Supplementary Fig. s7 compares the T₂ and ${\mathrm{T}}_2^{\ast }$ maps from the same slice: (a) without any iteration and (b) with LLR + phase update, where the SNR improvements from LLR + phase updates can be clearly seen. It is noteworthy that the T₂ and ${\mathrm{T}}_2^{\ast }$ maps presented here serve as an initial demonstration for relaxometry imaging but are not fully optimized in terms of sampling, number of shots and echoes.

Fig. 11.

The results of 1.5 mm isotropic resolution data, including b = 0 image, T2 and T2* maps, mean DWI, FA and color-coded FA maps.

V. Discussion

In this study, a novel EPTI-based acquisition and reconstruction method has been developed for distortion-free diffusion imaging. A self-navigated Cartesian EPTI-based diffusion acquisition sequence is designed. Different phase components in the EPTI diffusion signal are analyzed and an approach to synthesize a fully phase matched diffusion navigator is developed. Finally, the rich magnitude and phase correlations in EPTI acquisition are exploited to enhance the reconstruction performance. In vivo experiments have demonstrated the high efficacy of the scEPTI acquisition and reconstruction for distortion-free diffusion imaging.

As in the initial EPTI [15], optimized CAIPI sampling in the k_y-t domain is used in scEPTI, which will promote a full use of coil sensitivity and spatiotemporal correlations. The proposed scEPTI is different from conventional multi-shot multi-echo EPI (ms-me-EPI) [37]-[39] in the following aspects. In conventional ms-me-EPI, each echo is still a conventional multi-shot EPI acquisition and thus subject to image distortion and blurring. The reconstruction of conventional ms-me-EPI is echo independent and no temporal correlations between different echoes are exploited. Lastly, the total number of echoes in conventional ms-me-EPI is usually limited (<10) because of long readout window at each echo and thus more ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ decay, whereas it is easy to acquire tens of echoes or even more than 100 echoes using EPTI.

As the initial EPTI [15] and PEPTIDE [16], [17], the proposed scEPTI samples uniformly at each TE, which maintains the capacity for relaxometry imaging. In addition to a direct ${\mathrm{T}}_2∕{\mathrm{T}}_2^{\ast }$ mapping from the b = 0 data, another valuable potential of the proposed scEPTI is simultaneous diffusion and relaxometry imaging, which might allow a more comprehensive revealing of the microstructure information [40], [41]. This potential is further boosted by the LLR constraint, which can effectively improve the accuracy of diffusion metrics (such as FA maps) at single TEs (especially TE₄₀ = 86 ms), as shown in Fig. 8.

The LLR constraint in this study is a data driven approach, which only assumes that the data is low-rank and does not require the explicit expression ($1∕T_2-1∕T_2^{\prime }$ or $1∕T_2+1∕T_2^{\prime }$). The results demonstrate an SNR improvement in the single-TE diffusion images, T₂ and ${\mathrm{T}}_2^{\ast }$ maps with LLR constraints (Fig. 6, 7, s5, s6 and s7), although there is no obvious SNR improvement in the combined images. The LLR constraint might cause blurring in the CSF regions and thus degrades CNR between brain parenchyma and CSF. The reason is that when diffusion encoding is added, the CSF signal is almost attenuated to the background noise level (due to the strong diffusivity of free water), which therefore does not satisfy the LLR property anymore. In this study, the blurring problem can be effectively mitigated by integrating phase update into the POCS iteration, which significantly improves the CNR between brainstem and CSF (Fig. 6 and s5). As in conventional ms-EPI [9], [10], LLR also exists along different diffusion encoding directions, which can be used to further improve the SNR performance. In this study, we mainly focus on the LLR along the temporal dimension, which is more specific for the EPTI acquisition and can be used for a single-direction diffusion encoded image volume. The LLR method in this study can be further optimized. For example, currently it cannot recover the images at the peripheral TEs because the initial input cannot be well recovered using GRAPPA-CK due to the kernel size limitation. Previous studies have also reported that EPTI magnitude correlation can be used in other ways, e.g., the subspace-based method, which can be used to recover images at all TEs [18], [21]. In the future, we can combine the subspace-based method with the current reconstruction to recover the diffusion images at all TEs, which might further boost the SNR of the final diffusion images and thus allow potentially higher acceleration.

Previously PEPTIDE has been proposed as a motion robust technique for simultaneous diffusion and relaxometry imaging [16]. As in conventional segmented EPI and PROPELLER EPI [42], similarities and differences exist between scEPTI and PEPTIDE. The key strengths of PEPTIDE include self-navigating and motion robustness: all blades cover the k-space center, which can be used to estimate the motion-induced phase variations and the macroscopic motion status in each shot. Similarly, the navigator image of the newly developed scEPTI can also record both the phase information and macroscopic motion status (Fig. 2) in each shot, which can allow incorporating macro-motion correction methods [43], [44] into the reconstruction. As a non-Cartesian sampling based on PROPELLER, PEPTIDE can be less efficient in terms of k-space coverage [42], which might require more shots and thus more scan time to accomplish the whole k-space than scEPTI. Regridding and density compensation operation are used in PEPTIDE (non-Cartesian sampling) reconstruction but can be omitted in the proposed scEPTI (Cartesian sampling), which might further simplify the reconstruction complexity and improve the reconstruction efficiency. The new scEPTI design might allow a shorter echo spacing time (ESP) compared to PEPTIDE. The shortest ESP depends on the maximum allowable PNS threshold, which varies from axis to axis [45]. In scEPTI, the readout direction can be set along the axis with the maximum allowable PNS threshold to achieve the shortest ESP. However, in PEPTIDE, due to the rotation character of different blades, the minimum ESP is dependent on the allowable PNS threshold of the whole rotation plane rather than a single axis and thus might be increased. A comprehensive comparison between the proposed scEPTI and PEPTIDE is out of the scope of the current study but will be of interest in the future.

There are several limitations in this study. First, we do not consider the B₀ field drift over time. The reason is that the B₀ field drift induced phase changes (Supplementary Fig. s8a vs s8d) is much smaller than the difference between φ_B0 and motion induced phase φ_diff (Supplementary Fig. s8a vs s8c), or φ_B0 at different TEs but in the same volume (Supplementary Fig. s8a vs s8b). Taking the dynamic B₀ field drift into account might further improve the reconstruction accuracy, as demonstrated by previous studies [15], [18]. The B₀ field drift can also be integrated into our framework by using field probes [46] or iteratively updating the B₀ background phase [15], [18]. Second, as a proof of concept, the current scEPTI protocol provides 60-mm slice coverage, which is not sufficient to cover the whole brain (~140 mm), due to scan time limitation. In the future, the proposed scEPTI can be combined with advanced acquisition methods such as simultaneous multi-slice [47] to improve the scan efficiency.

VI. Conclusion

In conclusion, a self-navigated Cartesian EPTI-based diffusion acquisition and reconstruction method has been proposed for distortion-free diffusion imaging. The rich magnitude and phase correlations in the EPTI diffusion signal enable a notable improvement in the reconstruction efficacy. High quality distortion-free diffusion and relaxometry images can be acquired with the proposed scEPTI method, rendering it an appealing approach for many neuroimaging applications.