Abstract
Assortativity is the tendency of individuals connected in a network to share traits and behaviors. Through simulations, we demonstrated the potential for bias resulting from assortativity by vaccination, where vaccinated individuals are more likely to be connected with other vaccinated individuals. We simulated outbreaks of a hypothetical infectious disease and vaccine in a randomly generated network and a contact network of university students living on campus. We varied protection of the vaccine to the individual, transmission potential of vaccinated-but-infected individuals, and assortativity by vaccination. We compared a traditional approach, which ignores the structural features of a network, with simple approaches which summarized information from the network. The traditional approach resulted in biased estimates of the unit-treatment effect when there was assortativity by vaccination. Several different approaches that included summary measures from the network reduced bias and improved confidence interval coverage. Through simulations, we showed the pitfalls of ignoring assortativity by vaccination. While our example is described in terms of vaccines, our results apply more widely to exposures for contagious outcomes. Assortativity should be considered when evaluating exposures for contagious outcomes.
Keywords: assortativity, contagious outcomes, infectiousness, interference, networks
Abbreviations
- eX-FLU Study
Study of Exclusion Criteria in a University Population
Interference—dependence of an individual’s potential outcome on their exposure status and the exposure status of others—has long been recognized in the vaccine literature (1–3). Previous work has delineated potential estimands (2, 4–6). The average unit-treatment (i.e., direct) effect, the contrast between average risk with vaccination versus no vaccination (2, 5), is a common estimand in epidemiology and is used to calculate direct vaccine effectiveness (2). For estimation of the unit-treatment effect, researchers must assume that all else is equal between vaccinated and unvaccinated individuals. Differential likelihood of exposure to a pathogen (pathogen exposure) by vaccination status has long been recognized as a violation of this principle (1, 2, 7, 8). Recent work has shown that some definitions for unit-treatment effects may result in differential pathogen exposures to contagious outcomes (9). Other work has demonstrated that it is possible to estimate the unit-treatment effect without explicit knowledge of the interference pattern in randomized trials (10). However, both of these previous results relied on vaccination assignment being independent of other units’ assignments, which may not readily extend to observational studies.
The previous literature has focused on clusters (11), where only members who belong to the same cluster can transmit to each other. Network-based approaches instead assume that transmission occurs between individuals connected by an edge, regardless of cluster membership. Prior work has demonstrated how the distribution of vaccination in a network affects the size of the outbreak (12, 13). In fact, distributions of vaccination in networks have been used as a strategy to reduce the number of overall infections, such as the ring vaccination strategies for smallpox (14) and Ebola (15). Within network analysis, assortativity is the tendency for individuals connected in a network to share similar traits and behaviors (16), potentially arising from various mechanisms (17). Regarding vaccines, previous work has observed assortativity for influenza vaccination (12). The occurrence of assortativity violates the assumption of all else being equal between vaccinated and unvaccinated individuals, possibly resulting in bias.
Our purpose in this paper is to explore bias of the unit-treatment risk ratio incurred by ignoring assortativity by vaccination, where vaccinated individuals are more likely to share connections with other vaccinated individuals. We present simulations for a hypothetical infectious disease outbreak demonstrating that assortativity by vaccination can lead to biased results, and we explore several simple remedies. These approaches operate by including network features in regression models to account for dependencies between observations. While we frame our simulations as a hypothetical vaccine, the biases that are demonstrated here can be generalized to other interventions on other contagious outcomes.
METHODS
Networks
We simulated outbreaks of a hypothetical infectious disease in a randomly generated network and an empirically observed network (see Web Figure 1, available online at https://doi.org/10.1093/aje/kwab167). The randomly generated network, hereafter referred to as the stochastic block network, was generated from a stochastic block random graph model. Stochastic block models generate networks with an underlying community structure by partitioning nodes into distinct sets and randomly creating edges at a specified probability for nodes within the same set and a different (in our case, lower) probability for nodes in discordant sets (see Web Appendix 1 for details). The observed network, referred to as the eX-FLU network, comes from the Study of Exclusion Criteria in a University Population (eX-FLU Study), a cluster-randomized trial assessing the efficacy of 3-day self-isolation among Michigan university students (18). During follow-up, participating students reported all contacts with other students in the study each week. From 10 weeks of self-reported contacts, a static network from the largest component was generated. The 3-day isolation intervention will have no impact on our simulations, since contacts were defined as any contact occurring during the full study and simulated variables are independent of the isolation intervention. Descriptions of the study networks are provided in Web Table 1.
Notation
Let 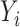 indicate whether an individual was infected over the course of the outbreak;
indicate whether an individual was infected over the course of the outbreak; 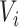 be vaccination status;
be vaccination status; 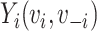 be the potential outcome under
be the potential outcome under 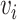 and
and 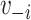 , where
, where 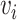 is the vaccination status of individual
is the vaccination status of individual 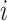 and
and 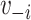 is the vaccination status of all other units; and α indicate the vaccination allocation strategy or policy which determines the probability of vaccination for each individual in the population. Therefore, the estimand is the unit-treatment risk ratio,
is the vaccination status of all other units; and α indicate the vaccination allocation strategy or policy which determines the probability of vaccination for each individual in the population. Therefore, the estimand is the unit-treatment risk ratio,
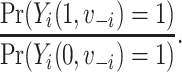 |
Network measures
When discussing an individual’s centrality, we refer to degree, the number of unique contacts (alternative measures of centrality exist (19)). We summarized contacts’ vaccination status through 2 exposure mappings we refer to as 1-step vaccination and 2-step vaccination. One-step vaccination summarizes the proportion vaccinated among an individual’s immediate contacts and is calculated via
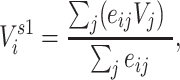 |
where 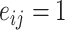 if an edge exists between node
if an edge exists between node  and node
and node 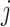 and
and 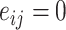 otherwise. One-step vaccination is equivalent to the percentage of immediate contacts who are vaccinated.
otherwise. One-step vaccination is equivalent to the percentage of immediate contacts who are vaccinated.
Two-step vaccination summarizes the proportion vaccinated among an individual’s contacts’ contacts. In our formulation, the 2-step treatment is calculated by taking the average of each contact’s 1-step vaccination, but immediate contact 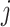 ’s 1-step vaccination does not include node
’s 1-step vaccination does not include node 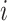 (i.e., individual
(i.e., individual 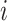 ’s vaccination status does not contribute to their 2-step vaccination). Our expression of the 2-step treatment is
’s vaccination status does not contribute to their 2-step vaccination). Our expression of the 2-step treatment is
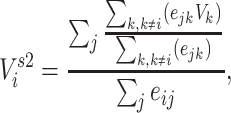 |
where 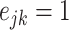 if an edge exists between node
if an edge exists between node 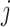 and node
and node 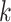 and
and 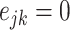 otherwise.
otherwise.
The assortativity of networks by vaccination status was calculated using the assortativity coefficient (16), a measure bounded between −1 and 1, where −1 and 1 indicate perfectly disassortative and assortative networks, respectively. An assortativity coefficient of 0 indicates there is no overall observed contact pattern by vaccination.
Louvain’s community detection algorithm with a resolution parameter of 1 was used to identify exclusive clusters (20), where clusters are exclusive groups of nodes embedded in the larger network. Within the network literature, those clusters are referred to as communities. Let 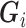 indicate a vector of dummy variables with a value of 1 if node
indicate a vector of dummy variables with a value of 1 if node 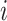 is in an exclusive cluster and 0 otherwise. Louvain’s algorithm identifies communities that maximize the number of connections within each set of nodes and minimize the number of outside connections, thereby finding a partition that reduces the number of paths for interference (21). By defining clusters through Louvain’s algorithm, assortativity by vaccination status was manipulated in simulations. Because of the small size of 6 disparate clusters in the eX-FLU network that were located between large clusters, these 6 clusters were considered structurally equivalent and regarded as a single cluster.
is in an exclusive cluster and 0 otherwise. Louvain’s algorithm identifies communities that maximize the number of connections within each set of nodes and minimize the number of outside connections, thereby finding a partition that reduces the number of paths for interference (21). By defining clusters through Louvain’s algorithm, assortativity by vaccination status was manipulated in simulations. Because of the small size of 6 disparate clusters in the eX-FLU network that were located between large clusters, these 6 clusters were considered structurally equivalent and regarded as a single cluster.
Regression models
We compared 4 different regression models for estimation of the unit-treatment risk ratio, termed 1) traditional, 2) cluster, 3) 1-step, and 4) 2-step. Because log-binomial models have known convergence issues, we instead used log-Poisson models to estimate the risk ratio. Log-Poisson moddels, when accounting for inflated variance with sandwich estimators, provide inference similar to that of log-binomial models but are more robust to convergence problems (22, 23). For all models, the unit-treatment risk ratio is estimated by 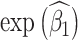 . The traditional model consists of the vaccination status of the individual:
. The traditional model consists of the vaccination status of the individual:
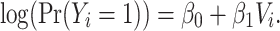 |
By not including some representation of 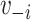 in the model, the traditional model implicitly stipulates random mixing by vaccination status.
in the model, the traditional model implicitly stipulates random mixing by vaccination status.
Next, the cluster model included indicator variables for the designated Louvain-identified cluster:
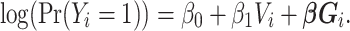 |
The cluster model includes 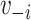 through the inclusion of cluster membership. This model assumes no (few) connections between clusters as well as no assortativity by vaccination within clusters.
through the inclusion of cluster membership. This model assumes no (few) connections between clusters as well as no assortativity by vaccination within clusters.
The 1-step model included individual vaccination status, 1-step vaccination (immediate contacts’ vaccination status), and degree:
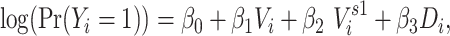 |
where 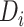 indicates degree. The 1-step model operationalizes
indicates degree. The 1-step model operationalizes 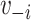 as an individual’s immediate contacts’ vaccination status. This restricts spillover effects to be a result of only immediate contacts, which we refer to as weak dependence. Because the vaccination status of immediate contacts is expressed through a summary measure, the model assumes that 1-step vaccination is an adequate parametric approximation of the mechanism of transmission. The above formation of the 1-step measure further implies that all contacts are equivalent.
as an individual’s immediate contacts’ vaccination status. This restricts spillover effects to be a result of only immediate contacts, which we refer to as weak dependence. Because the vaccination status of immediate contacts is expressed through a summary measure, the model assumes that 1-step vaccination is an adequate parametric approximation of the mechanism of transmission. The above formation of the 1-step measure further implies that all contacts are equivalent.
The 2-step model expanded the 1-step model by including 2-step vaccination (immediate contacts’ contacts’ vaccination status):
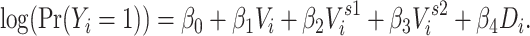 |
The 2-step model includes 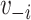 through both an individual’s immediate contacts’ vaccination status and their second-order contacts’ vaccination status. The extended sphere of influence similarly assumes that all contacts are equivalent and that both 1-step and 2-step vaccination are adequate parametric approximations of the transmission mechanism. In both 1-step and 2-step models,
through both an individual’s immediate contacts’ vaccination status and their second-order contacts’ vaccination status. The extended sphere of influence similarly assumes that all contacts are equivalent and that both 1-step and 2-step vaccination are adequate parametric approximations of the transmission mechanism. In both 1-step and 2-step models, 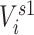 ,
, 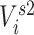 , and
, and 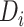 were modeled using restricted quadratic splines to allow for flexibility.
were modeled using restricted quadratic splines to allow for flexibility.
Simulations
All simulations were conducted with Python 3.5.1 (Python Software Foundation, Beaverton, Oregon) using the following libraries: NumPy 1.16.0 (24), Pandas 0.23.4 (25), NetworkX 2.2 (26), and Statsmodels 0.8.0 (27). Code for simulations is available on GitHub (28).
Outbreaks were simulated via the following process (see Web Appendix 2 for further details). First, vaccination was distributed to nodes according to the allocation strategy. Two randomly selected individuals were set as having initial infections. Then, over a period of discrete 20-time steps, infected nodes attempted to transmit the infection to their immediate contacts in a random order. After 20 cycles, the overall incidence of the infection was calculated. To reduce convergence issues, the 4 regression models were fitted to the generated data set if the incidence of the infection was greater than 5%. The above procedure was repeated 10,000 times.
To induce assortativity by vaccination, a 2-step randomization α was used, where clusters were randomized to different probabilities of vaccination and then each individual in the cluster was randomly assigned vaccination status (i.e., probability of vaccination was conditional on the cluster). Through this simulation approach, we controlled the expected overall proportion vaccinated and the assortativity coefficient.
Vaccine effects.
A variety of different combinations of possible vaccine mechanisms were studied (Web Table 2). For scenarios with protective effects of the vaccine for the individual receiving it (unit-treatment effects), vaccination reduced the probability of infection based on a single exposure to an infected individual, referred to as the “leaky” vaccine model (29). We modified the unit-treatment effect scenario using a gradient of no, weak, and moderate unit-treatment effects. The no unit-treatment effect vaccine did not alter the probability of infection for the individual. The “weak” unit-treatment effect vaccine had 0.7 times’ the probability of infection given a single exposure to the infection, and the “moderate” unit-treatment effect vaccine had 0.4 times’ the probability of infection compared with unvaccinated individuals.
Spillover effects consisted of 2 different mechanisms: infectiousness effects and contagion effects. Infectiousness effects reduce the infectiousness of vaccinated-but-infected individuals (30). Infectiousness effects were created by reducing the duration of infectiousness of the vaccinated-but-infected individual and reducing their probability of transmitting the infection. For the no-infectiousness-effect vaccine, the duration of infection (5 time steps) and the probability of transmitting (0.07) were the same between unvaccinated-and-infected and vaccinated-but-infected individuals. The “weak” infectiousness effect vaccine reduced the duration of infectiousness to 4 time steps and reduced the probability of transmitting by 0.9 times’ that of unvaccinated individuals. The “moderate” infectiousness effect vaccine reduced the duration of infectiousness to 3 time steps and reduced the relative infectiousness by 0.75 times. Contagion effects result from vaccinated individuals’ being less likely to develop the infection, thus preventing them from infecting their contacts, on average. Therefore, all vaccines with a protective unit-treatment effect had a marginal protective contagion effect.
The 9 unique combinations of unit-treatment (none, weak, moderate) and infectiousness (none, weak, moderate) effects were simulated for each of the 2 networks. Each of the previous combinations was further varied by the overall proportion of the population vaccinated from 25% to 50% in 5% increments, for a total of 108 unique combinations. Scenarios were simulated 10,000 times. Across all of the different scenarios, the mean assortativity coefficient was 0.1.
Assortativity.
To explore how varying the assortativity coefficient influenced the results, we selected the weak unit-treatment and weak infectiousness effect combination at an average of 40% vaccinated for further simulations. The mean assortativity of vaccination in the network was varied between 0 and 0.25 in 0.05 increments.
Metrics.
Estimated unit-treatment risk ratios were compared using 3 metrics: bias, root mean squared error, and 95% confidence interval coverage of the true risk ratio. Bias was defined as the regression-model–estimated log-transformed risk ratio subtracted from the true log-transformed risk ratio. The root mean squared error was the square root of the squared bias plus the empirical variance. Ninety-five percent confidence interval coverage was calculated as the proportion of estimated confidence intervals containing the true risk ratio.
True values.
For weak or moderate unit-treatment effects, 50,000 outbreaks were simulated with α corresponding to unconditional random assignment, with the true unit-treatment effect defined as the mean of the log-transformed risk ratio across all simulations for each combination of vaccine effects (see Web Appendix 2 and Web Table 3 for further details).
RESULTS
No unit-treatment effect
In scenarios of vaccines with no unit-treatment and no infectiousness effect (Figure 1, Web Figure 2), the traditional model was unbiased but had confidence interval coverage substantively below the expected level (95%) across all proportions of vaccination. In settings with no unit-treatment effect but a protective infectiousness effect, the traditional model was increasingly biased as the infectiousness effect increased. Cluster, 1-step, and 2-step models were less biased than traditional models (Figure 1, Web Figure 2) and had lower root mean squared error (Web Tables 4 and 5). The 95% confidence interval coverage of the true unit-treatment risk ratio for no effects was close to the nominal level in the stochastic block network. For the eX-FLU network, coverage was slightly below the nominal coverage for 1-step and 2-step models. With 25% of the overall population vaccinated, 1-step and 2-step models failed to converge about one-fourth of the time (Web Figure 3). Convergence issues were related to model separation (31). For other proportions vaccinated and the stochastic block network, failures were less than 5%.
Figure 1.
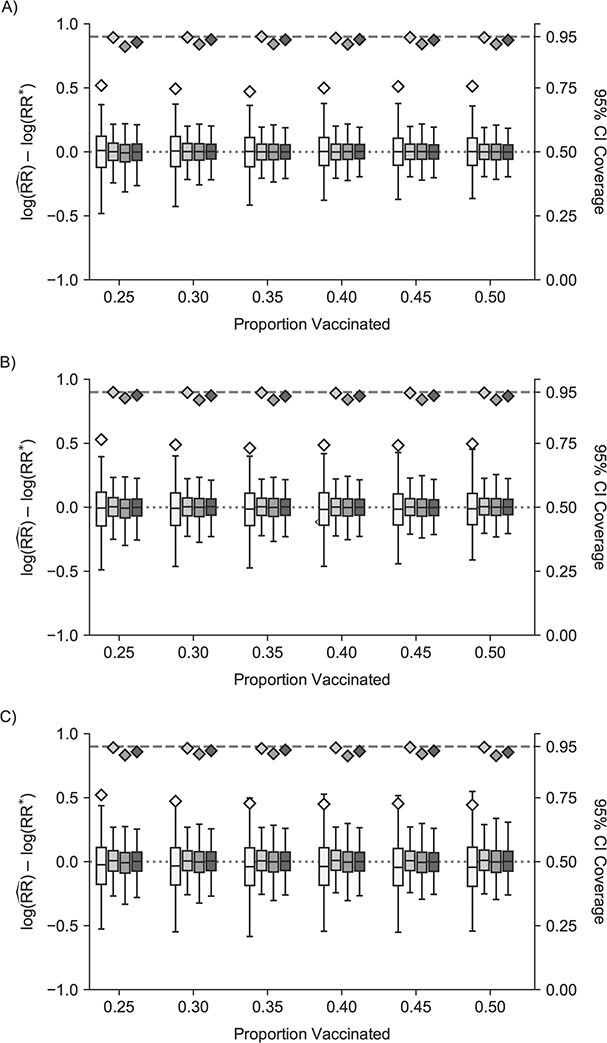
Study of Exclusion Criteria in a University Population (eX-FLU) simulation results for a hypothetical vaccine with no unit-treatment effect. A) No spillover; B) weak infectiousness effect; C) moderate infectiousness effect. From light to dark gray (left to right), results are shown for the traditional model, cluster model, 1-step model, and 2-step model. The y-axis and box plots show the bias, defined as the regression model log-transformed risk ratio (RR) minus the true log-transformed RR. Whiskers indicate the 2.5th and 97.5th percentiles. The z-axis and diamonds show the 95% confidence interval (CI) coverage, defined as the proportion of 95% CIs that contained the true value. The x-axis indicates the overall proportion of individuals vaccinated in the population in expectation. 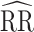 , estimated RR for the unit-treatment effect;
, estimated RR for the unit-treatment effect; 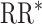 , true RR for the unit-treatment effect.
, true RR for the unit-treatment effect.
Weak unit-treatment effect
Estimates from traditional models were biased across the different infectiousness effects, and 95% confidence interval coverage was similarly poor (Figure 2, Web Figure 4). Cluster, 1-step, and 2-step models all had improved performance with regard to bias and root mean squared error (Web Tables 6 and 7). Similarly, 1-step and 2-step models had slightly below nominal coverage of the reference value. Nonconvergence followed a similar pattern (Web Figure 5).
Figure 2.
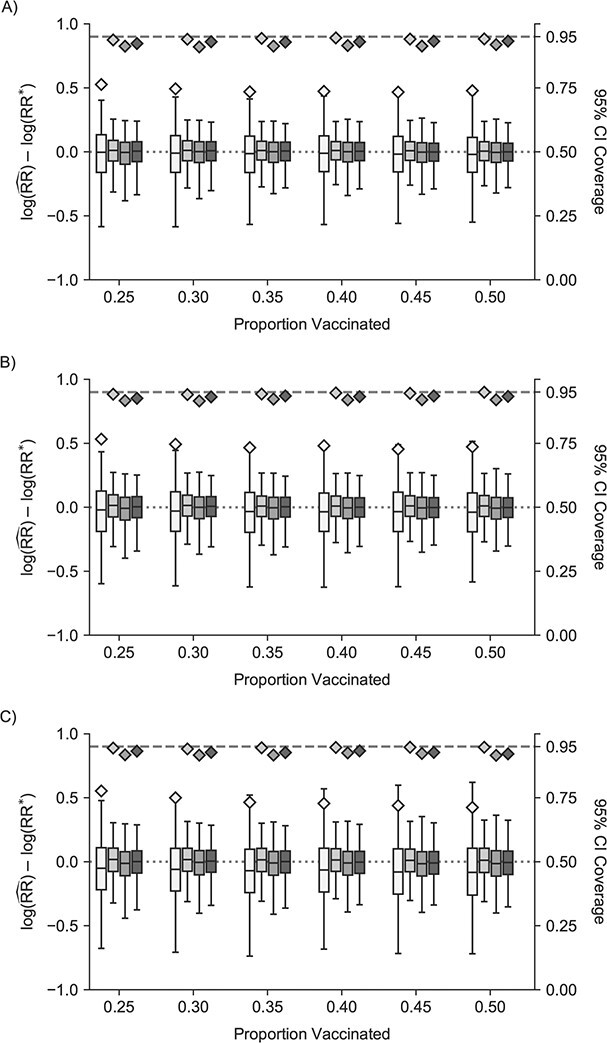
Study of Exclusion Criteria in a University Population (eX-FLU) simulation results for a hypothetical vaccine with a weak unit-treatment effect. A) No infectiousness effect; B) weak infectiousness effect; C) moderate infectiousness effect. From light to dark gray (left to right), results are shown for the traditional model, cluster model, 1-step model, and 2-step model. The y-axis and box plots show the bias, defined as the regression model log-transformed risk ratio (RR) minus the true log-transformed RR. Whiskers indicate the 2.5th and 97.5th percentiles. The z-axis and diamonds show the 95% confidence interval (CI) coverage, defined as the proportion of 95% CIs that contained the true value. The x-axis indicates the overall proportion of individuals vaccinated in the population in expectation.  , estimated RR for the unit-treatment effect;
, estimated RR for the unit-treatment effect;  , true RR for the unit-treatment effect.
, true RR for the unit-treatment effect.
Moderate unit-treatment effects
The traditional model was further biased from the reference value and had similarly poor confidence interval coverage (Figure 3, Web Figure 6). Cluster models were slightly biased toward the null, had confidence interval coverage slightly below 95%, and had smaller root mean squared error compared with the traditional model (Web Tables 8 and 9). The 1-step and 2-step models were biased away from the null, but less so than the traditional model. The 1-step and 2-step models had lower confidence interval coverage than the cluster model. Nonconvergence followed a similar pattern (Web Figure 7).
Figure 3.
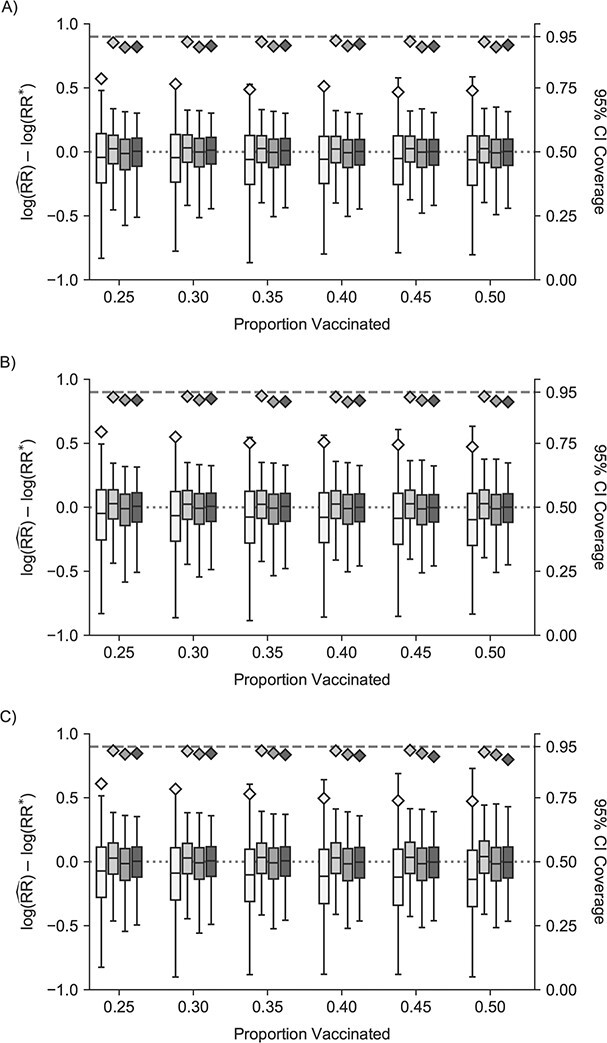
Study of Exclusion Criteria in a University Population (eX-FLU) simulation results for a hypothetical vaccine with a moderate unit-treatment effect. A) No infectiousness effect; B) weak infectiousness effect; C) moderate infectiousness effect. From light to dark gray (left to right), results are shown for the traditional model, cluster model, 1-step model, and 2-step model. The y-axis and box plots show the bias, defined as the regression model log-transformed risk ratio (RR) minus the true log-transformed RR. Whiskers indicate the 2.5th and 97.5th percentiles. The z-axis and diamonds show the 95% confidence interval (CI) coverage, defined as the proportion of 95% CIs that contained the true value. The x-axis indicates the overall proportion of individuals vaccinated in the population in expectation. 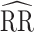 , estimated RR for the unit-treatment effect;
, estimated RR for the unit-treatment effect; 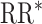 , true RR for the unit-treatment effect.
, true RR for the unit-treatment effect.
Assortativity
As the assortativity coefficient increased, the magnitude of the bias for the traditional model estimated unit-treatment risk ratio increased (Figure 4). This was true for both networks, with the stochastic block network bias increasing faster as a function of increased assortativity of treatment. The cluster, 1-step, and 2-step models remained less biased than the traditional model across all assortativity coefficients. The bias in the 1-step model also began to increase as assortativity increased, more notably in the stochastic block network. Nearly all models converged (Web Figure 8).
Figure 4.
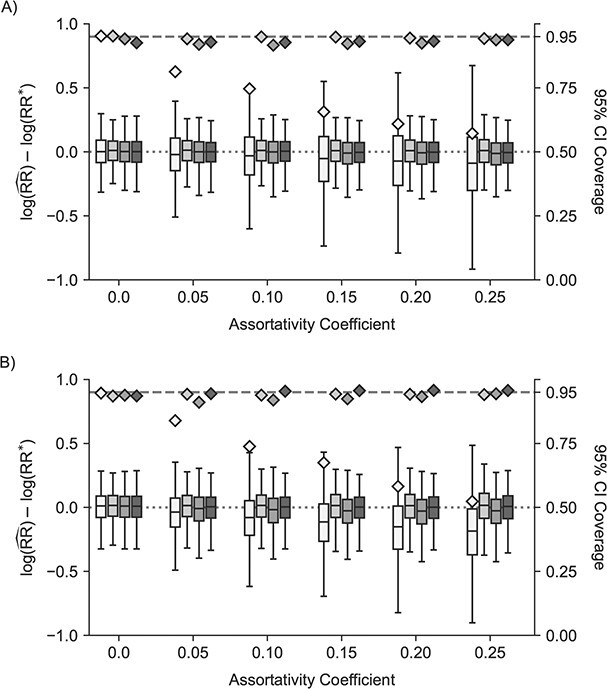
Study of Exclusion Criteria in a University Population (eX-FLU) and stochastic-block network simulation results for a hypothetical vaccine according to varying assortativity coefficients. A) eX-FLU network; B) stochastic-block network. From light to dark gray (left to right), results are shown for the traditional model, cluster model, 1-step model, and 2-step model. The y-axis and box plots show the bias, defined as the regression model log-transformed risk ratio (RR) minus the true log-transformed RR. Whiskers indicate the 2.5th and 97.5th percentiles. The z-axis and diamonds show the 95% confidence interval (CI) coverage, defined as the proportion of 95% CIs that contained the true value. The x-axis indicates the value for the assortativity coefficient in expectation. Higher values indicate greater assortativity. 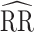 , estimated RR for the unit-treatment effect;
, estimated RR for the unit-treatment effect; 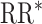 , true RR for the unit-treatment effect.
, true RR for the unit-treatment effect.
DISCUSSION
Through a variety of simulations, we demonstrated that estimates of the unit-treatment risk ratio were biased when either unit-treatment or infectiousness effects existed and the network was assortative by vaccination. We further demonstrated that bias increased as the assortativity by vaccination in the network increased. Our simulations add to previous work demonstrating that even if there is no unit-treatment or infectiousness effects of a vaccine, the confidence interval coverage can drop below the expected coverage in assortative networks. Poor confidence interval coverage means overestimated precision, more erroneous conclusions in the literature, and ultimately more conflicting studies, since investigators may mistakenly conclude that there is a protective or harmful unit-treatment effect more often than would be expected. This result is particularly concerning for vaccines or exposures that have no unit-treatment effects but have protective spillover effects, since assortativity can incorrectly lead to estimation of protective unit-treatment effects when ignored. An example of this scenario is malaria vaccines for prevention of human-to-mosquito transmission (32). Since the induced human immune response targets the invasion of the mosquito’s midgut by the malaria parasite, these vaccines are not expected to provide a direct benefit to vaccinated individuals but instead exert indirect effects by targeting the parasite in the mosquito stage to interrupt transmission. Finally, concerns regarding assortativity extend to other exposures related to infectious diseases. Assortativity has been observed for condom use (33), alcohol use (34), and other health behaviors related to sexually transmitted infections (33).
Assortativity by vaccination results in bias, since the assumption that each individual has an equal likelihood of pathogen exposure no longer holds (1, 2). Estimation of the unit-treatment risk ratio compares the incidence in vaccinated individuals with that in the unvaccinated, holding all else equal, where “all else equal” extends to include vaccination of contacts (2, 6). When vaccination is distributed randomly, this assumption holds in expectation. When assortativity by vaccination occurs, the comparison instead consists of some combination of unit-treatment and spillover effects, since contacts’ vaccination status differs by an individual’s vaccination status. Assortativity and protective spillover effects are expected to result in overestimation of the protectiveness of the unit-treatment risk ratio, as shown in the simulation results for scenarios of no unit-treatment effect but protective infectiousness effects. Our results are consistent with previous simulations in the context of no effect of tobacco use on human papillomavirus infection, which demonstrated that assortativity of tobacco use resulted in a harmful effect when only individual-level characteristics were considered (35). For scenarios with no unit-treatment or spillover effects, the traditional model was unbiased on average, but 95% confidence interval coverage was below nominal levels. By chance, a(n) (un)vaccinated individual becomes infected and subsequently infects immediate contacts who are more likely to have a similar vaccination status, leading to estimates further from the null. While these occurrences balance out over repetitions (hence why there is little bias in the scenario of no unit-treatment and spillover effects), the overestimation in either direction leads to reduced confidence interval coverage. Halloran and Struchiner (7) have proposed restricting analyses to only individuals who were exposed to the contagious agent in order to avoid this issue. However, this approach results in a reduced sample size, requires a precise definition for what constitutes exposure to the contagious agent, assumes that “all exposures to the infection are discrete and equivalent” (7, p. 145), and changes the estimand (i.e., conditions on infection of contacts).
Both the cluster and step models, which incorporated network effects into the models, outperformed the traditional model with regard to bias and confidence interval coverage across scenarios when vaccination was assortative. The cluster model performed well, as vaccination was randomly distributed within communities and there were relatively few connections between clusters. Despite the assumption of weak dependence being incorrect, the 1-step model outperformed the traditional model because it was able to capture some of the dependencies in the network. However, 95% confidence intervals were below the expected coverage levels of 95% in the eX-FLU network, and some residual bias was present (particularly under increasing assortativity). These observations are consistent with the 1-step modeling failing to sufficiently capture the full dependence structure in the network. The 2-step model was meant to capture additional dependencies in the network by expanding the sphere of influence allowed. Both of these approaches rely on strong parametric assumptions. Many alternative formations of the proposed 1-step vaccination exist (e.g., sum of contacts’ covariates, thresholds (36), etc.). Two-step vaccination has even more alternative formations, and care should be taken when selecting the summary measure. Additionally, 1-step and 2-step summary measures assume all contacts are equivalent, but these measures could instead be defined through a weighted network (e.g., number of sexual contacts between 2 individuals) or have multiple measures that are stratified by edge attributes (e.g., relationship types).
Our simple approaches of incorporating network information are based on the concepts of other approaches used to address interference. First, the cluster model operates similarly to methods that assume partial interference—that interference occurs within groups but not between groups (37). These approaches included 2-stage randomization (6), household studies (38), minicommunity studies (39), geography-based clusters (40), and extensions of inverse probability weights (41–43). The major advantage to partial interference is that use of exclusive group data allows for application of standard statistical theory (5, 11, 41). While our example consists of communities defined by the underlying network, there may be structural or environmental features that strongly determine contact patterns (e.g., classrooms, isolated villages, etc.) that are reasonable to use instead.
General interference instead allows for interference to occur between any 2 individuals in the sample, but it is often restricted to edges in a network. The 1-step and 2-step models are examples of general interference with restrictions on general interference to immediate or second-order contacts, respectively. Network summary measures have been proposed for risk assessment (44), outbreak detection (45), and use in estimation (46) and causal inference (47, 48). One example for causal inference is the extension to targeted maximum likelihood estimation that summarizes immediate contacts through parametric measures under the assumption of weak dependence (49–51). In order to address possible violations in the weak dependence assumption, use of longitudinal data, with the amount of time between follow-ups chosen to limit interference to immediate contacts, has been suggested (50, 51). Lastly, an extension of the g-formula (auto-g-computation) avoids the assumption of weak dependence and allows for any units connected in a network to be dependent (52).
The advantage of some previously described alternatives in the contexts of partial and general interference over our simple corrections are that those approaches retain marginal interpretations, allow alternative estimands outside of the unit-treatment risk ratio, and provide valid inferences. First, the proposed models that incorporate information from the network are conditional on the network summary measures used. While the marginal and conditional unit-treatment risk ratios were similar in our simulations, unit-treatment risk ratio estimates conditional on information from the network may not always closely approximate the marginal unit-treatment risk ratio. Approaches like inverse probability weights for partial interference (41, 42) or auto-g-computation (52) retain the focus on the marginal parameter. Second, there are a variety of other potential estimands of interest in a setting with interference. Our simulations focus solely on the unit-treatment risk ratio. However, the unit-treatment risk ratio in the context of differing 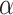 ’s or estimation of spillover effects is probably of interest as well.
’s or estimation of spillover effects is probably of interest as well.
There are several items readers should note regarding the interpretation of our simulations. First, our simulations predominantly used an assortativity coefficient of 0.10, which is a mild level of assortativity. Assortativity above this level has been observed for influenza vaccination among US high school students (12), suggesting the threats to validity may be even greater. Second, we relied on a static network of contacts in which all contacts had equal probabilities of transmission conditional on vaccination. Contacts in reality are more complex and vary over time. Third, the 1-step measure performed better in the eX-FLU network, which had a higher clustering coefficient than the stochastic block network, suggesting that the performance of these approaches depends on the underlying network structure. Further work on comparing approaches and their performance based on differing network characteristics is needed. Fourth, 1-step and 2-step summary measures are assumed to be adequate parametric representations of how contacts affect an individual. Alternative definitions for 1-step measures, their performance, and model selection are areas for future work. Some assortative networks in which exposure is less common may preclude the use of more flexible models because of separation (31), as seen in the 1-step and 2-step models for the eX-FLU network when the overall proportion vaccinated was 25%. Reducing the flexibility of the model, use of penalized regression, or use of Bayesian methods may help to alleviate issues (53), but estimation of the unit-treatment effect may not be possible when the assortativity coefficient is near 1 (e.g., almost no vaccinated individuals have all unvaccinated contacts). Lastly, the infection parameters were not chosen on the basis of a particular disease; rather, the parameters were selected so as to remain constant across the different simulation scenarios and networks and reduce the run times of infection cycles.
In conclusion, through a variety of simulated outbreaks, we have demonstrated that assortativity by vaccination can result in biased estimates of the unit-treatment risk ratio. While they are discussed in terms of a hypothetical vaccine and infection, our simulation results apply broadly to exposures on contagious outcomes. Methods for addressing assortativity should be considered when evaluating interventions or exposures for contagious outcomes.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Department of Epidemiology, Gillings School of Global Public Health, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina, United States (Paul N. Zivich, Allison E. Aiello); Carolina Population Center, Chapel Hill, North Carolina, United States (Paul N. Zivich, Allison E. Aiello); Department of Statistical Science, Trinity College of Arts and Sciences, Duke University, Durham, North Carolina, United States (Alexander Volfovsky); and Department of Sociology, Trinity College of Arts and Sciences, Duke University, Durham, North Carolina, United States (James Moody).
P.N.Z. was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD) (grant T32-HD091058). A.V. and A.E.A. received funding from the National Institute of Biomedical Imaging and Bioengineering (grant R01-EB025021). A.E.A. acknowledges receipt of NICHD grants T32-HD091058 and P2C HD050924. The eX-FLU Study was funded by the Centers for Disease Control and Prevention (grant U01-CK000185).
Software code used to conduct the simulations and the stochastic block network are available on GitHub (28).
Conflict of interest: none declared.
REFERENCES
- 1. Greenwood M, Yule GU. The statistics of anti-typhoid and anti-cholera inoculations, and the interpretation of such statistics in general. Proc R Soc Med. 1915;8(Sect Epidemiol State Med):113–194. [PMC free article] [PubMed] [Google Scholar]
- 2. Halloran ME, Haber M, Longini IM Jr, et al. Direct and indirect effects in vaccine efficacy and effectiveness. Am J Epidemiol. 1991;133(4):323–331. [DOI] [PubMed] [Google Scholar]
- 3. Ross R. An application of the theory of probabilities to the study of a priori pathometry. Part I. Proc R Soc Lond Ser A. 1916;92(638):204–230. [Google Scholar]
- 4. Struchiner CJ, Halloran ME, Robins JM, et al. The behaviour of common measures of association used to assess a vaccination programme under complex disease transmission patterns—a computer simulation study of malaria vaccines. Int J Epidemiol. 1990;19(1):187–196. [DOI] [PubMed] [Google Scholar]
- 5. Tchetgen Tchetgen EJ, VanderWeele TJ. On causal inference in the presence of interference. Stat Methods Med Res. 2012;21(1):55–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hudgens MG, Halloran ME. Toward causal inference with interference. J Am Stat Assoc. 2008;103(482):832–842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Halloran ME, Struchiner CJ. Causal inference in infectious diseases. Epidemiology. 1995;6(2):142–151. [DOI] [PubMed] [Google Scholar]
- 8. Morozova O, Cohen T, Crawford FW. Risk ratios for contagious outcomes. J R Soc Interface. 2018;15(138):20170696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Eck DJ, Morozova O, Crawford FW. Randomization for the direct effect of an infectious disease intervention in a clustered study population [preprint] arXiv. 2018. (doi: arXiv:1808.05593v1). Accessed May 26, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Sävje F, Aronow PM, Hudgens MG. Average treatment effects in the presence of unknown interference [preprint]. arXiv. 2017. (doi: arXiv:1711.06399). Accessed May 26, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Halloran ME, Hudgens MG. Dependent happenings: a recent methodological review. Curr Epidemiol Rep. 2016;3(4):297–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Barclay VC, Smieszek T, He J, et al. Positive network assortativity of influenza vaccination at a high school: implications for outbreak risk and herd immunity. PloS One. 2014;9(2):e87042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Salathé M, Khandelwal S. Assessing vaccination sentiments with online social media: implications for infectious disease dynamics and control. PLoS Comput Biol. 2011;7(10):e1002199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Fenner F, Henderson DA, Arita I, et al. Smallpox and Its Eradication. Geneva, Switzerland: World Health Organization; 1988. [Google Scholar]
- 15. Ebola ça Suffit Ring Vaccination Trial Consortium . The Ring Vaccination Trial: a novel cluster randomised controlled trial design to evaluate vaccine efficacy and effectiveness during outbreaks, with special reference to Ebola. BMJ. 2015;351:h3740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Newman ME. Mixing patterns in networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2003;67(2):026126. [DOI] [PubMed] [Google Scholar]
- 17. Cohen-Cole E, Fletcher JM. Is obesity contagious? Social networks vs. environmental factors in the obesity epidemic. J Health Econ. 2008;27(5):1382–1387. [DOI] [PubMed] [Google Scholar]
- 18. Aiello AE, Simanek AM, Eisenberg MC, et al. Design and methods of a social network isolation study for reducing respiratory infection transmission: the eX-FLU cluster randomized trial. Epidemics. 2016;15:38–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Landherr A, Friedl B, Heidemann JA. Critical review of centrality measures in social networks. Bus Inf Syst Eng. 2010;2(6):371–385. [Google Scholar]
- 20. Blondel VD, Guillaume J-L, Lambiotte R, et al. Fast unfolding of communities in large networks. J Stat Mech Theory Exp. 2008;2008(10):P10008. [Google Scholar]
- 21. Smith N, Zivich P, Frerichs L, et al. A guide for choosing community detection algorithms in social network studies: the question-alignment approach. Am J Prev Med. 2020;59(4):597–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. McNutt L-A, Wu C, Xue X, et al. Estimating the relative risk in cohort studies and clinical trials of common outcomes. Am J Epidemiol. 2003;157(10):940–943. [DOI] [PubMed] [Google Scholar]
- 23. Zou G. A modified Poisson regression approach to prospective studies with binary data. Am J Epidemiol. 2004;159(7):702–706. [DOI] [PubMed] [Google Scholar]
- 24. Harris CR, Millman KJ, van der Walt SJ, et al. Array programming with NumPy. Nature. 2020;585(7825):357–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. McKinney W. Data structures for statistical computing in Python. In: van der Walt S, Millman J, eds. Proceedings of the 9th Python in Science Conference (SciPy 2010) [electronic conference proceedings]. Austin, TX: SciPy Developers; 2010:56–61. https://conference.scipy.org/proceedings/scipy2010/pdfs/seabold.pdf. Accessed August 2, 2021. [Google Scholar]
- 26. Hagberg AA, Schult DA, Swart PJ. Exploring network structure, dynamics, and function using NetworkX. In: Varoquaux G, Vaught T, Millman J, eds. Proceedings of the 7th Python in Science Conference (SciPy 2008) [electronic conference proceedings]. Pasadena, CA: SciPy Developers; 2011:11–15. http://conference.scipy.org/proceedings/scipy2008/paper_2/. Accessed August 2, 2021. [Google Scholar]
- 27. Seabold S, Perktold J. Statsmodels: econometric and statistical modeling with Python. In: van der Walt S, Millman J, eds. Proceedings of the 9th Python in Science Conference (SciPy 2010) [electronic conference proceedings]. Austin, TX: SciPy Developers; 2010:92–96. https://conference.scipy.org/proceedings/scipy2010/pdfs/seabold.pdf. Accessed August 2, 2021. [Google Scholar]
- 28. Zivich P. Publications code. https://github.com/pzivich/publications-code. Published April 24, 2020. Accessed May 26, 2021.
- 29. Halloran ME, Haber M, Longini IM Jr. Interpretation and estimation of vaccine efficacy under heterogeneity. Am J Epidemiol. 1992;136(3):328–343. [DOI] [PubMed] [Google Scholar]
- 30. Ogburn EL, VanderWeele TJ. Vaccines, contagion, and social networks. Ann Appl Stat. 2017;11(2):919–948. [Google Scholar]
- 31. Albert A, Anderson JA. On the existence of maximum likelihood estimates in logistic regression models. Biometrika. 1984;71(1):1–10. [Google Scholar]
- 32. Nunes JK, Woods C, Carter T, et al. Development of a transmission-blocking malaria vaccine: progress, challenges, and the path forward. Vaccine. 2014;32(43):5531–5539. [DOI] [PubMed] [Google Scholar]
- 33. Schneider JA, Cornwell B, Ostrow D, et al. Network mixing and network influences most linked to HIV infection and risk behavior in the HIV epidemic among black men who have sex with men. Am J Public Health. 2013;103(1):e28–e36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Cheadle JE, Stevens M, Williams DT, et al. The differential contributions of teen drinking homophily to new and existing friendships: an empirical assessment of assortative and proximity selection mechanisms. Soc Sci Res. 2013;42(5):1297–1310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Lemieux-Mellouki P, Drolet M, Brisson J, et al. Assortative mixing as a source of bias in epidemiological studies of sexually transmitted infections: the case of smoking and human papillomavirus. J Hygiene. 2016;144(7):1490–1499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Rudolph AE, Young AM, Havens JR. Examining the social context of injection drug use: social proximity to persons who inject drugs versus geographic proximity to persons who inject drugs. Am J Epidemiol. 2017;186(8):970–978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Sobel ME. What do randomized studies of housing mobility demonstrate? J Am Stat Assoc. 2006;101(476):1398–1407. [Google Scholar]
- 38. Millar EV, Watt JP, Bronsdon MA, et al. Indirect effect of 7-valent pneumococcal conjugate vaccine on pneumococcal colonization among unvaccinated household members. Clin Infect Dis. 2008;47(8):989–996. [DOI] [PubMed] [Google Scholar]
- 39. Halloran ME. The minicommunity design to assess indirect effects of vaccination. Epidemiol Methods. 2012;1(1):83–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Ali M, Emch M, von Seidlein L, et al. Herd immunity conferred by killed oral cholera vaccines in Bangladesh: a reanalysis. Lancet. 2005;366(9479):44–49. [DOI] [PubMed] [Google Scholar]
- 41. Perez-Heydrich C, Hudgens MG, Halloran ME, et al. Assessing effects of cholera vaccination in the presence of interference. Biometrics. 2014;70(3):731–744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Barkley BG, Hudgens MG, Clemens JD, et al. Causal inference from observational studies with clustered interference, with application to a cholera vaccine study. Ann Appl Stat. 2020;14(3):1432–1448. [Google Scholar]
- 43. Papadogeorgou G, Mealli F, Zigler CM. Causal inference with interfering units for cluster and population level treatment allocation programs. Biometrics. 2019;75(3):778–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Altmann M, Wee BC, Willard K, et al. Network analytic methods for epidemiological risk assessment. Stat Med. 1994;13(1):53–60. [DOI] [PubMed] [Google Scholar]
- 45. Christakis NA, Fowler JH. Social network sensors for early detection of contagious outbreaks. PLoS One. 2010;5(9):e12948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Root ED, Giebultowicz S, Ali M, et al. The role of vaccine coverage within social networks in cholera vaccine efficacy. PLoS One. 2011;6(7):e22971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Aronow PM, Samii C. Estimating average causal effects under general interference, with application to a social network experiment. Ann Appl Stat. 2017;11(4):1912–1947. [Google Scholar]
- 48. Bowers J, Fredrickson MM, Panagopoulos C. Reasoning about interference between units: a general framework. Political Anal. 2013;21(1):97–124. [Google Scholar]
- 49. Sofrygin O, van der Laan MJ. Causal inference in longitudinal network-dependent data. In: van der Laan MJ, Rose S, eds. Targeted Learning in Data Science: Causal Inference for Complex Longitudinal Studies. 1st ed. (Springer Series in Statistics). New York, NY: Springer Publishing Company; 2018:349–371. [Google Scholar]
- 50. Sofrygin O, van der Laan MJ. Semi-parametric estimation and inference for the mean outcome of the single time-point intervention in a causally connected population. J Causal Inference. 2017;5(1):20160003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Ogburn EL, Sofrygin O, Diaz I, et al. Causal inference for social network data [preprint]. arXiv. 2017. (doi: arXiv:1705.08527v1). Accessed May 26, 2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Tchetgen Tchetgen EJ, Fulcher I, Shpitser I. Auto-g-computation of causal effects on a network. J Am Stat Assoc. 2021;116(534):833–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Greenland S, Mansournia MA, Altman DG. Sparse data bias: a problem hiding in plain sight. BMJ. 2016;352:i1981. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


