Stock market efficiency: An intraday case of study about the G-20 group

Abstract

Given the importance of the financial markets in the global context, data analysis and new statistical approach are always welcome, especially if we are referring to G-20 group (the world's richest countries). As we know, the pandemic outbreak of COVID-19 has affected the global economy, and its impact seems to be inevitable (as it was in 2020). From the perspective of what was raised above, this paper aims to analyze the stock market efficiency in 21 indexes of G-20. We are going to do our analysis with intraday scale (of hour), from May 2019 to May 2020. In order to be successful in this analysis, we applied the DFA and the DCCA methods, to identify or not two points:

• i)Are G-20 stock market efficient in their weak form?
• ii)With open/close values, it is possible to identify some type of memory in G-20 group?

The answer to these points will be given throughout this paper. For this purpose, the entire analysis will be divided into two different time-scale: Period I, time-scale less than five days and Period II, with time-scale greater than ten days. In the pandemic times of COVID-19, our results show that taking into account the DFA method, for time-scale shorter than 5 days, the stock markets tend to be efficient, whereas for time-scale longer than 10 days, the stock market tend to be inefficient. But, with DCCA method for cross-correlation analysis, the results for open/close indexes show different types of behaviors for each stock market index separately.

G-20 stock market; COVID-19; Time-series analysis

1. Introduction

The outbreak of COVID-19 has caused global concerns. On January 30, World Health Organization (WHO) declared the pandemic to be a global health emergency. The easy spread of this virus has caused uncertainty in the global population. This epidemic has also changed people's lifestyles, and (bi)millions of people have been placed in isolation to reduce the transmission of the virus. Companies have closed to control the spread of the virus, causing loss of income and leading to significant levels of unemployment. Worldwide, flights have been canceled and transportation systems have been shut down. The clear consequence of this episode is that economic activities have been disrupted and many countries and stock exchanges have dropped sharply [1], [2], [3], [4]. As the disease has spread rapidly around the world, there is an enormous amount of data concerning the COVID-19, as never before seen (in many countries with under-reporting) for: active, recovered, and dead cases. The social isolation, a way to contain the spread of the virus in society, caused the financial markets to fall sharply at the pandemic beginning (almost simultaneously). The recovery of each financial markets, since then, has occurred in a different way, some have recovered more quickly and others not so much. A way to study the effect of the pandemic spread (indirectly) can be done by the financial market, and with Econophysics techniques [5], [6], [7], [8], [9], [10], [11], [12], [13]. An adequate way of analyzing data (time-series) using statistical methods is applied the Detrended Fluctuation Analysis, DFA [14], the Detrended Cross-Correlation Analysis, DCCA [15], as well as, the DCCA cross-correlation coefficient, ${\rho }_{DCCA}$ [16]. DFA method can be applied to analyze the auto-correlation of a given time-series and can identify the level of financial markets efficiency [17], [18], while the DCCA can be applied to analyze long-range cross-correlations between two time-series [19], [20], [21], [22].

Thus, taking into account the pandemic period and the stock market indexes, in this paper we aim to identify the stock market efficiency, in its weak form, looking specifically at the main stock market indexes of the G20 group (with intraday data). For this proposal we applied the DFA method, which will assess the presence or not of long memories in these time-series, and also, with the DCCA method, we analyze the cross-correlation between Open/Close indexes of the stock markets individually, in order to assess whether the stock market adjust efficiently, see [23] for more details.

Therefore, the main objective of this paper is to contribute in the informational efficiency for G-20 group in the context of COVID-19. For this implementation, the paper was organized as follows in the text: Section 2.1, presents the state of the art regarding the literature on efficient market hypothesis; Section 2.2, introduces the methodology; Section 3, exhibit the results; and Section 4, concludes the paper.

2. Literature revision and methodology

2.1. Literature revision

The efficient market hypothesis, EMH, of Fame [24] claims that the financial markets are efficient in relation to the information. In other words, an investor is not able to consistently achieve returns above the market average (with a certain level of risk), considering only the publicly available information at the present time. There are three assumptions:

• •The weak hypothesis, that considers that the prices reflect all publicly available historical information;
• •The semi-strong hypothesis, where the prices reflect all publicly available information, and also that the prices change instantly to reflect the new public information;
• •The strong hypothesis, where the prices reflect instantly the hidden or privileged information.

Many articles have been published within this premise, such as: [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35], [36]. Therefore, according to the efficient market hypothesis, on the weak form, we intend to contribute with a new statistical approach, following the methodology presented right below.

2.2. Methodology

The two statistical methods to analyze the stock market indexes, the first for auto-correlation and the other for cross-correlation analysis (with its referred coefficient), will be described shortly below in two sub-sections.

2.2.1. Detrended fluctuation analysis, DFA [14]

The DFA algorithm, for long-range auto-correlation analysis, is presented here in six steps:

• 1 -Consider a time-series $\{x_i\}$ with $i=1,...,N$ (time-series length). We integrate $x_i$ to obtain $X_k={\sum }_{i=1}^k[x_i-<x>]$, where <x> is the time-series mean, and $k=1,...,N$;
• 2 -The signal, $X_k$, is divided into $(N-n)$ overlapping boxes of equal length n (time-scale). Each box containing $(n+1)$ values, that starts at i and ends at $(i+n)$;
• 3 -For each box, we compute the local trend (a linear least-squares fit) on $X_k$, in order to obtain the adjusted value, ${\tilde{X}}_{k,i}$, with $(i\le k\le i+n)$;
• 4 -
  The integrated signal $X_k$ is subtracted with ${\tilde{X}}_{k,i}$ (detrended) to obtain:

  $$f_{DFA}^2(n,i)=1/(n+1)\sum _{k=i}^{i+n}{(X_k-{\tilde{X}}_{k,i})}^2;$$ (1)
• 5 -
  Now, for a given time-scale of length n, $F_{DFA\text{-}x}(n)$ is calculated by:

  $$F_{DFA\text{-}x}(n)=\sqrt{\frac{1}{(N-n)}\sum _{i=1}^{N-n}{f}_{DFA}^2(n,i)};$$ (2)
• 6 -The above steps are repeated for a broad of time-scales, $4\le n\le N/4$, to provide a relationship between $F_{DFA\text{-}x}$ and n.

More details about the DFA algorithm can be seen at the link below. https://physionet.org/content/dfa/1.0.0/ Therefore, if long-range auto-correlation appear, then $F_{DFA\text{-}x}\sim n^{{\alpha }_{DFA}}$, and ${\alpha }_{DFA}$ is a self-affinity parameter representing the long-range auto-correlation, such that [37]:

exponent	type of signal
αDFA < 0.5	long-range anti-persistent
αDFA ≃ 0.5	uncorrelated, white noise
αDFA > 0.5	long-range persistent

DFA method is able to identify seasonal components [38], [39], [40], and $F_{DFA\text{-}x}(n)$ can be applied to discriminate different types of signals [41]. However, we can applied the DFA generalization to analyze cross-correlation between two time-series, that is, the DCCA method [15], through its robust coefficient, ${\rho }_{DCCA}$, described just below.

2.2.2. DCCA cross-correlation coefficient, ${\rho }_{DCCA}$[16]

For two time-series, $\{x_i\}$ and $\{y_i\}$, of equal length N, we compute $X_k={\sum }_{i=1}^k[x_i-<x>]$ and $Y_k={\sum }_{i=1}^k[y_i-<y>]$, with $k=1,\cdots ,N$. Then, we generalized the DFA algorithm (six steps described above in DFA algorithm) to find $f_{DCCA}^2(n,i)\equiv 1/(n+1){\sum }_{k=i}^{i+n}(X_k-{\tilde{X}}_{k,i})(Y_k-{\tilde{Y}}_{k,i})$ (covariance of the residuals) and the detrended function by:

$$F_{DCCA\text{-}x,y}^2(n)\equiv {(N-n)}^{-1}\sum _{i=1}^{N-n}{f}_{DCCA}^2(n,i).$$ (3)

But, for quantify the level of cross-correlation, the DCCA cross-correlation coefficient can defined as the ratio between the detrended cross-correlation function, $F_{DCCA\text{-}x,y}^2$, and the detrended auto-correlation function, $F_{DFA\text{-}x}$ and $F_{DFA\text{-}y}$, for the time-series $\{x_i\}$ and $\{y_i\}$, respectively:

$${\rho }_{DCCA}(n)\equiv \frac{F_{DCCA\text{-}x,y}^2(n)}{F_{DFA\text{-}x}(n)F_{DFA\text{-}y}(n)}.$$ (4)

Some properties of ${\rho }_{DCCA}$ naturally appear, the most important is that:

$$-1.0\le {\rho }_{DCCA}\le 1.0$$

In this case, ${\rho }_{DCCA}=0.0$ means there is no cross-correlation between $\{x_i\}$ and $\{y_i\}$, and it splits the level of cross-correlation between positive and the negative case. This coefficient has been tested on selected time-series [21], [42] and proved to be quite robust, mainly for statistical analysis between non-stationary time-series [43], [44], [45], [46], [47], [48], among other cases. It is noteworthy that there is the ${\rho }_{DCCA}$ generalization, for more than two time-series analysis, what we call multiple DCCA coefficient, $DM{C}_{\mathrm{\text{x}}}^2$ [49], [50].

3. Data, results and discussion

3.1. Data

For this project we acquired the Open (first value at this time) and the Close (last value at this hour) data indexes, related to the 20 largest world economies, briefly identified as G-20 group. The indexes were obtained from Thomson Reuters platform (values in local currency, $S_i$), with intraday resolution (hour) and with one year of data, see Table 1 with these indexes for more details. In addition to the top twenty financial market indexes, we included the S&P 500, or SPX, a stock market index that measures the stock performance of 500 large companies listed on stock exchanges in the United States. It is one of the most commonly followed equity indexes, and many consider it to be one of the best representations of the U.S. stock market. As each index based on its own criterion, and that they usually have a very high standard deviation around their mean value, here we will analyze the return, commonly applied in economic and financial time-series analysis, i.e.:

$$r_i\equiv \ln \left(\frac{S_{i+1}}{S_i}\right)$$ (5)

As an example, Fig. 1 present the SPX index and respectively the return, with Open(black line)/Close(red line) values. In the naked eye, by the Fig. 1 (a), it is practically impossible to identify an appreciable difference between the values. This figure shows that the return has mean around zero allowing us to analyze basically the fluctuations (volatility). Also, the time-series comprises a complex time, with the beginning in January of the global pandemic outbreak (COVID-19). The return reveals a high volatility in the subsequent months, and the Open/Close indexes go together in this process. For an initial analysis, in the section 3.2 we present the descriptive statistical for all indexes, with Open/Close values.

Table 1.

Stock Market indexes description, for all G-20 group.

Country (Cur.)	Index	Symbol	Start	End	N
Argentina (ARS)	S&P MERVAL	MERVAL	14/05/2019	14/05/2020	1700
Australian (AUD)	S&P/ASX 200	AS51	15/05/2019	14/05/2020	1783
Brazil (BRL)	BRAZIL IBOVESPA	IBOV	15/05/2019	15/05/2020	1990
Canada (CAD)	S&P/TSX Composite	SPTSX	14/05/2019	14/05/2020	1763
China (CNY)	Shanghai Stock Exchange	SHCOMP	15/05/2019	14/05/2020	1220
Europe (EUR)	EURO STOXX 50 Price	SX5E	20/05/2019	18/05/2020	2175
France (EUR)	CAC 40	CAC	20/05/2019	18/05/2020	2289
Germany (EUR)	DAX	DAX	15/05/2019	14/05/2020	2149
India (INR)	S&P BSE SENSEX	SENSEX	16/05/2019	15/05/2020	1717
Indonesia (IDR)	Jakarta Stock Exchange Composite	JCI	15/05/2019	14/05/2020	1658
Italy (EUR)	FTSE MIB	FTSEMIB	15/05/2019	14/05/2020	2160
Japan (JPY)	JPX Nikkei Index 400	JPNK400	15/05/2019	14/05/2020	1701
Mexico (MXN)	S&P/BMV IPC	MEXBOL	14/05/2019	14/05/2020	1765
Russia (RUB)	MOEX Russia	IMOEX	15/05/2019	14/05/2020	2268
Saudi Arabia (SAR)	Tadawul All Share	SASEIDX	15/05/2019	14/05/2020	1219
South Africa (ZAR)	FTSE/JSE Africa Top40 Tradeable	TOP40	15/05/2019	14/05/2020	2249
South Korea (KRW)	Korea Stock Exchange KOSPI	KOSPI	15/05/2019	14/05/2020	1728
Turkey (TRY)	Borsa Istanbul 100	XU100	15/05/2019	14/05/2020	2458
UK (GBP)	FTSE 100	UKX	15/05/2019	14/05/2020	2162
USA (USD)	Dow Jones Industrial Average	INDU	14/05/2019	14/05/2020	1970
USA (USD)	S&P 500	SPX	14/05/2019	14/05/2020	1769

Figure 1.

The SPX index as a function of time (a) and the return (b) respectively with Open (black line) and Close (red line) values. The vertical dot line represents the pandemic start by WHO.

3.2. Descriptive statistical

For all indexes the mean value is around zero, but with different standard deviation values, see Fig. 2 (a). The standard deviation, sd, is presented in descending order (for open case), with Merval, IBOV, and SENSEX being the highest values, and JPNK400, JCI and IMOEX the lowest values. In the point of view of the degree of asymmetry of the distribution, Skewness (sk), the values are in general negative, see Fig. 2 (b), that is, the distribution has a heavier left tail. Finally, on the rule of classical descriptive analysis, we measure the Kurtosis, “the peakedness”, of the distribution. The excess of kurtosis, with kurt=0, tells us that the distribution is well adjusted to the normal distribution. The results showed that the distributions are leptokurtic (more concentrated than the normal distribution), mainly in the MERVAl index, see Fig. 2 (c). We can see that the results (sd, sk, and kur) for Open/Close values are very similar for all indexes. Therefore, if we want to produce a more sophisticated statistic, that give us a better information about the Open/Close return, we must choose other statistical tools, as shown below, with DFA and DCCA methods.

Figure 2.

Descriptive statistics with (a) standard deviation, (b) skewness, and (c) kurtosis for Open/Close return.

3.3. DFA results

As an example of the procedure for calculating the fluctuation function, $F_{DFA}\times n$, we choose the SPX index, as shown in the Fig. 3. This figure shows the DFA method applied to Open (left panel) and Close (right panel) return index. With the fluctuation function, $F_{DFA}$, we realize there are two possible intervals for further analysis, that are:

• 1.Period I, with $n<5$ days;
• 2.Period II, with $n>10$ days.

To confirm our premise, the complete result for all indexes can be accessed in the Supplementary Figures, with $F_{DFA}\times n$. Also, the complete DFA analysis can be found in the Table 2, here with ${\alpha }_{DFA}$ value at Open/Close cases, described in the Periods I and II, respectively. It should be noted that in the Table 2, the column h/day, means the number of hours on the specified stock market on a trading day. Continuing the analysis via DFA, Fig. 4 summarizes all results for ${\alpha }_{DFA}$. Most indexes presented an exponent ${\alpha }_{DFA}$ similar, if we look at these two time periods. This fact can be seen easily by visual comparison between Figs. 4 (a,c) and Figs. 4 (b,d). Also, we can see in Figs. 4 (a,b) for Period I, that in the average ${\alpha }_{DFA}\simeq 0.50$ (see the last line in the Table 2), theoretically designated here as a stock market weakly efficient. However, individually we can identified $0.5<{\alpha }_{DFA}<0.5$. Therefore, in G-20 group, MERVAL, SASEIDX, and MEXBOL are among those who have the greatest persistence (${\alpha }_{DFA}>0.5$), while IMOEX, DAX, and CAC are anti-persistent stock market (${\alpha }_{DFA}<0.5$). However, for the Period II, the stock market indexes show persistent behavior, and on average the Open/Close indexes had the same values, ${\alpha }_{DFA}=0.65$. But, each index has its own ${\alpha }_{DFA}$ value, with FTSEMIB, SPTSX, and DAX the biggest and SHCOMP, SASEIDX, and MEXBOL the lowest values.

Figure 3.

F_DFA as a function of n for SPX return index with Open/Close cases. This figure is split in two-time domain: Period I with n < 5 and Period II with n > 10 days.

Table 2.

G-20 Stock Market indexes with α_DFA exponent for Period I (n ≤ 5 days) and Period II (n ≥ 10 days) and open/close cases.

	Country	Symbol	Open		Close		h/day
			Per. I	Per. II	Per. I	Per. II
1	Argentina	MERVAL	0.59	0.60	0.59	0.60	7
2	Australian	AS51	0.52	0.71	0.52	0.71	7
3	Brazil	IBOV	0.52	0.64	0.52	0.64	8
4	Canada	SPTSX	0.52	0.74	0.52	0.72	7
5	China	SHCOMP	0.51	0.51	0.53	0.52	5
6	Europe	SX5E	0.47	0.72	0.44	0.72	9
7	France	CAC	0.45	0.69	0.45	0.69	9
8	Germany	DAX	0.45	0.74	0.45	0.74	9
9	India	SENSEX	0.50	0.64	0.50	0.64	7
10	Indonesia	JCI	0.53	0.60	0.49	0.60	6
11	Italy	FTSEMIB	0.47	0.76	0.47	0.76	8
12	Japan	JPNK400	0.52	0.61	0.51	0.61	7
13	Mexico	MEXBOL	0.54	0.55	0.48	0.55	7
14	Russia	IMOEX	0.44	0.73	0.44	0.73	9
15	Saudi Arabia	SASEIDX	0.56	0.54	0.56	0.54	4
16	South Africa	TOP40	0.49	0.67	0.49	0.67	9
17	South Korea	KOSPI	0.51	0.62	0.51	0.62	7
18	Turkey	XU100	0.46	0.63	0.46	0.63	8
19	United Kingdom	UKX	0.48	0.67	0.48	0.67	9
20	USA	INDU	0.47	0.65	0.47	0.65	8
21	USA	SPX	0.51	0.65	0.45	0.65	7
	Mean value	Mean	0.50	0.65	0.49	0.65

Figure 4.

α_DFA for G-20 indexes: (a) Open case at the Period I, (b) Close case at the Period I, (c) Open case at the Period II, and (d) Close case at the Period II.

With the result presented by the DFA method, via ${\alpha }_{DFA}$ exponent, it was not possible in general to identify a significant difference between the Open/Close return index. However, it is possible to measure how much these values are mutually related, and for this task we can apply the DCCA method, and the robust DCCA cross-correlation coefficient, ${\rho }_{DCCA}$.

3.4. ${\rho }_{DCCA}$ results

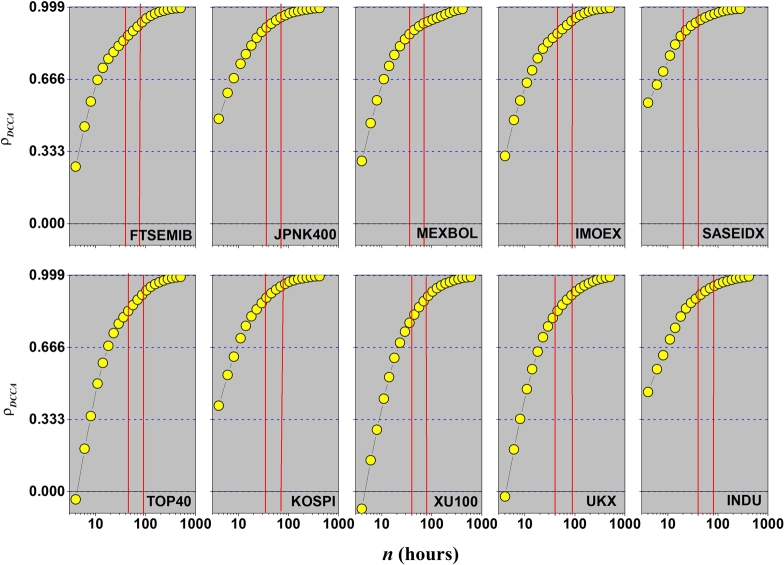
The objective in this sub-section was to apply the ${\rho }_{DCCA}$ between Open/Close return indexes. As an example of this application can be viewed in Fig. 5 with SPX index. Right now we can see ${\rho }_{DCCA}$ as a function of the time-scale n, with cross-correlation coefficient divided between ± weak, ± medium, and ± strong values (horizontal dash lines). For more technical details see [43]. Also, in the figure of ${\rho }_{DCCA}(n)$, we can see those two time Periods (I and II), with $n<5$ and $n>10$ days (vertical red lines). With ${\rho }_{DCCA}$ measured between Open/Close it is possible to see that its value is greater than 0, meaning there is a positive cross-correlation between the Open/Close return, but this cross-correlation is not perfect, with ${\rho }_{DCCA}<1$ for small time-scale, i.e., $n<5$ days. On the shortest time-scale, $n=4$ hours, ${\rho }_{DCCA}$ appears in the transition from weak to medium cross-correlation. However, ${\rho }_{DCCA}$ tends to strong cross-correlation quickly, with this effect in less than one business day. For long time-scale, namely $n>10$ days, ${\rho }_{DCCA}\sim 1$. The rest of the results for all indexes are presented in the Figs. 6 and 7 respectively, with ${\rho }_{DCCA}$ as a function of n. The results show that for time-scale $n>10$ days for all G-20 group, ${\rho }_{DCCA}$ tents to a perfect cross-correlation between the Open/Close return. However, for time-scale $n<5$ days there is a noticeable difference.

Figure 5.

ρ_DCCA as a function of n between Open/Close return with SPX index. The vertical lines represent respectively n = 35 (5 days) and n = 70 (10 days).

Figure 6.

ρ_DCCA as a function of n between open and close stock market (first 10 indexes).

Figure 7.

ρ_DCCA as a function of n between open and close stock market (last 10 indexes).

First, there are indexes with weak cross-correlation, such as: MERVAL, AS51, IBOV, SX5E, SENSEX, TOP40, XU100, and UKX Second, there are indexes in the transition from weak to medium cross-correlation: FTSEMIB, MEXBOL, IMOEX, and JCI Finally, there are indexes in the transition from medium to strong cross-correlation: SPTSX, SHCOMP, CAC, DAX, JPNK400, SASEIDX, KOSPI, and INDU It is important to highlight that the results for short time-scale only appear because originally intraday data, with time-scale of hours, was used. Continuing, it is clear to say that, for small time-scale, $n<5$ days, the results for ${\rho }_{DCCA}$ divided the G-20 group in three different samples: emerging (with weak cross-correlation), intermediate (with medium cross-correlation), and consolidated (with strong cross-correlation) economies. The exception noted here was seen for the United Kingdom, because this stock market presents hybrid results, and can have two interpretations: first due to the pandemic COVID-19, that all markets are currently subjected or because a causality referring to the BREXIT, see these papers [7], [51].

4. Conclusions

The COVID-19 pandemic outbreak has affected the global economy, and its impact on all financial markets is/was inevitable. In light of these events this article analyzes the stock market efficiency, in its weak form, among the G-20 group of more advanced economies with intraday data of price (in time-scale of hour), from May 2019 to May 2020 (one year). Here we analyze mainly two issues: (i) Are these stock markets efficient? If yes, (ii) could the presence of long-memories call into question the diversification of portfolios? In order to answer such questions, we performed two types of analysis with the return of prices, by auto-correlation (with DFA) and by cross-correlation (with DCCA).

Starting with DFA method, and with the premise that the most efficient stock market will be those with ${\alpha }_{DFA}=0.50$, we were able to identify first two time-scale, one with $n<5$ (Period I) and the other with $n>10$ days (Period II). For $n<5$ days the stock markets tend to be more efficient, with ${\alpha }_{DFA}\simeq 0.50$ on average. But, looking at individually, the following comparison can be performed between (${\alpha }_{DFA}$-open; ${\alpha }_{DFA}$-close): (i) for the Period I, ${\alpha }_{DFA}$-open ≃ ${\alpha }_{DFA}$-close, with a value close to 0.5, i.e., most efficient in their weak form. (ii) for the Period II, of long time-scale, the results present long-range auto-correlations with ${\alpha }_{DFA}\simeq 0.65$ on average, going out of its weak form of efficiency.

Therefore, the DFA method was unable to differentiate the opening from the closing index. Then, in order to improve the study of the efficiency of stock market with Open/Close values we applied ${\rho }_{DCCA}$ coefficient. The results show that for $n>10$ days, the value of ${\rho }_{DCCA}$ tends to 1.00 (perfect DCCA cross-correlation). However, for small time-scales, $n<5$ days, ${\rho }_{DCCA}$ show existence of weak cross-correlations in emerging economies (except UKX), and cross-correlations values ranging from medium to strong analyzing the consolidated economies. Thereby, it was possible to identify, in a short time-scale (less than 5 days), the most efficient stock markets. These results clearly answer the questions raised at the beginning of this paper.

Finally, as a suggestion, we will investigate the entire effect of the pandemic on the G-20 indexes. In this sense, our proposal will be to analyze these indexes for two periods, one before the COVID-19 and another during/“after” the COVID-19. Preliminary result in this direction can be see in the Supplementary Figures, for S&P 500 index.

Declarations

Author contribution statement

Gilney F. Zebende, Rui M. Santos Dias and Lazaro de Aguiar: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (310136/2020-2).

Data availability statement

Data associated with this study is available online at Thomson Reuters (https://finance.yahoo.com/quote/TRI/?guccounter=1)

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

Supplementary content related to this article has been published online at https://doi.org/10.1016/j.heliyon.2022.e08808.

No additional information is available for this paper.

Supplementary material

The following is the Supplementary material related to this article.

suplementaryf_v02_V2.pdf

Supplementary Figures.