SUMMARY
For microbiome biology to become a more predictive science, we must identify which descriptive features of microbial communities are reproducible and predictable, which are not, and why. We address this question by experimentally studying parallelism and convergence in microbial community assembly in replicate glucose-limited habitats. Here, we show that the previously observed family-level convergence in these habitats reflects a reproducible metabolic organization, where the ratio of the dominant metabolic groups can be explained from a simple resource-partitioning model. In turn, taxonomic divergence among replicate communities arises from multistability in population dynamics. Multistability can also lead to alternative functional states in closed ecosystems but not in metacommunities. Our findings empirically illustrate how the evolutionary conservation of quantitative metabolic traits, multistability, and the inherent stochasticity of population dynamics, may all conspire to generate the patterns of reproducibility and variability at different levels of organization that are commonplace in microbial community assembly.
In brief
Microbiomes may be described at different levels of organization: from strains to metabolic functions. The predictability of microbiome assembly often increases as we zoom out and look at their emergent functional behavior. Due to the significant challenges of studying microbiomes in their natural habitats, these recurrent patterns remain poorly understood. Here, we investigate laboratory ecosystems exhibiting a similar pattern of functional convergence despite fine-scale taxonomic divergence. By combining experiments and modeling, we provide a mechanistic explanation for these patterns.
Graphical Abstract
INTRODUCTION
The structure and function of microbial communities result from a complex interplay between selection, historical contingency, and chance events, in a manner that remains poorly understood (Costello et al., 2012). Integrating all of the deterministic and stochastic ecological processes that shape community assembly into a predictive theoretical framework is a major aspiration in microbiome biology. To meet this challenge, we must understand how each of these ecological forces influence the structure and functional attributes of microbial communities.
Several recent studies in a range of natural microbiomes, including those of systems as diverse as soils (Nelson et al., 2016), the oceans (Louca et al., 2016a), plants (Burke et al., 2011; Louca et al., 2016b), and the human gut (Human Microbiome Project Consortium, 2012; Turnbaugh et al., 2009), have reported intriguing generic patterns of convergence and variation at different levels of ecological organization. When binned by metabolic pathway, the fraction of the community metagenome that is devoted to different metabolic functions is often quantitatively reproducible in similar habitats (e.g., the same body part in different individuals) (Louca et al., 2018). Yet, these studies also find that the taxonomic composition (particularly at the genus level or lower) is generally highly variable in these habitats. This has led to the proposal that environmental selection determines the fractions of the metagenome devoted to certain metabolic functions, whereas the taxonomic composition is less constrained and more sensitive to chance events, environmental heterogeneity, historical contingency, and other processes (Louca et al., 2016b, 2018). In contrast to these findings, other recent studies have reported that seemingly important metabolic functions, such as the enzymatic degradation of growth-limiting polymers, may also be affected by historical contingency (Bittleston et al., 2020).
Reconciling these observations and explaining them within a single theoretical framework is challenging, due to fundamental limitations that are inherent to natural surveys. Namely, working under natural conditions makes it difficult to perform well-controlled manipulative experiments. This limitation makes it difficult to draw direct mechanistic links between physiological processes at the cellular level and the patterns of ecological convergence and variation that are observed at the community level. We cannot generally explain, for instance, why the specific ratios of different metabolic pathways are what they are in a given natural environment, nor how they should change in response to specific perturbations, such as nutrient shifts or antibiotic treatment. Perhaps one of the biggest challenges is that the selective pressures experienced by microbes in most natural habitats are not known exactly, nor do we have a detailed chronology of the historical events that may have led to the current state of a community.
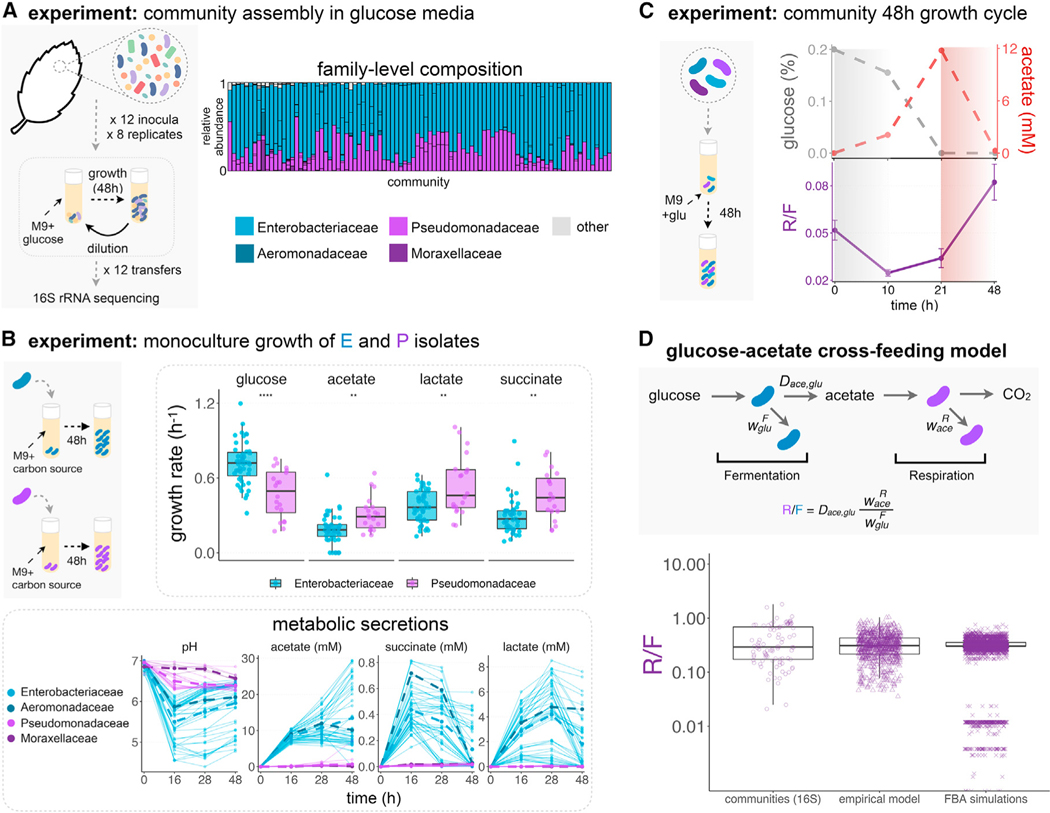
Some of these problems would be resolved if we were to study the assembly process in simpler and well-controlled habitats, where the selective and non-selective forces at play can be identified and mechanistically and quantitatively modeled (Carlson et al., 2020; Harcombe et al., 2014; Klitgord and Segrè, 2010; Sanchez and Gore, 2013; Zelezniak et al., 2015). To this end, we have recently investigated the self-assembly of hundreds of stable enrichment communities in replicate synthetic habitats of known biochemical composition and assembly history (Goldford et al., 2018). In these experiments, we found a strong convergence in community composition among replicate habitats at higher levels of taxonomy (i.e., family or higher), despite the presence of substantial variability at lower levels (i.e., genus). For instance, across N∼100 replicate glucose-limited habitats, communities in equilibrium adopted similar ratios of the two dominant taxonomic families (Enterobacteriaceae and Pseudomonadaceae), despite the different starting pools of species used to colonize each habitat. This is an example of ecological convergence (Figure 1A). At the same time, parallel community assembly experiments found that the species-level composition within each of these families was highly variable, diverging even across communities that were started from the same inoculum in identical habitats (Goldford et al., 2018).
Figure 1. Emergent metabolic structure in self-assembled microbial communities.
(A) Barplots show the relative abundance of the dominant families (Enterobacteriaceae, Pseudomonadaceae, Aeromonadaceae, and Moraxellaceae) in 92 communities started from 12 leaf or soil inocula (7–8 replicates each) after assembly in minimal media with glucose for 12 growth/dilution cycles (data from Goldford et al., 2018). Other families are shown in gray.
(B) Isolates belonging to different families were grown in monoculture for 48 h in minimal media supplemented with a single carbon source (CS) (glucose, acetate, lactate, or succinate) (N = 73, Figure S2). Each dot corresponds to an isolate’s maximum growth rate. Note that **** indicates p ≤ 0.0001, ** indicates p ≤ 0.01, two-sample t test. We measured the pH and quantified the amount of acetate, lactate, and succinate in the medium at various time points for all isolates. The dashed lines represent the mean concentrations for isolates of each family.
(C) Communities were thawed and grown in minimal media with glucose for a single incubation time. Samples were taken at 10, 21, and 48 h, and we measured the R/F ratio and the concentrations of glucose and acetate in the medium. Only one representative community (out of N = 9) is shown. See Figure S6 for other communities. The R/F ratio represents the mean ± SD of the CFU ratios calculated by bootstrapping (N = 1,000 replicates).
(D) Observed and predicted R/F ratio using a simple resource-partitioning model. The model assumes that the glucose is consumed by the fermentative specialist (F), whereas the acetate released as a metabolic by-product is consumed by the respirative specialist (R). Communities 16S: R/F ratio observed experimentally in the glucose communities described in Figure 1A (median = 0.29, Q1 = 0.17, Q3 = 0.69, N = 92). Empirically calibrated model: R/F ratio empirically calculated using parameters obtained from 47 Enterobacteriaceae isolates and 18 Pseudomonas isolates (STAR Methods; Figure S9) (median = 0.31, Q1 = 0.22, Q3 = 0.43, N = 846). FBA calibrated model: using Flux Balance Analysis, we calculated the biomass obtained from glucose fermentation by Enterobacteriaceae strains (F) and the biomass obtained from consumption of the F’s metabolic byproduct, acetate, by Pseudomonas strains (R). The predicted ratio between R and F biomass was calculated for 74 Pseudomonas metabolic models and 59 Enterobacteriaceae metabolic models. The simulations predict a median R/F ratio of ∼0.303 (Q1 = 0.302, Q3 = 0.356, N = 4,366) (Figures S9 and S10). Each dot represents a different Pseudomonas/Enterobacteriaceae pair.
However, the mechanisms responsible for these patterns of convergence and divergence at different levels of organization are unknown. It is tempting to hypothesize that, consistent with observations in natural habitats, family-level convergence in our laboratory-assembled communities may also reflect an emergent metabolic organization to which communities converge despite the unavoidable effects of chance, historical contingency, or idiosyncratic species interactions. As for the ecological processes leading to taxonomic variability at lower levels of taxonomy, we had originally speculated that alternative states in parallel assembly experiments may be due to sampling different taxa into different habitats from the same species pool (Goldford et al., 2018; Marsland et al., 2019). Alternatively, it is also possible that these represent alternative stable states, driven by multistability and stochasticity in population dynamics (Schröder et al., 2005).
In this paper, we set out to test these different hypotheses and to provide quantitative explanations for the observed quantitative patterns of convergence and variability at different levels of organization. To that end, we combine phenotypic assays and multi-replicated enrichment community experiments in defined media and link them with ecological and metabolic modeling. First, our findings indicate that quantitative nutrient utilization traits (i.e., growth rates and amount of nutrients secreted) are more deeply conserved than would be expected based on the shallow conservation of qualitative nutrient utilization traits in bacteria (Martiny et al., 2015). Second, we show that the previously observed convergent ratios of Pseudomonadaceae and Enterobacteriaceae in glucose enrichment communities reflect an emergent metabolic organization of microbial communities, where the latter specialize in the supplied glucose and the former in the organic acids released during overflow metabolism. Furthermore, we show that the ratio between the abundances of both functional guilds can be quantitatively explained by a simple resource-partitioning model. Third, we demonstrate that multistability explains the adoption of different compositions in replicate habitats and that the alternative community compositions are driven by the outcome of mutual inhibition between just two sub-dominant strains. Using dynamical systems theory, we can predict dynamical information, such as the location of the tipping points between alternative community states from the distribution of equilibrium abundances of just these two strains. Finally, we also show that, although alternative functional states are also possible when communities are propagated in isolation, these will collapse into a single functional state when connected through migration. Collectively, our work demonstrates the promise of using enrichment microbial community experiments and linking them with dynamical systems theory and systems biology models to quantitatively explain properties of experimental microbiomes—a step toward the aspiration of constructing a predictive theory of microbiome assembly (Costello et al., 2012; Estrela et al., 2021).
RESULTS
Family-level convergence reflects an emergent metabolic organization of self-assembled communities
As previewed above, we have recently found that natural bacterial communities that were serially passaged every 48 h in glucose minimal media self-assembled into stable communities containing N = 2–17 taxa, which coexist thanks to extensive cross-feeding interactions (Goldford et al., 2018). Despite their different starting inocula, these communities adopted highly reproducible compositions at the family (or higher) level of taxonomy, while varying widely in their composition at (or below) the genus level (Goldford et al., 2018). Communities were dominated by the Enterobacteriaceae (E), and in all cases the second most abundant family was the Pseudomonadaceae (P), at a median ratio of P/E = 0.27 (N = 92, Q1 = 0.15, Q3 = 0.70) (Figure 1A). The reasons for the strong reproducibility of community assembly at higher levels of taxonomic organization, and for the specific ratios of these two specific families, remain unknown. Based on simulations of community assembly using consumer-resource models, we had originally hypothesized that family-level convergence in our experiments may reflect an emergent metabolic organization that would map to the phylogeny through the conservation of quantitative metabolic traits at the family level (Goldford et al., 2018). Our mathematical models had suggested that the dominant family in our communities would be selected for their faster growth on the supplied resource, whereas the sub-dominant families would be selected by their competitive ability in the metabolic secretions (Goldford et al., 2018).
To evaluate the merits of this theory-motivated hypothesis, we collected 73 isolates (spanning a total of 11 genera) from 17 representative communities. Our isolates included members of the dominant Enterobacteriaceae family (N = 47 isolates) and the sub-dominant Pseudomonadaceae (N = 20 isolates), as well as other rarer families, such as Moraxellaceae (N = 3), Aeromonadaceae (N = 1), Alcaligenaceae (N = 1), and Comamonadaceae (N = 1) (STAR Methods). On average, our isolates represented 89.4% of the exact sequence variant (ESV)-level composition of the 17 communities from where they were collected (Figure S1; STAR Methods). We first measured the growth rates of all isolates in monoculture in the same M9 glucose minimal media where the communities had been originally assembled (STAR Methods). The vast majority of our isolates (72/73) were able to grow on glucose in monoculture (Figure S2). However, taken as a group, the Enterobacteriaceae isolates have much stronger growth rates in this medium than the Pseudomonadaceae isolates (mean(E, glu) = 0.72/h and mean(P, glu) = 0.47/h, p < 0.0001, two-sample t test, df = 32, N = 67; Figures 1B and S2). The finding that isolates belonging to the dominant family (Enterobacteriaceae) in our communities have, on average, a 60% growth advantage over the sub-dominant Pseudomonadaceae isolates is consistent with our hypothesis.
Although glucose is the only supplied resource, we have previously found that cross-feeding is rampant in these communities (Goldford et al., 2018). Because of their competitive disadvantage in the supplied glucose, we had hypothesized earlier that the permanence of Pseudomonadaceae in the community may be associated with stronger growth on the metabolic secretions of the Enterobacteriaceae. To identify what these byproducts may be, we used liquid-chromatography mass spectrometry (LC-MS) to analyze the most abundant secreted byproducts of glucose metabolism for a representative Enterobacter strain in our communities, as well as for E. coli MG1655 as a reference member of this family (STAR Methods). These two species also represent the two main forms of glucose fermentation typically found in the Enterobacteriaceae (Vivijs et al., 2015). The three dominant byproducts secreted by both strains into the environment during the exponential phase were acetate, lactate, and succinate (Figure S3), consistent with the known patterns of glucose overflow metabolism in Enterobacteriaceae (Vivijs et al., 2015). Of these, acetate was the most abundant, at a concentration of 4.7 ± 0.5 mM for E. coli and 6.0 ± 0.2 mM for Enterobacter after 28 h of growth. To test the generality of these secretion patterns, we quantified the amount of acetate, succinate, and lactate secreted by all of our Enterobacteriaceae isolates in glucose minimal media (STAR Methods). All three organic acids are strongly secreted by all the Enterobacteriaceae (at similar levels across isolates, with some genus-level variation Figure S4) but, as expected, to a much lesser extent by the Pseudomonadaceae (Figure 1B). Acetate, is in all cases, the dominant overflow byproduct (median = 8.5 mM, Q1 = 7.4 mM, and Q3 = 9.6 mM after 16 h of growth, N = 47).
If, as hypothesized above, the Pseudomonadaceae persist in our communities because of their growth advantage on the metabolic byproducts of the dominant Enterobacteriaceae, we should expect Pseudomonadaceae isolates to have a higher growth rate in the dominant organic acid (acetate), and possibly also in the others as well. To test this hypothesis, we measured the growth rates of all of our isolates in acetate, succinate, and lactate minimal media, separately (STAR Methods). Compared with the Enterobacteriaceae isolates, Pseudomonadaceae did indeed grow faster in acetate (mean(P, acetate) = 0.31/h versus mean(E, acetate) = 0.19/h, p < 0.01, two-sample t test, df = 31, N = 67), in succinate (mean(P, succinate) = 0.46/h versus mean(E, succinate) = 0.29/h, p < 0.01, two-sample t test, df = 27, N = 64), and also in lactate (mean(P, lactate) = 0.54/h versus mean(E, lactate) = 0.37/h, p < 0.01, two-sample t test, df = 24, N = 67) (Figures 1B, S2, and S5). Importantly, the vast majority of the isolates in our collection were also able to grow in all of the secreted nutrients (acetate, succinate, and lactate), regardless of the families they belonged to. Therefore, the difference in growth traits between families is quantitative rather than qualitative.
The outcome of these experiments is consistent with the theoretical explanation of family-level convergence due to quantitative (as opposed to qualitative) functional similarity, both in terms of niches created and in the growth response to the available resources. Thus, we propose that the Enterobacteriaceae in our communities (as well as the closely related Aeromonadaceae, which exhibits remarkably similar quantitative metabolic traits to the Enterobacteriaceae Figures 1B and S2) form a respiro-fermentative functional guild (F), which is selected due to their faster growth on the supplied glucose. In turn, the Pseudomonadaceae (together with the Moraxellaceae and Comamonadaceae) form a second functional group of respirative (R) bacteria, which is primarily selected by the organic acids released by the fermenters.
Because glucose is the only supplied resource at the beginning of each batch incubation, the scenario proposed above would predict that the fermentative (F) bacteria should initially increase in relative abundance over the respirative (R) group in the early phases of an incubation. This should lead to an early drop in the ratio between R/F abundances. By the time glucose is completely exhausted (which always occurs by 24 h of growth), the only carbon sources available are organic acids. Therefore, we should expect R specialists to have a growth advantage in the second half of the incubation, causing an increase in the R/F ratio. To test this prediction, we revived 9 stable communities from Goldford et al. (2018) (STAR Methods) and inoculated them on minimal glucose media at 30°C. We then measured the R/F ratio at different time points during a 48-h incubation (at 0, 10, 21, and 48 h), also quantifying the concentrations of glucose and acetate at each time. Consistent with our hypothesis, fermenters have a growth advantage in all communities (characterized by a drop in the R/F ratio) early on the incubation period (T = 0–10 h) when glucose is abundant (Figures 1C and S6). In turn, respirators have a growth advantage (characterized by an increase in the R/F ratio) in the second part of the incubation period (T = 21–48 h) (Figures 1C and S6), when glucose is absent but organic acids are abundant. Consistent with our hypothesis, the initial growth advantage of the F guild was accompanied by a depletion of glucose, whereas the later growth advantage of the R guild is concomitant with a depletion of acetate (Figures 1C and S6).
Although glucose is primarily metabolized by the F specialists and acetate is primarily metabolized by the R specialists, the latter do still grow (albeit less than F specialists do) within the first phase of the incubation where glucose is the only carbon source. This raises the question of whether R could be selected because of their growth on glucose rather than their significantly faster growth on the metabolic byproducts of F. To directly test this alternative hypothesis, we performed a new experiment where communities composed of three Enterobacteriaceae and one Pseudomonas were passaged under conditions that select for fast growth on glucose. For this, we shortened the incubation time to 12 h (instead of the usual 48 h), a time that is too short for a significant accumulation of organic acids and for the communities to reach stationary phase. As shown in Figure S7, under this scenario Pseudomonas are generally excluded from the communities and only Enterobacteriaceae are found. This provides further evidence that the R strains (such as Pseudomonas) are not selected for their growth on glucose but rather because of their fast growth on the organic acids secreted by the F strains.
In additional sets of assembly experiments, we have found that when communities lacked either Enterobacteriaceae or Pseudomonadaceae, these families were replaced at similar frequencies by members of other families with similar functional roles. For instance, Enterobacteriaceae can be replaced by Aeromonadaceae (Figures 1A and S8), another family of known respiro-fermentative bacteria that grow strongly in glucose (Figure S2) and produce the same organic acids as Enterobacteriaceae (Figure 1B). Likewise, we have observed that Pseudomonadaceae could be replaced by either Moraxellaceae (Figures 1 and S8) or Alcaligenaceae (Figure S8). These Alcaligenaceae do not metabolize glucose at all, and they are pure organic acid specialists. All of these enrichment communities have different family compositions but highly similar convergent ratios of organic acid respirators to glucose fermenters to the one found in Figure 1A (median R/F = 0.29, Q1 = 0.17, Q3 = 0.69, N = 92). This further supports the idea that family-level convergence reflects a convergent functional self-organization, which arises due to the evolutionary conservation of quantitative metabolic traits, such as the strength of niche construction and the growth-rate response to nutrients.
A simple metabolic model quantitatively explains the ratio of both functional groups
However, this does not explain why the observed ratio is R/F = 0.29. To test whether this ratio could be explained from simple metabolic principles, we develop a minimal two-species resource-partitioning model (STAR Methods). Briefly, the model assumes that all supplied glucose is consumed by the F specialist, whereas the excreted acetate is consumed by the R specialist. By empirically parameterizing the model with our collection of F and R isolates, we find a median predicted R/F ratio of 0.31 (Q1 = 0.22, Q3 = 0.43, N = 846), very close to the experimentally observed median R/F ratio of 0.29 (Q1 = 0.17, Q3 = 0.69, N = 92) in our communities (Figure 1D). We explore the generality of this result using constraint-based metabolic modeling (flux balance analysis [FBA]; STAR Methods) and a set of previously published genome-scale models for 74 Pseudomonadaceae (Nogales et al., 2020) and 59 Enterobacteriaceae (Orth et al., 2011) strains, which do not represent any of the isolates in our communities. We find a median R/F ratio of 0.303 (Q1 = 0.302, Q3 = 0.356, N = 4,366), which is also well aligned with the experimental R/F ratio of 0.29 in our glucose communities (Figures 1D, S9, and S10).
Our communities were grown on glucose as the single carbon source. Is the observed R/F ratio specific to growth on glucose or is this a more general signature of fast growth on sugars that lead to the release of organic acids on which organic acid specialists can grow? By assembling a new set of communities in five other single carbon sources (three sugars and two organic acids) under identical conditions as the glucose experiments, we find that the R/F ratio is quantitatively very similar to the R/F ratio of the glucose communities in all sugars tested, which include a hexose (fructose), a pentose (ribose), and a disaccharide (cellobiose), but increases when non-fermentable carbon sources (citrate and glutamine) are used (Figure S11). This finding is consistent with our model, which predicts that because respirators have a growth advantage on non-fermentable carbon sources relative to fermenters, respirators are favored and fermenters disfavored; therefore, the R/F ratio should increase.
Replaying the tape of community assembly a large number of times revealed multiple alternative community states at the ESV level
Despite their quantitatively convergent metabolic self-organization, communities often exhibited substantial taxonomic variation at the ESV and genus levels, even when all communities were started from the same inoculum (Goldford et al., 2018). Based on consumer-resource simulations, we had originally hypothesized that the observed variability in species-level composition may be caused by the random sorting of species into different replicate habitats; that is, some genera may be sampled only into some but not all of the habitats (Goldford et al., 2018). An alternative mechanism that may also explain taxonomic divergence in parallel assembly experiments is the existence of alternative stable states in population dynamics (Amor et al., 2020; Case, 1990; Dai et al., 2012; Faust et al., 2015; Fukami, 2015; Schröder et al., 2005; Shaw et al., 2019). Multi-stability is a common outcome of nonlinear dynamics, and it has been reported in a wide range of biological systems (Axelrod et al., 2015; Dai et al., 2012; Hirota et al., 2011; Ozbudak et al., 2004; Rauch et al., 2017; Sorek et al., 2013).
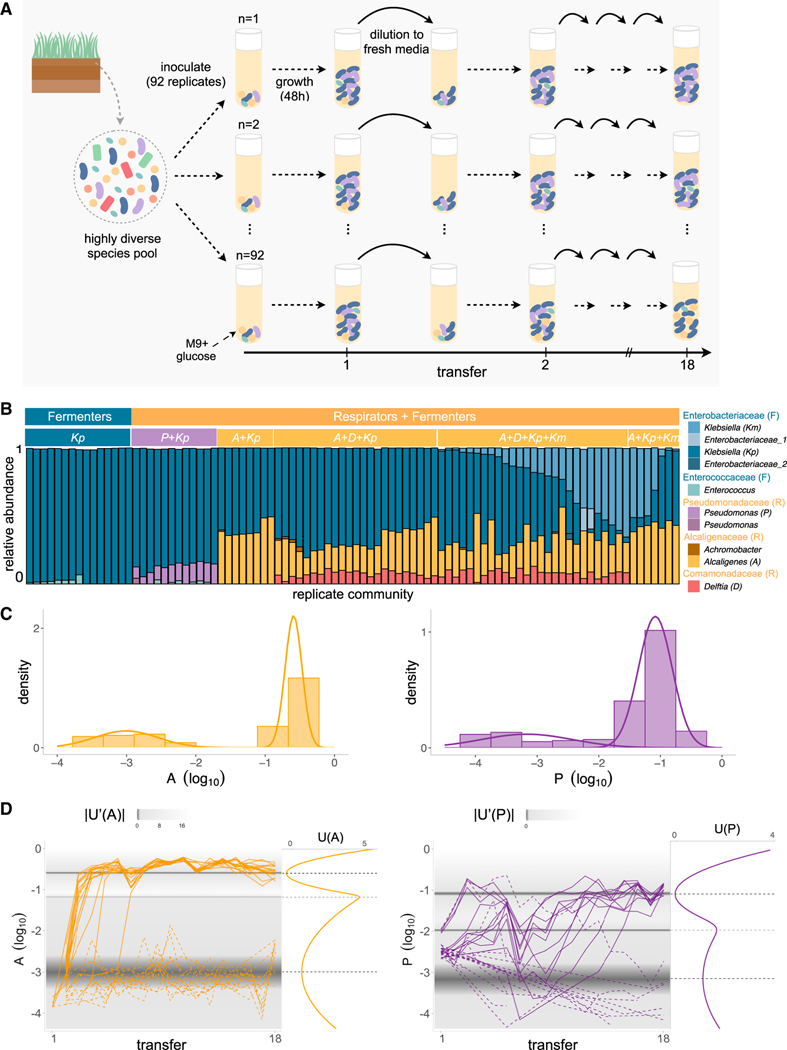
The number of replicates (eight per inoculum) used in the assembly experiment shown in Figure 1A is not high enough to unambiguously discriminate among these alternative (yet, compatible) hypotheses. This prompted us to start a new experiment with 92 parallel replicate communities, all seeded from the same environmental inoculum and propagated in minimal glucose media as we did before (Figure 2A). After 18 serial dilution transfers, most communities (77 out of 92) assembled into the metabolic structure described above, consisting of F and R specialists at proportions that fall within the range we had observed before (R/F = 0.46, Q1 = 0.34, Q3 = 0.65) (Figure 2B). We will leave the remaining 15 communities aside for now and return back to them in later sections of this paper.
Figure 2. Multiple alternative states at the metabolic and taxonomic level arise from assembly of replicate communities from a single inoculum.
(A) Schematic of experimental design: starting from a highly diverse soil microbial community, 92 communities were serially passaged in replicate habitats with glucose as the single carbon source for 18 incubation (growth/dilution) cycles (48 h each).
(B) Taxonomic profile of communities shown at the exact sequence variant (ESV) level (one color per ESV) with corresponding genus and family-level assignments. Only the ESVs with a relative abundance >0.01 are shown. After 18 transfers, we find that replicate communities self-assembled in two major functional groups, fermenters only (N = 15) or fermenters with respirators (N = 77). Within the fermenter functional group, we can see two alternative taxonomic compositions depending on whether one or two Klebsiella strains are present (Kp and Kp+Km). Within the respirator functional group, we can clearly identify three alternative taxonomic groups (Pseudomonas, Alcaligenes, and Alcaligenes + Delftia).
(C) Probability density distribution of the relative abundance of the dominant Alcaligenes (A) and Pseudomonas (P) ESVs at Transfer 18 all started from the same inoculum (N = 370 communities) (STAR Methods).
(D) Population dynamics of A and P for a subset of the communities represented in (C) (N = 31), where the background shows the absolute value of the derivative of the potential (U′ [x]) (left plots). The plots on the right of each timeseries show the potential (U[x]) (colored solid line) and the dark gray dashed lines show the local maximum (indicating the tipping point, x = −1.18 for A and x = −1.97 for P) between the two minima (indicating the stable states; light gray dashed line).
Consistent with previous experiments, our parallel assembly experiment resulted in communities with alternative taxonomic compositions. We identified two main states within the fermentative functional group and three alternative compositions within the respirative functional group. These alternative states are evident when we simply group together all communities that share the same set of ESVs above a threshold of 0.01 relative abundance (Figure 2B), and they are also generally consistent with the outcome of cluster analysis (Figure S12). The two main taxa in the R group are an ESV of the genus Alcaligenes (referred to further on as A) and an ESV of the genus Pseudomonas (referred to further on as P). Among the fermenters, the dominant taxa were two ESVs of the genus Klebsiella, hereafter referred to as Kp and Km, respectively (STAR Methods). The two, dominant respirator ESVs, Alcaligenes (A) and Pseudomonas (P), appear to be key determinants of taxonomic composition. They were never found together above an abundance of 0.01. In communities where A dominated the R guild, the F guild could contain either Kp alone, or both Kp and Km together above a 0.01 abundance threshold (R/F = 0.56, Q1 = 0.41, Q3 = 0.66). By contrast, when P dominates the R guild, the F guild would only contain one of these Klebsiella strains (Kp) but never the other, and it also may contain an ESV of the genus Enterococcus, which is, in turn, never found co-occurring with the A strain (R/F = 0.15, Q1 = 0.13, Q3 = 0.17). The composition of the respirator group is also strongly determined by its dominant taxa: the A strain may co-occur with a Delftia ESV (in N = 50 communities) and Achromobacter ESV (in N = 7 communities) and sometimes both (in N = 6 communities). The P strain, on the other hand, is never found together with neither Delftia nor Achromobacter. For simplicity, further on, we will refer to the state where A is the dominant member of the R guild as KA and to the state where P is the dominant member of the R guild as KP. However, note that these states may themselves contain several taxonomic alternative states. For instance, the KA state may not only consist of A coexisting with Kp but also with Km, Delftia, and/or Achromobacter.
The population dynamics of two R strains drive the formation of alternative stable states
What ecological mechanism governs whether a community will contain Pseudomonas or Alcaligenes as their dominant member of the R guild? A first hypothesis is random sampling: because there is no immigration, any community where either the A or the P strains were, by chance, not sampled into the habitat at the start of the experiment, will also not have these strains at the end (Goldford et al., 2018). Contrary to this hypothesis, we find that the P strain is still present below a relative abundance of 0.01 in ∼35% (23/65) of the A dominated communities (STAR Methods; Figure S13). Likewise, in ∼67% (8/12) of the P dominated communities, the A strain is also present below 0.01 relative abundance (STAR Methods; Figure S13). This result suggests that the alternative states we observed are in general not caused by randomly failing to inoculate either A or P in some of our habitats, nor is it caused by the stochastic extinction of established taxa during serial passaging.
The fact that both A and P may exist in either a low- or a high-abundance state in our replicate habitats suggests the possible existence of alternative stable states. For an initial exploration of this possibility we applied quasi-potential analysis (Hirota et al., 2011; Livina et al., 2010), an ecological method that has been recently applied to detect alternative states in the gut microbiome (Lahti et al., 2014). Quasi-potential analysis connects the probability density of a stochastic variable x (Q[x]) with the dynamical potential on which it moves (U[x]) through the Fokker-Planck equation (STAR Methods). This analysis allows us to derive the stable and unstable dynamical equilibria of the variable x, and we use it to separately estimate the potentials for A and P from their respective probability densities (N = 370 parallel communities) at transfer 18 (Figure 2C; STAR Methods).
For both strains, we detect a metastable state at low abundance and a stable equilibrium state at high abundance (indicated by the two local minima of the potentials, dark gray dashed lines), separated by a threshold (local maximum, light gray dashed line) (Figure 2D). To test whether the alternative equilibria and their switching thresholds are predictive of the assembly dynamics in our self-assembled communities, we sequenced the full temporal dynamics for a representative subset of 31 communities (Figure 2D). The predicted stable equilibria and thresholds for both strains are consistent with the observed population dynamics for each strain: when A or P jump over their predicted threshold they generally converge to the predicted high-abundance state, remaining there without switching back to the low-abundance state (Figure 2D).
These results are consistent with the existence of alternative stable states, but they fail to explain why we never see A and P together at high abundance. We hypothesize that this may be due to A and P mutually inhibiting one another when they are both at high abundance, so that once either of them reaches the high-abundance equilibrium, it prevents the other from switching to its own. This hypothesis would imply that, if we were to reconstitute communities with different initial abundances of A and P, we should find that neither of them may invade when rare if the other is at (or near) its high-abundance equilibrium.
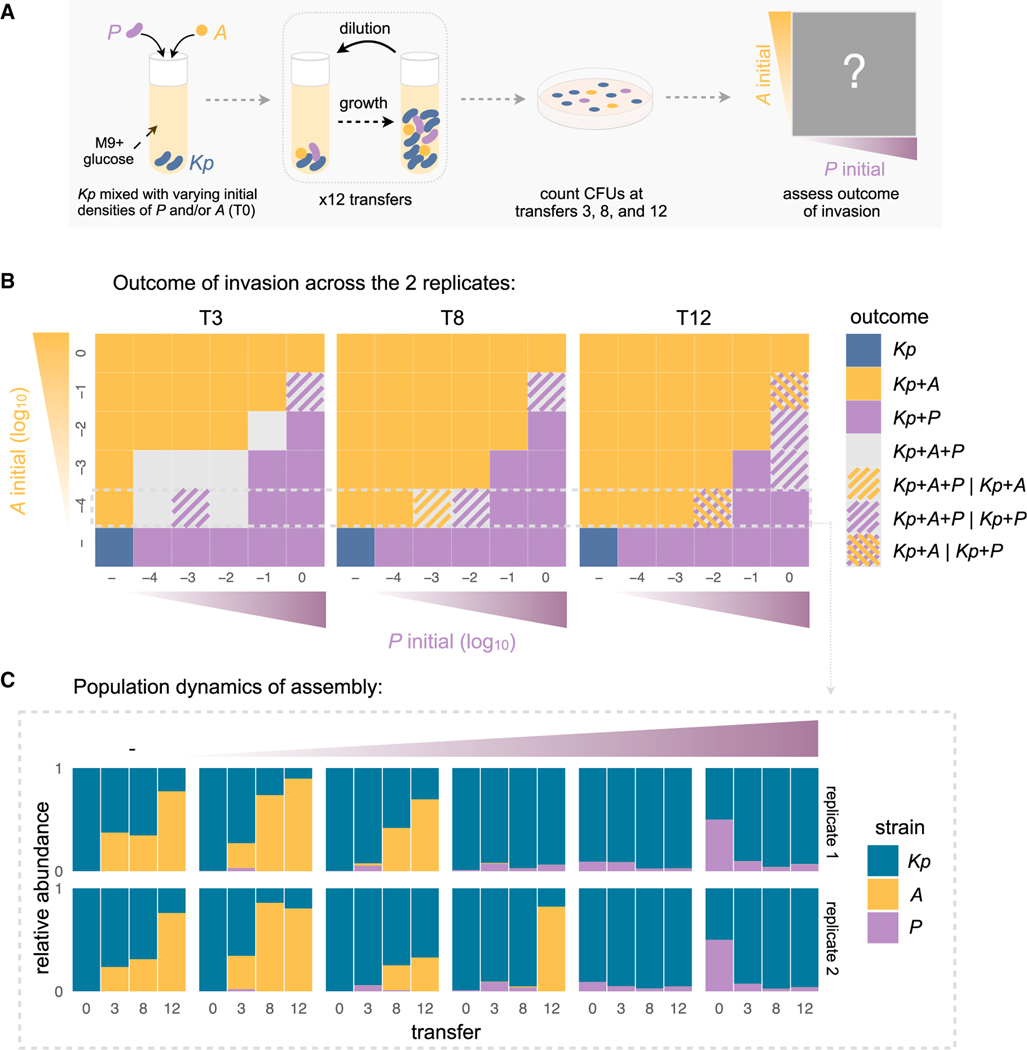
To test this hypothesis, we isolated the dominant strains (Kp, P, and A) and inoculated multiple populations of Klebsiella (Kp) with varying initial densities of A and P in minimal glucose media (Figure 3A). By starting multiple communities with regularly spaced densities of both species, and then allowing them to find their dynamical equilibria, we are also mapping out the basins of attraction of the stable equilibria in a two-dimensional phase portrait formed by A and P abundances (Chen et al., 2014; Sanchez and Gore, 2013) (Figure 3B; STAR Methods). To that effect, we passaged all these reconstituted communities for 12 growth-dilution cycles and measured their abundances at three different time points (Figure 3A) (STAR Methods). Consistent with the expectation of multistable population dynamics, we find that P and A both stably coexist with Kp, but generally not with one another regardless of their initial densities (Figures 3B, 3C, and S14). Importantly, and as expected from the multistability hypothesis, whether P or A is found in equilibrium depends on the initial state of the population in the phase portrait. In the upper-left side, where P starts at low and A at high abundance, communities converge to a state dominated by A (basin of attraction for A). In the lower-right part of the phase portrait, where the opposite is true, communities converge to a state dominated by P (basin of attraction for P) (Figure 3B). Although we kept the initial density of Kp constant across all treatments here, because Kp specializes primarily in the supplied glucose, it should equilibrate fast and therefore we expect the outcome to not be too affected by its initial abundance.
Figure 3. Multistable coexistence between two organic acid specialists explains the alternative attractors in community composition.
(A) We isolated the three dominant strains—Klebsiella (Kp), Alcaligenes (A), and Pseudomonas (P) that make up the two major alternative attractors and grew them in a pairwise coculture (Kp+A or Kp+P) or in a three-member consortia (Kp+A+P) by mixing Kp with different initial densities of A and/or P (see STAR Methods). These reconstituted communities were grown in the same conditions as the top-down assembly communities for 12 transfers (STAR Methods).
(B) Phase portrait showing the state of the community after T = 3, 8, and 12 transfers for 2 biological replicates. A square is colored yellow if a community that was started there contained A but not P at time T, and it is purple if it contained P but not A. It is gray if both A and P were present in both replicates. Squares with a seamless pattern show states where the two replicates exhibit different outcomes. We can see that the phase portrait is divided in two regions: the upper-left diagonal is made up by the basin of attraction of A dominated communities, whereas the bottom-right diagonal contains the basin of attraction for P dominated communities. A and P generally mutually exclude each other depending on their starting densities. See Figure S14 for the phase portraits of the two biological replicate experiments separately.
(C) Temporal dynamics of the relative abundance of each taxa for a subset of the communities shown in (B) (the 2 replicates are shown separately). See Figure S14 for the time series of all pairwise initial conditions of the phase portrait.
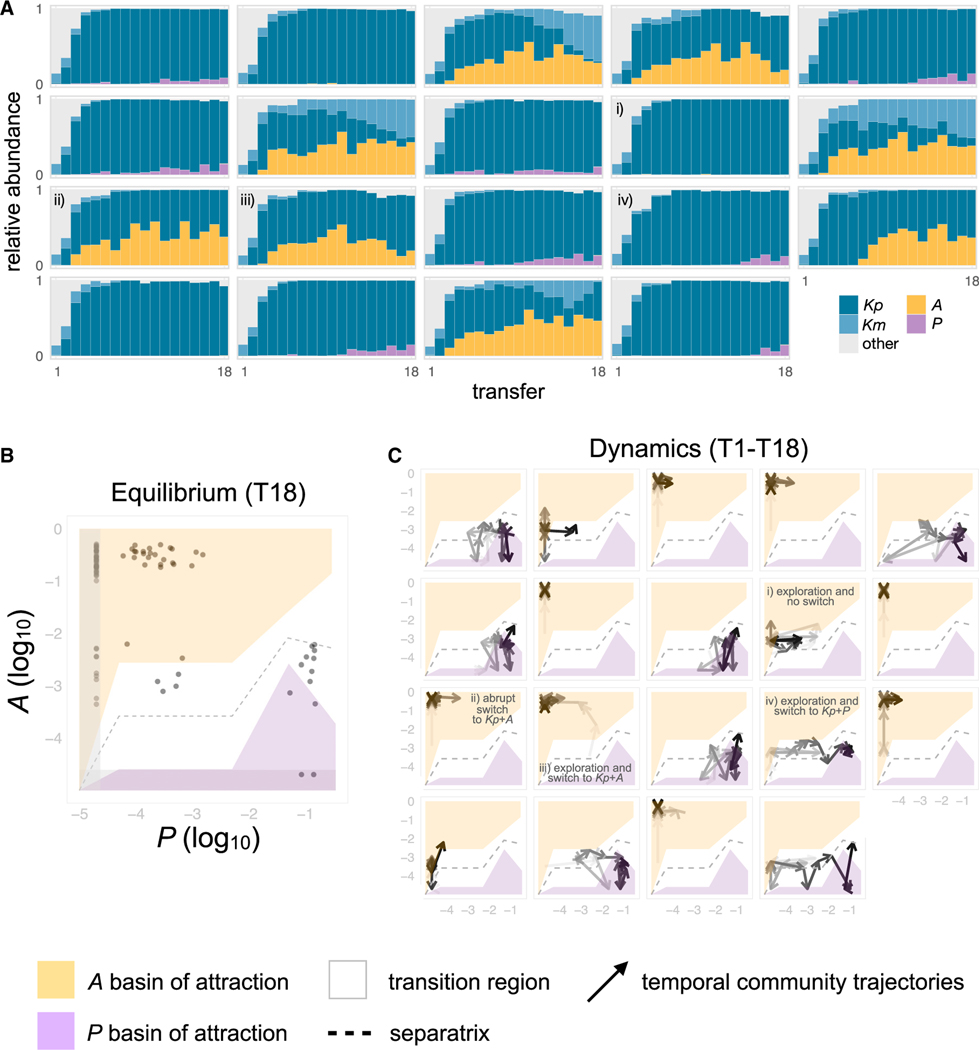
The outcome of the bottom-up invasion experiment in Figure 3B gives us the set of initial conditions of the basin of attractions for A and for P, which allows us to map the A-P phase portrait shown in Figures 4B and 4C. One may be skeptical of whether the basins of attraction inferred with this simple 3-member community will also describe our self-assembled communities, where many additional species are also present. To address this question, we projected the full temporal dynamics of the self-assembled communities (shown in Figure 4A) as trajectories over the A-P phase portrait mapped earlier (Figure 4C). The stable compositions of the self-assembled communities after 18 transfers fall within or very close to the basins of attraction inferred from the reconstituted, 3-species consortia (Figure 4). Communities start in a state where both P and A are low, and as time goes on, they fall into one of the two attractors and never switch back (Figure 4). Importantly for what follows, communities could also get trapped in the transition region where the separatrix between both basins of attraction is predicted to be, resulting in final states (after T = 18 transfers) where neither A nor P have yet reached their high-abundance state.
Figure 4. Multistable metabolic attractors between two organic acid specialists.
(A) Temporal dynamics for a subset of the replicate communities shown in Figure 2B (N = 19). Replicate communities were all started from the same inoculum and serially transferred to fresh minimal media with glucose every 48 h for a total of 18 growth-dilution cycles. Only the top four dominant ESVs (Kp, Km, P, and A) at transfer 18 are colored, other ESVs are shown in gray.
(B and C) Phase diagram showing the basins of attraction for Alcaligenes (A) dominated (yellow area) and for Pseudomonas (P) dominated (purple area) states, inferred from the outcome of the bottom-up invasion experiment in Figure 3B (STAR Methods), separated by a transition region (white area). The gray dashed line indicates the separatrix between the two basins of attraction. In (B), the dots show the relative abundance of A and P at Transfer 18 (N = 92) for the communities shown in Figure 2B. The gray shaded areas indicate the regions of low A and low P that are below the detection level of amplicon sequencing. In (C), overlaid are the trajectories of the relative abundance of A and P for all N = 19 communities shown in panel (A). The arrows become darker with time (i.e., from T1 to T18). At T0 (original inoculum), P was found at a relative abundance of 0.0086, whereas A was undetectable. We highlight four typical outcomes: the community explores the landscape and remains in the metastable state of low R/F (i), the community switches abruptly to the A dominated state (ii), the community explores the landscape and switches to the A dominated state (iii), and the community explores the landscape and switches to the P dominated state (iv).
Migration between communities funnels communities to functional convergence
Indeed, as already advanced in previous sections, a non-negligible fraction of the communities in Figure 2B (15/92) adopted an alternative functional state characterized by a low abundance of the respirative guild (R/F = 0.002, Q1 = 0.0014, Q3 = 0.0042). However, the results discussed above and shown in Figures 2, 3, and 4 suggest that these communities might be trapped in either a slow-dynamics transition region (near the separatrix) or in a metastable state. Previous theoretical and experimental work has shown that migration between communities can homogenize community composition, disfavoring metastable equilibria (Chase, 2003; Fodelianakis et al., 2019; Leibold et al., 2004; Stegen et al., 2013). Based on this premise, we hypothesized that opening the system by connecting communities through migration may destabilize this alternative functional state, pushing all communities toward the states with “typical” representation of both guilds.
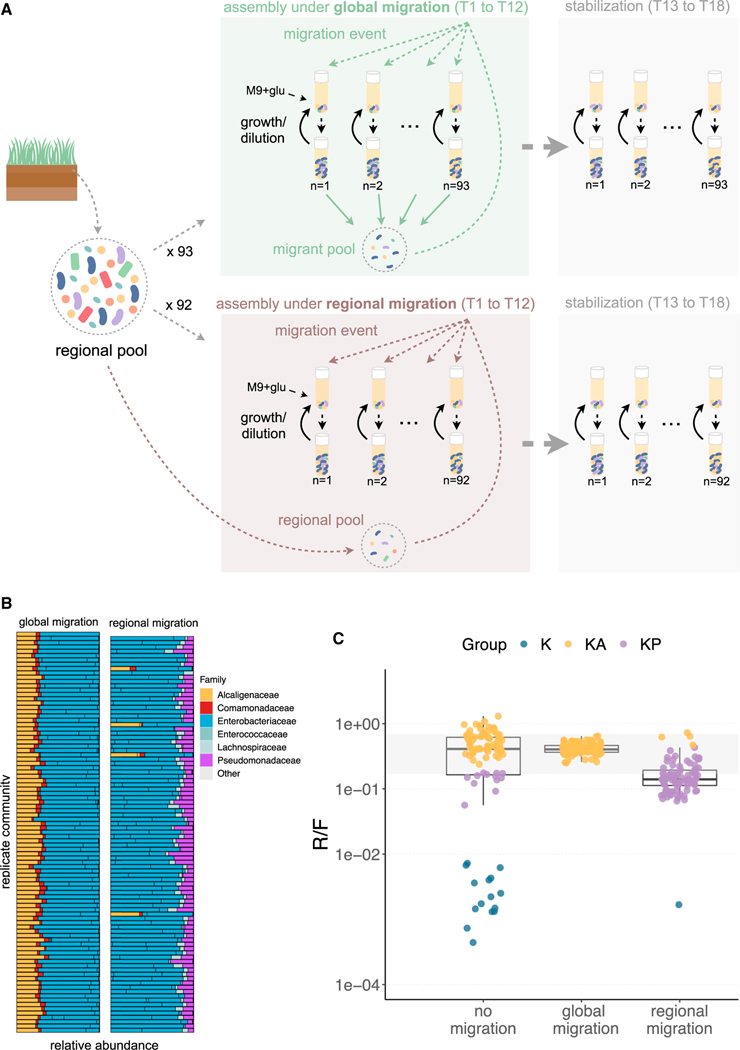
To test this hypothesis, we repeated our parallel community assembly experiments using the same initial inoculum in N = 93 identical habitats, but this time we also imposed migration between communities for twelve growth cycles (Figure 5A). We then allowed the communities to stabilize without migration for six additional transfers (Figure 5A). This experimental setup is similar to metacommunity dynamics with global dispersal (Leibold et al., 2004), and we hereafter refer to this treatment as “global migration” (Kryazhimskiy et al., 2012). Consistent with our hypothesis, we found that communities perturbed by global migration converged to a single metabolic attractor with a R/F = 0.40 (Q1 = 0.37, Q3 = 0.46, N = 93) (Figures 5B and 5C). At the taxonomic level, these communities all converged to the state most commonly observed in the closed system without migration, that is, the one dominated by the Enterobacteriaceae and Alcaligenaceae families (Figure 5B).
Figure 5. Opening the system through migration leads to functional convergence.
(A) Replicate communities all started from the same inoculum (and the same inoculum as in Figure 2) were assembled in an open system with global migration (N = 93)—that is, in addition to the normal transfer, each community received a small amount of migrants from a common migrant pool or with migration from the regional pool (i.e., inoculum) (N = 92) (STAR Methods). Communities were assembled under these migration scenarios for twelve growth cycles (T1–T12), after which migration was stopped, and communities were allowed to stabilize for six additional transfers without migration (T13–T18).
(B) Community composition at Transfer 18. ESVs with a relative abundance ≤0.01 are shown as “other”.
(C) R/F ratio of the communities at Transfer 18 for the no migration (Figure 2B), global migration, and regional migration (Figure 5B) treatments. Each dot represents a community and is colored by its taxonomic community state. The blue dots show communities mainly composed of fermenters, the yellow dots show communities where Alcaligenes is the dominant respirator, and the purple dots show communities where Pseudomonas is the dominant respirator. The gray shading area represents the interquartile range of the communities shown in Figure 1A.
To further validate this result, we repeated the same experiment, but this time, imposing migration from the regional pool for 12 transfers followed by stabilization for 6 transfers. This “regional migration” perturbation pushed all but one of the 93 communities away from the low R/F functional state, switching to either the Pseudomonas dominated state (n = 88) or the Alcaligenes dominated state (n = 4). This experiment also supports the hypothesis that the alternative, low R/F (∼0.002) functional state reflects either communities existing in a metastable state, or communities stuck near the separatrix. Given enough time, or sufficient perturbations, these low R/F communities will eventually collapse into a metabolic state with an R/F ratio that is comparable with those we had observed before and whose R/F ratios are also consistent with the predictions from our resource-partitioning model (Figure S15).
DISCUSSION
At the onset of this paper, we set out to address three questions that will help us understand the previously reported patterns of convergence and parallelism observed in multi-replicated microbial community assembly experiments. Does convergent family-level structure observed in these experiments reflect a convergent metabolic self-organization of our communities? If that is the case, can we quantitatively and mechanistically explain the ratios of different metabolic groups? What ecological processes may be responsible for the observed divergence at lower levels of taxonomy in parallel assembly experiments? Through a combination of experiments and mathematical models, we present strong evidence that the previously reported family-level convergence in minimal glucose-limited habitats reflects an emergent metabolic self-organization to which these communities converge. Bacteria belonging to the dominant family, mainly Enterobacteriaceae, are selected for their fast growth on the supplied glucose, and they all secrete similar amounts of organic acids as metabolic by-products (glucose fermenters, F). In turn, bacteria belonging to the sub-dominant family, mainly Pseudomonadaceae, are selected for their faster growth on the organic acids (respirative strategists, R).
To study the ecological mechanisms behind the observed divergence in species-level composition, we have replayed the proverbial tape of community assembly hundreds of times under different migration treatments. Our experiments indicate that both (1) alternative taxonomic compositions of the same functional guilds and (2) alternative functional states may arise from multi-stable population dynamics and that this multistability may be driven by interactions between just two key strains. These results indicate that the combination of multistability and stochasticity can generate historical contingency and lead to different taxonomic and functional structures in closed microbial communities assembled in parallel. This provides a potential explanation for a similar observation of alternative functional states in aquatic microcosms under serial passaging (Bittleston et al., 2020). We speculate that, similar to what we have found in our experiments, migration between these microcosms might eliminate this functional variation and lead instead to convergence.
Other studies that have reported functional variation in replicate habitats were performed under a single batch without passaging and involved competition for space (Zhou et al., 2013). Under these conditions, one would intuitively expect historical contingency to play an even larger role. By contrast, our experiments are done under serial passaging (rather than in a single batch) under a relatively high dilution factor (125x). This treatment replenishes nutrients and removes microbes from the habitat every 48 h, and this allows communities to reach a state of “generational” equilibrium (Sánchez et al., 2021). Our experiments were also done under a strong selection regime. How increasing stochasticity should affect community assembly at different levels of organization is still an open question, but one may speculate that the effect of neutral processes would be stronger as we do so (Aguirre de Cárcer, 2019; D’Andrea et al., 2020). Finally, although the ratio of respirative to fermentative bacteria is strongly convergent in our glucose-limited habitats, we should not necessarily expect all other metabolic functions to be equally convergent (Bittleston et al., 2020). The strength of the different selective pressures, the distribution of metabolic functions in the phylogeny, and other demographic and ecological processes, such as the nutrient flow rate through a system or the turnover rate, could all affect the degree of functional convergence. Putting together all of these and other ecological factors into a comprehensive theory of microbial community assembly will represent a major conceptual advance with the potential to unify disparate observations across different habitats and conditions (Bittleston et al., 2020; Fukami, 2015; Louca et al., 2018). Future work will be needed to help us understand how selective pressures constrain the functional assembly of microbial communities, and under which conditions we should expect the joint effects of chance and historical contingency to make it unpredictable. We hope that the work presented herein will help motivate new such studies.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Alvaro Sanchez (alvaro.sanchez@yale.edu).
Materials availability
This study did not generate new materials.
Data and code availability
The 16S rRNA sequencing abundance data are available at Dryad or Zenodo and are publicly available as of the date of publication. Accession numbers are listed in the key resources table.
The raw 16S rRNA amplicon sequences and metadata files have been deposited in the NCBI SRA database under accession number PRJNA761777 and PRJNA761387 and are publicly available as of the date of publication.
The whole-genome sequence reads for the 5 isolates have been deposited in the NCBI SRA database under accession number PRJNA749600.
The source data files and scripts used to generate the figures are available at https://github.com/sylestrela/Estrelaetal2021_FunctionalAttractors and Zenodo. DOI is listed in the key resources table.
The code for the FBA simulations are available at https://github.com/vilacelestin/Estrelaetal2021_FunctionalAttractors and Zenodo. DOI is listed in the key resources table.
Any additional information required to re-analyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT OR RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, peptides, and recombinant proteins | ||
|
| ||
| D-glucose | VWR | Cat. #0188 |
| Acetate | Sigma | Cat. #S8625 |
| D-lactate | Sigma | Cat. #71716 |
| succinate | Alfa Aesar | Cat. #419A3 |
|
| ||
| Critical commercial assays | ||
|
| ||
| glucose GO assay kit | Millipore | Cat. #GAGO20 |
| Acetate assay kit | Abcam | Cat. #ab204719 |
| D-Lactate assay kit | Abcam | Cat. #ab83429 |
| Succinate assay kit | Abcam | Cat. #ab204718 |
| DNeasy 96 Blood & Tissue kit | QIAGEN | Cat. #69582 |
| Quan-iTPicoGreen dsDNA Assay kit | Invitrogen | Cat. #P11496 |
| SequalPrep PCR cleanup and normalization kit | Invitrogen | Cat. #A1051001 |
|
| ||
| Deposited data | ||
|
| ||
| 16S rRNA sequencing abundance data | This study | https://doi.org/10.5061/dryad.5x69p8d3z |
| Genome scale metabolic models | This study | SRA: PRJNA749600 |
| Raw 16S rRNA amplicon sequences for communities assembled in glucose under different migration treatments | This study | SRA: PRJNA761777 |
| Raw 16S rRNA amplicon sequences for communities assembled in alternate carbon sources | This study | SRA: PRJNA761387 |
| Community abundance data | Goldford et al., 2018 | https://doi.org/10.5281/zenodo.3817698 |
|
| ||
| Software and algorithms | ||
|
| ||
| Source data files and code used to generate the figures. | This study |
https://github.com/sylestrela/Estrelaetal2021_FunctionalAttractors (https://doi.org/10.5281/zenodo.5510318) |
| Code for the FBA simulations. | This study |
https://github.com/vilacelestin/Estrelaetal2021_FunctionalAttractors (https://doi.org/10.5281/zenodo.5510298) |
| R (version 3.4.3) | (R Core Team, 2017) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.r-project.org/ |
RRID:SCR_001905 |
| DADA2 (version 1.6.0) | Callahan et al., 2016 | N/A |
| COBRApy (version 0.17.1) | Ebrahim A, Lerman JA, Palsson BO, Hyduke DR. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst Biol. 2013;7: 74. |
RRID:SCR_012096 |
| Mathematica (version 11.0.1.0) | Wolfram | RRID:SCR_014448 |
METHOD DETAILS
Resource partitioning model
To try to explain the observed R/F ratio to which our serially passaged enrichment communities converge after 12 transfers (Figure 1A), we develop a resource-partitioning model. Our working hypothesis is that most (though not necessarily all, as elaborated in the Methods S1; Figure S6) of the glucose is uptaken by the fermentative guild (F), while most (though, again, not all; Figure S6) of the organic acids they release as overflow byproducts (primarily acetate; Figure 1B) is captured by the respirative specialists (R). Therefore, we reasoned that the observed median R/F ratio may simply reflect the ratio between (i) the average amount of biomass that the respirative specialists may extract from the secreted acetate over the incubation period, and (ii) the average biomass the glucose specialists can extract from the supplied glucose over the incubation period. We illustrate and formalize this hypothesis in Figure 1D. With minimal additional assumptions, this resource partitioning hypothesis would predict an R/F ratio of
| (Equation 1) |
where is the average number of acetate molecules secreted per glucose molecule uptaken by the F specialists; is the average biomass yield of F specialists per glucose molecule over the entire incubation time, and is the average biomass yield of R specialists per acetate molecule uptaken over the entire incubation time. As described in the Methods S1, Equation 1 is an approximation, which includes only the effects of the two most abundant resources, glucose and acetate, while ignoring the other less abundant resources. In the Methods S1 we derive Equation 1, and explore additional limits where those other resources are also included.
An advantage of the model in Equation 1 is that it can be tested quantitatively. One could estimate the values of , , and that are characteristic of F and R bacteria in our communities, by measuring them in our collection of isolated taxa. If Equation 1 approximates the underlying ecology with sufficient realism, we should expect that evaluating it with those parameters should produce a value of the R/F ratio that is similar to that to which our enrichment communities converge. To test this model, we thus proceeded to estimate the value of for each of our F isolates, by measuring the total amount of acetate released at the time when glucose had just been exhausted, and dividing it over the amount of supplied glucose (STAR Methods and Methods S1). We then estimated and for each of our F and R isolates by growing them in monoculture in glucose and acetate media, respectively (STAR Methods and Methods S1; Figure S9A). In Figure 1D we plot the expected R/F ratio by evaluating Equation 1 with the parameter values obtained for all pairs of isolates in our collection. This empirically parameterized model gives us a median predicted R/F ratio of 0.31 (Q1=0.22, Q3=0.43, N=846), very close to the experimental R/F ratio of 0.29 (Q1=0.17, Q3=0.69, N=92) in our communities (Figure 1D).
To explore the generality of this result beyond the specific set of isolates in our communities, we set out to evaluate Equation 1 using constraint-based metabolic modeling (Flux Balance Analysis [FBA]; STAR Methods) and a set of previously published genome-scale models for 74 Pseudomonadaceae (Nogales et al., 2020) and 59 Enterobacteriaceae (Orth et al., 2011) strains, which do not necessarily represent any of the isolates in our communities. Because FBA assumes that microbes grow optimally, this approach will give us the expected R/F ratio that one should observe if Enterobacteriaceae and Pseudomonadaceae were using optimal metabolic strategies in glucose and acetate, respectively (STAR Methods). In Figure 1D, we show the result of evaluating Equation 1 by entering the computed values of , , and for all of the possible R-F pairs one can form from our set of genome-scale models (Figures S9B, S9C, and S10). The median R/F ratio was 0.303 (Q1=0.302, Q3=0.356, N=4366) which is also well aligned with the experimentally observed median R/F ratio of 0.29 (Q1=0.17, Q3=0.69, N=92) in our glucose communities (Figure 1D). Additional variations of this model that explored more stringent (but less realistic) limits, i.e. where the additional secreted byproducts are either all consumed by the R specialists or by the F specialists, or they are evenly split between R and F specialists, are discussed in the Methods S1 and Figure S16. All yielded R/F ratios that were within the range of values to which our empirical communities converged to. We also use FBA to show that oxygen is generally required for growth on acetate, lactate, and succinate (Methods S1; Figure S17). To confirm the validity of using genome-scale models from the literature, we also performed whole genome sequencing for 5 strains from our isolate collection (belonging to 5 different genera) (Figure 1B) and built genome-scale metabolic models of these strains (Methods S1). As shown in Figure S18, repeating our analysis using these models produced results that are in line with those observed for the library of published models.
Isolates collection
Isolates were collected from several communities previously stabilized in glucose minimal media and stored in 40% glycerol at −80C. The communities used were C1R2, C1R4, C1R6, C1R7, C2R4, C2R6, C2R8, C4R1, C7R1, C8R2, C8R4, C8R5, C10R2, C11R1, C11R2, C11R5, C11R6, where CXRY stands for initial environmental sample (inoculum) X replicate community Y (Goldford et al., 2018). These communities were plated in three different media: Tryptic Soy Agar (TSA) and minimal M9 supplemented with glucose or citrate at concentration 0.07 moles of carbon per liter. Isolates from these plates were streaked on the corresponding medium based on visual inspection of colony morphology after 2 and 5 days. Colonies from the streaked plates were streaked twice more on new plates, then cultured in the corresponding liquid medium (Tryptic Soy Broth (TSB), M9 glucose or M9 citrate) and stored at −80C with 40% glycerol.
Growth curves and maximum growth rate calculation
Isolates were streaked from glycerol on TSA plates and grown at 30C for 48h. Single colonies of each isolate were used to inoculate 500uL TSB in a deep-well plate. These pre-cultures were incubated at 30C without shaking for 48h. Pre-cultures were then diluted 1:1000 in M9 supplemented with either glucose (VWR, #0188), acetate (Sigma, #S8625), D-lactate (Sigma, #71716), or succinate (Alfa Aesar, #419A3) at a final concentration of 0.07 moles of carbon per liter. The final volume for the growth assays was 100uL in 384 well plates. Each isolate was assayed in two replicates. For computing the maximal exponential growth rate, the log(OD620) of each replicate was first smoothed by fitting a generalized additive model with an adaptive smoother, using the gam function from the mgcv package in R. This method allows for extraction of estimates of growth rate that are not biased by underlying assumptions when fitting predetermined models. The maximum of the derivative was taken as the exponential growth rate. We excluded the first 1h of growth, as well as all of the timepoints in the beginning of the curve that showed an OD<0.01, to avoid artifacts derived from measurement and fitting noise respectively.
LC-MS of E. coli and Enterobacter supernatant
E. coli MG1655 and an Enterobacter isolate from the glucose communities in (Goldford et al., 2018) were revived from frozen stock by streaking on LB Agar. Two replicate colonies of each strain were used to inoculate separate 50ml falcon tubes which contained 5ml of LB-Lennox and were incubated at 30C overnight (shaking at 200RPM). After ∼16h of growth, overnight cultures were brought into balanced exponential by three serial transfers into fresh LB (1ml of culture in 4ml of fresh media). The first two transfers were performed at 1h intervals whilst after the final transfer the cultures were allowed to grow for 1h and 30 min. Cells were centrifuged, washed and re-suspended 3 times, using 1.1x M9 media (containing no carbon source). After the final washing step, cells were normalized to an OD620 of 0.1. 500ul of M9 glucose in a 96 deep well plate was inoculated with 4ul of normalized cells, and grown at 30C. After 28h of growth, spent media was extracted using 0.2um AcroPrep filter plates. Spent media was submitted for a targeted metabolomics analysis carried out by the Metabolomics Innovation Center (TMIC), in Alberta, Canada, and described below.
The samples were analysed using a targeted quantitative metabolomics approach. This approach combines a direct injection mass spectrometry method with a reverse-phase LC-MS/MS custom assay. Together with an ABSciex 4000 QTrap (Applied Biosystems/MDS Sciex) mass spectrometer, this method allows the targeted identification and quantification of up to 143 different endogenous metabolites, including sugars, amino acids, biogenic amines & derivatives, acylcarnitines, uremic toxins, glycerophospholipids, and sphingolipids (Foroutan et al., 2019, 2020). This method combines the derivatization and extraction of analytes, and the selective mass-spectrometric detection using multiple reaction monitoring (MRM) pairs. For metabolite quantification, isotope-labeled internal standards and other internal standards are used. Mass spectrometric analysis was performed on an AB Sciex 4000 Qtrap® tandem mass spectrometry instrument (Applied Biosystems/MDS Analytical Technologies, Foster City, CA) equipped with an Agilent 1260 series UHPLC system (Agilent Technologies, Palo Alto, CA). The samples were delivered to the mass spectrometer by a LC method followed by a direct injection (DI) method. Data analysis was done using Analyst 1.6.2.
48h growth assay of single isolates
Isolates were revived from frozen stock and acclimated to growth on glucose minimal media (500uL) for 48h. 4uL of the grown cultures were then inoculated into 500uL fresh glucose media (4 replicates each) and samples were collected at different timepoints during the 48h growth cycle (one replicate used per timepoint, i.e. at 0h, 16h, 28h, and 48h). At each timepoint, 100uL of samples were collected, their OD620 was measured, followed by storage at −80C with 40% glycerol. The remaining samples were immediately centrifuged at 3000 rpm for 25min to separate the cells from the supernatant. The supernatant was transferred to a 96 well 0.2μm AcroPrep filter plate on top of a 96 well NUNC plate fitted with the metal collar adaptor and centrifuged at 3000 rpm for 10 min. The supernatant was immediately frozen at −80C until processing.
48h growth assay of communities
Previously stabilized communities in glucose minimal media for 12 serial transfers (Goldford et al., 2018) were revived from frozen stock and serially transferred for three passages on glucose minimal media, under the same experimental conditions as before. We selected a subset (N=9) of communities where fermenters and respirators were detected after three serial transfers. At the start of the fourth passage, 4 replicate 96-well plates were started. Samples were collected at different timepoints during the 48h growth cycle (one plate used per time point, i.e. at 0h, 10h, 21h and 48h). At each timepoint, 100ul of samples were taken and stored at −80C with 40% glycerol. The remaining samples were immediately centrifuged at 3000 rpm for 25min to separate the cells from the supernatant. The supernatant was processed as described above.
Glucose, acetate, lactate, and succinate assays
Glucose concentration was measured using the glucose GO assay kit from Millipore (GAGO20). Acetate concentration was measured using the Acetate assay kit (ab204719). D-lactate concentration was measured using the D-Lactate assay kit (ab83429). Succinate concentration was measured using the Succinate assay kit (ab204718). For each assay, the supernatant was diluted (if needed) to ensure that the OD readings are within the standard curve range.
pH measurement
Determination of pH was done using the same filtered supernatant as for the assays described above. Bromocresol purple (BCP) was used as a pH indicator. The standard curve was prepared by adding different amounts of HCl 1M to M9 without carbon, and by measuring pH with an electronic pH-meter. pH of the samples was interpolated on the standard curve as described in (Yao and Byrne, 2001).
Fermentation profile assignment
We assigned a fermentation profile- respirator (R) or fermenter (F) to all dominant families (Table S1). For instance, bacterial genera belonging to the Enterobacteriaceae family are well-known fermenters while bacterial species belonging to the genus Pseudomonas are well-known non-fermenters. Some rare taxa belong to families that cannot be assigned to R or F, thus they were not accounted for in the R/F ratio. These taxa are at very low abundance, and therefore their effect on the R/F ratio is negligible. When counting CFUs, R and F were distinguished by platting on chromogenic agar (HiCrome Universal differential Medium from Sigma). White colonies were counted as R and blue/purple colonies were counted as F. Each isolate was platted on chromogenic agar to confirm its R/F assignment. There is a positive correlation between the R/F ratio obtained by CFU counting and by 16S sequencing (slope= 0.46, intercept −0.066, R2=0.32; Figure S19) and the two ratios are within the same order of magnitude (Figure S20).
Short incubation time experiment
We had previously isolated the four dominant strains from one of the self-assembled communities shown in Figure 1A (Goldford et al., 2018). Three of the strains belong to the Enterobacteriaceae family– Klebsiella, Raoultella, Citrobacter- and one strain belongs to the Pseudomonadaceae family (Pseudomonas). Each strain was grown for 24h in chromogenic agar at 30C. A colony was picked and resuspended in 500uL PBS 1x. Cells were then centrifuged for 10 min at 3500 rpm, washed, and re-suspended in PBS 1x (3 times in total). After the final washing step, cells were normalized to an OD620 of 0.15 and the 4-strain community was established by mixing the strains 1:1:1:1. 4ul from the mixture was transferred into 500uL of m9+glucose 0.2% in 6 replicates and incubated at 30C. The cultures were then serially-transferred to fresh medium (1:125 dilution) every 48h for 5 transfers. After the 5th transfer, the cultures were propagated for 5 more transfers of 48h (control treatment) (N=6) or 12h each (N=6). The relative abundance of each family was determined by plating into chromogenic agar (Enterobacteriaceae appear as blue/purple colonies while Pseudomonas appear as white colonies).
Soil sample collection
A soil sample was collected from a natural site in West Haven (CT, USA) using sterilized spatula, placed into a sterile bottle, and returned to the lab. 10 g of soil sample were then placed into a new sterile bottle and soaked into 100mL of sterile PBS supplemented with 200 μg/mL cycloheximide to inhibit eukaryotic growth. The bottle was vortexed and allowed to sit for 48 hours at room temperature. After 48h, samples of the supernatant solution containing the ‘source’ soil microbiome were used as inoculum for the experiment (see section below) or stored at −80C after mixing with 40% glycerol.
Growth medium and ‘no migration’ experimental setup
92 replicate communities from the same source community were cultured separately in the wells of 96 deep-well plates (VWR). Each replicate community was initiated by inoculating 4uL from the source community into 500uL of M9 minimal media supplemented with glucose 0.2% (i.e., 0.07 C-mol/L) (as in (Goldford et al., 2018)). The communities were grown at 30C under static conditions for 48h. After 48h growth, 4uL from the grown culture was transferred to fresh media. This dilution-growth cycle was repeated 18 times. For the first two growth cycles, cycloheximide (200 μg/mL) was added to the media. OD620 was measured at the end of each growth cycle and samples of the grown communities were stored at −80C after mixing with 40% glycerol. In a parallel experiment, 93 replicate communities were started with a 10x inoculation size (40ul) from the same source community, and propagated as described above.
Migration between local communities experiment
Similar to the treatment without migration, each replicate community was initiated by inoculating 4uL from the source community into 500uL of M9 minimal media. At the end of each growth cycle, however, 4uL from each well was pooled into a ‘migrant pool community’ and diluted 10,000-fold. Each well of the fresh media was inoculated with 4uL of this migrant pool community in addition to the 4uL from the corresponding replicate community (well) from the previous growth cycle. Thus, each replicate community from the 96 deep-well plate represents a local community from the same meta-community where the local communities are linked through migration. This migration step was performed for the first 12 growth cycles, followed by 6 dilution-growth cycles without migration (normal transfer only). OD620 was measured at the end of each growth cycle and culture samples were stored at −80C after mixing with 40% glycerol.
Migration from the regional pool experiment
Each replicate community was started with 4uL from the same source community into 500uL of M9 minimal media. At the start of each growth cycle, 4uL from the source community was inoculated into fresh media in addition to the 4uL from the corresponding replicate community (well) from the previous growth cycle. Thus, each replicate community from the 96 deep-well plate represents a local community that is linked to its regional pool through migration. This migration step was performed for the first 12 growth cycles, followed by 6 dilution-growth cycles without migration (normal transfer only). OD620 was measured at the end of each growth cycle and culture samples were stored at −80C after mixing with 40% glycerol.
DNA extraction and library preparation
Samples to be sequenced were centrifuged for 30min at 3500rpm. DNA extraction was performed following the DNeasy 96 Blood & Tissue kit protocol for animal tissues (QIAGEN) including the pre-treatment step for Gram-positive bacteria. DNA concentration was quantified using the Quan-iT PicoGreen dsDNA Assay kit (Invitrogen) and normalized to 5ng/uL. 16S rRNA amplicon library preparation was conducted using a dual-index paired-end approach (Kozich et al., 2013) and has been described in detail in (Goldford et al., 2018). The PCR reaction products were purified and normalized using the SequalPrep PCR cleanup and normalization kit (Invitrogen).
Sequencing and taxonomy assignment
The community composition profile was based on 16S (V4) rRNA gene sequence analysis, a commonly used genetic marker for classifying bacteria as it is highly conserved between different species. The samples were sequenced at the Yale Center for Genome Analysis (YCGA) using the Illumina MiSeq (2×250 bp paired-end) sequencing platform. Post-sequencing processing of the raw sequences, namely demultiplexing and removing the barcodes, indexes and primers, was performed using QIIME (version 1.9, (Caporaso et al., 2010)). The generated fastq files for the forward and reverse sequences were analysed using the DADA2 pipeline (version 1.6.0) to infer exact sequence variants (ESVs) (Callahan et al., 2016). The forward and reverse reads were trimmed at position 240 and 160, respectively, and then merged with a minimum overlap of 100bp. All other parameters were set to the DADA2 default values. Chimeras were removed using the “consensus” method in DADA2. The taxonomy of each 16S exact sequence variant (ESV) was then assigned using the naïve Bayesian classifier method (Wang et al., 2007) and the Silva reference database version 128 (Quast et al., 2013) as described in DADA2. A single strain E. coli (n=10) and a commercial DNA mock community (D6305, Zymo Research, Irvin, CA, USA) (n=12) were used as positive controls to correct for spurious detection during amplicon sequencing (Figure S13). In Figure S20, the estimated 16S R/F ratio was corrected for amplicon abundance bias using a in-house cell mock community composed of 5 isolates (1 Klebsiella, 1 Raoultella, 1 Aeromonas and 2 Pseudomonas) all mixed 1:1 by OD, thus giving a theoretical R/F ratio of 0.6. This mock community was processed using the same DNA extraction and PCR protocols as the communities above and sequenced at Microbiome Insights Inc. (Vancouver, Canada).
Isolation of dominant taxa
We isolated the four most abundant ESVs, two belonging to the Enterobacteriaceae family, one Pseudomonas and one Alcaligenes, and verified their taxonomy by sequencing the full-length 16S rRNA gene (GENEWIZ). Taxonomy was assigned using both the Silva database (v1.2.11) and the RDP Naive Bayesian rRNA Classifier Version 2.11 (training set 16). The two reference datasets provided equivalent taxonomic assignments and confirmed the identity assigned to the 16S V4 rRNA sequences. One of the most dominant ESVs belonging to the Enterobacteriaceae family was unidentified at the genus level but isolation of that strain followed by Sanger sequencing on the full-length 16S rRNA gene revealed that it belongs to the genus Klebsiella. We therefore assigned that ESV to Klebsiella. The two Klebsiella isolates display different morphologies on glucose agarose plates and an indole test (Remel Kovacs Indole Reagent, #R21227) revealed that one of the isolates is indole positive while the other isolate is indole negative. Based on this distinction, we decided to refer to the two Klebsiella as Klebsiella positive (Kp) and Klebsiella negative (Km).
Mapping isolates to amplicon sequencing data
To match our isolates from Sanger sequencing (full-length 16S rDNA sequence) to the amplicon sequencing data (ESVs) of the communities, we performed a pairwise alignment using the function pairwiseAlignment from the R package Biostrings (Pagès et al., 2017), with alignment type set to “local”. For each isolate in a community, we aligned its full-length Sanger sequence with all possible ESVs from the same community and obtained the reported alignment scores. Sanger-ESV alignment with highest alignment score was picked. If two Sanger sequences were matched to one ESV, the one with lower alignment score was dropped (19 of 73 isolate Sanger sequences were dropped). In the 54 pairwise alignments, the shortest consensus length is 234 base pairs, with 45 full matches, eight one base pair mismatches, and one two base pair mismatches.
Bottom-up invasion experiment
We performed an invasion experiment between Klebsiella (Kp) (resident) and Pseudomonas and/or Alcaligenes (invaders) either alone (mono-invasion) or together (co-invasion). Prior to the start of the invasion experiment, the three strains were grown from frozen glycerol stocks alone into LB-agarose plates. For each strain, colonies were re-suspended into 1x M9 (without glucose) and normalized to an OD620 of 0.1. The normalized A and P stocks were then serially diluted independently 10-fold four times from 10−1 to 10-4. Note that here we refer to OD620 of 0.1 as the baseline OD (100). For the co-invasion assays, Alcaligenes and Pseudomonas were mixed together for all five A and P dilutions (100 to 10−4) generating 25 different A-P initial density combinations. Competitions were started by mixing 2uL of Kp with 2uL of the A:P mixtures (co-invasion) or 2uL of A or P monocultures (mono-invasion) at the 5 different dilutions into 500uL of M9 + glucose. In total, 36 invasion scenarios with different initial frequencies and densities of A and/or P (25 co-invasions, 10 mono-invasions, and Kp alone) were investigated in duplicate, setting the initial position of the population in the phase portrait shown in Figure 3. Strains were grown for 48h without shaking at 30C and then diluted 1:125 into fresh medium, and this growth-dilution cycle was repeated for 12 transfers. The relative abundance of each strain was estimated by plating (Colony-Forming Units) on LB-agarose plates.
Probability distributions and quasi-potential
In Figure 2C, shown are the probability density distributions of the relative abundance (log10) of the dominant Alcaligenes (A) and Pseudomonas (P) ESVs at Transfer 18 in the communities self-assembled from the same inoculum under the four different treatments described above, that is, in the ‘no migration’ (both low and high inocula), ‘global migration’, and ‘regional migration’ (n=370). For the bimodal distributions, the distribution parameters for each Gaussian (lambda, mu, and sigma) were obtained by fitting a mixture distribution with the normalmix EM function in R. The position of the local minimum in between the two local maxima were determined using the FindMinimum function in Mathematica.
The potential U(x) was derived using the Fokker-Planck equation. The potential U(x) and the probability density of x are connected through the Fokker-Planck equation (Lahti et al., 2014), where U(x) is given by:
where D is the noise level. Assuming that x is the log10 relative abundance of A (or P) at equilibrium (T18), we can derive the energy potential U(a) and U(p) from their probability distributions (P(a) and P(p)). Assuming that D=1,
and
The roots of the potential U(x) were calculated using the FindRoot function in Mathematica.
Phase diagram and separatrix
The phase diagram drawn in Figures 4B and 4C was obtained by analysis of the outcome of the bottom-up invasion experiment described above and shown in Figures 3 and S14. The ‘transition’ region was determined as follow. First, we identified the ‘flickering’ region of the A-P initial frequency space where the outcome either changed (e.g. from coexistence (gray) to A dominated state (yellow)) or remained gray at any point during one of the 3 transfers (T3, T8, T12) and in one or both of the 2 replicates analysed. The basin boundary of Alcaligenes was determined by taking, for each initial frequency, the mid-points between the initial frequencies inside the basin of attraction of Alcaligenes and inside the ‘flickering’ region that are closest to the transition line. Similarly, the basin boundary of Pseudomonas was determined by taking, for each initial frequency, the mid-points between the initial frequencies inside the basin of attraction of Pseudomonas and inside the ‘flickering’ region that are closest to the transition line. The separatrix shows the midline between the two boundaries. In Figure 4B, the datapoints where the relative abundance is below the detection threshold are arbitrarily set to a value of −4.33.
Community assembly in alternative carbon sources
Four replicate communities, all started from the same soil inoculum, were serially transferred every 48h in minimal medium supplemented with a single carbon source (glucose, fructose, cellobiose, ribose, citrate, and glutamine) for a total of 10 transfers. The single carbon sources were adjusted to equal C-molar concentrations. The serial transfers were performed under the same conditions as described in the ‘Growth medium and no migration experimental setup’ section above. The DNA extraction was performed with the DNeasy 96 Blood & Tissue kit for animal tissues (QIAGEN) as described above. The 16S rRNA gene amplicon library preparation and sequencing were performed by Microbiome Insights, Vancouver, Canada (www.microbiomeinsights.com). The library preparation was done as described above. The samples were sequenced on the Illumina MiSeq using the 300-bp paired end kit v3.chemistry.
QUANTIFICATION AND STATISTICAL ANALYSIS
Statistical details can be found in the figure legends, Results, or Methods. All statistical analysis was performed with R.
Supplementary Material
Highlights.
We study convergence and divergence in microbiome assembly in replicate habitats
Functional convergence reflects an emergent metabolic self-organization
Taxonomic divergence arises from multistability in population dynamics
Simple models can explain observed quantitative patterns in microbiome assembly
ACKNOWLEDGMENTS
We want to thank Jackie Folmar for assistance with platting and Nora Pyenson and Xin Sun for comments on the manuscript. We thank Sven Even Borgos and Juan Nogales for providing us with SBML versions of Pseudomonas genome-scale metabolic models. The funding for this work partly results from a Scialog Program sponsored jointly by Research Corporation for Science Advancement and the Gordon and Betty Moore Foundation through grants to Yale University (A.S.). This work was also supported by a young investigator award from the Human Frontier Science Program (RGY0077/2016), by a Packard Foundation Fellowship to A.S., and by the National Institutes of Health through grant 1R35 GM133467-01 to A.S. M.R.-G. was additionally supported by a Donnelley Postdoctoral Fellowship from the Yale Institute for Biospheric Studies.
Footnotes
DECLARATION OF INTERESTS
A.S. is a member of the Cell Systems Advisory Board. The authors otherwise declare no competing interests.
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.cels.2021.09.011.
SUPPORTING CITATIONS
The following references appear in the supplemental information: Arkin et al., 2018; Basan et al., 2015; Chen et al, 2017; Goldford et al., 2018; Mori et al., 2016; Paczia et al., 2012; Parks et al., 2015; Peng et al., 2012; Seemann, 2014.
REFERENCES
- Aguirre de Cárcer D. (2019). A conceptual framework for the phylogenetically constrained assembly of microbial communities. Microbiome 7, 142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amor DR, Ratzke C, and Gore J. (2020). Transient invaders can induce shifts between alternative stable states of microbial communities. Sci. Adv 6, eaay 8676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkin AP, Cottingham RW, Henry CS, Harris NL, Stevens RL, Maslov S, Dehal Paramvir, et al. (2018). KBase: The United States Department of Energy Systems Biology Knowledgebase. Nature Biotechnology 36(7), 566–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Axelrod K, Sanchez A, and Gore J. (2015). Phenotypic states become increasingly sensitive to perturbations near a bifurcation in a synthetic gene network. Elife 4, e07935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basan M, Hui S, Okano H, Zhang Z, Shen Y, Williamson JR, and Hwa T. (2015). Overflow Metabolism in Escherichia Coli Results from Efficient Proteome Allocation. Nature 528, 99–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittleston LS, Gralka M, Leventhal GE, Mizrahi I, and Cordero OX (2020). Context-dependent dynamics lead to the assembly of functionally distinct microbial communities. Nat. Commun 11, 1440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke C, Steinberg P, Rusch D, Kjelleberg S, and Thomas T. (2011). Bacterial community assembly based on functional genes rather than species. Proc. Natl. Acad. Sci. USA 108, 14288–14293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callahan BJ, McMurdie PJ, Rosen MJ, Han AW, Johnson AJA, and Holmes SP (2016). DADA2: high-resolution sample inference from Illumina amplicon data. Nat. Methods 13, 581–583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caporaso JG, Kuczynski J, Stombaugh J, Bittinger K, Bushman FD, Costello EK, Fierer N, Peña AG, Goodrich JK, Gordon JI, et al. (2010). QIIME allows analysis of high-throughput community sequencing data. Nat. Methods 7, 335–336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson HK, Lui LM, Price MN, Kazakov AE, Carr AV, Kuehl JV, Owens TK, Nielsen T, Arkin AP, and Deutschbauer AM (2020). Selective carbon sources influence the end products of microbial nitrate respiration. ISMEJ 14, 2034–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Case TJ (1990). Invasion resistance arises in strongly interacting species-rich model competition communities. Proc. Natl. Acad. Sci. USA 87, 9610–9614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase JM (2003). Community assembly: when should history matter? Oecologia 136, 489–498. [DOI] [PubMed] [Google Scholar]
- Chen A, Sanchez A, Dai L, and Gore J. (2014). Dynamics of a producer-freeloader ecosystem on the brink of collapse. Nat. Commun 5, 3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Huang T, Zhou Y, Han Y, Xu M, and Gu J. (2017). AfterQC: Automatic Filtering, Trimming, Error Removing and Quality Control for FastqData. BMC Bioinformatics 18, 80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costello EK, Stagaman K, Dethlefsen L, Bohannan BJM, and Relman DA (2012). The application of ecological theory toward an understanding of the human microbiome. Science 336, 1255–1262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Andrea R, Gibbs T, and O’Dwyer JP (2020). Emergent neutrality in consumer-resource dynamics. PLOS Comput. Biol 16, e1008102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai L, Vorselen D, Korolev KS, and Gore J. (2012). Generic indicators for loss of resilience before a tipping point leading to population collapse. Science 336, 1175–1177. [DOI] [PubMed] [Google Scholar]
- Estrela S, Sánchez Á, and Rebolleda-Gómez M. (2021). Multi-replicated enrichment communities as a model system in microbial ecology. Front. Microbiol 12, 657467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faust K, Lahti L, Gonze D, de Vos WM, and Raes J. (2015). Metagenomics meets time series analysis: unraveling microbial community dynamics. Curr. Opin. Microbiol 25, 56–66. [DOI] [PubMed] [Google Scholar]
- Fodelianakis S, Lorz A, Valenzuela-Cuevas A, Barozzi A, Booth JM, and Daffonchio D. (2019). Dispersal homogenizes communities via immigration even at low rates in a simplified synthetic bacterial metacommunity. Nat. Commun 10, 1314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foroutan A, Fitzsimmons C, Mandal R, Piri-Moghadam H, Zheng J, Guo A, Li C, Guan LL, and Wishart DS (2020). The bovine metabolome. Metabolites 10, 233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foroutan A, Guo AC, Vazquez-Fresno R, Lipfert M, Zhang L, Zheng J, Badran H, Budinski Z, Mandal R, Ametaj BN, and Wishart DS (2019). Chemical composition of commercial cow’s milk. J. Agric. Food Chem 67, 4897–4914. [DOI] [PubMed] [Google Scholar]
- Fukami T. (2015). Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst 46, 1–23. [Google Scholar]
- Goldford JE, Lu N, Bajić D, Estrela S, Tikhonov M, Sanchez-Gorostiaga A, Segrè D, Mehta P, and Sanchez A. (2018). Emergent simplicity in microbial community assembly. Science 361, 469–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harcombe WR, Riehl WJ, Dukovski I, Granger BR, Betts A, Lang AH, Bonilla G, Kar A, Leiby N, Mehta P, et al. (2014). Metabolic resource allocation in individual microbes determines ecosystem interactions and spatial dynamics. Cell Rep 7, 1104–1115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirota M, Holmgren M, Van Nes EH, and Scheffer M. (2011). Global resilience of tropical forest and savanna to critical transitions. Science 334, 232–235. [DOI] [PubMed] [Google Scholar]
- Human Microbiome Project Consortium (2012). Structure, function and diversity of the healthy human microbiome. Nature 486, 207–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klitgord N, and Segrè D. (2010). Environments that induce synthetic microbial ecosystems. PLoS Comput. Biol 6, e1001002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozich JJ, Westcott SL, Baxter NT, Highlander SK, and Schloss PD (2013). Development of a dual-index sequencing strategy and curation pipeline for analyzing amplicon sequence data on the MiSeq Illumina sequencing platform. Appl. Environ. Microbiol 79, 5112–5120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kryazhimskiy S, Rice DP, and Desai MM (2012). Population subdivision and adaptation in asexual populations of Saccharomyces cerevisiae. Evolution 66, 1931–1941. [DOI] [PubMed] [Google Scholar]
- Lahti L, Saloja€rvi J, Salonen A, Scheffer M, and de Vos WM (2014). Tipping elements in the human intestinal ecosystem. Nat. Commun 5, 4344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leibold MA, Holyoak M, Mouquet N, Amarasekare P, Chase JM, Hoopes MF, Holt RD, Shurin JB, Law R, Tilman D, et al. (2004). The metacommunity concept: a framework for multi-scale community ecology. Ecol. Lett 7, 601–613. [Google Scholar]
- Livina VN, Kwasniok F, and Lenton TM (2010). Potential analysis reveals changing number of climate states during the last 60 kyr. Clim. Past 6, 77–82. [Google Scholar]
- Louca S, Jacques SMS, Pires APF, Leal JS, Srivastava DS, Parfrey LW, Farjalla VF, and Doebeli M. (2016b). High taxonomic variability despite stable functional structure across microbial communities. Nat. Ecol. Evol 1, 15. [DOI] [PubMed] [Google Scholar]
- Louca S, Parfrey LW, and Doebeli M. (2016a). Decoupling function and taxonomy in the global ocean microbiome. Science 353, 1272–1277. [DOI] [PubMed] [Google Scholar]
- Louca S, Polz MF, Mazel F, Albright MBN, Huber JA, O’Connor MI, Ackermann M, Hahn AS, Srivastava DS, Crowe SA, et al. (2018). Function and functional redundancy in microbial systems. Nat. Ecol. Evol 2, 936–943. [DOI] [PubMed] [Google Scholar]
- Marsland R 3rd, Cui W, Goldford J, Sanchez A, Korolev K, and Mehta P. (2019). Available energy fluxes drive a transition in the diversity, stability, and functional structure of microbial communities. PLoS Comput. Biol 15, e1006793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martiny JBH, Jones SE, Lennon JT, and Martiny AC (2015). Microbiomes in light of traits: a phylogenetic perspective. Science 350, aac9323. [DOI] [PubMed] [Google Scholar]
- Mori M, Hwa T, Martin OC, De Martino A, and Marinari E. (2016). Constrained Allocation Flux Balance Analysis. PLoS Computational Biology 12, e1004913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson MB, Martiny AC, and Martiny JBH (2016). Global biogeography of microbial nitrogen-cycling traits in soil. Proc. Natl. Acad. Sci. USA 113, 8033–8040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nogales J, Mueller J, Gudmundsson S, Canalejo FJ, Duque E, Monk J, Feist AM, Ramos JL, Niu W, and Palsson BO (2020). High-quality genome-scale metabolic modelling of Pseudomonas putida highlights its broad metabolic capabilities. Environ. Microbiol 22, 255–269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orth JD, Conrad TM, Na J, Lerman JA, Nam Hojung, Feist AM, and Palsson BØ (2011). A comprehensive genome-scale reconstruction of Escherichia coli metabolism–2011. Mol. Syst. Biol 7, 535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozbudak EM, Thattai M, Lim HN, Shraiman BI, and Van Oudenaarden A. (2004). Multistability in the lactose utilization network of Escherichia coli. Nature 427, 737–740. [DOI] [PubMed] [Google Scholar]
- Paczia N, Nilgen A, Lehmann T, Gätgens J, Wiechert W, and Noack S. (2012). Extensive Exometabolome Analysis Reveals Extended Overflow Metabolism in Various Microorganisms. Microbial Cell Factories 11, 122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagès H, Aboyoun P, Gentleman R, and DebRoy S. (2017). Biostrings: efficient manipulation of biological strings. R package version 2. https://rdrr.io/bioc/Biostrings/.
- Parks DH, Imelfort M, Skennerton CT, Hugenholtz P, and Tyson GW (2015). CheckM: Assessing the Quality of Microbial Genomes Recovered from Isolates, Single Cells, and Metagenomes. Genome Research 25, 1043–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peng Yu, Henry C, Leung M, Yiu SM, and Chin Francis Y.L. (2012). IDBA-UD: A de Novo Assembler for Single-Cell and Metagenomic Sequencing Data with Highly Uneven Depth. Bioinformatics 28, 1420–1428. [DOI] [PubMed] [Google Scholar]
- Quast C, Pruesse E, Yilmaz P, Gerken J, Schweer T, Yarza P, Peplies J, and Glöckner FO (2013). The SILVA ribosomal RNA gene database project: improved data processing and web-based tools. Nucleic Acids Res 41, D590–D596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rauch J, Kondev J, and Sanchez A. (2017). Cooperators trade off ecological resilience and evolutionary stability in public goods games. J. R. Soc. Interface 14, 20160967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez A, and Gore J. (2013). Feedback between population and evolutionary dynamics determines the fate of social microbial populations. PLoS Biol 11, e1001547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez Á, Vila JCC, Chang C-Y, Diaz-Colunga J, Estrela S, and Rebolleda-Gomez M. (2021). Directed evolution of microbial communities. Annu. Rev. Biophys 50, 323–341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schröder A, Persson L, and De Roos AM (2005). Direct experimental evidence for alternative stable states: a review. Oikos 110, 3–19. [Google Scholar]
- Shaw LP, Bassam H, Barnes CP, Walker AS, Klein N, and Balloux F. (2019). Modelling microbiome recovery after antibiotics using a stability landscape framework. ISME J 13, 1845–1856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorek M, Balaban NQ, and Loewenstein Y. (2013). Stochasticity, bistabilityand the wisdom of crowds: a model for associative learning in genetic regulatory networks. PLoS Comput. Biol 9, e1003179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stegen JC, Lin X, Fredrickson JK, Chen X, Kennedy DW, Murray CJ, Rockhold ML, and Konopka A. (2013). Quantifying community assembly processes and identifying features that impose them. ISME J 7, 2069–2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turnbaugh PJ, Ridaura VK, Faith JJ, Rey FE, Knight R, and Gordon JI (2009). The effect of diet on the human gut microbiome: a metagenomic analysis in humanized gnotobiotic mice. Sci. Transl. Med 1, 6ra14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vivijs B, Haberbeck LU, Baiye Mfortaw Mbong V, Bernaerts K, Geeraerd AH, Aertsen A, and Michiels CW (2015). Formate hydrogen lyase mediates stationary-phase deacidification and increases survival during sugar fermentation in acetoin-producing enterobacteria. Front. Microbiol 6, 150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Garrity GM, Tiedje JM, and Cole JR (2007). Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl. Environ. Microbiol 73, 5261–5267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao W, and Byrne RH (2001). Spectrophotometric determination of freshwater pH using bromocresol purple and phenol red. Environ. Sci. Technol 35, 1197–1201. [DOI] [PubMed] [Google Scholar]
- Zelezniak A, Andrejev S, Ponomarova O, Mende DR, Bork P, and Patil KR (2015). Metabolic dependencies drive species co-occurrence in diverse microbial communities. Proc. Natl. Acad. Sci. USA 112, 6449–6454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou J, Liu W, Deng Y, Jiang Y-H, Xue K, He Z, Van Nostrand JD, Wu L, Yang Y, and Wang A. (2013). Stochastic assembly leads to alternative communities with distinct functions in a bioreactor microbial community. mBio 4, e00584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team (2017) R: A Language and Environment for Statistical Computing, Vienna, Austria. https://www.R-project.org/RCoreTeam. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The 16S rRNA sequencing abundance data are available at Dryad or Zenodo and are publicly available as of the date of publication. Accession numbers are listed in the key resources table.
The raw 16S rRNA amplicon sequences and metadata files have been deposited in the NCBI SRA database under accession number PRJNA761777 and PRJNA761387 and are publicly available as of the date of publication.
The whole-genome sequence reads for the 5 isolates have been deposited in the NCBI SRA database under accession number PRJNA749600.
The source data files and scripts used to generate the figures are available at https://github.com/sylestrela/Estrelaetal2021_FunctionalAttractors and Zenodo. DOI is listed in the key resources table.
The code for the FBA simulations are available at https://github.com/vilacelestin/Estrelaetal2021_FunctionalAttractors and Zenodo. DOI is listed in the key resources table.
Any additional information required to re-analyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT OR RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, peptides, and recombinant proteins | ||
|
| ||
| D-glucose | VWR | Cat. #0188 |
| Acetate | Sigma | Cat. #S8625 |
| D-lactate | Sigma | Cat. #71716 |
| succinate | Alfa Aesar | Cat. #419A3 |
|
| ||
| Critical commercial assays | ||
|
| ||
| glucose GO assay kit | Millipore | Cat. #GAGO20 |
| Acetate assay kit | Abcam | Cat. #ab204719 |
| D-Lactate assay kit | Abcam | Cat. #ab83429 |
| Succinate assay kit | Abcam | Cat. #ab204718 |
| DNeasy 96 Blood & Tissue kit | QIAGEN | Cat. #69582 |
| Quan-iTPicoGreen dsDNA Assay kit | Invitrogen | Cat. #P11496 |
| SequalPrep PCR cleanup and normalization kit | Invitrogen | Cat. #A1051001 |
|
| ||
| Deposited data | ||
|
| ||
| 16S rRNA sequencing abundance data | This study | https://doi.org/10.5061/dryad.5x69p8d3z |
| Genome scale metabolic models | This study | SRA: PRJNA749600 |
| Raw 16S rRNA amplicon sequences for communities assembled in glucose under different migration treatments | This study | SRA: PRJNA761777 |
| Raw 16S rRNA amplicon sequences for communities assembled in alternate carbon sources | This study | SRA: PRJNA761387 |
| Community abundance data | Goldford et al., 2018 | https://doi.org/10.5281/zenodo.3817698 |
|
| ||
| Software and algorithms | ||
|
| ||
| Source data files and code used to generate the figures. | This study |
https://github.com/sylestrela/Estrelaetal2021_FunctionalAttractors (https://doi.org/10.5281/zenodo.5510318) |
| Code for the FBA simulations. | This study |
https://github.com/vilacelestin/Estrelaetal2021_FunctionalAttractors (https://doi.org/10.5281/zenodo.5510298) |
| R (version 3.4.3) | (R Core Team, 2017) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.r-project.org/ |
RRID:SCR_001905 |
| DADA2 (version 1.6.0) | Callahan et al., 2016 | N/A |
| COBRApy (version 0.17.1) | Ebrahim A, Lerman JA, Palsson BO, Hyduke DR. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst Biol. 2013;7: 74. |
RRID:SCR_012096 |
| Mathematica (version 11.0.1.0) | Wolfram | RRID:SCR_014448 |