Comparative study of a mathematical epidemic model, statistical modeling, and deep learning for COVID-19 forecasting and management

Abstract

The COVID-19 pandemic has caused a global crisis with 47,209,305 confirmed cases and 1,209,505 confirmed deaths worldwide as of November 2, 2020. Forecasting confirmed cases and understanding the virus dynamics is necessary to provide valuable insights into the growth of the outbreak and facilitate policy-making regarding virus containment and utilization of medical resources. In this study, we applied a mathematical epidemic model (MEM), statistical model, and recurrent neural network (RNN) variants to forecast the cumulative confirmed cases. We proposed a reproducible framework for RNN variants that addressed the stochastic nature of RNN variants leveraging z-score outlier detection. We incorporated heterogeneity in susceptibility into the MEM considering lockdowns and the dynamic dependency of the transmission and identification rates which were estimated using Poisson likelihood fitting. While the experimental results demonstrated the superiority of RNN variants in forecasting accuracy, the MEM presented comprehensive insights into the virus spread and potential control strategies.

1. Introduction

COVID-19, caused by the virus SARS-CoV-2, was first identified in Wuhan, China, and subsequently spread across the globe. It is a respiratory infection with typical symptoms such as fever, cough, dyspnea, and breathing difficulties. In severe cases, the infection can cause pneumonia, acute respiratory syndrome, kidney failure, and death [1,2]. Since January 17, 2020, the reported cases have significantly risen, and COVID-19 has been listed as a public health emergency of international concern by the WHO. One of the most affected countries is the USA, with 9,518,763 cases and 236,737 confirmed deaths reported as of November 2, 2020 [3]. The virus is a significant threat to the health and safety of people worldwide. Two types of counter measures are required: (i) to forecast daily confirmed cases so that health-care systems can efficiently address significant challenges, such as testing and caring for a massive number of confirmed patients, and (ii) to understand the dynamics of the disease so that public health professionals can implement effective control measures to slow down and reduce the rapid growth of infections. With the exponential growth of COVID-19, hospitals encounter difficulties in ensuring essential supplies, such as ventilators, personal protective equipment, and test kits. Moreover, irrepressible outbreaks were caused by the lack of understanding of transmission mechanisms and insufficient public acceptance of control measures [4,5]. Therefore, it is important not only to estimate the number of confirmed cases but also to provide valuable insights into the outbreak mechanisms; this would facilitate the policy-making for epidemic control and resource utilization.

Mathematical epidemic models (MEM) have been widely used to estimate future trends of disease transmission, gain insight into disease dynamics, and plan control strategies to mitigate outbreaks [6,7]; though possess limitations, such as identifiability in data fitting, case specificity, and robustness [7]. Recently, researchers have been applying advanced statistical methods, and deep neural networks to overcome the limitations of fitting and achieve more accurate forecast [8,9]. However, these do not provide insight to disease transmission mechanism and implications to control.

Time series forecasting is a well-known challenge for infectious diseases. Many researchers have already attempted to forecast COVID-19 pandemic time series. Most studies have applied statistical models, conventional machine learning, and deep learning [[10], [11], [12], [13]]. Statistical models– such as autoregressive integrated moving average (ARIMA), single exponential, double exponential, moving average, and S-curve models–were employed to forecast daily new cases COVID-19 in India by using data from January 22, 2020 to April 13, 2020 [10]. Experimental results of the study showed that ARIMA(2,2,2) outperformed other methods with a minimum mean absolute percentage error (MAPE) of 4.1. Exponential smoothing models were implemented to forecast various trends and seasonal patterns with limited training data [11]. The research focused on real-time cumulative daily cases (from January 22, 2020 until March 11, 2020) in the US and produced ten-days-ahead forecasts, updating these forecasts every ten days. Another analysis focused on daily cumulative cases of COVID-19 in 10 Brazilian states and applied models such as ARIMA, cubist regression (CUBIST), random forest (RF), support vector machine (SVR), and stacking-ensemble learning for short-term forecasting: one, three, and six days ahead [12]. The study showed that the SVR achieved the best mean absolute error (MAE) and symmetric MAPE in the evaluation. Autoregressive time-series models based on the two-piece scale mixture normal distribution (which excludes the assumption of the symmetric distribution of error terms) were applied to cumulative confirmed and recovered cases in the world, using data from February 02, 2002 to April 30, 2020 [13]. Moving average, weighted moving average, and single exponential smoothing methods were applied to time-series data on COVID-19 confirmed cases, deaths, and recoveries in several countries [14].

Deep learning models, such as recurrent neural network (RNN) variants, have been extensively used to forecast epidemics of infectious diseases. Long short-term memory (LSTM), a variant of RNN, was applied to predict COVID-19 cases in India [15]. COVID-19 data from January 30, 2020 to April 4, 2020 were used in the experiment, where 80% of data were used for training, and the remaining 20% were used for forecasting. The model produced an error percentage of between 1.6 and 6.4 for days from April 5 to 9 for total confirmed cases. LSTM, Bidirectional-LSTM (Bi-LSTM), gated recurrent unit (GRU), and ARIMA were employed to forecast confirmed COVID-19 cases in 10 countries [16]. Confirmed cases from 01/22/2020 to October 5, 2020 and from November 5, 2020 to 6/27/2020 were considered as training and testing data, respectively. The experimental results of these studies showed that Bi-LSTM outperformed other methods in terms of MAE, root-mean-square error (RMSE), and R2 score. Another recent study applied five deep learning methods—RNN, LSTM, Bi-LSTM, GRU, and variational autoencoder (VAE)—to COVID-19 time-series data (01/22/2020 to 07/17/2020) to forecast new cases and recovered cases in six highly impacted countries: Italy, Spain, France, China, the USA, and Australia [17]. VAE outperformed other models in terms of RMSE, MAE, MAPE, explained variable (EV), and root-mean-squared logarithmic error (RMSLE). An LSTM-based network was applied to forecast COVID-19 transmission in Canada, Italy, and the USA [18]. Several variants of RNN, such as LSTM and GRU, were used for training (1/20/2020 to December 3, 2020) and forecasting of confirmed, negative, released, and deceased COVID-19 cases [19]. Accuracy and RMSE were used as evaluation metrics.

In addition to prediction, MEMs help us explore the disease dynamics and facilitate assessment of the efficacy of the potential preventive and control measures, particularly when relevant biological or epidemiological characteristics are not well understood. Although SARS-CoV-2 has caused one of the largest pandemics in human history, its biological and epidemic characteristics are yet to be explored. Scientists used diverse variations of the basic susceptible-exposed-infectious-removed (SEIR) model to explore important features of the transmission dynamics of the current epidemic. For instance, phase-based transmission [[20], [21], [22]], time-dependent transmission [[23], [24], [25]], piecewise transmission [20,24], state-dependent transmission, time-dependent identification [25], and the role of super-spreaders [26] are a few important features of the disease transmission mechanism addressed so far. Other important features—unreported cases and unreported case-mediated transmissions—were addressed in Refs. [20,21,23,[27], [28], [29]]. Further details on the existing literature can be found in Refs. [8,9,30]. Among these, many studies produced time-dependent estimates of crucial parameters [[23], [24], [25],31]. However, in the case of COVID-19, all countries take prompt actions to develop control strategies, deploy preventive measures, and encourage people to follow them. In addition, fear of disease [[32], [33], [34]] and sense of safety [35] modulate the transmission. Therefore, the parameters associated with disease spreading, transmission, and identification would evolve depending on the epidemic status. For example, Yang and Wang [26] assumed that the number of identified cases would stimulate public awareness and hence reduce transmission. Usherwood et al. [35], introduced dynamic dependency of the transmission rate on the level of caution and sense of safety modulated by the number of active infected and vaccinated population. Wang et al. [36], assumed the parameters explicitly depend on time, expressed each parameter as a polynomial function of time, and fit with data. Also, the heterogeneity in susceptibility due to fear, lockdown and spatial spreading is a crucial factor addressed in the literature [[37], [38], [39], [40], [41]]. Besides, infectious individuals do not always have noticeable symptoms from the beginning of the infectious lifetime. Therefore, with the expansion of testing facilities, the identification rate would also change and play a crucial role in epidemiology [42].

In this study, we intend to introduce dynamic dependency of transmission rate and identification rate in a deterministic SEIR type model. In addition, we consider a fraction of the total population as susceptible to account geographical spread. COVID-19 is an imported disease in the USA, where strict lockdowns were imposed as new cases surged. Therefore, a good number of people were in geographically distant places from the location of the initial infections or maintaining strict social distancing to avoid the risk of a transmissible contact. We assume these group of people as non-susceptible. However, over time, the epidemic spread nation-wide and non-susceptible individuals turn out to be susceptible (candidate for a possible exposure to the virus). Also, individual violations of lockdowns may be considered as a social contagion. We assume, susceptible individuals who could avoid contracting the disease would inspire non-susceptible quarantined individuals to violate the control measures. Therefore, we model this phenomenon as follows: non-susceptible individuals become susceptible by following the crowd.

The transmission rate in our MEM replicates the human response to epidemiological status [26]. With a high number of identified cases, the implementation of control measures will be strict, and people will be highly cautious about following the control measures to reduce the transmission. Finally, the identification rate in our model depends on the number of daily identified cases. We assume no limitations in testing facilities, and we increase the testing rate as long as the number of daily identified cases keeps increasing. Further details regarding the model parameters have been provided in the next section.

Importantly, the proposed MEM distinguishes the group of people with no plausible exposure to the virus because they strictly follow preventive measures or geographically at distant places form the virus exposure. In addition, the model shows the dynamic evolution of transmission and identification rates as the epidemic progress. These parameters evaluate public health initiatives and may suggest required modifications of control measures. In our study, we apply MEM, statistical models, and RNN variants to forecast daily cumulative cases and provide valuable insights into the outbreak's mechanism. Our study has three main contributions:

• I.We propose a framework for RNN variants that can provide more robust and reproducible forecast which is crucial for public health resource management.
• II.Our proposed MEM can provide reasonable forecasts with proper interpretation for the spreading, individual participation in preventive measures, transmission, and identification rates which are crucial for identifying and developing effective control measures.
• III.Lastly, we demonstrate the efficiency of neutral network modeling in forecasting with respect to that of MEMs.

2. Methodology

2.1. Autoregressive integrated moving average (ARIMA)

ARIMA, a classic time-series forecasting method, is a generalized model for the autoregressive moving average (ARMA) that combines the autoregressive (AR) process and the moving average (MA) process [43,44]. The AR term expresses the dependencies between an observation and a number of lagged observations (p). The MA term indicates the dependencies between observations and the residual error terms for a number of lagged observations (q). ARMA applies to a stationary process, whereas ARIMA can deal with non-stationary time-series data by leveraging an integrated step to convert the non-stationary series to a stationary series by differentiation. The general form of an ARIMA model is denoted as ARIMA(p,d,q), where p is the order of the AR part, d is the degree of differentiation, and q is the order of the MA part. Equation (1) is the mathematical expression of the ARIMA model:

$$y_t=c+{\phi }_1{y}_{t-1}+{\phi }_2{y}_{t-2}+\dots +{\phi }_p{y}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-\dots -{\theta }_q{\epsilon }_{t-q}$$ (1)

Here, $y_t$ and ${\epsilon }_t$ refer to the actual value of a time series and the random error (white noise) at time t, respectively. Moreover, c, ${\phi }_i$ and ${\theta }_j$ are a constant and the coefficients of the AR and MA parts, respectively.

2.2. Long short-term memory (LSTM)

TLSTM is an extended version of the RNN architecture that can learn long-term dependencies. LSTM can overcome the limitations of a conventional statistical model (such as ARIMA) by capturing non-linearity of sequential data and simultaneously generating more precise forecasting for time-series data [18]. LSTM addresses the vanishing gradient problem of RNN [45]. The building block of LSTM architecture is a memory block, which consists of a memory cell that can preserve information of the preceding time step with self-recurrent connections.

Fig. 1 displays an internal architecture of an LSTM memory cell. The cell consists of three controlling gates: input gate, forget gate, and output gate [46]. The forget gate decides what information should be preserved or removed from the memory cell by using a sigmoid activation function. Value updates are controlled by the input gates that leverage a tanh layer and a sigmoid layer [47]. The sigmoid function determines which value should be updated. The tanh layer generates potential values that can be added to the memory cell. The output gate uses the sigmoid function to identify the memory contribution to the cell output. Subsequently, the tanh activation is applied to capture non-linearity of the values. Finally, the output value is multiplied with the output of the sigmoid layer.

Fig. 1.

Internal architecture for memory cell.

Equation (2) describes the full mechanisms of an LSTM model for an input $x_t$ at time t, where $f_t,i_t,o_t$ and $c_t$ are the forget, input, and output gates, and the internal memory cell state at time t, respectively. Moreover, $h_t$ and $h_{t-1}$ are the values of the hidden layer of the LSTM memory cell at time steps t and t−1, respectively. Finally, ⊗ and σ denote element-wise multiplication and sigmoid activation function, respectively.

$$\begin{array}{l}{f}_t=\sigma \left(W_{f_h}\left[h_{t-1}\right],W_{f_x}\left[x_t\right],b_f\right)\\ i_t=\sigma \left(W_{i_h}\left[h_{t-1}\right],W_{i_x}\left[x_t\right],b_i\right)\\ c_t=f_t\times c_{t-1}+i_t\otimes tanh\left(W_{c_h}\left[h_{t-1}\right],W_{c_x}\left[x_t\right],b_c\right)\\ o_t=\sigma \left(W_{o_h}\left[h_{t-1}\right],W_{o_x}\left[x_t\right],b_o\right)\\ h_t=o_t\otimes tanh\left(c_t\right)\end{array}$$ (2)

LSTM architecture takes advantage of the gates that adjust the values of memory cells and provide an internal dynamic in a cooperative manner [48]. Considering this property of LSTM, it shows a superior ability to learn nonlinear statistical and temporal dependencies of real-world time-series data [47].

2.3. Gated recurrent unit (GRU)

GRU is an alternative version of LSTM that was introduced to avoid the vanishing gradient problem and boost the efficiency of LSTM [49]. GRU has a less complicated architecture than LSTM, with a reduced number of parameters to learn. Fig. 2 shows the architecture of a memory cell of GRU. It consists of two gates: update and reset gates. (In comparison, three gates are included in LSTM.) GRU solves the vanishing gradient problems of RNN by leveraging the two gates through controlling what information should be passed to the future states [17]. The input and forget gates in LSTM models are integrated into the GRU update gate, which determines how much information from previous steps should be passed to the future time steps. Similarly, to the output gate in LSTM, the reset gate in the GRU incorporates new input and previous memory and determines how much memory of past information should be forgotten.

Fig. 2.

Internal architecture for GRU memory cell.

Equation (3) displays the mathematical relationship of GRU components for an input $x_t$ at time t, where $Z_t,R_t,{\bar{H}}_t$, and $H_t$ are the update, reset, current cell state, and new memory cell state at time t, respectively. Here, $W_{xr},W_{xz}$, and $W_{hr}$ are weight parameters. Moreover, $b_r$ and $b_z$ are bias parameters.

$$\begin{array}{l}{Z}_t=\sigma \left(x_t{W}_{xz}+H_{t-1}{W}_{hz}+b_z\right)\\ r_t=\sigma \left(x_t{W}_{xr}+H_{t-1}{W}_{hr}+b_r\right)\\ {\bar{H}}_t=\text{tanh}(x_t{W}_{xh}+\left(R_t\otimes H_{t-1}\right)W_{hh}+b_h\\ H_t=Z_t\otimes H_{t-1}+(1-Z_t)\otimes {\bar{H}}_t\end{array}$$ (3)

2.4. Bidirectional RNN (BRNN)

Bidirectional recurrent neural network (BRNN) is an extension of RNN that was first developed by Schuster and Paliwal to enhance the amount of information in the network [50]. Fig. 3 shows the architecture of BRNN. A limitation of the standard RNN is that it cannot access the future-state information from the current state. However, BRNN links two hidden layers of opposite directions to the same input so that information from past and future steps can be accessed concurrently by the output layer at every time step.

Fig. 3.

Internal architecture for BRNN memory cell.

Equation (4) presents the mathematical relationship of BRNN components. Wherein, the forward, backward and output sequences are ${\overrightarrow{H}}_t$, ${\overleftarrow{H}}_t$, and $y_t$, respectively. Here, $W_{x\overrightarrow{H}}$, $W_{x\overleftarrow{H}}$, and $W_{\overrightarrow{H}y}$ weight parameters. Moreover, $b_{\overrightarrow{H}}$, $b_{\overleftarrow{H}}$, and $b_y$ are bias parameters.

$$\begin{array}{l}{\overrightarrow{H}}_t=\sigma (x_t{W}_{x\overrightarrow{H}}+{\overrightarrow{H}}_{t-1}{W}_{\overrightarrow{H}\overrightarrow{H}}+b_{\overrightarrow{H}})\\ {\overleftarrow{H}}_t=\sigma (x_t{W}_{x\overleftarrow{H}}+{\overleftarrow{H}}_{t-1}{W}_{\overleftarrow{H}\overleftarrow{H}}+b_{\overleftarrow{H}})\\ y_t={\overrightarrow{H}}_t{W}_{\overrightarrow{H}y}+{\overleftarrow{H}}_t{W}_{\overleftarrow{H}y}+b_y\end{array}$$ (4)

2.5. RNN-variants framework

The outputs of RNNs vary due to the stochastic nature of optimization and random initialization of weights. Hence, we propose a simple but effective frame work that can generate reproducible results for RNN variants. The framework initially performs n repetitions of the experiments for each day of the forecasting horizon. Subsequently, it uses the summary statistics of the repetitions to obtain reproducible results. We assumed that there were outliers in the distribution of n repetitions. The z-score method detected outliers in the distribution and removed any output outside of two standard deviations from the mean. Finally, the mean was calculated for each unit of forecasts. Fig. 4 shows the architecture of this framework.

Fig. 4.

Framework for RNN variants.

2.6. Mathematical epidemic model (MEM)

To model the COVID-19 outbreak in the USA using MEM, we assume that the entire population was divided into six compartments: non-susceptible self-quarantined individuals Q(t) who are aware and maintain social distance and preventive measures due to imposed lockdowns, susceptible individuals S(t) who do not maintain preventive measures or are vulnerable to plausible exposure to the virus, exposed individuals E(t) who have been exposed to the virus but have not yet transmitted the disease, infectious individuals I(t) who have started transmitting the disease irrespective of showing symptoms, confirmed individuals C(t) who have been tested positive and quarantined, and removed individuals R(t) who have recovered from the infection or died.

Geographically the USA is a large country with a low population density (174th among 232 countries arranged in descending order) [51], where lockdowns were imposed after the initial cases were detected. Therefore, all individuals were not vulnerable to plausible infectious contacts from the very beginning (i.e., S(0)≠N). We assume ${\alpha }_0$ fraction of the total population belonging to the susceptible compartment was initially vulnerable to infectious contacts. The remaining $1-{\alpha }_0$ fraction of the total population belonged to compartment Q at the beginning, i.e., $Q\left(0\right)=(1-{\alpha }_0)N$ , where N = Q + S + E + I + C + R is the total population.

The individuals in Q transferred to S at a rate $\alpha$. Here, $\alpha$ is correlated with the geographical spread of the epidemic, lockdowns, and individual lockdown violations or negligence. We assume that susceptible people who moved around without getting infected inspired non-susceptible people to move to the susceptible compartment. The individuals in S could acquire the infection if exposed to the virus through contact with any person belonging to compartment I at rate β and transfer to compartment E of the exposed individuals. The virus in the individuals belonging to compartment E was in latent stage and could not be transmitted.

After a certain period, the exposed individuals became infectious and transferred to compartment I at a rate of ξ. However, all infectious individuals were not identified (because of asymptomatic or mild symptomatic nature of the infection or a delayed onset of symptoms). When the infectious individuals were tested and identified, they were isolated and shifted to compartment C at a rate κ. The individuals in compartment C, recovered or died at rate ${\gamma }_2$ and proceeded to compartment R. If an individual remains unidentified (because of not expressing symptom or limited testing facilities), s/he recovers at rate ${\gamma }_1$.

There is little evidence of re-infection, which we neglected; thus, we assume that individuals remained recovered for the entire period of interest. As we were interested in understanding the epidemic for the current outbreak, we ignored the demographic changes and assumed that the total population N was constant.

$$\begin{array}{l}\frac{dQ\left(t\right)}{dt}=-\alpha S\left(t\right)Q\left(t\right)\\ \frac{dS\left(t\right)}{dt}=\alpha S\left(t\right)Q\left(t\right)-\beta \left(t\right)I\left(t\right)S\left(t\right)\\ \frac{dE\left(t\right)}{dt}=\beta \left(t\right)I\left(t\right)S\left(t\right)-\xi E\left(t\right)\\ \frac{dI\left(t\right)}{dt}=\xi E\left(t\right)-{\gamma }_{1}I\left(t\right)-\kappa \left(t\right)I\left(t\right)\\ \frac{dC\left(t\right)}{dt}=\kappa \left(t\right)I\left(t\right)-{\gamma }_{2}C\left(t\right)\\ \frac{dR\left(t\right)}{dt}={\gamma }_{1}I\left(t\right)+{\gamma }_{2}C\left(t\right)\end{array}$$ (5)

Among the parameters ${\alpha }_0,\alpha ,\xi ,{\gamma }_1$ and ${\gamma }_2$ were considered constant. Parameters β and κ were associated with human awareness and public health measures adopted by the government and, thus assumed to evolve over time with the epidemic. Following the work of Yang and Wang [26], we assume $\beta \left(t\right)=\frac{{\beta }_0}{1+c_{\beta }C\left(t\right)}$ to replicate the fact that higher values of C would stimulate both the public awareness and intensity of public health policy implications. Here, ${\beta }_0$ is the maximum possible transmission rate and $c_{\beta }$ is an adjustment coefficient. We also assumed no limitations in testing facilities. The daily testing rate was an increasing function of daily identified cases κ(t)I(t), to represent that the testing facilities improved as the number of identified surged. Therefore, as a simple approximation, we consider $\kappa \left(t\right)={\kappa }_0+c_{\kappa }\kappa \left(t\right)I\left(t\right)$, which gives $\kappa \left(t\right)=\frac{{\kappa }_0}{1-c_{\kappa }I\left(t\right)}$, where ${\kappa }_0$ is the lowest possible identification rate, and $c_{\kappa }$ is an adjustment. Fig. 5 illustrates MEM. The transmission and identification rates are written as β(C) and κ(I), respectively, to express the dynamic dependency of the parameters on the specified state variables.

Fig. 5.

Schematic diagram of the proposed MEM.

The next-generation matrix [52] for the MEM (5) is

$$\left[\begin{array}{ll}\frac{N{\beta }_0}{{\gamma }_1+{\kappa }_0}\hfill & \frac{N{\beta }_0}{{\gamma }_1+{\kappa }_0}\hfill \\ 0\hfill & 0\hfill \end{array}\right].$$

The basic reproduction number $R_0$ is defined as the average number of secondary infections produced by one infected individual throughout its entire infectious lifetime in a completely susceptible environment. It can be computed as the spectral radius of the matrix K. Therefore, $R_0=\rho \left(K\right)=\frac{N{\beta }_0}{{\gamma }_1+{\kappa }_0}$ for the MEM. According to our assumptions, the average infectious life time of an infected individual is $\frac{1}{{\gamma }_1+{\kappa }_0}$, throughout which the individual transmit the disease at per-capita rate ${\beta }_0$. Therefore, one infectedindividual transmits the virus to $N\times {\beta }_0\times \frac{1}{{\gamma }_1+{\kappa }_0}$ individuals on average. Hence, the definition of $R_0$ is justified. However, according to our assumption, rather than the whole population, a subset S of the whole population is susceptible. Therefore, instead of $R_0$, time-dependent effective reproduction number $R_{0E}\left(t\right)$ is of interest. Complying with the expression of $R_0$, we can define $R_{0E}\left(t\right)$ as $R_{0E}\left(t\right)=\frac{S\left(t\right)\beta \left(C\left(t\right)\right)}{{\gamma }_1+\kappa \left(I\left(t\right)\right)}$.

There are several estimates of the latent period. We consider $\frac{1}{\xi }=5$ days [53]. The infectious period is assumed to be $\frac{1}{{\gamma }_1}=22$ days [54]. The average stay in compartment C is $\frac{1}{{\gamma }_2}=\frac{9.3\times (100-18.4)+12.7\times 18.4}{100}=9.925$ days [55]. Therefore, the remaining unknown parameters are ${\alpha }_0,\alpha ,{\beta }_0,c_{\beta },{\kappa }_0$ and $c_{\kappa }$.

We intended to adopt the maximum likelihood method for fitting our model to the US data of cumulative daily identified cases $y\left(t_i\right)$. Let $X=\left(Q,S,E,I,C,R\right)\in {\mathbb{R}}_{+}^6$ denote the state variables, f be the right side of system (5), and $\hat{y}\left(t\right)={\int }_0^t\kappa \left(s\right)I\left(s\right)ds$ be cumulative identified cases. We assumed all $y\left(t_i\right)$ to be independent and follow the Poisson distribution with mean $\hat{y}\left(t_i\right)$. Hence, the fitting problem can be expressed as follows:

$$\begin{array}{l}\frac{d}{dt}X\left(\alpha ,{\beta }_0,c_{\beta },{\kappa }_0,c_{\kappa },t\right)=f\left(X,\alpha ,{\beta }_0,c_{\beta },{\kappa }_0,c_{\kappa },t\right)\\ \hat{y}\left(\alpha ,{\beta }_0,c_{\beta },{\kappa }_0,c_{\kappa },t\right)=\underset{0}{\overset{t}{\int }}\kappa \left(s\right)I\left(s\right)ds\\ X\left(0\right)=\left(N\left(1-{\alpha }_0\right),N{\alpha }_0-E\left(0\right)-I\left(0\right)-y\left(0\right),E\left(0\right),I\left(0\right),y\left(0\right),0\right)\\ X\left(t\right),\alpha ,{\beta }_0,c_{\beta },{\kappa }_0,c_{\kappa }\ge 0and1\ge {\alpha }_0\ge 0\end{array}$$ (6)

Therefore, the likelihood function can be expressed as, $L\left(y\left(t\right)|\hat{y}\left(t\right)\right)=\prod _0^{t_f}\frac{\hat{y}{\left(t_i\right)}^{y\left(t_i\right)}{e}^{-\hat{y}\left(t_i\right)}}{y\left(t_i\right)!}$, where $t_f$ is the final time. We know the value of $H\left(0\right)(=y\left(0\right))$ and $R\left(0\right)$ from the data. Moreover, we assume $E\left(0\right)=10,I\left(0\right)=10$. Our objective was to find ${\alpha }_0,\alpha ,{\beta }_0,c_{\beta },{\kappa }_0$ and $c_{\kappa }$ that maximize the probability of observing $y\left(t_i\right)$, i.e., to maximize the above likelihood function. To obtain the optimal fitting, we used the Nelder-Mead simplex method [56] which is implemented by “fminsearch” function of MATLAB. To comply with the “fminsearch” function, instead of maximizing the likelihood, we minimize the negative log-likelihood function given by, $NLL\left({\alpha }_0,\alpha ,{\beta }_0,c_{\beta },{\kappa }_0,c_{\kappa }\right)=-\sum _0^{t_f}\left(y\left(t_i\right)\ln \left(\hat{y}\left(t_i\right)\right)-\hat{y}\left(t_i\right)-\ln \left(y\left(t_i\right)!\right)\right)$.

3. Numerical results

3.1. Evaluation metrics

MAPE, RMSE, and MAE are common metrics for comparing forecasting methods applied to a single time series. MAPE is used as the primary performance metric throughout this study due to its advantage of interpretability. MAPE represents the absolute error as a percentage of the actual value. Equation (7) presents the mathematical definitions of MAPE, RMSE, and MAE, where $y_i$ and ${\hat{y}}_i$ are the i-th observed and forecasted values, respectively, and $\varkappa$ is the number of test data points.

$$\begin{array}{l}MAPE=\frac{1}{\varkappa }\sum _{i=1}^{\varkappa }\frac{\left|y_i-{\hat{y}}_i\right|}{y_i}\times 100\%\\ RMSE=\sqrt{\frac{1}{\varkappa }\sum _{i=1}^{\varkappa }{\left(y_i-{\hat{y}}_i\right)}^2}\\ MAE=\frac{1}{\varkappa }\sum _{i=1}^{\varkappa }|y_i-{\hat{y}}_i|\end{array}$$ (7)

3.2. Experiments

We considered cumulative identified data up to August 10, 2020 as training data, and the next 15 days were used as test data [57]. The original sequence from 01/22/2020 to 08/24/2020 of the cumulative number of confirmed COVID-19 cases showed an upward trend with non-constant mean and variance. Next, the series was converted into a stationary process by transforming $\stackrel{\prime }{x_i}=x_i^{\frac{1}{8}}$ and subsequently carrying out both the first and second differences of the series. The augmented Dickey-Fuller test was performed on the transformed series to validate stationarity. The test provided a significant p-value of 0.001, confirming that the series finally transformed into a stationary process after required transformation and differencing. Once the series was ready for modeling, a list of candidate models was selected by investigating the spikes of the autocorrelation function (ACF) and partial autocorrelation function (PACF). Finally, the model that generated minimum MAPE with the test data was selected as the best model to fit the cumulative daily number of confirmed cases of COVID-19 in the USA. In this process, ARIMA(2,3) model was selected as the best model (having the lowest MAPE). ACF, PACF, inverse autocorrelation function (IACF), and white noise probability of residual correlation of the ARIMA(2,3) were examined for diagnostic testing.

Fig. 6 illustrates the ACF, PACF, IACF, and white noise probability plots. The ARIMA(2,3) model satisfies all diagnostics criteria: ACF and PACF show no significant correlation of residuals; the IACF does not reveal any instability, and the white noise probability shows significance. We applied the min-max normalization technique to the time-series data to scale the original data to a fixed range of 0 and 1. The normalization ensures consistency of the data distribution. Moreover, it helps to avoid the exploding gradients problem in the training phase. The test data are normalized using the parameters of training data.

Fig. 6.

Diagnostic tests for ARIMA (2, 3) model using (a) Auto-correlation Function (ACF), (b) Partial Auto-correlation Function (PACF), (c) Inverse Auto-Correlation Function (IACF), and (d) White noise probability plots.

We applied different RNN variants on normalized datasets with default Keras initialization weights, where the Glorot uniform was the initializer for the kernel weights matrix, and the orthogonal initializer was used as the recurrent initializer. The bias vector was initialized with all zeros. The sigmoid activation function was used in the recurrent step. We used the rectified linear unit (ReLU) activation function in the hidden layer. The Adam optimization algorithm and mean squared error (MSE) were used as optimizer and loss function, respectively. LSTM, BRNN, and GRU units were used in the hidden layer for LSTM, BRNN, and GRU methods, respectively. The learning rate was fixed at 0.001. Hyperparameters were optimized using grid search. All experiments were performed with an identical setup to maintain consistency in the model evaluation process. In this process, we run all experiments 30 times, following the central limit theorem of the sampling distribution. Consequently, we used the z-score method to detect outliers and to remove outliers from the forecasting list. Finally, we considered the median as the summary metric of the remaining experiments was calculated for each day of forecasts, respectively.

The different RNN-variants network with optimized hyperparameters was applied with the time-series generator class in Keras. In the training phase, the generator uses the number of lagged observations as input with a fixed batch size of 1 as output that allows generating a one-step-ahead forecast after the last available date in the training set. We opted to employ recursive multistep time-series forecasting criteria that involved recursively applying the model for one-step-ahead forecasts until reaching the desired n-step forecast horizon. In this process, the prior-time-step forecast was fed to the model as an input to forecast the sequential time step.

We applied the reproducible framework to different RNN variants. The number of time steps in lagged observations, n, ranged from 1 to 12. Subsequently, we selected the time steps that produced minimum MAPE. Overall, we performed 12 × 30 = 360 experiments for each RNN variant. Table 1 displays the results (MAPE score) of LSTM, BRNN, and GRU for different numbers of lagged observations. The lowest MAPE score of 1.659 was achieved by LSTM with 2 days of lagged observations. BRNN generated a minimum MAPE score of 0.23 by using 3 days of lagged observations. In comparison, GRU produced minimum MAPE (0.53) with 9 days of lagged observations. Table 2 shows performance of all models in terms of MAPE, RMSE, and MAE. The results show that BRNN outperformed other methods in terms of MAPE, RMSE, and MAE. In addition, BRNN achieved the lowest MAPE score of 0.23, lowest RMSE score of $1.55\times {10}^4$, and lowest MAE score of 1.27 × ${10}^4$. The GRU was the second-best model and achieved a MAPE score of 0.53, RMSE score of $1.55\times {10}^4$, and MAE score of $1.27\times {10}^4$. Daily level forecasts for each implemented model are listed in Table 3 . The forecasting accuracy of MEM is not very promising. However, such models can provide a proper interpretation of the virus transmission.

Table 1.

Results for different RNN-variants with various lag observations.

lag days	LSTM	BRNN	GRU
1	2532.836	329.0414	25.7877
2	1.659383	1.791408	4.201779
3	2.48154	0.230536	3.065812
4	4.902399	1.421821	3.361842
5	3.796942	6.158511	1.857447
6	3.50816	5.370399	1.847813
7	6.204086	4.078184	2.030198
8	6.59439	4.608474	0.826541
9	6.000012	6.463311	0.53685
10	7.259901	6.579114	0.760299
11	3.796942	6.158511	0.547891
12	6.288304	5.042317	0.825948

Table 2.

Performance of the techniques. Comparison of errors produced by the methods.

	MAPE	RMSE( × 104)	MAE( × 104)
ARIMA	0.55	3.53	3.06
LSTM-RNN	1.65	10.84	9.21
Bidirectional-RNN	0.23	1.55	1.27
GRU-RNN	0.53	3.45	2.97
MEM	4.86	26.52	26.25

Table 3.

Daily forecast. Date wise forecasts of daily cumulative cases for COVID-19 by ARIMA, LSTM, BRNN, GRU and MEM.

	Observed	ARIMA	LSTM	BRNN	GRU	MEM
8/10/2020	5094400	5093842	5089235	5102212	5093363	4796503
8/11/2020	5141208	5133133	5132156	5154586	5142174	4848723
8/12/2020	5197411	5182345	5173231	5205310	5190243	4901292
8/13/2020	5248958	5229603	5212686	5257514	5237328	4954232
8/14/2020	5313252	5280036	5250555	5308244	5283285	5007492
8/15/2020	5361165	5328333	5286897	5358477	5328086	5061042
8/16/2020	5403213	5378814	5321762	5397716	5371706	5114869
8/17/2020	5438325	5419619	5355150	5445779	5414222	5168971
8/18/2020	5482416	5463496	5387138	5493529	5455689	5223362
8/19/2020	5529824	5499522	5417787	5541104	5496227	5278066
8/20/2020	5573847	5537796	5447168	5588474	5535862	5333120
8/21/2020	5622540	5572115	5475322	5635743	5574608	5388498
8/22/2020	5667112	5610835	5502327	5682983	5612491	5444175
8/23/2020	5701679	5644105	5528246	5730262	5649546	5500153

Fig. 7-a,b show the performance of the maximum likelihood fitting of MEM. The corresponding estimation of the parameters are shown in Table 4. The mathematical model produces poor predictions in comparison with statistical models and neural network (Please refer to Table 2 to find the comparison among errors). However, the estimated parameter values agree with the COVID-19 outbreak time line and answers crucial questions from the epidemic perspective for instance, how the disease has spread nationwide, how effective the preventive efforts were, how effective the screening was, how many of the infections could not be identified. At the beginning, approximately 8% people were in the susceptible compartment according to our estimation. Gradually lockdown was lifted, and disease spread. Thus, the individuals from Q transferred to S (Fig. 7c). Approximately 60% of the entire population was in compartment Q by August 10, 2020.

Fig. 7.

Maximum likelihood fitting of the MEM for (a) Cumulative identified (b) Daily identified (c)Evolution of susceptible S(t) and non-susceptible population Q(t) with time.

Table 4.

Maximum likelihood estimate of the parameters.

${\alpha }_0$	$\alpha$	${\beta }_0$	$C_{\beta }$	$q$	$C_q$
$0.0837$	$3.007\times {10}^{-11}$	$1.6438\times {10}^{-8}$	$2.150\times {10}^{-5}$	$0.1204$	$7.9573\times {10}^{-8}$

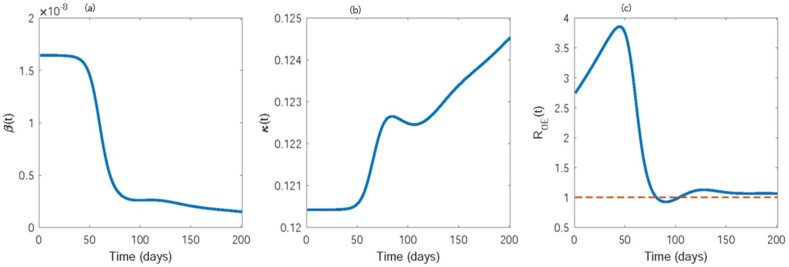
Fig. 8 shows the estimated evolution of the transmission rate, identification rate, and effective reproduction number. Both β(t) and κ(t) were at a steady level for approximately the first 30 days, which was followed by an abrupt decrease in β(t) and an abrupt increase in κ(t) until approximately the 85th day. Hence, the public health measures required time to become effective and create awareness among the individuals. Between the 30th to 85th day, awareness and testing facilities were improved remarkably. This result is correlated with the government effort of making COVID-19 test open to all on 6th March 2020 (45th day in our simulation) and investment of $50 billion dollar for COVID-19 testing facility expansion on 13th March 2020 [58]. Onward, β(t) continued to gently decrease, whereas κ(t) was increasing as a result of imposing social distancing guidelines from 16th March 2020 [58]. These results show the increased awareness regarding preventive measures, the improvement in expanding testing facilities, and the overall improvement in public health policies against the COVID-19 outbreak in the USA.

Fig. 8.

Maximum likelihood estimate of (a) transmission rate β(t), (b) identification rate κ(t), and (c) effective reproduction number $R_{0E}\left(t\right)$ have been shown as a function of time. The dashed line in (c) resembles the threshold value 1 for disease outbreak.

The effective reproduction number was 2.747 but increased to a maximum of 3.856 by the 45th day. Although public health efforts reduced the reproduction number, the increased number of susceptible individuals increased $R_{0E}\left(t\right)$. However, it fell abruptly after the 45th day and decreased below one by the 83rd day, owing to improved preventive efforts and testing facilities. This estimate agrees with the estimate produced by Macdonald et al. [41]. However, as the social distancing regulations are relaxed and business reopening started from 24th April 2020 (95th day in our simulation) [58], the number of susceptible individuals increased. As a result, $R_{0E}$ exceeds 1 by the 101th day. Therefore, although public health interventions temporarily suppressed the transmission, consistent increase in the number of susceptible individuals (due to releasing the lockdown and geographical spread) made it insufficient to retrieve and maintain $R_{0E}\left(t\right)$ below 1.

The daily number of estimated identified (blue shading) and unidentified (red shading) infected cases are compared in Fig. 9 -a. Because of inconsistent symptoms many of the infectious patients were unidentified. In addition, a decrease after the first peak is observed, which is followed by another increase, showing tendency toward a second peak. The estimated fraction of identified cases is plotted in Fig. 9-b. Although approximately 10% of the infectious people were identified at the beginning, this number increased with an improvement in testing facilities, and it was stabilized at approximately 53%. A crucial problem with improving the identification rate was the uncertainty in the symptom onset. However, as the fraction of identified cases was approximately 53%, there is a room for improvement in the identification rate and reduction in the infectious lifetime, which could be performed by contact tracing and quarantining people with plausible exposure.

Fig. 9.

(a) The red and blue area shows estimated unidentified ($I\left(t\right)$) and identified cases ($H\left(t\right)$) cases respectively. (b) The variation of fraction identified ($\frac{H\left(t\right)}{I\left(t\right)+H\left(t\right)}$) with time is shown. Though initially the fraction identified was very low, it settled down above 0.5 by the 200th day. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)

4. Discussion

The COVID-19 pandemic is exponentially spreading worldwide, causing an unprecedented global health crisis. Developing models that can reliably forecast the number of confirmed cases and provide useful information on the outbreak dynamics is critical. In this paper, we applied statistical models, a reproducible framework for RNN variants and a MEM to forecast the number of confirmed COVID-19 cases in the USA. Moreover, it helped to understand the transmission dynamics of the infection. We implemented five techniques: ARIMA, LSTM, BRNN, GRU, and MEM. In our study, LSTM, BRNN, and GRU exploited the presented framework for robust performance. Fifteen-days-ahead forecasts were provided based on historical data from January 22, 2020 to August 10, 2020 for the USA. The performance of the implemented techniques was evaluated using MAPE, RMSE, and MAE. The experimental results suggested the superiority of the reproducible framework in terms of forecasting accuracy. Better predictions facilitate resource management but cannot explain the mechanism and, therefore, are not effective for developing a control strategy.

Therefore, in addition to deep learning techniques, fitting of MEM has been performed. Predictive epidemic models generally estimate constant values of model parameters using least square fitting or estimate time-dependent value of the parameters using Markov chain Monte Carlo or Kalman filter derived techniques. Although the later techniques provide time-dependent estimates, they do not reveal the dynamic dependency of the parameters on the epidemic. The current COVID-19 outbreak has multifaceted underlying mechanisms (for instance, human participation in social distancing measures, expansion of testing facilities to improve identification rates, and the asymptomatic infectious period). Our model fitting not only provides time-dependent estimates of the transmission and identification rates but also reveals their dynamic dependency on the state variables. Furthermore, our model facilitates estimating the unreported fraction of infected individuals, which shows that the reported fraction of identified cases was increased with an improvement in testing facilities [59].

Dealing epidemic with deep learning and MEM comes with their own specific challenges. Deep learning techniques require handful of data to produce reliable prediction, while comes with the limitation of not revealing the transmission mechanism [60]. On the other hand, prediction with MEM is highly dependent on model assumptions, fitting technique and identifiability issue of the parameters [60,61]. In the present work, we implemented both type of approach on time series data of cumulative infected in the USA and found that these two types of approach serves two mutually exclusive purpose for managing disease outbreak. Deep learning techniques produce accurate prediction which is useful for distributing and managing public health resources. On the other hand, MEM helps to explore the transmission mechanism which helps to infer potential control strategies. Our analysis reveals that expansion of testing facility is very crucial for slowing down the spread. In the case of USA, expansion of testing facility along with social distancing measures reduced the effective reproduction number below $1$, which is the condition for disease extinction. As the lock down was released and more people become vulnerable to plausible exposure of the virus, the effective reproduction number surge back above $1$ and the epidemic takes off again. A delayed lock down release could eradicate the disease in the USA. As releasing lockdown increase susceptibility, preventive measures like using mask, disinfecting surfaces maintain distance in crowded places, etc. should be maintained with sufficient care to keep the effective reproduction number below $1$.

However, USA is a big country with geographical heterogeneity. Model implications could be more useful and accurate if smaller geographical units are considered. Our future research direction is to combine mathematical modeling with state of the art neural networks to produce interpretability and effective forecasting simultaneously over a network of smaller geographical units.

Author statement

Conceptualization: MM, MMA, SK; Data curation: MM, HS; Formal analysis: MM, MMA, SK; Funding acquisition: SK; Investigation: HS, SK; Methodology: MM, MMA, MIA; Project administration: HS, SK; Resources: SK; Supervision: HS, SK; Validation: MIA, SK; Visualization: MM, MMA; Roles/Writing - original draft: MM, MMA, MIA; Writing - review & editing: MM, MMA, SK.

Data and materials availability

Publicly available data have been used with citation of the source.

Declaration of competing interest

The authors declare no conflict of interest.

Biographies

Mohammad Masum is currently a fourth-year Ph.D. candidate in the School of Data Science and Analytics, Kennesaw State University, under Professor Hossain Shahriar's supervision. He holds an MS in Mathematical Sciences from East Tennessee State University, USA, and an MS in Applied Mathematics from the University of Dhaka, Bangladesh. His research interest includes developing Machine Learning and Deep Learning techniques for Health Informatics and the cybersecurity domains. He has published several peer-reviewed conference papers, available here. He is also a regular contributor at the online platform Medium.

M. A. Masud is now contributing as a post-doctoral researcher in Busan National University, South Korea. He is on leave from North South University holding the position of Assistant Professor. He completed Ph.D. from Kyungpook National University, South Korea. He has several articles published in peer-reviewed reputed journals. His research aim is to develop and use mathematical and computational tools to explore mechanisms in biology and medicine which are as diverse as epidemiology, immunology, conservation biology, to name just a few. These require skills in mathematical modeling, probabilistic modeling, stability and bifurcation analysis, optimal control theory, game theory.

Muhaiminul Islam Adnan, presently working as a lecturer in Mathematics at United International University, Bangladesh. He obtained his B.S in Mathematics and M.S in Applied Mathematics degree from the University of Dhaka, Bangladesh. He published several journal articles in the field of numerical analysis, Statistics and epidemiology. His research interest includes epidemic modeling, numerical analysis, Machine learning, data analysis, and health science.

Dr. Hossain Shahriar is currently an Associate Professor of Information Technology and BSIT/BASIT program co-ordinator. He received his Ph.D. in Computing from Queen's University. His current research interests include application security, health information security, connected health, blockchain application, and computing education. His research has appeared in various journals and conferences including Computers and Security, Information Security Journal: Global Perspective, Future Generation Computer Systems, Journal of Systems and Software, ACM Computing Surveys, Blockchain in Healthcare Today, and many conferences such as IEEE BigData, IEEE COMPSAC, SIGCSE, IEEE FIE, and ACM SAC.

Sangil Kim is an Associate Professor in Mathematics at Pusan National University and Deputy Director of Finance/Fishery/Manufacture Industrial Mathematics Center on Big Data. He is an author of many publications concerning Biomathematics, Numerical Modeling with Artificial Intelligence, Optimal Control Theory, Decomposition in main effects and interaction term in multiple contingency tables and Correspondence Analysis in presence the ordinal variables by means orthogonal polynomials and/or cumulative analysis.