Abstract
In this paper, a reinforcement learning based framework is developed for COVID-19 resource allocation. We first construct an agent-based epidemic environment to model the transmission dynamics in multiple states. Then, a multi-agent reinforcement-learning algorithm is proposed based on the time-varying properties of the environment, and the performance of the algorithm is compared with other algorithms. According to the age distribution of populations and their economic conditions, the optimal lockdown resource allocation strategies of Arizona, California, Nevada, and Utah in the United States are determined using the proposed reinforcement-learning algorithm. Experimental results show that the framework can adopt more flexible resource allocation strategies and help decision makers to determine the optimal deployment of limited resources in infection prevention.
Keywords: COVID-19, Reinforcement Learning, Agent-based Model, Resource Allocation
1. Introduction
The COVID-19 outbreak is a global pandemic with the widest impact that humans have encountered in the past century. The health care systems in many countries have been severely tested. In the early stage of the outbreak, many hospitals faced shortages of staff and medical supplies, and patients who could not be treated in time had higher mortality rates (Andrea, Charles, & Luciana, 2021). Even now, health systems in some areas are under pressure from shortages of medical supplies and beds.
Although some countries have developed vaccines against the SARS-CoV-2 virus, vaccination coverage in some countries remains low. As the outbreak continues and the virus mutates, vaccines become less effective against the new mutated virus. There are many measures to control COVID-19 pandemic, some of them can be timely deployed, such as lockdown, wearing face masks, and maintaining personal hygiene. Compared with limited and expensive medical resources, more effective use of such non-pharmaceutical interventions measures would not only alleviate the pressure on health systems, but also significantly reduce the number of additional deaths caused by delays in getting care.
In this paper, we construct an agent-based epidemic simulation environment for COVID-19. Based on the time-varying properties of the environment, a new multi-agent reinforcement-learning algorithm is also proposed herein. The proposed reinforcement learning algorithm is applied to explore the optimal lockdown resource allocation strategies.
The contributions of this paper are threefold: First, an agent-based multi-agent reinforcement-learning simulation environment for COVID-19 epidemic is proposed. This environment can not only simulates fine-grained interactions among people at specific locations, but also simulate the population flow between different U.S. states with different economic structures and age distributions. Second, a new multi-agent reinforcement-learning algorithm that can capture the time-varying nature of the environment is developed, and the results show that the algorithm has better performance. Third, real epidemic transmission data are used to calibrate the environment, so the simulation results are more consistent with the real situation. Then, the calibrated framework is used to explore the optimal lockdown resource allocation strategies among the four states in the United States.
2. Related Literature
Recent studies have identified that artificial intelligence (AI) techniques comprise a promising technology employed by various healthcare providers. Reinforcement learning is a machine learning technique that understands and automatically processes goal-oriented learning and decision-making problems. In recent years, reinforcement learning has been applied to many fields and achieved remarkable results (Eilers et al., 2014, Silver et al., 2017, Brown et al., 2019).
There are many literatures on the application of reinforcement learning methods in supply chain management and resource allocation (Shahrabi et al., 2017, Chen et al., 2020). For example, Xiang et al. (2020) developed a model for energy emergency supply chain coordination, which combined reinforcement learning and the emergency supply chain collaboration optimization with group consensus. Deng et al. (2020) studied the dynamic resource allocation of edge computing servers in the Internet of Things environment based on the reinforcement learning method. Liang, Ye, Yu, and Li (2019) explored the problem of applying reinforcement learning to wireless resource allocation in vehicular networks. Cui, Liu, and Nallanathan (2019) developed a multi-agent reinforcement learning framework to study the dynamic resource allocation of multi-Unmanned Aerial Vehicles communication networks in order to maximize long-term benefits. The simulation results show that the multi-agent reinforcement learning algorithm can achieve a good trade-off between performance gains and information exchange costs. Tian, Liu, Zhang, and Wu (2021) applied a multi-agent reinforcement learning to study the channel allocation and power control in heterogeneous vehicular networks and showed that this algorithm has advantages over other reinforcement learning based resource allocation schemes.
In the application of reinforcement learning to COVID-19 related research, some efforts have been chronicled in the literature. Ohi, Mridha, Monowar, and Hamid (2020) employed reinforcement learning to explore COVID-19 lockdown strategies and the experimental results showed that the strategy can strike a balance between controlling the spread of the epidemic and the economic development. Bednarski, Singh, and Jones (2021) applied reinforcement learning to the problem of redistribution of medical supplies, and the effectiveness of the algorithm was demonstrated experimentally.
To study the evolution of COVID-19, predict the timing of the next outbreak, and test the effects of intervention measures, many researchers have studied the construction of epidemic transmission models. There are three main types of epidemic transmission models: compartment models, network models and agent-based models. Since the agent-based model can clearly understand the current disease state of an individual and the interaction between the individual and other individuals, it has been widely used to study the transmission and response of COVID-19. Using population mobility data and demographic data, Aleta et al. (2020) constructed an agent-based model of COVID-19 transmission in the Boston metropolitan area. Willem et al. (2021) applied an agent-based model to simulate resident interactions in Belgium and found that it was critical to complete contact tracing within four days of symptom onset. Wilder et al. (2020) simulated the spread of COVID-19 by building an agent-based model that included household structure, age distribution and comorbidity. Larremore et al. (2021) used an agent-based model to investigate the effectiveness of repeat population screening.
The rest of this paper is organized as follows. Section 3 describes the multi-agent reinforcement learning algorithm proposed in this paper; that is, the multi-agent recurrent attention actor-critic (MARAAC) algorithm. Section 4 introduces the COVID-19 epidemic simulation environment designed in this study. Section 5 describes the simulation experiment settings. Section 6 presents the experiment results, and Section 7 concludes the paper.
3. Multi-Agent Recurrent Attention Actor-Critic Algorithm
3.1. Background
Markov Games. A Markov game is an extension of game theory to Markov decision processes-like environments (Littman, 1994). In general, a Markov game can be represented by the following:
where N is the number of agents and S the system state, which generally refers to the joint state of multiple agents. is the action set of these agents. T is the state-transition function and P is probability distribution. ; that is, the probability distribution of the next state is determined by the current system state and the current actions of all agents. represents the reward obtained by agent i after performing the joint action in state s. The goal of agent i is to maximize its discounted reward expectation . is the discount factor and is the reward obtained by agent i at time .
Attention Mechanism. In recent years, attention mechanisms have been applied in many areas of machine learning. In brief, an attention mechanism is a technique that allows the model to focus on and learn from important information. In the algorithm proposed herein, each agent can observe the information about observations and actions of other agents, and then incorporates the information into the estimation of its value function. An attention function can be described as mapping a query and a set of key-value pairs to an output. The output is a weighted sum of values, and the weight of each value is calculated by a compatibility function of the query with the corresponding key (Vaswani et al., 2017). The calculation formula for scaled dot-product attention is
where , and V represent queries, keys, and values, respectively.
Recurrent Neural Networks. Recurrent neural networks (RNNs) are neural networks with memories that are able to capture the information stored in the previous element of the sequence. However, the traditional fully connected RNNs have the drawbacks of gradient vanishing and gradient exploding, which makes it difficult to deal with time-series problems with long-term dependence. However, long short-term memory (LSTM) is universal and effective in capturing long-term time dependence (Greff, Srivastava, Koutník, Steunebrink, & Schmidhuber, 2016). As a variant of LSTM, the gated recurrent unit (GRU) simplifies the structure of LSTM while retaining its advantages. The GRU cell can be considered as a black box that contains the input state of the current moment and the hidden state of the previous moment, and the cell generates the hidden state of the current moment. The update formulas for all weights are expressed as follow:
| (1) |
where is the reset gate, is the update gate, and is the activation function.
3.2. Method
Consider a task with N agents. Let represent N random policies adopted by each agent and represent the parameter of policy . The action of agent i under observation can be expressed as . Adding recurrence allows the network to better estimate the underlying system state (Hausknecht & Stone, 2015). In this paper, a GRU is introduced in an agent’s policy learning according to the characteristics of time series in the environment to be used. Let the series of historical observations of agent i at time t be . Then, the action of agent i at time t can be written as , and
| (2) |
where are the hidden states of the GRU cell at times and t, and is bias. The policy of agent i is updated as follows:
| (3) |
where
| (4) |
where D is the replay buffer that stores the past experience and the temperature parameter determining the balance between maximizing entropy and rewards.
is called the advantage function, which is used to solve the multi-agent credit assignment problem. It comes from COMA’s counterfactual baseline method developed by Foerster, Farquhar, Afouras, Nardelli, and Whiteson (2018). By comparing the action value of agent i with the average action value of all agents, one can determine whether the increased reward is due to the current action of agent i or the action of other agents. That is, one can calculate the baseline in a single forward pass by outputting the expected return for every possible action that agent i can take. The expectation can be calculated as follows:
| (5) |
In Formula 4, is the Q-value function for agent i. Its input is the action taken by agent i and the environment observation received by agent i, where is a one-layer multi-layer-perceptron (MLP) embedding function and is a two-layer MLP. represents other agents’ contributions:
| (6) |
is an embedding function of agent j, which encodes agent j through an embedding function . h is a nonlinear activation function.
is the attention weight of agent j relative to agent i, which is embedded into a softmax function:
| (7) |
According to the above attention-mechanism settings, the parameters are shared between all agents. All critics are updated by minimizing a loss function:
| (8) |
where
| (9) |
where , and are the parameters of critic, policy, target critic, and target policy, respectively. is the temperature parameter. The structure of the algorithm is shown in Fig. 1 .
Fig. 1.
MARAAC structure.
The algorithm is trained in K parallel environments to improve the sample efficiency and reduce the variance of updates. Algorithm 1 is the pseudo code of MARAAC algorithm.
Algorithm 1
Multi-Agent Recurrent Attention Actor-Critic for N Agents
4. Agent-based COVID-19 epidemic simulation environment
In this section, we construct an agent-based epidemic transmission simulation environment. The environment simulates the contact of different individuals in different locations, including offices, schools, grocery stores, retail stores, restaurants, bars, and parks. The environment simulates a day as 24 discrete hours. In each hour, individuals can randomly decide whether to stay at home, go to work, go to school, travel to another city, and so on. The design of this environment is a modification of Capobianco et al. (2021), which supports simultaneous simulation of multiple cities, and residents can visit other cities. In this environment, multi-agent reinforcement learning is applied to simulate the impact of different government lockdown strategies on the spread of the epidemic. By assigning an agent to each city, the multi-agent reinforcement-learning algorithm can allocate different lockdown resources based on the characteristics of different states, so as to control the spread of the epidemic more effectively.
First, the environment randomly generates a specified number of people based on the pre-set age distribution of the population. Then, the population is divided into youth (aged 0–18), worker (aged 19–64), and elder (aged above 65) groups. These three groups have their own characteristics. The youth group are basically students. They spend most of their time in school and have relatively close contact with each other. Worker group usually work in their workplace during the day, and contact with other people. The elder group are retired and can travel around at any time.
The youths and workers go to school and work for 8 h per day on weekdays, and the elders randomly choose to stay at home, go to other locations or travel to other cities. On weekends, everyone can go to shops, entertainment locations or travel to other cities. When people travel in other cities, they will go to parks, restaurants, stores, and other locations. The outbreak will be accelerated by infected people traveling to other cities or susceptible people contacting infected individuals in other cities. Fig. 2 displays the difference in epidemic transmission with and without intercity travel. According to Fig. 2, the outbreak time of the epidemic is significantly earlier when the setting includes travel between multiple states. And the peak number of infections has also increased. At the end of the day, each person’s infection status is updated via an infection model, according to the other people they have been in contact with during the day.
Fig. 2.
Number of infections with and without intercity travel (The total population of the city is 1,000).
Location in the environment can set the number of staff and visitors respectively, and the contact probability among different people also varies in different locations. The environment also added a scaling factor for the contact rates of all locations to calibrate the environment. If , no scaling is performed. If , maximum scaling is applied. All locations configured in the environment include homes, offices, schools, hospitals, grocery stores, retail stores, restaurants, bars and parks. If a person is sick, depending on the strategy, he may be required to stay at home, otherwise he will follow his routine. If his condition becomes severe enough to require hospitalization, the environment will arrange hospitalization based on the availability of hospital beds.
The situation of people after infection is simulated by a SEAIRD infection model which consists of six states: susceptible (S), exposed (E), asymptomatic (A), infected (I), recovered (R), and death (D). A schematic overview of the SEAIRD model is shown in Fig. 3 .
Fig. 3.
SEAIRD model.
At the beginning of the epidemic simulation, some people will be randomly selected and set to be exposed. Then, the exposed people will transfer to one of the infectious states and interact with susceptible people. The probability that a susceptible person will be infected on a given day after contact with an infected individual is calculated as follows:
| (10) |
where
| (11) |
| (12) |
The in 10 is the probability that a susceptible person will not be infected after contact with an infected individual at time t. is the set of infected population that person i contacts at location j at time t. is the set of the total population in location j at time t. is the set of infected people in location j at time t. is the contact rate of people at location j. is the infection spread rate of each individual, which is used to show the difference in susceptibility between different people. Susceptible people become exposed after contact with infected individuals, and then transfer to different compartments with the probability P. The parameter settings used by the infection model are shown in Table 1 .
Table 1.
Parameters used in SEAIRD model
| Parameter | Description | Value | Source |
|---|---|---|---|
| exposed rate | Zhang et al. (2020) | ||
| symptomatic proportion | 57% | Gudbjartsson et al. (2020) | |
| pre-asymptomatic rate | He et al. (2020) | ||
| pre-symptomatic rate | He et al. (2020) | ||
| recovery rate in asymptomatic compartment | He et al. (2020) | ||
| recovery rate in symptomatic non-treated compartment | He et al. (2020) | ||
| rate from symptom onset to hospitalized | 0.1695 | ||
| h | symptomatic case hospitalization rate | [0.07018, 0.07018,4.735, 16.33, 25.54] | Verity et al. (2020) |
| rate of symptomatic individuals go to hospital | |||
| recovery rate in hospitalized compartment | fit to Austin admissions and discharge data | ||
| rate from hospitalized to death | fit to Austin admissions and discharge data | ||
| f | hospitalized fatality ratio | [4, 12.365, 3.122, 10.745, 23.158] | Verity et al. (2020) |
| death rate on hospitalized individuals | |||
| death rate on individuals that need hospitalization | [0.208, 0.206, 0.228, 0.284, 0.367] | Adjust from CDC (2020) | |
| rate from hospitalization needed to death | 0.3 | self defined | |
| infection spread rate | 0.023 | Calibrate according to real-world data | |
| scaling factor | 0.765 | Calibrate according to real-world data |
The schematic diagram of learning process of MARAAC algorithm in the simulation environment is shown in Fig. 4 . Based on Fig. 4, for an agent, during a learning process, the algorithm first passes the current lockdown resource allocation policy into the environment. The environment then lockdowns the locations according to the received policy and issued regulations for the population (wear masks, stay at home when sick, etc.). In the next time step (set to 7 days for this paper), people act according to the adjusted regulations. At the end of each day (24 o’clock each day), each person’s infection status is updated via the SEAIHRD model, based on the other people they have been in contact with during the day. Then, the current infection status information of all people is summaries into a five-element array containing only the information of susceptible, infected, hospitalized, recovered and dead as the observation information of the day. And the lockdown cost (based on lockdown situation at each location) and hospitalizations is calculated as reward information. Finally, at the end of current time step, all the observation information and reward information of 7 days are summarized as the final observation information and reward information, and feed back to the algorithm. The loss function is calculated and the reinforcement learning network parameters are updated based on the feedback information of the environment.
Fig. 4.
contact network.
5. Experiment Setting
5.1. Algorithm Performance Experiment
In order to study the performance of MARAAC algorithm proposed in this paper, we compare it with other two multi-agent Actor-Critic algorithms, i.e., Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm and Multi-Actor Attention Critic (MAAC) algorithm (Iqbal & Sha, 2019). The experiment uses a multi-agent SEAIRD compartment environment that contains different numbers of cities with inter-city travel; the reward of each agent is set to reduce the economic loss as much as possible while keeping the number of patients below the hospital capacity. To make the lockdown resource allocation strategy more in line with reality, the strategies are updated every 7 d (1 week). Each agent observes the 7-d history of epidemic transmission data and corresponding rewards of their cities at each step. We simulate the environment with 2, 4 and 8 agents respectively. Fig. 5, Fig. 6, Fig. 7 shows the average rewards per episode attained by various methods on the environment.
Fig. 5.
Agent rewards after 10,000 episodes in 8-agent environment.
Fig. 6.
Agent rewards after 10,000 episodes in 4-agent environment.
Fig. 7.
Agent rewards after 10,000 episodes in 2-agent environment.
As can be seen from these figures, although MADDPF can achieve a high reward in the early stage of the 8-agent and the 2-agent environment, the reward of the algorithm starts to decline and fluctuate, which is not stable. However, MAAC and MARAAC can converge smoothly during the whole training process. Among all environments, MARAAC converges faster than MAAC algorithm, and the final reward value is also larger. .
5.2. Simulation Environment Setting
To investigate the epidemic transmission dynamics in different types of states and the impact of population flow between different states on the epidemic transmission, we selected California, Arizona, Nevada, and Utah of the United States as in the experiment.
There are several reasons for choosing these four states. First, geographically, these four states border each other, and population flows among them are relatively frequent. In addition, these four states have different characteristics. California has the largest area, the largest population, and the most developed economy. Arizona also has a larger population than Nevada and Utah, and a different economic structure than California. Among the four states, Nevada has a relatively developed tourism industry, while Utah has the youngest population. The parameters of the environment are chosen on the different conditions of these states. Environment settings are given in Table 2 .
Table 2.
Environment Parameters
| State | Age distribution1 | Parameter2 | locations weight3 |
|---|---|---|---|
| Arizona | [12%, 13.3%, 14%, 12.8%, 12%, 11.9%, 11.5%, 8.4%, 4.1%] | Population: 1400; Home: 514, -, -; Office: 8, 150,0; School: 2, 30, 200; Hospital: 1, 30, 10; Grocery Store: 6, 5, 30;Retail Store: 6, 5, 30; Restaurant: 2,6,30; Bar: 3, 5, 30; Park: 3, 10, 300 | [0.780, 0.018, 0.110, 0.050, 0.010, 0.017, 0.015] |
| California | [12%, 13.1%, 14.5%, 14.5%, 12.8%, 12.5%, 10.6%, 6.4%, 3.6%] | Population: 7400; Homes: 2552, -, -;Office: 37, 150, 0; School: 8, 30, 200; Hospital: 7, 30, 10; Grocery Store: 30, 5, 30; Retail Store: 30, 5, 30; Restaurant: 14, 6, 30; Bar: 15, 5, 30; Park: 5, 10, 300 | [0.840, 0.017, 0.080, 0.035, 0.010, 0.006, 0.012] |
| Nevada | [12%, 12.7%, 13.2%, 14.3%, 12.8%, 12.8%, 11.4%, 7.6%, 3.1%] | Population: 600; Home: 222, -, -;Office: 2, 150, 0; School: 1, 50, 360; Hospital: 1, 18, 6; Grocery Store: 2, 5, 30; Retail Store: 2, 5, 30; Restaurant: 1, 8, 40; Bar: 15, 3, 30; Park: 10, 10, 300 | [0.670, 0.006, 0.085, 0.130, 0.045, 0.016, 0.048] |
| Utah | [15.7%, 16.3%, 16.2%, 14.1%, 12.1%, 9.4%, 8.6%, 5.1%, 2.5%] | Population: 600; Home: 193, -, -;Office: 2, 150, 0; School: 1, 50, 360; Hospital: 1, 18, 6; Grocery Store: 2, 5, 30; Retail Store: 2, 5, 30; Restaurant: 1, 6, 30; Bar: 5, 3, 30; Park: 10, 10, 300 | [0.800, 0.022, 0.110, 0.030, 0.010, 0.014, 0.014] |
Values given as nine-element vectors correspond to 0–9, 10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70–79, and 80 + year age groups, respectively. Data source:https://censusreporter.org/
Values given as three-element vectors correspond to number of locations, employee capacity, and visitor capacity, respectively.
Adjusted according to gross domestic product (GDP) data of each state in 2019 released by Bureau of Economic Analysis.
The objective function of the environment is to minimize the economic loss while keeping the number of individuals in critical condition below the hospital capacity M. Therefore, the reward function is
| (13) |
where are weights and Loc the location weight. represents the lockdown level at location i.
5.3. Parameter Calibration
The epidemic simulation environment used in this paper contains many artificial parameters. Although these parameters refer to the real world, it is still doubtful whether they can truly simulate the actual transmission situation. Therefore, real data are used to calibrate the parameters.
Specifically, we compared the average time to peak for deaths in the epidemic simulation environment against real data from Sweden 1 . Sweden can represent the countries in which the fewest restrictions were applied during the first wave of the epidemic and the transmission dynamics were the most ”natural”(Claeson et al., 2021). Bayesian optimization was applied to adjust the infection spread rate and scaling factor in the simulation environment. That is, we ran a grid search on the transmission rate in the range [0.005, 0.03], and on the social distancing rate in the range [0.5, 1]. Based on the experimental results, the spread rate and the social distancing rate were set to 0.023 and 0.765, respectively.
5.4. Sensitivity Analysis
This section mainly discusses how infection spread rate and scaling factor affect the spread of the epidemic under different values. The results are shown in Table 3 . For all states, the peak number of infections, the time to peak, and the eventual number of deaths all increased as the infection spread rate increased. As the scaling factor increased, the peak number of infections, the time to peak, and the eventual number of deaths decreased. The result is intuitive, as increased infection spread rate and contact rate both worsen the epidemic.
Table 3.
Sensitivity analysis of the environment
| States | Infection Spread Rate | Scaling Factor | ||||||
|---|---|---|---|---|---|---|---|---|
| value | infection peak | time to peak | deaths | value | infection peak | time to peak | deaths | |
| Arizona | 0.01 | 0.363 | 27 | 0.034 | 0 | 0.457 | 23 | 0.037 |
| 0.02 | 0.457 | 23 | 0.037 | 0.4 | 0.415 | 24 | 0.030 | |
| 0.03 | 0.511 | 18 | 0.043 | 0.7 | 0.324 | 26 | 0.041 | |
| California | 0.01 | 0.419 | 24 | 0.032 | 0 | 0.471 | 20 | 0.033 |
| 0.02 | 0.471 | 20 | 0.033 | 0.4 | 0.442 | 24 | 0.031 | |
| 0.03 | 0.514 | 18 | 0.034 | 0.7 | 0.342 | 29 | 0.028 | |
| Nevada | 0.01 | 0.295 | 30 | 0.022 | 0 | 0.337 | 22 | 0.047 |
| 0.02 | 0.337 | 22 | 0.047 | 0.4 | 0.333 | 31 | 0.035 | |
| 0.03 | 0.402 | 22 | 0.048 | 0.7 | 0.195 | 39 | 0.022 | |
| Utah | 0.01 | 0.330 | 27 | 0.022 | 0 | 0.393 | 23 | 0.047 |
| 0.02 | 0.393 | 23 | 0.047 | 0.4 | 0.388 | 29 | 0.035 | |
| 0.03 | 0.442 | 18 | 0.048 | 0.7 | 0.297 | 30 | 0.022 | |
5.5. Strategy Setting
The purpose of the experiment is to explore the optimal lockdown resource allocation strategy and investigate the performance of the multi-agent reinforcement-learning algorithm proposed in this paper, i.e., MARAAC, so as to provide more insights for the simulation and resource allocation strategy of the COVID-19 epidemic. To this end, two experiments were designed. In the first experiment, one agent was assigned to each state. In each step, each agent selected one allocation strategy to execute according to the five-level lockdown resource allocation strategies formulated in this paper. The details of five-level allocation strategies are provided in Table 4 . In the second experiment, each type of location in each state was assigned an agent. This allows the algorithm to fine-tune the allocation strategy of lockdown resources. At the beginning of the epidemic simulation, 1% of the population were randomly selected in each state as exposed individuals. To make the lockdown resource allocation strategy more in line with reality, the agents updated their strategies once per week (7 d) and the spread of the epidemic was simulated for 20 weeks (140 d).
Table 4.
Five-level allocation strategies
| Levels | Stay home if sick, Practice good hygiene | Wear facial coverings | Locked locations | Travel restrictions |
|---|---|---|---|---|
| Level 0 | False | False | None | False |
| Level 1 | True | True | None | True |
| Level 2 | True | True | School | True |
| Level 3 | True | True | School, Retail Store, Bar, Restaurant, Park | True |
| Level 4 | True | Ture | Office, School, Retail Store, Restaurant, Bar, Park | True |
6. Results
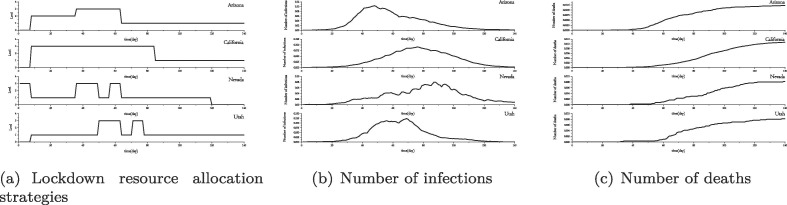
Fig. 8 displays the results of the first experiment. Fig. 8(a) shows the lockdown resource allocation strategies of the four states, and the curves of the number of infections and deaths in each state are displayed in Figs. 8(b) and (c), respectively. As can be seen from these figures, the algorithm has adopted different allocation strategies in different states based on the age distributions and economic conditions of different states. To summarize, the algorithm has accurately captured the outbreak situation. Among the four states, California has the largest population, so the algorithm implements a strict lockdown which will last for a long time. Arizona has a smaller population than California, so the lockdown is not so strict, but the number of infections has also been controlled within a certain range. Nevada and Utah have relatively small populations, but Nevada’s tourism industry is relatively developed, so stricter lockdown strategies are allocated at the beginning of the epidemic and travel restrictions are lifted when the epidemic situation becomes relatively stable. Utah, with its small and young population, has a lower probability of people developing a severe illness or dying after infection, so the state allocates few lockdown resources most of the time. It can be seen from the death toll that Utah had the lowest number of deaths despite having few lockdown resources.
Fig. 8.
Results of first experiment.
In order to evaluate the transfer-ability of the reinforcement learning algorithm, the trained algorithm was applied to the environment with a total population of 100,000, and the result is shown in Fig. 9 . As can been seen from Fig. 9, the results are robust, so the algorithm can quickly learn the strategy even if it is transferred to a larger environment.
Fig. 9.
Results of the first experiment in the environment with a total population of 100 000.
The results of the second experiment are displayed in Fig. 10 . The lockdown resource allocation strategies for the four aforementioned states are presented in Figs. 10 (a-d). The y axis represents the degree of lockdown resource allocation, where 0 indicates no lockdown resource and 1 means maximum lockdown resources. Figs. 10 (e and f) plot the curves of the number of infections and deaths in each state. As shown in these figures, the algorithm has adopted different lockdown strategies for different states. In short, the algorithm effectively captured the outbreak of the epidemic.
Fig. 10.
Results of the second experiment.
7. Conclusion
In this paper, a reinforcement learning based framework is constructed for COVID-19 resource allocation. First, we develop an agent-based COVID-19 epidemic simulation environment, which can not only simulate the interaction among people within a city, but can also simulate the population flow among different states (several U.S. states were chosen for simulation). Then, a multi-agent reinforcement-learning algorithm is proposed based on the time-varying properties of the environment, and the performance of the algorithm is compared with other algorithms. According to the age distribution of population and their economic conditions of Arizona, California, Nevada, and Utah in the United States, the optimal lockdown resource allocation strategies are determined using the proposed framework. The experimental results show that the algorithm can adopt the more flexible allocation strategy according to the age distribution of population and economic conditions, which provide insights for decision makers in supply chain management.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the Technology and Innovation Major Project of the Ministry of Science and Technology of China under Grant Nos. 2020AAA0108400, 2020AAA0108402 and 2020AAA0108404.
Footnotes
https://covid19.who.int/region/euro/country/se
References
- Aleta, A., Martin-Corral, D., y Piontti, A. P., Ajelli, M., Litvinova, M., Chinazzi, M., Dean, N. E., Halloran, M. E., Longini Jr. I.M., & Merler, S., et al. (2020). Modelling the impact of testing, contact tracing and household quarantine on second waves of covid-19. Nature Human Behaviour 4 (9) (pp. 964–971). [DOI] [PMC free article] [PubMed]
- Andrea, B., Charles, W., Luciana, & M. S. S. et al. (2021). Report 46 - factors driving extensive spatial and temporal fluctuations in covid-19 fatality rates in brazilian hospitals, [EB/OL], https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/report-46-Brazil/ (2021).
- Bednarski B.P., Singh A.D., Jones W.M. On collaborative reinforcement learning to optimize the redistribution of critical medical supplies throughout the covid-19 pandemic. Journal of the American Medical Informatics Association. 2021;28(4):874–878. doi: 10.1093/jamia/ocaa324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown N., Sandholm T. Superhuman ai for multiplayer poker. Science. 2019;365(6456):885–890. doi: 10.1126/science.aay2400. [DOI] [PubMed] [Google Scholar]
- Capobianco R., Kompella V., Ault J., Sharon G., Jong S., Fox S., Meyers L., Wurman P.R., Stone P. Agent-based markov modeling for improved covid-19 mitigation policies. Journal of Artificial Intelligence Research. 2021;71:953–992. [Google Scholar]
- CDC, 2020. Covid-19 laboratory-confirmed hospitalizations preliminary data as of sep 12 2020, [EB/OL], https://gis.cdc.gov/grasp/COVIDNet/COVID19_5.html.
- Chen R., Yang B., Li S., Wang S. A self-learning genetic algorithm based on reinforcement learning for flexible job-shop scheduling problem. Computers & Industrial Engineering. 2020;149:106778. [Google Scholar]
- Claeson M., Hanson S. Covid-19 and the swedish enigma. The Lancet. 2021;397(10271):259–261. doi: 10.1016/S0140-6736(20)32750-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui J., Liu Y., Nallanathan A. Multi-agent reinforcement learning-based resource allocation for uav networks. IEEE Transactions on Wireless Communications. 2019;19(2):729–743. [Google Scholar]
- Deng S., Xiang Z., Zhao P., Taheri J., Gao H., Yin J., Zomaya A.Y. Dynamical resource allocation in edge for trustable internet-of-things systems: A reinforcement learning method. IEEE Transactions on Industrial Informatics. 2020;16(9):6103–6113. [Google Scholar]
- Eilers D., Dunis C.L., von Mettenheim H.-J., Breitner M.H. Intelligent trading of seasonal effects: A decision support algorithm based on reinforcement learning. Decision Support Systems. 2014;64:100–108. [Google Scholar]
- Foerster, J., Farquhar, G., Afouras, T., Nardelli, N., Whiteson, S. (2018). Counterfactual multi-agent policy gradients. In Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 32, 2018.
- Greff K., Srivastava R.K., Koutník J., Steunebrink B.R., Schmidhuber J. Lstm: A search space odyssey. IEEE Transactions on Neural Networks and Learning Systems. 2016;28(10):2222–2232. doi: 10.1109/TNNLS.2016.2582924. [DOI] [PubMed] [Google Scholar]
- Gudbjartsson D.F., Helgason A., Jonsson H., Magnusson O.T., Melsted P., Norddahl G.L., Saemundsdottir J., Sigurdsson A., Sulem P., Agustsdottir A.B., et al. Spread of sars-cov-2 in the icelandic population. New England Journal of Medicine. 2020;382(24):2302–2315. doi: 10.1056/NEJMoa2006100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hausknecht, M., & Stone, P. (2015). Deep recurrent q-learning for partially observable mdps. In 2015 aaai fall symposium series.
- He X., Lau E.H., Wu P., Deng X., Wang J., Hao X., Lau Y.C., Wong J.Y., Guan Y., Tan X., et al. Temporal dynamics in viral shedding and transmissibility of covid-19. Nature Medicine. 2020;26(5):672–675. doi: 10.1038/s41591-020-0869-5. [DOI] [PubMed] [Google Scholar]
- Iqbal, S., & Sha, F. (2019). Actor-attention-critic for multi-agent reinforcement learning. In International Conference on Machine Learning, PMLR, 2019 (pp. 2961–2970).
- Larremore D.B., Wilder B., Lester E., Shehata S., Burke J.M., Hay J.A., Tambe M., Mina M.J., Parker R. Test sensitivity is secondary to frequency and turnaround time for covid-19 screening. Science Advances. 2021;7(1):eabd5393. doi: 10.1126/sciadv.abd5393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang L., Ye H., Yu G., Li G.Y. Deep-learning-based wireless resource allocation with application to vehicular networks. Proceedings of the IEEE. 2019;108(2):341–356. [Google Scholar]
- Littman M.L. Machine learning proceedings 1994. Elsevier; 1994. Markov games as a framework for multi-agent reinforcement learning; pp. 157–163. [Google Scholar]
- Ohi A.Q., Mridha M., Monowar M.M., Hamid M.A. Exploring optimal control of epidemic spread using reinforcement learning. Scientific Reports. 2020;10(1):1–19. doi: 10.1038/s41598-020-79147-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahrabi J., Adibi M.A., Mahootchi M. A reinforcement learning approach to parameter estimation in dynamic job shop scheduling. Computers & Industrial Engineering. 2017;110:75–82. [Google Scholar]
- Silver D., Schrittwieser J., Simonyan K., Antonoglou I., Huang A., Guez A., Hubert T., Baker L., Lai M., Bolton A., et al. Mastering the game of go without human knowledge. Nature. 2017;550(7676):354–359. doi: 10.1038/nature24270. [DOI] [PubMed] [Google Scholar]
- Tian, J., Liu, Q., Zhang, H., & Wu, D. (2021). Multi-agent deep reinforcement learning based resource allocation for heterogeneous qos guarantees for vehicular networks. IEEE Internet of Things Journal.
- Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., Polosukhin, I. (2017). Attention is all you need. In Advances in neural information processing systems, 2017 (pp. 5998–6008).
- Verity R., Okell L.C., Dorigatti I., Winskill P., Whittaker C., Imai N., Cuomo-Dannenburg G., Thompson H., Walker P.G., Fu H., et al. Estimates of the severity of coronavirus disease 2019: a model-based analysis. The Lancet Infectious Diseases. 2020;20(6):669–677. doi: 10.1016/S1473-3099(20)30243-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilder B., Charpignon M., Killian J.A., Ou H.-C., Mate A., Jabbari S., Perrault A., Desai A.N., Tambe M., Majumder M.S. Modeling between-population variation in covid-19 dynamics in Hubei, Lombardy, and New York City. Proceedings of the National Academy of Sciences. 2020;117(41):25904–25910. doi: 10.1073/pnas.2010651117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Willem L., Abrams S., Libin P.J., Coletti P., Kuylen E., Petrof O., Møgelmose S., Wambua J., Herzog S.A., Faes C., et al. The impact of contact tracing and household bubbles on deconfinement strategies for covid-19. Nature Communications. 2021;12(1):1–9. doi: 10.1038/s41467-021-21747-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang L. Energy emergency supply chain collaboration optimization with group consensus through reinforcement learning considering non-cooperative behaviours. Energy. 2020;210:118597. [Google Scholar]
- Zhang J., Litvinova M., Wang W., Wang Y., Deng X., Chen X., Li M., Zheng W., Yi L., Chen X., et al. Evolving epidemiology and transmission dynamics of coronavirus disease 2019 outside Hubei province, China: A descriptive and modelling study. The Lancet Infectious Diseases. 2020;20(7):793–802. doi: 10.1016/S1473-3099(20)30230-9. [DOI] [PMC free article] [PubMed] [Google Scholar]