修正SEIR传染病动力学模型应用于湖北省2019冠状病毒病(COVID-19)疫情预测和评估

Abstract

目的

建立可用于2019冠状病毒病（COVID-19）疫情评估的SEIR传染病动力学模型，并对湖北省COVID-19疫情进行预测和评估。

方法

考虑COVID-19潜伏期患者不易被有效隔离，且具有较强的传染能力，建立了联合考虑潜伏期传播能力和追踪隔离干预措施的COVID-19 SEIR传染病动力学模型。以2020年1月23日至2月24日的湖北省疫情数据为依据，拟合得到了新建立的修正SEIR模型的动力学参数。通过欧拉数值方法实现修正SEIR传染病动力学模型的求解，对湖北省疫情进行分析，评估防控隔离和集中收治等措施对疫情发展的影响。

结果

修正的SEIR传染病动力学模型对疫情的理论估计与湖北省疫情的实际情况较为符合。模型理论分析表明，防控隔离和医学追踪隔离等措施对疫情大面积传播有重要抑制作用；集中接收、分层治疗等重要措施对感染人数峰值的迅速回落起到了关键作用；此外，个人提高防范意识，采取严格自我防护措施，遏制了感染人数的新增。

结论

修正的SEIR传染病动力学模型可用于COVID-19传播态势分析，以便为制订未来的疫情干预决策提供一定的理论支持。

2019年12月初，湖北省武汉市暴发2019冠状病毒病(coronavirus disease 2019，COVID-19)，其病原体于2020年2月11日被国际病毒分类委员会命名为严重急性呼吸综合征冠状病毒2(severe acute respiratory syndrome coronavirus 2，SARS-CoV-2)。SARS-CoV-2以其高传播效率、严重感染后果以及捉摸不定的流行时间对人类健康构成持续的威胁。两个多月时间，COVID-19疫情已经从湖北省迅速蔓延至全国各地。

部分学者尝试通过动力学模型对COVID-19疫情发展态势进行研究和分析。2020年1月24日，英国学者Jonathan等 ^{[ 1]} 对疫情进行了初步估计，认为2月4日武汉市感染病例将达到19万例，这显然高估了疫情发展态势。2020年1月25日，西安交通大学健康科学中心Shen等 ^{[ 2]} 在现有流行病学资料和动力学模型的基础上，估计了SARS-CoV-2的基本和有效繁殖次数，并预测了疫情高峰时间和规模，估计感染人数最终在2万人以内，这已经低于2月7日公布的疫情数据。2020年1月31日，中国香港学者Wu等 ^{[ 3]} 利用武汉市2019年12月31日至2020年1月28日的病例数推算武汉市感染人数，推测1月25日感染人数超过6000，高于25日全国感染确诊人数1985例。最近，西安交通大学肖燕妮教授等基于SARS-CoV-2的传播机制，考虑密切跟踪隔离等干预策略，建立了疫情传播动力学模型。其对COVID-19传播风险进行了预测分析，预计疫情将在2月5日左右到达高峰 ^{[ 4]} ，而当前的疫情发展态势已经远远偏离了上述COVID-19疫情传播动力学研究的预测结果。近期，部分学者尝试利用SEIR模型推演湖北省、湖北省以外地区和全国的疫情拐点，但是模型中没有考虑防控措施、集中收治等因素对于疫情的遏制作用 ^{[ 5]} 。此外，有学者基于数据驱动的网络模型研究了武汉及周边地区复工对疫情发展的影响 ^{[ 6]} 。

考虑到在疫情发展初期，学者们开展疫情传播动力学研究时缺乏足够的原始数据，所以较难对疫情发展态势进行准确预测 ^{[ 1- 4]} 。再加上最近的证据表明不易被有效隔离的潜伏期患者具有较强的病毒传播能力，而研究人员之前建立的疫情传播动力学模型忽略了潜伏期患者导致的传播风险 ^{[ 4- 6]} 。因此，当前阶段仍有必要对COVID-19疫情传播规律进行研究，这对疫情的态势分析和防控指导等有着现实意义。本文将建立考虑潜伏期患者病毒传播能力和追踪隔离干预措施对疫情作用的修正SEIR传染病动力学模型。以实际数据为依据，参考已有文献报道，拟合得到新建立的SEIR模型的动力学参数。通过欧拉数值方法对湖北省疫情进行分析，讨论防控隔离和集中收治等措施对疫情发展的影响。

1 资料与方法

1.1 数据来源及假设

本文所采用的疫情数据来源于湖北省卫生健康委员会官方网站(http://wjw.hubei.gov.cn/)。2020年1月23日，面对疫情防控压力，湖北省武汉市宣布“封城”，随后湖北省其他城市也相继采取了“封城”举措，人员间的接触率相对稳定，故取2020年1月23日至2月24日的疫情数据进行研究。此外，根据国家统计局官方网站()公布的2018年人口统计数据，设定湖北省常住人口为5917万。

考虑到2020年1月23日湖北省大部分城市采取“封城”措施，故假设湖北省为一个封闭的节点，基本可以忽略省级人口流动。考虑到近期研究结果表明SARS-CoV-2在潜伏期就具有传染性，本文在已有疫情传播动力学模型 ^{[ 4]} 的基础上进行了修正。新模型一方面考虑了潜伏期患者的传播风险，另一方面也考虑了防控隔离等手段对于疫情演化的影响。此外，本模型尚未考虑无症状感染者的影响，未来可以在本模型的基础上考虑无症状感染者，使得模型更加贴合实际。

1.2 SEIR模型建模

经典SEIR模型将人群分为易感者(susceptible， S)、感染者(infected， I)、接触者(exposed， E)和康复人群(recovered， R)。该模型还假设人群中所有个体都有被感染的概率，当被感染个体痊愈后，会产生抗体，即康复人群 R不会再被感染。考虑到防治传染病的隔离措施，模型中的人群组别新增隔离易感者( S _q )、隔离接触者( E _q )和隔离感染者( I _q )。鉴于隔离感染者会立即送往定点医院隔离治疗，因此这部分人群在本模型中全部转化为住院患者 H。因此，本文修订的模型中 S、 I、 E分别指隔离措施遗漏的易感者、感染者和接触者。隔离易感者解除隔离后重新转变为易感者，而感染者和接触者对易感者均有不同程度的感染能力，使其转化为接触者。人群的转化关系如 图 1所示。

图1.

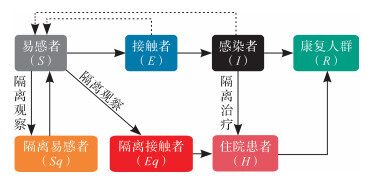
修正的SEIR传染病动力学模型中人群转化

假设隔离比例为 q，传染概率为 β，接触率为 c， ρ是有效接触系数，有效接触系数的参考值取1， ρc是有效接触率。易感者 S向隔离易感者 S _q 、隔离接触者 Eq、接触者 E的转化速率为 ρcq(1- β)、 ρcβq和 ρcβ(1- q)。同时考虑到非隔离的感染者 I和接触者 E对易感人群的影响，又有隔离解除的易感者 S _q 重新转变为 S，因此易感者人数控制方程为

其中 θ是接触者相对于感染者传播能力的比值，假设接触者与已表现出症状患者的传染能力相同，即 θ=1。λ是隔离解除速率，取 λ=1/14(隔离时长为14 d)。

用于COVID-19疫情的修正SEIR方程构建如下：

其中， σ为接触者向感染者的转化速率，取 σ=1/7(潜伏期为7 d)， α为病死率， δ _I 是感染者的隔离速率， γ _I 是感染者的恢复率。 δ _q 是隔离接触者向隔离感染者的转化速率， γ _H 是隔离感染者的恢复速率。

1.3 模型参数赋值及检验

对模型采用欧拉数值方法进行求解，时间步长为0.01(d)。需要声明的是，本文模型中的 I为当前感染者人数，定义为当天公布的确诊病例减去治愈病例和死亡病例。

上述SEIR模型参数赋值如 表 1所示，参数赋值与文献[ 6]中的参数赋值基本保持一致。由于文献[ 6]未考虑潜伏期患者的传染能力，高估了接触传染概率 β，所以本文对其给出的接触传染概率进行了调整，并且基于当前更多的原始数据对参数 q和 α等进行拟合优化，从而提高模型预测的准确性。

表1 修正的SEIR传染病动力学模型参数赋值

Table 1 Parameters in modified SEIR model

参 数	c	δ I	δ q	γ I
本文取值	2	0.13	0.13	0.007
文献[ 6]取值	1.6~4.8	0.132 66	0.125 9	0.330 29
取值说明	保持一致	保持一致	保持一致	基于实际治愈人数调整
参 数	γ H	β	q	α
本文取值	0.014	2.05×10 -9	1×10 -6	2.7×10 -4
文献[ 6]取值	0.116 24	2.101 1×10 -8	1.888 7×10 -7	1.782 6×10 -5
取值说明	基于实际治愈人数调整	文献[ 6]未考虑潜伏期患者传染能力，高估了接触传染概率	参考文献[ 6]并基于实际数据进行拟合优化	基于实际死亡人数调整

   c：接触率； δ _I ：感染者的隔离速率； δ _q ：隔离接触者向隔离感染者的转化速率； γ _I ：感染者的恢复速率； γ _H ：隔离感染者的恢复速率； β：传染概率； q：隔离比例； α：病死率.

动力学系统的初值参考2020年1月23日湖北省官方公布数据，部分参数进行了合理的估值，具体参数取值及其取值说明见 表 2。

表2 修正的SEIR传染病动力学模型初值设定

Table 2 Initial values of the modified SEIR dynamic model

变 量	S	E	I	S q	E q	H	R
取值	5917万	4007	524×1.5	2776	400(估)	I+E q	31
取值说明	湖北省总人口官方数据	2020年1月29日确诊人数与1月23日确诊人数的差值	官方数据基础上考虑了未检出比例	官方数据，尚接受医学观察	小于尚在接受医学观察人数	患者隔离与部分医学观察	官方数据

   S：易感者； E：接触者； I：感染者； S _q ：隔离易感者； E _q ：隔离接触者； H：住院患者； R：康复人群.

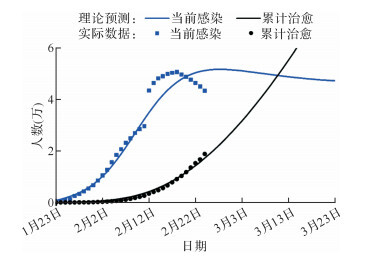
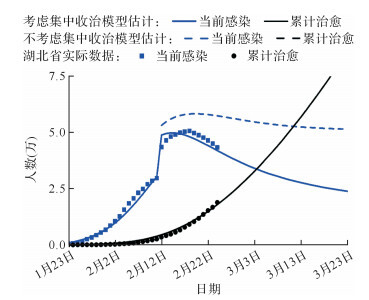
利用建构的SEIR模型分析发现，当前模型理论预测的感染人数与2020年1月23日至2月12日的实际数据吻合度较好( 图 2)。而当 θ=0(即不考虑潜伏期患者传染力)时(等同于文献[ 6]建立的SEIR模型)，模型理论估计得到的湖北省感染人数峰值达到16万，远高于湖北省疫情实际数据。由此可见，本文中修正的SEIR模型对疫情的理论估计更符合湖北省疫情的实际情况。

图2.

考虑潜伏期传染性和不考虑潜伏期传染性时修正的SEIR传染病动力学模型对感染人数和治愈人数的理论估计对比

湖北省疫情实际数据截至2020年2月24日.

2 结果与讨论

基于本文SEIR模型对湖北省疫情进行回溯研究，对湖北省疫情发展规律进行理论分析，并分析防控隔离和集中收治等措施对其疫情发展的影响。

2.1 湖北省COVID-19疫情分析

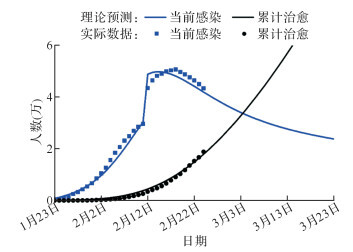
基于本文建立的SEIR模型估计湖北省的感染人数与2020年1月23日至2月11日实际感染人数吻合度较好( 图 3)。需要指出的是，本文模型及参数于2月5日前确立，而模型预测的2月6日至11日感染人数与后续报道的实际数据基本一致，研究结果初步证明该修正的SEIR模型对疫情走势的评估是可靠的。

图3.

修正的SEIR传染病动力学模型对湖北省2019冠状病毒病疫情走势的预测

模型及参数于2020年2月5日前确立并进行预测.

2月12日起，湖北省改变新增确诊病例的统计方式，将临床诊断病例计入新增病例中，官方公布的新增病例大幅上升。统计方式的改变导致官方公布的数据高于 图 3所示的理论模型预测结果。考虑前后的统计方法不同，因此对模型参数进行适当修正。通过考虑部分非二次确诊病例的计入导致平均感染系数较低，以及总病例数增大导致接触系数增大，使用调整参数后的SEIR模型计算感染人数理论结果，对应于2月12日之后临床诊断标准修改后的理论预测结果。理论预测的湖北省疫情结果与实际数据基本吻合，初步解释了2月12日新增病例数突增以及疫情后续发展趋势等( 图 4)，预计湖北省COVID-19感染人数2月19日左右达到顶峰，与疫情的实际情况基本一致。

图4.

针对临床诊断标准修改对SEIR模型再次修正后对湖北省2019冠状病毒病疫情走势的预测

湖北省疫情实际数据截至2020年2月24日.

2.2 防控隔离和隔离密切接触者对疫情的影响评估

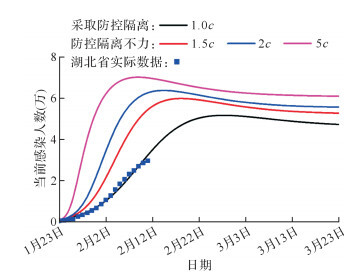
2020年1月24日起，湖北省启动重大突发公共卫生事件Ⅰ级响应，根据突发公共卫生事件处理需要，启动了必要的防控隔离措施，如限制或停止集市、集会、影剧院演出以及其他人群聚集的活动，并对流动人口采取预防工作，防止病毒在人与人之间过度扩散。这些防控隔离措施本质上是降低易感者的接触率 c。本文在理论分析中假定当前防控隔离措施下的接触率为2。通过增加接触率来模拟防控措施不力条件下的COVID-19发展态势，用于评估当前防控措施的效果。 图 5给出了更高易感者接触率下的疫情模拟(假设诊断标准未发生变化，即感染人数未突跳)。分析发现当前的严格管制和防控隔离等措施，已经对当前疫情大面积发展产生较好的抑制效果。如果2020年1月24日起没有采取政府倡导下的群众防控隔离，湖北省感染人数会迅速增长，并且可能达到当前感染人数的2倍以上( 图 5中粉色线)。此外，若未采取当前的严格管制和防控隔离等措施，将导致感染人数峰值更高且更快达到峰值，造成更大的生命财产损失和社会恐慌。

图5.

利用修正的SEIR传染病动力学模型评估防控隔离措施对疫情控制的影响

湖北省实际感染人数截至2020年2月11日.

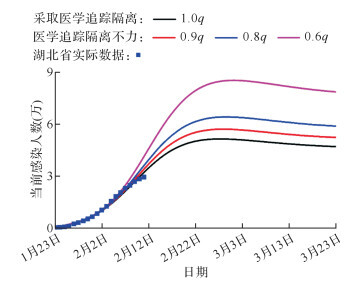
为了控制疫情，湖北省实施了严格的医学追踪隔离，如将与感染者接触过的人群进行为期14 d的隔离观察。本文模拟了追踪隔离措施，即追踪隔离比例下降对疫情发展的后果。如 图 6所示，当隔离比例下降为0.9、0.8和0.6倍时，感染人数的上升速率和峰值均会增加(假设诊断标准未发生变化，即感染人数未突跳)。尤其当取0.6 q时，感染人数峰值提高约两倍。由此可见，严格的医学追踪隔离是防止疫情发展的有效手段。

图6.

利用修正的SEIR传染病动力学模型评估医学追踪隔离等措施对疫情控制的影响

湖北省实际感染人数截至2020年2月11日.

2.3 集中收治和个人防护对疫情的影响评估

疫情暴发后，湖北省积极动员医院为疫情空出床位，同时国家部署雷神山医院、火神山医院、方舱医院等，集中接收、分层治疗患者。本文模拟了不采取集中收治措施时感染人数的发展趋势。感染者向住院者的转化速率对应本文模型中的参数 δ _I 。集中收治能力与参数 δ _I 成正比。从 图 7可以看出，从2月5日开始集中收治确诊患者对湖北省感染人数的迅速回落起到了关键作用，疫情峰值在2月19日左右出现，感染人数大幅降低。随着疫情的发展，集中收治对疫情的遏制效果逐渐凸显，预计在集中收治措施实施一个月之后感染人数降低约两万人。

图7.

利用修正的SEIR传染病动力学模型评估集中收治措施对疫情控制的影响

湖北省疫情实际数据截至2020年2月24日.

随着日常接触率增大，个人日常安全防护显得尤其重要。有效接触率为 c′= ρc。其中 c为日常接触率， ρ为有效接触系数。 图 8分析了有效接触系数降低对疫情发展的影响(假设诊断标准未发生变化)，设置人员之间接触率 c=10。有效接触系数分别取0.5、0.25和0.1时，如 图 8红色、蓝色和粉色数据线所示。个人日常防护措施将在保障个人安全的同时，对遏制疫情的发展起到重要作用。严格的日常安全防护有助于感染人数峰值时间的提前，并且有助于峰值人数的降低。在严格个人防护措施下( ρ=0.1， 图 8中粉色曲线)，感染人数峰值可下降接近50 %。

图8.

利用修正的SEIR传染病动力学模型评估日常安全防护对疫情控制的影响

湖北省疫情数据截至2020年2月11日.

3 结语

综上所述，本文收集整理了2020年1月23日至2月24日的确诊、疑似病例人数等官方数据，通过建立修正的SEIR传染病动力学模型对湖北省疫情发展规律进行了分析，并利用模型估计了防控隔离和集中收治等措施对疫情发展的影响。分析结果表明：①防控隔离和医学追踪隔离是有效遏制COVID-19大面积传播的重要措施。政府倡导下的居家防控隔离措施对疫情大面积传播有重要抑制作用，对感染者所接触过的人员进行严格医学追踪隔离也有效地防止了疫情的过快增长。②集中接收、分层治疗等重要措施对感染人数峰值的迅速回落起到了关键作用，对疫情发展有重要控制效果。个人安全防护措施的提升会极大遏制疫情发展，采取严格自我防护措施，起到遏制感染人数过快增长的作用。

本文构建的SEIR模型对湖北省COVID-19疫情进行回溯分析，研究结果确认了该模型在传染病传播态势分析上是可靠的，可以为制订未来的疫情干预决策提供一定的理论支持。但是，模型不可避免地会与现实存在一定差异，进而导致分析预测结果存在一定的偏差。

Funding Statement

国家自然科学基金（11802225）