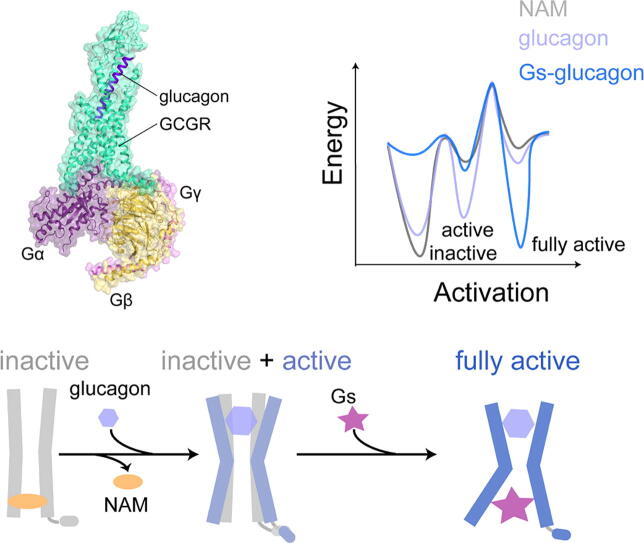
Graphical abstract
Keywords: GPCR, Molecular dynamics simulations, Markov state model, Allosteric modulator
Abstract
Class B G protein-coupled receptors (GPCRs) are important targets in the treatment of metabolic syndrome and diabetes. Although multiple structures of class B GPCRs–G protein complexes have been elucidated, the detailed activation mechanism of the receptors remains unclear. Here, we combine Gaussian accelerated molecular dynamics simulations and Markov state models (MSM) to investigate the activation mechanism of a canonical class B GPCR, human glucagon receptor–GCGR, including the negative allosteric modulator-bound inactive state, the agonist glucagon-bound active state, and both glucagon- and Gs-bound fully active state. The free-energy landscapes of GCGR show the conformational ensemble consisting of three activation-associated states: inactive, active, and fully active. The structural analysis indicates the high dynamics of GCGR upon glucagon binding with both active and inactive conformations in the ensemble. Significantly, the H8 and TM6 exhibits distinct features from the inactive to the active states. The additional simulations demonstrate the role of H8 in the recruitment of Gs. Gs binding presents a crucial function of stabilizing the glucagon binding site and MSM highlights the absolute requirement of Gs to help the GCGR reach the fully active state. Together, our results reveal the detailed activation mechanism of GCGR from the view of conformational dynamics.
1. Introduction
Seven transmembrane (TM) proteins–G protein-coupled receptors (GPCRs)–are the most successful targets in the human genome, and account for the therapeutic targets of one-third of approved drugs [1], [2], [3], [4], [5], [6]. Under normal physiological conditions, the endogenous ligands bind to the orthosteric sites of the receptor and activate the receptor by inducing conformational rearrangements. Upon activation, the intracellular transducers (such as G proteins) are recruited to the binding sites located at the intracellular region of the receptor for initiating the exchange of guanine nucleotide and then stimulating multiple intracellular signaling events [7], [8], [9], [10], [11].
The class A GPCRs adopt the quintessential activation mechanism, where endogenous ligands binding leads to outward movements of the intracellular end of TM6 and TM5 and inward movement of the intracellular end of TM7. These movements open the intracellular cavity of the receptors for accommodating G proteins. It is well-established that the agonist alone binding to the class A GPCRs induces the large magnitude of conformational changes, and shift the conformational ensemble towards a fully active state [12], [13], [14], [15]. In comparison to the class A GPCRs, the activation mechanism of class B GPCRs is poorly understood, which hinders the drug discovery of class B GPCRs. Structural comparison between class A and class B GPCR highlights that class B GPCRs adopt a distinct active state, such as the formation of a sharp bend in the PxxG motif of the TM6. Furthermore, class B GPCRs miss many conserved motifs that play key roles in the activation of class A GPCRs, such as the NPxxY motif of the TM7 [16], [17], [18], [19], [20], [21]. These discrepancies imply that the activation mechanism of class B GPCRs differs from that of the class A GPCRs Thus, there is a pressing demand for exploring the underlying activation mechanism in the class B GPCRs, to better understand their biology, biophysics, and medicinal chemistry.
Class B GPCRs (the secretin peptide receptors) play a crucial role in maintaining hormonal homeostasis in the human body. The structure of class B GPCRs consists of an extracellular domain (ECD) and a seven-transmembrane domain (TMD) [22], [23], [24], [25], [26], [27]. The human glucagon receptor (GCGR) is a prototypical class B GPCR. It mediates the glucose homeostasis in response to the endogenous ligand (peptide hormone glucagon), and is considered a crucial target for the treatment of obesity and type 2 diabetes [28], [29], [30], [31], [32], [33]. Recently, multiple GCGR complexes have been reported. Compared with other class B GPCRs, both the inactive and active states of crystal or cryo-electron microscopy (cryo-EM) structures of GCGR are determined, including the inactive conformation of the full-length GCGR bound to the negative allosteric modulator (NAM) (NNC0640) and antigen-binding fragment (Fab) (PDB ID: 5XEZ) [34], [35], the active conformation of GCGR bound to a partial agonist (a glucagon analog, NNC1702) (PDB ID: 5YQZ) [36] and the fully active conformation of GCGR bound to the full agonist (ZP3780, a soluble glucagon analog) and Gs protein (PDB ID: 6WPW) [16]. Based on the crystal or cryo-EM structures of GCGR, the conformational changes of a 12-residue segment (termed as salk) and the extracellular loop 1 (ECL1) during the peptide binding are observed, which deepen the molecular underpinning of peptide recognition by GCGR. However, crystal or cryo-EM structures usually represent one snapshot of the conformational ensemble. As a result, crystallographic information is not sufficient to elaborate the allosteric communication mechanism of the conformational transition from the endogenous ligand binding site to the intracellular transducer binding site.
Molecular dynamics (MD) simulations that stand on the static crystal structure can predict atomic-level motion and capture the dynamic information of conformational transitions [37], [38], [39], [40], [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51], [52]. As a result of computation and algorithmic promotion, MD simulations have become an important source of complementary information in crystallography and a primary tool for mechanism research [53], [54], [55], [56], [57], [58], [59], [60], [61], [62], [63], [64], [65]. Furthermore, MD simulations in combination with Markov state models (MSM) have widely applied to explore the thermodynamics and kinetics of biomolecules [66], [67] and to investigate a slew of biophysical problems, such as protein folding [68], allosteric regulation [69], and molecular mechanism of conformational transition [70].
Gaussian accelerated molecular dynamics (GaMD) is an efficient approach to enable enhanced sampling of distinct biomolecular conformations. By adding a harmonic boost potential to smoothen the system potential energy surface, GaMD captures rare conformations that are inaccessible by conventional MD simulations Compared with other enhanced sampling methods such as metadynamics, GaMD has the advantage of no need to set predefined reaction coordinates and reducing the energetic noise [71], [72], [73], [74].
Here, we performed GaMD (a total of 15 μs) in the combination of MSM to investigate the activation mechanism and conformational landscape of GCGR. The GaMD simulations reveal that the conformational ensemble consists of three different states in the receptor activation. Furthermore, the present work uncovers the allosteric communication driven by different binding events. Gs binding not only stabilizes the intracellular–binding domain but also reduces the fluctuation of glucagon–binding domain, which keeps the GCGR in a fully active state. MSM verifies that Gs is absolutely required for the receptor to reach the fully active state, which is identical to previous structural and experimental studies. Furthermore, the simulations reveal the glucagon-dependent conformational change of H8 and indicate the significant role of H8 in receptor activation. We propose that H8 may initiate the engagement of Gs during the activation process. Together, our study may promote the structure-based design of allosteric modulators for class B GPCRs.
2. Materials and methods
2.1. Structure preparation
Three model systems were built for MD simulations, consisting of the GGGR–NAM complex, GGGR–glucagon complex, GGGR–glucagon–Gs complex. The GGGR–NAM complex (named as NAM–binding system) was built by crystal structure of GCGR (PDB ID: 5XEZ). The extra residues in antibody (mAb1) protein and ligands were removed from GCGR, and the missing residues in the ICL3 domain of GCGR structure were added into the receptor using the Discovery Studio. The GGGR–glucagon complex (named as glucagon–binding system) was built by crystal structure of GCGR (PDB ID: 5YQZ). The extra ligands were removed from GCGR, and the missing residues in the ICL3 domain of GCGR structure were added into the receptor, using the Discovery Studio. The GGGR–glucagon–Gs complex (named as glucagon–Gs–binding system) was built by crystal structure of GCGR (PDB ID: 6WPW). The extra ligands and residues in antibody (Nb35) protein were removed from GCGR, and the missing residues in the ICL3 domain of GCGR structure were added into the receptor. All the mutant and modified residues were mutated back to standard amino acids. Then, the obtained complexes were oriented in the Orientations of Proteins in membrane (OPM) server [75]. The structures were inserted to the DOPC membrane in the CHARMM-GUI server. Next, the systems were embedded in water molecules according to the number of 80 water molecules per one lipid molecule. A salt concentration of 0.15 mol/L KCL was used to balance the charge. Finally, we obtained the coordinate and topology for Amber by the input generation of the CHARMM-GUI [76].
2.2. Simulation protocols
We used Amber-package to perform Gaussian Accelerated Molecular Dynamics (GaMD) simulation. The program of the Amber-tleap was used to generate the coordinate file and topology files for the stimulation [77]. The lipid 14 force filed parameters was used to model the molecule of the DOPC, the ff14SB force filed was employed for proteins and Peptide ligands, and the TIP3P model was applied to the water molecules. In addition, we generated the force filed for NAM (NNC0640) by the Antechamber package of the Amber. Upon generating the correct input files, the simulations were performed with the four steps, following a protocol that employed in previous study [78], [79], [80], [81]. First, the two rounds of energy minimizations were carried out for each system using the steepest descent algorithms with the restriction of 500 kcal mol−1Å−2. The first minimization with a restraint of 500 kcal mol−1Å−2 on receptor and ligand, while water and counterions were minimized in 50,000 cycles (25000 steepest descent cycles and 25,000 conjugate gradient cycles). Second, all atoms were subjected to 50,000 cycles of steepest descent and 50,000 cycles of conjugate gradient minimization without any restraint. After that, each system was gradually thermalized from 0 K to 310 K in 500 ps under isothermal − isovolumetric (NVT) conditions. Finally, system equilibration was achieved by a 11 ns in an isothermal − isobaric (NPT) ensemble.
Then, the Gamd simulations were divided into multiple jobs, following the published manual [73], [79]. In the Gamd simulations, the system threshold energy was set as E = Vmax. To obtain the maximum, minimum, average, and standard deviation values (Vmax, Vmin, Vav, and σV) of the system potential, 100 ns conventional MD (cMD) simulations with no boost potential were performed. The greatest σ0 and k0 were determined through cMD simulations. Second, 60 ns GaMD equilibration were carried out to collect boost potential. Last, the GaMD production simulations were performed with random velocities and the dual-boost potential, including five independent 1 μs simulations for each system using a time step of 2 fs. During the simulation, the cutoff of 10 Å was used for short-range electrostatic and van der Waals interactions. The particle mesh Ewald (PME) method was employed to evaluate the long-range electrostatic interactions. The SHAKE algorithm was employed for covalent bonds involving hydrogen. The temperature of the system was kept at 300 K using the Langevin dynamics with the coupling time constant of 1.0 ps. The coordinates of the snapshots were collected every 200 ps, for a total of 50,000 frames for each system.
2.3. Principal component analysis (PCA)
PCA is a normal method to analyze large-scale collective motions occurring in biological macromolecules along MD simulations. This statistical technique captures large-amplitude motions of the system by reducing the lot of degrees of freedom to a vital subspace set. To describe the system motions, we calculated and diagonalized the covariance matrix of the receptor Cα atoms to generate a new set of coordinates (named as eigenvectors). The eigenvectors also called Principal Component–PC, and the eigenvalue is associated with the mean square fluctuation contained in the trajectory projected along the eigenvector. Because the first PC (named as PC1) corresponds to the largest amplitude motion of system, the dynamics along PC1 usually represents the “essential dynamics” of system [82]. In the current work, the covariance matrix of the protein Cα atoms was mass-weighted to compute the principal motions of the protein. In detail, the sampled conformations corresponding to the trajectories were projected onto the collective coordinate space that defined by PC1, in terms of the initial structure of the receptor for each system. Then, the visualization of major motions for each system were presented as porcupine plots. To capture differences of the essential properties of structural-dynamic among three systems and keep the comparability, all systems had its trajectory superposed onto the inactive state of GCGR (PDB ID: 5XEZ) and projected along with the first PC (PC1).
2.4. Markov modeling and timescale validation
Markov state models (MSMs) were built for each system using the PyEMMA, following the protocols in the PyEMMA website (http://www.emma-project.org/latest/) [83], [84]. According to the previous analysis of GCGR conformational ensemble, we defined and calculated the parameters that we used in the conformational landscape as the input files for the PyEMMA analysis. First, we validated the Markovian property of combined system using the implied timescale test. We clustered the two-dimensional trajectory of each system into 200 microstates with a maximum k-means iteration number of 200. And the multiple transition probability matrixes (TPMs) were constructed with a specific lag time. TPMs reflect the possibility of transition among all microstates and determine the relaxation timescales (also termed as implied timescale) through Equation (1):
| (1) |
where represents the lag time for constructing TPMs, and is the eigenvalue of the TPM. The relaxation timescale for the transition of microstate relaxes in time is calculated using the Equation.
In practice, the implied timescale is generated from the eigen decomposition of TPMs under the situation that the sequence of eigenvalues corresponds to the sequence of transition. The first eigenvalue () reflects the slowest transition. If the cruve (especially for ) starts to be flattened from a specific lag time, we consider that the system is Markovian mode [85]. As shown in Fig. S5B, the τi curves start to be flattened from a lag time than 40 ns. Thus, for the more accurate MSM analysis, we specified the lag time of 40 ns for all systems.
2.5. PCCA+ analysis and capture the representative structures
Based on the results of timescale test, we used the Perron cluster (PCCA +) analysis to assign the microstates to several metastates. In order to validate our MSM estimation in metastates, we employed the method of Chapman-Kolmogorov (CK) test to check whether the transition probability estimated by MSM analysis is highly close to the practical transition process [86]. When we clustered 200 microstates into 5 metastates for the system, we can see a suitable agreement between models estimated and predictions of the model (Fig. S6). The CK test well validated the Markov model in a 5 metastates that we constructed for GCGR.
Then, using the mdtraj package, we extracted the structures close to the microstate cluster centers of each metastate into the trajectories for the corresponding metastates [87]. Next, using the obtained trajectories, the representative structure of each metastate was captured according to the similarity score Sij. In according to the Equation [2], the structure with the highest Sij among the trajectories was considered as the most representative conformation of the metastate. The dij is the RMSD between the conformations i and j, while dscale is the standard deviation of d.
| (2) |
Furthermore, we calculated the proportions and all representative structures, and mapped the structures onto the landscape generated from the cluster method.
2.6. Cross-correlation analysis
Here, we perform Correlation analysis to identify the coupled motions between Cα atoms (i and j) in the simulation systems. “Pearson-like” cross-correlation (CCij) analysis is a method to calculate the collinear correlations between the atoms i and j [88]. The CCij matrix can be computed as a normalization of the covariance matrix:
| (3) |
where and represent the position vectors of atoms i and j. Positive values of the coefficients represent lockstep motions between atoms i and j, and negative values of indicate relative motions. The magnitude of coefficients represent the strength of the correlation.
2.7. Generalized-correlation analysis
The method of Generalized-Correlation ) analysis was used to capture the dynamic correlations motions in the MD systems [89]. Comparing with the traditional Pearson cofficients, GCij analysis has the advantage of capturing the non-liner correlations by calculating the correlations independently on the relative orientation of the atomic fluctuations. In this analysis, two variables of position vectors ( and ) will be considered correlated when their joint probability distribution, , is smaller than the product of their marginal distributions, ∙ . The mutual information (MI) is a measure of the degree of correlation between and defined as function of and ∙ according to:
| (4) |
Notably, MI is closely related to the definition of the Shannon entropy, . For the expectation value of a random variable r, has a probability distribution described as function [5]:
| (5) |
Thus, the can be computed as:
| (6) |
where and are the marginal Shannon entropies, and is the joint entropy, providing a link between correlations of the motions and information content. The g_correlation tool, as implemented in GROMACS 3.3 [90], was employed to calculate the marginal entropies and and the joint entropy by means of the k-nearest neighbor distances algorithm [91], applied to the fluctuations of atomic positions from MD simulations. Since MI varies from 0 to + ∞, normalized generalized correlation () coefficients, ranging from 0 (independent variables) to 1 (fully correlated variables), are defined as:
| (7) |
where d is the dimensionality of and (d = 3).
2.8. Community network analysis (CNA)
Using the NetworkView plugin in VMD [92], we computed the community organizations of different systems based on the correlation coefficient matrix. The protocols and cutoff followed the guideline of Dynamic Network Analysis. In this analysis, each Cα atom was recognized as a node. First, the coefficient was for Cα pairs were calculated by function [7] was calculated as:
| (8) |
Where and represents the positions of the and Cα atoms.
The edge connections (the inter-node distances) are defined using the coefficients according to function [9]:
| (9) |
where i and j represent the two nodes and was calculated using function [8]. Two nodes are considered connected if Cα atom of the two residues is within 4.5 Å for at least the 75 % of the simulation time. The resulting dynamical network weighted by , with information on the critical nodes that are important for the communication within system. In the weighted network, a set of “communities” can be identified. These local substructures can be obtained with the Girvan-Newman algorithm, which is a divisive algorithm that uses the “edge betweenness” partitioning criterion [93]. These communities do not necessarily correspond to the domain definitions of the protein, and the members of the same community can be distant in sequence. Communities are groups of nodes in which the network connections are dense but between which they are sparse. The allosteric signal is assumed to travel from the communities with the various identity members. The width of an edge (edge betweenness), defined as the number of shortest paths that pass through the edge in the network, is used to measure the importance of the edge for communication within the network. The edges with the highest betweenness connect many pairs of nodes and form the link between different communities. High edge betweenness associates with pairs of residues that are important for the communication flow within the weighted network.
In the community network graph, different communities of are represented as spheres connected by bonds. The width of the bonds connecting the communities is proportional to the sum of edge betweenness, is a measure of the strength of the communication between different communities.
3. Results
3.1. Different binding events induce distinct conformational dynamics
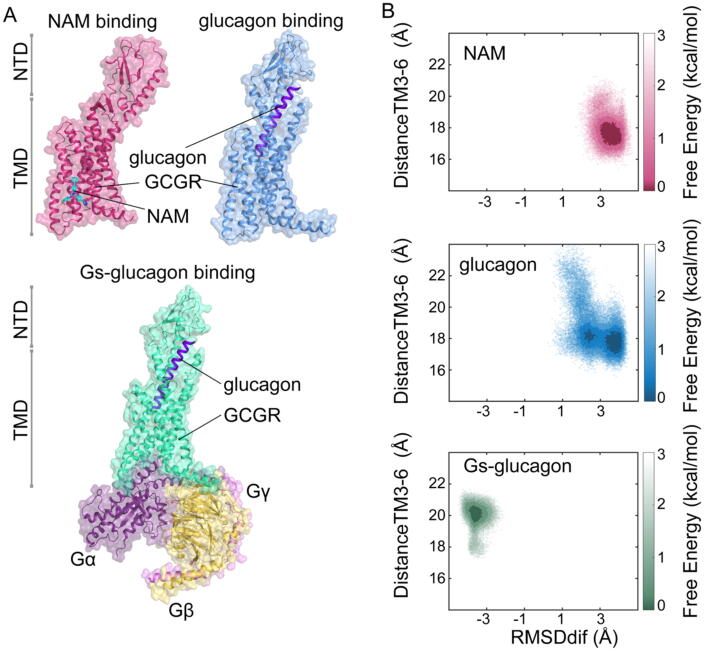
To uncover the molecular mechanism of GCGR activation, a 1 μs GaMD simulation was performed for three systems, including the NAM-bound inactive state, the agonist glucagon-bound active state, and both glucagon- and Gs-bound fully active state in five replicas (totally 15 μs) to enhance sampling and cover broad conformational space (see Materials and methods). To assess the conformational ensemble of GCGR, we defined two order parameters, RMSDdif and distanceTM3−TM6, for characterizing the free-energy landscape. It is well-established that the outward of TM6 is a hallmark in the process of receptor activation and thus the RMSD differences of TM6 in the distinct binding events of GCGR can uncover conformational changes [16]. In our analysis, RMSDdif was calculated as the Cα atoms of RMSD difference of TM6 between the fully active (Gs–glucagon binding) conformation (PDB ID: 6WPW) and the inactive (NAM binding) conformation (PDB ID: 5XEZ). The smaller value of RMSDdif represents the more approaching to the fully active state. The distance between the centers of mass of the intracellular ends of TM3 (G2463.51, L2473.52, Y2483.53, L2493.54, and H2503.55; superscripts indicate the Ballesteros − Weinstein numbering for GPCR residues), and TM6 (Y3436.34, K3446.35, F3456.36, R3466.37, and L3476.38) was calculated as the second collective variable (distanceTM3−TM6). The larger value of distanceTM3−TM6 means the more outward movements of TM6.
Different binding events sample distinct conformational ensemble of GCGR as revealed by the analysis of two-dimensional landscapes (RMSDdif and distanceTM3−TM6) (Fig. 1B and Fig. S1). NAM binding stabilized a major conformation located in regions with RMSDdif of approximatively 3–4 Å and distanceTM3−TM6 of approximatively 18 Å. Upon glucagon binding to the receptor, GCGR underwent larger fluctuations compared to the NAM-bound state, suggesting significantly conformational plasticity of the receptor in the presence of glucagon. Noticeably, glucagon stabilized two representative conformations of GCGR with different locations, one resembling the NAM-bound state, and the other with RMSDdif of approximatively 2.5 Å and distanceTM3−TM6 of approximatively 18 Å. However, in both Gs–glucagon-bound system, the receptor conformational space was restrained in regions with RMSDdif of approximatively −3.5 Å and distanceTM3−TM6 of approximatively 20 Å, which was opposite to the conformational ensemble of NAM-or glucagon-bound systems. Together, we identified the conformational ensemble of GCGR associated with the different binding event-driven activation (NAM, glucagon, and Gs–glucagon). We observed that the conformational ensemble of GCGR contained three distinct conformations. Glucagon binding stabilized two different conformations, one located at a similar position to the NAM binding system and the other at a different position from both NAM and Gs–glucagon binding systems. This observation indicated that the conformational ensemble of GCGR may consist of three conformational states in the activation process. Indeed, previous MD simulations also suggested that GPCRs adopt multiple intermediate states in the progress of activation [40] and recent nuclear magnetic resonance (NMR) spectroscopy on the adenosine A2A receptor (A2AR) has revealed that the active ensemble of A2AR encompasses at least three distinct conformations [96], further supporting our MD simulation results.
Fig. 1.
GCGR adopts a distinct free–energy landscape under different binding conditions. (A) Overview of the complexes used in our simulation. Top left corner, NAM-bound system (GCGR–NNC06040 complex, PDB ID: 5XEZ). The GCGR is colored in red, and the NAM (NNC0640) is colored in cyan. Top right corner, glucagon-bound system (GCGR–glucagon complex), which is built based on the GCGR–NNC1702 complex (PDB ID: 5YQZ). The receptor is colored in blue, and the glucagon is colored in purple. Bottom, the Gs–glucagon-bound system (GCGR–Gs–glucagon complex), which is built based on the GCGR–ZP3780–Gs complex (PDN ID: 6WPW). The receptor is colored in green, the glucagon is colored in purple, and the Gs is colored in terms of subunits (Gα, dark-purple; Gβ, yellow; Gγ, violet) (B) Free–energy landscapes of GCGR in the presence of NAM, glucagon, and Gs–glucagon. Top, the free–energy landscapes of GCGR in the NAM-bound system, and the energy is presented by the depth of red. Medium, the free–energy landscapes of GCGR in the glucagon-bound system, and the energy is presented by the depth of blue. Bottom, the free energy landscapes of GCGR in the Gs–glucagon-bound system, and the energy are presented by the depth of green. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2. Glucagon binding leads to the high dynamics of GCGR
The conformational landscapes suggest that GCGR is more dynamic in the presence of glucagon. To test this hypothesis, principal component analysis (PCA) was performed to capture the differential dynamics (Fig. 2A). We defined the orthosteric site of glucagon as the agonist binding domain (ABD) (Fig. S2), which consists of ECL1-2 and the extracellular ends of TM1 − TM3 and TM5 − TM7. The allosteric site of NNC06040 was named as the NAM binding domain and the Gs binding site was defined as the intracellular binding domain (IBD), which includes ICL2-3 and the intracellular ends of TM1 − TM3, TM5 − TM7, and H8 (Fig. S2). The visualization of principal component 1 (PC1) showed that glucagon binding induced more dynamic movement of IBD than the other two systems. For example, no obvious motion of the IBD was observed in both NAM- and Gs–glucagon-bound systems. The crystal structure of GCGR–NNC0640 has shown that the binding site of NAM locates at the intracellular end of the TM6, which restrains the conformational movement of the TM6. While the addition of Gs decreases the motions of both IBD and ABD (Fig. 2A). The root-mean-square-fluctuation (RMSF) analysis was further performed to measure protein flexibility (Fig. S3). In agreement with the PCA analysis, the IBD of GCGR in the presence of glucagon was highly flexible. Upon NAM or Gs − glucagon binding, the flexibility of the IBD region was reduced.
Fig. 2.
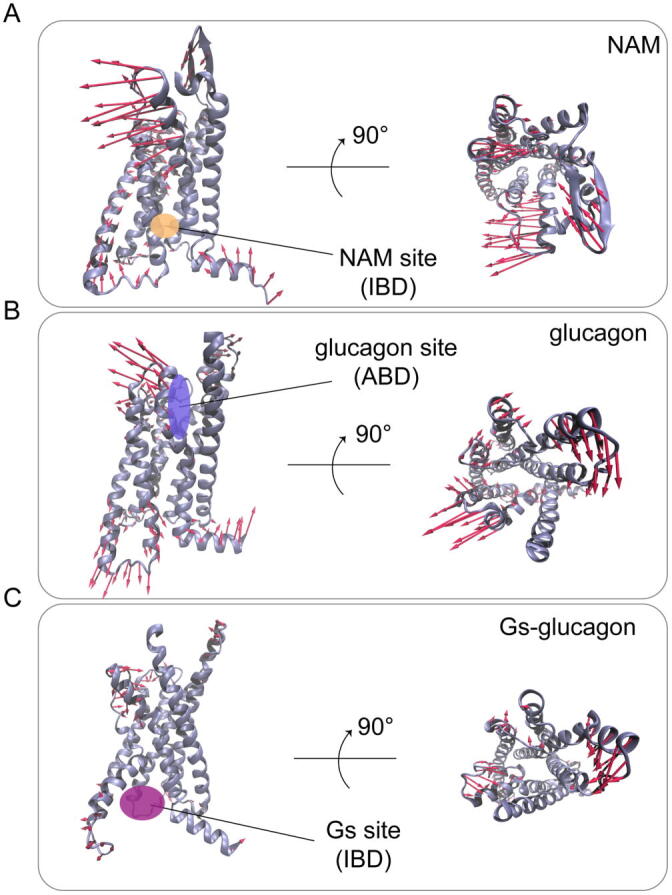
Glucagon binding induces high flexibility of GCGR along with the dynamics and stabilizes two conformation states. (A) The motion of the first principal component corresponds to the three systems: NAM-bound system (top), glucagon-bound system (medium), Gs–glucagon-bound system (bottom). The red arrows represent the direction, with length proportional to the intensity of the motion. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
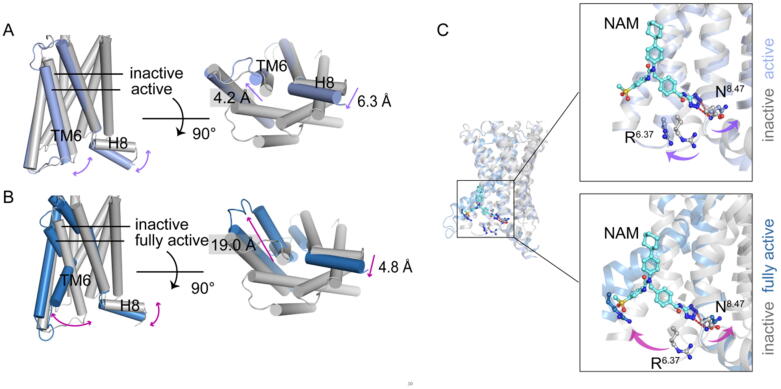
Simultaneously, we extracted the representative conformations of three systems using Mdtraj package [87]. In agreement with the results of free-energy landscapes (Fig. 1B), structural alignment showed that GCGR presented three different conformations (inactive, active, and fully active), with the most distinguishing conformational differences of the TM6 and H8 (Fig. 3A). The representative conformation of the NAM-bound system resembles the crystal structure of NNC0640-bound GCGR (PDB ID: 5XEZ). The TM6 conformation presents no outward movement of the intracellular end of TM6, with a lack of a sharp bend of the conserved PxxG motif (P3566.47 − LL − G3596.50) in the TM6 (Fig. S4A). As a result, this conformation was named the “inactive” state. The representative conformation of the Gs–glucagon-bound system equals the crystal structure of full agonist–Gs bound GCGR (PDB ID: 6WPW). Compared with the inactive state, the intracellular end of TM6 of this conformation moves farther away from the transmembrane core (around 19.0 Å). Thus, this conformation of both Gs–glucagon-bound receptor was named as the fully active (Fig. 3B). However, glucagon binding stabilizes two different conformations. One presents a similar feature of the intracellular end of TM6 and H8 to the inactive state (Fig. S4). Nevertheless, a distinct conformation with the unique feature of TM6 and H8 from the inactive state and fully active state was found. The outward extent of the intracellular end of the MT6 is between the inactive and fully active states (around 4.2 Å), and the H8 moves towards the intracellular end of the receptor. Comparing the inactive state, the PxxG motif in the TM6 presents no sharp bend (Fig. S4B and C), but the conformational rearrangements located at NAM binding site were observed. For example, the N8.47 moves towards TM1, leading to the rupture of the hydrogen bonding interactions between NAM and N8.47. In addition, R6.37 moves away from the TM7 accompanied by the outward movement of the intracellular end of the TM6, breaking the hydrophobic interactions between NAM and R6.37 (Fig. 3C). These rearrangements indicated that this conformation represents an active–like conformation with the impaired NAM binding site. Thus, we defined the second representative conformation of glucagon-bound GCGR as the active state.
Fig. 3.
Glucagon binding stabilizes two different conformation states. (A) and (B) Representative conformations of GCGR of three systems along with simulations. The inactive state is colored in gray, the active state is colored in light blue, and the fully active state is colored in dark blue. The double arrow curves present the major difference between different states. The distance between different states is computed by the Cα atom of the last residue (K6.35) in the intracellular end of TM6, which is the measurement of the outward movement of TM6. (C) Conformational change on the NAM site. The site residues are shown as sticks, and the color is corresponding to the states (inactive, gray; active, light blue; fully active, dark blue.) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.3. Gs binding rewires the orthosteric site and is required for activation of GCGR
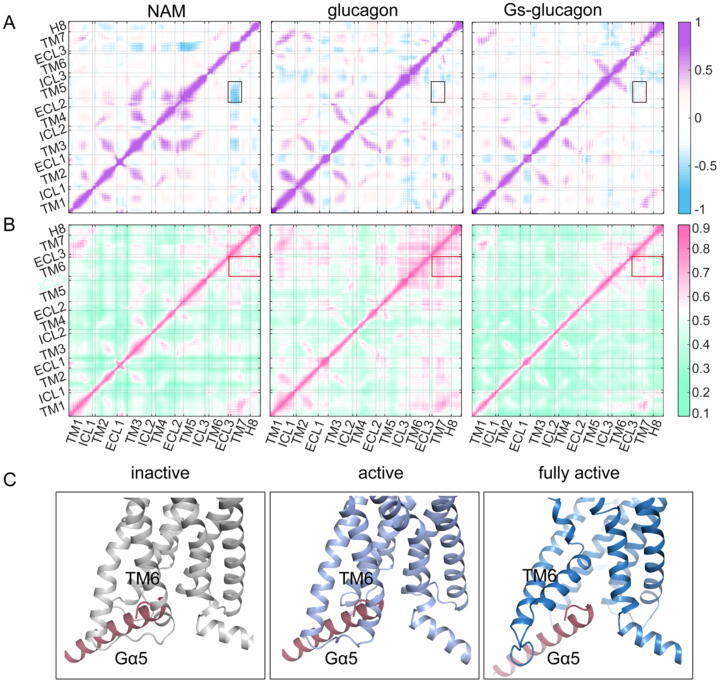
The results of PCA and RMSF showed that the addition of Gs reduced the fluctuation of ABD (Fig. 2 and Fig. S3), suggesting that Gs plays an important role in the stabilization of the orthosteric site. To validate this hypothesis, two correlation analyses were carried out. The traditional Person cross-correlation (CCij) analysis is a well-known method to measure the collinear correlations between two atoms. The negative coefficients represent the relative motions and the positive coefficients represent the lockstep motions) motions and the absolute value of coefficients are proportional to the correlation. The generalized correlation (GCij) is a power scheme to compute the non-linear correlations based on the mutual information between atoms. We employed the CCij analysis to evaluate the coupled linear motion (Fig. 4A) and the GCij analysis to monitor the non-linear correlation (Fig. 4B). The CCij pattern showed that the NAM binding yielded more coupled motions between the residues at the ABD. For instance, the highly relative motions between the ECL2, the extracellular end of TM5, and the extracellular end of TM7 (Fig. 4A). The more coupled motions indicated the instability of ABD, which was in line with the result of PCA. Therefore, NAM binding exerted the inhibitory function on GCGR not only by restraining the movement of TM6 but also by decreasing the stability of the ABD to impair the affinity of glucagon. In contrast, the glucagon binding induced the non-linear correlated motions between the residues at both the ABD and IBD, such as the high correlation between the extracellular end of TM7, the H8, and the intracellular end of TM6 (Fig. 4B). This was consistent with the high dynamics of GCGR in the presence of glucagon. Strikingly, no significant coupled motions in the Gs–glucagon-bound system, which was identical to the PCA results. Furthermore, we computed the probability distributions of correlation coefficients of GCij. The GCij coefficients of glucagon–Gs-bound system distributed with a peak of approximatively 0.5, while NAM-bound and glucagon-bound systems distributed with a peak of approximatively 0.6, which indicated that the GCij correlation of the whole system was much weaker in the presence of glucagon and Gs (Fig. S5A). Thus, the coupled motions of ABD and IBD were dominantly decreased after the binding of Gs. Collectively, these results suggested that Gs plays a vital role in stabilizing the IBD and further rewiring the ABD, and is a positive regulator for glucagon binding affinity.
Fig. 4.
Gs binding decreases the correlated motions in the ABD and IBD and is required for the activation of GCGR. (A) Cross-correlation (CCij) map for NAM-bound (left), glucagon-bound (medium), and Gs–glucagon-bound systems. The CCij is colored in blue (for CCij ≤ 0, relative motions) to purple (for CCij ≥ 0, lockstep motions). (B) The generalized correlation (GCij) map for NAM-bound (left), glucagon-bound (medium), and Gs–glucagon-bound systems. GCij is colored green (uncorrelated) to violet (correlated). (C) The structural alignment between the Gα5 of Gs and IBD of GCGR. The Gα5 of Gs is colored in raspberry, and the IBD of GCGR is colored in terms of states (inactive, gray; active, light blue; fully active, dark blue). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
To shed light on the role of Gs in the activation of GCGR, we aligned the Gs onto three representative conformations of GCGR (inactive, active, and fully active states). All conformations except the fully active state had steric clashes with the helix α5 of Gs (Gα5), a major domain of Gs that interacts with the IBD of GCGR. Although the TM6 in the glucagon-bound GCGR adopted the open conformation, the intracellular cavity of this agonist-induced active state cannot accommodate the Gα5 binding (Fig. 4C). Thus, we concluded that GCGR can’t reach the fully active state in the glucagon alone binding and the Gs is required for the receptor to achieve activation.
3.4. MSM reveals the transitions between different states
MSM is a precise method to summarize the equilibrium of the conformational ensemble, quantifying the thermodynamic properties (such as transitions timescale). According to the parameters used in the free-energy landscape, we combined all the trajectories to build an MSM for calculating the transition between different states using PyEMMA [94]. A 200-microstate MSM was constructed and then validated the Markovian of the properties by timescale validation. As shown in Fig. S5B, the τi curves of the system started to be flattened from a lag time of 40 ns. Thus, the lag time of 40 ns was used for the following analysis. Based on the results of the timescale test, the Perron cluster (PCCA+) analysis was used to assign the microstates to 5 metastates, which were further confirmed by a Chapman–Kolmogorov test (Fig. S6). Then, using the Mdtraj package, we extracted the representative structure of all metastates and calculated the proportion of each metastate. The metastases (whose proportion was occupied by the top-three) were mapped onto the free-energy landscapes (Fig. S7).
Based on the parameters of the cluster, three metastases were selected as the representative conformations corresponding to the inactive, active, and fully active states. The proportions of three representative conformations were 54.1%, 10.3%, and 32.3% for the inactive, active, and fully active states, respectively (Fig. S7). As shown in Fig. 5A, the transition path theory (TPT) was used to map the transition timescales among the inactive, active, and fully active states. The transition time from the inactive to active states (82.9 μs) was significantly longer than that from the active to the inactive state (9.11 μs). This observation was supported by the previous data that GCGR was normally stabilized in the inactive state in the presence of glucagon, and the active conformation also exited in its ensemble with a smaller proportion [16]. The transition from the active to the fully active states (4073.4 μs) was far longer than the timescale from the inactive to active states or the active to inactive states. This result indicated that the transition from the active to the fully active state was extremely slow when the agonist glucagon alone was bound. As such, it is an absolute requirement of the Gs to reach the fully active state of GGCR.
Fig. 5.
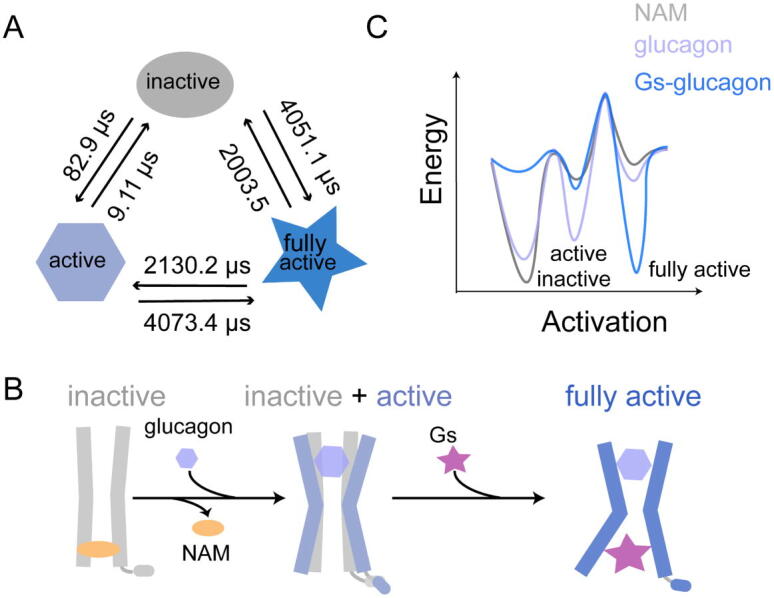
Gs binding induces the transition from the active to the fully active states. (A) The transition timescales among the inactive, active, and fully active states. The circle presents the inactive state (gray), the hexagon represents the active state (light blue), and the fully active state is shown in hexagon (dark blue) (B) The model of conformational transition between the inactive, active, and fully active states. (C) Model of the simplified free energy landscape for describing the effect of NAM, glucagon, and Gs on the equilibrium among the inactive, active, and fully active conformations of GCGR. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
From the perspective of the conformational ensemble, the detailed transition mechanism of GCGR activation was highlighted (Fig. 5B and C). NAM binding selects and stabilizes the inactive conformation of GCGR, with the influence of the stability of ABD. Upon glucagon binding to the GCGR, the glucagon stabilizes two different conformations (inactive and active states). Glucagon plays a partial active function in receptor activation, with the stabilization of a metastable conformation that may be beneficial to the binding of Gs. Gs selects the active state of GCGR, and induces the receptor to further open the intracellular cavity to reach the fully active state. Meanwhile, Gs stabilizes the ABD and IBD of the receptor to keep the receptor in a fully active state. Thus, Gs plays a dual allosteric communication in the activation of GCGR.
3.5. Multiple allosteric pathways of information transfer
To investigate the pathway of allosteric communication driven by different binding events, we performed community network analysis for three systems. Analyzing the NAM-bound system, a strong communication path was found between the transmembrane helix. The TM7 of GCGR formed two communities (8 and 9), which indicated the increased stability of IBD. However, the communications linking to the ECL1 (community 5) were weaker than other linkages. For example, the communication between community 3 and community 5, which indicated the instability of ABD (Fig. 6A). These observations were in line with the results of PCA and MSM. Thus, NAM binding may regulate the ABD through the TM7 of GCGR through a pair of critical nodes (F7.44 and F7.48) connecting the TM7 related communities. The two hydrophobic residues are underneath the ABD (Fig. S8) and NAM binding may influence the stability of ABD by impacting the hydrophobic interactions in the ABD.
Fig. 6.
GCGR presents different allosteric communication in the presence of glucagon. The community networks for NAM-bound system (A), glucagon-bound system (B), and Gs–glucagon-bound system. The communities are shown as circles with different colors. The edges represent the connections among communities and the width is proportional to the cumulative betweenness of community edges. The receptors are shown as the cartoon and colored by community distribution.
Upon the Gs binding, a new communication between the community “6′′” and “7′′” emerged, which was formed by residues from the intracellular ends of TM5 and TM6 and ICL3. The critical nodes are the H209 and D211 of ICL3 (Fig. S8), which could form salt bridges and enhance the stability of IBD. Compared with the NAM- or glucagon-bound systems, the communication between the ECL1 and TM3 (community 8′′ and 9′′) was enhanced in the Gs–glucagon-bound system (Fig. 6C), which might explain the stabilizing effect of Gs for the ABD. In the glucagon-bound system, the residues of TM7 only formed one community (10′). The communications between ECL1 and TM3 (community 3′ and the community 5′) were weak, which was identical to the PCA and RMSF. Notably, a new community (11′) of H8 was formed and communicated with the community (10′) of TM7 related community (Fig. 6B). The critical nodes are C7.58 and N8.47. Several residues of TM7 (such as R7.35 and D7.42) locate in the glucagon binding pocket, and make polar interactions with glucagon. Mutation and structural experiments have confirmed the N8.47 is important to Gs activation and forms hydrogen bonding interactions with Gs (Fig. S8) [95]. The H8 consists of many polar residues (N8.47-KEVQSELRRR-W8.61), and the key residues of the Gα5 that account for binding are also polar (385–392: DIIQRMHLRQYE). Thus, we speculate that the activation of receptor by glucagon may depend on the H8 domain, and the polar residues at the H8 domain, especially the N8.47, may initiate the engagement of Gs to the receptor via attractions between the polar residues.
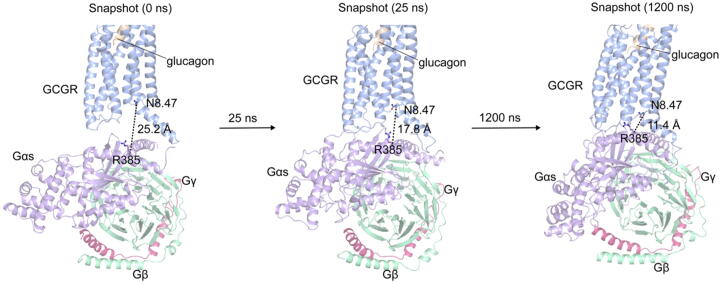
To further demonstrate the function of H8, we added the Gs into the glucagon-bound GCGR and performed additional MD simulations. As shown in Fig. 7, the Gs approached the H8 of the receptor along with the simulation. We calculated the distance between the N8.47 and the E392 of Gα5 and this distance decreased from 25.2 to 10.8 Å, which indicated that the polar residues (especially the N8.47) of H8 initiated the engagement of the Gs to the receptor (Fig. S9). This observation supported the receptor activation by glucagon through the H8 domain, and the polar residues of H8 especially N8.47 help the receptor to recruit the Gs.
Fig. 7.
The H8 of GCGR plays a vital role in receptor activation. The snapshots of GCGR were extracted in the simulation. The distance between the H8 and the Gα5 was calculated using the Cα atoms of N8.47 from GCGR and R385 from Gs. The proteins are shown as cartoon. The receptor is colored in light blue, the glucagon is colored in yellow, and the Gs is colored in terms of subunits (Gα, light purple; Gβ, light green; Gγ, red). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
Multi-microsecond GaMD simulations elaborate the changes in the conformational ensemble of GCGR. We performed five independent replicas for each simulation system and observed the analogous free-energy landscapes (Fig. S10). Combing with the correlation, MSM, and community analyses, we observed a distinct and allosteric coupling motion between the IBD and ABD driven by three different binding events, including the NAM, glucagon, and Gs − glucagon. NAM binding restrains the motion of TM6 and impairs the stability of the ABD, which represents negative cooperativity between the IBD and ABD. Upon glucagon binding, it initiates the movement of TM6 and H8 and leads to positive cooperativity between the IBD and ABD. Two major conformations are stabilized by glucagon, the inactive and active states. The active conformer presents a different conformation of TM6 and H8, which is distinct from the fully active state. In the glucagon-bound GCGR, the H8 plays a significant role in attracting Gs to the IBD. However, the active conformation cannot accommodate the binding of Gs, and it further needs the Gs to reach the fully active state. Gs plays an induced-fit role in the late process of activation, which triggers the opening of the intracellular end of TM6 and stabilizes the IBD. Furthermore, Gs binding rewires the orthosteric site and stabilizes the ABD, which is beneficial to glucagon binding.
NMR researches have demonstrated that the conformational diversity of GPCR in the presence of agonists is revealed by the existence of the inactive state in the conformational ensemble of A2AR in presence of agonists [96]. We found that the conformational ensemble of GCGR also includes an inactive state in the presence of glucagon. Accumulating evidence suggests that GPCRs adopt multiple intermediate conformations in the proceeds of activation. For example, the crystal experiment has reported two different active conformers of neurotensin receptor 1 [97], [98], [99]. In agreement with these works, our MD simulations revealed a new intermediate (active state) and obtained the conformational ensemble consisting of three different states of GCGR. Previously, researchers proposed that the intermediate and fully active state distributes with a higher activation energy barrier for GCGR than β2 adrenergic receptor (class A GPCR). Glucagon shifts the conformation population by increasing the frequency of the intermediate. Our analysis provides the evidence for this hypothesis. Indeed, we observe and validate the inactive and an intermediate (named active state in our study) of GCGR in the glucagon-bound system.
Previous fluorophore monobromobimane-labeling experiments revealed slight conformational changes of the intracellular end of TM6 and proposed that the effect of glucagon associated with receptor activation may act on other intracellular regions near the TM6 [16]. Encouragingly, our simulations provide the answer to this mystery. Through the structural alignment, we highlighted the significant differences of H8 between the inactive states. Furthermore, the results of community analysis show that an important community of H8 is formed in response to glucagon binding, and the N8.47 is the key residue in the allosteric communication of H8. It indicates that the activation of the receptor by glucagon may depend on the H8, especially the N8.47. Further simulations supported the notion that the N8.47 of H8 help the receptor recruit to the Gs upon glucagon binding, with the approaching of Gs to the N8.47 of H8 along the simulation.
Crystal and MD analysis highlighted the role of induced–fit of Gs on the activation of GCGR [16], [100]. Indeed, our MSM analysis revealed that Gs is required for triggering the intracellular end of TM6 to open the IBD of the receptor for Gs binding. The stabilizing effect of Gi protein has been reported on class A of GPCR–adenosine A1 receptor (A1R) [101]. In line with class A of GPCR, the Gs protein has a stabilizing effect on the ABD and IBD of GCGR to keep the fully active state of the receptor. Previous single-molecule fluorescence spectroscopy (FRET) provided a detailed explanation for the increased agonist efficacy observed with a positive agonist modulator (PAM) [102]. We here revealed that NAM can allosterically influence the glucagon binding affinity. NAM induced the fluctuations of ABD and restricted TM6 movement, which was supported by the crystal structure of GCGR − NN06040 (PDB ID: 5XEZ).
The distinct allosteric regulation between the ABD and IBD may benefit the optimization of allosteric modulators of class B GPCRs. This study may provide an alternative way for the discovery of novel allosteric modulators of GCGR, which will promote the development of structure-based drug discovery and precision-tuned therapeutics. A possible limitation of this work is that we don’t observe a metastable conformation that resembles the fully active state in the glucagon alone bound-GCGR, which may be solved by longer timescale simulations. In addition, it will be interesting to check the conformational landscape of PAM/ago–PAM ligand binding systems. Yet, such structures have not been solved by the cryo-electron microscopy or X-ray crystallography so far. There are no accessible initial structures to run MD simulations. Based on the current study, we propose that the PAM binding system might display the conformational landscape with the active state representative conformation. In the ago-PAM binding system, the landscape may display two kinds of states. The large frequency is active state, and the smaller frequency is the fully active state. These predictions might be verified through MD simulations if these initial structures are solved.
5. Conclusion
Our work described the activation–associated free–energy landscapes of GCGR, with a newly discovered active state conformation. The structural and MSM analysis illuminate how the conformational ensemble shifts in the progress of the receptor activation, which stays in step with previous NMR and crystal results of GPCRs. We demonstrate the detailed effect of glucagon and Gs binding in the receptor activation and extend the allosteric mechanism of GCGR activation. Glucagon binding induces the conformational changes in the TM6 and H8 and plays the role of shifting conformational ensemble by increasing the population of the active state. Two different states (inactive and active) of GCGR are observed in the glucagon-bound system. The active state of GCGR facilitates the binding of Gs, with the H8 resembling the fully active state. We propose that the active state of H8 attracts the Gs to the IBD by polar interactions, and then Gs binding induces the conformational changes of the intracellular end of TM6 to open the Gs binding cavity. Furthermore, Gs plays a role of dual stabilization for the binding of Gs and glucagon to stabilize the fully active state. Overall, this study may provide a promising guidance for the allosteric modulator design of class B GPCRs.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported partly by grants from the National Natural Science Foundation of China (No. 22077082) and Shanghai Frontiers Science Center of Cellular Homeostasis and Human Diseases.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.csbj.2022.01.015.
Contributor Information
Ting Chen, Email: pipidan@126.com.
Shaoyong Lu, Email: lushaoyong@sjtu.edu.cn.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Ma P., Zemmel R. Value of novelty? Nat Rev Drug Discov. 2002;1(8):571–572. doi: 10.1038/nrd884. [DOI] [PubMed] [Google Scholar]
- 2.Lappano R., Maggiolini M. G protein-coupled receptors: novel targets for drug discovery in cancer. Nat Rev Drug Discov. 2011;10(1):47–60. doi: 10.1038/nrd3320. [DOI] [PubMed] [Google Scholar]
- 3.Hauser A.S., Chavali S., Masuho I., Jahn L.J., Martemyanov K.A., Gloriam D.E., et al. Pharmacogenomics of GPCR Drug Targets. Cell. 2018;172(1-2):41–54.e19. doi: 10.1016/j.cell.2017.11.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Saikia S., Bordoloi M., Sarmah R. Established and In-trial GPCR Families in Clinical Trials: A Review for Target Selection. Curr Drug Targets. 2019;20(5):522–539. doi: 10.2174/1389450120666181105152439. [DOI] [PubMed] [Google Scholar]
- 5.Sriram K., Insel P.A. G Protein-Coupled Receptors as Targets for Approved Drugs: How Many Targets and How Many Drugs? Mol Pharmacol. 2018;93(4):251–258. doi: 10.1124/mol.117.111062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lu S., Zhang J. Small Molecule Allosteric Modulators of G-Protein-Coupled Receptors: Drug-Target Interactions. J Med Chem. 2019;62(1):24–45. doi: 10.1021/acs.jmedchem.7b01844. [DOI] [PubMed] [Google Scholar]
- 7.Changeux J.-P., Christopoulos A. Allosteric modulation as a unifying mechanism for receptor function and regulation. Diabetes, Obes Metab. 2017;19(Suppl 1):4–21. doi: 10.1111/dom.12959. [DOI] [PubMed] [Google Scholar]
- 8.Wang J., Hua T., Liu Z.-J. Structural features of activated GPCR signaling complexes. Curr Opin Struct Biol. 2020;63:82–89. doi: 10.1016/j.sbi.2020.04.008. [DOI] [PubMed] [Google Scholar]
- 9.Wang W., Qiao Y., Li Z. New Insights into Modes of GPCR Activation. Trends Pharmacol Sci. 2018;39(4):367–386. doi: 10.1016/j.tips.2018.01.001. [DOI] [PubMed] [Google Scholar]
- 10.Duc N.M., Kim H.R., Chung K.Y. Structural mechanism of G protein activation by G protein-coupled receptor. Eur J Pharmacol. 2015;763(Pt B):214–222. doi: 10.1016/j.ejphar.2015.05.016. [DOI] [PubMed] [Google Scholar]
- 11.Inoue A., Raimondi F., Kadji F.M.N., Singh G., Kishi T., Uwamizu A., et al. Illuminating G-Protein-Coupling Selectivity of GPCRs. Cell. 2019;177(7):1933–1947.e25. doi: 10.1016/j.cell.2019.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tehan B.G., Bortolato A., Blaney F.E., Weir M.P., Mason J.S. Unifying Family A GPCR Theories of Activation. Pharmacol Ther. 2014;143(1):51–60. doi: 10.1016/j.pharmthera.2014.02.004. [DOI] [PubMed] [Google Scholar]
- 13.Weis W.I., Kobilka B.K. The Molecular Basis of G Protein-Coupled Receptor Activation. Annu Rev Biochem. 2014;87:897–919. doi: 10.1146/annurev-biochem-060614-033910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kalogriopoulos N.A., Rees S.D., Ngo T., Kopcho N.J., Ilatovskiy A.V., Sun N., et al. Structural basis for GPCR-independent activation of heterotrimeric Gi proteins. Proc Natl Acad Sci USA. 2019;116(33):16394–16403. doi: 10.1073/pnas.1906658116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhou Q., Yang D., Wu M., Guo Y.u., Guo W., Zhong L.i., et al. Common activation mechanism of class A GPCRs. Elife. 2019;8:e50279. doi: 10.7554/eLife.50279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hilger D., Kumar K.K., Hu H., Pedersen M.F., O’Brien E.S., Giehm L., et al. Structural insights into differences in G protein activation by family A and family B GPCRs. Science. 2020;369(6503) doi: 10.1126/science.aba3373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Krumm B., Roth B.L. A Structural Understanding of Class B GPCR Selectivity and Activation Revealed. Structure. 2020;28(3):277–279. doi: 10.1016/j.str.2020.02.004. [DOI] [PubMed] [Google Scholar]
- 18.Liang Y.-L., Belousoff M.J., Zhao P., Koole C., Fletcher M.M., Truong T.T., et al. Toward a Structural Understanding of Class B GPCR Peptide Binding and Activation. Mol Cell. 2020;77(3):656–668.e5. doi: 10.1016/j.molcel.2020.01.012. [DOI] [PubMed] [Google Scholar]
- 19.Karageorgos V., Venihaki M., Sakellaris S., Pardalos M., Kontakis G., Matsoukas M.-T., et al. Current understanding of the structure and function of family B GPCRs to design novel drugs. Hormones. 2018;17(1):45–59. doi: 10.1007/s42000-018-0009-5. [DOI] [PubMed] [Google Scholar]
- 20.Langer I. Conformational switches in the VPAC1 receptor. Br J Pharmacol. 2012;166(1):79–84. doi: 10.1111/j.1476-5381.2011.01616.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yin Y., de Waal P.W., He Y., Zhao L.-H., Yang D., Cai X., et al. Rearrangement of a polar core provides a conserved mechanism for constitutive activation of class B G protein-coupled receptors. J Biol Chem. 2017;292(24):9865–9881. doi: 10.1074/jbc.M117.782987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lagerström M.C., Schiöth H.B. Structural diversity of G protein-coupled receptors and significance for drug discovery. Nat Rev Drug Discov. 2008;7(4):339–357. doi: 10.1038/nrd2518. [DOI] [PubMed] [Google Scholar]
- 23.Hollenstein K., de Graaf C., Bortolato A., Wang M.-W., Marshall F.H., Stevens R.C. Insights into the structure of class B GPCRs. Trends Pharmacol Sci. 2014;35(1):12–22. doi: 10.1016/j.tips.2013.11.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.George L., Minos-Timotheos M., Vlasios K., Maria V., Thomas M. Family B G Protein-coupled Receptors and their Ligands: From Structure to Function. Curr Med Chem. 2017;24(31):3323–3355. doi: 10.2174/0929867324666170303162416. [DOI] [PubMed] [Google Scholar]
- 25.de Graaf C., Song G., Cao C., Zhao Q., Wang M.-W., Wu B., et al. Extending the Structural View of Class B GPCRs. Trends Biochem Sci. 2017;42(12):946–960. doi: 10.1016/j.tibs.2017.10.003. [DOI] [PubMed] [Google Scholar]
- 26.Culhane K.J., Liu Y., Cai Y., Yan E.C.Y. Transmembrane signal transduction by peptide hormones via family B G protein-coupled receptors. Front Pharmacol. 2015;6:264. doi: 10.3389/fphar.2015.00264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liao C., Remington J.M., May V., Li J. Molecular Basis of Class B GPCR Selectivity for the Neuropeptides PACAP and VIP. Front Mol Biosci. 2021;8 doi: 10.3389/fmolb.2021.644644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lin G., Liu Q., Dai A., Cai X., Zhou Q., Wang X.i., et al. Characterization of a naturally occurring mutation V368M in the human glucagon receptor and its association with metabolic disorders. Biochem J. 2020;477(13):2581–2594. doi: 10.1042/BCJ20200235. [DOI] [PubMed] [Google Scholar]
- 29.Gelling R.W., Du X.Q., Dichmann D.S., Rømer J., Huang H., Cui L., et al. Lower blood glucose, hyperglucagonemia, and pancreatic α cell hyperplasia in glucagon receptor knockout mice. Proc Natl Acad Sci. 2003;100(3):1438–1443. doi: 10.1073/pnas.0237106100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vuguin P.M., Charron M.J. Novel insight into glucagon receptor action: lessons from knockout and transgenic mouse models. Diabetes, Obes Metab. 2011;13:144–150. doi: 10.1111/j.1463-1326.2011.01447.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vega R.B., Whytock K.L., Gassenhuber J., Goebel B., Tillner J., Agueusop I., et al. A Metabolomic Signature of Glucagon Action in Healthy Individuals With Overweight/Obesity. J Endocr Soc. 2021;5(9):bvab118. doi: 10.1210/jendso/bvab118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Janah L., Kjeldsen S., Galsgaard K.D., Winther-Sørensen M., Stojanovska E., Pedersen J., et al. Glucagon Receptor Signaling and Glucagon Resistance. Int J Mol Sci. 2019;20(13):3314. doi: 10.3390/ijms20133314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wewer Albrechtsen N.J. Glucagon receptor signaling in metabolic diseases. Peptides. 2018;100:42–47. doi: 10.1016/j.peptides.2017.11.016. [DOI] [PubMed] [Google Scholar]
- 34.Zhang H., Qiao A., Yang L., Van Eps N., Frederiksen K.S., Yang D., et al. Structure of the glucagon receptor in complex with a glucagon analogue. Nature. 2018;553(7686):106–110. doi: 10.1038/nature25153. [DOI] [PubMed] [Google Scholar]
- 35.Wang Y., Yu Z., Xiao W., Lu S., Zhang J. Allosteric binding sites at the receptor–lipid bilayer interface: novel targets for GPCR drug discovery. Drug Discov Today. 2021;26(3):690–703. doi: 10.1016/j.drudis.2020.12.001. [DOI] [PubMed] [Google Scholar]
- 36.Slosky L.M., Caron M.G., Barak L.S. Biased Allosteric Modulators: New Frontiers in GPCR Drug Discovery. Trends Pharmacol Sci. 2021;42(4):283–299. doi: 10.1016/j.tips.2020.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Adcock S.A., McCammon J.A. Molecular dynamics: survey of methods for simulating the activity of proteins. Chem Rev. 2006;106(5):1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chan-Yao-Chong M., Durand D., Ha-Duong T. Molecular Dynamics Simulations Combined with Nuclear Magnetic Resonance and/or Small-Angle X-ray Scattering Data for Characterizing Intrinsically Disordered Protein Conformational Ensembles. J Chem Inf Model. 2019;59(5):1743–1758. doi: 10.1021/acs.jcim.8b00928. [DOI] [PubMed] [Google Scholar]
- 39.Ye W., Wang W., Jiang C., Yu Q., Chen H. Molecular dynamics simulations of amyloid fibrils: an in silico approach. Acta Biochim Biophys Sin (Shanghai) 2013;45(6):503–508. doi: 10.1093/abbs/gmt026. [DOI] [PubMed] [Google Scholar]
- 40.Dror R.O., Arlow D.H., Maragakis P., Mildorf T.J., Pan A.C., Xu H., et al. Activation mechanism of the β2-adrenergic receptor. Proc Natl Acad Sci USA. 2011;108(46):18684–18689. doi: 10.1073/pnas.1110499108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Suzuki S., Nakamura T., Saito R., Terauchi Y., Kawai K., Takimoto-Kamimura M., et al. Structural change of retinoic-acid receptor-related orphan receptor induced by binding of inverse-agonist: Molecular dynamics and ab initio molecular orbital simulations. Comput Struct Biotechnol J. 2020;18:1676–1685. doi: 10.1016/j.csbj.2020.06.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Baldessari F., Capelli R., Carloni P., Giorgetti A. Coevolutionary data-based interaction networks approach highlighting key residues across protein families: The case of the G-protein coupled receptors. Comput Struct Biotechnol J. 2020;18:1153–1159. doi: 10.1016/j.csbj.2020.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kaynak B.T., Bahar I., Doruker P. Essential site scanning analysis: A new approach for detecting sites that modulate the dispersion of protein global motions. Comput Struct Biotechnol J. 2020;18:1577–1586. doi: 10.1016/j.csbj.2020.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Navarro G., Gonzalez A., Campanacci S., Rivas-Santisteban R., Reyes-Resina I., Casajuana-Martin N., et al. Experimental and computational analysis of biased agonism on full-length and a C-terminally truncated adenosine A2A receptor. Comput Struct Biotechnol J. 2020;18:2723–2732. doi: 10.1016/j.csbj.2020.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Abramyan A.M., Yano H., Xu M., Liu L., Naing S., Fant A.D., et al. The Glu102 mutation disrupts higher-order oligomerization of the sigma 1 receptor. Comput Struct Biotechnol J. 2020;18:199–206. doi: 10.1016/j.csbj.2019.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Che K., Muttenthaler M., Kurzbach D. Conformational selection of vasopressin upon V1a receptor binding. Comput Struct Biotechnol J. 2021;19:5826–5833. doi: 10.1016/j.csbj.2021.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jiang J.-H., Xu X.-Q., Jiang W.-G., Wang T., Liu X., Zeng L.-G., et al. Discovery of the EL-0052 as a potential anesthetic drug. Comput Struct. Biotechnol J. 2021;19:710–718. doi: 10.1016/j.csbj.2021.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Qiu W., Lv Z., Xiao X., Shao S., Lin H. EMCBOW-GPCR: A method for identifying G-protein coupled receptors based on word embedding and wordbooks. Comput Struct Biotechnol J. 2021;19:4961–4969. doi: 10.1016/j.csbj.2021.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.An X., Bai Q., Bing Z., Liu H., Yao X. Insights into the molecular mechanism of positive cooperativity between partial agonist MK-8666 and full allosteric agonist AP8 of hGPR40 by Gaussian accelerated molecular dynamics (GaMD) simulations. Comput Struct Biotechnol J. 2021;19:3978–3989. doi: 10.1016/j.csbj.2021.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kiriakidi S., Chatzigiannis C., Papaemmanouil C., Tzakos A.G., Cournia Z., Mavromoustakos T. Interplay of cholesterol, membrane bilayers and the AT1R: A cholesterol consensus motif on AT1R is revealed. Comput Struct Biotechnol J. 2021;19:110–120. doi: 10.1016/j.csbj.2020.11.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Pal A., Curtin J.F., Kinsella G.K. Structure based prediction of a novel GPR120 antagonist based on pharmacophore screening and molecular dynamics simulations. Comput Struct Biotechnol J. 2021;19:6050–6063. doi: 10.1016/j.csbj.2021.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Felline A., Schiroli D., Comitato A., Marigo V., Fanelli F. Structure network-based landscape of rhodopsin misfolding by mutations and algorithmic prediction of small chaperone action. Comput Struct Biotechnol J. 2021;19:6020–6038. doi: 10.1016/j.csbj.2021.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Paul A., Samantray S., Anteghini M., Khaled M., Strodel B. Thermodynamics and kinetics of the amyloid-β peptide revealed by Markov state models based on MD data in agreement with experiment. Chem Sci. 2021;12(19):6652–6669. doi: 10.1039/d0sc04657d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Romo T.D., Grossfield A., Pitman M.C. Concerted interconversion between ionic lock substates of the beta(2) adrenergic receptor revealed by microsecond timescale molecular dynamics. Biophys J. 2010;98(1):76–84. doi: 10.1016/j.bpj.2009.09.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Byun J.A., VanSchouwen B., Akimoto M., Melacini G. Allosteric inhibition explained through conformational ensembles sampling distinct “mixed” states. Comput Struct Biotechnol J. 2020;18:3803–3818. doi: 10.1016/j.csbj.2020.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jang H., Zhang M., Nussinov R. The quaternary assembly of KRas4B with Raf-1 at the membrane. Comput Struct Biotechnol J. 2020;18:737–748. doi: 10.1016/j.csbj.2020.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lu S., Chen Y., Wei J., Zhao M., Ni D., He X., et al. Mechanism of allosteric activation of SIRT6 revealed by the action of rationally designed activators. Acta Pharm Sin B. 2021;11(5):1355–1361. doi: 10.1016/j.apsb.2020.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Hernández-Alvarez L., Oliveira Jr A.B., Hernández-González J.E., Chahine J., Pascutti P.G., de Araujo A.S., et al. Computational study on the allosteric mechanism of Leishmania major IF4E-1 by 4E-interacting protein-1: Unravelling the determinants of m7GTP cap recognition. Comput Struct Biotechnol J. 2021;19:2027–2044. doi: 10.1016/j.csbj.2021.03.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Marasco M., Kirkpatrick J., Nanna V., Sikorska J., Carlomagno T. Phosphotyrosine couples peptide binding and SHP2 activation via a dynamic allosteric network. Comput Struct Biotechnol J. 2021;19:2398–2415. doi: 10.1016/j.csbj.2021.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Foutch D., Pham B., Shen T. Protein conformational switch discerned via network centrality properties. Comput Struct Biotechnol J. 2021;19:3599–3608. doi: 10.1016/j.csbj.2021.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Aledavood E., Forte A., Estarellas C., Javier Luque F. Structural basis of the selective activation of enzyme isoforms: Allosteric response to activators of β1- and β2-containing AMPK complexes. Comput Struct Biotechnol J. 2021;19:3394–3406. doi: 10.1016/j.csbj.2021.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Li X., Wang C., Peng T., Chai Z., Ni D., Liu Y., et al. Atomic-scale insights into allosteric inhibition and evolutional rescue mechanism of Streptococcus thermophilus Cas9 by the anti-CRISPR protein AcrIIA6. Comput Struct Biotechnol J. 2021;19:6108–6124. doi: 10.1016/j.csbj.2021.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Wang Y., Ji D., Lei C., Chen Y., Qiu Y., Li X., et al. Mechanistic insights into the effect of phosphorylation on Ras conformational dynamics and its interactions with cell signaling proteins. Comput Struct Biotechnol J. 2021;19:1184–1199. doi: 10.1016/j.csbj.2021.01.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Qiu Y., Yin X., Li X., Wang Y., Fu Q., Huang R., et al. Untangling dual-targeting therapeutic mechanism of epidermal growth factor receptor (Egfr) based on reversed allosteric communication. Pharmaceutics. 2021;13(5):747. doi: 10.3390/pharmaceutics13050747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Suomivuori C.-M., Latorraca N.R., Wingler L.M., Eismann S., King M.C., Kleinhenz A.L.W., et al. Molecular mechanism of biased signaling in a prototypical G protein-coupled receptor. Science. 2020;367(6480):881–887. doi: 10.1126/science.aaz0326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Noé F., Schütte C., Vanden-Eijnden E., Reich L., Weikl T.R. Constructing the equilibrium ensemble of folding pathways from short off-equilibrium simulations. Proc Natl Acad Sci. 2009;106(45):19011–19016. doi: 10.1073/pnas.0905466106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Narayan B., Yuan Y., Fathizadeh A., Elber R., Buchete N.V. Long-time methods for molecular dynamics simulations: Markov State Models and Milestoning. Prog Mol Biol Transl Sci. 2020;170:215–237. doi: 10.1016/bs.pmbts.2020.01.002. [DOI] [PubMed] [Google Scholar]
- 68.Zhou H., Dong Z., Verkhivker G., Zoltowski B.D., Tao P., MacKerell A. Allosteric mechanism of the circadian protein Vivid resolved through Markov state model and machine learning analysis. PLoS Comput Biol. 2019;15(2):e1006801. doi: 10.1371/journal.pcbi.1006801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Chodera J.D., Noé F. Markov state models of biomolecular conformational dynamics. Curr Opin Struct Biol. 2014;25:135–144. doi: 10.1016/j.sbi.2014.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lu S., He X., Yang Z., Chai Z., Zhou S., Wang J., et al. Activation pathway of a G protein-coupled receptor uncovers conformational intermediates as targets for allosteric drug design. Nat Commun. 2021;12(1):4721. doi: 10.1038/s41467-021-25020-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Chen J., Zhang S., Wang W., Pang L., Zhang Q., Liu X. Mutation-Induced Impacts on the Switch Transformations of the GDP- and GTP-Bound K-Ras: Insights from Multiple Replica Gaussian Accelerated Molecular Dynamics and Free Energy Analysis. J Chem Inf Model. 2021;61(4):1954–1969. doi: 10.1021/acs.jcim.0c01470. [DOI] [PubMed] [Google Scholar]
- 72.Huang Y.-M., McCammon J.A., Miao Y. Replica Exchange Gaussian Accelerated Molecular Dynamics: Improved Enhanced Sampling and Free Energy Calculation. J Chem Theory Comput. 2018;14(4):1853–1864. doi: 10.1021/acs.jctc.7b01226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Miao Y., Feher V.A., McCammon J.A. Gaussian Accelerated Molecular Dynamics: Unconstrained Enhanced Sampling and Free Energy Calculation. J Chem Theory Comput. 2015;11(8):3584–3595. doi: 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Miao Y., McCammon J.A. Gaussian Accelerated Molecular Dynamics: Theory, Implementation, and Applications. Annu Rep Comput Chem. 2017;13:231–278. doi: 10.1016/bs.arcc.2017.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lomize M.A., Pogozheva I.D., Joo H., Mosberg H.I., Lomize A.L. OPM database and PPM web server: resources for positioning of proteins in membranes. Nucleic Acids Res. 2012;40(D1):D370–D376. doi: 10.1093/nar/gkr703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Lee J., Cheng X.i., Swails J.M., Yeom M.S., Eastman P.K., Lemkul J.A., et al. CHARMM-GUI Input Generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM Simulations Using the CHARMM36 Additive Force Field. J Chem Theory Comput. 2016;12(1):405–413. doi: 10.1021/acs.jctc.5b00935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Wang J., Wolf R.M., Caldwell J.W., Kollman P.A., Case D.A. Development and testing of a general amber force field. J Comput Chem. 2004;25(9):1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 78.Duan Y., Wu C., Chowdhury S., Lee M.C., Xiong G., Zhang W., et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J Comput Chem. 2003;24(16):1999–2012. doi: 10.1002/jcc.10349. [DOI] [PubMed] [Google Scholar]
- 79.Ni D., Wei J., He X., Rehman A.U., Li X., Qiu Y., et al. Discovery of cryptic allosteric sites using reversed allosteric communication by a combined computational and experimental strategy. Chem Sci. 2021;12(1):464–476. doi: 10.1039/d0sc05131d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Feng L.i., Lu S., Zheng Z., Chen Y., Zhao Y., Song K., et al. Identification of an allosteric hotspot for additive activation of PPARγ in antidiabetic effects. Sci Bull. 2021;66(15):1559–1570. doi: 10.1016/j.scib.2021.01.023. [DOI] [PubMed] [Google Scholar]
- 81.Wu J., Li D., Liu X., Li Q., He X., Wei J., et al. IDDB: A comprehensive resource featuring genes, variants and characteristics associated with infertility. Nucleic Acids Res. 2021;49(D1):D1218–D1224. doi: 10.1093/nar/gkaa753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Amadei A., Linssen A.B.M., Berendsen H.J.C. Essential dynamics of proteins. Proteins Struct Funct Bioinforma. 1993;17(4):412–425. doi: 10.1002/prot.340170408. [DOI] [PubMed] [Google Scholar]
- 83.Cunial F., Alanko J., Belazzougui D., Birol I. A framework for space-efficient variable-order Markov models. Bioinformatics. 2019;35(22):4607–4616. doi: 10.1093/bioinformatics/btz268. [DOI] [PubMed] [Google Scholar]
- 84.Husic B.E., Pande V.S. Markov State Models: From an Art to a Science. J Am Chem Soc. 2018;140(7):2386–2396. doi: 10.1021/jacs.7b12191. [DOI] [PubMed] [Google Scholar]
- 85.Swope W.C., Pitera J.W., Suits F., Pitman M., Eleftheriou M., Fitch B.G., et al. Describing Protein Folding Kinetics by Molecular Dynamics Simulations. 2. Example Applications to Alanine Dipeptide and a β-Hairpin Peptide. J Phys Chem B. 2004;108(21):6582–6594. [Google Scholar]
- 86.Prinz J.-H., Wu H., Sarich M., Keller B., Senne M., Held M., et al. Markov models of molecular kinetics: Generation and validation. J Chem Phys. 2011;134(17):174105. doi: 10.1063/1.3565032. [DOI] [PubMed] [Google Scholar]
- 87.McGibbon R., Beauchamp K., Harrigan M., Klein C., Swails J., Hernández C., et al. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys J. 2015;109(8):1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Hünenberger P.H., Mark A.E., van Gunsteren W.F. Fluctuation and Cross-correlation Analysis of Protein Motions Observed in Nanosecond Molecular Dynamics Simulations. J Mol Biol. 1995;252(4):492–503. doi: 10.1006/jmbi.1995.0514. [DOI] [PubMed] [Google Scholar]
- 89.Lange O.F., Grubmüller H. Generalized correlation for biomolecular dynamics. Proteins Struct Funct Bioinforma. 2006;62(4):1053–1061. doi: 10.1002/prot.20784. [DOI] [PubMed] [Google Scholar]
- 90.Lindahl E., Hess B., van der Spoel D. GROMACS 3.0: a package for molecular simulation and trajectory analysis. Mol Model Annu. 2001;7(8):306–317. [Google Scholar]
- 91.Floyd R.W. Algorithm 97: Shortest path. Commun ACM. 1962;5(6):345. [Google Scholar]
- 92.Sethi A., Eargle J., Black A.A., Luthey-Schulten Z. Dynamical networks in tRNA:protein complexes. Proc Natl Acad Sci USA. 2009;106(16):6620–6625. doi: 10.1073/pnas.0810961106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Girvan M., Newman M.E.J. Community structure in social and biological networks. Proc Natl Acad Sci USA. 2002;99(12):7821–7826. doi: 10.1073/pnas.122653799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Scherer M.K., Trendelkamp-Schroer B., Paul F., Pérez-Hernández G., Hoffmann M., Plattner N., et al. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J Chem Theory Comput. 2015;11(11):5525–5542. doi: 10.1021/acs.jctc.5b00743. [DOI] [PubMed] [Google Scholar]
- 95.Qiao A., Han S., Li X., Li Z., Zhao P., Dai A., et al. Structural basis of Gs and Gi recognition by the human glucagon receptor. Science. 2020;367(6484):1346–1352. doi: 10.1126/science.aaz5346. [DOI] [PubMed] [Google Scholar]
- 96.Huang S.K., Pandey A., Tran D.P., Villanueva N.L., Kitao A., Sunahara R.K., et al. Delineating the conformational landscape of the adenosine A2A receptor during G protein coupling. Cell. 2021;184(7):1884–1894.e14. doi: 10.1016/j.cell.2021.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Van Eps N., Caro L.N., Morizumi T., Kusnetzow A.K., Szczepek M., Hofmann K.P., et al. Conformational equilibria of light-activated rhodopsin in nanodiscs. Proc Natl Acad Sci USA. 2017;114(16):E3268–E3275. doi: 10.1073/pnas.1620405114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Gregorio G.G., Masureel M., Hilger D., Terry D.S., Juette M., Zhao H., et al. Single-molecule analysis of ligand efficacy in β2AR–G-protein activation. Nature. 2017;547(7661):68–73. doi: 10.1038/nature22354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Kato H.E., Zhang Y., Hu H., Suomivuori C.-M., Kadji F.M.N., Aoki J., et al. Conformational transitions of a neurotensin receptor 1–Gi1 complex. Nature. 2019;572(7767):80–85. doi: 10.1038/s41586-019-1337-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Mattedi G., Acosta-Gutiérrez S., Clark T., Gervasio F.L. A combined activation mechanism for the glucagon receptor. Proc Natl Acad Sci USA. 2020;117(27):15414–15422. doi: 10.1073/pnas.1921851117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Cao A.M., Quast R.B., Fatemi F., Rondard P., Pin J.-P., Margeat E. Allosteric modulators enhance agonist efficacy by increasing the residence time of a GPCR in the active state. Nat Commun. 2021;12(1):5426. doi: 10.1038/s41467-021-25620-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Draper-Joyce C.J., Bhola R., Wang J., Bhattarai A., Nguyen A.T.N., Cowie-Kent I., et al. Positive allosteric mechanisms of adenosine A1 receptor-mediated analgesia. Nature. 2021;597(7877):571–576. doi: 10.1038/s41586-021-03897-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.