Abstract
A growing number of studies show that the uneven spatial distribution of COVID-19 deaths is related to demographic and socioeconomic disparities across space. However, most studies fail to assess the relative importance of each factor to COVID-19 death rate and, more importantly, how this importance varies spatially. Here, we assess the variables that are more important locally using Geographical Random Forest (GRF), a local non-linear regression method. Through GRF, we estimated the non-linear relationships between the COVID-19 death rate and 29 socioeconomic and health-related factors during the first year of the pandemic in the USA (county level). GRF outputs are compared to global (Random Forest and OLS) and local (Geographically Weighted Regression) models. Results show that GRF outperforms all models and that the importance of variables highly varies by location. For example, lack of health insurance is the most important factor in one-third (34.86%) of the US counties. Most of these counties are (concentrated mainly in the Midwest region and South region). On the other hand, no leisure-time physical activity is the most important primary factor for 19.86% of the US counties. These counties are found in California, Oregon, Washington, and parts of the South region. Understanding the location-based characteristics and spatial patterns of socioeconomic and health factors linked to COVID-19 deaths is paramount for policy designing and decision making. In this way, interventions can be designed and implemented based on the most important factors locally, avoiding thus general guidelines addressed for the entire nation.
Keywords: spatial Machine learning, Random forest, COVID-19, USA
1. Introduction
COVID-19 has posed a severe threat against human life significantly impacting various aspects of social and economic activity (Grekousis and Liu 2021). Considering the unprecedented and acute impact on human well-being and society's sustainability, the United Nations declared the pandemic a social, human, and economic crisis (United Nations 2020). However, the epidemic does not only impact the socioeconomic characteristics of a community, but it is also shaped (in terms of transmission and severity) by these characteristics. In response, many researchers and organisations across the world rushed into a fight against COVID-19 to understand how the spatial spread and mortality patterns of this novel disease are related to the socioeconomic characteristics of the underlying communities (Grekousis et al., 2021). This would assist in designing more efficient health policies and implement targeted non-pharmaceutical interventions (Fu and Zhai, 2021).
Machine learning has been proved a determinative weapon to this fight (Roy and Ghosh, 2020). Machine learning is a set of computer algorithms that improve automatically through training without being explicitly programmed (Mitchell 1997; Lecun et al., 2015). In essence, machine learning is a process whereby computers learn by example using various algorithms and methods, test their gained knowledge, and use it to solve complex problems (Grekousis 2019). Such algorithms are popular in many geographically related fields, such as geodemographics (Grekousis 2021), natural hazards (Pradhan and Kim, 2020), remote sensing classification (Georganos et al., 2018), built-environment relation with physical and mental health (Wang et al., 2019), emergency medical services (Grekousis and Liu, 2019), demography (Andreopoulos et al., 2021), and epidemiology (Bannick et al., 2020).
In the context of the COVID-19 pandemic, machine learning algorithms have been used mainly from the following three standpoints: a) clinical, b) epidemiological, and c) societal (Roy and Ghosh, 2020). On the clinical and epidemiological front, efforts have been made to apply machine learning for various topics, including virus classification (Randhawa et al., 2020), vaccine design (Ong et al., 2020), compartmental modeling (i.e., Susceptible-Infectious-Recovered; Yang et al., 2020), and estimating the expected COVID-19 deaths (Sujath et al., 2020). From the societal standpoint, machine learning has been applied to assess the crucial role of demographics (i.e., age, gender), socioeconomic (i.e., occupation, income), and health status (i.e., underlying health conditions) as key risk factors of COVID-19 transmission and mortality (Torrats-Espinosa, 2021; Mollalo et al., 2021, Desmet et al., 2021; Ghahramani and Pilla, 2021).
Most of the existing non-geographically-oriented works do not consider the spatial variation of COVID-19 death rate and its determinants. However, the spatial variation in COVID-19 deaths reflects fundamental demographic and socioeconomic differences across space that must be considered. For example, the clustered concentration of COVID-19 deaths demonstrates spatial dependency of the confounding variables (Maiti et al., 2021). Neglecting the spatial aspect in COVID-19 analysis infers model inaccuracies as spatial dependence and spatial autocorrelation presence may distort the results of non-spatial statistics (Grekousis 2020). Current machine learning approaches cannot fully capture spatial analysis tasks unless they have trivial autocorrelation structure (Werner et al., 2021). In a broader context, understanding all sorts of considerations that make spatial data special is not always feasible by traditional aspatial machine learning (Werner et al., 2021). A way to partially address the above issues is through spatial machine learning.
Spatial machine learning is a set of georeferenced-data-driven techniques that incorporate spatial awareness and geographic attributes (i.e., location, distance, proximity, neighborhood, spatial weights) in the calculations and setting up of the algorithms. Spatial machine learning is, more simply, when spatial data, methods, and algorithms extend the casual machine learning process (Kalisky et al., 2019).
Examples of spatial machine learning methods that have been used to examine community drivers of COVID-19 are: Geographically Weighted Regression (GWR) (Lak et al., 2021), Multiscale Geographically Weighted Regression (MGWR) (Mansour et al., 2021), Spatial Lag Model (SLM) and Spatial Error Model (SEM) (Sannigrahi et al., 2020).
In the context of the US, income inequality, median household income, the percentage of black females, and the percentage of nurse practitioners were found to be significant explanatory variables of an MGWR model used to explain the spatial variability of COVID-19 incidence in the US from January 22, 2020, to April 9, 2020 (Mollalo et al., 2020). Another study applied spatial lag modeling over seven categories of socio-economic factors (gender, race, age, income, pollution, health insurance, health conditions) (Baum and Henry, 2020). The study found strong evidence of county-level socioeconomic factors influencing the spatial spread of COVID-19 confirmed cases in the US for Spring 2020. A spatial lag regression approach was applied for COVID-19 cases and deaths (registered from January 22 to June 30, 2020) based on 34 potential risk factors in counties across the US (Andersen et al., 2021). The study revealed that the most vulnerable communities were located in New England, the Southeast, and the Southwest and were associated with a larger proportion of black individuals. A spatial lag model was used in another study to analyse the predictors (including political attributes) of COVID-19 death as of August 31, 2020 (Feinhandler et al., 2020). Spatial autoregressive models were used to assess the associations between COVID-19 deaths (as reported by August 2020) and the percentage of individuals engaged in farm work, uninsured individuals, and individuals living below the poverty level (Fielding-Miller et al., 2020). Global spatial lag and spatial error models, and local spatial regression models (GWR, MGWR) were applied to measure the associations between a set of explanatory factors and COVID-19 deaths at the county scale for the US from March to July 2020 (Maiti et al., 2021). The above work also included time in the local models by analysing monthly COVID-19 cases and deaths. Lastly, spatial lag, spatial error, and combined spatial lag and error models were used to examine the role of spatial structure in shaping geographic disparities in the COVID-19 confirmed cases (Sun et al., 2020). Results showed that spatial models could better estimate COVID-19 confirmed cases.
The above studies have improved our understanding of the spatial spread and mortality patterns of COVID-19. However, they are based on the assumption that the relationships between the COVID-19 deaths and the socioeconomic factors studied are linear (without providing any stromg evidence that proves this assumption). In reality, the relationships between risk factors and various death causes are not always linear (Zaccardi et al., 2017, Quiñones et al., 2021). Therefore, it is essential to deal with the non-linear relationships in a local regression model to explore the spatial variation of COVID-19 deaths concerning various socioeconomic and health factors. As such, the existing literature has left a significant research gap concerning the use of non-linear non-parametric local machine learning techniques.
Another noteworthy gap is that existing research in analysing the spatial determinants of US COVID-19 deaths limits its reference period to the first US pandemic wave, failing to address the subsequent ones.
Here we fill these gaps in two ways. First, we assess the non-linear relationships between the COVID-19 death rate and 29 socioeconomic and health factors across 3021 counties of the US. Second, we extend the reference period to include the entire first year of the pandemic in the US (February 6, 2020, until February 5, 2021).
To fill the first gap we use Geographical Random Forest (GRF), a local non-linear non parametric spatial machine learning method (Georganos et al., 2021). In this way, we identify the factors that are more important locally. GRF can successfully handle spatial heterogeneity and overcome many limitations that Geographically Weighted Regression (GWR) or other linear spatial regression models exhibit (Georganos et al., 2021; Luo et al., 2021, Quiñones et al., 2021).
In contrast to GWR or other linear spatial regression methods, GRF does not need to make assumptions regarding the relationships between independent and dependent variables (such as linearity) as well as the relationships among the predictors (collinearity) (Quiñones et al., 2021). In this sense, GRF is considered superior to linear spatial regression models, provided that the data size is large and its hyper-parameters are fine-tuned (Janitza et al., 2018). Even though, we analysed the relationships between the risk factors and COVID-19 death rate through partial dependence plots to bring more evidence on the existence of non-linearity and, therefore, the need to apply GRF. Our analysis showed that almost all risk factors are non-linearly related to COVID-19 death rates. In addition, we compared the outputs of GRF to GWR and OLS (ordinary least squares) for the same set of variables. Results showed that GRF outperformed RF, GWR, and OLS. The above findings further strengthen the choice of non-linear spatial machine learning methods (GRF) in complex spatial analysis problem. Lastly, we present in detail the major differences between GRF and GWR in the methods section.
Regarding the second gap, by analysing COVID-19 death rates for the first year of the pandemic we can better trace the geographical shifts of COVID-19 hot spots reported over time. For example, during the first wave, urban counties on the west coast were hit first (Zhai et al., 2021). Over time hotspots of deaths and cases moved east and to rural counties (Desmet et al., 2021). As such, early studies identified different COVID-19 determinants compared to later ones. For instance, preliminary studies (Feinhandler et al., 2020; Hamidi et al., 2020) found a positive relationship between COVID-19 deaths and population density in metropolitan areas. However, this association was later rejected by others (Desmet et al., 2021; Carozzi et al., 2020), who argued that density might have affected the time of the outbreak in each county (densely populated areas were more likely to experience an early epidemic outbreak), but not COVID-19 deaths. Therefore, we believe that a broader reference period is preferred to infer about factors associations of a dynamic phenomenon. For this reason, we analysed data for the first year of the pandemic.
Currently, only one study has applied a spatial non-linear machine learning regression method to study COVID-19 mortality for the US (Luo et al., 2021). Specifically, a geographically-weighted random forest regression (GW-RF) was proposed to evaluate the variations in COVID-19 deaths and risk factors across the continental USA from January 22, 2020, to June 26, 2020 (Luo et al., 2021). The authors present GW-RF briefly without referring to the hyperparameters or the method's settings. For this reason, we cannot directly compare GW-RF with GRF used in this research which is fully documented in (Kalogirou et al., 2019).
To the authors’ knowledge, this is the first study that explores the spatial variation in the non-linear relationships between COVID-19 death rate and multiple societal and health factors for the first year of the pandemic in the US. In addition, it assesses and maps how the importance of these factors on the COVID-19 death rate varies spatially. Hopefully, this will assist decision-makers in implementing more targeted interventions to control and prevent the COVID-19 epidemic.
2. Material and methods
2.1. Material
An initial set of demographic and socioeconomic variables was obtained from the US Census Bureau (US Census Bureau, 2021a, US Census Bureau, 2021b). Underlying health condition variables were compiled from the US Centers for Disease Control and Prevention (CDC 2020a). COVID-19 deaths were obtained at the county level from USAFacts and cover the first year of the epidemic from February 6, 2020- the first death registered in the US- to February 5, 2021 (USAFacts 2021). The death rate per county is the cumulative deaths by February 5, 2021) per 100,000 inhabitants. The population of each county was derived from the US Census Bureau 2015–2019 American Community Survey (US Census Bureau, 2021a, US Census Bureau, 2021b). Fifty-nine counties reported no deaths by February 5, 2021, and were removed from the study. Another 28 counties were removed as outliers (having outlying values in COVID-19 death rate). A set of n = 3021 counties was finally analysed. The geographical boundaries of the counties, states, and regions refer to the year 2019, at a 1:5 million geographical scale, and were obtained from the Census Bureau's MAF/TIGER geographic database (US Census Bureau 2019).
Contrary to other studies that do not consider multicollinearity an issue for random forest regression (Luo et al., 2021), in this study, we excluded those variables with a variance inflation factor (VIF) of more than 7.5. Highly correlated variables (those with r > 0.70 were also removed. Tracing and removing highly correlated variables are important in random forest regression (Strobl et al., 2008). From the modeling perspective, any correlated variable can be selected as a predictor without significantly affecting the model's predictive performance. However, once one of the correlated variables is used, the importance of others is reduced. This happens because the correlated variable not picked initially (we assume two variables highly correlated) has a lower chance of picked later since the former variable has already explained the output variation for both of them (Gregorutti et al., 2017). Therefore, when interpreting data, this can drive us to the wrong conclusion of a lower importance of one variable over the other, when in fact, their relationships with the dependent variable are similar (Toloşi et al., 2011). From an initial set of 76 variables compiled from several sources, a set of 29 variables was finally retained after removing variables exhibiting multicollinearity (Table 1 ).
Table 1.
Names, descriptions and sources of the variables.
| Theme | Variable Name | Description | Source |
|---|---|---|---|
| Demographic | Population density | Population density per square km | U.S. Census US Census Bureau, 2019 |
| %Age 20-39 | % Population by age: 20–39 years | ||
| %Age 40-59 | % Population by age: 40–59 years | ||
| %Age 60-79 | % Population by age: 60–79 years | ||
| %Age 80+ | % Population by age: 80 years and over | ||
| %African American | % Population by race: Black or African American alone | ||
| %Asian | % Population by race: Asian alone | ||
| %Disabled | % Civilian noninstitutionalized population with a disability | ||
| Households | Household size | Average household size | U.S. Census US Census Bureau, 2019 |
| Housing Characteristics | %No vehicles | % Occupied housing units with no vehicles available | U.S. Census US Census Bureau, 2019 |
| %Housing problem | Percentage of households with at least 1 of 4 housing problems: overcrowding, high housing costs, lack of kitchen facilities, or lack of plumbing facilities | ||
| Education | %> Bachelor | % Population 25 years and over bachelor's degree | U.S. Census US Census Bureau, 2019 |
| Employment | %Work construction and trade sector | % Workers in construction, manufacturing, wholesale trade, transportation, warehousing, utilities and retail trade | U.S. Census US Census Bureau, 2019 |
| %Work services sector | % Workers in information, finance, insurance, real estate, rental, leasing, professional, scientific, management, administrative and waste management services | ||
| %Work social sector | % Workers in educational services, health care, and social assistance | ||
| Economic | Median income | Households median annual income (in 1000 dollars) | U.S. Census US Census Bureau, 2019 |
| %Unemployment | % Unemployment rate for population 20–64 years | ||
| %No insurance | % Current lack of health insurance among adults aged 18–64 years 2018 age-adjusted prevalence | CDC Centers for Disease Control and Prevention, 2020a, CDC Centers for Disease Control and Prevention, 2020b | |
| %Poverty | % Below poverty level population for whom poverty status is determined | U.S. Census US Census Bureau, 2019 | |
| Commuting | %Private transportation | % Worker 16 years and over by means of transportation to work: car, truck, or van drove alone | U.S. Census US Census Bureau, 2019 |
| %Walking | % Worker 16 years and over by means of transportation to work: walk | ||
| %Work from home | % Worker 16 years and over who worked from home | ||
| Commuting time | Mean travel time to work (minutes) for workers 16 years and over who did not work from home | ||
| Health Condition | Heart disease mortality | Heart disease mortality per 100,000 population age-adjusted, spatially smoothed, 3-year average. 2016–2018 | CDC Centers for Disease Control and Prevention, 2020a, CDC Centers for Disease Control and Prevention, 2020b |
| %Asthma | % Current asthma among adults aged ≥18 years 2018 age-adjusted prevalence | ||
| %Obesity | % Obesity among adults aged ≥18 years 2018 age-adjusted prevalence | ||
| %Sleep<7hrs | % Sleeping less than 7 h among adults aged ≥18 years 2018 age-adjusted prevalence | ||
| %No leisure-time PA | % no leisure-time physical activity among adults aged ≥18 years 2018 age-adjusted prevalence | ||
| %Smokers | % Current smoking among adults aged ≥18 years 2018 age-adjusted prevalence | ||
| Coordinates | X,Y | Counties' centroids coordinates | U.S. Census US Census Bureau, 2019 |
| COVID-19 | Deaths per 100k | Cumulative COVID-19 deaths per 100,000 population as of February 5th, 2021 | USAFacts 2021 |
2.2. Methods
2.2.1. Random forest
Random forest (RF) is a non-parametric machine learning method for classification and regression analysis (Breiman 2001). RF does not require an assumption about the statistical distribution of the data, making the method suitable in the case of non-linear relationships among the variables (Catani et al., 2013).
RF is a group of un-pruned classification or regression trees created from a random selection of samples derived from the training data (Ali et al., 2012). The ‘forest’ is an ensemble of decision trees usually trained with the bagging method. Briefly, the RF algorithm basic steps are:
-
1
From a given training set select n samples randomly with replacement (n usually equals with 2/3 of the training data). The other third, the so-called out-of-bag (OOB) set, is kept out of training and is used to estimate the RF's goodness of fit.
-
2
From each sample with k variables, randomly select a subset (m < k) and create a decision tree.
-
3
Each tree grows with a constant m to its largest extent without pruning until it cannot be split.
-
4
The prediction/classification result for each tree is calculated.
-
5
The most commonly occurring class/vote (for classification) or the average prediction (for regression) of all trees is used to create the final output.
There is no need for cross-validation or using a separate test set to validate RF models (Breiman 2001). Validation is estimated internally during the algorithm run using the out of bag (OOB) method, which measures the prediction error of random forests using bootstrap aggregating. The third of the data from each tree initially kept out of the training (see step 1 above), is used to estimate the OOB error (for classification), or the OOB mean square error (MSE), and the OOB R 2 (for regression). OOB and cross-validation are different methods of validating a machine learning method. However, the OOB method is less computationally demanding and tests the model while trained (Janitza et al., 2018). The OOB method is also used to assess the importance of each independent variable. A standard method to calculate importance is calculating the increase in the Mean Squared Error (%IncMSE; Georganos et al., 2021). This method randomly permutes the values in the OOB sample of each variable in turn and calculates the OOB error. If the OOB error increases with the permuted values, this indicates that the variable is important. The higher the change, the more important the variable is to predict the dependent variable.
2.2.2. Geographical random forest
Geographical random forest (GRF) is an extension of the traditional RF and its used both as a predictive model and as a tool to address spatial heterogeneity (Georganos et al., 2021). The core idea of GRF is similar to the local regression analysis framework of the traditional GWR (geographically weighted regression). GRF consists of several local sub-models rather than a single global model. To address spatial heterogeneity, GRF is calibrated locally using a spatial weights matrix and random forest trees. In other words, for each location i, a local RF is computed using only nearby observations. A simplistic version of the regression equation of the aspatial RF is (1)
| (1) |
where is the dependent variable for the ith observation, is the non-linear prediction of RF based on a set of x independent variables, and e is the error term. The GRF extends equation (1) to use each time only a subset of the original dataset (2) (Georganos et al., 2021).
| (2) |
where is the prediction of the RF model calibrated on location i, and are the co-ordinates of the centroid of the spatial unit i. A different sub-model is built for every spatial unit, including only its neighboring units. The neighborhood, or else kernel, is created based either on a distance threshold value (bandwidth-fixed kernel) or the number of nearest neighbors (adoptive kernel). When the aerial size of the spatial units varies a lot (as in our case study), the adoptive kernel is preferred. For this reason, we used the adaptive kernel and tested GRF models using different bandwidth values.
To assess the goodness-of-fit and overall performance of the GRF model, the following standard metrics are calculated: coefficient of determination R 2 (3), Root Mean Square Error (RMSE) (4), and the Mean Absolute Error (MAE) (5),
| (3) |
| (4) |
| (5) |
where is the actual value for observation i, is the predicted value for observation i, is the average value of the dependent variable, n is the total sample size. To implement the RF and GRF analyses, we used the R package ‘randomForest’ (Liaw et al., 2002) and ‘SpatialML’ (Kalogirou and Georganos, 2019), respectively. A more thorough presentation of GRF can be found at Georganos et al. (2021) and Kalogirou and Georganos, 2019.
GRF and random forests are less prone to overfitting by creating multiple trees, with each tree trained slightly differently (Breiman et al., 2001; Zhao et al., 2012). Even if a tree overfits, it overfits differently from the rest. On that note, random forests outperform the solution generated by a single decision tree as multiple overfitting classifiers are combined to reduce the overfitting. Therefore, GRF and random forests are considered robust classifiers that avoid overfitting as long as the dataset is large and the hyper-parameters are properly selected (Janitza et al., 2018). To avoid overfitting in this study and similar to other works (Luo et al., 2021, Quiñones et al., 2021), we fine-tuned hyper-parameters employing Random Grid Search (RGS) and used a large dataset of 3021 data points (counties) and 29 variables.
2.2.3. Confounding variables, variables selection, and outliers
An important issue that should be considered is how RF and GRF handle confounding variables. This study uses the randomization method that has become a standard in applied machine learning to manage confounding variables (Brownlee 2020). Randomization is applied in random forests and GRF in many different levels (Gallicchio et al., 2017). Each tree is built from samples drawn randomly with replacement from the training set. At each node of the tree, a subset of the variables in the data is selected at random, and only these variables are considered for the partition at the node. This random selection of variables reduces the similarity of trees coming from different bootstrap samples (Altman and Krzywinski, 2017). This reduces the potential for confounding by generating groups that are comparable concerning known and unknown confounding variables (Pourhoseingholi, 2012). In this sense, randomization of experiments is the key to controlling for confounding variables in machine learning experiments (Brownlee 2020).
Following the example of other studies that apply random forests or GRF (Quiñones et al., 2021; Luo et al., 2021; Georganos et al., 2021), we do not analyse confounding variables with other traditional techniques, and we rely on the randomization procedures embedded in the RF machine learning technique.
Apart from controlling for confounding variables, several advantages are achieved through randomization in RF and GRF, such as improved variable selection, reducing overfitting, and better predictions (Gallicchio et al., 2017).
Randomization in variable selection is a significant difference from other linear spatial regression models. For example, GWR uses a fixed number of variables for the entire training process. On the other hand, GRF selects a different set of variables through randomization for the same location and tests which ones are more important in the local model. In other words, GWR or other linear spatial regression models conduct variable selection before training. In contrast, variable selection is made during training in GRF, thus testing many different variable combinations.
The difference in variable selection methods between GWR and GRF has another implication. GWR models tend to use a relatively small number of variables as it is hard to interpret the local coefficients that explain the effect of the independent variables on the dependent for a large number of factors. Specifically, GWR allows for mapping the local coefficients of the independent variables. This offers a comprehensive view of the spatial variability of coefficient values and allows for tracing potential clustering (Grekousis 2020). Still, the local coefficients of a variable can not be compared (at least directly) with the coefficients of the remaining variables (especially when they are many). Therefore, it is not easy to assess which independent variable is associated to a higher degree, relative to the rest, with the dependent one by only plotting the local coefficients. On the other hand, GRF allows for plotting the relative importance of a large number of variables for every location, which is straightforward and extremely helpful when it comes to decision-making.
Another important difference between GRF and GWR is that the linear model in GRW is susceptible to outliers while GRF is less sensitive. The reason is that a random forest is an ensemble of Classification and Regression Trees (CART) fitted to independent bootstrap samples of the data. In this way, outliers may be left out when creating bootstrap samples, making overfitting less likely and improving variable selection (Altman and Krzywinski, 2017).
3. Results
RF and GRF were applied to a large set of 29 variables to analyse the COVID-19 death rate across 3021 counties (spatial units) in the US. Before fitting the RF and the GRF model, and to avoid overfitting, we used Random Grid Search to find the optimal values for the hyper-parameters. After testing various combinations of hyper-parameters values through K-fold cross-validation, we used the following settings for the GRF: adoptive kernel, bandwidth = 300 nearest neighbors, number of trees to grow (ntree) = 2,000, number of variables randomly sampled as candidates at each split (mtry) = 8. We also run OLS (ordinary least squares), RF, and GWR to compare with the GRF output. Table 2 presents models' assessment metrics, indicating that GRF is more accurate than GWR, RF, and OLS, having higher R 2 and lower RMSE and MAE.
Table 2.
Model assessment metrics.
| Model | RMSE | MAE | R2 | OOB R2 |
|---|---|---|---|---|
| OLS | 74.83 | 57.19 | 0.30 | NAa |
| GWR | 70.25 | 55.20 | 0.55 | NAa |
| RF | 71.31 | 54.59 | 0.63 | 0.38 |
| GRF | 67.29 | 50.31 | 0.76 | 0.43 |
NA: Not applicable.
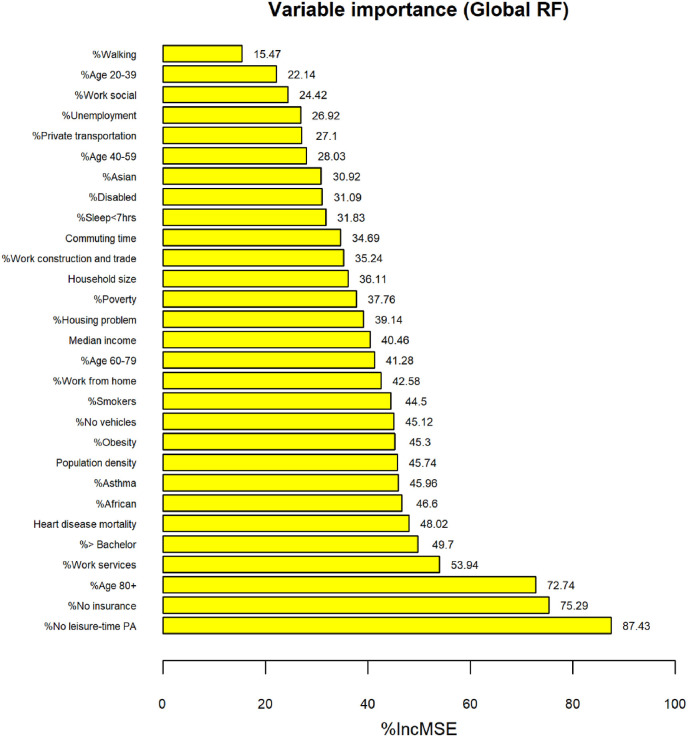
The importance of the independent variables for the RF is depicted in Fig. 1 . The higher the increase in the mean squared error (%IncMSE), the more important the variable. Health-related factors (heart disease mortality, asthma, obesity), education (percentage of people with higher than a bachelor's degree), socioeconomic factors (percentage of people with no medical insurance, percentage of people with no leisure-time physical activity), and demographic variables (people over 80 years old, and percentage of African-American population) are listed in the top 10 most important variables concerning COVID-19 death rate.
Fig. 1.
RF variable importance. A higher increase (%) in mean squared error (%IncMSE) corresponds to higher importance.
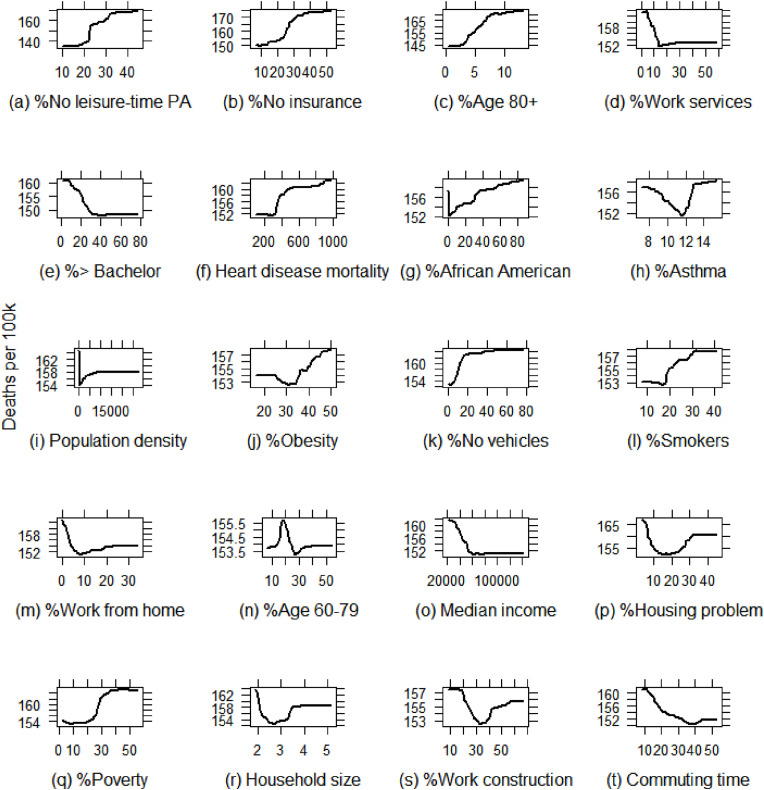
Partial dependence plots (PDPs) for the risk factors variables with the highest importance (top 20 generated based on the RF model) were built to characterize the non-linear relationship between the risk factors and COVID-19 death rate (Fig. 2 ). PDPs can display the expected target response as a function of the input features of interest and reveal whether the relationship between the target and a feature is linear, monotonic, curvilinear, or more complex (Friedman, 2001). Results show that most risk factors are not linearly associated with COVID-19 death rate (i.e., no leisure-time PA, Fig. 2a, no insurance, Fig. 2b, heart disease mortality, Fig. 2f, asthma, Fig. 2h, smokers, Fig2l). For example, the negative non-linear effect of average household size on COVID-19 death rate is observed when the average household size is lower than three, while the average household size is positively associated (non-linearly) with COVID-19 death rate when the average household size is higher than three (Fig 2r).
Fig. 2.
Partial dependence plots for the top 20 most important risk factors.
We notice linear relationships for a few variables but only within specific ranges. For example, there is a positive linear relationship between Age 80+ and COVID-19 death rate at the range of 3%–7%, but after that point, the effect is marginal (Fig. 2c). Similarly, there is an almost linear negative association between median income and COVID-19 death rate at the range of 20.000–80,000 US dollars, but after that, the effect is not evident (Fig 2o).
Overall, results show that nearly all relations are non-linear, further strengthening the necessity for applying non-linear regression models. We have no reasons to assume that non-linearity would disappear at the local models, and therefor we apply GRF to handle non-linearity.
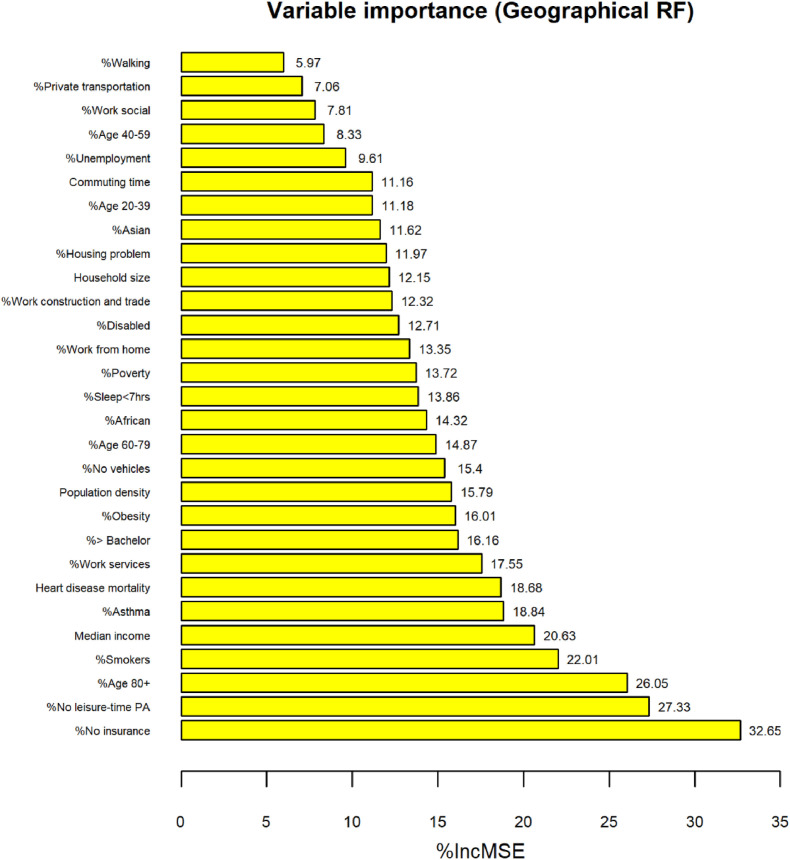
Fig. 3 depicts the average local importance value (%IncMSE) per variable on the COVID-19 death rate in the GRF model. We observe that the risk factors are ordered quite similarly to the global model (Fig. 1). For example, no insurance is ranked first (higher %IncMSE) and no leisure-time physical activity second in GRF. The order is reversed in RF. However, some differences in order are also noticed. Median income is ranked as the fifth most important variable for modeling COVID-19 death rate in GRF and 15th in the RF. Similarly, the percentage of African Americans is ranked 14th in GRF but 7th in RF.
Fig. 3.
Average local importance per variable in the GRF model. A higher increase (%) in mean squared error (%IncMSE) corresponds to higher importance.
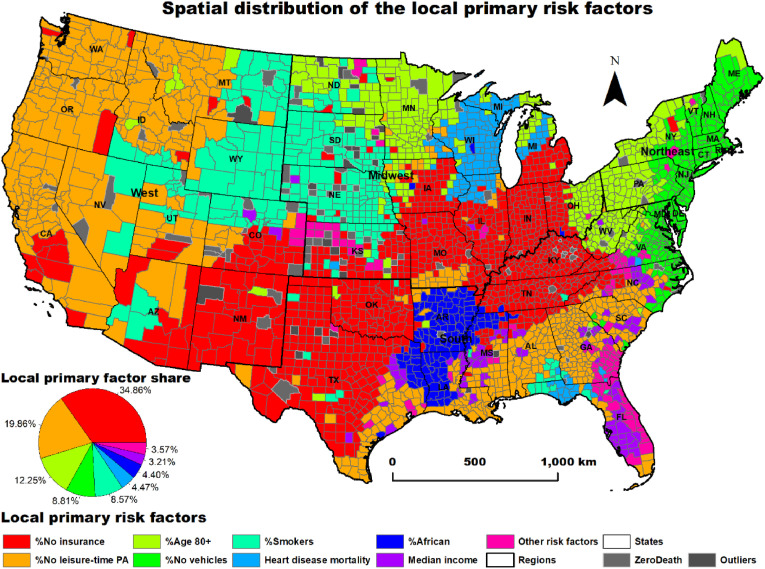
We also calculated the proportion of counties having the same local primary risk factor (factor with the highest importance) (Table 3 ). For example, lack of health insurance is the factor with the highest importance in 34.86% of counties.
Table 3.
Counties having the same factor with the highest importance (primary factor).
| Local primary factors | Share of counties (%) |
|---|---|
| Lack of health insurance (%) | 34.86 |
| No leisure-time physical activity (%) | 19.86 |
| Aged over 80 years (%) | 12.25 |
| No vehicles (in occupied housing units) (%) | 8.81 |
| Smokers (%) | 8.57 |
| Heart disease mortality rate | 4.47 |
| African American (%) | 4.40 |
| Households' median annual income | 3.21 |
| Other risk factors | 3.57 |
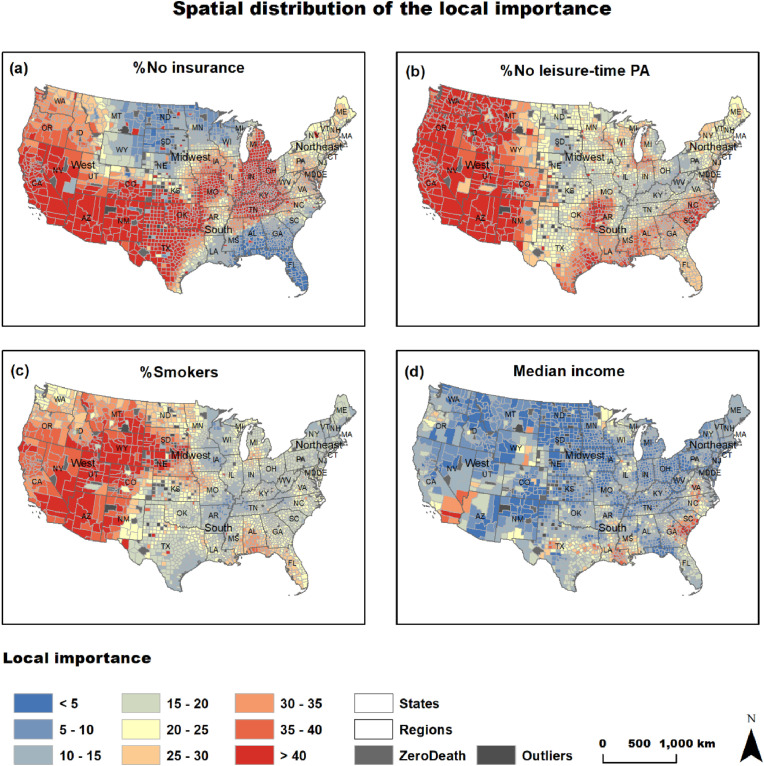
Not surprisingly, socioeconomic and health-related factors such as lack of insurance (34.86%), no leisure-time physical activity (19.86%), smokers (8.57%), heart disease mortality (4.47%) were ranked as the most influential factors to COVID-19 death rate in 67.76% of the US counties (Table 3, Fig. 4 ). Population aged over 80 (12.25%), housing units with no vehicles available (8.81%), African-American population (4.40%), and annual median (3.21%) income were also ranked top. The geographical pattern of the primary factors is interesting (Fig. 4). No insurance is dominant in southern states of the Midwest regions (i.e., Kansas, Montana, Illinois, Indiana), New Mexico, Texas, Oklahoma, Kentucky, and Tennessee. No leisure-time physical activity is the most influential factor mainly in the western part of the West region (California, Oregon, Washington), and in South region states of Alabama, Georgia, and South Carolina. Population aged over 80 is the most important factor in Minnesota and parts of North Dakota, Ohio, West Virginia, New York, and Pennsylvania. Smokers is the local primary factor mainly in Wyoming, South Dakota, and Nebraska. The percentage of African-American population is influential in 4.40% of the counties primarily located in Arkansas, Mississippi, and Louisiana. Lastly, median income is not concentrated in a specific region, although we observe a small cluster in Florida.
Fig. 4.
Spatial distribution of importance of key factors.
To further analyse the spatial distribution of the local variable importance, we map the following top factors: no insurance, no leisure-time physical activity, smokers, and median income (Fig. 5 ). This map depicts the importance value (%IncMSE) of each local factor no matter if it is primary or not. No insurance (Fig. 5A) has high importance not only in parts of the Midwest and South regions (that was the primary factor as shown in Fig. 4) but also in the West region (i.e., California, Oregon, Washington, Nevada, and Arizona) where no leisure-time physical activity is the primary risk factor. This means that no insurance is a critical factor to COVID-19 death rate across most US counties except for northern Midwest states and Alabama, Georgia, and Florida in the South region. No leisure-time physical activity dominates the West region (see Figs. 4 and 5b) and the South region. Smokers is also an important factor in the West and parts of Midwest regions and southern states such as Alabama and Florida (Fig. 5C). Lastly, median income is important in southern California and counties of the South region (Texas, Louisiana, Georgia, South Carolina, North Carolina, and Virginia, Fig. 5D). Further analysis of the above results is discussed in the following section.
Fig. 5.
Primary local factor per county.
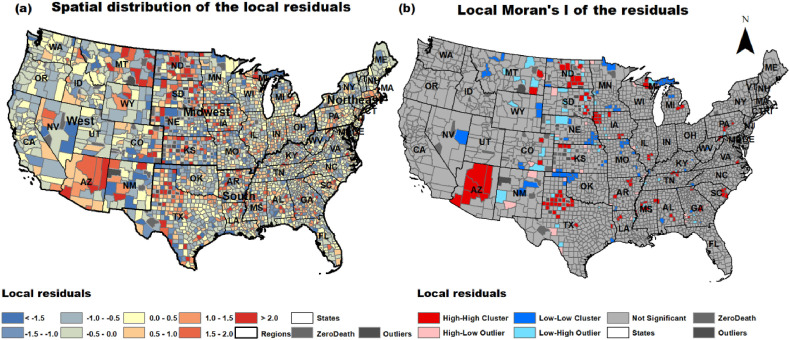
To better understand how GRF addressed spatial heterogeneity, we map the spatial distribution of the standardised residuals (Fig. 6 a). We also estimate spatial autocorrelation through local Moran's I to trace potential clustering in the residuals (Fig. 6b). Results show that spatial clustering of residuals is not evident in most areas and that they are randomly scattered. This indicates that GRF has addressed spatial heterogeneity in most locations. However, the checkboard-like pattern with large over or under predictions in nearby locations (mainly across the Great Plains and Texas; Fig. 6a) and the existence of clusters and spatial outliers in the same areas (Fig. 6b), indicate that counties exhibiting severe over-prediction were adjacent to counties with under-predictions. This pattern was also observed in other works that analysed COVID-19 through spatial regression methods (Sun et al., 2020). It's unclear why other regression methods and GRF applied here cannot address this problem. This can be partially explained by the fact that spatial heterogeneity is common in US counties (Mollalo et al., 2020) or that additional variable should be included in the model. Even with this caveat, the residuals map offers a better understanding of where the model is misspecified, allowing us to trace hidden drivers.
Fig. 6.
(a) Spatial distribution of the standardised local residuals. (b) Local Moran's I of standardized residuals.
4. Discussion
This cross-sectional ecological study reports a county-level analysis of the cumulative COVID-19 death rate for the first year of the epidemic in the US since February 5, 2020. We applied two non-linear regression models, namely RF and GRF and two linear ones (OLS and GWR). Results showed that the local GRF model outperformed all models. This indicates that GRF can handle spatial heterogeneity and identify the factors that explain local variance in the COVID-19 death rate, something confirmed in other studies (Georganos et al., 2021; Luo et al., 2021). This study aims to identify the importance of key demographic, socioeconomic, and health-related factors on the COVID-19 death rate. Of the top eight most influential local risk factors, four are socio-economic (no leisure-time physical activity, lack of insurance, no vehicle, median annual income), two are health-related (smoking, heart disease), and two are demographic (over 80 years old, African-American population). Below, we discuss the findings related to these factors and highlight their implications.
4.1. No leisure physical activity
No leisure-time physical activity is defined as not participating in any physical activities such as running, walking for exercise, or gardening. Limited physical activity or, even worst, no physical activity could dramatically increase the risk of many severe health disorders (i.e., diabetes, cancer, and cardiovascular disease), thus increasing the severity of potential COVID-19 infection (Lippi et al., 2020). Furthermore, reduced or no leisure-time physical activity has been linked to experiencing unpleasant emotions such as sadness, anger, or frustration and, in general, to mental health and mental wellbeing (Huang et al., 2021; Liu et al., 2019). In combination with prolonged quarantines, physical activity's absence triggers post-traumatic stress and depression (Brooks et al., 2020). With many states imposing statewide quarantine, or stay-at-home orders in attempts to hinder the spread of COVID-19, it is not surprising that this factor is ranked high across the US. No leisure-time physical activity is the most important primary factor for 19.86% of the counties concentrated mainly in California, Oregon, Washington, and parts of the South region (i.e., Alabama, Georgia, South Carolina) (Fig. 4). However, as shown in Fig. 5B, the importance of this factor is high across the entire West region and most of the counties of the South region. We also notice that in the part of the South region that African-American population is the primary factor, a cluster of high values of the importance of no leisure-time physical activity collocates (Figs. 4 and 5B).
This is an important lesson extracted from our study as we found that the lack of leisure physical activity is the second most important risk factor across the US and is also spatially clustered in specific regions. This could inform local governments to promote outdoor or indoor physical activities with specific regulations in places where the importance is higher. As local lockdowns, quarantines, and stay-at-home orders are still in effect in many places worldwide, staying active and maintaining physical exercise should be prioritised for mental and physical health (Lippi et al., 2020). As physical activity is linked to a person's overall physical and mental health, we suggest that local and regional governments encourage physical activities during epidemics as an alternative way to build a stronger immune system.
4.2. Health related variables
From the health-related variables, smoking and heart disease were ranked at the top eight local primary factors for the COVID-19 death rate. Studies have shown that smoking is a risk factor for the progression of COVID-19, with smokers having higher odds of infection and mortality from COVID-19 than non-smokers (Reddy et al., 2021, Patanavanich and Glantz, 2020). The percentage of smokers was the most important local primary risk factor in 8.57% of the counties concentrated mainly in Wyoming, South Dakota, Nebraska, and northern Colorado. There is also a small cluster of counties with smoking as the primary factor in south Alabama and Florida, which is surrounded by counties having heart disease as the primary risk factor. Heart disease is also dominant in Wisconsin and parts of Illinois and Michigan and has been associated with higher COVID-19 mortality in other studies (Núñez-Gil et al., 2021).
Studies have shown that underlying medical conditions are highly prevalent among COVID-19 patients that are hospitalised (Stokes et al., 2020). Our analysis confirms this result and locates the population's enclaves at higher risk. In this respect, the estimations of the importance of the underlying medical factors at the county level can be used together with data on intensive care units admissions or available beds for efficient planning to mitigate the epidemic and decrease mortality rates. Areas, for example, with risk factors highly related to underlying health conditions could use additional resource investment, including hospital beds, staffing, ventilators, or other supplies in need to treat an expected high flow of COVID-19 patients with specific health problems (Razzaghi et al., 2020). As such, the implications of our anlaysis in designing effective health policies could be significant.
4.3. African-American population
Many studies have identified the African-American population as a determinant of the COVID-19 death rate (Andersen et al., 2021; Feinhandler et al., 2020). This can be attributed to the high prevalence of factors that adversely affect health, including poverty, low-quality nutrition, lack of insurance, and limited access to health care in many African-American communities (Yancy 2020; Hamidi et al., 2020). The importance of the African-American share on COVID-19 death rates is higher in the South region, in states (i.e., Arizona, Louisiana), and counties that historically have high proportions of African-Americans. This finding is critical from a policy perspective as it may lead to more tailored and effective strategies for this subpopulation.
4.4. Age over 80
A population aged over 80 is related to high COVID-19 death rates (Dowd et al., 2020). According to CDC, people in the US over 85 years have a 630 times greater average death rate than those aged between 18 and 29 years (CDC 2020b). For example, as of May 17, 2021, 80.5% of deaths in the US were people over 65 years old, while 31.4% of deaths were individuals aged 85 and above (CDC 2021). We found that this risk factor clusters in parts of the Midwest and Southeast regions. We suggest that identifying and mapping age-related spatial clustering be prioritised to improve critical care forecasts and health care system preparedness (Verhagen et al., 2020).
4.5. Household median income and lack of medical insurance
Household median income is ranked the fifth most important local risk factor. Median income has been linked to COVID-19 mortality in many studies (Maiti et al., 2021; Mollalo et al., 2020). For example, a Multiscale Geographical Weight Regression model used to explain the spatial variability of COVID-19 incidence in the US from January 22, 2020, to April 9, 2020, found median income to be a significant determinant (Mollalo et al., 2020). The above study identified higher coefficient values of median income in similar areas (parts of West region and South region) with areas having high importance value in this study.
In general, the poorer populations are more likely to lack access to medical insurance and health care services which may inflate mortality rates (Ahmed et al., 2020). Our study shows that the lack of insurance is the most important factor in 34.86% of the US counties. These counties are concentrated in parts of the West, South, and Midwest regions. On the other hand, no insurance is ranked relatively low in the states of the east coast. People with no insurance are more likely to work in service-oriented industries with a lower ability to work from home (Chin et al., 2020). In consequence, they are more susceptible to COVID-19 (Chin et al., 2020).
We should emphasise that the medical cost of COVID-19 treatment is high in the absence of health insurance. It is estimated as being 14,366 US dollars on median values per single symptomatic SARS-CoV-2 patient needing hospitalisation (Bartsch et al., 2020).
The fact that lack of insurance is the most important factor across the US counties is a significant finding. The high cost of medical treatment can be an extra obstacle for seeking health care to a hospital for people with adequate income but no insurance. Late treatment of COVID-19 infection may be fatal (Bartsch et al., 2020). This highlights the importance of medical insurance that gives access to the health care system, and like others, we strongly support robust social security and health system at the national, regional, and local levels (Batty 2020).
4.6. Housing units with no vehicles
Housing units with no vehicles available was the most influential factor for 8.81% of the counties. Counties most influenced by this factor lie on the Atlantic coast stretching from Virginia up to Maine and belong mainly to the northeast megalopolis (also known as northeast corridor, or Bos-Wash) consisting of Boston, New York, Philadelphia, and Baltimore, and Washington D.C. urbanised areas. It is the most populous megalopolis in the US with over 50 million residents and the world's largest economic output estimated at 4 trillion US dollars (Florida 2019).
The fact that the absence of a car within a housing unit was ranked as the most important factor in these areas highlights the effect of choosing between private and public transportation as an important causal mechanism in the spread of COVID-19 and underlines the significance of interconnected communities (Seto et al., 2021).
The study has the following limitations. First, a finer scale of analysis would provide a deeper understanding of the importance and effect of the studied variables on the COVID-19 death rate. Yet, the finest spatial scale that COVID-19 death data is available for the contiguous US at the county level at least for the time that this paper is written (summer 2021). Second, and similar to others (Luo et al., 2021; Snyder and Parks, 2020), we did not account for different containment policies applied across the US. Although shelter-in-place orders, lockdowns, and social distancing varied, it would be beyond the scopes of this study to systematically analyse these differences across space (counties) and time (duration and stringency). To account for this limitation, we analysed cumulative data referring to the end of the first year of the epidemic. We expect that gradually people would take precautions not only because they were ordered but mainly due to the public sentiment for protection. Therefore, analysing data for the first year could partially address this limitation. However, future research should also include the policy measures and how they affected COVID-19 death rate. Lastly, another limitation is that COVID-19 deaths at any given time may be underreported (Fineberg 2020). For example, people dying at home from COVID-19, may not have been tested for the virus and as such their death is attributed to other reasons. Although COVID-19 deaths may be underestimated, we expect this will not change the relationship between risk factors and death rate. Thus, we assume that our results are not biased as we did not conduct a predictive analysis but an exploratory one. For this reason, and similar to others (Andersen et al., 2021; Stokes et al., 2020), we rely on the confirmed COVID-19 deaths at the county level.
5. Conclusions
Machine learning has been widely used to analyse the dynamics of COVID-19 and identify the critical risk factors that contribute to higher mortality rates (Roy and Ghosh, 2020). At present, existing works that study the spatial variation of COVID-19 deaths use mostly linear spatial machine learning methods (i.e., geographically weighted regression). However, assuming that relations of risk factors to COVID-19 mortality are linear cannot be easily justified due to the imbalanced distribution of COVID-19 deaths and the complex interrelations with its risk factors (Luo et al., 2021). We apply a non-linear non-parametric geographical random forest model that can address both spatial heterogeneity and non-linear relationships. By examining how the importance of risk factors spatially varies, we found that different factors are associated with the COVID-19 death rate across the continental US. This shows that GRF, due to its capability to handle spatial heterogeneity, can identify how factors' importance spatially varies. This is more straightforward to inform policymaking compared to local coefficients that linear regression models provide. For example, our findings imply that local and regional governments (mainly in the West region) should encourage physical activities during COVID-19 epidemic as their absence is the primary important factor for high COVID-19 death rates. Additionally, we show that lack of medical insurance is the most important factor in 34.86% of the US counties. Governments should focus more on improving social security systems and invest more on medical insurance so that people get adequate and affordable medical treatment.
Concluding, county, state, and national policies and health specialists can benefit from such results by examining the local factors that are more likely to be associated with COVID-19 death rate, increasing their ability to respond timely. In this sense, prevention approaches and disease pharmaceutical or non-pharmaceutical interventions can be tailored and, hopefully, more effective in saving lives.
Funding
No funding
Declaration of competing interest
The authors declare no conflict of interest.
References
- Ahmed F., Ahmed N.E., Pissarides C., Stiglitz J. Why inequality could spread COVID-19. Lancet Public Health. 2020;5:e240. doi: 10.1016/S2468-2667(20)30085-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ali J., Khan R., Ahmad N., Maqsood I. Random forests and decision trees. Int. J. Comput. Scie. Issues (IJCSI). 2012;9(5):272. [Google Scholar]
- Altman N., Krzywinski M. Ensemble methods: bagging and random forests. Nat. Methods. 2017;14(10):933–935. [Google Scholar]
- Andersen L.M., Harden S.R., Sugg M.M., Runkle J.D., Lundquist T.E. Analyzing the spatial determinants of local Covid-19 transmission in the United States. Sci. Total Environ. 2021;754:142396. doi: 10.1016/j.scitotenv.2020.142396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andreopoulos P., Kalogeropoulos K., Tragaki A., Stathopoulos N. Could historical mortality data predict mortality due to unexpected events? ISPRS Int. Geo-Inf. 2021;10:283. [Google Scholar]
- Bannick M.S., McGaughey M., Flaxman A.D. Ensemble modelling in descriptive epidemiology: burden of disease estimation. Int. J. Epidemiol. 2020;49:2065–2073. doi: 10.1093/ije/dyz223. [DOI] [PubMed] [Google Scholar]
- Bartsch S.M., Ferguson M.C., McKinnell J.A., O'Shea K.J., Wedlock P.T., Siegmund S.S., Lee B.Y. The potential health care costs and resource use associated with COVID-19 in the United States. Health Aff. 2020;39:927–935. doi: 10.1377/hlthaff.2020.00426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batty M. The Coronavirus crisis: what will the post-pandemic city look like? Environment and Planning B: Urban Anal. City Sci. 2020;47(4):547–552. [Google Scholar]
- Baum C.F., Henry B. Vol. 1009. Boston College Working Papers in Economics; 2020. Socioeconomic factors influencing the spatial spread of COVID-19 in the United States; p. 2020.https://ideas.repec.org/p/boc/bocoec/1009.html [Google Scholar]
- Breiman L. Random forests. Mach. Learn. 2001;45:5–32. [Google Scholar]
- Brooks S.K., Webster R.K., Smith L.E., Woodland L., Wessely S., Greenberg N., Rubin G.J. The psychological impact of quarantine and how to reduce it: rapid review of the evidence. Lancet. 2020;395:912–920. doi: 10.1016/S0140-6736(20)30460-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownlee J. eBook; 2020. Statistical Methods for Machine Learning.https://machinelearningmastery.com/statistics_for_machine_learning/ [Google Scholar]
- Carozzi F., Provenzano S., Roth S. 2020. Urban Density and Covid-19.https://ssrn.com/absract=3643204 IZA Discussion Paper No. 134402020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catani F., Lagomarsino D., Segoni S., Tofani V. Landslide susceptibility estimation by random forests technique: sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013;13:2815–2831. [Google Scholar]
- CDC Centers for Disease Control and Prevention . 2020. Leading indicators for chronic diseases and risk factors.https://chronicdata.cdc.gov/ Available online. [Google Scholar]
- CDC Centers for Disease Control and Prevention . 2020. COVID-19 hospitalization and death by age.https://www.cdc.gov/coronavirus/2019-ncov/covid-data/investigations-discovery/hospitalization-death-by-age.html Available online. [Google Scholar]
- CDC Centers for Disease Control and Prevention . 2021. CDC COVID data tracker.https://covid.cdc.gov/covid-data-tracker/#demographics Available online: accessed 17 May. [Google Scholar]
- Desmet K., Wacziarg R. Understanding spatial variation in COVID-19 across the United States. J. Urban Econ. 2021:103332. doi: 10.1016/j.jue.2021.103332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowd J.B., Andriano L., Brazel D.M., Rotondi V., Block P., Ding X., Liu Y., Mills M.C. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. U.S.A. 2020;117:9696–9698. doi: 10.1073/pnas.2004911117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feinhandler I., Cilento B., Beauvais B., Harrop J., Fulton L. In Healthcare; Multidisciplinary Digital Publishing Institute. Vol. 8. 2020. Predictors of death rate during the COVID-19 pandemic; p. 339. 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fielding-Miller R.K., Sundaram M.E., Brouwer K. Social determinants of COVID-19 mortality at the county level. PLoS One. 2020;15 doi: 10.1371/journal.pone.0240151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fineberg H.V. The toll of covid-19. JAMA. 2020;324:1502–1503. doi: 10.1001/jama.2020.20019. [DOI] [PubMed] [Google Scholar]
- Florida R . 2019. The real powerhouses that drive the world's economy.https://www.bloomberg.com/news/articles/2019-02-28/mapping-the-mega-regions-powering-the-world-s-economy Available online: [Google Scholar]
- Friedman J.H. Greedy function approximation: a gradient boosting machine. Ann. Stat. 2001;29(5):1189–1232. [Google Scholar]
- Fu X., Zhai W. Examining the spatial and temporal relationship between social vulnerability and stay-at-home behaviors in New York City during the COVID-19 pandemic. Sustain. Cities Soc. 2021;67:102757. doi: 10.1016/j.scs.2021.102757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gallicchio C., Martín-Guerrero J.D., Micheli A., Soria-Olivas E. 2017. Randomized machine learning approaches: recent developments and challenges.http://www.i6doc.com/en/ ESANN 2017 Proceedings, European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), 26-28 April. i6doc.com publ., ISBN 978-287587039-1. Available from: [Google Scholar]
- Georganos S., Grippa T., Vanhuysse S., Lennert M., Shimoni M., Kalogirou S., Wolff E. Less is more: optimizing classification performance through feature selection in a very-high-resolution remote sensing object-based urban application. GIScience Remote Sens. 2018;55(2):221–242. [Google Scholar]
- Georganos S., Grippa T., Niang Gadiaga A., Linard C., Lennert M., Vanhuysse S., Mboga N., Wolff E., Kalogirou S. Geographical random forests: a spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021;36:121–136. [Google Scholar]
- Ghahramani M., Pilla F. Leveraging artificial intelligence to analyze the COVID-19 distribution pattern based on socio-economic determinants. Sustain. Cities Soc. 2021;69:102848. doi: 10.1016/j.scs.2021.102848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gregorutti B., Michel B., Saint-Pierre P. Correlation and variable importance in random forests. Stat. Comput. 2017;27:659–678. [Google Scholar]
- Grekousis G. Artificial neural networks and deep learning in urban geography: a systematic review and meta-analysis. Comput. Environ. Urban Syst. 2019;74:244–256. [Google Scholar]
- Grekousis G. Cambridge University Press; 2020. Spatial Analysis Methods and Practice: Describe–Explore–Explain through GIS. [Google Scholar]
- Grekousis G. Local fuzzy geographically weighted clustering: a new method for geodemographic segmentation. Int. J. Geogr. Inf. Sci. 2021;35:152–174. [Google Scholar]
- Grekousis G., Liu Y. Where will the next emergency event occur? Predicting ambulance demand in emergency medical services using artificial intelligence. Comput. Environ. Urban Syst. 2019;76:110–122. [Google Scholar]
- Grekousis G., Liu Y. Digital contact tracing, community uptake, and proximity awareness technology to fight COVID-19: a systematic review. Sustain. Cities Soc. 2021;71:102995. doi: 10.1016/j.scs.2021.102995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grekousis G., Wang R., Liu Y. Applied Geography; 2021. Mapping the Geodemographics of Racial, Economic, Health, and COVID-19 Deaths Inequalities in the Conterminous US; p. 102558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamidi S., Sabouri S., Ewing R. Does density aggravate the COVID-19 pandemic? Early findings and lessons for planners. J. Am. Plann. Assoc. 2020;86:495–509. [Google Scholar]
- Huang B., Xiao T., Grekousis G., Zhao H., He J., Dong G., Liu Y. Greenness-air pollution-physical activity-hypertension association among middle-aged and older adults: evidence from urban and rural China. Environ. Res. 2021;195:110836. doi: 10.1016/j.envres.2021.110836. [DOI] [PubMed] [Google Scholar]
- Janitza S., Hornung R. On the overestimation of random forest's out-of-bag error. PLoS One. 2018;13(8) doi: 10.1371/journal.pone.0201904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kalisky S., Mani A. 2019. How gis and machine learning work together.https://www.esri.com/content/dam/esrisites/en-us/about/events/media/UC-2019/technical-workshops/tw-6165-494.pdf Available online: [Google Scholar]
- Kalogirou S., Georganos S. 2019. SpatialML, R package.https://cran.r-project.org/web/packages/SpatialML/SpatialML.pdf Available online: [Google Scholar]
- Lak A., Sharifi A., Badr S., Zali A., Maher A., Mostafavi E., Khalili D. Spatio-temporal patterns of the COVID-19 pandemic, and place-based influential factors at the neighborhood scale in tehran. Sustain. Cities Soc. 2021:103034. doi: 10.1016/j.scs.2021.103034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecun Y., Bengio Y., Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- Liaw A., Wiener M. Classification and regression by randomForest. R. News. 2002;2:18–22. [Google Scholar]
- Lippi G., Henry B.M., Sanchis-Gomar F. Physical inactivity and cardiovascular disease at the time of coronavirus disease 2019 (COVID-19) Eur. J. Prev. Cardiol. 2020;27:906–908. doi: 10.1177/2047487320916823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y., Wang R., Grekousis G., Liu Y., Yuan Y., Li Z. Neighbourhood greenness and mental wellbeing in Guangzhou, China: what are the pathways? Landsc. Urban Plann. 2019;190:103602. [Google Scholar]
- Luo Y., Yan J., McClure S. Distribution of the environmental and socioeconomic risk factors on COVID-19 death rate across continental USA: a spatial non-linear analysis. Environ. Sci. Pollut. Res. 2021;28:6587–6599. doi: 10.1007/s11356-020-10962-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maiti A., Zhang Q., Sannigrahi S., Pramanik S., Chakraborti S., Cerda A., Pilla F. Exploring spatiotemporal effects of the driving factors on COVID-19 incidences in the contiguous United States. Sustain. Cities Soc. 2021;68:102784. doi: 10.1016/j.scs.2021.102784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansour S., Al Kindi A., Al-Said A., Al-Said A., Atkinson P. Sociodemographic determinants of COVID-19 incidence rates in Oman: geospatial modelling using multiscale geographically weighted regression (MGWR) Sustain. Cities Soc. 2021;65:102627. doi: 10.1016/j.scs.2020.102627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell T. McGraw Hill; Boston,USA: 1997. Machine Learning. [Google Scholar]
- Mollalo A., Vahedi B., Rivera K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020;728:138884. doi: 10.1016/j.scitotenv.2020.138884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollalo A., Rivera K.M., Vahabi N. Spatial statistical analysis of pre-existing mortalities of 20 diseases with COVID-19 mortalities in the continental United States. Sustain. Cities Soc. 2021;67:102738. doi: 10.1016/j.scs.2021.102738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Núñez-Gil I.J., Fernández-Ortiz A., Eid C.M., Huang J., Romero R., Becerra-Muñoz V.M., Uribarri A., Feltes G., Trabatoni D., Fernandez-Rozas I., Viana-Llamas M.C. Underlying heart diseases and acute COVID-19 outcomes. Cardiol. J. 2021;28:202–214. doi: 10.5603/CJ.a2020.0183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ong E., Wong M.U., Huffman A., He Y. COVID-19 coronavirus vaccine design using reverse vaccinology and machine learning. Front. Immunol. 2020;11:1581. doi: 10.3389/fimmu.2020.01581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patanavanich R., Glantz S.A. Smoking is associated with COVID-19 progression: a meta-analysis. Nicotine Tob. Res. 2020;22:1653–1656. doi: 10.1093/ntr/ntaa082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pourhoseingholi M.A., Baghestani A.R., Vahedi M. Vol. 5. 2012. How to control confounding effects by statistical analysis. Gastroenterology and hepatology from bed to bench; p. 79. (2) [PMC free article] [PubMed] [Google Scholar]
- Pradhan A.M.S., Kim Y.T. Rainfall-induced shallow landslide susceptibility mapping at two adjacent catchments using advanced machine learning algorithms. ISPRS Int. Geo-Inf. 2020;9:569. [Google Scholar]
- Quiñones S., Goyal A., Ahmed Z.U. Geographically weighted machine learning model for untangling spatial heterogeneity of type 2 diabetes mellitus (T2D) prevalence in the USA. Sci. Rep. 2021;11(1):1–13. doi: 10.1038/s41598-021-85381-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randhawa G.S., Soltysiak M.P., El Roz H., de Souza C.P., Hill K.A., Kari L. Machine learning using intrinsic genomic signatures for rapid classification of novel pathogens: COVID-19 case study. PLoS One. 2020;15 doi: 10.1371/journal.pone.0232391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Razzaghi H., Wang Y., Lu H., Marshall K.E., Dowling N.F., Paz-Bailey G., Twentyman E.R., Peacock G., Greenlund K.J. Estimated county-level prevalence of selected underlying medical conditions associated with increased risk for severe COVID-19 illness—United States, 2018. MMWR Morb. Mortal. Wkly. Rep. 2020;69:945. doi: 10.15585/mmwr.mm6929a1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy R.K., Charles W.N., Sklavounos A., Dutt A., Seed P.T., Khajuria A. The effect of smoking on COVID, A.ia, A.ajuria, A.Kari, L. Machine learning using i. J. Med. Virol. 2021;93:1045–1056. doi: 10.1002/jmv.26389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy S., Ghosh P. Factors affecting COVID-19 infected and death rates inform lockdown-related policymaking. PLoS One. 2020;15 doi: 10.1371/journal.pone.0241165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sannigrahi S., Pilla F., Basu B., Basu A.S., Molter A. Examining the association between socio-demographic composition and COVID-19 fatalities in the European region using spatial regression approach. Sustain. Cities Soc. 2020;62:102418. doi: 10.1016/j.scs.2020.102418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seto C., Khademi A., Graif C., Honavar V.G. 2021. Commuting Network Spillovers and COVID-19 Deaths across US Counties. arXiv. arXiv:2010.01101. [Google Scholar]
- Snyder B.F., Parks V. Spatial variation in socio-ecological vulnerability to Covid-19 in the contiguous United States. Health Place. 2020;66:102471. doi: 10.1016/j.healthplace.2020.102471. [DOI] [PubMed] [Google Scholar]
- Stokes E.K., Zambrano L.D., Anderson K.N., Marder E.P., Raz K.M., Felix S.E.B., Tie Y., Fullerton K.E. Coronavirus disease 2019 case surveillance—United States, January 22–May 30, 2020. MMWR Morb. Mortal. Wkly. Rep. 2020;69:759. doi: 10.15585/mmwr.mm6924e2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strobl C., Lb A., Kneib T., Augustin T.A.Z. Conditional variable importance for random forests. BMC Bioinf. 2008;9:307. doi: 10.1186/1471-2105-9-307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sujath R., Chatterjee J.M., Hassanien A.E. A machine learning forecasting model for COVID-19 pandemic in India. Stoch. Environ. Res. Risk Assess. 2020;34:959–972. doi: 10.1007/s00477-020-01827-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun F., Matthews S.A., Yang T.C., Hu M.H. A spatial analysis of the COVID-19 period prevalence in US counties through June 28, 2020: where geography matters? Ann. Epidemiol. 2020;52:54–59. doi: 10.1016/j.annepidem.2020.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toloşi L., Lengauer T. Classification with correlated features: unreliability of feature ranking and solutions. Bioinformatics. 2011;27:1986–1994. doi: 10.1093/bioinformatics/btr300. [DOI] [PubMed] [Google Scholar]
- Torrats-Espinosa G. Using machine learning to estimate the effect of racial segregation on COVID-19 mortality in the United States. Proc. Natl. Acad. Sci. U.S.A. 2021;118 doi: 10.1073/pnas.2015577118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- United Nations . 2020. Liquidity and debt solutions to invest in the SDGs: the time to act is now.https://www.un.org/sites/un2.un.org/files/sg_ policy_brief_on_liquidity_and_debt_solutions_march_2021.pdf Available online: [Google Scholar]
- US Census Bureau . 2021. Census Bureau's MAF/TIGER geographic database. Available online: https://www.census.gov/geographies/mapping-files/time-series/geo/carto-boundary-file.html. accessed on 20 January. [Google Scholar]
- US Census Bureau . 2021. 2015-2019 American community Survey 5-year estimates.https://data.census.gov/cedsci/ Available online: accessed on 10 February. [Google Scholar]
- USAFacts . 2021. US Coronavirus cases and deaths.https://usafacts.org/visualizations/coronavirus-covid-19-spread-map/ Available online: accessed on 10 February. [Google Scholar]
- Verhagen M.D., Brazel D.M., Dowd J.B., Kashnitsky I., Mills M. 2020. Mapping hospital demand: demographics, spatial variation, and the risk of “hospital deserts” during COVID-19 in England and Wales. OSF Preprints. [DOI] [Google Scholar]
- Wang R., Liu Y., Lu Y., Zhang J., Liu P., Yao Y., Grekousis G. Perceptions of built environment and health outcomes for older Chinese in Beijing: a big data approach with street view images and deep learning technique. Comput. Environ. Urban Syst. 2019;78:101386. [Google Scholar]
- Werner M., Dax G., Laass M. 2021. Computational Challenges for Artificial Intelligence and Machine Learning in Environmental Research. INFORMATIK 2020. [Google Scholar]
- Yancy C.W. COVID-19 and african americans. JAMA. 2020;323:1891–1892. doi: 10.1001/jama.2020.6548. [DOI] [PubMed] [Google Scholar]
- Yang Z., Zeng Z., Wang K., Wong S.S., Liang W., Zanin M., Liu P., Cao X., Gao Z., Mai Z., Liang J. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020;12:165. doi: 10.21037/jtd.2020.02.64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaccardi F., et al. Non-linear association of BMI with all-cause and cardiovascular mortality in type 2 diabetes mellitus: a systematic review and meta-analysis of 414,587 participants in prospective studies. Diabetologia. 2017;60:240–248. doi: 10.1007/s00125-016-4162-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhai W., Liu M., Fu X., Peng Z.R. American inequality meets COVID-19: uneven spread of the disease across communities. Ann. Assoc. Am. Geogr. 2021:1–21. [Google Scholar]
- Zhao Y., Chen F., Zhai R., Lin X., Wang Z., Su L., Christiani D.C. Correction for population stratification in random forest analysis. Int. J. Epidemiol. 2012;41(6):1798–1806. doi: 10.1093/ije/dys183. [DOI] [PMC free article] [PubMed] [Google Scholar]