Abstract
The post-COVID-19 period is likely to be characterised by an intensified stabilisation-sustainability trade-off. This paper revisits the design of the Stability and Growth Pact’s debt rule in the context of two debates on fiscal policies: first, the implications of the low interest environment for debt sustainability and the appropriate interaction of fiscal and monetary policies and, second, the reform of the EU fiscal governance framework. In both debates the choice of government debt anchor and the speed of adjustment take centre stage. The debt rule appears predestined to fulfil the role of debt anchor. However, our analysis shows that its existing design gives rise to a pro-cyclical bias that has hampered its implementation in a low-growth and inflation environment. We propose two parametric changes to better balance the objectives of macroeconomic stabilisation and debt sustainability: first, accounting for persistent deviations of inflation from the central bank’s target; and, second, a reduced speed of adjustment. Putting a reformed debt rule at the centre of the EU fiscal governance framework would allow reducing the latter’s complexity without the need to revise the EU Treaties.
Keywords: COVID-19, Debt overhang, Interest rates, Fiscal policy, Public debt sustainability, Fiscal rules, Fiscal governance
1. Introduction
Government debt ratios are set to increase significantly in the wake of COVID-19. An intensified stabilisation-sustainability trade-off is therefore to be expected in the coming years – notably in countries with high government debt ratios – since fiscal policies will need to square the goals of supporting the post-crisis recovery while addressing debt overhangs.
In this context, the present paper links to two ongoing debates on fiscal policies: first, the implications of low interest-rate growth differentials for debt sustainability and the appropriate interaction of fiscal and monetary policy, second, the reform of the EU fiscal governance framework. In both debates the choice of government debt anchor and the speed of adjustment towards the target value take centre stage. Regarding the calibration of fiscal adjustment, political-economy constraints are an important factor when assessing debt policies in practice. Empirical evidence on fiscal fatigue (Ghosh et al., 2013) and scarce historical examples of debt adjustments based on persistent and very large primary budgetary surpluses (see, e.g., Eichengreen and Panizza, 2016) suggest that feasibility constraints need to be reflected in the parametrisation of fiscal rules in order to ensure political implementability. At the same time, the literature on the political economy of budgetary institutions typically finds that stronger budgeting procedures and more stringent fiscal rules contribute to fiscal discipline and restrain government debt (e.g. Hallerberg et al., 2007; Reuter, 2015; Bergman et al., 2016; Reuter, 2019).
From an economic point of view there is widespread agreement that fiscal policies have to ensure debt sustainability, while contributing to macroeconomic stabilisation. However, there is less agreement on the optimal pace of debt adjustment, especially in the current environment characterised by low interest-growth differentials. For example, Blanchard (2019) recently argued that a longer-term outlook of (safe) interest rates below GDP growth rates implies that the issuance of public debt comes without fiscal costs. In the absence of a binding inter-temporal budget constraint welfare costs of issuing public debt may be low, calling for a reassessment of appropriate debt policies and fiscal frameworks (Blanchard et al., 2019). The theoretical literature in general suggests a low pace of debt adjustment is optimal in the absence of sovereign risk (see, e.g., Benigno and Woodford, 2004 and Schmitt-Grohé and Uribe, 2004). However, if public debt is perceived as risky, the presence of multiple equilibria and possible expectation-driven increases in interest rates may call for a relatively swift adjustment to prudent levels of debt (see, e.g., Calvo, 1988; Corsetti et al., 2014; Cantore et al., 2017 and Lorenzoni and Werning, 2019). This latter point is particularly relevant for European Monetary Union (EMU), where several countries have experienced significant and volatile spreads vis-à-vis the German Bund since the financial crisis, suggesting that sovereign risk considerations need to be factored in when designing optimal debt policies in EMU.
While there is thus a controversial debate in the theoretical literature on the optimal design of debt feedback rules, there is widespread agreement that debt rather than deficits should have the anchoring function in fiscal rules. Also, there seems to be an emerging consensus in the policy domain that a revised fiscal framework should be centred on such a debt anchor but combined with an operational target in the form of an expenditure rule (see, e.g., European Fiscal Board, 2018 and Bénassy-Quéré et al., 2018). At first sight, this would suggest that the EU fiscal framework’s debt rule introduced in 2011 should take centre stage in a reform towards simplification of the framework, which is widely seen as necessary (see e.g. Juncker et al., 2015; European Commission, 2017; Deroose et al., 2018; European Fiscal Board, 2019; Kamps and Leiner-Killinger, 2019; Debrun and Jonung, 2019 and European Commission, 2020). The debt rule was introduced in the fiscal framework precisely to strengthen the focus on debt ratios, by a concrete operationalisation of the European Treaty’s 60% of GDP debt criterion. Concretely, the debt rule requires EU Member States with debt ratios above 60% to reduce the excess over the debt criterion by one twentieth per year. However, in practice the debt rule has hardly played a role in the implementation of the EU fiscal framework, partly due to shortfalls in fiscal consolidation but also due to its inbuilt pro-cyclicality, with requirements increasing significantly in a low-growth and low-inflation environment (see, e.g., European Central Bank, 2016a), leading to complaints that strict implementation of the debt rule would be self-defeating (see e.g. European Commission, 2019a, p. 15)
In the main body of this paper we first present a stylised model to highlight the main economic trade-offs related to the adjustment of government debt. While simple, the framework captures the main features of fiscal rules typically also present in more sophisticated general equilibrium frameworks. A fiscal reaction function is derived to economically assess the SGP’s debt rule, highlighting the inbuilt pro-cyclicality of adjustment requirements under the current parametrisation. Backward-looking simulations over the period 1999–2019 provide ample evidence for the pro-cyclicality of the debt rule both in economic good times and bad times. In particular, a major shortcoming of the existing debt rule is the failure to account for persistent deviations of inflation from the central bank’s price stability objective. We show that the overshooting of inflation in a number of EMU Member States ahead of the financial crisis created a false impression of safety, while the undershooting of inflation after the crisis in several EMU Member States significantly tightened requirements under the existing debt rule. In both situations the existing debt rule was not consistent with an effective backing of fiscal policy for monetary policy in the latter’s pursuit of its price stability objective.
We propose a set of parametric changes to the SGP debt rule with a view to better integrating macroeconomic stabilisation considerations and longer-term fiscal sustainability concerns. The former are taken into account through a “nominal” cyclical adjustment which corrects for fluctuations of nominal GDP growth around a country’s real GDP growth potential and the ECB’s price stability objective.1 The proposed approach goes beyond the current method by not only removing the impact of the (real) cyclical components of headline budget balances but also adjusting the accumulation of debt for snowball effects related to nominal growth diverging from the real GDP growth potential plus a 2% trend inflation component. This serves two purposes. First, adjusting the accumulation of debt for positive and negative deviations from trend inflation reinforces the counter-cyclical modulation of adjustment requirements. Second, if implemented and adhered to, our approach would help to better align fiscal policies in euro area Member States with the ECB’s monetary policy objective to achieve price stability, thereby promoting a better macroeconomic policy-mix. Using a standard New Keynesian framework, Hauptmeier et al. (2022) show that a fiscal policy rule that targets both output and inflation gaps counter-cyclically increases welfare by reducing the frequency of lower bound episodes and related economic distortions.
Simulation analysis for euro area countries suggests that the proposed “nominal” cyclical adjustment would significantly smoothen adjustment requirements compared to the status quo without impairing the debt sustainability objective. Our simulations also suggest that for countries with very high debt the “1/20” adjustment speed of the current framework becomes particularly demanding when growth is persistently low. Therefore, in order to avoid that fiscal adjustment becomes self-defeating, the speed of adjustment under the debt rule could be reduced from currently 5% of the distance to the debt reference value to, for example, 3%. In order to assess the sensitivity of our simulations to the underlying macroeconomic assumptions we show two “low for long” scenarios which assume that inflation and interest rates, respectively, remain at the presently low levels for an extended period of time. Given that our “nominal” cyclical adjustment approach filters out the cumulative impact of inflation differentials vis-à-vis 2%, the resulting adjustment requirements are insulated from inflation shocks.
Our paper offers the following lessons for the debate on reforming the EU fiscal framework. First, our proposal for a reform of the SGP’s debt rule offers a way to address its economic weaknesses and to put it at the centre of a revised EU fiscal framework. All other elements of the framework should be made consistent with the newly designed debt rule. For example, the so-called medium term objectives should be adjusted to be consistent with achieving the debt target at the recommended speed of adjustment, and the same applies for an expenditure rule should this be made the operational target. Our paper is agnostic on whether a structural balance rule or a expenditure rules should be made the single operational target under a revised framework; both would work in principle if aligned with the requirements of our debt rule proposal, which would provide the anchor.2
Second, focussing the fiscal framework on the achievement of a debt target would create fiscal space compared to the current framework.3 This space could be used to finance public investment in priority areas such as climate change, digitalisation, infrastructure and research and development. While there have been calls for a specific treatment of public investment under the existing SGP framework (see, e.g., European Fiscal Board, 2019 and Blanchard et al., 2019), this would risk in a further complication rather than simplification of the framework. A symmetric treatment of the 60% of GDP reference level, by implying convergence towards the fiscal anchor also from below, may be an alternative way to create budgetary room for additional investment, and this without the need for special exemptions. Such symmetric treatment could also be useful in a situation where monetary policy reaches the effective lower bound and debt dynamics move towards an undershooting of the debt target as was the case in a number of euro area countries before the COVID-19 crisis. Fiscal policy would thus support monetary policy in such circumstances, allowing the latter to achieve its goal faster and with fewer side effects (Lagarde, 2019).
Third, our proposal does not require revisions of EU primary law. Article 126 of the Treaty on the Functioning of the European Union, which focusses on the identification of “gross policy errors”, would not need to be amended, and the 60% of GDP debt reference value would be preserved. Instead, secondary legislation would need to be adjusted to give more prominence to the debt rule and to amend its parametrisation. In addition, the medium-term objectives – if retained – should be modified such as to ensure consistency with the desired speed of adjustment to the debt target, and the same would apply for the expenditure benchmark — again, if retained.
The remainder of the paper is organised as follows. Section 2 first discusses the economic literature on the optimal pace of debt adjustment and presents a stylised model that highlights the main economic trade-offs. These are then linked to the basic setup of the SGP’s debt rule. A description of the current framework is then provided in Section 3 before turning to our proposal for a “nominal” cyclical adjustment approach and comparing it to the status quo. Section 4 explains the simulation approach and presents backward- and forward-looking debt simulations for selected euro area countries, highlighting the impact of a number of changes both to the parametric settings of the debt rule as well as the underlying macroeconomic assumptions. Conclusions are drawn in Section 5.
2. The (political-)economics of debt adjustment
The literature on the political economy of budgetary institutions typically finds that stronger budgeting procedures and more stringent fiscal rules contribute to fiscal discipline and restrain government debt (e.g. Hallerberg et al., 2007; Reuter, 2015; Bergman et al., 2016; Reuter, 2019). In a monetary union setting, Muscatelli et al. (2012) argue that such fiscal rules should focus on longer-term debt rather than short-term nominal deficit targets since the latter imply inefficient stabilisation in the face of adverse shocks and therefore pro-cyclicality. Uniform deficit targets – as the ones contained in the SGP framework – are achieved without significant government effort in economic good times but require pro-cyclical tightening during cyclical downswings. At the same time, the one-size fits all approach linked to deficit targets imposes relatively stronger fiscal discipline on countries with low debt and – as a result – more limited sustainability risk.
From an economic point of view, the optimal speed of debt reduction depends on an evaluation of the trade-off between risks related to elevated debt levels on the one hand and the objective of fiscal policy to provide macroeconomic stabilisation in economic downturns on the other. Theory suggests that in the absence of sovereign risk government debt optimally follows a near random walk process to avoid short-term volatility in taxes and prices (see, e.g., Benigno and Woodford, 2004 and Schmitt-Grohé and Uribe, 2004). The presence of sovereign risk however provides incentives to reduce government debt and related vulnerabilities (Adam, 2011, Cantore et al., 2017, Lorenzoni and Werning, 2019). Iara and Wolff (2014) provide evidence for euro area countries suggesting that stronger fiscal rules in euro area countries tend to reduce sovereign risk premia in the presence of market stress.
The macroeconomic stabilisation objective of fiscal policies on the other hand is reinforced in a low interest rate environment (Blanchard, 2019; Coenen et al., 2020) when the central bank can be expected to operate in proximity to the effective lower bound on nominal interest rates more frequently.4 At the same time, such circumstances render fiscal policy more effective as a stabilisation tool (e.g. Christiano et al., 2011). The report of the Work stream on monetary-fiscal policy interactions (2021) in the context of the ECB’s strategic review discusses the interplay between both policies with a particular focus on lower bound episodes, suggesting that a proper synchronisation can support a swifter achievement of macroeconomic stabilisation objectives.
Besides purely economic considerations, political-economy constraints are an important factor when assessing debt policies and the speed of debt adjustment in practice. Empirical evidence suggests a declining sensitivity of the primary balance to increases in debt (Ghosh et al., 2013). Such fiscal fatigue may reflect feasibility constraints which would need to be reflected in the parametrisation of fiscal rules to ensure implementability. Eichengreen and Panizza (2016) provide historical evidence suggesting that debt adjustments based on persistent and very large primary budgetary surpluses are rare. Since such surpluses constitute a common pool they are difficult to maintain in the absence of strong budgetary institutions (see, e.g., de Haan et al., 2013).
2.1. Optimal debt adjustment — conceptual considerations
Below we present a stylised model which aims to capture the main economic trade-offs related to the adjustment of government debt (see also Kanda, 2011 and Carnot, 2014). The starting point is the standard debt accumulation equation
| (1) |
where , and label the initial debt-to-GDP ratio, nominal GDP growth and the primary balance-to-GDP ratio, respectively. Abstracting from stock flow adjustments, debt at time depends on the size of two terms: First, the lagged debt ratio multiplied with the growth-adjusted interest rate , where
| (2) |
The (implicit) interest rate captures a benchmark rate plus a spread that depends on the deviation of debt in the previous year from the debt target . The debt target could for instance reflect a level of debt that ensures a sufficient safety margin with respect to the fiscal limit (Bi, 2012). In our stylised framework, we let the interest rate spread increase linearly with the distance to the debt target. While typically the literature assumes non-linearity (e.g. Cantore et al., 2017), our simple approach is sufficient to introduce the notion of sovereign risk and therefore to create an economic incentive to reduce government debt. quantifies the interest sensitivity to the debt overhang. Second, the primary balance ratio can be decomposed into a structural and cyclical component:
| (3) |
where labels the cyclically-adjusted primary budget balance ratio and , the cyclical sensitivity of the budget balance, times , the output gap, captures the operation of automatic fiscal stabilisers. The output gap evolves according to the dynamic equation
| (4) |
where denotes the speed of output gap closure. and label the fiscal multiplier and the fiscal stance (discretionary fiscal policy action), respectively.
The fiscal policy maker is assumed to minimise the following quadratic loss function when setting the fiscal stance
| (5) |
This setup captures the trade-off between, on the one hand, cyclical considerations reflected by the weight and, on the other hand, debt sustainability considerations which receive a weight , assuming . Differentiation with respect to the fiscal stance () and plugging in (2), (3), (4) gives the following fiscal reaction function5
| (6) |
where
| (7) |
| (8) |
The implications of the initial cyclical conditions in the fiscal reaction function (6) are not clear-cut. This relates to the fact that the loss function on the one hand penalises negative and positive output gaps while increasing output gaps are generally desirable from a fiscal sustainability point of view given that larger cyclical components improve the budget balance. The relative importance of these two channels depends on the relative weighting of the loss function objectives but also on the sensitivity of the budget to cyclical conditions and the size of the fiscal multiplier . As an example, let us assume that the government assigns equal weight to both the stabilisation and sustainability objective, i.e. . Moreover, setting in line with the European Commission’s 2018 estimate for the average budgetary sensitivity in euro area countries implies that for . Under these relatively plausible assumptions the optimal fiscal stance would be contractionary (expansionary) in the presence of a positive (negative) initial output gap.
Turing to the second term on the right-hand side of Eq. (6), we assume that , therefore ruling out self-defeating fiscal consolidation.6 This implies that . The optimal fiscal stance will depend on several factors influencing debt sustainability. Along the lines of Blanchard (2019), the differential between the benchmark interest rate and the growth rate of the economy will, if negative, point towards a less restrictive fiscal stance, all other things equal (first term in square brackets on the right-hand side of Eq. (6)). In the opposite direction, sovereign risk premia, captured by the parameter , will point towards a more restrictive fiscal stance when the initial debt ratio is above the debt target (second term in square brackets on the right-hand side of Eq. (6)). Finally, the need for fiscal adjustment declines with the initial cyclically-adjusted primary balance ().
2.2. Debt rule design and pro-cyclicality
In view of the analysis of the functioning of the European debt rule in the remainder of this paper it is useful to formulate the following debt motion equation which captures the different components of debt adjustment.
| (9) |
At this stage we introduce a stylised debt rule which captures the main features of the European framework which is described in detail in Section 3. The parameter labels the speed of adjustment which is applied to the distance from the debt target . The debt adjustment is composed of four components: the fiscal policy stance (first term on the rhs of Eq. (9)), the cyclically-adjusted primary balance in (second term), the budgetary impact of the cycle (operation of automatic stabilisers; third term) and the snowball effect (fourth term). Note that the debt adjustment is not only directly affected by the cycle via the cyclical component of the budget balance but also indirectly given that higher nominal GDP growth reduces the snowball effect in the debt accumulation equation.
Given the fixed adjustment requirement, Eq. (9) implies that the fiscal policy stance will move pro-cyclically in the presence of shocks to any of the macroeconomic parameters that affect the accumulation of debt. These need to be fully absorbed by the fiscal policy stance . So in case the output gap declines, any related budgetary shortfalls, e.g. due to lower cyclical taxes, would need to be compensated for by a more restrictive fiscal stance. The same holds true for the case of lower inflation and nominal GDP growth.
Relaxing the debt adjustment rule through a cyclical modulation of in line with Eq. (6) would reduce this pro-cyclicality via two inbuilt features. First, the direct conditioning on the lagged output gap (the first term). Second, the responsiveness of the rule to both the lagged debt ratio and the debt overhang depends on the nominal trend GDP growth rate of the economy, not actual growth. Therefore, cyclical variation in nominal GDP growth is not captured in the reaction function. Favourable snow-ball effects in economic good times (related to relatively strong growth and inflation dynamics) do not imply a deceleration in the fiscal adjustment. Symmetrically, when growth and price developments weaken during recessions, causing unfavourable debt dynamics, the optimal fiscal stance according to Eq. (6) would not tighten pro-cyclically. An issue that arises in this context is which trend component to chose for price developments in order to determine the nominal trend growth rate . A straightforward choice is to link the nominal component to the inflation objective of the central bank. This would imply that the fiscal policy stance becomes less (more) contractionary in times of inflation below (above) the inflation target, implying symmetric fiscal support for the monetary policy authority to achieve the inflation objective.
2.3. Debt rule design and fiscal targets
Abstracting from cyclical considerations, i.e. assuming , Eq. (9) can be rearranged to highlight the implications of different parameter settings for primary balance targets
| (10) |
The primary balance ratio required to comply with the stylised debt rule depends in particular on the adjustment speed , the interest growth differential and the initial level of debt (). Table 1 gives an overview of primary balance targets for different parameter constellations and a debt target in line with the SGP. Five debt regimes are distinguished ranging between low debt at 30% of GDP (which implies that there is fiscal space relative to the debt target) and very high debt at 170% of GDP. In addition, primary balance targets are computed for different levels of the interest-growth differential, i.e. negative at , zero (which implies that the first term in Eq. (10) disappears) and positive at 1%. Finally, the speed of adjustment is varied between 5% (SGP 1/20 rule) and a significantly slower pace of 1%).
Table 1.
Primary balance targets.
|
|
||||||
|---|---|---|---|---|---|---|
| 30 | 60 | 100 | 140 | 170 | ||
| (1) | (2) | (3) | (4) | (5) | ||
| 0.01 | −1.2 | 0.6 | 3.0 | 5.4 | 7.2 | |
| 0.05 | 0.00 | −1.5 | 0.0 | 2.0 | 4.0 | 5.5 |
| −0.01 | −1.8 | −0.6 | 1.0 | 2.6 | 3.8 | |
| 0.01 | −0.6 | 0.6 | 2.2 | 3.8 | 5.0 | |
| 0.03 | 0.00 | −0.9 | 0.0 | 1.2 | 2.4 | 3.3 |
| −0.01 | −1.2 | −0.6 | 0.2 | 1.0 | 1.6 | |
| 0.01 | 0.0 | 0.6 | 1.4 | 2.2 | 2.8 | |
| 0.01 | 0.00 | −0.3 | 0.0 | 0.4 | 0.8 | 1.1 |
| −0.01 | −0.6 | −0.6 | −0.6 | −0.6 | −0.6 | |
Note: The calculations assume nominal growth . labels the speed of debt adjustment, the interest-growth differential and the lagged debt ratio.
Columns (1) and (2) in Table 1 show that for countries that have reached the debt target, the interest-growth differential determines the debt-stabilising primary balance ratio. In line with the arguments put forward by Blanchard (2019) a country can run persistent primary deficits if . Note that treating the 60% of GDP reference level for the debt ratio as a symmetric target would imply convergence towards the fiscal anchor from above and below. For the macroeconomic policy mix, such a symmetric treatment could be useful in a situation where monetary policy reaches the effective lower bound and debt dynamics move towards an undershooting of the debt target. In this context, Leeper (2016) emphasises the risk of asymmetric fiscal responses to monetary policy, i.e. fiscal tightening when interest rates rise, but no fiscal loosening when interest rates fall. In the latter case, fiscal policy fails to accommodate the monetary easing to raise inflation.
On the other hand from columns (4) and (5) it becomes apparent that the combination of very high debt, positive interest-growth differentials and high speed of adjustment imply quite demanding targets for the primary balance ratio which would be difficult to sustain for extended periods when factoring in fiscal fatigue (see, e.g., Ghosh et al., 2013). Here, moving to a somewhat lower pace of debt adjustment (e.g. ) could support political feasibility while ensuring significant convergence towards the debt anchor.
While in the theoretical literature on fiscal policies much of the analysis is cast in terms of the implications for the primary balance, in the policy discussion the focus often is on implications for the overall balance. The EU fiscal framework, for example, highlights two deficit levels: first, the 3% of GDP headline deficit reference value (often misunderstood to be a target in itself), the breach of which may trigger a so-called Excessive Deficit Procedure; and, second, the medium-term objective for the structural balance (which is meant to be the overarching target in the framework), which is set at a deficit no larger than 0.5% of GDP for Member States with debt above 60% of GDP and no larger than 1% of GDP for Member States with debt below 60% of GDP.
The above analysis can be easily recast in terms of the overall deficit, i.e. including interest payments. The target deficit ratio, , consistent with debt reduction at the desired pace can be written as
| (11) |
Table 2 shows the implied deficit targets for alternative values of the economy’s nominal growth rate and the initial debt ratio. As expected deficit targets are the less stringent the higher the nominal growth rate. However, the table also reveals that deficit targets get more stringent the higher the initial debt ratio only if the pace of debt reduction is larger than the steady-state nominal growth rate. It is easy to see that the deficit target is invariant to the debt ratio for .
Table 2.
Overall budget deficit targets.
|
|
||||||
|---|---|---|---|---|---|---|
| 30 | 60 | 100 | 140 | 170 | ||
| (1) | (1) | (2) | (3) | (3) | ||
| 0.035 | 2.5 | 2.0 | 1.4 | 0.7 | 0.2 | |
| 0.05 | 0.030 | 2.4 | 1.7 | 0.9 | 0.1 | −0.5 |
| 0.025 | 2.2 | 1.5 | 0.4 | −0.6 | −1.4 | |
| 0.035 | 1.9 | 2.0 | 2.2 | 2.3 | 2.4 | |
| 0.03 | 0.030 | 1.8 | 1.7 | 1.7 | 1.7 | 1.7 |
| 0.025 | 1.6 | 1.5 | 1.2 | 1.0 | 0.8 | |
| 0.035 | 1.3 | 2.0 | 3.0 | 3.9 | 4.6 | |
| 0.01 | 0.030 | 1.2 | 1.7 | 2.5 | 3.3 | 3.9 |
| 0.025 | 1.0 | 1.5 | 2.0 | 2.6 | 3.0 | |
Note: labels the speed of debt adjustment, the nominal GDP growth rate and the lagged debt ratio.
For the average euro area Member State – which has grown nominally at a rate around 3% over the EMU period – a deficit target of around 1.75% of GDP would be consistent with convergence to the reference value for a speed of adjustment of 3%. This would create space of slightly more than 1% of GDP for the average euro area Member State.7 Also, compared to the current parametrisation of the debt rule, the required tightening in the deficit target would be less drastic as either nominal growth falls short of this value or the initial debt ratio increases.
3. Debt rule design in practice
3.1. The design of the European debt rule
The Treaty on the Functioning of the European Union (TFEU) in Art. 126 specifies that compliance with the debt criterion requires a country’s debt ratio to be either below 60% of GDP or “sufficiently diminishing and approaching the reference value at a satisfactory pace”. In the context of the “Six Pack Reform” the debt criterion was operationalised in 2011. According to the so called “debt benchmark”, a country’s government debt ratio is considered sufficiently diminishing “if the differential with respect to the reference value has decreased over the previous three years at an average rate of one twentieth per year”.8 The formula for the so called “backward-looking” debt reduction benchmark reads as follows:
| (12) |
where denotes the SGP’s backward-looking debt reduction benchmark in year . Art. 2(1a) Reg. 1467/97 mentions two additional configurations for the debt reduction benchmark, i.e. a forward-looking one which covers a two-year ahead period based on a “no-policy-change” assumption and the cyclically-adjusted debt reduction benchmark whereas compliance is assessed vis-à-vis the least demanding indicator.9 The latter will be discussed in more detail in the next section.
The gap between the actual debt ratio in a given year and the debt reduction benchmark then quantifies the necessary adjustment to comply with the debt rule, i.e.
| (13) |
If an EU Member State breaches the debt reduction benchmark in a given year, i.e. if the debt ratio exceeds the benchmark value, Art. 126(3) TFEU requires the European Commission to issue a report in which it assesses whether the respective country is in compliance with the Treaty’s debt criterion. In the report the European Commission – according to Art. 2(3) Reg. 1467/97 – shall take into account all relevant factors which may significantly affect the assessment of compliance with the deficit and debt criteria, including developments in the medium-term economic and budgetary position.
To date the SGP’s debt rule has been a binding constraint mainly for countries with very high debt ratios, notably for Belgium and Italy for which the European Commission issued Art. 126(3) reports on a regular basis since 2015. While gaps in relation to the fulfilment of the debt rule have been significant in these two countries, a number of mitigating relevant factors were put forward as justification for not opening a debt-based excessive deficit procedure. Several reports argued that unfavourable economic conditions related, in particular, to low inflation and negative real growth would lead to an unwarranted fiscal tightening. This line of argument underlines the analysis shown in Section 2. Pro-cyclicality of the SGP’s debt rule has been put forward frequently as an obstacle to its effective implementation (see, e.g., European Central Bank, 2016a).
3.2. Reducing procyclicality via a “nominal” cyclical adjustment of the debt rule
The cyclical adjustment of fiscal balances is a standard method to assess the impact of the economic environment on fiscal developments. Underlying budget balances are computed by applying estimated tax and spending elasticities to the output gap and removing the resulting cyclical component (see, e.g., Mourre and Princen, 2014, and Price et al., 2014). Such cyclical adjustment is “real” in the sense that the correction takes into account deviations of real GDP from its potential. However, as discussed earlier the accumulation of government debt is not only affected by the cyclical components of the budget balance but also by developments in nominal GDP via the “denominator effect” .
As mentioned in Section 3.1, the current version of the debt rule in the Stability and Growth Pact framework includes a cyclically-adjusted configuration (see Section 2.2.1.2 in European Commission (2019b) for details) which reads as follows
| (14) |
and stand for the nominal level of debt and GDP, respectively. The growth rates of real potential GDP and the GDP deflator are denoted by and . labels the cyclical component of the budget balance. Eq. (14) shows that the cyclically-adjusted debt reduction benchmark of the SGP implies two adjustments to the debt ratio: First, the contemporaneous level of debt is corrected for the sum of the cyclical deficit components of the current and the previous two years. Second, nominal GDP in the denominator is corrected for deviations of real from potential GDP growth. This cyclical adjustment however does not take into account two factors, notably the multi-year snowball effects related to cyclical changes in primary balances (empirically rather small) and the impact of cyclical changes in inflation (empirically important). We will show in the following that the latter in particular has sizable quantitative implications for the accumulation of debt.
Note therefore that an alternative cyclical adjustment of the debt ratio could be done on the basis of the following adaptation of the standard debt accumulation equation:
| (15) |
where denotes the nominal cyclically adjusted debt ratio.10 Note that the correction of the snowball term (relative to Eq. (1)) works via two adjustments of the decomposed nominal GDP growth rate. First, the real GDP growth rate is replaced by , i.e. the growth rate of potential GDP. Second, the growth rate of the GDP deflator is replaced by the ECB’s 2% inflation target. The nominal potential growth rate of the economy is then given by . The correction for deviations from this nominal growth potential implies that the debt ratio is cyclically adjusted in “nominal” terms, i.e. that deviations of inflation from 2% are treated as a cyclical fluctuation. Jarociński and Lenza (2018) for example argue that a reliable measure of the output gap should also capture deviations of inflation from its trend. This warrants an explanation.
While obviously price developments show strong cyclical patterns it is less straightforward to set a benchmark or potential rate for inflation than for GDP growth. Of course, the 2% inflation target of the ECB is a natural reference point for euro area countries. At the same time, government debt ratios are based on nominal GDP levels which implies that our nominal cyclical-adjustment approach uses the GDP deflator as the relevant price variable. Of course, the ECB targets HICP inflation rather than the growth of the GDP deflator and there are conceptual differences between the two. The former measures the change in the prices of domestic and foreign consumer goods and services purchased by euro area households while the GDP deflator captures the prices of all final products produced by the domestic economy. As a result, discrepancies between the two indicators can be related to several factors, including movements in import prices. However, while a temporary decoupling of HICP inflation and the growth rate of the GDP deflator can occur, both indicators tend to show significant co-movement over longer time periods (see European Central Bank, 2016b). Moreover, given the multi-year smoothing and forward-looking nature of the proposed nominal cyclical adjustment, temporary discrepancies are of minor relevance for the approach. At the same time, the GDP deflator arguably constitutes a suitable nominal anchor as it constitutes a broad indicator of underlying domestic price developments (including in the public sector).
Treating 2% as the benchmark rate in the context of our cyclical-adjustment of debt serves two purposes. First, adjusting the accumulation of debt for positive and negative deviations from the inflation objective implies that adjustment requirements under the debt rule would vary in a counter-cyclical way with economic conditions. This is the core aspect of our approach that would help to bring the debt rule more in line with the features of the theoretical fiscal reaction function derived in Section 2. Second, if implemented and adhered to, such a rule would gear fiscal policies in euro area Member States to the ECB’s inflation target. This would support its achievement, notably in view of the trend decline in interest rates which, if persistent, implies that the lower bound on nominal interest rates could constrain monetary policy more frequently. As a result of its strategy review, the ECB has revised its monetary policy framework in July 2021, notably to account for the effective lower bound (ELB) as an occasionally binding constraint when reacting to disinflationary shocks with standard interest rate policies. The communication related to the strategy review also emphasises the importance of counter-cyclical fiscal policies.11 In this context, Blanchard et al. (2019) argue in favour of a change of the European fiscal framework in order to ensure that Member States conduct their fiscal policies “in a way that supports the ECB in attaining its stability objective”. Employing a New Keynesian DSGE framework, Hauptmeier et al. (2022) show that a fiscal rule that responds counter-cyclically to both the output gap and inflation increases welfare by reducing the frequency of zero lower bound episodes and alleviating related distortions.
Fig. 1 highlights the impact of our nominal cyclical adjustment approach on debt accumulation for the example of Italy over the 1999–2019 period. It compares nominally adjusted debt developments with the ones implied by the real adjustment method under the current debt rule. Italy is taken as an example here because, first, it is one of the countries that entered EMU with a debt level above 100% of GDP and, second, inflation showed significant positive deviations from 2% in the early 2000s as well as significant negative deviations after the Great Financial Crisis, which helps to highlight the quantitative impact of our approach, also in comparison to the current SGP method. Fig. 1(b) shows that the pro-cyclical pattern of the snowball effect on the accumulation of debt is somewhat reduced by the SGP method, which accounts for deviations of real GDP growth from that of potential GDP. This can be seen in particular during the recessions in Italy in 2008/09 and 2012/13 when large snowball effects implied rapid increases in the debt ratio while the real cyclical adjustment smoothes these cyclical peaks. Note, however, that the nominal cyclical adjustment implies significant additional smoothing especially during two periods, i.e. between 2001–04 when inflation developments exceeded 2% and as of 2010 when growth rates in the GDP deflator persistently remained below the price stability definition. Fig. 1(b) highlights this additional smoothing that further reduces the procyclical pattern of the snowball effect, which is larger in the high inflation period before the crises and lower thereafter.
Fig. 1.
Cyclically adjusted debt — SGP method vs proposed nominal cyclical adjustment (Italy, 1999–2019).
AMECO and own computations.
This has significant quantitative implications for the requirements under the debt rule. Fig. 1(c) shows the gaps vis-à-vis the debt reduction benchmark computed in line with Eq. (13) over 1999–2019. Actual gaps are compared to the ones based on the two different cyclical adjustment methods. Note that for the case of Italy the nominal cyclical adjustment implies a significant smoothing of the gaps vis-à-vis both values based on actual numbers and the ones based on the SGP’s real cyclical adjustment method. This results from the fact that the former not only treats fluctuation of real GDP growth around potential GDP growth as cyclical factors but also deviations of inflation from the price stability definition, which therefore also do not impact on the nominally adjusted debt reduction benchmark in a given year. As stated above, this implies a significant additional smoothing of the adjustment requirements over the cycle. Concretely, adjustment requirements will be lower not only when growth is below potential but also in times when inflation is below the inflation target and vice versa. The inbuilt pro-cyclicality of the current debt rule is thereby reduced.
4. Simulations
In order to quantitatively assess the implications of the nominal cyclical adjustment method for the debt rule described in Section 3.2, this section presents simulation analysis for selected euro area countries and the euro area aggregate. Section 4.2 will start with backward-looking simulations for the period 1999–2019. A particular focus, particularly in the backward-looking part, will lie on those countries for which the debt rule has been a binding constraint in recent years, notably Italy and Belgium. The forward-looking simulations shown in Section 4.3 then cover the period until 2031.
4.1. Assumptions
As regards data sources, the simulations are done using the European Commission’s AMECO database (Autumn 2021 Economic Forecast vintage), which provides data and projections until 2023. As of 2024, fiscal and macroeconomic assumptions are in line with the European Commission’s 2020 Debt Sustainability Monitor (DSM) (see European Commission, 2021). The Autumn 2021 T+10 assumptions for potential GDP growth rates are taken from the Output Gaps Working Group of the Economic Policy Committee. In line with the European Commission’s baseline assumptions, underlying for example the debt sustainability analysis presented most recently in the 2020 DSM, we assume that output gaps gradually close within three years after the end of the projection horizon of the European Commission forecast, i.e. from 2024 to 2026.12 At the same time, the growth rate of the GDP deflator gradually converges towards 2% over 8 years.
The fiscal adjustment scenarios require additional assumptions. Here we assume an aggregate fiscal multiplier of 0.7. Concretely, a 1 percentage point of GDP fiscal contraction – as measured by the change in the underlying fiscal balance – will reduce the real GDP growth rate by 0.5 percentage point and the growth rate of the GDP deflator by 0.2 percentage point in the same year. This seems to be a reasonable assumption in light of the available empirical evidence. In their meta analysis Gechert and Rannenberg (2018) for example show a mean value of 0.35 for the real fiscal multiplier related to unspecified public deficit shocks.13 Moreover, all adjustment scenarios are based on the assumption of fixed implicit interest rates. Cyclical semi-elasticities which are needed to recompute the cyclical components in the adjustment scenarios are in line with the European Commissions’ standard assumptions,14 and kept constant beyond the projection horizon of the Commission forecast.
4.2. Backward-looking simulations
4.2.1. Actual versus cyclically adjusted debt rule scenarios
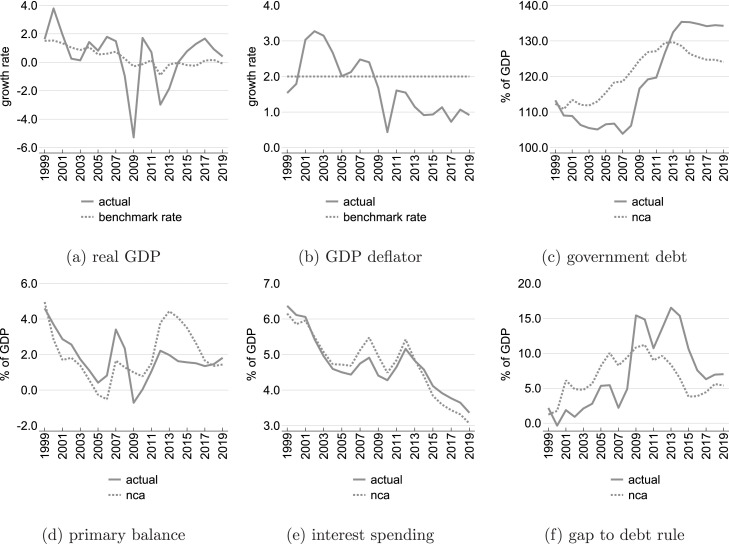
While the SGP’s debt rule in its current operationalisation has only been in place since 2011 it is still informative to see how selected euro area countries as a whole would have performed against this benchmark from the start of EMU in 1999 onwards. In the following we focus on the two country examples of Italy and Belgium (see Appendix Fig. A.2 for additional simulations for the euro area as well as Germany and France). Fig. 2 shows actual fiscal and macroeconomic developments for Italy for the years 1999–2019. It contrasts these actual developments with simulations based on the proposed “nominal” cyclical adjustment method described in Section 3.2.
Fig. A.2.
Debt simulations — actual versus cyclically adjusted (1999–2019).
Notes: “Actual” refers to historical data. “nca” labels nominal cyclically-adjusted figures.
AMECO and own computations.
Fig. 2.
Debt simulations — actual versus cyclically adjusted (Italy, 1999–2019).
Notes: Historical data labelled as “actual”. Nominal cyclically adjusted figures are labelled “nca”. Benchmark rates correspond to potential GDP growth (real GDP) and 2% (GDP deflator).
AMECO and own computations.
Fig. 2, Fig. 2 depict the benchmark values for growth and inflation that are used for the cyclical adjustment, i.e. potential GDP growth and the 2% inflation norm, against actual developments. While in Italy real GDP growth fluctuated around the growth potential in the years before the 2008/09 recession, the GDP deflator growth rate significantly exceeded 2% in most years. Note that – as shown in Fig. 2(c) – this implies that the cyclically adjusted debt ratio exceeds the actual debt ratio over the pre-crisis period and only drops below the actual ratio around the time of the 2012/13 economic downturn (“nominal” cyclical adjusted ratios are labelled “nca”).
The decline in the government debt ratio from around 110% at the start of EMU to around 100% in 2007 was mainly driven by favourable macroeconomic developments, notably relatively high inflation, while in nominally-adjusted terms debt increased. This is in line with the notion that economic good times before the crisis were not used to build buffers. As can be seen in Fig. 2, Fig. 2 declines in interest spending following EMU accession were more than offset by lower primary surpluses. Fig. 2(f) finally depicts gaps vis-à-vis the debt reduction benchmark (1/20 rule), both actual and in nominal cyclically adjusted terms. These reflect the differences in actual and nominal cyclically adjusted debt developments, i.e. larger gaps before the 2008/09 recession owing to structural debt increases and lower gaps in the aftermath of the crisis when weak economic developments accelerated the accumulation of debt via a stronger snowball effect. As highlighted in Section 3.2 the cyclical adjustment smoothes the requirements under the debt rule over the cycle, thereby reducing the inbuilt pro-cyclicality.
The case of Belgium looks somewhat different, as can be seen from Fig. 3. While starting in 1999 with a similar ratio of government debt-to-GDP as Italy, fluctuations around the benchmark rates for growth and inflation seem to broadly balance out over the period ahead of the 2008/09 downturn (see Fig. 3, Fig. 3). Therefore, the difference between the actual and the nominal cyclically adjusted debt ratio shown in Fig. 3(c) is relatively small. Contrary to Italy, the significant decline in the interest spending ratio was (on average) not offset by lower primary surplus ratios, as can be seen in Fig. 3, Fig. 3, respectively. As a result, government debt fell from around 115% to below 90% of GDP in 2007, and this decline was driven only to a very limited extent by cyclical factors. It is noteworthy that Belgium shows negative gaps to the debt reduction benchmark throughout the pre-crisis period, both in actual and cyclically adjusted terms as is highlighted in Fig. 3(f). Contrary to Italy, Belgium therefore can be seen as having taken advantage of pre-crisis economic good times to build buffers. Our cyclical-adjustment approach brings this out very clearly, whereas this is concealed when comparing developments in actual debt for Italy versus Belgium. Also, in the case of Belgium, emerging sizeable gaps vis-à-vis the debt reduction benchmark as of 2008/09 are explained to a significant extent by deficit-debt adjustments related to financial sector recapitalisations.
Fig. 3.
Debt simulations — actual versus cyclically adjusted (Belgium, 1999–2019).
Notes: Historical data labelled as “actual”. Nominal cyclically adjusted figures are labelled “nca”. Benchmark rates correspond to potential GDP growth (real GDP) and 2% (GDP deflator).
AMECO and own computations.
4.2.2. Backward-looking counterfactual scenarios
In order to assess the fiscal and macroeconomic implications of a hypothetical fiscal adjustment in line with the requirements of the debt rule in Italy and Belgium, this section provides counterfactual simulation analysis. Again, we focus on these two countries here because they entered EMU with high levels of debt and have also been constrained by the SGP’s debt rule in recent years. As explained in Section 4.1, the mechanistic simulations presented below are based on a fiscal multiplier analysis which is static in nature.15 The counterfactual compliance scenarios assume an immediate adjustment in 1999 to the primary balance needed to comply (on average) with the SGP’s 1/20th debt benchmark over 1999–2007, i.e. before the 2008/09 recession.16 We specifically look at the pre-crisis period in this section because it has been argued that fiscal adjustment in the economic good times before the Great Financial Crisis could have implied the build-up of fiscal space beforehand and limited the rise in debt ratios as a result of the economic shock.
Concretely, debt targets over periods are computed according to the following equation
| (16) |
which is parametrised in line with the current SGP debt benchmark ( and of GDP) while abstracting from the three year averaging for simplicity. This will remain the benchmark for now.
In a next step, the standard debt accumulation Eq. (1) can be extended to periods and solved for the (constant) primary balance ratio that if maintained ensures achievement of the intermediate debt ratio target . For the backward-looking counterfactuals below we assume that the primary balance is adjusted as of 1999 according to the following target
| (17) |
where is the debt target to be reached in 2007.17
Turning to the results for Italy, charts 4(a)–4(c) compare actual developments against two different counterfactual scenarios, i.e. one that assumes compliance with the 1/20th debt reduction benchmark (labelled “ (SGP)”) and a second one that assumes compliance based on our nominal cyclical adjustment method described in Section 3.2 (labelled “ (nca)”). As can be seen from Fig. 4(a), actual debt developments in Italy were in (hypothetical) compliance with the 1/20th rule until around 2002 before sizable gaps vis-à-vis the debt benchmark emerged in the years up to 2007 (see Fig. 4(b)). Actual government debt reached around 104% of GDP in 2007, while compliance with the debt benchmark would have required a decline of the debt ratio to around 92%. Note that an additional debt adjustment of around 6 percentage points of GDP would have been required to comply in nominal cyclically adjusted terms, implying a drop of government debt to around 86% by 2007.
Fig. 4.
Counterfactual adjustment scenarios (1999–2007).
Notes: Historical data labelled as “actual”. Nominal cyclically adjusted figures are labelled “nca”. corresponds to the speed of debt adjustment.
AMECO and own computations.
Fig. 4(b) depicts the developments in the primary balance ratio that would have been required for actual and cyclically-adjusted compliance, respectively. For the former a primary balance of on average around 3% of GDP would have been necessary, while larger primary surpluses of close to 4% of GDP (on average over 1999–2007) would have been needed to comply in cyclically adjusted terms. This comparison highlights the implications of the cyclical adjustment method put forward in Section 3.2. Given that debt accumulation in Italy was alleviated by a favourable snowball effect related in particular to relatively strong GDP deflator growth (see Fig. 2(b)), the implicit debt target for 2007 is reduced to compensate for the cyclical influence. The implication is that the rule would have prescribed Italy to roughly maintain its primary balance at the level reached at the start of EMU, i.e. saving rather then spending the “EMU interest dividend”. Fig. 4(c) highlights the implications of the two counterfactual adjustment paths for nominal GDP growth, suggesting that macroeconomic costs of compliance with the debt rule would have been moderate.
Figs. 4(d)–4(f) show the same set of fiscal and macroeconomic variables for Belgium, again depicting the differences between actual developments and the two counterfactual adjustment scenarios. Note that for Belgium both compliance scenarios lie above the actual debt ratio development over the entire pre-crisis period, implying over-achievement over 1999–2007 (see Fig. 4(d)). Given the limited impact of the cyclical adjustment over this period, the 2007 debt target values for the two counterfactuals are very similar at somewhat below 100% of GDP. Actual debt in 2007 stood at below 90% of GDP. Consequently, the primary balance level could have been reduced from around 5% of GDP on average over 1999–2007 to around 4% of GDP on average while still achieving compliance with the debt reduction benchmark (see Fig. 4(f)).
4.3. Forward-looking simulations
4.3.1. Baseline scenarios
The forward-looking adjustment scenarios are computed equivalently to the approach for the backward-looking counterfactuals explained in Section 4.2.2. We now choose an intermediate debt target to be achieved in 2031 while the primary balance is adjusted to the respective target values in 2023. The latter reflects the likely deactivation of the SGP’s general escape clause and return to country-specific fiscal surveillance as of 2023. The ten-year horizon up to 2031 is in line the 2020 DSM (see European Commission, 2021). As explained in Section 4.1, our simulations use the Autumn 2021 European Commission Economic Forecast for 2019–23 and, as of 2024, the baseline fiscal and macroeconomic assumptions from the 2020 DSM and the Output Gaps Working Group. Assumptions regarding the fiscal multiplier are equivalent to the ones used for the backward-looking counterfactual adjustment scenarios.
Table 3 provides an overview of fiscal positions – both current and projected – in euro area Member States (excl. Greece) and the euro area aggregate, notably 2019 and 2022 debt ratios (“”) and primary balances (“”) (see columns (1)–(4)). Column (5) shows projected18 interest-growth differentials. As highlighted in Section 2.3, constitutes an important determinant of the underlying debt dynamics. Columns (6)–(9) finally include target primary balances to be achieved over the 2023–31 period in order to ensure compliance with different parametrisations of the debt rule. The existing 1/20 rule is labelled (“”). We also show three primary balance targets computed on the basis of our nominal cyclical adjustment method (labelled as “nca”), i.e. one requiring the SGP’s 1/20 adjustment and two based on lower speeds of adjustment amounting to and .
Table 3.
Overview of adjustment requirements.
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|||
| % of GDP | 2019 | 2022 | 2019 | 2022 | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |
| AT | 70.6 | 79.4 | 2.0 | −1.5 | −2.4 | −1.1 | −1.0 | −1.3 | −1.6 |
| BE | 97.7 | 113.1 | 0.1 | −3.6 | −1.8 | 0.4 | 0.0 | −0.8 | −1.8 |
| CY | 91.1 | 97.6 | 3.5 | −0.2 | −0.8 | 0.4 | −0.7 | −1.3 | −2.0 |
| DE | 58.9 | 69.2 | 2.3 | −2.1 | −2.3 | −1.1 | −1.4 | −1.6 | −1.7 |
| EE | 8.6 | 20.4 | 0.1 | −2.1 | −4.5 | −2.8 | −2.9 | −2.2 | −1.4 |
| ES | 95.5 | 118.2 | −0.6 | −2.0 | −1.1 | 1.2 | 0.6 | −0.3 | −1.4 |
| FI | 59.5 | 71.2 | −0.1 | −1.7 | −3.0 | −1.4 | −1.2 | −1.4 | −1.6 |
| FR | 97.5 | 113.7 | −1.7 | −4.2 | −2.4 | −0.3 | −0.3 | −1.1 | −2.1 |
| IE | 57.2 | 52.3 | 1.8 | −2.4 | −4.8 | −2.8 | −2.6 | −2.5 | −2.3 |
| IT | 134.3 | 151.4 | 1.9 | −2.8 | −1.1 | 2.4 | 2.2 | 0.8 | −0.8 |
| LT | 35.9 | 44.1 | 1.4 | −2.5 | −2.6 | −1.5 | −2.0 | −1.8 | −1.5 |
| LU | 22.3 | 25.6 | 2.6 | 0.7 | −3.4 | −2.3 | −2.3 | −1.7 | −1.1 |
| LV | 36.7 | 50.7 | 0.1 | −3.4 | −2.5 | −1.5 | −1.9 | −1.7 | −1.6 |
| MT | 40.7 | 62.4 | 1.8 | −3.9 | −2.6 | −1.5 | −1.7 | −1.7 | −1.7 |
| NL | 48.5 | 56.8 | 2.5 | −2.0 | −1.6 | −1.1 | −1.5 | −1.4 | −1.4 |
| PT | 116.6 | 123.9 | 3.1 | −1.1 | −1.1 | 1.4 | 1.3 | 0.4 | −0.8 |
| SK | 48.1 | 60.0 | −0.1 | −3.2 | −3.9 | −2.4 | −2.1 | −2.1 | −2.1 |
| SN | 65.6 | 76.4 | 2.1 | −4.9 | −3.2 | −1.9 | −2.1 | −2.4 | −2.7 |
| EA | 84.0 | 96.4 | 0.9 | −2.6 | −2.1 | −0.2 | −0.4 | −1.0 | −1.6 |
Notes: Debt and the primary balance ratio are labelled and , respectively. Nominal cyclically adjusted figures are labelled “nca”. corresponds to the speed of debt adjustment.
Primary balances in 2022 are shown in cyclically-adjusted terms.
Interest-growth differentials are shown in percent.
AMECO and own computations.
It can be seen from Table 3 that for most euro area Member States primary balance ratios in 2022 are projected to deteriorate significantly compared to 2019 levels also due to fiscal support measures taken in the context of the Corona pandemic. As a result, debt ratios are set to rise by on average around 12pp of GDP by 2022. The aggregate debt ratio of somewhat below 100% masks significant cross-country heterogeneity in debt positions, which are projected to range from around 20% of GDP in Estonia to above 150% of GDP in Italy. There are several countries, for which significant improvements in the primary balance ratio would be required to comply with the existing parametrisation of the SGP’s debt rule as of 2023. Comparing columns (4) and (6) however also suggests that several countries would not require significant discretionary fiscal consolidation (or could even loosen fiscal policies) to achieve the primary balance target. This also captures the expected unwinding of negative cyclical components in the wake of the economic recovery.
Going forward, those euro area countries with debt exceeding the 60% reference value by a wide margin are likely to face an intensified stabilisation-sustainability trade-off, given on the one hand the need to support the economic recovery while at the same time significant adjustment in the primary balance ratio will be needed in the medium-term to address the COVID-19 related debt overhang. This is the case in particular for Italy, which is also among the countries with the least favourable interest-growth differential of around over the 2023–2031 period. In addition, high debt ratios at well above 100% require sizeable budgetary improvements in Belgium, France and Spain despite the more favourable outlook for the interest-growth differential. Under the current parametrisation of the debt rule, adjustment requirements amount to around 3pp of GDP in Spain, 4pp of GDP in Belgium and France and roughly 5 pp of GDP in the case of Italy. Switching to our nominal cyclical adjustment method provides some relief with some cross-country heterogeneity (see column (7)). For the euro area as a whole the nominal cyclical adjustment reduces the primary balance target by around 0.2pp of GDP, reflecting a relatively small output and inflation gap in 2022, which the procedure corrects for. The primary balance target is around 0.6pp of GDP lower in the case of Spain, which according to the Commission forecast still has negative output gap of around 2% of GDP in 2022 while GDP deflator growth is projected at around 1.6%. In many cases, the effect of the cyclical adjustment is limited due to relatively low inflation and output gaps at the end of the European Commission’s projection horizon. In Section 4.3.2, we will highlight the implications of an alternative scenario with persistently low growth and inflation. In our baseline scenario, reducing the adjustment speed would rather result in a significantly lower the primary balance target for high debt countries. For example, imposing reduces the consolidation requirement by around 1 pp of GDP in Belgium, Italy, Spain and France.
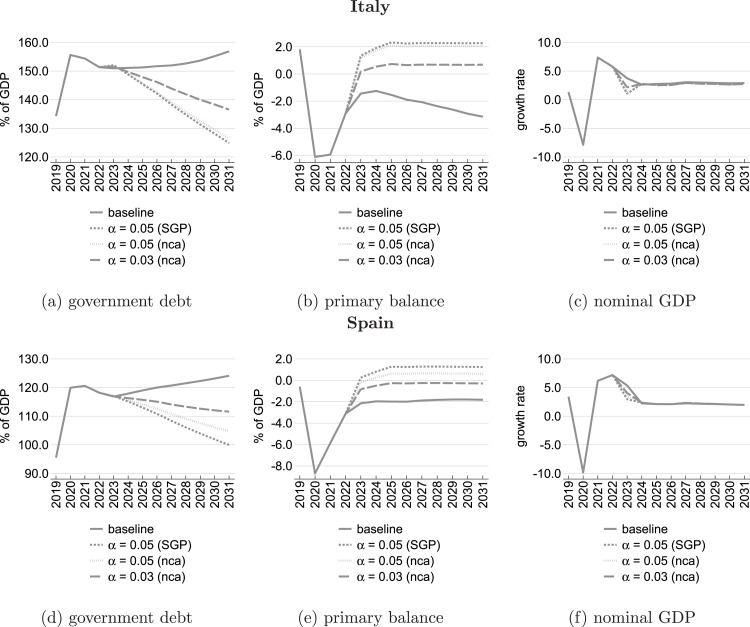
To get an impression of the dynamics, Fig. 5 shows the baseline projections together with the three adjustment scenarios for Italy and Spain (see Fig. A.3, Fig. A.4 in the Appendix for additional simulations). These projections, which are based on a no-policy-change assumption, show upward sloping debt trajectories for Italy and Spain, following a temporary reduction in debt as a ratio to GDP related to the denominator effect of above-potential GDP growth over 2021–23. Increased debt accumulation in the medium term would result inter alia from ageing-related spending increases. Depending on the speed of adjustment and the choice of using unadjusted versus nominal cyclically adjusted figures, debt as a ratio to GDP would decline to between around 125 and 135% in Italy and 100 and 110% of GDP in Spain if the countries fully complied with the respective debt rule specification. Under the current parametrisation of the debt rule this would require an improvement of the primary balance ratio to a surplus of around 2% and 1.5% of GDP in Italy and Spain, respectively. Fig. 5(c) highlights that a related and immediate fiscal consolidation would have significant adverse economic effects, notably for the case of Italy, based on our standard fiscal multiplier assumptions. Moving to a somewhat lower adjustment speed of 3% would limit adverse multiplier effects.
Fig. 5.
Counterfactual adjustment scenarios (2023–2031).
Notes: “Baseline” refers to the European Commission 2021 autumn forecast until 2023. Own simulations thereafter. corresponds to the speed of debt adjustment and “nca” to nominal cyclically-adjusted figures.
AMECO and own computations.
Fig. A.3.
Counterfactual adjustment scenarios (2023–2031).
Notes: “Baseline” refers to the European Commission 2021 autumn forecast until 2023. Own simulations thereafter. corresponds to the speed of debt adjustment and “nca” to nominal cyclically-adjusted figures.
AMECO and own computations.
Fig. A.4.
Counterfactual adjustment scenarios (2023–2031)
Notes: “Baseline” refers to the European Commission 2021 autumn forecast until 2023. Own simulations thereafter. corresponds to the speed of debt adjustment and “nca” to nominal cyclically-adjusted figures.
AMECO and own computations.
4.3.2. Low for long scenarios
As discussed in Section 4.1, the baseline assumptions employed by the European Commission imply a gradual closing of output gaps, a normalisation of interest rates as well as convergence of inflation towards 2%. In this section, we provide some counterfactual simulation analysis where we deviate from the baseline assumptions regarding interest rates and inflation. Linked to the economic debate on longer-term downward trends in inflation and growth (see, e.g., Jorda et al., 2019 and Rachel and Summers, 2019) we show a stylised scenario for the case of Italy highlighting the implications of persistent low nominal growth for the accumulation of debt.
Concretely, in the “low growth and inflation scenario” we assume that GDP deflator growth over the years 2023–31 remains at the projected 2022 level of around 1.5% and annual real GDP growth is 0.5pp lower than in the baseline (see Fig. 6(c)). By 2031, the cumulative deviation of government debt from the baseline scenario amounts to around 20pp of GDP. Complying with the 1/20 debt benchmark of the SGP would therefore require an adjustment to a higher primary balance ratio of around 3.5% of GDP (compared to around 2% of GDP under the baseline assumptions; see Fig. 5(b)). Instead, the adjustment requirement based on the proposed nominal cyclical adjustment approach remains unaffected.19 This relates to the fact that inflation differentials vis-à-vis the 2% inflation norm and their implications for the accumulation of debt are filtered out. The same holds true for fluctuations around the growth potential.
Fig. 6.
Low growth and inflation scenario (Italy 2023–2031).
Notes: “Baseline” refers to the European Commission 2021 autumn forecast until 2023. Own simulations thereafter. corresponds to the speed of debt adjustment and “nca” to nominal cyclically-adjusted figures.
AMECO and own computations.
5. Conclusions
Large COVID-19 related debt overhangs in several countries will need to be addressed once euro area economies have moved to a self-sustained recovery. The Stability and Growth Pact’s debt rule – which was introduced in 2011 as a response to the European debt crisis to operationalise the Treaty’s debt criterion – is in principle in place to guide debt policies going forward. However, its effective implementation has been hindered in the past by its inbuilt pro-cyclicality and very demanding adjustment requirements for high-debt countries, especially in a low growth and inflation environment.
This paper therefore proposes parametric changes to the existing debt rule which aim to remove some of its economic weaknesses, while requiring only limited changes to secondary EU legislation. First, a “nominal” cyclical adjustment, which treats fluctuations of nominal GDP around the real GDP growth potential and deviations of inflation from a 2% norm as cyclical factors, would support a modulation of adjustment requirements over the cycle. It would also help to better align fiscal and monetary policies when inflation rates remain below the price stability objective. Second, a reduction in the debt adjustment parameter from currently 5% of the distance to the debt reference value of 60% of GDP to, for example, 3% would imply lower primary balance targets for high-debt Member States. As a result, compliance would become more feasible both from an economic and political point of view. Third, a symmetric treatment of the debt reference level would imply convergence towards the debt anchor also from below. Unlike with the 3% deficit reference value of the Stability and Growth Pact, a symmetric treatment of the debt reference value would reduce existing heterogeneity in euro area debt positions. This could be useful in a situation where monetary policy reaches the effective lower bound and debt dynamics move towards an undershooting of the debt target as was the case in a number of euro area countries before the COVID-19 crisis. Fiscal policy would thus support monetary policy in such circumstances, allowing the latter to achieve its goal faster and with fewer side effects.
Acknowledgements
We would like to thank our editor, Jan-Egbert Sturm, and three anonymous referees for their comments and suggestions. We also thank Othman Bouabdallah, Nicolas Carnot, Jacopo Cimadomo, Servaas Deroose, Philip Lane, Martin Larch, Eric Leeper, Philipp Mohl, Gilles Mourre, Lucio Pench, Philipp Rother as well as participants at the DG ECFIN workshop “Fiscal rules in Europe: Design and Enforcement” which took place at the European Commission in Brussels on 28 January 2020 for valuable comments and suggestions. The opinions expressed herein are those of the authors and do not necessarily reflect those of the European Central Bank or the Eurosystem.
Footnotes
The rate of 2% we choose to calibrate the trend inflation component refers to the change in the GDP deflator and not to the HICP, which is the price index underlying the ECB’s definition of price stability.
Several contributions favour an expenditure-based indicator over the current structural balance approach of the SGP, given arguably better cyclical properties of the former (see, e.g., Andrle et al., 2015; Bénassy-Quéré et al., 2018 and Holm-Hadulla et al., 2012).
Kamps and Leiner-Killinger, 2019 show that the current medium-term objectives for euro area Member States – structural deficits of no more than 0.5% of GDP for countries with debt above 60% of GDP – are inconsistent with debt ratios converging to 60% of GDP. For the average euro area Member State, with nominal growth expected to be around 3% over the long term, convergence of the debt ratio to 60% of GDP would be consistent with a steady-state deficit ratio of 1.75% of GDP.
See overview note of the ECB’s monetary policy strategy published on 8 July 2021..
For expositional convenience, we follow Fournier (2019) in defining all ratios in the model with respect to (nominal) potential GDP. The growth potential of the economy is accordingly assumed to be time-constant. However, also from an economic point of view it is useful to evaluate debt dynamics relative to potential rather than actual GDP developments.
For a standard value of the budget sensitivity (), fiscal consolidation becomes self-defeating – in the sense that fiscal consolidation does not improve the budget balance – at multipliers above 2.
Such number is significant when assessed against recent calls to create room for public investment. Blanchard et al. (2019), for example, argue for “golden rule accounting”, allowing for debt financing of net public investment. In turn, net public investment of 1 to 1.5% of GDP would be sufficient to restore public capital stocks to pre-crisis levels (Kamps, 2006; Checherita-Westphal et al., 2014).
See Art. 2(1a) of Council Regulation 1467/97.
Note that a three year transitional period was applied for Member States subject to an excessive deficit procedure started before 8 November 2011. See Section 2.2.1.3. in European Commission (2019b) for details. In this paper we abstract from transitional considerations.
Note that the computation of the cyclically-adjusted debt ratio according to Eq. (15) requires the setting of a base year in which the unadjusted debt ratio serves as the reference point. Concretely, when implementing the nominal cyclical adjustment of the debt ratio for the period 1999–2019 as shown for example in Fig. 1(a) the (unadjusted) debt ratio in 1998 serves as the starting point.
See footnote 4.
We do not cover Greece in our paper given its specific debt structure and arrangements following the economic adjustment programme.
In the Appendix we provide additional simulations which show the sensitivity of the debt projections with respect to alternative assumptions for the fiscal multiplier (see Fig. A.1).
See Box 1.3 in European Commission, 2019b.
Note that we assume that shocks to real GDP growth will not have persistent effects on the output gap. We therefore adjust potential growth rates in T+1 and T+2 in order to offset the real multiplier effect at time T.
Note that the adjustment in the primary balance does not factor in contemporaneous multiplier effects ex ante. This is why the counterfactual primary balance ratio is not constant over the 1999–2007 period but shows variation which is related to GDP multiplier effects affecting the denominator and the cyclical component (see Section 4.1).
Note that primary balance targets are nominally adjusted by replacing the effective interest rates by the ones computed on the basis of the benchmark rates for growth and inflation, i.e. .
Column (5) of Table 3 depicts the average projected interest-growth differential over the 2023–31 horizon.
In Fig. 6, for ease of reference, we show only the nominal cyclically-adjusted benchmark for . Likewise, for the primary surplus requirement would not be affected in a low inflation scenario.
Appendix.
See Fig. A.1, Fig. A.2, Fig. A.3, Fig. A.4.
Fig. A.1.
Sensitivity to fiscal multiplier assumptions.
AMECO and own computations.
Data availability
Data will be made available on request.
References
- Adam K. Government debt and optimal monetary and fiscal policy. Eur. Econ. Rev. 2011;55:57–74. [Google Scholar]
- Andrle M., Bluedorn J., Eyraud L., Kinda T., Brooks P.K., Schwartz G., Weber A. IMF; 2015. Reforming Fiscal Governance in the European Union. IMF Staff Discussion Note 115/09. [Google Scholar]
- Bénassy-Quéré A., Brunnermeier M., Enderlein H., Farhi E., Fratzscher M., Fuest C., Gourinchas P.-O., Martin P., PisaniFerry J., Rey H., Schnabel I., di Mauro N.V.B.W., Zettelmeyer J. CEPR; 2018. Reconciling Risk Sharing with Market Discipline: a Constructive Approach to Euro Area Reform. Policy Insight 91. [Google Scholar]
- Benigno P., Woodford M. NBER Macroeconomics Annual 2003. 2004. Optimal monetary and fiscal policy: A linear- quadratic approach; pp. 271–364. [Google Scholar]
- Bergman U.M., Hutchison M.M., Jensen S.E.H. Promoting sustainable public finances in the European Union: The role of fiscal rules and government efficiency. Eur. J. Political Econ. 2016;44:1–19. [Google Scholar]
- Bi H. Sovereign default risk premia, fiscal limits, and fiscal policy. Eur. Econ. Rev. 2012;56(3):389–410. [Google Scholar]
- Blanchard O. Public debt and low interest rates. Amer. Econ. Rev. 2019;109(4):1197–1229. [Google Scholar]
- Blanchard O., Leandro A., Zettelmeyer J.K. Mimeo; 2019. Revisiting the EU Fiscal Framework in an Era of Low Interest Rates. [Google Scholar]
- Calvo G. Servicing the public debt: The role of expectations. Amer. Econ. Rev. 1988;78(4):647–661. [Google Scholar]
- Cantore C., Levine P., Melina G., Pearlman J. Optimal fiscal and monetary policy, debt crisis and management. Macroecon. Dyn. 2017;23(3):1166–1204. [Google Scholar]
- Carnot N. 2014. Evaluating fiscal policy: a rule of thumb. European Economy - Economic Papers 526. [Google Scholar]
- Checherita-Westphal C., Hughes Hallett A., Rother P. Fiscal sustainability using growth-maximizing debt targets. Appl. Econ. 2014;46(6):638–647. [Google Scholar]
- Christiano L., Eichenbaum M., Rebelo S. When is the government spending multiplier large? J. Political Econ. 2011;119(1):78–121. [Google Scholar]
- Coenen, G., Montes-Galdón, C., Smets, F., 2020. Effects of state-dependent forward guidance, large-scale asset purchases and fiscal stimulus in a low-interest-rate environment. Working Paper Series 2352. European Central Bank.
- Corsetti G., Kuester K., Meier A., Müller G.J. Sovereign risk and belief-driven fluctuations in the euro area. J. Monet. Econ. 2014;61:53–73. [Google Scholar]
- Debrun X., Jonung L. Under threat: Rules-based fiscal policy and how to preserve it. Eur. J. Political Econ. 2019;57:142–157. Fiscal Frameworks in Europe. [Google Scholar]
- Deroose S., Carnot N., Pench L., Mourre G. 2018. EU fiscal rules: Root causes of its complexity. VoxEU blog, 14 September. [Google Scholar]
- Eichengreen B., Panizza U. A surplus of ambition: can europe rely on large primary surpluses to solve its debt problem? Econ. Policy. 2016;31(85):5–49. [Google Scholar]
- European Central Bank B. 2016. Government debt reduction strategies in the euro area. ECB Economic Bulletin, Issue 3 / 2016 (Article 2) [Google Scholar]
- European Central Bank B. 2016. What accounts for the recent decoupling between the euro area GDP deflator and the HICP excluding energy and food? ECB Economic Bulletin, Issue 6 / 2016 (Box 5) [Google Scholar]
- European Commission B. 2017. Reflection paper on the deepening of the economic and monetary union. 31 May. [Google Scholar]
- European Commission B. 2019. Italy: Report prepared in accordance with article 126(3) of the treaty on the functioning of the European union. 5 June. [Google Scholar]
- European Commission B. 2019. Vade mecum on the stability and growth pact - 2019 edition. Institutional Paper 101. [Google Scholar]
- European Commission B. 2020. Economic governance review communication. 5 February. [Google Scholar]
- European Commission B. 2021. Debt sustainability monitor 2020. Institutional Paper 143. [Google Scholar]
- European Fiscal Board B. 2018. 2018 Annual report of the European fiscal board. 10 October. [Google Scholar]
- European Fiscal Board B. 2019. Assessment of EU fiscal rules with a focus on the six and two-pack legislation. 11 September. [Google Scholar]
- Fournier, J.-M., 2019. A buffer-stock model for the government: Balancing stability and sustainability. IMF Working Paper No. 19/159.
- Gechert S., Rannenberg A. Which fiscal multipliers are regime-dependent? A meta-regression analysis. J. Econ. Surv. 2018;32(4):1160–1182. [Google Scholar]
- Ghosh A.R., Kim J.I., Mendoza E.G., Ostry J.D., Qureshi M.S. Fiscal fatigue, fiscal space and debt sustainability in advanced economies. Econ. J. 2013;123(566):F4–F30. [Google Scholar]
- de Haan J., Jong-A-Pin R., Mierau J.O. Do budgetary institutions mitigate the common pool problem? New empirical evidence for the EU. Public Choice. 2013;156:423–441. [Google Scholar]
- Hallerberg M., Strauch R., von Hagen J. The design of fiscal rules and forms of governance in European Union countries. Eur. J. Political Econ. 2007;23(2):338–359. [Google Scholar]
- Hauptmeier, S., Kamps, C., Radke, L., 2022. Fiscal Rules and the Zero Lower Bound. manuscript. European Central Bank.
- Holm-Hadulla F., Hauptmeier S., Rother P. The impact of numerical expenditure rules on budgetary discipline over the cycle. Appl. Econ. 2012;44(25):3287–3296. [Google Scholar]
- Iara A., Wolff G.B. Rules and risk in the Euro area. Eur. J. Political Econ. 2014;34:222–236. [Google Scholar]
- Jarociński M., Lenza M. An inflation-predicting measure of the output gap in the euro area. J. Money Credit Bank. 2018;50(6):1189–1224. [Google Scholar]
- Jorda O., Marti C., Nechio F., Tallman E. Why is inflation low globally? FRBSF Econ. Lett. 2019 2019-19, 15 July. [Google Scholar]
- Juncker J.-C., Tusk D., Dijsselbloem J., Draghi M., Schulz M. European Commission; 2015. 22 June. [Google Scholar]
- Kamps C. Is there a lack of public capital in the European Union? EIB Papers. 2006;10(1):72–93. [Google Scholar]
- Kamps C., Leiner-Killinger N. Taking stock of the functioning of the EU fiscal rules and options for reform. J. Econ. Stat. 2019;239(5-6):861–894. [Google Scholar]
- Kanda, D., 2011. Modeling optimal fiscal consolidation paths in a selection of European countries. IMF Working Paper 11/164.
- Lagarde C. 2019. The future of the euro area economy. Speech at the Frankfurt European Banking Congress, 22 November. [Google Scholar]
- Leeper E.M. Why central banks should care about fiscal rules. Sveriges Riksbank Econ. Rev. 2016;3:109–125. [Google Scholar]
- Lorenzoni G., Werning I. Slow moving debt crises. Amer. Econ. Rev. 2019;109(9):3229–3263. [Google Scholar]
- Mourre C., Princen S. 2014. Adjusting the budget balance for the business cycle: the EU methodology. European Economy, Economic Papers 536. [Google Scholar]
- Muscatelli V.A., Natale P., Tirelli P. A simple and flexible alternative to stability and growth pact deficit ceilings. Is it at hand? Eur. J. Political Econ. 2012;28(1):14–26. [Google Scholar]
- Price, R.W., Dang, T., Guillemette, Y., 2014. New tax and expenditure elasticity estimates for EU budget surveillance. OECD Economics Department Working Paper No. 1174.
- Rachel L., Summers L.H. On falling neutral real rates, fiscal policy and the risk of secular stagnation. Brook. Pap. Econ. Activity. 2019 Spring, 1-54. [Google Scholar]
- Reuter W.H. National numerical fiscal rules: Not complied with, but still effective? Eur. J. Political Econ. 2015;39:67–81. [Google Scholar]
- Reuter W.H. When and why do countries break their national fiscal rules? Eur. J. Political Econ. 2019;57:125–141. [Google Scholar]
- Schmitt-Grohé S., Uribe M. Optimal fiscal and monetary policy under sticky prices. J. Econ. Theory. 2004;114(2):198–230. [Google Scholar]
- Work stream on monetary-fiscal policy interactions S. ECB; 2021. Monetary-Fiscal Policy Interactions in the Euro Area. ECB Occasional Paper Series 273. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data will be made available on request.