Testing the safe-haven properties of gold and bitcoin in the backdrop of COVID-19: A wavelet quantile correlation approach

Abstract

We test the suitability of Gold and Bitcoin as safe-haven instruments in the backdrop of the Covid-19 related equity market meltdown by implementing the newly proposed Wavelet Quantile Correlation. We employ daily returns of Bitcoin, Gold, DJIA, CAC40, NSE50, S&P 500, NASDAQ, and EUROSTOXX from 05–01–2015 to 31–12–2020. Our results show that Gold consistently exhibits safe haven properties for all the markets except NSE in the long and short run, while Bitcoin provided mixed results. We find that Gold can act as an effective hedge and diversifier as well.

1. Introduction

Equity markets worldwide witnessed a severe meltdown due to the unprecedented impact of Covid-19 on the global economy. DJIA crashed by 2997 points on March 16, 2020; the biggest fall in a day since the 1987 crash. CAC 40 witnessed a drop of 9% in a single day. Among the emerging markets, NSE50 lost 3100 points in March 2020 alone, almost around 27% of its value. S&P 500 Circuit breakers were triggered four times during March 2020. Similar behaviour was found in other equity and commodity markets, resulting in overall uncertainty. Investors normally flock towards safe-haven assets to protect their investment during such instances.

Baur and Lucey (2010) define hedge, diversifier, and safe haven as follows:

Hedge: An asset that is uncorrelated or negatively correlated with another asset or portfolio on average. A strict hedge is (strictly) negatively correlated with another asset or a portfolio on average.

Diversifier: An asset that is positively (but not perfectly correlated) with another asset or portfolio on average.

Safe haven: An asset that is uncorrelated or negatively correlated with another asset or portfolio in times of market stress or turmoil.

Precious metals act as a traditional safe haven as risk-averse investors flock to them during times of crisis. However, the COVID-19 pandemic created a meltdown in the precious metals markets during January-March 2020. Prices of silver and platinum fell by 22% and 26%, respectively, while Gold continued an upward swing from the 3rd week of March at the same time as the bear market rally in the US. Prices of silver and other precious metals had rallied positively in the later part of 2020.

Traditionally, investors have used Gold as a safe-haven asset. (Baur and Lucey, 2010; Ji et al., 2020). Other precious metals like Silver, Palladium and Platinum are less preferred as their safe haven property are found to be valid only over the short time horizon (Bredin et al., 2017; Lahiani et al., 2021). However, Gold's safe-haven property is found to be time-varying (Shahzad et al., 2019a, Akhtaruzzaman et al., 2021) and market-specific (Beckmann et al., 2015; Shahzad et al., 2019b). Further, there are studies that question Gold's safe-haven ability (Dee et al., 2013; Baur and Glover, 2016; Klein, 2017 to name some).

Of late, researchers have identified cryptocurrencies, especially Bitcoin, as a potential safe-haven instrument (Bouri et al., 2017b; Shahzad et al., 2019). The rationale is that they exist outside the traditional financial system, and therefore, are impervious to the shocks influencing it (Dyhrberg, 2016; Corbet et al., 2018). Further, Bitcoin is identified as a portfolio diversifier (Dyhrberg, 2016; Guesmi et al., 2019) and a short-term hedge (Bouri et al., 2017a; Bouri et al., 2017b).

During January-March 2020, Bitcoin, whose prices had hit a five-month high around $10,500 in February, slipped below $8000, and on March 13, plunged 39% in a single day, eventually hitting a low of $4106. However, Bitcoin prices recovered fast and reached as high as $20,000 by mid of December 2020, and thus emerged as a potential safe haven asset.

Recent studies have concluded that Bitcoin is at the most a weak safe-haven (Shahzad et al., 2019; Nagy and Benedek, 2021), especially during turbulent times such as the Covid-19 crisis (Conlon and McGeee, 2020; Syuhada et al., 2021). Due to the mixed evidence on the safe-haven properties of Gold and Bitcoin and the unprecedented impact of COVID-19 on financial markets, we need a proper re-examination of their safe haven properties.

The commonly used methodology to test the safe-haven properties of an asset is the multivariate GARCH based regression proposed by Ratner and Chiu (2013). However, we cannot extract information across different frequencies using this method. Similarly, we have the GVAR based method of Diebold and Yilmaz's (2012) method and its extensions. Diebold and Yilmaz (2012) proposed the directional spillover models based on GVAR estimation. They further extended it with the dynamic connectedness methods proposed in Diebold and Yilmaz (2014). Later, Baruník and Křehlík (2018) extended the method by implementing a Fourier-based decomposition to capture dynamic spillover across different frequencies. Giudici and Pagnottoni (2019a, 2019b) employed a VECM based extension of DY2012 to address cointegrated behaviour and found that connectedness between Bitcoin exchanges is dynamic. Similarly, Ji et al. (2021) found that safe asset withdrawal is essential in determining a Bitcoin exchange's position in the connectedness network. Using DY2014 methodology, Giudici et al. (2021) explored the possibility of stablecoins to offset the foreign exchange shocks and found that a basket-based stable coin can preserve its values during times of market turmoil.

While these methods help capture the directional and dynamic connectedness behaviour, they cannot capture tail dependence, which is necessary to determine the safe haven property of an asset. Considering these methodological issues, we propose a methodology to extract safe haven property across different time horizons.

2. Data and methodology

We employ daily log-returns of DJIA, CAC40, NSE 50, NASDAQ, S&P 500, EURO STOXX, Bitcoin, and Gold from 05-Jan-2015 to 31–12–2020. These indices are relatively important in their market capitalisation and represent diverse constituents and geographies.

We propose a new methodology, namely Wavelet Quantile Correlation (WQC), to test the safe-haven nature of Bitcoin and Gold. Li et al. (2015) define the Quantile Correlation (QC) between two variables X and Y as follows:

Let Q _τ,X be the τ^th quantile of X and Q _τ,Y(X) be the τ^th quantile of Y conditional upon X. Q _τ, Y(X) is independent of X if and only if the random variables I(Y − Q _τ, Y) > 0 and X is independent. Here I(.) is the indicator function. For 0 < τ < 1, the quantile covariance is defined as:

qcov_t(Y,X) = cov{I(Y − Q _τ,Y > 0), x} = E(φ_τ(Y − Q _τ,Y)(X − E(X))

φ_τ(w) = τ − I(w < 0). We calculate QC as:

$$qco{r}_t\left(X,Y\right)=\frac{qco{v}_t\left(Y,X\right)}{\surd \left(var\right({\varphi }_{\tau }\left(Y-Q_{\tau ,Y}\right)var\left(X\right)}$$

Using the QC, we can measure the correlation between the asset pairs across different quantiles. If an asset exhibits safe haven properties, its correlation with the other asset should be negative during extreme conditions, captured by QC in the lower quantiles. However, this only solves part of the problem.

Conventional investment theory assumes that investment decisions are invariant to the time horizon. However, Kristoufek (2013) employed Fractal Market Hypothesis (Peters,1994) and showed that investors make their decisions based on the investment horizons they are operating. We assume that investors have varied preferences across different timescales while picking a safe-haven asset. We can identify these dynamics by analysing the dependence structure across different timescales. Towards this, we introduce Wavelet Quantile Correlation (WQC). The methodology is intuitive and straightforward.

First, we decompose the asset pairs X_t and Y_t using a maximal overlapping discrete wavelet transform (MODWT), proposed by Perciwal and Walden (2000). We explain MODWT briefly below.

Consider a signal X[i] of length T where T= 2^J for some integer J. Let h ₁[i] and g ₁[i] be the low-pass filter and the high-pass filter, defined by an orthogonal wavelet. At the first level, X[i] is convolved with h ₁[i] to obtain the approximation coefficients a ₁[i] and with g ₁[i] to obtain the detail coefficients d ₁[i]. Here, a ₁[i] and d ₁[i] is of length N.

$$a_1\left[i\right]=h_1\left[i\right]*s\left[i\right]={\Sigma }_k{h}_1\left[i-k\right]s\left[k\right]$$

$$d_1\left[i\right]=g_1\left[i\right]*s\left[i\right]={\Sigma }_k{g}_1\left[i-k\right]s\left[k\right]$$

Next, we filter a ₁[i] using the same scheme but with modified filters h ₂[i] and g ₂[i], obtained by dyadic up-sampling h ₁[i] and g ₁[i]. We continue this process recursively. For J = 1,2.....J ₀–1,where J ₀ ≤ J, we can calculate the approximate and detailed coefficients as:

$$a_{j+1}\left[i\right]=h_{j+1}\left[i\right]*a_j\left[i\right]={\Sigma }_k{h}_{j+1}\left[i-k\right]a_j\left[i\right]$$

$$d_{j+1}\left[i\right]=g_{j+1}\left[i\right]*a_j\left[i\right]={\Sigma }_k{g}_{j+1}\left[n-k\right]a_j\left[j\right]$$

Where h _j + 1[i] = U(h_j[i]) and g _j + 1[i] = U(g_j[i]).

U is the up-sampling operator that inserts a zero between every adjacent pair of time-series elements.

After applying a J level decomposition to X_t and Y_t and obtaining the detail coefficients, we apply QC to the pair of wavelet details d _j[X] and d _j[Y] for all J, and thus obtain WQC for each level J. We define the WQC for two-time series X and Y at a given decomposition level J, and quantile τ as:

$$WQ{C}_{\tau }\left(d_j\left[X\right],d_j\left[Y\right]\right)=\frac{qco{v}_{\tau }\left(d_j\left[Y\right],d_j\left[X\right]\right)}{\sqrt{var\left({\varphi }_{\tau }\left(d_j\left[Y\right]-Q_{\tau ,d_j\left[Y\right]}\right)\right)var\left(d_j\left[X\right]\right)}}$$

We extract information at the scales of 4–8 days, 16–32 days, and 128–256 days to roughly capture the behaviour across one trading week, one trading month, and one trading year.

3. Results and discussion

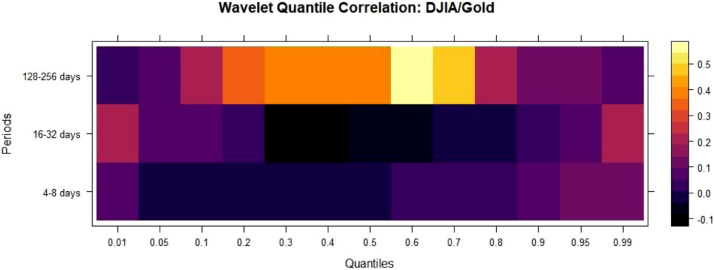
If an asset exhibits safe-haven properties, its correlation with the other assets should be negative during market turbulence, visible at lower quantiles. For DJIA/Gold Fig. 1 , QC is minimal and positive in the lower quantiles for one trading month and one trading year, indicating diversifier property. QC is negative across the low and median quantiles for one trading week, indicating safe haven and hedge property. QC is negative across the median quantiles for one trading month, indicating hedge property.

Fig. 1.

WQC between DJIA/Gold.

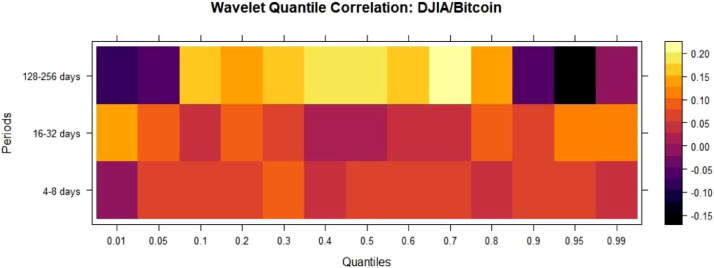
For DJIA/Bitcoin Fig. 2 , QC is minimal and positive at lower quantiles for one trading week and one trading month, indicating diversifier property. However, QC is negative at one trading year at lower quantiles, indicating safe haven property in the long run.

Fig. 2.

WQC between DJIA/Bitcoin.

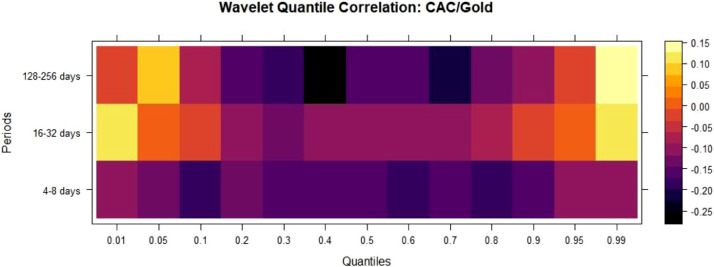
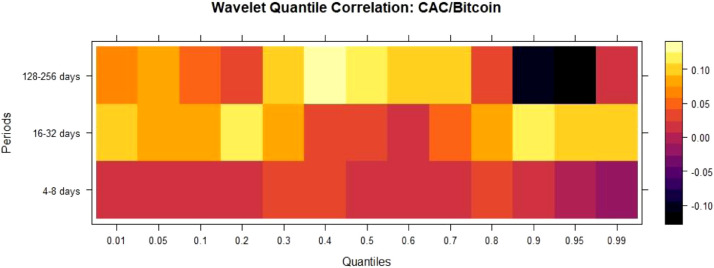
For CAC/Gold Fig. 3 , QC is negative in lower and median quantiles for 4–8 and 128–256 days, indicating safe haven and hedge properties. QC is negative across median quantiles for 16–32 days, indicating hedge property. For CAC/Bitcoin Fig. 4 , QC is positive and minimal in almost all the quantiles across all the timescales, indicating diversifier property.

Fig. 3.

WQC between CAC40/Gold.

Fig. 4.

WQC between CAC40/Bitcoin.

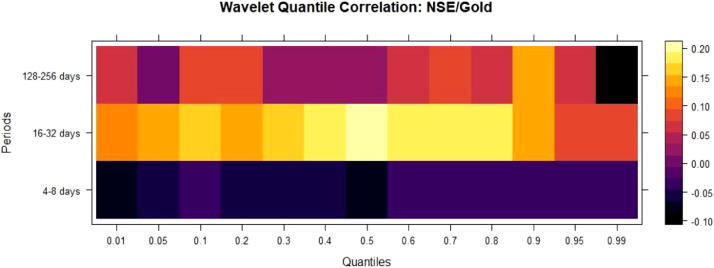
QC between NSE50/Gold Fig. 5 is negative in lower and median quantiles for the 4–8 days scales, indicating safe haven and hedge property. QC is minimal but mostly positive across all quantiles for the other scales, indicating diversifier property.

Fig. 5.

WQC between NSE/Gold.

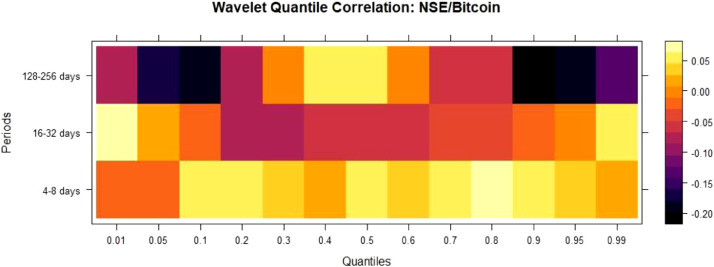
For NSE/Bitcoin Fig. 6 , we observe QC negative for lower quantiles at 4–8 days, indicating safe haven property. QC is negative across the median quantiles up to one trading month(16–32 days), confirming hedge property.

Fig. 6.

WQC between NSE/Bitcoin.

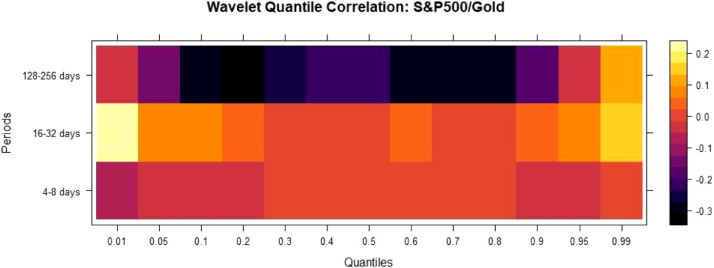
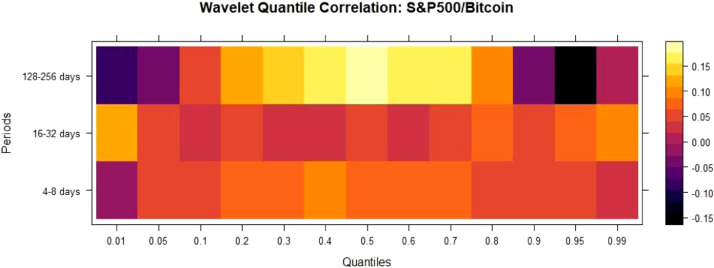
For S&P 500/Gold Fig. 7 , QC is negative in the lower and median quantiles for 4–8 days and 128–256 days, thus confirming safe haven and hedge property. We find QC negative in the median quantiles for 16–32 days, indicting hedge property. For S&P500/Bitcoin Fig. 8 , QC is minimal and positive across all quantiles & scales.

Fig. 7.

WQC between S&P 500/Gold.

Fig. 8.

WQC between S&P 500/Bitcoin.

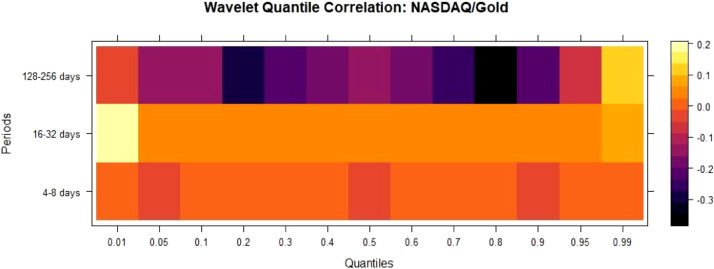
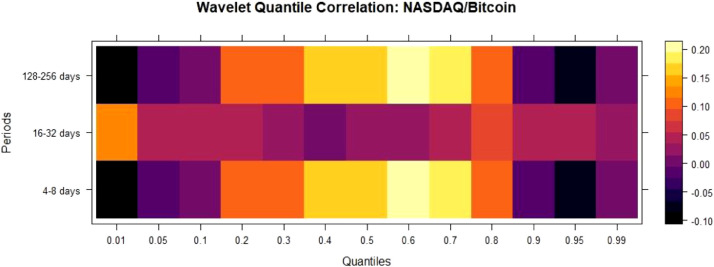
For NASDAQ/Gold Fig. 9 , QC is minimal and negative for the lower and median quantiles for 4–8 days and 128–256 days. QC is negative in the median quantiles for 4–8 days and 16–32 days. Thus, we can employ Gold as a safe haven in the short and long run and as a hedge in the short and medium run. For NASDAQ/Bitcoin Fig. 10 , we find safe haven properties at short-run(4–8 days) and long-run(128–256 days) as QC is negative across lower quantiles for these scales.

Fig. 9.

WQC between NASDAQ/Gold.

Fig. 10.

WQC between NASDAQ/Bitcoin.

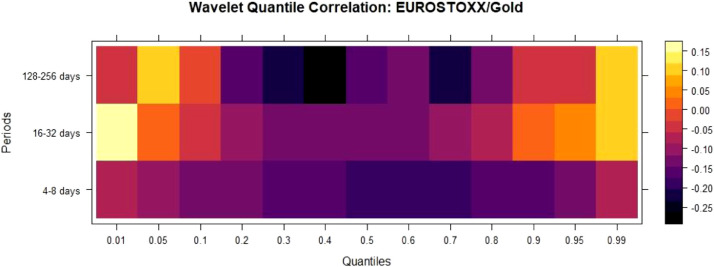
For EUROSTOXX/Gold Fig. 11 , QC is negative in the lower and median quantiles for 4–8 days and 128–256, indicating safe haven and hedge property. For 16–32 days, QC is negative in the median scales, implying hedge property. For EUROSTOXX/Bitcoin Fig. 12 , we observe negative QC in the lower quantiles for short(4–8 days) and long (128–256) run, indicating safe haven property.

Fig. 11.

WQC between EUROSTOXX/Gold.

Fig. 12.

WQC between EUROSTOXX/Bitcoin.

We see that Gold exhibits safe haven property both in the long and short-run irrespective of differences in Index constitution and Market capitalisation. However, for an emerging market such as NSE, Gold only exhibits safe haven property in the short run. Our results confirm the findings of Shahzad et al., al.(2019a) and Akhtaruzzaman et al., al.(2021) that the safe haven property of Gold is time-varying. For Bitcoin, we see a separate dynamic altogether. For NASDAQ and EURO STOXX, Bitcoin exhibits safe haven property both in the short-run and long run. In contrast, for DJIA, safe haven property is present only in the long run. For NSE, we see only short-run safe haven property. For CAC40 and S&P 500, Bitcoin exhibit no safe haven property. Further, we observe significant right tail dependence in the long run between Bitcoin and stock markets, indicating that Bitcoin can act as a diversifier in the long run.

4. Concluding remarks

We tested the suitability of Gold and Bitcoin as safe-haven instruments employing the newly proposed Wavelet Quantile Correlation. Our results showed that Gold consistently exhibited both short-run and long-run safe haven properties. In contrast, Bitcoin exhibited short-run and long-run safe-haven properties only for NASDAQ, EUROSTOXX, and short-run safe haven property for NSE50. Bitcoin did not exhibit any safe haven property for a highly market capitalised index such as S&P500. Further, we found that Gold demonstrates better hedge ability in the medium run.

We found that Bitcoin exhibits long-run diversifier properties. Bitcoin's safe-haven property varied across markets and scales, especially in the short run. During a crisis, investors would be largely bothered by the short-run dynamics. Using Bitcoin as a safe haven asset would not be advisable in such a scenario. We suggest that investors use Gold as a safe haven instrument as we find its safe-haven property market invariant.

Considering the volatile nature of Bitcoin prices, we feel that the investment aspect of Bitcoin and other cryptocurrencies needs further attention. In future research, we intend to extend our study by incorporating directional spillovers using frequency decomposition (Baruník and Křehlík, 2018) and non-linear dependencies (Nagy and Benedek,2021).

Declaration of Competing Interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.