Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2022 Jan 19;13(3):822–829. doi: 10.1021/acs.jpclett.1c03835

Systematic Assessment of the Accuracy of Subunit Counting in Biomolecular Complexes Using Automated Single-Molecule Brightness Analysis

John S H Danial †,‡,§,*, Yuri Quintana †, Uris Ros †,∥, Raed Shalaby †,∥, Eleonora G Margheritis ⊥, Sabrina Chumpen Ramirez ⊥, Christian Ungermann ⊥, Ana J Garcia-Saez †,∥,*, Katia Cosentino †,⊥,*
PMCID: PMC8802318  PMID: 35044771

Abstract

graphic file with name jz1c03835_0006.jpg

Analysis of single-molecule brightness allows subunit counting of high-order oligomeric biomolecular complexes. Although the theory behind the method has been extensively assessed, systematic analysis of the experimental conditions required to accurately quantify the stoichiometry of biological complexes remains challenging. In this work, we develop a high-throughput, automated computational pipeline for single-molecule brightness analysis that requires minimal human input. We use this strategy to systematically quantify the accuracy of counting under a wide range of experimental conditions in simulated ground-truth data and then validate its use on experimentally obtained data. Our approach defines a set of conditions under which subunit counting by brightness analysis is designed to work optimally and helps in establishing the experimental limits in quantifying the number of subunits in a complex of interest. Finally, we combine these features into a powerful, yet simple, software that can be easily used for the analysis of the stoichiometry of such complexes.

Assembly into nanoscopic oligomeric complexes is a common mechanism that allows biomolecules to perform their cellular activities.1−3 Determining the structural organization of these complexes is paramount to understanding their functions. High-resolution structural characterization methods, such as X-ray diffraction or cryo-electron microscopy, provide angstrom-resolution atomic maps but require the biological complex under study to be purifiable with a high yield, to be preserved in its entirety along with, possibly, its native physiological environment during the purification step, and to be stoichiometrically homologous. Super-resolution microscopy methods can chart the architecture of many of these nanoscopic complexes directly inside their cellular environments with nanometer resolution;4−7 however, precise molecular counting using super-resolution microscopies is a formidable task that remains challenging.5,8−12

Single-molecule fluorescence analysis has emerged as a powerful strategy for measuring the stoichiometry of small and large biomolecular complexes.13−20 Two major approaches comprising subunit counting by this analytical toolkit are known as stepwise photobleaching21 and single-molecule brightness analysis.22 In stepwise photobleaching analysis, the number of photobleaching steps exhibited by a single oligomer is counted and correlated with the number of subunits contained within. Counting the number of photobleaching steps has, traditionally, been performed manually or by the use of some algorithms.23 However, both approaches require trained users that are able to isolate actual photobleaching steps from artifacts derived from high noise levels, the presence of one or several photo-blinking steps, and temporal variations in the intensity of the excitation source. These problems were recently addressed by training and deploying convolutional and long–short-term memory deep learning neural network (CLDNN) to classify different oligomeric species on the basis of the number of photobleaching steps they exhibit.24 Despite the high accuracy of this network in discerning oligomers with up to five subunits, automated and manual classification based on step counting remains extremely challenging for larger assemblies.

Single-molecule brightness analysis is not limited by the mentioned factors and has the potential to quantify the stoichiometry of small to medium-sized macromolecular complexes.22 In this method, the number of underlying subunits of an oligomeric species is obtained by comparing its brightness to a calibration curve theoretically calculated from the measured average brightness of monomers. Monomers, selected on the basis of the stepwise photobleaching analysis, can be obtained by different strategies: from a sample with a mixture of different oligomers, from partial bleaching of protein complexes,15 or from non-activated or mutant forms of the protein of interest, which are unable to oligomerize.17 Paramount to the accurate quantification of stoichiometry is the selection of “clean” intensity traces of the monomeric species, which are not affected by any intensity variations other than imaging noise. Equally important is the accurate measurement of the brightness of oligomeric species, which is irrespective of high noise, early photobleaching, the presence of multiple photoblinking steps, and other nonspecific intensity variations.

Despite the enormous power of single-molecule brightness analysis and the unique niche it occupies within the family of methods used to quantity absolute molecular copy numbers, it suffers from a number of important limitations.

(1) The fluorescence intensity of the monomeric and oligomeric particles may take a wide range of values. Detecting these particles with high fidelity (i.e., low false negative and positive rates) requires subjective changes of the detection parameters by the end user. This process hampers the automation of data processing and the accuracy of the eventual subunit counting.

(2) The maximum number of resolved oligomers is strictly connected to the quality of the monomer calibration. Therefore, the selection of clean, single-step intensity traces for monomer calibration is paramount for resolving higher-order oligomers; however, traditionally this step is performed manually. In addition to the potential introduction of human error during the classification process, this is a complicated task due to the need for tens to hundreds of such traces for appropriate calibration, which needs to be repeated for each data set due to any subtle change in the experimental setup or in the sample preparation.

(3) Although the theory behind single-molecule brightness analysis has been extensively scrutinized, the experimental conditions under which this method is designed to operate optimally have never been systematically navigated. This prevented the optimized application of this method and in some cases may have led to incorrect conclusions about the underlying biological system.

(4) The accuracy of this method in quantifying multiple stoichiometric occurrences (e.g., dimeric, trimeric, tetrameric, etc.) of protein complexes, as well as any change in the proportion of oligomeric species as a function of protein concentration, was not systematically assessed before. This prevented the end users from understanding the analytical limits of this approach and judging its applicability to the system of their interest.

(5) Fitting the intensity distributions to multiple Gaussians may not perfectly match the real data introducing false stoichiometry assessments.

To address these important limitations, we have developed SAS (Stoichiometry Analysis Software), a fully automated software pipeline for analyzing the stoichiometry of oligomeric complexes imaged by fluorescence microscopy. By employing SAS to quantify the number of complex subunits by brightness analysis, we could carefully assess the accuracy of this method and provide the users with guidelines for the optimal experimental and analytical conditions to employ for reliable and accurate stoichiometry measurements of protein complexes.

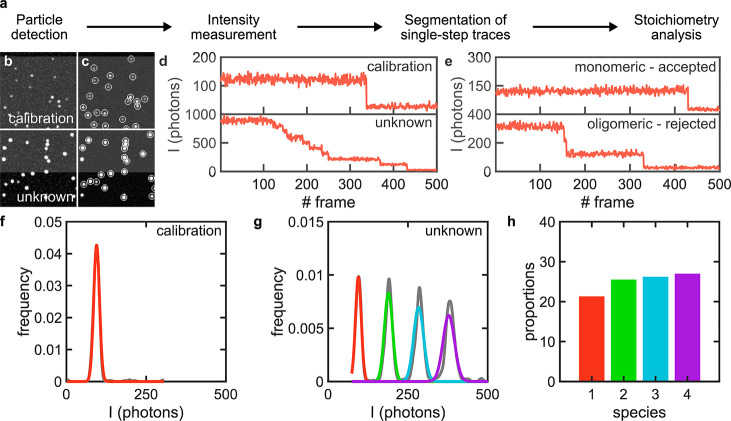
SAS uses a simple, but robust, parameter-free, single-molecule particle detection algorithm based on a multilayer convolutional neural network (DeepSinse), which was previously found to exhibit 4–5 times lower false positive and negative rates compared to the best-in-class, domain specific detection algorithm based on wavelet filtering on a remarkably wide range of signal-to-noise ratios (SNRs).25 Importantly, SAS requires no human input for optimized detection (Figure 1a–c and Figure S1; see Methods). The time-dependent intensity traces of the detected molecules are extracted from the acquired frame stacks by measuring the background-corrected intensities in regions of interest (ROIs) centered around the centroids of each detected particle (Figure 1c,d; see Methods). In SAS, data to be processed need to be classified as either “calibration” or “unknown” (Figure 1b–d). The “calibration” data set will be used to find the brightness values of monomeric species. For this purpose, we fed the extracted intensity traces into a trace annotator that selects clean, single-step traces by calculating and normalizing the gradient (i.e., slope) of each trace and picking up traces with a single peak gradient above a preset threshold (Figure 1e and Figure S2; see Methods). The selected traces are then used to construct a distribution curve from a kernel density function and fitting it to a Gaussian mixture model (GMM) to account for the fact that some of the selected single-step traces are not monomeric due to the photobleaching of two, or more, fluorophores at the same time within the same complex (Figure 1f; see Methods). The mean and standard deviation of the intensity values in the fitted Gaussian curve corresponding to the monomeric population are, subsequently, used to construct an idealized Gaussian mixture that represents the distribution of the higher-order oligomeric species. By overimposing these multiple Gaussians on the intensity distribution of all detected particles from the “unknown” data set, we calculate the proportion of each species from the area of each Gaussian curve (Figure 1g; see Methods). Finally, the calculated proportions are corrected for incomplete labeling using a binomial probability density function to yield the true stoichiometry of the underlying biological complex (Figure 1h; see Methods). The quality of the monomeric calibration Gaussian curve is critical in the brightness analysis approach as the width of the intensity distribution defines the maximum number of species that can be resolved. The selection of monomeric traces by SAS is reliable even for wide and complex simulated and experimental intensity distributions (see, for example, the calibration distribution of experimental data in Figure S3). However, this step needs particular attention and scrutiny by the final end user.

Figure 1.

Figure 1

Open in a new tab

Overview of the mode of operation of SAS. (a) SAS workflow. (b,c) Exemplary simulated, ground-truth images of single molecules for a set of calibration (stoichiometry: 50% monomers, 25% dimers, and 25% trimers) and unknown (stoichiometry: equal proportions of monomers to 16-mer) species (b) before detection and (c) after detection where detected particles are encircled with white circles. (d) Exemplary intensity traces of two randomly chosen particles from the calibration and unknown data sets after conversion from signal counts to photons. (e) Examples of monomeric and oligomeric traces extracted from the calibration data set that are automatically annotated by SAS. (f) Kernel density function of the intensity distribution underlying the calibration data set (gray) and the Gaussian curve representing the monomeric population (red). (g) Kernel density function of the intensity distribution underlying the unknown data set (gray) and the Gaussian mixture representing the monomeric population (red, green, cyan, and purple). (h) Bar graph of the proportion of the species underlying the unknown data set (color code as in panel g).

We then assessed the performance of the software and the accuracy of counting using single-molecule brightness analysis by simulating ground-truth data under a wide range of experimental conditions (see Methods). To this end, we evaluated the error in the calculated versus simulated proportions of species when varying the density of particles, SNR, number of subunits per complex (at a constant particle density), number of monomeric particles selected for calibration, variation in the intensity of each molecule, the bin size of the kernel probability distribution function (pdf), the particle intensity distribution width (i.e., σ) to ROI radius (SRR) from which the intensity traces are extracted, and the pixel size (Figure 2a–h). Under all simulated conditions, the error in the assignment of oligomeric species did not exceed 15% while reaching, in many cases, <5%. Variations in the density of particles, number of subunits per complex, and pixel size did not result in substantial changes to the error (<3%) within the simulated ranges.

Figure 2.

Figure 2

Open in a new tab

Assessment of the accuracy of subunit counting under different simulated experimental conditions. Measurement of the error against the (a) density of particles, (b) signal-to-noise ratio (SNR), (c) maximum number of subunits per complex, (d) number of monomeric particles selected for calibration, (e) intercomplex variation in photon count, (f) kernel probability distribution function (pdf) bin size, (g) ratio of the σ, or standard deviation, of the point spread function (PSF) of the underlying particles to ROI radius (SRR), and (h) pixel size. Base parameters used across all simulations (except for those varied): number of time frames, 500; number of movies for calibration and unknown species (each), at least 10; maximum photon count, 10; intercomplex variation in photon count, 0%; σ of the PSF of each complex, 130 nm; stoichiometry of the calibration species , 50% monomers, 25% dimers, and 25% trimers; stoichiometry of the unknown species, 50% monomers and 50% dimers. See the supplementary data for camera parameters.

Our analysis shows that the bin size for generating a kernel pdf, as well as the number of calibration particles, may be a critical parameter to consider for fitting the intensity distributions, as increasing the bin size further increases the error rate while decreasing the number of calibration particles decreases the error rate. SAS employs a bin size of five photons, which provides an error of 3%, to ensure that the intensity information is not lost and the fitting procedure is not oversensitive to fine fluctuations in the intensity curve.

Expectedly, decreasing the SNR to 3.54, which is remarkably low for single-molecule experiments, affects the fidelity of the stoichiometry measurements, resulting in an error of 13.96%. A marginal improvement of the SNR to 5.68 yields a large improvement in the error (=5.01%). Any improvement to the SNR beyond 5–10 yields diminishing returns on the error (>2%). This result indicates that while the use of bright fluorophores and efficient detection setups is necessary to improve the detection efficiency, beyond a certain point, it is not necessarily correlated with improved counting accuracy by SAS. In contrast, our simulations indicate that intensity variation is a critical parameter to the accuracy of counting. Intensity variations of >25% can yield error values of >5%. These results favor the use of stable fluorophores that exhibit a narrow emission spectrum and minimal photoblinking, as well as flat-field illumination schemes that minimize spatial variations in the excitation profile and unpolarized light as the excitation source to ensure fluorophores under different orientations are equally excited.

Finally, the SRR affects the accuracy of counting. Surprisingly, however, our simulations indicate an optimal ratio of 0.75 at which the error is minimized to 1.69%. One possible explanation for this important finding is that for ROIs smaller than the full width of the particles the extracted intensities are inaccurate given that a large portion of the point spread function (PSF) lies outside of the borders of the ROIs, yet for ROIs much larger than the full width of the particles, noise affects the extracted intensities. Our simulations point to the importance of accurately measuring the mean standard deviation of the underlying particles in choosing the ROI radius.

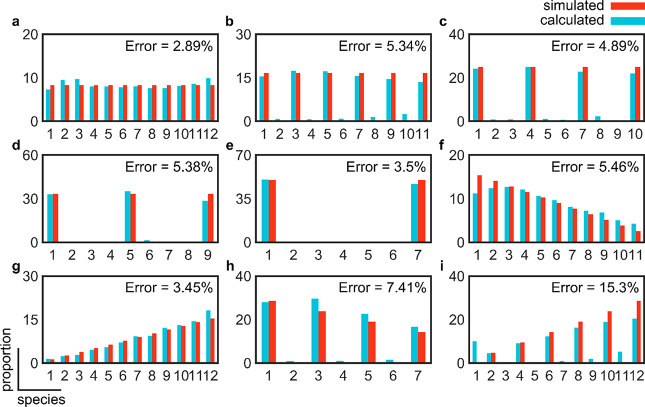
Then, we assessed the accuracy of subunit counting for different stoichiometric configurations (Figure 3a–i). To do this, we simulated nine different stoichiometric configurations with a maximum of 12 subunits where the proportion of species is constant (Figure 3a–e), decreasing (Figure 3f,h), or increasing (Figure 3g,i) with the number of subunits. The underlying species were also allowed to take monomeric up to hexameric units. Under all simulated configurations, the error did not exceed 15%. The accuracy of counting was particularly minimized when the proportion of species was held constant under all stoichiometries (Figure 3a–e). Although the error of the measurements was excellent throughout, we have noticed that, particularly where we have simulated increasing or decreasing proportions, a large fraction of the species was not recognized. This finding suggested that in a typical experiment, where not all single molecules assemble into higher-order oligomers and where these oligomers add dimeric or higher-order units, larger complexes might not be recognized in the analysis.

Figure 3.

Figure 3

Open in a new tab

Assessment of the accuracy of subunit counting under different simulated stoichiometric configurations. Starting from a monomer as the basic unit, we assessed the measurement of the error for equal proportions (8.33%) of (a) monomeric species, (b) dimeric species, (c) trimeric species, (d) tetrameric species, (e) hexameric species, (f) decreasing proportions (15.4% monomers, 14.1% dimers, 12.8% trimers, 11.5% tetramers, 10.3% pentamers, 9.0% hexamers, 7.7% heptamers, 6.4% octamers, 5.1% 9-mers, 3.8% 10-mers, 2.6% 11-mers, and 1.3% 12-mers) based on monomeric units, (g) increasing proportions (same as panel f but in reverse order) based on monomeric units, (h) decreasing proportions (28.6% monomers, 23.9% trimers, 19.0% pentamers, 14.3% heptamers, 9.5% 9-mers, and 4.8% 11-mers) based on the addition of dimeric units, and (i) increasing proportions (same as panel h but in reverse order) based on the addition of dimeric units.

To investigate the reason behind the poorer performance of the software in quantifying the number of subunits in the mentioned stoichiometric configurations, we paid closer attention to the fittings of the idealized Gaussian mixture to the kernel density function of the unknown species. We found that marginal shifts in the mean intensity values of the calibration curves would propagate to high-order oligomers beyond 8–10 subunits causing obvious misfits to the idealized mixture of Gaussians as suggested in Figure 1g. Furthermore, this issue could be more severe in a real, experimental setting where the intensity distribution of the underlying species might not follow the idealized Gaussian mixture due to imaging artifacts or photoquenching.

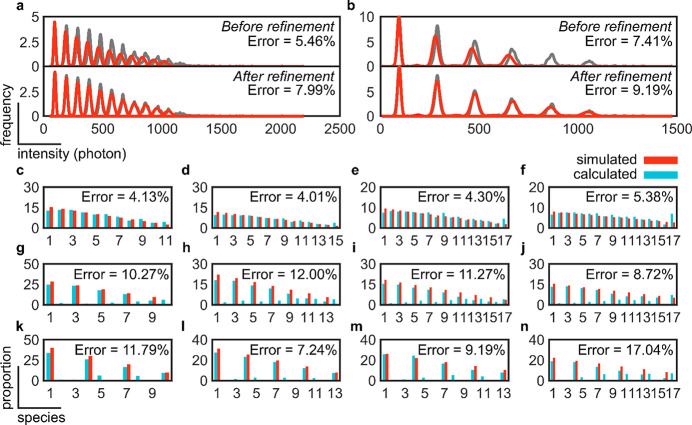
To solve this issue, we implemented a fitting refinement step in which the mean intensity value of the calibration curve is scanned in a ±10 photons region, with one-photon resolution, and the residual error is calculated after fitting with the Gaussian mixture model. The refined mean intensity value of the calibration curve is chosen where the residual error is minimum. Given that the mean intensity value of the monomer species is changed, we expect that the error would increase (i.e., be worsened) at the expense of recovering a larger number of species. Following this improvement, we first assessed two challenging configurations (Figure 3f,h). As expected, our assessments reveal an increase in the error from 5.46% to 7.99%, for the configuration based on the addition of monomers, and from 7.41% to 9.19%, for the configuration based on the addition of dimers (Figure 4a,b). The advantages of using a refinement step were particularly observed in this last configuration where the number of recognized species increased from 7 to 11 out of a simulated 12 (Figure 4b). In all of the above, the SNR was set to 10.74 and the intercomplex variation in photon count was set to 0% to ensure that none of these important photophysical parameters would complicate or affect our assessment of the accuracy of counting.

Figure 4.

Figure 4

Open in a new tab

Assessment of the accuracy of subunit counting under real experimental conditions and challenging stoichiometric configurations. Kernel density distribution functions and error measurements for 12-mer stoichiometries based on the addition of (a) monomeric or (b) dimeric units before and after refinement simulated at an SNR of 10.74 (photon count of 10) and intercomplex variation in photon count of 0%. Kernel density distributions are colored gray, and the Gaussian mixture is colored red. Error measurements based on the addition of (c–f) monomeric, (g–j) dimeric, or (k–n) trimeric units of high-order oligomers: (c, g, and k) 12-mer, (d, h, and l) 16-mer, (e, i, and m) 20-mer, and (f, j, and n) 24-mer. Simulations were performed at an SNR of 5.68 (photon count of 5) and an intercomplex variation in photon count of 20%. Proportions of each species can be found in the supplementary data.

Next, we conducted a final round of assessment to establish the absolute limits of accurate counting with single-molecule brightness analysis using the introduced refinement step for more challenging experimental conditions (i.e., an SNR of 5.68 and an intercomplex variation in photon count of 20%) and stoichiometric configurations (from 12- to 24-mers with a decreasing proportion of species) (Figure 4c–n). On average, the error was lowest for the configurations based on monomeric, followed by dimeric, and finally trimeric units. All error measurements were <15% except for the 24-mer in trimeric configuration, where the measured error was 17.04%. Finally, and because of the refinement step, high-order species were recognized in all cases; however, low proportions of species that were not simulated in the configurations based on the addition of dimeric and trimeric units were also produced.

Importantly, the end user needs to be aware that the refinement step helps to increase the accuracy at the expense of sensitivity. This step can be included in or excluded from the analysis, as illustrated in the GUI (Figure S1), thus leaving to the end user the choice between accuracy or sensitivity, according to the specific experimental and analytical need.

In summary, this extensive analysis has shown the following.

(1) The SNR and intercomplex variation in photon count play an important role in dictating the accuracy as well as the number of recognized species within a complex of interest. While marginal improvements in the SNR yield noticeable improvements to the accuracy of counting quickly followed by diminishing returns, the intercomplex variation in photon count has to be minimized at all times to maximize the accuracy of counting and number of recognized species.

(2) The ROI size has to be optimized manually by the user in case the mean standard deviation in the PSF of the imaged complexes is known.

(3) The stoichiometric occurrence does not affect the accuracy of measurements, but relevant factors are the basic unit (i.e., monomeric, dimeric, or trimeric) and whether the proportion of species increases or decreases with the number of subunits.

(4) Refining the mean intensity value of the calibration species can recover high-order species, but at the expense of a reduced counting sensitivity as well as uncovering additional species that are absent in reality. The use of the refinement step is dependent on whether the user is interested in accurate or more comprehensive measurements of stoichiometry.

Having extensively assessed the accuracy of counting with single-molecule brightness analysis, we, finally, validated SAS on biological samples whose stoichiometry is known a priori, as reported from either structural studies or prior subunit counting measurements performed manually. In addition, the chosen samples had to satisfy the following requirements: (1) The labeling efficiency had to be previously reported to ensure that any unlabeled species are accurately accounted for. Furthermore, the labeling efficiency had to be reported under exactly the same labeling conditions and using the same fluorophore as label in our experimental validation. (2) Highly compacted structures, in which the underlying fluorophores are located close to one another, were avoided. In doing so, we wanted to ameliorate the hard to simulate effects of fluorophore quenching on the measured intensity of the complex of interest. (3) For the purpose of validation, the complex of interest would be known to take stable stoichiometries that would not change during the course of an experiment or under slightly different conditions. This is to ensure that our results would, to the best of our knowledge, match those reported. (4) The complex of interest has to be assembled from its individual components in vitro and in situ. Oligomeric complexes that can be imaged only inside their physiological, cellular environment were excluded as their densities, as well as the behavior of the host cellular system, cannot be appropriately controlled.

We identified the Bcl-2-associated-X-protein (BAX), which is known to assemble into multiple species based on dimer units,17 and the lipid scramblase Atg9, which has been recently reported to assemble as a homotrimer,26−29 as candidate systems. To this end, we reconstituted labeled BAX oligomers into a supported lipid bilayer (SLB) and imaged them under a TIRF microscope (see Methods). We then compared the proportion of species measured using SAS with those measured manually as reported in ref (17) (Figure 5a–e and Figure S3). Our measurements show excellent agreement with those reported, revealing the dimeric stoichiometry of BAX. Moreover, because of the entirely automated pipeline of SAS, it took us 3 min to process one data set, which typically took hours to days to process through the manual selection of clean traces, as well as optimization of detection under various experimental conditions. Similarly, stoichiometry experiments on Atg9 complexes processed by SAS showed excellent agreement with the literature data, with Atg9 assembling predominantly as a trimer [with minor high-order aggregates/complexes based on trimer units (Figure 5f)].

Figure 5.

Figure 5

Open in a new tab

Comparison of subunit counting accuracy with a manual (semiautomated) pipeline and SAS applied on experimental data. (a) Calibration data set of monomeric Bax labeled with ATTO 488 dye. (b) Set of unknown stoichiometries of labeled BAX molecules. Scale bar, 5 μm. Subunit counting of BAX performed (c) manually and using SAS (d) before and (e) after refinement. (f) Subunit counting of Atg9 performed using SAS.

In summary, here we have systematically and extensively assessed the accuracy of subunit counting using brightness analysis. We have established the experimental conditions and assessed complex stoichiometric configurations, under which this method can count with accuracies exceeding 85%. Our analysis serves as an important resource for experimentalists in need of accurately counting the copy number of proteins in a variety of stoichiometric configurations and under a wide range of challenging experimental conditions. To perform this analysis, we developed a fully automated computational pipeline that is simple to use and serves as a fundamental tool for future experiments of this type. We expect our analysis, and software, to empower the use of optical microscopy in structural studies of complex, large, and heterogeneous macromolecular assemblies with single-molecule sensitivity.

Acknowledgments

This work was supported by a research associateship from King’s College, University of Cambridge, awarded to J.S.H.D., a scholarship from the International Max-Planck Research School and the University of Tubingen awarded to R.S., Deutsche Forschungsgemeinschaft (DFG) Grant UN111/13-1 awarded to C.U., DFG GA164/3-1, starting (Grant 309966) and consolidator (APOSITE) ERC grants awarded to A.J.G.S., and an Elite Postdoctoral Fellowship from the Baden-Wuerttemberg Foundation and DFG Grant INST 190/194-1 awarded to K.C.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c03835.

  • Methods, including simulation of ground-truth data, workflow for single-molecule detection, calibration and particle analysis, and sample preparation for experimental validation; GUI of SAS (Figure S1); gallery of randomly accepted and rejected traces selected by SAS (Figure S2); graphs of the intensity distributions obtained from the experimental data (Figure S3); and stoichiometric configurations and experimental conditions simulated in this study (Table S1) (PDF)

  • Supplemental data (ZIP)

Author Contributions

J.S.H.D. and Y.Q. contributed equally to this work. K.C. and A.J.G.-S. conceived the study. J.S.H.D., Y.Q., A.J.G.-S., and K.C. designed the study with the contributions of U.R. and R.S. K.C. performed BAX experiments. E.G.M. and S.C.R. performed Atg9 experiments. J.S.H.D. and Y.Q. wrote the software. K.C. performed the manual analysis. J.S.H.D. and E.G.M. performed the software analysis. K.C., J.S.H.D., U.R., and R.S. assessed performance. K.C., C.U., and A.J.G.S. provided supervision and infrastructure. All authors contributed to writing the manuscript.

The authors declare no competing financial interest.

Notes

Updated versions of the source code for SAS, as well as guiding instructions, can be obtained from https://github.com/jdanial/SAS.

Supplementary Material

jz1c03835_si_001.pdf (748.3KB, pdf)
jz1c03835_si_002.zip (6.1MB, zip)

References

  1. Szymborska A.; de Marco A.; Daigle N.; Cordes V. C.; Briggs J. A. G.; Ellenberg J. Nuclear Pore Scaffold Structure Analyzed by Super-Resolution Microscopy and Particle Averaging. Science 2013, 341 (6146), 655–658. 10.1126/science.1240672. [DOI] [PubMed] [Google Scholar]
  2. Salvador-Gallego R.; Mund M.; Cosentino K.; Schneider J.; Unsay J.; Schraermeyer U.; Engelhardt J.; Ries J.; García-Sáez A. J. Bax Assembly into Rings and Arcs in Apoptotic Mitochondria Is Linked to Membrane Pores. EMBO J. 2016, 35 (4), 389–401. 10.15252/embj.201593384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Song L.; Hobaugh M. R.; Shustak C.; Cheley S.; Bayley H.; Gouaux J. E. Structure of Staphylococcal α-Hemolysin, a Heptameric Transmembrane Pore. Science 1996, 274 (5294), 1859–1865. 10.1126/science.274.5294.1859. [DOI] [PubMed] [Google Scholar]
  4. Mund M.; van der Beek J. A.; Deschamps J.; Dmitrieff S.; Hoess P.; Monster J. L.; Picco A.; Nédélec F.; Kaksonen M.; Ries J. Systematic Nanoscale Analysis of Endocytosis Links Efficient Vesicle Formation to Patterned Actin Nucleation. Cell 2018, 174 (4), 884–896.e17. 10.1016/j.cell.2018.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Thevathasan J. V.; Kahnwald M.; Cieśliński K.; Hoess P.; Peneti S. K.; Reitberger M.; Heid D.; Kasuba K. C.; Hoerner S. J.; Li Y.; Wu Y.-L.; Mund M.; Matti U.; Pereira P. M.; Henriques R.; Nijmeijer B.; Kueblbeck M.; Sabinina V. J.; Ellenberg J.; Ries J. Nuclear Pores as Versatile Reference Standards for Quantitative Superresolution Microscopy. Nat. Methods 2019, 16 (10), 1045–1053. 10.1038/s41592-019-0574-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Rust M. J.; Bates M.; Zhuang X. Sub-Diffraction-Limit Imaging by Stochastic Optical Reconstruction Microscopy (STORM). Nat. Methods 2006, 3 (10), 793–796. 10.1038/nmeth929. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Xu K.; Zhong G.; Zhuang X. Actin, Spectrin, and Associated Proteins Form a Periodic Cytoskeletal Structure in Axons. Science 2013, 339 (6118), 452–456. 10.1126/science.1232251. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fricke F.; Beaudouin J.; Eils R.; Heilemann M. One, Two or Three? Probing the Stoichiometry of Membrane Proteins by Single-Molecule Localization Microscopy. Sci. Rep. 2015, 5 (1), 14072. 10.1038/srep14072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hummer G.; Fricke F.; Heilemann M. Model-Independent Counting of Molecules in Single-Molecule Localization Microscopy. Mol. Biol. Cell 2016, 27 (22), 3637–3644. 10.1091/mbc.e16-07-0525. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Karathanasis C.; Fricke F.; Hummer G.; Heilemann M. Molecule Counts in Localization Microscopy with Organic Fluorophores. ChemPhysChem 2017, 18 (8), 942–948. 10.1002/cphc.201601425. [DOI] [PubMed] [Google Scholar]
  11. Jungmann R.; Avendaño M. S.; Dai M.; Woehrstein J. B.; Agasti S. S.; Feiger Z.; Rodal A.; Yin P. Quantitative Super-Resolution Imaging with QPAINT. Nat. Methods 2016, 13 (5), 439–442. 10.1038/nmeth.3804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Stein J.; Stehr F.; Schueler P.; Blumhardt P.; Schueder F.; Mücksch J.; Jungmann R.; Schwille P. Toward Absolute Molecular Numbers in DNA-PAINT. Nano Lett. 2019, 19 (11), 8182–8190. 10.1021/acs.nanolett.9b03546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Das S. K.; Darshi M.; Cheley S.; Wallace M. I.; Bayley H. Membrane Protein Stoichiometry Determined from the Step-Wise Photobleaching of Dye-Labelled Subunits. ChemBioChem 2007, 8 (9), 994–999. 10.1002/cbic.200600474. [DOI] [PubMed] [Google Scholar]
  14. Thompson J. R.; Cronin B.; Bayley H.; Wallace M. I. Rapid Assembly of a Multimeric Membrane Protein Pore. Biophys. J. 2011, 101 (11), 2679–2683. 10.1016/j.bpj.2011.09.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Anderluh A.; Klotzsch E.; Reismann A. W. A. F.; Brameshuber M.; Kudlacek O.; Newman A. H.; Sitte H. H.; Schütz G. J. Single Molecule Analysis Reveals Coexistence of Stable Serotonin Transporter Monomers and Oligomers in the Live Cell Plasma Membrane*. J. Biol. Chem. 2014, 289 (7), 4387–4394. 10.1074/jbc.M113.531632. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hastie P.; Ulbrich M. H.; Wang H.-L.; Arant R. J.; Lau A. G.; Zhang Z.; Isacoff E. Y.; Chen L. AMPA Receptor/TARP Stoichiometry Visualized by Single-Molecule Subunit Counting. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (13), 5163–5168. 10.1073/pnas.1218765110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Subburaj Y.; Cosentino K.; Axmann M.; Pedrueza-Villalmanzo E.; Hermann E.; Bleicken S.; Spatz J.; García-Sáez A. J. Bax Monomers Form Dimer Units in the Membrane That Further Self-Assemble into Multiple Oligomeric Species. Nat. Commun. 2015, 6 (1), 8042. 10.1038/ncomms9042. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Calebiro D.; Rieken F.; Wagner J.; Sungkaworn T.; Zabel U.; Borzi A.; Cocucci E.; Zürn A.; Lohse M. J. Single-Molecule Analysis of Fluorescently Labeled G-Protein–Coupled Receptors Reveals Complexes with Distinct Dynamics and Organization. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (2), 743–748. 10.1073/pnas.1205798110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. McGuire H.; Aurousseau M. R. P.; Bowie D.; Blunck R. Automating Single Subunit Counting of Membrane Proteins in Mammalian Cells. J. Biol. Chem. 2012, 287 (43), 35912–35921. 10.1074/jbc.M112.402057. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jenner A.; Shalaby R.; Cosentino K.. Chapter Three - Quantitative Single-Molecule Imaging of Protein Assembly in Membranes. In Advances in Biomembranes and Lipid Self-Assembly; Iglič A., Rappolt M., García-Sáez A. J., Eds.; Advances in Biomembranes and Lipid Self-Assembly; Academic Press, 2020; Vol. 31, pp 81–128. 10.1016/bs.abl.2020.02.004 [DOI] [Google Scholar]
  21. Ulbrich M. H.; Isacoff E. Y. Subunit Counting in Membrane-Bound Proteins. Nat. Methods 2007, 4 (4), 319–321. 10.1038/nmeth1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Schmidt T.; Schütz G. J.; Gruber H. J.; Schindler H. Local Stoichiometries Determined by Counting Individual Molecules. Anal. Chem. 1996, 68 (24), 4397–4401. 10.1021/ac960710g. [DOI] [Google Scholar]
  23. Ulbrich M. H.Counting Molecules: Toward Quantitative Imaging. In Far-Field Optical Nanoscopy; Tinnefeld P., Eggeling C., Hell S. W., Eds.; Springer Series on Fluorescence; Springer: Berlin, 2015; pp 263–291. 10.1007/4243_2011_36 [DOI] [Google Scholar]
  24. Xu J.; Qin G.; Luo F.; Wang L.; Zhao R.; Li N.; Yuan J.; Fang X. Automated Stoichiometry Analysis of Single-Molecule Fluorescence Imaging Traces via Deep Learning. J. Am. Chem. Soc. 2019, 141 (17), 6976–6985. 10.1021/jacs.9b00688. [DOI] [PubMed] [Google Scholar]
  25. Danial J. S. H.; Shalaby R.; Cosentino K.; Mahmoud M. M.; Medhat F.; Klenerman D.; Garcia Saez A. J. DeepSinse: Deep Learning Based Detection of Single Molecules. Bioinformatics 2021, 37, 3998. 10.1093/bioinformatics/btab352. [DOI] [PubMed] [Google Scholar]
  26. Matoba K.; Kotani T.; Tsutsumi A.; Tsuji T.; Mori T.; Noshiro D.; Sugita Y.; Nomura N.; Iwata S.; Ohsumi Y.; Fujimoto T.; Nakatogawa H.; Kikkawa M.; Noda N. N. Atg9 Is a Lipid Scramblase That Mediates Autophagosomal Membrane Expansion. Nat. Struct. Mol. Biol. 2020, 27 (12), 1185–1193. 10.1038/s41594-020-00518-w. [DOI] [PubMed] [Google Scholar]
  27. Maeda S.; Yamamoto H.; Kinch L. N.; Garza C. M.; Takahashi S.; Otomo C.; Grishin N. V.; Forli S.; Mizushima N.; Otomo T. Structure, Lipid Scrambling Activity and Role in Autophagosome Formation of ATG9A. Nat. Struct. Mol. Biol. 2020, 27 (12), 1194–1201. 10.1038/s41594-020-00520-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Guardia C. M.; Tan X.-F.; Lian T.; Rana M. S.; Zhou W.; Christenson E. T.; Lowry A. J.; Faraldo-Gómez J. D.; Bonifacino J. S.; Jiang J.; Banerjee A. Structure of Human ATG9A, the Only Transmembrane Protein of the Core Autophagy Machinery. Cell Rep. 2020, 31 (13), 107837. 10.1016/j.celrep.2020.107837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gómez-Sánchez R.; Rose J.; Guimarães R.; Mari M.; Papinski D.; Rieter E.; Geerts W. J.; Hardenberg R.; Kraft C.; Ungermann C.; Reggiori F. Atg9 Establishes Atg2-Dependent Contact Sites between the Endoplasmic Reticulum and Phagophores. J. Cell Biol. 2018, 217 (8), 2743–2763. 10.1083/jcb.201710116. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz1c03835_si_001.pdf (748.3KB, pdf)
jz1c03835_si_002.zip (6.1MB, zip)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES