Existence of Functional Connectome Fingerprint during Infancy and Its Stability over Months

Abstract

The functional connectome fingerprint is a cluster of individualized brain functional connectivity patterns that are capable of distinguishing one individual from others. Although its existence has been demonstrated in adolescents and adults, whether such individualized patterns exist during infancy is barely investigated despite its importance in identifying the origin of the intrinsic connectome patterns that potentially mirror distinct behavioral phenotypes. To fill this knowledge gap, capitalizing on a longitudinal high-resolution structural and resting-state functional MRI dataset with 104 human infants (53 females) with 806 longitudinal scans (age, 16–876 d) and infant-specific functional parcellation maps, we observe that the brain functional connectome fingerprint may exist since infancy and keeps stable over months during early brain development. Specifically, we achieve an ∼78% individual identification rate by using ∼5% selected functional connections, compared with the best identification rate of 60% without connection selection. The frontoparietal networks recognized as the most contributive networks in adult functional connectome fingerprinting retain their superiority in infants despite being widely acknowledged as rapidly developing systems during childhood. The existence and stability of the functional connectome fingerprint are further validated on adjacent age groups. Moreover, we show that the infant frontoparietal networks can reach similar accuracy in predicting individual early learning composite scores as the whole-brain connectome, again resembling the observations in adults and highlighting the relevance of functional connectome fingerprint to cognitive performance. For the first time, these results suggest that each individual may retain a unique and stable marker of functional connectome during early brain development.

SIGNIFICANCE STATEMENT Functional connectome fingerprinting during infancy featuring rapid brain development remains almost uninvestigated even though it is essential for understanding the early individual-level intrinsic pattern of functional organization and its relationship with distinct behavioral phenotypes. With an infant-tailored functional connection selection and validation strategy, we strive to provide the delineation of the infant functional connectome fingerprint by examining its existence, stability, and relationship with early cognitive performance. We observe that the brain functional connectome fingerprint may exist since early infancy and remains stable over months during the first 2 years. The identified key contributive functional connections and networks for fingerprinting are also verified to be highly predictive for cognitive score prediction, which reveals the association between infant connectome fingerprint and cognitive performance.

Introduction

The human brain during infancy, especially within the first 2 years after birth, undergoes exceptionally rapid development in both structure (Gilmore et al. 2018; Li et al., 2014c) and function (Gao et al., 2015; Zhang et al., 2019) that could largely shape later behavioral and cognitive performance. Although many infant neuroimaging studies have revealed the brain growth patterns during 0 and 2 years old (Gilmore et al., 2010; Li et al., 2015, 2016), they are largely performed at the population level. Hence, we still lack critical knowledge on the individualized brain organization and development during infancy, which is essential for mapping individual brain characteristics to individual behavior phenotypes (Kanai and Rees, 2011; Mueller et al., 2013; Wee et al., 2018; Girault et al., 2019) and exploring personalized diagnosis and treatment of mental disorders (Orru et al., 2012; Wolfers et al., 2015). As a key solution, infant brain fingerprinting is used to discover reliable and robust individualized brain organization patterns that are capable of accurately distinguishing one individual from others, like fingerprints. This is critical for providing fundamental insight into the individual-level unique, stable, and relatively invariant patterns (Finn et al., 2015; Horien et al., 2019) during rapid infant brain development.

To date, from the perspective of morphology and structural connectivity, the brain folding and structural connectome fingerprinting in infants and neonates has been investigated (Duan et al., 2020; Ciarrusta et al., 2021), which enables accurate identification of an infant from its neonatal brain, highlighting the uniqueness of cortical folding and structural connectivity patterns. But infant functional connectome fingerprinting using longitudinal resting-state functional MRI rs-fMRI), which is critical for understanding the origin of the individualized intrinsic brain functional organization and development, still remains uninvestigated. Actually, the fingerprinting capability of functional connectome has been observed in the cohorts of older children (Miranda-Dominguez et al., 2018), adolescents (Kaufmann et al., 2017), youths (Demeter et al., 2020), adults (Finn et al., 2015; Liu et al., 2018; Miranda-Dominguez et al., 2018; Horien et al., 2019), and even older adults (Horien et al., 2019), almost covering the whole life span, indicating that individualized functional connectome distinguishability is substantial and reproducible. Moreover, the existence of interindividual variability of functional connectivity has been revealed in preterm neonates (Xu et al., 2019; Stoecklein et al., 2020). The individual uniqueness in the neonatal functional connectome (36.9 - 44.1 weeks of postmenstrual age) has been reported by (Wang et al., 2021). Although the individual uniqueness was validated by a split-half approach with only a short time interval (1 min) between two sessions, and the age range of individuals is relatively small, it promisingly hints at the existence of an infant functional connectome fingerprint. Meanwhile, some functional connections in higher order association cortices are consistently identified as the most distinctive connections for both individual identification and cognitive performance prediction (Finn et al., 2015; Liu et al., 2018; Miranda-Dominguez et al., 2018; Horien et al., 2019), highlighting the association between the connectome fingerprint and cognitive functions and behaviors.

In this study, capitalizing on a longitudinal high-resolution structural MRI (sMRI) and rs-fMRI dataset acquired from the University of North Carolina (UNC)/University of Minnesota Baby Connectome Project (BCP; Howell et al., 2019), state-of-the-art infant-tailored sMRI and fMRI processing pipelines (Li et al., 2019), a fine-grained infant-specific functional parcellation map along with an infant-tailored functional connection selection, and validation strategy, we aim to provide the delineation of an infant functional connectome fingerprint by examining the following: (1) whether the individualized functional connectome pattern exists during early brain development and keeps stable over months to years, (2) which functional connections and networks manifest the most individualized uniqueness during infancy, (3) how the functional connectome fingerprint evolves with early brain development, and (4) the relationship between brain functional connectome fingerprint and early cognitive performance. Answering these points is of neuroscientific significance not only for systematically understanding the origin of individualized brain functional organization patterns but also the crucial impact of infancy to one's lifetime.

Materials and Methods

To study the existence and stability of a functional connectome fingerprint, we use 104 subjects with 806 longitudinal high-resolution sMRI and rs-fMRI scans acquired from the BCP (Howell et al., 2019). In the identification procedure, feature selection is introduced because subsets of connections are found to have higher identification accuracy than the whole-brain connectome. Then, an identification-specific cross-validation was specifically designed for the analysis involving feature selection. Next, the factors that affect the identification accuracy were studied by pinpointing the most contributive edges for identification, comparing identification rates with shorter time duration, coarser brain parcellation, and more longitudinal information. The gender and head motion effects were also examined. Furthermore, to delineate how the functional connectome fingerprint evolves during infancy, we performed identification tests on five adjacent age groups (0–6 months, 6–9 months, 9–12 months, 12–18 months, and 18–24 months of age). Finally, we examined the relevance of a functional connectome fingerprint to cognitive performance by studying the similarity in contributive edges and networks between infant individual identification and individual early learning composite (ELC) cognitive score predictions.

Subjects and image acquisition

Subjects in this study are from the BCP (Howell et al., 2019). For the study of normal early brain development, all infants recruited in BCP were born at the gestational age of 37–42 weeks and were free of any major pregnancy and delivery complications. We used 104 subjects (53 females, 51 males) with 806 longitudinal scans acquired at different ages ranging from 16 to 874 d. All infant MRIs were acquired during infants' natural sleep using a 3T Siemens Prisma MRI scanner with a Siemens 32-channel head coil. T1-weighted images (208 sagittal slices) were obtained by using the three-dimensional magnetization-prepared rapid gradient echo sequence: repetition time (TR), echo time (TE), and inversion time (TI) = 2400, 2.24, 1600 ms, respectively; flip angle = 8°, and resolution = 0.8 × 0.8 × 0.8 ${\text{mm}}^3$. T2-weighted images (208 sagittal slices) with turbo spin-echo sequences (turbo factor = 314, echo train length = 1166 ms): TR, TE = 3200, 564 ms, respectively; and resolution = 0.8 × 0.8 × 0.8 ${\text{mm}}^3$ using a variable flip angle. All structural MRI data were assessed visually for excessive motion, insufficient coverage, and/or ghosting to ensure sufficient image quality for processing. For the same cohort, rs-fMRI scans were also acquired using a blood oxygenation level-dependent (BOLD) contrast-sensitive gradient echo echo-planar sequence: TR = 800 ms, TE = 37 ms, flip angle = 80°, field of view = 208 × 208 mm, 72 axial slices per volume, resolution = 2 × 2 × 2 ${\text{mm}}^3$, total volumes = 420 (5 min 47 s). fMRI scans include anterior to posterior scans and posterior to anterior scans, which are two opposite phase-encoding directions for better correction of geometric distortions. Here, in BCP, setting same scanning parameters for all the subjects at different ages may not be the optimal protocols for some ages but would largely avoid the inconsistency and uncertainty resulting from different scan protocols, which is beneficial for our study. We also used cognitive data that were collected within a month around each fMRI data collection. Specifically, we used ELC cognitive scores defined in Mullen Scales of Early Learning (Yitzhak et al., 2016), which is a composite of the expressive language, fine motor, receptive language, and visual reception scores. We selected age-equivalent scores for our study because they are more suitable for research related to longitudinal cognitive scores (Mullen, 1989).

Image processing

All structural and functional MRIs were processed following state-of-the-art infant-tailored pipelines (Li et al., 2019; Zhang et al., 2019), which have been extensively validated in many infant studies (Meng et al., 2016, 2018; Wang et al., 2019). All T1-weighted and T2-weighted MRIs were processed by iBEAT V2.0 Cloud (https://www.ibeat.cloud/) with the following main steps: (1) skull stripping by a learning-based method (Shi et al., 2012); (2) cerebellum and brainstem removal by a deep-learning-based model (densely connected U-Net); (3) intensity inhomogeneity correction by the N3 framework (Sled et al., 1998); (4) tissue segmentation using an age-specific deep-learning-based framework (Wu et al., 2017; Wang et al., 2018), which was visually inspected to ensure sufficient accuracy; and (5) noncortical structures filling and left/right hemisphere separation (Li et al., 2014b). After that, for each hemisphere of each scan, the topologically correct and geometrically accurate inner (white/gray matter interface), middle, and outer (gray matter/cerebrospinal fluid interface) cortical surfaces were reconstructed using a topology-preserving deformable surface method based on tissue segmentation results (Li et al., 2014a). The inner cortical surface, which has vertex-to-vertex correspondences with the middle and outer cortical surfaces, was further smoothed, inflated, and mapped onto a standard sphere (Fischl et al., 1999). Each spherical surface of each subject was aligned onto its age-group-specific template in the University of North Carolina 4D Infant Cortical Surface Atlas (https://www.nitrc.org/projects/infantsurfatlas/; Li et al., 2015; Wu et al., 2019) using Spherical Demons (Yeo et al., 2010), thus warping all cortical surfaces across subjects and ages to a common space. Then all cortical surfaces were accordingly resampled using the same mesh tessellation, thus establishing cortical vertex-to-vertex correspondences among individual surfaces. Infant rs-fMRI preprocessing was conducted according to an infant-specific functional pipeline in the following steps (Li et al., 2019; Zhang et al., 2019): (1) correction of head motion and spatial distortion using the Functional MRI of the Brain Software Library (FSL); 2) registration of fMRI scans onto the corresponding structural MRI scans by boundary-based registration (Greve and Fischl, 2009) via aligning fMRIs to the tissue segmentation map obtained from T1- and T2-weighted images to avoid inaccurate alignment because of the substantially different image appearances at different ages, (3) resampling fMRI data in the native space through a one-time resampling strategy by concatenation of the above two transformations, (4) removing linear trends in the data based on a conservative high-pass filtering with a σ of 1000 s, (5) decomposing each fMRI signal into 150 components using individual independent component analysis by MELODIC (Multivariate Exploratory Linear Optimized Decomposition into Independent Components) in FSL, and (6) removing noisy components based on a deep-learning model (Kam et al., 2019). At each cortical vertex on the resampled middle cortical surface, its representative fMRI time series were extracted (Glasser et al., 2016).

Infant-specific functional parcellation and network definition

An infant-specific fine-grained cortical functional parcellation map with 602 cortical ROIs, as shown in Figure 1C, was constructed based on 1064 longitudinal resting-state fMRI scans from 197 subjects during the first 2 years after birth (also from BCP data) using the following steps (Wang et al., 2020): (1) An individual gradient density map of functional connectivity for each scan was computed (Gordon et al., 2016), (2) the group-average functional gradient density map was generated by averaging the individual gradient density maps, and (3) a watershed method was applied on a group-average functional gradient density map to generate the corresponding functional parcellation map (Gordon et al., 2016). Each individual's cortical surfaces were then parceled into 602 ROIs by aligning them onto the obtained group-level infant-specific functional parcellation map, which has been validated by the measures of reproducibility and homogeneity following the ways in Gordon et al. 2016. Then, all time series within each ROI were averaged and further correlated with those from all the others. A $602\times 602$ functional connectivity matrix was derived by calculating Pearson's correlation coefficient between the time series courses (low-frequency band of interest, 0.01–0.1 Hz) of each pair of ROIs. Fisher's r to z transformation was conducted to improve the normality of the functional connectivity. For the subjects who had multiple scan directions and sessions at the same age, we combined all the corresponding functional connectivity matrices via averaging to reduce noise (Cao et al., 2019). During the processing, all cortical surfaces from individual scan spaces were warped to the Human Connectome Project (HCP) 32k_LR space and were further resampled to meshes with 32,492 vertices. To obtain the networks definition, we registered Yeo's seven-network atlas (Yeo et al., 2011) to the HCP 32k_LR space; the networks are shown in Figure 1C.

Figure 1.

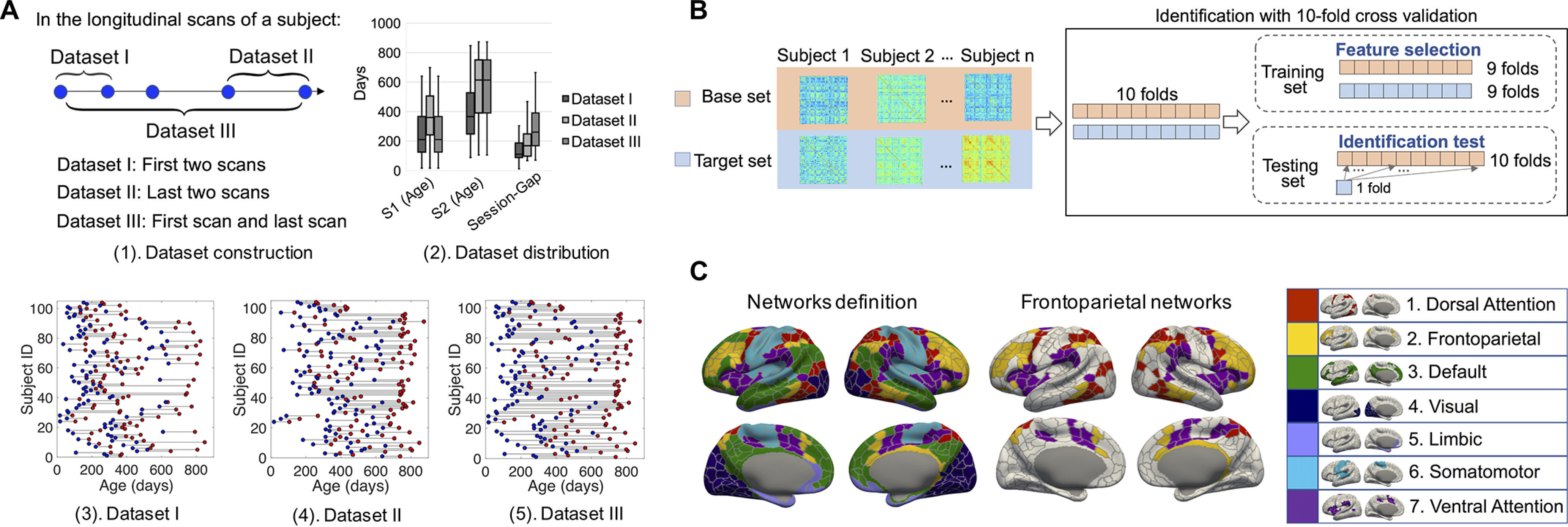
The process of dataset description, identification-specific cross-validation, and network definition. A, Dataset construction and description. To study the fingerprinting using datasets with different distributions of age and session gaps, we generated three datasets from 806 longitudinal scans from 104 subjects, each with at least two longitudinal scans. Datasets I–III consisted of all the first two scans, all the last two scans, and all the first and last scans, respectively. A(3)–(5), The scan distribution of Datasets I–III, where the blue and red points represent the scans acquired from session 1 and session 2, respectively. For detailed age distribution information of the three datasets, the box plots of the scan age of session 1 (S1), session 2 (S2), and the session gap between S1 and S2 are shown in A(2). B, Identification procedure with one round of 10-fold cross-validation. Each subject has a pair of scans acquired from two sessions that constitute a base set and a target set for the identification test. First, the target set and base set were partitioned into 10 folds by correspondingly partitioning the subjects set; the training set consists of nine folds from target and base sets; the testing set consists of the remaining fold of the target set and the whole base set. Then, a feature selection procedure was implemented to obtain the edge set with the largest SD among subjects. Finally, infant identification was conducted on the testing set. C, Node and network definition. We leveraged an infant-specific fine-grained brain functional parcellation map with 602 cortical nodes (ROIs) defined from the BCP dataset (Wang, 2020). Seven networks were then grouped from the nodes according to a popular network template (Yeo et al., 2011) for comparison with the results obtained in adults.

Experimental design and statistical analysis

Identification test

Datasets preparation

Among the 104 subjects with 806 longitudinal rs-fMRI scans, 47 subjects have 2 longitudinal scans, 28 subjects have 3 longitudinal scans, and 29 subjects have 4 or more longitudinal scans after combining the scans acquired from the same subject at the same age (multiple scan directions and sessions). To study the impact of the distribution of subject age and session gap (the time interval between two fMRI sessions) on infant brain connectome fingerprinting, three representative datasets (i.e., Datasets I–III) were derived. Figure 1A illustrates how these datasets were generated and the age distribution of each dataset. In every dataset, each subject has a pair of longitudinal scans acquired from two sessions at different ages, with session 1 being earlier than session 2. The basic information of the three datasets is shown in Figure 1A and Table 1. The mean $\pm$ SD of the mean framewise displacement (FD) power before processing and the number of DVARS (SD of intensity difference between successive time points) outliers after processing are also included in Table 1. Motion outliers were identified by thresholding the DVARS at the 75th percentile plus 1.5 times the interquartile range.

Table 1.

The demographic information of the three datasets

Datasets	Age (minimum - maximum)	Age (mean ± SD)	Session gap (minimum - maximum)	Session gap (mean ± SD)	Mean FD	DVARS outlier
Dataset I	16 - 848 D	335 ± 205 D	12 - 589 D	147 ± 93 D	0.28$\pm$ 0.16 mm	2.97 ± 5.28
Dataset II	17 - 874 D	463 ± 211 D	68 - 589 D	191 ± 120 D	0.27$\pm$ 0.12 mm	2.36 ± 4.22
Dataset III	16 - 874 D	410 ± 243 D	70 - 665 D	298 ± 176 D	0.27$\pm$ 0.15 mm	2.64 ± 4.80

D, Days.

Feature-selection-based identification test

Although all the prior research on functional connectome fingerprinting used all the edges for individual identification, and there is evidence that more edges are beneficial for higher identification accuracy in adults (Byrge and Kennedy, 2019), we found that proper selection of edges can improve the identification accuracy in infants (Fig. 2). Thus, we proposed feature-selection-based identification via estimating the differential capability of an edge by its SD across subjects. Because feature selection was involved in the identification process, we designed an identification-specific 10-fold cross-validation and repeated it 20 times for the infant identification analysis.

Figure 2.

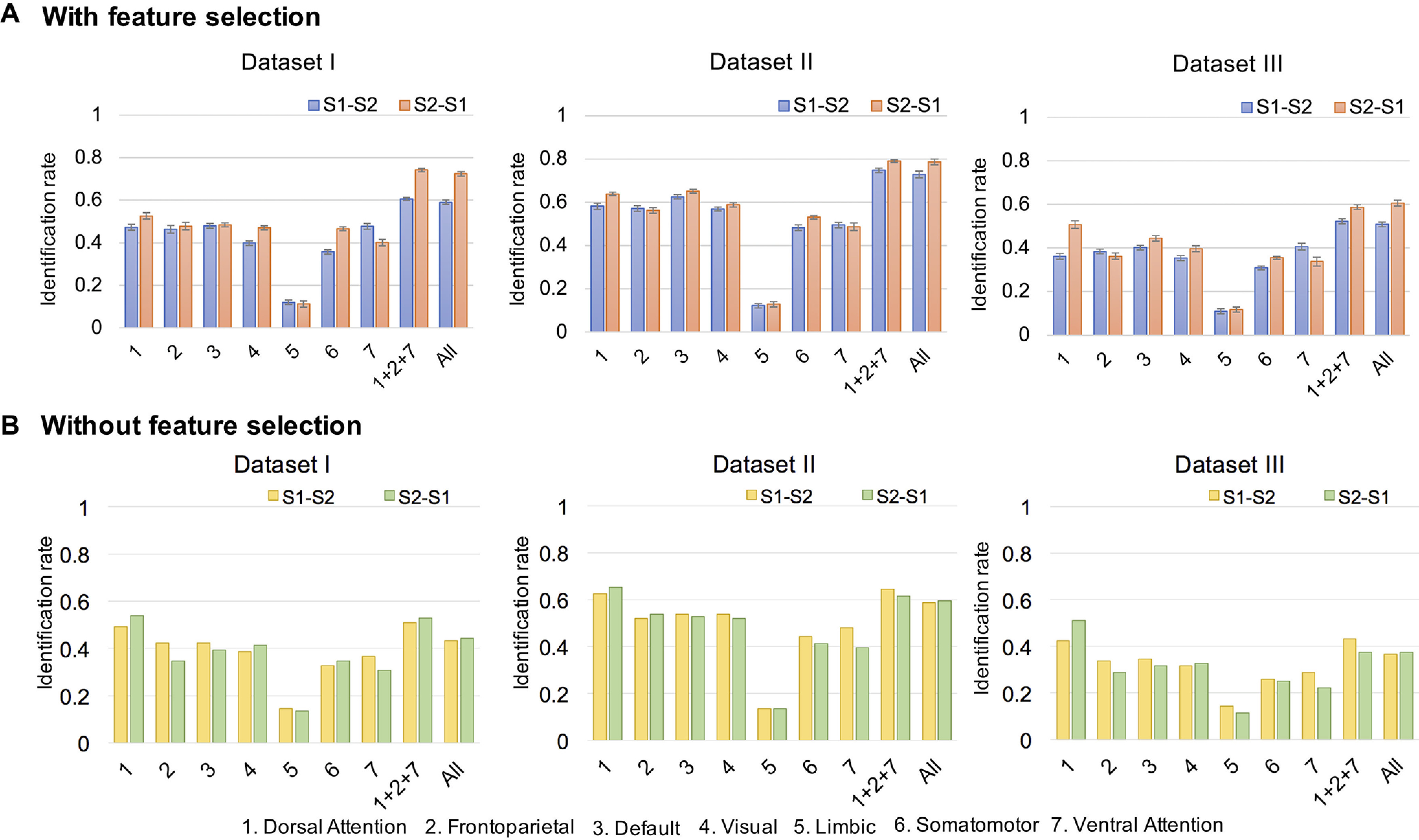
The identification rates across session pairs and networks. Identification rates based on whole-brain connectivity (All), frontoparietal networks (1 + 2 + 7), and seven individual networks. The color of the bars, blue/red in the top row and yellow/green in the bottom row, indicates different session pairs as base set, target set, where session 2 (S2) was acquired later than session 1 (S1) and the error bar in figure A is the SD of identification rates. A, The identification rates obtained with feature selection and identification-specific cross-validation. B, The identification rates obtained without feature selection.

Target set, base set, and identification rate

The individual infant identification test was performed across paired scans consisting of one target set, $T=\{X_i^t,i=1,2,\cdots ,n\}$, and one base set, $B=\{X_j^b,j=1,2,\cdots ,n\}$, where $X_i^t$ and $X_j^b$ are all flattened vectors of the upper triangle of the whole-brain connectivity matrix (602 nodes, 180,901 edges) and the subscripts $i$ and $j$ denote the subject index. With the requirement that $X_i^t$ and $X_i^b$ are acquired from the $i^{th}$ subject at different ages, each subject has two longitudinal fMRI scans from two different sessions. In the process of identification, one target matrix, $X_i^t$, was selected from the target set $T$, and Pearson's correlation coefficient was used to measure the similarity between $X_i^t$ and all the matrices in base set $B$. The corresponding similarity matrix is defined as follows: $H={\left(h_{ij}\right)}_{n\times n}$, $h_{ij}=corr(X_i^t,X_j^b)$. The identity in $B$ having the largest similarity with $X_i^t$ was regarded as the predicted identity of $X_i^t$, that is, as follows:

$$Identity\left(X_i^t\right)=argma{x}_{j}corr(X_i^t,X_j^b).$$

After this identification process was implemented iteratively for all the subjects in $T$, the identification rate was measured as the percentage of subjects whose identity was correctly predicted among the total number of subjects. The differential identifiability of similarity matrix is defined as ${\text{I}}_{\text{diff}}=({\text{I}}_{\text{self}}-{\text{I}}_{\text{others}})\times 100,$ where ${\text{I}}_{\text{self}}$ and ${\text{I}}_{\text{others}}$ are the average diagonal elements and the off-diagonal element of similarity matrix $\text{H}$, respectively.

Feature selection and identification-specific cross-validation

All the connections (including negative correlations) in the connectome were considered as possible features for identification. In the iterative analysis, features were selected on the training set, and infant identification was implemented on the testing set. First, the target set $T$ and base set $B$ were partitioned into 10 folds by correspondingly partitioning the subjects set; a training set is represented as $\{T_{tr},B_{tr}\}$ and constituted 9 folds from $T$ and $B$; a testing set is represented as $\{T_{te},B\}$ and constituted the remaining fold of target set and the whole base set $B$. Of note, the testing set should be constructed as $\{T_{te},B_{te}\}$ if we follow the conventional method of cross-validation, where $B_{te}$ is the remaining fold of the base set. It means for each $X_i^t$ in $T_{te}$, the identity of $X_i^t$ will be determined within $B_{te}$, which obviously decreases the difficulty of identification and leads to a false high accuracy. Thus, we proposed an identification-specific cross-validation and set the testing set as $\{T_{te},B\}$. Then, a feature selection procedure was implemented by ranking features according to their SD across subjects in the training set, retaining only features with the highest SD values bigger than the thesholded percentile. For each edge $e$ in the connectome, the SD of $e$ was computed as follows:

$$SD\left(e\right)=0.5\times (\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^{\left|T_{tr}\right|}(e_i-\frac{1}{\left|T_{tr}\right|}{{\displaystyle \sum }}_{i=1}^{\left|T_{tr}\right|}{e}_i)}{\left|T_{tr}\right|}}+\sqrt{\frac{{{\displaystyle \sum }}_{j=1}^{\left|B_{tr}\right|}(e_j-\frac{1}{\left|B_{tr}\right|}{{\displaystyle \sum }}_{j=1}^{\left|B_{tr}\right|}{e}_j)}{\left|B_{tr}\right|}}),$$

where $e_i$ and $e_j$ are the edges of $i^{th}$ and $j^{th}$ subject in $T_{tr}$ and $B_{tr}$, respectively; $|\cdot |$ represents the number of subjects in the set. Third, infant identification was conducted on the testing set by taking $T_{te}$ and $B$ as the target set and the base set, respectively. After the identification process was implemented iteratively for all the subjects in the target set $T$, the identification rate was measured as the percentage of subjects whose identity was correctly predicted among the total number of subjects.

Network-based identification test

In addition to conducting the identification test based on the whole-brain connectivity, we also tested the identification performance of the seven networks (Yeo et al., 2011). We repeated 20 times of 10-fold cross-validation described above separately for each network and only included the within-network edges for identification. The mean and SD of the identification rate over all cross-validations were also used to show the predictive power of each network.

Factors affecting identification test

Contributive edges and networks

In the identification test, 20 times of 10-fold cross-validation were implemented. Because the training set in each iteration was slightly different, 200 different sets of edges were selected as the features for further identification or prediction. The selected frequency was used to measure the edgewise contribution, which was computed in the following steps: (1) A binary 200 $\times$ 180,901 matrix was generated to represent the 200 different sets of selected edges with each row representing the selected edges in one iteration, where the elements 1 and 0 indicate the corresponding edge is selected and not selected, respectively; (2) each row of the matrix was normalized by the number of the selected features in this iteration; and (3) the values of each column were averaged to obtain the selected frequency of the edge. Then, the selected frequency of the within- or between-network edges were summed up and normalized by the total number of the corresponding edges to measure the network-wise contribution, respectively.

Identification with shorter time duration

To investigate the identification capability of the functional connectome over shorter acquisition durations, we performed whole-brain-based identification on the 104 subjects while varying the number of time points used to calculate connectivity matrices. With the same starting point, each subject's full 5 min 47 s rs-fMRI run was truncated to $\{\frac{4}{5},\frac{3}{5},\frac{2}{5},\frac{1}{5},\frac{1}{6}\}\times 420$ time points. For each reduced time series, 20 times of 10-fold identification-specific cross-validation were implemented to obtain the corresponding identification rate.

Identification with coarser parcellation of brain

To investigate the effect of the specific choice of parcellation maps on identification, we repeated the identification experiments using connectivity matrices calculated from the 360-node (Glasser et al., 2016) and 68-node (Desikan et al., 2006) parcellation maps by aligning the cortical surface onto the UNC 4D Infant Cortical Surface Atlas (Wu et al., 2019). As the identification test implemented with 602 nodes, 20 times of 10-fold identification-specific cross-validation were implemented to obtain the corresponding identification rate.

Identification based on two-base set and two-target set

In an effort to validate accumulated uniqueness across longitudinal scans, we also tested a design option in which two longitudinal matrices were included in the base set or target set for each subject. In the ordinary identification test design, there was only one scan in the target set and one corresponding scan in the base set for each subject. Adding an additional longitudinal scan acquired on a different age has the potential to improve the identification performance. Therefore, we designed two identification tests by adding one longitudinal scan to the base set and target set. Fifty-seven subjects with more than two longitudinal scans were used to generate three datasets, that is, MM-Dataset I, MM-Dataset II, and MM-Dataset III, where “MM” means two longitudinal matrices (M) were used during the identification and is used to differentiate these datasets with the ones used in the standard identification. Each subject has three scans in every dataset. MM-Dataset I, MM-Dataset II, and MM-Dataset III consisted of the first three scans, the last three scans, and the first/middle/last scans, respectively, where middle is defined as the biggest integer smaller than half of the longitudinal scan number of the subject. For the identification based on a two-base set, we created a base set that included two connectivity matrices obtained from the scans acquired longitudinally as follows: $B=\{\left(X_i^1,X_i^2\right),i=1,\cdots ,57\}$. To predict the subject identity, we linearly project the current target matrix $Y_j$ ($j=1,\cdots ,57$) to the subspace spanned by the pair $\left(X_i^1,X_i^2\right)$ to obtain a projection ${\widehat{Y}}_j$ and then computed the correlation between $Y_i$ and ${\widehat{Y}}_j$ to find the best match. On the other side, for the identification based on a two-target set, we created a target set that included two connectivity matrices obtained from the scans acquired longitudinally as follows: $D=\{\left(Y_j^1,Y_j^2\right),i=1,\cdots ,57\}$. To predict the subject identity, we linearly project the base set matrix $X_i$ to the subspace spanned by the pair $\left(Y_j^1,Y_j^2\right)$ to obtain a projection ${\widehat{X}}_i$ and then computed the correlation between $X_i$ and ${\widehat{X}}_i$ to find the best match.

In each dataset, because every subject has three scans acquired at three sessions ($t_1,t_2,t_3$), the two-base set identification was implemented on the base-target pairs of ($t_1,t_2)$-$t_3$, ($t_1,t_3)$-$t_2$, ($t_2,t_3)$-$t_1$, and the two-target set identification was performed on the base-target pairs of $t_1$-($t_2,t_3)$, $t_2$-($t_1,t_3)$, $t_3$-($t_1,t_2)$. The identifications with a normal base set and target set (i.e., including only one connectivity matrix for each subject) were implemented on the pairs of $t_1$-$t_2$, $t_1$-$t_3$, $t_2$-$t_3$, $t_2$-$t_1$, $t_2$-$t_3$, $t_3$-$t_1$. The identification rates of the two-base set and two-target set were the average of identification rates of 20 times of 10-fold cross-validation across three base-target pairs.

Effects of gender and head motion

To test the gender effect, the identification rates were broken down to males and females, and then the paired t test across three datasets and two base-target pairs were adopted for determining whether there is significant gender difference in the identification test. To examine the possibility that the identification resulted from the individual characteristic of movement patterns, we used motion estimates solely to implement the identification test. Specifically, (1) we calculated motion vector for each scan based on DVARS; (2) the mean and SD of the DVARS across all scans were computed; (3) 60 bins that spanned the grand mean $\pm$ SD were specified, and the motion distribution vectors were computed correspondingly; (4) the motion distribution vector of a subject having multiple scan directions and sessions at the same age was obtained by averaging the motion distribution vectors of the corresponding scans; and (5) the functional connections were replaced by the motion distribution vectors in the three datasets, and the identification tests were implemented the same way as for using the functional connections for infant identification.

Identification in adjacent age groups

To further investigate whether the identification rate is related to the age of the subjects and whether the contribution of the seven networks to identification and their individual identification performances change along with brain development, we tested the identification rate with five adjacent datasets across different age groups, that is, 0–6 months, 6–9 months, 9–12 months, 12–18 months, 18–24 months (with 19, 21, 14, 30, and 15 subjects, respectively). The scan acquired at an age within 30 d from the age group was included in the corresponding dataset to increase the number of subjects in each dataset. We repeated 20 times of 10-fold identification-specific cross-validation with the same procedure shown in Figure 1B for each age group and assessed the identification performance by averaging the accuracies over all cross-validations.

Association between connectome distinctiveness and age

After the identification process was implemented iteratively for all the subjects across Dataset I, Dataset II, and Dataset III, in a dataset, the connectome distinctiveness of each subject was defined as the percentage of it being correctly identified across 20 times of 10-fold cross-validation based on a base-target pair of session 1 to session 2. The scan age of this subject at session 1 was taken as the corresponding age for the connectome distinctiveness. The (age, connectome distinctiveness) pairs in Datasets I–III were concatenated together. Then, with this concatenated dataset, we repeatedly fitted a smooth curve with automatic estimation of the smoothness parameters (Fjell et al., 2010) between connectome distinctiveness and age, with mean and SD computed across 10,000 bootstraps.

Cognitive score prediction

To explore whether the most contributive networks for a functional connectome fingerprint are also predictive for infant cognitive performance, the whole brain and the frontoparietal connectivity profile, were separately used to predict the ELC score in the Mullen Scales of Early Learning assessment (Yitzhak et al., 2016). The ELC score is the aggregation of scores of the fine motor, visual reception, receptive language, and expressive language domains. A dataset of 232 scans with corresponding ELC cognitive scores was used (143 subjects, males/females = 64/79). Comparing with the identification test, 39 more subjects were included in ELC score prediction for better model fitting and feature analysis based on machine learning.

We used random forest (RF) to perform the ELC prediction, which is widely used as a supervised machine-learning method (Kesler et al., 2017; Wlaszczyk et al., 2019) and could well address the data scarcity of the ELC score prediction because of the bootstrapping strategy. In the RF-based analysis, the number of ensemble trees equals 20, and the minimum number of observations per tree leaf equals five (as the default in MATLAB), whereas a different number of ensemble trees from 5 to 60 were tried in our experiment and achieved similar results. We used 20 times of 10-fold cross-validation to estimate the prediction performance. Each subject belongs to only the training set or the testing set in each fold to ensure the independence of the data in training and testing. Feature selection and prediction modeling were implemented in the training set, and the ELC score prediction was performed on the testing set. The following steps were used for the prediction of the ELC. First, feature selection was implemented on the training set. Only the edges with the highest Pearson's correlation coefficient with the ELC score, corresponding to p < 0.001, were retained for modeling (different p values of 0.1, 0.05, 0.01, and 0.005 were tried in our experiment and achieved similar results). Then, the selected edges were separated into two tails, those positively correlated with ELC and those negatively correlated with ELC. By summing all the absolute correlation values of all the edges in the corresponding feature set, two single-subject summary statistics were generated based on the selected edges, that is, positive whole-brain network strength and negative whole-brain network strength. For an individual connectivity matrix, the two summary statistics were defined as follows:

$$S_{Positive}={\displaystyle \sum }_e\left|r_e\right|m_e^{+}$$

$$S_{Negtive}={\displaystyle \sum }_e\left|r_e\right|m_e^{-},$$

where $r_e$ is the Pearson's correlation between the two nodes of edge $e$, and $m_e^{+}=1$, $m_e^{-}=0$ when $r_e>0$, otherwise $m_e^{+}=0$, $m_e^{-}=1$. Moreover, RF was adopted to model the relationship between the two single-subject summary statistics ($S_{Positive}$, $S_{Negtive}$) and the dependent variable ELC, because the bootstrapping strategy used in RF and the summarized features could well address the data scarcity issue in ELC prediction. Finally, the ELC scores of the unseen subjects in the testing set were predicted with the trained RF model. With all the 20 times of 10-fold cross-validation finished, the predicted values obtained from each time of 10-fold cross-validation were averaged as the final predicted value to estimate the overall performance of the model. The mean absolute error and Pearson's correlation of the predicted and observed scores yielded the indexes of the accuracy performance. To estimate the predictive power of each edge, we computed the frequency of this edge being selected across all iterations. To further explore the contribution of the networks to ELC prediction, the frequencies of the within- and between-network edges were summed and normalized by the total number of the corresponding network edges. The contribution of the edges was summarized separately with the negatively and positively correlated feature set.

Results

Infant identification with brain functional connectome

Whole-brain-based identification

Using the feature-selection-based identification test, we obtained identification rates well above chance with all the three datasets (Fig. 2A). The results demonstrate that the functional connectome fingerprint may exist during early infancy and keep stable over months. Specifically, the identification rates (mean $\pm$ SD) of 104 infants over 20 times of 10-fold cross-validation were 58.99 $\pm$ 1.05% (Dataset I), 72.88 $\pm$ 1.52% (Dataset II), and 50.87 $\pm$ 0.98% (Dataset III) based on a base-target pair of session 1-session 2 and 72.36 $\pm$ 0.98% (Dataset I), 78.61 $\pm$ 1.32% (Dataset II), and 60.72 $\pm$ 1.33% (Dataset III) of the reverse session 2-session 1. With relatively older ages of the scans, Dataset II reaches the best performance in the three datasets, indicating that the individualized functional connectome patterns tend to be more stable with increasing age. Meanwhile, with the largest session gap distribution, the relatively lower accuracy obtained by Dataset III reveals increasing identification difficulty with the longer interval between sessions. We also performed 1000 times of permutation testing to estimate the statistical significance of these identification rates. The mean identification rates over 1000 permutation testing were 1.02 $\pm$ 1.02% (Dataset I), 1.03 $\pm$ 1.13% (Dataset II), and 1.07 $\pm$ 1.04% (Dataset III) based on a base-target pair of session 1-session 2, and 1.06 $\pm$ 1.00% (Dataset I), 1.01 $\pm$ 0.97% (Dataset II), and 1.10 $\pm$ 0.95% (Dataset III) of the reverse session 2-session 1, whereas the corresponding p values were all equal to zero.

Network-based identification

We next used each of the seven functional networks (Fig. 1C) and certain combinations of these networks to examine which functional networks manifest more individualized uniqueness during early brain development. Although all the single networks led to lower identification rates than the whole-brain connectome (Fig. 2A), the one-tailed paired t test across three datasets and two base-target pairs showed that the dorsal attention network (network 1) and default network (network 3) are the only two networks that achieved higher identification rates than all the other four networks (dorsal attention network, $p<{10}^{-2}\sim {10}^{-4}$; default network, $p<{10}^3\sim {10}^{-4}$). There is no significant difference in identification rates achieved by the dorsal attention network and the default network. Among all the combinations of any two networks and three networks, after implementing identification tests on them, the combination of the dorsal attention network (network 1), frontoparietal network (network 2), and ventral attention network (network 7), referred to as the frontoparietal networks (Finn et al., 2015; networks 1 + 2 + 7), led to the highest average identification rate across the two base-target pairs. Specifically, it reached 60.53 $\pm$ 0.58% (Dataset I), 74.76 $\pm$ 0.98% (Dataset II), and 52.36 $\pm$ 1.15% (Dataset III) based on the base-target pair of session 1-session 2 and 74.18 $\pm$ 0.78% (Dataset I), 79.09 $\pm$ 0.61% (Dataset II), and 58.80 $\pm$ 1.00% (Dataset III) of the reverse session 2-session 1. Based on the one-tailed paired t test across 20 times of 10-fold cross-validation, frontoparietal networks tend to have significantly higher capability of infant identification than the whole-brain connectome in five ($t_{(19)}=2.61\sim 5.39$, $p<{10}^{-3}\sim {10}^{-6})$ of six base-target pairs over three datasets.

Factors affecting identification accuracy

Contributive edges for identification

Although no studies have yet showed that more edges could decrease identification accuracy, we observed that the identification rates with all the edges in whole-brain connectivity were only 43.27% (Dataset I), 58.65% (Dataset II), and 36.54% (Dataset III) based on a base-target pair of session 1-session 2 and 44.23% (Dataset I), 59.62% (Dataset II), and 37.50% (Dataset III) of the reverse session 2-session 1. The performance of the whole-brain connectivity was significantly lower than the identification with SD-based feature selection (Mann–Whitney U test on the six identification tests on three datasets over two base set-target set directions, rank sum = 54, one-tailed $p=0.0076$). The network-based identification rates without feature selection are shown in Figure 2B. The benefit of feature selection is demonstrated by comparing Figure 2, A and B. Moreover, Figure 3 demonstrates that including low contributive edges for identification may degrade accuracy. First, as shown in Figure 3A, the superiority of diagonal elements compared with nondiagonal is more obvious in the cross-subject similarity matrix obtained with selected edges. Second, in Figure 3B, the differential identifiability of the cross-subject similarity matrices obtained by whole-brain edges is lower than the ones obtained by the selected edges thresholded at the 95th percentile of the SD values. Third, Figure 3C illustrates that the identification rate increases as the threshold becomes greater and sharply decreases after reaching the peak value with the threshold equal to 0.95 ∼ 0.98. Of note, the results shown in Figure 3, A and C, were only based on Dataset II for illustrating the importance of feature selection, and the corresponding results obtained from Dataset I and Dataset III were similar.

Figure 3.

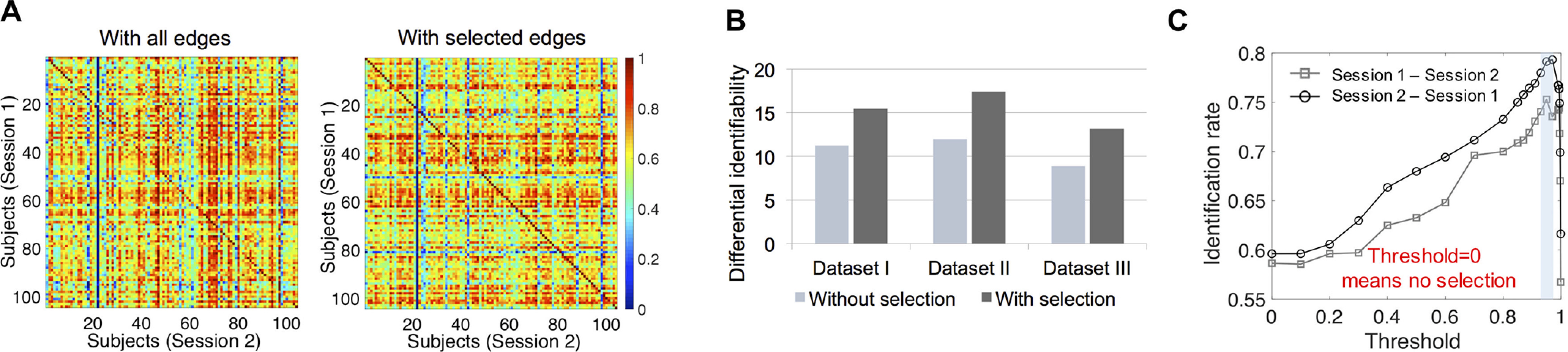
The importance of feature selection in the identification test of infants. A, The 104 × 104 cross-subject similarity matrices based on whole-brain edges and the selected edges thresholded at the 95th percentile of the SD values (Dataset II). Session 2 (S2) was acquired later than session 1 (S1). All the elements in the similarity matrices have been normalized by the maximum of each row. B, The average differential identifiability of corresponding cross-subject similarity matrices obtained with whole-brain edges and the selected edges thresholded at the 95th percentile of the SD values (Datasets I–III). C, The effect of the threshold for feature selection on identification accuracy. After the differential capability of the edges was ranked according to their SD across subjects, different thresholds of percentiles determine the edges retained for further identification. The shaded area represents the optimal area of the identification rate. In experiments, the threshold for each fold was determined by its performance on the training set.

The discriminative power of each edge (edgewise contribution) was measured by the average frequency with which this edge was selected across all iterations. As the results of the edgewise contribution in the three datasets are similar (two-tailed paired t tests on the three pairs of the datasets, $p=1$), we only show the contribution analysis based on Dataset II in Figure 4A. Approximately 69% of the edges with a high contribution to identification were intranetwork connections. Approximately 38 and 50% of the high contributive edges were linked to the dorsal attention network and visual network, respectively, which suggests they possess high intersubject variability and play an important role in the infant brain functional fingerprint.

Figure 4.

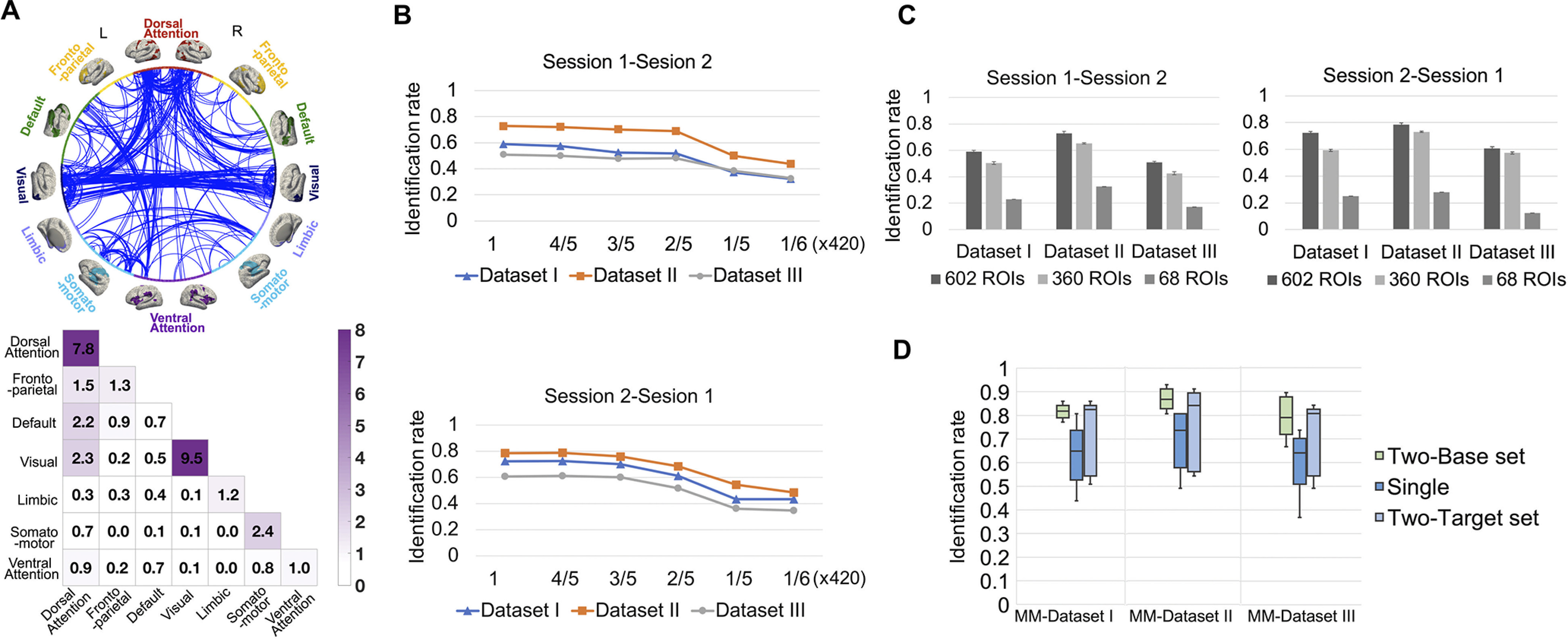
Factors affecting identification accuracy. A, Contributive edges for identification. The circle map shows the most contributive edges to identification, where the whole edge set was thresholded at the 99.9th percentile for better visualization. The 602 nodes in the whole brain are grouped into seven networks in the left (L) and right (R) hemisphere, respectively. The color (purple) in the colored matrix (bottom) shows the summed normalized contribution within and between networks. B, Identification with shorter time duration. We performed identification with a truncated rs-fMRI run, where $\left\{\frac{4}{5},\frac{3}{5},\frac{2}{5},\frac{1}{5},\frac{1}{6}\right\}$ time points with the same starting point were used to compute connectivity matrices; different curves in the figures show the identification performance obtained from three different datasets (Datasets I–III). C, Effect of parcellation scheme. We calculated the connectivity profiles of the scans based on 360-node and 68-node cortical parcellation maps and compared the identification performance of different parcellation schemes. D, Identification with two-base set including two longitudinal connectivity matrices as the base set or two-target set including two longitudinal connectivity matrices as the target set. The box plots show the performance of identification with the two-base set, two-target set, and single matrix on the three datasets (i.e., MM-Dataset I, MM-Dataset II, and MM-Dataset III) generated from 57 subjects with >2 longitudinal scans. The error bar is the SD of identification rates.

Identification with shorter time duration

We next evaluated the distinguishability of the functional connectome fingerprint associated with the rs-fMRI BOLD signal acquisition duration. The identification rates obtained by the truncated rs-fMRI run with $\left\{\frac{4}{5},\frac{3}{5},\frac{2}{5},\frac{1}{5},\frac{1}{6}\right\}\times 420$ time points were investigated. We observed that although longer time series tend to improve identification accuracy, shorter time courses with more than ∼250 time points were able to relatively preserve the identification capability in connectivity profiles (Fig. 4B), and the identification performance degraded sharply with fewer than ∼70 time points. The number of time points at which the identification accuracy decreases was consistent across the three datasets (I–III). Thus, during infancy, the minimal rs-fMRI acquisition duration required for accurate identification is not affected by the distribution of session gap and subject age.

Identification with coarser parcellation of brain

As shown in Figure 4C, the identification rates using the 360-node atlas were 50.43 $\pm$ 1.10% (Dataset I), 65.29 $\pm$ 0.53% (Dataset II), and 42.69 $\pm$ 1.18% (Dataset III) based on a base-target pair of session 1-session 2 and 59.33 $\pm$ 0.83% (Dataset I), 73.08 $\pm$ 0.54% (Dataset II), and 57.36 $\pm$ 0.72% (Dataset III) of the reverse session 2-session 1. The identification rates using the 68-node atlas were 23.08 $\pm$ 0.00% (Dataset I), 32.69 $\pm$ 0.00% (Dataset II), and 17.31 $\pm$ 0.00% (Dataset III) based on a base-target pair of session 1-session 2 and 25.00 $\pm$ 0.00% (Dataset I), 27.88 $\pm$ 0.00% (Dataset II), and 12.50 $\pm$ 0.00% (Dataset III) of the reverse session 2-session 1. Compared with our 602-node fine-grained infant-dedicated cortical functional parcellation map, the identification rates with low-resolution parcellation were obviously reduced.

Identification based on two-base set and two-target set

The functional connectome fingerprint should be stable and be maintained across ages to a certain extent. In an effort to validate accumulated uniqueness across longitudinal scans, we performed an identification test using an expanded base set and expanded target set with two longitudinal connectivity matrices on three datasets (i.e., MM-Dataset I, MM-Dataset II, and MM-Dataset III) with different distributions of scan age and session gap. In all cases, the identification rate was improved using the two-base set or two-target set (detailed results with Mann–Whitney U test on the three datasets, respectively: rank sum = 8695, 8950, and 8453, two-sided $p<{10}^{-22},{10}^{-26},{10}^{-19}$ on two-base set vs single-matrix base set; rank sum = 7333, 7075, and 7376, two-sided $p<{10}^{-8},{10}^{-6},{10}^{-8}$ on two-target set vs single-matrix target set). Specifically, for the identification based on the two-base set, the average identification rates of 20 times of 10-fold cross-validation increased substantially to 82.16 $\pm$ 3.13% (MM-Dataset I), 86.84 $\pm$ 3.82% (MM-Dataset II), and 79.21 $\pm$ 7.41% (MM-Dataset III), respectively (average identification rates were respectively 63.49 $\pm$ 12.3%, 69.23 $\pm$ 11.43%, and 59.41 $\pm$ 11.69% with the normal single-matrix base set and single-matrix target set on the three datasets). For the identification based on the two-target set, the average identification rate of 20 times of 10-fold cross-validation increased to 73.71 $\pm$ 14.41% (MM-Dataset I), 76.87 $\pm$ 15.47% (MM-Dataset II), and 71.78 $\pm$ 13.49% (MM-Dataset III), respectively. This suggests that the uniqueness can be better captured by longitudinal information (Fig. 4D).

Effects of gender and head motion

After breaking down the identification rates according to gender, the paired t test across three datasets and two base-target pairs shows there is no significant difference between males and females ($p=0.2920$). Furthermore, the average identification rate with motion estimates vectors on the three datasets over two base-target pairs is 0.96%, which is even lower than the identification rate of chance level over 1000 permutation testing (average identification rate is 1.1%). Thus, it is unlikely that identifiability is related to idiosyncratic patterns of head motion.

Identification in adjacent age groups

The relevance of subject age to identification rate and the contribution of the seven networks to identification were tested with five adjacent datasets across different age groups, that is, 0–6 months, 6–9 months, 9–12 months, 12–18 months, and 18–24 months. As shown in Figure 5A, the frontoparietal networks (networks 1 + 2 + 7) still led to comparable identification rates as the whole-brain connectivity at all age groups. As the age increases, the advantages of high-order networks in independently identifying the identity become more obvious. We also explored the contribution of the edges and networks in each age group (Fig. 5B) following the same procedures described before. Similar pattern was found in the distribution of the most contributive edges to identification throughout the first 2 years after birth, revealing the stability of the functional connectome fingerprint across early brain development. First, the connections within the dorsal attention network and visual network make the largest contributions across all age groups. Second, the internetwork connections involving the dorsal attention network usually contribute more to the identification compared with other internetwork connections without the dorsal attention network. Finally, within-network connections are more distinctive than between-network connections. Moreover, to further study the association between connectome distinctiveness and age, we defined the connectome distinctiveness with the identification tests based on Datasets I–III, which is the average accuracy across 20 times of 10-fold cross-validation on all the three datasets based on a base-target pair of session 1-session 2. The scan age of each subject at session 1 was taken as the corresponding age with the connectome distinctiveness. The relationship between connectome distinctness and age is demonstrated by a smooth curve based on the automatic estimation of the smoothness parameter (Fjell et al., 2010) between them (Fig. 5C), with mean and SD computed across 10,000 bootstraps. There is a clear tendency that connectome distinctiveness increases with age (Fig. 5C).

Figure 5.

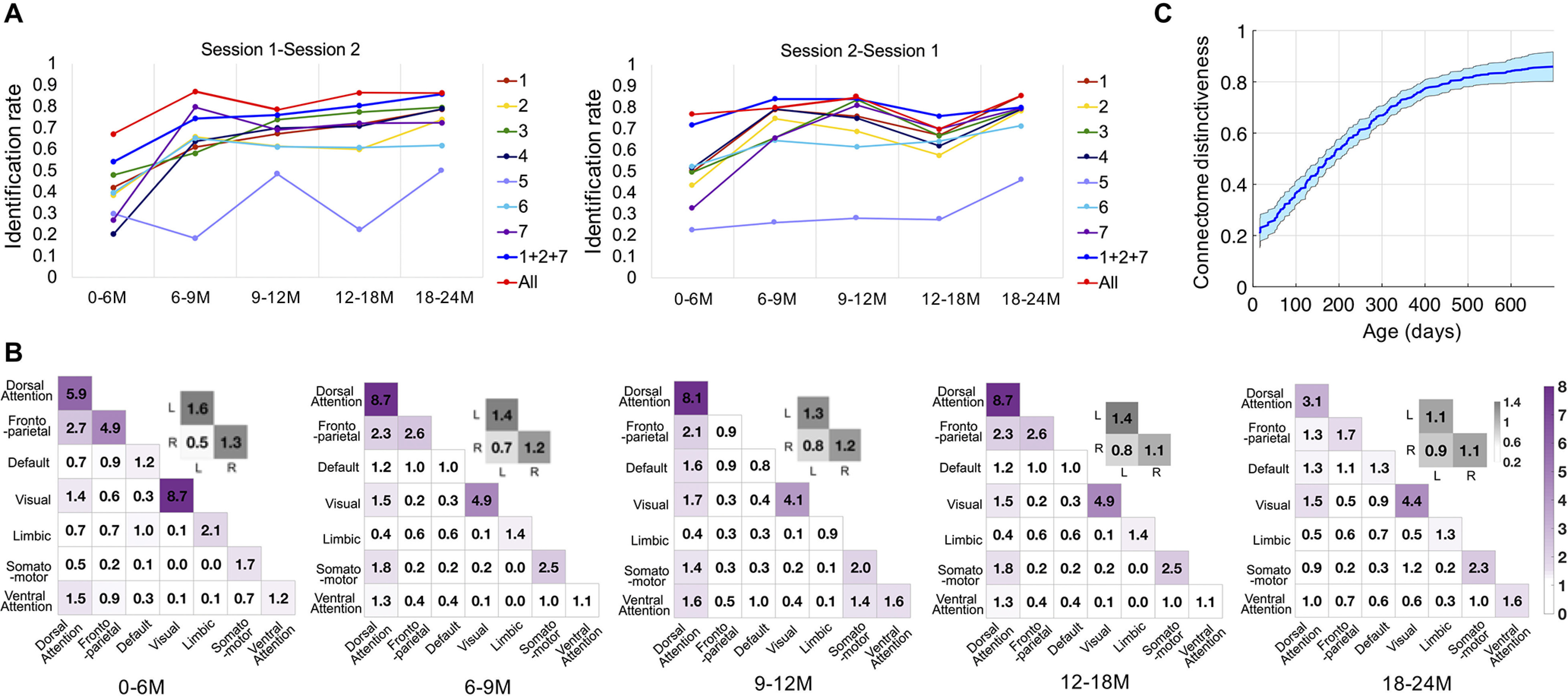
Identification in adjacent age groups. M, Month. A, The identification accuracies at five age groups of the first 2 years after birth. At different age groups, the identification rates based on the whole-brain connectivity (All), frontoparietal networks (1 + 2 + 7), and seven individual networks are represented by dots in the figure. The base set/target set sequences are shown in the top of each figure; that is, sessions 1 and 2 are the base set in the left figure and right figure, respectively. B, The contributive edges for the identification in the five age groups. The color (purple) in the colored matrices (bottom) shows the summed normalized contribution within and between networks; the color gray in the colored matrices shows the summed standardized contribution within and between left (L) and right (R) hemispheres. C, Association between connectome distinctiveness and age. The mean and SD of the smooth function fitting across 10,000 bootstraps are represented by the blue curve and shaded area, respectively.

Cognitive score prediction

In adults, it has been shown that the frontoparietal networks are the most discriminative for individuals and also have high capability in cognitive behavior prediction (Finn et al., 2015; Liu et al., 2018). Here, we explore whether this fact still holds for infants.

We found that both whole-brain connectivity ($r=0.36,p<{10}^{-9}$) and frontoparietal connectivity ($r=0.34,p<{10}^{-7}$) generated significant predictions (Fig. 6A). The dorsal attention network and somatomotor network demonstrated more predictive power for cognitive behavior. Different from the distribution of the most contributive edges for identity identification, internetwork edges showed a higher contribution to ELC prediction (Fig. 6B). Approximately 89.1 and 58.5% of the edges with a high contribution to ELC prediction were intranetwork connections in positively and negatively correlated edge sets, respectively.

Figure 6.

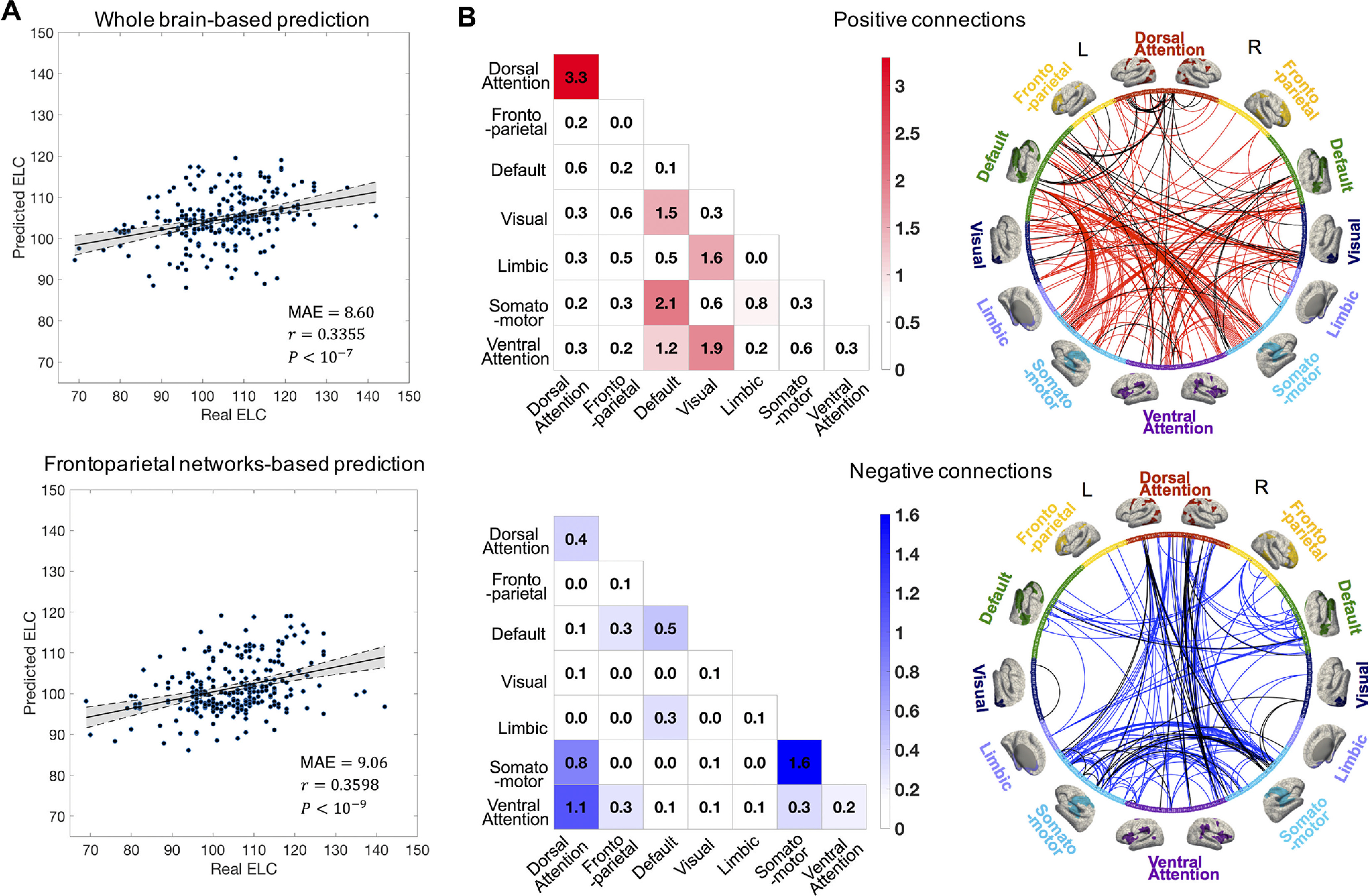
Cognitive score prediction based on functional connectome. A, ELC score prediction results based on the whole-brain connectivity and frontoparietal networks. Scatter plot shows the averaged predicted ELC from the 20 times 10-fold cross-validation and the real observed ELC. Each dot represents the predicted and real ELC pair from one subject; the gray area indicates 95% confidence interval for the best-fit line. B, The contributive edges for ELC score prediction. The contribution of the edges was summarized separately with a negatively and positively correlated edge set. The color in the colored matrices shows the summed standardized contribution of within and between networks. The circle map shows the contribution of the edges to the ELC score prediction, where the whole edge set was thresholded at the 99.9th percentile for better visualization; the 602 parcels in the whole brain are grouped into seven networks. The black lines in the circle map represent the most contributive edges for both cognitive prediction and infant identification.

Discussion

By performing functional connectivity-based individual identification in infants, for the first time we demonstrate that the individualized functional connectome pattern may exist during early infancy and remains stable over months. Both the primary and high-order systems capture the characteristics of individual uniqueness in brain functional organization. Notably, the frontoparietal networks exhibit comparable capability as the whole-brain connectivity in identity identification and cognitive performance prediction during infancy, resembling the prior research about the functional connectome fingerprint in older children (Miranda-Dominguez et al., 2018), adolescents (Kaufmann et al., 2017), and adults (Finn et al., 2015; Horien et al., 2019), as well as individual uniqueness in neonates (Wang et al., 2021). Moreover, we demonstrate the stability of the brain functional fingerprint by the relative high identification rates using datasets of large session gaps, and also suggest the potential of inferring individual behavior phenotypes based on the functional connectome during infancy.

The functional connectome fingerprint exists and evolves during infancy

The identifiability of a functional connectome appears to be established during early infancy as the infant functional connectivity has become unique enough for individual identification (the average identification rate on three datasets reaches 65.76%, with the average session gap approaching 212 d). Despite rapid brain development during infancy, we achieved statistically significant identification rates based on the functional connectivity pattern. Together with the prior literature showing the existence of a functional connectome fingerprint in older children/adolescents/youths (7–15 years old (Miranda-Dominguez et al., 2018), 8–22 years old (Kaufmann et al., 2017), 9–19 years old (Demeter et al., 2020), 11–29 years old (Horien et al., 2019), adults (22–36 years old; Finn et al., 2015; Liu et al., 2018), and older adults (59–72 years old (Horien et al., 2019), we suggest, at the population level, the functional connectome may have identifiability in some extent across the whole life span, which echoes the hypothesis of the life-long existence of a cortical folding-based fingerprint (Duan et al., 2020).

Although the functional connectome fingerprint exists from early infancy and may last the whole life, the strength of the identifiability is different at different periods of life. We observed an increasing pattern of the association between connectome distinctiveness and age (Fig. 5C). Meanwhile, in the longitudinal design of the identification test based on five adjacent age groups (Fig. 5A), the identification accuracy during 0 ∼ 6 months was mostly lower than that of the older age groups. The difference in identification rates between Dataset I and Dataset II also supports the difficulty in identification when involving younger subjects. Here, the session gap effect is ruled out because the average session gap of Dataset I is smaller compared with that of Dataset II. It can be speculated that the brain functional connectome fingerprint goes through a gradual process of formation during the course of brain development. Actually, many previous studies about the functional (Tau and Peterson, 2010; Gao et al., 2013) and structural (Schneider et al., 2004; Geng et al., 2012) development of the infant brain have suggested that the first infantile year could be characterized as the construction process of the backbone of most functional networks and thus possesses low intersubject variability. Although the magnitude of interindividual difference gradually increases after fundamental construction, the individualization of the functional connectome tends to be strengthened. Our results suggest that the functional connectome fingerprint is not static but evolves during infancy, which also aligns with the hypothesis that the brain functional connectome is undergoing a process of individualization during adolescence (Kaufmann et al., 2017).

Frontoparietal networks are the most distinguishing functional systems even during infancy

The frontoparietal networks have been demonstrated to perform best in defining the uniqueness of individuals from neonates to adults (Vanderwal et al., 2017; Horien et al., 2019; Wang et al., 2021). Our findings illustrate the superior distinctiveness of frontoparietal networks in infants by showing their high and stable discriminative capability (averaged on the three datasets, the frontoparietal networks reach an identification rate of 66.62% compared with the rate of 65.76% obtained by the whole-brain connections). Interestingly, as the high-order association cortices, the frontoparietal networks are consistently recognized as being immature and continuously developing (Smyser et al., 2011; Cao et al., 2017a,b). How could the frontoparietal networks keep uniqueness and stability during brain development is an intricate problem. Gao et al. (2014) suggested that the prolonged maturation of higher order systems offers an opportunity for the development of intersubject variability, and Mueller et al. (2013) interpreted it as the result of environmental factors. But these determinants may not explain all the contributive connections with high uniqueness because the primary networks, also identified as contributive networks in our study, are always recognized as well-established systems in prenatal development with little environmental influence. Our results may suggest that the functional connectome fingerprint is a specific pattern tightly related to only a very small portion of connections (Using only 5% connections can reach significantly higher identification accuracy than using the whole-brain connections.), which maintain high stability (despite slightly evolving and completing), whereas the rest of the connections are heavily affected by brain development.

The basic pattern in the infant functional connectome fingerprint is relatively stable over months

Using connectome-based identification in three datasets, we demonstrate that the functional connectome fingerprint remains stable over months because of the satisfactory identification over big session gaps (the mean is 147 ∼ 298 d). Although longer session gaps may lead to lower intrasubject stability and are prone to degrade identification accuracy, the statistically significant identification accuracies still demonstrate the stability of the functional connectome fingerprint, consistent with previous studies suggesting that the uniqueness of the functional connectome is stable for a few months in older adults and 1–2 years in adolescents (Horien et al., 2019). Existing reports have provided evidence that brain networks are largely stable with trivial variation in networks over time, especially during rest (Vakhtin et al., 2014; Laumann et al., 2017), and are dominated by individual factors such as genetics (Gratton et al., 2018). Meanwhile, given that existing studies in neonates and infants suggest a more fundamental role of genetic factors (Lee et al., 2015; Sadeghi et al., 2017) over environmental factors in the stability of brain organization, we speculate that the functional fingerprint may be largely linked to genetics.

Potential factors to boost identification rate

Some factors could potentially increase the identification rate. First, eliminating the edges with low intersubject variability could benefit the identification in infants. It has been observed that a small portion of functional connections is sufficient to obtain similar identification accuracy comparing with the whole-brain connections (Byrge and Kennedy, 2019). In our study, the connections with low intersubject variability are prone to reduce identification accuracy. This factor may be more prominent for infants because of the confounding effect of immature functional patterns. Second, a parcellation with higher resolution has the potential to improve identification. The increased identification rate obtained by a fine-grained parcellation (Fig. 4C), resembling the results in adults (Finn et al., 2015), may imply that the functional fingerprint is a delicate pattern. Third, uniqueness could be boosted with more reference scans. We found, as expected, the identification accuracies significantly increased with a two-based set or two-target set, again in agreement with the findings in adults (Finn et al., 2015), and possibly resulted from the stability of the functional fingerprint.

Association exists between functional connectome fingerprints and cognitive performance

We also demonstrated that the frontoparietal networks highly contribute to the ELC score prediction as well as identity identification, which is consistent with existing studies demonstrating the relationship between individual uniqueness and cognitive behavior (Cole et al., 2012; Kaufmann et al., 2017; Horien et al., 2019). This result reveals the association between functional fingerprints and cognitive performance during infancy. Meanwhile, difference exist in the individualized connectome characteristics between identification and behavior prediction. The strong dependence of cognitive score on the across-network connectivity suggests the domination of large-scale coordination of brain activity in cognitive behavior (Power et al., 2011). By comparison, the involvement of more within-network connectivity in the uniqueness of individual connectome patterns reveals the importance of localized stability in the functional fingerprint.

Additional considerations

In our study, subjects older than 876 d in the BCP dataset were not included because they were typically scanned while watching movies rather than sleeping, and the functional connectivity may show different patterns with different engagement of visual and auditory stimuli (Vakhtin et al., 2014; Horien et al., 2019). Employing longitudinal pediatric scans acquired across different scan paradigms and during longer intervals up to years may further test the stability of the functional connectome fingerprinting. Our recent work on sleep-to-awake functional connectome prediction based on deep learning may be beneficial for the related study (Hu et al., 2021). Another consideration is that we only used static functional connectivity to investigate the individualized pattern of the functional connectome. Examining whether the dynamic functional connectivity and some derived dynamic measures (Liu et al., 2018) can characterize individual uniqueness of infants would further improve our understanding of the stable inherent traits and ongoing changes of the infant connectome fingerprint.

Conclusion

In summary, our findings reveal that the functional connectome fingerprint appears to be established during early infancy and, more importantly, maintains stability over the span of months, despite rapid early brain development. Complementary to the reports of the individualized patterns of functional connectome in adolescents, adults, and older adults, our results highlight the existence of individualized functional connectivity patterns during infancy, thus filling a knowledge gap in neurodevelopment and completing the full picture of the functional connectome fingerprint across the whole life span after birth. The necessity of functional connection selection during our study emphasizes the specificity of the functional connectome fingerprint during infancy as well. By demonstrating the distinctness of high-order association cortices and the differential contribution of various networks in individual identification, we characterize, for the first time, the network mechanisms underlying the functional connectome fingerprint in infants. Our findings support the potential application of an individualized functional connectome in measuring individual personal traits and tracking the progression of mental disorders during early brain development.