Abstract
Predictive coding accounts of brain functions profoundly influence current approaches to perceptual synthesis. However, a fundamental paradox has emerged, that may be very relevant for understanding hallucinations, psychosis, or cognitive inflexibility: in some situations, surprise or prediction error-related responses can decrease when predicted, and yet, they can increase when we know they are predictable. This paradox is resolved by recognizing that brain responses reflect precision-weighted prediction error. This presses us to disambiguate the contributions of precision and prediction error in electrophysiology. To meet this challenge for the first time, we appeal to a methodology that couples an original experimental paradigm with fine dynamic modeling. We examined brain responses in healthy human participants (N = 20; 10 female) to unexpected and expected surprising sounds, assuming that the latter yield a smaller prediction error but much more amplified by a larger precision weight. Importantly, addressing this modulation requires the modeling of trial-by-trial variations of brain responses, that we reconstructed within a fronto-temporal network by combining EEG and MEG. Our results reveal an adaptive learning of surprise with larger integration of past (relevant) information in the context of expected surprises. Within the auditory hierarchy, this adaptation was found tied down to specific connections and reveals in particular precision encoding through neuronal excitability. Strikingly, these fine processes are automated as sound sequences were unattended. These findings directly speak to applications in psychiatry, where specifically impaired precision weighting has been suggested to be at the heart of several conditions such as schizophrenia and autism.
SIGNIFICANCE STATEMENT In perception as Bayesian inference and learning, context sensitivity expresses as the precision weighting of prediction errors. A subtle mechanism that is thought to lie at the heart of several psychiatric conditions. It is thus critical to identify its neurophysiological and computational underpinnings. We revisit the passive auditory oddball paradigm by manipulating sound predictability and use a twofold modeling approach to simultaneous EEG-MEG recordings: (1) trial-by-trial modeling of cortical responses reveals a context-sensitive perceptual learning process; (2) the dynamic causal modeling (DCM) of evoked responses uncovers the associated changes in synaptic efficacy. Predictability discloses a link between precision weighting and self-inhibition of superficial pyramidal (SP) cells, a result that paves the way to a fine description of healthy and pathologic perception.
Keywords: Bayesian learning, dynamic causal modeling, EEG-MEG fusion, mismatch negativity, predictive coding, trial-by-trial modeling
Introduction
Brain responses to surprise are essential to understand how the brain adapts to changing or uncertain environment. In perception research, the abundant literature dedicated to surprise-related electrophysiological components has largely contributed to frame perception processes into regularity learning, independently of attention engagement. This important turn leverages on influential computational predictive brain theories (Dayan et al., 1995; Friston, 2012), with predictive coding algorithm in particular (Friston, 2005; Spratling, 2017). Under this view, evoked responses are treated as surprise or prediction errors indexing the discrepancy between predictions established through regularity learning and current sensations (Schröger et al., 2015; Auksztulewicz and Friston, 2016; Heilbron and Chait, 2018; Lumaca et al., 2019). These dynamic errors drive belief updating to ensure an on-going adaptation to changes. However, recent work points to a fundamental paradox that clearly deserves attention to further refine perceptual models (Auksztulewicz et al., 2017; Southwell et al., 2017; Heilbron and Chait, 2018; Fitzgerald and Todd, 2020; Meyniel, 2020; Walsh et al., 2020). Namely, prediction error related brain responses were found to decrease with reduced (or predicted) surprise but also to increase in some contexts where surprise becomes predictable.
Predictive brain theories resolve this paradox by considering the precision (or confidence) the brain assigns to predictions and sensory inputs so that evoked responses to surprise would reflect precision-weighted prediction errors. In short, these computational views of brain functions posit that the brain processes every information (internal predictions and incoming sensations) in a probabilistic way, meaning that the brain would not only estimate the most likely value of information but also its associated precision (the mean and inverse variance of the corresponding probability distribution, respectively). Precision provides a formal way to control the gain of prediction errors according to their contextual relevance for an efficient and flexible perceptual processing (Friston, 2008, 2009; Clark, 2013; Mathys et al., 2014). Precision-weighted prediction errors correspond to the “precision weight × prediction error” product. The resulting filtering of prediction errors directly speaks to the fact that the same surprising event may convey an important message in some contexts but not in others. This points to the difference between expected and unexpected surprise induced by rare events delivered within a predictable (structured) or random (uncertain) environment, respectively. Precisions hence make perception context-sensitive and are expected to be larger in a more predictable context (PC). This is assumed to result from a hierarchical learning process whereby higher-order belief updating adjusts the precision of first-order (sensory) prediction errors. This implies two opposite effects at the sensory level: (1) a higher precision afforded by predictability, yielding efficient belief updating, hence (2) lower prediction errors. The initial paradox thus turns into a challenge, namely, to isolate the physiological representations of precision and prediction error, respectively.
We here address this timely question by proposing an auditory oddball experimental paradigm with a predictability manipulation to generate expected and unexpected surprises. These could be indexed by the mismatch negativity (MMN; Friston, 2005; Winkler, 2007). We conducted simultaneous EEG and MEG recordings (Lopes da Silva, 2013) to measure subtle changes of brain activity during passive listening. Passive listening has been used here primarily to study implicit, automatic learning processes and to avoid the presumably confounding effect of voluntary attention on the adjustment of precision weights (Feldman and Friston, 2010; Parr and Friston, 2019). We could indeed measure a smaller MMN under predictability based on these EEG data (Lecaignard et al., 2015). However, evoked response analysis (average-based) prevents from testing Bayesian learning directly, nor to seek separate evidence for precision and prediction errors in brain responses (the MMN as a precision-weighted prediction error combines both quantities indistinctly). Here, we pursue our investigation using a neurocomputational dynamic modeling scheme. In short, at the cognitive (computational) level, trial-by-trial modeling of reconstructed cortical responses could evidence Bayesian learning and its automatic adaptation to predictability, an effect which translates into a larger account of past (relevant) information. We then addressed the issue of disentangling learning quantities at the physiological level, using dynamic causal models (DCMs). Predictability effect was measured as changes in the synaptic strength within a fronto-temporal network, revealing distinct mechanisms for the encoding of precision weights and prediction errors.
Materials and Methods
A general view of the present neurocomputational approach is provided in Figure 2. Before testing the predictability effect onto perceptual learning and associated synaptic connectivity, we first conducted a control analysis aiming at characterizing such learning at play for the processing of unexpected sounds (in both contexts) at the cognitive level (using trial-by-trial computational modeling) and the physiological level (using DCM).
Figure 2.
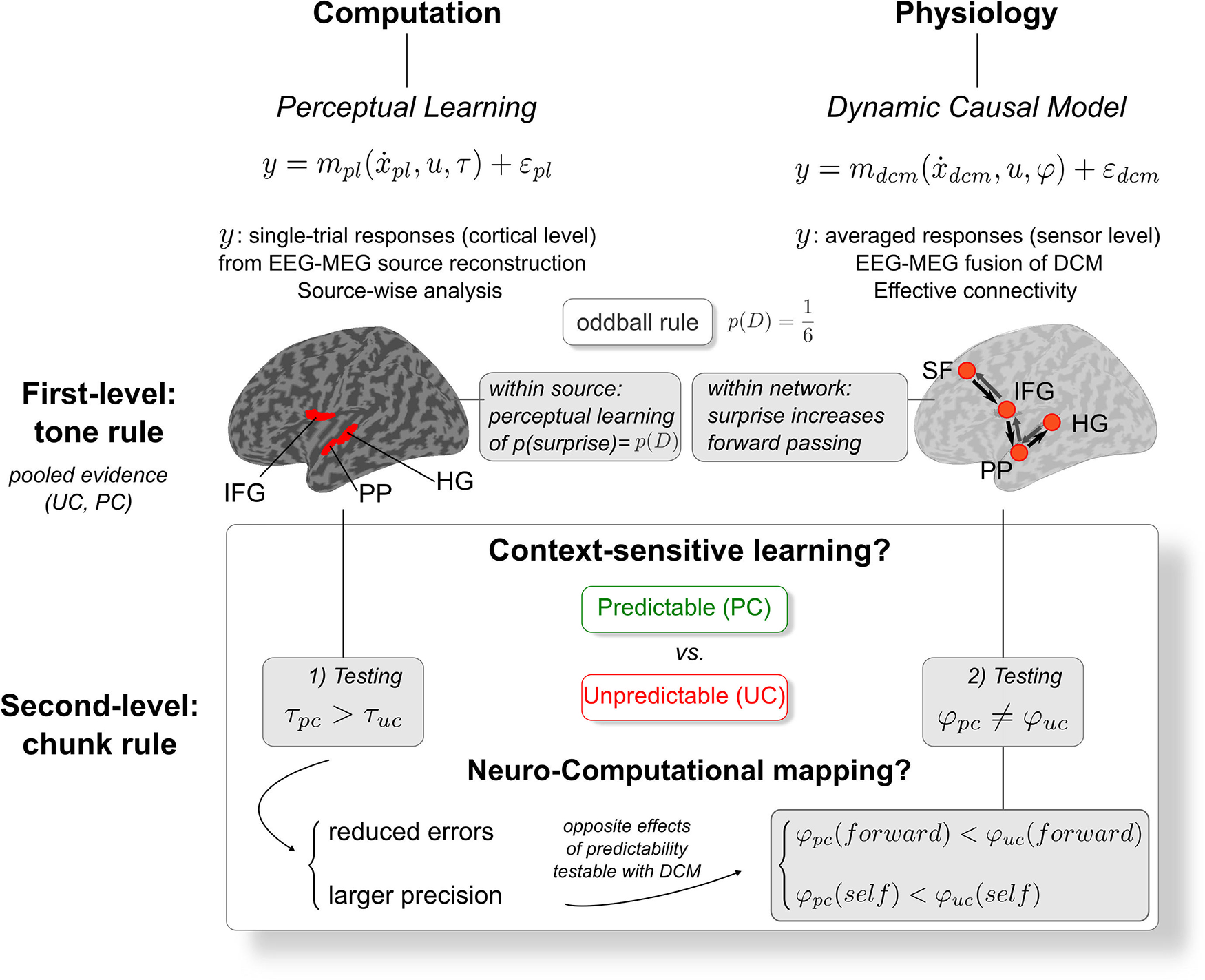
Neurocomputational framework. Representation of the current approach deployed at both the cognitive and physiological levels to address the automatic adaptive learning at play during auditory processing, and to disambiguate the mapping of precision weights and prediction errors onto physiological responses. First-level analysis (upper panel): the expected perceptual learning of the oddball rule is first tested at the computational level (left) as well as its physiological implementation within a fronto-temporal hierarchy (right). Second-level analysis (lower panel): adaptation of this learning to the manipulation of predictability is then tested through the examination of model parameters for each condition (UC, PC), both at the computational (left) and physiological (right) levels. Gray boxes highlight the specific differences that were tested. Different learning time constants τ (left) would support hierarchical learning with opposite effects on precision weighting and prediction errors, that are testable (hence separable) using DCM. First-level and second-level rules are described in Figure 1A. Dynamic models: pl (perceptual learning), dcm (dynamic causal model); cortical sources: HG (Heschl's gyrus), PP (planum polare), IFG (inferior frontal gyrus), SF (superior frontal); experimental contexts: PC/pc (predictable context), UC/uc (unpredictable context). D: deviant. Forward/self: DCM forward/self-inhibition connection strength parameters.
Participants
Twenty healthy volunteers (10 female, mean age 25 ± 5 years, ranging from 18 to 35) participated in the study. The previous EEG report (Lecaignard et al., 2015) involved two participants that were excluded here because of noisy MEG signals. All participants had no history of neurologic or psychiatric disorder and reported normal hearing. All participants gave written informed consent and were paid for their participation. Ethical approval was obtained from the appropriate regional ethics committee on Human Research (CPP Sud-Est IV-2010-A00301-38).
Experimental design
Predictable and unpredictable sound sequences embedding a typical frequency oddball rule [conditions PC and unpredictable context (UC)] were used in the present study. Control sequences using an intensity deviance were also delivered to the participants; the corresponding datasets have been analyzed previously (Lecaignard et al., 2015, 2021). Participants were instructed to ignore the sounds and watch a silent movie of their choice with subtitles. Predictable sound sequences comprised 16 cycles that were each made of a repeating 42-tone pattern following the deterministic incrementing rule depicted in Figure 1A. Unpredictable sequences corresponded to pseudo-random oddball sequences typically used in oddball paradigms, with specific controls for the number of standards in between two deviants to mirror the predictable sequences. Despite their differing statistical structure, both sequence types had the same deviant probability (p = 0.17) and the same distribution of deviants among standards (there were exactly the same number of chunks of repeating standards before a deviant in both conditions, with chunk size varying from 2 to 8 standards). Each condition (UC, PC) was delivered twice, in separated runs (made of 674 stimuli each) to enable reversing the role of the two sounds (500/550 Hz; standard/deviant). Further details about stimuli and sequence can be found in (Lecaignard et al., 2015). All stimuli were delivered using Presentation software (Neurobehavioral Systems).
Figure 1.
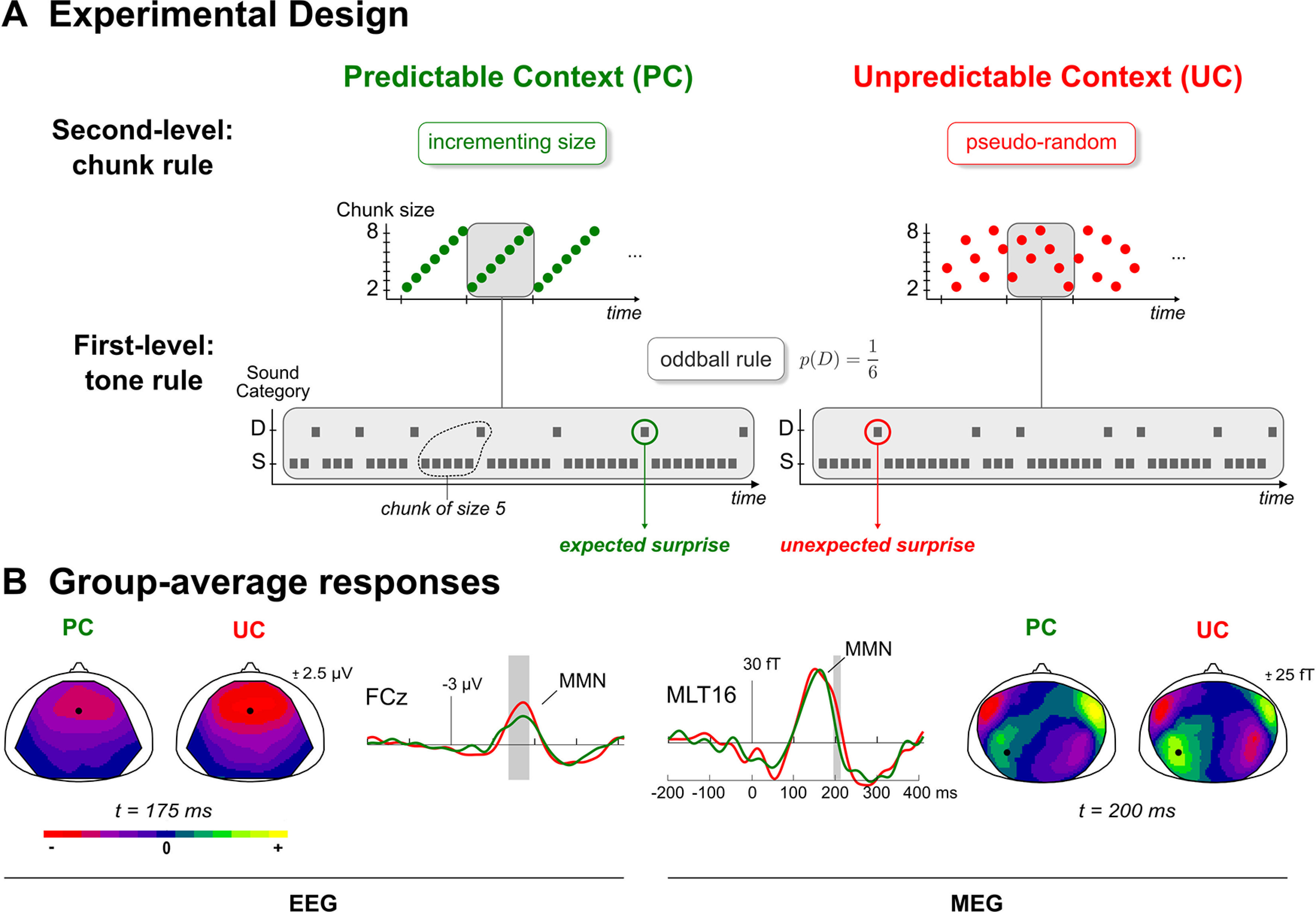
A, Experimental design. Schematic view of the predictability manipulation applying to typical oddball sound sequences. PC (left, green) involves cycles of ordered transitions between segments of repeating standards (chunks), which become shuffled in the UC (right, red). Deviant probability remains the same in both context (p = 1/6). Gray rectangles delineate an exemplary cycle for both sequences. S: Standard, D: Deviant. B, Group-average difference responses. For each modality (EEG, left; MEG, right), scalp maps of grand-average difference (deviant – standard) responses at latency showing a significant predictability effect for both contexts (PC: green; UC: red). Middle plots: traces at sensors showing a significant MMN reduction under predictability (EEG: FCz; MEG: MLT16; location on related scalp map is represented by a black circle); gray areas indicate the significant time intervals for these sensors (permutation tests with multiple comparison correction, p < 0.05).
Data acquisition and preprocessing
Simultaneous MEG and EEG recordings were conducted in a magnetically shielded room with a whole-head 275-channel gradiometer (CTF-275 by VSM Medtech Inc.) and the CTF-supplied EEG recording system (63 electrodes), respectively. Signal was amplified, bandpass filtered (0.016–150 Hz), digitized (sampling frequency 600 Hz), and stored for off-line analysis. First-order spatial gradient noise cancellation was applied to MEG signal. EEG reference and ground electrodes were placed on the tip of the nose and left shoulder, respectively. Digitization of electrode locations (Fastrak, Polhemus) and acquisition of individual T1-weighted magnetic resonance imaging images (MRIs; Magnetom Sonata 1.5 T, Siemens) were conducted for coregistration purposes in distributed source reconstruction (see below).
Preprocessing of data using the ELAN package (Aguera et al., 2011) and MATLAB routines included the following: rejection of data segments affected by head movements (larger than 15 mm relative to the average position over sessions) or SQUID jumps, power-line filtering (stop-band filters centered on 50, 100, and 150 Hz with bandwidth of ±2 Hz), indpendent component analysis (ICA) correction for ocular artifacts (EEGlab routines; http://sccn.ucsd.edu/eeglab/index.html), rejection of trial epochs (from −200 to 410 ms after stimulus onset) with signal amplitude range (over entire epoch) exceeding 2000 fT for MEG data and 150 μV for EEG data, and 2- to 45-Hz bandpass digital filtering (bidirectional Butterworth, fourth order). Importantly, we only used time epochs that survived the procedures applied for artifact rejection for both modalities. Finally, trial epochs were imported in SPM (Wellcome Department of Imaging Neuroscience; http://www.fil.ion.ucl.ac.uk/spm) and were down-sampled (200 Hz) for data reduction and low-pass filtered (20 Hz low-pass digital filter, bidirectional Butterworth, fifth order) to get rid of high-frequency noise. EEG data were re-referenced to the averaged mastoid electrodes for compatibility with the forward model used in both cognitive modeling and DCM. Group-average deviance responses obtained in EEG and MEG in both UC and PC conditions are shown in Figure 1B. The difference between conditions was tested over a temporal window spanning the MMN (from 100 to 210 ms) using permutation tests with correction for multiple comparisons (we replicated the statistical analysis applied to the 2- to 45-Hz nose-referenced EEG data in Lecaignard et al., 2015). A significant reduction of the mismatch response under predictability was found in EEG over fronto-central electrodes (21 sensors), from 138 to 188 ms, and to a lesser extent in MEG over a right anterior gradiometer cluster (11 sensors) from 100 to 120 ms, and a left posterior one (nine sensors) from 195 to 210 ms.
Computational modeling (cognitive level)
Trial-wise reconstructed cortical data
For a given peri-stimulus time, learning and non-learning models were each fitted to the time series made by the changes in cortical activity over trials. Precisely, single-trial cortical data were obtained in a preparatory step involving the distributed source reconstruction of fused EEG-MEG data. Advanced methods were employed for source inversion with realistic forward models for both modalities [boundary element model (BEM); Gramfort et al., 2010], Bayesian framework enabling multiple sparse priors (Mattout et al., 2006; Friston et al., 2008), EEG-MEG fusion (Henson et al., 2009), and group-level inference (Litvak and Friston, 2008). Source inversions were all performed with the SPM software (SPM8 release). Source inversions were all performed with the SPM software (SPM8 release). First, six cortical clusters could be identified from the inversion of the MMN peak (from 150 to 200 ms) in condition UC (Lecaignard et al., 2021). These sources (whose spatial extent is shown on in Fig. 3A) were located in the left and right Heschl's gyrus (HG), planum polare (PP), and inferior frontal gyrus (IFG), respectively. Critically, they subsequently served as spatial priors to constrain the inversion of entire single-trial epochs (from −200 to +410 ms). This constraint addresses the lack of reliable spatial information when dealing with (noisy) single-trial data. We resolved this issue by assuming the stationarity of the spatial locations of the cortical sources underlying auditory evoked responses, which we indeed validated with that same datasets and over the entire epoch (Lecaignard et al., 2021). In total, 674 trials per run, per condition and per participant were reconstructed. Within each cluster and for each trial, reconstructed cluster-node activities were averaged to derive a cluster-level and single-trial trace being informed by both EEG and MEG data. These single trial responses could be averaged using exactly the same scheme as employed at the sensor level to derive group-average deviance responses in each condition. The above-mentioned statistical analysis over the 100- to 210-ms window here disclosed a significant mismatch reduction under predictability (p < 0.05, uncorrected) in right HG (from 160 to 185 ms), right PP (from 110 to 140 ms) and left IFG (from 150 to 165 ms). This gives confidence in our overall procedure for inferring cortical single-trial activities.
Figure 3.
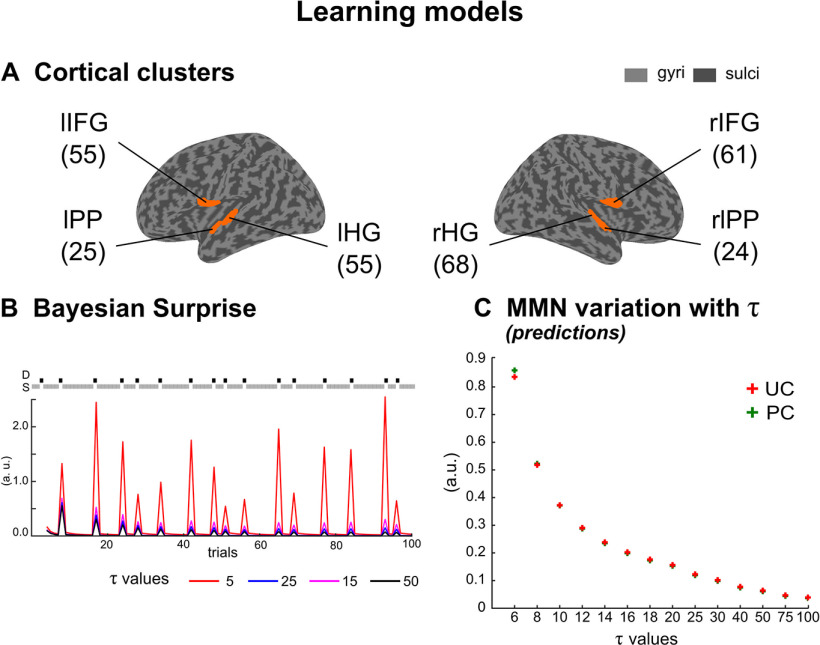
Perceptual learning models. A, Each cluster of interest is represented (orange) over the inflated cortical surface of the SPM template brain (Mattout et al., 2007). These six clusters are left, right HG (lHG, rHG), left, right PP (lPP, rPP) and left, right IFG (lIFG, rIFG). Total number of nodes in each cluster is indicated in parenthesis. B, Bayesian surprise as a function of (arbitrary units, a.u.). Illustration of different BS trajectories obtained with varying , for the first 100 stimuli of a typical UC oddball sequence. Two comments should be made: (1) BS decreases as increases and (2) whatever , BS is larger for deviants (D, black squares) than for standards (S, gray squares). C, Learning model predictions of the MMN amplitude as a function of (group average) for UC (red) and PC (green) sound sequences (see Materials and Methods). Note that in both contexts, MMN amplitude decreases similarly as increases.
Learning model
We considered a learning model which assumes that the brain learns from each stimulus exposure the probability to have a deviant, to predict the next sound category (with in the case of a deviant and in the case of a standard). We define with the Bernoulli distribution, and with and the parameters of the distribution , corresponding in the current case to deviant and standard counts, respectively. At trial , we have:
| (1) |
Where the first expression reflects the prediction about before new observation, while the second one pertains to the updating of the belief on , after having observed . The posterior distribution of is in the form of a distribution ( distribution is conjugate to the distribution), leading to the following updated expression of at trial :
| (2) |
With the gamma Euler function, and and following update equations:
| (3) |
We defined precision-weighted prediction error as the Kullback–Leibler (KL) divergence between the prior and the posterior distributions of , also referred to as a Bayesian surprise (Ostwald et al., 2012). At trial , it expresses as:
| (4) |
With the digamma Euler function. Importantly for our investigation, the size of the temporal integration window was parameterized by which enters standard and deviant count updates as follows:
| (5) |
From Equation 5, we see that the larger the , the larger the weight applying to past observations, leading to a more informed learning (an illustration can be found in Fig. 7A). Variation of BS with the size of the temporal integration window is shown in Figure 3B.
Figure 7.
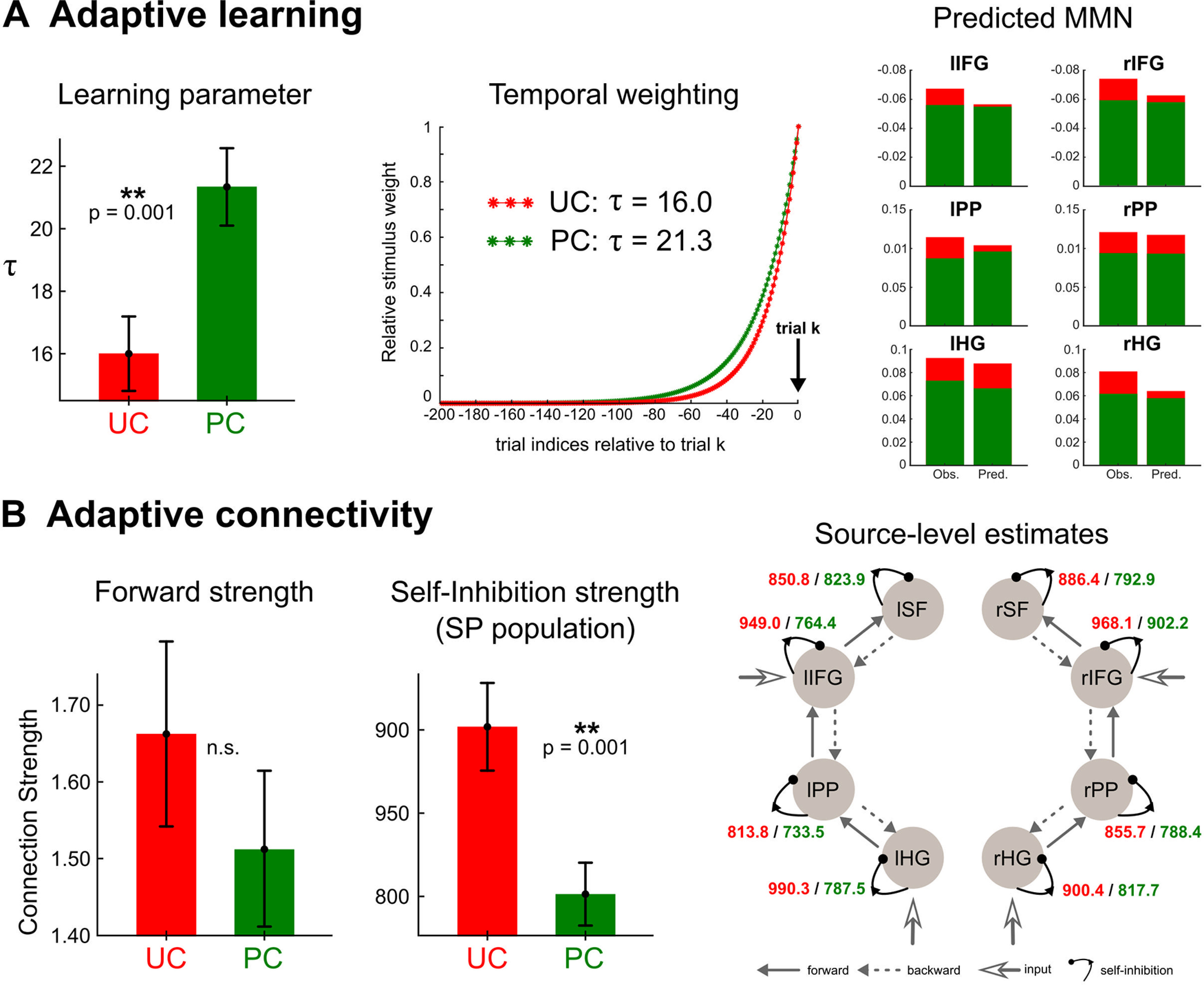
Effect of predictability on auditory processing. A, Cognitive modeling (perceptual learning). Left plot, Effect of predictability on learning parameter . Posterior estimates of averaged at the group level and over the six clusters exhibited a significant difference between conditions. Middle plot, Downweighting of past observations obtained with the posterior estimates of for conditions UC (red) and PC (green), respectively. Right plot, Group-level observed (Obs.) and predicted (Pred.) MMN amplitude within each cluster, and for condition UC (red) and PC (green). Each value gathers time samples that exhibited a significant learning effect in the first-level analysis and was computed following the scheme described for the pseudo-MMN computation (detailed in the main text). B, Physiologic counterpart (DCM). Effect of predictability onto effective connectivity obtained with the fusion of EEG and MEG DCMs. Left and middle plots, Posterior estimates of forward and self-inhibition strengths measured in both conditions (UC: red, PC: green), averaged over the group and over the connections within the DCM. SP: superficial pyramidal; a.u.: arbitrary units. Right plot, Source-based self-inhibition strengths showing a significant predictability effect. Values for each condition (UC: red, PC: green) are displayed over a typical DCM graph representation. Labels of cortical sources as in Figure 4.
First-level analysis (Fig. 2, upper left panel)
We first tested the learning model against alternative cognitive processes that did not involve perceptual learning. Models were all defined as a two-level linear model of the form:
| (6) |
Where indicates the reconstructed cortical activity informed by a fused EEG-MEG source inversion in the form of a vector of trial-by-trial activity at a particular sample of the peristimulus time; is defined for each model and represents the predicted trajectory of precision-weighted prediction error over the sound sequence;and refer to Gaussian observation parameters and Gaussian noise, respectively. Vector was defined for each time sample of the [−50 + 350] ms epoch and for each cluster of the MMN cortical network identified at the group level (six clusters). We considered a model space of seven cognitive models partitioned into three families, largely inspired by models used in a previous tactile oddball study (Ostwald et al., 2012):
Family famnull is made of a single model, the null model (M0) assuming that the brain response to every tone is the same, or equivalently that fluctuations in reconstructed cortical signals only reflect random noise (i.e., in Eq. 6).
Family famnoL contains two non-learning or static models, namely, change detection (CD) and linear CD (LinCD). Both assume that the brain simply compares each incoming sensation to the preceding one. In model CD, at trial is assigned to 0 if the stimulus is equal to the preceding one, and 1 otherwise. Model LinDC is similar to CD but assigns a prediction error proportional to the number of preceding sounds that differ from the one being currently observed (Ostwald et al., 2012; Lieder et al., 2013).
Family famL includes the learning model described above, assuming that the brain estimates the probability to hear a standard (under a Bernoulli distribution). We considered four different values for (2, 6, 10 and 100), leading to four models in famL. Precision-weighted prediction error is here defined as the Bayesian surprise (mismatch between the prior and the posterior distribution of ).
These models were all fitted to the reconstructed cortical activity in both PC and UC conditions. For each source and at each time sample of the peristimulus interval, model inversions were performed using the VBA toolbox (Daunizeau et al., 2014), individual UC and PC data (four runs) were processed all at once (multisession model fitting), bad trials (with regard to sensor-level artifact rejection) were processed such that associated signals would not corrupt parameter optimization while their related stimuli entered model dynamics (these sounds were observed by the brain).
Second-level analysis (Fig. 2, lower left panel)
Inversion of the learning model (which was found outperforming others in the first-level analysis) was here performed separately in each context, and critically, time constant parameter was no longer fixed but inferred from data confrontation. Beyond the memory-based interpretation (the brain may arguably not be able to deal with long-gone, past information), this parameter endows the learning model with a flexible way to integrate past information and formalizes brain adaptation to its environment. From Figure 3B, it can be seen that the precision-weighted prediction error, here defined as a Bayesian surprise, decreases with , reflecting the better predictions induced from a larger account of past information. In order to test whether sound transition alone, which differs across UC and PC contexts, is sufficient to explain the reduced MMN observed under predictability, we simulated group-level MMN for different values of . For each subject, we computed individual trial-by-trial precision-weighted prediction error trajectories induced by UC and PC sequences for in , using VBA. We then selected the values obtained for each standard preceding a deviant and for each deviant (in keeping with sensor-level trial rejection). Using exactly the same procedure that had been used to compute the event-related difference response at the sensor level, we could simulate the group-average MMN amplitude in conditions UC and PC (arbitrary units).
Model inversion was performed in each of the six clusters, and at every time sample spanning the MMN (precisely we considered the samples that exhibited this model as winning in the first-level). Bad trials were treated as in the first-level analysis. The number of samples consequently varied across clusters, leading to a total of 33 samples. Overall, 66 inversions were conducted per subject (1 model, 2 conditions, 33 samples). Each inversion provided a posterior estimate for parameter informed by EEG and MEG data. To evaluate the quality of fit, the percentage of explained variance was computed based on the observed and predicted MMN within each cluster and for each condition (using averaged estimates across samples). Therefore, the predicted MMN was obtained following the procedure described above to compute the simulated MMN.
Statistical analysis
In the first-level analysis, the three model families were compared with each other using an RFX family-level inference (Penny et al., 2010). In subsequent second-level analysis, we assumed a constant value of within the time interval used for model inversion (spanning the MMN). We therefore averaged estimates across samples for each cluster. Predictability effect could thus be analyzed by conducting a repeated-measures ANOVA on these posterior estimates with factors condition (UC, PC), hemisphere (left, right), and sources (HG, PP, IFG).
DCM (physiological level)
DCM analysis was performed with SPM12 (Wellcome Department of Imaging Neuroscience; https://www.fil.ion.ucl.ac.uk/spm/). DCM architecture includes interconnected sources, each with four neuronal subpopulations (Auksztulewicz et al., 2018); corresponding extrinsic and intrinsic dynamics induced by sensory inputs are specified by the canonical microcircuit (CMC) neural mass model, which we here consider to exploit its relevance to test predictive coding predictions (Bastos et al., 2012; Brown and Friston, 2013; Moran et al., 2013). Forward connections originate in superficial pyramidal (SP) subpopulation and target the spiny stellate cells of the higher-level source, and could reflect precision-weighted prediction errors. Backward connections link deep pyramidal subpopulation to spiny stellate cells, and are assigned to predictions. Intrinsic connections here appeal to the gain of SP cells (self-inhibition connection) and are associated to the precision weight.
EEG and MEG evoked responses
Averaged responses evoked by standards just preceding a deviant and by deviants were considered for all DCM analyses. Time interval of 0 to 220 ms after sound onset was used for model inversion. It was defined from sensor-level (EEG and MEG) statistical analysis on deviance responses to ensure it encompasses the MMN (and no later components). A Hanning window was applied to time-series to ensure that system's dynamics was set to zero before being excited. Data reduction was achieved using the default SPM procedure adjusted for the current Openmeeg forward models (BEM). On average across subjects, it selected 8 (±2.7) and 13 spatial modes with EEG and MEG data, respectively (intersubject variability is because of the individual anatomic information that was used to refine the inversion scheme; here, it here appears to exert a larger effect in EEG than MEG).
First-level analysis (Fig. 2, upper right panel)
Inspired by previous DCMs of the MMN (Garrido et al., 2009a; Auksztulewicz and Friston, 2016), and guided by current learning model predictions, we addressed the two following questions: what is the structure of the network engaged in typical oddball sequence processing (at play in both UC and PC contexts)? Within this auditory network, what modulation of effective connectivity supports deviant compared with standard tone processing? Contrary to the above-cited studies, these questions were treated one after the other (we used two model spaces depicted in Fig. 4C). The reason for this was to highlight the fact that the modulation of the effective connectivity by predictability (an effect that was examined next in the second-level analysis, see below) could be found at both levels (as we shall see, we expected an effect at the network level).
Figure 4.
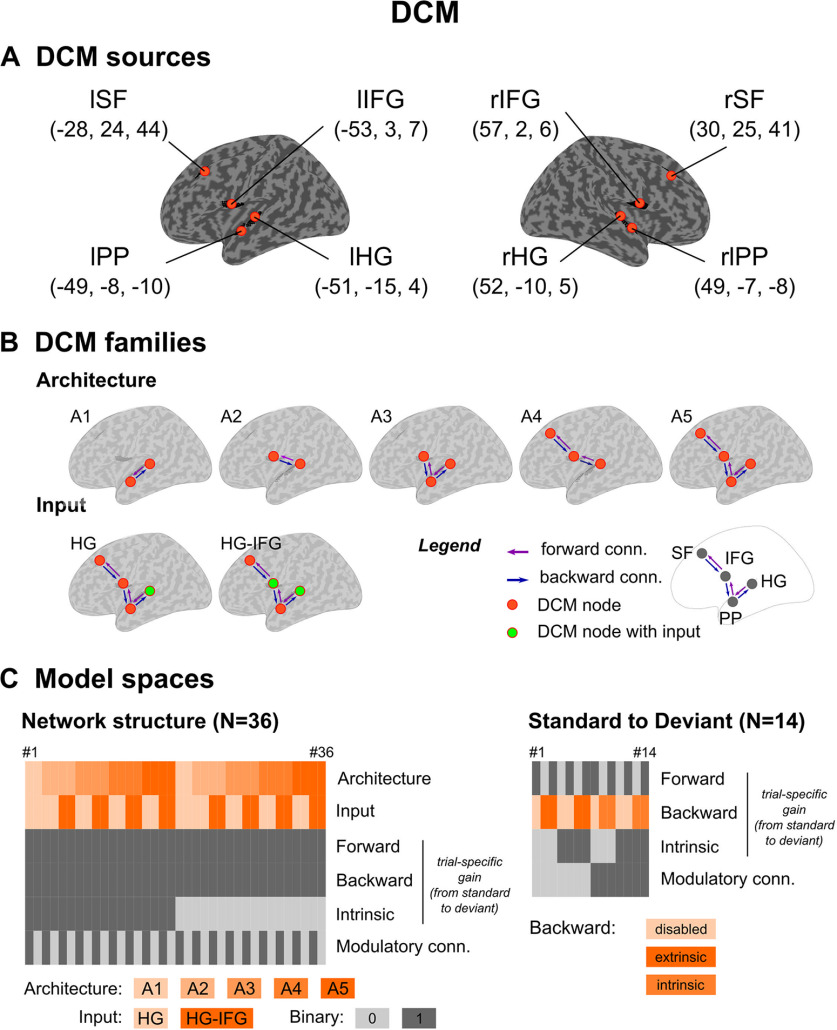
DCM. A, Cortical sources for DCM analysis. Each source is indicated schematically with orange dots on the inflated cortex, with corresponding MNI coordinates (mm) in parenthesis. B, Model families. Upper row, Schematic view of the five model families designed to test DCM architecture in deviance processing. Bottom row, The two model families of DCM input, HG and HG-IFG. Color codes of extrinsic connections (conn.) and DCM source (or node) are provided in the legend. C, Model spaces. Network structure analysis (left): DCM specifications for each of the 36 models (in columns). Frontal, backward and intrinsic trial-specific gains, as well as modulatory connections correspond to binary options (enabled = 1, disabled= 0) applying to the entire network. Standard-to-deviant modulation analysis (right), following the same logic of display. Backward trial-specific gains were disabled or applied onto either extrinsic or intrinsic connections depending on modulatory connections (as detailed in the main text).
Most reports of the DCM of the MMN entailed a three-level hierarchy (Garrido et al., 2009b; Auksztulewicz and Friston, 2015; Phillips et al., 2015; Chennu et al., 2016). We considered the six above-mentioned sources of the MMN. However, the complementary EEG and MEG topographical information regarding the predictability modulation of the MMN peak led us to test an additional level in the superior frontal area (SF), with more details below. Each of the eight resulting clusters led to an equivalent current dipole (ECD) located at the averaged position of local maxima over the different time intervals. MNI coordinates are provided in Figure 4A. The resulting four-level DCM structure was composed of eight sources distributed bilaterally over (from the lowest to the highest level) HG, PP, IFG, and SF. We connected these sources with extrinsic (forward and backward) connections. Alternative hypotheses entailed two-level and three-level networks allowing to test the hierarchical depth as well as the contribution of PP and SF sources, leading to five model families (A1, A2, A3, A4, and A5). Regarding DCM inputs, all models included a direct input to bilateral HG. In addition, inputs targeting IFG sources (known to receive direct thalamic afferents) were tested as the source-reconstructed EEG and MEG evoked responses suggested that frontal regions were activated prior to temporal ones (Deouell, 2007). The input factor thereby included two levels (HG and HG-IFG). Importantly, we did not address the presence or absence of trial-specific modulations (standard-to-deviant changes in connection strength) applying to extrinsic and intrinsic connections; this aspect is treated in the following. We therefore assumed forward and backward trial-specific modulations, as already reported in several MMN DCM studies (Garrido et al., 2009b), and we integrated over the two possible hypotheses (presence or absence) for the intrinsic modulation. DCM with CMC also includes extrinsic modulatory connections to enable the top-down indexation of subpopulation SP excitability on the output activity of higher-level feedbacking sources. These connections and self-inhibition ones constitute two different ways to modulate SP excitability, in an activity-dependent and activity-independent manner following the terminology proposed in recent studies (Auksztulewicz et al., 2018; Rosch et al., 2019). We integrate over the two alternative hypotheses (presence or absence of modulatory connections). The resulting model space to investigate DCM architecture thus comprised a total of 36 DCMs (Fig. 4C, left).
Next, we addressed the trial-specific gain (standard-to-deviant modulation) applying on forward, backward, and intrinsic connections within the winning DCM structure (architecture A5 and double-input HG-IFG). For forward and intrinsic gains, two model families were considered each (present or absent at all or none connections). Regarding backward gains, when considering modulatory connections, they apply to activity-dependent intrinsic connections (activity-dependent gain; Auksztulewicz et al., 2018; see their Fig. 4); otherwise they modulate extrinsic backward strength. This led us to consider three model families with respect to backward gains and their possible modulatory effects (1) disabled, (2) enabled as an extrinsic modulation, and (3) enabled as an intrinsic modulation. A total of 14 models composed this model space (Fig. 4C, right).
Each model inversion was performed in condition UC and PC and for EEG and MEG data separately (leading to four inversions per subject and per model, with 36 + 14 models per subject). We used default values of SPM12 as prior expectations and prior variance for each DCM parameter to be estimated. Each DCM inversion involved standard response (as the initial state of the system) and deviant response (resulting from the experimental perturbation). Regarding DCM sources, we maintained dipole locations fixed (but not their orientation) to inform spatially DCM inversion with the group-level MEG-EEG information. For each modality (EEG, MEG), the forward model used for DCM inversion was the above-mentioned realistic BEM computed with Openmeeg software (Gramfort et al., 2010).
Second-level analysis (Fig. 2, lower right panel)
Here, we test for a predictability effect on the synaptic connectivity established for typical oddball processing (first-level analysis winning DCM: architecture A5 with HG-IFG inputs). In particular, we compare the forward and self-inhibition connection strengths obtained in each context in the first-level DCM analysis. A significant reduction in both parameters in condition PC would confirm the expected separate physiological accounts for prediction error and precision weighting (more details are provided in Results). The corresponding statistical analysis is described below.
Fusion of EEG and MEG DCMs
We integrated EEG and MEG data into a single DCM analysis, assuming that their complementarity would improve the inference on brain activity, as it was empirically evidenced for classical source reconstruction (Lecaignard et al., 2021). Fusion of EEG and fMRI data for DCM was also demonstrated to outperform unimodal (fMRI) scheme, in the context of simulated auditory mismatch responses (Wei et al., 2020). This fusion operates sequentially, by inverting EEG data first based on uninformative priors over parameters, to then guide with EEG-informed priors the subsequent fMRI data inversion. This way, unplausible hypotheses (given EEG) are thus ruled out. Here, we adopt a slightly different approach, which consists in modeling EEG and MEG data independently (based on uninformative priors) and then derive a posterior estimate of model parameters based on both inferences using the Bayesian machinery. These estimates informed by both modalities are referred to as p-MEEG. Each modality thus selects plausible hypotheses which are then combined based on their respective evidence to derive multimodal posterior estimates. Both approaches illustrate the great potential of the Bayesian framework to flexibly integrate multimodal information in a principled fashion.
Precisely, the proposed procedure rests on the assumption of conditional independence of EEG and MEG data under the quasi-static approximation of Maxwell equations, which is largely admitted for signals below 1 kHz (as is the case here). Denoting EEG and MEG data byand , respectively, we have:
| (7) |
And posterior model evidence of model can be approximated using unimodal EEG and MEG model evidences:
| (8) |
Consequently, the variational free energy approximation to p-MEEG model log-evidence could be obtained by:
| (9) |
With and the free energy values for EEG and MEG, respectively. Besides, the posterior distribution of some DCM parameter under model writes given:
| (10) |
Which can be re-formulated as follows to reveal the posterior distributions of deriving from unimodal inversion of EEG and MEG data:
| (11) |
DCM approach assumes every parameter to have of the form of a Gaussian distribution. Hence prior distribution expresses as We also denote , and the posterior distribution of given EEG data, MEG data and EEG-and-MEG data, respectively. We have and the mean and variance of the distribution resulting from the multiplication of and . From Equation 11 and the analytical expressions of and (detailed in most statistic books), we derive:
| (12) |
Statistical analysis
In the first-level analysis, we combined p-MEEG DCMs obtained across conditions (UC, PC) using similar Bayesian reasoning as for the EEG and MEG fusion (log-posterior model evidences in UC and PC were summed across conditions). We first quantitatively evaluated the architecture and the input families using family-level inference (Penny et al., 2010) with an RFX model, based on the p-MEEG approximations of model evidence (. Next, regarding the standard-to-deviant modulation of synaptic connectivity, family level inference (RFX model) was conducted over the forward, backward and intrinsic trial-specific gain parameters. As each of these three family comparisons indicated significant modulations, we subsequently examined their corresponding direction of change (a gain value larger than one would indicate larger connection strength in deviants than in standards, and vice versa). For each connection type (forward, backward, intrinsic), we used Bayesian model averaging (BMA; Penny et al., 2006) to derive group-level posterior estimates averaged across model space (with model-evidence weighting) and across subjects, and we average these estimates (per connection type) over the entire network.
In the second-level analysis, for each context, we computed individual p-MEEG BMA estimates of forward and self-inhibition connection strengths, and their respective trial-specific gain (standard-to-deviant modulation). For the forward related parameters, we conducted a repeated-measures ANOVA over individual BMA estimates with factors condition (UC, PC), hemisphere (left, right), and level (temporal, fronto-temporal, frontal); in the self-inhibition related parameter, this latter factor was replaced by factor source (HG, PP, IFG, SF).
Throughout the paper, ANOVAs were performed using R software (The R Foundation; https://www.r-project.org/).
About the contribution of SF sources
In the first-level DCM analysis, we tested the relevance of an additional frontal level in oddball processing dynamics. This hypothesis emerged from the following observation: the predictability effect was larger at fronto-central sites in EEG (Lecaignard et al., 2015) and at temporal gradiometers in MEG (Fig. 1B), in a way that suggests generators expressing poorly on frontal gradiometers. We could indeed identify bilateral clusters of activity in this region over the significant time intervals reported in Lecaignard et al. (2015), with however limited precision. In short, left and right frontal clusters (36 and 29 nodes, respectively, p < 0.05 with family wise error (FWE) whole-brain correction) were found for the early deviance effect, and a left contribution of 34 nodes for the MMN interval (with p < 0.001 not corrected). Despite the poor spatial precision, SF sources could still contribute to better fit the data (if frontal generators are truly involved) as they impose a strong temporal constraint on DCM dynamics (Attal et al., 2012). However, we decided not to include the SF clusters in the above-mentioned computational modeling to avoid the issue of fitting single trial cortical responses reconstructed from uncertain spatial information.
Results
We address the automatic context sensitivity of auditory processing, at both the cognitive and physiological levels. Following the scheme presented in Figure 2, we first examine the processing of deviant sounds (in both contexts) at the cognitive and the physiological levels, in the aim to evidence Bayesian learning at play in a fronto-temporal hierarchy, as reported in pioneering work in the field (Garrido et al., 2009a; Ostwald et al., 2012). Second, using trial-by-trial computational modeling we test whether the brain adapts its learning style to the contextual manipulation during unattentional listening. Results provide clear predictions regarding the mapping of precision and prediction error onto physiology, which we next test using DCM (Kiebel et al., 2009; Bastos et al., 2012).
Perceptual learning in oddball processing (Fig. 2, upper left panel)
As shown in Figure 5, the Null hypothesis (famnull) was found to outperform the other families, at every time sample and every cortical source, except for the time interval of the MMN. Precisely, posterior exceedance probability of family famL was found to be significantly greater than the ones of the other families between 150 and 200 ms (six samples), in the left and right HG, between 130 and 180 ms (six samples) and at 150 ms (one sample) in the left and right PP, respectively, and between 130 and 200 ms (eight samples) and between 140 and 190 ms (six samples) in the left and right IFG, respectively. Noticeably, in the latency range of the P3a described in Lecaignard et al. (2015), the Null hypothesis could also be challenged by learning models, as suggested by the increase of famL posterior exceedance probability, an effect most visible in left IFG.
Figure 5.
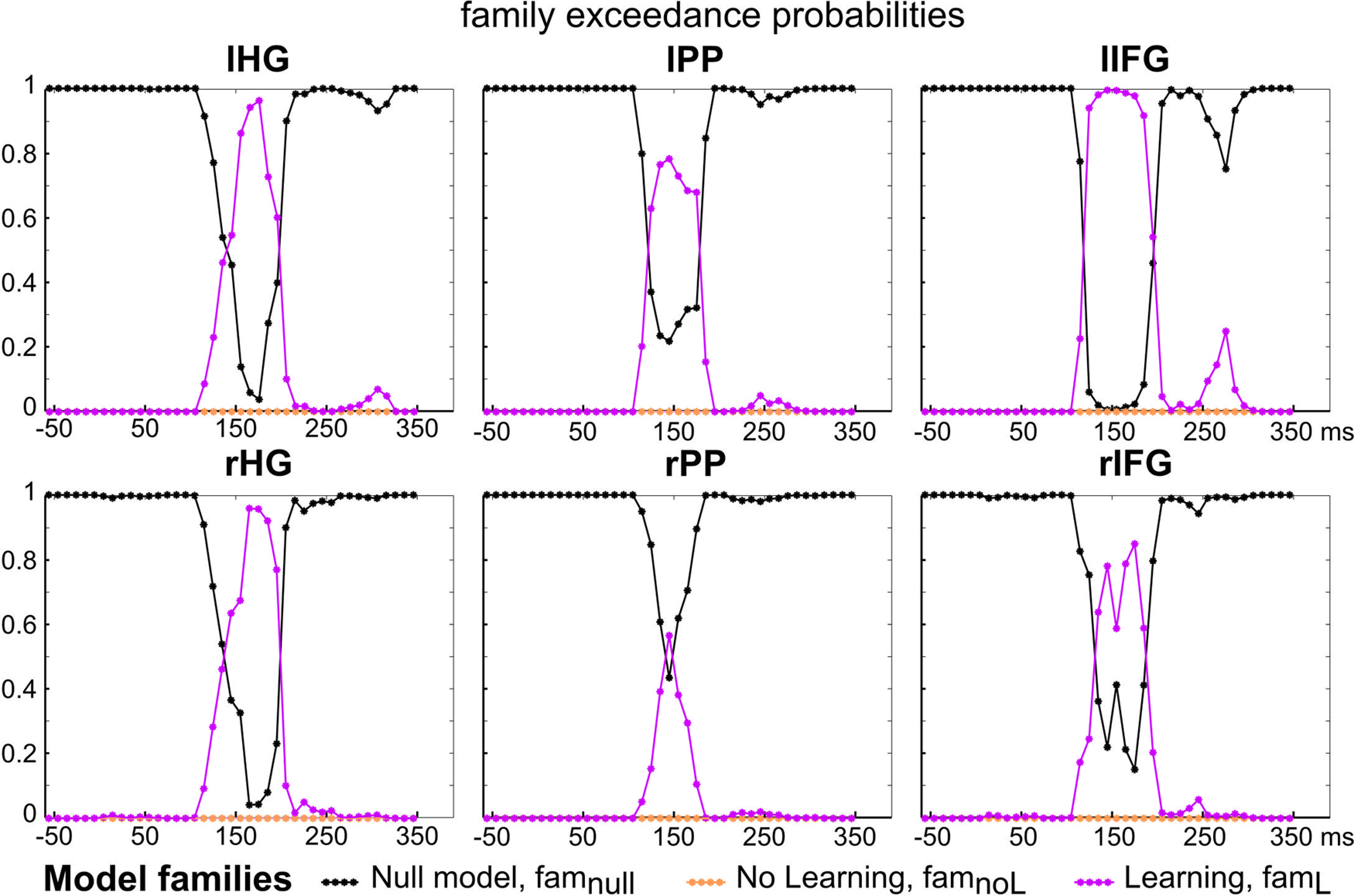
Computational modeling of deviance processing. Family-wise Bayesian model comparison. For each cluster and at each time sample, family inference provides the estimated posterior family exceedance probability of each model family (famnull: black, famnoL: orange, famL: pink).
Effective connectivity in oddball processing (Fig. 2, upper right panel)
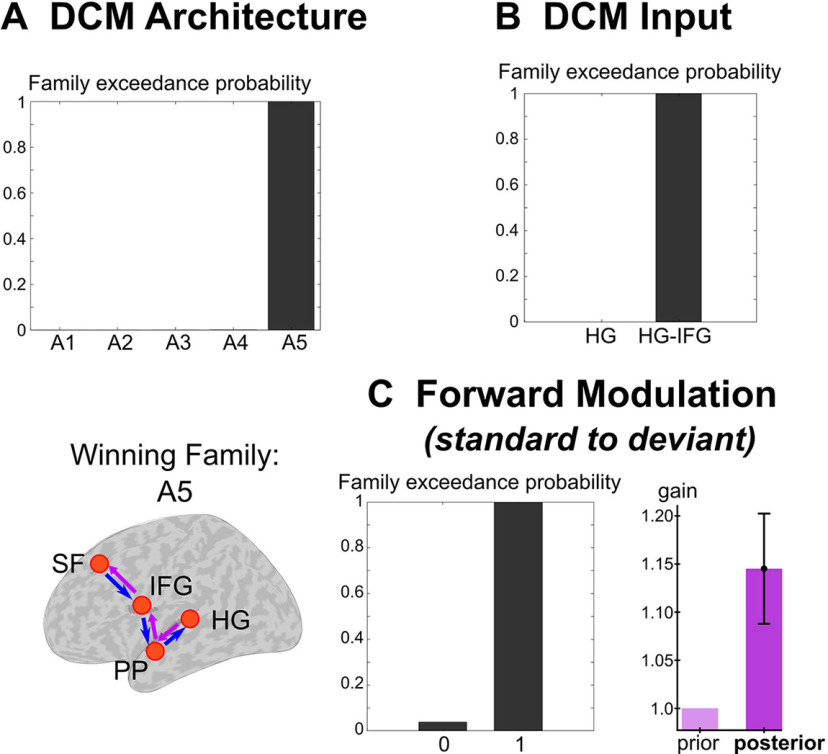
Regarding DCM architecture, explained variance averaged across models (n = 36) and subjects was equal 92.5% (SD ±10.5) and 78.1% (±11.6) in EEG and MEG, respectively (condition UC), and to 91.9% (±12.1) and 78.1% (±11.6) in EEG and MEG, respectively (condition PC). In the p-MEEG modality, family level inference revealed that family A5 outperformed other model families with a posterior confidence probability (pcp) and posterior exceedance probability (pep) of 0.68 and >0.99, respectively (Fig. 6A). Regarding the DCM inputs (Fig. 6B), family level inference was clearly in favor of models with inputs arriving in both HG and IFG sources (pcp/pep: 0.82/>0.99).
Figure 6.
DCM of deviance processing, using p-MEEG. A, Family inference for DCM architecture: family exceedance probabilities (upper left) and corresponding network for the winning family A5 (lower left). B, Family inference for DCM inputs. C, Family inference for standard-to-deviant trial-specific modulation for the forward connectivity. Family exceedance probabilities of the model families with disabled (0) and enabled modulation (1) is provided (left) and group-level BMA estimates of gain values (in condition UC) averaged over the DCM network is represented (right). Prior value of gain (light purple) was set to 1 assuming no standard-to-deviant modulation. Labels for the cortical sources and model families are provided in the main text.
Regarding deviance-related changes in connectivity, explained variance averaged across models (n = 14) was equal to (results for condition UC/condition PC): 96.5% (±5.1)/97.8% (±2.7), for EEG, and 87.1% (±7.4)/87.5% (±5.5) for MEG. We found evidence for forward, backward and intrinsic deviant modulation (pcp/pep: 0.82/>0.99; 0.73/0.99; 0.73/0.99, respectively) in line with pioneering DCMs of the MMN (Garrido et al., 2009b; Auksztulewicz and Friston, 2016). Group-level BMA posterior estimates of trial-specific gain (gathering the entire network and both conditions) fit well with predictive coding message-passing expectations. In particular, we found larger forward coupling for deviants (Fig. 6C; average and standard error across the network of group-level BMA estimates of forward trial-specific gain. UC: 1.145 ± 0.057, present in five out of six forward connections; PC: 1.027 ± 0.042, four out of six connections). We also found the expected increase of backward gain (UC: 1.179 ± 0.073, five out of six connections; PC: 1.307 ± 0.112, five out of six connections) and a decrease of the intrinsic gain (UC: 0.947 ± 0.064, five out of eight connections. PC: 0.956 ± 0.047, five out of eight connections).
Contextual adaptation of perceptual learning (Fig. 2, lower left panel)
First, simulated MMNs for a given value show a similar amplitude across contexts (Fig. 3C). This suggests that the reduced MMN measured in condition PC does not emerge from the sound sequence structure alone but results from an adaptive hierarchical learning. To put it another way, similar values between conditions would indicate the context insensitivity of prediction errors (i.e., a fairly rigid perceptual learning process, as could be expected in some psychiatric conditions such as schizophrenia or autism; Adams et al., 2013; Friston et al., 2014). The learning model with values inferred for each cluster and each condition separately yields MMN predictions (Fig. 7A, right plot) with an explained variance at the group level equal to 88.8% (SD ±8.0). As expected, larger values were found with condition PC compared with condition UC (F(1,19) = 10.13; p = 0.002). On average across sources, is equal to 16.0 and to 21.3 with UC and PC, respectively (Fig. 7A, left plot). The ANOVA showed no other significant effect (all p > 0.12). As can be seen in Fig. 7A, middle plot, the different values in UC and PC generate different downweightings of past observations, with a larger amount of information integrated during perceptual learning in the PC.
Separate neural correlates of prediction error and precision (Fig. 2, lower right panel)
We next examined how the adaptation of learning (larger ) manifests at the physiological level, based on the computational interpretation of specific DCM connections (see Materials and Methods). Precisely, we expected predictability to have the following effects. (1) A reduction of forward connection strength. Indeed, this extrinsic connection is thought represent the precision-weighted prediction error for which our results converge toward a diminution under predictability (smaller MMN and smaller Bayesian surprise; see Fig. 3B). (2) A reduction of self-inhibition connection strength. This intrinsic connection controls the excitability of the SP cells, where the forward connection originates from. As an inhibitory parameter, a low value translates into a large SP synaptic gain. Self-inhibition connection and SP activity have been proposed to index the precision weighting and the prediction error, respectively (Feldman and Friston, 2010; Bastos et al., 2012; Brown and Friston, 2013; Moran et al., 2013; Fogelson et al., 2014; Auksztulewicz et al., 2017). Observing a lower self-inhibition strength in condition PC would establish a direct mapping of this parameter onto precision weighting (which, as detailed in the introduction, is larger in predictable environment).
Regarding first prediction, as can be seen in Figure 7B, left, predictability yielded a reduced forward connection strength on average across the network (average with SE: 1.51 ± 0.10 and 1.66 ± 0.12, in PC and UC, respectively), an effect which is largest at the lowest level of the network (PC/UC, level temporal: 1.52 ± 0.10/2.05 ± 0.24; level fronto-temporal: 1.41 ± 0.16/1.50 ± 0.21; level frontal: 1.61 ± 0.24/1.44 ± 0.17). However, these effects do not reach statistical significance (condition: F(1,19) = 0.84; p = 0.36; condition × level: F(1,19) = 1.82; p = 0.17). Second prediction was fulfilled as self-inhibition connection strength was measured significantly reduced in condition PC compared with condition UC (801.4 ± 18.9 and 901.9 ± 26.3, respectively; F(1,19) = 10.52; p = 0.001; as shown in Fig. 7B, middle, right). This result establishes a link between self-inhibition and precision, as both adapt consistently to predictability (Fig. 2, lower panel). No main effect of Hemisphere, nor Source, and no interaction between factors (condition, hemisphere, source) could be observed using ANOVA (p ≥ 0.12 for all but the main effect of condition). Finally, the ANOVA conducted on standard-to-deviant modulation applying on forward connection strength and self-inhibition parameters did not disclose any significant main effect of condition (forward: F(1,19) = 2.50; p = 0.12; self-inhibition: F(1,19) = 0.01; p = 0.90). This suggests that the contextual effect of our predictability manipulation apply indistinctively to standard and deviant stimuli processing.
Discussion
This work addressed the hierarchical processing of sensory information during unattentional listening through its adaptation to the statistical structure of the environment. Complementary cognitive and neurophysiological modeling of oddball responses collected during different contexts of predictability reveals the occurrence of perceptual learning within a fronto-temporal hierarchy, as expected in the predictive coding framework. Moreover, it formally demonstrates that this predictive process is shaped by predictability in a way that optimizes the integration of relevant sensory information over time. Computationally speaking, this adaptation relies on the tuning of the precision weighting of prediction errors, a process which is known to be a cornerstone of Bayesian information processing (Mathys et al., 2014). We therefore show with a mechanistic and dynamical approach that during passive oddball listening, the more predictable the environment, the more efficient the sound processing. Besides, for the first time the neural encoding of precision weight could be distinguished from the prediction error per se and directly attributed to inhibitory mechanisms. Remarkably, the hypothesis of evoked responses reflecting hidden precision-weighted prediction errors (Friston, 2005) that was considered along this work is substantiated empirically by the present findings obtained with complementary neuro- and computational generative models of evoked responses.
Rare but robust empirical supports for predictive coding at play during oddball processing have been reported this past decade, obtained at the psychological level with trial-by-trial computational modeling (Ostwald et al., 2012; Lieder et al., 2013; Stefanics et al., 2018; Weber et al., 2020) and at the physiological level with DCM (Garrido et al., 2009a; Moran et al., 2013; Fogelson et al., 2014; Chennu et al., 2016; Lumaca et al., 2021). Novel evidence at both levels of analysis is provided here in the controlled work using exactly the same brain data informed by simultaneous EEG and MEG. The major contribution of this work, in the perspective of testing predictive coding more finely, lies in the fact that we could evidence the automatic tuning of the precision weighting of sensory errors and relate it to inhibitory mechanisms. This was made possible with the proposed model-driven contextual manipulation, where a second-order rule applies on the first-order oddball one.
At the cognitive level, our results demonstrate quantitatively brain's ability to grasp implicitly the larger informational content of the PC to derive a more informed and more efficient learning at the sensory level (by means of a larger temporal integration window). The larger efficiency in sensory processing translates into more accurate sensory predictions and more rapid adaptation to unexpectedness (Mathys et al., 2014). Predictable deviants remain surprising as a significant MMN in condition PC was measured in EEG and MEG (see also Fig. 3B). Beyond the passive nature of the experiment yielding arguably inaccurate predictions, this result actually demonstrates a hierarchical process that enables selecting low-level surprises (expected surprise still remains a surprise). Beside, our findings could provide a mechanistic explanation to the better task performances reported in target detection when listening to regular compared with random auditory streams (Southwell et al., 2017), and also during the processing of words and music stimuli under contextual expectancy (Tillmann et al., 1998). Similar facilitation of sensory processing in a structured environment was also suggested in a visual discrimination study (Rohenkohl et al., 2012), where temporal expectation was found to decrease reaction time, and could be associated to an increase of the sensory gain using a diffusion model. This result is comparable to the present precision adaptation, that here occurs without attentional (active) processing.
At the neural level, the effect of predictability on forward connection strength did not prove significant. Regarding self-inhibition connection, our findings establish empirically a direct link between precision and self-inhibition within supragranular cortical layers. Several DCM studies strongly supported this mapping, as they reported consistent modulations of self-inhibition by some experimental manipulations hypothesized to influence precision under predictive coding, namely, a cholinergic neuromodulation (Moran et al., 2013), sensory precision (Brown and Friston, 2012), selective attention (Brown and Friston, 2013), and predictability (Auksztulewicz et al., 2017). Here, it is the automatic contextual adaptation of sensory processing that we reveal computationally and physiologically that fills the missing link enabling to relate precision and self-inhibition directly. From a methodological perspective, this findings add to recent efforts to increase model plausibility to account for electrophysiological data (Phillips et al., 2016; Pinotsis et al., 2017).
The present approach (contextual manipulation and neurocomputational modeling) allowed us to test hierarchical learning in auditory processing, although the perceptual model is not hierarchically organized (it is based on a simple Bernoulli distribution). This aspect prevents from addressing the computational role of each DCM level, which is beyond the scope of this work. Here, hierarchical process was evaluated using our experimental manipulation, looking specifically at its effect on a single model parameter (a time constant that shapes learning evolution over trials). In hierarchical systems, higher levels process the most stable or slowly changing stimulus features, and associated predictions constitute top-down constraints on lower levels (Friston and Kiebel, 2009). In addition, increasing second-order statistic reliability has been theoretically demonstrated to increase the precision-weighting of sensory errors (Friston, 2008; Kanai et al., 2015). The reduced value under predictability fits very well with the top-down influence of contextual learning on sensory processing. Hierarchical learning models would be relevant to address the mechanisms by which the brain adapts to the context (an important direction discussed below). They should be employed with a slightly different paradigm to include the necessary transitions between contexts. Such models have already proven useful in characterizing the dynamics of learning an oddball rule changing over stable and volatile episodes (Meyniel, 2020; Weber et al., 2020).
Future research in testing predictive brain theories for perception has to address the mechanisms which subsume the adaptation of learning, including the dynamics of precision tuning. From a psychological perspective we aim at investigating more finely the present predictability adaptation in relation to attentional processes, guided by the computational account of attention (Friston, 2005). Under this view, attention serves to collect contextually-informative sensations to optimize perception and learning (Auksztulewicz and Friston, 2016; Parr and Friston, 2019), through either the precision weighting of sensory channels (Feldman and Friston, 2010) or action. The view of attention as the tuning of precision echoes our findings obtained without participant's awareness of the experimental manipulation. Interestingly, predictive brain theories have led to consider under the same framework the opposite effect of voluntary attention (an increase) and predictability (a decrease) on evoked response amplitudes reflecting precision-weighted prediction errors. In Chennu et al. (2013) and in Auksztulewicz and Friston (2015), both factors could be manipulated orthogonally using different task instructions during perception of oddball-like sound sequences. These two studies revealed different modulations of mismatch responses at different latencies, and related attention to self-inhibition using DCM, respectively. Chennu and colleagues reported a reduced MMN when attention was explicitly engaged toward (local) tone transitions compared with (global) multitone patterns. This fits with the present reduced MMN in the predictable condition considering that a more informed learning of the oddball rule (providing better predictions) could be at play either through an explicit attentional engagement or, in our case, through the implicit learning of the contextual information. Therefore, we argue that likewise but without the voluntary orientation of attention, predictability acts as an implicit attentional process, enhancing the efficiency of sensory processing. Similar effect of voluntary attention and predictability on precision (an increase) emphasizes the great potential of separating prediction error and precision accounts to predict (and test) their respective effects on evoked responses, instead of addressing precision-weighted prediction errors as a whole (Heilbron and Chait, 2018). Bridging passive predictability processing and voluntary attention opens the way to mechanistically investigate attentional capture. This would involve experimental manipulations of precision and prediction error with appropriate hierarchical dynamic models to assess underlying activity, and feasibility was demonstrated here. We expect in particular novel insights from the manipulation of precision (in addition to typical modulations of global precision-weighted prediction errors), to assess whether voluntary attention can emerge from specific precision evolution reflecting a form of evidence accumulation.
In conclusion, a contextual manipulation of oddball paradigm combined with a neurocomputational dynamic modeling scheme was used to disentangle prediction error and precision neural representations. Contextual effect was found to increase the extent of temporal integration of past information, which implies lower sensory prediction errors amplified by a larger precision weighting. Findings in this paper (1) demonstrate the conclusive power of modeling approaches combining neuronal and cognitive levels and (2) emphasize the importance of accounting for the encoding of precision weighting when investigating perceptual learning and decision-making. Unfolding the mechanisms of precision tuning and encoding, especially at an implicit level, is a potentially critical step for clinical applications as alterations of these processes have been suggested to be at the core of several psychiatric disorders (Adams et al., 2013; Lawson et al., 2017; Friston, 2020; Haarsma et al., 2020). Applying such a simple oddball paradigm, only involving passive listening, coupled with computational and neurophysiological modeling could be of great value in this context.
Footnotes
This work was supported by a grant from the Agence Nationale de la Recherche of the French Ministry of Research ANR-11-BSH2-001-01 (to A.C. and F.L.) and a grant from the Fondation pour la Recherche Médicale (FRM; to O.B. and J.M.). This work was conducted in the framework of the LabEx CeLyA (“Centre Lyonnais d'Acoustique,” ANR-10-LABX-0060) and of the LabEx Cortex (“Construction, Function and Cognitive Function and Rehabilitation of the Cortex,” ANR-10-LABX-0042) of Université de Lyon, within the program “Investissements d'avenir” (ANR-11- IDEX-0007) operated by the French National Research Agency (ANR). We thank Sébastien Daligault and Pascal Calvat for programming support in interfacing with the CC IN2P3; CC-IN2P3 for providing computing resources and services needed for this work; Emmanuel Maby and Gaëtan Sanchez for helpful discussions; and Karl Friston and Florent Meyniel for valuable feedback on the manuscript.
The authors declare no competing financial interests.
References
- Adams RA, Stephan KE, Brown HR, Frith CD, Friston K (2013) The computational anatomy of psychosis. Front Psychiatry 4:47. 10.3389/fpsyt.2013.00047 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguera PE, Jerbi K, Caclin A, Bertrand O (2011) ELAN: a software package for analysis and visualization of MEG, EEG, and LFP signals. Comput Intell Neurosci 2011:1–11. 10.1155/2011/158970 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attal Y, Maess B, Friederici A, David O (2012) Head models and dynamic causal modeling of subcortical activity using magnetoencephalographic/electroencephalographic data. Rev Neurosci 23:85–95. [DOI] [PubMed] [Google Scholar]
- Auksztulewicz R, Friston K (2015) Attentional enhancement of auditory mismatch responses: a DCM/MEG study. Cereb Cortex 25:4273–4283. 10.1093/cercor/bhu323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auksztulewicz R, Friston K (2016) Repetition suppression and its contextual determinants in predictive coding. Cortex 80:125–140. 10.1016/j.cortex.2015.11.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auksztulewicz R, Barascud N, Cooray GK, Nobre AC, Chait M, Friston K (2017) The cumulative effects of predictability on synaptic gain in the auditory processing stream. J Neurosci 37:6751–6760. 10.1523/JNEUROSCI.0291-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Auksztulewicz R, Schwiedrzik CM, Thesen T, Doyle W, Devinsky O, Nobre AC, Schroeder CE, Friston K, Melloni L (2018) Not all predictions are equal: “what” and “when” predictions modulate activity in auditory cortex through different mechanisms. J Neurosci 38:8680–8693. 10.1523/JNEUROSCI.0369-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, Friston K (2012) Canonical microcircuits for predictive coding. Neuron 76:695–711. 10.1016/j.neuron.2012.10.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown HR, Friston K (2012) Dynamic causal modelling of precision and synaptic gain in visual perception - an EEG study. Neuroimage 63:223–231. 10.1016/j.neuroimage.2012.06.044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown HR, Friston K (2013) The functional anatomy of attention: a DCM study. Front Hum Neurosci 7:784. 10.3389/fnhum.2013.00784 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chennu S, Noreika V, Gueorguiev D, Blenkmann A, Kochen S, Ibáñez A, Owen AM, Bekinschtein TA (2013) Expectation and attention in hierarchical auditory prediction. J Neurosci 33:11194–11205. 10.1523/JNEUROSCI.0114-13.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chennu S, Noreika V, Gueorguiev D, Shtyrov Y, Bekinschtein TA, Henson R (2016) Silent expectations: dynamic causal modeling of cortical prediction and attention to sounds that weren't. J Neurosci 36:8305–8316. 10.1523/JNEUROSCI.1125-16.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark A (2013) Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav Brain Sci 36:181–204. 10.1017/S0140525X12000477 [DOI] [PubMed] [Google Scholar]
- Daunizeau J, Adam V, Rigoux L (2014) VBA: a probabilistic treatment of nonlinear models for neurobiological and behavioural data. PLoS Comput Biol 10:e1003441. 10.1371/journal.pcbi.1003441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dayan P, Hinton GE, Neal RM, Zemel RS (1995) The Helmholtz Machine. Neural Comput 7:889–904. 10.1162/neco.1995.7.5.889 [DOI] [PubMed] [Google Scholar]
- Deouell LY (2007) The frontal generator of the mismatch negativity revisited. J Psychophysiol 21:188–203. 10.1027/0269-8803.21.34.188 [DOI] [Google Scholar]
- Feldman H, Friston K (2010) Attention, uncertainty, and free-energy. Front Hum Neurosci 4:215. 10.3389/fnhum.2010.00215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzgerald K, Todd J (2020) Making sense of mismatch negativity. Front Psychiatry 11:468. 10.3389/fpsyt.2020.00468 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fogelson N, Litvak V, Peled A, Fernandez-del-Olmo M, Friston K (2014) The functional anatomy of schizophrenia: a dynamic causal modeling study of predictive coding. Schizophr Res 158:204–212. 10.1016/j.schres.2014.06.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K (2005) A theory of cortical responses. Philos Trans R Soc Lond B Biol Sci 360:815–836. 10.1098/rstb.2005.1622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K (2008) Hierarchical models in the brain. PLoS Comput Biol 4:e1000211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K (2009) The free-energy principle: a rough guide to the brain? Trends Cogn Sci 13:293–301. 10.1016/j.tics.2009.04.005 [DOI] [PubMed] [Google Scholar]
- Friston K (2012) The history of the future of the Bayesian brain. Neuroimage 62:1230–1233. 10.1016/j.neuroimage.2011.10.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K (2020) Bayesian dysconnections. Am J Psychiatry 177:1110–1112. 10.1176/appi.ajp.2020.20091421 [DOI] [PubMed] [Google Scholar]
- Friston K, Kiebel S (2009) Predictive coding under the free-energy principle. J Math Psychol 364:1211–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K, Harrison L, Daunizeau J, Kiebel S, Phillips C, Trujillo-Barreto N, Henson R, Flandin G, Mattout J (2008) Multiple sparse priors for the M/EEG inverse problem. Neuroimage 39:1104–1120. 10.1016/j.neuroimage.2007.09.048 [DOI] [PubMed] [Google Scholar]
- Friston K, Stephan KE, Montague R, Dolan RJ (2014) Computational psychiatry: the brain as a phantastic organ. Lancet Psychiatry 1:148–158. 10.1016/S2215-0366(14)70275-5 [DOI] [PubMed] [Google Scholar]
- Garrido MI, Kilner JM, Kiebel S, Friston K (2009a) Dynamic causal modeling of the response to frequency deviants. J Neurophysiol 101:2620–2631. 10.1152/jn.90291.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garrido MI, Kilner JM, Stephan KE, Friston K (2009b) The mismatch negativity: a review of underlying mechanisms. Clin Neurophysiol 120:453–463. 10.1016/j.clinph.2008.11.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gramfort A, Papadopoulo T, Olivi E, Clerc M (2010) OpenMEEG: opensource software for quasistatic bioelectromagnetics. Biomed Eng Online 9:45. 10.1186/1475-925X-9-45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haarsma J, Kok P, Browning M (2020) The promise of layer-specific neuroimaging for testing predictive coding theories of psychosis. Schizophr Res. Advance online publication. Retrieved Nov 13, 2020. doi: 10.1016/j.schres.2020.10.009. 10.1016/j.schres.2020.10.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heilbron M, Chait M (2018) Great expectations: is there evidence for predictive coding in auditory cortex? Neuroscience 389:54–73. 10.1016/j.neuroscience.2017.07.061 [DOI] [PubMed] [Google Scholar]
- Henson R, Mouchlianitis E, Friston K (2009) MEG and EEG data fusion: simultaneous localisation of face-evoked responses. Neuroimage 47:581–589. 10.1016/j.neuroimage.2009.04.063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanai R, Komura Y, Shipp S, Friston K (2015) Cerebral hierarchies: predictive processing, precision and the pulvinar. Philos Trans R Soc Lond B Biol Sci 370:20140169. 10.1098/rstb.2014.0169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiebel S, Garrido MI, Moran R, Chen CC, Friston K (2009) Dynamic causal modeling for EEG and MEG. Hum Brain Mapp 30:1866–1876. 10.1002/hbm.20775 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson RP, Mathys CD, Rees G (2017) Adults with autism overestimate the volatility of the sensory environment. Nat Neurosci 20:1293–1213. 10.1038/nn.4615 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecaignard F, Bertrand O, Gimenez G, Mattout J, Caclin A (2015) Implicit learning of predictable sound sequences modulates human brain responses at different levels of the auditory hierarchy. Front Hum Neurosci 9:505. 10.3389/fnhum.2015.00505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecaignard F, Bertrand O, Caclin A, Mattout J (2021) Empirical Bayes evaluation of fused EEG-MEG source reconstruction: application to auditory mismatch evoked responses. Neuroimage 226:117468. 10.1016/j.neuroimage.2020.117468 [DOI] [PubMed] [Google Scholar]
- Lieder F, Daunizeau J, Garrido MI, Friston K, Stephan KE (2013) Modelling trial-by-trial changes in the mismatch negativity. PLoS Comput Biol 9:e1002911. 10.1371/annotation/ca4c3cdf-9573-4a93-9542-3a62cdbb8396 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litvak V, Friston K (2008) Electromagnetic source reconstruction for group studies. Neuroimage 42:1490–1498. 10.1016/j.neuroimage.2008.06.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopes da Silva F (2013) EEG and MEG: relevance to neuroscience. Neuron 80:1112–1128. 10.1016/j.neuron.2013.10.017 [DOI] [PubMed] [Google Scholar]
- Lumaca M, Haumann NT, Brattico E, Grube M, Vuust P (2019) Weighting of neural prediction error by rhythmic complexity: a predictive coding account using mismatch negativity. Eur J Neurosci 49:1597–1609. 10.1111/ejn.14329 [DOI] [PubMed] [Google Scholar]
- Lumaca M, Dietz MJ, Hansen NC, Quiroga-Martinez DR, Vuust P (2021) Perceptual learning of tone patterns changes the effective connectivity between Heschl's gyrus and planum temporale. Hum Brain Mapp 42:941–952. 10.1002/hbm.25269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathys CD, Lomakina EI, Daunizeau J, Iglesias S, Brodersen KH, Friston K, Stephan KE (2014) Uncertainty in perception and the hierarchical gaussian filter. Front Hum Neurosci 8:825. 10.3389/fnhum.2014.00825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattout J, Henson RN, Friston KJ (2007) Canonical source reconstruction for MEG. Comput Intell Neurosci 2007:67613. 10.1155/2007/67613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mattout J, Phillips C, Penny WD, Rugg MD, Friston K (2006) MEG source localization under multiple constraints: an extended Bayesian framework. Neuroimage 30:753–767. 10.1016/j.neuroimage.2005.10.037 [DOI] [PubMed] [Google Scholar]
- Meyniel F (2020) Brain dynamics for confidence-weighted learning. PLoS Comput Biol 16:e1007935. 10.1371/journal.pcbi.1007935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran R, Campo P, Symmonds M, Stephan KE, Dolan RJ, Friston K (2013) Free energy, precision and learning: the role of cholinergic neuromodulation. J Neurosci 33:8227–8236. 10.1523/JNEUROSCI.4255-12.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostwald D, Spitzer B, Guggenmos M, Schmidt TT, Kiebel S, Blankenburg F (2012) Evidence for neural encoding of Bayesian surprise in human somatosensation. Neuroimage 62:177–188. 10.1016/j.neuroimage.2012.04.050 [DOI] [PubMed] [Google Scholar]
- Parr T, Friston K (2019) Attention or salience? Curr Opin Psychol 29:1–5. 10.1016/j.copsyc.2018.10.006 [DOI] [PubMed] [Google Scholar]
- Penny WD, Mattout J, Trujillo-Barreto N (2006) Bayesian model selection and averaging. Statistical Parametric Mapping: The analysis of functional brain images. London: Elsevier. [Google Scholar]
- Penny WD, Stephan KE, Daunizeau J, Rosa MJ, Friston K, Schofield TM, Leff AP (2010) Comparing families of dynamic causal models. PLoS Comput Biol 6:e1000709. 10.1371/journal.pcbi.1000709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips HN, Blenkmann A, Hughes LE, Bekinschtein TA, Rowe JB (2015) Hierarchical organization of frontotemporal networks for the prediction of stimuli across multiple dimensions. J Neurosci 35:9255–9264. 10.1523/JNEUROSCI.5095-14.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips HN, Blenkmann A, Hughes LE, Kochen S, Bekinschtein TA, Rowe JB; Cam-CAN (2016) Convergent evidence for hierarchical prediction networks from human electrocorticography and magnetoencephalography. Cortex 82:192–205. 10.1016/j.cortex.2016.05.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinotsis DA, Geerts JP, Pinto L, Fitzgerald THB, Litvak V, Auksztulewicz R, Friston K (2017) Linking canonical microcircuits and neuronal activity: dynamic causal modelling of laminar recordings. Neuroimage 146:355–366. 10.1016/j.neuroimage.2016.11.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohenkohl G, Cravo AM, Wyart V, Nobre AC (2012) Temporal expectation improves the quality of sensory information. J Neurosci 32:8424–8428. 10.1523/JNEUROSCI.0804-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosch RE, Auksztulewicz R, Leung PD, Friston KJ, Baldeweg T (2019) Selective prefrontal disinhibition in a roving auditory oddball paradigm under N-methyl-D-aspartate receptor blockade. Biol Psychiatry Cogn Neurosci Neuroimaging 4:140–150. 10.1016/j.bpsc.2018.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schröger E, Kotz SA, Sanmiguel I (2015) Bridging prediction and attention in current research on perception and action. Brain Res 1626:1–13. 10.1016/j.brainres.2015.08.037 [DOI] [PubMed] [Google Scholar]
- Southwell R, Baumann A, Gal C, Barascud N, Friston K, Chait M (2017) Is predictability salient? A study of attentional capture by auditory patterns. Philos Trans R Soc Lond B Biol Sci 372:20160105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spratling MW (2017) A review of predictive coding algorithms. Brain Cogn 112:92–97. 10.1016/j.bandc.2015.11.003 [DOI] [PubMed] [Google Scholar]
- Stefanics G, Heinzle J, Horváth AA, Stephan KE (2018) Visual mismatch and predictive coding: a computational single-trial ERP study. J Neurosci 38:4020–4030. 10.1523/JNEUROSCI.3365-17.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tillmann B, Bigand E, Pineau M (1998) Effects of global and local contexts on harmonic expectancy. Music Percept 16:99–117. 10.2307/40285780 [DOI] [Google Scholar]
- Walsh KS, McGovern DP, Clark A, O'Connell RG (2020) Evaluating the neurophysiological evidence for predictive processing as a model of perception. Ann NY Acad Sci 1464:242–268. 10.1111/nyas.14321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber LAE, Diaconescu AO, Mathys CD, Schmidt A, Kometer M, Vollenweider F, Stephan KE (2020) Ketamine affects prediction errors about statistical regularities: a computational single-trial analysis of the mismatch negativity. J Neurosci 40:5658–5668. 10.1523/JNEUROSCI.3069-19.2020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei H, Jafarian A, Zeidman P, Litvak V, Razi A, Hu D, Friston KJ (2020) Bayesian fusion and multimodal DCM for EEG and fMRI. Neuroimage 211:116595. 10.1016/j.neuroimage.2020.116595 [DOI] [PubMed] [Google Scholar]
- Winkler I (2007) Interpreting the mismatch negativity. J Psychophysiol 21:147–163. 10.1027/0269-8803.21.34.147 [DOI] [Google Scholar]