Abstract
The elastic properties of cells are important for many of their functions, however the development of label free noninvasive cellular elastography method is a challenging topic. We present a novel single-cell all-optical coherence elastography method that combines optical tweezers producing mechanical excitation on the cell membrane or organelle and phase-sensitive optical coherence microscopy measuring sample response and determining its mechanical properties. The method allows living cells imaging with a lateral resolution of 0.5 μm and an axial resolution up to 10 nm, making it possible to detect nanometer displacements of the cell organelles and to record the propagation of mechanical wave along the cell membrane in response to optical tweezers excitation. We also demonstrate applicability of the method on single living red blood cells, yeast and cancer cells. The all-optical nature of the method developed makes it a promising and easily applicable tool for studying cellular and subcellular mechanics in vivo.
1. Introduction
Mechanical properties of living cell define its response to the mechanical forces from microenvironment and influence many cellular functions such as adhesion and migration [1]. Cellular biomechanics also becomes the defining epigenetic factor for the shape, behavior and differentiation of the cell [2–4] and may be connected with various diseases. For example, changes of mechanical properties of red blood cells are associated with Sickle cell disease and hereditary cytoskeletal abnormalities [5,6], while mechanical interactions of cancer cells with their microenvironment define the cancer progression and metastatic process [7]. There is growing interest in studying the relationship between organelle biomechanics and cellular functions: for instance, nucleus deformation has been shown to affect cell differentiation and proprioception [8,9]. Research of living organisms in vivo are of great importance for determination of the relationship between the biomechanics of cells, organelles and the functions of the organism and its pathologies. Thus, development of noninvasive methods for studying the mechanical properties of cells and their organelles, which can shed light on the connection between biomechanics and the functional behavior of cells inside living organisms, is an urgent problem.
One of the most powerful noninvasive methods to study the mechanical properties of biological objects, mainly tissues, is optical coherence elastography (OCE), which is based on the use of optical coherence tomography (OCT) [10] for imaging, differentiation and registration of sample movement under mechanical excitation [11–14]. The highest resolution in OCE is achieved by using phase-sensitive optical coherence microscopy (OCM), which is a combination of OCT and confocal microscopy [15–18]. Unlike monochrome phase imaging methods [19–21], due to using light source with wide spectrum, OCM combines coherence and confocal gate sectioning to improves imaging resolution and allow measuring of nanometer cellular membrane displacements [15]. Mechanical excitation in the OCE is created using, for example, ultrasound pulses [22,23], air pulses [24,25], mechanical wave drivers [26] and radiation force [27]. Due to the characteristic size of the area of influence, these sources are suitable for tissue elastography and not for the individual cells. To study the mechanical properties of cells, a point excitation is used. For single-cell OCE, magnetomotive approach [28] was proposed, but this method is invasive because it requires to attach magnetic particles to the studied cell.
At the same time, other techniques provide point mechanical excitation to study the mechanical properties of cells. The gold standard for this is atomic force microscopy (AFM), which uses the movement of the cantilever to create a mechanical impact [29,30]. AFM allows studying with high accuracy both the biomechanics of single cells and their organelles [31]. In the Fluid-Based Deformation Cytometry and Micropipette Aspiration methods the motion of cellular parts is not measured directly, but other parameters are analysed, such as transit velocity or the time of cell transit through a microchannel [32]. Also, cells shape deformation under the acoustic pressure is studied using acoustic tweezers [33]. These techniques have a lot of advantages, such as high acting forces and possibility to measure elasticity of rigid cells. However, in these approaches the elastic properties of the whole cell are measured and there is no possibility to make subcellular mapping of cell mechanical response on the external excitation. Other powerful techniques include magnetic twisting cytometry [34], Brillouin microscopy [35], and optical tweezers (OT) [6,36–38]. The main disadvantages of AFM and magnetic twisting cytometry are their invasiveness and the use of probes, that limits the possibility of using these methods in vivo. OT and Brillouin microscopy are known to be the most contactless and non-invasive methods; however, the weak scattering cross section of Brillouin microscopy necessitates potentially harmful illumination intensities of the order of hundreds of milliwatts [39]. The use of short wavelengths increases the scattering cross section, but decreases the penetration depth. Mechanical excitation in OT is realized by action of gradient and scattering forces near the waist of tightly focused laser beam, that make it possible to create point excitation, trapping and rotation of objects, and can be used in combination with imaging methods [40–43]. For OCE of single living cells, optical tweezers can potentially be used as a source of mechanical excitation, allowing elastography to be pointwise, completely optical and, therefore, contactless.
In this paper, we demonstrate novel single-cell all-optical coherence elastography technique (SCAOCE) that combines optical tweezers to produce mechanical excitation on the cellular or subcellular structures and phase-sensitive optical coherence microscopy to measure sample response and thus to study its biomechanics. As a result, we have obtained an all-optical noninvasive method, that allows living cells imaging with submicron lateral resolution and nanometer axial resolution. The method potentially can take advantage of the OCM using objective with longer working distance and be used to image cells located millimeters deep inside biological tissue. This makes it possible to detect nanometer displacements of the cell organelles, and to map the cell membrane response to the OT excitation. We demonstrate applicability and correctness of the SCAOCE method on single living red blood cells, yeast and cancer cells.
Section 2 describes the experimental implementation of the SCAOCE method, the procedure for measuring and processing data. Section 3.1 describes the imaging of single living cells using the OCM module. The samples are discocytes (normal red blood cells, RBC) and spherocytes (spherical RBC) – as high contrast single cells with a characteristic shape. Cells are imaged with OCM without the use of optical tweezers, which allows testing the resolution of the OCM module and its ability to visualize the optical path difference map.
Elastographic measurements of single living cells with simple and complex internal structures are carried out in Section 3.2. Firstly, we use a simulation of the response of a cell with simple shape and structure and make a comparison of the obtained values with the literature data. The sample is a spherocyte – a cell with a spherical shape convenient for numerical calculations. Next, elastographic measurements of single cells with a complex internal structure, baker’s yeasts, are carried out. Finally, it is shown on cancer cells that the developed method can be successfully combined with the already existing rheology method based on optical tweezers [6,44], complementing it and improving the resolution of the latter.
2. Methods
2.1. Cell preparation
Single living RBC of discocyte (a) and spherocyte (b) types, yeast (c) and cancer (d) cells are used for experiments.
(a) For experiments with discocytes, 5 µl of fresh capillary blood was added to 1 ml of autologous plasma. (b) A hypotonic sodium phosphate buffer solution (tonicity 0.82) was used to prepare a sample with spherocytes. (c) For yeast cells sample, 1 gram of baker’s yeast (Saccharomyces cerevisiae) was taken. Yeast cells were incubated in a solution of 2 ml of water with 1 gram of sugar per hour at 30 °C. In each of cases (a, b, c) the solution with cells (40 µl) was placed between two cover slips. (d) For experiments with cancer cells, a mouse breast cancer culture (line 4T1) was taken, which was then mixed with 5-10 µm borosilicate microbeads with 0.1 mg/µl concentration. Experiments were carried out at room temperature (21 °C) during 2 hours after removing the culture from the incubator.
For each cell sample refractive index values were taken from the Ref. [45]. All the cells were attached to the substrate during the measurements.
2.2. Experimental setup
The SCAOCE experimental setup consists of two modules: OT and OCM ones. Preliminary imaging of the cell is carried out using phase-sensitive OCM, which provides information about the shape and internal structure of the cell. Then single-cell elastography is performed: OCM records the response of the cell to the OT mechanical excitation. In experiments with spherocytes the resulting imaging and elastographic data are then used in numerical simulations to estimate the mechanical properties of the cell sample.
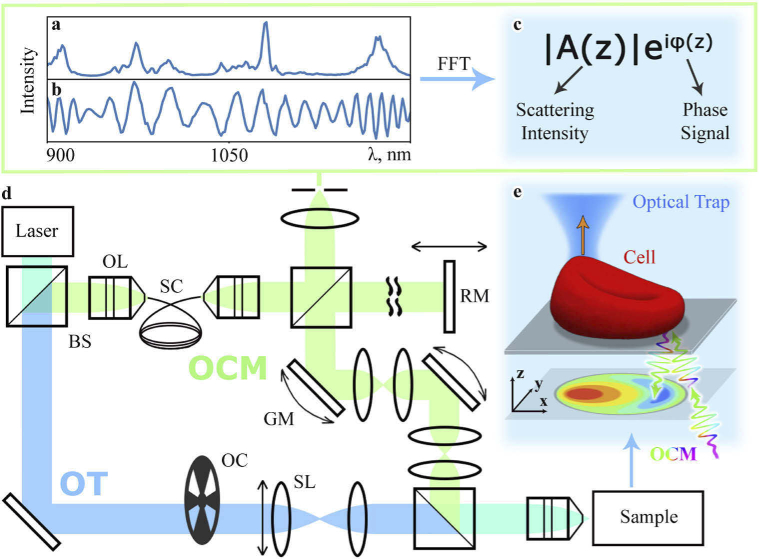
The OCM module is based on a combination of OCT and confocal microscopy (green rays in Fig. 1(d)). The radiation of the 1050-nm Yb-doped solid-state femtosecond laser (Avesta TEMA-70) is broadened by a nonlinear photonic crystal fiber NKT Photonics SC-5.0-1040 (Fig. 1(a)). The resulting 300-nm bandwidth radiation goes into Michelson interferometer containing the sample in the signal arm. Position of the mirror in the reference arm can be changed using optical translator (OptoSigma OSMS 20-85) to adjust the path difference. A system of galvanometer-mounted mirrors (Thorlabs GVS001) is used to scan sample in lateral directions. A high-aperture lens (Olympus UPLSAPO60XW) with numerical aperture of focuses signal beam at the sample. The effective aperture of the OCM signal beam is , the beam power in the sample is 0.5 mW. The radiation scattered by the sample is collected back by the objective, interferes with the reference beam (Fig. 1(b)), and is detected by the spectrometer (Ocean Optics NIR Quest 512). Lateral resolution is 0.5 µm, axial resolution (coherence gate) is 2 µm, confocal gate is also 2 µm.
Fig. 1.
Schematic of the SCAOCE technique. (a) Supercontinuum spectrum generated with photonic crystal fiber. (b) The spectrum resulting from interference between the reference and sample beams (normalized). (c) Scattering intensity and phase signal obtained from the spectrum (b) using fast Fourier transform (FFT). (d) The SCAOCE experimental setup scheme. OCM is optical coherence microscopy module, OL is objective lens, BS is beam splitter, SC – supercontinuum, RM is reference mirror, GM is galvanometer-mounted mirror. OT is optical tweezers module, OC is optical chopper, SL is steering lens. (e) The inset sketch shows schematic diagram of the SCAOCE experiment.
As excitation, the SCAOCE uses the action of optical tweezers, which allows manipulating the cell membrane or trapping individual organelles. The same laser acts as a trapping beam, periodic exposure is provided by an optical chopper, and the trap position is adjusted using a steering lens (blue rays in Fig. 1(d)). The trapping beam is focused at the sample by the same objective, the effective aperture for the optical tweezers beam is . The operating range of the OT radiation power in the sample is from 5 to 20 mW and the fluence is up to 20 in the focal point, which prevents optical damage of the sample [46,47].
2.3. Image postprocessing
The recorded signal is further processed using hand-made program code. At each sample scan point at a certain point in time we obtain the spectrum of the radiation caused by the interference between signal and reference beams (Fig. 1(b)). The spectrum is subjected to Fourier transform, and the dependence of the complex quantity on the sample depth is obtained (Fig. 1(c)). The depth distribution of the sample reflectivity (scattering intensity) is obtained from the amplitude . The phase is the phase of light reflected from the sample at depth (phase scan). Phase allows reconstructing height profile of the sample using the formula [48]:
| (1) |
where is a refractive index and is center wavelength of the signal beam spectrum (1050 nm). Equation (1) is used both for motion detection and imaging [17,48]. To correct the coherence gate curvature and compensate for the dispersion of the OCM beam in the optical elements during scanning, the normalization method [49] was used.
The value of the average standard deviation of the height of the substrate area (without a sample) obtained from the phase scans is used as the axial resolution. The height standard deviation is calculated in several areas of the substrate with the size of 2x2 µm, after which the obtained values are averaged. For raw scans, the average standard deviation is 50±20 nm, after the procedure of averaging and alignment along the scan lines, the imaging resolution reaches 10±5 nm. The main source of image noise is phase jitter between scan lines caused by mechanical noise in the setup. Validation of the Eq. (1) was performed on test data (see Supplement 1 (8.2MB, pdf) ).
2.4. Elastography
During the experiment, the cell is attached to the substrate, and the waist of the optical trap is located above the membrane surface (Fig. 1(e)). Periodic membrane movement is created by turning on and off the OT beam with the frequency of 2-3 Hz, the point of application of the OT does not change. For each point, 65 spectra are recorded with an exposure of 30 ms, thus the measurement time for every point is 1.95 seconds corresponding to 4-6 periods of turning on and off the optical tweezers. In terminology commonly used for OCE, all data was collected in M-B scan format in which 65 A-scans are repeated in the same location (M-scan) in 25 different horizontal locations (B-scan) across the imaging plane. The displacement of the cell membrane at a particular point under the excitation is calculated as the change in the height of the sample using Eq. (1). Further, the frequency and amplitude of oscillations of the cell membrane are determined from time dependence of membrane displacement using the Fourier transform. In addition to the OCM signal, the spectrometer also records the OT beam reflected from the sample. The fact that the narrow peak of the OT (1050±6 nm) is located inside the wide spectrum of OCT (1050±150 nm) provides an easy and accurate synchronization of the trap and cell response signals.
The elastography resolution is determined by the smallest value of the cell membrane displacement, which the method can distinguish against the background of noise caused by phase jitter. To estimate the noise, the response is also recorded from the stationary substrate. In experiments with spherocytes, yeast and cancer cells the SCAOCE resolution was up to the order of a few nanometers (see Supplement 1 (8.2MB, pdf) for the details of force estimation and phantom sample test).
2.5. Numerical simulations
To simulate the response of a spherocyte, the finite element method implemented in the COMSOL package was used. For simplicity of model calculations, a symmetric hemispherical domain with a radius of 3.1 µm covered with a 10-nm thick membrane [50] was simulated. The radius of the domain is equal to the cell radius determined with the experimental SCAOCE scans of the spherocyte, for which the elastography was performed. The lower part of the hemisphere was fixed at a substrate; a point force of 10 pN acted on a cell point near the edge. Force estimation was made using data from previous calibration of forces acted on red blood cells in optical trap with similar optical power [6]. In addition, the internal volume conservation condition and the condition of near-incompressibility of the membrane (Poisson’s ratio 0.47) were taken into account. A mechanical model of hyperelastic material (2-parametric Mooney-Rivlin) was used. The obtained response was compared to the experimental data.
3. Results and discussion
3.1. Cellular imaging with the SCAOCE
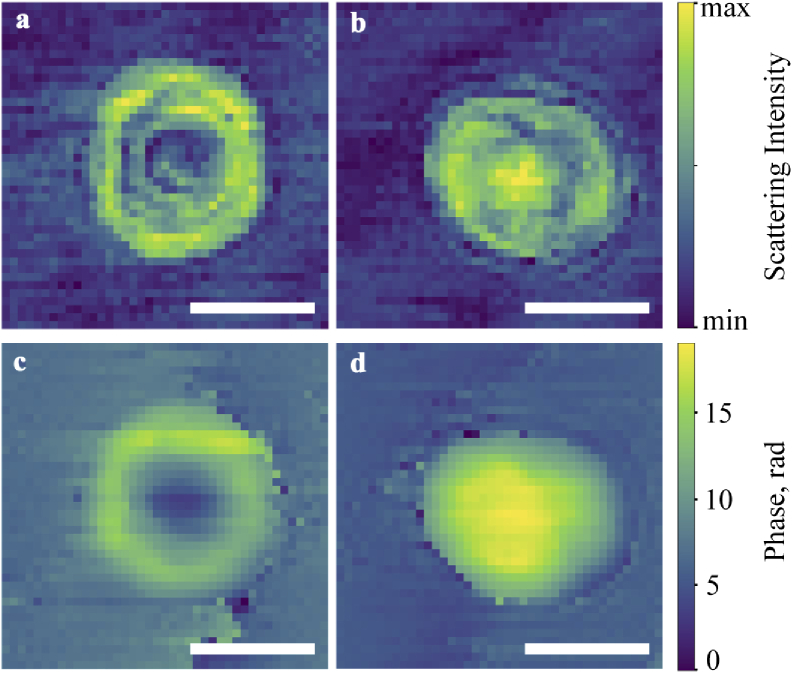
Single-cell imaging performed by the SCAOCE technique is demonstrated using RBC in two characteristic shapes of discocyte and spherocyte. Scattering intensity maps in Figs. 2(a, b) allow evaluating the shape of an object and the scattering of light in it. The cell diameter is 7.7 µm for a discocyte and 8 µm for a spherocyte, imaging step equals to 0.3 µm. Circular stripes on maps are associated with beam interference within the cell. The data on the shape of the sample is later used in numerical simulations.
Fig. 2.
Discocyte (left) and spherocyte (right) scattering intensity map (a, b) and shape visualization with phase scans (c, d), respectively. Scale bars are 5 µm.
In turn, phase scans in Figs. 2(c, d) make it possible to see the features of the cell surface. The discocyte has an expected biconcave shape with the concavity of 0.8 µm deep at the center. The spherocyte has a hemispherical shape, and the phase scan shows the top surface of the hemisphere. The central part of the scanned surface of the cell is on 0.9 µm higher than at the edges of scan. The side surface of spherocyte is not shown because it lies in the next lower pixel of OCM scan along z axis.
The first stage of experiments helped us to check the imaging resolution of the OCM module of the SCAOCE. It was shown that the method resolution is up to 10 nm and is primarily determined by the phase jitter that occurs during scanning. We decided to overcome this noise using periodic excitation and point-by-point registration in elastography. The experimental scans of RBC are consistent with the scans shown in other works [5,16,17].
3.2. Cellular and subcellular elastography with the SCAOCE
Microelastography was performed by the SCAOCE technique for single-cell living RBC, yeast and cancer cells. Most attention is paid to the study of RBC in the form of spherocyte, since its simple shape and well-known properties make the result easy to interpret. The spherocyte was placed on a substrate and therefore took the shape of hemisphere.
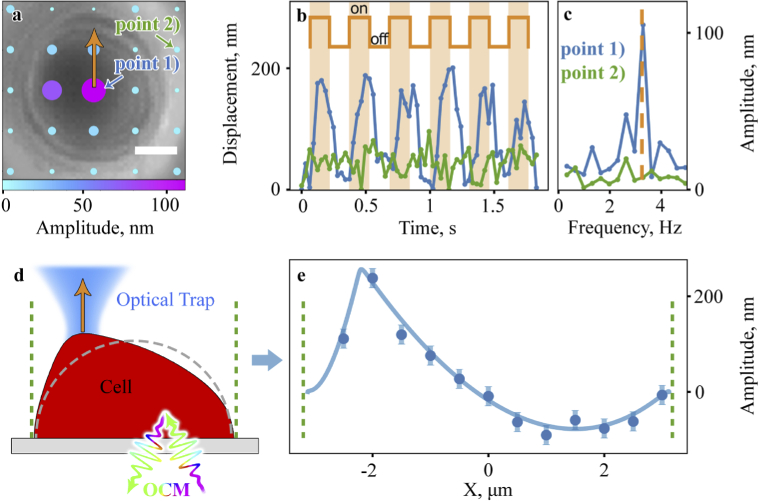
A two-dimensional map of the spherocyte response to external stimulation was constructed (Figs. 3(a)). OT were used to lift the central part of the cell membrane in one point (marked by arrow) with a frequency of 3.3 Hz. The movement of the membrane caused by mechanical excitation from the OT was recorded sequentially at 25 points of the cell and substrate (in the 2D plane).
Fig. 3.
Spherocyte dynamics study. (a) 2D spherocyte oscillation map, orange arrow depicts trap position, scale bar is 2 µm. (b) Cell oscillation in points 1) (blue) and 2) (green) for central excitation, the periods of switching on and off the OT beam are indicated by orange color and meander. (c) Cell oscillation spectrum in points 1) (blue) and 2) (green), dashed orange line depicts trap activation frequency. (d) Schematic diagram of the experiment with excitation of the edge of the cell. (e) 1D spherocyte oscillation distribution for edge excitation. Points depict experimental data; curve is finite element modeling results.
Figure 3(a) shows an optical microscope image of a spherocyte overlaid with a 2D cell response amplitude map, where the color and size of the dot correspond to the magnitude of the response. The OCM signals at points marked 1) and 2) are shown in the Fig. 3(b), where the first point corresponds to the center of the cell with the maximum response value, and the second one is a fixed point on the substrate. The periods of turning on and off the OT beam are indicated by orange color and meander. The spherocyte response frequency is 3.3 Hz and coincides with the on-off frequency of the OT. The maximum amplitude of the cell response at the center is 110 nm. The amplitude of the phase jitter at the points of the stationary substrate is on average 6.5 nm. The magnitude of the cell’s response drops significantly upon the moving away from the point of excitation. This is probably due to the large distance between the scanning points.
Further, a similar experiment was carried out, but now the point of application of excitation is located at the edge of the cell, the experiment concept is shown in Fig. 3(d). As in the previous experiment, the point of application of the optical tweezers remained constant. The SCAOCE scanning was carried out along the straight line in order to increase the lateral resolution without increasing the duration of measurements.
The dependence of the amplitude of the cell response on the transverse coordinate was obtained (Fig. 3(e)). The point of application of the optical tweezers corresponds to the maximum response amplitude (x = -2 µm). The amplitude of the response is from 5 nm to 200 nm at various points of the cell. A region of negative amplitude on the right side of the plot corresponds to the movement of the cell membrane in antiphase with external excitation, that is, when the OT were turned on, this part of the cell bend down. This indicates that the spherocyte reacts to the excitation like a ball or a drop, the proposed type of cell deformation is shown in Fig. 3(d). Experimentally measured mechanical response of the spherocyte membrane is in excellent agreement with results of numerical calculation. The values of the Mooney-Rivlin elasticity coefficients obtained as fitting parameters in the numerical simulation are of the order of , , which is in order consistent with experimental data obtained using other methods [50].
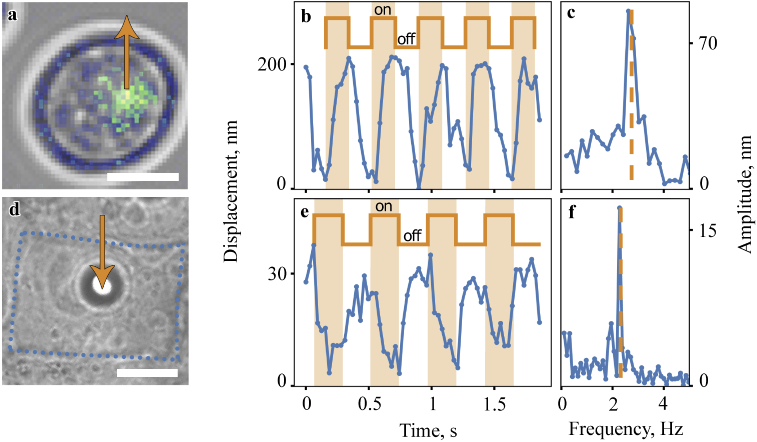
The next SCAOCE research subject were baker’s yeast cells as model organisms with a complex internal structure and optically contrasting nucleus. Figure 4(a) shows an optical microscope image of a yeast cell overlaid with a scattering intensity OCM scan. An OCM image of the cell was obtained to determine the position of the cell nucleus by the maximum scattering amplitude. Then the detected nucleus was periodically lifted using optical tweezers, the arrow indicates the location and direction of impact. Figure 4(b) shows the displacement of the cell nucleus position under the influence of periodic optical trapping. The periods of turning on and off the OT beam are indicated by color and meander. The amplitude and frequency of nucleus motion are obtained, the amplitude is 85 nm, the response frequency is 2.6 Hz and coincides with the frequency of turning on and off the OT beam (Fig. 4(c)). Due to the connection of the organelle with the cell and because of its small size, the whole cell oscillation was also observed during the nucleus excitation. When the cell was excited at points where strong scattering was not observed, the response was relatively weak or completely absent, probably because of the lack of optical trapping forces due to low refractive index contrast between object and medium [51].
Fig. 4.
Yeast cell and cancer cell dynamics. (a) Scattering intensity map is placed on top of the microscope image of the yeast cell revealing the nucleus location. (b) Yeast cell organelle oscillation and (c) oscillation amplitude. (d) Microscope image of the cancer cell, dotted line indicates cancer cell boundaries, microsphere diameter is 5 µm. (e) Cancer cell oscillation and (f) oscillation amplitude. Blue curves depict cell oscillations, the periods of turning on and off the OT beam are indicated by orange color and meander. Orange arrow depicts trap position and trapping force direction. Scale bars: 5 µm (a) and 10 µm (d).
For clinical applications of elastography, comparative experiments on pathological cells are of great interest. We applied the SCAOCE method to study the mechanical properties of mouse breast cancer cells.
In contrast to previous experiments, we found to be unable to capture the cell membrane or its organelles with an optical trap. Possible causes are the high stiffness of the structures of this cell and low contrast of the refractive index between the membrane, the medium, and the cytoplasm. In this case a different approach based on the use of microprobe at the cell surface [6,44] with the SCAOCE can be applied, similar to position tracking of optically trapped particles using optical diffraction tomography [52].
Borosilicate microspheres were added to the sample with the cell culture, and then were trapped and attached to the cell membrane (Fig. 4(d)). The waist of the optical trap was located below the center of the microsphere, thus, when the OT were turned on, the microsphere was pressed into the cell; when the trap was turned off, the cell restored its shape. At the same time, using a phase-sensitive OCM, the position of the particle was determined when the optical trap was turned on and off (Fig. 4(e)). The response amplitude is 17 nm, the response frequency is 2.3 Hz and coincides with the frequency of the optical trap switching (Fig. 4(f)). The significantly lower value of the response of the mouse breast cancer cell in comparison with the response of red blood cells and yeast cells also corresponds to the higher stiffness of cancer cells.
The SCAOCE method allows studying the mechanical properties of single cells in a noninvasive and completely optical way. The optical tweezers are used to create external excitation on the cell membrane pointwise and without a probe. Phase-sensitive optical coherence microscopy uses coherence and confocal gates simultaneously, which makes it possible to build images of cells with submicron accuracy and record nanometer membrane displacements from a specific point of the sample volume. The developed method allows studying the biomechanical properties of living single cells and individual cells within a culture, the performed numerical modeling shows good agreement with the literature data.
The measurements demonstrate that the method allows label-free manipulating the position of the organelle inside the cell without destroying the cell itself, and at the same time registering organelle position with nanometer accuracy. The experiment carried out indicates the prospects of using the SCAOCE method for subcellular noninvasive microelastography.
Despite all the listed advantages, the method also has some limitations. For example, in the case of more rigid cells, we have to use more powerful CW-laser sources or to abandon the concept of all-optical study and use attached microbeads to excite mechanical waves. The experiment demonstrates that the SCAOCE method in combination with the use of microparticles can also be applied to study the mechanical properties of membranes of relatively rigid cells, cells with a low contrast of refractive indices, and other cells in which, for some reason, it is impossible to carry out direct optical trapping of membranes. At the same time, the advantages of the SCAOCE method associated with its all-optical nature disappear, but the advantages associated with high sensitivity and the ability to visualize cell and map its response remain. Phase-sensitive OCM allows tracking the trajectory of the particle and cell membrane with nanometer precision, which cannot be done using optical tweezers alone.
4. Conclusions
A novel single-cell all-optical coherence elastography method (SCAOCE) that combines optical tweezers to produce mechanical excitation on the cell membrane or organelle and phase-sensitive OCM to visualize cell and map its response is demonstrated. Three types of samples are studied: living single cells with a simple internal structure (RBC), cells with a complex internal structure (yeast cells), as well as single cells within a culture (cancer cells). The elasticity coefficients of spherocyte membrane determined using the SCAOCE are in good agreement with the data reported in the literature using other methods.
The ability to determine the mechanical properties of single cells can be used in single-cell diagnostics – in the case of the presence of only a small number of cells of interest or the need for their minimal use. The use of a common laser source and objective lens for creating mechanical excitation and for visualization and mapping of the response can be an advantage of the method when it is used in vivo. For example, in the study of single cells in a living organism, to implement the method, it will be sufficient to use a single objective lens, brought up to the studied area. In endoscopic study, the method can be implemented using an optical fiber. At the same time, the completely optical nature of the method and the use of infrared radiation makes it possible to study noninvasively the mechanical properties of sufficiently deeply located cells and their organelles. This indicates that the developed SCAOCE method has great potential for in vivo single-cell biomedical diagnostics.
Acknowledgments
The authors thank Dr. Anastasiia S. Garanina for supporting samples of mouse breast cancer cells.
Funding
Russian Science Foundation10.13039/501100006769 (20-12-00371, numerical simulations); Russian Foundation for Basic Research10.13039/501100002261 (20-04-60526, sample preparation); Ministry of Education and Science of the Russian Federation10.13039/501100003443 (14.W03.31.0008, biomechanical measurements and 075-15-2020801, cellular imaging); MSU Interdisciplinary School “Photonic and Quantum technologies. Digital medicine”; MSU Quantum Technology Center).
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (8.2MB, pdf) for supporting content.
References
- 1.Wu P.-H., Aroush D. R.-B., Asnacios A., Chen W.-C., Dokukin M. E., Doss B. L., Durand P., Ekpenyong A., Guck J., Guz N. V., Janmey P. A., Lee J. S. H., Moore N. M., Ott A., Poh Y.-C., Ros R., Sander M., Sokolov I., Staunton J. R., Wang N., Whyte G., Wirtz D., “A comparison of methods to assess cell mechanical properties,” Nat. Methods 15(7), 491–498 (2018). 10.1038/s41592-018-0015-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Totaro A., Castellan M., Battilana G., Zanconato F., Azzolin L., Giulitti S., Cordenonsi M., Piccolo S., “YAP/TAZ link cell mechanics to notch signalling to control epidermal stem cell fate,” Nat. Commun. 8(1), 15206 (2017). 10.1038/ncomms15206 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fletcher D. A., Mullins R. D., “Cell mechanics and the cytoskeleton,” Nature 463(7280), 485–492 (2010). 10.1038/nature08908 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Davies P. F., Manduchi E., Jiménez J. M., Jiang Y.-Z., “Biofluids, cell mechanics and epigenetics: flow-induced epigenetic mechanisms of endothelial gene expression,” J. Biomech. 50, 3–10 (2017). 10.1016/j.jbiomech.2016.11.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Popescu G., Park Y., Choi W., Dasari R. R., Feld M. S., Badizadegan K., “Imaging red blood cell dynamics by quantitative phase microscopy,” Blood Cells, Mol., Dis. 41(1), 10–16 (2008). 10.1016/j.bcmd.2008.01.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lyubin E. V., Khokhlova M. D., Skryabina M. N., Fedyanin A. A., “Cellular viscoelasticity probed by active rheology in optical tweezers,” J. Biomed. Opt. 17(10), 101510 (2012). 10.1117/1.JBO.17.10.101510 [DOI] [PubMed] [Google Scholar]
- 7.Wirtz D., Konstantopoulos K., Searson P. C., “The physics of cancer: the role of physical interactions and mechanical forces in metastasis,” Nat. Rev. Cancer 11(7), 512–522 (2011). 10.1038/nrc3080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Almonacid M., Terret M.-E., Verlhac M.-H., “Nuclear positioning as an integrator of cell fate,” Curr. Opin. Cell Biol. 56, 122–129 (2019). 10.1016/j.ceb.2018.12.002 [DOI] [PubMed] [Google Scholar]
- 9.Venturini V., Pezzano F., Castro F. C., Häkkinen H.-M., Jiménez-Delgado S., Colomer-Rosell M., Marro M., Tolosa-Ramon Q., Paz-López S., Valverde M. A., Weghuber J., Loza-Alvarez P., Krieg M., Wieser S., Ruprecht V., “The nucleus measures shape changes for cellular proprioception to control dynamic cell behavior,” Science 370(6514), eaba2644 (2020). 10.1126/science.aba2644 [DOI] [PubMed] [Google Scholar]
- 10.Brezinski M. E., Optical Coherence Tomography: Principles and Applications (Elsevier, 2006). [Google Scholar]
- 11.Dolganova I. N., Aleksandrova P. V., Nikitin P. V., Alekseeva A. I., Chernomyrdin N. V., Musina G. R., Beshplav S. T., Reshetov I. V., Potapov A. A., Kurlov V. N., Tuchin V. V., Zaytsev K. I., “Capability of physically reasonable oct-based differentiation between intact brain tissues, human brain gliomas of different who grades, and glioma model 101.8 from rats,” Biomed. Opt. Express 11(11), 6780–6798 (2020). 10.1364/BOE.409692 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Larin K. V., Sampson D. D., “Optical coherence elastography–OCT at work in tissue biomechanics,” Biomed. Opt. Express 8(2), 1172–1202 (2017). 10.1364/BOE.8.001172 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang S., Larin K. V., “Optical coherence elastography for tissue characterization: a review,” J. Biophotonics 8(4), 279–302 (2015). 10.1002/jbio.201400108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Schmitt J. M., “Oct elastography: imaging microscopic deformation and strain of tissue,” Opt. Express 3(6), 199–211 (1998). 10.1364/OE.3.000199 [DOI] [PubMed] [Google Scholar]
- 15.Drexler W., Fujimoto J. G., Optical Coherence Tomography: Technology and Applications (Springer Science & Business Media, 2008). [Google Scholar]
- 16.Sarunic M. V., Weinberg S., Izatt J. A., “Full-field swept-source phase microscopy,” Opt. Lett. 31(10), 1462–1464 (2006). 10.1364/OL.31.001462 [DOI] [PubMed] [Google Scholar]
- 17.Joo C., Akkin T., Cense B., Park B. H., De Boer J. F., “Spectral-domain optical coherence phase microscopy for quantitative phase-contrast imaging,” Opt. Lett. 30(16), 2131–2133 (2005). 10.1364/OL.30.002131 [DOI] [PubMed] [Google Scholar]
- 18.Zhao Y., Chen Z., Saxer C., Xiang S., de Boer J. F., Nelson J. S., “Phase-resolved optical coherence tomography and optical doppler tomography for imaging blood flow in human skin with fast scanning speed and high velocity sensitivity,” Opt. Lett. 25(2), 114–116 (2000). 10.1364/OL.25.000114 [DOI] [PubMed] [Google Scholar]
- 19.Park Y., Best C. A., Badizadegan K., Dasari R. R., Feld M. S., Kuriabova T., Henle M. L., Levine A. J., Popescu G., “Measurement of red blood cell mechanics during morphological changes,” Proc. Natl. Acad. Sci. 107(15), 6731–6736 (2010). 10.1073/pnas.0909533107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee K., Kim K., Jung J., Heo J., Cho S., Lee S., Chang G., Jo Y., Park H., Park Y., “Quantitative phase imaging techniques for the study of cell pathophysiology: from principles to applications,” Sensors 13(4), 4170–4191 (2013). 10.3390/s130404170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Marquet P., Depeursinge C., Magistretti P. J., “Review of quantitative phase-digital holographic microscopy: promising novel imaging technique to resolve neuronal network activity and identify cellular biomarkers of psychiatric disorders,” Neurophotonics 1(2), 020901 (2014). 10.1117/1.NPh.1.2.020901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wu Z., Luu C. D., Ayton L. N., Goh J. K., Lucci L. M., Hubbard W. C., Hageman J. L., Hageman G. S., Guymer R. H., “Fundus autofluorescence characteristics of nascent geographic atrophy in age-related macular degeneration,” Invest. Ophthalmol. Visual Sci. 56(3), 1546–1552 (2015). 10.1167/iovs.14-16211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Song S., Le N. M., Huang Z., Shen T., Wang R. K., “Quantitative shear-wave optical coherence elastography with a programmable phased array ultrasound as the wave source,” Opt. Lett. 40(21), 5007–5010 (2015). 10.1364/OL.40.005007 [DOI] [PubMed] [Google Scholar]
- 24.Singh M., Wu C., Liu C.-H., Li J., Schill A., Nair A., Larin K. V., “Phase-sensitive optical coherence elastography at 1.5 million a-lines per second,” Opt. Lett. 40(11), 2588–2591 (2015). 10.1364/OL.40.002588 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wang S., Larin K. V., Li J., Vantipalli S., Manapuram R., Aglyamov S., Emelianov S., Twa M., “A focused air-pulse system for optical-coherence-tomography-based measurements of tissue elasticity,” Laser Phys. Lett. 10(7), 075605 (2013). 10.1088/1612-2011/10/7/075605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liang X., Boppart S. A., “Biomechanical properties of in vivo human skin from dynamic optical coherence elastography,” IEEE Trans. Biomed. Eng. 57(4), 953–959 (2009). 10.1109/TBME.2009.2033464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Leartprapun N., Iyer R. R., Untracht G. R., Mulligan J. A., Adie S. G., “Photonic force optical coherence elastography for three-dimensional mechanical microscopy,” Nat. Commun. 9(1), 2079 (2018). 10.1038/s41467-018-04357-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Crecea V., Graf B. W., Kim T., Popescu G., Boppart S. A., “High resolution phase-sensitive magnetomotive optical coherence microscopy for tracking magnetic microbeads and cellular mechanics,” IEEE J. Sel. Top. Quantum Electron. 20(2), 25–31 (2013). 10.1109/JSTQE.2013.2280501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Alcaraz J., Buscemi L., Grabulosa M., Trepat X., Fabry B., Farré R., Navajas D., “Microrheology of human lung epithelial cells measured by atomic force microscopy,” Biophys. J. 84(3), 2071–2079 (2003). 10.1016/S0006-3495(03)75014-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Emad A., Heinz W. F., Antonik M. D., D’Costa N. P., Nageswaran S., Schoenenberger C.-A., Hoh J. H., “Relative microelastic mapping of living cells by atomic force microscopy,” Biophys. J. 74(3), 1564–1578 (1998). 10.1016/S0006-3495(98)77868-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Liu H., Wen J., Xiao Y., Liu J., Hopyan S., Radisic M., Simmons C. A., Sun Y., “In situ mechanical characterization of the cell nucleus by atomic force microscopy,” ACS Nano 8(4), 3821–3828 (2014). 10.1021/nn500553z [DOI] [PubMed] [Google Scholar]
- 32.Byun S., Son S., Amodei D., Cermak N., Shaw J., Kang J. H., Hecht V. C., Winslow M. M., Jacks T., Mallick P., Manalis S. R., “Characterizing deformability and surface friction of cancer cells,” Proc. Natl. Acad. Sci. 110(19), 7580–7585 (2013). 10.1073/pnas.1218806110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Liu H.-C., Gang E. J., Kim H. N., Lim H. G., Jung H., Chen R., Abdel-Azim H., Shung K. K., Kim Y.-M., “Characterizing deformability of drug resistant patient-derived acute lymphoblastic leukemia (all) cells using acoustic tweezers,” Sci. Rep. 8(1), 15708 (2018). 10.1038/s41598-018-34024-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Wang N., Ingber D. E., “Control of cytoskeletal mechanics by extracellular matrix, cell shape, and mechanical tension,” Biophys. J. 66(6), 2181–2189 (1994). 10.1016/S0006-3495(94)81014-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Antonacci G., Braakman S., “Biomechanics of subcellular structures by non-invasive brillouin microscopy,” Sci. Rep. 6(1), 37217 (2016). 10.1038/srep37217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fazal F. M., Block S. M., “Optical tweezers study life under tension,” Nat. Photonics 5(6), 318–321 (2011). 10.1038/nphoton.2011.100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Khokhlova M. D., Lyubin E. V., Zhdanov A. G., Rykova S. Y., Sokolova I. A., Fedyanin A. A., “Normal and system lupus erythematosus red blood cell interactions studied by double trap optical tweezers: direct measurements of aggregation forces,” J. Biomed. Opt. 17(2), 025001 (2012). 10.1117/1.JBO.17.2.025001 [DOI] [PubMed] [Google Scholar]
- 38.Guck J., Ananthakrishnan R., Mahmood H., Moon T. J., Cunningham C. C., Käs J., “The optical stretcher: a novel laser tool to micromanipulate cells,” Biophys. J. 81(2), 767–784 (2001). 10.1016/S0006-3495(01)75740-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Antonacci G., Beck T., Bilenca A., Czarske J., Elsayad K., Guck J., Kim K., Krug B., Palombo F., Prevedel R., Scarcelli G., “Recent progress and current opinions in brillouin microscopy for life science applications,” Biophys. Rev. 12(3), 615–624 (2020). 10.1007/s12551-020-00701-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Stetciura I. Y., Yashchenok A., Masic A., Lyubin E. V., Inozemtseva O. A., Drozdova M. G., Markvichova E. A., Khlebtsov B. N., Fedyanin A. A., Sukhorukov G. B., Gorin D. A., Volodkin D., “Composite sers-based satellites navigated by optical tweezers for single cell analysis,” Analyst 140(15), 4981–4986 (2015). 10.1039/C5AN00392J [DOI] [PubMed] [Google Scholar]
- 41.Shilkin D. A., Lyubin E. V., Soboleva I. V., Fedyanin A. A., “Direct measurements of forces induced by bloch surface waves in a one-dimensional photonic crystal,” Opt. Lett. 40(21), 4883–4886 (2015). 10.1364/OL.40.004883 [DOI] [PubMed] [Google Scholar]
- 42.Habaza M., Gilboa B., Roichman Y., Shaked N. T., “Tomographic phase microscopy with 180 rotation of live cells in suspension by holographic optical tweezers,” Opt. Lett. 40(8), 1881–1884 (2015). 10.1364/OL.40.001881 [DOI] [PubMed] [Google Scholar]
- 43.Yevnin M., Kasimov D., Gluckman Y., Ebenstein Y., Roichman Y., “Independent and simultaneous three-dimensional optical trapping and imaging,” Biomed. Opt. Express 4(10), 2087–2094 (2013). 10.1364/BOE.4.002087 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mills J., Qie L., Dao M., Lim C., Suresh S., “Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers,” Molecular & Cellular Biomechanics 1, 169 (2004). [PubMed] [Google Scholar]
- 45.Liu P. Y., Chin L., Ser W., Chen H., Hsieh C.-M., Lee C.-H., Sung K.-B., Ayi T., Yap P., Liedberg B., Wang K., Bourouina T., Leprince-Wang Y., “Cell refractive index for cell biology and disease diagnosis: past, present and future,” Lab Chip 16(4), 634–644 (2016). 10.1039/C5LC01445J [DOI] [PubMed] [Google Scholar]
- 46.Saytashev I., Arkhipov S. N., Winkler N., Zuraski K., Lozovoy V. V., Dantus M., “Pulse duration and energy dependence of photodamage and lethality induced by femtosecond near infrared laser pulses in drosophila melanogaster,” J. Photochem. Photobiol., B 115, 42–50 (2012). 10.1016/j.jphotobiol.2012.06.009 [DOI] [PubMed] [Google Scholar]
- 47.Bourgeois F., Ben-Yakar A., “Femtosecond laser nanoaxotomy properties and their effect on axonal recovery in c. elegans,” Opt. Express 15(14), 8521–8531 (2007). 10.1364/OE.15.008521 [DOI] [PubMed] [Google Scholar]
- 48.Choma M. A., Ellerbee A. K., Yang C., Creazzo T. L., Izatt J. A., “Spectral-domain phase microscopy,” Opt. Lett. 30(10), 1162–1164 (2005). 10.1364/OL.30.001162 [DOI] [PubMed] [Google Scholar]
- 49.Graf B. W., Adie S. G., Boppart S. A., “Correction of coherence gate curvature in high numerical aperture optical coherence imaging,” Opt. Lett. 35(18), 3120–3122 (2010). 10.1364/OL.35.003120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Xu D., Kaliviotis E., Munjiza A., Avital E., Ji C., Williams J., “Large scale simulation of red blood cell aggregation in shear flows,” Journal of Biomechanics 46(11), 1810–1817 (2013). 10.1016/j.jbiomech.2013.05.010 [DOI] [PubMed] [Google Scholar]
- 51.Neuman K. C., Block S. M., “Optical trapping,” Rev. Sci. Instrum. 75(9), 2787–2809 (2004). 10.1063/1.1785844 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Kim K., Yoon J., Park Y., “Simultaneous 3D visualization and position tracking of optically trapped particles using optical diffraction tomography,” Optica 2(4), 343–346 (2015). 10.1364/OPTICA.2.000343 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.