Abstract
Multiphoton fluorescence microscopy enables deep in vivo imaging by using long excitation wavelengths to increase the penetration depth of ballistic photons and nonlinear excitation to suppress the out-of-focus fluorescence. However, the imaging depth of multiphoton microscopy is limited by tissue scattering and absorption. This fundamental depth limit for two-photon microscopy has been studied theoretically and experimentally. Long wavelength three-photon fluorescence microscopy was developed to image beyond the depth limit of two-photon microscopy and has achieved unprecedented in vivo imaging depth. Here we extend the theoretical framework for characterizing the depth limit of two-photon microscopy to three-photon microscopy. We further verify the theoretical predictions with experimental results from tissue phantoms. We demonstrate experimentally that high spatial resolution diffraction-limited imaging at a depth of 10 scattering mean free paths, which is nearly twice the transport mean free path, is possible with multiphoton microscopy. Our results indicate that the depth limit of three-photon microscopy is significantly beyond what has been achieved in biological tissues so far, and further technological development is required to reach the full potential of three-photon microscopy.
1. Introduction
Optical microscopy plays a key role in advancing our understanding of biological systems. The high spatiotemporal resolution of noninvasive optical imaging techniques make them unique in their ability to answer specific biological questions [1–4]. Multiphoton microscopy (MPM) enables deep imaging within turbid media with high spatial resolution [5–7]. The nonlinear nature of multiphoton excitation reduces out-of-focus (background) fluorescence generation. Additionally, by using longer wavelengths to excite widely available fluorophores, the excitation photons are scattered less and can form a sharp focus deeper inside turbid media [5,8]. Over the last few decades, two-photon microscopy (2PM) has become the gold standard of deep in vivo imaging, enabling access to depths beyond the superficial layers [9–12]. While 2PM can penetrate deeper than one-photon confocal fluorescence microscopy when imaging the same fluorophores, it is eventually limited by contrast degradation due to background fluorescence generation [8]. As powerful ultrafast lasers have become more accessible, the depth limit of 2PM has been reached and quantitatively characterized [8,12]. For example, both theoretical and experimental investigations in the past have shown that the fundamental depth limit for 2PM is approximately 0.8 mm penetration depth when imaging mouse brain vasculature in vivo at the excitation wavelength of 920 nm [8,13].
To overcome the depth limit of 2PM, long wavelength three-photon fluorescence microscopy (3PM) was developed. 3PM takes advantage of the optimal excitation wavelength windows for deep tissue imaging at 1300 nm and 1700 nm and further suppresses background fluorescence because of higher order nonlinear excitation [5,14,15]. 3PM has since achieved unprecedented imaging depths; examples include 3PM of neuronal activity with single-cell resolution in the mouse hippocampus [6] or through the intact skull of adult mice and zebrafish [7,16], imaging mouse brain vasculature and blood flow at >2 mm depth [17], imaging the physiological response of the subplate of the mouse visual cortex [12,18,19], two-photon (2P) and three-photon (3P) volumetric imaging for simultaneous monitoring of both the cortical layers and the subcortical regions [20], and recording neuronal activities at >1.1 mm depth in the visual cortex of freely moving rats with a head-mounted miniature 3P microscope [21]. However, while the depth limit of 2PM has been extensively studied, systematic studies of depth limits of 3PM lack. Most of the current work that examines the depth limit of 3PM has employed theoretical simulations without experimental verifications [12,22]. The depth limit for 3PM has not yet been established theoretically or experimentally. New theoretical and experimental investigations are needed to fully understand the capability of 3PM and define the boundaries of high spatial resolution deep tissue imaging.
We follow the analytical model of Theer and Denk, where the spatiotemporal distribution of scattered and ballistic photons in a turbid media are analytically modeled to find a depth limit [8]. We extend this model to three- and four-photon (4P) excitation. Furthermore, we perform controlled experiments to quantitatively compare the depth limit of 2PM and 3PM and investigate the depth limit of 3PM in a variety of experimental conditions. Our theoretical and experimental data contradict published results from numerical simulation that showed loss of spatial resolution is the limiting factor in deep imaging with 3PM [22]. We demonstrate high spatial resolution imaging at depths of approximately 10 scattering mean free paths, which is nearly twice the transport mean free path (TMFP), the commonly acknowledged depth limit of imaging techniques using ballistic photons [23,24]. Our results unequivocally show that the depth limit of 3PM is significantly beyond what has been achieved in biological tissues so far. Our work will not only deepen the understanding of deep tissue imaging but will also motivate future technology development to reach the full potential of 3PM.
2. Theoretical analysis
To quantitatively describe the spatial distribution of fluorescence, we must find the distribution of excitation light inside a scattering medium. Ballistic photons are exponentially attenuated by tissue scattering and absorption, which are characterized by the scattering mean free path and absorption length . The combined effect of absorption and scattering is represented by the effective attenuation length ( ):
| (1) |
The EAL is often used as the unit of depth in characterizing the optical imaging depth limit [8,15]. In our experiments, which mimic biological imaging conditions, scattering is the dominant cause of ballistic photon attenuation (i.e., and ). This assumption holds for most biological tissues in vivo between 700 nm and 1700 nm (typical wavelength window for MPM) except for within the wavelength range of strong water absorption between approximately 1400 nm and 1550 nm.
The power of ballistic photons as a function of depth can be characterized by:
| (2) |
where is the optical power at the surface of the media and is the distance traveled within the media. While absorption simply removes the excitation photons from the focal volume, scattering re-distributes the light intensity and increases the excitation outside of the focal volume. Multiphoton excited fluorescence signal from the focal volume (defined as the signal, S) is mostly generated by the ballistic photons. Therefore, the excitation power at the sample surface must exponentially increase as a function of depth to maintain sufficient power at the focus for detectable signal generation (Eq. (2)). As the imaging depth increases, the amount of fluorescence excitation outside the focal volume (defined as the out-of-focus background, B), which contains no high spatial resolution information, eventually overwhelms S. The signal-to-background ratio (SBR) characterizes the image contrast. The imaging depth limit can be defined by choosing a depth at which a required SBR value is reached. We chose the depth limit as the depth at which SBR = 1, which has been commonly used in the past [8,12,25].
To simplify the analytical modeling, the ballistic photons inside a sample can be formulated as an exponentially decaying Gaussian beam with the beam waist at the focus plane. An additional temporal component is added in the case of pulsed lasers to represent the temporal pulse shape. Assuming a Gaussian temporal distribution, the intensity of ballistic photons can be described as:
| (3) |
where P is the normalized power through a transverse plane, z is the position along optical axis measured from the focus plane, is the radial distance from the optical axis, is the radius of the beam, is the pulse half width, and is the effective attenuation coefficient .
When the beam is focused inside a scattering medium, it travels from a transparent medium to the absorbing-scattering environment of the sample. The light that travels inside the sample has two components: the ballistic photons that follow the Gaussian distribution (Eq. (3)) and the scattered photons that deviate from this path. The spatial distribution of light depends on many factors including the angular distribution of the scattered light. Scattering angular distribution is characterized with the anisotropy factor, g. In biological samples, scattering is mostly in the forward direction and the value of g is typically between of 0.8 and 1 [24].
The ballistic photons traveling inside the sample are governed by the focusing geometry and the properties of the sample. As the beam travels deeper inside the sample, the rays at larger convergence angles experience larger attenuation and cause the effective numerical aperture (NA) of the system to reduce with depth. The effective NA (NAeff) in the sample at focus depth z can be approximated by using propagation laws of Gaussian beams as follows [8]:
| (4) |
where , n is the refractive index of the medium, and is the far-field angular spread of the Gaussian beam. Using this approximation, we find the intensity distribution of the ballistic photons inside a scattering medium.
We follow the model developed by Theer and Denk to find the intensity of the scattered light ( ) [8]. A beam spread function is defined to analytically compute the mean and variance of the spatial and temporal distribution of the scattered light. The scattered intensity is then calculated by finding the convolution of the ballistic intensity with the beam spread function. Detailed description of the model is shown in Supplement 1 (2.5MB, pdf) .
Fluorescence produced by an -photon process can be described as follows:
| (5) |
The axial distribution of fluorescence is found by integrating the radial and temporal components (Fig. 1(a),(b))). To quantify the SBR given an axial intensity distribution, the signal is found by integrating the axial distribution of the fluorescence over increasing intervals around the focus depth, until a plateau in the value of S is reached (Fig. S1). We normalized the integration range to the Rayleigh length of the Gaussian beam as defined by
| (6) |
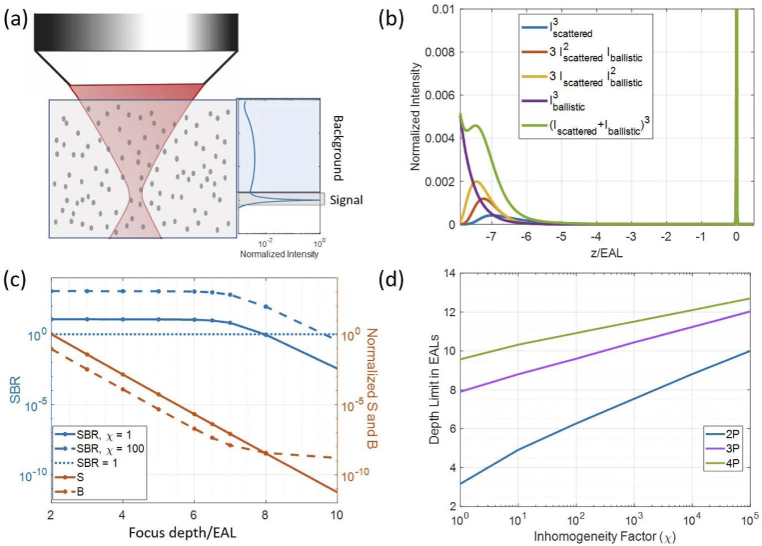
Fig. 1.
Intensity distribution simulations for typical imaging parameters in biological sample with NA of 1. The parameters used for 2P imaging are: g = 0.88, λ = 920 nm, τ = 100 fs, EAL = 150 µm. The parameters used for 3P imaging are: g = 0.81, λ = 1280 nm, τ = 50 fs, EAL = 300 µm. The parameters used for 4P imaging are: g = 0.73, λ = 1680 nm, τ = 50 fs, EAL = 380 µm. (a) Schematic illustration of a focused Gaussian beam inside a scattering medium, with the corresponding axial fluorescence distribution as a function of depth shown on the right. (b) Example of the axial distribution of 3P excited fluorescence intensity calculated at a focus depth of 8 EALs inside a scattering medium. Values are normalized to the maximum fluorescence at the focus. (c) S, B, and SBR values for 3P excited fluorescence at various focus depths inside a scattering medium. SBR is plotted for inhomogeneity factor (χ) of 1 and 100. S and B values are normalized to the S value at a focus depth of 2 EALs for clarity. Data points are plotted with markers and a line connects them to find the intersection with SBR = 1 (dotted line). (d) Depth limit (depth at which SBR=1) as a function of inhomogeneity factor for 2P, 3P, and 4P excited fluorescence inside a scattering medium.
As shown in Fig. S1, the signal reaches an asymptotical value for all focus depths. We chose a full integration range of and for 3P and 2P intensity distributions, respectively. The background value is determined by subtracting the signal from the total integrated fluorescence of the entire depth. The change in 2P and 3Ps S, B, and SBR with increasing focus depth is shown in Fig. S2.
An important factor in determining the background fluorescence is the fraction of the volume that is occupied by fluorophores since fluorescence is directly proportional to concentration [26]. This effect can be quantified by defining an inhomogeneity factor:
| (7) |
Assuming the features of interest are larger than the focal volume, the background fluorescence can be scaled inversely with the inhomogeneity factor and the SBR can be calculated for samples with different inhomogeneity factors (Fig. 1(c),(d))). Since fluorophore distribution in biological samples can vary, this representation of the depth limit allows us to adjust the values according to the sample properties. The depth limit will increase as the contribution of background decreases with increasing inhomogeneity, as shown in Fig. 1(d). Using the theoretical models described above, we have also investigated the effect of NA and pulse width of the excitation light on SBR (Fig. S3 and S4).
3. Experimental setup
To verify the theoretical analysis above, we performed experimental measurements in tissue phantoms, which allow us to precisely control all the sample and imaging parameters. We embedded polystyrene beads in an agarose solution to create controlled absorbing and scattering tissue phantoms. We used 1 gram of high melting point agarose per 100 mL of water as our base medium so that we could stabilize the beads for resolution measurement while emulating biological samples with its absorption properties. To control the scattering and inhomogeneity factor we added a combination of 1-µm diameter fluorescent beads (Fluoresbrite Yellow Green Microspheres, 17154 Polysciences, Inc.) and 1-µm diameter non-fluorescent beads (Polybead Microspheres, 07310 Polysciences, Inc.). While keeping the agarose solution above its gelling point, the two types of beads were mixed with a vortex mixer, then mixed thoroughly with the agarose solution before pouring into the sample container to solidify.
Images were obtained using a commercial multiphoton microscope (Bergamo II system B242, Thorlabs Inc.). A high numerical aperture objective lens (XLPLN25XWMP2, Olympus, NA 1.05) was used for the experiments. The back aperture was approximately filled. The excitation source was a non-collinear optical parametric amplifier (NOPA, Spectra Physics) pumped by an amplifier (Spirit 1030-70, Spectra Physics). For 3PM and 2PM, the excitation wavelengths were 1280 nm and 920 nm, respectively. To reach the depth limit while maintaining low average power on the sample surface, low repetition rates of 333 kHz and 2 MHz were used for 3PM and 2PM, respectively. The full width at half maximum (FWHM) pulse width was measured to be 120 fs at 920 nm and 50 fs at 1280 nm, assuming sech2 pulse intensity profile.
Images were collected at approximately 1 frame per second over a field-of-view (FOV) of 67 µm by 67 µm with 512 by 512 pixels. The point spread function (PSF) of both 2PM and 3PM images was characterized in shallow regions (<1 EAL) to verify diffraction-limited performance of the microscope. To find the EAL of the samples, z-stacks were taken. To represent the signal at the corresponding depth, the top 0.01% or 0.1% (depending on the inhomogeneity factor) of the brightest pixels of each image in the z-stack were averaged and normalized to the cubic or square (for 3P and 2P, respectively) of the power used. The signal value obtained by averaging the top 0.01% or 0.1% (depending on the inhomogeneity factor) of the brightest pixels of each image was used to calculate the SBR of each image (Fig. 2(c) and 4(c)). The background of each image was determined by averaging 90 percent of pixels with the lowest pixel counts. The slope of fluorescence signal versus depth in the semi-log plot was used to calculate the EAL [26]. All powers reported are values measured after the objective lens. For some samples, the EALs measured from the z-stacks were further verified with values measured with a spectrophotometer (Cary-5000-UV-Vis-NIR spectrometer, Agilent).
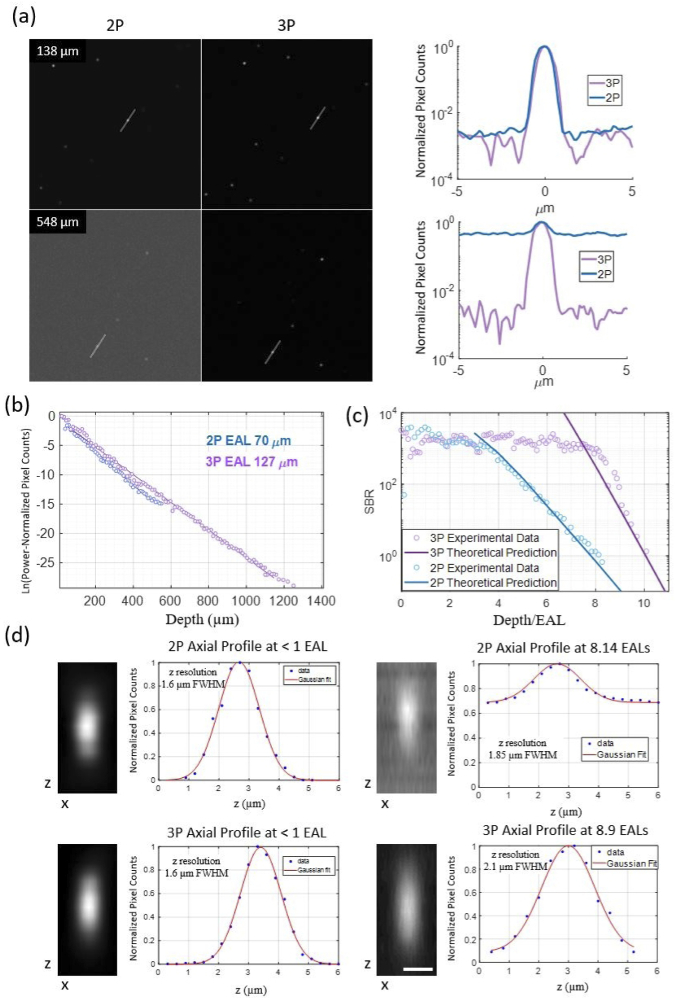
Fig. 2.
2PM and 3PM characterization in a tissue phantom with inhomogeneity factor of 4545. (a) SBR comparison of 2PM and 3PM at different depths. Left panel: 67 µm by 67 µm FOV images collected at different depths as marked on the top left corner of the image. A 5 pixel-wide line was drawn on one fluorescent bead to acquire a line intensity profile. Right panel: Line profiles of images shown on the left. (b) Measured effective attenuation lengths (EALs) at 920 nm and 1280 nm. (c) Experimentally measured and theoretically predicted SBR vs depth of 2PM and 3PM. (d) Measured axial resolution in shallow and deep regions. Zoomed-in XZ images of beads were collected with fine z steps of 0.3 µm. Scale bar indicates 1 µm.
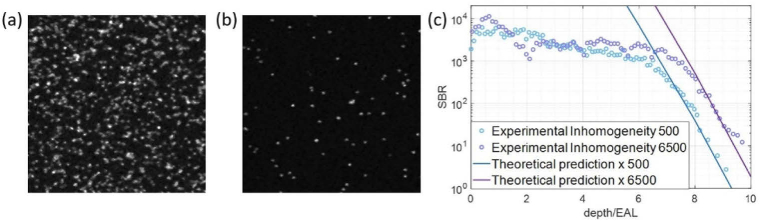
Fig. 4.
Inhomogeneity-dependent 3PM depth limit. Images are average intensity projections of 67 µm by 67 µm FOV images collected over 20 µm depth at 1 µm steps. (a) Sample with inhomogeneity factor of 500, which is equivalent to 0.2% of the volume labeled. (b) Sample with inhomogeneity factor of 6500. (c) SBR vs depth for the samples in (a) and (b).
4. Experimental results
4.1. 2PM and 3PM depth limit
We quantitatively characterized 2PM and 3PM images of tissue phantoms at various depths in order to experimentally determine the depth limits. A tissue phantom with a concentration of beads per microliter was created using a combination of fluorescent and non-fluorescent beads. From the z-stack images, we measured the EALs to be 70 µm at 920 nm and 127 µm at 1280 nm (Fig. 2(b)). The calculated scattering mean free path using Mie theory was 142 µm for wavelength of 1280 nm and 80 µm for wavelength of 920 nm. The specific bottle of nonfluorescent polystyrene beads used for this sample had a mean diameter value of 1.06 µm with a coefficient of variation of 3%. We attribute the difference between the measured and the calculated values to the variation in bead diameters. The Maximum powers of 74 mW at 1280 nm and 55 mW at 920 nm were used to obtain the deepest 3PM and 2PM images, respectively. Using the concentration of the bead solutions, an inhomogeneity factor of 4545 (∼0.02% fluorescent volume) was calculated for this sample. We verified the inhomogeneity factor experimentally by taking a fine z-stack of images spanning a portion of the sample depth and then counting the number of beads within the measurement volume. To quantitatively compare the experimentally measured and theoretically calculated SBR values at each depth, the theoretically calculated SBR at was scaled up by the inhomogeneity factor.
The SBRs of 2PM and 3PM images are similar in the shallow regions given the limited dynamic range of the microscope (Fig. 2(a)). At depths where 2PM images start to have noticeable background, 3PM has no measurable background generation. For this scattering sample, we reach an SBR of 1 at ∼560 µm (8 EALs) for 2PM, but with 3PM, we can penetrate deeper than 1270 µm, reaching beyond 10 EALs (Fig. 3(b)). As shown in Fig. 2(c), the SBRs measured in the sample in the deep regions are in good agreement with the theoretical predictions for both 2PM and 3PM. In the shallower regions, the theoretically calculated SBRs are too high to be experimentally verified with our microscope, particularly for 3PM. We note that the SBRs in these shallow regions are inconsequential for determining the depth limit of 2PM and 3PM.
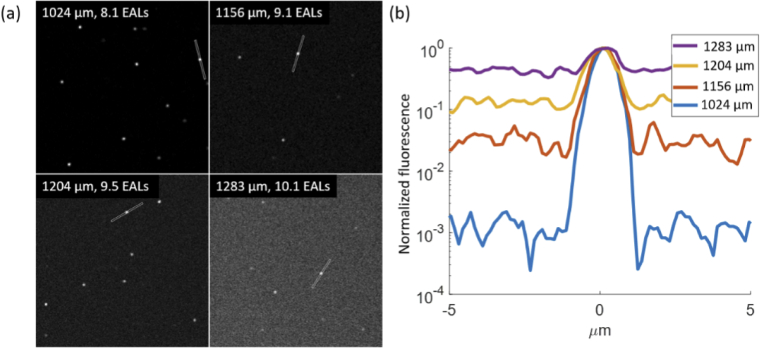
Fig. 3.
3PM beyond the TMFP of sample characterized in Fig. 2. (a) Images at various depths with 5 pixel-wide lines drawn on a fluorescent bead. FOV: 67 µm by 67 µm. (b) Fluorescence intensity profiles of the corresponding lines in (a).
Individual beads are clearly resolvable even in the deepest images. To quantify the spatial resolution, we collected images of beads with a FOV of 6.7 µm by 6.7 µm with 256 by 256 pixels and at 0.3 µm z-steps in both the shallow and deep regions. The axial fluorescence intensity profiles are shown in Fig. 2(d). The FWHM are measured to be 1.6 µm for both 2PM and 3PM in the shallow region. The diffraction-limited resolution of the microscope for 2PM and 3PM is calculated to be 1.3 µm and 1.4 µm for NA = 1, respectively [27]. In the deeper regions the axial resolution degrades in high NA conditions due to attenuation of light at large convergence angles. The axial resolution in the deeper regions was measured to be 1.85 µm and 2.1 µm for 2PM and 3PM, respectively. The small degradation of the axial resolution (∼ 30% or less) in the deeper regions is expected due to the reduction of the effective NA when focusing in scattering samples. The lateral width of the beads was measured to have a FWHM of 0.75 µm and 0.8 µm in shallow regions and 0.82 µm and 0.79 µm in the deep regions for 3PM and 2PM, respectively. The diffraction-limited lateral resolution of our 3P imaging system is ∼ 0.4 µm (FWHM). The FWHM of the fluorescent beads in our images (∼ 0.8 µm) is noticeably smaller than the diameter of the beads (1.0 µm), which can be explained by the spherical geometry of the beads and possibly the non-uniform distribution of the fluorophores within the beads. The graininess of the PSF images was caused by photon shot noise.
Figure 3 shows the decline of SBR in 3PM images of the sample. Images with SBR of above 1 were obtained at the depth of 10 EALs. We found close to diffraction-limited resolution near the depth limit (∼9 EAL deep in Fig. 2(d)), indicating that resolution degradation is not the limiting factor in reaching the depth limit. This finding contradicts a previous report that, based on numerical simulation, degradation of spatial resolution limits the imaging depth of 3PM [22].
With the anisotropy factor of the tissue phantoms calculated to be 0.82 using Mie scattering theory, the TMFP for the samples in our experimental conditions is [28]:
| (8) |
Therefore, Fig. 3 shows that high spatial-resolution MPM can reach nearly twice the depth of the TMFP.
4.2. Inhomogeneity-dependent 3PM depth limit
To test the effects of inhomogeneity on the depth limit, we used samples with varying ratios of fluorescent to non-fluorescent beads. The tissue phantom with high inhomogeneity factor contained beads per microliter and the tissue phantom with low inhomogeneity factor contained beads per microliter. The scattering lengths were calculated using Mie theory to be 135 µm and 149 µm for the high inhomogeneity sample and the low inhomogeneity sample, respectively. We measured EALs to be 120 µm for the low inhomogeneity sample and 144 µm for the high inhomogeneity sample. The inhomogeneity of the samples differs by a factor of ∼13 (Fig. 4), which results in slightly less than 1 EAL difference in the 3PM depth limit. This result matches well with the theoretical calculation (Fig. 4(c)). Diffraction-limited resolution was obtained in both samples at ∼9 EALs deep in the sample.
5. Discussion and conclusion
MPM is a powerful tool for deep imaging due to reduction of the out-of-focus fluorescence and use of long wavelength photons that penetrate deeper into scattering tissue. While 2PM can reach deep within scattering tissue by using longer excitation wavelengths compared to one photon excitation, the optimal wavelengths for deep penetration in biological samples (i.e., ∼1300 nm and 1700nm) coincide with the 3P excitation wavelengths of the most commonly available fluorophores [5]. Additionally, the higher-order excitation in 3PM reduces the generated background fluorescence, producing high-SBR images beyond depths (normalized to the EALs) that are accessible to 2PM. While 4PM would further reduce background generation, we note that SBR is not the current experimental limitation for deep imaging with 3PM.
The TMFP is often stated as the fundamental limit for diffraction-limited optical microscopy since the ballistic photons are drastically attenuated by the time they reach this depth [23,24]. As we show with our experimental results, MPM can surpass this limit while maintaining a diffraction-limited resolution, even in densely labeled samples (e.g. with 3PM). Our results provide an intuitive understanding of three-dimensionally resolved optical microscopy as a competition between the in-focus signal and the out-of-focus background photons: the greater the reduction of the background photons, relative to the signal, the greater our chances of detecting the signal. While TMFP provides a length scale that describes the intensity distribution of the excitation beam, it does not characterize the nonlinearly generated signal and background. In MPM, the ‘fundamental’ depth limit is not caused by photons being able to reach a certain depth but rather the ability to distinguish the fluorescence photons that are generated at the focus from those that are from outside the focal volume, which is characterizable by the SBR.
The inhomogeneity factor is a key consideration in determining the depth limit since the amount of background generated by excitation light distribution is directly proportional to fluorophore distribution [26]. By linear fitting of the depth limit (normalized by EAL) as a function of logarithm of shown in Fig. 1(d) ranging from to , we found that the depth limit for 2PM and 3PM can be approximately expressed as:
| (9) |
| (10) |
Our theoretical results show that for approximately every 17 times increase in inhomogeneity, an additional EAL in depth will be accessible with 3PM. For 2PM the inhomogeneity needs to increase 6 times for each additional EAL of accessible depth. These results closely match our experimental findings. Equations (9 and 10) show that when the inhomogeneity factor is ∼ , the depth limit for 2PM can eventually overtake that of 3PM. While such cross-over of 2PM and 3PM depth limits is theoretically interesting, such sparse labeling has little practical consequence. The inhomogeneity factor of , which corresponds to having a single 1 µm fluorescent bead in a volume of in a tissue phantom, is most likely irrelevant to in vivo imaging. Therefore, within the practical range of in vivo imaging, the EAL-normalized depth limit of 3PM is larger than that of 2PM. By examining the differences in the depth limit (Fig. 1(d)) it is clear that the advantage of 3PM over 2PM in penetration depth (normalized by the EAL) is more pronounced in densely labeled samples (i.e., samples with smaller inhomogeneity). For example, our simulations show that the normalized depth limit of 3PM for (similar to mouse cortex vasculature density) is approximately 9.4 EALs compared to depth limit of 5.9 EALs for 2PM, a difference of 3.5 EALs. For , the difference is reduced to approximately 2.9 EALs.
We plotted the axial fluorescence profile (Fig. 1(b)), SBR as a function of depth (Fig. 1(c)), and the imaging depth limit as a function of inhomogeneity (Fig. 1(d)) using depth (z) normalized by the EAL. Such plots capture the effects of a variety of parameters on imaging depth limit. Intuitively, represents the signal attenuation as a function of imaging depth (Eq. (3)) and is the most important parameter for defining the depth limit. On the other hand, the SBR also depends on the value of the EAL. Therefore, the coefficients in Eqs. (9 and 10) will depend on not only the imaging parameters (e.g., NA and pulse width) but also the EAL values. The EALs of biological samples can vary based on tissue properties. Fig. S5 shows that SBR increases with increasing values of EAL when plotted against the normalized depth, although the increase does not appear to be large enough to significantly change the depth limit (in units of z/EAL).
The deepest in vivo 3PM so far is at the depth of ∼6 EALs when imaging mouse brain vasculature [17]. Our results show that the current in vivo imaging depth achieved by 3PM is practically limited by the signal strength of 3P excitation. We used bright fluorescent beads in tissue phantoms to generate sufficient signal strength to reach the 3P depth limit. From the power levels at the surface of the sample, we estimated that the fluorescent beads we used are thousands of times brighter than typical in vivo imaging settings, e.g., imaging mouse brain vasculature. Therefore, brighter fluorophores together with schemes to enhance signal generation can lower excitation power requirements, making deeper regions more accessible [29,30]. Additionally, using lower repetition rate lasers [31,32] or adaptive excitation sources to reduce the effective repetition rate [33] can further improve the signal strength. Adaptive optics can also be used to enhance the 3P signal strength [34–39] by correcting the low order optical aberrations in biological samples. Combinations of some or all of these techniques can be employed to achieve the signal strength needed for reaching the 3P depth limit in vivo.
In summary, we extended the analytical model of Theer and Denk for 2PM to three- and four-photon excitation and performed controlled experiments to compare the depth limit of 2PM and 3PM. We also demonstrated the depth limit of 3PM in a variety of experimental conditions. We found that the analytical model is in good agreement with the experiments. Our experimental results show that loss of resolution (i.e., degradation of the point spread function) does not limit the imaging depth of 3PM. We show high spatial resolution at an imaging depth of > 10 scattering mean free paths, which is nearly twice the TMFP, the commonly acknowledged depth limit of imaging techniques using ballistic photons. We further studied the dependence of imaging depth limit on the staining inhomogeneity. Our results show that the depth limit of 3PM is significantly beyond what has been achieved in biological tissues so far. Our work will not only deepen the understanding of deep tissue imaging but will also motivate future technology development to reach the full potential of 3PM.
Funding
National Science Foundation10.13039/100000001 (DBI-1707312); Cornell Neurotech Mong Fellowship.
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Supplemental document
See Supplement 1 (2.5MB, pdf) for supporting content.
References
- 1.Choquet D., Sainlos M., Sibarita J.-B., “Advanced imaging and labelling methods to decipher brain cell organization and function,” Nat. Rev. Neurosci. 22(4), 237–255 (2021). 10.1038/s41583-021-00441-z [DOI] [PubMed] [Google Scholar]
- 2.Deisseroth K., Schnitzer M. J., “Engineering approaches to illuminating brain structure and dynamics,” Neuron 80(3), 568–577 (2013). 10.1016/j.neuron.2013.10.032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nowzari F., Wang H., Khoradmehr A., Baghban M., Arandian A., Muhaddesi M., Nabipour I., Zibaii M. I., Najarasl M., Taheri P., Latifi H., Tamadon A., “Three-Dimensional Imaging in Stem Cell-Based Researches,” Front. Vet. Sci. 8, 657525 (2021). 10.3389/fvets.2021.657525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bocklitz T., Silge A., Bae H., Rodewald M., Legesse F. B., Meyer T., Popp J., “Non-invasive imaging techniques: from histology to in vivo imaging,” in Molecular Imaging in Oncology , (Springer International Publishing, 2020), pp. 795–812. [DOI] [PubMed] [Google Scholar]
- 5.Horton N. G., Wang K., Kobat D., Clark C. G., Wise F. W., Schaffer C. B., Xu C., “In vivo three-photon microscopy of subcortical structures within an intact mouse brain,” Nat. Photonics 7(3), 205–209 (2013). 10.1038/nphoton.2012.336 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ouzounov D. G., Wang T., Wang M., Feng D. D., Horton N. G., Cruz-Hernández J. C., Cheng Y.-T., Reimer J., Tolias A. S., Nishimura N., Xu C., “In vivo three-photon imaging of activity of GCaMP6-labeled neurons deep in intact mouse brain,” Nat. Methods 14(4), 388–390 (2017). 10.1038/nmeth.4183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wang T., Ouzounov D. G., Wu C., Horton N. G., Zhang B., Wu C.-H., Zhang Y., Schnitzer M. J., Xu C., “Three-photon imaging of mouse brain structure and function through the intact skull,” Nat. Methods 15(10), 789–792 (2018). 10.1038/s41592-018-0115-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Theer P., Denk W., “On the fundamental imaging-depth limit in two-photon microscopy,” J. Opt. Soc. Am. A 23(12), 3139–3149 (2006). 10.1364/JOSAA.23.003139 [DOI] [PubMed] [Google Scholar]
- 9.Lecoq J., Orlova N., Grewe B. F., “Wide. Fast. Deep: recent advances in multiphoton microscopy of in vivo neuronal activity,” J. Neurosci. 39(46), 9042–9052 (2019). 10.1523/JNEUROSCI.1527-18.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Attardo A., Fitzgerald J. E., Schnitzer M. J., “Impermanence of dendritic spines in live adult CA1 hippocampus,” Nature 523(7562), 592–596 (2015). 10.1038/nature14467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Trachtenberg J. T., Chen B. E., Knott G. W., Feng G., Sanes J. R., Welker E., Svoboda K., “Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex,” Nature 420(6917), 788–794 (2002). 10.1038/nature01273 [DOI] [PubMed] [Google Scholar]
- 12.Takasaki K., Abbasi-Asl R., Waters J., “Superficial bound of the depth limit of two-photon imaging in mouse brain,” eNeuro 7(1), ENEURO.0255-19.2019 (2020). 10.1523/ENEURO.0255-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang T., Wu C., Ouzounov D. G., Gu W., Xia F., Kim M., Yang X., Warden M. R., Xu C., “Quantitative analysis of 1300-nm three-photon calcium imaging in the mouse brain,” eLife 9, e53205 (2020). 10.7554/eLife.53205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang T., Xu C., “Three-photon neuronal imaging in deep mouse brain,” Optica 7(8), 947–960 (2020). 10.1364/OPTICA.395825 [DOI] [Google Scholar]
- 15.Wang M., Wu C., Sinefeld D., Li B., Xia F., Xu C., “Comparing the effective attenuation lengths for long wavelength in vivo imaging of the mouse brain,” Biomed. Opt. Express 9(8), 3534–3543 (2018). 10.1364/BOE.9.003534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chow D. M., Sinefeld D., Kolkman K. E., Ouzounov D. G., Akbari N., Tatarsky R., Bass A., Xu C., Fetcho J. R., “Deep three-photon imaging of the brain in intact adult zebrafish,” Nat. Methods 17(6), 605–608 (2020). 10.1038/s41592-020-0819-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liu H., Deng X., Tong S., He C., Cheng H., Zhuang Z., Gan M., Li J., Xie W., Qiu P., Wang K., “In vivo deep-brain structural and hemodynamic multiphoton microscopy enabled by quantum dots,” Nano Lett. 19(8), 5260–5265 (2019). 10.1021/acs.nanolett.9b01708 [DOI] [PubMed] [Google Scholar]
- 18.Yildirim M., Sugihara H., So P. T. C., Sur M., “Functional imaging of visual cortical layers and subplate in awake mice with optimized three-photon microscopy,” Nat. Commun. 10(1), 177 (2019). 10.1038/s41467-018-08179-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yildirim M., Hu M., Le N. M., Sugihara H., So P. T. C., Sur M., “Quantitative third-harmonic generation imaging of mouse visual cortex areas reveals correlations between functional maps and structural substrates,” Biomed. Opt. Express 11(10), 5650–5673 (2020). 10.1364/BOE.396962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Weisenburger S., Tejera F., Demas J., Chen B., Manley J., Sparks F. T., Martínez Traub F., Daigle T., Zeng H., Losonczy A., Vaziri A., “Volumetric Ca2+ imaging in the mouse brain using hybrid multiplexed sculpted light microscopy,” Cell 177(4), 1050–1066.e14 (2019). 10.1016/j.cell.2019.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Klioutchnikov A., Wallace D. J., Frosz M. H., Zeltner R., Sawinski J., Pawlak V., Voit K.-M., Russell P. S. J., Kerr J. N. D., “Three-photon head-mounted microscope for imaging deep cortical layers in freely moving rats,” Nat. Methods 17(5), 509–513 (2020). 10.1038/s41592-020-0817-9 [DOI] [PubMed] [Google Scholar]
- 22.Cheng X., Sadegh S., Zilpelwar S., Devor A., Tian L., Boas D. A., “Comparing the fundamental imaging depth limit of two-photon, three-photon, and non-degenerate two-photon microscopy,” Opt. Lett. 45(10), 2934–2937 (2020). 10.1364/OL.392724 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Liu Y., Lai P., Ma C., Xu X., Grabar A. A., Wang L. V., “Optical focusing deep inside dynamic scattering media with near-infrared time-reversed ultrasonically encoded (TRUE) light,” Nat. Commun. 6(1), 5904 (2015). 10.1038/ncomms6904 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ntziachristos V., “Going deeper than microscopy: the optical imaging frontier in biology,” Nat. Methods 7(8), 603–614 (2010). 10.1038/nmeth.1483 [DOI] [PubMed] [Google Scholar]
- 25.LaViolette A. K., Xu C., “Shot noise limits on binary detection in multiphoton imaging,” Biomed. Opt. Express 12(11), 7033–7048 (2021). 10.1364/BOE.442442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Xu C., Webb W. W., “Multiphoton excitation of molecular fluorophores and nonlinear laser microscopy,” in Topics in Fluorescence Spectroscopy (Springer, 1997), Vol. 5, pp. 471–540. [Google Scholar]
- 27.Wang M., Kim M., Xia F., Xu C., “Impact of the emission wavelengths on in vivo multiphoton imaging of mouse brains,” Biomed. Opt. Express 10(4), 1905–1918 (2019). 10.1364/BOE.10.001905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zipfel W. R., Williams R. M., Webb W. W., “Nonlinear magic: multiphoton microscopy in the biosciences,” Nat. Biotechnol. 21(11), 1369–1377 (2003). 10.1038/nbt899 [DOI] [PubMed] [Google Scholar]
- 29.Liu Y., Zhang C., Wang L. V., “Effects of light scattering on optical-resolution photoacoustic microscopy,” J. Biomed. Opt. 17(12), 126014 (2012). 10.1117/1.JBO.17.12.126014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hontani Y., Xia F., Xu C., “Multicolor three-photon fluorescence imaging with single-wavelength excitation deep in mouse brain,” Sci. Adv. 7(12), eabf3531 (2021). 10.1126/sciadv.abf3531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zarowny L., Aggarwal A., Rutten V. M. S., Kolb I., Patel R., Huang H.-Y., Chang Y.-F., Phan T., Kanyo R., Ahrens M. B., Allison W. T., Podgorski K., Campbell R. E., “Bright and high-performance genetically encoded Ca2+ indicator based on mneongreen fluorescent protein,” ACS Sens. 5(7), 1959–1968 (2020). 10.1021/acssensors.0c00279 [DOI] [PubMed] [Google Scholar]
- 32.Theer P., Hasan M. T., Denk W., “Two-photon imaging to a depth of 1000 µm in living brains by use of a Ti:Al2O3 regenerative amplifier,” Opt. Lett. 28(12), 1022–1024 (2003). 10.1364/OL.28.001022 [DOI] [PubMed] [Google Scholar]
- 33.Charan K., Li B., Wang M., Lin C. P., Xu C., “Fiber-based tunable repetition rate source for deep tissue two-photon fluorescence microscopy,” Biomed. Opt. Express 9(5), 2304–2311 (2018). 10.1364/BOE.9.002304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Li B., Wu C., Wang M., Charan K., Xu C., “An adaptive excitation source for high-speed multiphoton microscopy,” Nat. Methods 17(2), 163–166 (2020). 10.1038/s41592-019-0663-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rodríguez C., Chen A., Rivera J. A., Mohr M. A., Liang Y., Sun W., Milkie D. E., Bifano T. G., Chen X., Ji N., “An adaptive optics module for deep tissue multiphoton imaging in vivo,” bioRxiv: 2020.11.25.397968 (2020). [DOI] [PMC free article] [PubMed]
- 36.Tang J., Germain R. N., Cui M., “Superpenetration optical microscopy by iterative multiphoton adaptive compensation technique,” Proc. Natl. Acad. Sci. U. S. A. 109(22), 8434–8439 (2012). 10.1073/pnas.1119590109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ji N., Milkie D. E., Betzig E., “Adaptive optics via pupil segmentation for high-resolution imaging in biological tissues,” Nat. Methods 7(2), 141–147 (2010). 10.1038/nmeth.1411 [DOI] [PubMed] [Google Scholar]
- 38.Sinefeld D., Paudel H. P., Ouzounov D. G., Bifano T. G., Xu C., “Adaptive optics in multiphoton microscopy: comparison of two, three and four photon fluorescence,” Opt. Express 23(24), 31472–31483 (2015). 10.1364/OE.23.031472 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Booth M. J., “Adaptive optics in microscopy,” Philos. Trans. R. Soc., A 365(1861), 2829–2843 (2007). 10.1098/rsta.2007.0013 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.