CDR loop interactions can determine heavy and light chain pairing preferences in bispecific antibodies

ABSTRACT

As the current biotherapeutic market is dominated by antibodies, the design of different antibody formats, like bispecific antibodies, is critical to the advancement of the field. In contrast to monovalent antibodies, which consist of two identical antigen-binding sites, bispecific antibodies can target two different epitopes by containing two different antigen-binding sites. Thus, the rise of new formats as successful therapeutics has reignited the interest in advancing and facilitating the efficient production of bispecific antibodies. Here, we investigate the influence of point mutations in the antigen-binding site, the paratope, on heavy and light chain pairing preferences by using molecular dynamics simulations. In agreement with experiments, we find that specific residues in the antibody variable domain (Fv), i.e., the complementarity-determining region (CDR) L3 and H3 loops, determine heavy and light chain pairing preferences. Excitingly, we observe substantial population shifts in CDR-H3 and CDR-L3 loop conformations in solution accompanied by a decrease in bispecific IgG yield. These conformational changes in the CDR3 loops induced by point mutations also influence all other CDR loop conformations and consequentially result in different CDR loop states in solution. However, besides their effect on the obtained CDR loop ensembles, point mutations also lead to distinct interaction patterns in the V_H-V_L interface. By comparing the interaction patterns among all investigated variants, we observe specific contacts in the interface that drive heavy and light chain pairing. Thus, these findings have broad implications in the field of antibody engineering and design because they provide a mechanistic understanding of antibody interfaces, by identifying critical factors driving the pairing preferences, and thus can help to advance the design of bispecific antibodies.

Introduction

Monoclonal antibodies have become one of the fastest-growing classes of biopharmaceutical proteins and are the most successful clinical therapeutic targets against a variety of diseases.^1–4 Antibodies are developed by the immune system to identify and neutralize foreign molecules.⁵ The function of an antibody depends on its three-dimensional structure, which determines specificity and biological activity. Typically antibodies consist of two identical heavy and light chains and are characterized by a unique modular anatomy that facilitates their engineering and design.⁶

The immunoglobulin heavy and light chains are composed of various discrete protein domains. Generally, antibodies can be divided into a crystallizable fragment (Fc) and two identical antigen-binding fragments (Fabs). The Fab can further be subdivided into constant (C_H1-C_L) and variable (V_H-V_L) domains. Both Fab interfaces are mutually stabilized by the high cooperation between the V_H–V_L and C_H1–C_L domains. Comparison of the V_H-V_L and the C_H1-C_L heterodimers revealed that the C_H1-C_L heterodimer is more stable than the V_H–V_L heterodimer.^6,7 However, the individual C_H1 domain is not stable in folded form and requires interactions with either the chaperone BiP⁸ or the C_L domain for folded state stability.⁹ The variable domains of both the heavy and the light chain (V_H and V_L) shape the antigen-binding site, i.e., the paratope, and are responsible for antigen binding and recognition.¹⁰ The paratope is composed of up to six hypervariable complementarity-determining region (CDR) loops. In this study for comparability of all antibodies, the term paratope is defined by all six CDR loops.^11–13

The Fc consists of a C_H2–C_H2 and a C_H3–C_H3 dimer and is strongly involved in modulating both the adaptive and innate immune response.¹⁴ Mutations in the C_H3–C_H3 interface have been shown to affect domain association preferences and influence antibody stability.^14,15 In particular, the design of bispecific antibodies, which can recognize two different epitopes, profited from these advances in engineering C_H3–C_H3 interfaces. The concept of bispecific antibodies, i.e., combining specificities of two antibodies and thereby simultaneously addressing different antigens or epitopes, was introduced in the 1960s. Thereby, bispecific antibodies expand the functionalities of traditional antibodies by more efficiently targeting effector cells to kill tumor cells, enhancing tissue specificity, and targeting two signaling pathways at the same time.

Bispecific antibodies can be assembled from up to two different heavy and light chains, respectively.^16,17 However, the complex hetero-tetrameric composition makes it challenging to produce bispecific IgGs, as the co-expression of the four different chains can lead to nine mispairings in addition to the desired bispecific IgG. Thus, to avoid chain mispairings and to allow efficient production of bispecific IgGs, understanding of heavy/heavy and heavy/light chain pairings and their resulting interfaces for heterodimerization is critical.^18–22 A major advance in designing bispecific antibodies was the invention of the “knobs-into-holes” (KiH) technology for C_H3–C_H3 interfaces.²³ The concept of the KiH technology was to introduce mutations in the two C_H3 domains to promote/favor the formation of the heterodimer by altering the complementarity between the C_H3 domains. Up to now, numerous variations of this approach have been developed following different strategies to optimize the heterodimer formation, by altering charge polarity in the interfaces or considering alternative mutations.

More recently, several different strategies have been developed to circumvent heavy and light chain mispairings and to favor heterodimerization in Fabs, i.e., mutating interface residues of V_L-C_L and V_H-C_H1 and the domain crossover (CrossMab) technology.^{18,21,22,24,25} Another obvious and attractive solution to circumvent light chain mispairings is the use of common light chain, which prevents mispairings without additional engineering efforts.²⁶ However, the use of common chains (both heavy and light) can have detrimental effects on stability and immunogenicity of the engineered molecules and also constrain the choice of antibodies than can be used for making bispecific IgGs.^27–32

To elucidate the heavy and light chain pairing preferences in Fabs, Joshi et al. investigated the influence of point mutations of CDR loop residues on the resulting bispecific IgG yield and identified that specific residues in the CDR-H3 loop and CDR-L3 loop contribute to the high bispecific IgG yield.¹⁸ Thus, here we use molecular dynamics simulations to characterize changes in the conformational diversity, interaction patterns and biophysical properties of the CDR loops and the V_H-V_L interface of an anti-MET Fab and the anti-IL-13 Fab as a consequence of these specific point mutations in the CDR3 loops. Especially, as it has been shown that a strong pairing preference in one Fab arm can be sufficient for high bispecific yield,¹⁸ these findings provide a mechanistic understanding of antibody interfaces and thereby contribute to optimizing the engineering of bispecific antibodies.

Results

In a recent study, the CDR3 loops of the anti-MET Fab and the anti-IL-13 Fab were shown to contribute to high bispecific yield of the anti-MET/EGFR antibody and the anti-IL-13/IL-4 antibody, respectively.^18,33 Here, we applied a well-established enhanced sampling technique in combination with molecular dynamics simulations to characterize and understand the influence of point mutations in the CDR3 loops on the heavy and light chain pairing preferences of the anti-MET Fab and an anti-IL-13 Fab (PDB accession code: 4K3J and 4I77, respectively).³³ SI Table S1 summarizes the investigated variants and the aggregated simulation times. As the mutations were introduced in the CDR-L3 or CDR-H3 loops, we first characterized the conformational diversity of these CDR loops to identify conformational rearrangements that determine specific interface pairing preferences. Figure 1 and SI Figure S1 illustrate the structures of the anti-MET Fab and of the anti-IL-13 Fab, highlighting the CDR3 loop residues, that are mutated in the different investigated variants.

Figure 1.

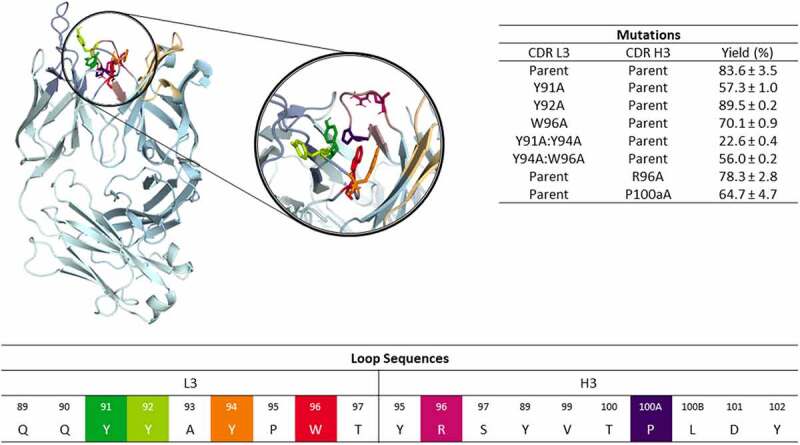
Structure of the anti-MET antibody showing a close-up of the CDR-L3 and CDR-H3 loop residues. The mutated residues are color-coded according to the sequence representation depicted below. The different variants including the experimentally determined bispecific IgG yields are summarized on the right.¹⁸ Ribbon representation of the X-ray structure of the anti-MET Fab showing that CDR-L3 mutations in this study are distributed over the length of the CDR-L3 loop and in the beginning and the end of the CDR-H3 loop.

CDR-H3 loop

Figure 2 shows the free energy landscapes of the CDR-H3 loop variants of the anti-MET Fab. To characterize and compare the conformational spaces of all anti-MET Fab variants, we performed a principal component analysis (PCA) for both the CDR-L3 and CDR-H3 loops for all investigated variants of the anti-MET antibody (Figure 1) in a combined PCA coordinate system. We observe a population shift of the dominant CDR-H3 loop conformations in solution, which goes hand in hand with a reduction in anti-EGFR/MET bispecific IgG yield. To further strengthen this observation, we provide the respective state probabilities in SI Figure S2. The bispecific IgG yield has been defined as the percentage of correctly assembled bispecific IgG in the purified pool of different IgG species and has been estimated by using mass liquid chromatography-mass spectrometry.^18,22,34 Furthermore, we also observe differences in the flexibility of the CDR-H3 loop between the different variants, which is reflected in a broader conformational space. Similar findings can be observed for the anti-IL-13 Fab. SI Figure S3 shows the free energy surfaces of the CDR-H3 loop for the anti-IL-13 Fab, which also indicates that a decrease in bispecific IgG yield is accompanied by population shifts and an increase in flexibility.

Figure 2.

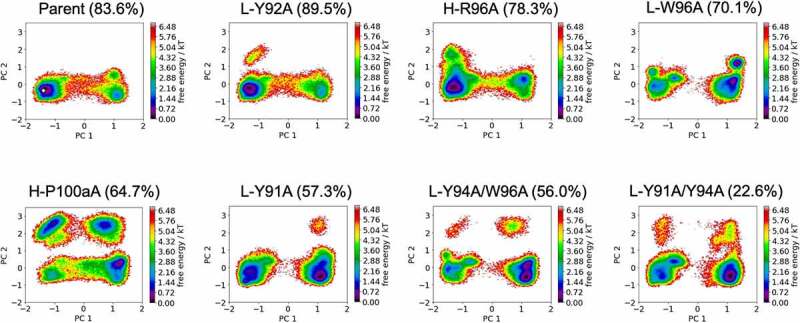
Free energy surfaces of the CDR-H3 loop in a combined coordinate system of all investigated anti-MET Fab variants, sorted by descending bispecific IgG yield. The crystal structure of the Parent (PDB accession code: 4K3J) is projected into the free energy landscape and depicted as white dot. The percentages in the heading refer to the experimentally determined bispecific yields for the anti-MET Fab variants, respectively. Conformational spaces of the CDR-H3 loop ensembles showing a substantial population shift of the CDR-H3 loop from the binding competent state toward a side minimum resulting in a drop in bispecific IgG yield.

In Figure 3, we provide tICA plots in a combined tICA space of the Parent anti-MET Fab and the L-Y91A/Y94A mutant showing the free energy surfaces of the CDR-H3 loop. tICA is a dimensionality reduction technique, which was applied to identify the slowest movements of the CDR-H3 loop and to obtain a kinetic discretization of the sampled conformational space. Based on the tICA, we calculated the Markov-state model (MSM), transition kinetics, state probabilities and representative macrostate ensembles (Figure 3). We find transition timescales in the low microsecond timescale between different CDR-H3 loop macrostates, which are rather fast compared to correlated rearrangements of all CDR loops, which can occur in the millisecond timescale.³⁵ Additionally, we observe a strong population shift of the dominant CDR-H3 loop ensemble in solution between the Parent and the double mutant. This is particularly interesting, as the double mutation L-Y91A/Y94A in the CDR-L3 loop results in a significant reduction of bispecific yield (from 82% to 22%). Shifts of the dominant CDR-H3 loop conformations in solution also directly result in conformational rearrangements of the CDR-L3 loop, as the CDR3 loop movements are strongly correlated.

Figure 3.

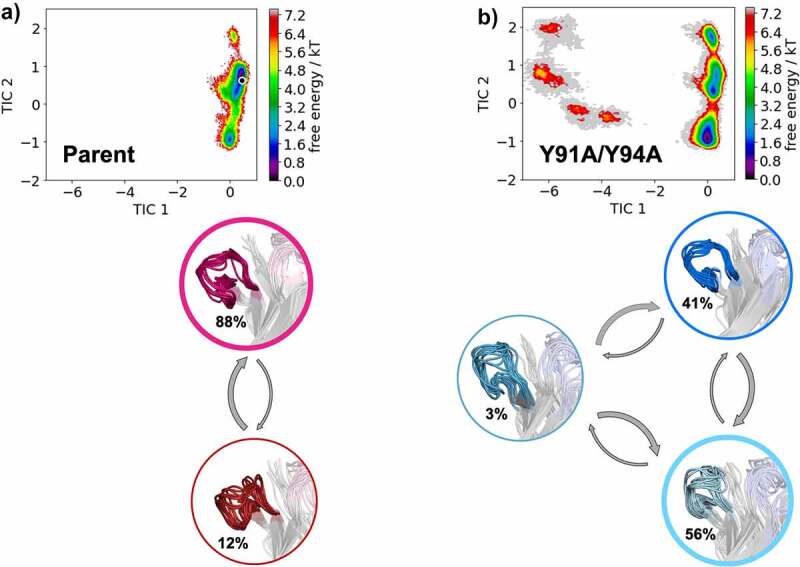
Free energy landscape of the CDR-H3 loop for both the Parent (a) and the double mutant L-Y91A/Y94A (b) presented in a kinetic coordinate system (tICA space). Based on the tICA, we calculated a Markov-state model, which allows us to reconstruct thermodynamics and kinetics of conformational CDR-H3 loop transitions. The crystal structure is projected in the tICA space for the parent and illustrated as white dot. The thickness of the circles corresponds to the state probabilities. The transition timescales between different CDR-H3 loop conformations occur in the low microsecond timescale. Free energy landscapes and representative ensemble structures of the CDR-H3 loop for the Parent and the bispecific yield reducing double mutant show a population shift away from the dominant binding competent CDR-H3 loop conformation in solution resulting from two-point mutations in the CDR-L3 loop.

CDR-L3 loop

Figure 4 shows the free energy landscapes of the CDR-L3 loop for all studied anti-MET Fab variants in a combined PCA coordinate system. In line with the results for the CDR-H3 loop, we see population shifts of the dominant CDR-L3 loop conformation in solution and find differences in flexibility for all investigated CDR-L3 loop variants. The respective state probabilities for the CDR-L3 loop ensembles are presented in SI Figure S4. As the CDR-H3 and CDR-L3 loops are located at the center of the antigen-binding site, conformational rearrangements of the CDR3 loops strongly influence the shape of the paratope. Thus, these observed structural rearrangements of the CDR3 loops induce global conformational changes to all CDR loops.

Figure 4.

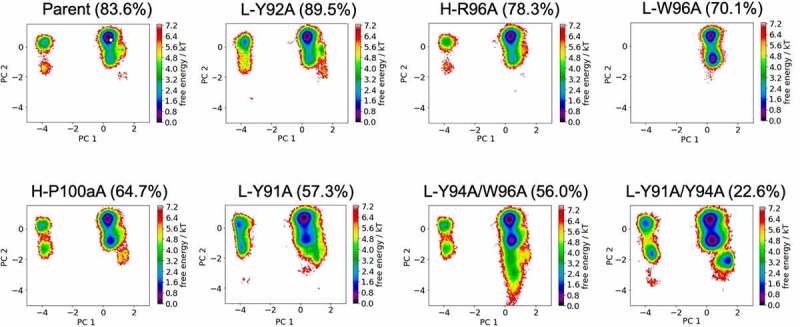
Free energy surfaces of the CDR-L3 loop in a combined coordinate system with all investigated anti-MET Fab variants, sorted by descending bispecific IgG yield. The crystal structure of the Parent (PDB accession code: 4K3J) is projected into the free energy landscape and depicted as white dot. The percentages in the heading refer to the experimentally determined bispecific yields for the anti-MET Fab variants, respectively. CDR-L3 loop conformational spaces show that a drop in bispecific IgG yield is accompanied by a strong population shift from the dominant CDR-L3 loop conformations in solution toward a side minimum.

Conformational diversity of all six CDR loops and interface dynamics

Figure 5 shows the results of the MSMs, including the free energy surfaces for all six antibody CDR loops, the interdomain orientations and the macrostate ensembles with respective state probabilities for both the Parent and the L-Y91A/Y94A mutant anti-MET Fab. While we find a strong shift of the relative interdomain orientation V_H-V_L between the highest populated macrostate (blue) and the other macrostates (green and purple) for the L-Y91A/Y94A mutant, we observe no shift for the Parent. To better understand the influence of point mutations on the whole Fab dynamics of the anti-MET Fab, we also calculated the elbow angle and C_H1-C_L interdomain orientations for the obtained macrostate ensembles of the Parent and the L-Y91A/Y94A mutant (SI Figure S5). The elbow angle is defined as the angle between the pseudo-two-fold axes relating V_H to V_L and C_H1 to C_L.^36,37 Surprisingly, we also find substantial shifts of the dominant elbow angle and C_H1-C_L interdomain angle distributions, as a consequence of two-point mutations in the CDR-L3 loop. We observe similar results for all CDR loops of the anti-IL-13 Fab Parent and the bispecific yield-reducing L-R96A mutant Fab. The free energy surfaces and the respective MSMs of all CDR loops for both the Parent and the L-R96A mutant are presented in (SI Figures S6 and S7). The L-R96A mutation leads to a population shift of the CDR loop conformations in solution, which is accompanied by a 6° shift in the interdomain orientation, compared to the Parent anti-IL-13 Fab.

Figure 5.

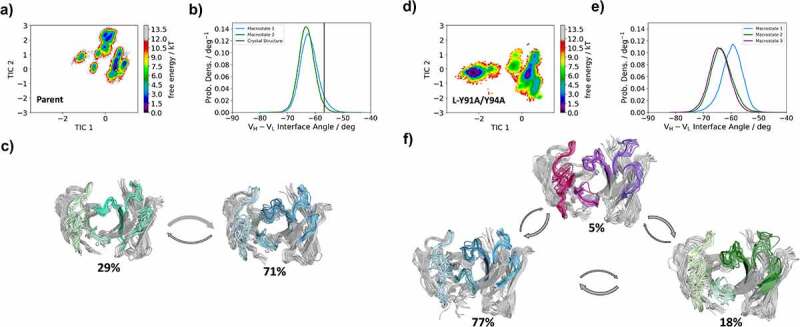
Free energy landscape of all antibody CDR loops for both the Parent and the double mutant L-Y91A/Y94A anti-MET Fab showing the Markov-state model, the respective macrostate ensembles and the and interdomain angle distributions (HL torsion angle). The macrostate ensembles (c and f) are arranged according to the shape of the tICA free energy surface (a and d). The macrostate ensembles depict the light chain on the left in lighter colors, while the heavy chain is shown on the right in darker colors. (b and e) V_H-V_L interdomain angle distributions (HL torsion angle) have been calculated with ABangle and color-coded according to the respective macrostates. The available crystal structure is projected into the free energy surface (displayed as white dot) and into the interdomain angle distribution (illustrated as vertical line). Free energy surfaces and the representative ensemble structures of all CDR loops for the Parent show no shift in the interdomain orientation as a consequence of conformational rearrangements of the CDR loops. However, we observe that the yield reducing double mutant results in conformational rearrangements of all CDR loops, compared to the Parent and leads to a substantial shift in the relative interdomain orientation toward a smaller V_H-V_L interface angle.

Characterization of interface interactions

As the interface orientations were strongly influenced by modifications in the CDR3 loops, we also calculated the contacts between the V_H-V_L domains. Figure 6 shows an “open-book” representation of the V_H and V_L interfaces color-coded according to the number of interdomain contacts for the Parent, the L-Y92A mutant and the double mutant L-Y91A/Y94A. In agreement with the experimentally determined bispecific IgG yield, we find identical interdomain interaction patterns for the Parent and the L-Y92A mutant and substantially different contacts for the yield-reducing double mutant L-Y91A/Y94A. We chose these three interfaces, as they have the biggest spread in experimentally determined bispecific IgG yield. Apart from coloring the interfaces, we also provide the interdomain contact distributions (contacts/frame) for the two mutants compared with the Parent. By comparing these distributions, we see a substantial decrease in the number of contacts per frame for the double mutant L-Y91A/Y94A, while the Parent and the L-Y92A mutant show a nearly identical contact per frame distribution. To capture the differences in the interface interactions more quantitatively, we also calculated the interface interaction energies for the three in-detailed discussed Fabs and find significant differences in the van der Waals interaction energies between the Parent and the double mutant (−99 $\pm$ 6 kcal/mol and −82 $\pm$ 8 kcal/mol, respectively), while the L-Y92A mutant revealed similar van der Waals interaction energies compared to the Parent (−100 $\pm$ 5 kcal/mol). The electrostatic interaction energies differ to a smaller extent between the Parent and the double mutant (104 $\pm$ 30 kcal/mol and −87 $\pm$ 34 kcal/mol) and again the Y92A mutant reveals comparable interaction energies to the Parent (−101 $\pm$ 28 kcal/mol). In line with these observations, we also find substantial changes in the interface interaction patterns and interdomain contact distributions (contacts/frame) for the anti-IL-13 Fab (SI Figure S8). These changes are also reflected in the interface interaction energies (SI Table S2). The Parent reveals a substantially higher electrostatic interaction energy in the interface of 133 $\pm$ 31 kcal/mol, while the yield reducing L-R96A mutation leads to an electrostatic interaction energy −77 $\pm$ 27 kcal/mol. The van der Waals interface interaction energy of the Parent (−91 $\pm$ 5 kcal/mol) is only slightly higher compared to the mutant (−81 $\pm$ 6 kcal/mol). The interface interaction energies are summarized in SI Table S2. Additionally, we provide the average heavy atom distances of the interdomain salt-bridge interactions for both the anti-MET Fab and the anti-IL-13 Fab in SI Table S3.

Figure 6.

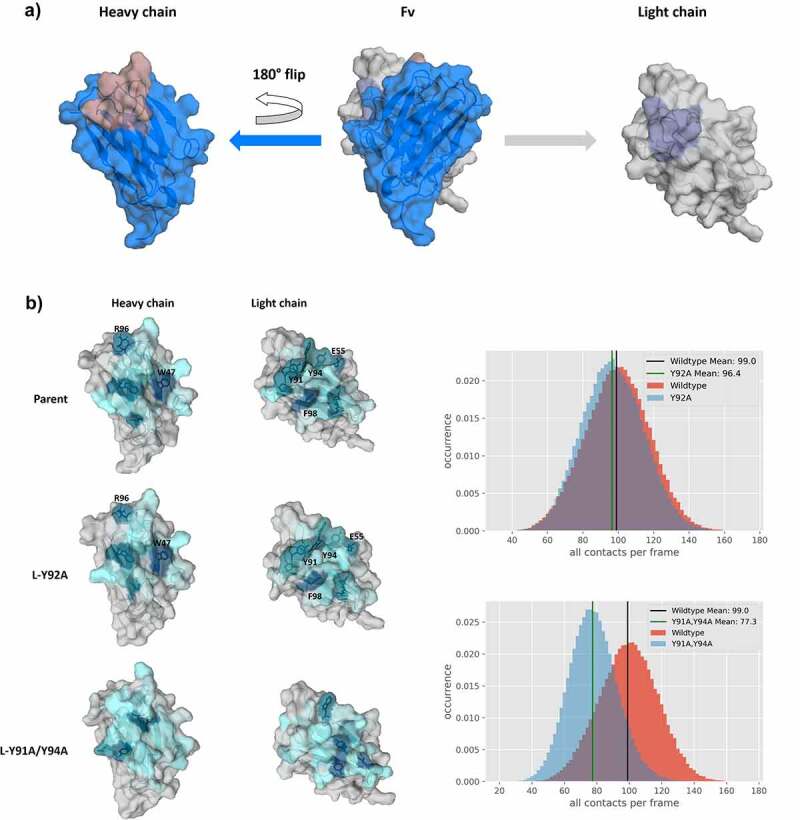
“Open-book” representation of the V_H and V_L interfaces, color-coded according to the number of interdomain contacts per frame. a) illustrates the orientation of the domains, highlighting CDR-L3 and CDR-H3 loops, respectively. b) Comparison of interdomain interaction patterns between the Parent, the bispecific yield increasing L-Y92A mutant and the L-Y91A/Y94A double mutant. To have a more quantitative representation of the difference in interdomain contacts, we provide distributions showing the interdomain contacts per frame. The color-gradient (gray to blue) corresponds to the number of interdomain interactions each residue is forming (the higher the number of contacts, the darker are the shades of blue). Comparison of the “open-book” representation of the V_H-V_L interfaces shows clear reduction in the interdomain interactions for the yield reducing double mutant compared to the Parent, while another variant, which results in an increase of bispecific yield, reveals nearly identical interface patterns compared to the Parent.

Discussion

In this study, we characterize the role of point mutations in the CDR3 loops on cognate heavy and light chain pairing preferences for an anti-MET Fab and an anti-IL-13 Fab³³ and provide structural and mechanistical explanations for their differences in bispecific IgG yield.¹⁸ As identified by Joshi et al., the pairing of the heavy and light chains in the anti-MET Fab and the anti-IL-13 Fab dominate the bispecific yield.¹⁸

Bispecific antibodies are based on the idea of having two different antigen binding sites within one molecule.¹⁶ Alongside technical advances and innovations in the field of antibody engineering, this concept has resulted in more than 100 bispecific antibody formats.^16,38,39 One of the most attractive of these is the bispecific IgG format, as it allows for long serum half-life and effector functions. However, the production of bispecific IgGs is challenging because of their complex hetero-tetrameric composition and the premise that specific pairing of these two distinct heavy and light chains must be achieved.^18,22,34 The concept of modifying the interfaces to favor heterodimerization over homodimerization in the C_H3-C_H3 dimer was ignited by the KiH approach, which has already motivated numerous studies to find variations of this technique, e.g., introducing charge pairs.^20,23,40,41 These interface modifications have also advanced the understanding of heavy and light chain assembly pathways and preferences in the Fab, namely V_H-V_L and C_H1-C_L domains.^18,19,21,22 Here, we elucidate the influence of CDR3 loop mutations on the respective pairing preferences by characterizing CDR loop states, interdomain and elbow angle dynamics and interface interaction patterns for the anti-MET Fab and the anti-IL-13 Fab. The mutations introduced in the CDR-L3 and CDR-H3 loops, which play a critical role in shaping the V_H-V_L interface (Figures 2 and 4), have been shown to co-determine the bispecific IgG yield. Thus, differences in sequence and structure of the V_H-V_L domains can drive heavy and light chain pairing preferences, independently of the constant domains.^18,21,22

To structurally elucidate the consequences of CDR3 loop mutations on the respective pairing preferences, we first characterized the free energy landscapes of both the CDR-L3 and CDR-H3 loops (Figures 2 and 4) of the anti-MET Fab. In line with a reduction in experimentally determined bispecific IgG yield, we find population shifts of the dominant CDR-H3 and CDR-L3 loop states. Even though the mutations were mainly introduced in the CDR-L3 loop, we identified substantial conformational changes in the CDR-H3 loop (Figure 2, SI Figures S2, S3). As all CDR loop movements are strongly correlated,^35,42–44 we also provide the free energy surfaces for all CDR loops of the Parent and the L-Y91A/Y94A mutant, which reveals a reduced bispecific IgG yield, from 82% to 22%. In agreement with the findings for the CDR3 loops, we observe a substantial population shift of the dominant CDR loop conformations in solution (Figure 5), which can contribute to the drastic decrease in bispecific IgG yield. In agreement with this observation for the anti-MET Fab, we find a strong population shift of the dominant CDR loop conformations as a consequence of a single point mutation in the CDR-L3 loop for the L-R96A variant, compared to the Parent anti-IL-13 Fab. Additionally, we find that the conformational rearrangements resulting from the L-R96A mutation also lead to a 6° shifted interdomain angle distribution for the mutant, compared to the Parent anit-IL-13 Fab (SI Figures S6 and S7). As conformational changes of all CDR loops can be directly transmitted to V_H-V_L interdomain orientations, we provide in Figure 5(b,e) the V_H-V_L interdomain angle distributions for the individual macrostates of the anti-MET Fab. For the double mutant L-Y91A/Y94A we find again that conformational changes in the antigen-binding site also shift the relative V_H-V_L interdomain angle (HL torsion angle) distributions because of two mutations in the CDR-L3 loop. This observation supports the idea, that optimizing the V_H-V_L interface, which is dominated by CDR loop interactions, can substantially improve the efficiency of heavy and light chain assembly, without modifying the constant domains. Thus, the assembly of heavy and light chains in the V_H-V_L interface and in the C_H1-C_L interface can occur independently. The first chain association might involve the assembly of V_H and V_L, which was shown to dominate the association of specific heavy and light chains, followed by assembly of the C_H1 and C_L domains.²¹ However, also a simultaneous association of both domains cannot be excluded.²² Thus, different CDR3 loop conformations induce conformational rearrangements of all six CDR loops, which directly co-determine the cognate heavy and light chain pairing preferences. Additionally, the observed shifts of the dominant CDR loop ensembles in solution strongly indicate that the point mutations in the CDR3 loops influence antigen binding.⁴⁵

To further characterize the Fv interface, we colored the V_H-V_L interface residues based on the number of interdomain interactions formed. Figure 6 shows an “open-book” view of the V_H and V_L domains for the double mutant L-Y91A/Y94A, the L-Y92A mutant and the Parent. Already from the interaction patterns mapped on the interface, we find highly similar contacts between the Parent and the L-Y92A mutant, which is also reflected in the distribution showing the number of all contacts per frame. The double mutant on the other hand differs substantially in the observed interaction patterns and the distribution of the number of contacts per frame is shifted substantially. In particular, the dominant ionic interaction between H-R96 and L-E55 is weakened substantially by the introduction of the mutations in the CDR-L3 loop (L-Y91A/Y94A). L-E55, which is situated in the CDR-L2 loop, has already been previously discussed to play a critical role in co-determining the CDR-H3 loop conformation, as it not only interacts with the CDR-H3 loop, but also contributes to stabilize the V_H-V_L interface.^43,46,47 Additionally, the stacking interactions of the H-W47 with L-F98 and L-Y91/Y94 are abolished. In agreement with these results, we find substantial differences in the van der Waals interaction energies for the Parent and the double mutant, while we only find smaller differences in the electrostatic interaction energies. These differences in the interface interaction patterns can also be observed for the anti-IL-13 Fab (SI Figure S8). While the L-D94A mutant shows highly similar interface interaction patterns compared to the Parent, the L-R96A mutation reveals distinct interaction patterns. These differences in the interface interaction patterns of the L-R96A variant are also reflected in a shift of the interdomain contact distributions, resulting in a reduced number of contacts per frame. The mutation of residue L-R96 to alanine leads to the loss of the dominant ionic interaction with residue H-D95. Additionally, the L-R96A mutation abolishes an interaction with residue H-W47, which results in a formation of a different interaction network of H-W47 with residues L-D94. Astonishingly, even though both L-D94 and L-R96 are located in the CDR-L3 loop, the respective mutations (L-D94A and L-R96A) reveal reversed effects. While L-R96 forms a network of stabilizing interdomain interactions with various residues located in the heavy chain, residue L-D94 mainly interacts with the solvent or only with residue H-K56 situated in the CDR-H2 loop. Thus, the mutation of L-D94 to an alanine does not interfere with the crucial interdomain interaction network and even results in a structural stabilization, which is reflected in an increase in interdomain interactions (SI Figure S8), in a decreased conformational space (SI Figure S3) and in a higher bispecific IgG yield.

Thus, by taking CDR loop ensembles, relative interdomain orientations, and the respective interface characteristics into account, we can provide a mechanistic explanation of the effect of the introduced point mutations on the pairing preferences. As both Fab interfaces (V_H-V_L and C_H1-C_L) show a high cooperation between each other, we additionally analyzed the distributions of the C_H1-C_L angle (AB torsion angle) and the elbow angle (SI Figure S5). We see shifts in the dominant C_H1-C_L and the elbow angle distributions, which are in line with the findings for the CDR loops and the V_H-V_L angle distributions.

In conclusion, we show that point mutations in the CDR-H3 and CDR-L3 loops, which have been shown to strongly determine heavy and light chain pairing preferences, induce substantial conformational rearrangements in the antigen-binding site, resulting in different dominant solution structures. As a consequence of conformational changes of all CDR loops, we find substantial shifts in the V_H-V_L interface angle, C_H1-C_L angle and elbow angle distributions, which are accompanied by a reduction in bispecific IgG yield. However, we not only observe shifts in the interface angle distributions, but we also see distinct V_H-V_L interface interaction patterns between different variants, which elucidate their different heavy and light chain pairing preferences.

Methods

Dataset

As starting structures for our simulations, we used the anti-MET Fab and an anti-IL-13 Fab (PDB accession code: 4K3J and 4I77, respectively). Both antibodies have been part of a study that investigated the influence of CDR3 loop residues on the resulting bispecific IgG yield of the anti-EGFR/MET and the anti-IL-13/IL-4 antibody.¹⁸ Previous studies determined the bispecific IgG yield by using liquid chromatography in combination with an extended mass range Orbitrap-based high-resolution mass spectrometer and defined the bispecific IgG yield as percentage of correctly assembled bispecific IgG in the purified pool of different IgG species.^18,22,34 This means that a high bispecific yield for the anti-EGFR/MET and anti-IL-13/anti-IL-4 antibodies is consistent with a cognate heavy and light chain pairing preference.

The different variants of the anti-MET and the anti-IL-13 antibody, which strongly influence bispecific IgG yield, differ in point mutations in the CDR-L3 and CDR-H3 loop. The starting structures of the different variants were prepared in MOE by mutating the respective residues. The in-total 13 Fab variants were protonated using the Protonate3D tool.^48,49 Charge neutrality was ensured by using the uniform background plasma approach in AMBER.^50–52 Using the tleap tool of the AmberTools20⁵⁰ package, the crystal structures were soaked in cubic water boxes of TIP3P water molecules with a minimum wall distance of 10 Å to the protein.⁵³ The structures were described with the AMBER force field 14SB.⁵⁴ The antibody fragments were carefully equilibrated using a multistep equilibration protocol.⁵⁵

Metadynamics simulations

To enhance the sampling of the conformational space, well-tempered bias-exchange metadynamics^56–58 simulations were performed in GROMACS^59,60 with the PLUMED 2 implementation.⁶¹ As an enhanced sampling technique, we chose metadynamics because it allowed us to focus the enhanced sampling on predefined collective variables (CV). The sampling is accelerated by a history-dependent bias potential, which is constructed in the space of the CVs.^56,58,62 As collective variables, we used a well-established protocol, boosting a linear combination of sine and cosine of the ψ torsion angles of all six CDR loops calculated with functions MATHEVAL and COMBINE implemented in PLUMED 2.^{35,61,63–66} As discussed previously, the ψ torsion angle captures conformational transitions comprehensively.⁶⁷ The underlying method presented here has been validated in various studies against a large number of experimental results. The simulations were performed at 300 K in an NpT ensemble using the GPU implementation of the pmemd module⁶⁸ to be as close to the experimental conditions as possible and to obtain the correct density distributions of both protein and water. We used a Gaussian height of 10.0 kJ/mol and a width of 0.3 rad. Gaussian deposition occurred every 1000 steps and a biasfactor of 10 was used. 500 ns of bias-exchange metadynamics simulations were performed for the prepared Fab structures. The resulting trajectories were aligned to the whole Fv and clustered with the program cpptraj^51,69 using the average linkage hierarchical clustering algorithm with a root mean square deviation cutoff criterion of 1.2 Å resulting in a large number of clusters. The cluster representatives for the antibody fragments were equilibrated and simulated for 100 ns using the AMBER 20⁵⁰ simulation package. The number of clusters and the accumulated simulation time for the 13 Fab (8 anti-MET Fab variants and 5 anti-IL-13 Fab variants) are summarized in SI Table S1.

Molecular dynamics simulations and further analyses

Molecular dynamics simulations were performed in an NpT ensemble using the pmemd.cuda module of AMBER 20.⁵¹ Bonds involving hydrogen atoms were restrained with the SHAKE algorithm,⁷⁰ allowing a time step of 2.0 femtoseconds. Atmospheric pressure (1 bar) of the system was set by weak coupling to an external bath using the Berendsen algorithm.⁷¹ The Langevin thermostat⁷² was used to maintain the temperature during simulations at 300 K.

With the obtained trajectories we performed a time-lagged independent component analysis (tICA) using the python library PyEMMA 2 employing a lag time of 10 nanoseconds. tICA was applied to identify the slowest movements of the investigated Fab and consequently to obtain a kinetic discretization of the sampled conformational space.⁷³ Based on the tICA conformational spaces, thermodynamics and kinetics were calculated with an MSM⁷⁴ by using PyEMMA 2, which uses the k-means clustering algorithm⁷⁵ to define microstates and the PCCA+ clustering algorithm⁷⁶ to coarse grain the microstates to macrostates. MSMs are network models that provide valuable insights for conformational states and transition probabilities between them, as it is possible to sufficient accurately identify the boundaries between two states.⁷⁴ The states are defined based on kinetic criteria, which allow the boundaries between free energy wells to be identified. Basically, MSMs coarse-grain the system’s dynamics, which reflect the free energy surface and ultimately determine the system’s structure and dynamics. Thus, MSMs provide important insights and enhance the understanding of states and transition probabilities and facilitate a quantitative connection with experimental data.^74,77

We performed tICA analyses and calculated MSMs for all CDR loops and the CDR3 loops of all 8 anti-MET variants and 5 anti-IL-13 variants following the Chothia nomenclature.¹²

tICA is a dimensionality reduction technique, detecting the slowest-relaxing degrees of freedom and facilitating the kinetic clustering, which is crucial for building an MSM. It linearly transforms a set of high-dimensional input coordinates to a set of output coordinates, by finding a subspace of good reaction coordinates. Thereby, tICA finds coordinates of maximal autocorrelation at a given lag time. The lag time sets a lower limit to the timescales considered in the tICA and the MSM. tIC 1 and tIC2 represent the two slowest degrees of freedom of the systems.

The sampling efficiency and the reliability of the MSM (e.g., defining optimal feature mappings) can be evaluated with the Chapman-Kolmogorov test,^78,79 by using the variational approach for Markov processes⁸⁰ and monitoring the fraction of states used, since the network states must be fully connected to calculate probabilities of transitions and the relative equilibrium probabilities. To build the MSM, we used the backbone torsions of the respective CDR loop following the Chothia nomenclature,⁸¹ defined 100 microstates using the k-means clustering algorithm and applied a lag time of 10 ns.

We then used the resulting macrostate ensembles to investigate correlations between the different CDR loop states, relative interdomain orientations (V_H-V_L and C_H1-C_L) and the elbow angle.

Relative V_H and V_L orientations using ABangle

ABangle is a computational tool^82–85 to characterize the relative orientations between the antibody variable domains (V_H and V_L) using six measurements (five angles and a distance). A plane is projected on each of the two variable domains. Between these two planes, a distance vector C is defined. The six measures are then two tilt angles between each plane (HC1, HC2, LC1, LC2) and a torsion angle (HL) between the two planes along the distance vector C (dc). The ABangle script can calculate these measures for an arbitrary Fv region by aligning the consensus structures to the found core set positions and fitting the planes and distance vector from this alignment. This online available tool was combined with an in‐house python script to reduce computational effort and to visualize our simulation data over time. The in‐house script makes use of ANARCI⁸⁶ for fast local annotation of the Fv region and pytraj from the AmberTools package⁵⁰ for rapid trajectory processing. To better visualize shifts in the relative V_H-V_L interdomain orientation we performed the Gaussian kernel density estimation (KDE) on the HL angle, to obtain probability density distributions. To calculate the KDE, we used the recently published implementation of KDE in C++.⁸⁷

C_H1-C_L interdomain orientation calculations and elbow angle calculations

While computational tools to fully characterize the Fv region of antibodies are already available, no such tools were published for other immunoglobulin domain interfaces, such as the C_H1-C_L interface.⁸² The Orientation of Cylindrical Domains approach⁸⁸ automatically creates a suitable coordinate system to characterize these interfaces for any user-provided reference structure. Using this tool, a reference coordinate system is created based on user-defined reference structures consisting of an atomic structure and two domain selections over these atoms. To this end, the reference structure for each domain is generated by considering a center axis linking the two centers of mass of the different domains, and the first principal axis P of inertia of each domain corresponding to the lowest eigenvalue of the inertia tensor. Each individual domain is aligned to the world coordinate system by aligning this principal axis to the z unit vector and the center axis as close as possible to the x unit vector, yielding a reference structure for each domain. To map the coordinate system onto a sample structure, the references are aligned to the sample and the alignment transformations are applied to the xyz unit vectors. The transformed z vectors (A1/ B1) and y vectors (A2/B2) as well as the center axis are then used to calculate six orientational measures: Two tilt angles for each vector toward the center axis (AC1, AC2, BC1, BC2), the length of the center axis (dC) and a torsion angle (AB) between the two intersecting planes composed of A1, the center axis and B1.

As measure for the elbow-angle, we calculated a torsion angle between the center of mass of variable domain, a defined vector between the COMs of the switch regions and the COM of the constant region.³⁵

Funding Statement

This work was supported by the Austrian Science Fund [P30565, P30737, P34518, DOC30].

Abbreviations

CDR	Complementarity-determining region
Fab	Antigen-binding fragment
Fc	Crystallizable fragment
Fv	Variable domain
MSM	Markov-state model
PCCA	Perron-cluster cluster analysis
tICA	Time-lagged independent component analysis

Disclosure statement

No potential conflict of interest was reported by the author(s).

Supplementary material

Supplemental data for this article can be accessed on the publisher’s website.