Overhauser Dynamic Nuclear Polarization with Selectively Deuterated BDPA Radicals

Abstract

The Overhauser effect (OE), commonly observed in NMR spectra of liquids and conducting solids, was recently discovered in insulating solids doped with the radical 1,3-bisdiphenylene-2-phenylallyl (BDPA). However, the mechanism of polarization transfer in OE-DNP in insulators is yet to be established, but hyperfine coupling of the radical to protons in BDPA has been proposed. In this paper we present a study that addresses the role of hyperfine couplings via the EPR and DNP measurements on some selectively deuterated BDPA radicals synthesized for this purpose. Newly developed synthetic routes enable selective deuteration at orthogonal positions or perdeuteration of the fluorene moieties with ²H incorporation of >93%. The fluorene moieties were subsequently used to synthesize two octadeuterated BDPA radicals, 1,3-[α,γ-d₈]-BDPA and 1,3-[β,δ-d₈]-BDPA, and a BDPA radical with perdeuterated fluorene moieties, 1,3-[α,β,γ,δ-d₁₆]-BDPA. In contrast to the strong positive OE enhancement observed in degassed samples of fully protonated h₂₁-BDPA (ε ~ +70), perdeuteration of the fluorenes results in a negative enhancement (ε ~ −13), while selective deuteration of α- and γ-positions (a_iso ~ 5.4 MHz) in BDPA results in a weak negative OE enhancement (ε ~ −1). Furthermore, deuteration of β- and δ-positions (a_iso ~ 1.2 MHz) results in a positive OE enhancement (ε ~ +36), albeit with a reduced magnitude relative to that observed in fully protonated BDPA. Our results clearly show the role of the hyperfine coupled α and γ ¹H spins in the BDPA radical in determining the dominance of the zero and double-quantum cross-relaxation pathways and the polarization-transfer mechanism to the bulk matrix.

Graphical Abstract

1. INTRODUCTION

Dynamic nuclear polarization (DNP) has emerged as a powerful method to overcome the inherent low sensitivity of nuclear magnetic resonance (NMR) spectroscopy by transferring the large polarization of unpaired electron spins to the nuclei of interest, typically ¹H.^1-3 DNP provides sensitivity enhancements of 2–3 orders of magnitude, enabling the study of biomolecules and materials that are sensitivity limited^4-13 and where structural studies using dipole recoupling are difficult.^14-18 The success of these experiments has stimulated the sustained development of continuous-wave (CW) solid-state devices and gyrotrons that generate microwave powers ranging from several hundred milliwatts to tens of watts, respectively. In turn, these sources provide microwave irradiation to drive electron or electron–nuclear spin transitions that facilitate CW-DNP, enabling experiments at magnetic fields up to 21.1 T.^19-26

There are four known CW-DNP mechanisms: the solid effect (SE), cross effect (CE), thermal mixing (TM), and the Overhauser effect (OE). The SE involves microwave excitation of weakly allowed forbidden zero-quantum (ZQ) or double-quantum (DQ) transitions in coupled electron–nuclear spin systems.^27-30 The CE involves coupled electron–electron–nuclear spin systems where microwave irradiation at the resonance frequency of one of the two participating electron spins alters the equilibrium polarization difference between the electrons. A fraction of the polarization difference is subsequently transferred to the nucleus via three-spin transitions when the difference between the electron resonance frequencies matches the nuclear resonance frequency.^30-34 TM is similar to the CE, except the dipolar interaction between electron spins is homogeneous, and the consequent fast electron spectral diffusion holds the electron spin system in local equilibrium.^35-37 In contrast to other CW-DNP mechanisms that can all be described by time-independent electron–nuclear and electron–electron interactions, the OE relies on the time dependence of the electron–nuclear couplings to drive the electron–nuclear cross-relaxation. Microwave irradiation of the allowed single quantum (SQ) electron transition results in ZQ and DQ cross-relaxation processes that occur at unequal rates and drive the buildup of nuclear polarization. The positive or negative sign of the observed nuclear enhancement is determined by the relative sizes of the ZQ and DQ cross-relaxation rates, respectively.

In the early 1950s the OE was the initial DNP mechanism proposed for studies of conducting solids,² and it was experimentally verified shortly thereafter by Carver and Slichter.^38,39 Much more recently, the OE in insulators was observed by using the narrow line radicals SA-BDPA⁴⁰ and BDPA,⁴¹ which were under investigation initially as polarizing agents for SE-DNP. These recent experiments demonstrated that among the CW-DNP mechanisms in solids, the OE has three crucial advantages. First, the allowed SQ transition is saturated at modest microwave powers, enabling low-power microwave sources for DNP.⁴¹ Second, unlike the other CW-DNP techniques, the enhancement factor of the OE is proportional to the external magnetic field strength, making it an attractive choice among DNP methods to pursue at high magnetic fields.^41,42 Third, the OE enhancement factor is observed to be proportional to the magic angle spinning (MAS) frequency. The observation is rationalized by a source-sink diffusion model with paramagnetic impurities or dissolved oxygen serving as polarization sinks.⁴³ Furthermore, the OE in insulating solids doped with BDPA has been observed at temperatures ranging from 1.2 K to room temperature.^42,44

The source of the time dependence in the electron–nuclear hyperfine couplings that drives cross-relaxation in insulating solids remains unknown. Recently, Pylaeva et al. proposed intramolecular charge transfer mediated by the mixed-valence nature of BDPA as the source of electron–nuclear hyperfine fluctuations. They computationally predicted that the oscillation of hyperfine couplings in the spin system was a consequence of electron hopping between the fluorene moieties and suggested that the rate of oscillation falls in the range required for the OE.^45,46 Guided by this insight, they recently synthesized two new mixed-valence radicals, namely tetrakis(4-methoxyphenyl)benzene-1,4-diamine radical and tetrakis(4-methoxyphenyl)benzene-1,3-diamine radical and, in the solvent tetrachloroethylene (TCE), demonstrated higher OE enhancements with these radicals than in samples doped with BDPA.⁴⁷

Although DNP experiments were initially reported in 1953 and BDPA has been used for 50 years as a polarizing agent, the details of the polarization transfer mechanism from the radical to the bulk nuclei via either the SE, CE, or OE-DNP have only recently been investigated. The three-spin solid effect was used to shed light on the mechanism of polarization transfer in trityl radicals showing that the spin diffusion barrier is <6 Å, and the first polarization transfer step is to ¹H spins on the trityl molecule itself.⁴⁸ In H₂O–glycerol matrices polarization is then transferred to glycerol molecules clustered near trityl radicals and is further relayed to the bulk solvent via spin diffusion. Note that trityl spectra do not display resolved hyperfine structure. In a second set of experiments, Stern et al. developed microwave gated hyperpolarization resurgence (HypRes) as an approach that allows separation of the contribution of nuclear spin diffusion from the efficiency of the core DNP mechanism.⁴⁹ These experiments were applied in the context of CE-DNP to bis-nitroxides and determined the spin diffusion barrier to be <3 Å.

In this paper we discuss the roles of electron–nuclear hyperfine interactions in the BDPA radicals responsible for the OE-DNP transfer by performing EPR and DNP experiments on selectively deuterated BDPA. Selective deuteration attenuates the specific isotropic couplings and consequently modulates the difference between ZQ and DQ cross-relaxation rates active in the electron–nuclear spin systems. Synthetic routes were developed to synthesize three BDPA radicals, with ²H labels on entire fluorene moieties or selectively on positions 1, 3, 6, 8 (alternatively labeled α and γ) on the fluorene moieties and the orthogonal positions 2, 4, 5, 7 (alternatively labeled β and δ). We show that the protons with a_iso ~ 5.4 MHz isotropic hyperfine couplings at positions 1, 3, 6, 8 in the fluorene moieties are crucial in obtaining positive DNP enhancements via the OE in BDPA. Furthermore, we present preliminary evidence that the protons at positions 2, 4, 5, 7 on the fluorene moieties, with weaker isotropic couplings, aid substantially in the efficient relay of polarization from the strongly coupled protons on the radical to the bulk ¹H in the surrounding matrix.

2. EXPERIMENTAL METHODS

2.1. Synthesis and Sample Preparation.

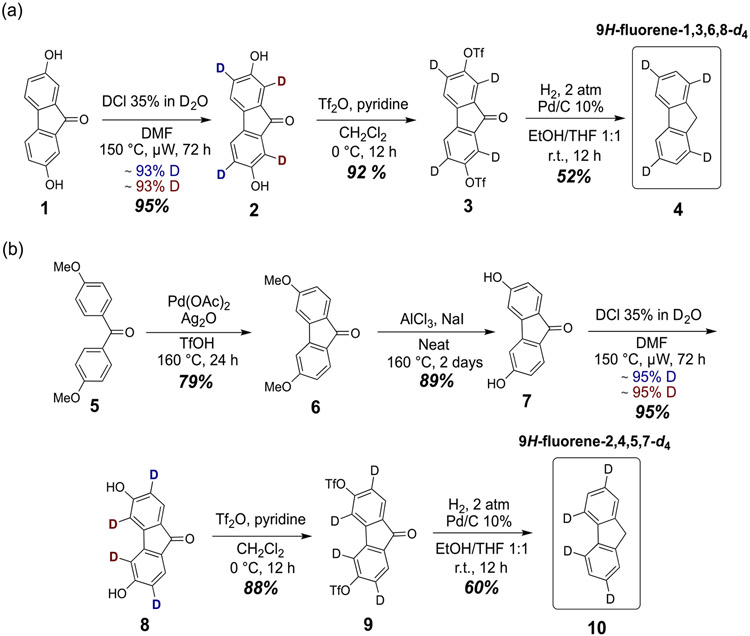
Investigation of the OE in 1,3-bisdiphenylene-2-phenylallyl (BDPA) radicals required the development of synthetic routes that would enable selective ²H labeling of orthogonal positions on the fluorene moieties, i.e., 1, 3, 6, 8 and 2, 4, 5, 7. Conventionally, the deuteration of aromatic compounds requires harsh reaction conditions, costly catalysts, and/or extended reaction times as aromatic hydrogens are not labile and often lead to poor deuterium incorporation.^50-55 Efficient direct H/D exchange at alternating positions on arenes is typically achieved by using activating groups, specifically ortho/para directors such as phenols and anilines.^56-58

Several deuteration techniques were attempted and were ultimately unsuccessful, including selective bromination and nitration of fluorene followed by deuterium substitution and synthesis of fluorene moieties from commercial deuterated arenes. None of these methods either yielded the desired products or deuteration patterns. Instead, deuterium incorporation into arenes was achieved through an acid-catalyzed electrophilic aromatic hydrogen exchange of phenolic systems, which was rationalized to be efficient for fluorene derivatives 1 and 7 (Scheme 1). This method allows deuteration at the positions ortho to the hydroxyl groups, which is desirable for the deuteration patterns targeted in this study. Note that the para positions are blocked in both substrates. The starting materials used in these synthetic routes are dihydroxyfluorenone derivatives, and so the resulting products contain hydroxyl and carbonyl groups that will have to be removed. Lastly, this type of reaction is performed in acidic aqueous media, in which all fluorene derivatives suited for the synthesis of targeted substrates are not soluble, and therefore the use of nonaqueous solvents was required.

Scheme 1.

Synthetic Routes to Selectively Deuterated Fluorenes (a) 9H-Fluorene-1,3,6,8-d₄ and (b) 9H-Fluorene-2,4,5,7-d₄

Scheme 1 shows the synthetic routes developed for the key synthetic intermediates 9H-fluorene-1,3,6,8-d₄ and 9H-fluorene-2,4,5,7-d₄. Fluorenone derivatives were used primarily due to compound 1 being inexpensive and commercially available. Compound 7 was synthesized through modified literature procedures.^59,60 Fluorenone derivative 6 was obtained from diaryl ketone 5 through a Pd-catalyzed oxidative cyclization in a 79% yield. The aryl methoxy groups were subsequently cleaved by using aluminum chloride and sodium iodide to give compound 7 in an 89% yield. The solubility of starting materials 1 and 7 in acidic aqueous media was insufficient for synthesis even at elevated temperatures, so a a 1:1 mixture of 35% DCl in D₂0 and DMF was used. Microwave-assisted methods also proved to integral in our synthesis. Reactions were initially conducted with conventional heating, and minimal conversion was observed after 3 days at 140 °C. The high boiling polar solvents DMSO, DMAc, and NMP yielded low conversion. Deuterium incorporation was monitored by NMR every 12 h and reached >93% and >95% after 72 h through microwave assistance by using a power of 75 W to reach a reaction temperature of 150 °C for compounds 2 and 8, respectively. Both compounds were ultimately obtained in a yield of 95%. Decomposition of the DMF resulted in pressure buildup inside the microwave vial, which had to be released periodically for a total of five times. The hydroxyl groups were subsequently converted into triflates by using triflic anhydride to give compounds 3 and 9 in 92% and 88% yields, respectively. Removal of the triflate groups was accomplished by palladium-catalyzed hydrogenolysis using hydrogen gas. During the characterization of the latter reaction, a minor product was isolated and was identified as final compound 4. This led to the conclusion that the carbonyl group of the fluorenone could be removed as well through reductive hydrogenation. By increasing the temperature of reaction from room temperature to 50 °C, complete reduction of respective carbonyls gave key intermediates 4 and 10 as the major products in 52% and 60% yields, respectively.

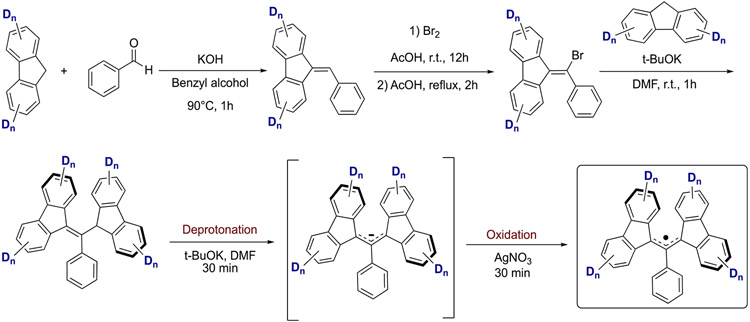
Scheme 2 details the general synthetic route to BDPA radicals once selectively deuterated fluorene moieties were obtained, which was based on a previous report.⁶¹ Condensation of selectively deuterated fluorene moieties with benzaldehyde yielded 9-benzylidene-9H-fluorene derivatives, which were subjected to a two-step process by alkene bromination followed by dehydrobromination to yield 9-(bromo(phenyl)methylene)-9H-fluorene derivatives. These derivatives were then condensed with deuterated fluorene derivatives via a nucleophilic addition–elimination sequence to form the neutral precursor to BDPA radicals (BDPA-H). Finally, the radical formation was performed by deprotonation of BDPA-H intermediates, followed by one-electron oxidation of the resulting anion using silver nitrate. For further experimental details on the synthesis of selectively deuterated BDPA radicals, we refer the reader to the Supporting Information.

Scheme 2.

General Synthetic Route to Selectively Deuterated BDPA Radicals

2.2. EPR Experiments at 0.34 T/9.6 GHz/X-Band.

The EPR samples were prepared by dissolving the BDPA in anhydrous toluene at 50 μM concentrations. h₂₁-BDPA (1,3-bisdiphenylene-2-phenylallyl 1:1 benzene complex) was purchased from Millipore-Sigma (St. Louis, MO), and dissolved paramagnetic oxygen in the solvent was removed by using five freeze–pump–thaw cycles. Continuous-wave, room temperature EPR spectra were recorded using a 5 mm OD Suprasil gastight EPR tube (Wilmad, Buena, NJ) and a Bruker Elexsys E580 spectrometer at 0.34 T/9.6 GHz (X-band). We note that the repeated freeze–pump–thaw cycles were essential to obtain a high-resolution EPR spectra. Similar results were not obtained with repeated freeze–thaw cycles, without pumping.

2.3. MAS DNP Experiments at 8.9 T/380 MHz/250 GHz.

2.5 wt % of h₂₁-BDPA in complex with benzene, 1,3-[α,β,γ,δ-d₁₆]-BDPA, 1,3-[α,γ-d₈]-BDPA, or 1,3-[β,δ-d₈]-BDPA was doped into a mixture of 95/5 mol % d₁₄ and h₁₄-o-terphenyl (oTP). In molar concentrations, this corresponds to ~57 mM of h₂₁-BDPA, ~65 mM of 1,3-[α,β,γ,δ-d₁₆]-BDPA, and ~66 mM of 1,3-[α,γ-d₈]-BDPA and 1,3-[β,δ-d₈]-BDPA in the oTP mixture. The doped mixture was then codissolved in deuterated chloroform, which was later removed by evaporation under vacuum. The resulting thin film was finely ground and packed in a 4 mm sapphire rotor (with an ID of 2.45 mm), between a Kel-F spacer and a top-cap (Revolution NMR). The packed sample was subsequently degassed with five freeze–pump–thaw cycles by using a home-built 3D-printed adapter. Samples were heated to ~58 °C during thaw cycles and rapidly freeze-quenched to promote oTP glass formation.⁶² Additional details on home-built adapter are provided in the Supporting Information.

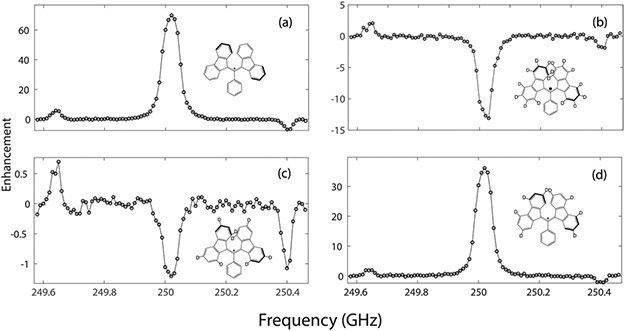
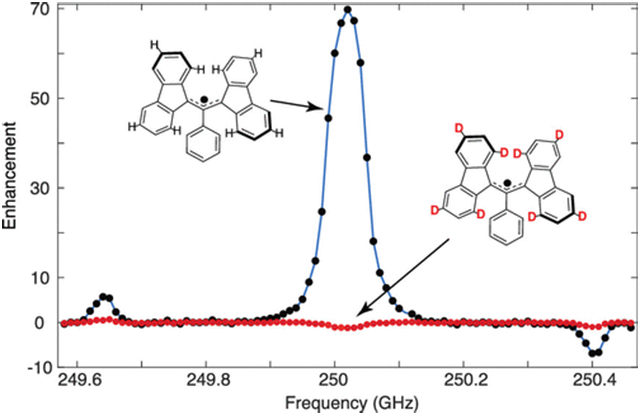
DNP experiments were performed on a 8.92 T/380 MHz/250 GHz DNP spectrometer⁶³ at a MAS frequency of ω_r/2π = 5 kHz and at 90 K (calibrated by using KBr).⁶⁴ The microwave pulses were first generated by a 10 GHz local oscillator (LO) source, which is then frequency-multiplied ×2 and ×3 to 60 GHz, before being mixed with a ~2.5 GHz signal from an arbitrary waveform generator (Keysight AWG M8190A). The resultant 62.5 GHz signal is filtered, amplified, and fed into two frequency doublers in an amplifier-multiplier chain (VDI AMC 691) yielding a 220 mW, 250 GHz microwave beam. The DNP frequency profiles (Figure 2) were obtained by varying the frequency of the signal from the AWG. Further details of this instrumentation will be discussed in a future publication.

Figure 2.

DNP Zeeman frequency profiles for samples containing (a) h₂₁-BDPA, ε = 70, (b) 1,3-[α,β,γ,δ-d_l6]-BDPA, ε = −13, (c) 1,3-[α,γ-d₈]-BDPA, ε = −1, and (d) 1,3-[β,δ-d₈]-BDPA, ε = 36.

The NMR experiment involved a train of 48 ¹H saturation pulses with Rabi frequency of ω_1H/2π = 83 kHz and 3 μs pulse width, with interpulse delays of 220 μs. This was followed by a recovery period before the signal was acquired by using a solid echo sequence. The spin–lattice relaxation time T₁ and the DNP buildup time T_B were estimated by fitting a monoexponential to the signal intensities with varying recovery periods. The DNP enhancement was determined by using $\epsilon =\frac{I-I_0}{I_0}$, where I denotes the microwave on NMR signal at a recovery period of 5T_B,OE and I₀ is the microwave off signal at a recovery period of 5T₁.

3. RESULTS

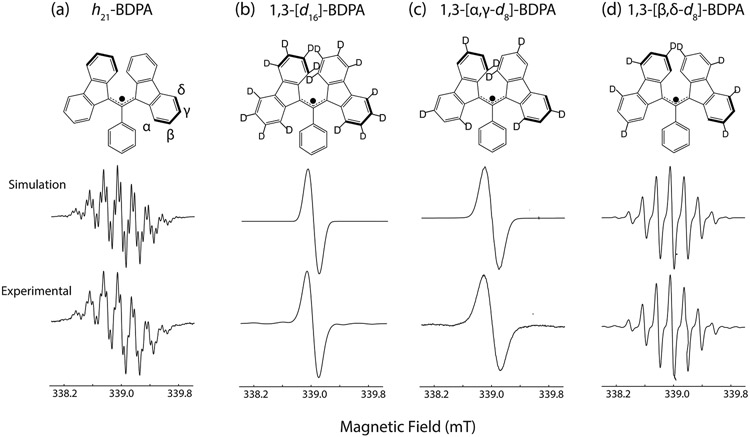
The strong coupling network of the fully protonated BDPA (h₂₁-BDPA) is verified by the excellent agreement between the EPR spectra and the numerical simulations (Figure 1) performed by using EasySpin⁵⁹ and the isotropic coupling constants (in MHz) listed in Table 1. The coupling constant data were taken from the published EPR and ENDOR spectra of Dalal et al.⁶⁵ Note that the inclusion of three couplings from the ¹H spins on the phenyl ring (ortho, meta, and para) in the simulation is necessary to reproduce the experimentally observed line shape.

Figure 1.

The 9.5 GHz solution EPR simulation and experimental spectra of (a) h₂₁-BDPA, (b) 1,3-[α,β,γ,δ-d₁₆]-BDPA, (c) 1,3-[α,γ-d₈]-BDPA, and (d) 1,3-[β,δ-d₈]-BDPA with molecular structures given in the top row. Middle row: simulated 9.5 GHz spectra using EasySpin and ¹H couplings from Dalal et al.⁶⁵ Bottom row: experimental solution state, CW EPR spectra recorded in degassed toluene samples.

Table 1.

¹H and ²H Hyperfine Couplings (in MHz) Used in the EasySpin Simulations of the EPR Spectra Shown in Figure 1^a

	α	β	γ	δ	o-, p-	m-
h21-BDPA	−5.54	1.38	−5.29	1.09	−0.5	−0.15
1,3-[α,β,γ,δ-d16]-BDPA	−0.85	0.21	−0.81	0.17	−0.5	−0.15
1,3-[α,γ-d8]-BDPA	−0.85	1.38	−0.81	1.09	−0.5	−0.15
1,3-[β,δ-d8]-BDPA	−5.54	0.21	−5.29	0.17	−0.5	−0.15
number of spins	4	4	4	4	3	2

^aThe positions on the fluorene ring are indicated in the first row, and the coupling constants of the ¹H or ²H at those positions are listed in the following rows for the four radicals. The total number of spins of each type is listed in the bottom row. Values and assignment of HFCs for h₂₁ BDPA were taken from Dalal et al.⁶⁵

A similar study was repeated on the selectively deuterated BDPA, where the introduction of ²H reduces the magnitude of the hyperfine coupling by a factor of γ¹_H/γ²_H ~ 6.51. The deuteration at the α- and γ-positions of the fluorene moieties (1,3-[α,γ-d₈]-BDPA) with a_iso ~ −5.54 and −5.29 MHz couplings, respectively, causes the EPR spectrum to collapse to a single broad line (Figure 1c). Similarly, introduction of ²H at the β- and δ-positions which removes the 1.38 and 1.09 MHz couplings from those ¹H spins and yields a nine-line pattern. We note the weak feature at 339 ± 0.8 mT present in the experimental trace is likely due to the remaining ~5% protonation of β- and δ-positions of the fluorene moieties. Finally, complete deuteration of all fluorene moiety protons to yield 1,3-[α,β,γ,δ-d₁₆]-BDPA results in a single EPR line that is reduced in breadth relative to that of 1,3-[α,γ-d₈]-BDPA. Nevertheless, in all four cases, the simulations are well matched the main experimental features, verifying that the introduction of specific ²H labels modified the hyperfine structure of the EPR spectrum in the expected manner and confirming the chemical structure of the target radicals.

Figure 2 shows the ¹H DNP enhancement as a function of microwave irradiation frequency obtained for oTP doped with the polarizing agents h_2l-BDPA, 1,3-[α,β,γ,δ-d_l6]-BDPA, 1,3-[β,γ-d₈]-BDPA, and 1,3-[β,δ-d₈]-BDPA. A large OE enhancement of ε = 70 was observed at 250.02 GHz for h₂₁-BDPA. Note that the SE enhancements obtained for h₂₁-BDPA with the diode source are small (ε = 5.8) because of the Rabi frequency. Deuteration of all the positions on the fluorene moieties resulted in a negative enhancement of ε = −13, while deuteration of only the strongly hyperfine coupled protons (−5.54 and −5.29 MHz) at positions 1, 3, 6, 8 on the fluorene moieties to yield 1,3-[α,γ-d₈]-BDPA also resulted in a very weak, negative OE enhancement ε = −1. This result clearly demonstrates that these large hyperfine couplings are primarily responsible for mediating the OE in h₂₁-BDPA. Deuteration of the weakly HF coupled protons at positions 2, 4, 5, 7 on the fluorene moieties, as in 1,3-[β,δ-d₈]-BDPA, results in an attenuated positive OE enhancement of ~36. Additionally, DNP enhancements were observed at 249.64 and 250.40 GHz for the positive and negative SE conditions. However, the magnitudes of the observed SE enhancements were an order of magnitude lower than that of the OE enhancements for all three radicals. Table 2 shows the spin–lattice relaxation times (T₁), the DNP buildup times measured at the OE condition (T_B,OE) and the positive SE condition (T_B,SE), and the observed enhancement values for the four polarizing agents. The enhancement values reported here are extracted from the frequency profile data depicted in Figure 2. Please refer to Table S3 for the enhancement values with error estimates which are generally ±10%.

Table 2.

Experimentally Measured Spin–Lattice Relaxation Times (T₁), DNP Buildup Times with the Microwaves at the OE Frequency (T_B,OE), and the Positive SE Frequency (T_B,SE) as Well as Enhancement Values Calculated for the OE (ε_OE) and the Positive SE (ε_SE)^a

radical	T1 (s)	TB,OE (s)	TB,SE (s)	ε OE	ε SE	εOE (normalized)
h21-BDPA	42.7 ± 3.3	43.6 ± 2.3	42.4 ± 2.2	70 ± 3	5.8	70
1,3-[α,β,γ,δ-d16]-BDPA	66.4 ± 4.0	74.0 ± 5.8	74.7 ± 5.0	−13 ± 1	1.9	−10
1,3-[α,γ-d8]-BDPA	66.7 ± 4.9	71.6 ± 6.4	70.4 ± 5.7	−1 ± 0.2	0.5	−3
1,3-[β,δ-d8]-BDPA	36.8 ± 1.2	41.3 ± 2.0	39.6 ± 1.6	36 ± 4	1.8	23

^aThe errors were estimated from intensities obtained following 180 s of microwave radiation. The last column has the OE enhancement values normalized by their relative radical concentrations.

The T₁ for h₂₁-BDPA and 1,3-[β,δ-d₈]-BDPA were found to be comparable at ~43 and ~37 s, respectively. In contrast, the T₁ for 1,3-[α,β,γ,δ-d₁₆]-BDPA and 1,3-[α,γ-d₈]-BDPA were much longer and comparable at ~66 and ~67 s, respectively, consistent with the absence of the strongly coupled ¹H spins at α,γ-positions. A similar trend was observed with the DNP buildup times. Table 2 also shows the calculated enhancement values for the OE DNP and the positive SE DNP.

4. DISCUSSION

The observed enhancement of ~70 for 2.5 wt % h₂₁ -BDPA in 95/5 mol % d₁₄ and h₁₄-oTP matrix is, to our knowledge, the highest reported in the literature normalized for the field and spinning frequency. Chaudhari et al. have reported an enhancement of ~60 for 2.5 wt % BDPA in 95/5 wt % d₁₄ and h₁₄-oTP spinning at 5 kHz, but at a higher field of 18.8 T, a temperature of ~128 K and in a ZrO₂ 1.3 mm rotor.⁴³ We note the electron Rabi field in a ZrO₂1.3 mm rotor system was calculated to be 19 μT/W^1/2,⁶⁶ whereas the reported experimental value for the 4 mm system used in this study is 13 μT/W^1/2,⁶⁷ indicating that the standard 1.3 mm system may have superior excitation efficiency for the electron spin transitions for the same incident microwave power. Moreover, the currently reported enhancement was obtained by using a solid-state microwave source with an output power of only 220 mW. Thus, we attribute the improved DNP enhancements obtained in this study to the efficiency of freeze–pump–thaw degassing cycles. This hypothesis is supported by noting that the enhancement factor improves by 75% for the degassed sample compared to the nondegassed h₂₁-BDPA sample (see Figure S39 and Table S2). Our experimental observation here is in good agreement with similar observations reported in the literature, where removal of paramagnetic oxygen by using freeze–thaw cycles on a BDPA-doped 1,1,2,2-tetrachloroethane (TCE) sample also demonstrated improved enhancement factors, and the observation was rationalized by using a source-sink model.⁴³

We note the concentration of active h₂₁-BDPA radical in commercial samples was only 50% of the anticipated value, as determined by measuring the extinction coefficient via UV–vis experiments (see Figure S34a and Table S1).⁶⁸ Using matrix-assisted laser desorption ionization-time of flight mass spectrometry (MALDI-TOF-MS), a significant fraction of the samples were determined to be hydroxylated BDPA (HO-BDPA) and hydroperoxylated BDPA (HO-O-BDPA). These impurities were readily removed from the sample by using silica gel chromatography, and the purity of the radical was verified by further UV–vis experiments (see Figure S34b); however, subsequent exposure of purified BDPA radical to air resulted in rapid formation of the hydroxylated species, as suggested in a previous publication.⁶⁹ Further details on h₂₁-BDPA purity and determination of sample concentration are provided in the Supporting Information.

Relative radical concentrations between each BDPA sample were determined by using EPR to compare the magnitude of the enhancements among BDPA derivatives. The relative ratio of electron spins among the four samples—h₂₁-BDPA, 1,3-[α,β,γ,δ-d₁₆]-BDPA, 1,3-[α,γ-d₈]-BDPA, and 1,3-[β,δ-d₈]-BDPA—was determined to be ~2.2:3.1:1:3.4, respectively. Further details on DNP sample concentration determination are provided in the Supporting Information.

As mentioned earlier, the OE involves a two-spin system of one electron and one nucleus. Here, the nucleus is ¹H and the observed NMR signal is primarily that of the bulk ¹H spins in the oTP matrix, after the spins equilibrate with the hyperpolarized ¹H spins in and immediately around the radical. The overall DNP enhancement observed in the bulk ¹H spins thus results from the cumulative contribution of both positive and negative hyperpolarization originating in the protons coupled to the electron. Deuteration of all the sites on the fluorene moieties in 1,3-[α,β,γ,δ-d₁₆]-BDPA results in an OE enhancement of ε = −13 and suggests that the dipolar couplings between the electron and the ¹H spins on the phenyl ring of the BDPA radical and the ¹H spins on h₁₄-oTP in the vicinity of the radical drive the observed negative enhancement. The dominance of the dipolar hyperfine couplings results in a DQ cross-relaxation rate that is larger than the ZQ cross-relaxation rate, and this difference generates a negative enhancement of nuclear polarization. It is noted here that this DNP result in consistent with prior DNP data on d₂₁-BDPA in polystyrene (PS) presented by Can et al., in which a weak negative enhancement was observed.⁴¹

Deuteration of only the most strongly coupled sites on the fluorenes in 1,3-[α,γ-d₈]-BDPA also results in a negative enhancement, but of a smaller magnitude, ε = −1. This establishes the role of the strong α,γ couplings for efficient, positive OE-DNP enhancement observed in h₂₁-BDPA. The smaller magnitudes of the negative enhancements observed in 1,3-[α,β,γ,δ-d₁₆]-BDPA and 1,3-[α,γ-d₈]-BDPA are consistent with the fact that the dominant hyperfine couplings present in these samples are smaller relative to the couplings in samples with protonated α,γ-positions on the fluorene moieties. Second, the change in the observed enhancement from ε = −13 in 1,3-[α,β,γ,δ-d₁₆]-BDPA to ε = −1 in 1,3-[α,γ-d₈]-BDPA suggests that weakly coupled protons in the β,δ-positions also help mediate ZQ OE DNP, albeit at a lesser extent compared to the α,γ-protons. The argument holds true even upon considering a factor of ~3.1 in radical concentrations between the two samples as measured by EPR. We note that the magnitude of the OE-DNP enhancement measured in the bulk ¹H is expected to be directly proportional to the BDPA radical concentration, while the sign of the observed OE-DNP enhancement is independent of the radical concentration. The sign depends only on the relative strengths of the isotropic and dipolar couplings and consequently on the relative dominance between the ZQ and DQ cross-relaxation pathways in the contributing electron–nuclear spin systems. This assumes the relaxation parameters remain reasonably constant and are insensitive to deuteration.

Deuteration of the weakly hyperfine coupled sites of the fluorene moieties in 1,3-[β,δ-d₈]-BDPA yields a positive enhancement of ε = 36. The result, when contrasted with the observation of a negative enhancement of ε = −13 in 1,3-[α,β,γ,δ-d₁₆]-BDPA, provides additional evidence for the importance of the strongly coupled ¹H spins on the α,γ-positions in obtaining a strong positive OE enhancement. Moreover, if we normalize the signal by relative radical concentration, the relative enhancement obtained for 1,3-[β,δ-d₈]-BDPA is roughly 33% that of h₂₁-BDPA. As we have deduced earlier from the DNP results of 1,3-[α,β,γ,δ-d₁₆]-BDPA and 1,3-[α,γ-d₈]-BDPA, the positive enhancement of the ¹H spins on the β,δ-positions in h₂₁-BDPA are modest and, by themselves, cannot account for the attenuation in the enhancement of 1,3-[β,δ-d₈]-BDPA relative to that of h₂₁-BDPA. This suggests that the protons at positions β,δ on the fluorenes may play a significant role in the process of spin diffusion in h₂₁-BDPA, facilitating the transfer of polarization from the protons at positions α,γ to the bulk ¹H spins in the oTP matrix. The absence of these protons in 1,3-[β,δ-d₈]-BDPA may simply be contributing to the attenuation of the DNP enhancement in the bulk ¹H. It is noted here that any potential differences in electron spin–lattice relaxation times, T_1e, could also contribute to the observed difference in enhancements between the two radicals. However, the absence of eight coupled protons in 1,3-[β,δ-d₈]-BDPA compared to h₂₁-BDPA is expected to result in longer T_1e for 1,3-[β,δ-d₈]-BDPA, which, in theory, should enable more efficient OE for electron–nuclear subsystems involving the protons at positions α,γ on the fluorene moieties.

As listed in Table 2, the nuclear relaxation times, T_1n, are found to be about ~43 and ~37 s for samples doped with h₂₁-BDPA and 1,3-[β,δ-d₈]-BDPA, respectively. They are measured to be longer at ~66 and ~67 s for samples doped with 1,3-[α,β,γ,δ-d₁₆]-BDPA and 1,3-[α,γ-d₈]-BDPA, respectively. These observations are consistent with the presence or absence of the strong isotropic HF couplings of the electron with the proton spins at α,γ-positions in the BDPA radicals.

The observed solid effect enhancement was an order of magnitude lower than the OE enhancement due to the low microwave power (220 mW) available from the AMC source. The OE utilizes microwave excitation of allowed SQ electron spin transitions, in contrast to the SE which relies upon the weakly allowed forbidden spin transitions and requires significantly greater microwave power to induce DNP enhancements. The solid effect enhancement was observed to be attenuated in all three deuterated BDPA radicals relative to h₂₁-BDPA.

5. CONCLUSIONS

In conclusion, we present a synthetic methodology to generate deuterated BDPA radicals with ²H at all the positions on the fluorene moieties and selectively at positions 1, 3, 6, 8 and 2, 4, 5, 7 on the fluorene moieties. The synthesis of these radicals enabled the first experimental observations into the role of specific hyperfine coupled protons at these positions in generating both OE and SE DNP enhancements. Perdeuteration of the fluorene moieties entirely results in a moderate negative enhancement, while in the case of 1,3-[α,γ-d₈]-BDPA, where the strong hyperfine coupled protons are deuterated, a weak negative OE enhancement was observed. This highlights the primary role of the protons at 1,3,6,8-positions in the fluorene moieties in generating a strong positive OE enhancement as observed in insulating solids doped with h₂₁-BDPA radicals. Second, deuteration of the weakly coupled protons in 1,3-[β,δ-d₈]-BDPA resulted in a positive OE enhancement that was attenuated in magnitude relative to h₂₁-BDPA. We argue that in h₂₁-BDPA the weakly hyperfine coupled protons at 2,4,5,7-positions of the fluorene moieties may aid in efficient spin diffusion to the bulk ¹H, thereby enabling a larger positive OE enhancement. Finally, the OE enhancement of 70 obtained with only 220 mW of microwave power in a fully degassed BDPA-oTP sample emphasizes the relevance of the OE as a DNP method of choice and the possibility for a wider application using low-cost solid-state microwave sources. The results presented offer insights into the mechanisms of OE-DNP and may allow for the rational design of further OE-DNP polarizing agents for use under high field DNP.