Abstract
The aim of this study was to compare weekly accumulative load during the in-season competitive period by professional soccer players according to the amount of time played in official matches (90-min, >60-min, <60-min, and 0-min) regarding the players’ position. Twenty-four professional outfield football players were monitored by GPS devices during training sessions and official matches and the accumulative weekly load were calculated for the following external load variables: total distance (TD; m), high speed running (HSR; >19.8 km·h-1), sprint meters (SPR; >25.2 km·h-1), high metabolic load distance (HMLD; >25.5 W·kg-1), number of accelerations (ACC; >3 m·s-2) and decelerations (DEC; <-3 m·s-2). This study revealed that players (as a whole o per demarcation) with more match playing time had a higher accumulative weekly load for most of the variables, but particularly at TD and HMLD (90-min and >60-min vs. <60-min and 0-min), HSR (90-min vs. <60-min and 0-min) and SPR (90-min vs. <60-min and 0-min). In addition, less positional variation was observed in relation to the competition requirements. This information would allow coaches to refine the required load with the objective of optimizing performance to soccer players.
Keywords: Football, GPS, Periodization, Training load, Positional role
INTRODUCTION
Football (soccer) is a complex sport where a multitude of tactical, technical and physical elements modulate performance [1]. Contemporary approaches examining the integrative nature of the game, in which an array of factors are synthesised, provide greater insights into a player’s positional and match requirements [2–3]. These multifaceted demands accumulate across the season, particularly when matches are played with minimal recovery [4]. Accordingly, practitioners modify training and competition demands during the season by alternating load and rotating the squad [5]. In order to achieve a balance between acute and chronic loads, the applied scientist must have an in-depth knowledge of competition and training loads within the microcycle [6]. Thus, enabling optimal conditioning for performance but more importantly identifying players that are inadequately loaded and therefore potentially susceptible to injury [7–8]. Although, some have examined the properties of the training microcycle in relation to the days before competition [9–10–11–12], limited research exists regarding the accumulative load of players achieving match time versus those with limited exposure to competition.
Using global positioning system (GPS) technology in both training and official matches is an effective tool for monitoring the accumulative player load. Despite this technology being widely used within football to quantify training demands, its use in official matches is less common [13]. Thus, limited research exists on the comparison of external loads among players within the microcycle based on official match time. Stevens et al. [14] demonstrated that the load of nonstarter sessions was generally lower than regular training, but this study only provided a basic breakdown of load (starters vs. non starters) without differentiating between match exposure times (e.g. 0-min vs. <60-min vs. >60-min vs. 90-min). Competing in weekly matches seems to act as an important physiological, mechanical and neuromuscular stimulus for various fitness parameters [15–16–17]. Thus, creating a discrepancy in total load between those getting regular match time versus those with partial or no match time [14]. Furthermore, players completing more match minutes perceived training to be harder the following week compared to those with less match time [18]. However, research has yet to establish if this finding is related to a higher training load or accumulated fatigue. Moreover, the tactical role of a player seems to be a key determinant of their match physical performance, so it is imperative that the conditioning stimulus has a positional element to it [19–20]. As it is common for defensive positions to complete more match time and offensive players to be regularly replaced [21], it might be prudent to determine if position specific trends exist regarding accumulative load. This would enable bespoke conditioning practices to be developed that account for the players weekly load and tactical role in the team. Accordingly, this study aimed to compare weekly accumulative load according to the amount of time played in official matches (e.g., 90-min, >60-min, <60-min and 0-min) and in relation to a players’ position.
MATERIALS AND METHODS
Participants
Twenty-four professional outfield football players participated in this study (age; 20 ± 2 yr, body mass; 70.2 ± 6.1 kg and stature; 1.78 ± 0.1 m). Players belonged to a reserve squad of a Spanish La Liga club that also competed in the UEFA Champions League. Data were collected during the competitive season as part of the players’ daily monitoring. Outfield players not completing a full microcycle were excluded from the analysis. Data arose as a condition of the players’ employment whereby they were assessed daily, thus no authorization was required from an institutional ethics committee [22]. Nevertheless, this study complied with the Declaration of Helsinki and players provided informed consent before participating.
Design
GPS data were collected from 37 competitive matches and 42 training weeks during the 2015–16 season. This enabled absolute and relative external training loads to be quantified across the microcycle for players accumulating various match exposures. Sessions were performed on a natural grass surface within a pitch dimension of 105 × 68 m. The team systematically played in a 4–3–3 formation, with two full backs (FB), two central defenders (CD), one midfielder (MD), two offensive midfielders (OMF) and three forwards (FW). The players were grouped by the number of minutes they played in the previous match (Table 1): the full match (90-min), more than 60-min of the match but did not complete it (>60-min), less than 60-min of the match (<60-min) and did not play in the match (0-min).
TABLE 1.
Number of files for each group and position.
| Game Exposure |
|||||
|---|---|---|---|---|---|
| 90-min | > 60-min | < 60-min | 0-min | Total files | |
| CD | 9 | 2 | 5 | 10 | 26 |
| FB | 17 | 3 | 4 | 10 | 34 |
| MF | 6 | 1 | 3 | 2 | 12 |
| OMF | 7 | 4 | 7 | 12 | 30 |
| FW | 9 | 4 | 5 | 2 | 20 |
| Total | 48 | 14 | 24 | 36 | 122 |
CD = central defender; FW = forward; MF = midfielder; WMF = wide midfielder; FB = full back; 0-min: group of players with 0 minutes in competition; < 60-min: group of players with less than 60 minutes in competition; > 60-min: group of players with more than 60 minutes in competition; 90-min: group of players with 90 minutes in competition.
Structured Microcycle
Due to variations in the number of days between matches [12–14], the present study only analysed training weeks where players had six days between successive matches and the training week composed of five training sessions that had a clear focus on an upcoming match [23]. Based on the recommendations of Akenhead et al. [13], training load data were qualified with respect to the number of days before or after a match (MD minus or plus). The training sessions that are contextualised below were composed of integrated content (e.g., tactical, technical and physical factors were amalgamated):
MD+1: was the session the day after competition where players were split into two training groups. The first group included players who had played >60-min of previous match (90-min and >60-min). The aim of this session was to recover after the match, so the term “recovery session” was used, MD+1 recovery (MD+1R). These players conducted low-impact exercises combined with regeneration exercises. The second group included players who had played <60-min of previous match (<60-min and 0-min). This group worked within a technical circuit followed by a small positional game and a small-sided game (SSG) with goalkeepers within an assigned area which ranged between 30 and 60 m2 per player. This session attempted to reproduce competitive loads, so the term “compensatory session” was used, MD+1 compensatory (MD+1C). The session MD-4, MD-3, MD-2 and MD-1 were common for players, regardless of the number of minutes played in previous official match. The content of each of the sessions has been described by Martin-Garcia et al. [11].
Physical variables
Activity profiles of players were monitored during each match and training session using a portable 10 Hz GPS unit (Viper Pod, 50 g, 88 × 33 mm, Statsports Viper, Northern Ireland). Each unit was placed in a specially designed vest, inside a mini pocket positioned between the shoulder blades. Quantifying the devices accuracy indicated a 2.5% estimation error in distance covered, with accuracy improving as the distance covered increased and the speed of movement decreased [24]. In order to avoid inter-unit error, each player used the same device during the study period [25–26]. Upon completion of each match and session, GPS data were extracted using proprietary software (Viper, Statsports, Ireland). The total distance (TD; m), high-speed running (HSR; m >19.8 km·h-1) and sprinting (SPR; m >25.2 km·h-1) distances were quantified along with the number of intense accelerations/decelerations (ACC/DEC; >3 m·s-2), and high metabolic load distance (HMLD; m >25.5 W·kg-1). The mean value of each training group (90-min; >60-min; <60-min, and 0-min) was expressed in absolute values and the estimated accumulative load in relation to the mean external load registered during official matches. In the case of players without official match records, the mean values of the position they occupy in the game system were applied (e.g. three offensive midfielders and one central defender).
Statistical analysis
All statistical analyses were conducted using SPSS for Windows 16.0 (SPSS Inc., Chicago, USA). Homogeneity of variance was examined by conducting Levene’s test. A one-way ANOVA was used to evaluate differences in dependent variables across various groups (90-min, >60-min, <60-min, and 0-min). This analysis also was implemented regarding player’ positions (CD, FW, MF, WMF and FB). In the event of a difference occurring, Bonferroni post-hoc tests were used to identify any localised effects or Dunnett’s T3 post-hoc test was applied when the variances were not homogeneous. The data are presented as means and standard deviations and alpha was set at p <0.05. Effect sizes (ES) were calculated to determine meaningful differences. Magnitudes of difference were classed as [27]: trivial (<0.2), small (>0.2–0.6), moderate (>0.6–1.2), large (>1.2–2.0), and very large (>2.0–4.0).
RESULTS
Absolute Accumulative Load
Table 2 presents the absolute values obtained from each training group (90-min, >60-min, <60-min, and 0-min) across variables. The 0-min group had a lower accumulative load than the 90-min group for TD, HSR, SPR, HMLD, ACC, DEC (p <0.01, ES: 0.7–3.2) and the >60-min group for TD, HSR, HMLD (p <0.01, ES: 1.3–2.5). The <60-min group had a lower accumulative load than the 90-min group for TD, HSR, SPR and HMLD (p <0.01, ES: 0.7–1.9). The >60-min group had a higher accumulative load than <60-min group for TD, HMLD (p <0.05, ES: 1.1–1.3) and the 0-min group for TD, HSR and HMLD (p <0.01, ES: 0.8–2.1). Positional differences were evident across all groups (Table 2), specifically FB in the 0-min group demonstrating consistently higher loads than MF for HSR (p <0.01, ES: 1.4) and SPR (p <0.01, ES: 1.7) and FW for HMLD (p <0.05, ES: 1.0). FB in <60-min group also had higher weekly loads than OMF for HSR (p <0.01, ES: 3.2) and SPR (p <0.01, ES: 3.6). In the >60-min group, MF and OMF also demonstrated greater loads than FW for HMLD (p <0.05, ES: 0.9–2.2) and ACC (p <0.05, ES: 1.0–4.1. For the 90-min group, FB had higher loads than CD and MF for HSR (p <0.01, ES: 1.0–2.3) and SPR (p <0.01, ES: 1.4–2.4), while OMF had accumulated more load than FW for HMLD (p <0.01, ES: 1.7), ACC (p <0.01, ES: 1.9) and DEC (p <0.01, ES: 1.2).
TABLE 2.
Absolute accumulated values per external load variables (mean ± SD) obtained from each player’s group during a training microcycle plus match.
| Variables | Position | 0–min | < 60–min | > 60–min | 90–min | ES;p |
|---|---|---|---|---|---|---|
| TD | CD | 21957.6 ± 1764.8 | 25945.6 ± 3179.9 | 29387.9 ± 5027.4 | 30378.1 ± 1323.3* | ES: 0.4–5.4;p < 0.001 |
| FB | 22657.5 ± 3051.8 | 27200.0 ± 2714.8* | 28906.7 ± 1855.4* | 32093.4 ± 1998.5e,*,† | ES: 1.6–3.8;p < 0.001 | |
| MF | 23423.1 ± 1603.9 | 25643.6 ± 5250.0 | 33700.2 ± 2603.2e,*,† | 32143.1 ± 1474.0e,* | ES: 0.8–4.9;p = 0.002 | |
| OMF | 23604.9 ± 2896.2 | 24064.6 ± 5164.0 | 32296.7 ± 3410.1e,*,† | 33930.5 ± 1672.6e,*,† | ES: 0.7–4.1;p < 0.001 | |
| FW | 19983.4 ± 2519.1 | 24670.5 ± 3436.0* | 27395.2 ± 728.0* | 28006.1 ± 2967.1 | ES: 0.2–2.8;p = 0.012 | |
| AVG | 22715.6 ± 2644.8 | 25328.4 ± 3899.6* | 29690.6 ± 2755.3*,† | 31327.2 ± 2656.9*,† | ES: 0.6–3.2;p < 0.001 | |
| ES;p | ES: 0.1–1.3; p = 0.335 | ES: 0.4–0.7; p = 0.773 | ES: 0.4–4.1; p = 0.101 | ES: 1.1–2.4; p < 0.001 | . | |
|
| ||||||
| HSR | CD | 537.2 ± 119.5 | 806.1 ± 295.2 | 821.1 ± 16.8* | 1027.4 ± 245.1* | ES: 0.9–2.5;p < 0.001 |
| FB | 991.0 ± 456.9c | 1479.1 ± 240.1a,c,d | 1477.4 ± 462.1a,e | 1625.4 ± 384.0a,c,e,* | ES: 0.4–1.5;p = 0.003 | |
| MF | 434.4 ± 124.6 | 582.5 ± 180.3 | 1152.9 ± 266.6*,† | 837.2 ± 230.5* | ES: 1.3–3.7;p = 0.027 | |
| OMF | 676.6 ± 263.9 | 636.1 ± 261.0 | 1284.6 ± 298.8a,*,† | 1289.6 ± 388.2*,† | ES: 0.0–1.9;p < 0.001 | |
| FW | 466.2 ± 98.2 | 863.0 ± 452.4 | 969.0 ± 177.1 | 1221.3 ± 314.0* | ES: 0.9–2.6;p = 0.037 | |
| AVG | 700.1 ± 348.5 | 850.7 ± 409.8 | 1147.4 ± 244.5* | 1277.9 ± 427.9*,† | ES: 0.3–1.5;p < 0.001 | |
| ES;p | ES: 0.9–1.4; p = 0.007 | ES: 1.6–4.1; p = 0.003 | ES: 0.5–1.8; p = 0.124 | ES: 0.9–2.3; p < 0.001 | . | |
|
| ||||||
| SPR | CD | 104.8 ± 65.9 | 119.1 ± 93.4 | 134.6 ± 22.8 | 202.0 ± 95.0 | ES: 0.8–1.2;p = 0.068 |
| FB | 225.5 ± 124.1c,d,e | 374.5 ± 116.8d | 324.1 ± 160.6a,c,d,e | 381.3 ± 147.4a,c,d,* | ES: 0.1–1.1;p = 0.043 | |
| MF | 57.6 ± 29.7 | 62.9 ± 24.8 | 184.8 ± 30.7* | 77.6 ± 34.9 | ES: 3.1–4.2;p = 0.034 | |
| OMF | 86.3 ± 61.5 | 62.2 ± 61.5 | 139.1 ± 73.4 | 200.9 ± 80.4*,† | ES: 0.8–1.9;p = 0.002 | |
| FW | 35.9 ± 13.3 | 193.4 ± 174.9 | 170.0 ± 119.8 | 247.6 ± 113.9c | ES: 0.4–2.1;p = 0.292 | |
| AVG | 125.5 ± 103.2 | 152.2 ± 147.8 | 188.9 ± 81.5 | 254.0 ± 150.5*,† | ES: 0.5–1.0;p < 0.001 | |
| ES;p | ES: 1.2–1.7; p = 0.001 | ES: 1.2–3.6; p = 0.002 | ES: 1.1–1.5; p = 0.290 | ES: 1.0–2.4; p < 0.001 | . | |
|
| ||||||
| HMLD | CD | 2716.9 ± 229.0 | 3454.1 ± 513.5* | 3684.4 ± 315.5* | 3891.7 ± 325.2* | ES: 0.6–4.1;p < 0.001 |
| FB | 3381.5 ± 948.4e | 4389.8 ± 403.4 | 4310.4 ± 668.5 | 4958.2 ± 702.3a,c,e,* | ES: 0.9–2.0;p < 0.001 | |
| MF | 3075.9 ± 114.4 | 3553.7 ± 908.9 | 5077.1 ± 304.4a,e,*,† | 4023.7 ± 547.3*,† | ES: 2.0–9.4;p = 0.054 | |
| OMF | 3233.9 ± 614.2e | 3224.3 ± 1032.0 | 5315.5 ± 861.6a,b,e,*,† | 5125.7 ± 707.1a,c,e,*,† | ES: 0.3–2.5;p < 0.001 | |
| FW | 2506.3 ± 133.3 | 3413.4 ± 506.4 | 3882.5 ± 245.0* | 3940.2 ± 683.1* | ES: 0.1–2.3;p = 0.019 | |
| AVG | 3093.5 ± 675.0 | 3543.3 ± 779.6 | 4403.4 ± 479.1*,† | 4465.8 ± 806.2*,† | ES: 0.1–1.8;p < 0.001 | |
| ES;p | ES: 0.2–1.0; p = 0.119 | ES: 1.2–1.4; p = 0.188 | ES: 0.3–2.2; p = 0.025 | ES: 0.2–1.7; p < 0.001 | . | |
|
| ||||||
| ACC | CD | 530.8 ± 71.8 | 633.6 ± 84.5* | 586.5 ± 118.0 | 621.2 ± 37.7* | ES: 0.2–1.3;p = 0.014 |
| FB | 613.0 ± 152.4 | 721.0 ± 19.2 | 652.3 ± 130.8 | 676.1 ± 155.4 | ES: 0.3–0.8;p = 0.624 | |
| MF | 626.6 ± 28.3 | 705.3 ± 162.6 | 796.0 ± 108.3e | 630.9 ± 101.6 | ES: 0.6–2.4;p = 0.445 | |
| OMF | 521.9 ± 160.4 | 552.4 ± 192.1 | 783.5 ± 143.2e,* | 737.9 ± 100.2e,* | ES: 0.4–1.7;p = 0.005 | |
| FW | 405.0 ± 82.0 | 452.0 ± 92.3 | 491.6 ± 54.2 | 514.3 ± 133.0 | ES: 0.2–0.9;p = 0.526 | |
| AVG | 551.9 ± 137.0 | 597.2 ± 154.0 | 634.5 ± 110.9 | 640.6 ± 142.6* | ES: 0.0–0.6;p = 0.020 | |
| ES;p | ES: 0.1–3.9; p = 0.180 | ES: 0.1–3.8; p = 0.033 | ES: 0.1–4.1; p = 0.023 | ES: 0.4–1.9; p = 0.011 | . | |
|
| ||||||
| DEC | CD | 501.4 ± 57.6 | 574.6 ± 80.4 | 498.0 ± 131.5 | 553.7 ± 42.3 | ES: 0.4–0.8;p = 0.098 |
| FB | 588.4 ± 145.7 | 652.5 ± 12.7e | 637.7 ± 132.3a,e | 688.9 ± 134.5a,e | ES: 0.3–0.7;p = 0.281 | |
| MF | 629.0 ± 30.3a,e | 659.3 ± 155.9 | 767.0 ± 120.7a,e | 593.6 ± 63.1 | ES: 0.8–2.2;p = 0.307 | |
| OMF | 500.0 ± 153.4 | 486.0 ± 165.9 | 767.0 ± 115.2a,e,*,† | 680.4 ± 73.0a,e,* | ES: 1.0–1.9;p = 0.002 | |
| FW | 442.0 ± 90.5 | 478.6 ± 69.9 | 464.6 ± 38.1 | 507.0 ± 92.9 | ES: 0.3–0.7;p = 0.590 | |
| AVG | 532.2 ± 129.4 | 553.3 ± 129.3 | 604.5 ± 107.5 | 616.1 ± 119.1* | ES: 0.1–0.7;p = 0.008 | |
| ES;p | ES: 0.3–3.0; p = 0.191 | ES: 0.1–1.6; p = 0.071 | ES: 0.0–3.7; p = 0.007 | ES: 0.1–1.2; p < 0.001 | . | |
CD = central defender; FW = forward; MF = midfielder; WMF = wide midfielder; FB = full back; 0-min: group of players with 0 minutes in competition; < 60-min: group of players with less than 60 minutes in competition; > 60-min: group of players with more than 60 minutes in competition; 90-min: group of players with 90 minutes in competition; TD = distance covered; HSR = high speed running (m > 19.8 km·h-1); SPR = sprint (m > 25.2 km·h-1); HMLD = high metabolic load distance (m); ACC = accelerations (n > 3 m·s-2); DEC = decelerations (n < -3 m·s-2).
Relative Accumulative Load
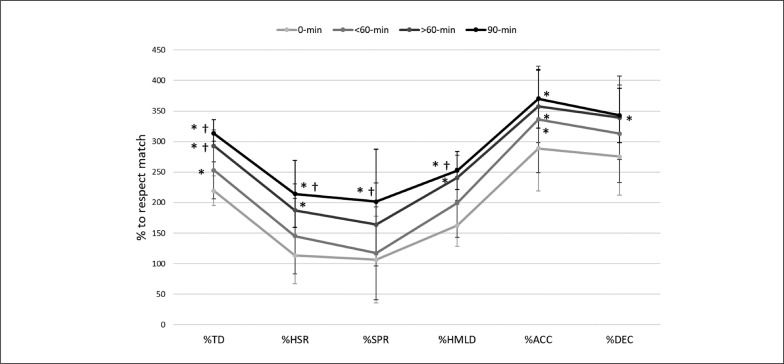
Figure 1 displays the relative accumulative load for each training variable regarding the training groups without considering the position of the players in the system. The 0-min group had a lower relative accumulative load than the 90-min group for TD, HSR, SPR, HMLD, ACC, DEC (p <0.01, ES: 0.7–3.2) and the >60-min group for TD, HSR HMLD (p <0.05, ES: 1.3–2.5). The 90-min group had a higher accumulative load than the 0-min group for TD, HSR, SPR, HMLD, ACC, DEC (p <0.01, ES: 1.3–4.5), in addition to the <60 and >60-min groups for TD, HSR, SPR and HMLD (p <0.05, ES: 1.0–3.5).
FIG. 1.
Relative accumulative load for each training variable regarding the training groups without considering the position of the players in the system.
0-min: group of players with 0 minutes in competition; < 60-min: group of players with less than 60 minutes in competition; > 60-min:group of players with more than 60 minutes in competition; 90-min: group of players with 90 minutes in competition; TD = distance covered; HSR = high speed running (m > 19.8 km·h-1); SPR = sprint (m > 25.2 km·h-1); HMLD = high metabolic load distance (m); ACC = accelerations (n > 3 m·s-2); DEC = decelerations (n < -3 m·s-2).
Table 3 presents the accumulative load for each training group (90-min, >60-min, <60-min, and 0-min) relative to match load and across variables and playing positions. Compared to the absolute accumulated load data, less relative differences were evident across position (Table 3). In the 0-min group, FB demonstrated higher accumulative loads than OMF for HMLD (p <0.05, ES: 1.1) while FB and FW loaded more than MF for ACC (p >0.05, ES: 1.3–1.8). For the >60-min group, OMF accumulated more weekly load than CD, MF and FW for both ACC (p >0.05, ES: 1.0.-1.3) and DEC (p >0.05, ES: 1.2–1.4). Within the 90-min group, FB were consistently loaded more during the week than MF for TD, SPR, HMLD, ACC and DEC (p <0.05, ES: 0.9–1.6).
TABLE 3.
Relative accumulated values per external load variables (mean ± SD) for each player’s group during a training microcycle plus match.
| Variables | Position | 0–min | < 60–min | > 60–min | 90–min | ES;p |
|---|---|---|---|---|---|---|
| %TD | CD | 224.3 ± 18.5 | 268.0 ± 32.9 | 301.2 ± 53.6e | 312.8 ± 15.5* | ES: 0.5–5.2; p < 0.001 |
| FB | 228.3 ± 28.5 | 279.1 ± 27.1* | 297.0 ± 19.0* | 323.9 ± 23.1c,*,† | ES: 1.2–3.8; p < 0.001 | |
| MF | 214.9 ± 14.7 | 235.3 ± 48.2 | 309.3 ± 13.4e,* | 292.8 ± 13.5* | ES: 1.2–6.6; p = 0.003 | |
| OMF | 210.0 ± 24.8 | 225.2 ± 59.6 | 299.3 ± 19.4* | 313.4 ± 22.9*,† | ES: 0.6–4.3; p < 0.001 | |
| FW | 217.7 ± 27.4 | 264.8 ± 45.7 | 279.1 ± 24.9 | 309.2 ± 26.7* | ES: 1.2–3.4; p = 0.026 | |
| AVG | 219.5 ± 24.2 | 253.2 ± 47.0* | 293.0 ± 26.0*,† | 313.4 ± 22.8*,† | ES: 0.9–4.0; p < 0.001 | |
| ES;p | ES: 0.2–0.7; p = 0.435 | ES: 0.4–1.1; p = 0.294 | ES: 0.2–1.4; p = 0.705 | ES: 0.4–1.5; p = 0.036 | . | |
|
| ||||||
| %HSR | CD | 120.1 ± 25.9 | 182.0 ± 72.1 | 196.0 ± 35.3 | 234.8 ± 64.9* | ES: 0.6–2.2;p = 0.002 |
| FB | 139.1 ± 50.9 | 174.8 ± 20.5 | 233.3 ± 65.5* | 237.4 ± 47.7* | ES: 0.1–2.0;p < 0.001 | |
| MF | 96.7 ± 27.7 | 129.7 ± 40.1 | 256.6 ± 32.1*,† | 177.4 ± 38.8* | ES: 2.1–5.4;p = 0.012 | |
| OMF | 97.7 ± 51.5 | 105.8 ± 65.3 | 196.4 ± 36.3* | 205.8 ± 60.0*,† | ES: 0.2–2.0;p < 0.001 | |
| FW | 70.6 ± 14.8 | 142.1 ± 54.9 | 136.1 ± 47.0 | 179.3 ± 27.8* | ES: 0.9–4.2;p = 0.033 | |
| AVG | 113.5 ± 46.6 | 145.3 ± 61.7 | 187.6 ± 43.2* | 214.3 ± 54.9*,† | ES: 0.5–2.0;p < 0.001 | |
| ES;p | ES: 0.5–1.5; p = 0.125 | ES: 0.1–1.1; p = 0.187 | ES: 0.4–2.8; p = 0.090 | ES: 0.1–1.3; p = 0.014 | . | |
|
| ||||||
| %SPR | CD | 98.0 ± 70.7 | 106.5 ± 79.7 | 144.8 ± 69.0 | 189.9 ± 92.2 | ES: 0.5–1.1;p = 0.086 |
| FB | 143.7 ± 72.3 | 140.8 ± 26.9 | 248.3 ± 79.6e,d | 250.0 ± 83.3c,e,* | ES: 0.0–1.4;p = 0.003 | |
| MF | 153.0 ± 78.8 | 167.0 ± 65.8 | 490.4 ± 93.5 a,b,d,e,*,†,□ | 146.4 ± 69.6 | ES: 4.4–4.6;p = 0.008 | |
| OMF | 83.6 ± 55.3 | 72.6 ± 89.6 | 133.6 ± 34.6 | 213.7 ± 67.1*,† | ES: 1.4–1.8;p < 0.001 | |
| FW | 21.1 ± 7.8 | 143.2 ± 72.3 | 80.8 ± 63.6 | 150.6 ± 60.5 | ES: 0.1–2.4;p = 0.064 | |
| AVG | 106.6 ± 70.7 | 117.1 ± 76.2 | 164.2 ± 68.1 | 201.6 ± 85.7*,† | ES: 0.4–1.2;p < 0.001 | |
| ES;p | ES: 0.1–2.1; p = 0.057 | ES: 0.3–1.1; p = 0.326 | ES: 2.8–5.6; p < 0.001 | ES: 0.5–1.3; p = 0.011 | . | |
|
| ||||||
| %HMLD | CD | 177.3 ± 14.8 | 226.5 ± 34.8 | 241.6 ± 12.7* | 254.7 ± 21.2* | ES: 0.7–4.2;p < 0.001 |
| FB | 180.9 ± 35.7d | 225.4 ± 22.0 | 246.0 ± 28.1* | 270.4 ± 27.1c,* | ES: 0.9–2.9;p < 0.001 | |
| MF | 153.8 ± 5.7 | 177.8 ± 45.5 | 254.0 ± 33.6* | 221.1 ± 30.0* | ES: 1.1–4.6;p = 0.025 | |
| OMF | 139.7 ± 36.6 | 163.3 ± 76.4 | 267.0 ± 60.7e,*,† | 245.5 ± 35.0*,† | ES: 0.5–2.9;p < 0.001 | |
| FW | 156.9 ± 8.3 | 211.1 ± 53.3 | 213.5 ± 48.5 | 245.3 ± 26.7 | ES: 0.9–3.6;p = 0.131 | |
| AVG | 162.5 ± 34.2 | 199.7 ± 56.4 | 240.7 ± 36.7* | 252.6 ± 31.1*,† | ES: 0.3–2.8;p < 0.001 | |
| ES;p | ES: 0.1–1.1; p = 0.019 | ES: 0.0–1.0; p = 0.219 | ES: 0.2–1.0; p = 0.576 | ES: 0.6–0.9; p = 0.004 | . | |
|
| ||||||
| %ACC | CD | 296.6 ± 42.4 | 354.1 ± 44.9 | 331.2 ± 72.6 | 349.3 ± 23.8* | ES: 0.2–1.3;p = 0.020 |
| FB | 319.0 ± 55.9c | 358.6 ± 12.5 | 352.3 ± 33.6 | 396.3 ± 38.2c,* | ES: 1.1–1.7;p = 0.001 | |
| MF | 250.8 ± 11.3 | 282.3 ± 65.1 | 318.6 ± 40.2* | 329.9 ± 50.0* | ES: 0.2–1.9;p = 0.168 | |
| OMF | 261.0 ± 92.8 | 320.3 ± 148.9 | 420.8 ± 91.4a,c,e,* | 362.4 ± 52.5* | ES: 0.9–1.7;p = 0.034 | |
| FW | 326.2 ± 66.0c | 353.2 ± 59.0 | 328.7 ± 57.5 | 382.9 ± 55.7 | ES: 0.5–1.0;p = 0.656 | |
| AVG | 288.8 ± 70.0* | 336.5 ± 87.1* | 357.6 ± 59.1* | 370.4 ± 48.0* | ES: 0.2–1.4;p < 0.001 | |
| ES;p | ES: 0.1–1.8; p = 0.227 | ES: 0.1–1.8; p = 0.752 | ES: 0.9–1.3; p = 0.346 | ES: 0.3–1.4; p = 0.006 | . | |
|
| ||||||
| %DEC | CD | 290.9 ± 34.9 | 339.3 ± 47.2 | 299.1 ± 98.4 | 329.3 ± 22.3 | ES: 0.3–1.2;p = 0.078 |
| FB | 304.2 ± 56.9 | 340.8 ± 37.5 | 334.7 ± 53.7 | 368.3 ± 45.2c,* | ES: 0.6–1.3;p = 0.018 | |
| MF | 248.6 ± 11.9 | 260.6 ± 61.6 | 303.2 ± 45.6 | 299.6 ± 37.8 | ES: 0.1–1.8;p = 0.279 | |
| OMF | 237.8 ± 71.7 | 273.2 ± 124.4 | 415.9 ± 75.9a,c,e,*,† | 339.9 ± 37.2* | ES: 1.4–2.5;p = 0.002 | |
| FW | 327.7 ± 67.1 | 346.5 ± 37.2 | 303.5 ± 68.3 | 344.6 ± 47.0 | ES: 0.0–0.8;p = 0.635 | |
| AVG | 275.2 ± 62.8 | 313.0 ± 80.0 | 339.1 ± 68.4 | 342.8 ± 44.4* | ES: 0.1–1.3;p < 0.001 | |
| ES;p | ES: 0.4–1.3; p = 0.040 | ES: 0.1–1.8; p = 0.295 | ES: 1.2–1.4; p = 0.231 | ES: 0.5–1.6; p = 0.005 | . | |
CD = central defender; FW = forward; MF = midfielder; WMF = wide midfielder; FB = full back; 0-min: group of players with 0 minutes in competition; < 60-min: group of players with less than 60 minutes in competition; > 60-min: group of players with more than 60 minutes in competition; 90-min: group of players with 90 minutes in competition; TD = distance covered; HSR = high speed running (m > 19.8 km·h-1); SPR = sprint (m > 25.2 km·h-1); HMLD = high metabolic load distance (m); ACC = accelerations (n > 3 m·s-2); DEC = decelerations (n < -3 m·s-2).
DISCUSSION
This study findings revealed that players with more match playing time had a higher accumulative weekly load for most of the external load variables, but particularly at HSR and SPR. Moreover, position specific accumulative load trends were evident in players completing more match time, with less positional variation when expressed relative to match requirements.
Accumulative weekly load has previously been examined in English [13], Dutch [15] and Spanish League players [18–28]. This is particularly relevant as cultural and competition demands across leagues could result in distinct loading variations in attempt to optimise performance. Interestingly, when comparing external loads across various European leagues, starters consistently display higher accumulative demands than non-starters [14–15–18] with match time being the major determinant of this difference. However, comparisons across studies are difficult as researchers generally use generic descriptors for starters and nonstarters. For instance, assigning players into two or three accumulative load groups based on match time [14–15–18–28]. To complicate matters, studies use distinct loading metrics, thresholds, GPS devices, and these further limits comparability between studies. The present analysis is the most granular to date, and not only compares four groups of players based on match time but also explores this as a function of their playing position.
The data demonstrated that the 0-min and <60-min groups were lower for most external loading variables in comparison to >60-min and 90-min groups, with very little difference between the 90-min and the >60-min group. This finding could potentially justify the practices employed by some elite clubs that split the squad for MD+1 work based on greater or less than <60-min played in previous official matches [11]. For instance, professional Spanish team use a MD+1R session for players completing >60 min to aid recovery, as opposed to MD+1C that is for players completing <60 min and is a compensatory session in an attempt to replicate loading during an official match [11]. This is imperative, as matches seems to act as an important physiological, mechanical and neuromuscular stimulus for various fitness parameters [15–16–17]. As the MD+1C session encompassed both positional games and SSG in reduced pitch dimensions, it seems that this adequately mimicked the ACC and DEC match demands as differences were only present between the 90 and 0-min group [29]. This is not surprising as Martin-Garcia et al. [11] reported that ACC and DEC demands during a MD+1C session exceeded 80% of that performed in official match. Specifically, the ACC and DEC demands attained by the 90-min group equate to the load accumulated in 3.5 matches, which aligns with those reported by Stevens et al. [14], with the starter group also reaching more than three matches in high intensity ACC and DEC. In contrast, weekly ACC and DEC load in the 0-min group was equivalent to about three weekly matches, while other external load variables demonstrate weekly demands of between 1–2 matches. In agreement with the present findings, Stevens et al. [14] also found that ACC and DEC load variables displayed the lowest differential between starters and nonstarters compared to other external load variables.
Match running performances studies reveal that HSR and SPR are important physical actions, determinants many times for its connection with scoring opportunities [30], and also has been evidenced when comparing differences between performance level and playing positions [20–31–32]. The data demonstrate that HSR and SPR weekly accumulation was double for the 90-min vs the 0-min group. Despite this, the 0-min group still reached an average weekly accumulation value of one match for HSR and SPR. Interestingly, Stevens et al. [14] reported values of 1.5 and 0.5 for HSR and SPR for substitutes in one and two matches per week, respectively. Unfortunately, comparisons are difficult as this study only quantified one group for non-starters with no differentiation between substitutes and players who did not play at all. As previously discussed, strategies to replicate the match demands of nonstarters in MD+1C seems to be optimal for ACC and DEC [11]. However, the present results reveal that this session does not seem to provide sufficient overload to develop HSR and SPR capabilities as these external load variables only reach 20–30% of match play demands [11]. Research has indicated that pitch running without the ball or position specific circuits that encompass supra-maximal running alongside technical actions and some directional changes could achieve the necessary overload for HSR and SPR metrics [33]. Although the relationship between the workload and the likelihood of injury is highly complex, influenced by different moderators [34] and in need of more research before conclusions can be drawn, weekly HSR and SPR management could be important [35]. This is especially important as a relationship between weekly HSR load and the probability of injury seems to be U-shaped whereby a moderate amount seems to have a protective effect [36]. Thus, perhaps both groups might present a certain risk of injury, in some cases due to under-stimulation (0-min group) and in other cases due to over-stimulation (90min group). Thus, future research should modify MD+1C sessions using a multi-modal approach to optimise the training stimulus for players with partial or no limited match time.
The tactical role of a player seems to be a powerful determinant of their match physical performance, so it is imperative that the conditioning stimulus has a positional element to it [2]. It is worth noting that during official matches of this same team studied, CB and MF (~300–400 m) cover less HSR than FW and FB (~600–800 m). Interestingly, FB produce the greatest HSR and SPR load and MF typically the lowest load compared to other positions from MD-4 across to MD-1 [11]. Thus, training load and match running metrics are directly aligned to enable players to be conditioned for their distinct tactical role in the team. Although interpreting positional trends from a low sample size requires caution, it was clear to see that this trend was not always evident for various metrics across the various weekly accumulative load groups. Crucially, as football is a submaximal sport whereby players are likely to be working within their physical capacity for long periods, it is imperative to remember that players tax a high proportion of this capacity during intense periods of the match [37]. Thus, inadequate match time could impact a player’s ability to maintain a high work rate if required during various phases of match-play. As selected positions within the modern game have higher physical requirements [19], it might be wise to ensure these positions are loaded more during compensatory sessions when not gaining match time. This is especially important for FB to enable them to cope with a dual tactical role that includes defensive (e.g. recovery running) and offensive (e.g. overlapping and running the channel) physical-tactical actions [2]. Research also highlights that most substitutions occurred at halftime and between the 60- to 85-min [38] and these include more attacking positions as the second half progresses [21]. Thus, as offensive players are more likely to gain some match time, bespoke conditioning work might need to be incorporated to account for defensive players not been regularly introduced and attaining 0 min per week regularly.
Some of the main limitations of the study are due to not considering the specific load in the training made outside the field (indoor), not incorporating internal load variables (heart rate or RPE) or the effective differences in minutes that may exist within the same group (61 minutes vs. 89 minutes). However, the use of four groups depending on the minutes played in the previous match (90 minutes, >60 minutes, <60 minutes and 0 minutes) provides new and practical information to the coaches.
CONCLUSIONS
In summary, this study revealed that players with more match playing time had a higher accumulative weekly load for most of the variables, but particularly at HSR and SPR. Moreover, position specific accumulative load trends were evident in players completing more match time, with less positional variation when expressed relative to match requirements.
Acknowledgments
The authors thank all the athletes who participated in the study. The authors did not report any potential conflicts of interest. The authors gratefully acknowledge the support of a Spanish government subproject Mixed method approach on performance analysis (in training and competition) in elite and academy sport [PGC2018-098742-B-C33] (2019-2021) [del Ministerio de Ciencia, Innovación y Universidades (MCIU), la Agencia Estatal de Investigación (AEI) y el Fondo Europeo de Desarrollo Regional (FEDER)], that is part of the coordinated project New approach of research in physical activity and sport from mixed methods perspective (NARPAS_MM) [SPGC201800X098742CV0].
Conflict of interest
The authors did not report any potential conflicts of interest.
Practical applications
Knowing external training loads is important for applied professionals, particularly when it comes to optimizing position-specific loads. As competitive match play is an important stimulus for developing the physiological capacities of players regularly completing games, it is imperative that practical strategies are implemented to offset any reductions in the fitness of players getting limited game time. Thus, the MD-1, MD and MD+1 sessions could be the most appropriate sessions to try to compensate for the absence of competitive stimulus in order to synchronize the weekly training loads of all the team members with a view to having all the effective with the fitness and the necessary freshness with which to be able to compete every week.
REFERENCES
- 1.Bradley PS, Ade JD. Are current physical match performance metrics in elite soccer fit for purpose or is the adoption of an integrated approach needed? Int J Sports Physiol Perform. 2018;13(5):656–664. doi: 10.1123/ijspp.2017-0433. [DOI] [PubMed] [Google Scholar]
- 2.Ade J, Fitzpatrick J, Bradley PS. High-intensity efforts in elite soccer matches and associated movement patterns, technical skills and tactical actions. Information for position-specific training drills. J Sports Sci. 2016;34(24):2205–2214. doi: 10.1080/02640414.2016.1217343. [DOI] [PubMed] [Google Scholar]
- 3.Bradley PS, Mascio MD, Mohr M, Fransson D, Wells C, Moreira A, et al. Can modern trends in elite football match demands be translated into novel training and testing modes? Aspertar Sports Med J. 2018;7(1):46–52. [Google Scholar]
- 4.Moreira A, Bradley P, Carling C, Arruda AF, Spigolon LM, Franciscon C, Aoki MS. Effect of a congested match schedule on immune-endocrine responses, technical performance and session-RPE in elite youth soccer players. J Sports Sci. 2016;34(24):2255–2261. doi: 10.1080/02640414.2016.1205753. [DOI] [PubMed] [Google Scholar]
- 5.Carling C, Le Gall F, McCall A, Nedelec M, Dupont G. Squad management, injury and match performance in a professional soccer team over a championship-winning season. Eur J Sport Sci. 2015;15(7):573–582. doi: 10.1080/17461391.2014.955885. [DOI] [PubMed] [Google Scholar]
- 6.Gabbett T. The training-injury prevention paradox: Should athletes be training smarter and harder? Br J Sports Med. 2016;50(5):273–280. doi: 10.1136/bjsports-2015-095788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Drew MK, Finch CF. The relationship between training load and injury, illness and soreness: a systematic and literature review. Sports Med. 2016;4(6):861–883. doi: 10.1007/s40279-015-0459-8. [DOI] [PubMed] [Google Scholar]
- 8.Gabbett TJ, Whiteley R. Two Training-Load Paradoxes: Can We Work Harder and Smarter, Can Physical Preparation and Medical Be Teammates? Int J Sports Physiol Perform. 2017;12(s2):S2–50. doi: 10.1123/ijspp.2016-0321. [DOI] [PubMed] [Google Scholar]
- 9.Coutts A, Reaburn P, Piva TJ, Murphy A. Changes in selected biochemical, muscular strength, power, and endurance measures during deliberate overreaching and tapering in rugby league players. Int J Sports Med. 2007;28(02):116–124. doi: 10.1055/s-2006-924145. [DOI] [PubMed] [Google Scholar]
- 10.Fessi MS, Zarrouk N, Di Salvo V, Filetti C, Barker AR, Moalla W. Effects of tapering on physical match activities in professional soccer players. J Sport Sci. 2016;34(24):2189–2194. doi: 10.1080/02640414.2016.1171891. [DOI] [PubMed] [Google Scholar]
- 11.Martín-García A, Gómez Díaz A, Bradley PS, Cos F, Casamichana D. The Quantification of a Professional Football Teams External Load Using a Microcycle Structure. J Strength Cond Res. 2018;32(12):3511–3518. doi: 10.1519/JSC.0000000000002816. [DOI] [PubMed] [Google Scholar]
- 12.Owen AL, Djaoui L, Newton M, Malone S, Mendes B. A contemporary multi-modal mechanical approach to training monitoring in elite professional soccer. Sci Med Football. 2017;1(3):216–221. doi: 10.1080/24733938.2021.1942539. [DOI] [PubMed] [Google Scholar]
- 13.Akenhead R, Harley JA, Tweddle SP. Examining the external training load of an English Premier League football team with special reference to acceleration. J Strength Cond Res. 2016;30(9):2424–2432. doi: 10.1519/JSC.0000000000001343. [DOI] [PubMed] [Google Scholar]
- 14.Stevens TG, de Ruiter CJ, Twisk JW, Savelsbergh GJ, Beek PJ. Quantification of in-season training load relative to match load in professional Dutch Eredivisie football players. Sci Med Football. 2017;1(2):117–125. [Google Scholar]
- 15.Anderson L, Orme P, Di Michele R, Close GL, Morgans R, Drust B, et al. Quantification of training load during one-, two-and threegame week schedules in professional soccer players from the English Premier League: Implications for carbohydrate periodisation. J Sport Sci. 2016;34(13):1250–1259. doi: 10.1080/02640414.2015.1106574. [DOI] [PubMed] [Google Scholar]
- 16.Morgans R, Di Michele R, Drust B. Soccer match play as an important component of the power-training stimulus in Premier League players. Int J Sports Physiol Perform. 2017;13(5):665–667. doi: 10.1123/ijspp.2016-0412. [DOI] [PubMed] [Google Scholar]
- 17.Young WB, Newton RU, Doyle TLA, Chapman D, Cormack S, Stewart C, et al. Physiological and anthropometric characteristics of starters and non-starters and playing positions in elite Australian Rules Football: A case study. J Sci Med Sport. 2005;8(3):333–345. doi: 10.1016/s1440-2440(05)80044-1. [DOI] [PubMed] [Google Scholar]
- 18.Azcárate U, Yanci J, Los Arcos A. Influence of match playing time and the length of the between-match microcycle in Spanish professional soccer players’ perceived training load. Sci Med Football. 2018;2(1):23–28. [Google Scholar]
- 19.Bush MD, Archer DT, Hogg R, Bradley PS. Factors influencing physical and technical variability in the English Premier League. Int J Sports Physiol Perform. 2015;10(7):865–872. doi: 10.1123/ijspp.2014-0484. [DOI] [PubMed] [Google Scholar]
- 20.Bradley PS, Sheldon W, Wooster B, Olsen P, Boanas P, Krustrup P. High-intensity running in English FA Premier League soccer matches. J Sport Sci. 2009;27(2):159–168. doi: 10.1080/02640410802512775. [DOI] [PubMed] [Google Scholar]
- 21.Bradley PS, Lago-Peñas C, Rey E. Evaluation of the match performances of substitution players in elite soccer. Int J Sports Physiol Perform. 2014;9(3):415–424. doi: 10.1123/ijspp.2013-0304. [DOI] [PubMed] [Google Scholar]
- 22.Lacome M, Simpson BM, Cholley Y, Lambert P, Buchheit M. Small-sided games in elite soccer: Does one size fits all? Int J Sports Physiol Perform. 2018;13(5):568–576. doi: 10.1123/ijspp.2017-0214. [DOI] [PubMed] [Google Scholar]
- 23.Malone JJ, Di Michele R, Morgans R, Burgess D, Morton JP, Drust B. Seasonal training-load quantification in elite English premier league soccer players. Int J Sports Physiol Perform. 2015;10(4):489–497. doi: 10.1123/ijspp.2014-0352. [DOI] [PubMed] [Google Scholar]
- 24.Beato M, Bartolini D, Ghia G, Zamparo P. Accuracy of a 10 Hz GPS unit in measuring shuttle velocity performed at different speeds and distances (5–20 M) J Hum Kinet. 2016;54(1):15–22. doi: 10.1515/hukin-2016-0031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Buchheit M, Simpson BM. Player-tracking technology: Halffull or half-empty glass? Int J Sports Physiol Perform. 2017;12(s2):S2–35. doi: 10.1123/ijspp.2016-0499. [DOI] [PubMed] [Google Scholar]
- 26.Castellano J, Alvarez-Pastor D, Bradley PS. Evaluation of research using computerised tracking systems (Amisco and Prozone) to analyse physical performance in elite soccer: A systematic review. Sports Med. 2014;44(5):701–712. doi: 10.1007/s40279-014-0144-3. [DOI] [PubMed] [Google Scholar]
- 27.Batterham AM, Hopkins WG. Making meaningful inferences about magnitudes. Int J Sports Physiol Perform. 2006;1(1):50–57. [PubMed] [Google Scholar]
- 28.Los Arcos A, Mendez-Villanueva A, Martínez-Santos R. In-season training periodization of professional soccer players. Biol Sport. 2017;34(2):149–155. doi: 10.5114/biolsport.2017.64588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Castellano J, Casamichana D. Differences in the number of accelerations between small-sided games and friendly matches in soccer. J Sports Sci Med. 2013;12(1):209–210. [PMC free article] [PubMed] [Google Scholar]
- 30.Hinijosa A, Castellano J. Influencia de la distancia recorrida en diferentes rangos de velocidad en la anotación de un gol en fútbol. Retos. 2017;31(1):188–192. [Google Scholar]
- 31.Buchheit M, Simpson BM, Hader K, Lacome M. Occurrences of near-to-maximal speed running bouts in elite soccer: insights for training prescription and injury mitigation. Sci Med. 2020 doi: 10.1080/24733938.2020.1802058. In press. [DOI] [PubMed] [Google Scholar]
- 32.Mohr M, Krustrup P, Bangsbo J. Match performance of high-standard soccer players with special reference to development of fatigue. J Sports Sci. 2003;21(7):519–528. doi: 10.1080/0264041031000071182. [DOI] [PubMed] [Google Scholar]
- 33.Ade J, Harley J, Bradley PS. The physiological response, time-motion characteristics and reproducibility of various speed endurance drills in elite youth soccer players: Small sided games vs generic running. Int J Sports Physiol Perform. 2014;9(3):471–479. doi: 10.1123/ijspp.2013-0390. [DOI] [PubMed] [Google Scholar]
- 34.Windt J, Zumbo BD, Sporer B, MacDonald K, Gabbett TJ. Why do workload spikes cause injuries, and which athletes are at higher risk? Mediators and moderators in workload–injury investigations. Br J Sports Med. 2017:993–994. doi: 10.1136/bjsports-2016-097255. [DOI] [PubMed] [Google Scholar]
- 35.Hader K, Rumpf MC, Hertzog M, Kilduff LP, Girard O, Silva JR. Monitoring the Athlete Match Response: Can External Load Variables Predict Post-match Acute and Residual Fatigue in Soccer? A Systematic Review with Meta-analysis. J Sports Med. 2019:5(1):48. doi: 10.1186/s40798-019-0219-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Malone S, Owen A, Mendes B, Hughes B, Collins K, Gabbett T. High-speed running and sprinting as an injury risk factor in soccer: Can well-developed physical qualities reduce the risk? J Sci Med Sport. 2017;21(3):257–262. doi: 10.1016/j.jsams.2017.05.016. [DOI] [PubMed] [Google Scholar]
- 37.Paul DJ, Bradley PS, Nasis G. Factor affecting running performance in elite soccer players: Shedding some light on the complexity. Int J Sports Physiol Perform. 2015;10(4):516–519. doi: 10.1123/IJSPP.2015-0029. [DOI] [PubMed] [Google Scholar]
- 38.Rey E, Lago-Ballesteros J, Padrón-Cabo A. Timing and tactical analysis of player substitutions in the UEFA Champions League. Int J Perf Anal Spor. 2015;15(3):840–850. [Google Scholar]