Abstract
Deep learning (DL) has achieved promising performance in detecting common abnormalities from the 12-lead electrocardiogram (ECG). However, diagnostic redundancy exists in the 12-lead ECG, which could impose a systematic overfitting on DL, causing poor generalization. We, therefore, hypothesized that finding an optimal lead subset of the 12-lead ECG to eliminate the redundancy would help improve the generalizability of DL-based models. In this study, we developed and evaluated a DL-based model that has a feature extraction stage, an ECG-lead subset selection stage and a decision-making stage to automatically interpret multiple common ECG abnormality types. The data analysed in this study consisted of 6877 12-lead ECG recordings from CPSC 2018 (labelled as normal rhythm or eight types of ECG abnormalities, split into training (approx. 80%), validation (approx. 10%) and test (approx. 10%) sets) and 3998 12-lead ECG recordings from PhysioNet/CinC 2020 (labelled as normal rhythm or four types of ECG abnormalities, used as external text set). The ECG-lead subset selection module was introduced within the proposed model to efficiently constrain model complexity. It detected an optimal 4-lead ECG subset consisting of leads II, aVR, V1 and V4. The proposed model using the optimal 4-lead subset significantly outperformed the model using the complete 12-lead ECG on the validation set and on the external test dataset. The results demonstrated that our proposed model successfully identified an optimal subset of 12-lead ECG; the resulting 4-lead ECG subset improves the generalizability of the DL model in ECG abnormality interpretation. This study provides an outlook on what channels are necessary to keep and which ones may be ignored when considering an automated detection system for cardiac ECG abnormalities.
This article is part of the theme issue ‘Advanced computation in cardiovascular physiology: new challenges and opportunities’.
Keywords: arrhythmias, electrocardiogram, deep learning, subset selection
1. Introduction
Over the past decades, computerized interpretation of the electrocardiogram (CIE) has been introduced to clinical settings for aiding the physician's interpretation. However, achieving physician-level accuracy in detecting cardiac arrhythmias is challenging for current CIE [1]. Conventional CIE relies on domain expert knowledge to engineer useful features based on the electrocardiogram (ECG) data, but it faces the challenge of feature quality and robustness [2]. In recent years, substantial advances in CIE have been made, driven primarily by deep learning (DL) [3]. DL is a representation-learning method, a subfield in machine learning that allows a machine to be fed raw data and automatically discover the representations, namely features needed for detection or classification [4]. DL enables an ‘end-to-end’ paradigm, which can take large amounts of the original data as input and output its decision without domain expert knowledge. With this ‘end-to-end’ approach and the widespread digitization of ECG data, DL substantially improves the accuracy of heart rhythm interpretation [3,5–7].
A major challenge in machine learning is overfitting, which happens because a model is picking up some patterns that are just caused by random chance rather than by true properties of the unknown relationship [8]. This phenomenon is most likely to happen when the amount of training data is not much larger than the number of extracted features, causing poor generalization [2,8]. In the conventional CIE, techniques like dimensionality reduction [9,10] and feature selection [11,12] have been applied to reduce the model complexity for good generalization. Deep neural networks (DNNs) have a huge number of parameters, compared with conventional machine learning models, and a much stronger ability to recognize patterns from the input data. However, DNNs have a much higher chance to encounter the overfitting problem. Computer scientists and mathematicians have made numerous efforts to restrict the solution space of DL models for better generalization, such as L1/L2 regularization [13], dropout [14] and early stopping [15].
The necessity to tackle the overfitting problem is critical for DL-based CIE, especially for interpreting the 12-lead ECG. Compared with single-lead ECG, the 12-lead ECG provides a more comprehensive evaluation of cardiac electrical activity in clinical settings [7]. However, diagnostic redundancy exists in the 12-lead ECG (particularly in the frontal leads); thus, when using the complete 12-lead ECG as input to train DL models, a systematic overfitting problem is often encountered. The systematic overfitting problem in CIE caused by the redundancy in the 12-lead ECG has been mostly ignored until recently. Van de Leur et al. [16] trained a DNN using the eight independent ECG leads for automatic ECG interpretation. Zhou et al. [17] suggested that a DL model could have better generalizability when using an optimal ECG-lead subset obtained from the 12-lead ECG but did not prove it. Therefore, DL-based CIE would likely benefit in generalizability from eliminating redundancies in the 12-lead ECG and determining what ECG leads constitute an optimal subset.
In this study, we aimed to solve the signal-level ECG classification problem for ECG abnormality detection, with a focus on addressing the issue of overfitting and generalizability of DL-based CIE. We hypothesized that finding an optimal ECG-lead subset to eliminate the diagnostic redundancy would decrease overfitting and improve the generalizability of the DL-based CIE. To test the hypothesis, a DL-based model was developed that has multiple stages for automated interpretation of eight ECG abnormality types: atrial fibrillation (AF), first-degree atrioventricular block (I-AVB), left bundle branch block (LBBB), right bundle branch block (RBBB), premature atrial contraction (PAC), premature ventricular contraction (PVC), ST-segment depression (STD) and ST-segment elevated (STE). The model incorporates a forward stepwise subset selection approach that iteratively finds single-lead ECGs that improve the classification performance most to determine an optimal ECG-lead subset for the ECG abnormality interpretation. We trained the proposed model on a dataset and evaluated it on an independent external dataset. We show that using an optimal ECG-lead subset (leads II, aVR, V1, V4) results in better generalizability of the proposed model compared with using the complete 12-lead ECG.
2. Methods
(a) . Data description and preparation
In this study, two datasets were used for model development and evaluation: the China Physiological Signal Challenge 2018 (CPSC 2018) dataset [18] and the PhysioNet/Computing in Cardiology (CinC) 2020 dataset [19,20]. Table 1 presents the details of the two datasets, including recording lengths and annotations. The CPSC 2018 dataset consists of 6877 12-lead ECG recordings from 477 subjects recorded at the sampling rate of 500 Hz. The recordings were annotated as normal rhythm or eight common abnormality types: AF, I-AVB, LBBB, RBBB, PAC, PVC, STD and STE. The PhysioNet/CinC 2020 dataset consists of 3998 12-lead ECG records sampled at 500 Hz. The ECGs were annotated as normal rhythm or four common abnormality types: AF, AVB, BBB and ST-segment changes (STC).
Table 1.
An overview of the datasets used in this study.
| data source | no. of recordings | sampling frequency (Hz) | length (s) | annotations (recordings of a label/total recordings) |
|---|---|---|---|---|
| China Physiological Signal Challenge 2018 (CPSC 2018) [18] | 6877 (female: 3178; male: 3699) | 500 Hz | 6–60 | normal (918/6877); |
| atrial fibrillation (AF) (1221/6877); | ||||
| first-degree atrioventricular block (I-AVB) (722/6877); | ||||
| left bundle branch block (LBBB) (236/6877); | ||||
| right bundle branch block (RBBB) (1857/6877); | ||||
| premature atrial contraction (PAC) (616/6877); | ||||
| premature ventricular contraction (PVC) (700/6877); | ||||
| ST-segment depression (STD) (869/6877); | ||||
| ST-segment elevated (STE) (220/6877) | ||||
| PhysioNet/CinC 2020 [19,20] | 3998 (female: 1895; male: 2103) | 500 Hz | 10 | normal (1752/3998); |
| atrial fibrillation (AF) (487/3998); | ||||
| atrioventricular block (AVB) (709/3998); | ||||
| bundle branch block (BBB) (258/3998); | ||||
| ST-segment changes (STC) (1044/3998) |
The CPSC 2018 dataset was divided into a training set (approx. 80% = 5492 recordings), a validation set (approx. 10% = 693 recordings) and a held-out test set (approx. 10% = 692 recordings). A multi-stage DL-based model was trained to detect 8 ECG abnormality types on the CPSC 2018 dataset. The PhysioNet/CinC 2020 dataset served as an external test set to evaluate the generalizability of the trained multi-stage DL-based model. Due to the difference in labels between the CPSC 2018 dataset and the PhysioNet/CinC 2020 dataset, during the external test on the PhysioNet/CinC 2020 dataset, we merged the proposed model decision of LBBB and RBBB as BBB, and also merged STD and STE as STC.
(b) . Multi-stage DL-based model development
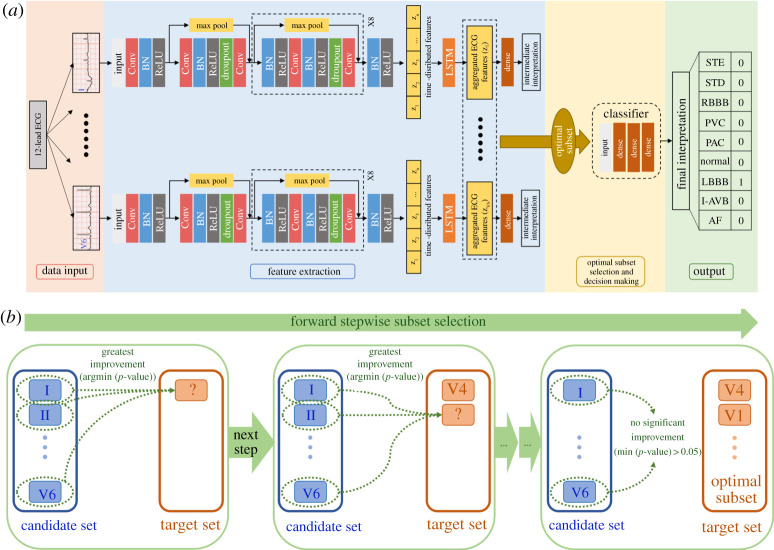
We developed a multi-stage DL-based model to automatically detect ECG abnormality types, which takes as input the raw 12-lead ECG data with variable length and outputs an abnormality interpretation for the whole signal. The proposed model, illustrated in figure 1a, consists of three modules: (i) a feature extraction module that automatically extracts features from each lead of the raw 12-lead ECG data, (ii) an optimal ECG-lead subset selection module that is used to find an optimal minimal lead subset and (iii) a decision-making module that uses features extracted from the optimal ECG-lead subset to interpret ECG abnormality types.
Figure 1.
(a) The multi-stage DL-based model for ECG abnormality classification consists of a feature extraction module, an optimal ECG-lead subset selection module and a decision-making module. The blocks with max pooling shortcuts are the residual blocks. BN, batch normalization layer; Conv, convolutional layer; ReLU, rectified linear unit activation; LSTM, long short-term memory layer; AF, atrial fibrillation; I-AVB, first-degree atrioventricular block; LBBB, left bundle branch block; RBBB, right bundle branch block; PAC, premature atrial contraction; PVC, premature ventricular contraction; STD, ST-segment depression; STE, ST-segment elevated. (b) An illustration of the forward stepwise subset selection process. In each step, the candidate single-lead ECG that introduces the greatest performance improvement, i.e. the one with the smallest p-value < 0.05, is selected to the target set. (Online version in colour.)
(i) . Feature extraction module
First, a single-lead feature extraction neural network (fFE) was developed. We next deployed 12 such single-lead neural networks of the same architecture in the feature extraction module and passed separately each of the leads of the 12-lead ECG to one of the networks. The single-lead ECG signals as inputs to the networks are represented in the form of one-dimensional time-varying potential signals XECG with a variable length of time. The architecture of the single-lead neural network consisted of a residual convolutional neural network (ResCNN) (fResCNN) [3,21] and a long short-term memory (LSTM) layer (fLSTM) [22]. In the architecture, the ResCNN detected local features of the single-lead ECG signals and compressed them into a sequence of feature vectors . The length of the sequence depends on the length of the input signal; the dimensionality of the feature vectors depends on the number of filters used in the convolutional layers. The LSTM layer directly connected to the end of ResCNN then fused the sequence of time-distributed features from the ResCNN into aggregated features, which were contained in a fixed-length vector ZECG and represented signal features of this single-lead ECG. The process is represented as
| 2.1 |
and
| 2.2 |
Lastly, there was a fully connected dense layer using the aggregated features to interpret eight ECG abnormality types. The ECG abnormality interpretations of the 12 single-lead feature extraction networks obtained in the training process, termed intermediate interpretations in this study, were not part of the final interpretations.
The details of the single-lead feature extraction network are as follows. There were nine residual blocks, and each residual block had two convolutional layers. Each convolutional layer had 32 filters with a width of 5. Within each residual block, the first and the second convolutional layers were performed with a stride of 1 and 2, respectively. The shortcut connection of each residual block had a max-pooling layer with a pool size of 2. In this manner, every residual block downsampled its inputs by a factor of 2. Following each convolutional layer, a rectified linear unit (ReLU) activation [23] and a batch normalization layer [24] were applied. The ReLU reduced the vanishing gradient problem and created sparsity, allowing for fast and effective training of DNNs. The batch normalization layer standardized the inputs and helped stabilize the parameter updating procedure. Within each residual block, a dropout layer [14] with a probability of 0.3 was applied as a regularization method to improve generalization. Finally, an LSTM layer with a size of 32 and a dense layer with an output size of 9 followed by the convolutional residual blocks were applied to interpret eight ECG abnormality types. The dense layer had a sigmoid activation, which allowed the network to detect each ECG abnormality type in a binary classification manner and learn to classify recordings with multiple labels. The hyperparameters above characterizing the network architecture are tuned with a grid search method. The major hyperparameters considered in the grid search tuning include the number of residual blocks, the number of convolutional filters, the probability of dropout and the size of LSTM layer.
(ii) . Optimal subset selection and decision-making modules
A forward stepwise subset selection method [8], as illustrated in figure 1b, was used to find an optimal ECG-lead subset of the 12-lead ECG. Briefly, we iteratively selected a stepwise optimal single-lead ECG from the 12-lead ECG until the addition of any single-lead ECG no longer improved the classification performance significantly. Specifically, we divided the 12-lead ECG into a target set and a candidate set. Initially, the target set was null, and the candidate set contained the complete 12-lead ECG. In each step, we tested the addition of each single-lead ECG from the candidate set to the target set by training a decision-making classifier with random initialization of weights 10 times independently and evaluating it on the validation set each time. We used F1 score to measure the multi-class classification performance (see Model evaluation section for details about the scoring function), thus, in each step, we had 10 estimates of the validation F1 score from the 10 independent trainings for the addition of each candidate single-lead ECG. We conduct the two-sample t-test between two groups of F1 scores using, respectively, the target set and the target set with the addition of a candidate single-lead ECG. From the two-sample t-test, a p-value measuring the statistical improvement of F1 scores were calculated for the addition of each candidate single-lead ECG. Among all the candidate single-lead ECGs, we chose the one whose inclusion gave the model the most statistically significant improvement of validation F1 score, i.e. the one with smallest p-value < 0.05. That single-lead ECG was then moved from the candidate set to the target set. When the addition of any single-lead ECG could not improve the model to a statistically significant extent for a 0.95 confidence, i.e. the p-values for all candidate single-lead ECGs were greater than 0.05, we took the selected target set to be the optimal ECG-lead subset of 12-lead ECG. After finding an optimal ECG-lead subset, we continued the process above until all the 12-lead ECGs were added into the target set to see what change would be brought to the model by additional single-lead ECGs.
| Algorithm 1. Forward stepwise subset selection. |
| Variables: |
| —Candidate set |
| —Target set |
| —Single-lead ECG |
| —F1 scores for the addition of single-lead ECG |
| —The best F1 scores in step i |
| —The p-value measuring the improvement for the addition of single-lead ECG |
| —The best single-lead ECG in step i |
| Pseudo code: |
| Initialize |
| , , |
| For i in 1:12 |
| For in |
| Calculate by training a model using for 10 times |
| Calculate by conducting t-tests between and |
| If min < 0.05 |
| Xbest,i = argmin(PECG) |
| Remove from , Add to |
| Else |
| Break |
| Output as the optimal subset |
A feed-forward neural network (FNN) was used as the decision-making classifier, which interpret ECG abnormality types from extracted ECG features. The FNN consists of an input layer with variable size based on the number of ECG leads incorporated, a hidden layer with a size of 64, a following hidden layer with a size of 32, and an output layer with a size of 9 and a sigmoid activation. The hyperparameters for this FNN, including the number of hidden layers and the size of each hidden layer, are selected using grid search tuning to maximize the classifier's performance. The FNN took concatenated features from selected ECG leads and outputted an interpretation of ECG abnormality types as probabilities. We set a probability threshold of 0.5 and accepted the ECG abnormality types with probabilities higher than the threshold to turn the probability outputs into one-hot encoded labels, with each digit corresponding to one ECG abnormality type in a binary format.
(c) . Training strategies
The 12 single-lead feature extraction neural networks and the FNN classifier were trained with Xavier initialization of the weights [25] and Adam optimizer with the default parameters (β1 = 0.9 and β2 = 0.999) [26]. The training of models in this study suffers from class imbalance problems as revealed in table 1. For each class of abnormalities, the negatively labelled recordings greatly outnumbered the positively labelled recordings. The weighted binary cross entropy (WCE) as a loss function was used to tackle the problem of class imbalance.
| 2.3 |
where nc is the number of signals labels as ECG abnormality class c; is the true label of the ith signal in class c; is the signal's predicted probability for the ECG abnormality class; is the class weight used to balance the contribution from each ECG abnormality class to WCE.
During training, an adaptive learning rate was applied by tracking the validation loss. The adaptive learning rate was initialized as 0.001 and decayed by a factor of 10 when the validation loss did not improve for three consecutive epochs. A maximum epoch limit is set to 100 and an early stopping strategy [15] with a patience of 10 epochs was used to prevent overfitting. Most training experiments stopped within 50 epochs by the early stopping strategy and the maximum epoch limit was never reached. All experiments were conducted on a workstation with AMD Ryzen 7 2700X 8-Core CPU @ 4.00 GHz, 64 GB RAM and NVIDIA GeForce RTX 2060 GPU.
(d) . Model evaluation
In the study, the held-out internal test set (approx. 10% of CPSC 2018) and the external PhysioNet/CinC 2020 dataset were used to evaluate the classification performance of the multi-stage DL-based model trained from the CPSC 2018 dataset (approx. 80%). The F1 score and AUC (area under the receiver operating characteristic (ROC) curve/sensitivity versus 1 − specificity curve) were adopted for evaluating the classification performance. The F1 score and ROC curves were calculated from true positive (TP), true negative (TN), false positive (FP) and false negative (FN).
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
We calculated class-specific F1 scores and AUC for each ECG abnormality type with a one-versus-rest strategy [27,28], i.e. considering each class of ECG abnormality as a binary classification problem, which measured the ability of detecting each specific abnormality from the whole population. We also calculated overall F1 scores in the multi-class classification problem, measuring the ability in correctly detecting all ECG abnormality types. For the recordings with multiple labels, their contributions to the overall F1 scoring function were normalized to ensure an equal contribution from each recording. For example, if a recording has six labels, and our model identifies three labels correctly, identifies one label incorrectly and misses two labels, then we increase the TP by 3/6, FP by 1/6, FN by 2/6 for the F1 scoring functions, respectively. Statistical comparisons of the multi-stage DL-based model performance metrics using either the optimal ECG-lead subset or the complete 12 lead includes firstly testing the normality of the data using the Shapiro–Wilk test, and then testing the difference through the independent two-sample t-test if the data is normally distributed or through the nonparametric Mann–Whitney U-test if the data is not normally distributed.
3. Results
(a) . Optimal ECG-lead subset selection
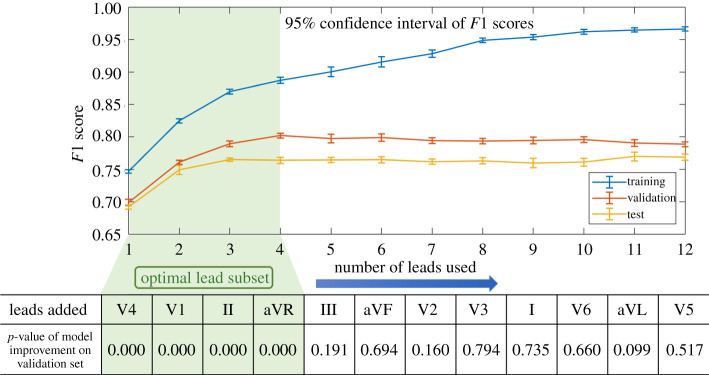
Figure 2 illustrates the forward stepwise subset selection process that (i) the F1 score increases on the training set with the addition of single-lead ECGs, and (ii) the F1 score increases on the validation set at first but remains within stable ranges on the validation set (F1 = 0.789–0.799) and the held-out test set (F1 = 0.760–0.770) after ECGs from four leads are added. Statistical results yield that the four single-lead ECGs (leads II, aVR, V1, V4) improved the validation F1 scores significantly (p < 0.05), and the addition of another single-lead ECG did not improve the model significantly afterwards. This result suggested that the proposed model was picking up patterns that were not generalizable after the model complexity exceeds a particular interval (marked by green in figure 2). In other words, although the extra complexity (e.g. adding additional single-lead ECGs) enabled the proposed model to build more complicated relationships on the training set, it could not generalize well to the validation set and the test set.
Figure 2.
Optimal ECG-lead subset selection by the forward stepwise subset selection method. The table at the bottom shows the single-lead ECGs selected in every step and the p-values quantifying the improvements they caused. Significant improvement is defined as p-value < 0.05. (Online version in colour.)
(b) . Performance evaluation
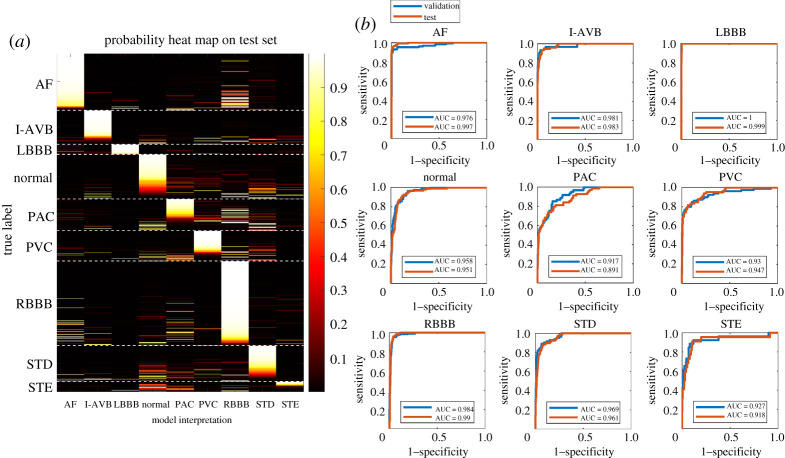
We evaluated the classification performance of the multi-stage DL-based model on the held-out test set using the optimal ECG-lead (II, aVR, V1, V4) subset. In figure 3a, a heat map shows the interpretation output in probabilities of the ECG abnormality types for 692 recordings on the held-out test set. The heatmap illustrates that the multi-stage DL-based model correctly detected AF, I-AVB, LBBB and RBBB with high probabilities. The ROC curves plotted in figure 3b highlight that the detection of AF, LBBB and RBBB had AUC greater than 0.99 on the held-out test set, reflecting an excellent classification. The probability outputs in the heatmap (figure 3a) also illustrated that the proposed model was able to identify concurrent abnormalities in agreement with the statistics of the multi-labelled recordings in the CPSC 2018 dataset. Particularly, many AF recordings and PAC recordings were detected to have high probabilities for RBBB, which agrees with the statistical findings that AF/RBBB (172 recordings out of 476 multi-label recordings) and PAC/RBBB (55 recordings) are the first and second most common concurrent pairs in the dataset, respectively.
Figure 3.
Evaluation of our model using the optimal ECG-lead subset (II, aVR, V1, V4) in the classification of the ECG abnormality types. (a) A heat map illustrates the interpretation output in probabilities of the ECG abnormality types on the held-out test set using the optimal ECG-lead subset. From a vertical view, the distribution of the bright bars in a column reflects the performance of detecting a specific ECG abnormality from population. For instance, in the column of LBBB, the bright bars aligned well with the true LBBB patients, reflecting an excellent performance in LBBB detection. From a horizontal view, whether bright bars concentrate in the correct column reflects the performance of classifying a recording to its true abnormality class out of nine labels. For instance, in the rows of AF patients, the bright bars concentrated in the AF column correctly, but there are several bright bars in the RBBB column, which could be due to multi-labelled recordings or misclassification. (b) ROC curves show the classification performance of our model for interpreting each of the ECG abnormality types on the validation and held-out test sets. (Online version in colour.)
Table 2 reports comparisons of the ECG abnormality classification performance of the proposed model using the optimal 4-lead subset and the complete 12-lead ECG. All the data groups are tested to be normally distributed in the Shapiro–Wilk test. On the CPSC 2018 dataset, using the optimal 4-lead subset was significantly better than using the complete 12-lead ECG for classifying the eight common ECG abnormality types on the validation set (F1 score = 0.802 versus F1 score = 0.789, p-value = 0.000); there was no statistical difference in performance on the held-out test set. On the external test dataset, the model with the optimal 4-lead subset significantly outperformed the model using the complete 12-lead ECG (F1 score = 0.547 versus F1 score = 0.537, p-value = 0.000) for detecting four ECG abnormality types. The results suggest that the multi-stage DL-based model with a 4-lead (II, aVR, V1, V4) subset selection had better generalizability on the validation set and on the external test set.
Table 2.
A comparison of our model's overall F1 scores between using the optimal ECG-lead subset and using the complete 12-lead ECG on different datasets. p-values were calculated using the independent two-sample t-test between the overall F1 scores using the optimal 4-lead ECG and using the complete 12-lead ECG. A p-value < 0.05 means the optimal 4-lead ECG system provides a significant improvement in classifying ECG abnormalities over the complete 12-lead ECG.
| datasets | F1 scores using the optimal 4-lead ECG | F1 scores using the complete 12-lead ECG | p-value | |
|---|---|---|---|---|
| CPSC 2018 (8 ECG abnormality types) | validation | 0.802 ± 0.004 | 0.789 ± 0.004 | 0.000 |
| held-out test | 0.764 ± 0.005 | 0.769 ± 0.005 | 0.123 | |
| PhysioNet/CinC 2020 (4 ECG abnormality types) | external test | 0.547 ± 0.001 | 0.537 ± 0.001 | 0.000 |
4. Discussion
In this study, we developed a novel multi-stage DL-based model for automatic ECG abnormality classification. An optimal ECG-lead subset selection module was introduced to regularize the proposed model for improving generalizability. The results show that using the optimal ECG-lead subset outperforms significantly the use of the complete 12-lead ECG on the external test set, which supports our hypothesis that eliminating the redundancy can decrease overfitting and improve generalizability. To our knowledge, this is the first study to integrate a forward stepwise subset selection method with a DL-based model for ECG abnormality classification. Most studies previously attempted to overcome overfittings using general computational and mathematical techniques that were not task-specific. In addition to the common techniques used to overcome overfitting, the optimal ECG-lead subset selection algorithm we developed is specifically tailored to the 12-lead ECG and improves the generalizability of the DL-based CIE using a new approach. This study provides an outlook on what leads are necessary to keep and which ones may be ignored when considering an automated detection system for the cardiac ECG abnormalities at hand.
In the feature extraction module of the proposed model, we deployed a novel DNN that integrated a ResCNN with an LSTM, a type of recurrent neural network (RNN), to automatically extract high-quality features from arbitrary-length ECG signals. Although CNNs and RNNs have been separately applied in CIE in previous studies [3,6,29], there were limitations. CNNs require fixed-length input data when dealing with varied-length ECG signals, which could cause information loss or noise added. RNNs are capable of processing ECG signals with an arbitrary length, but they are considered to be less powerful than CNNs across a wide range of tasks [30]. Therefore, our DNN, as a combination of a CNN and an RNN, has the complementary advantages of these two networks, achieving efficient feature extraction.
The optimal 4-lead subset obtained by this data-driven approach provides valuable insights for CIE when considering an automatic system for ECG abnormality detection. As a 4-lead subset, it consisted of two limb leads, II and aVR, which contained all information needed to derive the other four limb leads, and two unipolar precordial leads V1 and V4, providing assessments in the horizontal plane from the vantage points of the septal surface and the anterior ventricular wall, respectively. The quasi-orthogonal four leads (leads II, aVR, V1 and V4) play a particularly important role in the ECG abnormality classification. Lead II, which is favoured among the 12 leads by physicians for a quick impression of an ECG recording due to its clearest signal [31], had decent overall performance here in classifying the eight ECG abnormality types. Lead V1 used in the clinic to detect RBBB by recognizing the distinct ‘m-shaped’ ‘RSR’ complex marker [32] exhibited supreme performance in classifying RBBB here. Although lead aVR is historically ignored in clinical practice, it is a valuable lead to diagnose acute coronary syndromes and narrow complex tachycardia [33,34]. As a comparison, lead I, which is used in the Apple Watch [35] and KardiaMobile [36] for AF detection, achieved ordinary performance in our study. Furthermore, our results indicated that the lead aVR performed ECG abnormality classifications with appreciable accuracy and thus deserves a further study.
The presented optimal subset selection module could be further improved. Currently, it selected a general ECG-lead subset optimized from a training set to classify all the ECG abnormality types. However, the clinical diagnostic criteria of cardiac arrhythmia types are often lead-specific, so a future research direction would be to select class-specific ECG-lead subsets rather than one general ECG-lead subset, which could improve the classification performance and provide more valuable insights. In addition, the resulting optimal 4-lead subset depends on the eight types of ECG abnormalities on our training dataset (AF, I-AVB, LBBB, RBBB, PAC, PVC, STD and STE). The optimal ECG-lead subset may change when considering new ECG abnormalities types or on new datasets. Finally, compared with an exhaustive search of all possible ECG-lead combinations, the presented forward stepwise subset selection algorithm provides a more efficient way to selectively search the solution space, but the result may not be global optimal.
There are several limitations to the study. Firstly, there are major difficulties in comparing our results with other studies in ECG interpretation. The values of performance metrics we reported cannot be compared directly due to the difference between the datasets or the different strategies of the metric calculation. Chen et al. [37] won the CPSC 2018 competition on 12-lead ECG interpretation with an overall F1 score of 0.837. Their classification of AF also ranked first in AF detection with an F1 score of 0.933. Although we used the same CPSC 2018 dataset, the results they reported were based on a hidden test set that was unavailable to us. Secondly, we split the CPSC 2018 dataset by signals but not by individual patients due to difficulties in tracking the patient of each ECG signal. In addition, the proposed multi-stage DL-based model had a relatively poor performance in detecting STE. The poor performance in detecting STE may be in part due to disagreements among physicians in interpreting STE [38] or the scarcity of data (STE had the least number of recordings in this dataset). Finally, the data analysed in this study had varying signal quality and were labelled by different physicians with various criteria, which may influence the performance of our model.
5. Conclusion
This study addressed the issue of overfitting and generalizability of DL-based CIE. To improve the generalizability, an ECG-lead subset selection module within a novel multi-stage DL-based model eliminated the redundancies of the 12-lead ECG. The subset selection module determined an optimal 4-lead subset (leads II, aVR, V1, V4), from which the model classifies ECG abnormality types significantly better than the classification from the complete 12-lead ECG. The results demonstrated the efficacy of the proposed subset selection approach and the feasibility of representing a complete 12-lead ECG by the optimal 4-lead subset to improve DL models' generalizability in the ECG abnormality classification.
Acknowledgements
The authors thank Binxin Liu from Cornell University for providing valuable discussions about the algorithm development.
Data accessibility
The China Physiological Signal Challenge 2018 dataset is publicly available from http://2018.icbeb.org/ (https://doi.org/10.1166/jmihi.2018.2442). The PhysioNet/CinC 2020 dataset is publicly available from https://storage.cloud.google.com/physionet-challenge-2020-12-lead-ecg-public/PhysioNetChallenge2020_Training_E.tar.gz (https://doi.org/10.13026/f4ab-0814). The algorithm was developed based on the open source toolkits Keras (https://keras.io/) and scikit-learn (https://scikit-learn.org/). The project is open source, and code for the algorithm development and evaluation and a demo model with weights are available from https://github.com/c-lai/DL_ECG_classification.
Authors' contributions
All the co-authors of this manuscript have contributed to the conception and design of the study, and the analysis and interpretation of the data and results. The first author drafted the manuscript and all the co-authors contributed to the critical revision of the manuscript and its final approval.
Competing interests
We declare we have no competing interests.
Funding
This work was supported by NIH (grant nos. R01HL142496 and R01HL126802) to N.T., Leducq 16CVD02 to N.T.
References
- 1.Schläpfer J, Wellens HJ. 2017. Computer-interpreted electrocardiograms: benefits and limitations. J. Am. Coll. Cardiol. 70, 1183-1192. ( 10.1016/j.jacc.2017.07.723) [DOI] [PubMed] [Google Scholar]
- 2.Lyon A, Mincholé A, Martínez JP, Laguna P, Rodriguez B. 2018. Computational techniques for ECG analysis and interpretation in light of their contribution to medical advances. J. R. Soc. Interface 15, 20170821. ( 10.1098/rsif.2017.0821) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hannun AY, Rajpurkar P, Haghpanahi M, Tison GH, Bourn C, Turakhia MP, Ng AY. 2019. Cardiologist-level arrhythmia detection and classification in ambulatory electrocardiograms using a deep neural network. Nat. Med. 25, 65-69. ( 10.1038/s41591-018-0268-3) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lecun Y, Bengio Y, Hinton G. 2015. Deep learning. Nature 521, 436-444. ( 10.1038/nature14539) [DOI] [PubMed] [Google Scholar]
- 5.Acharya UR, Fujita H, Lih OS, Hagiwara Y, Tan JH, Adam M. 2017. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 405, 81-90. ( 10.1016/j.ins.2017.04.012) [DOI] [Google Scholar]
- 6.Chang K-C, Hsieh P-H, Wu M-Y, Wang Y-C, Chen J-Y, Tsai F-J, Shih ESC, Hwang M-J, Huang T-C. 2020. Usefulness of machine-learning-based detection and classification of cardiac arrhythmias with 12-lead electrocardiograms. Can. J. Cardiol. 37, 94-104. ( 10.1016/j.cjca.2020.02.096) [DOI] [PubMed] [Google Scholar]
- 7.Ribeiro AH, et al. 2020. Automatic diagnosis of the 12-lead ECG using a deep neural network. Nat. Commun. 11, 1760. ( 10.1038/s41467-020-15432-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.James G, Witten D, Hastie T, Tibshirani R. 2013. An introduction to statistical learning. Berlin, Germany: Springer. [Google Scholar]
- 9.Nasiri JA, Naghibzadeh M, Yazdi HS, Naghibzadeh B. 2009. ECG arrhythmia classification with support vector machines and genetic algorithm. In 2009 Third UKSim European Symposium on Computer Modeling and Simulation, Athens, Greece, 25–27 November 2009, pp. 187–192. New York, NY: IEEE. ( 10.1109/ems.2009.39) [DOI]
- 10.de Chazal P, O'Dwyer M, Reilly RB. 2004. Automatic classification of heartbeats using ECG morphology and heartbeat interval features. IEEE Trans. Biomed. Eng. 51, 1196-1206. ( 10.1109/TBME.2004.827359) [DOI] [PubMed] [Google Scholar]
- 11.Melgani F, Bazi Y. 2008. Classification of electrocardiogram signals with support vector machines and particle swarm optimization. IEEE Trans. Inf. Technol. Biomed. 12, 667-677. ( 10.1109/titb.2008.923147) [DOI] [PubMed] [Google Scholar]
- 12.Mar T, Zaunseder S, Martinez JP, Llamedo M, Poll R. 2011. Optimization of ECG classification by means of feature selection. IEEE Trans. Biomed. Eng. 58, 2168-2177. ( 10.1109/tbme.2011.2113395) [DOI] [PubMed] [Google Scholar]
- 13.Ng AY. 2004. Feature selection, L 1 vs. L 2 regularization, and rotational invariance. In Proceedings of the twenty-first international conference on Machine learning, Banff, Canada, 4–8 July 2004, p. 78. New York, NY: ACM. ( 10.1145/1015330.1015435) [DOI]
- 14.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. 2014. Dropout: a simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 15, 1929-1958. [Google Scholar]
- 15.Prechelt L. 2012. Early stopping — but when? In Lecture notes in computer science (eds G Montavon, GB Orr, K-R Muüller), pp. 53-67. Berlin, Germany: Springer. [Google Scholar]
- 16.van de Leur RR, Lennart JB, Efstratios G, Irene EH, Jeroen FVDH, Nick CC, Pieter AD, Rutger JH, René VE. 2020. Automatic triage of 12-lead ECGs using deep convolutional neural networks. J. Am. Heart Assoc. 9, e015138. ( 10.1161/JAHA.119.015138) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhou S, Sapp JL, Wahab AA, Trayanova N. 2020. Deep-learning applied to electrocardiogram interpretation. Can. J. Cardiol. 37, 17-18. ( 10.1016/j.cjca.2020.03.035) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Liu F, et al. 2018. An open access database for evaluating the algorithms of electrocardiogram rhythm and morphology abnormality detection. J. Med. Imaging Health Inform. 8, 1368-1373. ( 10.1166/jmihi.2018.2442) [DOI] [Google Scholar]
- 19.Alday EAP, et al. 2020. Classification of 12-lead ECGs: the PhysioNet/computing in cardiology challenge 2020. PhysioNet. 41, 124003. ( 10.13026/f4ab-0814) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ary LG, Amaral LA, Glass L, Hausdorff JM, Ivanov PC, Mark RG, Mietus JE, Moody GB, Peng CK, Stanley HE. et al. 2000. PhysioBank, PhysioToolkit, and PhysioNet. Circulation 101, e215-e220. ( 10.1161/01.CIR.101.23.e215) [DOI] [PubMed] [Google Scholar]
- 21.He K, Zhang X, Ren S, Sun J.. 2016. Identity Mappings in Deep Residual Networks. ArXiv160305027 Cs.
- 22.Hochreiter S, Schmidhuber J. 1997. Long short-term memory. Neural Comput. 9, 1735-1780. ( 10.1162/neco.1997.9.8.1735) [DOI] [PubMed] [Google Scholar]
- 23.Nair V, Hinton GE.. 2010. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on International Conference on Machine Learning, Haifa, Israel, 21–14 June 2010, pp. 807–814. Madison, WI: Omnipress.
- 24.Ioffe S, Szegedy C. 2015. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. ArXiv150203167 Cs.
- 25.Glorot X, Bengio Y. 2010. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, Sardinia, Italy, 13–15 May 2010, pp. 249–256. JMLR Workshop and Conference Proceedings.
- 26.Kingma DP, Ba J. 2014. Adam: A method for stochastic optimization. ArXiv Prepr. ArXiv14126980.
- 27.Hand DJ, Till RJ. 2001. A simple generalisation of the area under the ROC curve for multiple class classification problems. Mach. Learn. 45, 171-186. ( 10.1023/A:1010920819831) [DOI] [Google Scholar]
- 28.Fawcett T. 2006. An introduction to ROC analysis. Pattern Recognit. Lett. 27, 861-874. ( 10.1016/j.patrec.2005.10.010) [DOI] [Google Scholar]
- 29.Raghunath S, et al. 2020. Prediction of mortality from 12-lead electrocardiogram voltage data using a deep neural network. Nat. Med. 26, 886-891. ( 10.1038/s41591-020-0870-z) [DOI] [PubMed] [Google Scholar]
- 30.Bai S, Kolter JZ, Koltun V.. 2018. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. ArXiv180301271 Cs.
- 31.Beebe R, Myers J. 2012. Professional paramedic, volume I: foundations of paramedic care. Clifton Park, NY: Delmar Cengage Learning. [Google Scholar]
- 32.Surawicz B, Knilans T. 2008. Chou's electrocardiography in clinical practice: adult and pediatric, 6th edn. Philadelphia, PA: Saunders. [Google Scholar]
- 33.Gorgels APM, Engelen DJM, Wellens HJJ. 2001. Lead aVR, a mostly ignored but very valuable lead in clinical electrocardiography**Editorials published in the Journal of the American College of Cardiologyreflect the views of the authors and do not necessarily represent the views of JACCor the American. J. Am. Coll. Cardiol. 38, 1355-1356. ( 10.1016/s0735-1097(01)01564-9) [DOI] [PubMed] [Google Scholar]
- 34.Williamson K, Mattu A, Plautz CU, Binder A, Brady WJ. 2006. Electrocardiographic applications of lead aVR. Am. J. Emerg. Med. 24, 864-874. ( 10.1016/j.ajem.2006.05.013) [DOI] [PubMed] [Google Scholar]
- 35.Perez MV, et al. 2019. Large-scale assessment of a smartwatch to identify atrial fibrillation. N. Engl. J. Med. 381, 1909-1917. ( 10.1056/NEJMoa1901183) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Goldenthal IL, et al. 2019. Recurrent atrial fibrillation/flutter detection after ablation or cardioversion using the AliveCor KardiaMobile device: iHEART results. J. Cardiovasc. Electrophysiol. 30, 2220-2228. ( 10.1111/jce.14160) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chen T-M, Huang C-H, Shih ESC, Hu Y-F, Hwang M-J. 2020. Detection and classification of cardiac arrhythmias by a challenge-best deep learning neural network model. iScience 23, 100886. ( 10.1016/j.isci.2020.100886) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.McCabe JM, et al. 2013. Physician accuracy in interpreting potential ST-segment elevation myocardial infarction electrocardiograms. J. Am. Heart Assoc. 2, e000268. ( 10.1161/JAHA.113.000268) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The China Physiological Signal Challenge 2018 dataset is publicly available from http://2018.icbeb.org/ (https://doi.org/10.1166/jmihi.2018.2442). The PhysioNet/CinC 2020 dataset is publicly available from https://storage.cloud.google.com/physionet-challenge-2020-12-lead-ecg-public/PhysioNetChallenge2020_Training_E.tar.gz (https://doi.org/10.13026/f4ab-0814). The algorithm was developed based on the open source toolkits Keras (https://keras.io/) and scikit-learn (https://scikit-learn.org/). The project is open source, and code for the algorithm development and evaluation and a demo model with weights are available from https://github.com/c-lai/DL_ECG_classification.