Rapid Fluorescence Lifetime Imaging Reveals That TRPV4 Channels Promote Dysregulation of Neuronal Na⁺ in Ischemia

Abstract

Fluorescence imaging is an indispensable method for analysis of diverse cellular and molecular processes, enabling, for example, detection of ions, second messengers, or metabolites. Intensity-based approaches, however, are prone to artifacts introduced by changes in fluorophore concentrations. This drawback can be overcome by fluorescence lifetime imaging (FLIM) based on time-correlated single-photon counting. FLIM often necessitates long photon collection times, resulting in strong temporal binning of dynamic processes. Recently, rapidFLIM was introduced, exploiting ultra-low dead-time photodetectors together with rapid electronics. Here, we demonstrate the applicability of rapidFLIM, combined with new and improved correction schemes, for spatiotemporal fluorescence lifetime imaging of low-emission fluorophores in a biological system. Using tissue slices of hippocampi of mice of either sex, loaded with the Na⁺ indicator ING2, we show that improved rapidFLIM enables quantitative, dynamic imaging of neuronal Na⁺ signals at a full-frame temporal resolution of 0.5 Hz. Induction of transient chemical ischemia resulted in unexpectedly large Na⁺ influx, accompanied by considerable cell swelling. Both Na⁺ loading and cell swelling were dampened on inhibition of TRPV4 channels. Together, rapidFLIM enabled the spatiotemporal visualization and quantification of neuronal Na⁺ transients at unprecedented speed and independent from changes in cell volume. Moreover, our experiments identified TRPV4 channels as hitherto unappreciated contributors to neuronal Na⁺ loading on metabolic failure, suggesting this pathway as a possible target to ameliorate excitotoxic damage. Finally, rapidFLIM will allow faster and more sensitive detection of a wide range of dynamic signals with other FLIM probes, most notably those with intrinsic low-photon emission.

SIGNIFICANCE STATEMENT FLIM is an indispensable method for analysis of cellular processes. FLIM often necessitates long photon collection periods, requiring the sacrifice of temporal resolution at the expense of spatial information. Here, we demonstrate the applicability of the recently introduced rapidFLIM for quantitative, dynamic imaging with low-emission fluorophores in brain slices. RapidFLIM, combined with improved correction schemes, enabled intensity-independent recording of neuronal Na⁺ transients at unprecedented full-frame rates of 0.5 Hz. It also allowed quantitative imaging independent from changes in cell volume, revealing a surprisingly strong and hitherto uncovered contribution of TRPV4 channels to Na⁺ loading on energy failure. Collectively, our study thus provides a novel, unexpected insight into the mechanisms that are responsible for Na⁺ changes on energy depletion.

Introduction

Fluorescence microscopy is an essential tool for biology. Because of the recent surge in the development of highly selective probes, it has become one of the most widely used approaches for studying cellular properties and signaling in living cells and tissues (Lichtman and Denk, 2011; Rodriguez et al., 2017). Notwithstanding its superior sensitivity and versatility, fluorescence imaging has always been hampered by the fact that only a small percentage of emitted photons is actually detected, necessitating stronger excitation intensities, which may lead to photobleaching and photodamage (Yang and Yuste, 2017). Moreover, analysis is often based on quantification of overall emission intensities, which is prone to artifacts resulting from uncontrollable changes in focal plane and/or fluorophore concentrations, requiring correction, for example, by pseudoratiometric imaging (Gerkau et al., 2018). Introduction of fluorescence lifetime imaging microscopy (FLIM) has circumvented this pitfall because it is essentially independent of the concentration of the fluorophore (Becker, 2015). FLIM, based on time-correlated single-photon counting (TCSPC; Lakowicz, 2006), has thereby enabled quantitative analysis of ion concentrations and second messenger signaling in the cellular cytosol (Wilms et al., 2006; Yellen and Mongeon, 2015; Zheng et al., 2015; Laviv et al., 2016; Chang et al., 2019; King et al., 2020; Laviv et al., 2020) or in subcellular compartments (Zhang et al., 2020).

Classic TCSPC-based FLIM often requires long collection times (many tens of seconds to >1 min) to generate a distribution plot of photon arrival times enabling the fitting of its decay (Zhang et al., 2020). This is especially critical for fluorophores with low quantum yields such as the available chemical indicators for intracellular Na⁺ and Cl^-. Former FLIM-based studies using these dyes thus suffer from low temporal resolution or only show static images (Roder and Hille, 2014; Rungta et al., 2015; Untiet et al., 2017; Meyer et al., 2019). Long collection times are partly caused by the so-called dead-time artifacts, which strongly reduce the amount of usable photons (Becker, 2015). Dead-time artifacts describe the detection of apparently shorter lifetimes when the photon count rate surpasses a certain threshold (usually 1–5% of the laser repetition rate).

To overcome this limitation, rapidFLIM was introduced, reducing the dead time from ∼100 ns to ∼0.7 ns (Patting et al., 2018; Wahl et al., 2020). Dead-time artifacts are therefore virtually nonexistent, resulting in much higher possible photon count rates and enabling higher imaging frequencies. The latter is particularly important for revealing the often short-lived and spatially constrained transient changes that are of interest in a typical biological experiment. Events occurring in the second or subsecond range, such as intracellular ion signals in neurons or glial cells, for example, are of critical relevance in the development, communication, and cellular plasticity of the CNS (Volterra et al., 2014; Padamsey et al., 2019; Verkhratsky et al., 2020).

Here, to the best of our knowledge, we demonstrate for the first time the applicability of rapidFLIM for dynamic quantitative measurement of changes in the fluorescence lifetime of a dim fluorophore in a biological system. We show that rapidFLIM is well suited for dynamic imaging of intracellular Na⁺ concentrations, [Na⁺]_i, using the chemical indicator dye ION-NaTRIUM-Green-2 (ING2). We also present an improved correction for electrical pulse pile-up resulting in lifetimes that are stable over the complete measurement even at high count rates. Our work furthermore reveals that rapidFLIM enables the detection of transient changes in [Na⁺]_i of mouse neurons in situ at hitherto unsurpassed frame rates. Taking advantage of this new implementation and corrections of rapidFLIM, we show that even brief metabolic inhibition results in an unexpectedly large increase in neuronal [Na⁺]_i, accompanied by substantial cellular swelling. Moreover, our work identifies TRPV4 channels as a new pathway involved in cellular breakdown of Na⁺ homeostasis.

Materials and Methods

Ethical approval

The present study was conducted in strict accordance with the institutional guidelines of the Heinrich Heine University Düsseldorf as well as the European Community Council Directive (2010/63/EU). All experiments using brain slices were communicated to and approved by the Animal Welfare Office at the Animal Care and Use Facility of the Heinrich Heine University Düsseldorf (Institutional Act No. O52/05). In accordance with the recommendations of the European Commission (Close et al., 1997), animals up to 10 d old were killed by decapitation, whereas older mice were anesthetized with CO₂ and then quickly decapitated.

rapidFLIM based on time-correlated single-photon counting

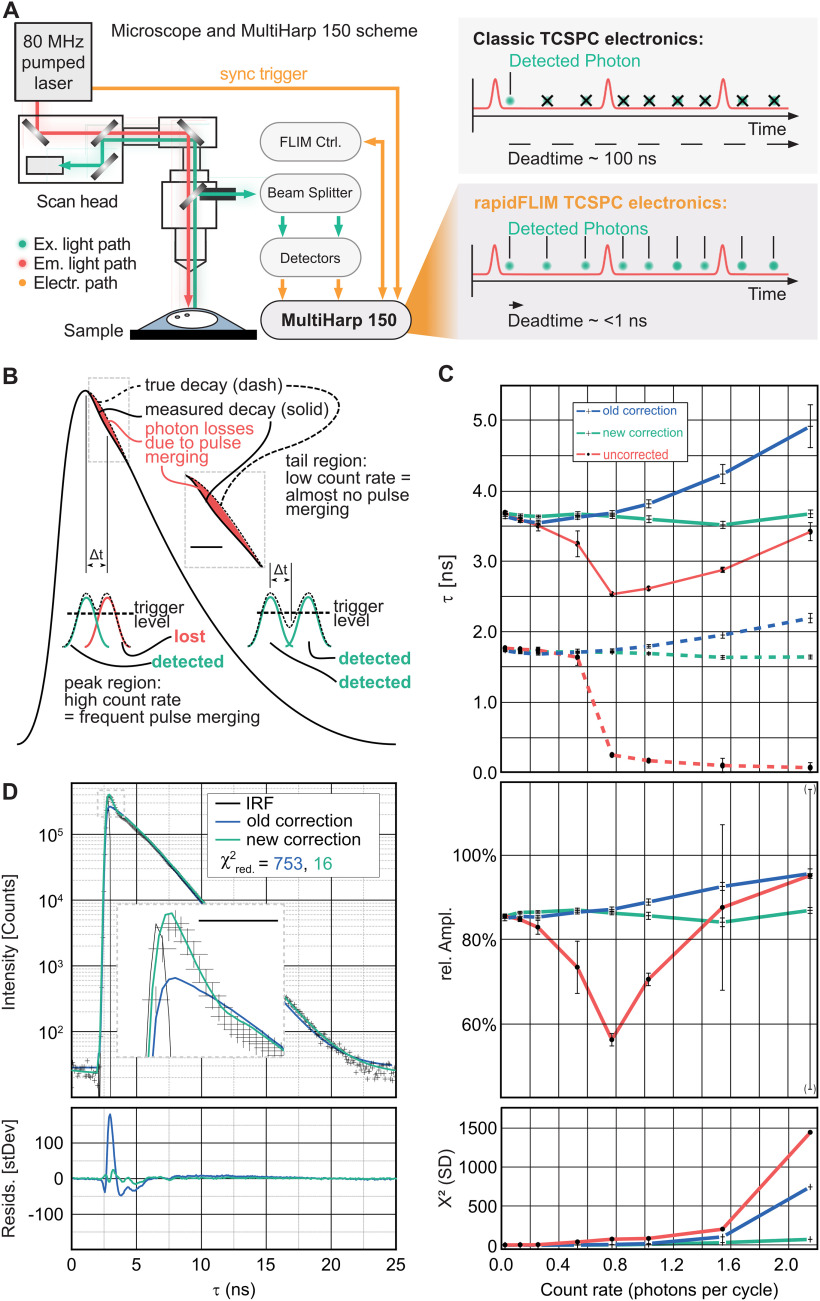
Classic TCSPC electronics as well as most single photon counting detectors have dead times in the order of several tens of nanoseconds (Fig. 1A; Becker, 2015). Measurements at count rates of more than ∼5% of the excitation exhibit biased photon loss (a count rate exceeding 10 mega counts per second was typical for this study.). The emergence of hybrid photodetectors and superconducting nanowire single-photon detectors brought about improved time resolution and short dead times below 10 ps (Michalet et al., 2008; Zadeh et al., 2018). To fully use the benefits of these detectors, new rapid TCSPC electronics with the shortest possible dead time were developed (Wahl et al., 2020). Based on the latter, the MultiHarp 150 (PicoQuant) has a timing resolution of 80 ps and features a dead time of only 650 ps. In combination with PMA Hybrid 40mod detectors (PicoQuant) that feature an electrical pulse width of 500 ps, dead-time effects are nonexistent in good approximation. This approach, permitting higher photon counts, was introduced as rapidFLIM (Fig. 1A; Patting et al., 2018; Wahl et al., 2020).

Figure 1.

Measurement principle and electrical pulse pile-up corrections. A, Experimental setup and schematic of photon losses in the recorded stream of photon events of classical TCSPC electronics compared with rapidFLIM TCSPC electronics and the MultiHarp 150. B, Biased photon losses because of pulse merging. A duty cycle of 40 MHz, resulting in an interpulse duration of 25 nanoseconds (ns). Inset, A 2× temporal magnification of the area where the photon losses occur. Scale bar, 2 ns. C, Mixture of Atto655 and AttoRh14, measured at 20 MHz excitation rate and fitted biexponentially at different count rates for the uncorrected model, the former correction, and the new correction. Top, Fast (solid line) and slow (dashed line) component of the measured lifetime. Middle, Relative amplitude fast component of the measured lifetime, Bottom, Weighted residuals trace. Error bars indicate statistical fitting errors corresponding to 1 SD of the fitting parameters as calculated by a bootstrap error analysis, whereas the central point indicates the best fit parameter set. D, Decay fit for Atto655, excitation and count rate 40 MHz; former correction (blue) versus new correction (green) and uncorrected (red). Crosses are the measured data points. Inset, A 6× temporal magnification. Scale bar, 1 ns.

However, at high count rates (exceeding ∼5% of the excitation rate), photon emissions at intervals shorter than the electrical pulse width will result in their overlap and thus merged detector pulses (Fig. 1B), a phenomenon called electrical pulse pile-up. As the TCSPC electronics cannot distinguish the original pulses, the two events are counted as one. To compensate for these effects, the following correction scheme was developed (Patting et al., 2018). At a known excitation rate f_exc and a known pulse count N, each discrete time t_i (a time channel in a TCSPC decay curve) can be associated with a differential or instantaneous count rate. Using this differential count rate, one can approximate the photon losses in each channel, given that the true decay curve is known. As all physically meaningful parameters that describe the decay behavior are extracted via a nonlinear fit, the corresponding model decay Dec_Mod(t) can be used as an approximation to this unknown true decay curve. Once the fit matches the measured data, this approximation is justified. As the corrections are incorporated into the fitting model itself, the measured data remain unchanged, and Dec_Corr(t_i) can be fit to the measured decay as usual by means of a maximum likelihood estimation (Fig. 1C).

It should be noted, however, that this correction method is an approximation that does not account for the following effect: Whenever a merged photon pair is detected by the TCSPC electronics, the lost photon is always the second to arrive at the detector. As a consequence, the losses do not aggregate exactly at the peak region, but slightly later. Here, we therefore introduced a new correction algorithm. For a given pulse pair resolution interval (Δt), any photon arriving ≤Δt later than a precedin photon will be lost, regardless of whether the latter was detected. This is different from dead-time effects, where subsequent photons will be lost only if the preceding one was detected and had started the dead time. The losses can be calculated from the undistorted decay curve, as approximated by the fitting model, Dec_Mod(t). The probability p_det-j that a photon in TCSPC bin t_j can be detected is equal to the probability that no photon whatsoever has previously arrived at the detector within Δt.

Let {T_j} represent the set of TCSPC bins t_i located within Δt preceding TCSPC bin t_j. Assuming statistically independent TCSPC bins, the probability p_{det j} of no photon occurrence within Δt can be expressed as the product of the probabilities π that no photon arrived in each t_i as follows:

$$p_{\det j}={\displaystyle {\displaystyle \prod }_{i,t_i\in \left\{T_i\right\}}{\overline{p}}_i}={\displaystyle {\displaystyle \prod }_{i,t_i\in \left\{T_i\right\}}(1-p_i)}.$$ (1)

Given the overall count rate N (units, photons/excitation cycle) and the shape of the model decay Dec_Mod(t), one can calculate the probabilities π for a photon to arrive within the same excitation cycle as the photon in TCSPC bin t_j; π is in good approximation in the following:

$$p_i=N\cdot De{c}_{Mod}(t_i)/{\displaystyle \sum _{k}De{c}_{Mod}(t_k)=:N\cdot De{c}_{Mod}{|}_{norm}(t_i)}.$$ (2)

The summation over index k stretches over all time bins t_k and serves as a normalization of the model decay Dec_Mod. As the decay consists of discrete channels, its integral is a sum, with the goal to yield the total number of photons in it. Using Equation 1 as a measure for the photon losses, the corrected model equation calculates as follows:

$$De{c}_{Corr}(t_j)=De{c}_{Mod}(t_j)\cdot {\displaystyle \prod _{i,t_i\in \left\{T_j\right\}}\left(1-p_i\right)}=De{c}_{Mod}(t_j)\cdot {\displaystyle \prod _{i,t_i\in \left\{T_j\right\}}\left(1-N\cdot De{c}_{Mod}{|}_{norm}(t_i)\right)}.$$ (3)

Typically, the TCSPC bins are equally spaced. Introducing a homogeneous bin width w, the TCSPC bins t_i within the interval Δt can be expressed analytically, and Equation (3) can be written as follows:

$$De{c}_{Corr}(t_j)=De{c}_{Mod}(t_j)\cdot {\displaystyle \prod _{i=j-\Delta t/w}^j\left(1-N\cdot De{c}_{Mod}{|}_{norm}(t_i)\right)}.$$ (4)

It is noteworthy here that as in previous studies (Patting et al., 2018), the correction applies exclusively to the fitting model equation. No manipulation or correction of raw data (i.e., the decay curves) is necessary. The nonlinear optimization algorithms used here are state of the art, namely a Marquardt–Levenberg fitting algorithm (Marquardt, 1963). In this study we used the fitting engine provided with the acquisition software (SymPhoTime 64, PicoQuant).

Δt can be estimated in the following ways. (1) The Δt parameter can be calibrated in a global fit over a series of decays measured at different count rates from a known fluorophore with a preferably monoexponential decay. For estimation, Δt and the lifetime parameter are calculated as global parameters throughout the series. It is important to cover at least the range of count rates that are expected to be encountered during the experiment. (2) For direct estimation from the experimental data, once a photon is measured, no further photon can be detected by the same detector within Δt. For each detector a histogram is calculated of the time intervals between subsequent photons. Δt represents an eventless hole [0–Δt]. Note that because of the intensity fluctuations of the electrical pulses, the sharp rise of events at the upper border of the interval is somewhat smeared out. It is best practice to use 50% of the subsequent maximum of events as a cutoff limit. Comparing the accuracy of both approaches, under favorable conditions, the first one may yield slightly more accurate results, but on the other hand it is prone to suffering from fitting inaccuracies, whereas the second is more stable and of sufficient accuracy for most purposes and does not require an additional calibration measurement. In our experiments exclusively, the second approach was used to determine Δt.

Preparations, salines, and drug application

Brain tissue slices were prepared from BALB/c mice (both sexes). For generation of acute hippocampal tissue slices, animals of postnatal days (P) 14–20 were anaesthetized, decapitated, and their brains removed. Brains were immediately placed in ice-cold preparation saline, containing the following (in mm): 125 NaCl, 2.5 KCl, 0.5 CaCl₂, 6 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose, bubbled with 95% O₂/5% CO₂, pH 7.4, and an osmolarity of 310 ± 5 mOsm l⁻¹. Subsequently, brains were separated into hemispheres and cut into 250-μm-thick slices in a parasagittal orientation using a vibrating blade microtome (HM 650V, Thermo Fisher Scientific). After cutting, slices were incubated at 34°C for 30 min in standard artificial cerebrospinal fluid (s-ACSF), containing the following (in mm): 125 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 26 NaHCO₃, and 10 glucose, bubbled with 95% O₂/5% CO₂, pH of 7.4, and an osmolarity of 310 ± 5 mOsm l⁻¹. Subsequently, slices were kept in s-ACSF at room temperature (21 ± 1°C) for up to 6 h.

Organotypic hippocampal tissue slice cultures were prepared as described previously (Stoppini et al., 1991; Gerkau et al., 2019b). Briefly, brain slices were obtained from P6–P8 mice under sterile conditions and immediately transferred onto Biopore membranes (Millicell standing insert, Merck Millipore). Slices were kept in an incubator at 36.5°C for at least 10 d at an interface between humidified carbogen (95% O₂/5% CO₂) and culture medium (Gee et al., 2017). Medium containing minimum essential medium (catalog #M7278; Sigma-Aldrich), 20% heat-inactivated horse serum (Thermo Fisher Scientific), 1 mm L-glutamine, 0.01 mg/ml insulin, 14.5 mm NaCl, 2 mm MgSO₄, 1.44 mm CaCl₂, 0.00,125% ascorbic acid, and 13 mm D-glucose was replaced every 3 d. Organotypic slices were used for experiments between 10 and 21 d in culture.

During experiments, slices were continuously perfused with s-ACSF. Unless otherwise noted, experiments were performed at room temperature. For experiments at near-physiological temperature (33 ± 1°C), slices were perfused with a high-temperature ACSF (ht-ACSF) containing the following (in mm): 132 NaCl, 2.5 KCl, 2 CaCl₂, 1 MgCl₂, 1.25 NaH₂PO₄, 20 NaHCO₃, and 10 glucose, bubbled with 95% O₂/5% CO₂, pH 7.4, adjusted with potassium hydroxide (KOH). In saline containing a low Na⁺ concentration, NaCl was substituted with N-methyl-D-glucamine chloride (NMDG-Cl), resulting in a residual Na⁺ of 27.25 mm.

Bath application of glutamate was performed by perfusing slices with s-ACSF to which 1 mm glutamate was added. For local pressure application, glutamate was dissolved in HEPES-buffered saline composed of the following (in mm): 125 NaCl, 2.5 KCl, 2 CaCl₂, 2 MgCl₂, 1.25 NaH₂PO₄ and 25 HEPES, pH 7.4 (adjusted with KOH). This solution was filled into a fine-tipped glass pipette (tip diameter <1 µm), which was inserted into the tissue, and glutamate ejected using a pressure application system (PDES nxh, npi electronic). Chemical ischemia (c.i.) was induced by perfusing slices with glucose-free s-ACSF or ht-ACSF, additionally containing sodium azide (NaN₃; 5 mm) and 2-deoxyglucose (2-DG; 2 mm). The duration of perfusion was 2 min for mild c.i. or 5 min for moderate c.i. For severe c.i., the concentration of NaN₃ was increased to 10 mm, and the saline perfused for 5 min.

Intensity-based and fluorescence lifetime imaging of sodium

For imaging of sodium (Na⁺), the membrane-permeable form of the chemical Na⁺ indicator ION-NaTRIUM-Green-2-AM (ING2; catalog #AB142802 and catalog #2011F, Mobitec) was pressure injected into the stratum radiatum and stratum oriens of hippocampal brain tissue slices as reported previously (Meier et al., 2006; Langer et al., 2017). In vitro measurements illustrating the novel correction algorithm (Fig. 1) were performed using a pulsed laser at 640 nm with a pulse rate of 40 MHz (PicoQuant); emission was collected using a 640/70 bandpass filter. Intensity-based, multiphoton imaging and FLIM of ING2 were performed using a custom-built laser-scanning microscope based on a Fluoview300 system (Olympus), equipped with a water immersion objective (NIR Apo 60×, numerical aperture 1.0, Nikon Instruments Europe). Laser pulses (<100 fs, 840 nm) were generated at 80 MHz by a mode-locked Titan Sapphire laser (Mai Tai, Spectra-Physics).

For intensity-based imaging during in situ calibration experiments, fluorescence emission <700 nm was directed to the internal Fluoview photomultiplier tubes (Olympus), and images were acquired at ∼1 Hz. Fluorescence collected from selected regions of interest (ROIs), representing cell bodies of CA1 pyramidal neurons, was analyzed offline using Fluoview 5.0 (Olympus Europe) and OriginPro software (OriginLab). For each ROI, changes in fluorescence emission (ΔF) induced by chemical ischemia were corrected for bleaching, normalized to the respective baseline (F₀) before chemical ischemia, and depicted as ΔF/F₀ (percentage).

Average fluorescence lifetimes (FL) were measured using TCSPC with a spatial resolution of 0.57 × 0.57 µm per pixel. Fluorescence emission was bandpass filtered (534/30, catalog #F39-533, AHF Analysentechnik) and directed to a phosphomolybdic acid (PMA) hybrid photodetector (PicoQuant). TCSPC electronics (MultiHarp 150, PicoQuant) and acquisition software (SymPhoTime 64, PicoQuant) were used for obtaining FL. Pixel dwell time was 3.81 µs for frames consisting of 512 × 512 or 56 × 56 pixels, with a typical frame rate of 1 s or 0.1 s per image, respectively. ROIs, representing cell bodies of CA1 pyramidal neurons, were selected in the intensity image, and only those with a total photon count of >5000 photons were used for analysis. To evaluate cellular autofluorescence, photon counts were taken from unstained tissue at a depth of about −40 µm. When summing up the emission from 20 frames, individual pixels yielded a photon count of 0–5 counts, typical size ROIs (representing cell bodies of CA1 pyramidal neurons) of ∼300 counts, and full frames of ∼200,000 counts. Subsequent dye loading increased the photon count per pixel to ∼500 counts, that of the ROIs to ∼100,000 counts, and that of the entire frame to ∼43,000,000 counts. Overall, the contribution of autofluorescence to the emitted signal thus amounted to ∼0.5%.

Acquired images were analyzed using SymPhoTime 64 software version 2.6 (PicoQuant) and a custom-written routine (Multi Frame Batch FLIM). Decay curves were analyzed by iterative reconvolution of the instrument response function (IRF) with newly implemented corrections for rapidFLIM (see above and below, Results), IRF_(t), with a biexponential model function, y_(t), using the following Equations 5 and 6:

$$y(t)={\displaystyle \sum _{k=0}^{n-1}IRF\otimes {|}_{Bkgr}{{}_{{}_{IRF}}}_{Shif{t}_{IRF}}}{A}_k\exp \left(\frac{t}{{\tau }_k}\right)+Bkg{r}_{Dec},$$ (5)

where τ_i is the characteristic decay times and A_k is the respective amplitudes, Bkgr_Dec is the decay background, and the dot cross product symbol is used to denote the convolution of the IRF, corrected by the IRF background (Bkgr_IRF) and the IRF shift (Shift_IRF). The amplitude weighted average lifetime, τ_AVG, was calculated as follows:

$${\tau }_{AVG}=\frac{{\displaystyle \sum _{k=0}^{n-1}{A}_k{\tau }_k}}{{\displaystyle \sum _{k=0}^{n-1}{A}_k}}.$$ (6)

For illustration purposes, all depicted images of fluorescence lifetime show the Fast LifeTime (fLT), which was calculated from the distance between the average of the measured TCPSC histogram and the average of the IRF histogram. As this process is not relying on complex fitting algorithms, it is less prone to statistical noise arising from low photon counts. Images of fLT thus require much less photon counts than those constructed from average fluorescence lifetimes. ING2 is a dim fluorophore and suffers from low photon emission. Only in static images with a frame binning of 30 and more (Fig. 4D), single pixel photon counts were sufficient to generate a pixel-by-pixel average lifetime image. All images depicting dynamic changes, with a low frame binning did not have enough pixel-per-pixel photon counts to calculate an image because of the dim nature of our probes. Note that for data analysis, ROI-based fits with exclusively τ_AVG were used, as this is more accurate than fLT.

Figure 4.

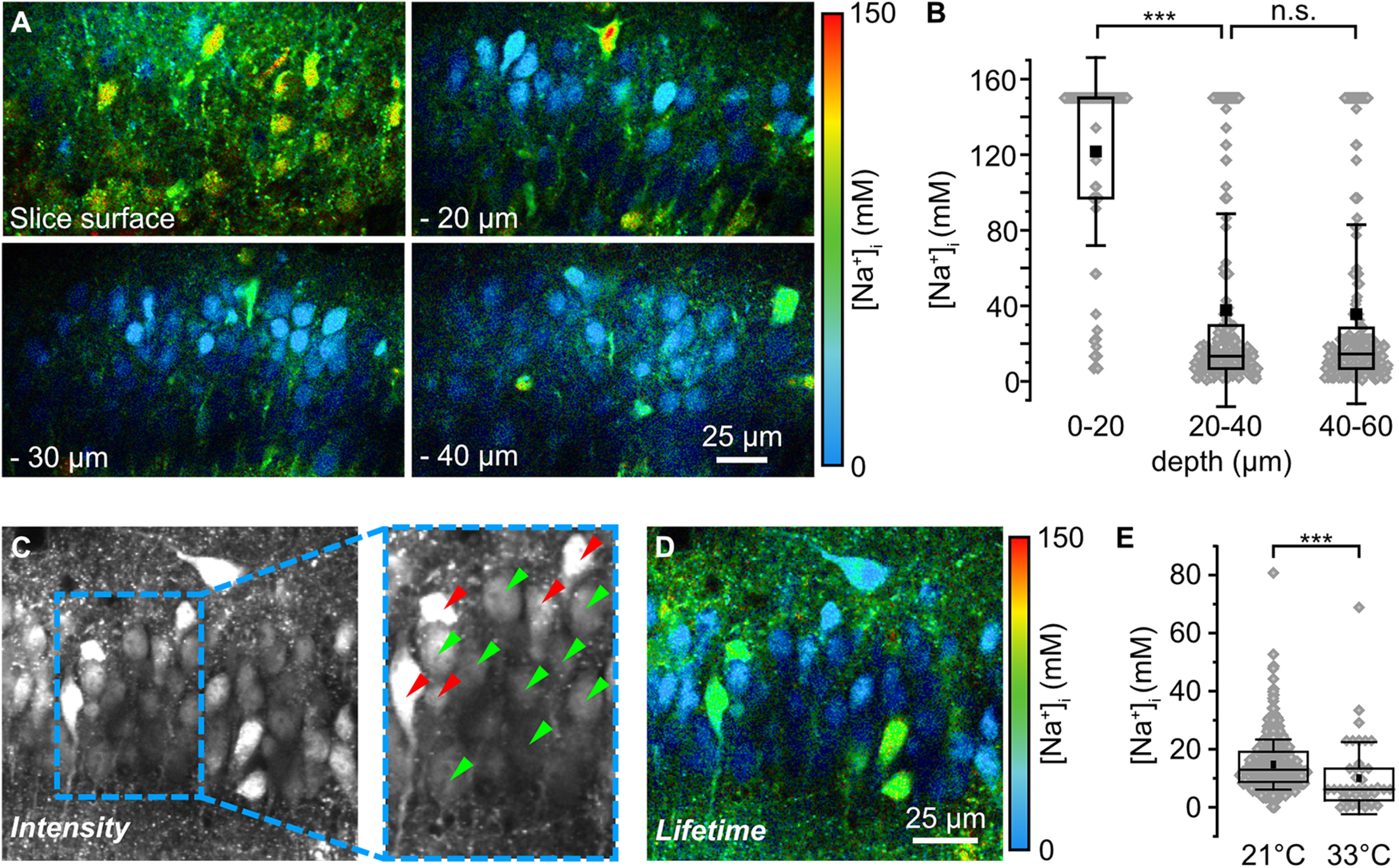
Baseline [Na⁺]_i of CA1 pyramidal neurons in acute tissue slices. A, Color-coded FL images of the CA1 pyramidal cell layer of an ING2-loaded acute tissue slice at different depths (slice surface, −20, −30, and −40 µm). Images are depicted with a 30 s temporal binning; cyan colors represent low [Na⁺], red colors represent high [Na⁺] as indicated by the bar (right). B, Box plots illustrating baseline [Na⁺] of neurons at the slice surface (n = 91), at depths of 20–40 µm (n = 358) and of 40–60 µm (n = 246). Note that the distribution of [Na⁺]_i across all cells was similar (p = 0.49) between 20–40 µm and 40–60 µm. C, Intensity image (temporal binning of 30 s) of an ING2-loaded acute slice taken at a depth of −25 µm. Inset, A magnification of 1.5× (right). Green arrowheads mark cells that were analyzed further based on their morphologic appearance and brightness in the intensity image. Red arrowheads point to cells that were excluded from further analysis based on the same criteria. D, Color-coded FL image (temporal binning of 30 s) of the same region depicted in C. E, Box plots illustrating baseline [Na⁺] of neurons at 21°C (n = 397, N > 5) and 33°C (n = 44, N = 5) at a depth between −20 and −60 µm. B, E, Box plots show mean (square), median (line), 25/75 percentiles (box), SD (whiskers), and single data points (gray diamonds). One-way ANOVA with Tukey's post hoc tests were used for normal distributed data; otherwise, Mann–Whitney tests were used; ***p < 0.001.

Calibration of ING2

To determine the Na⁺ selectivity of ING2 in vitro, the dye was dissolved at 5 μm in calibration salines consisting of the following (in mm): 10 HEPES, 26 K⁺-gluconate, 0–150 [Na⁺], 0-150 [K⁺] (NaCl + KCl = 150 mm), pH titrated to 7.4 with KOH. The K⁺ sensitivity was tested using calibration salines at a fixed [Na⁺] of 20 mm while varying [K⁺] between 30 and 150 mm. NMDG was added as required to maintain iso-osmolarity. To analyze the pH dependence of ING2, calibration salines at a fixed [Na⁺] of 20 mm ([K⁺] = 130 mm) and a pH titrated to values between 5.0 and 8.0 were used. The Ca²⁺ sensitivity was tested using a Ca²⁺-buffer kit (catalog #59100, Biotium) containing component A (10 mm K⁺-EGTA, 100 mm KCl, and 10 mm MOPS, pH 7.2) and component B (10 mm Ca²⁺-EGTA, 100 mm KCI, and 10 mm MOPS, pH 7.2). Both components were mixed accordingly to yield final concentrations of 0, 0.065, 0.15, 1.35, or 39.8 μm free Ca²⁺ in solution. The influence of viscosity was tested using a saline with 20 mm Na⁺ ([K⁺] = 130 mm), to which 0, 1, 2, 3, or 5% of a 80 kDa dextran (00892; Sigma-Aldrich) was added. To test the influence of an addition of ionophores on the fluorescence lifetime of ING2 (Yurinskaya et al., 2020), calibration salines with a [Na⁺] of 0 or 150 mm were prepared as stated above, to which 3 μm gramicidin (Na⁺-ionophore; Sigma-Aldrich), 10 μm monensin (Na⁺/H⁺-exchanger; Sigma-Aldrich), or both were added. Each in vitro measurement was repeated three times.

To determine the Na⁺ sensitivity of ING2 in situ, organotypic tissue slices were perfused with calibration salines containing the following (in mm): 10 HEPES, 26 K⁺-gluconate, 0-150 [Na⁺], 0-150 [K⁺] (NaCl + KCl = 150 mm), pH titrated to 7.3 with KOH, to which 3 μm gramicidin, 10 μm monensin, and 1 mm ouabain (Na⁺/K⁺-ATPase inhibitor; Calbiochem, Merck) were added to permeabilize cellular plasma membranes for Na⁺ (Rose and Ransom, 1996; Meier et al., 2006). On exposure of a slice with a calibration saline at a given [Na⁺], the fluorescence intensity of ING2 was continuously recorded until a stable plateau value was reached (Fig. 3B). Subsequently, intensity-based imaging was switched to FLIM. Photons were collected until a peak intensity of >1,000,000 photons, which corresponds to a total of >10,000,000 photons for the global photon distribution (full-frame image, 512 × 512 pixels), was attained. Afterward, the intensity-based imaging was commenced again (Fig. 3B). Obtained normalized changes in fluorescence intensity (ΔF/F₀) as well as the amplitude-weighted average lifetimes (τ_AVG) were plotted as a function of [Na⁺] and fitted with OriginPro software (OriginLab). Michaelis–Menten kinetics were used to describe the correlation between ΔF/F₀ or τ_AVG and [Na⁺].

Figure 3.

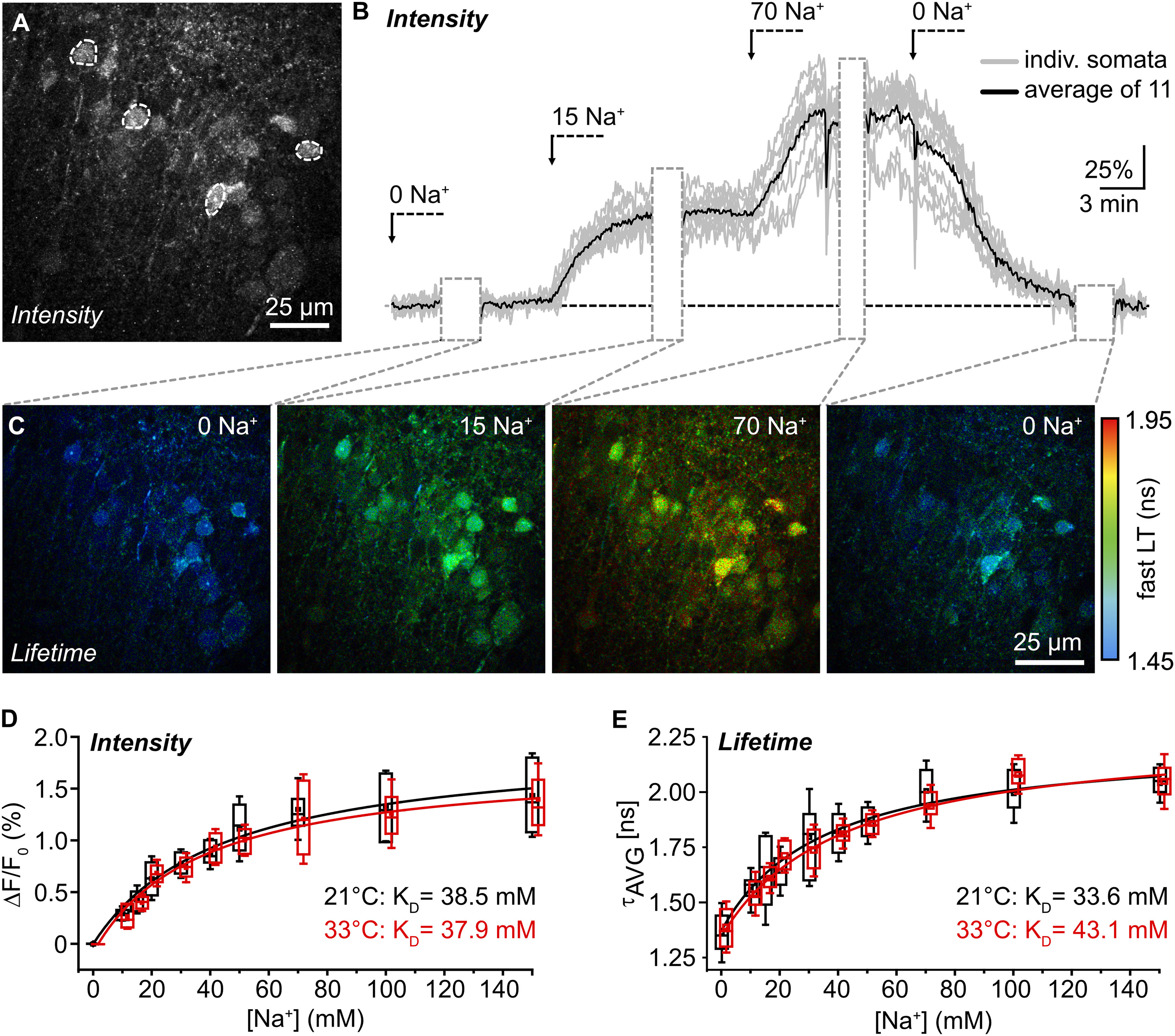
In situ calibration of ING2. A, ING2-fluorescence of the CA1 region of an organotypic tissue slice. Dashed white lines delineate ROIs drawn around cell bodies from which fluorescence intensity was recorded as shown in B. B, Normalized changes in cellular ING2 fluorescence intensity on changes in [Na⁺] in one experiment. Gray trace, individual somata; black trace, average. Gray boxes, periods during which FL was recorded as shown in C. C, Same experiment showing color-coded FL images of ING2 taken at different [Na⁺] with a temporal binning of 15–27 s. Right, Color code. D, Box plots illustrating ING2 fluorescence intensity at different [Na⁺], normalized to 0 mm Na⁺, at 21°C (black; n = 29–81), and at 33°C (red; n = 38–52). Red lines are Michaelis–Menten fits. E, Same illustration as in D for τ_AVG at 21°C (n = 21–135) and 33°C (n = 21–135). N ≥ 3 slices for each [Na⁺] and condition (D, E).

To report changes in Na⁺ based on τ_AVG, all data points were cropped to 0 mm (minimum) and 150 mm (maximum) Na⁺, respectively, because these are the boundaries that can naturally occur. Any values below or above these concentrations are because of noise imposed by the techniques used and physically improbable. Values lower than 0 mm or exceeding 150 mm were therefore set to their respective boundary. Of note, although our standard perfusion saline contained 152.25 mm Na⁺, data were cropped to 150 mm for the sake of simplicity.

Experimental design and statistical analysis

Experiments were performed on animals of both sexes. For in situ measurements, slices from at least three different animals were used. For analysis of changes in [Na⁺]_i of CA1 pyramidal neurons, the observation window was set to ∼20 min (corresponding to ∼1250 frames). This limit was dictated by the total file size (which is related to the total photon count) and hardware restrictions. Typical experiments each required a random-access memory size of 150 gigabytes; the time needed for saving the file after the experiment was ∼5–10 min; the time required for calculation was ∼8 h. All data were analyzed blind to the analyst. Unless stated otherwise, data are presented in Tukey's box-and-whisker plots indicating median (line), mean (square), interquartile range (25/75, box) and SD (whiskers). Additionally, all individual data points are plotted in gray diamonds. Average fluorescence lifetime data were constrained to the boundaries of the calibration (lower limit, 0 mm; upper limit, 150 mm Na⁺). Data points that mathematically exceeded these limits were restricted. Data were tested with the Kolmogorov–Smirnov test for normal distribution. Normally distributed data were statistically analyzed by one-way ANOVA followed by a post hoc Bonferroni test. Data not normally distributed were analyzed with a Mann–Whitney (MWU) test for significance. The results of the statistical tests are as follows: *0.01 ≤ p < 0.05, **0.001 ≤ p <0.01, and ***p < 0.001; n represents the number of cells analyzed, and N represents the number of independent experiments (in vitro) or slice preparations (in situ).

Data availability

The data that support the findings of this study are available from the corresponding author on reasonable request.

Results

Improved correction approach for high count rate imaging

rapidFLIM exploits ultra-low dead-time photodetectors together with rapid TCSPC electronics, enabling photon count rates of up to multiple detections per excitation cycle (Fig. 1A). Whenever subsequent detector pulses merge, the first photon will be detected, whereas photons arriving later within the pulse pair resolution interval Δt (see above, Materials and Methods) will be lost, necessitating a correction (Patting et al., 2018). However, these previous approaches have been an approximation that do not take into account that the maximum losses will not be centered around the peak of a decay curve but will occur ∼Δt later (Fig. 1B), reducing the precision of the fitted parameters.

To overcome this, we developed an improved correction, which yields results with higher precision (Fig. 1B–D). We compared decay fits for the fluorescent dyes Atto 655 and Atto Rh14 at 40 MHz excitation, taken at several count rates up to 40 MHz (i.e., 1.0 photon per excitation cycle; Fig. 1C). Although the former correction describes the photon losses when averaged over the peak region, the bias for later photon losses is neglected, leading to trends in the residuals and visible deviations between measured decay and fit. The new correction scheme substantially improved the fit between model and measured decay, and the trends in the residuals were reduced by a factor of ∼50 (Fig. 1D). For the uncorrected fitting model, both lifetimes and relative amplitudes of the mixture show strong trends with count rates above 0.2 (Fig. 1C). Although the former correction improves the results, there are still trends in the lifetimes as well as the relative amplitudes of the exponential components of ∼10% at count rates above 1. The new correction scheme yields lifetimes that are stable over the complete measurement range up to ∼2 photons per cycle. Moreover, the relative amplitude of the fast component remains equally stable over the complete range of count rates, indicating a stable analysis (Fig. 1C).

FLIM of ING2 in vitro and in situ

To test the suitability of rapidFLIM for dynamic cellular imaging with dim fluorophores, we chose the fluorescent dye ING2, a standard chemical indicator for intensity-based imaging of intracellular [Na⁺]. First, we analyzed its Na⁺ sensitivity and selectivity in vitro (Fig. 2). ING2 was dissolved in salines with [Na⁺] varying from 0 to 150 mm, and the amplitude-weighted average fluorescence lifetime (τ_AVG) was determined (n = 3; Fig. 2A). τ_AVG increased with increasing [Na⁺], ranging from 0.360 ± 0.040 ns in the nominal absence of Na⁺ (0 mm Na⁺) to 1.477 ± 0.023 ns under near-saturating conditions (150 mm Na⁺). Fitting the data points using a Michaelis–Menten plot (R² = 0.998), revealed an apparent K_D of 8.9 ± 0.4 mm for Na⁺ (Fig. 2A). Subsequently, we analyzed the sensitivity of ING2 to changes in [K⁺] or pH at a fixed [Na⁺] of 20 mm. τ_AVG was essentially insensitive to both ions in the ranges tested (20–150 mm K⁺; pH, 6–8; each n = 3; Fig. 2B,C). Furthermore, ING2 was found to be insensitive to changes in [Ca²⁺] between 0 and 40 μm (determined at 0 mm Na⁺; n = 3; Fig. 2D). In addition, the effect of viscosity was analyzed by adding 80 kDa dextran at 0–5%, and no change in τ_AVG was detected (n = 3; Fig. 2E). Finally, the influence of monensin and gramicidin, ionophores used for in situ calibrations, was tested. At both 0 and 150 mm Na⁺, neither the addition of one of the ionophores, nor of both, resulted in a change in τ_AVG (n = 3; data not shown). Together, these experiments demonstrate that ING2 is well suited for FLIM of Na⁺. Moreover, they show that ING2 exhibits essentially no sensitivity to K⁺ or H⁺ and does not respond to changes in viscosity nor to ionophores used for its calibration in situ.

Figure 2.

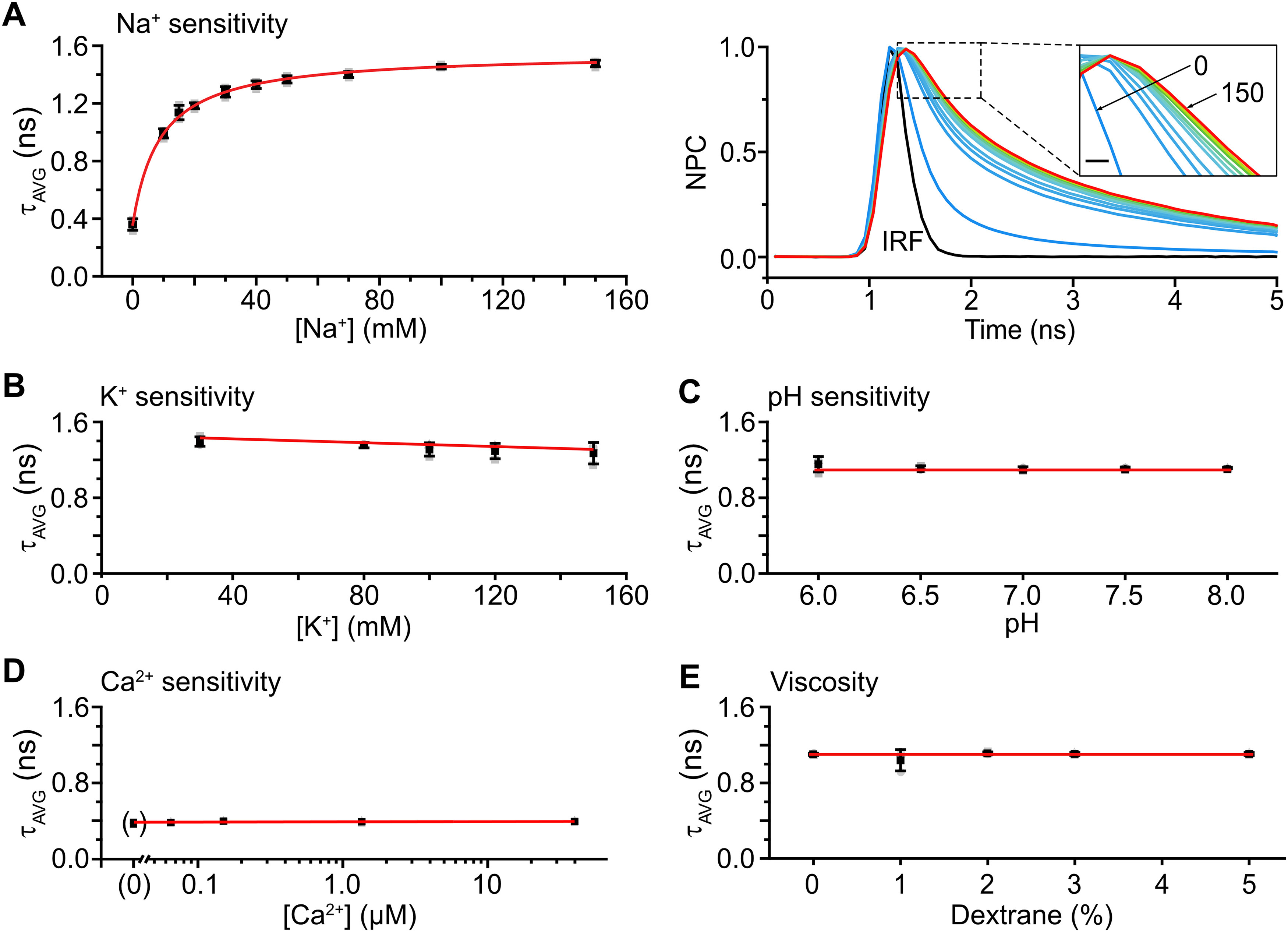
Calibration and ion sensitivity of ING2 in vitro. A, Left, Mean values of τ_AVG ± SD at different [Na⁺] ranging from 0 to 150 mm depicted in black, individual data points in gray. The red line represents a Michaelis–Menten plot revealing an apparent K_D of 8.9 mm for Na⁺. Gray squares represent individual data points. Right, Normalized photon count (NPC) of ING2 after pulsed excitation at different [Na⁺]. Inset, An enlargement of the fluorescence decays between 1.2 and 2.1 ns. Scale bar, 200 ps. The color illustrates different [Na⁺] with blue representing low (0 mm) and red representing high [Na⁺] (150 mm). The black trace shows the IRF of the optical pathway. B–D, Mean values of τ_AVG ± SD at fixed [Na⁺] of 20 mm depicted in black, individual values in gray. Red lines represent linear fits of the data shown. B, The τ_AVG at [K⁺] of 30, 80, 100, 120, and 150 mm. C, The τ_AVG, pH 6.0, 6.5, 7.0, 7.5, and 8.0. D, The τ_AVG at a [Ca²⁺] of 0, 0.065, 0.15, 1.35, and 39.8 μm. Note that these experiments were performed at 0 mm [Na⁺]. E, The τ_AVG on addition of 1, 2, 3, 4, and 5% dextran to the saline.

Next, we calibrated ING2 inside CA1 pyramidal neurons using intensity-based imaging combined with rapidFLIM. In situ calibrations require stable recordings of cellular fluorescence emission for at least 40–60 min. Calibrations were thus performed in organotypic tissue slices, which, because of their reduced thickness and adherence to the culturing membrane (Lerchundi et al., 2019), provide better optical accessibility as well as less tissue movement than acutely isolated slices. Moreover, in this set of experiments, two sets of detectors were combined (internal Fluoview photomultipliers as well as PMA hybrid photodetectors), enabling online evaluation of fluorescence intensity together with TCSPC.

Organotypic slice cultures were bolus loaded with ING2-AM (Fig. 3A) and then perfused with nominally Na⁺-free calibration saline. After recording a stable baseline, fluorescence emission was directed to the TCSPC detectors (Fig. 3B,C). Photons were collected at 0.2 Hz until >10,000,000 photons had been counted in total. Subsequently, intensity-based imaging was resumed, and after 3–5 more minutes, salines with a defined [Na⁺] (10–150 mm) were washed in sequentially. After recording the resulting changes in fluorescence intensity, photons were again directed to the FLIM detectors, and FL was determined for each condition (Fig. 3B,C).

The relation between normalized changes in intensity (ΔF/F₀) and [Na⁺]_i followed Michaelis–Menten kinetics (R² = 0.97), revealing an apparent K_D of 38.5 ± 5.7 mm at 21°C (n = 29–81 neurons, N ≥ 3 slices for each [Na⁺]; Fig. 3D). The K_D determined based on τ_AVG was in the same range, amounting to 33.6 ± 6.5 mm (n = 21–135; Fig. 3E). At near-physiological temperature (33°C), a K_D of 37.9 ± 5.1 mm (R² = 0.98) was determined based on intensity (n = 38–52); the K_D derived from the τ_AVG was 43.1 ± 9.5 mm (n = 21–135; Fig. 3D,E). In summary, these results show that intensity-based imaging and FLIM of ING2 report changes in [Na⁺]_i with a comparable apparent affinity to Na⁺ at both room and near-physiological temperatures. Moreover, they are in line with earlier reports showing that the apparent K_D of chemical sodium indicators is significantly higher inside cells as compared with in vitro conditions (Despa et al., 2000; Roder and Hille, 2014; Naumann et al., 2018; Meyer et al., 2019).

Determination of baseline [Na⁺]_i of CA1 pyramidal neurons

As a next step, we used rapidFLIM of ING2 to determine baseline [Na⁺]_i of CA1 pyramidal neurons in acute brain tissue slices. Laser power for experiments was chosen so that autofluorescence from unstained tissue was negligible. Imaging in unstained slices yielded a total photon account of <500 photons from ∼400 frames overall from the entire field of view. Loading slices with ING2, in contrast, resulted in photon counts of ∼1 billion under comparable conditions. CA1 pyramidal neurons were identified based on their characteristic morphology in images of ING2 intensity following the criteria described below. For adequate fitting of the lifetime, a sufficient number of photons was needed. Therefore, a photon threshold of 5000 counts per ROI (representing somata of CA1 pyramidal neurons) was set for analysis.

In line with the well-established reduced cellular viability at the slice surface, most neurons located at a depth of 0–20 µm from the surface showed very high [Na⁺]_i (>50 mm; n = 91, N = 6; Fig. 4A,B). The large majority of cells for which FLIM reported nonphysiologically high [Na⁺]_i were characterized by a distorted cell body (e.g. deformation of cell membrane, swollen appearance). Cell bodies with high [Na⁺]_i and distorted morphology were still observed 20–60 µm below the slice surface (Fig. 4A,C), but at these depths, the majority of cells exhibited a [Na⁺]_i <20 mm (20–40 µm, 65%, mean 37.7 ± 51.1 mm, median 13.3 mm, n = 358, N = 10; and 40-60 µm, 59%, mean 35.6 ± 47.4 mm, median 14.5 mm, n = 246, N = 10, MWU, p = 0.49141; Fig. 4B,C).

At depths >60 µm, somatic photon counts were drastically reduced, precluding FLIM of ING2 (data not shown). Of note, all available Na⁺ indicators including ING2 suffer from low quantum efficacy and are generally much dimmer than any of the commonly used Ca²⁺ indicator dyes such as Oregon Green BAPTA-1 or Fluo4. Unfortunately, this restricted imaging in deeper tissue layers as with increasing depth, brightness declines because of a combination of lower dye concentration, lower excitation intensity, and higher loss of emitted photons because of increased scattering.

Based on these findings, all following measurements were taken in somata located 20–60 µm below the slice surface. Moreover, before switching to FLIM, somata were evaluated based on their morphology as reported by ING2 fluorescence intensity. Importantly, this initial visual inspection was made under baseline conditions, before any other manipulations were performed. Only cells with a clearly perpendicular orientation in the stratum pyramidale of the CA1 region which had an even, pear-shaped soma, and were the proper approximate size were analyzed (Fig. 4C, green arrowheads). Cells that met one or multiple of the following criteria were discarded (Fig. 4C, red arrowheads): (1) cell body not oriented perpendicular to the CA1 pyramidal cell layer, (2) cells did not show the typical pyramidal-like shape, (3) unevenly shaped soma/distorted silhouette, (4) swollen cell body, (5) overly bright nucleus, and (6) a saturated appearance in the image. In addition, cells with a strongly distorted primary apical dendrite were excluded. Based on these criteria, ∼30–50% of the cells within the field of view were discarded from analysis. Subsequent analysis of FL of ING2 revealed that neurons chosen following this procedure displayed a mean [Na⁺]_i of 14.7 mm ± 9 mm at 21°C (median 13.0 mm; n = 488, N > 5; Fig. 4D,E). At 33°C, mean [Na⁺]_i was significantly lower, averaging 10.8 ± 13.6 mm (median 6.2 mm; n = 44, N = 5; MWU, p = 8.69E-07; Fig. 4E).

Dynamic, quantitative Na⁺ imaging in hippocampal neurons using rapidFLIM

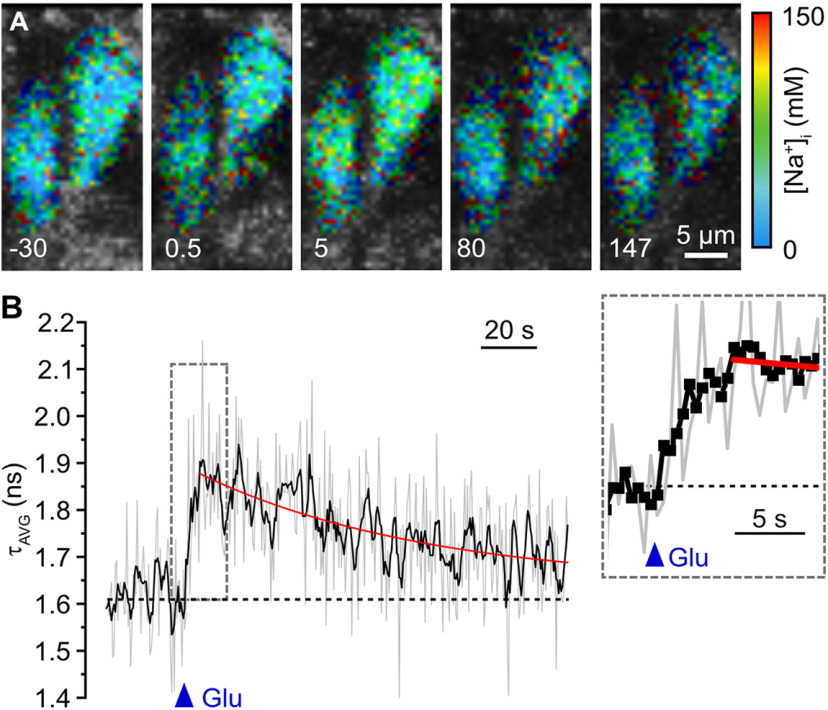
We then probed for the suitability of rapidFLIM to monitor changes in [Na⁺]_i. To induce a transient elevation in neuronal [Na⁺]_i, we bath applied 1 mm glutamate for 10 s (n = 58, N = 5). rapidFLIM, performed at 0.2 Hz, reliably reported both the rise as well as the decay phase of the resulting Na⁺ transients (Fig. 5A–C; Movie 1). On average, [Na⁺]_i increased by 69.6 ± 35.9 mm within ∼70 s, and thereafter monoexponentially decayed back to baseline within 2–3 min (Fig. 5C,F; Movie 1). Next, glutamate was pressure applied. rapidFLIM at full-frame (512 × 512 pixels), requiring 2 s to collect enough photons, reported a transient increase in [Na⁺]_i by 30.2 ± 16.3 mm (n = 61, N > 5); this maximum was already reached at the first data point collected after a stimulation for 100 milliseconds (Fig. 5D–F; Movie 2). To increase the temporal resolution of rapidFLIM of ING2, we repeated pressure application of glutamate (for 200 ms) at reduced frame size (Fig. 6A). When recording frames of 56 × 56 pixels (n = 35, N = 4), photon collection from cell bodies required 0.5 s. At this frequency of image generation (2 Hz), the rising phase of glutamate-induced changes in fluorescence lifetime of ING2 (and [Na⁺]_i, respectively), was reported well when averaging multiple neurons in the field of view (3–4 cells; Fig. 6B).

Figure 5.

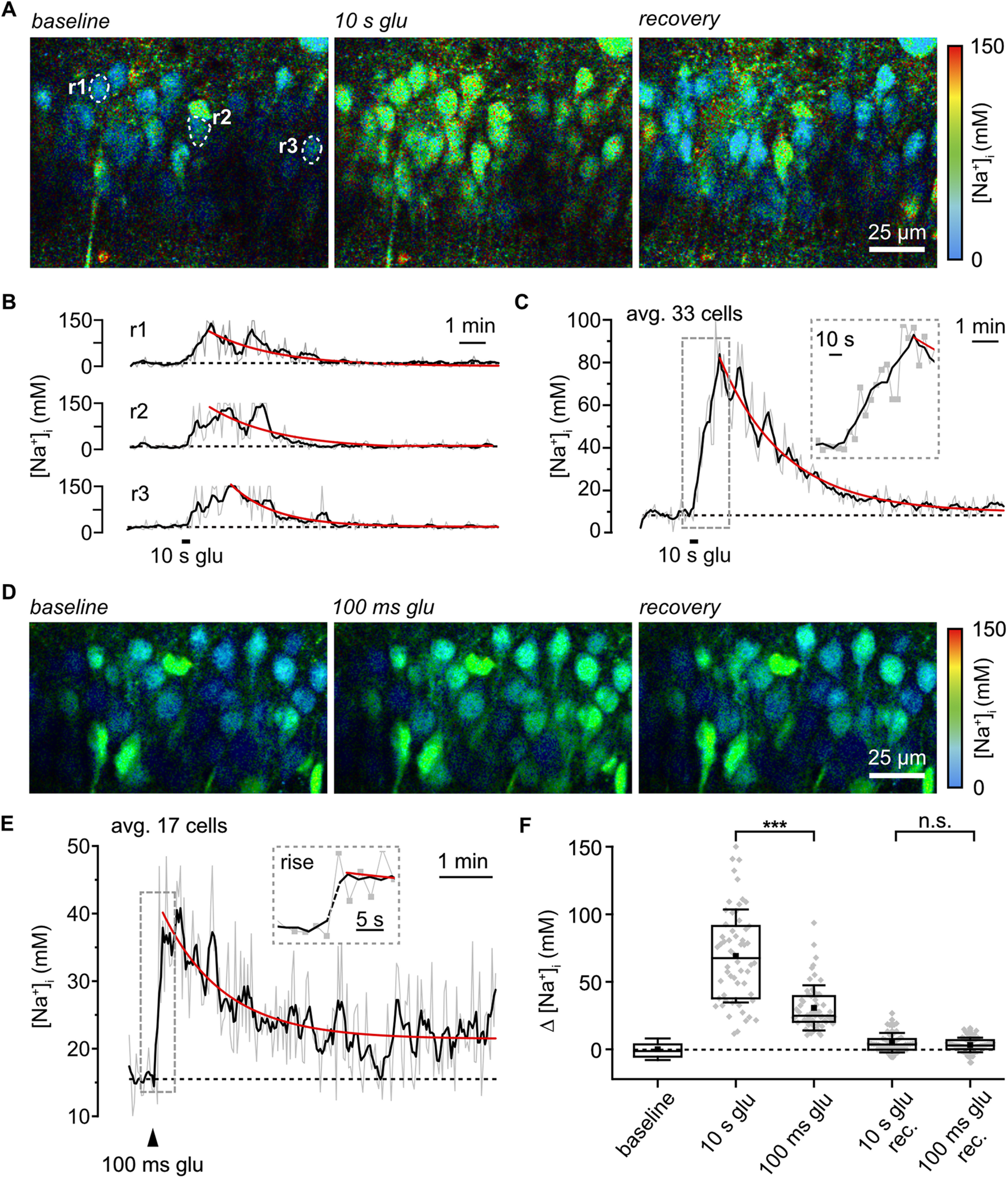
Detection of Na⁺ signals by rapidFLIM. A, Color-coded FL images, depicted with a 30 s temporal binning, of the CA1 region of an ING2-loaded acute slice. Right, Color code. Left: [Na⁺]_i at baseline conditions. Center, Change in [Na⁺] (binned from 70 to 99 s) after bath application of glutamate (1 mm/10 s). Right, Recovery at ∼12 min after termination of glutamate application. Dashed white lines illustrate ROIs (r1–3) analyzed in B. B, Glutamate-induced [Na⁺]_i changes in r1–3. C, Same experiment as in A and B, showing average [Na⁺]_i change in 33 neurons. Inset:, [Na⁺]_i increase at higher time resolution; gray squares, individual data points. D, FL images as in A. Right, Color code. Left, [Na⁺]_i at baseline. Center, Change in [Na⁺] after pressure application of glutamate (1 mm/100 ms; binned from 2 to 31 s after the puff). Right, Recovery (∼5 min after puff). E, Same experiment as in D showing averaged glutamate-induced [Na⁺]_i change from 17 somata. Inset, A [Na⁺]_i increase at higher time resolution; gray squares, individual data points. Gray lines, raw data; black lines, rolling average of five points; red line, monoexponential fits of the recovery phase (B, C, E). F, Box plot showing means (square), median (line), 25/75 percentiles (box), and SD (whiskers) of peak changes in [Na⁺]_i in response to glutamate (10 s, n = 58, N = 5; 100 ms, n = 62, N = 5) and on recovery after 5–10 min. Gray diamonds, single data points. Mann–Whitney test was used for comparison; ***p < 0.001.

Figure 6.

Glutamate-induced changes in ING2-FL. A, Color-coded fluorescence lifetime images (excerpts, 28 × 56 pixels) of the soma of a CA1 neuron in an ING2-loaded acute tissue slice. Right, Color code. An experiment in which the frame size was cropped to 56 × 56 pixels; frame rate was 10 Hz. Images depicted are bins of five frames, resulting in a final temporal resolution of 2 Hz. Numbers (−30, 0.5, 5, 80, and 147) are the corresponding time points, with 0 corresponding to the moment of a pressure application of glutamate (1 mm/200 ms). Note the change in image brightness (intensity/photon count) and color (fluorescence lifetime) in response to glutamate. B, Same experiment as in A showing glutamate-induced changes in fluorescence lifetime (τ_AVG; 5 frames binned). Gray lines, raw data of four cells; black lines, rolling average of the raw data; red line, monoexponential fit of the recovery phase. Blue triangle, time point of glutamate application. Inset, The τ_AVG at 5× higher temporal resolution; black squares represent individual data points of the averaged trace. Scale bar, 5 µm.

Movie 1.

rapidFLIM reveals global increases in neuronal Na⁺ in response to bath application of glutamate.

Movie 2.

rapidFLIM reveals local changes in neuronal Na⁺ on pressure application of glutamate.

In summary, these results demonstrate that rapidFLIM of ING2 allows determination of somatic baseline [Na⁺]_i in neurons in tissue slice preparations. Moreover, they show that under the given experimental conditions, rapidFLIM enables the quantitative detection of changes in [Na⁺]_i at an unprecedented temporal resolution of 0.5 Hz (full frame) to 2 Hz at reduced frame size (56 × 56 pixels), surpassing former FLIM approaches with Na⁺ indicator dyes severalfold (Roder and Hille, 2014; Meyer et al., 2019).

Analysis of Na⁺ loading under ischemic conditions using rapidFLIM

Ischemic conditions result in rapid cell swelling, which can reduce the cytosolic concentration of the soluble indicator and thus distort intensity-based investigation of ion concentrations. Here, we used rapidFLIM of ING2 for determination of changes in neuronal [Na⁺]_i in response to metabolic inhibition. To mimic conditions accompanying ischemic stroke, we induced a c.i. by exposing ING2-loaded acute slices to glucose-free saline containing NaN₃ (5 mm) and 2-DG (2 mm) for inhibition of mitochondrial respiration and glycolysis. Switching from s-ACSF to this saline for 2 min (i.e., mild c.i.) resulted in a transient increase in neuronal [Na⁺]_i by on average 46.3 ± 28.8 mm (n = 90, N = 5) as reported by rapidFLIM (Fig. 7A–C). Peak [Na⁺]_i of 60.4 ± 31.7 mm was reached within ∼4 min after which [Na⁺]_i fully declined back to baseline. Normalized changes in fluorescence intensity (ΔF/F_o) extracted from the FL traces followed a similar time course during this manipulation (n = 54, N = 5; Fig. 7B). Increasing the period of metabolic inhibition to 5 min (i.e., moderate c.i.) resulted in a significant increase in [Na⁺]_i loading by 96.0 ± 31.2 mm (n = 169, N = 5; MWU, p = 9.24E-24). Peak [Na⁺]_i of 111.0 ± 31.7 mm was reached after ∼8 min, and cells did not fully recover within the observation window (Fig. 7A–C). Although experiments were restricted to 20 min for technical reasons (see above, Materials and Methods), [Na⁺]_i still declined at this time point (Fig. 7B), indicating that cells might fully recover after this period.

Figure 7.

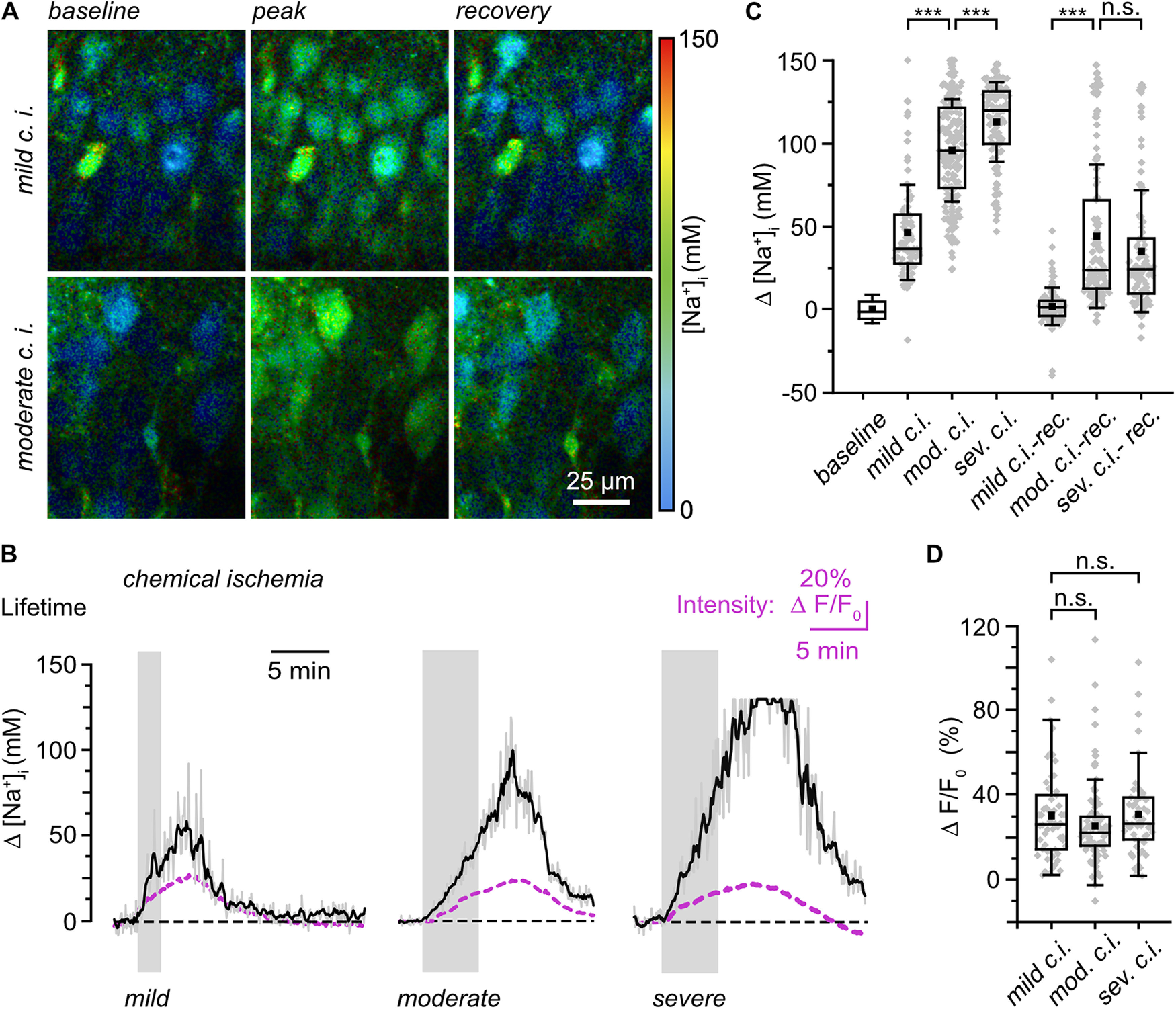
Effects of chemical ischemia on [Na⁺]_i. A, Color-coded FL images, depicted with a 30 s temporal binning, of the CA1 layer of an ING2-loaded acute tissue slice. Right, Color code. Top, Image of [Na⁺]_i at baseline conditions (left); change in [Na⁺] on mild chemical ischemia taken ∼5 min after starting perfusion with the metabolic inhibitors (middle); recovery taken ∼20 min after starting perfusion with inhibitors (right). Bottom, Same illustration showing the effect of moderate chemical ischemia at ∼7 min and 16 min, respectively in another experiment. B, Changes in [Na⁺]_i reported by rapidFLIM in three different experiments on mild (left), moderate (middle), and severe (right) chemical ischemia as indicated by the gray boxes. Gray traces, individual cell bodies; black traces, averages of all neurons analyzed in one particular experiment (n = 35, 40, and 21, respectively). Note that data points were constrained to the minimum/maximum value of the calibration (0 and 150 mm Na⁺). Purple traces, averaged changes in fluorescence intensity taken from the same ROIs as for determination of the FL. C, Box plot illustrating changes in [Na⁺]_i in response to mild (n = 158, N = 5), moderate (n = 169, N = 5), or severe (n = 104, N = 5) chemical ischemia and their recovery as determined 5–7 min after the metabolic inhibition. D, Box plot illustrating normalized changes in fluorescence intensity (ΔF/F₀) taken at the peak of the [Na⁺]_i changes as reported by rapidFLIM (B) in response to mild (n = 54, N = 5), moderate (n = 96, N = 5), or severe (n = 52, N = 5) chemical ischemia. C, D, Means (square), median (line), 25/75 percentiles (box), SD (whiskers), and single data points (gray diamonds). Mann–Whitney or one-way ANOVA with Tukey's post hoc tests were used for comparison; ***p < 0.001.

When extracting changes in fluorescence intensity from lifetime measurements, we found that the average increase in fluorescence intensity (ΔF/F_o) on moderate c.i., determined at the peak of the [Na⁺]_i change as reported by rapidFLIM, was comparable to that induced by mild c.i. (n = 96, N = 5; MWU, p = 0.185; Fig. 7B,D). This strongly indicates that intensity-based analysis of changes in ING2 fluorescence does not correctly report changes in intracellular Na⁺ concentrations under these conditions.

Finally, slices were exposed to saline in which the NaN₃ concentration was increased to 10 mm for a duration of 5 min to induce severe metabolic failure (i.e., severe c.i.). In response to this, neuronal [Na⁺]_i rose by 113.0 ± 23.9 mm (n = 104, N = 5; Fig. 7B,C). In more than a third of neurons (38/104), [Na⁺]_i even equilibrated with extracellular [Na⁺], reaching values of ∼150 mm close to full saturation of ING2 (Fig. 7B,C). Peak [Na⁺]_i was reached after ∼8 min, and cells partially recovered within the observation time (Fig. 7B). Again, changes in fluorescence intensity did not follow the relative increase in [Na⁺]_i reported by rapidFLIM for the different manipulations. Instead, their average amplitude did not exceed those reached in response to mild c.i. (n = 52, N = 5; ANOVA, p = 0.895; Fig. 7B,D). Together, these experiments strongly suggest that intensity-based imaging of ING2 is not suited for determination of neuronal [Na⁺]_i during metabolic inhibition. rapidFLIM of ING2, in contrast, reports increasing amplitudes of [Na⁺]_i loading in response to increasing severity of metabolic inhibition, indicating that changes in [Na⁺]_i are reported reliably.

A likely reason for the observed distortion of changes in fluorescence intensity evoked by moderate and severe c.i. are changes in dye concentration resulting from changes in cell volume. To probe for cell swelling in response to metabolic failure, we determined the size of individual somata based on images of ING2 fluorescence intensity (Fig. 8A). Under baseline conditions, cell bodies had an average area of 95.8 ± 28.7 µm² (n = 100, N = 5). In response to severe c.i., cell body size increased significantly by 21.2 ± 22.3 µm² as determined at peak [Na⁺]_i (∼8 min after wash in; n = 100, N = 5; ANOVA, p = 4.18E-08; Fig. 8A,B).

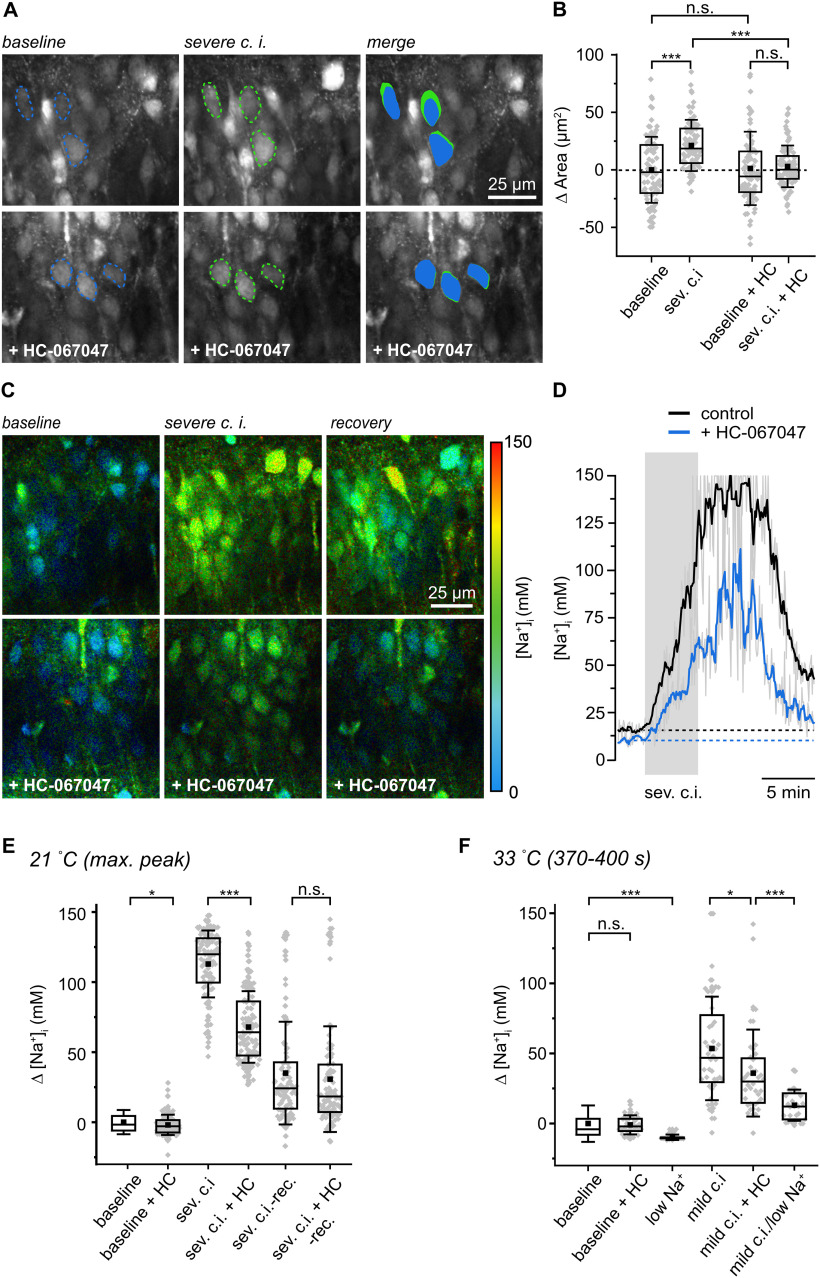
Figure 8.

Role of TRPV4 in cell swelling and neuronal Na⁺ loading. A, Top, Fluorescence intensity of the CA1 layer of an ING2-loaded acute slice at baseline (left) and on severe chemical ischemia (center) taken 11 min after starting perfusion with the metabolic inhibitors. Dashed lines delineate the circumference of three somata. Right, Merge, blue, baseline conditions; green, on chemical ischemia. Bottom, Analog experiment and illustration, with HC-067047 (10 μm). B, Box plots illustrating peak changes in cell body areas on severe chemical ischemia in control (n = 100, N = 5) and with HC-067047 (HC, n = 124, N = 5). C, Color-coded FL images, depicted with a 30 s temporal binning, of the CA1 layer of an ING2-loaded acute slice. Right, Color code. Top, Image of [Na⁺]_i at baseline (left); peak change in [Na⁺] taken ∼11 min after induction of severe chemical ischemia (middle); recovery taken ∼17 min after induction of ischemia (right). Bottom, Analog experiment and illustration, with HC-067047. D, Changes in [Na⁺]_i in response to severe chemical ischemia in a control experiment (black trace, rolling average of 21 neurons) and with HC-067047 (blue trace, rolling average of 29 neurons). Gray traces, raw average traces of 21 and 29 neurons. Note that data points were restricted to the minimum/maximum of the calibration (0 and 150 mm Na⁺). E, Changes in [Na⁺]_i on addition of HC-067047 (n = 124, N = 5), during severe ischemia (n = 104, N = 5), severe ischemia in the presence of HC-067047 (n = 124, N = 5), and recovery as determined 16 min after metabolic inhibition. F, Changes in [Na⁺]_i at 33°C on addition of HC-067047 (n = 40, N = 4) and at low [Na⁺] (n = 30, N = 4). Moreover, changes in [Na⁺]_i as determined 370–400 s after induction of mild ischemia are shown in control (n = 44, N = 5), with HC-067047 (n = 40, N = 4), and in low [Na⁺]-saline (n = 29, N = 4). Box plots illustrating means (square), median (line), 25/75 percentiles (box), SD (whiskers), and single data points (gray diamonds; B, E, F). Note that for illustration purposes, one data point reflecting soma size at baseline with HC-067047 added (140 µm²) is not shown in B. Mann–Whitney or one-way-ANOVA with Tukey's post hoc tests were used for comparison; ***p < 0.001, *p < 0.05.

Earlier reports (Hoshi et al., 2018) identified the osmotically regulated unspecific cation channel TRPV4 (transient receptor potential vanilloid 4) as an important contributor to the development of brain edema after ischemia. We thus tested the effect of bath application of the selective TRPV4 antagonist HC-067047 on ischemia-induced neuronal swelling. The addition of 10 μm HC-067047 under control conditions did not cause a change in neuronal areas (n = 124, N = 5; ANOVA, p = 0.40 794), but prevented the increase in cell body size in response to severe c.i. (mean change, 3.0 ± 18.1 µm²; n = 86, N = 5; ANOVA, p = 4.18E-08; Fig. 8A,B). Next, we analyzed the influence of HC-067047 on [Na⁺]_i. The addition of HC-067047 resulted in a slightly lower baseline [Na⁺]_i as compared with control conditions (12.8 ± 7 mm; n = 124, N = 5; MWU, p = 0.023; Fig. 8E). In the presence of HC-067047, the average peak amplitude of [Na⁺]_i elevations induced by severe c.i. was significantly decreased to 68.0 ± 25.5 mm (n = 124, N = 5; MWU, p = 5.99E-24; Fig. 8C–E; Movie 3). When analyzing changes in ING2 intensity, we found that the mean peak amplitude of changes in fluorescence intensity was similar for both severe ischemia and for severe ischemia with HC-067047 (data not shown). This result indicates that intensity-based measurement of changes in [Na⁺]_i is more reliable when swelling is suppressed by the blocker, again highlighting the superiority of an intensity-independent measurement of [Na⁺]_i when using laser-scanning-based imaging from a focal plane under conditions accompanied by cellular volume changes and tissue movement.

Movie 3.

Na⁺ loading and cell swelling induced by transient ischemia are significantly dampened by inhibition of TRPV4 channels.

TRPV4 is also activated by elevating temperature (Güler et al., 2002; Shibasaki et al., 2007, 2015), and we performed experiments at near-physiological temperatures (33°C) to address this parameter. To this end, tissue slices were slowly heated from room temperature (21 ± 1°C) to 33°C (±1°) and kept at this higher temperature for 15–30 min before exposing them to chemical ischemia. Notably, cell swelling in response to metabolic inhibition was greatly enhanced under these conditions and within ∼8 min on induction of moderate or severe c.i., the cell bodies of pyramidal neurons had moved out of the focal plane, precluding their imaging. We therefore analyzed somatic areas and [Na⁺]_i after a mild c.i. and at 370–400 s after wash in of the metabolic inhibitors, a period at which cells were still clearly visible.

Neurons exhibited a decreased baseline [Na⁺]_i of 10.8 ± 13.6 mm at 33°C (Fig. 4E). The addition of HC-067047 did not alter baseline [Na⁺]_i at 33°C (9.2 ± 6.5 mm; n = 40, N = 4; MWU, p = 0.3974; Fig. 8F). Mild c.i. resulted in an increase of [Na⁺]_i by 51.6 ± 35.5 mm (n = 44, N = 5; Fig. 8F), similar to the value determined at room temperature at this time point (46.3 ± 28.8 mm; n = 90, N = 5; MWU, p = 0.3624; data not shown). During perfusion with HC-067047, this Na⁺ increase was significantly reduced to 34.0 ± 29.8 mm (n = 40, N = 4; ANOVA, p = 0.02116; Fig. 8F). A significant reduction of the Na⁺ increase was also observed in saline with a strongly reduced resting [Na⁺] (27.25 mm). Under this condition, baseline [Na⁺]_i was 0.7 ± 1.9 mm (n = 30, N = 4; MWU, p = 1.30E-08), and mild c.i. resulted in an increase by 13.3 ± 11.1 mm only (n = 29, N = 4; Fig. 8F).

Together, these results suggest that activation of TRPV4 is a major contributor to cell swelling in response to inhibition of cellular metabolism. Moreover, TRPV4 activation generates significant Na⁺ influx under both room and near-physiological temperatures.

Discussion

With classical time-correlated single photon counting devices, stable fitting of the fluorescence lifetime decay necessitates relatively long acquisition times per pixel and/or high laser excitation intensities, both of which stress the probe and may induce photodamage (Becker, 2015; Liu et al., 2019). Long collection times, moreover, constrain the achievable temporal resolution and thereby the possibility to record fast signals. Several strategies were developed to overcome these limitations (Levitt et al., 2020). A ratiometric method, based on splitting the decay curve into early and late segments, enabled imaging of intracellular Ca²⁺ transients in brain tissue with the indicator OregonGreen BAPTA-2 (OGB2) at high frame rates (Minge et al., 2017; Zheng et al., 2018). In combination with line scanning (and thus at the expense of spatial information) this approach allowed registration of Ca²⁺ signals at ≤100 Hz (Zheng et al., 2015; Minge et al., 2017).

Compared with OGB1/2, fluorophores suitable for FLIM-based detection of Cl^- or Na⁺, however, exhibit severalfold lower quantum yield and/or smaller dynamic range (Sagolla et al., 2013; Zheng et al., 2018). FLIM of the Cl⁻ indicator MQAE thus necessitated photon collection for tens of seconds to faithfully report intracellular Cl⁻ concentrations in mouse cerebellar tissue slices (Hille et al., 2009; Untiet et al., 2017). Long photon collection times (≥20 s) also applied for FLIM of intracellular Na⁺ using the CoroNaGreen or ANG2 (a former version of ING2 used here; Roder and Hille, 2014; Rungta et al., 2015; Meyer et al., 2019).

Employing rapidFLIM in the present study, involving new TCSPC electronics registering almost all photons detected by the PMTs, enabled unbiased determination of neuronal baseline [Na⁺]_i in brain slices, confirming earlier investigations with intensity-based approaches (Mondragão et al., 2016). In addition, it allowed FLIM-based recording of glutamate-induced neuronal Na⁺ dynamics at the so-far unprecedented speed of 0.5 Hz full frame. Although such temporal resolution can be easily obtained and even surpassed with intensity-based imaging (Baranauskas et al., 2013; Mondragão et al., 2016; Miyazaki and Ross, 2017), the latter suffers from artifacts introduced by changes in dye concentration that can distort measurements. This is especially evident on cell swelling, precluding quantitative determination of [Na⁺]_i based on changes in the emission intensity of Na⁺ indicators (Rungta et al., 2015).

It is long established that [Na⁺]_i increases can trigger cell swelling and drive development of cerebral edema, which, for example, accompany ischemic stroke (Kahle et al., 2009; Rungta et al., 2015). Knowledge of the mechanisms and time course of Na⁺-dysregulation is thus indispensable to elucidate the pathways responsible for cell damage and excitotoxic injury in the brain. Here, rapidFLIM of ING2, in contrast to intensity-based imaging, enabled quantitative dynamic determination of neuronal Na⁺ loading on metabolic inhibition also under conditions accompanied by cell swelling. Our measurements show substantial increases in [Na⁺]_i with increasing severity of chemical ischemia up to its equilibration with extracellular [Na⁺]. Such strong Na⁺ loading, accompanied by increases in extracellular [K⁺] by 50–60 mm may apply in the core region of an ischemic stroke, driving reverse operation of neuronal glutamate transport (Rossi et al., 2000).

Our work identifies TRPV4 channels as major pathways responsible for neuronal swelling on transient chemical ischemia. Activation of TRPV4 was also observed following oxygen-glucose deprivation (Hoshi et al., 2018). The latter work showed that TRPV4 channels generate swelling of acute mouse brain slices in response to removal of oxygen and glucose. Moreover, the study revealed that brain edema induced by traumatic brain injury is attenuated in TRPV4 knock-out mice in vivo, confirming earlier observations with this model (Lu et al., 2017). Other work has demonstrated involvement of TRPV4 in Ca²⁺ influx into neurons and astrocytes during spreading depolarizations in the ischemic penumbra of mouse neocortex in vivo, presumably driving accumulation of extracellular glutamate (Rakers et al., 2017), as well as in brain edema formation (Jie et al., 2015) on middle cerebral artery occlusion. Activation of TRPV4 is thus not restricted to the chemical ischemia model used here but is also observed in other models of energy depletion in vitro and in vivo.

We found that TRPV4 was involved in the generation of significant Na⁺ influx at both room (21 ± 1°C) and near-physiological temperatures (33 ± 1°C) during chemical ischemia. Several studies describe an activation threshold of TRPV4 at 33–34°C (Güler et al., 2002; Shibasaki et al., 2007), whereas others demonstrate activation at lower temperatures (Güler et al., 2002; Watanabe et al., 2002). The latter is in line with the work by Hoshi et al. (2018) performed in acute mouse brain tissue slices. This study showed that increasing the temperature to 33°C results in a significant increase in brain swelling on oxygen-glucose deprivation mediated by TRPV4 activation, indicating efficient activation of TRPV4 already at 33°C in this preparation.

Interestingly, however, the TRPV4 inhibitor HC-067047 reduced the peak amplitude of chemical ischemia-induced Na⁺ elevations at both room temperature and 33°C to a similar degree (to ∼60% and to ∼65%, respectively). This result indicates that the contribution of TRPV4 and TRPV4-related mechanisms to neuronal Na⁺ loading on energy deprivation was not primarily dependent on temperature. Activation of TRPV4 under our experimental conditions might also have been induced by other stimuli such as osmotic stress, mechanical stimuli, or intracellular signaling cascades, for example, by phosphorylation by protein kinase A or PKC (Vriens et al., 2004; White et al., 2016; Shibasaki, 2020). Of note, tissue slices in the present study were slowly heated to 33°C and kept at this temperature for 15–30 min before exposing them to chemical ischemia. The apparent lack of temperature sensitivity may thus at least partly be because of a phasic response behavior of TRPV4 as heat-evoked TRPV4-mediated currents have been shown to rapidly inactivate in response to heat stimuli (Güler et al., 2002; Watanabe et al., 2002; Hoshi et al., 2018). Moreover, TRPV4 closely interacts with different ion channels, including Ca²⁺-sensitive large conductance K⁺ channels, changing its gating properties (White et al., 2016). The described polymodal responsiveness to osmotic and thermal stimulation and the manifold intracellular pathways that influence activation and conductance of TRPV4 channels indicate that TRPV4 activation on energy failure may not necessarily require high body temperatures (37°C) but that is mediated by a combination of these interacting stimuli.

TRPV4 is thus a new and highly relevant addition to the battery of other pathways that result in Na⁺ influx identified earlier including voltage- and ligand-gated ion channels (Somjen, 2004; Pietrobon and Moskowitz, 2014). As compared with other members of the TRP channel superfamily, TRPV4 has a moderate Ca²⁺/Na⁺ permeability of 6–10 Ca²⁺ per Na⁺ (Yu et al., 2019). The observation that TRPV4 channels promote Na⁺ loading of neurons under ischemic conditions is a surprising finding. In addition to direct Na⁺ influx through TRPV4 channels, several mechanisms secondary to TRPV4 opening may come into play. These, yet unidentified pathways may include increased activation of NMDA-receptors in response to opening of TRPV4, as previously shown to occur in hippocampal neurons (Shibasaki et al., 2007; Li et al., 2013). TRPV4 activation will depolarize cells and amplify the ischemia-induced neuronal depolarization, which could further increase channel-mediated Na⁺ influx. Another possibility is that activation of TRPV4 and the resulting cellular swelling will lead to shrinkage of the extracellular space. TRPV4-related shrinkage is likely to increase the extracellular acidification induced by energy depletion, which will enhance activation of acid-sensing ion channels (ASICs; Leng et al., 2014). The latter may cause additional Na⁺ influx through ASICs and/or increased activation of AMPA receptors (and resulting in increased Na⁺ influx through the latter; Quintana et al., 2015). Moreover, reversal of the Na⁺/Ca²⁺ exchanger NCX1 (Gerkau et al., 2018) and resulting transporter-mediated Na⁺ influx might play a role. Na⁺ loading on activation of TRPV4 will aggravate both neuronal swelling and depolarization (Rungta et al., 2015; Dijkstra et al., 2016). Moreover, it will decrease the driving force for Na⁺-dependent secondary transporters necessary to ensure cellular function (Kintner et al., 2007) but also accelerate depletion of cellular ATP through activation of Na⁺/K⁺-ATPase (Erecińska and Silver, 1994). TRPV4 may thus represent a promising target to ameliorate cellular damage and infarct size following a stroke.

Furthermore, we conclude that improved rapidFLIM will pave the way to a better understanding of the mechanisms of intracellular Na⁺ signaling and dysregulation also under challenging conditions accompanied by large volume changes such as brain ischemia. It will set the stage for future quantitative determination of baseline [Na⁺]_i in different cellular domains such as dendrites, dendritic spines, or fine astrocytic processes, information that so far is only available at the level of neuronal or astrocyte somata (Gerkau et al., 2019a; Rose et al., 2020). Moreover, the possibility of registering a significantly larger proportion of emitted photons will greatly improve usability and applicability of other probes with low quantum yields and low dynamic range. Because of the substantially increased photon yield, rapidFLIM will permit frame scanning at substantially increased speed, thereby enabling better temporal resolution without the need to sacrifice spatial information by reducing the number of scanned pixels, for example, by line or point scan. This will especially be relevant for analysis of the occurrence, spatial extent, and spread of cellular signals generated locally. Dynamic rapidFLIM-based TCSPC will thereby serve as a valuable new tool to uncover and study the spatiotemporal properties of fast cellular signals in biological probes.